Improvement of Lunar Surface Dating Accuracy Utilizing Crater Degradation Model: A Case Study of the Chang’e-5 Sampling Area

Abstract

Taking the Chang’e-5 (CE-5) sampling area as an example, this study carried out an investigation on improving the crater size-frequency distribution (CSFD) dating accuracy of lunar surface geologic units based on the crater degradation model. We constructed a three-parted crater degradation model, which consists of the diffusion equation describing crater degradation and equations describing the original crater profile for small craters (D < 1 km) and larger craters (D ≥ 1 km). A method that can improve the accuracy of CSFD dating was also proposed in this study, which utilizes the newly constructed degradation model to simulate the degradation process of the craters to help determine the crater degradation process and screen out the craters suitable for CSFD analysis. This method shows a good performance in regional dating. The age determined for the CE-5 sampling area is 2.0 ± 0.2 Ga, very close to the 2.03 ± 0.004 Ga of isotopic dating result of the returned sample. We found that the degradation state of the craters simulated by our constructed degradation model is highly consistent with the real existing state of the craters in terms of their topographic, geomorphological, and compositional (e.g., FeO) features. It fully demonstrates that the degradation model proposed in this study is effective and reliable for describing and distinguishing the degradation state of craters over time due to the cumulative effects of small craters. The proposed method can effectively distinguish between diffusively degraded (which conform to the degradation model) and non-diffusively degraded (which do not conform to the degradation model) craters and improve the CSFD accuracy through the selection of the craters. This not only provides an effective solution to the problem of obtaining a more “exact” frequency distribution of craters, which has long plagued the practical application of the CSFD method in dating the lunar surface but also advances our understanding of the evolutionary history of the geologic units of the study area. The results of this work are important for the in-depth study of the formation and evolution of the moon, especially for lunar chronology.

1. Introduction

Craters are the main geomorphic feature on the lunar surface. They can be preserved for a long period because of the absence of atmosphere and water on the lunar surface and weak geologic activities; however, they could be degraded by coverage from later impact ejecta or terrain relaxation over time. The degradation of a crater refers to the gradual darkening, filling, and even disappearing of a crater under the influences of micrometeorite bombardment and other spatial environments [1]. The degradation process of crater morphology can reflect the geological activities experienced by the crater and the area where the crater is located, show the topographic diffusion pattern of the lunar surface, and infer the evolutionary process experienced by the lunar surface [2,3,4]. Techniques for measuring crater size-frequency distributions over spectrally homogeneous regions [5] and combined analysis of the lunar surface CSFD dating and the degradation state of crater morphology can help improve the dating accuracy of lunar surface geologic units and provide insight into the geological history and thermal evolution of the moon.

Culling [6] established a functional relationship (the topographic diffusion equation) between the profile height of lunar surface topography and the time to simulate the evolution of the lunar landscape. Soderblom [7] believed that the degradation process of a crater caused by the cumulative effect of later impacts is a diffusion phenomenon that can be represented by the diffusion equation. The diffusion equation can be used to fit the degradation process of a crater on the lunar surface. In other words, it can be used to represent the morphological variation of the crater and the geologic units where the crater is located as a function of time under the influence of non-external forces [3,8,9,10,11,12,13]. However, when a certain area of the lunar surface is subjected to strong external geological forces (e.g., large impacts, eruptions of a lava flow, landslides, and ejecta coverage), the diffusion equation is no longer suited for the description of the degraded state of the crater within this area [3]. The diameter and size of craters at the moment of formation depend on the characteristics of the impactor (density, velocity, and incidence angle) and the characteristics of the target surface. After formation, most fresh, primitive, and simple craters have a consistent shape profile [4]. Based on mare craters with diameters ranging from 0.8 to 5 km (accounting for >30% of the lunar maria), Fassett et al. [4] constructed a degradation model that simulates the change in the characteristic state of craters using the diffusion equation and quantitatively provided the mean diffusivity suitable to the degradation of the crater’s (<3 Ga) profile height over time. According to this established degradation model, the degradation rate of different sizes of craters is different. Under the same topographic diffusion rate, small craters degrade faster than large craters, and the retention time of large craters is longer than that of small craters. When the diameter of craters doubles, their retention time on the lunar surface will increase by about four times [4]. Xie et al. [2] modified the crater degradation model proposed by Fassett et al. [4] and further provided the original crater profile suitable for small craters (diameter less than 1 km) on the basis of the observed data of fresh craters [14], continuous ejecta blanket [15], distribution pattern of ejecta [16], and uplift structure of the crater rim [17]. Following the work of Fassett et al. [4], Du et al. [18] subdivided craters into three categories: the simple crater (1 ≤ D ≤ 15 km), the transitional crater (15 < D ≤ 20 km), and the complex crater (D > 20 km). For each category, original crater profiles suitable for the lunar mare and highland were proposed, and altogether there are six types of the original crater profile. Therefore, by combining the above-mentioned studies, a crater degradation model applicable to arbitrary crater size can be constructed, which enables the simulation of the degradation state of arbitrary crater morphology over time.

The method of estimating the absolute model age (AMA) of lunar surface geologic units using the crater size-frequency distribution (CSFD) [19,20,21,22,23] has been widely applied in lunar chronology [5,24,25,26,27,28] and has been extended to the dating of other terrestrial planets such as Mars and Mercury [20,21,29,30,31,32]. Despite the universality of the CSFD method, in some specific applications, different researchers often produce different AMAs in the same area. It seems that there is a large uncertainty in the dating results. For example, the estimated age of the CE-5 landing area using the CSFD method varies from 1.21 Ga to 3.46 Ga [24,28,33,34,35,36,37,38], and the estimated difference between the maximum age and minimum age is 2.25 Ga. After careful analysis and exclusion of the interference from the identification and elimination of the secondary crater, we believe that in addition to different counting areas, different images, and different crater counting methods the influence of complex geological processes that the study area has undergone on CSFD results when counting craters is commonly overlooked. It is difficult to detect complex geological processes (e.g., coverage of lava flow) only through the composition and spectral properties [36]. For craters in the same degradation state, a larger crater will appear substantially fresher than its smaller counterparts, and some of the large craters on older geologic units are preserved because the morphological change rate is smaller than that of smaller craters [4]. This results in the coexistence of old craters on old geologic units and young craters on young geologic units, thus making the crater statistics include craters formed on different geologic units with different evolutionary experiences. This makes it difficult to obtain “exact” crater statistics when using CSFD statistics for dating. In this study, we use the degradation model to simulate the degradation of craters, and screen out two types of craters with different evolutionary processes: diffusively degraded craters that conform to the crater degradation model represent young craters formed on young geologic units, and non-diffusively degraded craters that do not fit the crater degradation model represent old craters formed on old geologic units. The degradation process of craters is used to infer the geological activity experienced in the region, and for different geologic units, all craters accumulated on that geologic unit are selected for CSFD dating.

In December 2020, CE-5, China’s first lunar sample return mission, successfully landed in the mare plain in the northeastern Oceanus Procellarum, with a longitude and latitude of 51.916°W and 43.058°N, and it returned 1731 g of lunar samples. Isotope measurements showed that CE-5 basalt was formed at 2.03 ± 0.004 Ga [39]. In this work, based on the craters identified in the CE-5 sampling area, we proposed to use the crater degradation model to simulate the topography degradation of the crater and compared the simulated degradation state of the crater with the existing state, so as to analyze the evolution experience of the crater, and selected all craters on the geologic unit with the same degradation experience to carry out the dating study of the CSFD method in the study area. This paper first describes a method to improve the accuracy of CSFD according to the spatial randomness analysis and degradation process analysis of the crater. Then, in conjunction with the dating results, the method was further discussed and analyzed in terms of its overall effectiveness and the validation of the crater degradation analysis method. Finally, the main findings of this work were summarized, and future research directions were discussed.

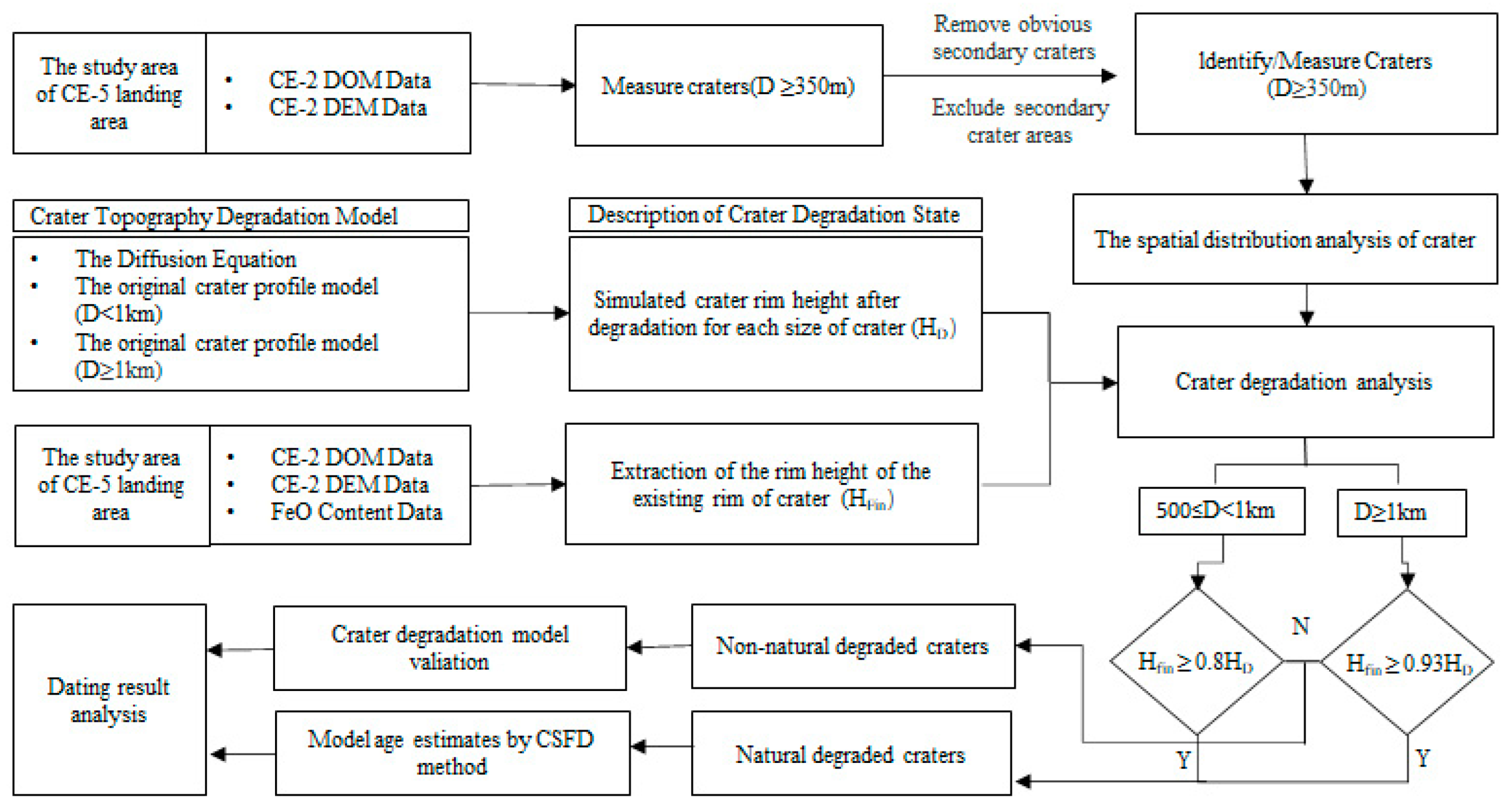
2. Methods

To improve the accuracy of the CSFD method, we identified the craters within the study area, simulated the topography degradation of craters using the crater degradation model, and compared it with the existing morphological state of the crater; we selected all craters on the geologic unit with the same degradation experience by analyzing the degradation process of craters. The flowchart of this study is shown in Figure 1, which mainly consists of four steps including the selection of the study area and data preparation, spatial randomness evaluation of the crater distribution, analysis of the crater degradation process, and the CSFD dating of the investigated area.

2.1. Selection of Study Area and Data Preparation

A region surrounding the CE-5 landing site was selected as the investigated area of this work (green square in Figure 2). Based on the 7 m/pixel digital orthophoto map (DOM) of the CE-2 CCD stereo camera [40], we mapped the craters within the study area using the CraterTools extension of ArcMap [41] and removed the obvious secondary craters (blue area in Figure 2) through their chain- and cluster-shaped distributional features. Finally, 353 craters ≥ 350 m in diameter were identified in the study area (red circle in Figure 2). The total area of crater count area is 5331.06 km².

2.2. Randomness Evaluation of the Crater Distribution

One prerequisite for calculating the geological age of the lunar surface using the CSFD method is that the craters should meet the spatial distribution of randomness rather than clustering [19]. Therefore, it is necessary to evaluate the randomness of the crater distribution within the study area. The spatial distribution analysis of craters regards each crater within the study area as a point of an equal probability distribution, and the positions are randomly distributed within the region. Therefore, randomly distributed craters satisfy the Poisson distribution law [42]. Through a detailed investigation of the spatial distribution of craters, Michael et al. [42] proposed to utilize the Monte Carlo Method to simulate the statistical features of the Mean Closest Neighbor Distance (MCND) or the Mean 2nd-Closest Neighbor Distance (M2CND) of craters’ distribution within the study area. This study analyzed the clustering of craters by the comparison between the simulated (conform to the Poisson distribution) and the measured M2CNDs of the craters within the study area, thereby realizing the randomness evaluation of crater distribution.

The specific steps are as follows: (1) We identified all craters within the study area, divided the craters into different groups according to their diameter range, and calculated the number of craters for each size group. (2) We conducted Monte Carlo simulations for each group. First, we generated craters of the same size and number as the measured data within the study area. Then, we calculated the ratio of MCND/M2CND among these craters and repeated this several times to obtain the histogram of MCND/M2CND of craters. (3) We compared the measured MCND/M2CND with the simulated (calculated) MCND/M2CND and assessed the randomness of the craters’ distribution for each size group. If the measured value was smaller than the lower limit of the histogram, the spatial distribution of craters was non-random and clustered (Figure 3a); if the measured value was within the range of the confidence interval of the histogram, the spatial distribution of the crater was random, and its randomness can be expressed as confidence percentage. The area in the histogram that was larger than the average of the measured MCND/M2CND was termed the non-clustered confidence percentage (Figure 3b). If the measured value was higher than the upper limit of the histogram, the craters were more ordered than random (Figure 3c). In this work, we used this method to analyze the randomness of the crater distribution of the study area, excluded craters of non-random distribution for each size group, and selected craters within the non-clustered confidence interval to participate in the subsequent dating analysis.

2.3. Crater Degradation Process Analysis

Another prerequisite for calculating the geological age of the lunar surface using the CSFD method is the selection of craters for dating on homogeneous units [19]. However, due to the complex geological processes experienced by the geologic units, some newly formed geologic units not only contain the craters created by subsequent impacts but also retain some larger size craters of the old geologic units [43,44,45,46] and/or some craters with different experiences caused by other erosion mechanisms [47]. The degradation experience of craters in the study area needs to be discriminated, and craters with the same evolutionary experience are selected to determine the age of the host layer. In this work, we proposed a method to simulate the degradation process of craters using the crater degradation model. By comparing the simulated degradation state of craters with the measured existing state of craters, we could determine their degradation experience.

2.3.1. Simulation of Degradation State of Crater

In this study, a new model to simulate the degradation state of craters was proposed. Based on the degradation model established by Fassett et al. [4], we combined the diffusion equation with the original crater profiles established by Xie et al. [2] and Du et al. [18]. The newly constructed crater degradation model consisted of the diffusion equation (Equation (1)) and the original crater profiles for small (D < 1 km) (Equation (2)) and large (D ≥ 1 km) (Equation (3)) craters. It should be noted that we selected the mare crater (1 ≤ D ≤ 15 km) model for Equation (3) from the six models established by Du et al. [18] according to the actual situation of the study area and craters within it.

$$\frac{\partial h}{\partial t}=k{\nabla }^{2}h$$

(1)

Equation (1) is the diffusion equation used to describe the degradation of the height of the crater rim over time. H is the elevation of the point on the crater profile at a distance r from the center of the crater, and t is the degradation time. k is diffusivity, which was set as 5.5 m²/Myr in this work [4].

$$\mathrm{H}=\left\{\begin{array}{cc}\hfill {\mathrm{h}}_0-{\mathrm{d}}_0,& \mathrm{r}/{\mathrm{R}}_0\le 0.2\hfill \\ \hfill {\mathrm{C}}_{\mathrm{w}1}({\mathrm{r}/{\mathrm{R}}_0)}^{1.06}+{\mathrm{C}}_{\mathrm{w}2},& 0.2<\mathrm{r}/{\mathrm{R}}_0\le 1\hfill \\ \hfill 0.033{\mathrm{R}}_0({\mathrm{r}/{\mathrm{R}}_0)}^{-3}+{\mathrm{C}}_{\mathrm{s}\mathrm{u}}({\mathrm{r}/{\mathrm{R}}_0)}^{-6}+{\mathrm{C}}_{\mathrm{c}\mathrm{e}},& 1<\mathrm{r}/{\mathrm{R}}_0\le {\mathrm{R}}_{\mathrm{c}\mathrm{e}}/{\mathrm{R}}_0\hfill \\ \hfill 0,& \mathrm{r}>{\mathrm{R}}_{\mathrm{c}\mathrm{e}}\hfill \end{array}\right.$$

(2)

Equation (2) is used to simulate the original profile of small craters (D < 1 km). Here, H is the elevation of the point on the crater profile at a distance r from the center of the crater, r is the distance from the target point selected along the crater profile to the crater center, and R₀ is the radius of the crater. h₀ is the original height of the crater rim, and it is defined as h₀ = 0.024D₀^1.058 [14]. D₀ = 2R₀ is the diameter of the crater. d₀ is the depth from the crater rim to the bottom, and it is defined as d₀ = 0.08D₀^1.13. R_ce is the mean ejecta radius, and it is defined as R_ce = 1.12D₀^1.006. C_w1, C_w2, C_su, and C_ce are a set of equations that are expressed as: C_w1 = d₀/0.08184, C_w2 = (h₀ − d₀) − 0.1816C_w1, C_su = (h₀ − 0.033R₀ (1 − (R_ce/R₀)⁻³))/(1 − (R_ce/R₀)⁻⁶), and C_ce = −0.033R₀(R_ce/R₀)⁻³ − C_su(R_ce/R₀)⁻⁶.

$$\mathrm{H}=\left\{\begin{array}{c}-0.165,\mathrm{r}/{\mathrm{R}}_0\le 0.2\\ -0.292{(\mathrm{r}/{\mathrm{R}}_0)}^3+0.489{(\mathrm{r}/{\mathrm{R}}_0)}^2+0.028\mathrm{r}/{\mathrm{R}}_0-0.188,0.2<\mathrm{r}/{\mathrm{R}}_0\le 1\\ -0.081{(\mathrm{r}/{\mathrm{R}}_0)}^3+0.419{(\mathrm{r}/{\mathrm{R}}_0)}^2-0.731(\mathrm{r}/{\mathrm{R}}_0)+0.430,1<\mathrm{r}/{\mathrm{R}}_0\le 1.7\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} 0,\mathrm{r}/{\mathrm{R}}_0>1.7\end{array}\right.$$

(3)

Equation (3) is used to simulate the original profile of larger craters (1 km ≤ D ≤ 15 km). Definitions of H, r, and R₀ are the same as that of Equation (2).

For craters with diameters less than 15 km, the diffusion degradation process of the crater can be obtained by solving the diffusion Equation (1) by setting the initial boundary conditions and the final boundary conditions. The initial boundary condition is the initial state of the crater (for a crater of arbitrary diameter, Equations (2) and (3) can simulate the initial profile model of the crater, as shown in (Figure 4a)), and the final boundary condition is the crater degradation until it is unrecognizable (the elevation of all points on the crater profile is 0); using these two boundary conditions to solve Equation (1), the crater degradation from the initial crater rim height H₀ to the crater rim height H_D after t years of degradation (Figure 4b)is obtained, thus obtaining the change of the diffusion degradation state of the crater with time.

In this study, we calculated the rim height (H_D) of craters (0 < D ≤ 15 km) after experiencing the degradation process of 0.8 Ga, 1.0 Ga, 1.5 Ga, 2.0 Ga, 2.5 Ga, 3.0 Ga, 3.16 Ga, and 3.85 Ga years. The relationship between the rim height and diameter of craters of varying sizes and experiencing different degradation times is shown in Figure 5.

2.3.2. Discrimination of Crater Degradation Process

For any region of the lunar surface, if the existing crater rim height is approximately the same as the simulated degraded crater rim height, the degradation process of the crater conforms to the degradation law described by the degradation model. However, if the existing crater rim height deviates significantly from the simulated degraded crater rim height, it means that the crater is subjected to external geological forces in addition to diffusive weathering after the formation of the crater. To facilitate subsequent discussions, we classified craters that conform to the degradation model as diffusively degraded craters and those that do not conform to the degradation model as non-diffusively degraded craters. According to this feature of craters, we analyzed and identified the degradation process of the craters within the study area.

First, the existing crater rim height (H_Fin) was calculated. For one crater, based on 7 m/pixel CE-2 DEM data, the 3D Analyst tool in ArcMap software was used to extract three elevation profiles crossing the center of this crater at 60° intervals (Figure 6a). We calculated the height of the crater rim to the lunar surface for three elevation profiles (H_Fin1~H_Fin6) and took the average of the six rim heights as the existing crater rim height (H_Fin) of this crater (Figure 6).

Second, the degradation experience of crater morphology was identified. We NPF. For craters with 1 km ≥ D ≥ 0.5 km, if H_Fin ≥ 0.8H_D, the degradation of the crater is assessed to be in accordance with the degradation law represented by the degradation model and belongs to diffusive degradation (black dots in Figure 7a); otherwise, the degradation of the crater is assessed to be not in accordance with the degradation law represented by the degradation model and belongs to non-diffusive degradation (red dots in Figure 7a). Because the larger the diameter of the crater, the smaller the degree of change of the crater’s shape with time; for craters with D > 1 km, if H_Fin ≥ 0.93H_D, the degradation of the crater is assessed to be in accordance with the degradation law expressed by the degradation model and belongs to diffusive degradation (black dots in Figure 7b); vice versa, the degradation of the crater is assessed to be not in accordance with the degradation law expressed by the degradation model and belongs to non-diffusive degradation (red dots in Figure 7b). By comparison, the craters in the study area were classified as diffusively degraded or non-diffusively degraded according to their degradation experience; the non-diffusively degraded craters were excluded, and the diffusively degraded ones were selected for the subsequent CSFD dating.

2.4. CSFD Dating of CE-5 Landing Area

The CSFD method is based on the assumption that the craters on the lunar surface have random distribution and that the accumulated craters in the older regions are more than those in the younger regions. It is a method of estimating the age of geologic units by counting the number of craters accumulated on their surface since their formation [19,21]. Neukum [44] and Ivanov [23] made a statistic on the number and diameter of craters for Mare Serenitatis, Montes Apennius, Mare Orientale, Mare Crisium, Mendeleev crater (floor), Apollo 15 landing site, Apollo 16 landing site, and Orientale Basin and derived a crater production function that can represent the relationship between the size and frequency of craters (Equation (4)) [21]:

$${\log }_{10}\left({\mathrm{N}}_{\mathrm{c}\mathrm{u}\mathrm{m}}\right)={\mathrm{a}}_0+{\sum }_{\mathrm{j}=1}^{11}{{\mathrm{a}}_{\mathrm{j}}\left[{\log }_{10}\mathrm{D}\right]}^{\mathrm{j}}.$$

(4)

Here, N_cum is the number of craters per km², D is the crater diameter (in units of km) suitable to the area with crater diameter between 0.01 km and 300 km, and a₀~a₁₁ are coefficients, and their values are shown in

Table 1. Coefficient of craters production function.

Coefficient	NPF1983 [21]	NPF2001 [20]
a0	−3.0768	−3.0876
a1	−3.6269	−3.557528
a2	+0.4366	+0.781027
a3	+0.7935	+1.021521
a4	+0.0865	−0.156012
a5	−0.2649	−0.444058
a6	−0.0664	+0.019977
a7	+0.0379	+0.086850
a8	+0.0106	−0.005874
a9	−0.0022	−0.006809
a10	−5.18 × 10−4	+8.25 × 10−4
a11	+3.97 × 10−5	+5.54 × 10−5

Note: NPF1983 originally came from the German version of Neukum’s doctoral thesis written in 1983, which was later translated into English [21].

.

Subsequent studies slightly modified the coefficients of Neukum Production Function (NPF) based on the new statistical data [20,23,48], and the two production functions were termed as NPF983 and NPF2001, respectively. By calculating the relationship between the radiometric ages of Apollo samples and the cumulative frequency of craters counted from the image, Neukum obtained a crater chronology function (Equation (5)):

$$\mathrm{N}\left(\ge 1\right)=5.44·{10}^{-14}\left[\exp \left(6.93\mathrm{T}\right)-1\right]+8.38·{10}^{-4}\mathrm{T}$$

(5)

where T is the absolute model age in Ga, and N (1) is the cumulative crater (D ≥ 1 km) frequency.

N (1) of any size region can be obtained using Equation (4), and then, according to Equation (5), the absolute model age of the region can be acquired. This is the basic idea of the CSFD dating method. The CSFD method has been commonly accepted in the field of lunar and planetary science. The researchers then synthesized these formulas and wrote the software called Craterstats [49].

3. Results

3.1. Randomness Assessment of Crater Distribution

The craters with diameters between 350 m and 8 km were separated into eight different size ranges for randomness analysis. Results show that the measured clustering of craters with D ≥ 500 m lies within most of the range of the simulated histogram, indicating that the spatial distribution of D ≥ 500 m craters is random (Figure 8).

3.2. Crater Degradation Process Analysis

Based on the above randomness evaluation results, we analyzed the degradation process for 107 craters with D ≥ 500 m of the study area. The craters were subdivided into 0.5 km ≤ D < 1 km and D ≥ 1 km two size range groups, and their simulated rim height H_D after 1.0 Ga, 2.0 Ga, and 3.0 Ga degradation and their currently existing rim height H_Fin were calculated Figure 9.

It can be seen from Figure 9 that within the range of 0.5 km ≤ D < 1 km, all 95 craters conform to the degradation model. Of 12 craters with D ≥ 1 km, 7 follow and 5 do not follow the degradation model. Our results show that 102 of the craters with diameter D ≥ 0.5 km are diffusively degraded craters and 5 craters are non-diffusively degraded craters. It is concluded that the degradation experience of the five craters that do not fit the crater degradation model is different from that of the 102 craters that fit the crater degradation model. The five craters that do not fit the degradation model may be formed in the old geologic units, while the 102 craters that fit the degradation model may be formed in the new geologic units.

3.3. Age of the Study Area

A total of 102 craters belonging to diffusive degradation were selected as input to the CSFD for estimating the absolute age of the study area. Using NPF1983 and NPF2001, the calculated N(1) values for this study area are 1.68 × 10⁻³ km⁻² and 1.67 × 10⁻³ km⁻², respectively, and the corresponding ages for the geologic unit where the study area is located are 2.0 Ga and 1.99 Ga, respectively (Figure 10).

4. Discussion

4.1. Dating Result Analysis

The age of the CE-5 landing area (2.0 ± 0.2 Ga) obtained by the method in this paper is very close to the radiometric age of the CE-5 samples. The effectiveness of the method to improve the accuracy of the CSFD method by selecting craters using crater degradation models is verified. Without crater screening, the dating result of the study area using all craters (D ≥ 500 m) is 3.24 Ga (purple line in Figure 11). This is similar to the ages of the geologic unit around the CE-5 landing area (3.27 Ga and 3.35 Ga) estimated by Jia et al. [37] and the ages of the geologic unit near the CE-5 landing area (3.44 Ga and 3.4 Ga) calculated by Hiesinger et al. [24]. Only three large non-diffusively degraded craters (6.36 km, 6.03 km, and 4.34 km) have a calculated age of 3.96 Ga (this age is only to make a rough estimate of the time; indeed it has a large uncertainty and just provides age constraints). The SFD curves of the unscreened craters (purple line in Figure 11) have a clear ‘kink’ (Neukum 1975), inferring that a resurfacing event may have occurred in the study area and the cover of lava flow results in the crater rim height of non-diffusively degraded crater is significantly lower than that fit by the crater degradation model. From the dating results of the craters screened in this paper, all unscreened craters and three large craters, it is assumed that all craters in the study area were not formed at the same time and that the craters can be roughly divided into those formed on the older geologic unit with an age of about 3.24 Ga or even older with non-diffusive degradation and those formed on a young geologic unit at 2.0 Ga with diffusive degradation. In summary, this study proposes a method to simulate the crater degradation process by using a crater degradation model, to distinguish the degradation experience of craters by comparing the degradation state of existing craters with that of the craters simulated by the crater degradation model, to screen the craters, and to improve the accuracy of CSFD. The results show that this method can effectively distinguish craters that have experienced non-diffusive degradation caused by external geological effects (lava flow and other different types of erosion and degradation mechanisms) from those that have experienced diffusive degradation. For the different geologic units, all craters accumulated on the geologic unit were selected for CSFD dating, effectively improving the CSFD accuracy.

4.2. Method Analysis

In this section, we screened seven diffusively degraded craters and five non-diffusively degraded craters with diameters D ≥ 1 km. To test the effectiveness of the established crater degradation model, we conducted a further analysis of the degradation state of these screened craters combining their simulated profiles of the degradation process, existing elevation profile, and maps of image and FeO content. It can be seen from Figure 12 that the seven diffusively degraded craters have similar simulated profiles of the degradation process as their existing elevation profiles (Figure 12(a1–a7,b1–b7)). They have a clear contour and relatively complete rim (Figure 12(c1–c7)); they are consistent with the fact that they are not affected by other external forces and exhibit the morphological characteristics of Eratosthenian craters [51]. The contents of FeO in the ejecta, interior, and rim of these craters are different, which also conforms to the distribution characteristics and patterns of FeO content of Eratosthenian craters [51,52]. In contrast to the seven diffusively degraded craters, the simulated profiles of the five non-diffusively degraded craters differ greatly from the elevation profiles of their existing state (Figure 13(a1–a5,b1–b5)). The rims of these craters are covered by mare materials and severely degraded. They exhibit the morphological characteristics of the Nectarian/Imbrian craters [51]. In addition, the FeO contents within and outside these craters are relatively consistent; this is in accordance with the compositional distribution characteristics of craters that are degraded by other geological forces besides diffusive degradation [51]. We speculate that after the formation of these craters, in addition to experiencing diffusive degradation, they may also be affected by the continuous development of underlying ridges as well as the coverage or burial of external forces such as mare materials.

The analysis method for the crater degradation process proposed in this study is reasonable, feasible, and has certain accuracy. Through simulating the diffusively degradation process by the constructed crater degradation model and comparing it with the existing state of the craters, the diffusively and non-diffusively degraded craters in the investigated area can be effectively distinguished. This provides strong support for understanding the evolution of geologic units in the study area. After the screening of craters, more “accurate” crater frequency distribution can be obtained, effectively improving the CSFD accuracy for geologic units.

5. Conclusions

In this study, we proposed a method to simulate the crater degradation process using a crater degradation model and improved the accuracy of CSFD dating by identifying the crater degradation experience and selecting the craters. We selected the study area around the CE-5 sampling site and conducted beneficial exploration and practice on the CSFD dating of the study area in combination with the crater randomness evaluation and degradation process analysis. The main findings are as following:

(1)

Using the method proposed in this work, the CSFD dating result for the CE-5 landing area is 2.0 Ga, which is close to the basalt age of 2.030 ± 0.004 Ga of CE-5 samples measured by Pb-Pb isotope dating technology [39]. This fully validates the effectiveness of the method proposed in this study to improve the accuracy of the CSFD method by using crater degradation models to simulate crater degradation experiences and realize the screening of the craters.

(2)

The degradation state simulated by the constructed crater degradation model is highly consistent with the existing state of the crater in terms of their geomorphology and material composition (FeO). For craters that degrade due to the cumulative effect of subsequent impacts and diffusive weathering, simulating the degradation process using the crater degradation model constructed in this study is practical and reliable. The description of the degradation state of crater over time is effective and credible.

(3)

The analysis and judgment method for the degradation process of craters proposed in this study can effectively distinguish between diffusively degraded craters and non-diffusively degraded craters, realize the selection of craters, and have significant effects on improving the accuracy of the CSFD method. For a long time, how to obtain more “accurate” data on the frequency distribution of craters for CSFD dating has been a problem that needs to be solved. The crater selection method proposed in this study not only explores the solution to the problem and proposes an effective solution, but also provides reference information for the study of the evolution of lunar surface geologic units and provides strong support for an in-depth understanding of the evolutionary process of regional stratigraphic units.

(4)

The method proposed in this study has achieved high accuracy in dating the CE-5 sampling area. Since CE-5 sampling area belongs to the lunar mare region, we have chosen an original profile equation suitable for the mare craters with a diameter ranging between 1 km and 15 km to establish the degradation model. In the future, we will further carry out method testing and validation in a wider range of areas, and it is expected to accumulate more beneficial experiences.