Abstract
The lunar crater production function describes the general pattern of the size–frequency distribution of craters on the lunar surface, and it is the foundation of the surface dating method via crater counting. In addition, the lunar crater production function has been extended to other celestial bodies and used to analyze the meteorite flux of the inner solar system. The basic process of establishing the lunar crater production function is to map in an ideal way the primary craters in different geological units, and then to normalize all of the corresponding size–frequency distributions using a mathematical model. Currently, the most widely used lunar crater production functions have been established based on the images acquired in the last century. However, now they can be refined with newly obtained high-resolution images. In this research, we mapped all of the primary craters in 13 regions on the lunar surface with the images acquired using the narrow angle camera and wide angle camera onboard the Lunar Reconnaissance Orbiter, and then we fitted the lunar crater production function with a polynomial. The resultant new lunar crater production function is largely comparable with the previous results, and the difference is mainly at the large diameter end. We analyzed the uncertainty of model fitting as well as the difference in the crater measurements and demonstrated the reliability of the new production function. It is expected to refine the lunar surface dating models, which can provide more accurate information on the impact rate in related studies.
1. Introduction
Absolute ages provide vital information in establishing the geologic history of the solar system solid bodies. However, extensive direct isotopic dating has been possible so far only for Earth. For the Moon, a widely used surface dating method is based on the crater size–frequency distribution (CSFD), which has been elaborated upon in the research of Neukum [1] and is the subject of many papers [2,3]. The rationale of the approach is to fit the observed CSFD of a counting area belonging to the same geologic unit to a known crater production function (PF) [4,5], which is further used to derive the absolute ages along with a chronology function (CF) calibrated to isotopic dating from lunar samples [2].
The lunar crater production function (PF) describes the relationship between the number of craters and the corresponding size, which is determined by measuring the crater size–frequency distributions (SFDs) in different geological units of the Moon. The lunar crater PF has been widely used in lunar surface dating. In addition, the lunar crater PF has also been used to derive information on the impact rate of the near-Earth objects (NEOs) and the corresponding SFD of meteorites for the Moon [1,6]. Therefore, the PF is one of the cornerstones of the crater SFD-based dating method.
The PF describes the general law of the crater SFD, and there have been many studies to derive crater SFD laws. For example, Hartmann [7] gave a slope of −2.1 to a straight line plot of vs. using the crater counts of Young [8] and Brown [9], where N is the incremental crater number corresponding to constant . After measuring craters on three areas of the Moon’s surface, Cross [10] proposed a power-law, i.e., (note here that is the cumulative crater number per unit area, and D is the crater diameter. is a constant). Hawkins [11] suggested that the power-law slope is variable, as shown by Hartmann’s experimental observations [12]. Chapman [13] and Neukum [14] also pointed out that a simple power-law cannot fit the distribution of a crater size–frequency well over a wide diameter range and concluded that the exponent is size-dependent, i.e., should be a function of D.
Neukum and his colleagues carried out a series of studies to find the SFD of the lunar primary impact crater populations [1,15,16,17]. Instead of using a simple power-law or piece-wise exponential functions, Neukum [1] fitted the lunar crater CSFD with a polynomial of the 11th degree in and derived the most widely used lunar PF—the Neukum PF (NPF). However, the crater counts used to construct the NPF were from the images of Apollo and Lunar Orbiter missions in the last century, which in general were of low resolution and had a poor quantity. The crater diameter was manually measured and calculated according to the scale [18]. Tens of years have passed and much better images (in terms of both geometric and radiometric qualities, as well as the spatial resolution of small features) of the Moon have been obtained [19]. Therefore, it is necessary to check and update the previous lunar crater PF using newly acquired high-resolution images.
Based on the high-resolution images acquired using the narrow angle camera (NAC) and the wide angle camera (WAC) onboard the Lunar Reconnaissance Orbiter (LRO), we carefully measured the craters in a total of 13 areas to refine the lunar crater PF and we hope that it can be used in related studies in the future.
2. Data Sets
Small craters with diameters smaller than 1 km were mapped in the high-resolution Lunar Reconnaissance Orbiter Camera (LROC) NAC images with incidence angles of 50–80° [20]. The LROC NAC provides a resolution of 0.5–2.5 m at different flight altitudes [21]. They are publicly available from the Planetary Data System Geosciences Node [22]. The information relating to the NAC images used in this study is shown in Table 1.

Table 1.
Information on the LROC NAC images used in this study.
The LROC WAC is a push-frame camera that has resolutions of 75–384 m/pixels depending on the orbital altitude [21]. The instrument team had produced a global mosaic product comprising over 15,000 images acquired between November 2009 and February 2011 [23]. This product was used in the current study for mapping large counting areas and checking and extracting large craters in these areas (to be elaborated upon in Section 4.7) using the crater database provided by Robbins et al. [24]. In addition, the elevation data, SLDEM2015, were used as auxiliary data, especially to check the craters that were not clear in the images.
Jia et al. [25] released a crater catalog of the Chang’e-5 (CE-5) landing area based on a digital orthophoto map (DOM) generated from over 700 LROC NAC images. This crater catalog was used to extract craters in the CE-5 landing area.
Robbins [24] published a global database of lunar impact craters that is estimated to be a complete census of all craters with D > 1–2 km. The database is the result of a fully manual effort rather than an automated effort, is very reliable, and has been widely used since publication. It was used in this study to extract craters with diameters greater than ~1 km in the large areas (as will be shown in Section 4.7).
3. Method
To establish the lunar crater PF, the first step was to map the crater populations and measure their diameters in different geologic regions. The NAC images were processed using the Integrated Software for Imagers and Spectrometers (ISIS) program [26], and then imported into ArcGIS for mapping craters. The procedure of crater CSFD measurements has been detailed in several previous studies [4,27]. In summary, in order to obtain the crater CSFD of a geological unit, we firstly had to determine the surface area of the geological unit, and then measure the diameters of each primary impact crater within the unit. The crater CSFDs from different areas were subsequently normalized, and the lunar crater PF was finally obtained by fitting the normalized CSFD with a function. The overall workflow is shown in Figure 1.
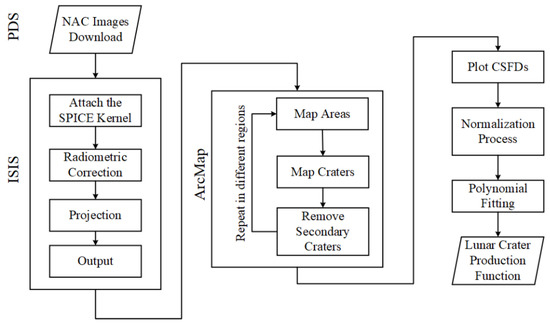
Figure 1.
Workflow of this research. All downloaded LROC NAC images were firstly processed in the ISIS program and then imported into ArcGIS to map the counting areas and craters. The CSFD of each counting area was then obtained and finally normalized to a polynomial to obtain the lunar crater PF.
3.1. NAC Images Processing
The experiment data record (EDR) NAC images were downloaded directly via the NASA Planetary Data System Geosciences Node [22], and preprocessed using the ISIS program provided by USGS. SPICE kernels were attached to each NAC image using the command of “spiceinit”, and radiometric corrections and the removal of echo effects were realized using the commands of “lronaccal” and “lronacecho”. Finally, the images were converted to map projection using the “cam2map” command [28]. The processed NAC images were then imported into ArcGIS for mapping craters. The NAC images used in this study can be found in Table 1.
3.2. Counting Area Mapping
It only makes sense to measure CSFD in an area that has the same age. If an initially fresh surface area was subsequently cratered with time, a certain SFD would be developed and remain constant, provided that no craters were removed via erosion and degradation [17]. Crater equilibrium refers to the state of a surface at which craters of the given size are being produced and being destroyed at the same rate [29]. Crater equilibrium is relevant mainly for small size domains and it should be avoided as the correlation between the crater SFD and surface age break-down, as it occurs. Furthermore, the CSFD of this area was only applicable for the primary craters because the distribution of the secondary craters was not random. Therefore, the measurements had to be performed in regions which had preserved all of the primary crater populations. The general criteria for counting area mapping are as follows:
(1) The counting area should belong to the same geological unit, that is, it should have been formed at an instant in the geological history.
(2) Counting areas should not include secondary craters as much as possible, i.e., counting areas should be far away from the ejecta field of large impact craters. The areas with craters of irregular forms or those distributed in chains, clusters, or herringbone patterns should be excluded [30,31,32].
(3) The counting area should be large enough to provide enough larger craters to obtain reasonable numerical statistics, since the accuracy of the result decreases for smaller count areas.
According to the criteria for the counting areas mentioned above, 13 counting areas (2 counting areas in the Orientale basin) were selected for mapping craters and fitting the lunar crater PF. In addition, the reasons for selecting them as counting areas include (1) these regions have flat terrain over a continuous geological unit, and provide good conditions for mapping craters; (2) these regions have been extensively studied in the past decades, especially with regard to geological unit, crater counting, and dating, providing many references and facilitating comparisons; and (3) these areas provide a large number of craters of various sizes, meaning we could build a PF across a wide diameter range. Figure 2 shows the locations of the counting areas used in this study.

Figure 2.
Locations of all of the counting areas used in this study. The basemap is a WAC image global mosaic. (a) Distribution of nine areas on the lunar nearside. (b) Distribution of three areas on the lunar farside.
3.3. Mapping Craters
Currently, there are two categories of crater mapping methods, i.e., automatic identification via computer and manual interpretation. Although it is time-consuming, manual crater mapping is usually deemed to be much more reliable and is often considered to be the golden standard for evaluating the automatic identification of results [33,34,35]. The main features for the visual identification of impact craters can be summarized as follows:
- (1)
- The interior of the impact crater is of high contrast in optical imagery for most cases due to shadowing effects.
- (2)
- The impact crater rim is generally circular or elliptical in shape.
- (3)
- The crater is usually expressed as an elevated rim surrounding a depressed cavity. Some shallow or degraded craters may not have elevated rims, but they can still be identified based on the shadowing effect.
In this study, small craters (D ≤ 1 km) were manually mapped in the counting areas with the help of the “CraterTools” add-in of ArcGIS [36] using either a single NAC image or several NAC images after geometric correction. During the crater mapping, obvious secondary craters, which display characteristic morphologies such as irregular forms and distribution in chains and clusters, were removed. After completing the identification of craters in a counting area, the result of crater mapping should be checked, and possible secondary craters should be further identified and removed based on the traces of the ejecta. However, independent secondary craters from distant impact events and a small number of smaller secondary craters cannot be excluded [37]. Therefore, it is unavoidable to mix a few secondary craters into the small craters. In addition, in some cases, it is necessary to identify the overlapping relationship between the crater and the ejecta with the naked eye, which is somewhat subjective.
Large craters (D > 1 km) were extracted as follows: First, the craters within the counting area were selected from the crater database published by Robbins [24]. Then, the selected craters were manually checked based on the WAC global mosaic and some modifications were made, including adding the mis-mapped craters and removing the secondary craters.
3.4. PF Normalization and Fitting
As we have stated above, the general size–frequency of craters on the lunar surface was assumed to be constant, and the relationship of crater frequencies for areas with different ages can be expressed as follows:
where refers to the cumulative crater frequency which is larger than diameter D for the area with age , refers to the crater frequency which is larger than diameter D for the area with age , and c is a constant. The above equation indicates that for the same crater diameters D, the crater frequency at the age can be converted to simply by multiplying a factor c. This is exactly the basis of the normalization of the lunar crater production. Therefore, determining the factor c can normalize the crater SFDs with different ages to each other and eliminate the difference in age.
However, there is usually a slight difference in the factor c for two or more geological units with the same diameters. In this case, the normalization factor c was simply equal to the average in the overlapping crater size interval (e.g., [15,17]). A more sophisticated method is to minimize the variance among the interval diameters between the two SFDs at different geological ages, and it can be expressed as follows:
where is the cumulative crater frequency at the geological age , is the cumulative crater frequency at the geological age , is the crater diameter in the overlapping interval between two observed SFDs, and is the normalization factor from to . The above equation can minimize the disagreement between the normalized SFDs. The CSFD of CE-5 was used as the standard distribution, and the normalization factor for the CSFD of other regions was calculated in the overlapping diameter range according to Formula (2). The CSFD of other regions was then multiplied by the normalization factor to obtain the normalized CSFD. The normalization process extends the standard distribution to both diameter ends and normalizes the CSFDs of other regions to CE-5, obtaining the CSFD curve and thus representing the age of CE-5. Finally, the PF was obtained by directly using the polynomial to fit the normalized CSFD.
4. Results
There were 13 counting areas used to build the lunar crater PF in this study, and LROC NAC images were used to map craters in 6 of them. In this section, we first present the counting areas and the mapped craters therein, and then we provide the new lunar crater PF.
4.1. Apollo 15 Landing Site (A15LS)
The Apollo 15 lunar module landed on the edge of Mare Imbrium, to the east of Hadley Rille [38]. The mare region on either side of the Rille is homogenous and both sides of it are suitable as crater counting areas. This area was first studied by Neukum et al. [17] using the Apollo 15 photographs. They plotted the crater frequency in a rough schematic draft with diameters greater than 250 m. Robbins et al. [39] also plotted the crater size frequency in this region; however, they used a much larger counting area including the mare surface in the west of the Rille. It is important to point out that Robbins et al. [39] manually removed many secondary craters in the mare surface. To be conservative, we refer to the counting area used by Neukum et al. [17] and mapped an area of ~244 km2 as the counting area in this study. To avoid possible contamination by secondary craters from the ejecta of the crater Autolycus in the northwest, the western boundary was set at 3.15°E (Figure 3a).
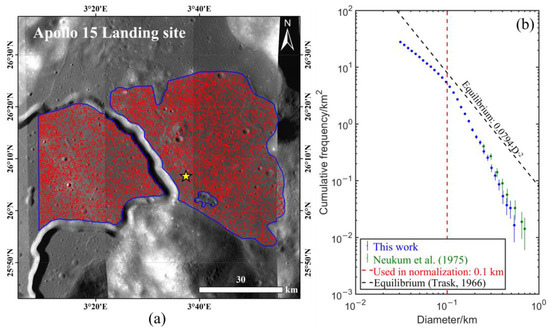
Figure 3.
Counting area and mapped craters surrounding A15LS and the corresponding CSFD in comparison with Neukum et al. [17]. (a) Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles). The yellow star indicates the Apollo 15 lander location. Note that the area encircled by the small blue polygon has been removed as it includes many secondary craters. Two pairs of LRO NAC images were used for this region: M104490494 and M1108260533. (b) The CSFD derived in this study (blue) in comparison with that of Neukum et al. [17] (green). The red dashed line represents the diameter range used in the normalization. The lunar equilibrium function [41] is shown by the black dashed line.
As a result, a total of 7044 craters with D > 30 m were mapped. The crater CSFD is shown in Figure 3b. Because similar areas were used, their results are also shown in Figure 3b for comparison. Neukum et al. [17] only presented the CSFD of craters with D > 250 m in a 213 km2 region. The CSFD of this study was slightly lower than that by Neukum et al. [17], but still within the error bar. The completeness diameter represents the minimum diameter of the completely identified craters and can generally only be estimated empirically. Robbins et al. [40] proposed a new technique based on kernel density estimation (KDE) to calculate the completeness diameter of craters. Using this method, the completeness diameter was calculated to be ~80 m. The lunar equilibrium function [41] was used to figure out whether the crater population had reached equilibrium. In this area, craters with diameters of ~100 m may have hit quasi-equilibrium. Therefore, only craters with D > 100 m were contained in the normalization process.
4.2. Mare Region West of Delisle
Another mare region used in this study lies in the west of Mare Imbrium, which is ~40 km from the crater Delisle and is shielded by Delisle β rise from the contamination of secondary craters (Figure 4a). König [15] utilized Apollo 15 photographs to measure craters in this region when constructing the PF. Using the NAC image M1203903057L, we mapped 2042 craters with D > 20 m in a counting area of ~31 km2. The measurement results of this study and of König [15] are shown in Figure 4b for comparison. The completeness diameter of craters in this study was calculated as 23.7 m. However, craters with D < ~130 m may have reached equilibrium. Only the craters with D > ~130 m were used in establishing PF.
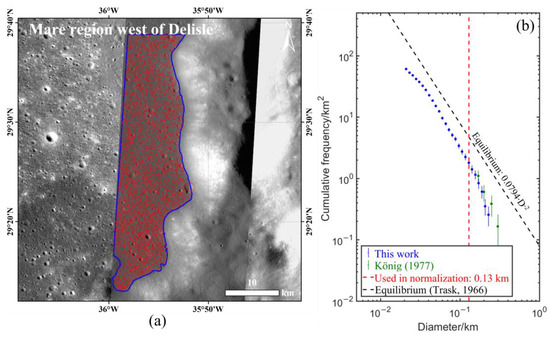
Figure 4.
Counting area and mapped craters in the west of Delisle and the corresponding CSFD in comparison with CSFD derived by König [15]. (a) Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles) in NAC image M1203903057L. (b) The CSFD in this study (blue) in comparison with that by König [15] (green). The lunar equilibrium function [41] is shown by the black dashed line.
4.3. Light Mantle Region of Apollo 17 Landing Site (A17LS)
The Apollo 17 lunar module landed in the Tauraus–Littrow valley [42]. The counting area was selected on the light mantle that was roughly five kilometers away from A17LS. A recent study by Jolliff et al. [43] pointed out that the light mantle material originated from the landslide material of South Massif. König [15] and Hiesinger et al. [44] mapped craters on the light mantle.
This region is suitable for mapping small craters as it is young and small craters have not been in equilibrium, but caution must be taken for those craters that are not completely buried by the landslide materials. Therefore, we did not use the region on the northeast of the light mantle like the previous two studies did, because the landslide material here was thinner and therefore many smaller craters may not have been completely buried. In addition, we also removed some craters that may not have been completely buried according to the superposition relationship between the ejecta of craters and landslide materials and the prominence of the craters’ rims. Obviously, both the studies of König [15] and Hiesinger et al. [44] mapped all of the visible craters (Figure 5b). The counting area in this study was ~6.55 km2 and 1948 craters were totally mapped (Figure 5a). The completeness diameter was determined as 10.8 m and the crater density did not reach equilibrium (Figure 5b).
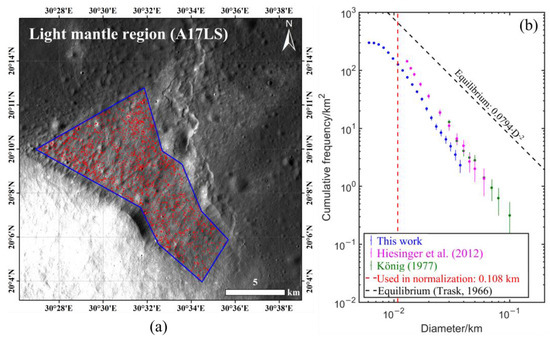
Figure 5.
Counting area and mapped craters surrounding the Apollo 17 lunar module landing site and the corresponding CSFD in comparison with König [15] and Hiesinger et al. [44]. (a) Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles) in NAC image M192760872L. (b) The CSFD derived in this study (blue) in comparison with that of König [15] (green) and of Hiesinger et al. [44] (purple). The lunar equilibrium function [41] is shown by the black dashed line.
4.4. North Ray Crater (Apollo 16LS)
The North Ray crater is a 950 m diameter crater in the Descartes Highlands, approximately 5 kilometers away from the Apollo 16 lunar module landing site (8.97°S, 15.50°E) [45]. Previous research has shown that North Ray is a young crater with a geological age of about 49 million years [46].
Using the NAC image M129187331 with a resolution of 0.5 m/pixel, the same 4 counting areas defined in König [15] were mapped in this study. We removed the craters that may not have been buried completely by the ejecta using the technique mentioned in Section 4.3. About 5800 craters were extracted on the continuous ejecta of North Ray (Figure 6a). The completeness diameter of the craters mapped in this study was calculated to be 4.7 m. However, craters with diameters of ~8 m were close to equilibrium. To be conservative, the normalization process involved the craters with D > ~8 m. There are some steep slopes in the southern sub-region of Figure 6a that may have a slightly lower density of small craters on their surfaces compared to the surrounding flat surface. However, considering that the area of the steep slopes was small compared to the entire counting area, and that most of the small craters were not used in the normalization process and PF construction, the area of these slopes was not excluded.
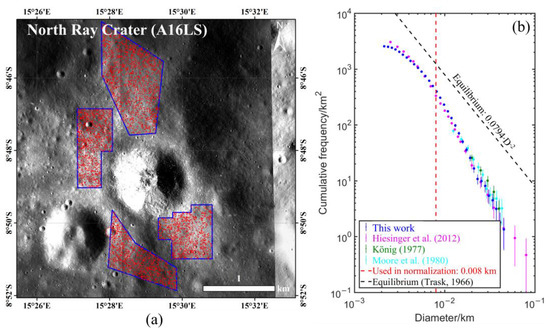
Figure 6.
Counting area and mapped craters in the ejecta of North Ray crater and the corresponding CSFD in comparison with König [15], Moore et al. [47], and Hiesinger et al. [44]. (a) Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles) in NAC image pair M129187331. (b) The CSFD derived in this study (blue) in comparison with that of König [15] (green), Moore et al. [47] (cyan), and Hiesinger et al. [44] (purple). The lunar equilibrium function [41] is shown by the black dashed line.
Hiesinger et al. [44] used the same counting areas and image data as this study. In addition, Moore et al. [47] (1980) measured the craters in this region. Their results and the derived CSFD in this research are also shown in Figure 6b. Robbins et al. [39] also mapped craters in a similar area and plotted an unbound CSFD, which differs from our representation and is not plotted in Figure 6b for comparison.
4.5. Cone Crater (Apollo 14LS)
Cone crater is a 350 m diameter crater in the Fra Mauro highlands [48], roughly 1 kilometer northeast of the Apollo 14 Landing Site (A14LS). Moore et al. [47] and Plescia et al. [49] measured craters near this region. In this study, the counting area we used was defined by Robbins et al. [39], which was mapped outside from the rim to a 0.5–1 crater diameter. In Figure 7a, there may be some unexcluded steep slopes in the western part of the counting area, accounting for about 6% of the total counting area. Steep slopes erase small craters more severely than flat terrain, but considering that this area is small, the impact of it on the crater measurements in the entire area is limited, and so it has not been excluded. The counting area was ~0.48 km2 on the ejecta blanket of Cone crater, and 517 craters were mapped in total (Figure 7a). Since the ejecta in this area was also not very thick, we carefully mapped the craters over the ejecta blanket. The CSFDs derived in this research along with that of Moore et al. [47] are shown in Figure 7b. Our CSFD is slightly higher than that of Moore et al.’s [47], but is still within the error bar. The completeness diameter of the mapped craters was calculated as 4.5 m and the equilibrium was not observed in this area.
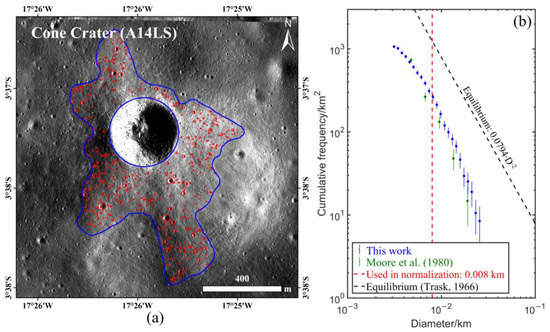
Figure 7.
Counting area and mapped craters in the ejecta of Cone crater and the corresponding CSFD in comparison with that of Moore et al. [47]. (a) Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles) in NAC image M114071006L. (b) The CSFD in this study (blue) in comparison with that by Moore et al. [47] (green). The lunar equilibrium function [41] is shown by the black dashed line.
4.6. Aristarchus Crater
Aristarchus is a 40 km diameter crater located in the lunar Oceanus Procellarum [50]. The reason to select it as a counting area is mainly to bridge the preceding small craters and the large craters in other areas. The counting area was ~31.9 km2 on its continuous ejecta blanket on the southwest edge of the crater, and 2709 craters were mapped in total (Figure 8a). Figure 8b shows the CSFD derived in this research and in the previous studies of König [15] and Zanetti et al. [51]. The completeness diameter was calculated as 30 m and the equilibrium was not observed in this area. Therefore, the normalization process contained the craters with D > ~30 m.
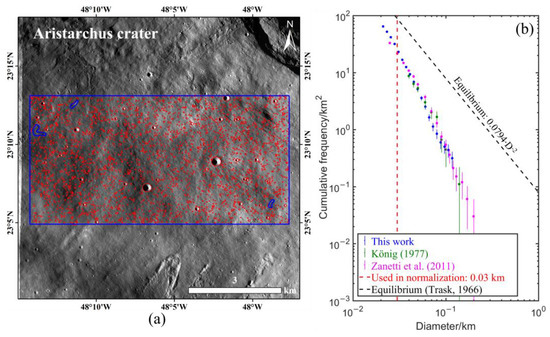
Figure 8.
Counting area and mapped craters in the ejecta of Aristarchus crater and the corresponding CSFD in comparison with König [15] and Zanetti et al. [51]. (a) Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles) in NAC image pair M102472092. (b) The CSFD in this study (blue) in comparison with that by König [15] (green) and Zanetti et al. [51] (purple). The lunar equilibrium function [41] is shown by the black dashed line.
4.7. Other Regions
Jia et al. [25] mapped all of the craters larger than 200 m in a geological unit surrounding the Chang’e-5 landing site, in which the possible secondary craters along with the host areas were removed (the authors also took part in this work). Thus, the results by Jia et al. [25] were directly used in this research.
To obtain as many craters as possible, it is better to select old geological units and large areas in mapping craters with D ≥ 1 km. In this case, we referred to the crater database published by Robbins et al. [24] and the geological units were determined using the geological map by Fortezzo et al. [52]. Using the method described in Section 3.2, we mapped large craters (D > 1 km) in these areas (see Figure 9, Figure 10 and Figure 11). Four counting areas of Mare Serenitatis, Mare Crisium, Mendeleev crater, and the Orientale basin were selected in this research (Figure 9). The CSFDs of the four areas are shown in Figure 12a.
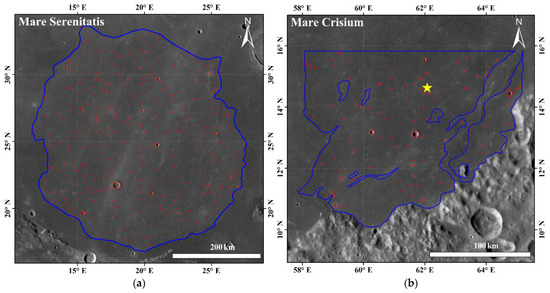

Figure 9.
Counting areas (encircled by the blue polygons) and mapped craters (shown in red circles) in a WAC image global mosaic [23]. (a) The interior of Mare Serenitatis. (b) The area in the southeast of the Mare Crisium. The yellow star indicates the Luna 24 lander location. (c) The bottom of the Mendeleev crater. (d) The area in the Orientale basin between the Cordillera ring and the Rook ring.
Another counting area was on the entire continuous ejecta blanket defined by Yue et al. [53]. According to the work of Yue et al. [53], the ejecta from the impact event decreased the population of craters with D < ~11.5 km, and probably buried all of the craters with D < ~5.5 km. With the help of the geological map by Fortezzo et al. [52], we mapped the craters with D > 10 km above the ejecta blanket (secondary craters were removed). These craters accumulated after the impact event of the Orientale basin and represent the age of the basin. The counting area and crater mapping are shown in Figure 10. The CSFD can be found in Figure 12a.

Figure 10.
Counting area (blue circle) and counted craters (red circles) on the ejecta of the Orientale basin defined by Yue et al. [54]. Only craters with D > 10 km above the ejecta blanket were mapped.
In addition, we mapped craters in the South Pole Aitken (SPA) basin (Figure 11). The SPA basin is the largest and the oldest impact structure on the Moon [55]. According to the counting area selection criteria (3) mentioned in Section 3.1, the SPA basin constitutes a sufficiently large coherent geological unit, which is suitable for mapping large craters. The outer ring of the SPA basin provided by Garrick et al. [56] was used as the boundary of the counting area in this study. We removed the basalt units located inside the SPA basin because they had different geological ages. Finally, we mapped an area of 4.0 × 106 km2 and counted 58,847 craters with D ≥ 2 km, and for clarity only the craters with D ≥ 10 km are shown in Figure 11. The CSFD derived in this area can be found in Figure 12a.
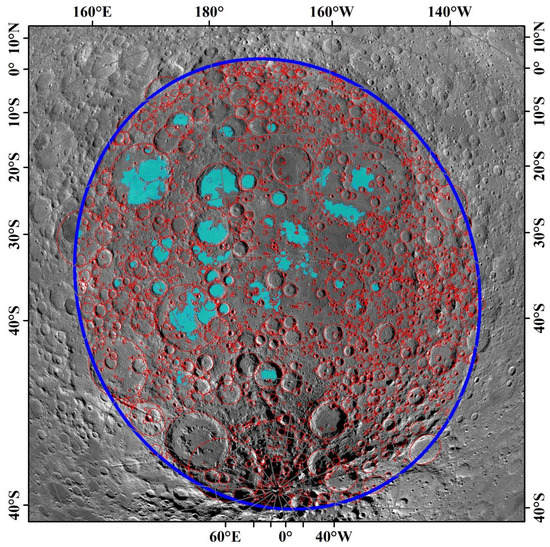
Figure 11.
Counting area (blue circle) and counted craters (red circles) within the SPA basin (only the craters with D ≥ 10 km are shown in the figure). The regions marked by cyan are the basalt units located in the SPA basin and they were excluded from the counting area.
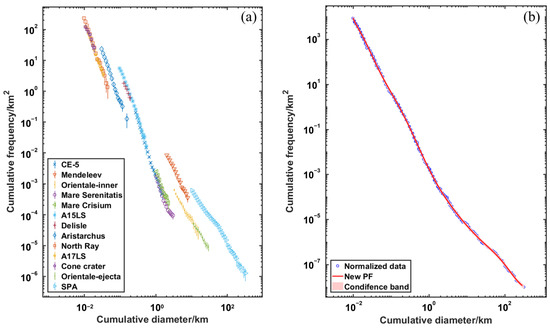
Figure 12.
All of the CSFDs and the normalization in this research. (a) The derived CSFDs in the different areas in this research. (b) The normalization result and the fitted lunar crater PF, in which the CSFD from the CE-5 landing area was used as the reference.
4.8. New PF Fitting
Table 2 shows the numerical details of crater counts. Figure 12a shows all of the CSFDs derived in this research. In the normalization, the CSFD from the CE-5 landing area was used as the reference because it had the largest diameter range. Figure 12b shows the normalization result. Similar to Neukum [1], we also used an 11th-degree polynomial to fit the normalized CSFD using the non-linear least square method because it fit the normalized CSFD well and did not appear to be overfitting. The confidence band with 95% confidence of the fitting curve is also shown in Figure 12b. The width of the confidence band increased with an increasing crater diameter, but the statistical uncertainties were within a factor of 50% (average: 20%). The resulting lunar crater PF had a similar form to the NPF:
where are the coefficients and only depends on the geological age of the mapped area, while the others are the constants for the lunar surface and they reflect the general pattern of the crater size frequency distribution. Table 3 lists all of the coefficients of the new lunar crater PF in the CE-5 landing area.

Table 2.
Summary data of crater counts of the 13 counting areas in this study.

Table 3.
Coefficients of the new lunar crater PF in the CE-5 landing area.
The new PF is valid for crater diameters between 0.01 km and 300 km. It is very close to that of Neukum [1] and Neukum et al. [57] with D < ~1 km (Figure 13), and only slightly lower than their result in the diameter range of ~30–100 m. For D < ~100 km, the new lunar crater PF is very similar to that of Neukum [1] and greatly different from that of Neukum et al. [57], while in the larger diameter range, the new PF gradually approaches that of Neukum et al. [57]. The reasons for these differences are discussed in Section 5.3.
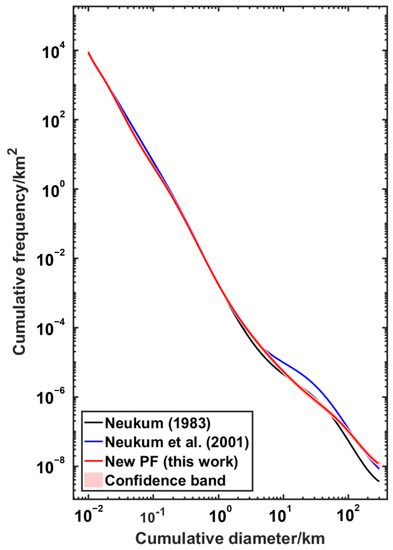
Figure 13.
The new PF derived in this research compared with that of Neukum [1] and Neukum et al. [57].
5. Discussion
5.1. Explanations for Disputed Areas
The new PF was constructed using the crater CSFDs from a total of 13 areas. Although the criteria for counting area mapping were established in Section 3.1, we provide further explanation of the three areas discussed below, which may be controversial.
5.1.1. Aristarchus Crater
The counting area was on the continuous ejecta blanket on the southwest of Aristarchus crater, in a small area next to the crater rim (Figure 8a). The ejecta blanket is so bright that it is easy to recognize. The work of Zanetti et al. [51] almost explicitly demonstrates the possibility of self-secondary cratering, which refers to secondary craters that formed on the ejecta deposit of the primary crater that made those secondaries. They suggested that the continuous ejecta blanket was contaminated by self-secondary craters (SSCs).
We must clarify that the influence of SSC in our counting area may be extremely limited. The formation mechanism of SSC determines the distribution pattern of increasing crater density with increasing distance from the crater rim within one crater radius from the parent crater rim. In addition, the thickness of the ejecta blanket decreases dramatically with the distance from the rim of the parent crater [58]. As this area is close to the crater rim, the ejecta blanket here is very thick, showing that it has resurfaced, and the density of the SSC is extremely low.
5.1.2. Ejecta of the Orientale Basin
This area is one of the few continuous surfaces suitable for counting the large craters with a diameter of tens of kilometers. It seems risky to measure craters in this area because the ejecta of the impact event did not completely bury all of the pre-existing craters [53]. However, the pre-existing craters around the Orientale basin were covered by thick ejecta, which could be easily distinguished according to their morphology and the superposition relationship between the ejecta materials. In addition, the geological map by Fortezzo et al. [52] provided information on the crater superimposed materials of the Orientale group. In conclusion, according to the overlapping relationship between the ejecta materials and the morphology of the craters, we identified the craters (D > 10 km) superimposed on the ejecta blanket of the Orientale basin. Figure 14a shows the CSFDs (not normalized) of the two areas in the Orientale basin, which are almost identical. Therefore, these craters can represent the age of the impact event of the basin.
5.1.3. South Pole Aitken (SPA) Basin
The SPA basin is the largest basin on the lunar surface. Obviously, the entire SPA basin does not only contain a single geological unit. Numerous different units have been identified within it [59], mainly including large impact basins (e.g., Apollo basin) and basalt units. The area of basalt units has been removed in this study. The superposition of large impact basins has indeed eliminated some pre-existing craters in the region, which may be difficult to avoid in the measurements of craters in large counting areas. However, considering that (1) the area of these impact basins is very small compared with the entire SPA basin and (2) we focused on the craters with D > 20 km in this area, we believe that it is feasible to measure craters in the SPA basin.
Figure 14 shows that the CSFD of the craters with D < 30 km in the SPA basin is very consistent with those of the two counting areas in the Orientale basin (the craters with D < 20 km are also very consistent, even if these craters are not included in the normalization process).
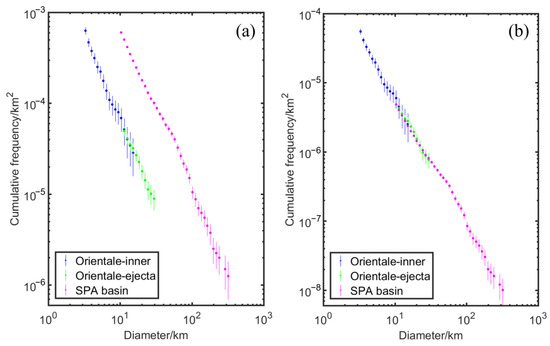
Figure 14.
The CSFDs and the normalized version of three areas in this study. (a) The CSFDs of Orientale—inner (blue), Orientale—ejecta (green), and SPA basin (purple). (b) The CSFD normalized to CE-5.
5.2. Compared with NPF
Figure 13 shows the new PF derived in this study, NPF (1983), and NPF (2001). The reasons for comparing with NPFs are that (1) we all used the method based on crater counts rather than the theoretical model, and (2) NPF-based chronology represents the current best interpretation for lunar cratering chronology [60].
5.2.1. Differences in Measurements
Similarly to NPF (1983), our new PF differs from NPF (2001) above ~1 km. The reason for the difference is that Neukum et al. [57] re-estimated the large crater part of the PF with new crater counts on the ejecta of the Orientale basin [61], which contains craters with a diameter of ~2–20 km. As mentioned earlier, extracting craters from the ejecta blanket surface requires distinguishing the superimposed relationship between the ejecta material and the craters. There are many craters on the ejecta blanket of the Orientale basin that are visible in the LROC WAC images, but are located below the ejecta blanket. The larger the diameter and the deeper the depth of the crater, the better the visibility. Therefore, if craters located above the ejecta blanket cannot be distinguished, the crater CSFD will be biased toward lower counts at the small diameter end and higher counts at the large diameter end, resulting in an S-shaped CSFD curve that does not match the crater production curve.
We measured craters in two areas of the Orientale basin as mentioned in Section 4.7, and the CSFDs were very consistent with each other (see Figure 14a). We compared the crater counts added in NPF (2001) with our results and found that their CSFD was lower than ours in the range of D < ~11 km (the maximum difference was ~40%, and the difference decreased with an increase in D) and higher than ours in the diameter range above ~11 km (before ~15 km, the difference was very small, but between 15–20 km, the maximum difference reached ~30%). A similar S-shape feature was observed in the study of Yue et al. [53]. They suggested that the ejecta from the Orientale impact event reduced the population of craters below ~11.5 km in diameter [53], which means that the craters included in the ejecta blanket do not belong to the geological unit with the same age (the craters not completely buried by the ejecta belong to the pre-existing surface). Therefore, it is necessary to identify the craters above the ejecta, which is what we did in this study. Although, Neukum et al. [57] did not provide a specific counting area or identify which craters were mapped. We believe that it is almost impossible to identify all of the craters located above the ejecta blanket in such a wide diameter range (~2–20 km).
The new PF differs from the NPF (both versions) at the large diameter end. Both versions of the NPF used crater counts in the highlands (again, without specifying the location of the counting area). The crater counts we used in this study came from the SPA basin. We did not attempt to measure craters in the highlands because the surface of the lunar highlands was thought to be saturated (e.g., [62,63]). Therefore, the CSFD of craters in the lunar highlands did not represent the geological age of the surface [64]. Furthermore, the thickness and strength of the megaregolith between maria and highlands vary greatly. Gardened highlands material is known to result in a different crater size for a given impactor compared to the impact of more competent volcanic maria. This could shift the local PF left or right (in diameter space) and yield a final, merged PF that does not accurately represent any single terrain.
5.2.2. Uncertainty Involved in Model Fitting
Although our measurements are more reliable than previous studies at the large diameter end, the uncertainty of model fitting due to the small absolute number of large craters may be one of the reasons for the difference between the new PF and NPFs. Therefore, we computed the confidence band of the new PF (Figure 13). The width of the 95% confidence band indeed increased with increasing diameter, but the maximum uncertainty of the fit was below 50%, with an average uncertainty of about ±20%. This indicates that the new PF, fitted with an 11th-degree polynomial, fits the normalized CSFD well.
Since the confidence band of the NPF was not discussed in previous studies, we can only compare the NPF curve with the new PF using a confidence band. The confidence band of the model shows the uncertainty range of the model fitting. Figure 13 shows that even at the large diameter end with the widest confidence band, the NPF2001 is still not within the confidence band of the new PF. This indicates that the difference in the large diameter end between the models is not due to the uncertainty of the model fitting, but is determined by the crater measurements.
5.2.3. Cumulative Fit of Measured Crater CSFD
The production function is generally used to fit the measured crater CSFD, derive the N(1) value, and then date the area. Therefore, the ability of the production function to describe the measured crater CSFD can be used as an indicator to evaluate the production function. In order to intuitively compare the difference between the new PF and the NPF at the large diameter end, we collected some work on large crater counts. Three crater CSFDs were used here, where the data of the Nectarian and pre-Nectarian terrains come from the work of Marchi et al. [65], and the data of terrestrial craters come from the Earth Crater Database [66]. They were not included in the counting areas of constructing PF. The cumulative fit results are shown in Figure 15.
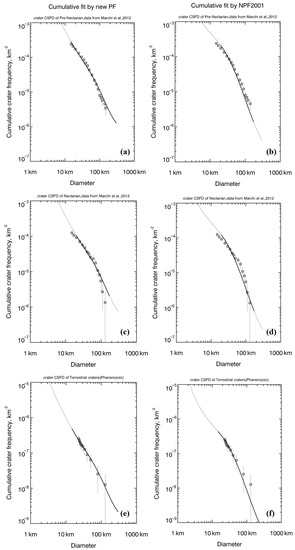
Figure 15.
Cumulative fit by new PF (left column) and cumulative fit by NPF2001 (right column). (a,b) Crater CSFD of pre-Nectarian terrains; data can be found in Marchi et al. [65]; (c,d) crater CSFD of Nectarian basin; data can be found in Marchi et al. [65]; and (e,f) crater CSFD of terrestrial craters; data can be found in Earth Impact Database [66].
Figure 15 shows that the crater CSFD with a diameter of ~10–100 km is shallower than the NPF and closer to the new PF. These cases show that the new PF has better consistency with the crater CSFDs at the large diameter end.
In conclusion, a significant difference between our new PF and the NPF (2001) is due to the incorrect extraction of the craters on the ejecta of the Orientale basin. Based on the geological unit map by Fortezzo et al. [52], we only identified craters (D > 10 km) superimposed on the ejecta blanket, and obtained a more accurate production curve in this diameter range (10–30 km). In addition, the three cases shown in Figure 15 prove that the new PF is more accurate at the large diameter end.
5.3. Influence of Topography Degradation and Terrain Properties
It has been proposed that topography degradation and terrain properties can modify the crater CSFD [67], especially for the small crater CSFD, because topography degradation enlarges the crater diameter, and smaller craters are enlarged faster than larger ones [68]. In addition, for the same impactor, the lunar maria and highlands may result in different crater sizes, which could shift the local crater CSFD left or right (in diameter space).
The counting areas used to construct the new PF in this study were mainly located on (a) the surface of young ejecta; (b) mare basalts; and (c) the interior or ejecta blanket of large impact basins. These areas have different terrain properties and degrees of topography degradation. However, in the normalization process, the following were found: (1) The four counting areas mentioned in Section 4.3, Section 4.4, Section 4.5 and Section 4.6, located on the surface of the young ejecta, have similar terrain properties and different ages/degradation degrees. The normalized CSFDs overlap consistently. (2) The two counting areas “Orientale—inner” and “Orientale—ejecta” in Figure 14 are of the same age/degradation, but have significantly different terrain properties. The CSFDs of the two regions are very consistent (Figure 14a). (3) Adding the CSFD of the SPA basin on the basis of (2), the age/degradation degree and terrain properties of the three areas are different, and the normalized CSFD is also very consistent. This shows that even though the crater SFDs are probably affected by topography degradation and terrain properties, they are still relatively consistent over the diameter range of 3–20 km.
Overall, since the new PF is constructed via observed crater diameters, it must include a certain level of terrain effects. This approach assumes a constant shape of the PF, with only the absolute number of craters changing over time, which ignores many influencing factors, including terrain properties and topography degradation. Therefore, the new PF represents the cumulative distribution of craters that includes the terrain effects rather than the original crater records.
6. Conclusions
Based on high-resolution LROC NAC images, WAC images, and SLDEM, we surveyed a total area of about 6.1 × 106 km2 and identified over 1.4 × 105 craters in 13 selected areas on the lunar surface and made corresponding analyses such as on crater completeness diameter and equilibrium state. All of the CSFDs from the different areas were normalized to those in the CE-5 landing area, and based on which the new lunar crater PF was derived using the non-linear least squares method. The new PF is valid for craters between 0.01 km and 300 km, and there was a moderate difference between the larger diameters compared with the previous PFs. We discussed the difference in relation to the NPF and found that (1) the lunar crater PF is very stable in the diameter range of 10 m–1 km, and our measurements of high-resolution images confirm the steep slope of the PF. (2) The most significant difference between the new PF and NPF (2001) may be caused by the incorrect crater counts in Orientale, and the new PF is more reliable at the large diameter end. (3) As with the previous PFs, the new PF includes unquantifiable terrain effects.
With the new lunar crater PF and the isotopically measured ages of lunar samples, a new lunar chronology function is expected to be established. In addition to surface dating, the new lunar crater PF can provide insights into the cratering history on the surface of the Moon, and can be extended to other inner solar system bodies [54,69]. It can also shed light on the analysis of the evolution of the asteroids and related bombardment rate in the near-Earth region.
Author Contributions
Conceptualization, Z.Y.; methodology, J.L. and Z.Y.; investigation, Z.Y., K.D. and Y.L.; writing—original draft preparation, J.L.; writing—review and editing, Z.Y., S.G. and K.D.; project administration, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (grant no. 2022YFF0503100) and the National Natural Science Foundation of China (grant nos. 41972321 and 42230206).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
The authors thank all those who worked on the NASA Planetary Data System archive to make the LROC imagery and SLDEM publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Neukum, G. Meteoriten Bombardement und Datierung Planetarer Oberflächen; University of Munich: Munich, Germany, 1983. [Google Scholar]
- Stöffler, D.; Ryder, G. Stratigraphy and isotope ages of lunar geologic units: Chronological standard for the inner solar system. Space Sci. Rev. 2001, 96, 9–54. [Google Scholar] [CrossRef]
- Stöffler, D.; Ryder, G. Cratering history and lunar chronology. Rev. Mineral. Geochem. 2006, 60, 519–596. [Google Scholar] [CrossRef]
- Hiesinger, H.; Jaumann, R.; Neukum, G.; Head III, J.W. Ages of mare basalts on the lunar nearside. J. Geophys. Res. Planets 2000, 105, 29239–29275. [Google Scholar] [CrossRef]
- Michael, G.; Neukum, G. Planetary surface dating from crater size–frequency distribution measurements: Partial resurfacing events and statistical age uncertainty. Earth Planet. Sci. Lett. 2010, 294, 223–229. [Google Scholar] [CrossRef]
- Stuart, J.S.; Binzel, R.P. Bias-corrected population, size distribution, and impact hazard for the near-Earth objects. Icarus 2004, 170, 295–311. [Google Scholar] [CrossRef]
- Hartmann, W.K. On the distribution of lunar crater diameters. Commun. Lunar Planet. Lab. 1964, 2, 197–204. [Google Scholar]
- Young, J. A statistical investigation of diameter and distribution of lunar craters. J. Br. Astron. Assoc. 1940, 50, 309–326. [Google Scholar]
- Brown, H. The density and mass distribution of meteoritic bodies in the neighborhood of the earth’s orbit. J. Geophys. Res. 1960, 65, 1679–1683. [Google Scholar] [CrossRef]
- Cross, C. The size distribution of lunar craters. Mon. Not. R. Astron. Soc. 1966, 134, 245–252. [Google Scholar] [CrossRef]
- Hawkins, G.S. Asteroidal fragments. Astron. J. 1960, 65, 318. [Google Scholar] [CrossRef]
- Hartmann, W.K. Terrestrial, lunar, and interplanetary rock fragmentation. Icarus 1969, 10, 201–213. [Google Scholar] [CrossRef]
- Chapman, C.; Haefner, R. A critique of methods for analysis of the diameter-frequency relation for craters with special application to the Moon. J. Geophys. Res. 1967, 72, 549–557. [Google Scholar] [CrossRef]
- Neukum, G.; Schneider, E.; Mehl, A.; Storzer, D.; Wagner, G.A.; Fechtig, H.; Bloch, M.R. Lunar craters and exposure ages derived from crater statistics and solar flare tracks. In Proceedings of the Lunar and Planetary Science Conference Proceedings, New York, NY, USA, 10–13 January 1972. [Google Scholar]
- König, B. Investigations of Primary and Secondary Impact Structures on the Moon and Laboratory Experiments to Study the Ejecta of Secondary Particles. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 1977. [Google Scholar]
- Neukum, G.; Ivanov, B. Crater size distributions and impact probabilities on Earth from lunar, terrestrial-planet, and asteroid cratering data. Hazards Due Comets Asteroids 1994, 359, 359–416. [Google Scholar]
- Neukum, G.; König, B.; Arkani-Hamed, J. A study of lunar impact crater size-distributions. Moon 1975, 12, 201–229. [Google Scholar] [CrossRef]
- Greeley, R.; Gault, D.E. Precision size-frequency distributions of craters for 12 selected areas of the lunar surface. Moon 1970, 2, 10–77. [Google Scholar] [CrossRef]
- Kereszturi, A.; Steinmann, V. Characteristics of small young lunar impact craters focusing on current production and degradation on the Moon. Planet. Space Sci. 2017, 148, 12–27. [Google Scholar] [CrossRef]
- Antonenko, I.; Robbins, S.; Gay, P.L.; Lehan, C.; Moore, J. Effects of Incidence Angle on Crater Detection and the Lunar Ioschron System: Preliminary Results from the CosmoQuest MoonMappers Citizen Science Project. In Proceedings of the 44th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2013. [Google Scholar]
- Robinson, M.S.; Brylow, S.; Tschimmel, M.; Humm, D.; Lawrence, S.J.; Thomas, P.C.; Denevi, B.W.; Bowman-Cisneros, E.; Zerr, J.; Ravine, M.A. Lunar reconnaissance orbiter camera (LROC) instrument overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- NASA. Planetary Data System Geosciences Node Orbital Data Explorer (ODE). Available online: https://ode.rsl.wustl.edu/moon/ (accessed on 2 May 2023).
- Wagner, R.; Speyerer, E.; Robinson, M.S.; LROC Team. New mosaicked data products from the LROC team. In Proceedings of the 46th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2015. [Google Scholar]
- Robbins, S.J. A new global database of lunar impact craters > 1–2 km: 1. Crater locations and sizes, comparisons with published databases, and global analysis. J. Geophys. Res. Planets 2019, 124, 871–892. [Google Scholar] [CrossRef]
- Jia, M.; Yue, Z.; Di, K.; Liu, B.; Liu, J.; Michael, G. A catalogue of impact craters larger than 200 m and surface age analysis in the Chang’e-5 landing area. Earth Planet. Sci. Lett. 2020, 541, 116272. [Google Scholar] [CrossRef]
- Sides, S.; Becker, T.; Becker, K.J.; Edmundson, K.L.; Backer, J.W.; Wilson, T.J.; Weller, L.A.; Humphrey, I.R.; Berry, K.L.; Shepherd, M.R. The USGS Integrated Software for Imagers and Spectrometers (ISIS 3) instrument support, new capabilities, and releases. In Proceedings of the 48th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 20–24 March 2017. [Google Scholar]
- Group, C.A.T.W. Standard techniques for presentation and analysis of crater size-frequency data. Icarus 1979, 37, 467–474. [Google Scholar]
- Henriksen, M.; Manheim, M.; Burns, K.N.; Seymour, P.; Speyerer, E.J.; Deran, A.; Boyd, A.K.; Howington-Kraus, E.; Rosiek, M.; Archinal, B. Extracting accurate and precise topography from LROC narrow angle camera stereo observations. Icarus 2017, 283, 122–137. [Google Scholar] [CrossRef]
- Gault, D.E. Saturation and equilibrium conditions for impact cratering on the lunar surface: Criteria and implications. Radio Sci. 1970, 5, 273–291. [Google Scholar] [CrossRef]
- Gou, S.; Yue, Z.; Di, K.; Cai, Z.; Liu, Z.; Niu, S. Absolute model age of lunar Finsen crater and geologic implications. Icarus 2021, 354, 114046. [Google Scholar] [CrossRef]
- McEwen, A.S.; Bierhaus, E.B. The importance of secondary cratering to age constraints on planetary surfaces. Earth Planet. Sci. Lett. 2006, 34, 535–567. [Google Scholar] [CrossRef]
- Hargitai, H.; Kereszturi, Á. Encyclopedia of Planetary Landforms; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Di, K.; Li, W.; Yue, Z.; Sun, Y.; Liu, Y. A machine learning approach to crater detection from topographic data. Adv. Space Res. 2014, 54, 2419–2429. [Google Scholar] [CrossRef]
- Salamunićcar, G.; Lončarić, S.; Pina, P.; Bandeira, L.; Saraiva, J. MA130301GT catalogue of Martian impact craters and advanced evaluation of crater detection algorithms using diverse topography and image datasets. Planet. Space Sci. 2011, 59, 111–131. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, W.; Zhou, C. A Chang’E-1 global catalog of lunar impact craters. Planet. Space Sci. 2015, 112, 42–45. [Google Scholar] [CrossRef]
- Kneissl, T.; van Gasselt, S.; Neukum, G. Map-projection-independent crater size-frequency determination in GIS environments—New software tool for ArcGIS. Planet. Space Sci. 2011, 59, 1243–1254. [Google Scholar] [CrossRef]
- Shi, K.; Yue, Z.; Di, K.; Liu, J.; Dong, Z. The gardening process of lunar regolith by small impact craters: A case study in Chang’E-4 landing area. Icarus 2022, 377, 114908. [Google Scholar] [CrossRef]
- Allen, J.P. Apollo 15: Scientific Journey to Hadley-Apennine: The stunning beauty of the most recent lunar landing site is surpassed by the rich scientific harvest which it yielded. Am. Sci. 1972, 60, 162–174. [Google Scholar]
- Robbins, S.J. New crater calibrations for the lunar crater-age chronology. Earth Planet. Sci. Lett. 2014, 403, 188–198. [Google Scholar] [CrossRef]
- Robbins, S.J.; Riggs, J.D.; Weaver, B.P.; Bierhaus, E.B.; Chapman, C.R.; Kirchoff, M.R.; Singer, K.N.; Gaddis, L.R. Revised recommended methods for analyzing crater size-frequency distributions. Meteorit. Planet. Sci. 2018, 53, 891–931. [Google Scholar] [CrossRef]
- Trask, N.J. Size and spatial distribution of craters estimated from the Ranger photographs. Icarus 1966, 6, 270–276. [Google Scholar] [CrossRef]
- Arvidson, R.; Crozaz, G.; Drozd, R.J.; Hohenberg, C.M.; Morgan, C.J. Cosmic ray exposure ages of features and events at the Apollo landing sites. Moon 1975, 13, 259–276. [Google Scholar] [CrossRef]
- Jolliff, B.L.; Wang, K.; Korotev, R.; Simon, S.; Papike, J.J.; Shearer, C.K. Apollo Next Generation Sample Analysis: What to expect among Rock Fragments in Apollo 17 Core Samples 73001 and 73002. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2020. [Google Scholar]
- Hiesinger, H.v.; Van Der Bogert, C.H.; Pasckert, J.H.; Funcke, L.; Giacomini, L.; Ostrach, L.R.; Robinson, M.S. How old are young lunar craters? J. Geophys. Res. Planets 2012, 117, E00H10. [Google Scholar] [CrossRef]
- Orloff, R.W.; Harland, D.M. The Definitive Sourcebook; Springer: Greer, SC, USA, 2006. [Google Scholar]
- Marti, K.; Lightner, B.; Osborn, T.W. Krypton and xenon in some lunar samples and the age of North Ray Crater. In Proceedings of the Lunar Science Conference, Houston, TX, USA, 1 January 1973. [Google Scholar]
- Moore, H.; Boyce, J.; Hahn, D. Small impact craters in the lunar regolith—Their morphologies, relative ages, and rates of formation. Moon Planets 1980, 23, 231–252. [Google Scholar] [CrossRef]
- Head, J.W.; Hawke, B. Geology of the Apollo 14 region/Fra Mauro/-Stratigraphic history and sample provenance. In Proceedings of the Lunar Science Conference, Houston, TX, USA, 17–21 March 1975. [Google Scholar]
- Plescia, J. Insight into Impact Crater Crustal Structure using Gravity Data. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2011. [Google Scholar]
- Mustard, J.F.; Pieters, C.M.; Isaacson, P.J.; Head, J.W.; Besse, S.; Clark, R.N.; Klima, R.L.; Petro, N.E.; Staid, M.I.; Sunshine, J.M. Compositional diversity and geologic insights of the Aristarchus crater from Moon Mineralogy Mapper data. J. Geophys. Res. Planets 2011, 116, E00G12. [Google Scholar] [CrossRef]
- Zanetti, M.; Hiesinger, H.; van der Bogert, C.H.; Reiss, D.; Jolliff, B.L. Aristarchus crater: Mapping of impact melt and absolute age determination. In Proceedings of the 42nd Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 7–10 March 2011. [Google Scholar]
- Fortezzo, C.; Spudis, P.; Harrel, S.L. Release of the digital unified global geologic map of the Moon at 1: 5,000,000-Scale. In Proceedings of the 51st Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2020. [Google Scholar]
- Yue, Z.; Yang, M.; Jia, M.; Michael, G.; Di, K.; Gou, S.; Liu, J. Refined model age for Orientale Basin derived from zonal crater dating of its ejecta. Icarus 2020, 346, 113804. [Google Scholar] [CrossRef]
- Yue, Z.; Di, K.; Wan, W.; Liu, Z.; Gou, S.; Liu, B.; Peng, M.; Wang, Y.; Jia, M.; Liu, J. Updated lunar cratering chronology model with the radiometric age of Chang’e-5 samples. Nat. Astron. 2022, 6, 541–545. [Google Scholar] [CrossRef]
- Jolliff, B.L.; Gillis, J.J.; Haskin, L.A.; Korotev, R.L.; Wieczorek, M.A. Major lunar crustal terranes: Surface expressions and crust-mantle origins. J. Geophys. Res. Planets 2000, 105, 4197–4216. [Google Scholar] [CrossRef]
- Garrick-Bethell, I.; Zuber, M.T. Elliptical structure of the lunar South Pole-Aitken basin. Icarus 2009, 204, 399–408. [Google Scholar] [CrossRef]
- Neukum, G.; Ivanov, B.A.; Hartmann, W.K. Cratering records in the inner solar system in relation to the lunar reference system. In Proceedings of the Chronology and Evolution of Mars: Proceedings of an ISSI Workshop, Bern, Switzerland, 10–14 April 2000. [Google Scholar]
- McGetchin, T.R.; Settle, M.; Head, J.W. Radial thickness variation in impact crater ejecta: Implications for lunar basin deposits. Earth Planet. Sci. Lett. 1973, 20, 226–236. [Google Scholar] [CrossRef]
- Ohtake, M.; Uemoto, K.; Yokota, Y.; Morota, T.; Yamamoto, S.; Nakamura, R.; Haruyama, J.; Iwata, T.; Matsunaga, T.; Ishihara, Y. Geologic structure generated by large-impact basin formation observed at the South Pole-Aitken basin on the Moon. Geophys. Res. Lett. 2014, 41, 2738–2745. [Google Scholar] [CrossRef]
- Marchi, S.; Mottola, S.; Cremonese, G.; Massironi, M.; Martellato, E. A new chronology for the Moon and Mercury. Astron. J. 2009, 137, 4936. [Google Scholar] [CrossRef]
- Ivanov, B.; Neukum, G.; Wagner, R. Impact craters, NEA, and Main Belt asteroids: Size-frequency distribution. In Proceedings of the Lunar and Planetary Science Conference, Johnson Space Center, Houston, TX, USA, 4 March 1999. [Google Scholar]
- Head III, J.W.; Fassett, C.I.; Kadish, S.J.; Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E. Global distribution of large lunar craters: Implications for resurfacing and impactor populations. Science 2010, 329, 1504–1507. [Google Scholar] [CrossRef]
- Richardson, J.E. Cratering saturation and equilibrium: A new model looks at an old problem. Icarus 2009, 204, 697–715. [Google Scholar] [CrossRef]
- Soderblom, J.M.; Evans, A.J.; Johnson, B.C.; Melosh, H.J.; Miljković, K.; Phillips, R.J.; Andrews-Hanna, J.C.; Bierson, C.J.; Head, J.W.; Milbury, C. The fractured Moon: Production and saturation of porosity in the lunar highlands from impact cratering. Geophys. Res. Lett. 2015, 42, 6939–6944. [Google Scholar] [CrossRef]
- Marchi, S.; Bottke, W.F.; Kring, D.A.; Morbidelli, A. The onset of the lunar cataclysm as recorded in its ancient crater populations. Earth Planet. Sci. Lett. 2012, 325, 27–38. [Google Scholar] [CrossRef]
- Planetary and Space Science Centre. Earth Impact Database. Available online: http://passc.net/EarthImpactDatabase/New%20website_05-2018/Index.html (accessed on 2 May 2023).
- Craddock, R.A.; Howard, A.D. Simulated degradation of lunar impact craters and a new method for age dating farside mare deposits. J. Geophys. Res. Planets 2000, 105, 20387–20401. [Google Scholar] [CrossRef]
- Fassett, C.I.; Thomson, B.J. Crater degradation on the lunar maria: Topographic diffusion and the rate of erosion on the Moon. J. Geophys. Res. Planets 2014, 119, 2255–2271. [Google Scholar] [CrossRef]
- Ivanov, B.; Neukum, G.; Wagner, R. Size-frequency distributions of planetary impact craters and asteroids. In Collisional Processes in the Solar System; Springer: Berlin/Heidelberg, Germany, 2001; pp. 1–34. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).