Abstract
An important research direction in the field of traffic light recognition of autonomous systems is to accurately obtain the region of interest (ROI) of the image through the multi-sensor assisted method. Dynamic evaluation of the performance of the multi-sensor (GNSS, IMU, and odometer) fusion positioning system to obtain the optimum size of the ROI is essential for further improvement of recognition accuracy. In this paper, we propose a dynamic estimation adjustment (DEA) model construction method to optimize the ROI. First, according to the residual variance of the integrated navigation system and the vehicle velocity, we divide the innovation into an approximate Gaussian fitting region (AGFR) and a Gaussian convergence region (GCR) and estimate them using variational Bayesian gated recurrent unit (VBGRU) networks and a Gaussian mixture model (GMM), respectively, to obtain the GNSS measurement uncertainty. Then, the relationship between the GNSS measurement uncertainty and the multi-sensor aided ROI acquisition error is deduced and analyzed in detail. Further, we build a dynamic estimation adjustment model to convert the innovation of the multi-sensor integrated navigation system into the optimal ROI size of the traffic lights online. Finally, we use the YOLOv4 model to detect and recognize the traffic lights in the ROI. Based on laboratory simulation and real road tests, we verify the performance of the DEA model. The experimental results show that the proposed algorithm is more suitable for the application of autonomous vehicles in complex urban road scenarios than the existing achievements.
1. Introduction
Environment and self-state perception, path planning and decision, and trajectory tracking and control are three important components of the autonomous drive system [1]. In the perception module, the different measuring principles among the various sensors determine that they have excellent complementarities [2]. Therefore, multi-sensor data fusion is one of the key technologies of autonomous driving perception systems [3,4] and is also an important research direction. Based on the sensing data of the road environment, position, and attitude obtained with the perception module, the autonomous vehicle plans its path with high-precision maps [5] and implements trajectory tracking and control by sending throttle, braking, and direction control commands to the linear control chassis [6].
Intelligent recognition of traffic lights has always been an indispensable function of autonomous driving vehicles [7]. Compared with the communication-based V2I [8], the vision-based recognition scheme has the incomparable unique advantages of low cost, autonomy, security, and other aspects. At the same time, vision-based recognition schemes are vulnerable to interference from weather, lighting conditions, external light sources, and other factors, and there are still huge technical challenges [9,10].
The traditional machine vision algorithms, such as AdaBoost and SVM, have the advantage of high efficiency, but the precision of object recognition is relatively low, which is difficult to meet the requirements. Since deep learning was proposed, it has made rapid progress [11], especially with the breakthrough made by AlexNet [12], in the ILSVRC challenge [13]; VGGNet [14], GoogleNet [15], and ResNet [16] have been proposed and applied. Yann LeCun [17] applied multi-scale CNN to recognize traffic lights for the first time in 2011, and its accuracy rate exceeded the human level, which caused widespread concern at that time. Subsequently, with the introduction and application of Faster-CNN [18] and YOLO [19], the recognition accuracy was further improved [20]. However, there is still a big gap between the accuracy of the deep learning algorithm and the actual application in autonomous vehicles. At the same time, the above models still have some deficiencies in real-time [21].
Under the influence of a complex external environment, vision-based traffic signal recognition will become extremely difficult [22], so it is necessary to integrate traditional machine learning, deep learning, prior maps, and multi-sensor data fusion technologies to meet the application requirements [23,24]. It is important to emphasize that multi-sensor fusion positioning-assisted ROI acquisition is a significant method to improve recognition accuracy [25]. Moreover, the smaller the size of the ROI, the greater the improvement of recognition accuracy. However, the reduction in the ROI size will increase the probability of object information loss. Therefore, it is extremely important to obtain the optimal ROI size according to the accuracy of the multi-sensor fusion positioning system.
The complex urban road environment presents great technical challenges for traffic light recognition. However, the achievements are insufficient; therefore, a DEA model-based improved algorithm was proposed. The main contributions of this paper can be summarized as follows.
- By analyzing the distribution characteristics of the odometer/GNSS residual sequence, we propose an approximate Gaussian estimation (AGE) method.
- Based on AGE, we integrate the VBGRU and GMM and propose an online measurement uncertainty calculation method for the multi-sensor fusion positioning system.
- Based on the above two contributions, a DEA model was built to realize the conversion of dynamic uncertainty to the optimal ROI size and further improve the accuracy of the multi-sensor assisted traffic light recognition algorithm.
In the second section, we will introduce the relevant work. In the third section, we will deduce the AGE and GNSS measurement uncertainty principle and introduce the DEA model construction method in detail. In the fourth section, the schemes of the simulation test and urban road test will be introduced, and the advantages of our algorithm will be discussed according to the test results. Finally, we summarize the conclusions of this paper in the fifth section.
2. Related Works
The deep learning network has shown excellent performance in image recognition. By combining it with prior map-assisted ROI acquisition, the accuracy has been greatly improved. Based on the proposed AGE method, this paper constructs a DEA model to optimize the ROI and further improve the accuracy of traffic light recognition in complex environments. Therefore, we will introduce the relevant work from three aspects: deep learning, prior map, and GNSS measurement uncertainty.
2.1. Deep Learning-Based Traffic Light Recognition
In consideration of the superior performance of deep learning in image recognition, it is increasingly used in traffic light recognition research. Weber [26] improved the AlexNet network and further proposed a Deep Traffic Light Recognition (DeepTLR) network, which achieved a significant improvement in performance compared to manual feature schemes. Taking advantage of the simplicity and efficiency of the AlexNet model, Feng Gao [27] combined deep learning with traditional machine vision and proposed a traffic light recognition scheme based on a hybrid strategy. The two-step deep learning models have great advantages in small object recognition. Therefore, Kim [28] and Hyun-Koo [29] designed recognition schemes based on the Faster-RCNN model. Moreover, by comparing the accuracy of multiple deep learning models in six color spaces, the latter concluded that the combination of Faster R-CNN and Inception-Resnet-v2 is superior to other schemes.
Compared with two-stage deep learning algorithms, one-stage algorithms, such as SSD and YOLO, have significant advantages in computing efficiency and are more suitable for scenarios with limited computing resources and high real-time requirements, such as autonomous vehicles. Behrendt [30] proposed a traffic light recognition and tracking algorithm based on YOLO, which combined a stereo camera and vehicle odometer. The detection speed of an image with a resolution of 1280 × 720 reached 10 frames per second. In addition, based on YOLO, Wang [31] proposed a solution that combined high/low exposure dual-channel architecture, which is very suitable for the autonomous driving systems in a highly dynamic environment. In the practical application of image recognition, the high loss of small objects is the defect of the one-stage deep learning algorithm. By improving the defects of the SSD model in the small target recognition, Julian [32] proposed Traffic Light-SSD (TL-SSD). Meanwhile, Ouyang [33] designed a traffic light detector based on lightweight CNN and fused it with the heuristic ROI detector. In addition, by combining CNN with traditional machine vision, Saini [34] also implemented a novel recognition scheme.
It should be emphasized that most of the above research results are based on general lighting environments and ordinary road conditions. However, there are a lot of extreme lighting, severe weather, and complex roads in the application, and the performance of the traditional algorithms is largely restricted. In complex scenarios, the acquisition and dynamic optimization of the ROI are important research directions in the field of traffic light recognition.
2.2. Prior Map-Based Traffic Light Recognition
The most important value of prior map assistance is that it can obtain the ROI in advance and greatly reduce the impact of environmental interference. Based on the unmanned vehicle platform developed by Google, Fairfield [25] designed and implemented a priori map-assisted traffic light recognition scheme. First, a priori map is constructed using differential GPS, IMU, and LiDAR. Then, with the help of navigation data and prior knowledge, the system accurately obtains the relevant objects in the image. The road test results show that the accuracy of the scheme is up to 99%, and the recall rate is 62%. From the perspective of algorithm optimization, Levinson [10] analyzed the error mechanism of image recognition in the process of prior map matching, location, and recognition in detail, and proposed a fusion recognition scheme on this basis. The road test showed that, taking advantage of a priori map, the comprehensive accuracy of the traditional algorithm reached 94% in the intersection at morning, noon, and night. Although the accuracy of green and yellow lights is especially low, the false positive probability of the former is as high as 1.35%, which is still far from the actual requirements. In addition, in the traffic light recognition scheme assisted by a priori map, road slope is usually the key factor for the ROI acquisition. The performance of the algorithm can be further improved by modifying the slope parameters in the road model [35]. The above schemes usually rely on high-precision navigation equipment, while Barnes [36] proposed a scheme based on low-cost GPS and verified its effectiveness through road tests.
In the prior map-assisted traffic light recognition scheme, the deep learning algorithm has better development prospects than the traditional machine vision algorithm. Combining auxiliary ROI acquisition with CNN, John [9] proposed two traffic light recognition schemes by analyzing the characteristics of the two typical scenes of day and night. In the prior map assistance scheme proposed by Posatti [37], relevant traffic lights are obtained according to vehicle control commands, which effectively improves the recognition accuracy of the latest deep learning model. In addition, Li [23] combined deep learning with ROI detection and proposed an improved recognition scheme based on multi-sensor data assistance.
Undoubtedly, the accurate acquisition of the ROI is the key factor to improve recognition accuracy. Based on Multi-sensor Data Fusion-AlexNet (MSDF-AlexNet), Li [38] improved the ROI accuracy by building an adaptive dynamic adjust (ADA) model and proposed an innovative algorithm. The ADA model divides the urban road environment into three modes, RTK, accuracy degradation, and navigation interruption, and adjusts the optimal size of the ROI through empirical values. Therefore, the main disadvantage of the ADA model is that the accuracy of the GNSS measurement error estimation is insufficient. Measurement uncertainty is an effective method to evaluate sensor error. In the next section, this paper will introduce the research progress of the measurement uncertainty of GNSS in detail.
2.3. Measurement Uncertainty of GNSS
The measurement uncertainty originated from the theory of uncertainty relationship proposed by German physicist Heisenberg in quantum mechanics in 1927. In 1963, the National Bureau of Standards (NBS) of the United States proposed a quantitative representation of uncertainty. To further unify the expression method and specification of measurement uncertainty, the Conference International des Poids et Mesures (CIPM) organized seven international organizations in different fields to jointly draft a guidance document on measurement uncertainty in 1986 and formally issued the Guide to the expression of Uncertainty in Measurement (GUM) in 1993 [39]. According to the definition of the GUM, the evaluation methods of measurement uncertainty are mainly divided into two types: (1) Class A Method for Evaluating Random Errors by Probability and Statistics; and (2) Class B method for non-random error evaluation.
In the research of multi-sensor fusion localization algorithms, measurement uncertainty is often used to estimate the GNSS noise model. GNSS measurement uncertainty is affected by the receiver’s working state, signal quality, external environment, and other factors. Therefore, Zhao [40] divided uncertainty into deterministic components and random components and proposed an optimal linear fusion algorithm based on the dynamic measurement uncertainty theory. On this basis, Wei [41] used the dynamic measurement uncertainty theory to model the observation data, analyzed the observation noise through the monitoring coefficient and variation, and finally realized the improved integrated navigation algorithm using the FKF filter. LEE [42] analyzed the characteristics of the GNSS noise using the uncertainty theory and quantized seven factors affecting the quality of the GNSS signal through three parameters, which effectively improved the accuracy of the GNSS observation noise model. Moreover, the experimental results show that the accurate noise model is helpful to improve the precision of the GNSS.
It is an important research field of integrated navigation algorithms based on the uncertainty theory to obtain filter noise matrix parameters according to innovation estimation. Based on the online estimation of the system noise covariance Q and observation noise covariance, Cui [43] proposed an improved unscented Kalman filter algorithm, which effectively improved the accuracy of the integrated navigation system. Furthermore, to optimize the problem that the system uncertainty has a great impact on the accuracy of the vehicle navigation system, Xing [44] proposed an integrated navigation algorithm based on the fuzzy Innovation Adaptive Estimation-UKF (IAE-UKF) filter by using the innovation adaptive estimation method to adjust the current measurement noise variance online.
The complex and changeable urban road environment has a great impact on the performance of the GNSS. When autonomous vehicles are driving on urban roads, high buildings, overpasses, dense tree crowns, tunnels, and other GNSS-denied environments [45,46] lead to the decline in GNSS accuracy or even failure to work normally. From the perspective of measurement uncertainty, the above research achievements proposed a variety of algorithm optimization methods to improve the performance of integrated navigation systems. At the same time, we can also draw an important conclusion that measurement uncertainty is an important parameter to evaluate the performance of the GNSS in a dynamic environment.
The statistical characteristic of GNSS errors is very important for prior map-aided ROI acquisition. The ADA model based on empirical values is difficult to accurately estimate the uncertainty of the GNSS measurement. Based on the above achievements, we propose an optimal ROI acquisition method in complex environments based on measurement uncertainty in this paper. The main contribution of this scheme is that a new AGE method composed of the VBGRU and GMM is used to estimate the GNSS/IMU/odometer integrated navigation system.
By summarizing the above contents, Table 1 classifies the main existing methods and shows the innovativeness of the proposed methods through comparison.

Table 1.
Classification and comparison of existing achievements.
3. Improved Traffic Light Recognition Scheme Based on the DEA Model
In this paper, the ROI acquisition method was optimized and improved through the DEA model. The scheme principle will be introduced in detail below.
3.1. Principle of AGE
Innovation-based noise estimation is an effective method for optimizing integrated navigation filters. The innovation, represented by , is shown in Equation (1).
where and are the system observations measured and estimated at time , respectively; and , , , and are the observation matrix, state vector, state vector estimation, and measurement noise sequence of the system at time , respectively. It can be observed from Equation (1) that the innovation contains the error of one-step prediction, which can be used to estimate the system noise covariance matrix and the observation noise covariance matrix. If the measurement error of one sensor is relatively small, the residual error can be used to approximate the dynamic uncertainty of the other related sensor.
In the GNSS-denied environments, such as multipath effect, signal occlusion, and electromagnetic interference, the performance of the receiver will be greatly reduced [47]. Compared with the GNSS, the measurement data output by the odometer after online correction is more stable and reliable. Therefore, this paper proposed a method to calculate the dynamic uncertainty based on the GNSS/odometer velocity residuals.
3.1.1. Dynamic Uncertainty Based on the GNSS/Odometer Velocity Residual
The east and north velocity errors of the GNSS were expressed as and , respectively, and the noise model conforms to the Gaussian distribution, expressed as and . Assuming that and obey independent distribution, can be expressed as a two-dimensional Gaussian model, as shown in Equation (2).
where , , , and are the expectation and variance of velocity error, respectively; and is the noise covariance matrix. Due to the odometer outputs and the ground speed, the GNSS ground speed was expressed as Equation (3) on the basis of ignoring the vertical speed of the autonomous vehicle.
where and are the true value and error of the speed output by the odometer, respectively.
3.1.2. Approximate Gaussian Distribution of the GNSS Velocity Error Sequence
When , Equation (3) can be expressed as Equation (4).
where and conform to the Gaussian distribution . The probability density function (PDF) of the velocity residual sequence is a Rayleigh distribution. When , Equation (3) can be approximately expressed as Equation (5).
It can be observed from Equation (5) that the PDF of the velocity residual sequence can be approximated to a GMM. However, in the complex urban road environment with low speed and GNSS denied, the velocity of the autonomous vehicle is generally between the above two conditions, which can be expressed as Equation (6).
In Equation (6), the first two terms and the last term conform to the Gaussian distribution, while the third term is the weighted chi-square distribution. The PDF of can be expressed as shown in Equation (7).
3.1.3. Simulation Analysis of the Approximate Gaussian Distribution
From the above theoretical derivation, an important conclusion can be drawn. When the driving speed of an autonomous vehicle increases from 0 m/s to , the PDF of the innovation gradually evolves from a Rayleigh distribution to an approximate Gaussian distribution. Next, the conclusion was validated through a simulation experiment.
First, from (0 m/s, 0.05 m/s) to (20 m/s, 30 m/s), 24 sets of velocity parameters were simulated as shown in Table 2. Then, by setting the RMSE parameters of and to 0.3 m/s and generating Gaussian noise sequences with a length of 1000, 24 sets of velocity error sequences can be obtained. Furthermore, using Equation (8), the ground velocity () and its error sequence with a length of 1000 can be calculated. The PDF of 24 sets of error sequences is shown in Figure 1. It can be observed from Figure 1 that, as the speed gradually increases, the PDF of the error sequences gradually evolves from a Rayleigh distribution to an approximate Gaussian distribution.

Table 2.
East and north velocity parameters (m/s).
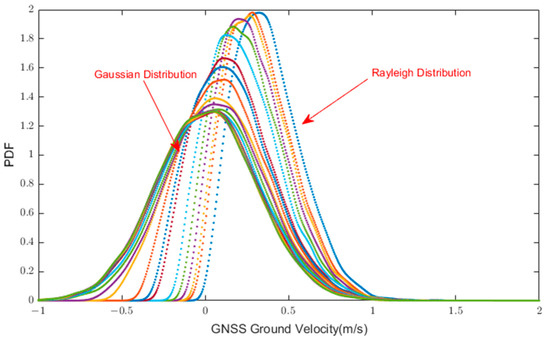
Figure 1.
Evolution diagram of the PDF of the error sequences.
3.2. AGE Scheme Design
3.2.1. Overall Design of the AGE Scheme
In order to analyze the distribution characteristics of the error sequences in more detail, the motion data from 0 to 6.7 m/s were simulated, and multiple sets of GNSS velocity measurement data were obtained by setting different error parameters. The specific process is as follows. First, with increments of (0.01 m/s, 0.005 m/s), a two-dimensional velocity parameter array with a length of 601 from (0, 0) to (6 m/s, 3 m/s) can be simulated. Meanwhile, the true velocity output by the GNSS receiver can be obtained. Then, with increments of 0.1 m/s, nine sets of the GNSS velocity RMSE parameter sequences () from 0.1 m/s to 0.9 m/s can be obtained. Further, expanding each group of the data in and into a two-dimensional array () produces the Gaussian distribution sequence (). Meanwhile, Equations (8) and (9) can be used to calculate the sequence of the ground velocity errors and variance , respectively. After estimation and correction by the integrated navigation system, the odometer measurement error can be ignored relative to the GNSS; therefore, was approximated as the GNSS/odometer velocity residual variance.
As the speed increases, the calculated noise variance will gradually converge to the noise variance set by the simulation test. By selecting a convergence point from each curve, a convergence function can be fitted. Based on , the curve can be divided into two regions: the point satisfying the condition of is the approximate Gaussian fitting region (AGFR), and the point satisfying the condition of is the Gaussian convergence region (GCR). The noise variance curve and the segmentation of the AGFR and the GCR are shown in Figure 2.
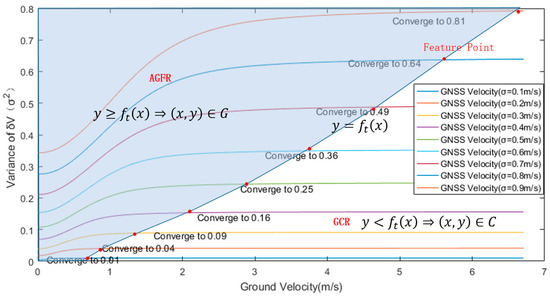
Figure 2.
The noise variance curve and the segmentation of the AGFR and GCR.
In Figure 2, the X-axis represents the ground speed of the autonomous vehicle, the Y-axis represents the variance of the GNSS/odometer residuals sequence, and each curve represents the relationship between the residuals variance and speed corresponding to a specific GNSS RMSE value. In the AGFR shown in the figure, the functional relationship corresponding to each curve has obvious nonlinear characteristics, which is suitable for deep learning models to estimate it. By analyzing the relationship between , , and , a VBGRU model was constructed to estimate the uncertainty of the GNSS measurement, which takes and as inputs to estimate . In the GCR, the residual variance gradually converges to the set GNSS variance, indicating that the residual sequence can already be approximated as a Gaussian distribution. Therefore, a mixed Gaussian model can be used to solve measurement uncertainty. Corresponding to the above two regions, different algorithms were used to estimate the uncertainty.
3.2.2. Uncertainty Estimation Method in the AGFR
In the AGFR, each nonlinear function curve corresponds to a determined RMSE parameter. Its essence is the relationship between the ground velocity residual variance and the speed growth under the different GNSS speed errors. Therefore, the output result corresponding to each group of data is not only related to the current value but also has an implicit relationship with the previous and subsequent data. In this paper, a VBGRU model was used to realize the estimation of the GNSS uncertainty in the AGFR.
The Recurrent Neural Network (RNN) is a commonly used sequential data processing model, which has the characteristics of memory and parameter sharing and has unique advantages for nonlinear sequential data feature learning [48]. The Long Short-term Memory (LSTM) network is an improved RNN. While inheriting the advantages of a chain network, it adds forgetting and memory mechanisms and combines short-term memory with long-term memory through the smart network structure design and optimal control of input, forgetting, and output gate. To a certain extent, it solves the problem of gradient disappearance and gradient explosion of the traditional RNN networks. Based on this, Jun [49] put forward an important improved LSTM network in 2014 and named it GRU. Its main feature is to combine the forgetting and input gate into the update gate, which realizes the prediction and estimation of parameters through the update and reset gate, greatly reducing the complexity of the model and improving the actual use effect. The VBGRU network [50] combines the Variable Bayesian Reference and GRU, introduces the uncertainty weight value into the model training process, and represents the model parameters through the normally distributed random variables, which greatly improves the adaptability and generalization of the model. The principle of VBI is shown in Figure 3. Different from the traditional GRU network, the weight parameters of the variable Bayesian GRU are not composed of determined values but are fitted to the nonlinear function through the random variables of the probability density distribution. More importantly, when it outputs the predicted value, it can also calculate its uncertainty, which is a maximum posteriori estimation method.
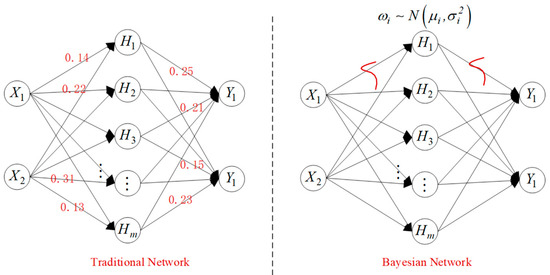
Figure 3.
Bayesian network schematic diagram.
3.2.3. Parameter Estimation Method in the GCR
In the GCR, the probability distribution function of the innovation is approximated to the Gaussian distribution as shown in Equation (5). Therefore, the GMM was used to realize the uncertainty estimation of the GNSS. The GMM decomposes a PDF into the overlap of several Gaussian functions. The variables of the function can be either one-dimensional or multidimensional, which can be expressed as Equation (10).
where represents a multidimensional Gaussian function, and is the normalization coefficient. The velocity residual expression in the GCR is shown in Equation (5), and the three noise sequences are all one-dimensional Gaussian distributions. By estimating the maximum likelihood of Equation (10), the GMM maximum likelihood function can be obtained as shown in Equation (11) and take the logarithm of both sides simultaneously to further obtain Equation (12).
where is the PDF of the Gaussian distribution. The Expectation Maximization (EM) algorithm was used to solve Equation (12) iteratively. First, based on Jensen inequality, the implicit variable expectation was calculated according to the current model parameter , and the lower bound of the likelihood function was obtained. Then, the model parameters were adjusted, and the lower bound was maximized to obtain a new parameter . The above two processes are iteratively calculated until the set convergence condition is satisfied. The calculation process of steps E and M are shown in Equations (13) and (14), respectively.
Equation (13) takes the partial derivative of and makes it equal to 0, and the estimation parameters , , and can be obtained, where is the measurement uncertainty of the GNSS.
3.3. DEA Model Construction
In a complex urban environment, the accuracy of the multi-sensor fusion positioning system changes dynamically. In the previous section, an estimation method of measurement uncertainty for the GNSS was proposed based on AGE. On this basis, a DEA model was constructed. Through joint calibration of sensors, GNSS, IMU, and the camera can be time and space unified. Then, using the position of the traffic light in the prior map, the corresponding pixel coordinate in the image [38] can be obtained. Meanwhile, the measurement uncertainty of the GNSS can be calculated based on AGE and further converted into ROI uncertainty through a model. The conversion model from measurement uncertainty to ROI error is shown in Equation (15). With Equation (15), the uncertainty of the ROI in the pixel coordinate system can be calculated.
where is the measurement uncertainty of the ROI in the pixel coordinate system; and are the measurement uncertainty in the ECEF coordinate system and camera coordinate system calculated with AGE, respectively; is the attitude transformation matrix from the ECEF coordinate system to the navigation coordinate system, as shown in (16); and is the attitude transformation matrix from the navigation coordinate system to the camera coordinate system, as shown in (17).
In Equations (16) and (17), and are the longitude and latitude of the autonomous vehicle, respectively, and , , and are pitch angle, roll angle, and heading angle, respectively.
3.4. Overall Scheme Design
With the help of multi-sensor data fusion, the ROI can be obtained and optimized, and then the YOLOv4 model was used to recognize the traffic lights. The algorithm scheme is shown in Figure 4.
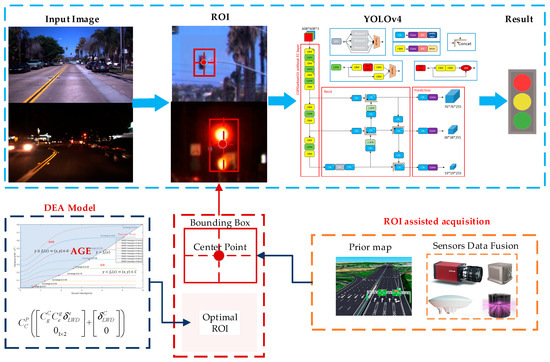
Figure 4.
Framework of the algorithm.
In Figure 4, the ROI acquisition algorithm was further improved and optimized. First, the multi-sensor assisted and a priori map were used to obtain the ROI, and its center point and boundary box were calculated. Then, a DEA model was built based on AGE to solve the measurement uncertainty online. Further, the sensor measurement uncertainty was converted into the ROI uncertainty area, and finally, the optimal ROI acquisition was achieved.
4. Experimental Verifications and Results
In this section, the DEA model was tested and verified based on the simulation data generated by the MATLAB platform first, and then the road tests were conducted on the autonomous driving platform developed by the National Engineering Laboratory for Integrated Command and Dispatch Technology (ICDT).
4.1. DEA Model Testing and Results
In this paper, the VBGRU and GMM were used to estimate the GNSS measurement uncertainty in the AGFR and GCR, respectively, and the performance of the GMM has been fully verified. Therefore, this paper mainly tested and evaluated the estimation accuracy of the VBGRU for the AGFR data. First, according to the method described in Section 3.2.1, the sample data for training and testing the VBGRU network model were simulated. At intervals of 0.05 m/s, 20 sets of the GNSS velocity RMES parameters between 0.05 m/s and 1 m/s can be obtained. At the same time, using 601 sets of velocity parameters , 12,020 sets of sample data can be obtained.
Nvidia DGX-1 was used as the training platform of the VBGRU model in this paper, which included four pieces of Tesla-V100-16G GPUs, two pieces of Intel Xeon Platinum 3.1 GHz processors, and 30 TB NVMe SSD storage space. On the Ubuntu 20.04 operating system platform, the VBGRU model was trained and tested based on the Python deep learning framework. Among the 12,020 sets of simulation data mentioned above, 9670 sets were used for the VBGRU model training, and the input and output parameters were and . In addition, 2350 sets of simulation data were used for the VBGRU model testing, and the actual estimation error and performance analysis of the model are shown in Figure 5a,b, respectively.
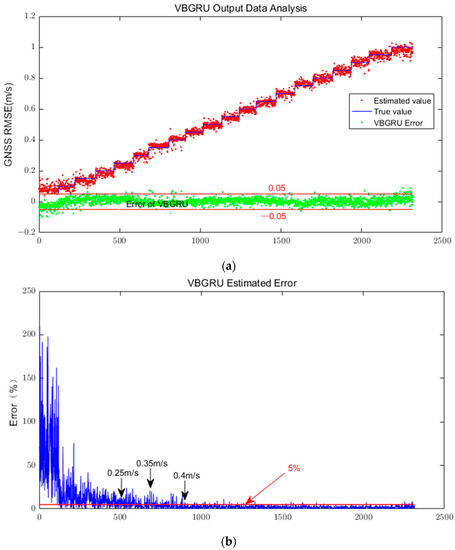
Figure 5.
The analysis chart of the VBGRU network estimation results. (a) Estimation error of the VBGRU network. (b) Error and truth ratio of the VBGRU network.
In Figure 5a, the X-axis represents 2350 sets of the VBGRU model test data, and the Y-axis represents the estimated value output from the model (RMSE of GNSS velocity). The blue stepped line represents the true value of RMSE, the red points represent the estimated value of the model, and the green points represent the difference between the red points and the blue line, which are the estimation errors of the model. Meanwhile, it can be observed that, in the process of increasing the RMSE of the GNSS from 0.05 m/s to 1 m/s, over 99% of the estimated values output by the VBGRU model have an error of less than 0.05 m/s. Obviously, the magnitude of the estimation error of the VBGRU model (0.05 m/s) is basically consistent with the GNSS velocity measurement error in the RTK state, which is significantly smaller than the error in the GNSS rejection environment (greater than 0.5 m/s) that this paper focuses on.
In Figure 5b, the X-axis also represents 2350 sets of test data, while the Y-axis represents the ratio between the estimation errors of the model and the true value. As described in Section 3.2.1, the RMSE value in the simulation data gradually increases from 0.05 m/s to 1 m/s. As shown in the figure, as the RMSE value gradually increases, the ratio of the error to the true value rapidly decreases. The figure shows the estimation errors corresponding to the RMSE parameters of 0.25 m/s, 0.35 m/s, and 0.4 m/s. It should be emphasized that, when the RMSE parameter value is greater than 0.4 m/s, the ratio of estimation error to the true value of the model will remain within the range of less than 5%. In the GNSS rejection scenario that this paper focuses on, the RMSE of the velocity parameter is generally greater than 0.5 m/s.
Therefore, an important conclusion can be drawn that the estimation accuracy of the VBGRU model meets the requirements of the optimal ROI acquisition algorithm.
4.2. Actual Road Test and Results
Based on the autonomous driving platform form the National Engineering Laboratory for ICDT (Figure 6a), the night test of urban roads was conducted in the Haidian District, Beijing (the test route is shown in Figure 6b).
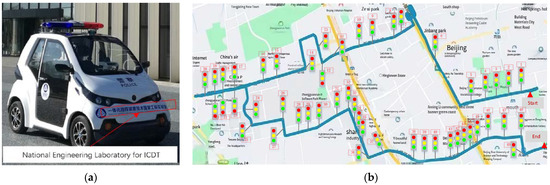
Figure 6.
Urban road test in the Haidian District, Beijing. (a) Autonomous driving platform. (b) Urban road test route map.
In Figure 6b, the road test route starts from the north gate of the Zhongguancun Dongsheng Science and Technology Park and ends at its south gate with a total length of 22.6 km, including 49 groups of traffic lights (13 groups of “straight + left” and 36 groups of “straight”), and 4599 image samples are collected. The test road passes through the auxiliary road of Beijing-Lhasa Expressway (G6), Tangjialing Road, Houchangcun Road, Xinxi Road, and Xiaoying East Road, including the GNSS-denied environments such as overpass, dense crown, and urban canyon. For ease of representation, 49 groups of traffic lights were numbered 1 to 49. A detailed description is shown in Table 3.

Table 3.
A detailed description of the traffic lights on the test route.
In the RTK road section, the existing achievements [38] can achieve excellent recognition accuracy through high-precision ROI acquisition, so the improvement effect of our algorithm is not obvious. However, in the GNSS rejection environment, the existing achievements have great room for improvement in recognition accuracy due to insufficient ROI acquisition accuracy. Figure 7 and Figure 8 show three typical GNSS rejection roads.
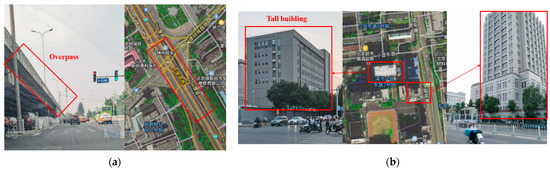
Figure 7.
GNSS rejection section (the overpass and tall buildings cause GNSS signal blocking and multipath effect). (a) Overpass on the G6 auxiliary road. (b) Tall building on the Houtun road.
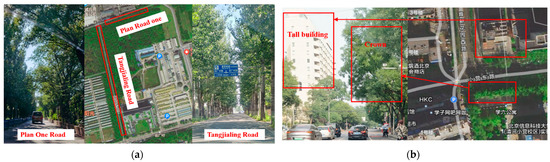
Figure 8.
GNSS rejection caused by the dense crown (the overpasses and tall buildings cause GNSS signal blocking and multipath effect). (a) Dense crown Plan One road and Tangjialing road. (b) Dense crown in Xiaoying East road.
In the above GNSS rejection test road segments, the corresponding traffic light numbers in Table 3 are 6, 14, 46, 48, and 49. The comparison and detailed analysis of the test results between the DEA and MSDA, YOLO are shown in Table 4.

Table 4.
Comparison of the recognition accuracy in the GNSS rejection road.
In Table 4, the symbol ‘√’ indicates that the traffic light recognition result is correct, while the symbol ‘×’ indicates that the result is incorrect. The above results do not include the missed detection rate. This is mainly considering that, in the scheme designed in this paper, the autonomous vehicles will only pass on traffic light sections when the recognition result is green, and missed detection will not affect the safety of the system. Meanwhile, it can be observed from Table 4 that the recognition accuracy of MSDA is significantly higher than that of YOLOv4 through multi-sensor assisted ROI acquisition. Further, DEA optimizes the ROI acquisition algorithm through GNSS measurement uncertainty and further improves the recognition accuracy. Typically, the recognition accuracy of MSDA for 13 # is as low as 80.15%, which is mainly due to the blocking of the GNSS signal caused by the dense crown of the Tangjialing road, which greatly reduces the ROI acquisition accuracy. The road test data were also analyzed according to the No. 1 to No. 49 listed in Table 3, as shown in Figure 9.
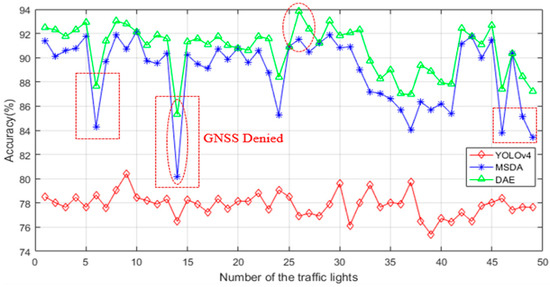
Figure 9.
Analysis of all traffic light recognition results.
In Figure 9, the X axis is the number of traffic lights, the Y axis is the recognition accuracy, and the three lines correspond to the YOLOv4, MSDA, and DAMM algorithms; the recognition accuracy achieved with the three algorithms is 77.79%, 88.65%, and 90.52%, respectively. Compared with YOLOv4, DEA achieved maximum improvement in the position of No. 26 by 17.69%. Meanwhile, in the GNSS rejection environment (rectangular box), the accuracy of MSDA and DEA is significantly reduced. However, the performance of the latter was improved to some extent by optimizing the ROI through the DEA model, as shown in No. 14, with a maximum increase of 5.14%.
5. Discussion
Visual-based traffic light recognition technology is one of the bottlenecks of the autonomous driving system in complex urban road scenarios. Current research shows that multi-sensor assisted ROI acquisition is an effective method to improve recognition accuracy, but there is still much room for improvement of the existing achievements. The smaller the size of the ROI, the greater the accuracy improvement of the image recognition algorithm. However, this also poses a risk of object information loss from the ROI. Therefore, it is important to accurately estimate the optimal ROI size based on the accuracy of sensor data. However, it is a difficult problem to accurately predict the uncertainty of the GNSS in the dynamic environment of urban roads.
To solve this problem, this paper presents a detailed theoretical analysis of the distribution of GNSS/odometer velocity residual data and proposes an AGE algorithm for the GNSS measurement uncertainty based on the VBGRU deep learning model. On this basis, this paper builds a DEA model by analyzing the relationship between the measurement uncertainty of the GNSS and the optimal size of the ROI, which can further optimize the ROI and improve the accuracy of traffic light recognition. The main contribution of this article is to propose a new ROI optimization algorithm, and through theoretical analysis, it can be concluded that this algorithm can achieve better recognition performance than existing achievements.
Based on the Nvidia DGX-1 hardware platform, this paper implements the DEA model and further utilizes MATLAB and the autonomous driving platform to simulate and test the performance of the algorithm, respectively. First, 12,020 sets of simulation data were generated based on MATLAB, 9670 of which were used for VBGRU model training and 2350 for model testing. The test results show that 99% of the estimation errors of the model are less than 0.05 m/s, and in the GNSS rejection environment, the ratio of the estimation error to the true value is less than 5%. Therefore, the estimation accuracy of the VBGRU model can meet the requirements of the scheme.
Furthermore, actual road tests were conducted in Haidian District, Beijing, and the improvement effect of the DEA model was verified by comparing it with the YOLOv4 and MSDA algorithms. The test results show that, in the RTK GNSS section, the recognition accuracy improvement of the DEA model compared to MSDA is not significant. However, in the GNSS rejection environment, the maximum improvement in recognition accuracy of the DEA model compared to YOLOv4 and MSDA reached 17.69% and 5.14%, respectively.
From the above discussion, the conclusion can be reached that the DEA model can dynamically optimize the size of the ROI according to the external environments and improve the accuracy of the multi-sensor fusion-assisted traffic light recognition algorithm in the complex environments. Although the algorithm proposed in this paper has made significant discoveries in ROI optimization, there are still some limitations. In the GNSS rejection environment, enlarging the ROI size by the AGE parameters can avoid the information loss of the objects, but the enlarged ROI cannot effectively suppress the impact of an extreme environment and bad weather on traffic light recognition, resulting in a decrease in accuracy. Therefore, we are researching the key technologies of multi-sensor fusion autonomous localization in GNSS rejection environments. This will have a positive effect on ROI-assisted acquisition and, thereby, effectively improve the performance of existing traffic signal recognition algorithms.
6. Conclusions
In this paper, a ROI optimization method based on the DEA model was proposed, which can effectively improve the recognition accuracy of traffic lights and help the application of the autonomous driving system on urban roads. The main innovations and contributions of this paper can be summarized as follows.
- According to the approximate Gaussian distribution of the odometer/GNSS residual sequence, an AGE method was proposed to estimate the measurement uncertainty of GNSS in complex environments.
- Based on the conversion relationship between multi-sensor data and the ROI, the estimation of AGE was converted into ROI uncertainty, and further, the DEA model was built.
- The DEA model was used to optimize the ROI online, and the experimental results show that the recognition accuracy of traffic lights was significantly improved.
Although the ROI optimization algorithm proposed in this paper improves the existing results to some extent, there is still a big gap between the actual requirements of the autonomous driving system in complex environments. In the field of vision-based traffic light recognition, the following research directions will have important theoretical value.
- Taking advantage of the complementarities between multiple optical spectra, the research on the infrared/visible light fusion recognition technology has good prospects.
- It is an excellent research direction to reduce the uncertainty of the navigation system and improve the ROI accuracy by combining the local positioning of the visual/LiDAR SLAM with the GNSS/odometer/IMU integrated navigation system.
- It is also an important research direction to combine classical machine vision with deep learning to improve its recognition accuracy in extreme light and severe weather.
Author Contributions
Conceptualization, Q.Z. and J.L.; methodology; software, Z.L.; validation, Z.L., Q.Z. and Y.L.; formal analysis, J.L.; investigation, resources, data curation.; writing—original draft preparation, writing—review and editing, Z.L.; visualization, Q.Z.; supervision, J.L.; project administration, J.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (No. 61533008, 61603181, 61673208, 61873125); National Key Research and Development Program of China (No. 2022YFC3004801); And The APC was funded by National Key Research and Development Program of China (No. 2022YFC3004801).
Data Availability Statement
Data sharing is not applicable to this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.; Li, Z. Key technology and application of intelligent connected patrol vehicles for security scenario. Telecommun. Sci. 2020, 36, 53–60. [Google Scholar]
- Muresan, M.P.; Giosan, I.; Nedevschi, S. Stabilization and Validation of 3D Object Position Using Multimodal Sensor Fusion and Semantic Segmentation. Sensors 2020, 20, 1110. [Google Scholar] [CrossRef] [PubMed]
- Nie, J.; Yan, J.; Yin, H.; Ren, L.; Meng, Q. A Multimodality Fusion Deep Neural Network and Safety Test Strategy for Intelligent Vehicles. IEEE Trans. Intell. Veh. 2021, 6, 310–322. [Google Scholar] [CrossRef]
- Jin, X.-B.; Yu, X.-H.; Su, T.-L.; Yang, D.-N.; Bai, Y.-T.; Kong, J.-L.; Wang, L. Distributed Deep Fusion Predictor for a Multi-Sensor System Based on Causality Entropy. Entropy 2021, 23, 219. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Cho, J.; Kim, D.; Huh, K. Intervention minimized semi-autonomous control using decoupled model predictive control. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 618–623. [Google Scholar] [CrossRef]
- Arikan, A.; Kayaduman, A.; Polat, S.; Simsek, Y.; Dikmen, I.C.; Bakir, H.G.; Karadag, T.; Abbasov, T. Control method simulation and application for autonomous vehicles. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Diaz, M.; Cerri, P.; Pirlo, G.; Ferrer, M.A.; Impedovo, D. A Survey on Traffic lights Detection. In International Conference on Image Analysis and Processing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 201–208. [Google Scholar]
- 3GPP. Study on Enhancement of 3GPP Support for 5G V2X Services: TR22.886, v.15.1.0; TSG: Valbonne, France, 2017. [Google Scholar]
- VJohn, V.; Yoneda, K.; Qi, B.; Liu, Z.; Mita, S. Traffic light recognition in varying illumination using deep learning and saliency map. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 2286–2291. [Google Scholar] [CrossRef]
- Levinson, J.; Askeland, J.; Dolson, J.; Thrun, S. Traffic lights mapping, localization, and state detection for autonomous vehicles. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 5784–5791. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural network. In Proceedings of the 25th International Conference on Neural Information Processing Systems—Volume 1 (NIPS’12); Curran Associates Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A.; Liu, W.; et al. Going deeper with convolutions. In Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sermanet, P.; LeCun, Y. Traffic sign recognition with multi-scale Convolutional Networks. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2809–2813. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, 6 June 2016; pp. 91–99. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv Preprint 2018, arXiv:1804. 02767. [Google Scholar]
- Jensen, M.B.; Philipsen, M.P.; Bahnsen, C.; Møgelmose, A.; Moeslund, T.B.; Trivedi, M.M. Traffic lights detection at night: Comparison of a learning-based detector and three model-based detectors. In Proceedings of the 11th Symposium on Visual Computing, Las Vegas, NV, USA, 14–16 December 2015; pp. 774–783. [Google Scholar]
- Hu, Q.; Paisitkriangkrai, S.; Shen, C.; van den Hengel, A.; Porikli, F. Fast detection of multiple objects in traffic scenes with a common detection framework. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1002–1014. [Google Scholar] [CrossRef]
- Symeonidis, G.; Groumpos, P.P.; Dermatas, E. Traffic Lights Detection in Adverse Conditions using Color, Symmetry and Spatiotemporal Information. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP), Rome, Italy, 24–26 February 2012. [Google Scholar]
- Li, Z.; Zeng, Q.; Zhang, S.; Liu, Y.; Liu, J. An image recognition algorithm based on multi-sensor data fusion assisted AlexNet model. J. Chin. Inert. Technol. 2020, 28, 219–225. [Google Scholar] [CrossRef]
- Wu, Y.; Geng, K.; Xue, P.; Yin, G.; Zhang, N.; Lin, Y. Traffic Lights Detection and Recognition Algorithm Based on Multi-feature Fusion. In Proceedings of the 2019 IEEE 4th International Conference on Image, Vision and Computing (ICIVC), Xiamen, China, 5–7 July 2019; pp. 427–432. [Google Scholar]
- Fairfield, N.; Urmson, C. Traffic light mapping and detection. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5421–5426. [Google Scholar]
- Weber, M.; Wolf, P.; Zollner, J.M. DeepTLR: A single deep convolutional network for detection and classification of traffic lights. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium, Gothenburg, Sweden, 19–22 June 2016; pp. 342–348. [Google Scholar] [CrossRef]
- Gao, F.; Wang, C. A hybrid strategy for traffic lights detection by combining classical and learning detectors. IET Intell. Transp. Syst. 2020, 14, 735–741. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H.; Hwangbo, M.; Choi, J.; Canny, J.; Kwon, Y.P. Deep Traffic lights Detection for Self-driving Cars from a Large-scale Dataset. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018; pp. 280–285. [Google Scholar]
- Kim, H.K.; Park, J.H.; Jung, H.Y. An Efficient Color Space for Deep-Learning Based Traffic lights Recognition. J. Adv. Transp. 2018, 2018, 2365414. [Google Scholar] [CrossRef]
- Behrendt, K.; Novak, L.; Botros, R. A Deep Learning Approach to Traffic Lights: Detection, Tracking, and Classification. In Proceedings of the International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar] [CrossRef]
- Wang, J.-G.; Zhou, L. Traffic lights Recognition with High Dynamic Range Imaging and Deep Learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1341–1352. [Google Scholar] [CrossRef]
- Müller, J.; Dietmayer, K. Detecting Traffic Lights by Single Shot Detection. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 266–273. [Google Scholar] [CrossRef]
- Ouyang, Z.; Niu, J.; Liu, Y. Deep CNN-Based Real-Time Traffic lights Detector for Self-Driving Vehicles. Ieee Trans. Mob. Comput. 2020, 19, 300–313. [Google Scholar] [CrossRef]
- Saini, S.; Nikhil, S.; Konda, K.R.; Bharadwaj, H.S.; Ganeshan, N. An efficient vision-based traffic lights detection and state recognition for autonomous vehicles. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 606–611. [Google Scholar] [CrossRef]
- Jang, C.; Cho, S.; Jeong, S.; Suhr, J.K.; Jung, H.G.; Sunwoo, M. Traffic light recognition exploiting map and localization at every stage. Expert Syst. Appl. 2017, 88, 290–304. [Google Scholar] [CrossRef]
- Barnes, D.; Maddern, W.; Posner, I. Exploiting 3D semantic scene priors for online traffic lights interpretation. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015; pp. 573–578. [Google Scholar] [CrossRef]
- Possatti, L.C.; Guidolini, R.; Cardoso, V.B.; Berriel, R.F.; Paixão, T.M.; Badue, C.; De Souza, A.F.; Oliveira-Santos, T. Traffic lights Recognition Using Deep Learning and Prior Maps for Autonomous Cars. arXiv Preprint 2019, arXiv:1906.11886v1. [Google Scholar] [CrossRef]
- Li, Z.; Zeng, Q.; Liu, Y.; Liu, J.; Li, L. An improved traffic lights recognition algorithm for autonomous driving in complex scenarios. Int. J. Distrib. Sens. Netw. 2021, 17, 155014772110183. [Google Scholar] [CrossRef]
- Guide to the Expression of Uncertainty in Measurement; International Organization for Standardization (ISO): Geneva, Switzerland, 1993.
- Zhao, Z.; Zhao, W. Optimal linear multi-sensor data fusion algorithm based on dynamic uncertainty theorty. Chin. J. Sci. Instrum. 2007, 28, 928–932. [Google Scholar]
- Wei, D.; Cao, L.; Han, X. Improved fading KF integrated navigation algorithm based on uncertainty. J. Navig. Position. 2021, 9, 73–82. [Google Scholar] [CrossRef]
- Lee, W.; Cho, H.; Hyeong, S.; Chung, W. Practical modeling of GNSS for autonomous vehicles in urban environments. Sensors 2019, 19, 4236. [Google Scholar] [CrossRef]
- Cui, D.; Wu, N.; Meng, F.-k. Unscented Kalman Filter based on Online Noise Estimation in Integrated Navigation. Commun. Technol. 2016, 49, 1306–1311. [Google Scholar] [CrossRef]
- Xing, D.-F.; Zhang, L.-J.; Yang, J.-H. Fuzzy IAE-UKF integrated navigation method introducing system uncertainty. Opt. Precis. Eng. 2021, 29, 172–182. [Google Scholar] [CrossRef]
- Meng, Q.; Hsu, L.-T. Integrity for Autonomous Vehicles and Towards a Novel Alert Limit Determination Method. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 996–1006. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, J.; Zeng, Q.; Feng, S.; Xu, R. Improved ARAIM fault modes determination scheme based on feedback structure with probability accumulation. GPS Solut. 2019, 23, 16. [Google Scholar] [CrossRef]
- Meng, Q.; Hsu, L.T. Integrity Monitoring for All-Source Navigation Enhanced by Kalman Filter based Solution Separation. IEEE Sens. J. 2020, 14, 15469–15484. [Google Scholar] [CrossRef]
- Tabas, S.S.; Samadi, S. Variational Bayesian Dropout with a Gaussian Prior for Recurrent Neural Networks Application in Rainfall–Runoff Modeling; IOP Publishing Ltd.: Bristol, UK, 2022. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. Eprint arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Jin, X.-B.; Gong, W.-T.; Kong, J.-L.; Bai, Y.-T.; Su, T.-L. A Variational Bayesian Deep Network with Data Self-Screening Layer for Massive Time-Series Data Forecasting. Entropy 2022, 24, 335. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).