A Redundant Measurement-Based Maximum Correntropy Extended Kalman Filter for the Noise Covariance Estimation in INS/GNSS Integration
Abstract
1. Introduction
- To make full use of the first- and second-order measurement statistics, the proposed method adopts the enhanced SOMD algorithm to estimate in real time. The RMCEKF is the first algorithm that combines the estimation of with observations only. Moreover, to get better numerical stability for the MCEKF, the matrix inverse operation is calculated by the Cholesky decomposition.
- To verify the effectiveness and performance of the RMCEKF, real road experiment data were used. The result showed that RMCEKF could achieve better estimation accuracy than the compared ones.
2. INS/GNSS Tightly Coupled Integration and EKF
2.1. Dynamic Model
2.2. Measurement Model
2.3. Navigation Filtering with the Standard EKF
3. Maximum Correntropy Extended Kalman Filter and Second Order Mutual Difference Method
3.1. Maximum Correntropy EKF
3.2. Limitations of MCEKF
3.3. Second Order Mutual Difference Algorithm for Estimation of Noise Variance
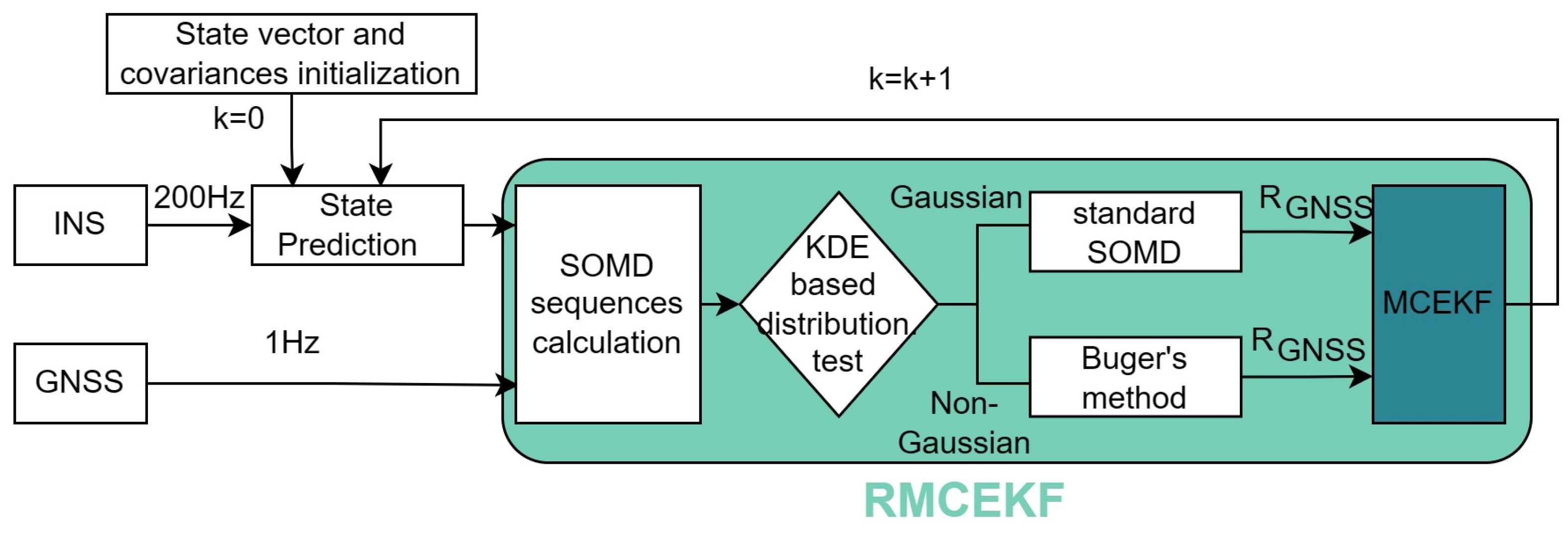
4. RMCEKF for the INS/GNSS Integration System
| Algorithm 1 The pseudocode of the RMCEKF. |
| Input: , , , , , . |
| Prediction: |
| 1. . |
| 2. . |
| Measurement update (when GNSS signal is available): |
| 1. Calculate the by (32)–(33). |
| 2. Gaussian distribution of test by KDE method [36]: |
| if |
| Calculate by (36). |
| Else |
| . |
| End |
| . |
| 3. , . |
| 4. , . |
| 5. . |
| 6. . |
| 7. |
| 8. if |
| go to 9. |
| Else |
| , go to 3. |
| End |
| 9. . |
| . |
| Outputs: , . |
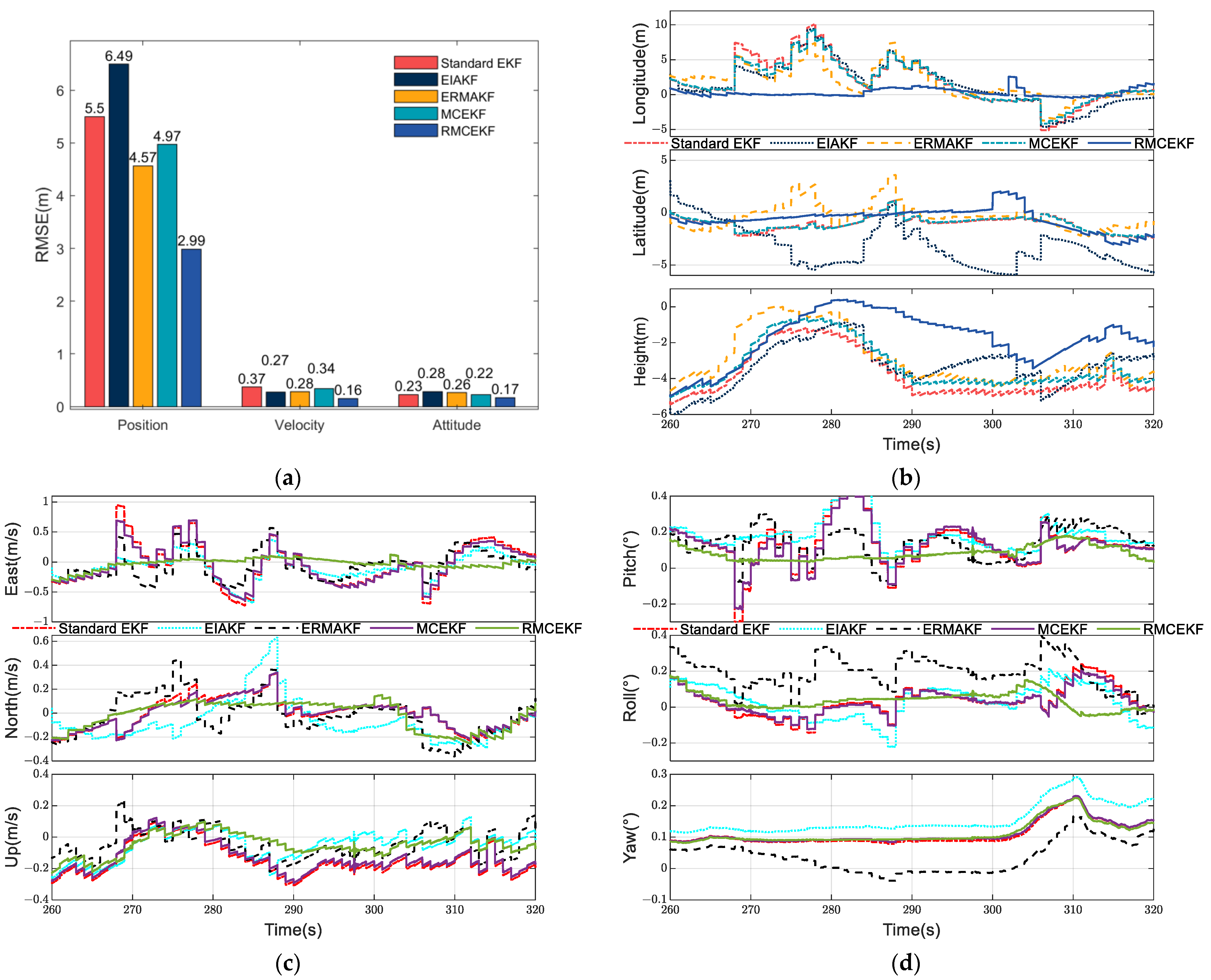
5. Experiment and Results
5.1. Estimation Accuracy Comparision in Foliage Environment
5.2. Estimation Accuracy Comparision in Dense Building Area
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Wu, W.; Zhang, S.; Wu, C.; Zhong, R. A GNSS/LiDAR/IMU Pose Estimation System Based on Collaborative Fusion of Factor Map and Filtering. Remote Sens. 2023, 15, 790. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, K.; Jiang, C.; Li, Z.; Yang, C.; Liu, D.; Zhang, H. Motion-Constrained GNSS/INS Integrated Navigation Method Based on BP Neural Network. Remote Sens. 2023, 15, 154. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Zhou, Q.; Che, H. An Adaptive Low-Cost INS/GNSS Tightly-Coupled Integration Architecture Based on Redundant Measurement Noise Covariance Estimation. Sensors 2017, 17, 2032. [Google Scholar] [CrossRef] [PubMed]
- Fang, W.; Jiang, J.; Lu, S.; Gong, Y.; Tao, Y.; Tang, Y.; Yan, P.; Luo, H.; Liu, J. A LSTM Algorithm Estimating Pseudo Measurements for Aiding INS during GNSS Signal Outages. Remote Sens. 2020, 12, 256. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Chan, C.; Li, B.; Song, X. Multi-sensor fusion methodology for enhanced land vehicle positioning. Inf. Fusion 2019, 46, 51–62. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Huang, Y.; Lu, Y.; Gao, L.; Xu, N.; Yu, Z. Estimation on IMU yaw misalignment by fusing information of automotive onboard sensors. Mech. Syst. Signal Process. 2022, 162, 107993. [Google Scholar] [CrossRef]
- Gao, L.; Xiong, L.; Xia, X.; Lu, Y.; Yu, Z.; Khajepour, A. Improved Vehicle Localization Using On-Board Sensors and Vehicle Lateral Velocity. IEEE Sens. J. 2022, 22, 6818–6831. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House: London, UK, 2008; pp. 363–387. [Google Scholar]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip AngleEstimation Based on Consensus Kalman Filter. IEEE Trans. Control. Syst. Technol. 2022, 31, 179–192. [Google Scholar] [CrossRef]
- Xiong, L.; Xia, X.; Lu, Y.; Liu, W.; Gao, L.; Song, S.; Yu, Z. IMU-based automated vehicle body sideslip angle and attitude estimation aided by GNSS using parallel adaptive Kalman filters. IEEE Trans. Veh. Technol. 2020, 69, 10668–10680. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Duník, J.; Biswas, S.K.; Dempster, A.G.; Pany, T.; Closas, P. State estimation methods in navigation: Overview and application. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 16–31. [Google Scholar] [CrossRef]
- Khodaparast, J. A Review of Dynamic Phasor Estimation by Non-Linear Kalman Filters. IEEE Access 2022, 10, 11090–11109. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 381–394. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE. 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature kalman filters. IEEE Trans. Autom. Control. 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, H. Student’s t-Kernel-Based Maximum Correntropy Kalman Filter. Sensors 2022, 22, 1683. [Google Scholar] [CrossRef]
- Shongwe, T.; Vinck, A.J.H.; Ferreira, H.C. A Study on Impulse Noise and Its Models. SAIEE Afr. Res. J. 2015, 106, 119–131. [Google Scholar] [CrossRef]
- Middleton, D. Non-Gaussian noise models in signal processing for telecommunications: New methods and results for class A and class B noise models. IEEE Trans. Inf. Theory 1999, 45, 1129–1149. [Google Scholar] [CrossRef]
- Ndo, G.; Labeau, F.; Kassouf, M. A markov-middleton model for bursty impulsive noise: Modeling and receiver design. IEEE Trans. Power Deliv. 2013, 28, 2317–2325. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, J.; Xu, X.; Pu, F. SAR Images Statistical Modeling and Classification Based on the Mixture of Alpha-Stable Distributions. Remote Sens. 2013, 5, 2145–2163. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Li, Z.; Zhao, Y.; Wang, R.; Habib, A. Optimization Method of Airborne LiDAR Individual Tree Segmentation Based on Gaussian Mixture Model. Remote Sens. 2022, 14, 6167. [Google Scholar] [CrossRef]
- Guangcai, W.; Xu, X.; Zhang, T. MM estimation-based robust cubature Kalman filter for INS/GPS integrated navigation system. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Mi, J.; Xu, Y.; Li, B.; Jiang, D.; Liu, W. A Robust Adaptive Filtering Algorithm for GNSS Single-Frequency RTK of Smartphone. Remote Sens. 2022, 14, 6388. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Chang, G.; Li, A. Huber-based novel robust unscented Kalman filter. IET Sci. Meas. Technol. 2012, 6, 502–509. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum correntropy Kalman filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; pp. 123–126. [Google Scholar]
- Qu, H.; Wang, M.; Zhao, J.; Zhao, S.; Li, T.; Yue, P. Generalized Asymmetric Correntropy for Robust Adaptive Filtering: A Theoretical and Simulation Study. Remote Sens. 2022, 14, 3677. [Google Scholar] [CrossRef]
- Liao, T.; Hirota, K.; Wu, X.; Shao, S.; Dai, Y. A Dynamic Self-Tuning Maximum Correntropy Kalman Filter forWireless Sensors Networks Positioning Systems. Remote Sens. 2022, 14, 4345. [Google Scholar] [CrossRef]
- Wang, S.Y.; Yang, J.Z. State Estimation under Outliers by the Maximum Correntropy Extended Kalman Filter. In Proceedings of the 2021 60th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Tokyo, Japan, 8–10 September 2021; pp. 1426–1431. [Google Scholar]
- Wang, D.; Zhang, H.; Ge, B. Adaptive Unscented Kalman Filter for Target Tacking with Time-Varying Noise Covariance Based on Multi-Sensor Information Fusion. Sensors 2021, 21, 5808. [Google Scholar] [CrossRef]
- Zhang, S. An Adaptive Unscented Kalman Filter for Dead Reckoning Systems. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009. [Google Scholar]
- Lu, D.H.; Wang, J.Q.; Xiong, K.; Hou, B.W.; He, Z.M. Strong tracking Kalman filter for non-Gaussian observation. Kongzhi Lilun Yu Yingyong/Control Theory Appl. 2019, 36, 1997–2004. [Google Scholar]
- Xie, S.B.; Zhang, Y.; Wen, K.R.; Zhang, S.; Liu, Z.M.; Qi, N.M. Motion estimation for non-cooperative target based on strong tracking cubature Kalman filter. Jilin Daxue Xuebao J. Jilin Univ. 2021, 51, 1482–1489. [Google Scholar]
- Wang, M.; Dong, X.; Qin, C.; Liu, J. Adaptive H-infinity Kalman filter based random drift modeling and compensation method for ring laser gyroscope. Measurement 2021, 167, 108170. [Google Scholar] [CrossRef]
- Gao, S.; Zhong, Y.; Li, W. Random weighting method for multisensory data fusion. IEEE Sens. J. 2011, 11, 1955–1961. [Google Scholar] [CrossRef]
- Gao, S.; Hu, G.; Zhong, Y. Windowing and random weighting-based adaptive unscented Kalman filter. Int. J. Adapt. Control Signal Process. 2015, 29, 201–223. [Google Scholar] [CrossRef]
- Gao, Z.; Mu, D.; Wei, W.; Zhong, Y.; Gu, C. Adaptive unscented Kalman filter based on maximum posterior estimation and random weighting. Aerosp. Sci. Technol. 2017, 71, 12–24. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, H.; Jiang, L. An Optimal Fusion Method of Multiple Inertial Measurement Units Based on Measurement Noise Variance Estimation. IEEE Sens. 2023, 23, 2693–2706. [Google Scholar] [CrossRef]
- Velazquez, J.R. Analysis and Development of Algorithms for Data Fusion in Sensor Arrays. Ph.D. Thesis, Universit Montpellier, Montpellier, France, 2020. [Google Scholar]
- Srinivas, P.; Kumar, A. Overview of architecture for GPS-INS integration. In Proceedings of the 2017 Recent Developments in Control, Automation & Power Engineering, Noida, India, 26–27 October 2017. [Google Scholar]
- Xu, X.; Nie, Z.; Wang, Z.; Wang, B.; Du, Q. Performance Assessment of BDS-3 PPP-B2b/INS Loosely Coupled Integration. Remote Sens. 2022, 14, 2957. [Google Scholar] [CrossRef]
- Zhai, R.; Yuan, Y. A Method of Vision Aided GNSS Positioning Using Semantic Information in Complex Urban Environment. Remote Sens. 2022, 14, 869. [Google Scholar] [CrossRef]
- Chiang, K.W.; Duong, T.T.; Liao, J.K. The performance analysis of a real-time integrated INS/GPS vehicle navigation system with abnormal GPS measurement elimination. Sensors 2013, 13, 10599–10622. [Google Scholar] [CrossRef]
- Zhao, Y. Performance evaluation of Cubature Kalman filter in a GPS/IMU tightly-coupled navigation system. Signal Proc. 2016, 119, 67–79. [Google Scholar] [CrossRef]
- Kong, X.; Nebot, E.M.; Durrant-Whyte, H. Development of a nonlinear psi-angle model for large misalignment errors and its application in INS alignment and calibration. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 1430–1435. [Google Scholar]
- Santamaría, I.; Pokharel, P.P.; Principe, J.C. Generalized correlation function: Definition, properties, and application to blind equalization. IEEE Trans. Signal Process. 2006, 54, 2187–2197. [Google Scholar] [CrossRef]
- Xiong, W.; Schindelhauer, C.; So, H.C.; Wang, Z. Maximum Correntropy Criterion for Robust TOA-Based Localization in NLOS Environments. Circuits Syst. Signal Process. 2021, 40, 6325–6339. [Google Scholar]
- Mohiuddin, S.M.; Qi, J. Maximum Correntropy Extended Kalman Filtering for Power System Dynamic State Estimation. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ge, B.S.; Zhang, H.; Fu, W.X.; Yang, J.B. Enhanced Redundant Measurement-Based Kalman Filter for Measurement Noise Covariance Estimation in INS/GNSS Integration. Remote Sens. 2020, 12, 3500. [Google Scholar] [CrossRef]
- Ghaleb, F.; Zainal, A.; Rassam, M.; Abraham, A. Improved vehicle positioning algorithm using enhanced innovation-based adaptive Kalman filter. Pervasive Mob. Comput. 2017, 40, 139–155. [Google Scholar] [CrossRef]
- Chen, X.; Yu, J.M.; Yu, W.; Truong, T.K. GPS L1CA/BDS B1I Multipath Channel Measurements and Modeling for Dynamic Land Vehicle in Shanghai Dense Urban Area. IEEE Trans. Veh. Technol. 2020, 69, 14247–14263. [Google Scholar] [CrossRef]
- Xia, X.; Meng, Z.; Han, X.; Li, H.; Tsukiji, T.; Xu, R.; Zhang, Z.; Ma, J. Automated Driving Systems Data Acquisition and Processing Platform. arXiv 2022, arXiv:2211.13425. [Google Scholar]
- Liu, W.; Quijano, K.; Crawford, M.M. YOLOv5-Tassel: Detecting Tassels in RGB UAV Imagery With Improved YOLOv5 Based on Transfer Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8085–8094. [Google Scholar] [CrossRef]



| Gyroscope Parameters | Accelerator Parameters | |
|---|---|---|
| Measurement range | ±495 deg/s | ±10 g |
| Bias stability(In-run) | ≤0.05 deg/hr | ≤100 μg |
| Non-linearity (Scale factor) | ≤100 ppm | ≤100 ppm |
| Random walk | 0.012 deg/√hr | ≤100 μg/√Hz |
| Raw Data Rate | 200 Hz | 200 Hz |
| Horizontal Position Accuracy of GNSS (RMS) | ||
| Single point L1/L2 | 1.2 m | |
| SBAS | 60 cm | |
| DGPS | 40 cm | |
| Algorithm | Longitude (m) | Latitude (m) | Height (m) | East Velocity (m/s) | North Velocity (m/s) | Up Velocity (m/s) | Pitch (°) | Roll (°) | Yaw (°) |
|---|---|---|---|---|---|---|---|---|---|
| Standard EKF | 5.4944 | 1.2624 | 5.6871 | 0.6415 | 0.2246 | 0.2221 | 0.2785 | 0.2165 | 0.0485 |
| EIAKF | 6.4422 | 1.8996 | 4.5233 | 0.6779 | 0.3255 | 0.1585 | 0.2784 | 0.2645 | 0.0454 |
| ERMAKF | 5.0846 | 1.9428 | 4.1101 | 0.2884 | 0.2544 | 0.1006 | 0.2783 | 0.3518 | 0.0312 |
| MCEKF | 5.1309 | 1.1844 | 5.3577 | 0.6000 | 0.2009 | 0.2183 | 0.2616 | 0.2032 | 0.0483 |
| RMCEKF | 3.9347 | 2.6159 | 3.2446 | 0.3112 | 0.2588 | 0.1792 | 0.1710 | 0.1294 | 0.0497 |
| Algorithm | Longitude (m) | Latitude (m) | Height (m) | East Velocity (m/s) | North Velocity (m/s) | Up Velocity (m/s) | Pitch (°) | Roll (°) | Yaw (°) |
|---|---|---|---|---|---|---|---|---|---|
| Standard EKF | 3.1620 | 1.7765 | 4.1326 | 0.3017 | 0.1075 | 0.1870 | 0.1653 | 0.0830 | 0.1347 |
| EIAKF | 2.9980 | 4.7459 | 3.2645 | 0.1961 | 0.1597 | 0.1011 | 0.1921 | 0.0888 | 0.1837 |
| ERMAKF | 2.6209 | 1.4191 | 3.4597 | 0.2152 | 0.1456 | 0.1037 | 0.1620 | 0.1902 | 0.0868 |
| MCEKF | 2.8755 | 1.7279 | 3.6706 | 0.2758 | 0.1020 | 0.1733 | 0.1573 | 0.0750 | 0.1361 |
| RMCEKF | 1.4543 | 1.4129 | 2.1926 | 0.0853 | 0.1031 | 0.0783 | 0.0884 | 0.0538 | 0.1346 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Zhang, H.; Huang, H.; Ge, B. A Redundant Measurement-Based Maximum Correntropy Extended Kalman Filter for the Noise Covariance Estimation in INS/GNSS Integration. Remote Sens. 2023, 15, 2430. https://doi.org/10.3390/rs15092430
Wang D, Zhang H, Huang H, Ge B. A Redundant Measurement-Based Maximum Correntropy Extended Kalman Filter for the Noise Covariance Estimation in INS/GNSS Integration. Remote Sensing. 2023; 15(9):2430. https://doi.org/10.3390/rs15092430
Chicago/Turabian StyleWang, Dapeng, Hai Zhang, Hongliang Huang, and Baoshuang Ge. 2023. "A Redundant Measurement-Based Maximum Correntropy Extended Kalman Filter for the Noise Covariance Estimation in INS/GNSS Integration" Remote Sensing 15, no. 9: 2430. https://doi.org/10.3390/rs15092430
APA StyleWang, D., Zhang, H., Huang, H., & Ge, B. (2023). A Redundant Measurement-Based Maximum Correntropy Extended Kalman Filter for the Noise Covariance Estimation in INS/GNSS Integration. Remote Sensing, 15(9), 2430. https://doi.org/10.3390/rs15092430








