A Method for Merging Multi-Source Daily Satellite Precipitation Datasets and Gauge Observations over Poyang Lake Basin, China
Abstract
1. Introduction
2. Materials and Methods
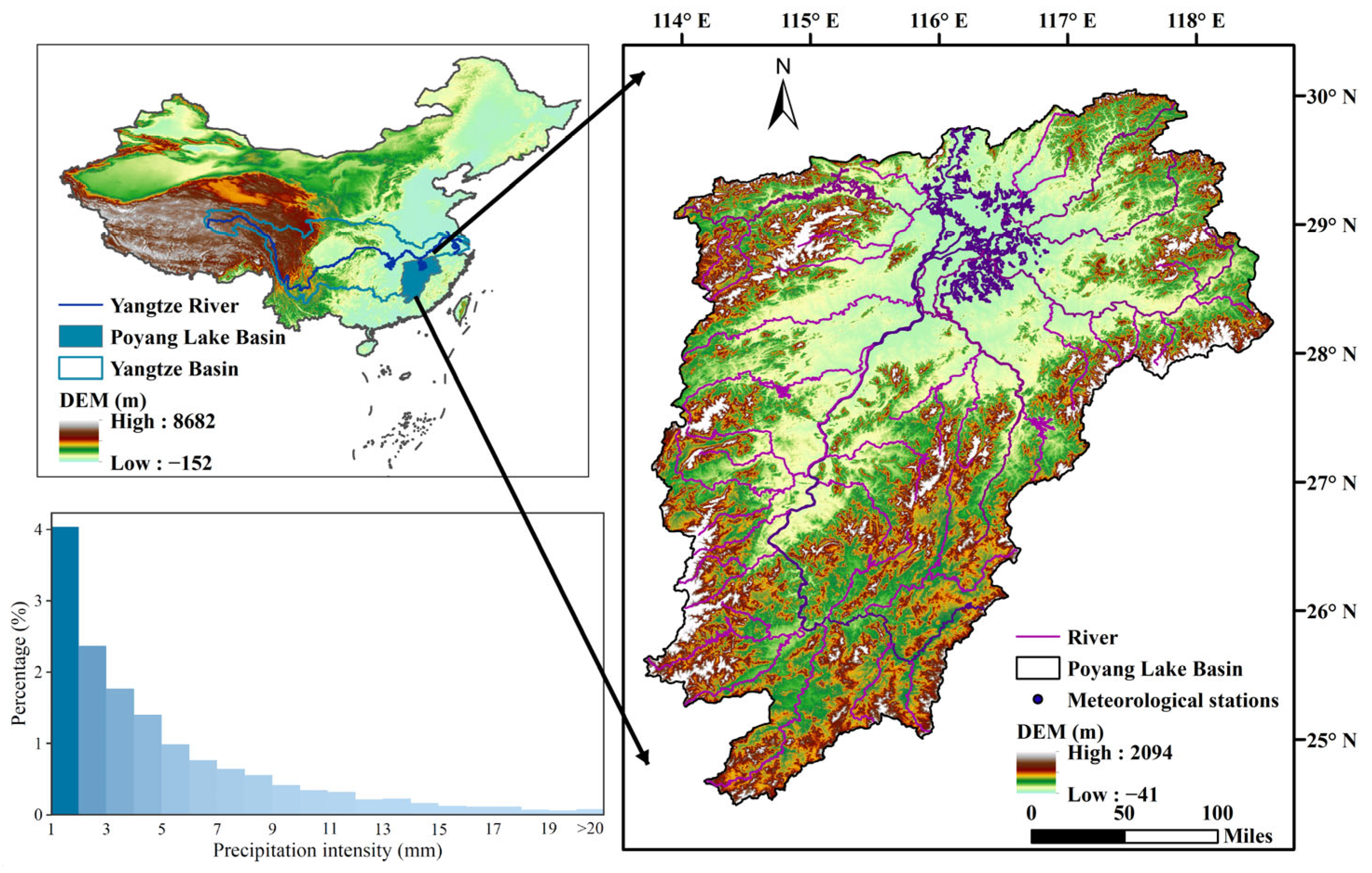
2.1. Materials
2.2. Methods
2.2.1. RESF Model
2.2.2. RESF-Based Downscaling
2.2.3. RESF-Based Data Fusion
2.2.4. Model Validation
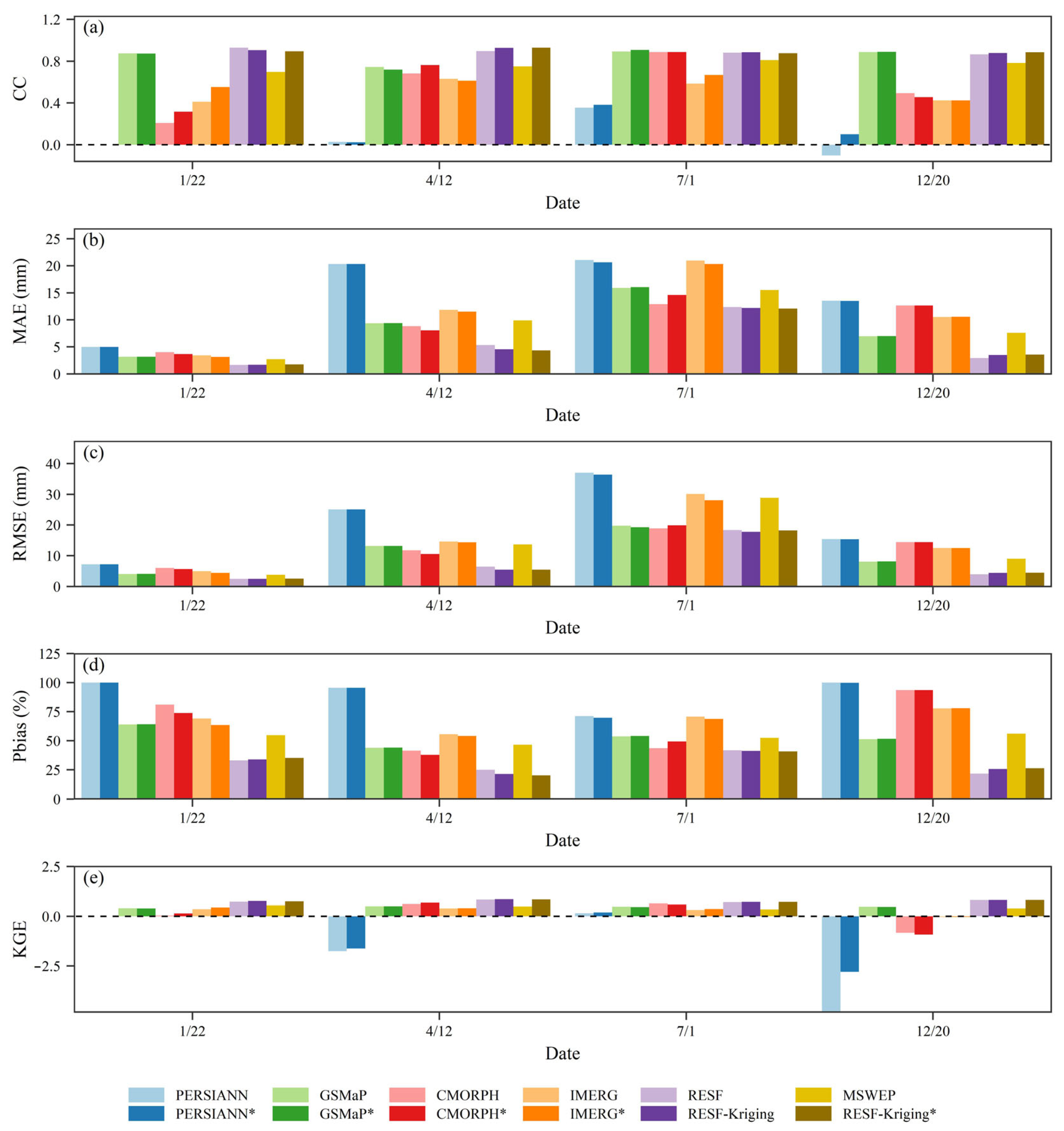
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Zhou, Y.; Hu, B.; Liang, Z.; Shi, Z. Downscaling annual precipitation with TMPA and land surface characteristics in China. Int. J. Climatol. 2017, 37, 5107–5119. [Google Scholar] [CrossRef]
- Navas, R.; Delrieu, G. Distributed hydrological modeling of floods in the Cévennes-Vivarais region, France: Impact of uncertainties related to precipitation estimation and model parameterization. J. Hydrol. 2018, 565, 276–288. [Google Scholar] [CrossRef]
- Loritz, R.; Hrachowitz, M.; Neuper, M.; Zehe, E. The role and value of distributed precipitation data in hydrological models. Hydrol. Earth Syst. Sci. 2021, 25, 147–167. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Rahimi, A.R. On-line detection of errors in tipping-bucket raingauges. J. Hydrol. 2003, 278, 197–212. [Google Scholar] [CrossRef]
- Yang, Z.W.; Hsu, K.L.; Sorooshian, S.; Xu, X.Y.; Braithwaite, D.; Zhang, Y.; Verbist, M.J. Merging high-resolution satellite-based precipitation fields and point-scale rain gauge measurements-A case study in Chile. J. Geophys. Res. Atmos. 2017, 122, 5267–5284. [Google Scholar] [CrossRef]
- Looper, J.P.; Vieux, B.E. An assessment of distributed flash flood forecasting accuracy using radar and rain gauge input for a physics-based distributed hydrologic model. J. Hydrol. 2012, 412–413, 114–132. [Google Scholar] [CrossRef]
- Pan, X.; Li, X.; Yang, K.; He, J.; Zhang, Y.; Han, X. Comparison of downscaled precipitation data over a mountainous watershed: A case study in the Heihe River Basin. J. Hydrometeorol. 2014, 15, 1560–1574. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.L.; Lu, J.Z.; Fu, X.K.; Zhang, Y.F.; Liang, D.; Xu, Q.Q. Precipitation projections using a spatiotemporally distributed method: A case study in the Poyang Lake watershed based on the MRI-CGCM3. Hydrol. Earth Syst. Sci. 2019, 23, 1649–1666. [Google Scholar] [CrossRef]
- Bardossy, A.; Pegram, G. Combination of radar and daily precipitation data to estimate meaningful sub-daily point precipitation etremes. J. Hydrol. 2017, 544, 397–406. [Google Scholar] [CrossRef]
- Huffman, G.J.; Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; et al. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG). NASA Algorithm Theoretical Basis Document, version 06, 38p. 2019. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V06.pdf (accessed on 12 December 2022).
- Tang, G.Q.; Martyn, P.C.; Simon, M.P.; Ma, Z.Q.; Yang, H. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-hourly 0.04 degrees global precipitation climate data record for heavy precipitation studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Yong, B.; Gourley, J.J.; Qi, W.; Lu, D.; Liu, J.; Ren, L.; Hong, Y.; Zhang, J. Recent global performance of the Climate Hazards group Infrared Precipitation (CHIRP) with Stations (CHIRPS). J. Hydrol. 2020, 591, 125284. [Google Scholar] [CrossRef]
- Okamoto, K.; Ushio, T.; Iguchi, T.; Takahashi, N.; Iwanami, K. The global satellite mapping of precipitation (GSMaP) project. In Proceedings of the 25th IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2005), Seoul, Republic of Korea, 25–29 July 2005; pp. 3414–3416. [Google Scholar]
- Li, Y.L.; Tao, H.; Yao, J.; Zhang, Q. Application of a distributed catchment model to investigate hydrological impacts of climate change within Poyang Lake catchment (China). Hydrol. Res. 2016, 47, 120–135. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document (ATBD) Version 2015, 4; NASA: Washington, DC, USA, 2015. [Google Scholar]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25 degrees global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Canedo-Rosso, C.; Hochrainer-Stigler, S.; Pflug, G.; Condori, B.; Berndtsson, R. Drought impact in the Bolivian Altiplano agriculture associated with the El Nino-Southern Oscillation using satellite imagery data. Nat. Hazards Earth Syst. Sci. 2021, 21, 995–1010. [Google Scholar] [CrossRef]
- Zhong, R.; Chen, X.; Lai, C.; Wang, Z.; Lian, Y.; Yu, H.; Wu, X. Drought monitoring utility of satellite-based precipitation products across mainland China. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Brodeur, Z.P.; Steinschneider, S. Spatial Bias in Medium-Range Forecasts of Heavy Precipitation in the Sacramento River Basin: Implications for Water Management. J. Hydrometeorol. 2020, 21, 1405–1423. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef]
- Hinge, G.; Hamouda, M.A.; Long, D.; Mohamed, M.M. Hydrologic utility of satellite precipitation products in flood prediction: A meta-data analysis and lessons learnt. J. Hydrol. 2022, 612, 128103. [Google Scholar] [CrossRef]
- Islam, A.; Yu, B.; Cartwright, N. Assessment and comparison of five satellite precipitation products in Australia. J. Hydrol. 2020, 590, 125474. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Chen, S.; Xiong, L.; Ma, Q.; Kim, J.S.; Chen, J.; Xu, C.Y. Improving daily spatial precipitation estimates by merging gauge observation with multiple satellite-based precipitation products based on the geographically weighted ridge regression method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Huang, J.F.; Sheng, S.X.; Mansaray, L.R.; Liu, Z.X.; Wu, H.Y.; Wang, X.Z. A new downscaling-integration framework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, W.C.; Zhang, Z.J.; Wang, S.H.; Zhang, B.; Cheema, M.J.M.; Shalamzari, M.J. Reconstructing high-resolution gridded precipitation data using an improved downscaling approach over the high altitude mountain regions of Upper Indus Basin (UIB). Sci. Total Environ. 2021, 784, 147140. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.M.; Liu, P.; Xia, J.; Zhao, Y.J.; Dong, Y. Merging multisatellite and gauge precipitation based on geographically weighted regression and long-short-term memory network. Remote Sens. 2022, 14, 3939. [Google Scholar] [CrossRef]
- Yumnam, K.; Guntu, R.K.; Rathinasamy, M.; Agarwal, A. Quantile-based Bayesian model averaging approach towards merging of precipitation products. J. Hydrol. 2022, 604, 127206. [Google Scholar] [CrossRef]
- Wu, H.C.; Yang, Q.L.; Liu, J.M.; Wang, G.Q. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Zhang, L.L.; Li, X.; Zheng, D.H.; Zhang, K.; Ma, Q.M.; Zhao, Y.B. Merging multiple satellite-based precipitation products and gauge observations using a novel double machine learning approach. J. Hydrol. 2021, 594, 125969. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q. An improved statistical approach to merge satellite rainfall estimates and rain gauge data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Verdin, A.; Funk, C.; Rajagopalan, B.; Kleiber, W. Kriging and local polynomial methods for blending satellite-derived and gauge precipitation estimates to support hydrologic early warning systems. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2552–2562. [Google Scholar] [CrossRef]
- Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalayan region. J. Geophys. Res. Atmos. 2015, 120, 12458–12473. [Google Scholar] [CrossRef]
- Hussain, S.T.; Lei, S.; Akram, T.; Haider, M.J.; Hussain, S.H.; Ali, M. Kurt Lewin’s change model: A critical review of the role of leadership and employee involvement in organizational change. J. Innov. Knowl. 2018, 3, 123–127. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gaugesatellite merged precipitation analyses. J. Geophys. 2011, 116, D21106. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Molinos, J.G.; Shi, L.L.; Zhang, M.; Wu, Z.S.; Zhang, H.; Xu, J. Divers and changes of the Poyang Lake wetland ecosystem. Wetland 2019, 39, S35–S344. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, S.; Guo, H.; Chen, G.Y.; Jiang, T. Interactions of the Yangtze river flow and hydrologic processes of the Poyang Lake, China. J. Hydrol. 2007, 347, 90–100. [Google Scholar] [CrossRef]
- Gao, J.H.; Jia, J.J.; Kettner, A.J.; Xing, F.; Wang, Y.P.; Xu, X.N.; Yang, Y.; Zou, X.Q.; Gao, S.; Qi, S.H.; et al. Changes in water and sediment exchange between the Changjiang River and Poyang Lake under natural and anthropogenix conditions, China. Sci. Total Environ. 2014, 481, 542–553. [Google Scholar] [CrossRef]
- Murakami, D.; Yoshida, T.; Seya, H.; Griffith, D.A.; Yamagata, Y. A Moran coefficient-based mixed effects approach to investigate spatially varying relationships. Spat. Stat. 2017, 19, 68–89. [Google Scholar] [CrossRef]
- Zhao, N.; Jiao, Y.M.; Zhang, L.L. Projections of precipitation change from CMIP6 based on a new downscaling method in the Poyang Lake basin, China. J. Hydrol.-Reg. Stud. 2022, 42, 101138. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, Q.; Ye, X.C. Dry/wet conditions monitoring based on TRMM rainfall data and its reliability validation over Poyang Lake Basin, China. Water 2013, 5, 1848–1864. [Google Scholar] [CrossRef]
- Su, J.; Lu, H.; Ryu, D.; Zhu, Y. The Assessment and Comparison of TMPA and IMERG Products Over the Major Basins of Mainland China. Earth Space Sci. 2019, 6, 2461–2479. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high-resolution precipitation products. J. Geophys. Res. 2010, 115, D02114. [Google Scholar]
- Ning, S.W.; Song, F.; Udmale, P.; Jin, J.L.; Thapa, B.R.; Ishidaira, H. Error analysis and evaluation of the latest GSMap and IMERG precipitation products over eastern China. Adv. Meteorol. 2017, 2017, 1803492. [Google Scholar] [CrossRef]
- Yang, T.; Li, Q.; Chen, X.; De Maeyer, P.; Yan, X.; Liu, Y.; Zhao, T.; Li, L. Spatiotemporal variability of the precipitation concentration and diversity in Central Asia. Atmos. Res. 2020, 241, 104954. [Google Scholar] [CrossRef]
- Arshad, M.; Ma, X.; Yin, J.; Ullah, W.; Ali, G.; Ullah, S.; Liu, M.; Shahzaman, M.; Ullah, I. Evaluation of GPM-IMERG and TRMM-3B42 precipitation products over Pakistan. Atmos. Res. 2021, 249, 105341. [Google Scholar] [CrossRef]
- Mega, T.; Ushio, T.; Matsuda, T.; Kubota, T.; Kachi, M.; Oki, R. Gauge-Adjusted Global Satellite Mapping of Precipitation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1928–1935. [Google Scholar] [CrossRef]
- Kubota, T.K.; Aonashi, T.; Ushio, S.; Shige, Y.N.; Takayabu, M.; Kachi, Y.; Arai, T.; Tashima, T.; Masaki, N.; Kawamoto, T.; et al. Satellite Precipitation Measurement; Springer: Cham, Switzerland, 2020; Volume 67, pp. 355–373. [Google Scholar]
- Jafarzadeh, A.; Pourreza-Bilondi, M.; Siuki, A.K.; Moghadam, J.R. Examination of Various Feature Selection Approaches for Daily Precipitation Downscaling in Different Climates. Water Resour. Manag. 2021, 35, 407–427. [Google Scholar] [CrossRef]
- Anselin, L.; Rey, S.J. Modern Spatial Econometrics in Practice: A Guide to GeoDa, GeoDaSpace and PySAL; GeoDa Press LLC: Chicago, IL, USA, 2014. [Google Scholar]
- Ullah, S.; Zuo, Z.K.; Zhang, F.Z.; Zheng, J.H.; Huang, S.F.; Lin, Y.; Iqbal, I.; Sun, Y.Y.; Yang, M.; Yan, L. GPM-based multitemporal weighted precipitation analysis using GPM_IMERGDF product and ASTER DEM in EDBF algorithm. Remote Sens. 2020, 12, 3162. [Google Scholar] [CrossRef]
- Chorbanpour, A.K.; Hessels, T.; Moghim, S.; Afshar, A. Comparison and assessment of spatial downscaling methods for enhancing the accuracy of satellite-based precipitation over Lake Urmia Basin. J. Hydrol. 2021, 596, 126055. [Google Scholar]
- Griffith, D.A. Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR). Environ. Plan. A 2008, 40, 2751–2769. [Google Scholar] [CrossRef]
- Griffith, D.; Chun, Y. Spatial Autocorrelation and Spatial Filtering. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1477–1507. [Google Scholar] [CrossRef]
- Chen, F.G.; Gao, Y.Q.; Wang, Y.G.; Li, X. A downscaling-merging method for high-resolution daily precipitation estimation. J. Hydrol. 2020, 581, 124414. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.X.; Chen, C.F.; Zhao, M.W.; Fan, Z.M. An improved statistical downscaling scheme of tropical rainfall measuring mission precipitation in the Heihe River basin, China. Int. J. Climatol. 2018, 38, 3309–3322. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, B.S.; Ma, Z.Q.; Chen, X.H.; Qiu, J.; Liu, D. Comprehensive comparisons of state-of the art gridded precipitation estimated for hydrological applications over southern China. Remote Sens. 2020, 12, 3997. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First results from version 7 TRMM 3B43 precipitation product in combination with a new downscaling-calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Liu, Z.F.; Xu, Z.X.; Charles, S.P.; Liu, L. Evaluation of two statistical downscaling models for daily precipitation over an arid basin in China. Int. J. Climatol. 2011, 31, 2006–2020. [Google Scholar] [CrossRef]
- Jing, W.L.; Yang, Y.P.; Yue, X.F.; Zhao, X.D. A spatial downscaling algorithm for satellite-based precipitation over the Tibetan Platetu based on NDVI, DEM and land surface temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, N. A Method for Merging Multi-Source Daily Satellite Precipitation Datasets and Gauge Observations over Poyang Lake Basin, China. Remote Sens. 2023, 15, 2407. https://doi.org/10.3390/rs15092407
Zhao N. A Method for Merging Multi-Source Daily Satellite Precipitation Datasets and Gauge Observations over Poyang Lake Basin, China. Remote Sensing. 2023; 15(9):2407. https://doi.org/10.3390/rs15092407
Chicago/Turabian StyleZhao, Na. 2023. "A Method for Merging Multi-Source Daily Satellite Precipitation Datasets and Gauge Observations over Poyang Lake Basin, China" Remote Sensing 15, no. 9: 2407. https://doi.org/10.3390/rs15092407
APA StyleZhao, N. (2023). A Method for Merging Multi-Source Daily Satellite Precipitation Datasets and Gauge Observations over Poyang Lake Basin, China. Remote Sensing, 15(9), 2407. https://doi.org/10.3390/rs15092407





