Estimation of Net Ecosystem Productivity on the Tibetan Plateau Grassland from 1982 to 2018 Based on Random Forest Model
Abstract
1. Introduction
2. Materials and Methods
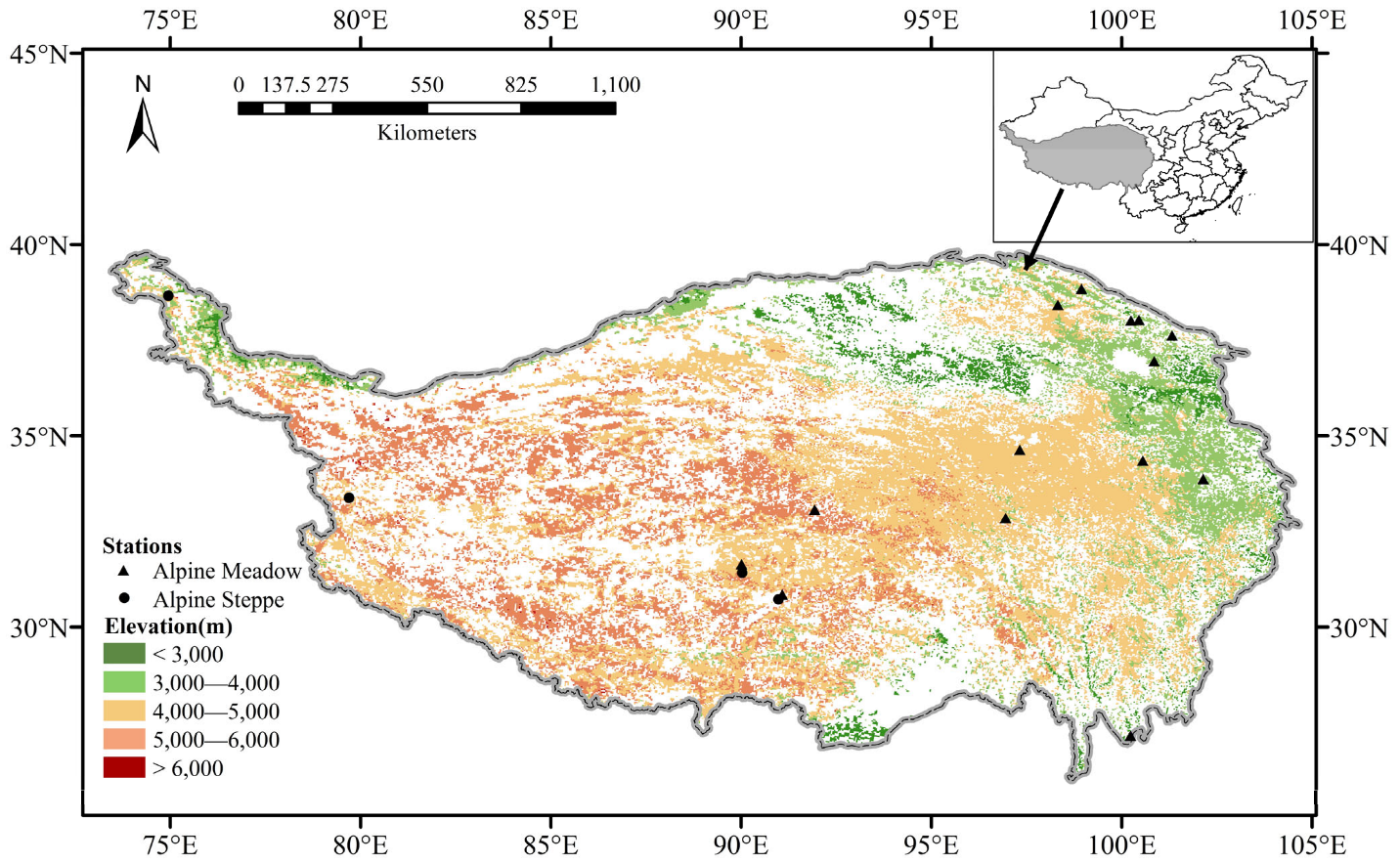
2.1. Study Area
2.2. Data Collection
2.2.1. Eddy-Covariance-Flux Data
2.2.2. Meteorological Data
2.2.3. Remote-Sensing Data
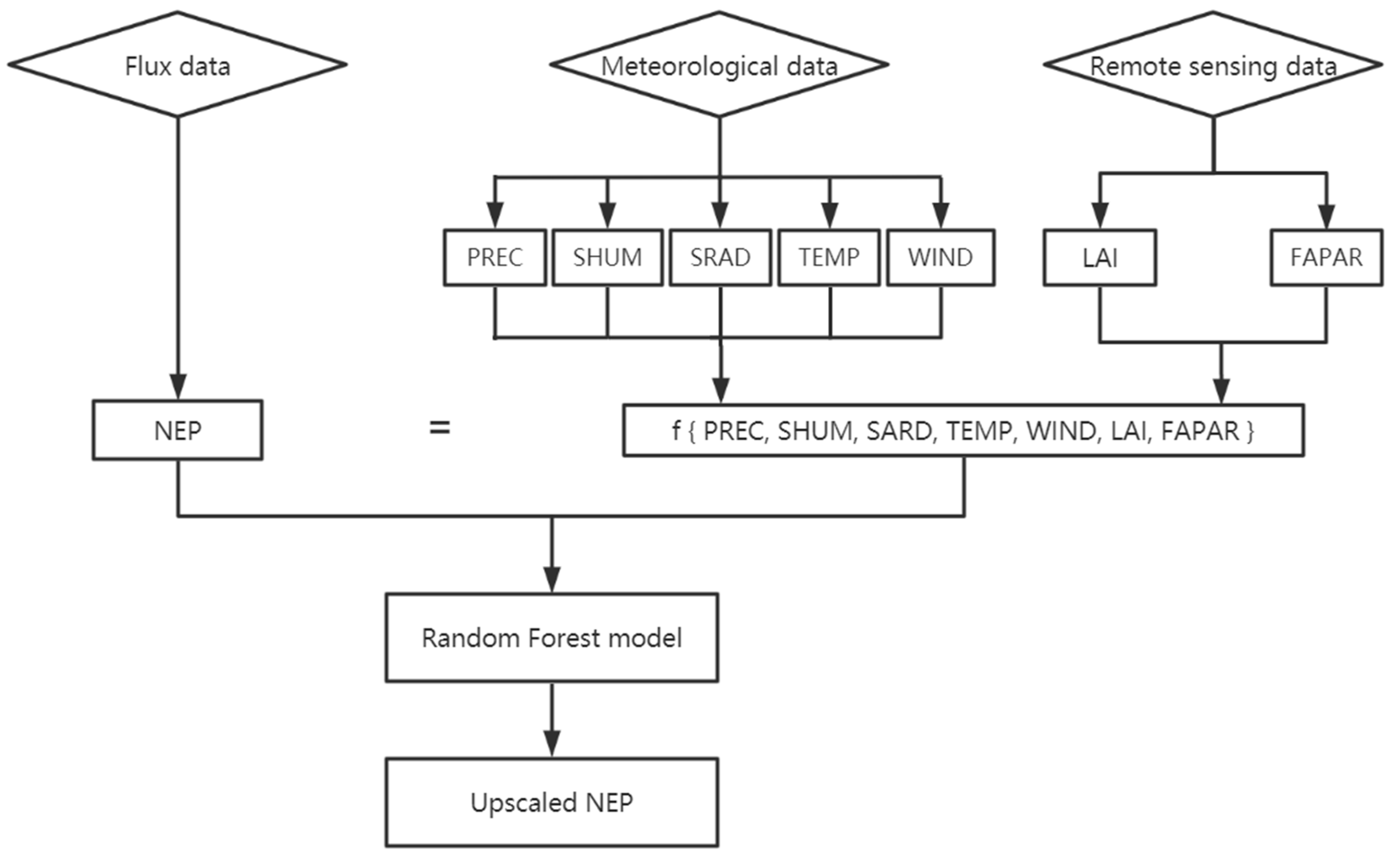
2.3. Random Forest Model
2.4. Data Analysis
2.4.1. Theil-Sen Median Trend Analysis of the Annual NEP
2.4.2. Partial Correlation Analysis between NEP and Climate Factors
3. Results
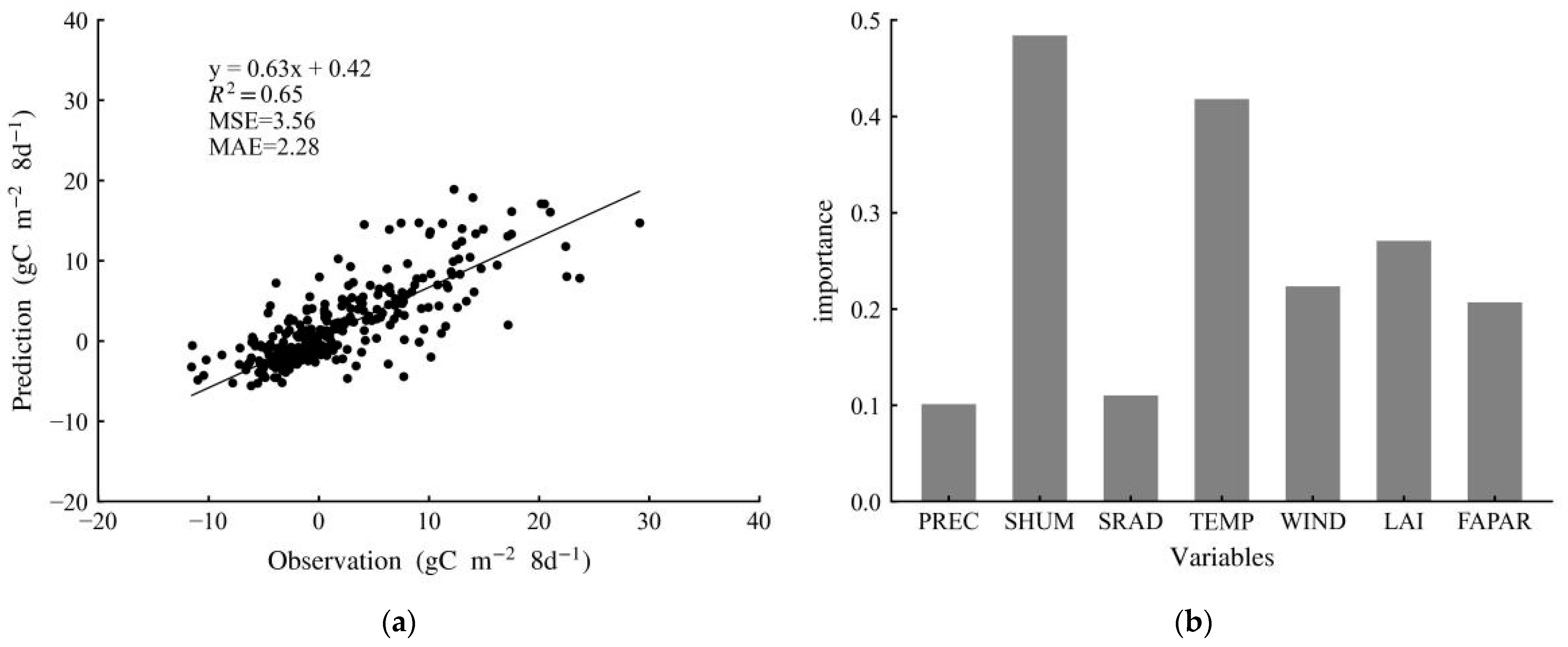
3.1. Performance of Estimation of NEP Using the Random Forest Model
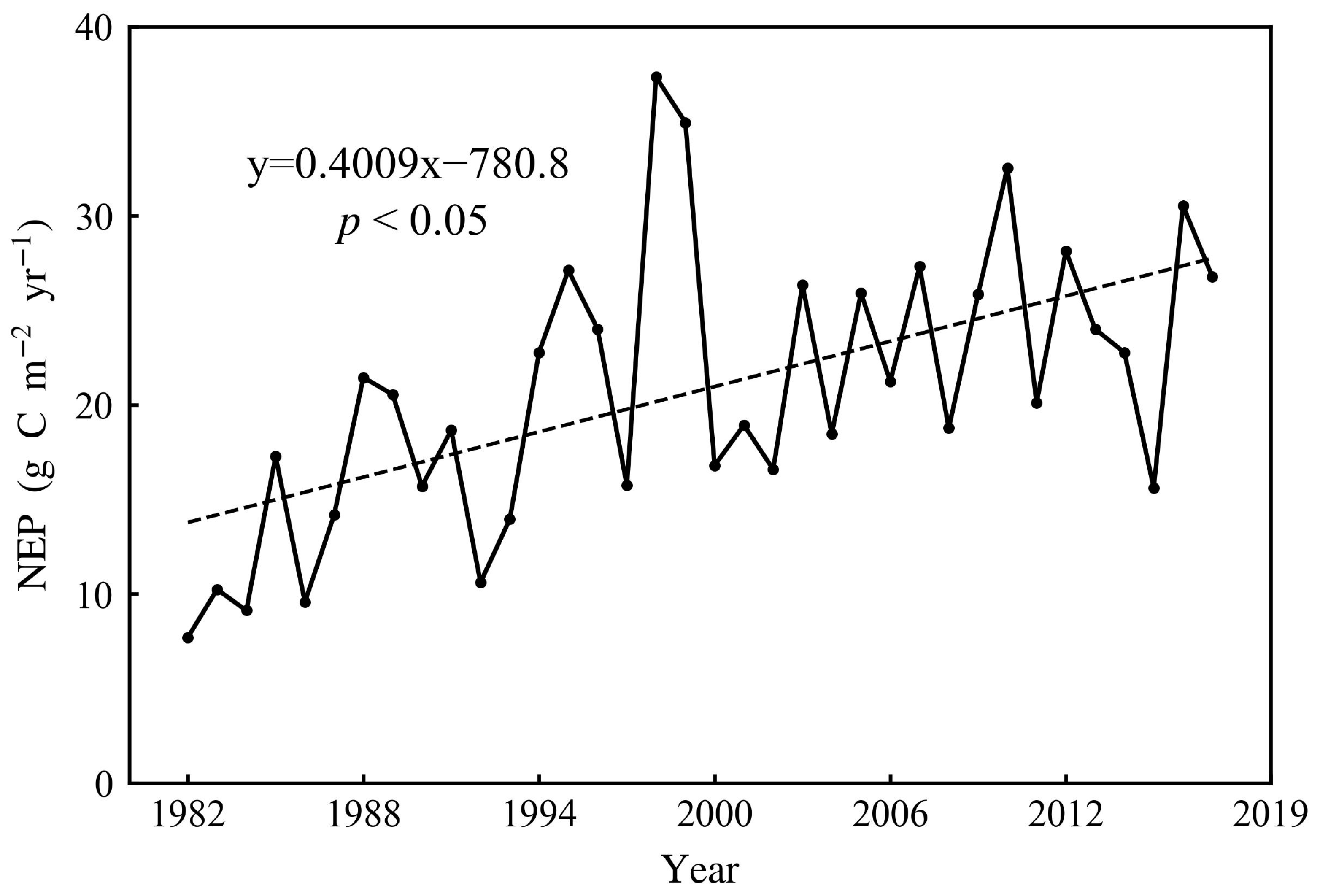
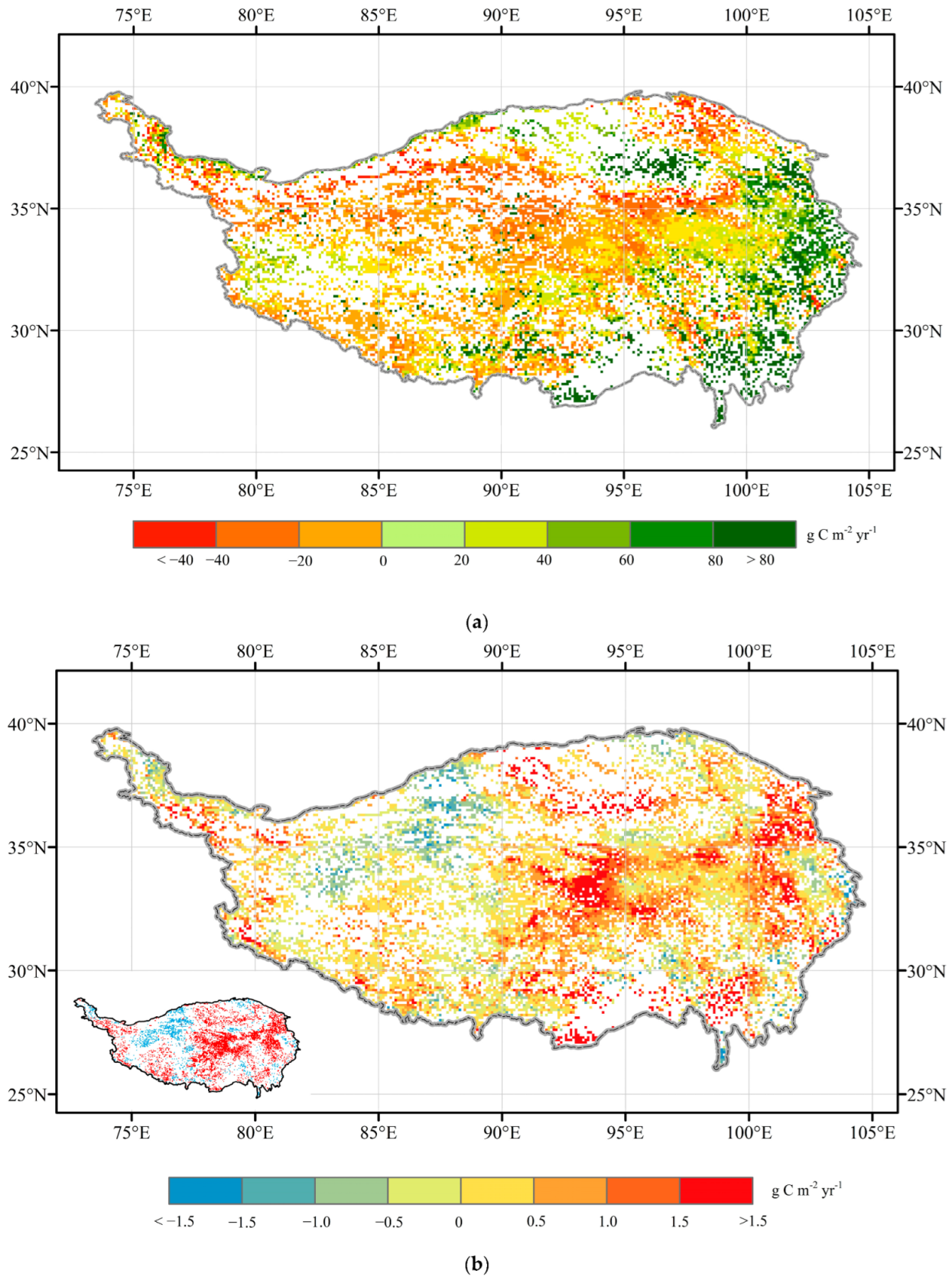
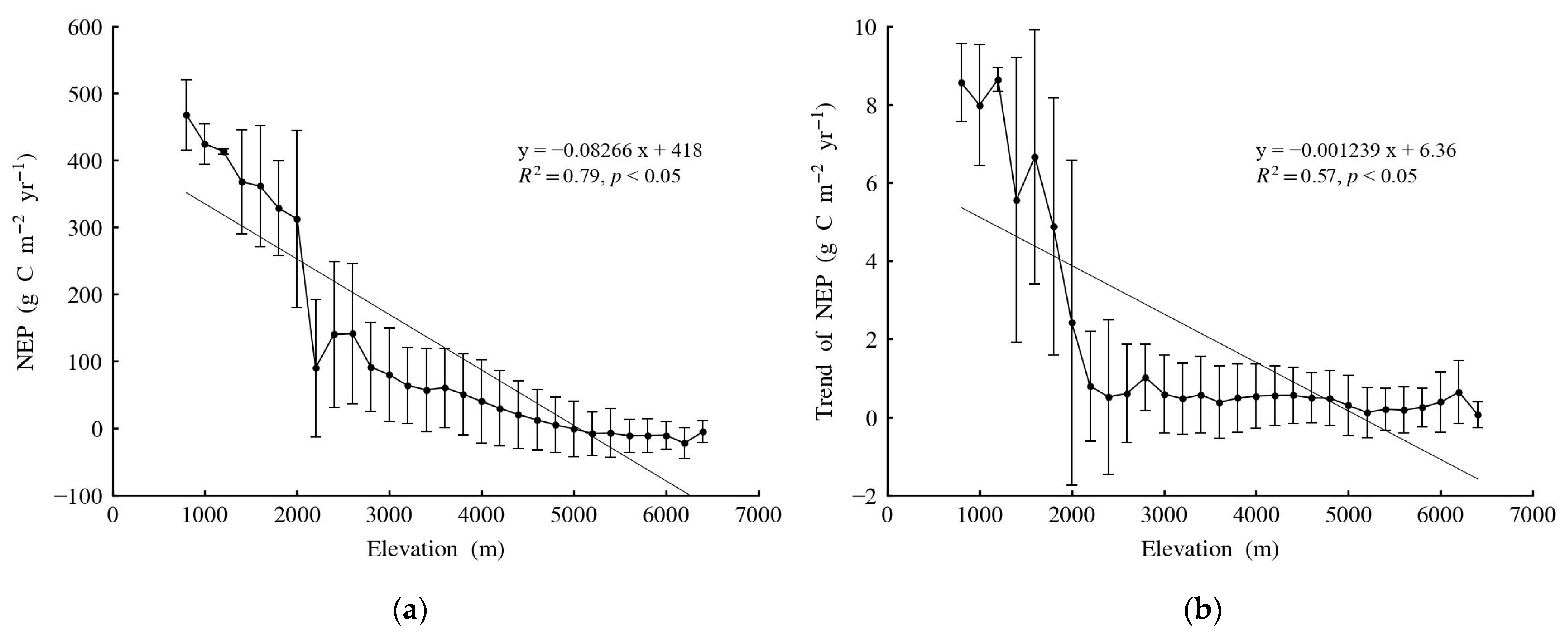
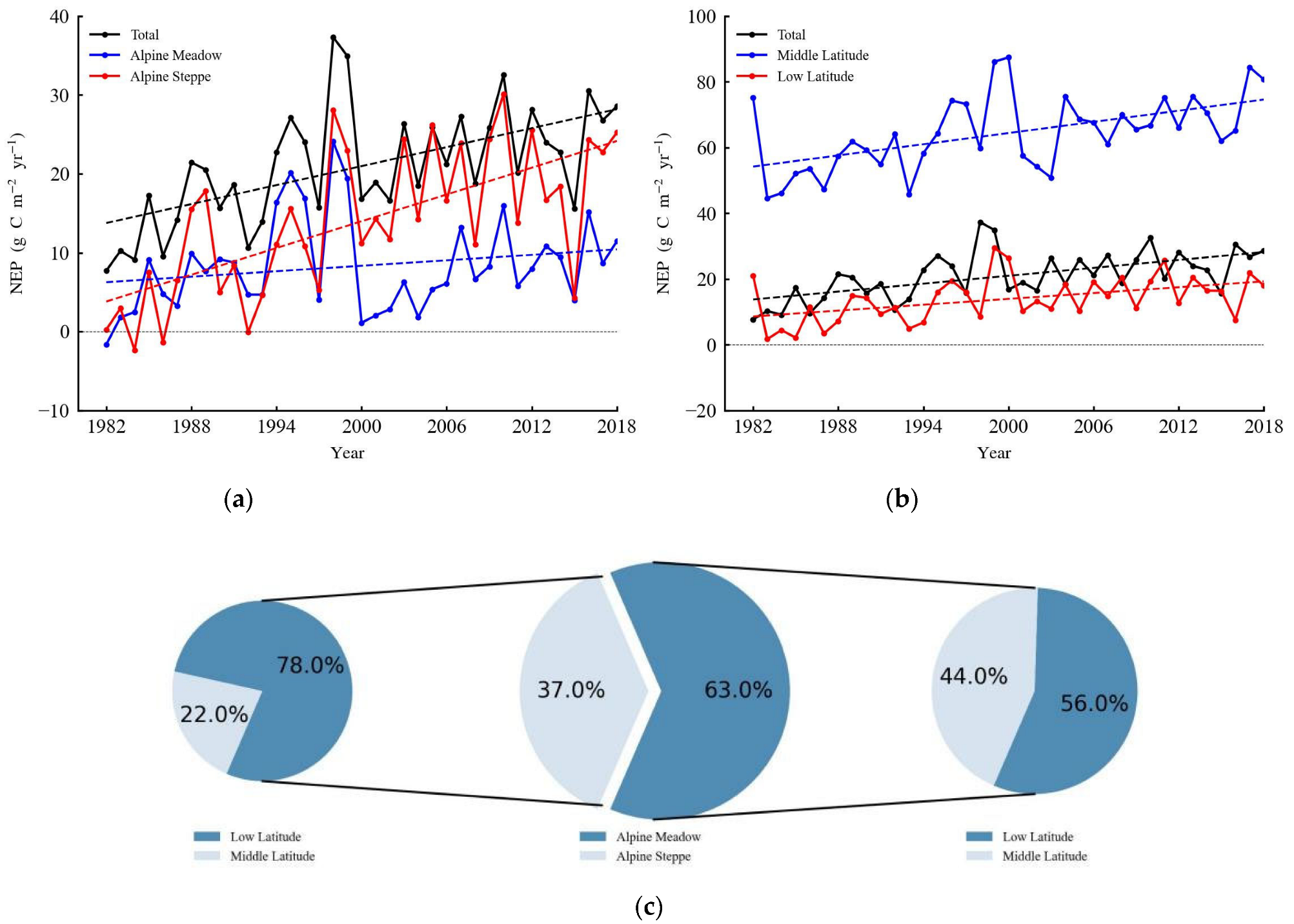
3.2. Spatial and Temporal Patterns of NEP
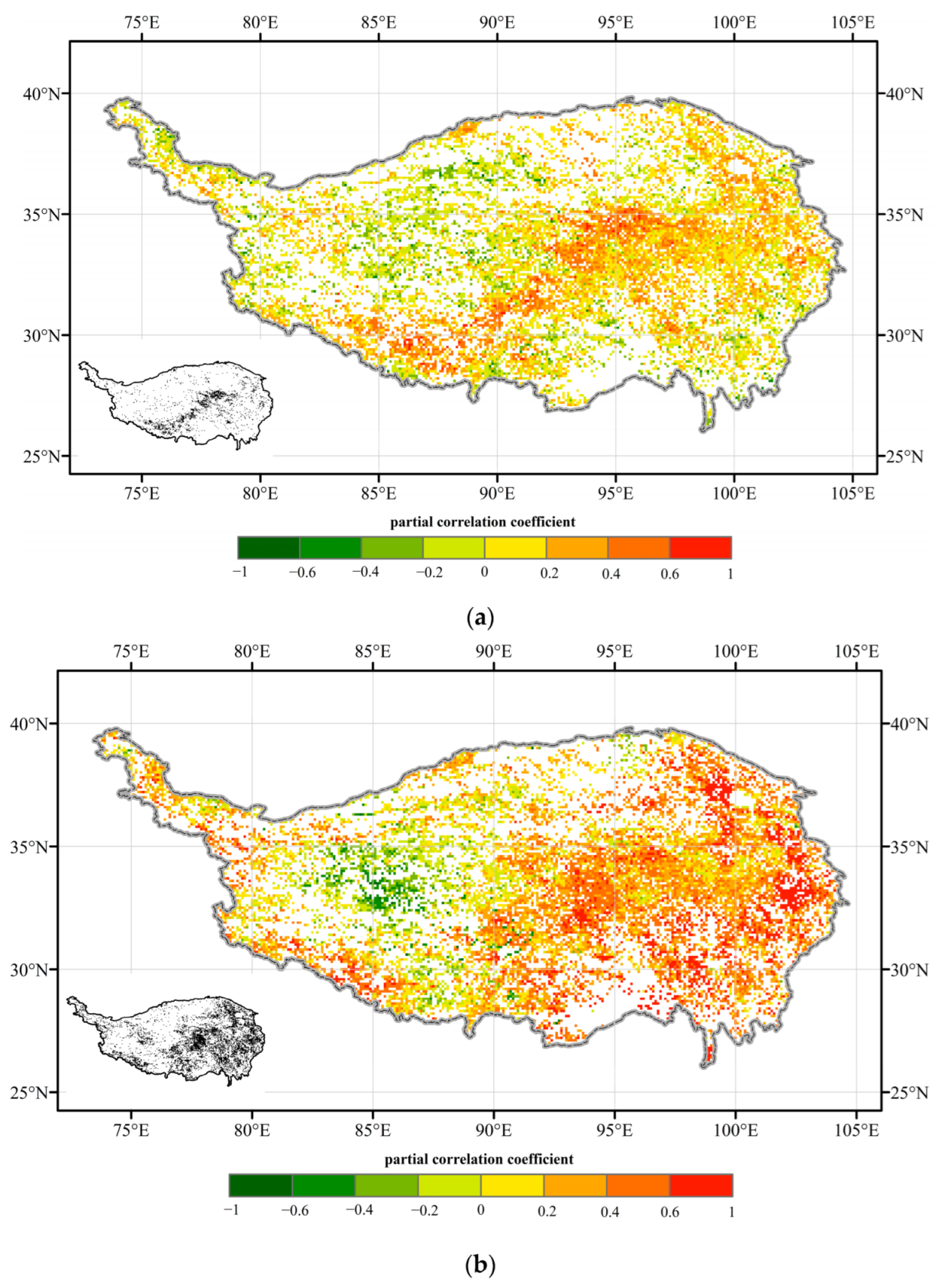
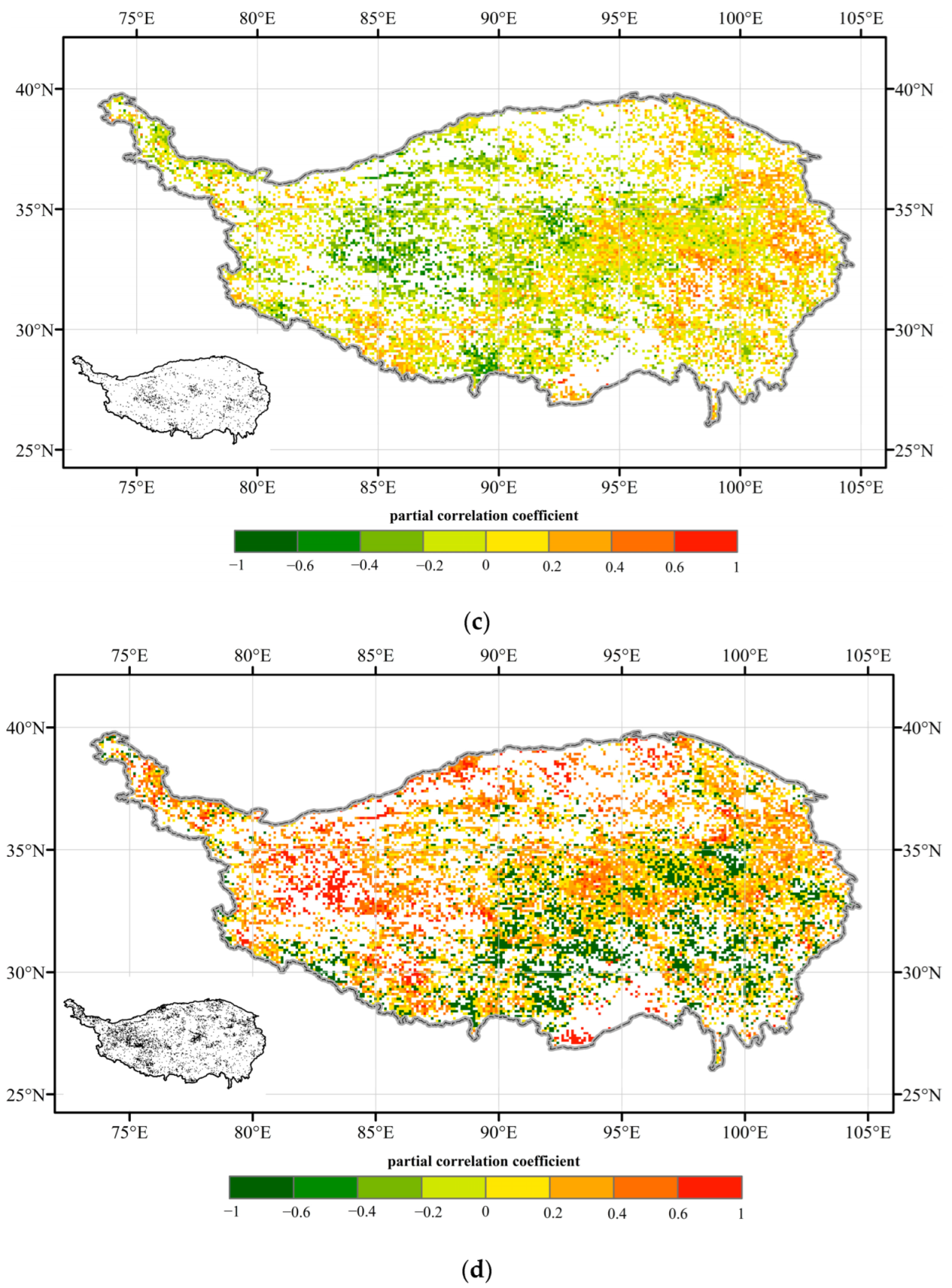
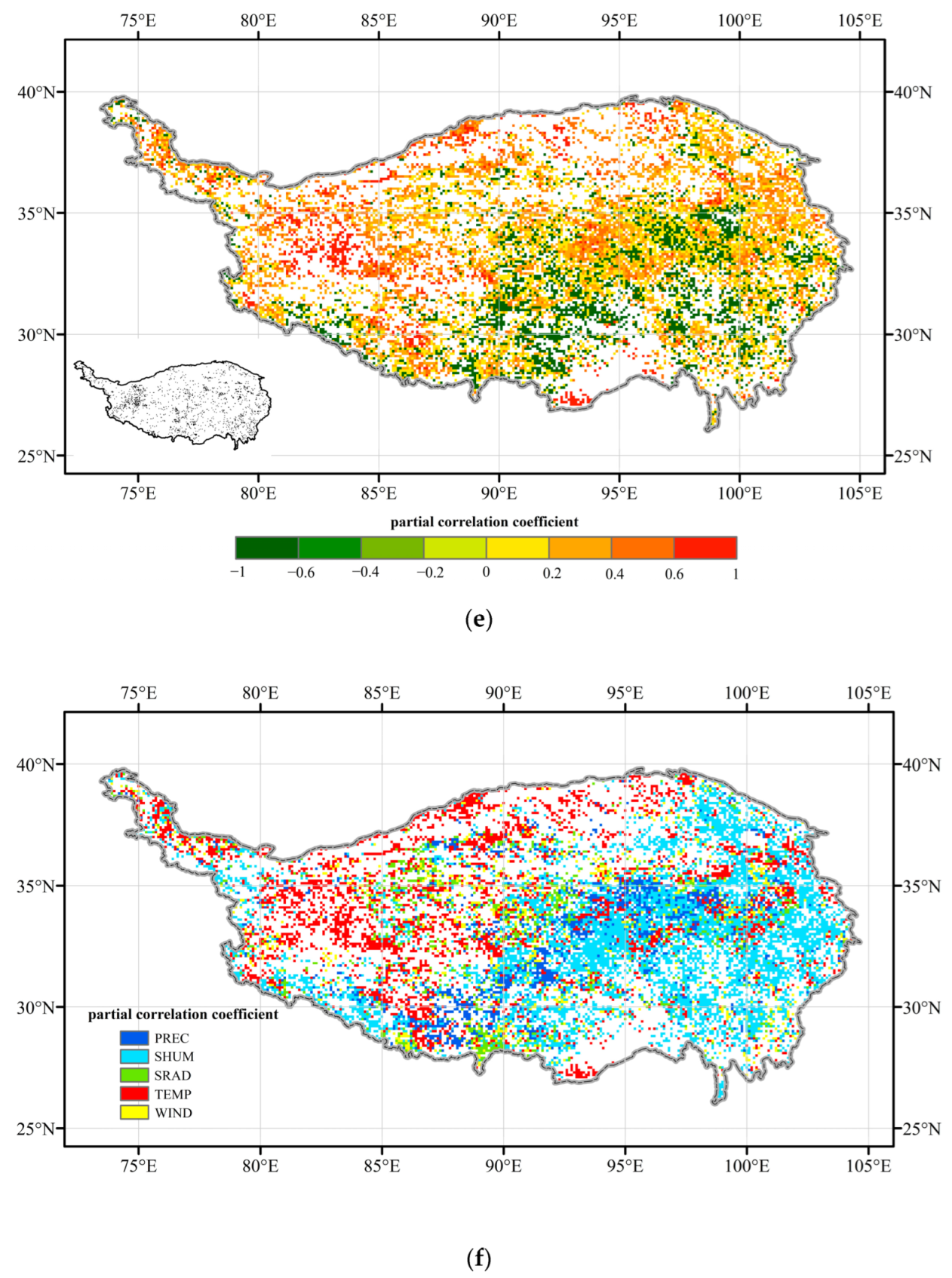
3.3. Driving Factors of NEP
4. Discussion
4.1. Driving Factors of Grassland Carbon Sink across the TP
4.2. The Size of Carbon Sink over the TP
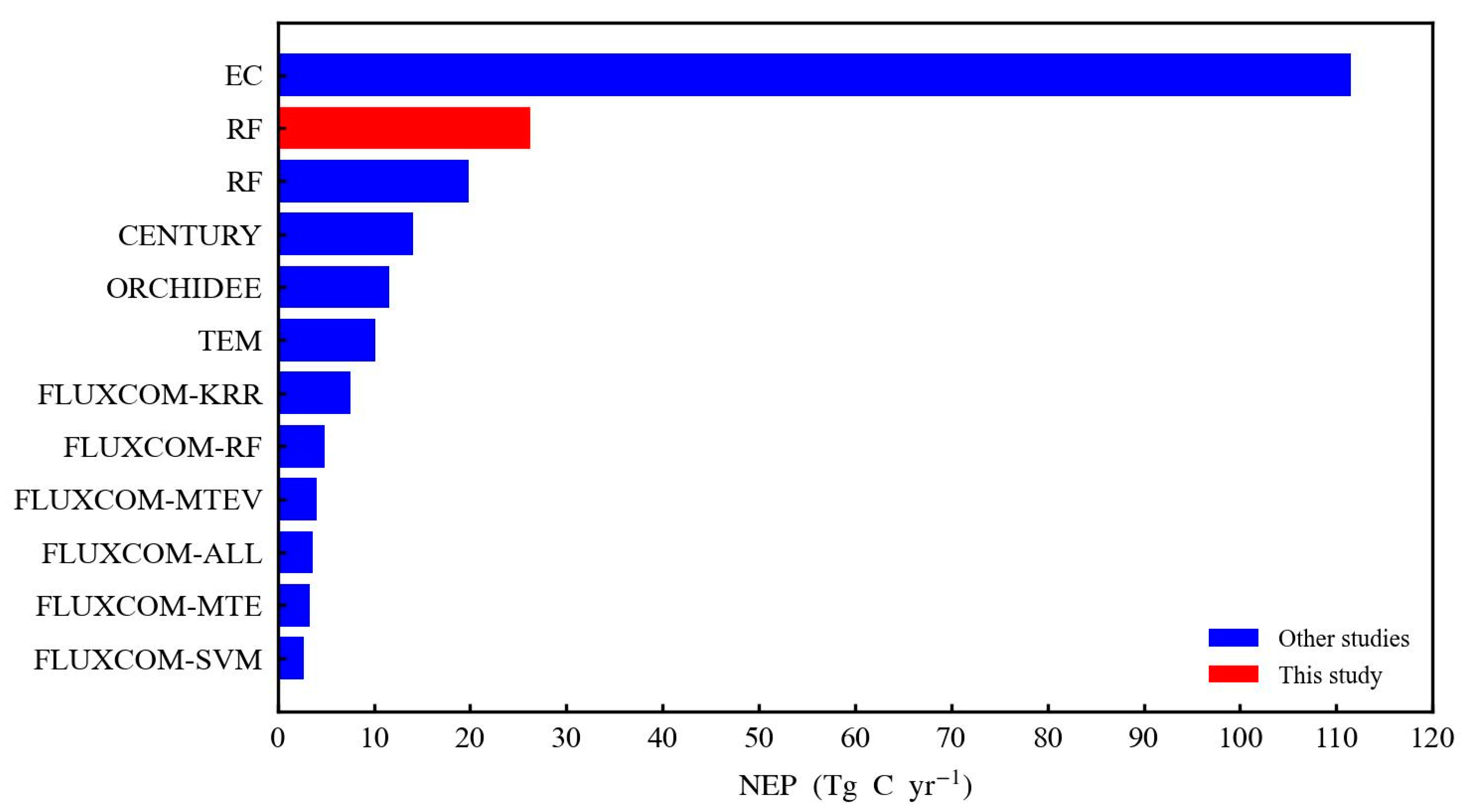
4.3. Comparison with Other Studies
4.4. Uncertainty and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahlstrom, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef]
- Scurlock, J.M.O.; Hall, D.O. The global carbon sink: A grassland perspective. Glob. Change Biol. 1998, 4, 229–233. [Google Scholar] [CrossRef]
- Smith, P.; Lanigan, G.; Kutsch, W.L.; Buchmann, N.; Eugster, W.; Aubinet, M.; Ceschia, E.; Béziat, P.; Yeluripati, J.B.; Osborne, B.; et al. Measurements necessary for assessing the net ecosystem carbon budget of croplands. Agric. Ecosyst. Environ. 2010, 139, 302–315. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Baldocchi, D.D.; Chen, J.; Richardson, A.D.; Melillo, J.M.; Davis, K.J.; Hollinger, D.Y.; Wharton, S.; et al. Assessing net ecosystem carbon exchange of U.S. terrestrial ecosystems by integrating eddy covariance flux measurements and satellite observations. Agric. For. Meteorol. 2011, 151, 60–69. [Google Scholar] [CrossRef]
- Wagle, P.; Xiao, X.; Scott, R.L.; Kolb, T.E.; Cook, D.R.; Brunsell, N.; Baldocchi, D.D.; Basara, J.; Matamala, R.; Zhou, Y. Biophysical controls on carbon and water vapor fluxes across a grassland climatic gradient in the United States. Agric. For. Meteorol. 2015, 214–215, 293–305. [Google Scholar] [CrossRef]
- Fu, Y.; Zheng, Z.; Yu, G.; Hu, Z.; Sun, X.; Shi, P.; Wang, Y.; Zhao, X. Environmental influences on carbon dioxide fluxes over three grassland ecosystems in China. Biogeosciences 2009, 6, 2879–2893. [Google Scholar] [CrossRef]
- Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.H.; Dashtseren, A.; Delaloye, R.; Elberling, B.; Etzelmüller, B.; Kholodov, A. Northern Hemisphere permafrost map based on TTOP modelling for 2000–2016 at 1 km2 scale. Earth-Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
- Scottdenning, A.; Randall, D.A.; Jamescollatz, G.; Sellers, P.J. Simulations of terrestrial carbon metabolism and atmospheric CO2 in a general circulation model. Part 2: Simulated CO2 concentrations. Tellus 2010, 48, 543–567. [Google Scholar]
- Yu, G.; Zhu, X.; Fu, Y.; He, H.; Wang, Q.; Wen, X. Spatial patterns and climate drivers of carbon fluxes in terrestrial ecosystems of China. Glob. Change Biol. 2013, 3, 798–810. [Google Scholar] [CrossRef]
- Piao, S.; He, Y.; Wang, X.; Chen, F. Estimation of China’s terrestrial ecosystem carbon sink: Methods, progress and prospects. Sci. China, Ser. D Earth Sci. 2022, 65, 641–651. [Google Scholar] [CrossRef]
- Dragoni, D.; Schmid, H.P.; Grimmond, C.S.B.; Loescher, H.W. Uncertainty of annual net ecosystem productivity estimated using eddy covariance flux measurements. J. Geophys. Res. Biogeosci. 2007, 112, D17102. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, J.; Ma, Y.; Luo, Y.; Hu, Z.; Li, F.; Li, Y.; Gu, L.; Li, Z.; Yuan, L. Carbon fluxes and environmental controls across different alpine grassland types on the Tibetan Plateau. Agric. For. Meteorol. 2021, 311, 108694. [Google Scholar] [CrossRef]
- Sun, S.; Che, T.; Li, H.; Wang, T.; Ma, C.; Liu, B.; Wu, Y.; Song, Z. Water and carbon dioxide exchange of an alpine meadow ecosystem in the northeastern Tibetan Plateau is energy-limited. Agric. For. Meteorol. 2019, 275, 283–295. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O′Sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Le Quéré, C.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget 2022. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Lin, X.; Han, P.; Zhang, W.; Wang, G. Sensitivity of alpine grassland carbon balance to interannual variability in climate and atmospheric CO 2 on the Tibetan Plateau during the last century. Glob. Planet. Change 2017, 154, 23–32. [Google Scholar] [CrossRef]
- Yan, L.; Zhou, G.; Wang, Y.; Hu, T.; Sui, X. The spatial and temporal dynamics of carbon budget in the alpine grasslands on the Qinghai-Tibetan Plateau using the Terrestrial Ecosystem Model. J. Cleaner Prod. 2015, 107, 195–201. [Google Scholar] [CrossRef]
- Piao, S.; Tan, K.; Nan, H.; Ciais, P.; Fang, J.; Wang, T.; Vuichard, N.; Zhu, B. Impacts of climate and CO2 changes on the vegetation growth and carbon balance of Qinghai–Tibetan grasslands over the past five decades. Glob. Planet. Change 2012, 98–99, 73–80. [Google Scholar] [CrossRef]
- Wu, T.; Ma, W.; Wu, X.; Li, R.; Qiao, Y.; Li, X.; Yue, G.; Zhu, X.; Ni, J. Weakening of carbon sink on the Qinghai–Tibet Plateau. Geoderma 2022, 412, 115707. [Google Scholar] [CrossRef]
- Xu, L.; Yu, G.; He, N.; Wang, Q.; Ge, J. Carbon storage in China’s terrestrial ecosystems: A synthesis. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef]
- Yu, G.; Wen, X.; Sun, X.; Tanner, B.D.; Lee, X.; Chen, J. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Kim, Y.; Johnson, M.S.; Knox, S.H.; Black, T.A.; Dalmagro, H.J.; Kang, M.; Kim, J.; Baldocchi, D. Gap-filling approaches for eddy covariance methane fluxes: A comparison of three machine learning algorithms and a traditional method with principal component analysis. Glob. Change Biol. 2020, 26, 1499–1518. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Dong, S.; Li, S.; Xu, Y.; Liu, S.; Zhao, H.; Yeomans, J.; Li, Y.; Shen, H.; Wu, S. Using the random forest model and validated MODIS with the field spectrometer measurement promote the accuracy of estimating aboveground biomass and coverage of alpine grasslands on the Qinghai-Tibetan Plateau. Ecol. Indic. 2020, 112, 106114. [Google Scholar] [CrossRef]
- Cai, J.; Xu, K.; Zhu, Y.; Hu, F.; Li, L. Prediction and analysis of net ecosystem carbon exchange based on gradient boosting regression and random forest. Appl. Energy 2020, 262, 114566. [Google Scholar] [CrossRef]
- Zhou, Q.; Fellows, A.; Flerchinger, G.N.; Flores, A.N. Examining Interactions Between and Among Predictors of Net Ecosystem Exchange: A Machine Learning Approach in a Semi-arid Landscape. Sci. Rep. 2019, 9, 2222. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, W.; Gao, S.; Zhang, K.; Huang, N. Estimating deciduous broadleaf forest gross primary productivity by remote sensing data using a random forest regression model. J. Appl. Remote Sens. 2019, 13, 038502. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Zeng, J.; Matsunaga, T.; Tan, Z.H.; Saigusa, N.; Shirai, T.; Tang, Y.; Peng, S.; Fukuda, Y. Global terrestrial carbon fluxes of 1999–2019 estimated by upscaling eddy covariance data with a random forest. Sci. Data 2020, 7, 313. [Google Scholar] [CrossRef]
- Jung, M.; Schwalm, C.; Migliavacca, M.; Walther, S.; Camps-Valls, G.; Koirala, S.; Anthoni, P.; Besnard, S.; Bodesheim, P.; Carvalhais, N.; et al. Scaling carbon fluxes from eddy covariance sites to globe: Synthesis and evaluation of the FLUXCOM approach. Biogeosciences 2020, 17, 1343–1365. [Google Scholar] [CrossRef]
- Cutler, D.R.; Jr, T.; Beard, K.H.; Cutler, A.; Hess, K.T. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Z.; Wang, T.; Chen, A.; Wang, X.; Du, M.; Jia, G.; Li, Y.; Li, H.; Luo, W.; et al. A new estimation of China’s net ecosystem productivity based on eddy covariance measurements and a model tree ensemble approach. Agric. For. Meteorol. 2018, 253–254, 84–93. [Google Scholar] [CrossRef]
- Yu, B.; Chen, F.; Chen, H. NPP estimation using random forest and impact feature variable importance analysis. J. Spatial Sci. 2017, 64, 173–192. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Comprehensive Evaluation of Machine Learning Techniques for Estimating the Responses of Carbon Fluxes to Climatic Forces in Different Terrestrial Ecosystems. Atmosphere 2018, 9, 83. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.; Fang, J.; He, J. Variations in Vegetation Net Primary Production in the Qinghai-Xizang Plateau, China, from 1982 to 1999. Clim. Change 2006, 74, 253–267. [Google Scholar] [CrossRef]
- Gregory, J.M.; Jones, C.D.; Cadule, P.; Friedlingstein, P. Quantifying Carbon Cycle Feedbacks. J. Clim. 2009, 22, 5232–5250. [Google Scholar] [CrossRef]
- Kato, T.; Tang, Y.; Gu, S.; Hirota, M.; Du, M.; Li, Y.; Zhao, X. Temperature and biomass influences on interannual changes in CO2 exchange in an alpine meadow on the Qinghai-Tibetan Plateau. Glob. Change Biol. 2006, 12, 1285–1298. [Google Scholar] [CrossRef]
- Zheng, D. The system of physico-geographical regions of the Qinghai-Xizang (Tibet) Plateau. Sci. China Ser. D Earth Sci. 1996, 39, 410–417. [Google Scholar]
- Ding, J.; Chen, L.; Ji, C.; Hugelius, G.; Li, Y.; Liu, L.; Qin, S.; Zhang, B.; Yang, G.; Li, F.; et al. Decadal soil carbon accumulation across Tibetan permafrost regions. Nat. Geosci. 2017, 10, 420–424. [Google Scholar] [CrossRef]
- Xu, X.; Liu, J.; Zhang, S.; Li, R.; Tan, C.; Wu, S. Multi-Period Remote Sensing Monitoring Data Set of Land Use in China. Registration and Publication System of Resources and Environmental Science Data. 2018. Available online: https://www.resdc.cn/doi/doi.aspx?DOIid=54 (accessed on 20 April 2022). [CrossRef]
- Wei, D.; Qi, Y.; Ma, Y.; Wang, X.; Ma, W.; Gao, T.; Huang, L.; Zhao, H.; Zhang, J.; Wang, X. Plant uptake of CO(2) outpaces losses from permafrost and plant respiration on the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2021, 118, e2015283118. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Xu, M.; Xi, Y.; Zhu, J.; Zhang, X.; Wang, Y.; Li, Y.; Shi, P.; Yu, G. Ecosystem response more than climate variability drives the inter-annual variability of carbon fluxes in three Chinese grasslands. Agric. For. Meteorol. 2016, 225, 48–56. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, Y.; Xu, M.; Zhao, G.; Chen, N.; Zheng, Z.; Zhu, J.; Ji, X.; Wang, D.; Zhang, Y.; et al. Joint control of alpine meadow productivity by plant phenology and photosynthetic capacity. Agric. For. Meteorol. 2022, 325, 109135. [Google Scholar] [CrossRef]
- Hashimoto, H.; Wang, W.; Milesi, C.; White, M.A.; Ganguly, S.; Gamo, M.; Hirata, R.; Myneni, R.B.; Nemani, R.R. Exploring Simple Algorithms for Estimating Gross Primary Production in Forested Areas from Satellite Data. Remote Sens. 2012, 4, 303–326. [Google Scholar] [CrossRef]
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tramontana, G.; Ichii, K.; Camps-Valls, G.; Tomelleri, E.; Papale, D. Uncertainty analysis of gross primary production upscaling using Random Forests, remote sensing and eddy covariance data. Remote Sens. Environ. 2015, 168, 360–373. [Google Scholar] [CrossRef]
- Vincenzi, S.; Zucchetta, M.; Franzoi, P.; Pellizzato, M.; Pranovi, F.; Leo, G.A.D.; Torricelli, P. Application of a Random Forest algorithm to predict spatial distribution of the potential yield of Ruditapes philippinarum in the Venice lagoon, Italy. Ecol. Model. 2011, 222, 1471–1478. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Sala, O.E.; Gherardi, L.A.; Peters, D.P.C. Enhanced precipitation variability effects on water losses and ecosystem functioning: Differential response of arid and mesic regions. Clim. Change 2015, 131, 213–227. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, Z.; Chen, A.; Yuan, W.; Hou, G.; Han, D.; Liang, M.; Di, K.; Cao, R.; Luo, D. The global decline in the sensitivity of vegetation productivity to precipitation from 2001 to 2018. Glob. Change Biol. 2022, 28, 6823–6833. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Xu, M.; Zhu, J.; Chen, N.; Jiang, Y.; Huang, K.; Zu, J.; Liu, Y.; Yu, G. Water availability is more important than temperature in driving the carbon fluxes of an alpine meadow on the Tibetan Plateau. Agric. For. Meteorol. 2018, 256, 22–31. [Google Scholar] [CrossRef]
- Lin, S.; Wang, G.; Feng, J.; Dan, L.; Sun, X.; Hu, Z.; Chen, X.; Xiao, X. A Carbon Flux Assessment Driven by Environmental Factors Over the Tibetan Plateau and Various Permafrost Regions. J. Geophys. Res. Biogeosci. 2019, 124, 1132–1147. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Huang, M.; Yao, Y.; Ciais, P.; Piao, S. Changes in interannual climate sensitivities of terrestrial carbon fluxes during the 21st century predicted by CMIP5 Earth System Models. J. Geophys. Res. Biogeosci. 2016, 121, 903–918. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Yuan, X.; Zhu, B. Effects of warming on carbon and nitrogen cycling in alpine grassland ecosystems on the Tibetan Plateau: A meta-analysis. Geoderma 2020, 370, 114363. [Google Scholar] [CrossRef]
- Li, C.; Peng, F.; Xue, X.; You, Q.; Lai, C.; Zhang, W.; Cheng, Y. Productivity and Quality of Alpine Grassland Vary With Soil Water Availability Under Experimental Warming. Front. Plant Sci. 2018, 9, 1790. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.S.; Yang, X.X.; Ren, F.; Zhang, Z.H.; He, J.S. Non-growth season’s greenhouse gases emission and its yearly contribution from alpine meadow on Tibetan Plateau of China. Chin. J. Ecol. 2013, 32, 1994–2001. [Google Scholar]
- Ganjurjav, H.; Gao, Q.; Gornish, E.S.; Schwartz, M.W.; Liang, Y.; Cao, X.; Zhang, W.; Zhang, Y.; Li, W.; Wan, Y. Differential response of alpine steppe and alpine meadow to climate warming in the central Qinghai–Tibetan Plateau - ScienceDirect. Agric. For. Meteorol. 2016, 223, 233–240. [Google Scholar] [CrossRef]
- Saito, M.; Kato, T.; Tang, Y. Temperature controls ecosystem CO2 exchange of an alpine meadow on the northeastern Tibetan Plateau. Glob. Change Biol. 2009, 15, 221–228. [Google Scholar] [CrossRef]
- Piao, S.; Friedlingstein, P.; Ciais, P.; Peylin, P.; Reichstein, M. Footprint of temperature changes in the temperate and boreal forest carbon balance. Geophys. Res. Lett. 2009, 36, L07404. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Schwalm, C.R.; Huntingford, C.; Sitch, S.; Ahlström, A.; Arneth, A.; Camps-Valls, G.; Ciais, P.; Friedlingstein, P.; et al. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 2017, 541, 516–520. [Google Scholar] [CrossRef]
- Chen, S.; Zou, J.; Hu, Z.; Lu, Y. Climate and Vegetation Drivers of Terrestrial Carbon Fluxes:A Global Data Synthesis. Adv. Atmos. Sci. 2019, 36, 679–696. [Google Scholar] [CrossRef]
- Chen, H.; Ju, P.; Zhu, Q.; Xu, X.; Wu, N.; Gao, Y.; Feng, X.; Tian, J.; Niu, S.; Zhang, Y.; et al. Carbon and nitrogen cycling on the Qinghai–Tibetan Plateau. Nat. Rev. Earth Environ. 2022, 3, 701–716. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, W.; Xue, K.; Wang, S.; Zhang, L.; Hu, R.; Zeng, H.; Xu, X.; Li, Y.; Jiang, L.; et al. Grassland changes and adaptive management on the Qinghai–Tibetan Plateau. Nat. Rev. Earth Environ. 2022, 3, 668–683. [Google Scholar] [CrossRef]
- Tang, L.; Dong, S.; Sherman, R.; Liu, S.; Liu, Q.; Wang, X.; Su, X.; Zhang, Y.; Li, Y.; Wu, Y.; et al. Changes in vegetation composition and plant diversity with rangeland degradation in the alpine region of Qinghai-Tibet Plateau. Rangel. J. 2015, 37, 107–115. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Xiao, J.; Ma, M.; Tan, J.; Wang, X.; Geng, L. Carbon fluxes across alpine, oasis, and desert ecosystems in northwestern China: The importance of water availability. Sci. Total Environ. 2019, 697, 133978. [Google Scholar] [CrossRef]
- Zhang, X. Vegetation map of the People’s Republic of China (1:1 000 000 000). Geol. Press 2007. Available online: https://www.plantplus.cn (accessed on 20 April 2022). [CrossRef]
- Yu, G.; Zhang, L.; Sun, X.; Li, Z.; Fu, Y. Advances in carbon flux observation and research in Asia. Sci. China Ser. D Earth Sci. 2005, 21, 1–16. [Google Scholar]
- Wang, Y.; Wang, X.; Wang, K.; Chevallier, F.; Zhu, D.; Lian, J.; He, Y.; Tian, H.; Li, J.; Zhu, J.; et al. The size of the land carbon sink in China. Nature 2022, 603, E7–E9. [Google Scholar] [CrossRef]
- Ingrisch, J.; Biermann, T.; Seeber, E.; Leipold, T.; Li, M. Carbon pools and fluxes in a Tibetan alpine Kobresia pygmaea pasture partitioned by coupled eddy-covariance measurements and 13CO2 pulse labeling. Sci. Total Environ. 2015, 505, 1213–1224. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Z.; Ma, Y. Data processing uncertainties may lead to an overestimation of the land carbon sink of the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2022, 119, e2202343119. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Li, Y.; Gu, S.; Zhao, X.; Xu, S.; Yu, G. Carbon Dioxide Exchange Between the Atmosphere and an Alpine Shrubland Meadow During the Growing Season on the Qinghai-Tibetan Plateau. J. Integr. Plant Biol. 2005, 47, 271–282. [Google Scholar] [CrossRef]
- Sitch, S.; Huntingford, C.; Gedney, N.; Levy, P.E.; Lomas, M.; Piao, S.L.; Betts, R.; Ciais, P.; Cox, P.; Friedlingstein, P.; et al. Evaluation of the terrestrial carbon cycle, future plant geography and climate-carbon cycle feedbacks using five Dynamic Global Vegetation Models (DGVMs). Glob. Change Biol. 2008, 14, 2015–2039. [Google Scholar] [CrossRef]
- Zhu, X.J.; Yu, G.R.; Chen, Z.; Zhang, W.K.; Han, L.; Wang, Q.F.; Chen, S.P.; Liu, S.M.; Wang, H.M.; Yan, J.H.; et al. Mapping Chinese annual gross primary productivity with eddy covariance measurements and machine learning. Sci. Total Environ. 2022, 857, 159390. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Yi, C.; Fang, W.; Hendrey, G. A global study of GPP focusing on light-use efficiency in a random forest regression model. Ecosphere 2017, 8, e01724. [Google Scholar] [CrossRef]
- Tian, H.; Melillo, J.; Lu, C.; Kicklighter, D.; Liu, M.; Ren, W.; Xu, X.; Chen, G.; Zhang, C.; Pan, S.; et al. China’s terrestrial carbon balance: Contributions from multiple global change factors. Glob. Biogeochem. Cycles 2011, 25, GB1007. [Google Scholar] [CrossRef]
| Station | Latitude (°N) | Longitude (°E) | Altitude (m) | Period | Ecosystem | NEP (g C m−2 yr−1) | Reference |
|---|---|---|---|---|---|---|---|
| Ali | 4270 | 33.38 | 79.7 | 2010–2011 | Steppe | 206.9 | [41] |
| Arou | 3033 | 38.03 | 100.45 | 2015 | Meadow | 31.7 | [41] |
| Batang | 4003 | 32.85 | 96.95 | 2017–2018 | Meadow | 429.6 | [41] |
| Bange | 4700 | 31.42 | 90.03 | 2014–2015 | Steppe | 314.0 | [41] |
| Dashalong | 3739 | 38.84 | 98.94 | 2015 | Meadow | −21.8 | [41] |
| Dangxiong | 4333 | 30.85 | 91.08 | 2004–2011 | Meadow | −35.7 | [42] |
| Guoluo | 3980 | 34.35 | 100.55 | 2010–2012 | Meadow | 25.3 | [41] |
| Haibei | 3250 | 37.60 | 101.33 | 2002–2004 | Meadow | 120.9 | [41] |
| Haiyan | 3140 | 36.95 | 100.85 | 2010.7–2011.7 | Meadow | 66.9 | [41] |
| Maoniuping | 3560 | 27.17 | 100.23 | 2012–2015 | Meadow | 161.8 | [41] |
| Maduo | 4316 | 34.63 | 97.32 | 2014 | Meadow | 164.8 | [41] |
| Muztag | 3668 | 38.66 | 74.95 | 2016 | Steppe | 60.2 | [41] |
| NamCo | 4730 | 30.72 | 90.98 | 2008–2009 | Steppe | 17.1 | [41] |
| Naqu | 4598 | 31.64 | 90.01 | 2012–2018 | Meadow | 3.0 | [43] |
| Shule | 3885 | 38.42 | 98.32 | 2009–2011 | Meadow | 43.4 | [41] |
| Tanggula | 5133 | 33.07 | 91.93 | 2007 | Meadow | −75.8 | [41] |
| Yakou | 4148 | 38.01 | 100.24 | 2015 | Meadow | 151.6 | [41] |
| Zoige | 3430 | 33.89 | 102.14 | 2010 | Meadow | 156.4 | [41] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Zhang, Y.; Wang, X.; Zhu, J.; Zhao, G.; Zheng, Z.; Tao, J.; Zhang, Y.; Li, J. Estimation of Net Ecosystem Productivity on the Tibetan Plateau Grassland from 1982 to 2018 Based on Random Forest Model. Remote Sens. 2023, 15, 2375. https://doi.org/10.3390/rs15092375
Zheng J, Zhang Y, Wang X, Zhu J, Zhao G, Zheng Z, Tao J, Zhang Y, Li J. Estimation of Net Ecosystem Productivity on the Tibetan Plateau Grassland from 1982 to 2018 Based on Random Forest Model. Remote Sensing. 2023; 15(9):2375. https://doi.org/10.3390/rs15092375
Chicago/Turabian StyleZheng, Jiahe, Yangjian Zhang, Xuhui Wang, Juntao Zhu, Guang Zhao, Zhoutao Zheng, Jian Tao, Yu Zhang, and Ji Li. 2023. "Estimation of Net Ecosystem Productivity on the Tibetan Plateau Grassland from 1982 to 2018 Based on Random Forest Model" Remote Sensing 15, no. 9: 2375. https://doi.org/10.3390/rs15092375
APA StyleZheng, J., Zhang, Y., Wang, X., Zhu, J., Zhao, G., Zheng, Z., Tao, J., Zhang, Y., & Li, J. (2023). Estimation of Net Ecosystem Productivity on the Tibetan Plateau Grassland from 1982 to 2018 Based on Random Forest Model. Remote Sensing, 15(9), 2375. https://doi.org/10.3390/rs15092375







