Next Article in Journal
Estimation of Pb and Cd Content in Soil Using Sentinel-2A Multispectral Images Based on Ensemble Learning
Next Article in Special Issue
Snow Cover and Climate Change and Their Coupling Effects on Runoff in the Keriya River Basin during 2001–2020
Previous Article in Journal
Coupling Progressive Deep Learning with the AdaBoost Framework for Landslide Displacement Rate Prediction in the Baihetan Dam Reservoir, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 9
10.3390/rs15092297
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Unmanned Aerial Vehicle-Based Structure from Motion Technique for Precise Snow Depth Retrieval—Implication for Optimal Ground Control Point Deployment Strategy

by
Song Shu
1,*,
Ok-Youn Yu
2,
Chris Schoonover
2,
Hongxing Liu
3 and
Bo Yang
4
1
Department of Geography and Planning, Appalachian State University, Boone, NC 28608, USA
2
Department of Sustainable Technology and the Built Environment, Appalachian State University, Boone, NC 28608, USA
3
Department of Geography, The University of Alabama, Tuscaloosa, AL 35487, USA
4
Department of Urban and Regional Planning, San Jose State University, San Jose, CA 95192, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(9), 2297; https://doi.org/10.3390/rs15092297
Submission received: 5 February 2023 / Revised: 20 April 2023 / Accepted: 24 April 2023 / Published: 27 April 2023
(This article belongs to the Special Issue Remote Sensing of Cryosphere and Related Processes)
Browse Figures
Review Reports Versions Notes

Abstract

:
Unmanned aerial vehicle (UAV)-based snow depth is mapped as the difference between snow-on and snow-off digital surface models (DSMs), which are derived using the structure from motion (SfM) technique with ground control points (GCPs). In this study, we evaluated the impacts of the quality and deployment of GCPs on the accuracy of snow depth estimates. For 15 GCPs in our study area, we surveyed each of their coordinates using an ordinary global positioning system (GPS) and a differential GPS, producing two sets of GCP measurements (hereinafter, the low-accuracy and high-accuracy sets). The two sets of GCP measurements were then incorporated into SfM processing of UAV images by following two deployment strategies to create snow-off and snow-on DSMs and then to retrieve snow depth. In Strategy A, the same GCP measurements in each set were used to create both the snow-on and snow-off DSMs. In Strategy B, each set of GCP measurements was divided into two sub-groups, one sub-group for creating snow-on DSMs and the other sub-group for snow-off DSMs. The accuracy of snow depth estimates was evaluated in comparison to concurrent in-situ snow depth measurements. The results showed that Strategy A, using both the low-accuracy and high-accuracy sets, generated accurate snow depth estimates, while in Strategy B, only the high-accuracy set could generate reliable snow depth estimates. The results demonstrated that the deployment of GCPs had a significant influence on UAV-based SfM snow depth retrieval. When accurate GCP measurements cannot be guaranteed (e.g., in mountainous regions), Strategy A is the optimal option for producing reliable snow depth estimates. When highly accurate GCP measurements are available (e.g., collected by differential GPS in open space), both deployment strategies can produce accurate snow depth estimates.

1. Introduction

Over one billion of people around the world rely on snowmelt water for domestic, agricultural, and industrial activities [1]. Snow accumulation in the winter season shows a rapidly decreasing trend in recent decades for North America in terms of snow depth [2], snow cover extent [3], and snow mass [4]. In particular, the continental-scale snowmelt water originating from mountainous regions is in steep decline [5]. To better understand its impact on the environment and human activities, it is necessary to accurately monitor winter snow accumulation and its dynamics in mountain ranges.
The amount of water contained in snowpack (snow water equivalent, or SWE) is jointly determined by snow density and snow depth. It has been documented in previous studies that snow depth has much stronger spatial variation than snow density [6,7,8]. The accurate mapping of snow depth is therefore critical for the estimation of SWE. Traditionally, snow depth is monitored by automated sensors at weather stations or measured manually using a snow probe in field surveys. These methods are typically limited to point-based locations or cover very sparse areas. Remote sensing technologies have also been used to derive snow depth information, such as satellite laser altimetry [9], passive microwave remote sensing systems [10,11,12,13], and snow radar systems [14,15,16]. Although these technologies have made positive contributions to snow depth mapping in relatively open space with gentle topography, their performances are mostly unsatisfactory in mountain ranges where snow accumulation varies drastically along with rapid changes in topography and vegetation within a short distance [17,18,19]. It has been proven that accurate estimation of snow accumulation in mountain ranges is hampered by the complex topography and varying vegetation cover [20,21,22]. The airborne LiDAR system has also been used to retrieve snow depth [23] and is a promising technique for mapping snow accumulation in mountainous regions. This technique, because of its high cost, is inapplicable for monitoring snow accumulation dynamics since this requires frequent and repeated observations. A more nuanced, efficient, flexible, and economic method that can accommodate the mountain environment and simultaneously provide accurate snow depth mapping is needed, particularly for a relatively small area and for ephemeral snowpack.
In recent years, the possibility of retrieving snow depth with unmanned aerial vehicle (UAV)-based structure from motion (SfM) photogrammetry has been discussed in a number of studies [24,25,26,27,28,29,30,31,32,33,34] due to the advancement of UAV technology, the development of low-cost lightweight cameras, and the availability of open-source and commercial SfM software packages. Compared to airborne and spaceborne remote sensing platforms, the prominent advantages of UAV-based SfM photogrammetry are its lower demand of personnel training, lower cost for purchasing and maintaining the equipment, and much higher flexibility for inaccessible areas (e.g., cliffs and valleys) and undesirable weather conditions (e.g., rain, strong wind, and heavy cloud). The basic idea of this method is to collect overlapping photos of a study area (e.g., open or vegetated, flat or rugged) with a UAV-based optical camera on snow-on and snow-off dates. Then, digital surface models (DSMs) of the study area are generated for each of the two dates by stitching the overlapping photos with an SfM workflow that has been implemented in many software packages [35]. The surface elevation increase due to snow accumulation over the study area is then calculated by differencing the two DSMs and treated as snow depth estimates. In general, the snow depth accuracy varies from several centimeters to several decimeters depending on the surface roughness, ground topography, and underlying vegetation [26,28,32,34].
In addition to the environmental characteristics of the snow accumulation field (i.e., topography, vegetation, surface roughness, etc.), the quality of snow-on and snow-off DSMs generated by SfM is a more dominant factor that determines the accuracy of UAV-based snow depth estimates. Two options are mostly adopted in existing studies to constrain the errors in DSMs and to improve snow depth accuracy. The first one uses an expensive real-time kinematic (RTK) UAV to collect optical photos of which the coordinates can be georeferenced to an accuracy of 2–4 cm by on-board RTK correction [26,27,33]. The accurate photo locations are then used directly to constrain the DSM uncertainties. In the second option, a regular customer-grade UAV is used to collect photos. Then, ground control points (GCP) evenly distributed across the study area are incorporated in SfM processing to reduce DSM errors [24,25,28,29,32,34]. The GCPs are often accurately surveyed with an RTK or post-processing kinematic (PPK) differential global positioning system (DGPS). Vander Jagt, Lucieer and Wallace et al. [27] compared the two options and reported that incorporating GCPs in the generation of DSM can produce a lower root mean square error (RMSE) between UAV-based snow depth estimates and in-situ measurements than simply using RTK UAV. Additionally, if a minimal number of GCPs is jointly used with RTK UAV, the RMSE can be further reduced. Harder, Schirmer and Pomeroy et al. [26] also suggested that inclusion of GCPs for RTK UAV would result in a great reduction of DSM bias, thus increasing the accuracy of snow depth estimates. Both studies indicated the necessity of incorporating GCPs for accurate snow depth retrieval with UAV-based SfM photogrammetry.
RTK UAV is a promising solution for snow depth mapping over inaccessible areas (e.g., areas susceptible to snow avalanche) [33]. The much higher cost of an RTK UAV than a regular customer-grade UAV limits its wide application in snow depth mapping. Most existing studies used a regular UAV to collect photos and incorporated GCPs to constrain DSM errors [24,28,31,32,34] and then retrieve snow depth. Lee, Park, Choi and Kim et al. [24] evaluated the influence of the number of GCPs on the accuracy of UAV-based snow depth and concluded that areas with higher densities of GCPs tended to have more accurate snow depth estimates. In other words, the more GCPs included, the better the snow depth accuracy. In these studies, GCPs over the study area were surveyed twice, one for snow-on date and one for snow-off date. The snow-on GCPs were usually differently from the snow-off GCPs. The two different sets of GCPs were used to produce the snow-on and snow-off DSMs, respectively. With this strategy, the errors in snow-on GCP coordinates (x, y, z) were completely independent from the errors in snow-off GCP coordinates. These errors could be propagated independently into the corresponding snow-on and snow-off DSMs, thus affecting the retrieved snow depth accuracy. However, no study has investigated how the errors in GCP coordinates influence UAV-based snow depth retrieval and how to improve the accuracy of snow depth estimates when DGPS performance is hampered by the surrounding environment.
The overall objective of this paper was to assess in detail the influence of GCP errors on the accuracy of snow depth measurements estimated by UAV-based SfM photogrammetry. Specifically, this paper (1) assesses how the errors in GCP horizontal coordinates (x, y) and vertical height (z) influence the accuracy of snow depth estimates; and (2) discusses the optimal GCP deployment strategy that can accommodate the errors in GCP coordinates (x, y, z) to help produce better snow depth estimates. The remainder of this paper is organized as follows: Section 2 describes the study area and the collection of UAV-based photos and in-situ snow depth data. Section 3 introduces SfM concepts and GCP deployment strategies. Section 4 presents the performance of UAV-based snow depth retrieval using different GCP deployment strategies. Section 5 analyzes the results and discusses the strategy of improving snow depth estimates.

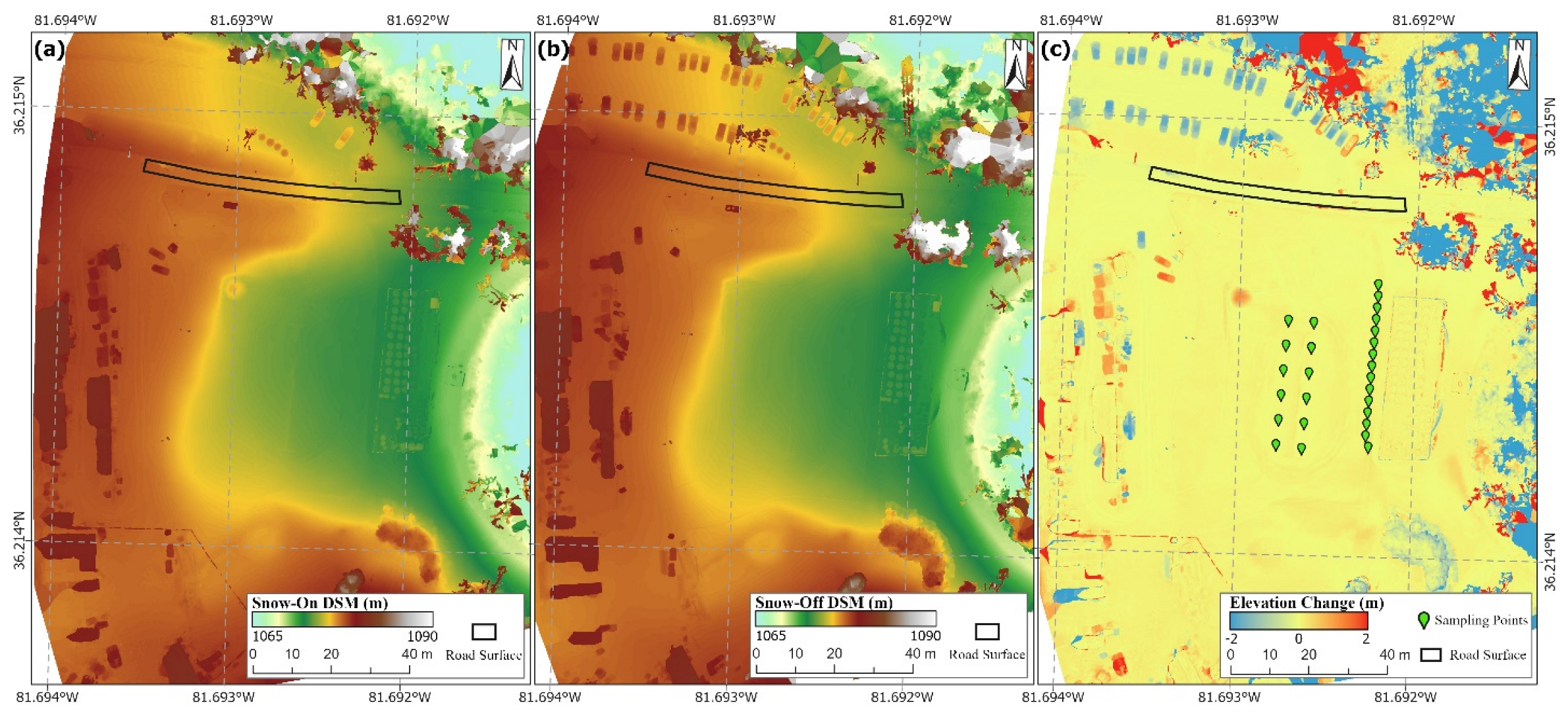
2. Study Area and Data Collection

Our study area was located in the southern Appalachian Mountains at 36.215°N and 81.693°W, close to the Blue Ridge Parkway, which is the longest linear national park way in the U.S. The elevation was about 1070 m above mean sea level. The study area was beside a wind turbine near the campus of Appalachian State University in Boone, western North Carolina. It was a small open space surrounded by trees and shrubs with different heights. As shown in Figure 1, the extent of the study area was approximately 120 m × 150 m. The surface elevation decreased gradually from the west to the east (as shown in Figure 2a,b), while the middle part of the study area was relatively flat with a slope less than 3°. This study area was chosen as an ideal place for experimenting UAV-based SfM snow depth retrieval for the following reason. In the winter, mountainous areas often experience frequent wind gusts, which have a strong redistributing effect on snow accumulation. Our study area was close to a wind turbine. It represented a typical small open space in the Appalachian Mountains for snow accumulation that is heavily influenced by winter wind. In this mountainous region, the mean annual snowfall can vary from several decimeters to two meters [36,37,38]. On 8 January 2021, a snow storm struck Boone and yielded an average snow accumulation of 10.16 cm (4 inches) on that day and another 5.08 cm (2 inches) in the morning of January 9 (National Weather Service, https://www.weather.gov/wrh/Climate?wfo=rnk, accessed on 23 April 2023).
We used a DJI Phantom 4 quadcopter UAV to collect photos of the study area right after snowfall at 3:30 p.m. on 9 January 2021 and after snowmelt at 3:40 p.m. on 24 February 2021. The DJI Phantom 4 is a customer-grade UAV that carries a low-cost CMOS camera, which well-suited the purpose of this study. The camera has a field of view (FOV) of 84° and focal length of 8.8 mm (comparable to 24 mm focal length on a 35 mm film camera). The dimension of each photo is 5472 × 3648. The photos were acquired at an above-ground height of 45.72 m (150 feet). The front and side overlapping rates are 70% and 80%, respectively. The ground sampling distance (spatial resolution) of the generated orthophoto and DSM is about 1.5 cm.
Concurrent in-situ snow depths accurate to one tenth of a centimeter were measured using a snow probe at 27 sampling points in the study area, as shown by the green points in Figure 1. These in-situ snow depths ranged from 5.0 to 29.3 cm. Compared to the 12 points on the left side, the 15 points on the right side had relatively higher depths (ranging from 15.0 to 29.3 cm) due to the blocking effect of the fence on the east of the 15 sampling points. We also surveyed 15 ground control points (red diamonds in Figure 1) across the entire study area using two GPS instruments, including the handheld Trimble GeoXH and the Trimble DA2 GNSS receiver. All 15 GCPs were free from snow cover on the two dates. The Trimble DA2 uses the real-time kinetic (RTK) technique and is able to achieve horizontal and vertical accuracies of 1 and 2 cm, respectively, under optimal conditions. The coordinates (x, y, z) measured by the Trimble GeoXH were not processed with any differential correction. The survey generated two sets of GCP measurements, one set with highly accurate coordinates and the other with low accuracy coordinates (hereinafter referred to as the high-accuracy and low-accuracy sets). To verify the accuracies of the two sets of GCPs, we also measured the coordinates of the 15 GCPs using a Nikon NPL-322 Series Total Stations, which provides measurements of the GCP coordinates at a millimeter-level accuracy for the spatial scale of our study area. Compared to the coordinates (x, y, z) measured by the total stations, the root mean square error (RMSE) values of the high-accuracy set coordinates were 3.08, 3.02, and 7.0 cm, respectively, and the RMSE values of the low-accuracy set coordinates were 30.25, 40.84, and 78.34 cm, respectively.

3. Methodology

In this study, the optical photos collected on the snow-on and snow-off dates were separately processed using ERSI Drone2Map software, which implemented the general SfM workflow described in Section 3.1 to generate orthophotos and DSMs for the two dates. The high-accuracy and low-accuracy sets of GCP measurements were incorporated into the SfM workflow following the strategies described in Section 3.2 in order to reduce the errors in DSMs and orthophotos and to georeference them to a real-world coordinate system. Figure 1a,b shows the orthophotos of the two dates. The SfM-based snow depth over the study area were then derived by subtracting snow-off DSM from snow-on DSM. Figure 2a,b shows the DSMs on the two dates and Figure 2c shows the derived elevation change. The accuracy of SfM-based snow depth (elevation change) was evaluated in comparison to the concurrent in-situ snow depths at the sampling points in Figure 2c (green points) with the metrics described in Section 3.3.

3.1. Generation of DSM and Orthophoto with SfM

The structure from motion (SfM) technique originated from the field of computer vision and has been implemented by many software packages, for example, ESRI Drone2Map used in this study. In general, the SfM workflow consists of the following five steps [39,40]: (1) identifying keypoints (e.g., corners, line ends, intersections, etc.) from each photo using the scale invariant feature transform (SIFT) algorithm [41,42]; (2) matching the correspondence keypoints in the overlapping areas of two adjacent photos using the approximate nearest neighbor k-dimensional trees approach [43]; (3) removing the outlier keypoints using the random sample consensus (RANSAC) approach [44]; (4) determining the extrinsic camera parameters (referred to as “motion”) for each photo, such as camera location and orientation, and simultaneously estimating the 3D position of each keypoint (referred to as “structure” or sparse point cloud) by solving and optimizing a set of collinearity equations [27]; (5) generating a dense 3D point cloud for each pixel on each photo based on the sparse point cloud and the camera parameters obtained in Step 4 by applying a patch-based multi-view stereo image matching [45].
In Step 4, initial values of the extrinsic camera parameters are first obtained from the EXIF tags of UAV-collected photos, and they are used to estimate the 3D positions of keypoints through collinearity equations [39]. The camera parameters and keypoint positions are then further refined by optimizing a non-linear cost function that represents the errors between the observed and estimated keypoint positions on UAV-collected photos. The optimization process is called bundle adjustment and is the step at which GCPs are incorporated. The objectives of incorporating GCPs are twofold. First, it can help constrain the non-linear cost function and refine the camera parameters and keypoint positions. Second, it helps georeference the original sparse point cloud from the arbitrary coordinate system to a real-world geographic or projected coordinate system. A seven-parameter linear similarity transformation (i.e., three global translation parameters, three rotation parameters, and one scaling parameter) is performed to achieve the georeferencing [39]. The coordinate system used for this study was NAD 1983 StatePlane North Carolina (2011). DSMs and orthophotos are then generated based on the refined camera parameters and dense 3D point cloud.

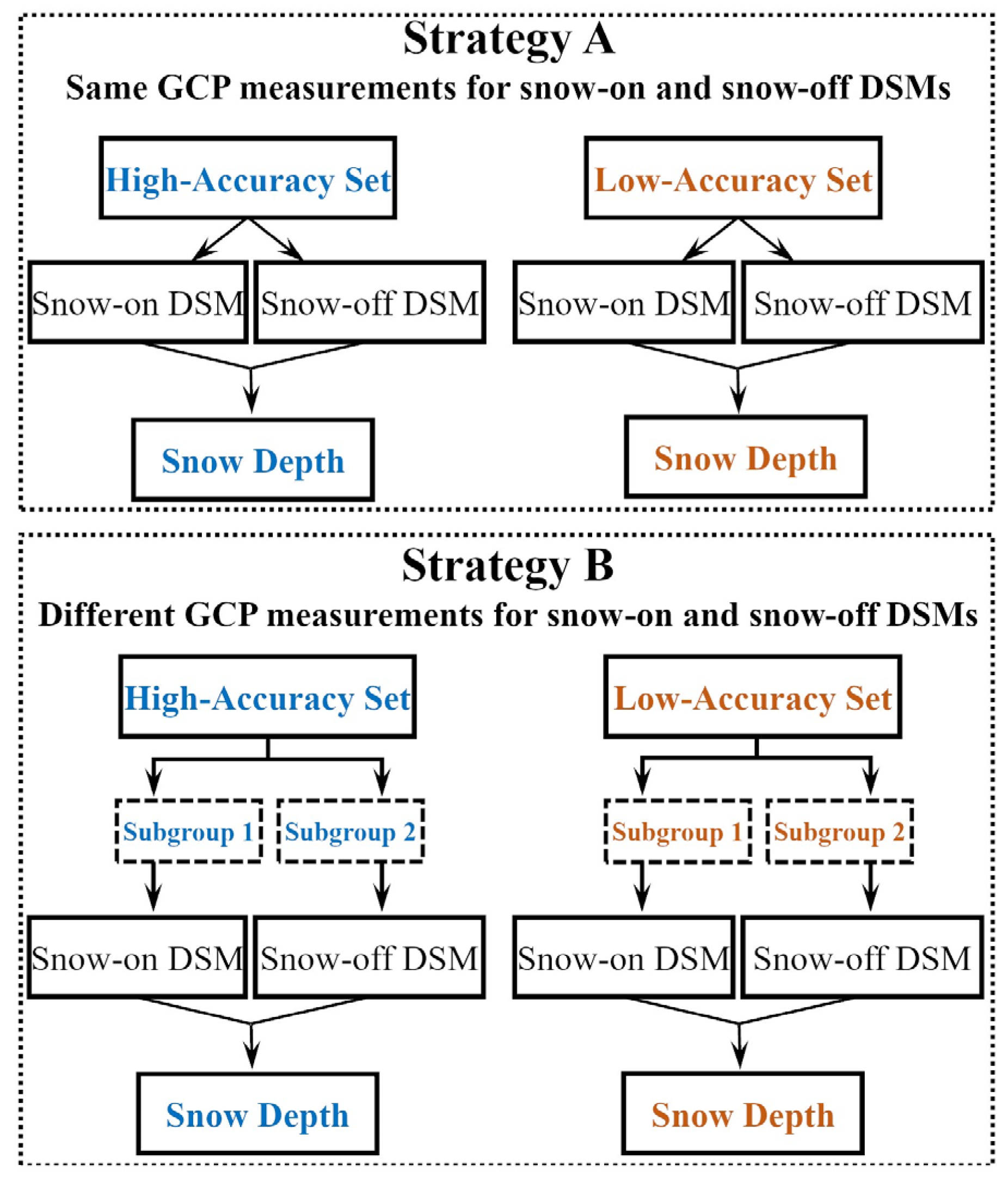
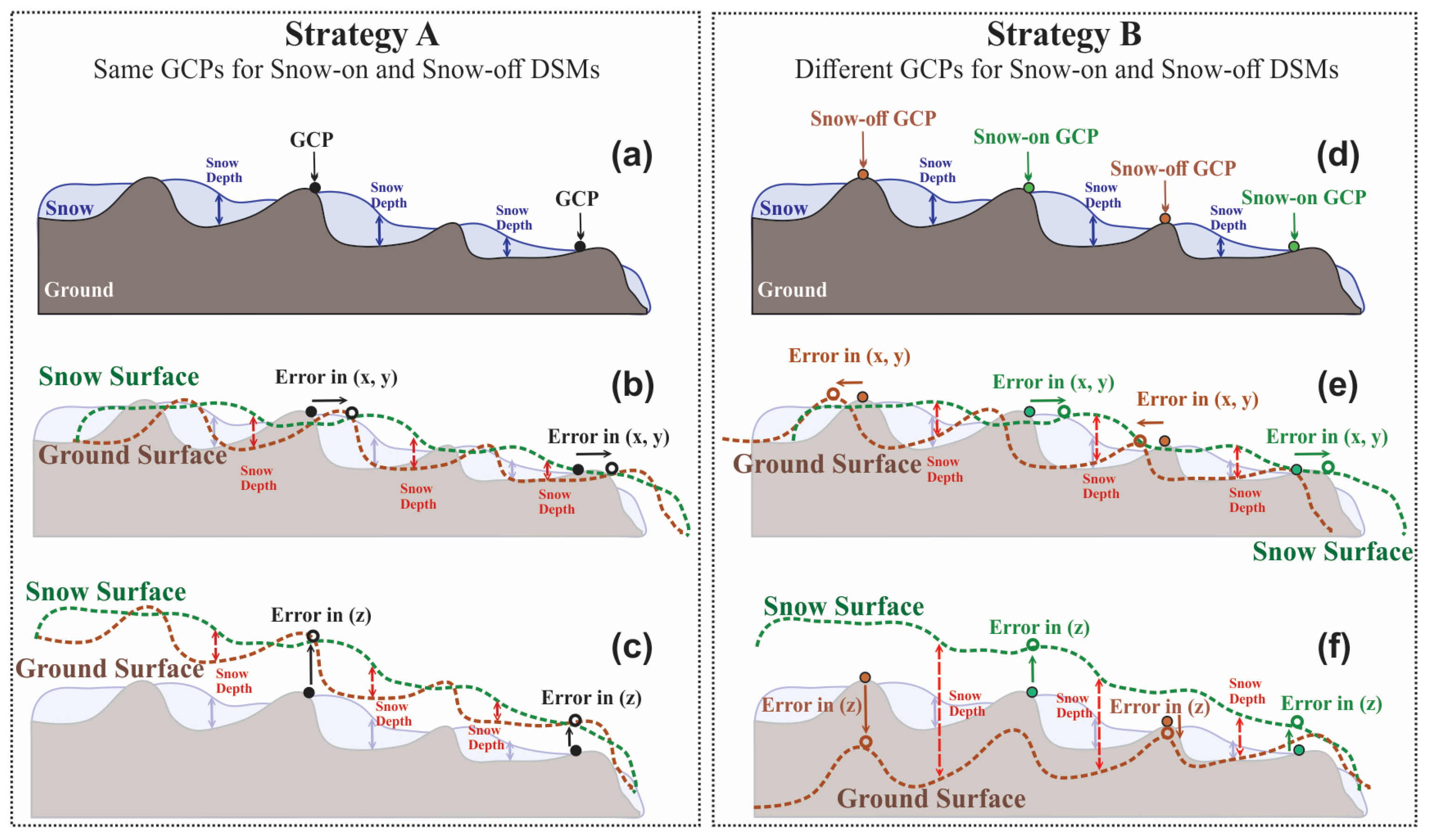
3.2. Strategy of Incorporating GCPs in SfM

Two sets of GCP measurements, the high-accuracy and low-accuracy sets, were collected for our study area. To assess the influences of GCP measurement accuracy and GCP deployment strategy on snow depth retrieval, each set of GCP measurements was incorporated into SfM by following two strategies to produce DSMs.
In Strategy A, the same GCP measurements in each set (hereinafter referred to as the Same-GCP strategy) were used to generate both the snow-on and snow-off DSMs and then to estimate snow depth, as shown in Figure 3. We incorporated all 15 GCP measurements at the beginning (Step 1 in Table 1) to generate the two DSMs and estimate snow depth. Then, we removed one GCP measurement at each of the following steps. For example, in Step 2 in Table 1, GCP 4 was removed. The coordinate measurements of the other 14 GCPs (1–3, 5–15) were used to produce the snow-on and snow-off DSMs.
In Strategy B, different GCP measurements in each set (hereinafter referred to as the Different-GCP strategy) were used to generate the snow-on and snow-off DSMs. As shown in Figure 3, the 15 GCP measurements in each set were divided into two subgroups, one subgroup for generating the snow-on DSMs and the other subgroup for the snow-off DSMs. At the beginning (Step 8 in Table 1), each subgroup had eight GCP measurements (with GCP 6 in Figure 1 shared by the two subgroups). Then, one GCP measurement was removed from each of the two subgroups at each step to generate the two DSMs. For example, in Step 9 in Table 1, GCP 3 was removed from subgroup 1 and GCP 10 was removed from subgroup 2. The remaining GCP measurements in the two subgroups were then used to produce the snow-on and snow-off DSMs, respectively. The GCPs in each sub-group were evenly distributed across the study area to ensure that the in-situ snow depth sampling points were encompassed by the GCPs.
Strategy B in this study, the Different-GCP strategy, replicated the approach used by most previous studies to incorporate GCPs and estimate snow depth [24,31,32,34]. Strategy A served as a reference for Strategy B. By comparing the results of the high-accuracy and low-accuracy sets under the two strategies, we were able to assess how SfM-based snow depth retrieval is influenced by the errors in GCP coordinate measurements and how GCP deployment strategies can help to mitigate the influence of the errors.
To further separate and evaluate the influences of horizontal (x, y) and vertical (z) coordinate errors on SfM-based snow depth retrieval, we replaced the GCP heights (z) in the low-accuracy set with the GCP heights in the high-accuracy set. This created a new set of GCPs with relatively inaccurate horizontal coordinates and accurate vertical coordinates, which was referred to as the accurate-Z set. We also created an accurate-XY set by replacing the GCP horizontal coordinates (x, y) in the low-accuracy set with the horizontal coordinates in the high-accuracy set. These two sets of GCPs were then incorporated into SfM following Strategy B in Table 1 to generate DSMs and estimate snow depth.

3.3. Assessment of SfM-Based Snow Depth Accuracy

For surfaces not covered by snow (e.g., the road surface in Figure 1, which had been cleared after snowfall), the elevation was supposed to remain the same in both snow-off and snow-on DSMs and the derived snow depth (i.e., elevation change) should be close to zero. When the snow depth estimates on the road surface have a systematic (positive or negative) deviation from zero, a bias between the two DSMs is observed. This bias could be wrongly interpreted as snow accumulation or depletion. This study used the road surface to estimate and remove bias in the derived snow depth. The bias was estimated as the mean value of snow depth within the black polygon on the road surface in Figure 1.
The accuracy of SfM-based snow depth was assessed in comparison to the in-situ snow depths measured at the 27 sampling points in Figure 1. At each sampling point, the SfM-based snow depth was estimated by an inverse-distance interpolation of the elevation changes in the surrounding 9 pixels (in a 3 × 3 neighborhood). The accuracy was measured by the Pearson correlation coefficient r [46], the root mean square error (RMSE), and the slope of regression between in-situ snow depth and SfM-based snow depth at the 27 sampling points. The RMSE represents the absolute accuracy of SfM-based snow depth. The smaller the RMSE, the higher the accuracy. The correlation coefficient r represents the capability of the SfM-based technique to capture the variation in snow depth across the study area. The closer the r value is to one, the stronger the capability. The slope of regression represents the tendency to over-estimate or under-estimate snow depth. Ideally, the slope value should be equal to one. If the intercept of regression equals zero, a slope of regression larger than one usually indicates a tendency to overestimate snow depth, whereas a slope less than one means a tendency to underestimate snow depth.

4. Results

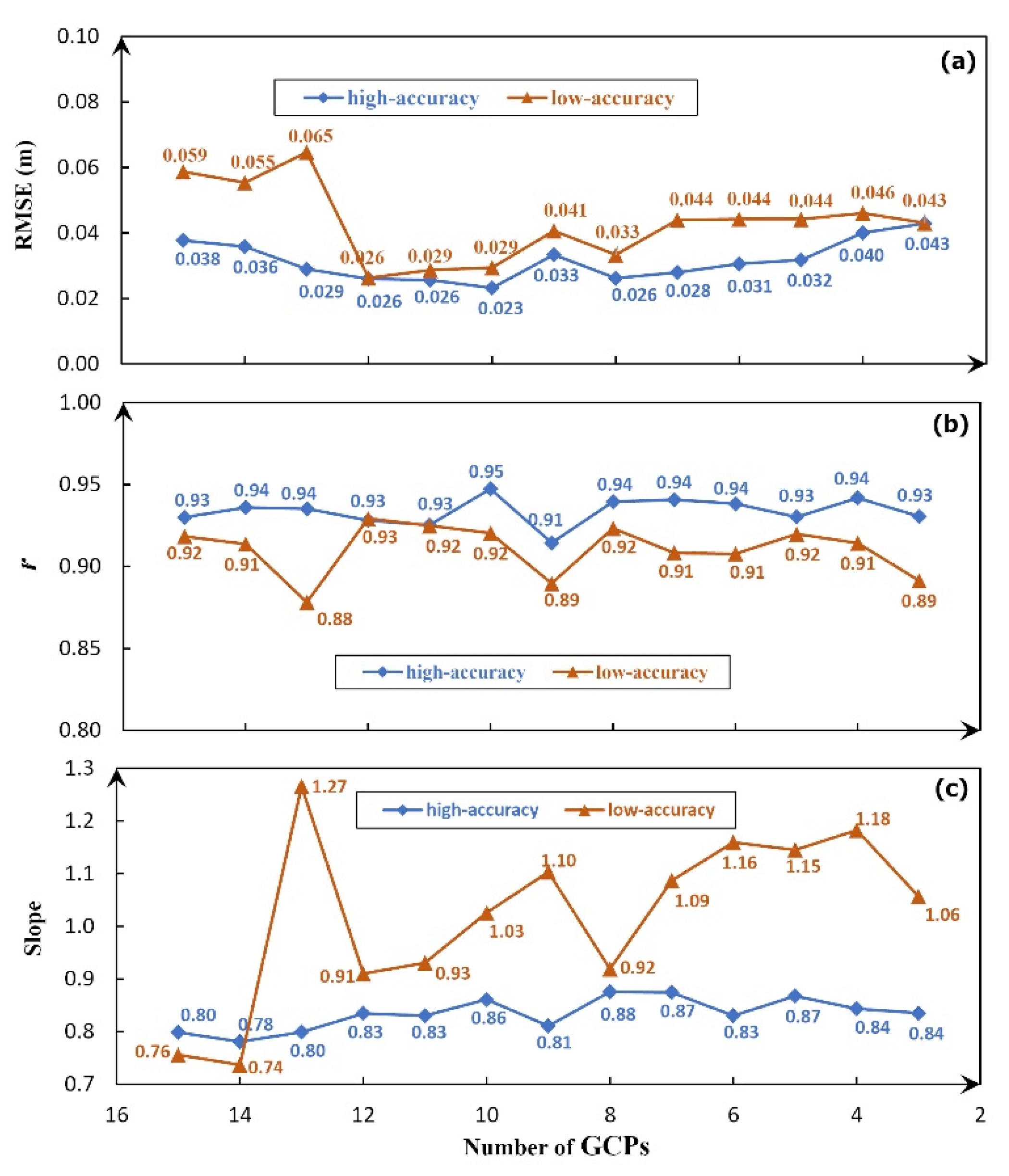
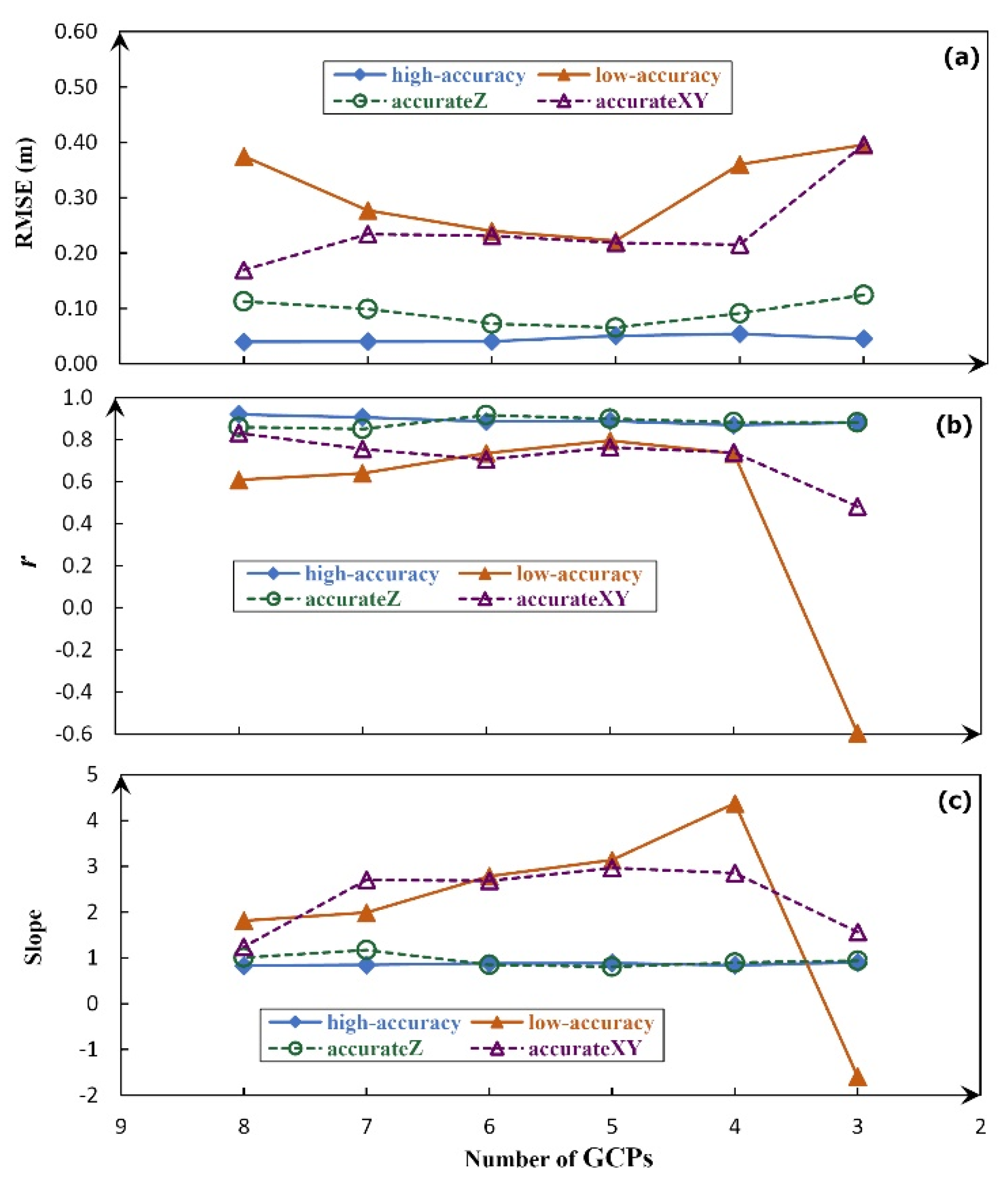
4.1. Strategy A: High-Accuracy Set Verses Low-Accuracy Set

The high-accuracy set of GCP measurements was first incorporated into SfM following Strategy A (the Same-GCP strategy) to generate DSMs and orthophotos for the two dates and then to derive snow depth estimates. The low-accuracy set was also incorporated in the same way to derive snow depth estimates. Figure 4 shows the scatterplots of SfM-based snow depth estimates against in-situ snow depths for the two sets of GCP measurements. Figure 5 shows the variations in RMSE, correlation coefficient r and linear regression slope along with the number of incorporated GCPs.
As expected, the high-accuracy set of GCP measurements produced better results than the low-accuracy set in terms of the three metrics. The RMSE values of the high-accuracy set ranged from 2.3 to 4.3 cm, slightly better than the RMSE values of the low-accuracy set that ranged from 2.6 to 6.5 cm. The correlation coefficient r and regression slope of the high-accuracy set remained quite stable along with the number of incorporated GCPs, as shown in Figure 5, whereas clear variations were observed for the low-accuracy set. The correlation coefficients were mostly higher than 0.9 for both sets.
The regression slope of the high-accuracy set was less than one (around 0.85) all the time, indicating an underestimation of snow depth. For the low-accuracy set, the regression slope was less than one when all GCPs were incorporated at the beginning. It increased with the removal of GCPs and remained mostly larger than one (around 1.1) when the number of GCPs was less than and equal to 10. This suggested that when using the low-accuracy set of GCPs, the snow depth was underestimated at the beginning, then became slightly overestimated as the number of GCP decreased. This trend can be clearly observed in Figure 4 when the number of GCPs decreased from 14 to 4.
Another interesting observation is that as shown in Figure 5a for both sets, the RMSE values gradually decreased as GCPs were removed at each step and then increased when GCPs were further removed. The highest accuracies occurred when the number of GCPs was 12 for the low-accuracy set and 10 for the high-accuracy set. This suggested that when using the Same-GCP strategy, more GCPs did not necessarily produce more accurate snow depth estimates. In general, the Same-GCP strategy helped generate highly accurate snow depth estimates. With this strategy, the low-accuracy set of GCPs could generate snow depth estimates with an accuracy comparable to that of the high-accuracy set. One thing to note is that in Figure 5 there was a relatively big jump in RMSE, r, and regression slope when the number of GCPs decreased to 13. This was possibly caused by the large errors in coordinate measurements of GCP 5 in Figure 1. After the removal of this GCP, the three indicators became more stable.

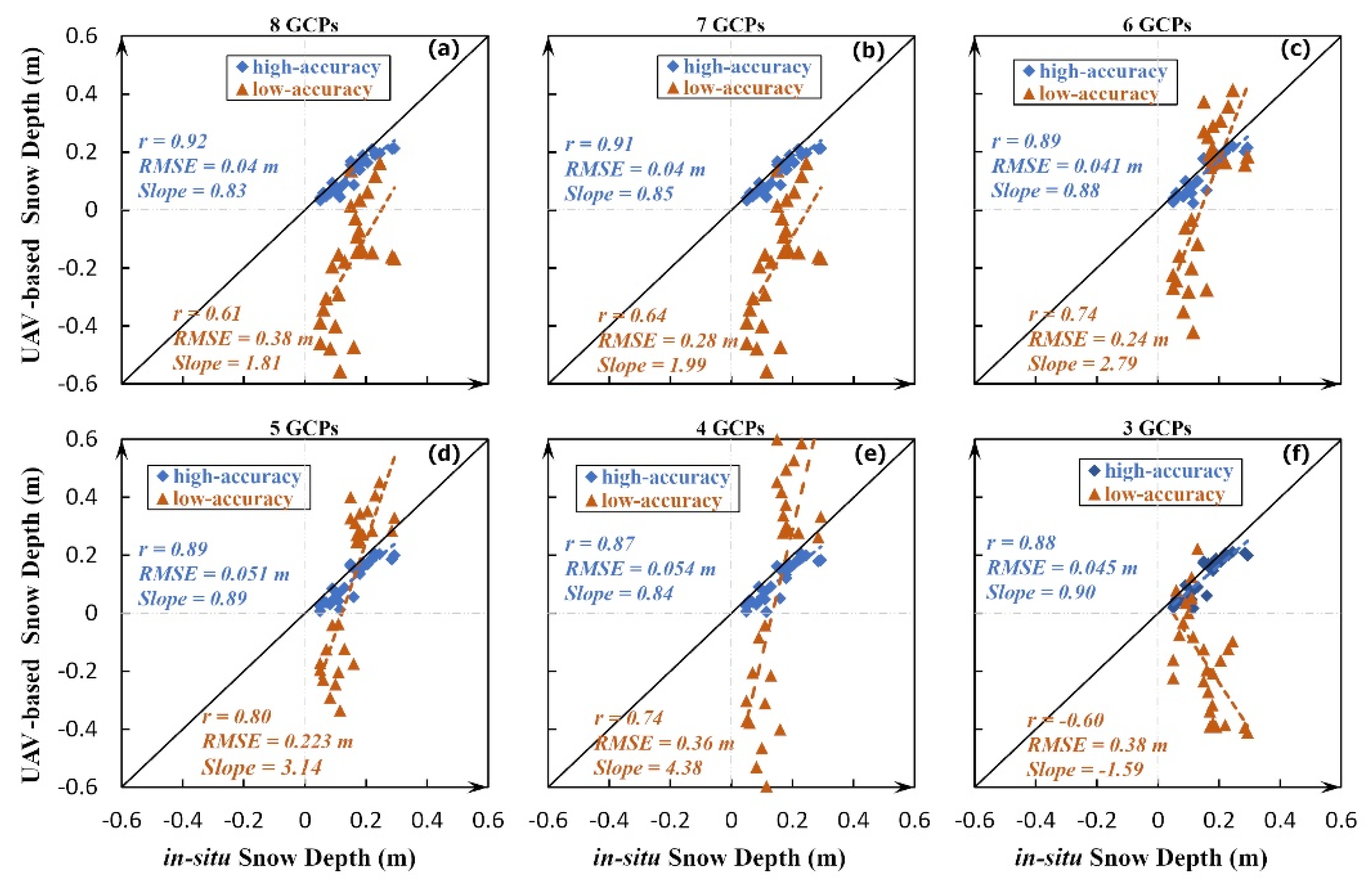
4.2. Strategy B: High-Accuracy Set Verses Low-Accuracy Set

The high-accuracy and low-accuracy sets of GCP measurements were also incorporated following Strategy B (the Different-GCP strategy) to estimate snow depth for our study area. Figure 6 shows the scatterplots of SfM-based snow depth estimates against in-situ snow depths. For the high-accuracy set of GCP measurements, the accuracy of SfM-based snow depth estimates was still quite high, even though its performance in terms of the three metrics was slightly inferior to that of Strategy A (the Same-GCP strategy). The correlation between snow depth estimates and in-situ snow depths was strong, with r varying from 0.87 to 0.92. The regression slopes remained stably less than one (around 0.85), which was consistent with Strategy A and indicated an underestimation of snow depth. The RMSE values were slightly higher than those in Strategy A and increased from 4.0 to 5.4 cm when the number of GCPs decreased from 8 to 3, indicating a degradation in accuracy when fewer GCPs were incorporated. This echoed the results observed by Lee, Park, Choi and Kim [24] that more GCPs produced better accuracy. In general, when using the high-accuracy set of GCP measurements, the influence of Strategy B on the accuracy of SfM-based snow depth estimates was limited. The snow depth accuracy was slightly inferior, but still comparable to that of Strategy A.
In contrast, when the low-accuracy set of GCP measurements was incorporated following Strategy B to retrieve snow depth, the accuracy was much lower than that of Strategy A. As shown in Figure 6, the RMSE values were high all the time and varied from 22.3 to 38 cm. Even though a correlation between SfM-based and in-situ snow depths could still be observed, the regression slopes were mostly much higher than one. The SfM technique heavily underestimated the snow depths for thin snow cover and produced negative snow depths, while it largely overestimated the snow depth for relatively thick snow. The fewer GCPs incorporated, the higher the slope. When the number of GCPs decreased to 3, a negative correlation between SfM-based and in-situ snow depths was observed, which was not reasonable for accurate snow depth mapping. By comparing the performances of the two sets of GCP measurements in Strategies A and B, it was reasonable to deduce that the errors in GCP horizontal and vertical coordinates (x, y, z) were propagated into SfM-based snow depths when using Strategy B to incorporate GCP measurements. It was also clear that Strategy A could effectively prevent the propagation of GCP coordinate errors and produce reliable SfM-based snow depths.

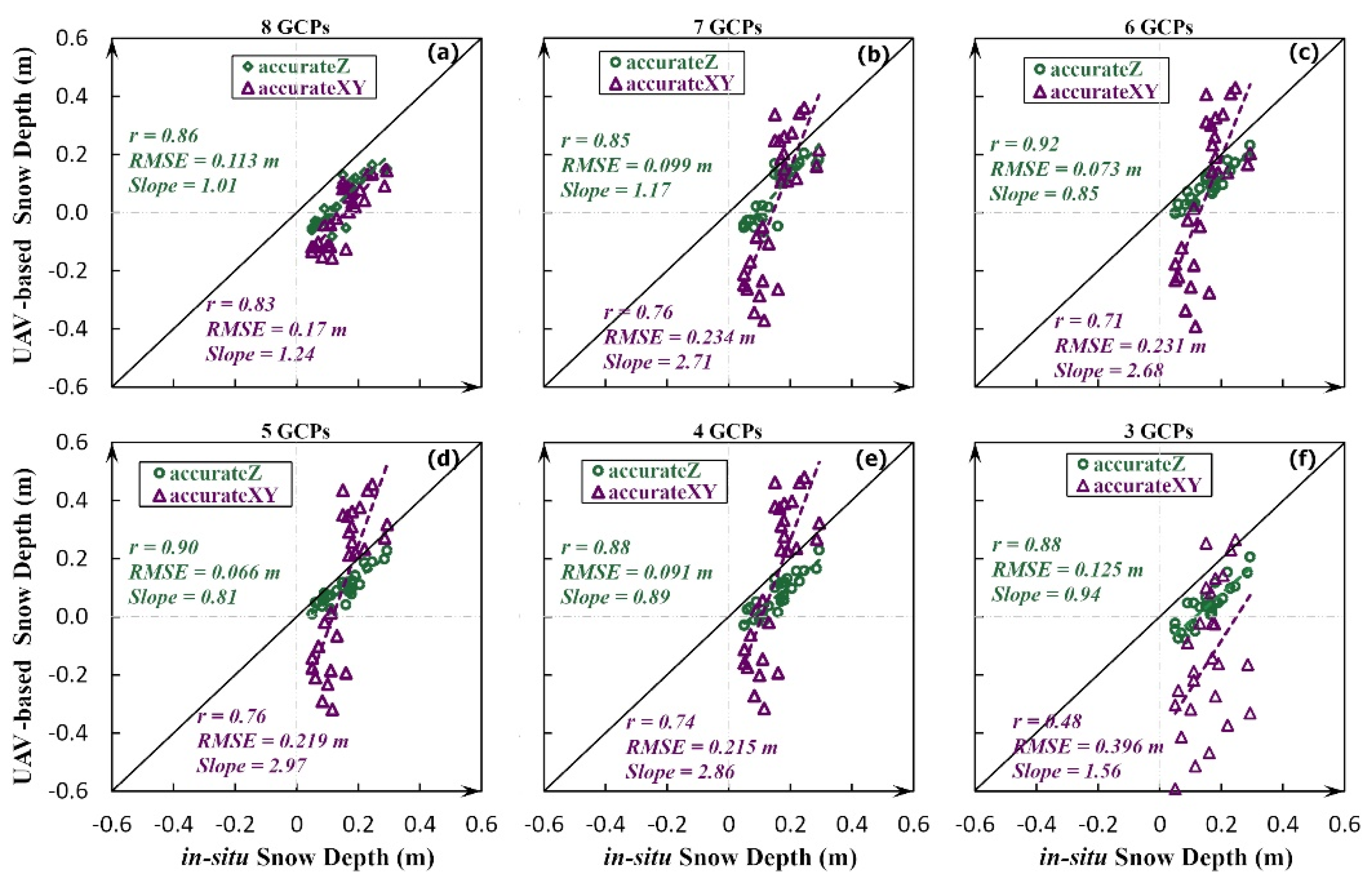
4.3. Strategy B: Accurate-Z Set Verses Accurate-XY Set

To further evaluate the individual influence of GCP horizontal coordinates (x, y) and vertical height (z) on SfM-based snow depth retrieval, the accurate-Z and accurate-XY sets of GCP measurements were incorporated separately following Strategy B to derive snow depth for our study area. Figure 7 shows the scatterplots of SfM-based and in-situ snow depths. Figure 8 summarizes and compares the results generated by incorporating the high-accuracy, low-accuracy, accurate-Z, and accurate-XY sets following Strategy B. As shown in Figure 7, the incorporation of the accurate-Z set produced evidently better snow depth estimates than the incorporation of the accurate-XY set. For the accurate-Z set, the RMSE values ranged from 6.6 to 12.5 cm, the correlation coefficient r varied from 0.85 to 0.92, and the regression slopes were in the range of 0.81–1.17. For the accurate-XY set, the RMSE values were much higher, ranging from 17 to 39.6 cm, the r decreased from 0.83 to 0.48 along with the removal of GCPs, and the regression slope was higher than one all the time. This comparison suggested that in this study the accuracy of GCP height (z) was more crucial than that of GCP horizontal coordinates (x, y) for accurate snow depth mapping using the SfM technique.
On the other hand, compared to the high-accuracy set in Strategy B, the result produced by incorporating the accurate-Z set was relatively inferior in terms of all three metrics, as shown in Figure 8. In particular, the incorporation of the accurate-Z set produced negative snow depth estimates for thin snow cover, as shown in Figure 7a,b,e,f. In addition, it can be observed from Figure 8 that the results produced by the accurate-XY set were generally better than the results produced by the low-accuracy set in Strategy B. These two observations indicated that even though GCP height (z) was more important for SfM-based snow depth retrieval, reducing the errors in GCP horizontal coordinates was still a necessary step to further improve SfM-based mapping of snow depth. In particular, this was more important for mountainous regions where acute topographic change can occur within a short distance.

5. Discussion

As observed in Section 4.1 and Section 4.2, the results generated by the high-accuracy and low-accuracy sets of GCP measurements in Strategies A (Same-GCP strategy) and B (Different-GCP strategy) were markedly different. The high-accuracy set produced reliable snow depth estimates in both strategies, whereas for the low-accuracy set, reliable snow depth estimates were only derived in Strategy A. The contrast highlights the effectiveness of Strategy A in mitigating the influence of GCP coordinates errors on SfM-based snow depth retrieval. It also entails a thorough discussion on how the errors in GCP coordinates are propagated in SfM-based snow depth estimates and how we should survey and incorporate GCPs in order to produce more accurate snow depth estimates.

5.1. Influence of GCP Coordinate Errors under Different GCP Deployment Strategies

As mentioned in Section 3.1, the role of GCPs in SfM workflow is twofold. It helps to optimize camera parameters and the 3D locations of keypoints (sparse point cloud) and then georeference the sparse point cloud. The DSMs and orthophotos are then generated based on the optimized camera parameters and the georeferenced sparse point cloud. Therefore, the optimizing and georeferencing processes are the two ways though which the errors in GCP coordinates (x, y, z) are propagated to the two DSMs and then to snow depth estimates. The optimizing process determines the 3D position of each keypoint relative to the surrounding keypoints. In other words, it determines the relative topographic undulation of the surface in our study area, on both the snow-off and snow-on dates. Georeferencing is achieved by using a linear similarity transformation [39]. It lines up the sparse point cloud (therefore, DSMs and orthophotos) with a real-world coordinate system through linear global translation, rotation, and scaling. These operations are applied in the same way to all points in the cloud. They are not involved in the determination of keypoints’ relative locations nor change the surface’s relative topographic undulation. When GCP measurements are incorporated, both the optimizing and georeferencing processes treat the GCP measurements as ground truth and try to minimize the overall discrepancy between the GCP measurements and the corresponding keypoints.
Figure 9 shows a schematic of the influence of GCP coordinate errors on snow depth estimates. Figure 9a–c illustrates the influence of coordinate errors on the snow-on and snow-off surface profiles when using Strategy A, while Figure 9d–f illustrates the influence of coordinate errors when using Strategy B. Figure 9a,d shows the true snow-on and snow-off surface profiles (snow and ground surfaces). As shown in the two figures, when the GCP coordinates are accurate and have no errors, the snow depth estimates are accurate for both strategies. These were the results observed in Section 4.1 and Section 4.2 when the high-accuracy set of GCP measurements was used.
If errors exist in GCP horizontal coordinates (x, y) and/or vertical height (z), when incorporating GCPs using the Same-GCP strategy (Strategy A), the snow-on and snow-off surface profiles will both be modified or transformed in the same way to best fit the GCPs. For example, as shown in Figure 9b, the snow-on and snow-off profiles were shifted to the right with the same distance. Similarly, in Figure 9c, both profiles were changed in the same way. Even though the errors in GCP (x, y) and (z) were propagated to the snow-on and snow-off profiles, they were canceled out when the two profiles were subtracted, thus generating quite reliable snow depth estimates. This was the result observed in Section 4.1 when the low-accuracy set of GCP measurements was used.
However, if the Different-GCP strategy (Strategy B) is used, the errors in GCP (x, y) and (z) are propagated separately and independently to the snow-off and snow-on profiles. As shown in Figure 9e, the snow-off profile was shifted to left whereas the snow-on profile was shifted to right due to the errors in GCP (x, y). In Figure 9f, the snow-off profile was shifted to a lower location than the true snow-off surface profile whereas the snow-on profile was dragged to a higher location than the true snow-on profile due to the errors in GCP (z). These errors were largely amplified when the snow-off profile was subtracted from snow-on profile, thus producing highly inaccurate snow depth estimates. This was the result observed in Section 4.2 when the low-accuracy set of GCP measurements was used.
Note that for legibility, the errors in horizontal coordinates (x, y) and in vertical height (z) are displayed separately in Figure 9b,e and Figure 9c,f. In addition, the snow-on and the snow-off surface profiles in Figure 9b,c,e,f maintain the same shapes of the true snow-on and snow-off surface profiles in Figure 9a,d, for the purpose of legibility. This may deliver a false message that the accuracy of snow depth estimates could be improved by manually co-registering the snow-on and snow-off DSMs, particularly for Figure 9e,f. In real situations, however, the GCP horizontal and vertical errors are entangled and can hardly be separated from each other. Therefore, simply reducing the horizontal or vertical errors cannot significantly improve the accuracy of snow depth estimates. This was the result observed in Section 4.3. Additionally, when inaccurate GCPs are incorporated into the SfM optimizing process, the errors in GCP coordinates would result in inaccurate camera parameters and sparse point clouds, which could largely change the relative locations of surface features on either the snow-on or snow-off DSMs. In other words, the shape of the snow-on and snow-off surface profiles in Figure 9b,c,e,f could be quite different from the shape of the true snow-on and snow-off profiles in Figure 9a,d. The errors caused by inaccurate camera parameters and sparse point clouds cannot be easily removed by co-registering the snow-on and snow-off DSMs. In fact, we co-registered the snow-on and snow-off DSMs generated by low-accuracy set in Section 4.2 and by the accurate-Z set in Section 4.3 to derive snow depth estimates. The results showed no big improvement in the accuracy of snow depth estimates.

5.2. Optimal GCP Deployment Strategy for UAV-Based SfM Snow Depth Retrieval

Existing studies have rarely investigated whether the GCP deployment strategy could help improve snow depth retrieval using the UAV-based SfM technique. Rigorous comparisons of the results reported by previous studies were not possible due to the huge differences in their study areas and snow cover conditions. However, such comparisons could provide a general sense of how the GCP deployment strategy may influence UAV-based SfM snow depth retrieval. For example, Harder et al. [26] used the same GCPs (the Same-GCP strategy in this study) to generate snow-on and snow-off DSMs and reported RMSE values of 8.5, 8.8, and 13.7 cm for areas with alpine, short, and tall vegetation, respectively. Fernandes et al. [25] used the Same-GCP strategy and reported RMSE values varying from 1.58 to 10.56 cm. Goetz et al. [32] and De Michele et al. [31] used different GCPs (the Different-GCP strategy in this study) to produce snow-on and snow-off DSMs and reported overall RMSE values of 15.2 and 14.3 cm, respectively. Lendzioch et al. [47] used the Different-GCP strategy and reported RMSE values of 16, 32, and 31 cm for open area (snow ablation), forest (snow accumulation), and forest (snow ablation), respectively.
In this study, we conducted a rigorous investigation of how different GCP deployment strategies could mitigate errors in GCP measurements and improve snow depth estimates. It is reasonable to conclude that the Same-GCP strategy is a better option than the Different-GCP strategy for accurately mapping snow depth with SfM-based photogrammetry technology. Even though DGPS (either PPK or RTK) is usually used to survey GCPs for SfM-based snow depth mapping, incorporating GCPs using the Same-GCP strategy can further improve the accuracy of snow depth estimates, as observed in Section 4.1 and Section 4.2. Furthermore, DGPS performs best in open space. In mountainous areas, its accuracy is often heavily hampered by the surrounding topography and vegetation. For example, the horizontal and vertical uncertainties of the DGPS used in this study were observed to be two times larger in the valley than in open space. The Same-GCP strategy was less susceptible to errors in GCP horizontal and vertical coordinates, as observed in Section 4. It is a more suitable option for mapping snow depth in mountainous regions.
The Same-GCP strategy requires the same set of GCP measurements for both snow-on and snow-off DSMs. In this study, the average snow depth was about 15 cm. We managed to identify 15 GCPs that were not covered by snow in our study area. In some areas, the snow can be thick enough to cover most of the surface features in a natural setting. In this case, it would be hard to identify GCPs that are free from snow cover on both snow-on and snow-off dates. A viable solution for those areas is to manually set up a series of GCPs that are higher than the snowpack and are maintained during the whole period between the snow-on and snow-off dates. For example, Fernandes et al. [25] used 30 cm square plywood and 15 cm diameter plastic disks as GCPs, which were suspended 1 and 1.3 m above ground surface. As observed in Section 4.1, when using the Same-GCP strategy, more GCPs did not necessarily improve snow depth accuracy. Actually, three GCPs were sufficient to produce snow depth estimates with quite high accuracy (4.3 cm for the high-accuracy and low-accuracy sets). This does not require significant extra labor effort in the field and is worthwhile for accurate snow depth mapping.
One thing to note is that the snow depth in our study area varied from 5 to 30 cm, with an average of about 15 cm. According to the experiments in this study, Strategy A performed best to retrieve snow depth in our study area. In the future, this strategy will be further tested in areas with relatively thick snow using the method discussed above and in areas with complex underlying surface conditions (e.g., grass, short shrubs), different topographic undulations, and various surrounding environments. In addition, when collecting drone optical photos for snow depth mapping, the drone should be flown following several communication protocols to avoid potential security issues, as denoted in [48,49].

6. Conclusions

This study investigated the influence of errors in GCP coordinates on the accuracy of snow depth estimates. Two sets of GCP measurements with different accuracy levels (high-accuracy and low-accuracy) were incorporated following two strategies (Same-GCP and Different-GCP) into SfM processing to generate snow-on and snow-off DSMs and derive snow depths for our study area. The results showed that the Different-GCP strategy tended to amplify and propagate GCP coordinate errors into snow depth estimates, thus heavily decreasing the accuracy. Conversely, if the Same-GCP strategy was applied, the GCP coordinate errors were propagated in the same way to the snow-on and snow-off DSMs and were canceled out when the two DSMs were subtracted to derive the snow depth estimates. These results therefore demonstrated that the Same-GCP strategy effectively mitigated the influence of GCP coordinate errors on SfM-based snow depth mapping and increased the accuracy of derived snow depth estimates. When using the Different-GCP strategy, increasing the number of GCPs improved the accuracy of snow depth estimates, which was consistent with the observations in a previous study [24]. When using the Same-GCP strategy, increasing the number of GCPs did not help produce better snow depth accuracy. In fact, three GCPs that enclosed the area of interest helped to produce highly accurate snow depth estimates.
After comprehensively evaluating the effectiveness of different sets of GCP measurements using the two strategies, the Same-GCP strategy—using the same GCP measurements to generate snow-on and snow-off DSMs—is highly recommended for UAV-based SfM snow depth retrieval. For areas in which thick snow covers most of the natural surface features and identifying the same GCPs on the two dates is difficult, man-made targets higher than the snow cover, e.g., the square plywood and plastic disks used by Fernandes et al. [25], are recommended to be set up and maintained for UAV flights collecting data throughout the whole snow season.

Author Contributions

S.S. and H.L. conceived the study; S.S., O.-Y.Y. and C.S. designed and performed the field surveys; S.S. performed formal analysis and drafted the original manuscript; S.S., H.L., O.-Y.Y., C.S. and B.Y. contributed to the review and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data in this study will be shared to readers upon request to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
  2. Kunkel, K.E.; Robinson, D.A.; Champion, S.; Yin, X.G.; Estilow, T.; Frankson, R.M. Trends and Extremes in Northern Hemisphere Snow Characteristics. Curr. Clim. Chang. Rep. 2016, 2, 65–73. [Google Scholar] [CrossRef]
  3. Dery, S.J.; Brown, R.D. Recent Northern Hemisphere snow cover extent trends and implications for the snow-albedo feedback. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
  4. Pulliainen, J.; Luojus, K.; Derksen, C.; Mudryk, L.; Lemmetyinen, J.; Salminen, M.; Ikonen, J.; Takala, M.; Cohen, J.; Smolander, T.; et al. Patterns and trends of Northern Hemisphere snow mass from 1980 to 2018. Nature 2020, 581, 294. [Google Scholar] [CrossRef]
  5. Musselman, K.N.; Addor, N.; Vano, J.A.; Molotch, N.P. Winter melt trends portend widespread declines in snow water resources. Nat. Clim. Chang. 2021, 11, 418. [Google Scholar] [CrossRef]
  6. Shook, K.; Gray, D. Small-scale spatial structure of shallow snowcovers. Hydrol. Process. 1996, 10, 1283–1292. [Google Scholar] [CrossRef]
  7. Jonas, T.; Marty, C.; Magnusson, J. Estimating the snow water equivalent from snow depth measurements in the Swiss Alps. J. Hydrol. 2009, 378, 161–167. [Google Scholar] [CrossRef]
  8. López-Moreno, J.I.; Fassnacht, S.; Heath, J.; Musselman, K.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef]
  9. Shu, S.; Liu, H.; Frappart, F.; Huang, Y.; Wang, S.; Hinkel, K.M.; Beck, R.A.; Yu, B.; Jones, B.M.; Arp, C.D.; et al. Estimation of snow accumulation over frozen Arctic lakes using repeat ICESat laser altimetry observations—A case study in northern Alaska. Remote Sens. Environ. 2018, 216, 529–543. [Google Scholar] [CrossRef]
  10. Chang, A.; Foster, J.; Hall, D. Nimbus-7 SMMR derived global snow cover parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef]
  11. Derksen, C.; Walker, A.; Goodison, B. Evaluation of passive microwave snow water equivalent retrievals across the boreal forest/tundra transition of western Canada. Remote Sens. Environ. 2005, 96, 315–327. [Google Scholar] [CrossRef]
  12. Green, J.; Kongoli, C.; Prakash, A.; Sturm, M.; Duguay, C.; Li, S. Quantifying the relationships between lake fraction, snow water equivalent and snow depth, and microwave brightness temperatures in an arctic tundra landscape. Remote Sens. Environ. 2012, 127, 329–340. [Google Scholar] [CrossRef]
  13. Kim, R.S.; Durand, M.; Liu, D. Spectral analysis of airborne passive microwave measurements of alpine snowpack: Colorado, USA. Remote Sens. Environ. 2018, 205, 469–484. [Google Scholar] [CrossRef]
  14. Brucker, L.; Markus, T. Arctic-scale assessment of satellite passive microwave-derived snow depth on sea ice using Operation IceBridge airborne data. J. Geophys. Res. C Ocean. 2013, 118, 2892–2905. [Google Scholar] [CrossRef]
  15. Kanagaratnam, P.; Markus, T.; Lytie, V.; Heavey, B.; Jansen, P.; Prescott, G.; Gogineni, S.P. Ultrawideband radar measurements of thickness of snow over sea ice. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2715–2724. [Google Scholar] [CrossRef]
  16. Kurtz, N.T.; Farrell, S.L. Large-scale surveys of snow depth on Arctic sea ice from Operation IceBridge. Geophys. Res. Lett. 2011, 38, L20505. [Google Scholar] [CrossRef]
  17. Liston, G.E.; Sturm, M. A snow-transport model for complex terrain. J. Glaciol. 1998, 44, 498–516. [Google Scholar] [CrossRef]
  18. Liston, G.E.; Elder, K. A distributed snow-evolution modeling system (snowmodel). J. Hydrometeorol. 2006, 7, 1259–1276. [Google Scholar] [CrossRef]
  19. Essery, R.; Pomeroy, J. Vegetation and topographic control of wind-blown snow distributions in distributed and aggregated simulations for an arctic tundra basin. J. Hydrometeorol. 2004, 5, 735–744. [Google Scholar] [CrossRef]
  20. Snauffer, A.M.; Hsieh, W.W.; Cannon, A.J. Comparison of gridded snow water equivalent products with in situ measurements in British Columbia, Canada. J. Hydrol. 2016, 541, 714–726. [Google Scholar] [CrossRef]
  21. Broxton, P.D.; Zeng, X.; Dawson, N. Why do global reanalyses and land data assimilation products underestimate snow water equivalent. J. Hydrometeorol. 2016, 17, 2743–2761. [Google Scholar] [CrossRef]
  22. Wrzesien, M.L.; Durand, M.T.; Pavelsky, T.M.; Howat, I.M.; Margulis, S.A.; Huning, L.S. Comparison of methods to estimate snow water equivalent at the mountain range scale: A case study of the California Sierra Nevada. J. Hydrometeorol. 2017, 18, 1101–1119. [Google Scholar] [CrossRef]
  23. Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef]
  24. Lee, S.; Park, J.; Choi, E.; Kim, D. Factors Influencing the Accuracy of Shallow Snow Depth Measured Using UAV-Based Photogrammetry. Remote Sens. 2021, 13, 828. [Google Scholar] [CrossRef]
  25. Fernandes, R.; Prevost, C.; Canisius, F.; Leblanc, S.G.; Maloley, M.; Oakes, S.; Holman, K.; Knudby, A. Monitoring snow depth change across a range of landscapes with ephemeral snowpacks using structure from motion applied to lightweight unmanned aerial vehicle videos. Cryosphere 2018, 12, 3535–3550. [Google Scholar] [CrossRef]
  26. Harder, P.; Schirmer, M.; Pomeroy, J.; Helgason, W. Accuracy of snow depth estimation in mountain and prairie environments by an unmanned aerial vehicle. Cryosphere 2016, 10, 2559–2571. [Google Scholar] [CrossRef]
  27. Vander Jagt, B.; Lucieer, A.; Wallace, L.; Turner, D.; Durand, M. Snow Depth Retrieval with UAS Using Photogrammetric Techniques. Geosciences 2015, 5, 264. [Google Scholar] [CrossRef]
  28. Cimoli, E.; Marcer, M.; Vandecrux, B.; Bøggild, C.E.; Williams, G.; Simonsen, S.B. Application of low-cost uass and digital photogrammetry for high-resolution snow depth mapping in the Arctic. Remote Sens. 2017, 9, 1144. [Google Scholar] [CrossRef]
  29. Avanzi, F.; Bianchi, A.; Cina, A.; De Michele, C.; Maschio, P.; Pagliari, D.; Passoni, D.; Pinto, L.; Piras, M.; Rossi, L. Centimetric accuracy in snow depth using unmanned aerial system photogrammetry and a multistation. Remote Sens. 2018, 10, 765. [Google Scholar] [CrossRef]
  30. Miziński, B.; Niedzielski, T. Fully-automated estimation of snow depth in near real time with the use of unmanned aerial vehicles without utilizing ground control points. Cold Reg. Sci. Technol. 2017, 138, 63–72. [Google Scholar] [CrossRef]
  31. De Michele, C.; Avanzi, F.; Passoni, D.; Barzaghi, R.; Pinto, L.; Dosso, P.; Ghezzi, A.; Gianatti, R.; Della Vedova, G. Using a fixed-wing UAS to map snow depth distribution: An evaluation at peak accumulation. Cryosphere 2016, 10, 511–522. [Google Scholar] [CrossRef]
  32. Goetz, J.; Brenning, A. Quantifying Uncertainties in Snow Depth Mapping From Structure From Motion Photogrammetry in an Alpine Area. Water Resour. Res. 2019, 55, 7772–7783. [Google Scholar] [CrossRef]
  33. Masný, M.; Weis, K.; Biskupič, M. Application of Fixed-Wing UAV-Based Photogrammetry Data for Snow Depth Mapping in Alpine Conditions. Drones 2021, 5, 114. [Google Scholar] [CrossRef]
  34. Bühler, Y.; Adams, M.S.; Bösch, R.; Stoffel, A. Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): Potential and limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef]
  35. Jiang, S.; Jiang, C.; Jiang, W. Efficient structure from motion for large-scale UAV images: A review and a comparison of SfM tools. ISPRS J. Photogramm. Remote Sens. 2020, 167, 230–251. [Google Scholar] [CrossRef]
  36. Perry, L.B.; Konrad, C.E. Relationships between NW flow snowfall and topography in the Southern Appalachians, USA. Clim. Res. 2006, 32, 35–47. [Google Scholar] [CrossRef]
  37. Perry, L.B.; Konrad, C.E.; Hotz, D.G.; Lee, L.G. Synoptic Classification of Snowfall Events in the Great Smoky Mountains, USA. Phys. Geogr. 2010, 31, 156–171. [Google Scholar] [CrossRef]
  38. Sugg, J.W.; Fuhrmann, C.M.; Perry, L.B.; Hall, D.K.; Konradll, C.E. Sub-regional snow cover distribution across the southern Appalachian Mountains. Phys. Geogr. 2017, 38, 105–123. [Google Scholar] [CrossRef]
  39. Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr. Earth Environ. 2015, 40, 247–275. [Google Scholar] [CrossRef]
  40. Carrivick, J.L.; Smith, M.W.; Quincey, D.J. Structure from Motion in the Geosciences; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
  41. Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
  42. Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 1152, pp. 1150–1157. [Google Scholar]
  43. Muja, M.; Lowe, D.G. Fast approximate nearest neighbors with automatic algorithm configuration. VISAPP 2009, 2, 2. [Google Scholar]
  44. Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
  45. Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
  46. Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
  47. Lendzioch, T.; Langhammer, J.; Jenicek, M. Estimating Snow Depth and Leaf Area Index Based on UAV Digital Photogrammetry. Sensors 2019, 19, 1027. [Google Scholar] [CrossRef]
  48. Krichen, M.; Adoni, W.Y.H.; Mihoub, A.; Alzahrani, M.Y.; Nahhal, T. Security Challenges for Drone Communications: Possible Threats, Attacks and Countermeasures. In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; pp. 184–189. [Google Scholar]
  49. Ko, Y.; Kim, J.; Duguma, D.G.; Astillo, P.V.; You, I.; Pau, G. Drone Secure Communication Protocol for Future Sensitive Applications in Military Zone. Sensors 2021, 21, 2057. [Google Scholar] [CrossRef]
Remotesensing 15 02297 g001 550
Figure 1. SfM-based orthophoto of the study area: (a) with snow cover on 9 January 2021, and (b) without snow cover on 24 February 2021. The ID number of each GCP is displayed in red color.
Figure 1. SfM-based orthophoto of the study area: (a) with snow cover on 9 January 2021, and (b) without snow cover on 24 February 2021. The ID number of each GCP is displayed in red color.
Remotesensing 15 02297 g001
Remotesensing 15 02297 g002 550
Figure 2. (a) DSM for snow-on date (9 January 2021); (b) DSM for snow-off date (24 February 2021); and (c) snow depth based on the difference between the two DSMs.
Figure 2. (a) DSM for snow-on date (9 January 2021); (b) DSM for snow-off date (24 February 2021); and (c) snow depth based on the difference between the two DSMs.
Remotesensing 15 02297 g002
Remotesensing 15 02297 g003 550
Figure 3. Strategies A and B of incorporating GCP measurements into SfM to estimate snow depth.
Figure 3. Strategies A and B of incorporating GCP measurements into SfM to estimate snow depth.
Remotesensing 15 02297 g003
Remotesensing 15 02297 g004 550
Figure 4. Scatterplots of SfM-based snow depth estimates against in-situ snow depth when using Strategy A to incorporate the high-accuracy and low-accuracy sets of GCPs. Only the scatterplots of an even number of GCPs are displayed. The number of GCPS decreases from (a) to (f).
Figure 4. Scatterplots of SfM-based snow depth estimates against in-situ snow depth when using Strategy A to incorporate the high-accuracy and low-accuracy sets of GCPs. Only the scatterplots of an even number of GCPs are displayed. The number of GCPS decreases from (a) to (f).
Remotesensing 15 02297 g004
Remotesensing 15 02297 g005 550
Figure 5. The performance of SfM-based snow depth retrieval when using Strategy A to incorporate the high-accuracy and low-accuracy sets of GCPs: (a) RMSE, (b) correlation coefficient r, and (c) linear regression slope.
Figure 5. The performance of SfM-based snow depth retrieval when using Strategy A to incorporate the high-accuracy and low-accuracy sets of GCPs: (a) RMSE, (b) correlation coefficient r, and (c) linear regression slope.
Remotesensing 15 02297 g005
Remotesensing 15 02297 g006 550
Figure 6. Scatterplots of SfM-based snow depth estimates against in-situ snow depth when using Strategy B to incorporate the high-accuracy and low-accuracy sets of GCPs. (a–f) the number of GCPs decreased from 8 to 3.
Figure 6. Scatterplots of SfM-based snow depth estimates against in-situ snow depth when using Strategy B to incorporate the high-accuracy and low-accuracy sets of GCPs. (a–f) the number of GCPs decreased from 8 to 3.
Remotesensing 15 02297 g006
Remotesensing 15 02297 g007 550
Figure 7. Scatterplots of SfM-based snow depth estimates against in-situ snow depth when using Strategy B to incorporate the accurate-Z and accurate-XY sets of GCP measurements. (a–f) the number of GCPs decreased from 8 to 3.
Figure 7. Scatterplots of SfM-based snow depth estimates against in-situ snow depth when using Strategy B to incorporate the accurate-Z and accurate-XY sets of GCP measurements. (a–f) the number of GCPs decreased from 8 to 3.
Remotesensing 15 02297 g007
Remotesensing 15 02297 g008 550
Figure 8. The performance of SfM-based snow depth retrieval when using Strategy B to incorporate the four sets of GCPs: (a) RMSE, (b) correlation coefficient r, and (c) linear regression slope.
Figure 8. The performance of SfM-based snow depth retrieval when using Strategy B to incorporate the four sets of GCPs: (a) RMSE, (b) correlation coefficient r, and (c) linear regression slope.
Remotesensing 15 02297 g008
Remotesensing 15 02297 g009 550
Figure 9. Influence of Strategies A and B on SfM-based snow depth estimates. (a–c) Strategy A. (d–f) Strategy B.
Figure 9. Influence of Strategies A and B on SfM-based snow depth estimates. (a–c) Strategy A. (d–f) Strategy B.
Remotesensing 15 02297 g009
Table
Table 1. GCPs incorporated at each step in Strategies A and B.
Table 1. GCPs incorporated at each step in Strategies A and B.
StepNumber of GCPs IncorporatedGCPs Incorporated in Strategy AGCPs Incorporated in Strategy B
Snow-On/Snow-OffSubgroup1: Snow-OnSubgroup2: Snow-Off
1151–15
2141–3, 5–15
3131–3, 6–15
4121–3, 6–9, 11–15
5111–3, 6, 8, 9, 11–15
6101, 3, 6, 8, 9, 11–15
791, 3, 6, 8, 9, 12–15
883, 6, 8, 9, 12–151, 3, 4, 6, 7, 9, 13, 152, 5, 6, 8, 10, 11, 12, 14
973, 6, 8, 9, 12, 13, 151, 4, 6, 7, 9, 13, 152, 5, 6, 8, 11, 12, 14
1063, 6, 8, 9, 12, 151, 4, 6, 9, 13, 152, 6, 8, 11, 12, 14
1153, 6, 8, 9, 151, 6, 9, 13, 152, 6, 8, 11, 14
1243, 6, 8, 91, 6, 9, 152, 6, 8, 11
1333, 6, 81, 9, 152, 6, 8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shu, S.; Yu, O.-Y.; Schoonover, C.; Liu, H.; Yang, B. Unmanned Aerial Vehicle-Based Structure from Motion Technique for Precise Snow Depth Retrieval—Implication for Optimal Ground Control Point Deployment Strategy. Remote Sens. 2023, 15, 2297. https://doi.org/10.3390/rs15092297

AMA Style

Shu S, Yu O-Y, Schoonover C, Liu H, Yang B. Unmanned Aerial Vehicle-Based Structure from Motion Technique for Precise Snow Depth Retrieval—Implication for Optimal Ground Control Point Deployment Strategy. Remote Sensing. 2023; 15(9):2297. https://doi.org/10.3390/rs15092297

Chicago/Turabian Style

Shu, Song, Ok-Youn Yu, Chris Schoonover, Hongxing Liu, and Bo Yang. 2023. "Unmanned Aerial Vehicle-Based Structure from Motion Technique for Precise Snow Depth Retrieval—Implication for Optimal Ground Control Point Deployment Strategy" Remote Sensing 15, no. 9: 2297. https://doi.org/10.3390/rs15092297

APA Style

Shu, S., Yu, O.-Y., Schoonover, C., Liu, H., & Yang, B. (2023). Unmanned Aerial Vehicle-Based Structure from Motion Technique for Precise Snow Depth Retrieval—Implication for Optimal Ground Control Point Deployment Strategy. Remote Sensing, 15(9), 2297. https://doi.org/10.3390/rs15092297

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop