Next Article in Journal
Coupling Progressive Deep Learning with the AdaBoost Framework for Landslide Displacement Rate Prediction in the Baihetan Dam Reservoir, China
Next Article in Special Issue
Applicability Assessment of Passive Microwave LST Downscaling over Semi–Homogeneous Desert Underlying Surface Based on Machine Learning
Previous Article in Journal
Permafrost Stability Mapping on the Tibetan Plateau by Integrating Time-Series InSAR and the Random Forest Method
Previous Article in Special Issue
Downscaling of SMAP Soil Moisture Data by Using a Deep Belief Network
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 9
10.3390/rs15092295
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Topological Generality and Spectral Dimensionality in the Earth Mineral Dust Source Investigation (EMIT) Using Joint Characterization and the Spectral Mixture Residual

by
Daniel Sousa
1,* and
Christopher Small
2
1
Department of Geography, San Diego State University, San Diego, CA 92182, USA
2
Lamont-Doherty Earth Observatory, Columbia University, Palisades, NY 10964, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(9), 2295; https://doi.org/10.3390/rs15092295
Submission received: 8 March 2023 / Revised: 18 April 2023 / Accepted: 25 April 2023 / Published: 27 April 2023
(This article belongs to the Special Issue New Advancements in the Field of Remote Sensing in Land Surface Processes)
Browse Figures
Versions Notes

Abstract

:
NASA’s Earth Surface Mineral Dust Source Investigation (EMIT) mission seeks to use spaceborne imaging spectroscopy (hyperspectral imaging) to map the mineralogy of arid dust source regions. Here we apply recent developments in Joint Characterization (JC) and the spectral Mixture Residual (MR) to explore the information content of data from this novel mission. Specifically, for a mosaic of 20 spectrally diverse scenes, we find: (1) a generalized three-endmember (Substrate, Vegetation, Dark; SVD) spectral mixture model is capable of capturing the preponderance (99% in three dimensions) of spectral variance with low misfit (99% pixels with <3.7% RMSE); (2) manifold learning (UMAP) is capable of identifying spatially coherent, physically interpretable clustering relationships in the spectral feature space; (3) UMAP yields results that are at least as informative when applied to the MR as when applied to raw reflectance; (4) SVD fraction information usefully contextualizes UMAP clustering relationships, and vice-versa (JC); and (5) when EMIT data are convolved to spectral response functions of multispectral instruments (Sentinel-2, Landsat 8/9, Planet SuperDove), SVD fractions correlate strongly across sensors, but UMAP clustering relationships for the EMIT hyperspectral feature space are far more informative than for simulated multispectral sensors. Implications are discussed for both the utility of EMIT data in the near-term and for the potential of high signal-to-noise (SNR) spaceborne imaging spectroscopy more generally, to transform the future of optical remote sensing in the years and decades to come.

1. Introduction

NASA’s Earth Mineral Dust Source Investigation (EMIT) mission is designed to study the mineralogy of Earth’s dust-forming regions using spaceborne imaging spectroscopy [1]. The EMIT instrument is a Dyson imaging spectrometer with an 11° cross-track field of view, with a fast (F/1.8) and wide-swath (1240 samples) optical system achieving roughly 7.4 nm spectral sampling across the 380–2500 nm spectral range at high signal-to-noise (SNR) [2]. EMIT was launched on 14 July 2022 via SpaceX Dragon and successfully autonomously docked to the forward-facing port of the International Space Station (ISS) [3]. EMIT data and algorithms are freely available for public use.
While the stated purpose of the EMIT mission is to measure surface mineralogy and mineral dust in the Earth’s dust-forming regions, these data also provide an unprecedented opportunity to advance our fundamental understanding of the spectral properties of the Earth’s surface more generally. Sensors like Landsat have collected multispectral satellite imagery for decades [4], but spaceborne hyperspectral (imaging spectroscopy) observations have been much more limited. Early missions like Hyperion [5] and HICO [6] were characterized by nontrivial noise limitations. High-quality airborne data from sensors like AVIRIS [7] are available, but with spatial and temporal coverage limitations inherent to airborne platforms. A new generation of spaceborne imaging spectrometers is now starting to come online, with significant involvement from multiple space agencies. Such missions include the Italian Space Agency’s PRISMA [8], DLR’s DESIS [9] and EnMAP [10], JAXA’s HISUI [11], as well as planned missions like the European Space Agency’s CHIME [12], NASA’s SBG [13] and more. EMIT is an exciting new contribution to this international constellation and marks an important step towards a comprehensive global hyperspectral monitoring system.
EMIT began collecting high-quality data shortly after launch, and a rapidly-growing library of scenes is already available for download. While geographic coverage of the EMIT mission is inherently limited by the orbital parameters of the ISS, the scenes that have been acquired to date sample broad spectral diversity spanning a wide range of biogeophysical settings. These novel data offer an unprecedented opportunity to test the utility of recent developments in spectral image analysis, including both characterization and modeling. In this analysis, we use the standard Level 2A EMIT surface reflectance data product. Notably, this product relies on a Bayesian optimal estimation approach [14] that differs in important ways from traditional direct radiative transfer model inversions [15].
Here, we use a compilation of 20 spectrally diverse EMIT scenes to investigate the differences between high SNR spaceborne hyperspectral data and simulated multispectral data from common sensors like Sentinel-2, Landsat, and SuperDove. Specifically, we apply two novel approaches to hyperspectral image analysis: joint characterization [16] and the spectral mixture residual [17]. Joint characterization assumes that important spectral signals may be distributed across multiple scales of variance and provides a way to characterize these signals in a physically interpretable way. The mixture residual uses spectral mixture analysis to isolate low-variance spectral signals (e.g., narrow mineral absorptions) from high-variance signals (e.g., land cover modulated variability in continuum shape and amplitude). Synthesizing these two novel approaches using a novel dataset, we address the following questions:
  • To what extent are EMIT reflectance spectra well characterized by a generalized three-endmember Substrate, Vegetation, Dark (SVD) model, such as has been shown effective for analysis of multispectral satellite imagery?
  • What quantitative and qualitative differences in spectral dimensionality and feature space topology are observed between EMIT reflectance and simulated multispectral data?
  • Does the spectral mixture model residual from EMIT data contain substantially more information than the mixture residual computed from multispectral data? If so, is this effectively captured by traditional dimensionality metrics like variance partition? And is this information also manifest topologically in the spectral feature space as a substantially different manifold structure?
  • To what extent can joint characterization be used to reveal subtle but physically meaningful spectral signals in EMIT data? Are these signals spatially coherent?

2. Materials and Methods

2.1. Data

Twenty EMIT scenes were selected on the basis of geographic and spectral diversity (Figure 1). Scenes span four continents, sampling important global deserts (Sahara, Arabia, Atacama, Taklamakan, Gobi, Great Basin, and Caspian), geologic structures (Zagros, Jabal Tuwaiq, Bushveld, Atacama, and the Hindu Kush), agricultural basins (San Joaquin, South African Cape, and the Hindu Kush), natural floristic diversity (Mata Atlântica, South African Cape, Okavango, and Sierra Nevada), as well as some cryospheric targets (Patagonia and Tian Shan) and human settlements (Los Angeles). While this compilation does not achieve comprehensive global sampling, at least some representation is included from most major biomes.
Data were downloaded in netCDF format from the USGS Land Processes Distributed Active Archive Center (LPDAAC) through the web portal: https://search.earthdata.nasa.gov/, accessed on 3 February 2023. Both reflectance and mask files were acquired. All 20 scenes were compiled into a single-image mosaic (Figure 2). For subsequent analysis, reflectance data were masked using the “Aggregate Flag” included in Band 7. SceneIDs are provided in Appendix A, Table A1.

2.2. Joint Characterization

Joint characterization (JC) combines complementary projections of the topology of the spectral feature space by combining global structure from the broad wavelength spectral continuum with a local structure related to narrow band absorption features. In this analysis, we applied JC to the EMIT mosaic described above. As detailed in [16] and refined in [18,19,20,21,22], the JC workflow was as follows:
  • Characterize spectral feature space on the basis of (statistically) global variance.
    a.
    Evaluate spectral mixture model and compute mixture residual.
  • Characterize spectral feature space on the basis of (statistically) local connectivity.
  • Evaluate the topology of global and local feature spaces separately.
  • Characterize joint feature space formed by both global and local basis vectors.
We provide further detail on each step in the following subsections.

2.2.1. Global Variance Characterization with PCA

The first step in joint characterization is to compute a set of basis vectors for the spectral feature space which capture the global variance structure of the data. For over a century, Principal Component Analysis (PCA) has been used to empirically estimate these basis vectors [23]. PCA is a generalizable, linear, invertible approach. PCA can be computed using the singular value decomposition described by the equation:
X = U Σ V
where X is the data matrix, U is the matrix of left singular vectors, Σ is the (diagonal) matrix of singular values, and V is the matrix of right singular vectors [24]. Here, we visualize the low-order global variance structure of the spectral feature space using bivariate distributions of values of the U matrix. Analysis of cumulative distributions of normalized singular values can also estimate data dimensionality [25,26]. We use this approach to compare the relative dimensionality of EMIT vs. simulated Landsat, Sentinel, and Planet spectra. We also note that other important and interesting approaches to dimensionality estimation exist [27,28].

Evaluation of Linear Spectral Mixture Model, Including Residual

Global variance characterization also provides a way to determine bounding spectral endmembers (EMs) and empirically evaluate linearity of spectral mixing [29]. Once identified, these EMs can then be used to estimate subpixel material abundances [30,31,32]. In addition, generalized EM fractions can provide a globally consistent parameter space for land cover mapping [33]. We take this approach here, using S, V, D fractions as one of our global variance metrics in the joint characterization step below. Interesting and potentially important information can also be captured in wavelength-dependent model misfit (i.e., mixture residual) [17,20]. The linear spectral mixture model can be represented as:
x = Mf + ε
where x is the vector of observed reflectance, M is the matrix of linear mixing equations, f is the subpixel fractional abundance of each EM, and ε is the vector of wavelength-explicit misfit [34]. Frequently, ε is summarized as a single statistic (e.g., root-mean-square error; RMSE). In addition to this summary statistic, we also retain the full ε-vector for each pixel. We treat this mixture residual as a source of potential information, evaluating its (global and local) feature space topology and spectral dimensionality.

2.2.2. Local Variance Characterization with UMAP

The second step in joint characterization is to evaluate (statistically) local variance in the data. Here, we do so using recent advances in the field of manifold learning. One conceptual framing of this approach can be considered as follows:
Each pixel reflectance vector occupies a position in high-dimensional feature space. Position in this feature space is a function of the generative physical processes underlying the spectral signature, plus measurement noise. Generative physical processes may be linear (single-scatter geometric optics) or nonlinear (intimate mixing); and span a broad range of amplitudes. The full set of generative physical processes of a large number of spectra describes a curvilinear manifold in high-dimensional feature space. Manifold learning algorithms seek to estimate this underlying manifold and use its structure to uncover useful information about the data.
Manifold learning has existed for decades. A wide range of algorithms exist, each with strengths and limitations. One of the earliest approaches was introduced as the Isometric Mapping (ISOMAP) algorithm [35]. Other approaches were rapidly developed, including Locally Linear Embedding (LLE) [36], Hessian Eigenmaps [37], spectral embedding/Laplacian eigenmaps [38], and Stochastic Neighbor Embedding [39,40]. For a review, see [41].
These approaches have been applied to hyperspectral imagery with varying success. Early recognition of the potential was noted by [42], with additional context provided by [43]. The application of locally linear embedding was rapidly adopted [44]. Important advances were then made by [45,46,47,48,49,50,51,52], including multi-algorithm comparisons and significant improvements in generalizability, computational optimization, and scalability.
The manifold learning algorithm we use in this analysis is Uniform Manifold Approximation and Projection (UMAP) [53]. UMAP was developed using a theoretical framework in Riemannian geometry and algebraic topology. The algorithm is designed to be scalable and computationally efficient, and additionally does not restrict the dimension of embedding. For a full exposition of the UMAP algorithm, the reader is referred to [53], but briefly, the steps are as follows. First, the data are modeled as a low-dimensional simplicial complex. Nonuniform data distribution is handled using a locally varying distance metric. Local connectivity is evaluated using fuzzy open sets. Fuzzy simplicial sets are then unioned together to form a single fuzzy simplicial complex, which can also be considered a weighted graph. Once this complex is determined, an embedding is found with optimal similarity to the fuzzy topological structure by minimizing cross-entropy:
Σ wh(e) log(wh(e)/wl(e)) + (1 − wh(e)) log ((1 − wh(e))/(1 − wl(e)))
where wh(e) is the weight of the 1-simplex e in the high-dimensional case and wl(e) is the weight of the 1-simplex e in the low-dimensional case. Here, we implement UMAP using the Python-based ‘umap-learn’ package. Both 2D and 3D UMAP embeddings were computed for the mosaic and individual EMIT scenes.

2.2.3. Evaluate the Topology of Global and Local Feature Spaces Separately

Once both global and local metrics are computed, connectivity structure and dimensionality are evaluated independently. Dimensionality is estimated from the singular value distribution as described above. The topology of global and local feature spaces is visualized. Endmember spectra, mixing relations, and clusters are evaluated, following [29].

2.2.4. Characterize Joint Feature Space

Global and local bases are then used to analyze the joint space. Patterns of global and local variance are investigated together to identify additional endmembers and clusters which are not evident or clearly interpretable using one approach alone.

3. Results

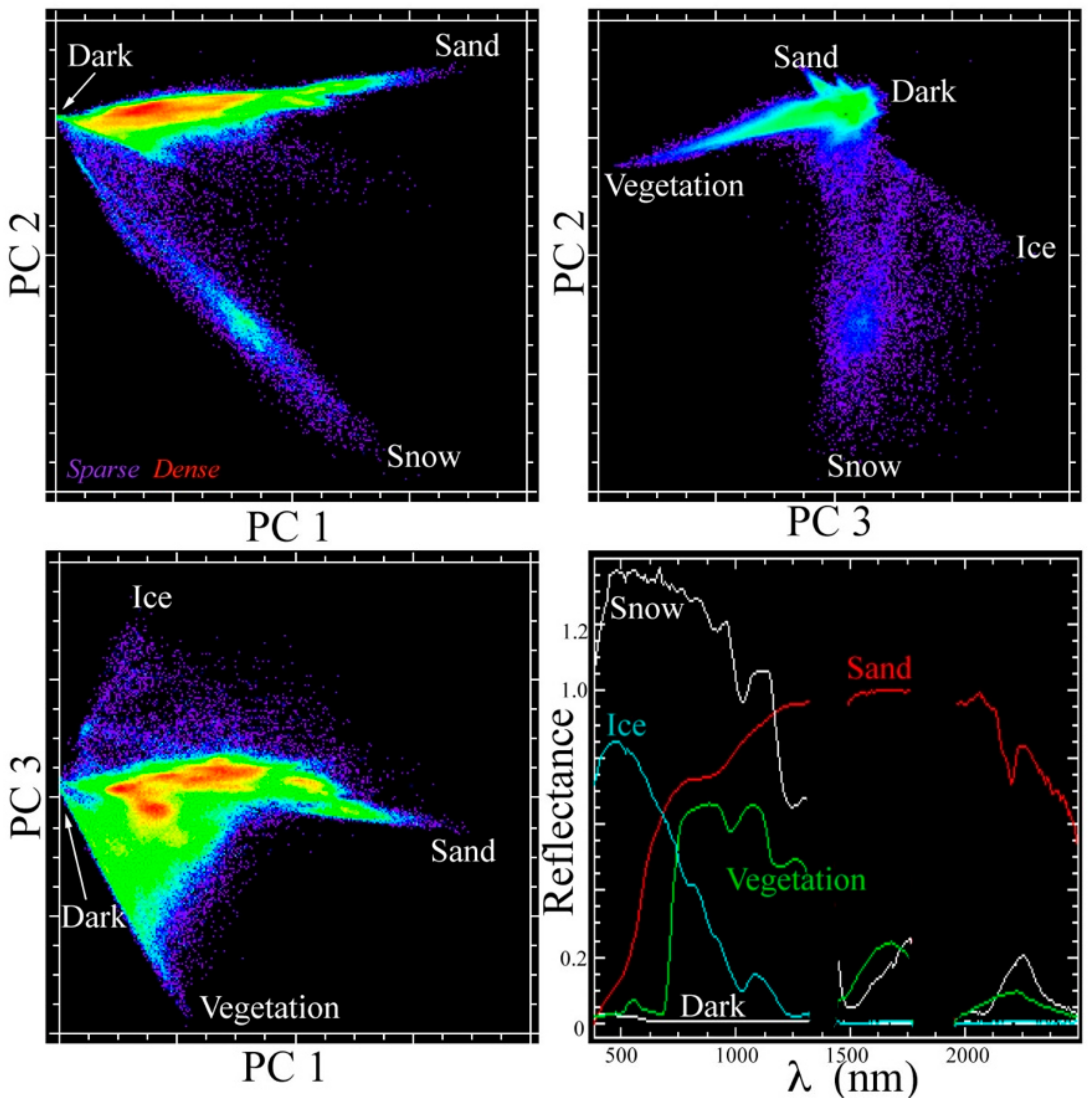
3.1. Variance-Based Spectral Feature Space—PCA

Figure 3 shows the low-order variance-based spectral feature space of the reflectance mosaic. The first three dimensions of these data are bounded by snow/ice (I); sand, soil, and rock substrates (S); illuminated photosynthetic vegetation (V); and dark targets like shadow and water (D). This low-order topology is consistent with previous regional compilations of AVIRIS imaging spectroscopy [17,54], as well as global compilations of Landsat [33,55,56], MODIS [57], and Sentinel-2 [18,19]. Significant spectral diversity in the S endmember is observed, associated with geologic variability in sediment, bedrock, and soil of the sparsely vegetated scenes in the mosaic. Reflectance spectra for generalized endmembers are shown in the lower right.
The image mosaic was then unmixed using the S, V, and D endmembers (EMs) and wavelength-specific mixture residual was retained, following [17]. Each endmember represents the mean of several pixel spectra near the respective apexes of the feature space shown in Figure 3. However, the S endmember is the mean of multiple sand spectra chosen to average out specific SWIR2 absorptions like that shown in Figure 4. It is projected onto a high amplitude specular reflection so as to have a maximum reflectance near 1.0, thereby bounding the space near the sand apex. The 3 EM SVD linear mixture model was found to yield a good fit for the preponderance of pixel reflectance spectra, with an average root-mean-square error (RMSE) of approximately 3.1%, and with 99% of pixels showing RMSE < 3.7%. The low-order feature space of the mixture residual mosaic is shown in Figure 4. The mixture residual effectively accentuates substrate EM variability by removing the high-variance component of spectral variability which is modeled by a simple linear mixing model. Multiple additional substrate EMs are clearly identifiable in the variance-based mixture residual feature space. Importantly, this endmember variability demonstrates correspondence to VNIR spectral curvature and narrow SWIR absorptions rather than simple differences in albedo.
In order to investigate EMIT’s information content relative to multispectral imagery, the reflectance mosaic was convolved using the spectral response functions of the Sentinel-2A, Landsat 8/9 OLI, and Planet SuperDove sensors. Variance-based characterization was then repeated, including computation of the mixture residual (i.e., wavelength-explicit misfit of the 3-EM linear spectral mixture model). The difference in information content was then quantified using the partition of variance captured by eigenvalues of the low-order PC dimensions of the reflectance and residual spectra from each sensor (Figure 5). Cumulative variance for the reflectance data (left) shows surprisingly little difference for EMIT data relative to Landsat and Sentinel-2, with minor differences persisting at Dimension 2 but near convergence by Dimension 3. SuperDove shows considerably lower dimensionality, presumably due to the absence of SWIR bands. In contrast, the partition of variance from mixture residual spectra (right) shows EMIT dimensionality to consistently exceed all multispectral sensors and Landsat/Sentinel to consistently exceed SuperDove. The multispectral feature spaces are effectively 2D and 3D, while EMIT’s hyperspectral feature space is at least 14D to 99.9% of the variance.

3.2. Manifold-Based Feature Space—UMAP

UMAP results for the EMIT mosaic, as well as convolved Sentinel, Landsat, and SuperDove mosaics, are shown in Figure 6. When UMAP is applied to reflectance spectra (top row), the greater information content of the EMIT mosaic is manifest as a more complex topology characterized by numerous tendrils with varying degrees of differentiation from the main body of the manifold. In contrast, the multispectral sensors demonstrate diminished complexity with fewer identifiable tendrils and a more continuous structure.
The difference in manifold structure between EMIT and multispectral spectra is further accentuated when UMAP is applied to the mixture residual mosaic (bottom row). Here, spectral differences within and among EMIT tiles result in clearly separated, well-defined clusters for EMIT. The multispectral sensors are not characterized by such spectral separability. For these data, manifolds are visibly well-connected, without such clearly separable gaps. The implications of this difference in manifold structure for both discrete and continuous image analysis are discussed below.

3.3. Joint Characterization

It has been noted previously that important information may exist at multiple scales of spectral variance in the same dataset and that such information may be usefully examined using Joint Characterization (JC), in which bivariate distributions are used to simultaneously visualize both global and local spectral features [16]. Figure 7 illustrates JC as implemented for the EMIT reflectance mosaic. Here, the S, V, and D endmember fractions are used as the global variance metric (x-axis), and UMAP dimensions are used as the local variance metric (y-axis). Tendrils at similar values of each mixture model fraction (similar x values but distinct y values) correspond to statistically distinct clusters with broadly similar overall spectral continua but distinct absorption features (e.g., endmember variability). These tendrils frequently correspond to spatially contiguous clusters of pixels in individual EMIT scenes. This is examined in greater detail below for three example EMIT scenes.

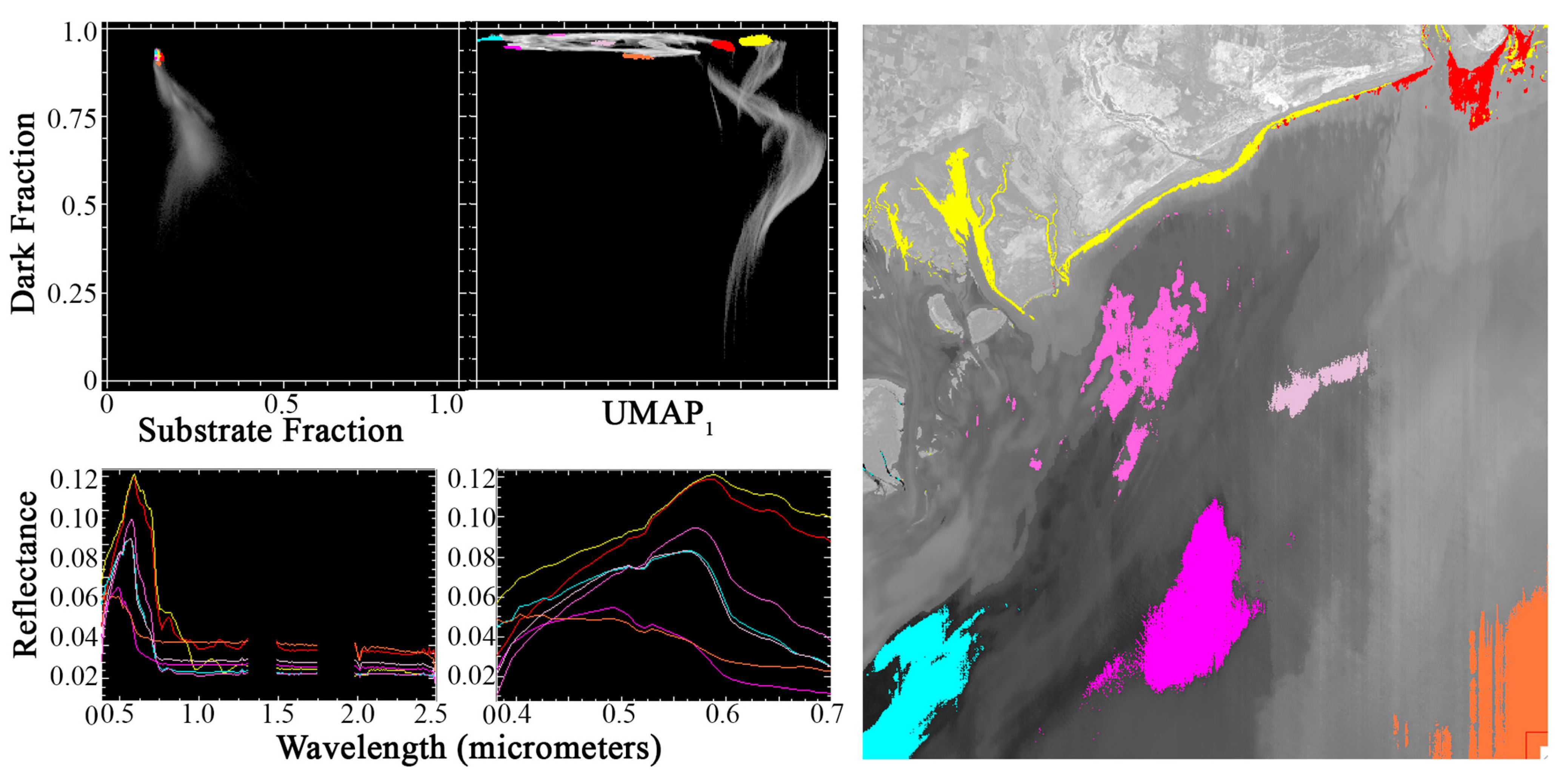
3.4. Single-Scene Examples

Joint characterization of individual EMIT scenes illustrates additional spectral feature space structure not apparent in the 20-scene mosaic. Figure 8 shows joint characterization as applied to vegetation spectra from the single San Joaquin scene. Red, yellow, and cyan regions of interest are identified and labeled (different colors) as clearly separable clusters from the JC scatterplot (upper right), then projected onto the SVD fraction space (upper left) for context. Average spectra from pixels in all three labeled regions of interest (bottom row) clearly correspond to photosynthetic vegetation. Differences in red edge slope, mesophyll reflectance and liquid water absorptions are present, as well as subtle differences in pigment absorption at visible wavelengths (lower right).
Figure 9 shows joint characterization as applied to substrate spectra from the single Atacama scene. Differently colored regions of interest are identified and labeled as clearly separable clusters from the JC scatterplot (upper right), then projected onto the SVD fraction space (upper left) for context. Average spectra from pixels in all regions of interest (bottom row) clearly correspond to exposed geologic substrates. All regions are substantially more absorptive than the global sand endmember (lower left, thick red). Differences in albedo and VNIR curvature are present, as well as specific absorption features in the 2.0 to 2.5-micron region (lower right).
Figure 10 shows joint characterization as applied to dark spectra from the single Bahia Union scene. Differently colored regions of interest are identified and labeled as clearly separable clusters from the JC scatterplot (upper right), then projected onto the SVD fraction space (upper left) for context. Average spectra from pixels in all regions of interest (bottom row) clearly correspond to different shallow and suspended sediment. Differences in overall brightness and VNIR curvature are present, likely corresponding to factors like bathymetry and turbidity (lower right).

4. Discussion

This analysis was guided by four major questions. We discuss lessons learned with respect to each question below.

4.1. Generality of the SVD Model

It has been acknowledged for decades that, for most of the Earth’s land surface, most variance in decameter-scale multispectral satellite imagery can be expressed in three dimensions. Early observations of the “brightness”, “greenness”, and “third” dimensions conceptualized by the Tasseled Cap [58,59] were subsequently extended to the domain of spectral mixture analysis with generalized global endmembers (EMs) corresponding to soil and rock Substrate, illuminated photosynthetic Vegetation, and Dark targets like shadow and water (S, V, and D) [33]. The SVD model has been repeatedly confirmed for larger compilations of Landsat [55,56], as well as decameter multispectral data with additional spectral bands from Sentinel-2 [19]. Decameter-to-meter spatial scaling has been characterized using Landsat:WorldView-2 image pairs [60], as well as decameter-to-hectometer spatial scaling using coincident Landsat:MODIS observations [57].
Spectral unmixing was largely developed in the context of imaging spectroscopy [30,31,32]. Models using soil, vegetation, and shadow have been applied to imaging spectroscopy data for decades, often with the addition of a non-photosynthetic vegetation (NPV) endmember (e.g., [30,61]). As noted above, the majority of such studies used airborne imaging spectroscopy and so largely operated at local to regional scales. Studies of compilations of AVIRIS flight lines have also been performed [28,54,62,63]. Such studies largely focus on the related but distinct concept of intrinsic dimensionality, e.g., [27,64,65]. Those that do focus on generality of the SVD model are limited in spatial scope by data availability to North America, primarily California [17,54,66]. Evaluation of the generality of the SVD model with geographically and spectrally diverse EMIT data was a primary objective of this study. To our knowledge, this is the most comprehensive study to date demonstrating the generality of the SVD model for imaging spectroscopy data and the first to do so with decameter spaceborne data.

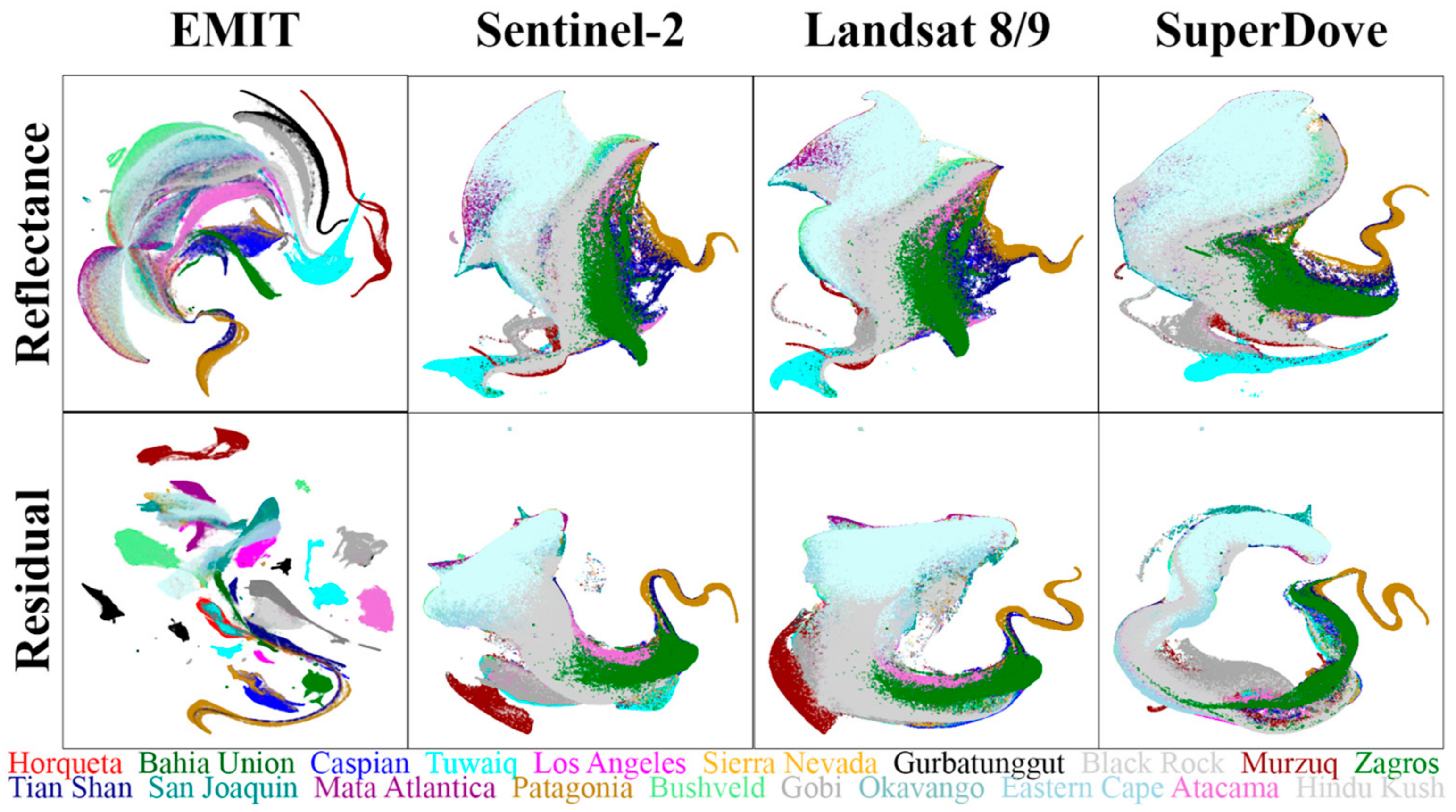
4.2. Feature Space Dimensionality and Topology: Hyperspectral vs. Multispectral

The cross-sensor generality of the SVD model is intrinsically related to similarity (or lack thereof) in spectral feature space dimensionality (variance partition) and topology. As noted above, the intrinsic dimensionality of imaging spectroscopy data has been studied previously, but studies have been limited by both data coverage and line-to-line differences in sensor calibration and atmospheric correction. The EMIT reflectance product used for this study is likely to exhibit substantially enhanced image-to-image radiometric stability relative to compilations of multiple flight lines from airborne sensors. The similarity in dimensionality between EMIT and simulated multispectral sensors when quantified using eigenvalues computed from reflectance—and dissimilarity when quantified using variance partition computed from the mixture residual—aligns with and extends previous results of [17,20] in clearly demonstrating that the greater spectral information content in hyperspectral image data can be effectively conceptualized as a greater departure from a simple three endmember linear mixing model. The fundamental differences in topology between the UMAP(MR) results for EMIT vs. all other sensors, discussed below, also strengthen and extend this finding.

4.3. Mixture Residual Efficacy: Hyperspectral vs. Multispectral

UMAP results from EMIT spectra at full spectral resolution indicate a demonstrably distinct manifold structure from all simulated multispectral sensors (Figure 6). While this distinction is observed when examining reflectance spectra, differences are much more apparent with the mixture residual. The separability among clusters of MR spectra both within and across EMIT scenes is unambiguous. This result strongly suggests that the spectral signatures captured by EMIT can differentiate biogeophysically distinct Earth surface materials which are not resolved by multispectral sensors like Landsat and Sentinel. The further loss of the distinct tendrils observed in Landsat and Sentinel in the SuperDove MR manifolds suggests that SWIR bands are especially important for the differentiation of these land cover types. This is particularly true for mineral absorptions in substrates, consistent with expectations of important information at SWIR wavelengths.

4.4. Efficacy of Joint Characterization with EMIT Data

Figure 7, Figure 8, Figure 9 and Figure 10 clearly indicate that Joint Characterization (JC) has significant potential to assist with exploratory analysis of high SNR decameter spaceborne imaging spectroscopy data. SVD mixture fractions provide natural quantities for the variance-based (global) axis of the JC. For this purpose, mixture model fractions have important advantages (e.g., physically interpretable) which are not generally true for other global metrics like PC dimensions. For the topology-based (local) axis of the JC, UMAP scores are clearly shown to provide useful information. Clusters identified from the JC space are consistently found to be statistically distinct and geographically coherent. Cluster position is not generally interpretable in UMAP space, but introducing S, V, and D fractions effectively provides physical order.

4.5. Limitations and Future Work

While the results of this study are promising, we do note some significant limitations. First, sampling is not truly global, so spectral diversity is underrepresented. While a wide range of geologic and floristic landscapes are sampled, several important areas are not yet included. Notably: (a) no scenes are included from Europe or Australia, (b) only one urban area (Los Angeles) is included, (c) only one major agricultural basin is sampled (San Joaquin), (d) no boreal (e.g., tundra) environments are included, and (e) cryospheric diversity is underrepresented. Future studies with greater data coverage may significantly extend these results, particularly in the form of more extreme endmember spectra.
Second, while the generalized SVD model is effective at modeling a wide range of terrestrial environments, it is intentionally exclusive of some materials. Such materials not well-fit by the SVD model include natural materials like evaporites, cryosphere (snow and ice), and shallow water substrates (e.g., reefs), as well as anthropogenic materials like roofing materials, plastics, and paint. While we recommend that regional analyses include both global and local EMs, it is likely that study areas that include significant areal coverage of evaporite pans, cryosphere, and/or urban areas may especially benefit from local EM selection and (potentially) mixture models with more than three endmembers.
Third, the results of this approach are inherently statistical, data-driven characterizations. Physical meaning, particularly of differences in cluster spectra identified from JC, does require user knowledge of reflectance spectroscopy. This approach is capable of identifying statistically distinct spectral signatures—but the interpretation of the physical meaning of those features is likely to benefit from models constructed for a different purpose. In particular, synergy with models which feature a direct physical interpretation like Tetracorder [67] is likely to be particularly interesting.
Fourth, this analysis uses the standard EMIT reflectance data product, which is derived from measured radiance spectra using the Optimal Estimation (OE)-based ISOFIT retrieval algorithm [68]. It is possible that significant differences might exist when compared to reflectance derived using different (non-Bayesian) atmospheric corrections and/or joint characterization of radiance. We suggest that further such intercomparisons represent important and interesting avenues for future work.

5. Conclusions

We analyze a spectrally and geographically diverse mosaic of 20 scenes from NASA’s novel Earth Mineral Dust Source Investigation (EMIT) mission. We evaluate the applicability of the generalized Substrate, Vegetation, Dark (SVD) linear mixture model from previous studies to these data and find the model to successfully fit the broad, high variance signatures in EMIT reflectance (average RMSE of non-masked pixels 3.1%; 99% of pixels < 3.7%). EMIT data are convolved to the spectral response functions of three common multispectral sensors. We find the partition of variance of EMIT reflectance spectra to be comparable to simulated Landsat and Sentinel reflectance spectra, but significant and consistent differences are present in the partition of variance among sensors for the spectral mixture residual. Similarly, the UMAP-estimated manifold structure for EMIT mixture residual is topologically distinct (more clustered) from the more continuous manifold structure of the multispectral mixture residuals. Joint characterization is found to effectively synergize the physical interpretability of the SVD mixture model with the statistical strengths of UMAP to effectively render additional potentially useful information. These results synthesize recent developments in hyperspectral high dimensional characterization, highlight the superb data quality from the novel EMIT mission, and demonstrate the quantitative and qualitative added value of spaceborne imaging spectroscopy over traditional multispectral satellite imaging.

Author Contributions

Conceptualization, D.S. and C.S.; methodology, D.S. and C.S.; formal analysis, D.S. and C.S.; investigation, D.S. and C.S.; resources, D.S. and C.S.; data curation, D.S. and C.S.; writing—original draft preparation, D.S.; writing—review and editing, D.S. and C.S.; visualization, D.S. and C.S.; funding acquisition, D.S. and C.S. All authors have read and agreed to the published version of the manuscript.

Funding

D.S. gratefully acknowledges funding from the USDA NIFA Sustainable Agroecosystems program (Grant #2022-67019-36397), the NASA Land-Cover/Land Use Change program (Grant #NNH21ZDA001N-LCLUC), the NASA Remote Sensing of Water Quality program (Grant #80NSSC22K0907), and the NSF Signals in the Soil program (Award #2226649). C.S. acknowledges the support of the endowment of the Lamont Doherty Earth Observatory of Columbia University.

Data Availability Statement

The data supporting this manuscript can be downloaded free of charge from the web portal listed in the main text.

Acknowledgments

D.S. thanks F.J.S. II for a lifetime of guidance and support. The authors thank two anonymous reviewers for constructive feedback.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. EMIT scenes used in this study. Latitude and longitude refer to the northwest corner of the scene.
Table A1. EMIT scenes used in this study. Latitude and longitude refer to the northwest corner of the scene.
TitleShort NameLatitudeLongitude
EMIT_L2A_RFL_001_20220909T145335_2225209_006Horqueta−41.53−68.60
EMIT_L2A_RFL_001_20220903T163129_2224611_012Bahia Union−39.24−62.09
EMIT_L2A_RFL_001_20220903T101734_2224607_026Eastern Cape−33.0123.50
EMIT_L2A_RFL_001_20220830T065605_2224205_022Tuwaiq24.7446.30
EMIT_L2A_RFL_001_20220828T174405_2224012_007Los Angeles34.99−118.51
EMIT_L2A_RFL_001_20220817T140711_2222909_021Murzuq26.3012.39
EMIT_L2A_RFL_001_20220815T042838_2222703_003Caspian40.1254.22
EMIT_L2A_RFL_001_20220815T025827_2222702_016Gurbantunggut45.6888.96
EMIT_L2A_RFL_001_20220814T223520_2222615_004Black Rock41.36−119.54
EMIT_L2A_RFL_001_20220814T160517_2222611_005Sierra Nevada38.45−119.69
EMIT_L2A_RFL_001_20220909T131308_2225208_011Atacama−21.95−69.18
EMIT_L2A_RFL_001_20220905T083937_2224806_033Bushveld−24.4626.61
EMIT_L2A_RFL_001_20220827T043253_2223903_002Tian Shan41.9577.10
EMIT_L2A_RFL_001_20220814T160505_2222611_004San Joaquin37.97−120.41
EMIT_L2A_RFL_001_20220901T034405_2224403_006Hindu Kush36.7368.68
EMIT_L2A_RFL_001_20220909T114035_2225207_003Mata Atlântica−22.75−44.88
EMIT_L2A_RFL_001_20220909T070044_2225204_005Okavango−18.8322.51
EMIT_L2A_RFL_001_20220912T154138_2225510_002Patagonia−49.58−74.14
EMIT_L2A_RFL_001_20220816T070436_2222805_008Gobi41.72104.40
EMIT_L2A_RFL_001_20220901T052019_2224404_013Zagros27.7055.64

References

  1. Green, R.O.; Thompson, D.R. EMIT Team NASA’s Earth Surface Mineral Dust Source Investigation: An Earth Venture Imaging Spectrometer Science Mission. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 119–122. [Google Scholar]
  2. Bradley, C.L.; Thingvold, E.; Moore, L.B.; Haag, J.M.; Raouf, N.A.; Mouroulis, P.; Green, R.O. Optical Design of the Earth Surface Mineral Dust Source Investigation (EMIT) Imaging Spectrometer. In Proceedings of the Imaging Spectrometry XXIV: Applications, Sensors, and Processing, Online, 24 August–4 September 2020; Volume 11504, p. 1150402. [Google Scholar]
  3. LP DAAC—New NASA Mission EMIT Launched to the International Space Station. Available online: https://lpdaac.usgs.gov/news/new-nasa-mission-emit-launched-to-the-international-space-station/ (accessed on 6 March 2023).
  4. Wulder, M.A.; Roy, D.P.; Radeloff, V.C.; Loveland, T.R.; Anderson, M.C.; Johnson, D.M.; Healey, S.; Zhu, Z.; Scambos, T.A.; Pahlevan, N. Fifty Years of Landsat Science and Impacts. Remote Sens. Environ. 2022, 280, 113195. [Google Scholar] [CrossRef]
  5. Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, S.L. Hyperion, a Space-Based Imaging Spectrometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1160–1173. [Google Scholar] [CrossRef]
  6. Corson, M.R.; Korwan, D.R.; Lucke, R.L.; Snyder, W.A.; Davis, C.O. The Hyperspectral Imager for the Coastal Ocean (HICO) on the International Space Station. In Proceedings of the IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; Volume 4, pp. IV–101–IV–104. [Google Scholar]
  7. Chapman, J.W.; Thompson, D.R.; Helmlinger, M.C.; Bue, B.D.; Green, R.O.; Eastwood, M.L.; Geier, S.; Olson-Duvall, W.; Lundeen, S.R. Spectral and Radiometric Calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG). Remote Sens. 2019, 11, 2129. [Google Scholar] [CrossRef]
  8. Candela, L.; Formaro, R.; Guarini, R.; Loizzo, R.; Longo, F.; Varacalli, G. The PRISMA Mission. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 253–256. [Google Scholar]
  9. Krutz, D.; Müller, R.; Knodt, U.; Günther, B.; Walter, I.; Sebastian, I.; Säuberlich, T.; Reulke, R.; Carmona, E.; Eckardt, A.; et al. The Instrument Design of the DLR Earth Sensing Imaging Spectrometer (DESIS). Sensors 2019, 19, 1622. [Google Scholar] [CrossRef] [PubMed]
  10. Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C. The EnMAP Spaceborne Imaging Spectroscopy Mission for Earth Observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
  11. Iwasaki, A.; Ohgi, N.; Tanii, J.; Kawashima, T.; Inada, H. Hyperspectral Imager Suite (HISUI)-Japanese Hyper-Multi Spectral Radiometer. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1025–1028. [Google Scholar]
  12. Nieke, J.; Rast, M. Towards the Copernicus Hyperspectral Imaging Mission for the Environment (CHIME). In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 157–159. [Google Scholar]
  13. Thompson, D.R.; Schimel, D.S.; Poulter, B.; Brosnan, I.; Hook, S.J.; Green, R.O.; Glenn, N.; Guild, L.; Henn, C.; Cawse-Nicholson, K. NASA’s Surface Biology and Geology Concept Study: Status and Next Steps. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3269–3271. [Google Scholar]
  14. Thompson, D.R.; Natraj, V.; Green, R.O.; Helmlinger, M.C.; Gao, B.-C.; Eastwood, M.L. Optimal Estimation for Imaging Spectrometer Atmospheric Correction. Remote Sens. Environ. 2018, 216, 355–373. [Google Scholar] [CrossRef]
  15. Gao, B.-C.; Montes, M.J.; Ahmad, Z.; Davis, C.O. Atmospheric Correction Algorithm for Hyperspectral Remote Sensing of Ocean Color from Space. Appl. Opt. 2000, 39, 887–896. [Google Scholar] [CrossRef]
  16. Sousa, D.; Small, C. Joint Characterization of Multiscale Information in High Dimensional Data. arXiv 2021, arXiv:2102.09669. [Google Scholar] [CrossRef]
  17. Sousa, D.; Brodrick, P.G.; Cawse-Nicholson, K.; Fisher, J.B.; Pavlick, R.; Small, C.; Thompson, D.R. The Spectral Mixture Residual: A Source of Low-Variance Information to Enhance the Explainability and Accuracy of Surface Biology and Geology Retrievals. J. Geophys. Res. Biogeosci. 2022, 127, e2021JG006672. [Google Scholar] [CrossRef]
  18. Sousa, D.; Small, C. Joint Characterization of Sentinel-2 Reflectance: Insights from Manifold Learning. Remote Sens. 2022, 14, 5688. [Google Scholar] [CrossRef]
  19. Small, C.; Sousa, D. The Sentinel 2 MSI Spectral Mixing Space. Remote Sens. 2022, 14, 5748. [Google Scholar] [CrossRef]
  20. Sousa, F.J.; Sousa, D.J. Hyperspectral Reconnaissance: Joint Characterization of the Spectral Mixture Residual Delineates Geologic Unit Boundaries in the White Mountains, CA. Remote Sens. 2022, 14, 4914. [Google Scholar] [CrossRef]
  21. Sousa, D.; Small, C. Joint Characterization of Spatiotemporal Data Manifolds. Front. Remote Sens. 2022, 3, 760650. [Google Scholar] [CrossRef]
  22. Small, C.; Sousa, D. Joint Characterization of the Cryospheric Spectral Feature Space. Front. Remote Sens. 2021, 2, 55. [Google Scholar] [CrossRef]
  23. Pearson, K. LIII. On Lines and Planes of Closest Fit to Systems of Points in Space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
  24. Strang, G. Introduction to Linear Algebra, 5th ed.; Wellesley-Cambridge Press: Cambridge, MA, USA, 2016. [Google Scholar]
  25. Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 2002; ISBN 1-139-42509-9. [Google Scholar]
  26. Menke, W.; Menke, J. Environmental Data Analysis with MatLab; Academic Press: Cambridge, MA, USA, 2016; ISBN 0-12-804550-7. [Google Scholar]
  27. Cawse-Nicholson, K.; Damelin, S.B.; Robin, A.; Sears, M. Determining the Intrinsic Dimension of a Hyperspectral Image Using Random Matrix Theory. IEEE Trans. Image Process. 2013, 22, 1301–1310. [Google Scholar] [CrossRef]
  28. Thompson, D.R.; Boardman, J.W.; Eastwood, M.L.; Green, R.O. A Large Airborne Survey of Earth’s Visible-Infrared Spectral Dimensionality. Opt. Express 2017, 25, 9186–9195. [Google Scholar] [CrossRef]
  29. Boardman, J.W. Automating Spectral Unmixing of AVIRIS Data Using Convex Geometry Concepts. In Proceedings of the JPL, Summaries of the 4th Annual JPL Airborne Geoscience Workshop, Washington, DC, USA, 25–29 October 1993; Volume 1, pp. 11–14. [Google Scholar]
  30. Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in Deserts: I. A Regional Measure of Abundance from Multispectral Images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
  31. Gillespie, A.; Smith, M.; Adams, J.; Willis, S.; Fischer, A.; Sabol, D. Interpretation of Residual Images: Spectral Mixture Analysis of AVIRIS Images, Owens Valley, California. In Proceedings of the Second Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop, Pasadena, CA, USA, 4–5 June 1990; NASA: Pasadena, CA, USA, 1990; pp. 243–270. [Google Scholar]
  32. Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral Mixture Modeling: A New Analysis of Rock and Soil Types at the Viking Lander 1 Site. J. Geophys. Res. Solid Earth 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
  33. Small, C. The Landsat ETM+ Spectral Mixing Space. Remote Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
  34. Settle, J.J.; Drake, N.A. Linear Mixing and the Estimation of Ground Cover Proportions. Int. J. Remote Sens. 1993, 14, 1159–1177. [Google Scholar] [CrossRef]
  35. Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319. [Google Scholar] [CrossRef] [PubMed]
  36. Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323. [Google Scholar] [CrossRef]
  37. Donoho, D.L.; Grimes, C. Hessian Eigenmaps: Locally Linear Embedding Techniques for High-Dimensional Data. Proc. Natl. Acad. Sci. USA 2003, 100, 5591. [Google Scholar] [CrossRef]
  38. Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
  39. Hinton, G.; Roweis, S.T. Stochastic Neighbor Embedding; Citeseer: Princeton, NJ, USA, 2002; Volume 15, pp. 833–840. [Google Scholar]
  40. van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
  41. Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality Reduction: A Comparative Review. J. Mach. Learn. Res. 2009, 10, 13. [Google Scholar]
  42. Landgrebe, D. Hyperspectral Image Data Analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
  43. Hérault, J.; Guérin-Dugué, A.; Villemain, P. Searching for the Embedded Manifolds in High-Dimensional Data, Problems and Unsolved Questions. In Proceedings of the ESANN 2002, Bruges, Belgium, 24–26 April 2002; pp. 173–184. [Google Scholar]
  44. Kim, D.H.; Finkel, L.H. Hyperspectral Image Processing Using Locally Linear Embedding. In Proceedings of the First International IEEE EMBS Conference on Neural Engineering, Capri, Italy, 20–22 March 2003; pp. 316–319. [Google Scholar]
  45. Bachmann, C.M.; Ainsworth, T.L.; Fusina, R.A. Exploiting Manifold Geometry in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 441–454. [Google Scholar] [CrossRef]
  46. Gillis, D.; Bowles, J.; Lamela, G.M.; Rhea, W.J.; Bachmann, C.M.; Montes, M.; Ainsworth, T. Manifold Learning Techniques for the Analysis of Hyperspectral Ocean Data. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Orlando, FL, USA, 28 March–1 April 2005; Volume 5806, pp. 342–351. [Google Scholar]
  47. Bachmann, C.M.; Ainsworth, T.L.; Fusina, R.A. Improved Manifold Coordinate Representations of Hyperspectral Imagery; Naval Research Laboratory Remote Sensing Division: Washington, DC, USA, 2005. [Google Scholar]
  48. Bachmann, C.M.; Ainsworth, T.L.; Fusina, R.A. Improved Manifold Coordinate Representations of Large-Scale Hyperspectral Scenes. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2786–2803. [Google Scholar] [CrossRef]
  49. Ainsworth, T.L.; Bachmann, C.M.; Fusina, R.A. Local Intrinsic Dimensionality of Hyperspectral Imagery from Non-Linear Manifold Coordinates. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1541–1542. [Google Scholar]
  50. Bachmann, C.M.; Ainsworth, T.L.; Fusina, R.A.; Montes, M.J.; Bowles, J.H.; Korwan, D.R. Bathymetric Retrieval from Manifold Coordinate Representations of Hyperspectral Imagery. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1548–1551. [Google Scholar]
  51. Mohan, A.; Sapiro, G.; Bosch, E. Spatially Coherent Nonlinear Dimensionality Reduction and Segmentation of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2007, 4, 206–210. [Google Scholar] [CrossRef]
  52. Bachmann, C.M.; Ainsworth, T.L.; Fusina, R.A. A Scalable Approach to Modeling Nonlinear Structure in Hyperspectral Imagery and Other High-Dimensional Data Using Manifold Coordinate Representations; SPIE: Bellingham, WA, USA, 2010; Volume 7695, pp. 92–98. [Google Scholar]
  53. McInnes, L.; Healy, J.; Melville, J. Umap: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
  54. Sousa, D.; Small, C. Multisensor Analysis of Spectral Dimensionality and Soil Diversity in the Great Central Valley of California. Sensors 2018, 18, 583. [Google Scholar] [CrossRef]
  55. Small, C.; Milesi, C. Multi-Scale Standardized Spectral Mixture Models. Remote Sens. Environ. 2013, 136, 442–454. [Google Scholar] [CrossRef]
  56. Sousa, D.; Small, C. Global Cross-Calibration of Landsat Spectral Mixture Models. Remote Sens. Environ. 2017, 192, 139–149. [Google Scholar] [CrossRef]
  57. Sousa, D.; Small, C. Globally Standardized MODIS Spectral Mixture Models. Remote Sens. Lett. 2019, 10, 1018–1027. [Google Scholar] [CrossRef]
  58. Kauth, R.J.; Thomas, G.S. The Tasselled Cap–a Graphic Description of the Spectral-Temporal Development of Agricultural Crops as Seen by Landsat. In Proceedings of the LARS Symposia, West Lafayette, IN, USA, 29 June–1 July 1976; p. 159. [Google Scholar]
  59. Crist, E.P.; Cicone, R.C. A Physically-Based Transformation of Thematic Mapper Data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 3, 256–263. [Google Scholar] [CrossRef]
  60. Small, C. Estimation of Urban Vegetation Abundance by Spectral Mixture Analysis. Int. J. Remote Sens. 2001, 22, 1305–1334. [Google Scholar] [CrossRef]
  61. Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R.O. Mapping Chaparral in the Santa Monica Mountains Using Multiple Endmember Spectral Mixture Models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
  62. Boardman, J.W.; Green, R.O. Exploring the Spectral Variability of the Earth as Measured by AVIRIS in 1999; Jet Propulsion Laboratory Special Publication: Pasadena, CA, USA, 2000. [Google Scholar]
  63. Asner, G.P.; Knapp, D.E.; Boardman, J.; Green, R.O.; Kennedy-Bowdoin, T.; Eastwood, M.; Martin, R.E.; Anderson, C.; Field, C.B. Carnegie Airborne Observatory-2: Increasing Science Data Dimensionality via High-Fidelity Multi-Sensor Fusion. Remote Sens. Environ. 2012, 124, 454–465. [Google Scholar] [CrossRef]
  64. Cawse-Nicholson, K.; Hook, S.J.; Miller, C.E.; Thompson, D.R. Intrinsic Dimensionality in Combined Visible to Thermal Infrared Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4977–4984. [Google Scholar] [CrossRef]
  65. Dai, J.; Vaughn, N.R.; Seeley, M.; Heckler, J.; Thompson, D.R.; Asner, G.P. Spectral Dimensionality of Imaging Spectroscopy Data over Diverse Landscapes and Spatial Resolutions. J. Appl. Remote Sens. 2022, 16, 044518. [Google Scholar] [CrossRef]
  66. Sousa, D.; Small, C. Which Vegetation Index? Benchmarking Multispectral Metrics to Hyperspectral Mixture Models in Diverse Cropland. Remote Sens. 2023, 15, 971. [Google Scholar] [CrossRef]
  67. Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.J.; Dalton, J.B.; McDougal, R.R.; Gent, C.A. Imaging Spectroscopy: Earth and Planetary Remote Sensing with the USGS Tetracorder and Expert Systems. J. Geophys. Res. E Planets 2003, 108, 1–44. [Google Scholar] [CrossRef]
  68. Thompson, D.R.; Brodrick, P.G.; Green, R.O.; Kalashnikova, O.; Lundeen, S.; Okin, G.; Olson-Duvall, W.; Painter, T. EMIT L2A Algorithm: Surface Reflectance and Scene Content Masks—Theoretical Basis; Earth Mineral dust source InvesTigation (EMIT); Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2020; p. 23. [Google Scholar]
Remotesensing 15 02295 g001 550
Figure 1. Index Map. Each of the 20 scenes used for this analysis is shown as a red dot. While the sample is not global, it does include a wide range of land cover, including globally significant hotspots for agriculture (San Joaquin), cryosphere (Patagonia and Tian Shan), desert (Taklamakan, Arabian, Saharan, and Gobi) and floristic diversity (South African Cape and Mata Atlântica).
Figure 1. Index Map. Each of the 20 scenes used for this analysis is shown as a red dot. While the sample is not global, it does include a wide range of land cover, including globally significant hotspots for agriculture (San Joaquin), cryosphere (Patagonia and Tian Shan), desert (Taklamakan, Arabian, Saharan, and Gobi) and floristic diversity (South African Cape and Mata Atlântica).
Remotesensing 15 02295 g001
Remotesensing 15 02295 g002 550
Figure 2. Mosaic of 20 spectrally diverse EMIT scenes.
Figure 2. Mosaic of 20 spectrally diverse EMIT scenes.
Remotesensing 15 02295 g002
Remotesensing 15 02295 g003 550
Figure 3. Three-dimensional spectral feature space and spectral endmembers. Scatterplots of orthogonal principal components reveal the straight edges and well-defined apexes of the spectral feature space. Density clustering along the substrate limb between dark and sand results from the geologic diversity of arid environments. However, no clusters are geographically specific. All are represented in multiple sample locations.
Figure 3. Three-dimensional spectral feature space and spectral endmembers. Scatterplots of orthogonal principal components reveal the straight edges and well-defined apexes of the spectral feature space. Density clustering along the substrate limb between dark and sand results from the geologic diversity of arid environments. However, no clusters are geographically specific. All are represented in multiple sample locations.
Remotesensing 15 02295 g003
Remotesensing 15 02295 g004 550
Figure 4. Three-dimensional mixture residual feature space and example spectra. Scatterplots of orthogonal principal components show some geographically distinct clusters (labeled) on the periphery, but the body of the distribution comingles residuals from almost all sample locations. Tuwaiq 1 and 2 correspond to bedrock and sand, respectively. The Zagros spectrum corresponds to shallow water in evaporite pans. The composite sand endmember used to compute the mixture residual is shown in red for comparison.
Figure 4. Three-dimensional mixture residual feature space and example spectra. Scatterplots of orthogonal principal components show some geographically distinct clusters (labeled) on the periphery, but the body of the distribution comingles residuals from almost all sample locations. Tuwaiq 1 and 2 correspond to bedrock and sand, respectively. The Zagros spectrum corresponds to shallow water in evaporite pans. The composite sand endmember used to compute the mixture residual is shown in red for comparison.
Remotesensing 15 02295 g004
Remotesensing 15 02295 g005 550
Figure 5. Partition of variance. Left: Cumulative normalized singular values for reflectance mosaic. Right: Cumulative normalized singular values for mixture residual mosaic. When computed from surface reflectance, all four sensors show >99% of spectral variance contained in the first three dimensions. After computing and removing the generalized (SVD) spectral mixture model, the partition of variance much more clearly reflects spectral differences among sensors. EMIT data show the highest dimensionality, with six additional dimensions required to capture 99% of the remaining variance. Sentinel-2 and Landsat 8 are comparable, each reaching 99% of the variance with two additional dimensions. SuperDove dimensionality is demonstrably lower, presumably as a result of the lack of SWIR bands. Note differences in both x and y-axis scaling between plots.
Figure 5. Partition of variance. Left: Cumulative normalized singular values for reflectance mosaic. Right: Cumulative normalized singular values for mixture residual mosaic. When computed from surface reflectance, all four sensors show >99% of spectral variance contained in the first three dimensions. After computing and removing the generalized (SVD) spectral mixture model, the partition of variance much more clearly reflects spectral differences among sensors. EMIT data show the highest dimensionality, with six additional dimensions required to capture 99% of the remaining variance. Sentinel-2 and Landsat 8 are comparable, each reaching 99% of the variance with two additional dimensions. SuperDove dimensionality is demonstrably lower, presumably as a result of the lack of SWIR bands. Note differences in both x and y-axis scaling between plots.
Remotesensing 15 02295 g005
Remotesensing 15 02295 g006 550
Figure 6. Effect of spectral resolution on manifold structure. Pixels from each EMIT scene are visualized using distinct colors. Both reflectance and residual feature space embeddings clearly segregate numerous individual EMIT scenes, while the multispectral embeddings depict them as comingled within a single continuum for each sensor. All embeddings shown here were generated with a n_neighbors value of 50.
Figure 6. Effect of spectral resolution on manifold structure. Pixels from each EMIT scene are visualized using distinct colors. Both reflectance and residual feature space embeddings clearly segregate numerous individual EMIT scenes, while the multispectral embeddings depict them as comingled within a single continuum for each sensor. All embeddings shown here were generated with a n_neighbors value of 50.
Remotesensing 15 02295 g006
Remotesensing 15 02295 g007 550
Figure 7. Joint characterization of the 20-scene mosaic spectral feature space. Two-dimensional UMAP embedding (upper left) shows distinct 2D continua for vegetation and substrates with distinct tendril continua for spectrally distinctive sands, bedrock lithology, and snow. Combining individual dimensions of the 2D UMAP manifold with individual S (lower left), V (lower right), and D (upper right) endmember fractions shows the physical properties of distinct spectra. Note geographically specific lithologic endmembers in Substrate + UMAP1 space in contrast to geographically comingled vegetation and non-photosynthetic vegetation (NPV) endmembers in Vegetation + UMAP2 space. Snow shows implausible vegetation fractions (in the range [0, 2]) because there is no snow EM in the SVD model. The UMAP embedding was generated using a n_neighbors value of 50.
Figure 7. Joint characterization of the 20-scene mosaic spectral feature space. Two-dimensional UMAP embedding (upper left) shows distinct 2D continua for vegetation and substrates with distinct tendril continua for spectrally distinctive sands, bedrock lithology, and snow. Combining individual dimensions of the 2D UMAP manifold with individual S (lower left), V (lower right), and D (upper right) endmember fractions shows the physical properties of distinct spectra. Note geographically specific lithologic endmembers in Substrate + UMAP1 space in contrast to geographically comingled vegetation and non-photosynthetic vegetation (NPV) endmembers in Vegetation + UMAP2 space. Snow shows implausible vegetation fractions (in the range [0, 2]) because there is no snow EM in the SVD model. The UMAP embedding was generated using a n_neighbors value of 50.
Remotesensing 15 02295 g007
Remotesensing 15 02295 g008 550
Figure 8. Joint characterization for discrimination of vegetation spectra in the San Joaquin Valley. Red, cyan, and yellow regions of interest are clearly separable in the joint space (top row, center) but not in the variance-based SVD fraction space (top row, left). Mean spectra from each region of interest (bottom row, left) show differences in mesophyll reflectance, red edge slope, liquid water absorption, and cellulose/lignin absorption features. All regions are more absorptive throughout visible wavelengths than the mosaic V endmember (green, bottom row, center). Clusters identified from JC are geographically coherent at the field scale in map space (right).
Figure 8. Joint characterization for discrimination of vegetation spectra in the San Joaquin Valley. Red, cyan, and yellow regions of interest are clearly separable in the joint space (top row, center) but not in the variance-based SVD fraction space (top row, left). Mean spectra from each region of interest (bottom row, left) show differences in mesophyll reflectance, red edge slope, liquid water absorption, and cellulose/lignin absorption features. All regions are more absorptive throughout visible wavelengths than the mosaic V endmember (green, bottom row, center). Clusters identified from JC are geographically coherent at the field scale in map space (right).
Remotesensing 15 02295 g008
Remotesensing 15 02295 g009 550
Figure 9. Joint characterization for discrimination of substrate spectra in the Atacama Desert. Red, cyan, yellow, magenta, green, and sienna regions of interest are clearly separable in the joint space (top row, center) but not in the variance-based SVD fraction space (top row, left). Mean spectra from each region (bottom row, left) show differences in amplitude and curvature throughout the spectrum, including minor but perceptible differences in SWIR wavelengths (bottom row, center). All regions are darker throughout VSWIR wavelengths than the mosaic S endmember (thick red). Clusters identified from JC are geographically coherent in map space (right).
Figure 9. Joint characterization for discrimination of substrate spectra in the Atacama Desert. Red, cyan, yellow, magenta, green, and sienna regions of interest are clearly separable in the joint space (top row, center) but not in the variance-based SVD fraction space (top row, left). Mean spectra from each region (bottom row, left) show differences in amplitude and curvature throughout the spectrum, including minor but perceptible differences in SWIR wavelengths (bottom row, center). All regions are darker throughout VSWIR wavelengths than the mosaic S endmember (thick red). Clusters identified from JC are geographically coherent in map space (right).
Remotesensing 15 02295 g009
Remotesensing 15 02295 g010 550
Figure 10. Joint characterization for discrimination of dark spectra in Bahia Union coastal ocean. Regions of interest (red, yellow, magenta, orchid, cyan, and orange) are clearly separable in the joint space (top row, right) but not in the variance-based SVD fraction space (top row, left). Mean spectra from each region (bottom row, left) show differences in amplitude and curvature throughout the spectrum, including significant differences at visible wavelengths (bottom row, right). Clusters identified from JC are geographically coherent in map space (right).
Figure 10. Joint characterization for discrimination of dark spectra in Bahia Union coastal ocean. Regions of interest (red, yellow, magenta, orchid, cyan, and orange) are clearly separable in the joint space (top row, right) but not in the variance-based SVD fraction space (top row, left). Mean spectra from each region (bottom row, left) show differences in amplitude and curvature throughout the spectrum, including significant differences at visible wavelengths (bottom row, right). Clusters identified from JC are geographically coherent in map space (right).
Remotesensing 15 02295 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sousa, D.; Small, C. Topological Generality and Spectral Dimensionality in the Earth Mineral Dust Source Investigation (EMIT) Using Joint Characterization and the Spectral Mixture Residual. Remote Sens. 2023, 15, 2295. https://doi.org/10.3390/rs15092295

AMA Style

Sousa D, Small C. Topological Generality and Spectral Dimensionality in the Earth Mineral Dust Source Investigation (EMIT) Using Joint Characterization and the Spectral Mixture Residual. Remote Sensing. 2023; 15(9):2295. https://doi.org/10.3390/rs15092295

Chicago/Turabian Style

Sousa, Daniel, and Christopher Small. 2023. "Topological Generality and Spectral Dimensionality in the Earth Mineral Dust Source Investigation (EMIT) Using Joint Characterization and the Spectral Mixture Residual" Remote Sensing 15, no. 9: 2295. https://doi.org/10.3390/rs15092295

APA Style

Sousa, D., & Small, C. (2023). Topological Generality and Spectral Dimensionality in the Earth Mineral Dust Source Investigation (EMIT) Using Joint Characterization and the Spectral Mixture Residual. Remote Sensing, 15(9), 2295. https://doi.org/10.3390/rs15092295

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop