High-Resolution and Efficient Neural Dual Contouring for Surface Reconstruction from Point Clouds
Abstract
1. Introduction
- We systematically summarize the related work on Neural Implicit Representation-based reconstruction, as detailed in Section 2. We also provide important insights in this topic from our perspective, including latent vector, local feature, network backbone, sharp boundary, and large-scale scenes. We also highlight the issue of “high-resolution” faced by existing works.
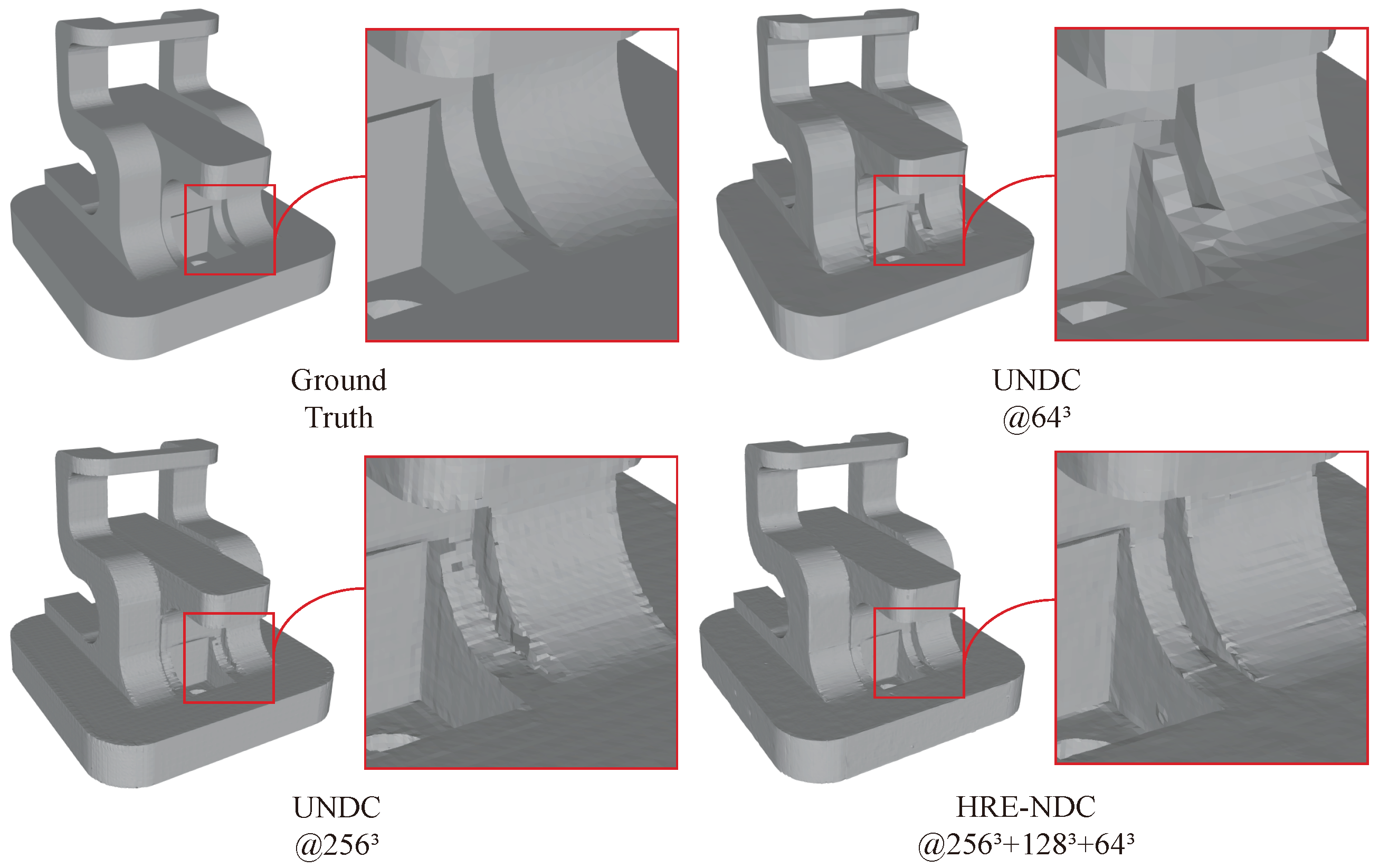
- To address the “high-resolution” problem, we introduce HRE-NDC, which is a highly efficient multiscale network structure for reconstructing mesh surfaces from point clouds. It incorporates a coarse-to-fine strategy and a series of effective techniques, significantly improving memory and time efficiency compared to prior works.
- HRE-NDC also raises the reconstruction quality by predicting residuals in our coarse-to-fine manner and using tailored activation functions to increase the network’s detail learning capacity. Our results surpass previous work in both quantitative and qualitative evaluations, providing results closest to the ground truth.
- We introduce a novel feature-preserving downsampling operation. Conventional downsampling operations such as MaxPool, AvgPool, nearest neighbor sampling, and bilinear sampling have a tendency to blur sharp features. Our downsampling algorithm focuses on preserving features at sharp edges and corners while downsampling only in smooth areas. By generating pseudo-targets at various scales using this downsampling, HRE-NDC is provided with effective supervision, leading to high-quality reconstruction results.
2. Related Work
2.1. Neural Implicit Representation-Based Reconstruction
2.2. Isosurface Extraction
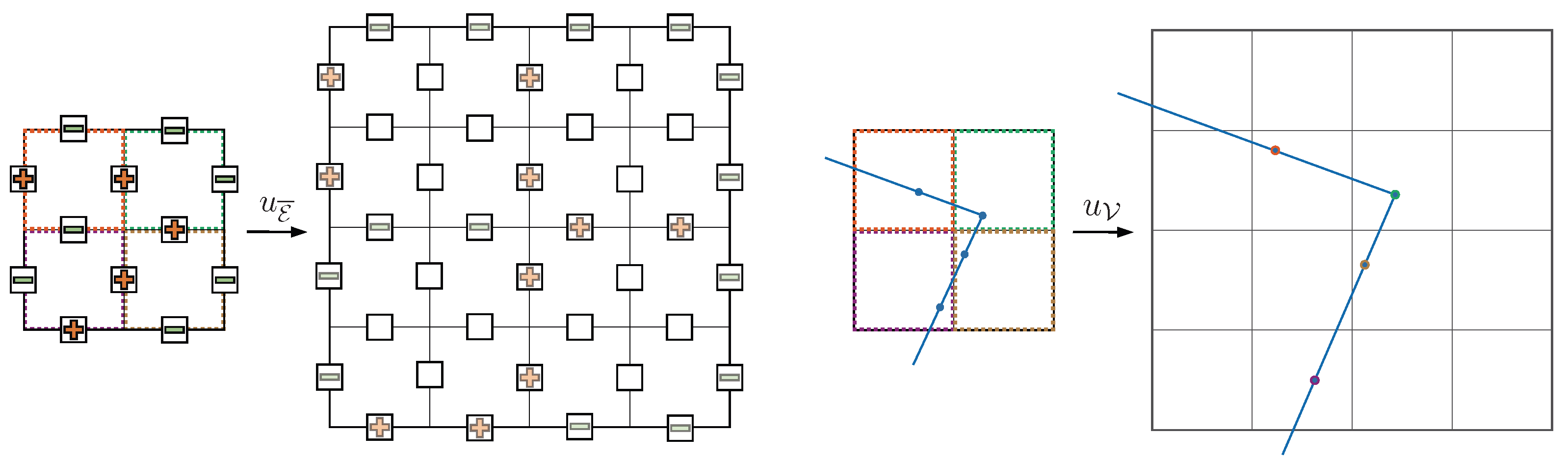
3. Method
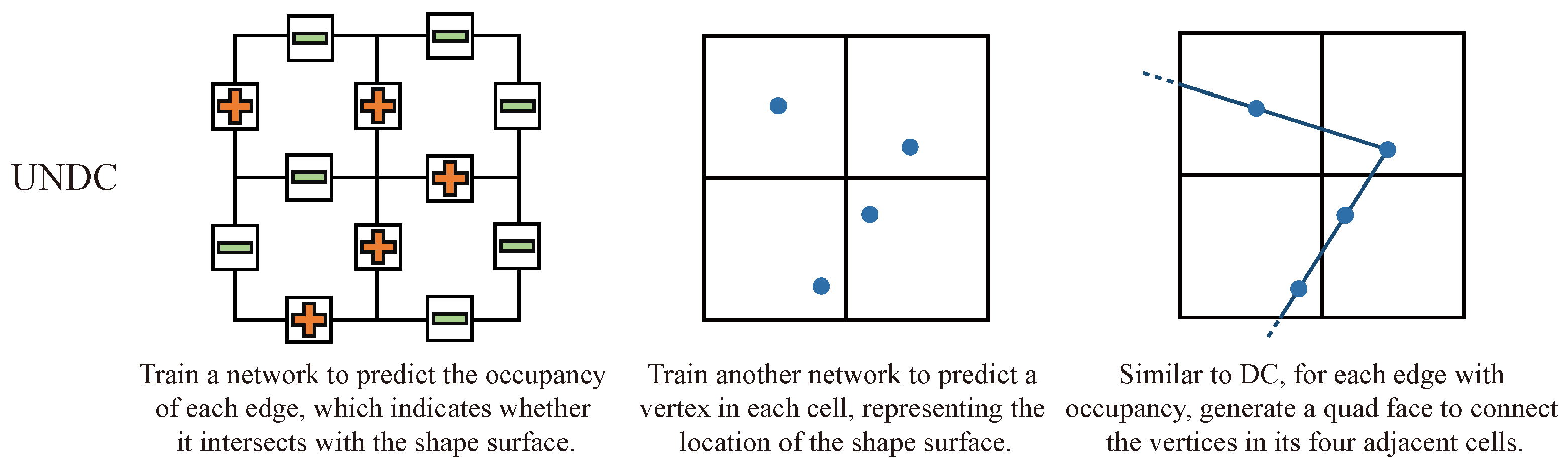
3.1. Baseline
3.2. Hre-Ndc
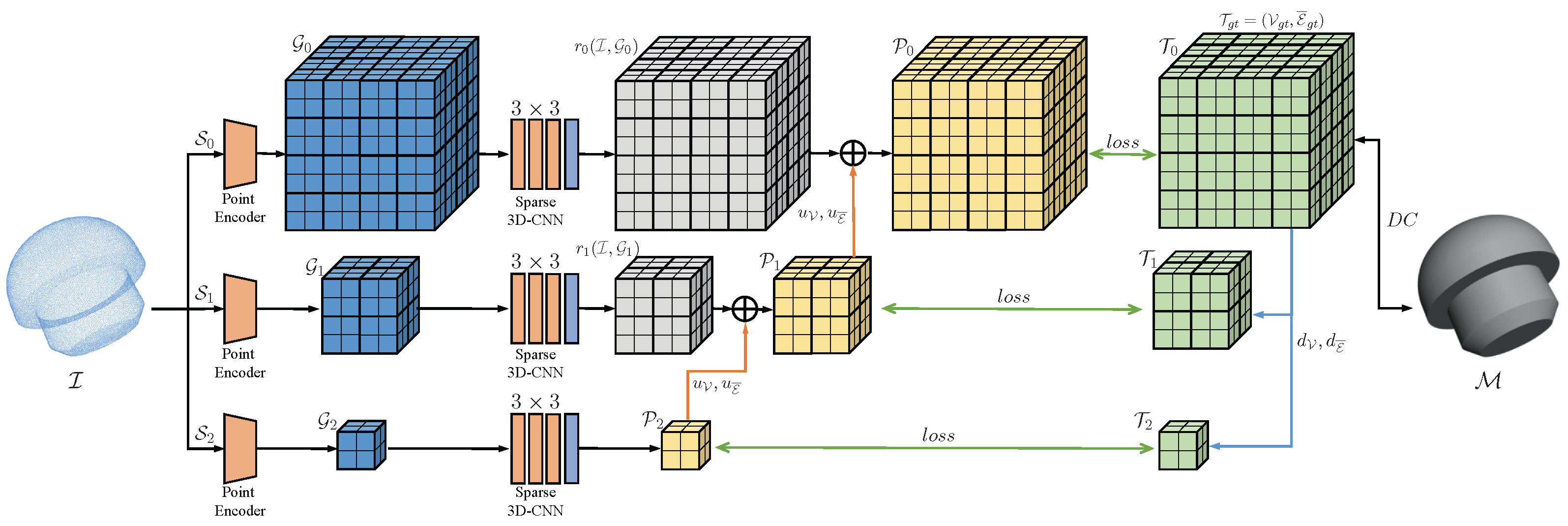
3.2.1. Network Architecture
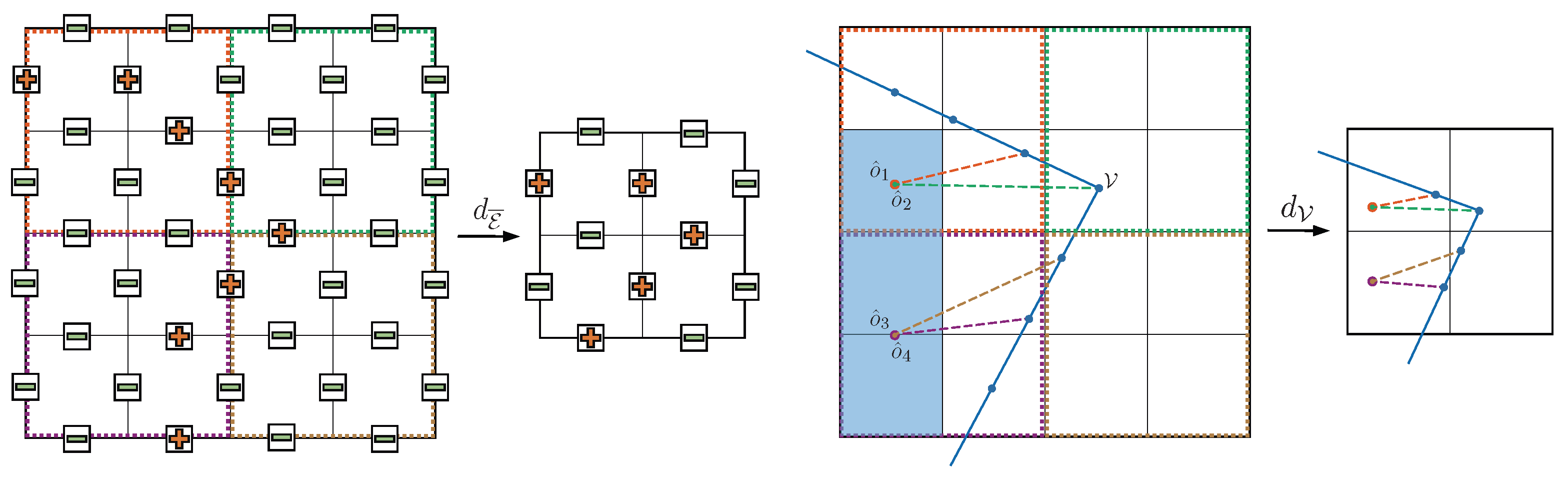
3.2.2. Feature Preserving Downsampling
3.2.3. Upsampling without Interpolation
3.2.4. Activation Functions
3.2.5. Masks and Sparse 3D-CNN
3.3. Training Strategy and Losses
4. Results
4.1. Datasets
- The Thingi10K [43] dataset, which contains over 10k 3D printing models uploaded by users, which is more challenging than ABC.
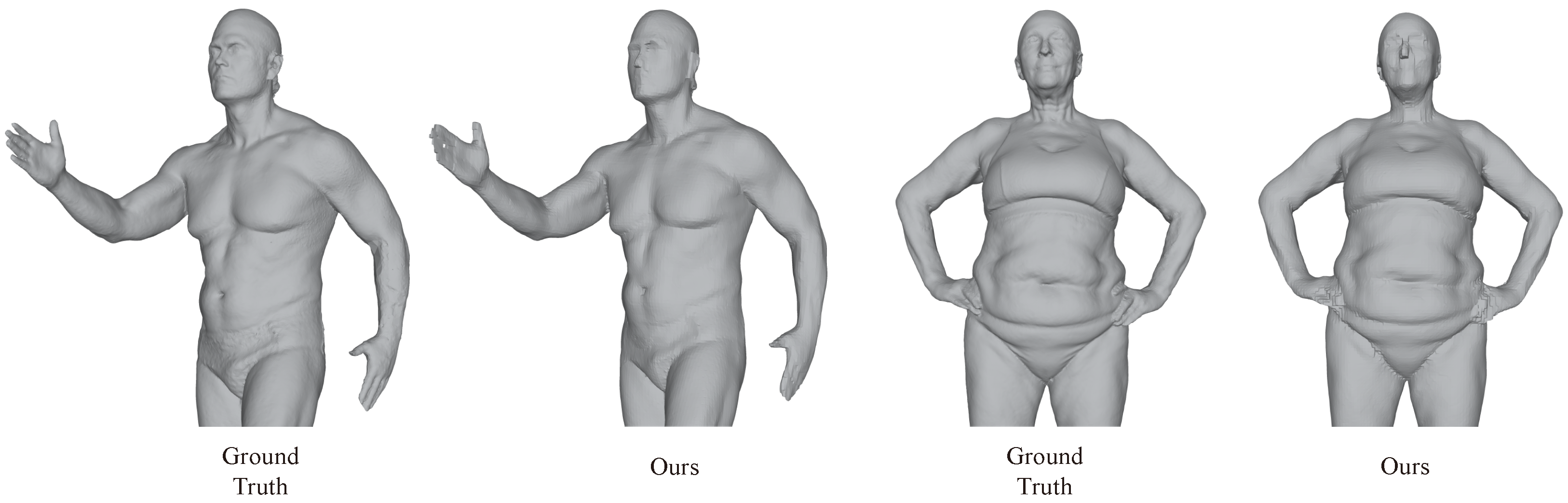
- The FAUST [44] dataset, which contains 100 human body models.
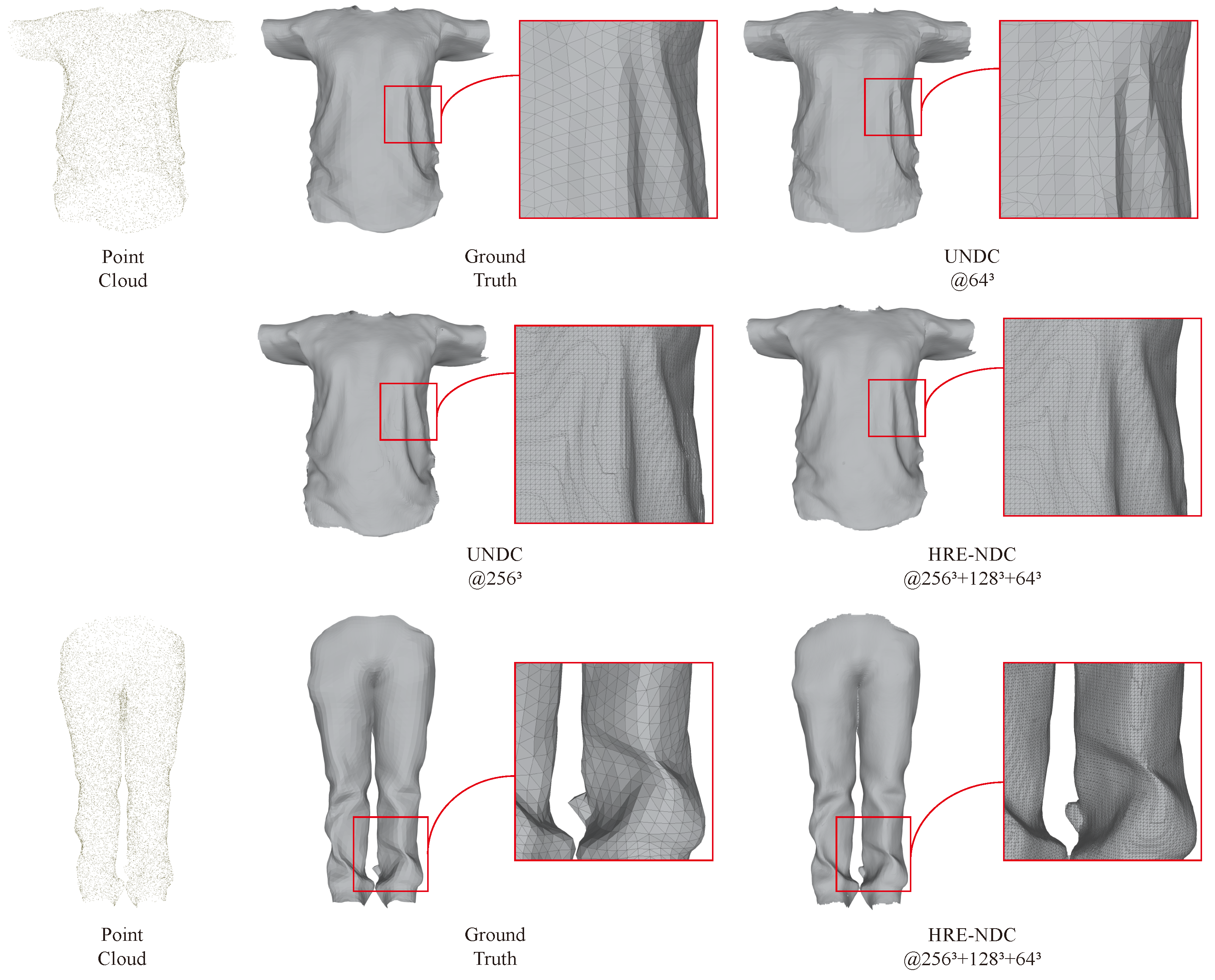
- The MGN dataset, a dataset containing clothes and open surfaces provided by MGN [45].
- Several rooms in the Matterport3D [46] dataset, which is used to test large indoor scan scenes.
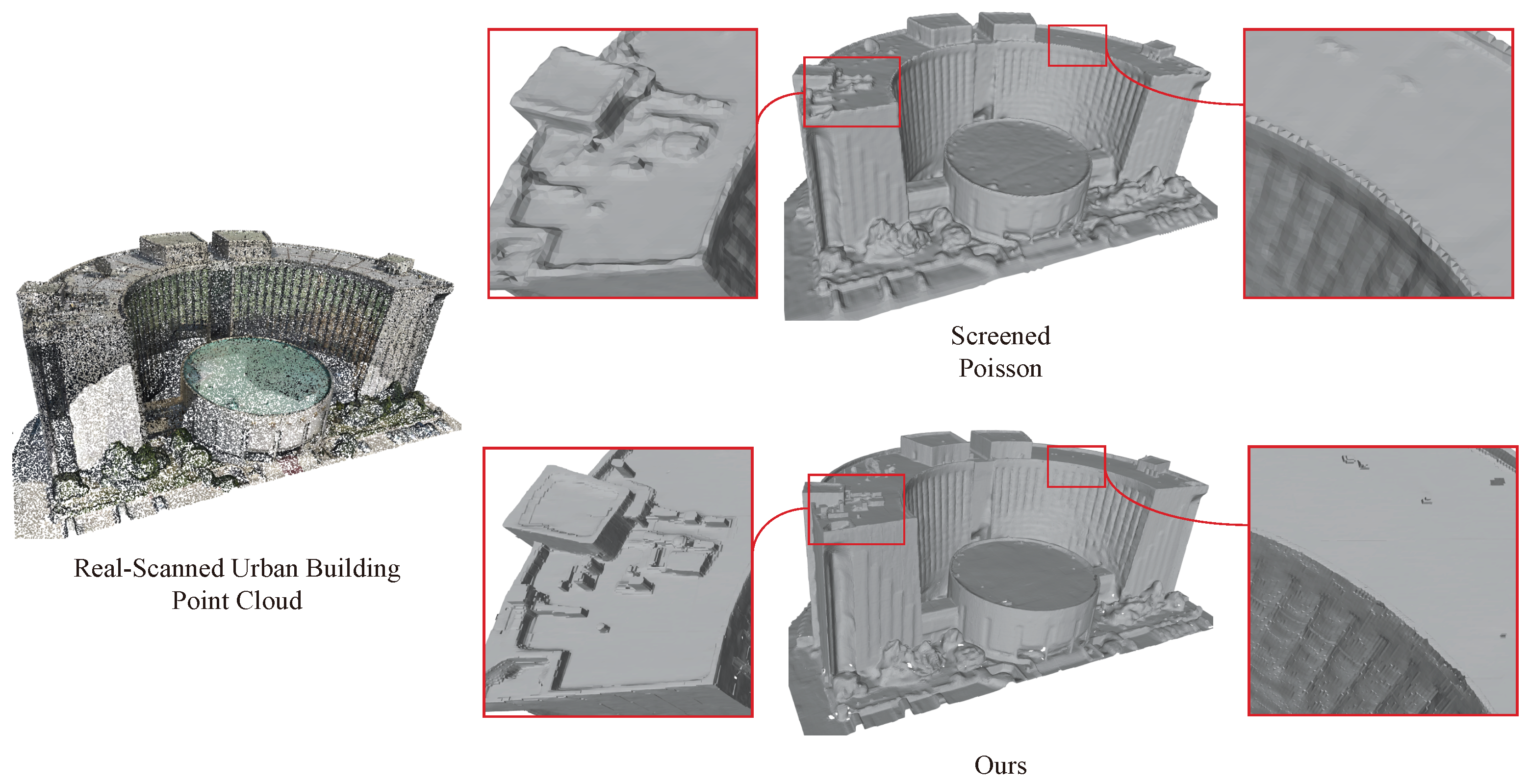
- Some real-scanned urban building data that we colllected ourselves.
4.2. Metircs
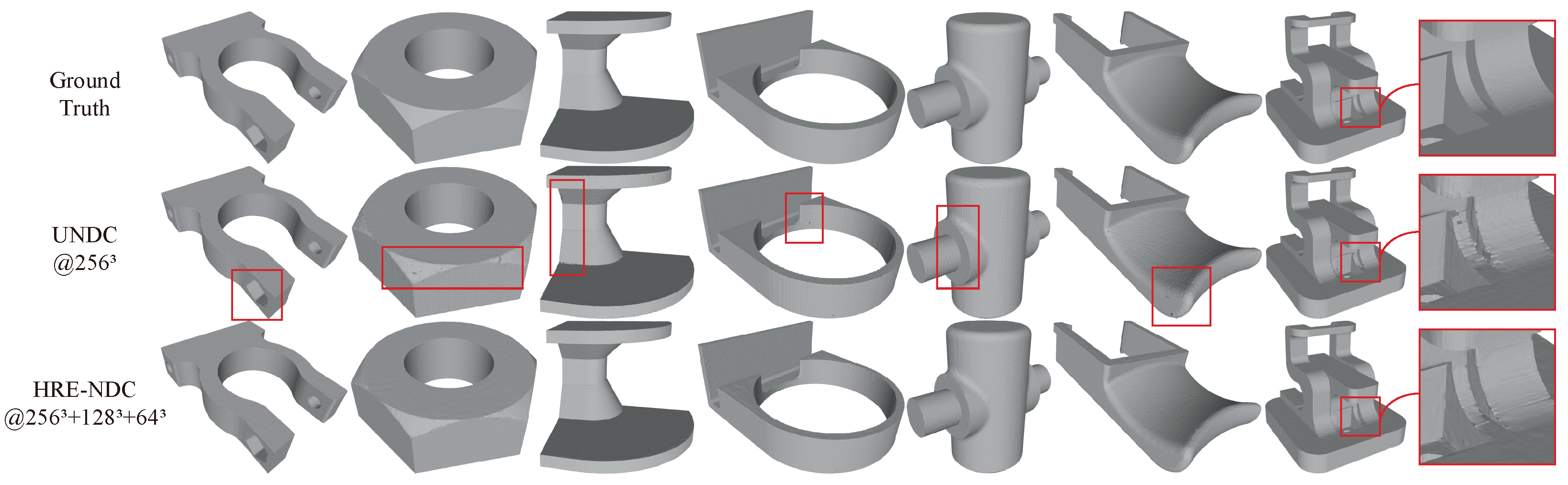
4.3. Comparison with Baseline
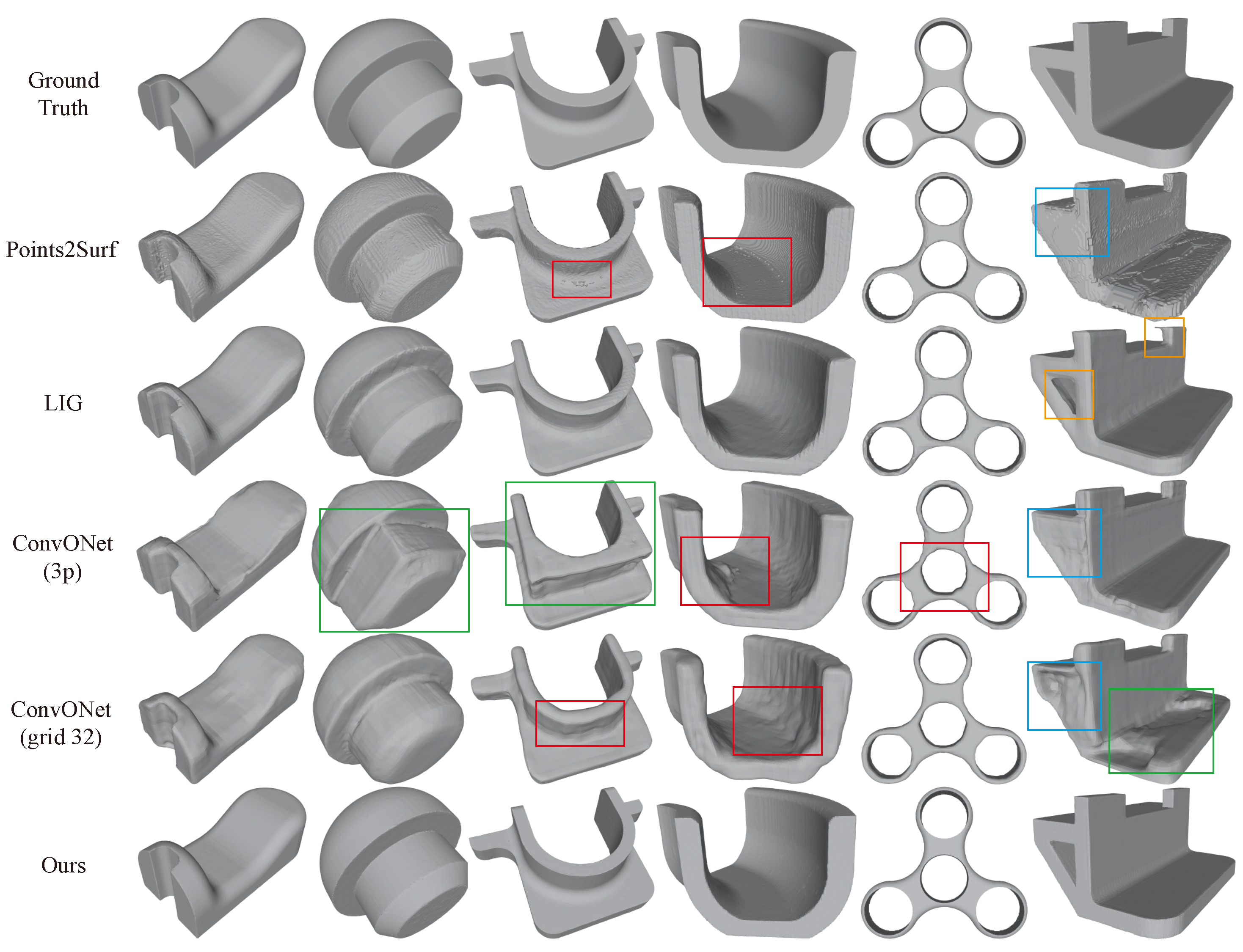
4.4. Comparison with Other NIR-Based Methods
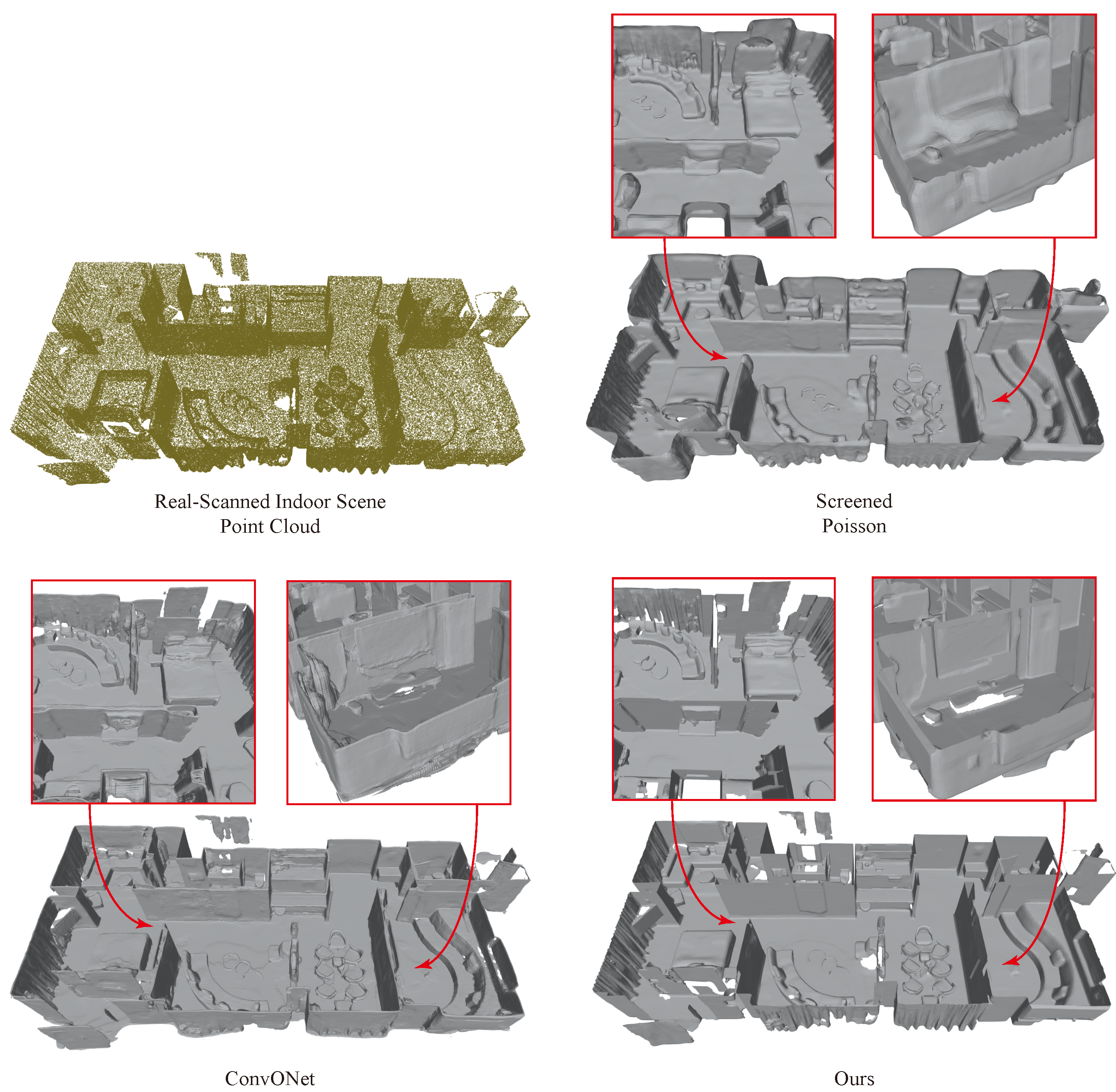
4.5. Reconstruction of Large Scenes
4.6. Generalization Performance Demonstration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berger, M.; Tagliasacchi, A.; Seversky, L.M.; Alliez, P.; Levine, J.a.; Sharf, A.; Silva, C.T.; Tagliasacchi, A.; Seversky, L.M.; Silva, C.T.; et al. State of the Art in Surface Reconstruction from Point Clouds. In Proceedings of the Eurographics 2014–State of the Art Reports, Strasbourg, France, 7 April 2014; Volume 1, pp. 161–185. [Google Scholar]
- Berger, M.; Tagliasacchi, A.; Seversky, L.M.; Alliez, P.; Guennebaud, G.; Levine, J.A.; Sharf, A.; Silva, C.T. A Survey of Surface Reconstruction from Point Clouds. Comput. Graph. Forum 2017, 36, 301–329. [Google Scholar] [CrossRef]
- Kaiser, A.; Ybanez Zepeda, J.A.; Boubekeur, T. A Survey of Simple Geometric Primitives Detection Methods for Captured 3D Data. Comput. Graph. Forum 2019, 38, 167–196. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, H. Learning Implicit Fields for Generative Shape Modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy Networks: Learning 3D Reconstruction in Function Space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Erler, P.; Guerrero, P.; Ohrhallinger, S.; Mitra, N.J.; Wimmer, M. Points2Surf: Learning Implicit Surfaces from Point Clouds. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 108–124. [Google Scholar] [CrossRef]
- Jiang, C.M.; Sud, A.; Makadia, A.; Huang, J.; Nießner, M.; Funkhouser, T. Local Implicit Grid Representations for 3D Scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Songyou, P.; Michael, N.; Lars, M.; Marc, P.; Andreas, G. Convolutional Occupancy Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Chen, Z.; Tagliasacchi, A.; Funkhouser, T.; Zhang, H. Neural Dual Contouring. ACM Trans. Graph. 2022, 41, 1–13. [Google Scholar] [CrossRef]
- Fan, H.; Su, H.; Guibas, L.J. A point set generation network for 3D Object Reconstruction from a single Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. A papier-mâché approach to learning 3D surface generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 216–224. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. ACM SIGGRAPH Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Evgcni, V. Chernyacv Marching Cubes 33: Construction of Topologically Correct. 1995. Available online: https://cds.cern.ch/record/292771/files/cn-95-017.pdf (accessed on 14 January 2023).
- Chibane, J.; Alldieck, T.; Pons-Moll, G. Implicit Functions in Feature Space for 3D Shape Reconstruction and Completion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Chen, Z.; Zhang, H. Neural Marching Cubes. ACM Trans. Graph. 2021, 40, 1–15. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hinton, G. Fast Learning of Sparse Representations with an Energy-Based Model. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Ju, T.; Losasso, F.; Schaefer, S.; Warren, J. Dual Contouring of Hermite Data. ACM Trans. Graph. 2002, 21, 339–346. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Kingma, D.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Choy, C.B.; Xu, D.; Gwak, J.; Chen, K.; Savarese, S. 3D-R2N2: A Unified Approach for Single and Multi-view 3D Object Reconstruction. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Garland, M.; Heckbert, P.S. Surface Simplification Using Quadric Error Metrics. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 3 August 1997; ACM Press: New York, NY, USA; Addison-Wesley Publishing Co.: Boston, MA, USA, 1997; pp. 209–216. [Google Scholar] [CrossRef]
- Chibane, J.; Mir, A.; Pons-Moll, G. Neural Unsigned Distance Fields for Implicit Function Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5105–5114. [Google Scholar]
- Alliez, P.; Giraudot, S.; Jamin, C.; Lafarge, F.; Mérigot, Q.; Meyron, J.; Saboret, L.; Salman, N.; Wu, S.; Yildiran, N.F. Point Set Processing. In CGAL User and Reference Manual, 5.1th ed.; 2022; Available online: https://geometrica.saclay.inria.fr/team/Marc.Glisse/tmp/cgal-power/Manual/how_to_cite_cgal.html (accessed on 20 March 2023).
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Dumoulin, V.; Visin, F. A guide to convolution arithmetic for deep learning. arXiv 2016, arXiv:1603.07285. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Graham, B.; Engelcke, M.; van der Maaten, L. 3D Semantic Segmentation with Submanifold Sparse Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Graham, B.; van der Maaten, L. Submanifold Sparse Convolutional Networks. arXiv 2017, arXiv:1706.01307. [Google Scholar]
- Koch, S.; Matveev, A.; Williams, F.; Alexa, M.; Zorin, D.; Panozzo, D.; Files, C.A.D. ABC: A Big CAD Model Dataset For Geometric Deep Learning. arXiv 2018, arXiv:1812.06216. [Google Scholar]
- Zhou, Q.; Jacobson, A. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv 2016, arXiv:1605.04797. [Google Scholar]
- Bogo, F.; Romero, J.; Loper, M.; Black, M.J. FAUST: Dataset and Evaluation for 3D Mesh Registration. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3794–3801. [Google Scholar] [CrossRef]
- Bhatnagar, B.; Tiwari, G.; Theobalt, C.; Pons-Moll, G. Multi-Garment Net: Learning to Dress 3D People From Images. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October 2019; pp. 5419–5429. [Google Scholar] [CrossRef]
- Chang, A.; Dai, A.; Funkhouser, T.; Halber, M.; Niessner, M.; Savva, M.; Song, S.; Zeng, A.; Zhang, Y. Matterport3D: Learning from RGB-D Data in Indoor Environments. In Proceedings of the 7th IEEE International Conference on 3D Vision, 3DV 2017, Qingdao, China, 10–12 October 2017. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]


| Method | Resolution | Epochs | Time/Epoch | Total Time | GPU Memory/Batch |
|---|---|---|---|---|---|
| UNDC | 250 | ≈12 min | ≈2 days | ≈4 G | |
| 100 | ≈150 min | ≈10.4 days | ≈70 G | ||
| 250 | ≈150 min | days | ≈70 G | ||
| HRE-NDC | 60 | ≈12 min | h | ≈3 G | |
| 30 | ≈39 min | ≈19.5 h | ≈11 G | ||
| 10 | ≈150 min | h | ≈41 G | ||
| + + | 100 | days |
| Method | CD | F1↑ | EDC | EF1↑ | Inference Time |
|---|---|---|---|---|---|
| UNDC (baseline) | 0.827 | 0.873 | 0.411 | 0.757 | s |
| HRE-NDC (ours) | 0.747 | 0.768 | 0.379 | 0.856 | s |
| Method | CD | F1 ↑ | EDC ↓ | EF1 | Inference Time |
|---|---|---|---|---|---|
| Points2Surf | 7.954 | 0.428 | 8.686 | 0.042 | s |
| LIG | 4.642 | 0.768 | 11.652 | 0.025 | s |
| ConvONet-3p | 18.134 | 0.536 | 4.113 | 0.105 | s |
| ConvONet-grid32 | 8.844 | 0.488 | 9.701 | 0.036 | s |
| UNDC | 0.753 | 0.873 | 0.822 | 0.757 | s |
| HRE-NDC(ours) | 0.726 | 0.832 | 0.752 | 0.856 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Xiao, J.; Liu, L.; Wang, Y.; Wang, Y. High-Resolution and Efficient Neural Dual Contouring for Surface Reconstruction from Point Clouds. Remote Sens. 2023, 15, 2267. https://doi.org/10.3390/rs15092267
Liu Q, Xiao J, Liu L, Wang Y, Wang Y. High-Resolution and Efficient Neural Dual Contouring for Surface Reconstruction from Point Clouds. Remote Sensing. 2023; 15(9):2267. https://doi.org/10.3390/rs15092267
Chicago/Turabian StyleLiu, Qi, Jun Xiao, Lupeng Liu, Yunbiao Wang, and Ying Wang. 2023. "High-Resolution and Efficient Neural Dual Contouring for Surface Reconstruction from Point Clouds" Remote Sensing 15, no. 9: 2267. https://doi.org/10.3390/rs15092267
APA StyleLiu, Q., Xiao, J., Liu, L., Wang, Y., & Wang, Y. (2023). High-Resolution and Efficient Neural Dual Contouring for Surface Reconstruction from Point Clouds. Remote Sensing, 15(9), 2267. https://doi.org/10.3390/rs15092267






