Clear-Air Bragg Scattering Observed above the Convective Boundary Layer in the Morning

Abstract

Reflected waves have been frequently observed via weather radar, even during sunny, cloudless days. Additionally, it is recognized that turbulence and biological scatterers can also dominate the scattering process. In previous studies, echo returns of turbulence from clear-air Bragg scattering (CABS) have been used to detect the height of the convective boundary layer (CBL). However, in a dual-frequency antenna multiplexing radar system, through which the dual-wavelength ratio (DWR) identifies the CABS clearly, CABS can be unexpectedly observed not only at the edge of the CBL but also above the CBL, highlighting the need for an expanded set of causes of clear-air echoes. It was further identified that the negative second derivative of horizontal wind speed, which is measured by a coherent Doppler Lidar, is consistent with the variation of the CABS layers’ height above the CBL. These results emphasize the presence of physical processes leading to turbulence in the troposphere, with implications for Bragg scattering studies and the theory of turbulence in general. This study will help the ecology of research better understand the laws of biological activity.

1. Introduction

Weather radars have been used to observe clouds and rain since World War II. Since then, clear-air echoes have usually been observed in sunny, cloudless weather conditions. One type of scattering of interest is clear-air Bragg scattering (CABS). Specifically, it was shown that CABS could be used to assist with radar calibration and detecting the height of the convective boundary layer (CBL) because layers of clear-air Bragg scattering are usually present near the top of the CBL [1,2,3]. In some cases, turbulent mixing between cloudy and drier environmental air can produce centimeter-scale variations in refractive index that can lead to strong CABS [4].

It is known that Bragg scattering is caused by turbulent inhomogeneities with sizes around one-half of a transmitted radar wavelength [5,6,7]. Due to the increase in the inner scale of turbulence with height, it is difficult to observe CABS in the X-band and even more so in the Ka-band due to their short wavelengths, which do not allow for backward scattering. Generally, Bragg scattering is observed as a layer at the top of the CBL and is mostly associated with refractivity and moisture gradients in dynamically unstable regions [8,9]. Turbulent mixing, penetrative convection, and detrainment/entrainment are considered the primary generation mechanisms of Bragg scattering [10,11].

However, the presence of CABS in the atmosphere has been overlooked for a considerable amount of time. Although turbulence-scattering mechanisms caused by turbulent inhomogeneities and biological scatterers, such as insects and birds, can dominate the scattering process of clear-air echoes, it is widely believed that insects and birds primarily cause most of the echoes [12]. The phenomenon of insects and birds gathering into layers during flight suggests that the fine layer echo is caused by biological flight. Therefore, CABS is generally considered to occur at the top of the CBL, which limits further research and development.

Unexpectedly, through dual-frequency observations, CABS was also observed above the CBL in the morning. A dual-frequency antenna multiplexing radar system (DFAMRS), which verified the systematic bias through a metal sphere hoisted by an unmanned aerial vehicle (UAV) [13] detected CABS that was significantly higher than CBL in the morning. Meanwhile, some large organisms were observed to float in these CABS layers. Comparison between CABS and the products of a coherent Doppler lidar (CDL) indicates that wind may be the main cause of CABS. The purpose of this paper is to introduce the relevant phenomena and deepen the understanding of CABS by proposing an expanded set of causes underlying clear-air echoes.

A brief description of DFAMRS used in this article to detect the layers of CABS is given in Section 2, together with a short introduction to coherent Doppler Lidar (CDL), which is used to obtain the CBL. The description of the observations of CABS (Section 3) is followed by a brief discussion about the relationship between CABS and wind (Section 4). Finally, Section 5 gives a summary and a plan for this work.

2. Materials and Methods

2.1. Materials

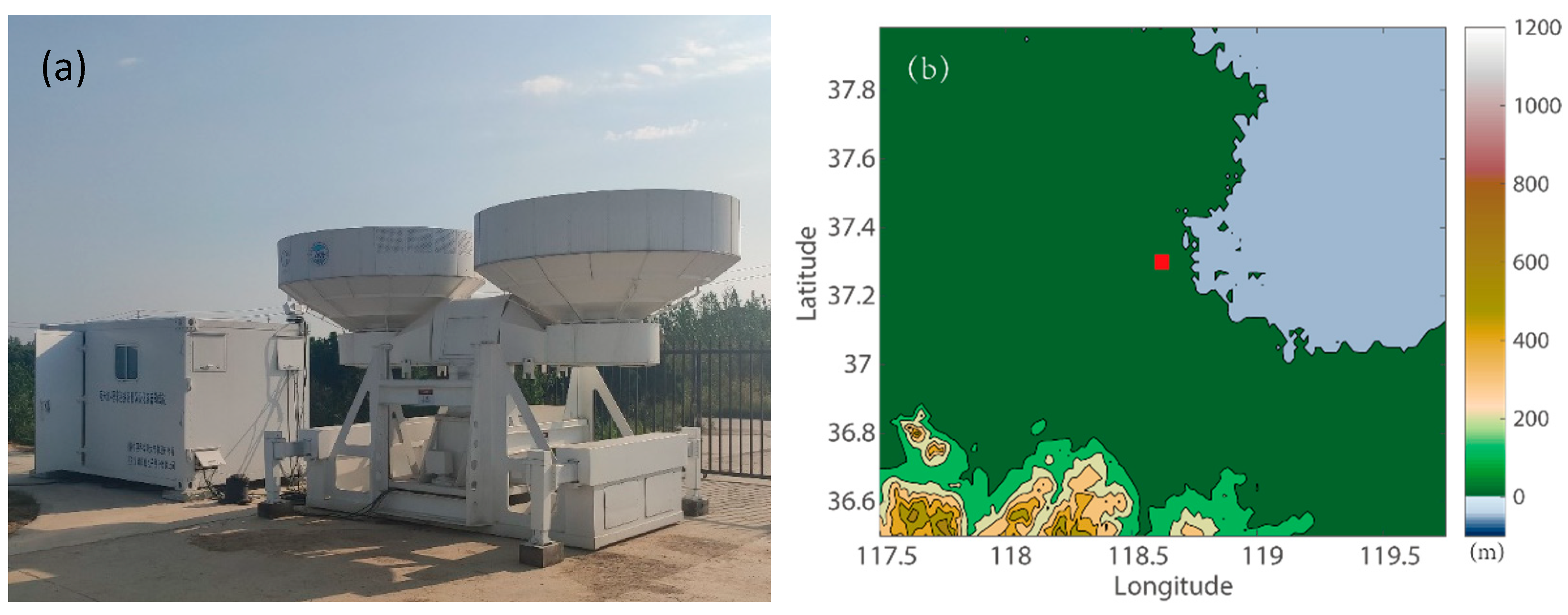
The dual-frequency antenna multiplexing radar system (DFAMRS), which was located in Dongying, Shandong as shown in Figure 1, was designed and manufactured by Sun Create Electronics Co. and the Institute of Atmospheric Physics, Chinese Academy of Sciences. The system consists of a data-processing center and X-band and Ka-band Doppler radar with antenna multiplexing. The X-band and Ka-band are equipped with all-solid-state transmitters based on frequency-modulated continuous wave (FMCW) technology. The multiplex Cassegrain antenna can ensure the temporal and spatial consistency of radio waves of two frequencies. The detailed system characteristics of the DFAMRS are shown in

Table 1. Specification of the dual-frequency antenna multiplexing radar system.

Specification	Ka-Band	X-Band
Wavelength	0.86 cm	3.2 cm
Minimum detectable Reflectivity	≤−30 dBz@5 km	≤−20 d Bz@5 km
Beam width	≤0.33°	≤1.0°
Sidelobe level	≤−23 dB	≤−28 dB
Pulse repetition interval	833~1667 μs	833~1667 μs
Range resolution	30 m	30 m

.

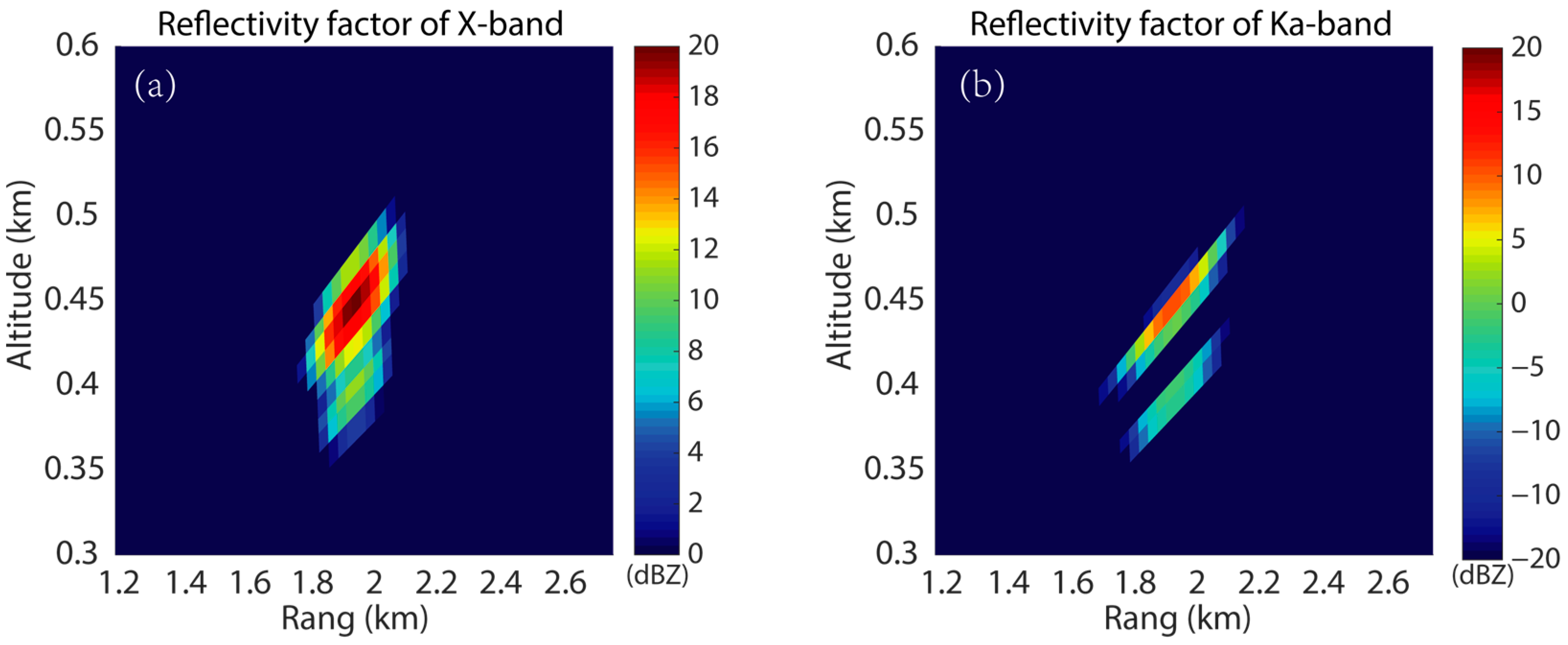
The accuracy of the reflectivity factor plays a crucial role in identifying CABS. For accurate remote-sensing data, a UAV is used to suspend a sphere for calibrating the dual-frequency antenna multiplexing radar system, as shown in Figure 2.

The position where the maximum reflectivity factor of the Ka-band appears is taken as the position of the metal sphere because the beam width of the Ka-band is smaller than that of the S-band. The average value of seven experiments is taken as the standard value in the calibration experiment.

Figure 2. Range–height cross-section of the reflectivity factor (unit: dBZ) at the X-band (a) and Ka-band (b) during calibration. The upper point echo is the UAV, and the lower point is the metal sphere.

Figure 2. Range–height cross-section of the reflectivity factor (unit: dBZ) at the X-band (a) and Ka-band (b) during calibration. The upper point echo is the UAV, and the lower point is the metal sphere.

During observations of CABS, the Wind3D-6000 coherent Doppler Lidar (CDL) is used. This tool is employed in wind-measuring applications because of its high measurement accuracy and spatial resolution. The detailed specifications of the Wind3D-6000 are shown in

Table 2. Specifications of Wind3D-6000.

Qualifications	Specifications
Wavelength (um)	1.55
Pulse repetition (kHz)	10
Sampling rate (GHz)	1
Data update rate (Hz)	4
Pulse width (ns)	100–400
Pulse energy (μJ)	150
Range resolution (m)	15–50

. The distance between the CDL and the DFAMRS was set as 1.5 km.

Lidar can be used to calculate the CBL depth. On the one hand, Lidar can identify the CBL depth as the gradient maximum of the backscattering profile [14,15] because the aerosol in the mixing layer is higher than that in the upper layer, which leads to a sharp gradient in the profiles of backscattering near the top of the CBL. On the other hand, vertical velocity variance can provide reliable CBL depths [16,17].

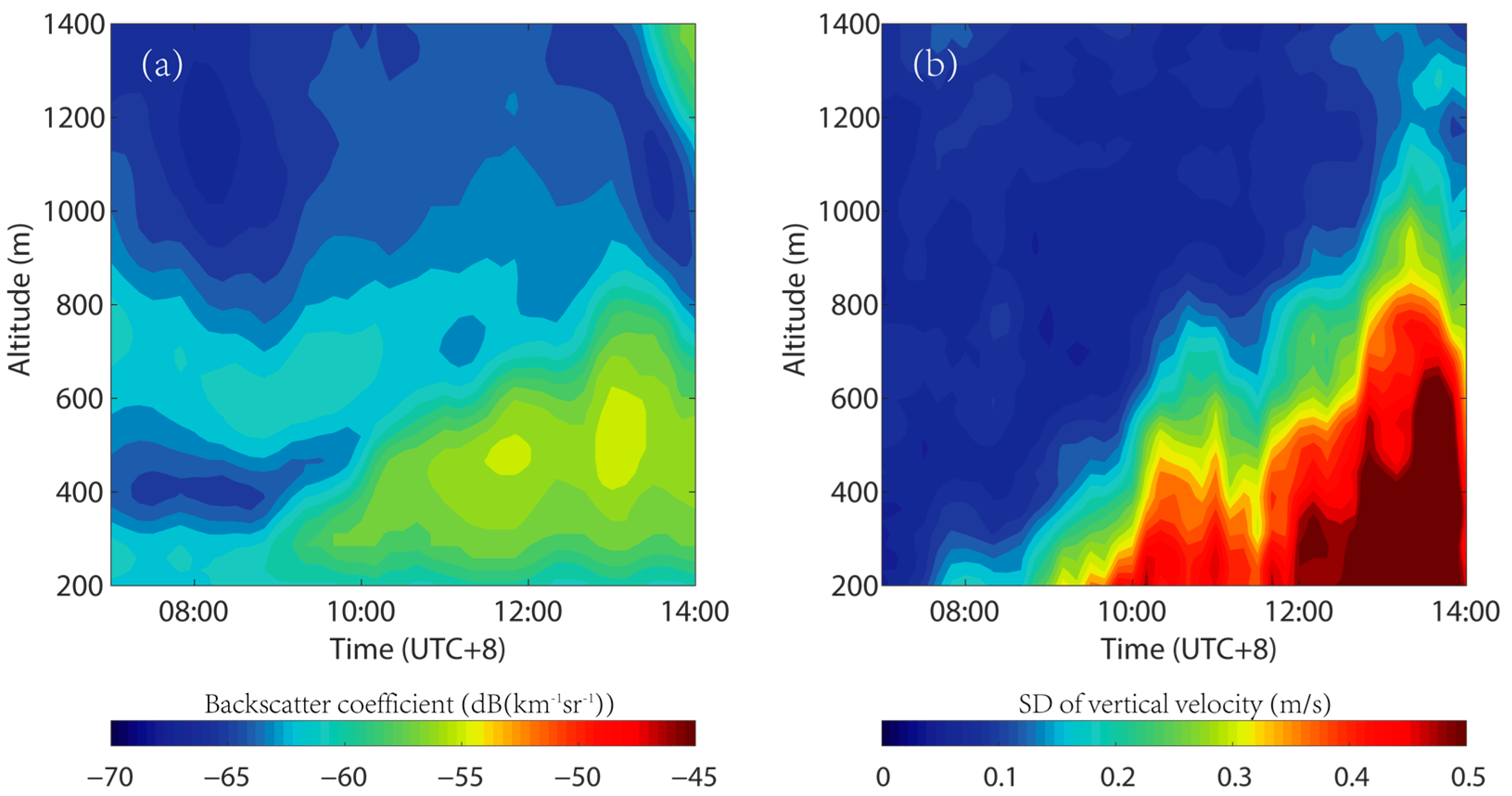
As shown in Figure 3, the distribution of the aerosol concentration and vertical velocity standard deviation is consistent. Both the backscatter and the standard deviation of vertical velocity (SDVV) indicate the depth of CBL. Since this study is focused on the morning, the SDVV was determined to be a better indicator for the CBL to avoid the influence of aerosol transport.

2.2. Bragg Scattering

Based on the Kolmogorov–Obukhov theory, Ottersten provided CABS reflectivity’s relationship with the atmospheric structure constant of the refractive index $C_n^2$ and radar wavelength $\lambda$ [8]. The radar reflectivity $\eta$ (or radar cross-section per unit volume) is given in Equation (1):

$$\eta =0.38C_n^2{\lambda }^{-1/3}.$$

(1)

According to Equation (1), the reflectivity factor $Z$ of CABS is given in Equation (2):

$$Z=\frac{0.38C_n^2{\lambda }^{11/3}}{{\pi }^5{K}^2}$$

(2)

where $K^2$ is a dielectric constant and is often taken to be 0.9 for water and 0.2 for ice, respectively. Thus, the dual-wavelength ratio (DWR) is

$$\frac{Z_1}{Z_2}={\left(\frac{{\lambda }_1}{{\lambda }_2}\right)}^{11/3}.$$

(3)

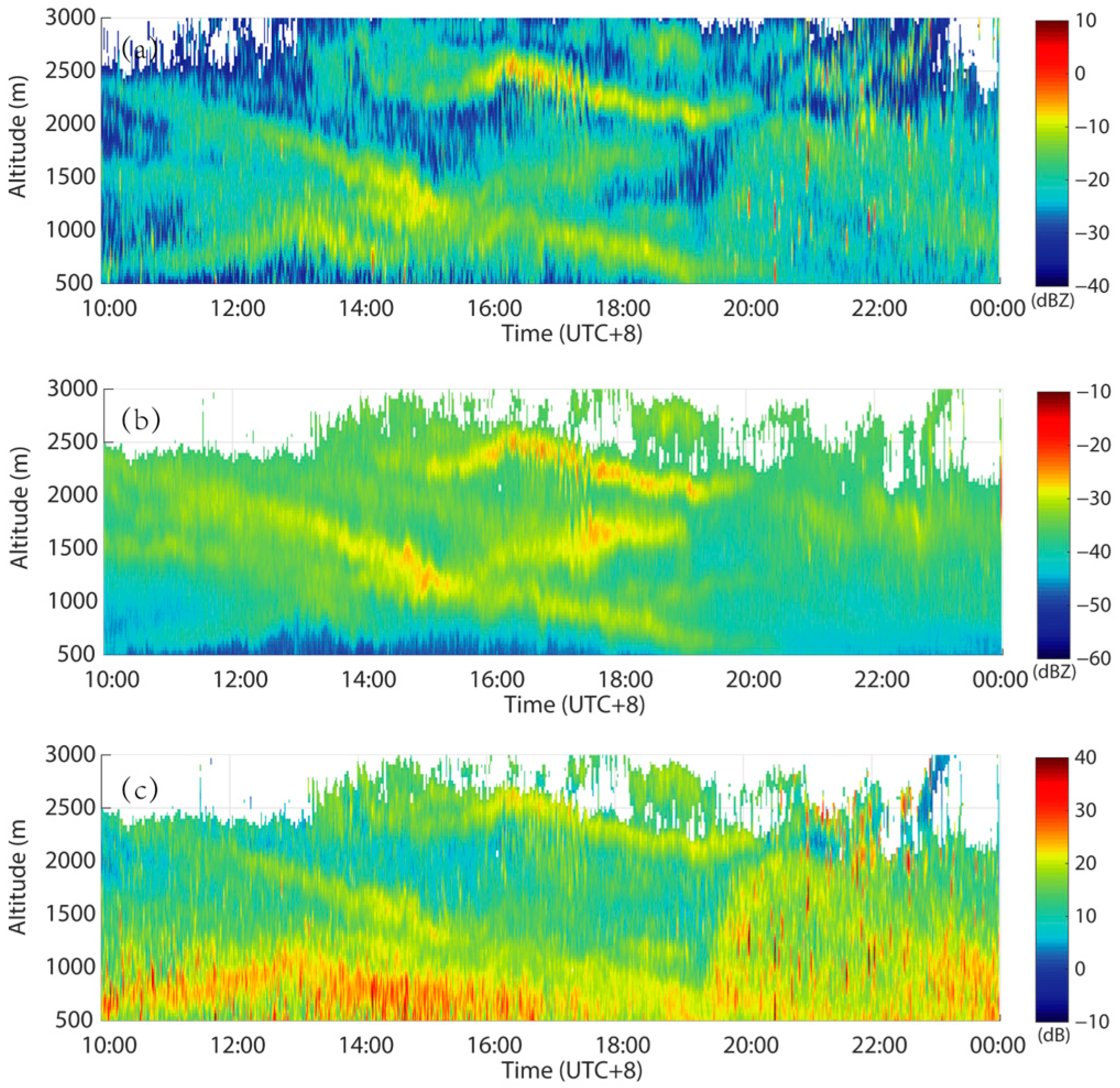
It is known that biological scattering and turbulent scattering have different DWR characteristics. The DWR of Bragg scattering is dependent on radar wavelength, as shown in Equation (3). However, the DWR changes in biological scattering are unpredictable due to the complex shapes of biological elements [6,18]. Hence, the CABS can be determined by the DWR. Based on the wavelengths of DFAMRS between the X-band and Ka-band, the theoretical DWR of Bragg scattering is 20.9 dB, which is presented using the yellow pattern in Figure 4c.

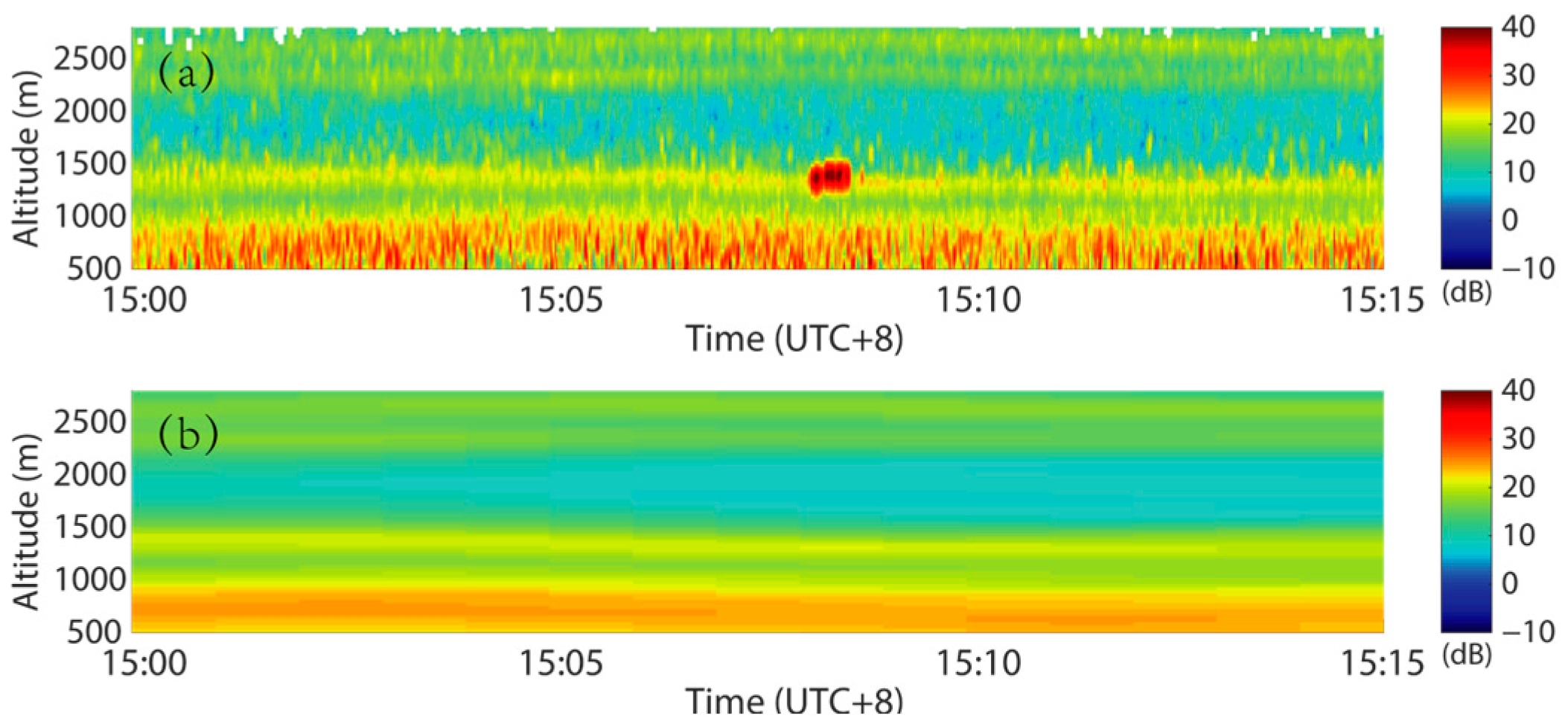
The particle scattering of atmospheric biota will affect the value of DWR, causing errors in the recognition of CABS. Therefore, preprocessing is necessary to filter point noise from organisms. DFAMRS outputs a profile of the reflectivity factor every 10 s. When biological activities are relatively modest, the radar beam cannot be filled by creatures continuously. Thus, the mode of the reflectivity factor values within 5 min is regarded as the signal without point noise because of the slow change in the meteorological signal, as shown in Figure 5. Notably, intense biological activity will make the preprocessing invalid. Fortunately, there are few creatures above the CBL.

3. Results

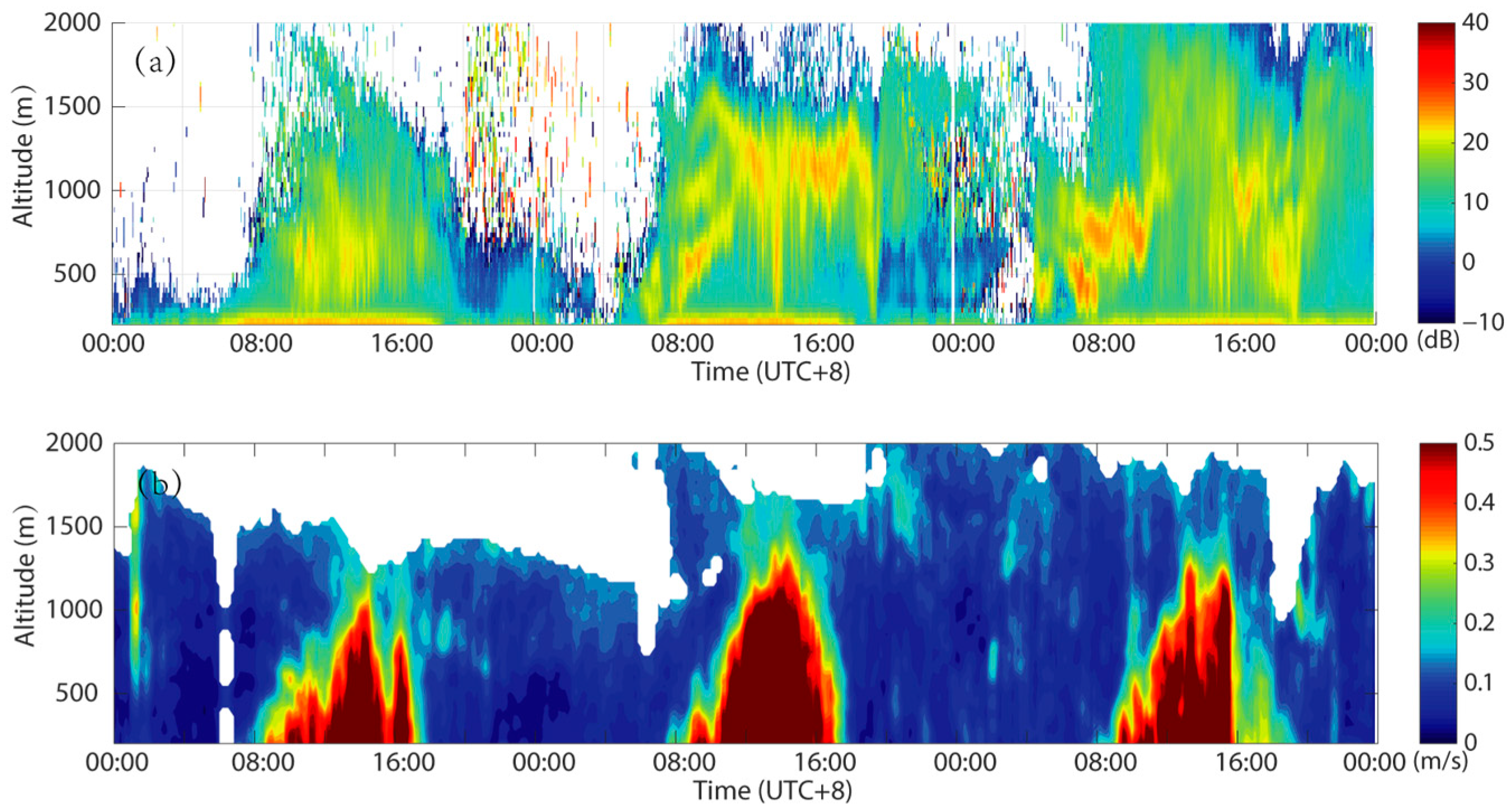
Co-varying with the CBL, the standard deviation of vertical velocity in Figure 6 also has apparent diurnal variation. The DWR also shows the same variation of CABS. Near the top of the CBL, the layers of CABS can be clearly observed. This result is consistent with other studies [1,2,11,19]. Interestingly, as shown in Figure 6, many chaotic point echoes can be observed at night, which can also be seen in Figure 4. These point echoes are caused by atmospheric biota.

Meanwhile, in the layers of CABS, there are some chaotic points with a large DWR. According to other studies, these points with larger DWR values are common in the biological scattering caused by large flying creatures. It is known that insects, as a means of conserving energy, use turbulent updraughts and downdraughts for transport [19,20]. Thus, although turbulence makes people experience bumps on a flight, it is reasonable to infer that these large organisms fly and float with the help of turbulence to save energy and obtain living advantages.

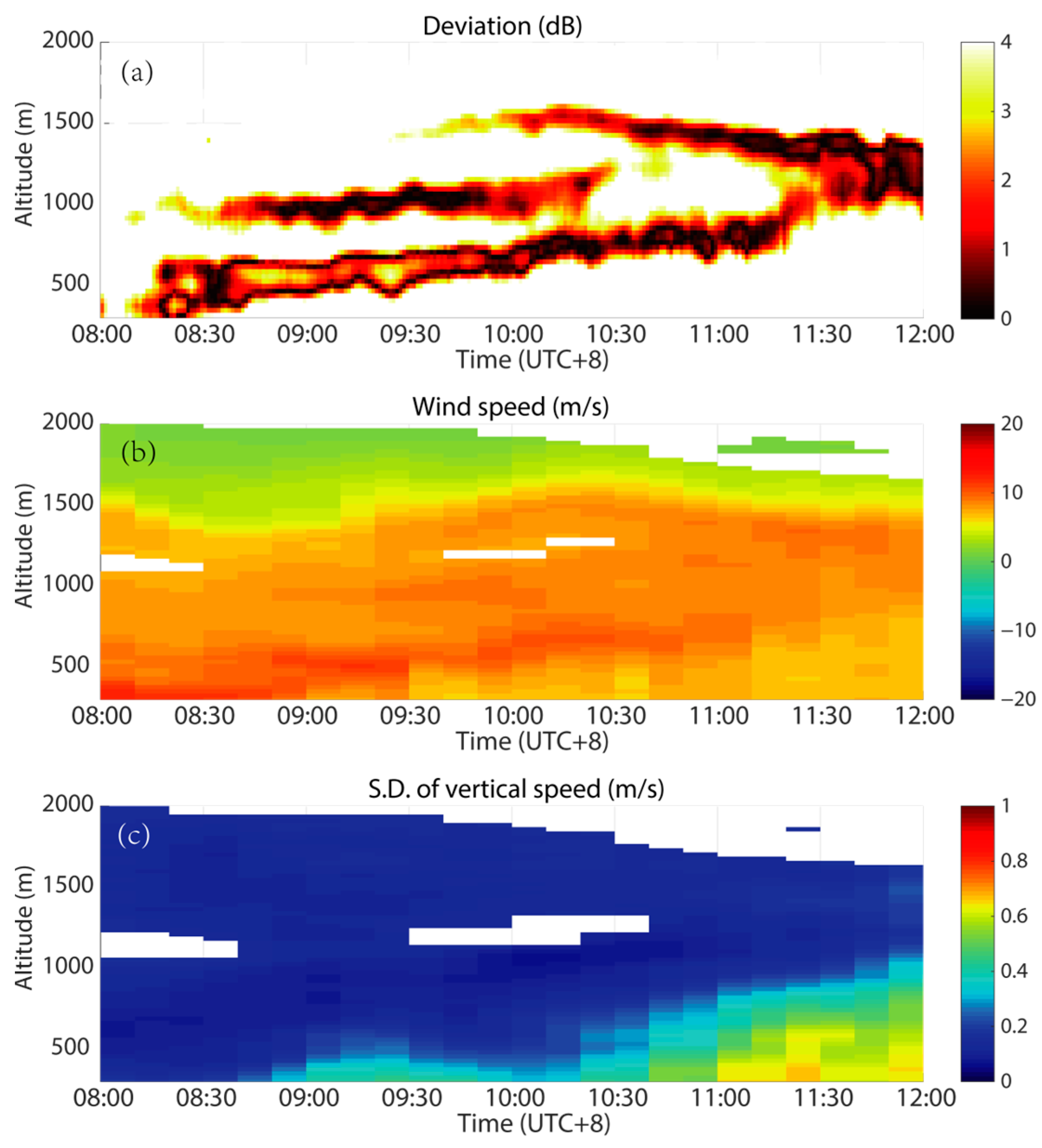
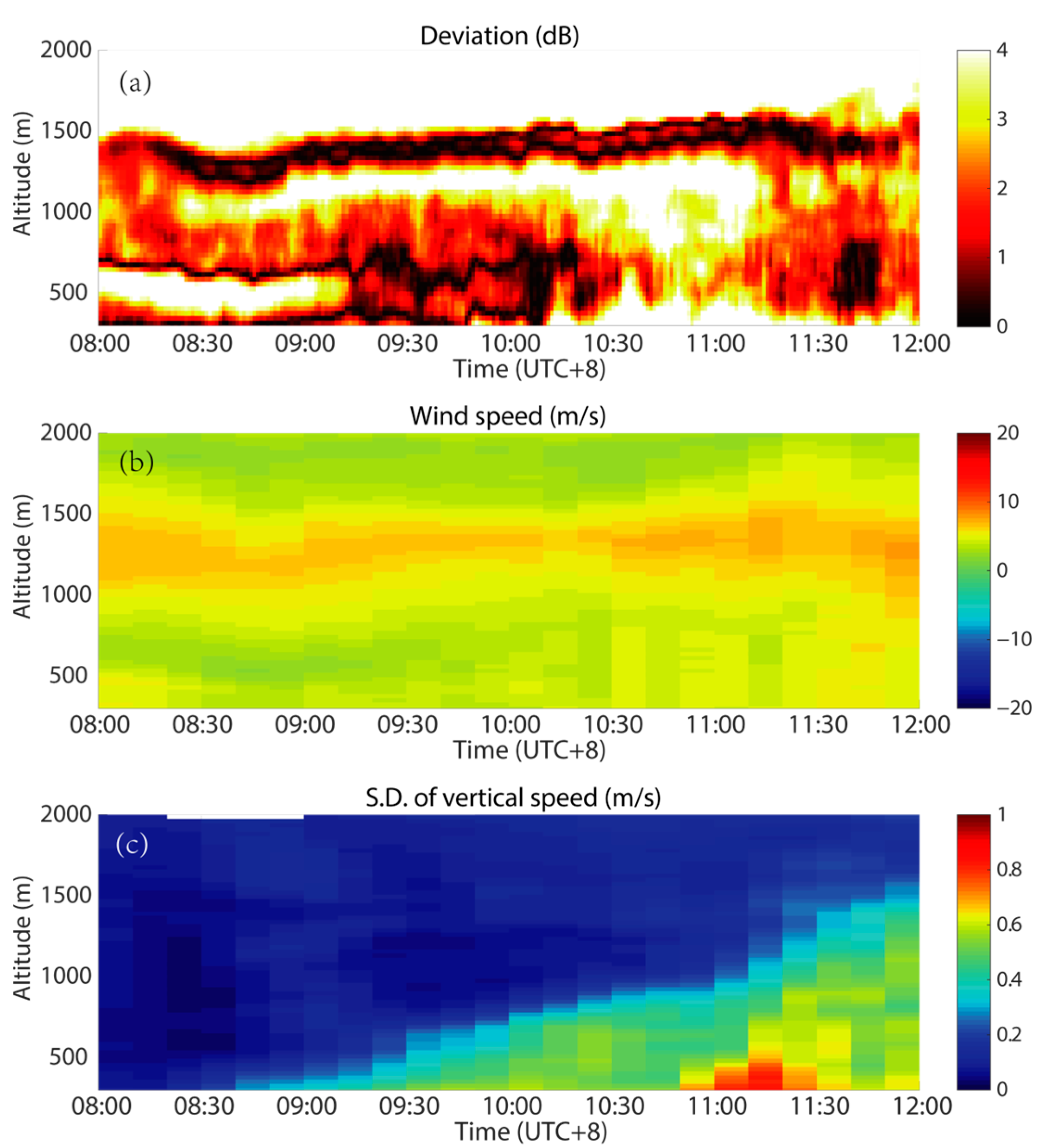
Contrary to expectations, the DFAMRS observed other layers of Bragg scattering above the CBL in the morning on 18 May and 22 May 2021, as shown in Figure 7 and Figure 8, respectively. Both layers are flat and near a height of 1.5 km, which is higher than the top of the CBL. The DFAMRS also observed three layers of CABS from 09:00 to 10:30 am on 18 May. This type of CABS typically has a thickness of 200 m and is relatively gentle, with a slower rate of change in the range of the X-band reflectivity factor from −10 to −30 dBZ. Thus, the refractive index structure constant ranges from 10⁻¹¹ to 10⁻¹³.

The heights of these layers intuitively have a large horizontal wind speed. However, similar layers of CABS are not always observed on other windy days. The results for 18 May show a thick layer with high wind speed, but the CABS layer is still thin. The wind shear also makes it difficult to explain the middle layer of CABS on 18 May.

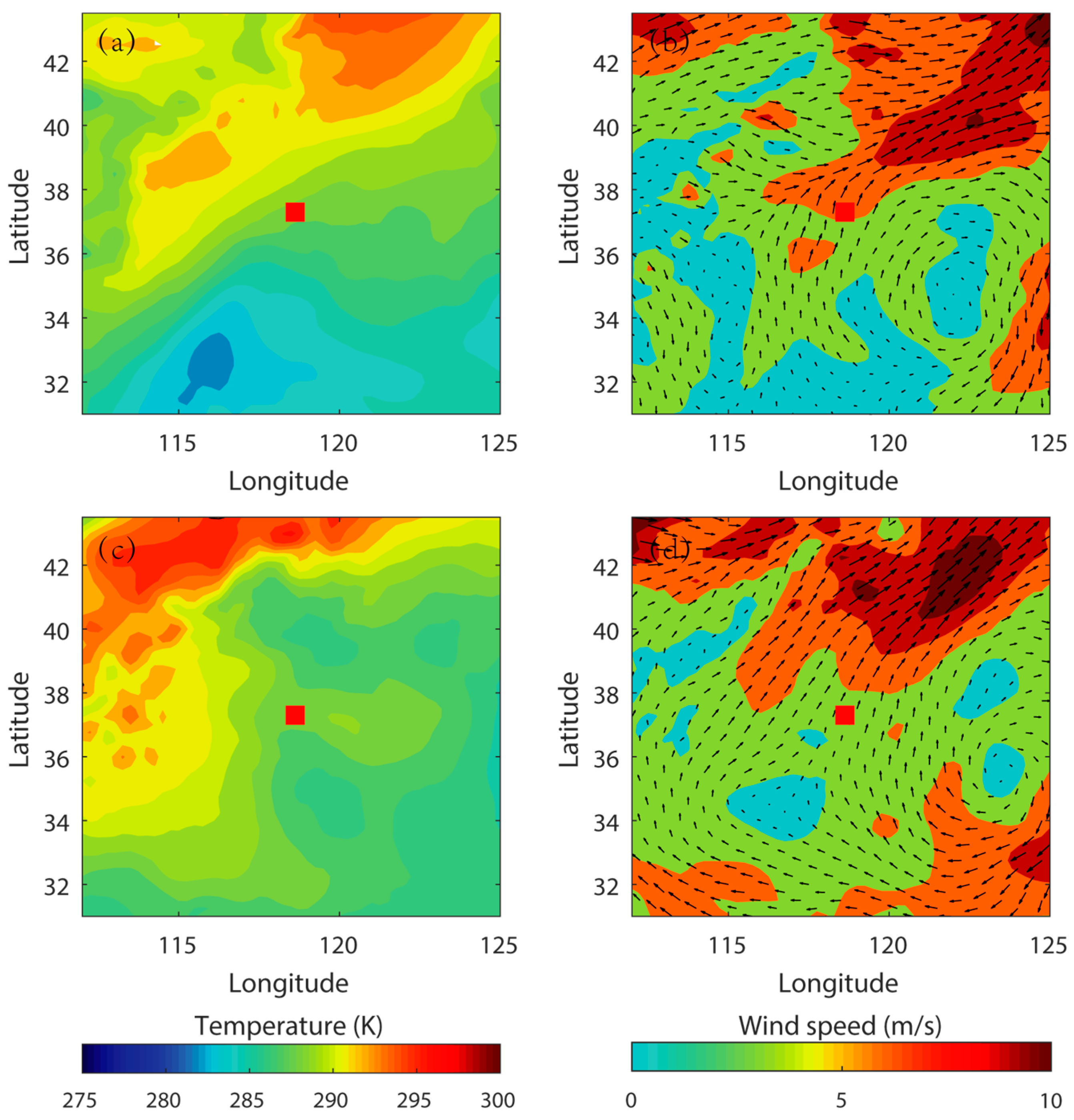
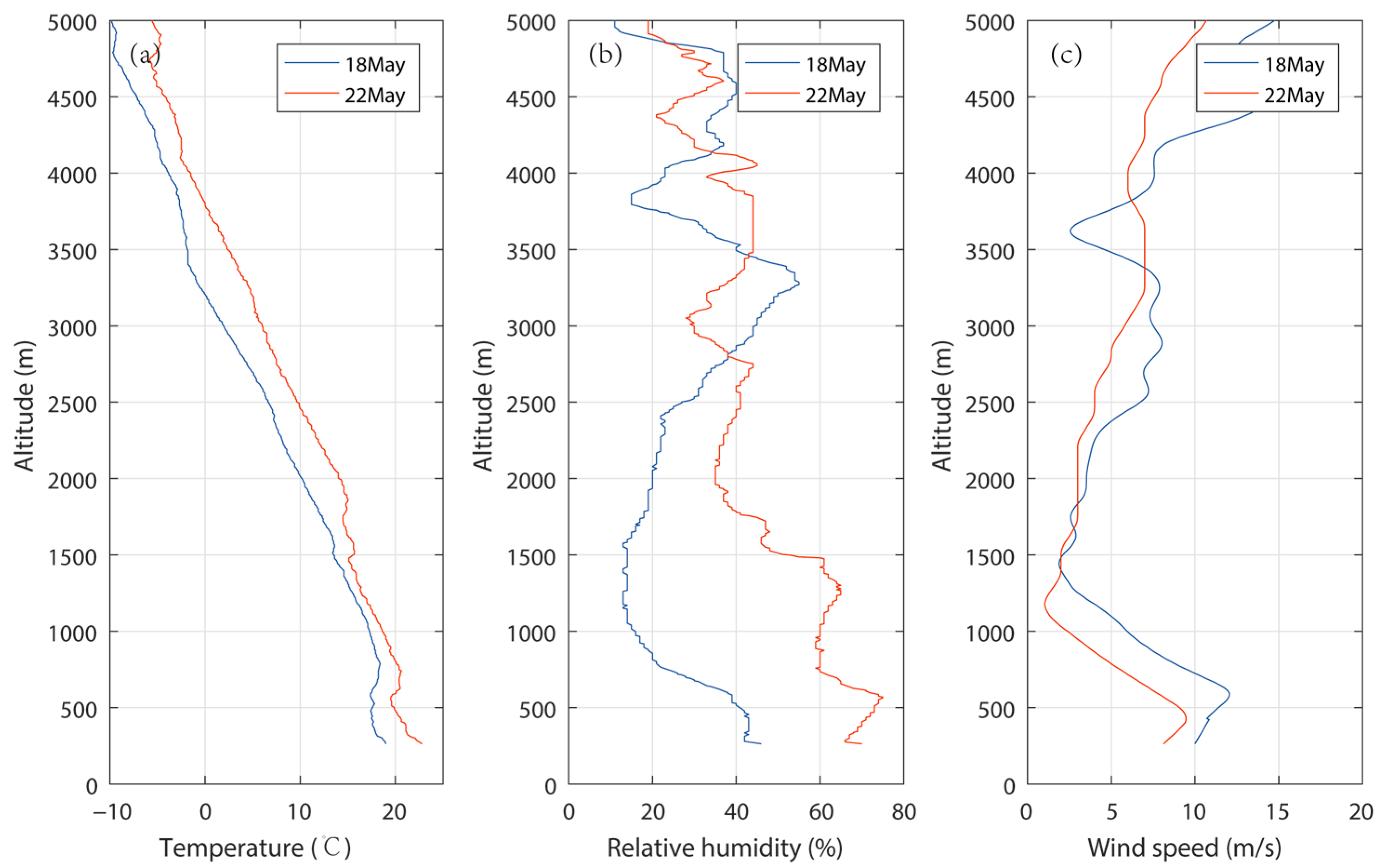
In the reanalysis field, as shown in Figure 9, there is no obvious weather process. A weak cyclone structure is present in the eastern part of the radar, but the radar is not located in the low-level jet. The sounding observations in Figure 10 also demonstrate the absence of low-level jets.

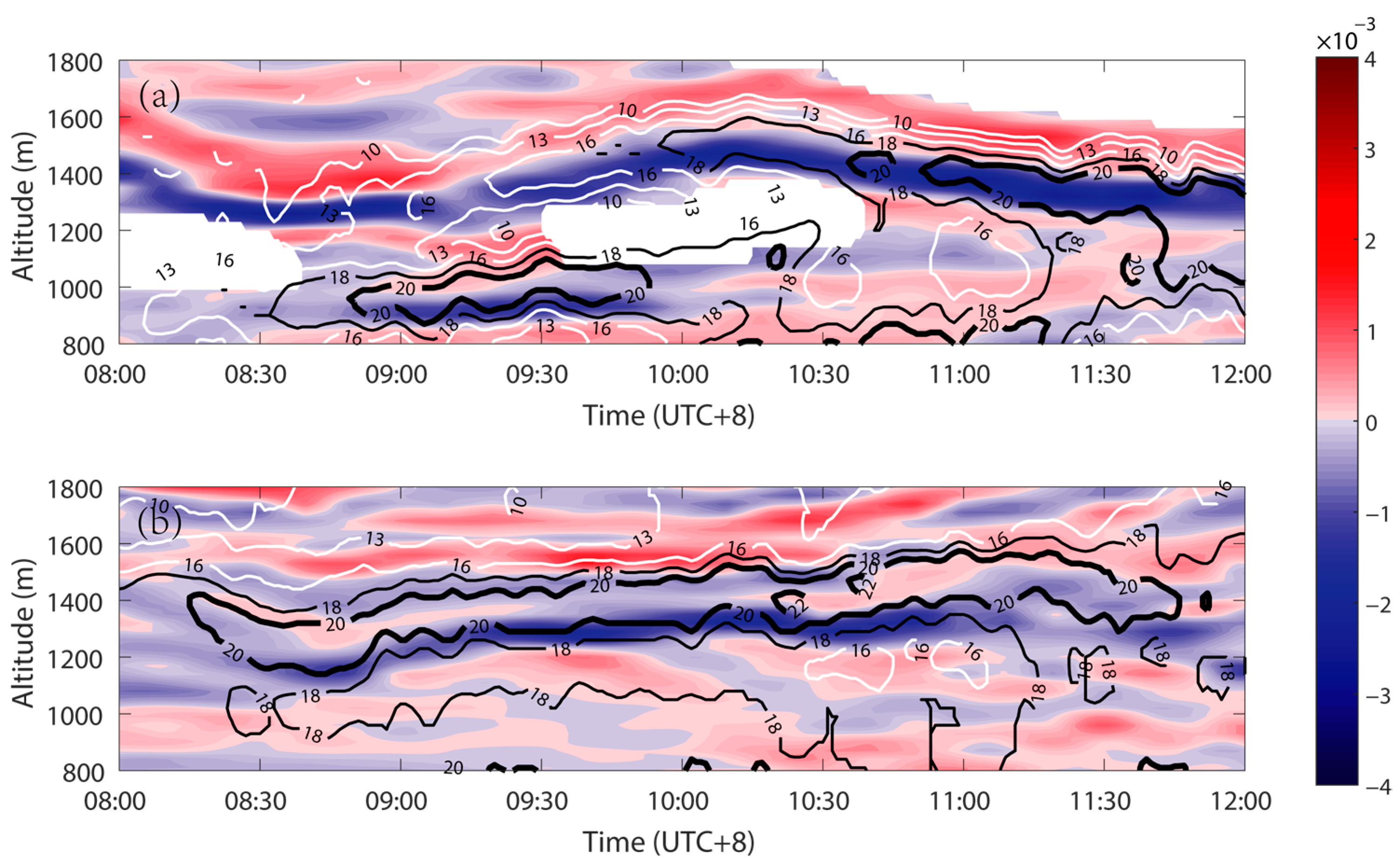
To our surprise, the vertical change rate of horizontal wind shear, which is the second derivative of horizontal wind speed, is more consistent with the height of the CABS layers. Figure 11 gives the co-varying patterns of the CABS layers and the negative second derivative, and the CABS layers are located in the position of the upper edge above the negative second derivative.

4. Discussion

Reflections from turbulent air are commonly observed on top of the CBL. Because of the penetrative convection and entrainment, thermals reciprocate in the layer [21]. This reciprocating activity generates turbulence and eventually causes Bragg scattering, but it is rarely directly observed in the echo of CABS above the CBL.

At first, we speculated that the horizontal wind shear caused the shear turbulence as a shear plane, but the corresponding relationship of CABS with the shear is less obvious than that with the negative second derivative of the wind.

Some researchers argue that mechanical energy, which depends on the wind speed gradient, does not cause turbulence, while the gradient of mechanical energy does [22], and that nonlinear instability is necessary for turbulence, not linear instability. Thus, the negative vertical change rate of horizontal wind shear may be the main factor that creates the layer of CABS. Notably, the relationship between the wind and CABS needs more experimental data to confirm.

Furthermore, an S-band weather radar near the DFAMRS did not observe these layers of CABS, possibly because the scale of turbulence was less than 5 cm and out of the range of Bragg scattering. This type of small-scale turbulence decays quickly above the CBL. Thus, it is normal for the S-band radar to be unable to observe the same CABS layer above the CBL.

5. Conclusions and Future Work

In this study, an antenna multiplexing radar system calibrated by a UAV featuring a metal sphere, with the DWR between the X-band and Ka-band, was used to determine the layers of CABS. We found that the CABS layer not only exists at the top of the CBL but can also be detected above the CBL. Such CABS echoes typically have a thickness of 200 m and exhibit a relatively gentle rate of change. The reflectivity factor of X-band echoes ranges from −10 to −30 dBZ, indicating a refractive index structure constant ranging from 10⁻¹¹ to 10⁻¹³.

This study demonstrated that echoes from the fine layer are not solely attributable to biological activities but can also be caused by meteorological factors above the convective boundary layer. As such, these results underscore the need to expand the range of potential causes of clear-air echoes. These thin layers of CABS above CBL have a relationship with the horizontal wind field. Based on existing data, CABS more closely coexists with a negative second derivative of horizontal wind speed.

However, the existing independent cases cannot support a more detailed analysis. The limited actual measurement range of the CDL causes some CABS cases to be abandoned. Equipment for wind measuring with higher power will be developed in an experiment to be undertaken in 2023. Future studies will also need some other meteorological parameters, such as profiles of the air temperature, relative humidity, and absolute humidity, which could be collected using a microwave radiometer. At the same time, the upgraded DFAMRS has a new dual-polarization detection mode, which could help detect the polarization characteristics of CABS layers above the CBL.