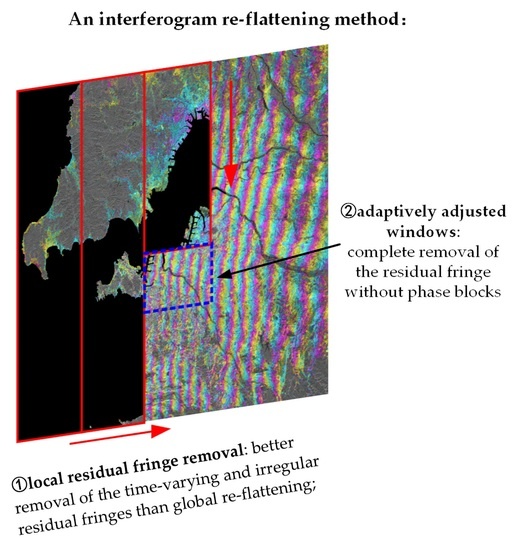
An Interferogram Re-Flattening Method for InSAR Based on Local Residual Fringe Removal and Adaptively Adjusted Windows
Abstract
1. Introduction
2. Related Work
2.1. Global Refinement and Re-Flattening Methods
2.1.1. Polynomial Refinement Method
2.1.2. Refinement and Re-Flattening Based on Baseline Correction
2.2. Flattening or Re-Flattening Methods Based on Manually Set Windows
3. Methods
3.1. Characteristics of Residual Fringes Caused by Baseline Errors
- The residual fringes conform to the first- or second-degree polynomial phase model locally;
- Residual fringes are time varying in azimuth;
- The time varying of residual fringes is irregular in the whole image.
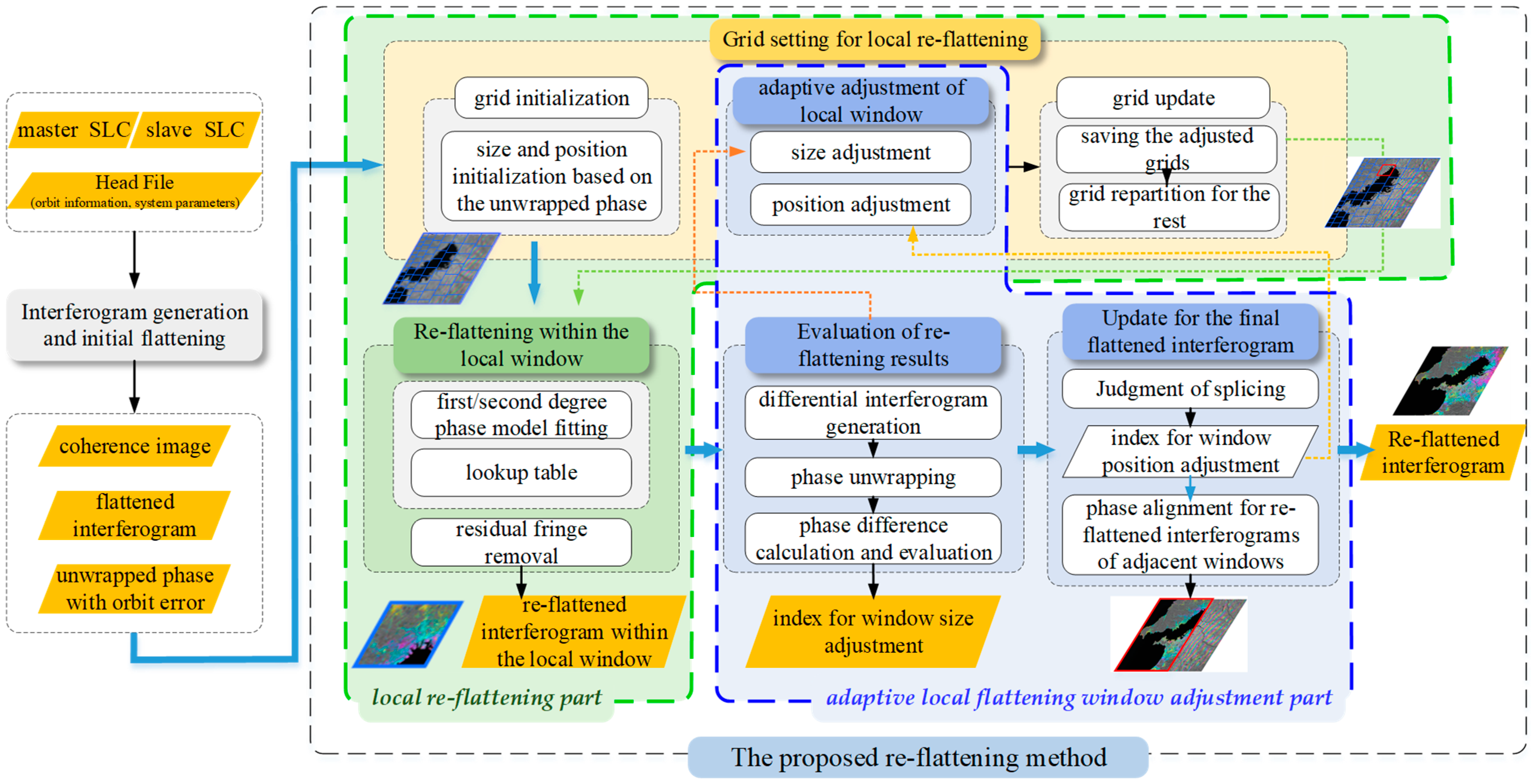
3.2. The Proposed Method: A Re-Flattening Method Based on Local Residual Fringe Removal and Adaptively Adjusted Windows
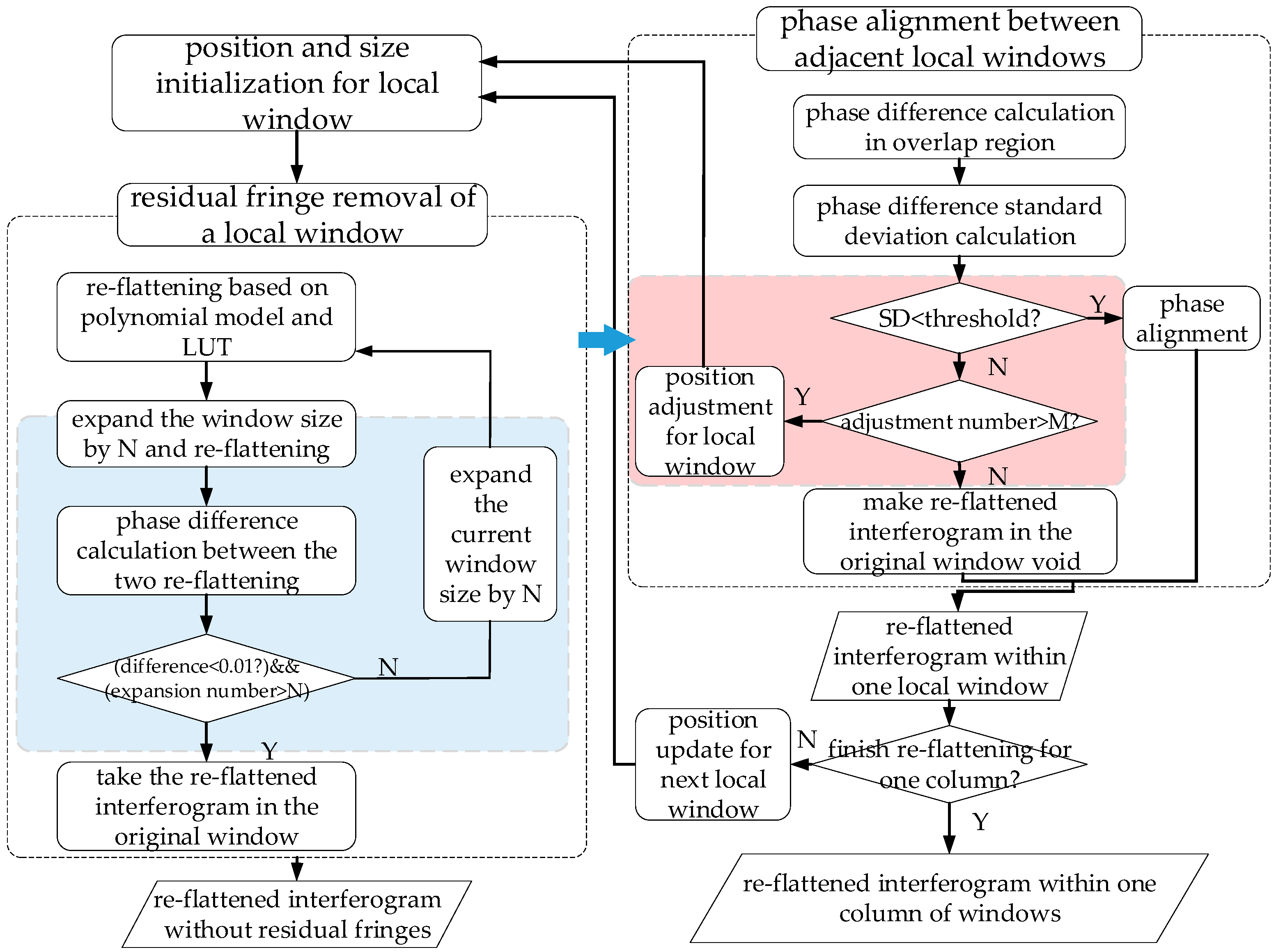
3.2.1. Principle of the Re-Flattening within A Local Window
3.2.2. Mechanism of Adaptive Adjustment for Re-Flattening Windows
4. Experiments
4.1. Experimental Data and Study Area
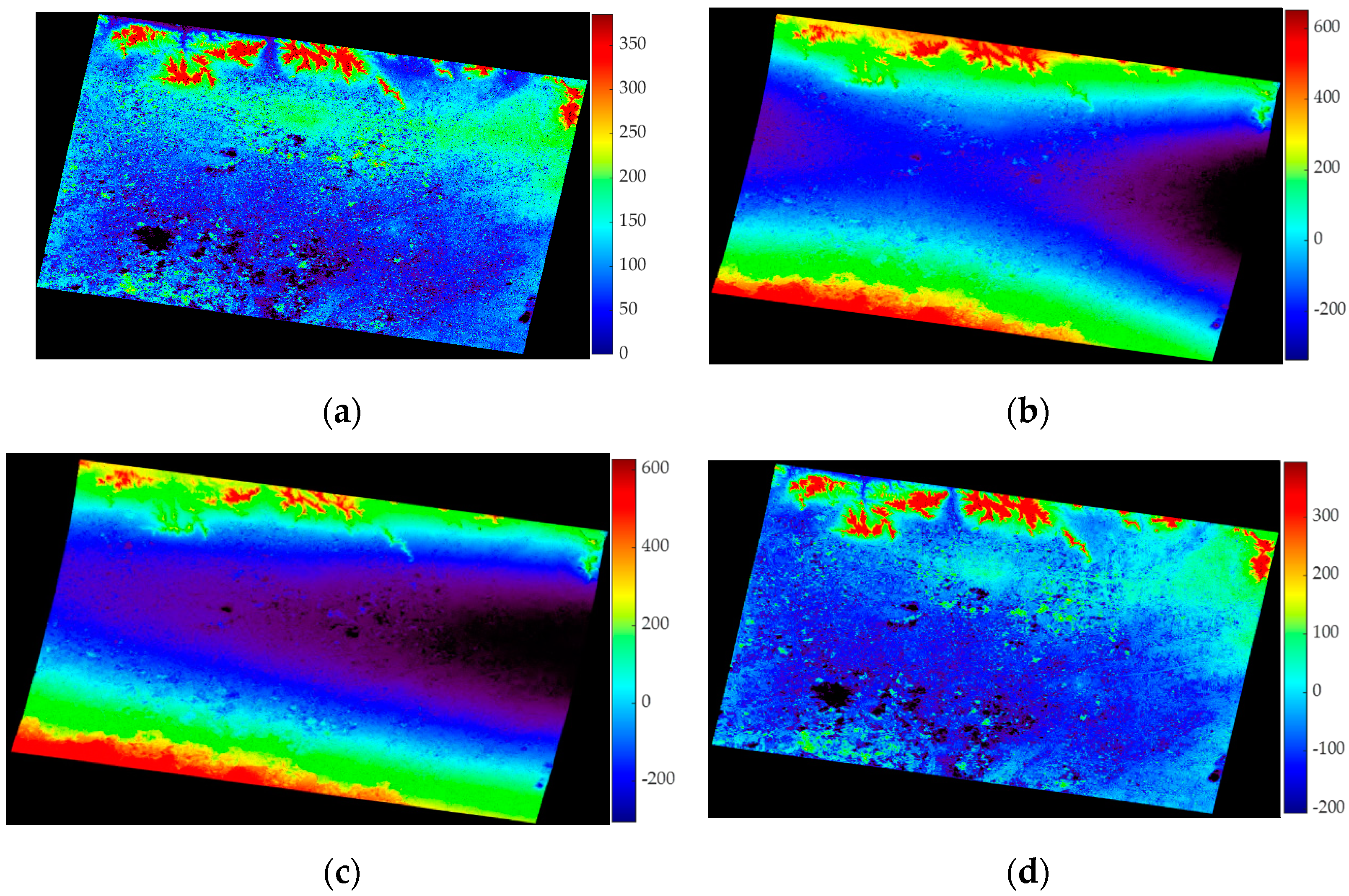
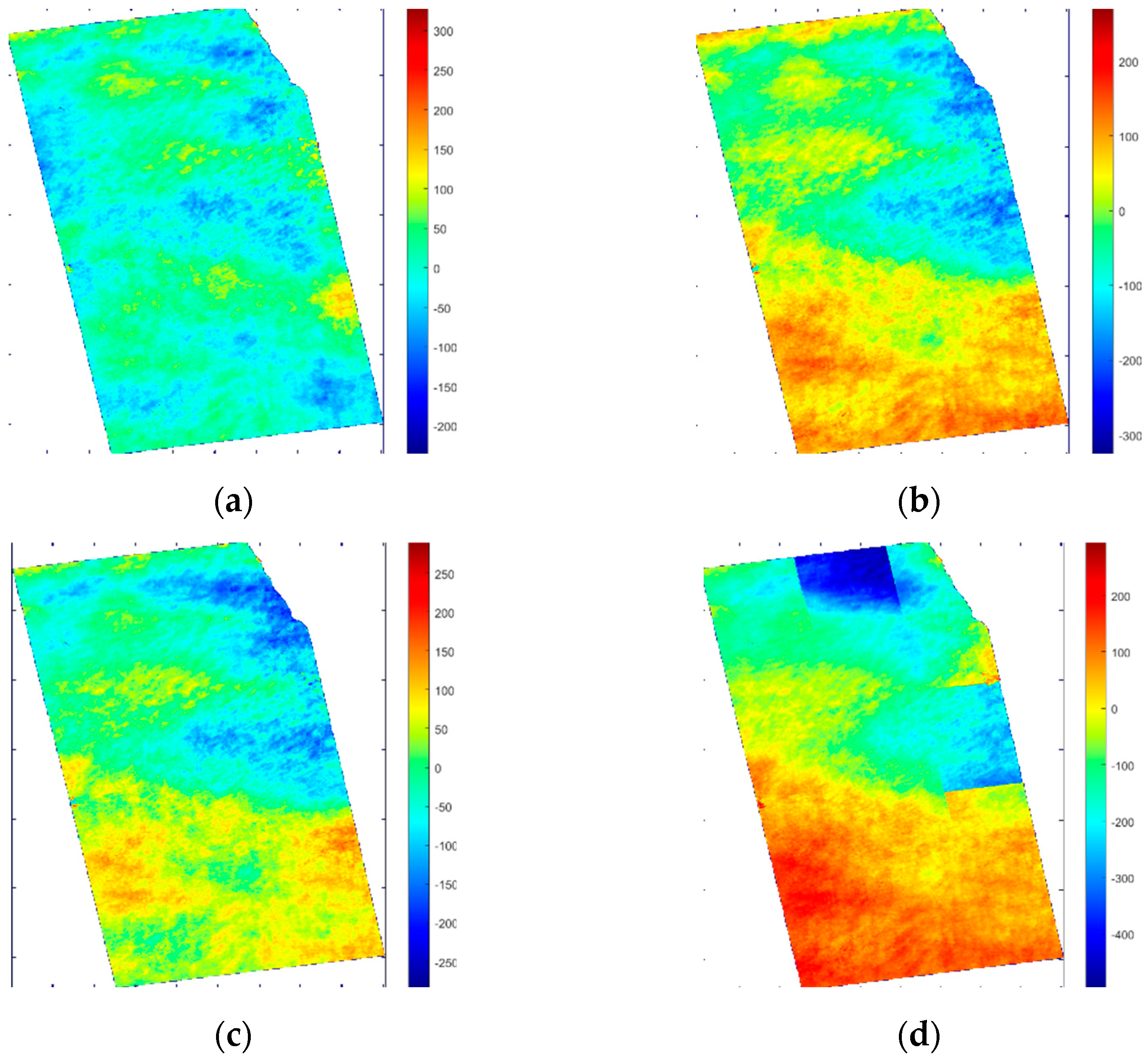
4.2. Re-Flattening Results and Qualitative Evaluations
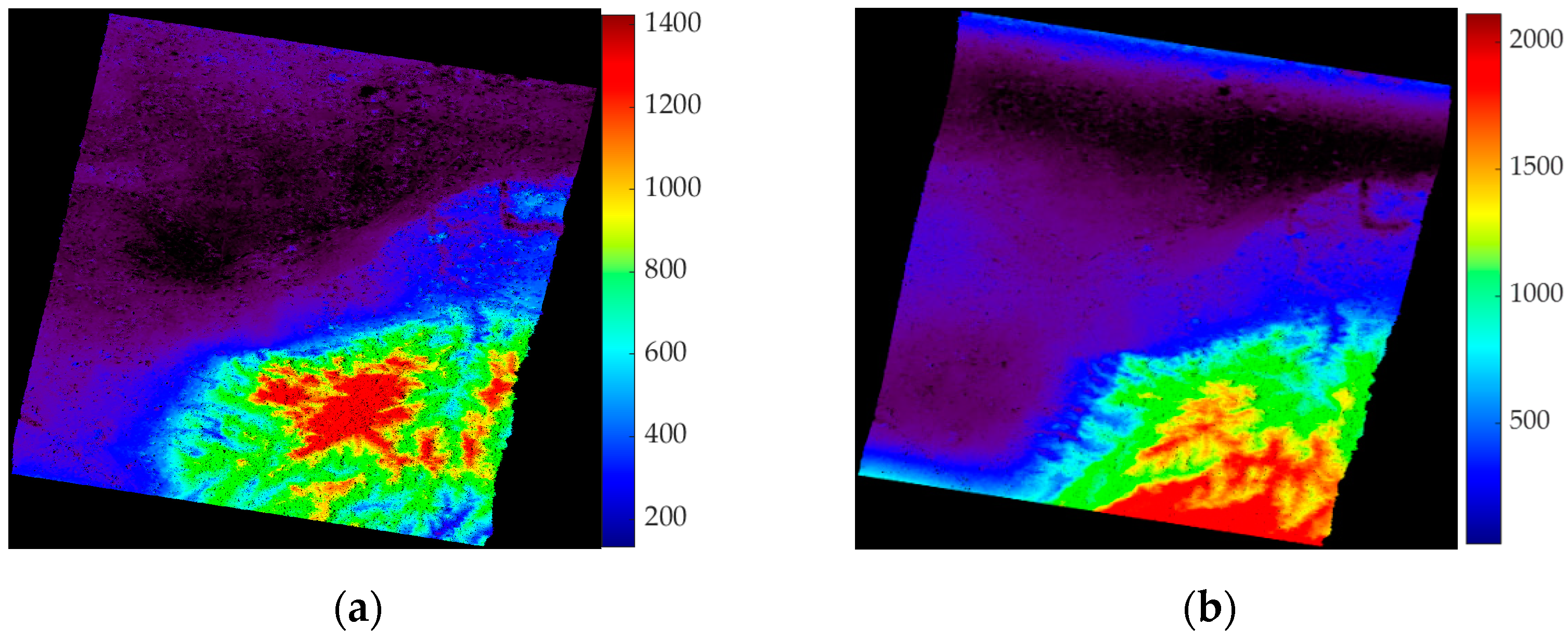
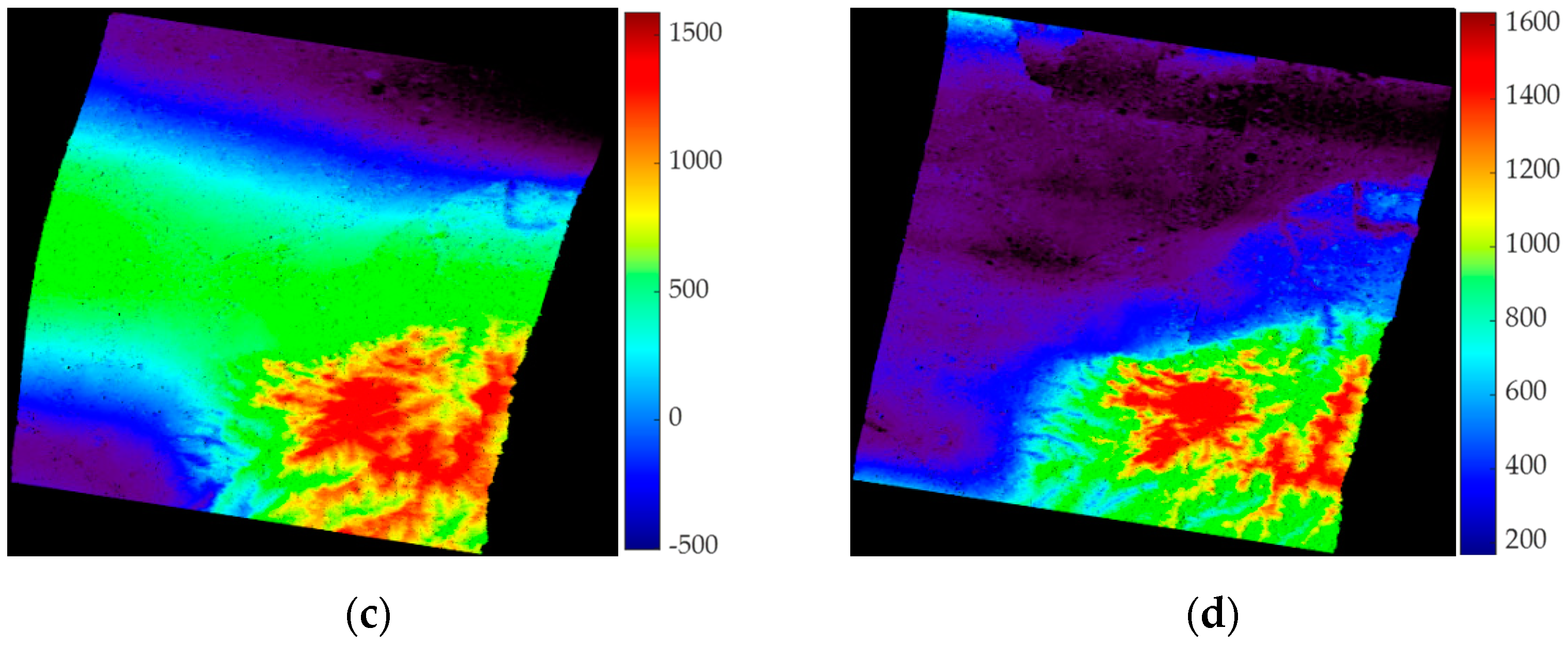
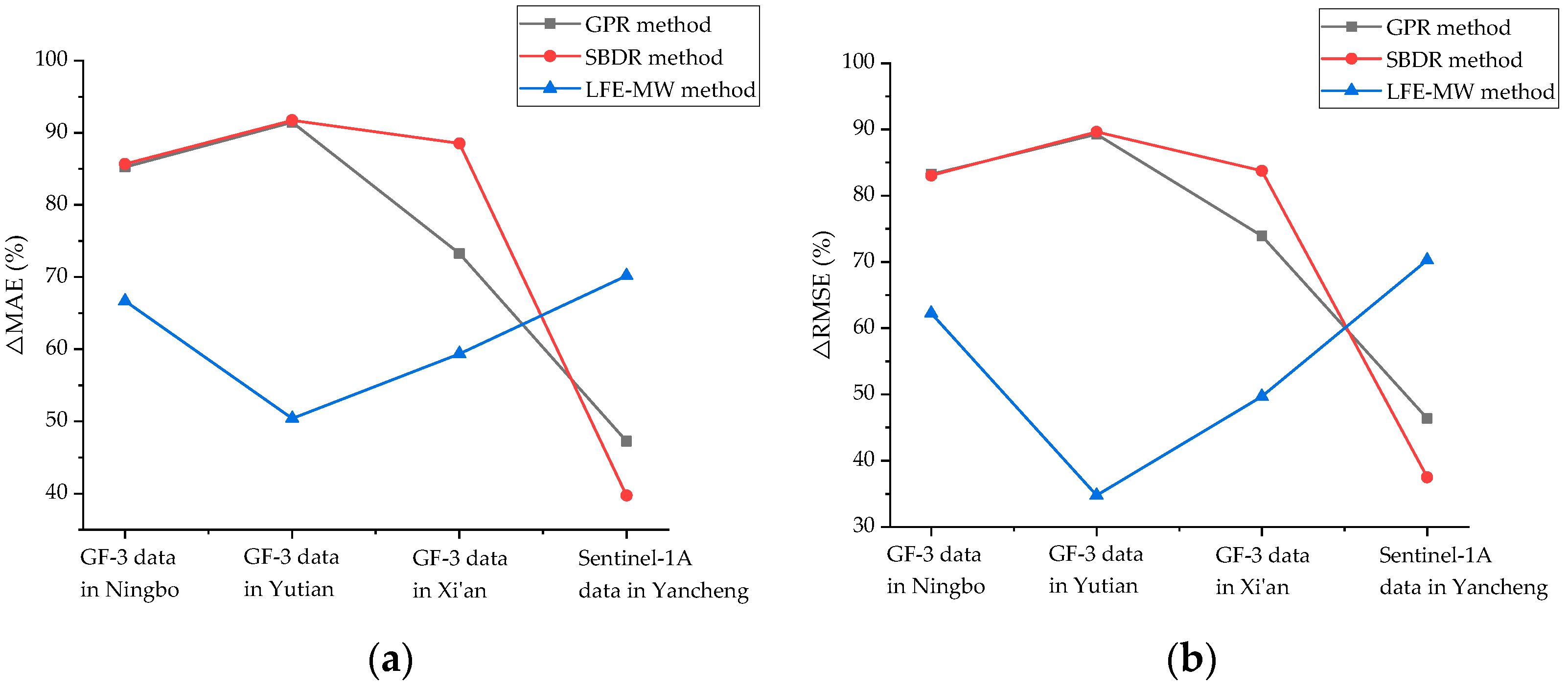
4.3. DEM Generation and Quantitative Evaluation
5. Discussion
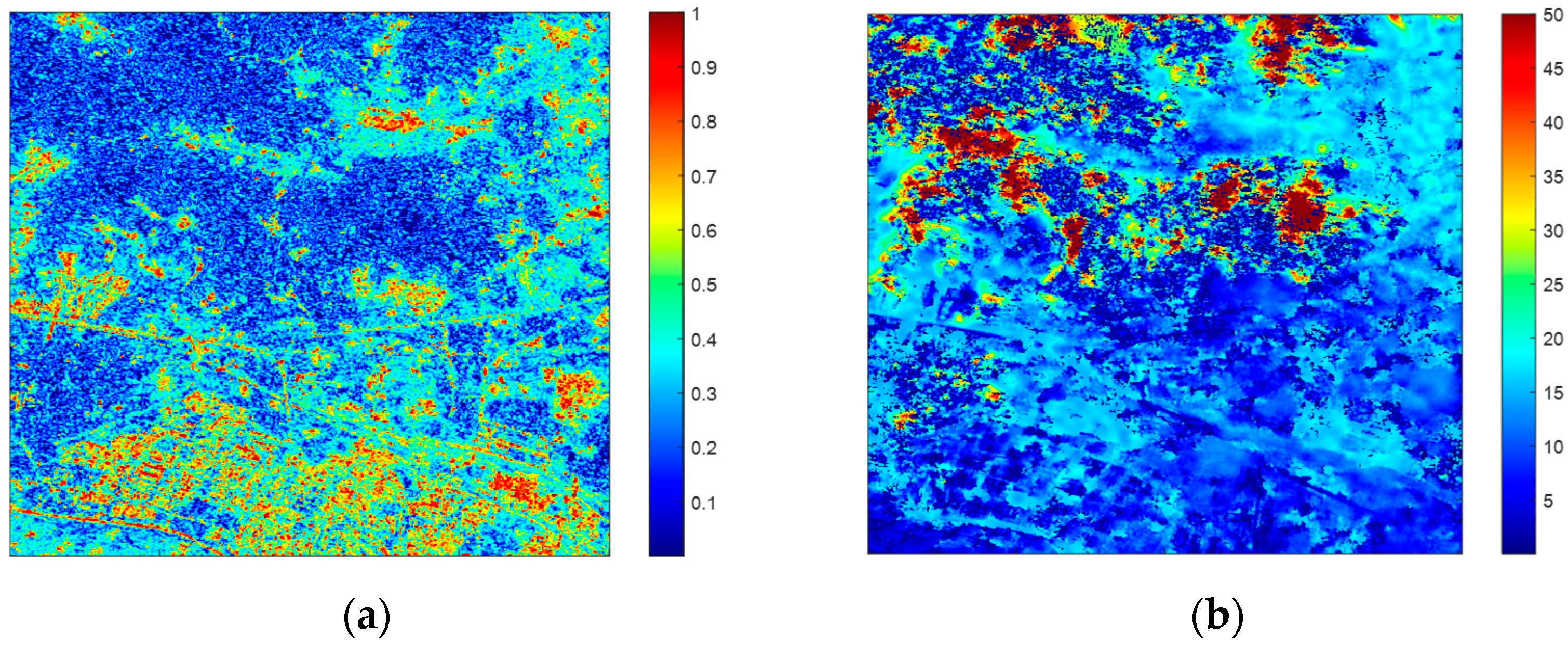
5.1. The Influence of Coherence on the Performance of the Proposed Re-Flattening Method
5.2. Comparison with the Result Based on TerraSAR-X Data with Similar Conditions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Short, N.; Brisco, B.; Couture, N.; Pollard, W.; Murnaghan, K.; Budkewitsch, P. A comparison of TerraSAR-X, RADARSAT-2 and ALOS-PALSAR interferometry for monitoring permafrost environments, case study from Herschel Island, Canada. Remote Sens. Environ. 2011, 115, 3491–3506. [Google Scholar] [CrossRef]
- Prush, V.B.; Lohman, R.B. Time-Varying Elevation Change at the Centralia Coal Mine in Centralia, Washington (USA), Constrained with InSAR, ASTER, and Optical Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 919–925. [Google Scholar] [CrossRef]
- Bayer, B.; Schmidt, D.; Simoni, A. The Influence of External Digital Elevation Models on PS-InSAR and SBAS Results: Implications for the Analysis of Deformation Signals Caused by Slow Moving Landslides in the Northern Apennines (Italy). IEEE Trans. Geosci. Remote Sens. 2017, 55, 2618–2631. [Google Scholar] [CrossRef]
- Sigmundsson, F.; Hreinsdottir, S.; Hooper, A.; Arnadottir, T.; Pedersen, R.; Roberts, M.J.; Oskarsson, N.; Auriac, A.; Decriem, J.; Einarsson, P.; et al. Intrusion triggering of the 2010 Eyjafjallajokull explosive eruption. Nature 2010, 468, 426–430. [Google Scholar] [CrossRef]
- Cochrane, T.A.; Egli, M.; Phillips, C.; Acharya, G. Development of a forest road erosion calculation GIS tool for forest road planning and design. In Proceedings of the International Congress on Modelling and Simulation: Land, Water, & Environmental Management: Integrating Systems for Sustainability, Christchurch, New Zealand, 1–5 December 2007. [Google Scholar]
- Buğday, E. Capabilities of using UAVs in forest road construction activities. Eur. J. For. Eng. 2018, 4, 56–62. [Google Scholar] [CrossRef]
- Tran, D.; Xu, D.; Dang, V.; Alwah, A.A.Q. Predicting Urban Waterlogging Risks by Regression Models and Internet Open-Data Sources. Water 2020, 12, 879. [Google Scholar] [CrossRef]
- Bhatt, C.M.; Srinivasa Rao, G. HAND (height above nearest drainage) tool and satellite-based geospatial analysis of Hyderabad (India) urban floods, September 2016. Arab. J. Geosci. 2018, 11, 600. [Google Scholar] [CrossRef]
- Li, D.; Zhu, X.; Huang, G.; Feng, H.; Zhu, S.; Li, X. A hybrid method for evaluating the resilience of urban road traffic network under flood disaster: An example of Nanjing, China. Environ. Sci. Pollut. Res. 2022, 29, 46306–46324. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi Samani, K.; Hosseini, S.A.; Lotfian, M.; Najafi, A. Planning road network in mountain forests using GIS and Analytic Hierarchical Process (AHP). Casp. J. Environ. Sci. 2010, 8, 151–162. [Google Scholar]
- Rouet-Leduc, B.; Jolivet, R.; Dalaison, M.; Johnson, P.A.; Hulbert, C. An identification method of potential landslide zones using InSAR data and landslide susceptibility. Geomat. Nat. Hazards Risk 2023, 14, 2185120. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Jolivet, R.; Dalaison, M.; Johnson, P.A.; Hulbert, C. Autonomous extraction of millimeter-scale deformation in InSAR time series using deep learning. Nat. Commun. 2021, 12, 6480. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Kelevitz, K.; Sadeghi, Z.; Wright, T.; Thompson, J.; Achim, A.M.; Bull, D. Detecting ground deformation in the built environment using sparse satellite InSAR data with a convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2940–2950. [Google Scholar] [CrossRef]
- Small, D.; Werner, C.; Nuesch, D. Base-Line Modeling for ERS-1 SAR Interferometry. In Proceedings of the IGARSS 93, Kogakuin Univ, Tokyo, Japan, 18–21 August 1993. [Google Scholar]
- Cao, Y.X.; Fan, Z.; Chen, Y. Flat Earth Removal and Baseline Estimation Based on Orbit Parameters Using Radarsat-2 Image. In Proceedings of the IGARSS 2013, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Geudtner, D.; Schwäbisch, M. An Algorithm for Precise Reconstruction of InSAR Imaging Geometry: Application to “Flat-Earth” Phase Removal, Phase-to-Height Conversion and Geocoding of InSAR-Derived DEMs. In Proceedings of the EUSAR ‘96 (1996), Königswinter, Germany, 26–28 March 1996. [Google Scholar]
- Kimura, H.; Todo, M. Baseline estimation using ground points for interferometric SAR. In Proceedings of the IGARSS 97, Singapore, 3–8 August 1997. [Google Scholar]
- Chen, X.T.; Zhu, X.F.; Wang, X.H.; Cai, Y. INSAR Flat-Earth Phase Removal Approach Based on DEM to Settlement Area. In Proceedings of the ITM Web of Conferences, Hangzhou, China, 29–31 July 2016. [Google Scholar]
- Gatelli, F.; Guamieri, A.M.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The Wave-Number Shift in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Moreira, J.; Schwabisch, M.; Fornaro, G. X-SAR Interferometry—First Results. IEEE Trans. Geosci. Remote Sens. 1995, 33, 950–956. [Google Scholar] [CrossRef]
- Lanari, R.; Fornaro, G.; Riccio, D.; Migliaccio, M.; Papathanassiou, K.P.; Moreira, J.R.; Schwabisch, M.; Dutra, L.; Puglisi, G.; Franceschetti, G.; et al. Generation of digital elevation models by using SIR-C/X-SAR multifrequency two-pass interferometry: The Etna case study. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1097–1114. [Google Scholar] [CrossRef]
- Xiang, Z.; Wang, K.Z.; Liu, X.Z. A Model-Spectrum-Based Flattening Algorithm for Airborne Single-Pass SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2009, 6, 307–311. [Google Scholar] [CrossRef]
- Peng, S.R.; He, K.X.; Wang, Y.N. A High Accurate Approach for InSAR Flat Earth Effect Removal. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009. [Google Scholar]
- Qu, C.Y.; Shan, X.J.; Zhang, G.H.; Song, X.G.; Zhang, G.F.; Liu, Y.H.; Guo, L.M. Influence of interferometric baseline on measurements of seismic deformation: A case study on the 1997 mani, tibet m 7.7 earthquake. Seismol. Geol. 2012, 34, 672–683. [Google Scholar]
- Xiang, Z.; Wang, K.Z.; Liu, X.Z.; Yu, W.X. Analysis of the InSAR Flattening Errors and Their Influence on DEM Reconstruction. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009. [Google Scholar]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Shirzaei, M.; Walter, T.R. Estimating the effect of satellite orbital error using wavelet-based robust regression applied to InSAR deformation data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4600–4605. [Google Scholar] [CrossRef]
- Liu, Z.; Jung, H.-S.; Lu, Z. Joint correction of ionosphere noise and orbital error in L-band SAR interferometry of interseismic deformation in southern California. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3421–3427. [Google Scholar] [CrossRef]
- Du, Y.; Fu, H.; Liu, L.; Feng, G.; Peng, X.; Wen, D. Orbit error removal in InSAR/MTInSAR with a patch-based polynomial model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102438. [Google Scholar] [CrossRef]
- Sahraoui, O.H.; Hassaine, B.; Serief, C.; Hasni, K. Radar interferometry with Sarscape software. In Proceedings of the Shaping Change XXIII FIG Congress, Munich, Germany, 8–13 October 2006. [Google Scholar]
- Polcari, M.; Albano, M.; Montuori, A. InSAR Monitoring of Italian Coastline Revealing Natural and Anthropogenic Ground Deformation Phenomena and Future Perspectives. Sustainability 2018, 10, 3152. [Google Scholar] [CrossRef]
- Sataer, G.; Sultan, M.; Emil, M.K. Remote Sensing Application for Landslide Detection, Monitoring along Eastern Lake Michigan (Miami Park, MI). Remote Sens. 2022, 14, 3474. [Google Scholar] [CrossRef]
- Xiao, B.; Zhao, J.S.; Li, D.S. The Monitoring and Analysis of Land Subsidence in Kunming (China) Supported by Time Series InSAR. Sustainability 2022, 14, 12387. [Google Scholar] [CrossRef]
- Gaber, A.; Darwish, N.; Koch, M. Minimizing the Residual Topography Effect on Interferograms to Improve DInSAR Results: Estimating Land Subsidence in Port-Said City, Egypt. Remote Sens. 2017, 9, 752. [Google Scholar] [CrossRef]
- Parihar, N.; Nathawat, M.S.; Das, A.K.; Mohan, S. Accuracy assessment of DEMs derived from multi-frequency SAR images. In Proceedings of the 3rd APSAR, Seoul, Republic of Korea, 26–30 September 2011. [Google Scholar]
- Xu, B.; Li, Z.; Zhu, Y.; Shi, J.; Feng, G. SAR Interferometric Baseline Refinement Based on Flat-Earth Phase without a Ground Control Point. Remote Sens. 2020, 12, 233. [Google Scholar] [CrossRef]
- Wang, H.Q.; Zhou, Y.S.; Fu, H.Q. Parameterized Modeling and Calibration for Orbital Error in TanDEM-X Bistatic SAR Interferometry over Complex Terrain Areas. Remote Sens. 2021, 13, 5124. [Google Scholar] [CrossRef]
- Lin, C.-y.; Chen, L.; Ge, S.-q. Research on method of flat earth effect removal based on refined local fringe frequency. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013. [Google Scholar]
- Ai, B.; Liu, K.; Li, X.; Li, D.H. Flat-earth phase removal algorithm improved with frequency information of interferogram. In Proceedings of the Geoinformatics 2008 and Joint Conference on GIS and Built Environment: Geo-Simulation and Virtual GIS Environments, Guangzhou, China, 28–29 June 2008. [Google Scholar]
- Yubin, Z.; Jie, Z.; Junmin, M.; Chenqing, F. An improved frequency shift method for ATI-SAR flat earth phase removal. Acta Oceanol. Sin. 2019, 38, 94–100. [Google Scholar] [CrossRef]
- Liu, G.; Hanssen, R.F.; Guo, H.; Yue, H.; Perski, Z. Nonlinear model for InSAR baseline error. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5341–5351. [Google Scholar] [CrossRef]
- Lu, H.; Suo, Z.; Li, Z.; Xie, J.; Zhao, J.; Zhang, Q. InSAR Baseline Estimation for Gaofen-3 Real-Time DEM Generation. Sensors 2018, 18, 2152. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Baran, I.; Stewart, M.P.; Kampes, B.M.; Perski, Z.; Lilly, P. A modification to the Goldstein radar interferogram filter. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2114–2118. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Ullah, Z.; Usman, M.; Jeon, M.; Gwak, J. Cascade multiscale residual attention cnns with adaptive roi for automatic brain tumor segmentation. Inf. Sci. 2022, 608, 1541–1556. [Google Scholar] [CrossRef]
- Ullah, Z.; Farooq, M.U.; Lee, S.H.; An, D. A hybrid image enhancement based brain MRI images classification technique. Med. Hypotheses 2020, 143, 109922. [Google Scholar] [CrossRef] [PubMed]















| Methods | Strengths | Weaknesses | |
|---|---|---|---|
| Global refinement and re-flattening methods | polynomial refinement method |
|
|
| re-flattening method based on baseline correction |
|
| |
| re-flattening methods based on manually set windows |
|
| |
| the proposed method |
|
| |
| Imaging Mode | Polarization | Resolution (Azimuth × Slant Range) | 2π Ambiguity Height | |
|---|---|---|---|---|
| GF-3 InSAR data in Ningbo | Fine Strip I | HH | 2.86 × 3.31 m | 31.05 m |
| GF-3 InSAR data in Yutian | Fine Strip I | HH | 3.13 × 3.61 m | 62.55 m |
| GF-3 InSAR data in Xi’an | Quad-Polarization Strip I | HH | 5.54 × 3.80 m | 109.98 m |
| Sentinel-1A InSAR data in Yancheng | IW | HH | 13.92 × 23.30 m | 224.12 m |
| Data\Indictor | Average Coherence | Ambiguity Height (m) | Method | MAE (m) | RMSE (m) |
|---|---|---|---|---|---|
| GF-3 InSAR data (Ningbo City) | 0.35 | 31.05 | the proposed method | 9.84 | 15.17 |
| GPR method | 66.60 | 90.60 | |||
| SBDR method | 68.65 | 89.45 | |||
| LFE-MW method | 29.52 | 40.21 | |||
| GF-3 InSAR data(Yutian County) | 0.24 | 62.55 | the proposed method | 11.27 | 17.86 |
| GPR method | 132.18 | 166.45 | |||
| SBDR method | 136.54 | 172.56 | |||
| LFE-MW method | 22.72 | 27.37 | |||
| GF-3 InSAR data (Xi’an City) | 0.46 | 109.98 | the proposed method | 32.92 | 53.95 |
| GPR method | 123.18 | 206.91 | |||
| SBDR method | 287.50 | 332.19 | |||
| LFE-MW method | 81.03 | 107.25 | |||
| Sentinel-1A InSAR data (Yancheng City) | 0.49 | 224.12 | the proposed method | 33.15 | 41.01 |
| GPR method | 62.84 | 76.48 | |||
| SBDR method | 55.00 | 65.61 | |||
| LFE-MW method | 111.22 | 137.95 |
| Data\Indicator | Average Coherence | Ambiguity Height (m) | MAE (m) | RMSE (m) |
|---|---|---|---|---|
| GF-3 InSAR data in Ningbo | 0.35 | 31.05 | 9.84 | 15.17 |
| TerraSAR-X InSAR data | 0.47 | 48.88 | 11.22 | 13.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, D.; Zhang, L.; Zou, B. An Interferogram Re-Flattening Method for InSAR Based on Local Residual Fringe Removal and Adaptively Adjusted Windows. Remote Sens. 2023, 15, 2214. https://doi.org/10.3390/rs15082214
Zhuang D, Zhang L, Zou B. An Interferogram Re-Flattening Method for InSAR Based on Local Residual Fringe Removal and Adaptively Adjusted Windows. Remote Sensing. 2023; 15(8):2214. https://doi.org/10.3390/rs15082214
Chicago/Turabian StyleZhuang, Di, Lamei Zhang, and Bin Zou. 2023. "An Interferogram Re-Flattening Method for InSAR Based on Local Residual Fringe Removal and Adaptively Adjusted Windows" Remote Sensing 15, no. 8: 2214. https://doi.org/10.3390/rs15082214
APA StyleZhuang, D., Zhang, L., & Zou, B. (2023). An Interferogram Re-Flattening Method for InSAR Based on Local Residual Fringe Removal and Adaptively Adjusted Windows. Remote Sensing, 15(8), 2214. https://doi.org/10.3390/rs15082214