Multiscale Entropy-Based Surface Complexity Analysis for Land Cover Image Semantic Segmentation
Abstract
1. Introduction
- (1)
- We made a quantification definition of pixel-level multiscale surface complexity that was encoded using an entropy-based convolution. The convolution operator was developed to calculate the local complexity for surface features.
- (2)
- We developed a deep learning algorithm to identify and extract multiscale surface complexity based on the input of spectral features and/or relevant geospatial variables. The robust learning algorithm can model the mapping relationship from the influencing factors to the surface complexity and improve its generalization.
- (3)
- We developed novel optimal sampling strategies based on complexity analysis and a constrained optimization of entropy-based invariance to improve the semantic segmentation of land cover images. Here, instead of emphasizing the innovation network structure, since the baseline UNet achieved the state-of-the-art test performance, we highlighted the importance of reducing the sampling and modeling bias for LULC semantic segmentation.
- (4)
- We evaluated the important influence of the complexity-informed optimal sampling and constrained optimization on the semantic segmentation of LULC using the typical Gaofen-2 satellite images. By comparing with representative deep learning methods including FCN-ResNet, global CNN, DeepLab V3, and Crossformer, we illustrated the innovative contributions of our method in reducing the sampling and modeling bias, which significantly improved the semantic segmentation of LULC.
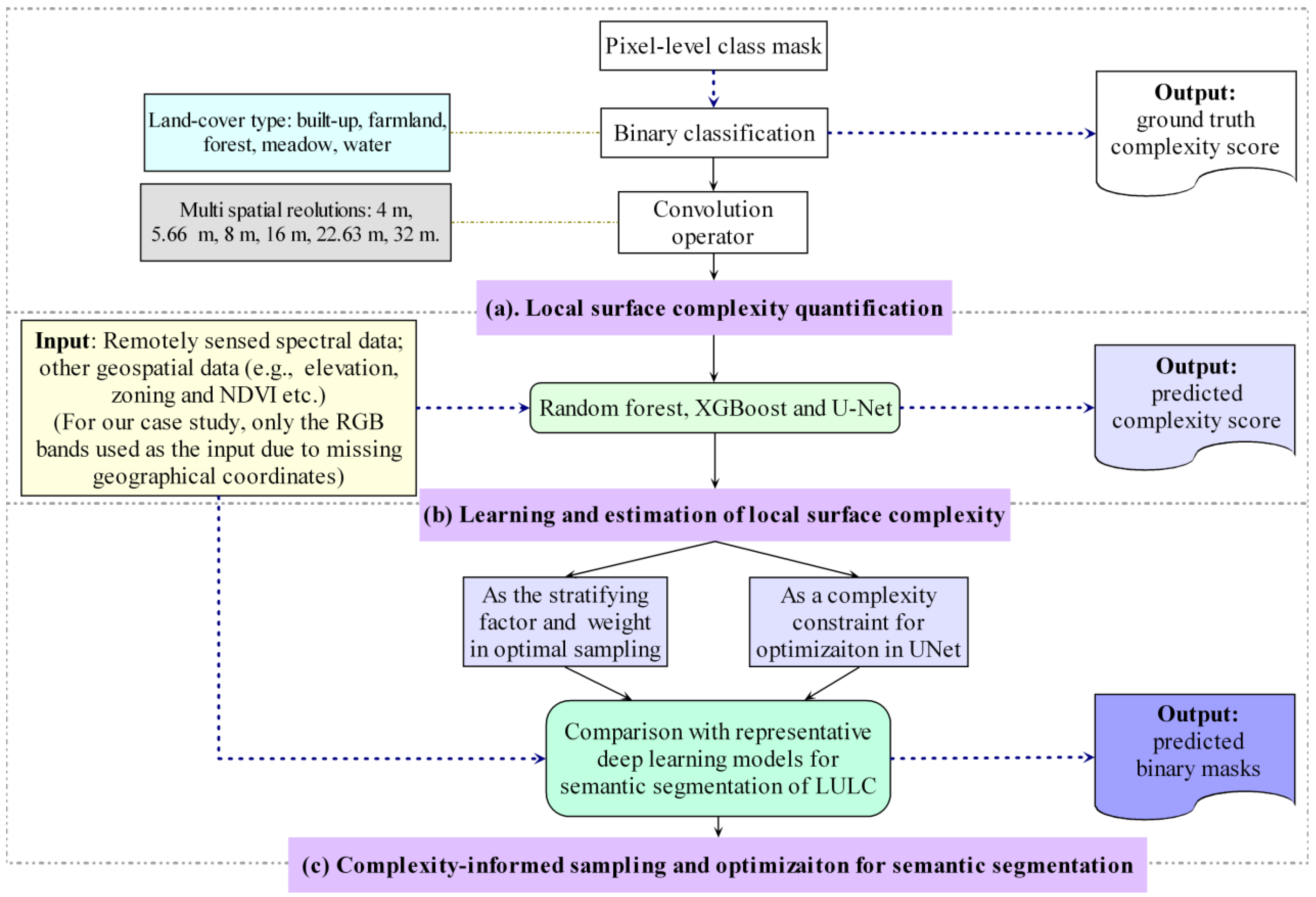
2. Methodology
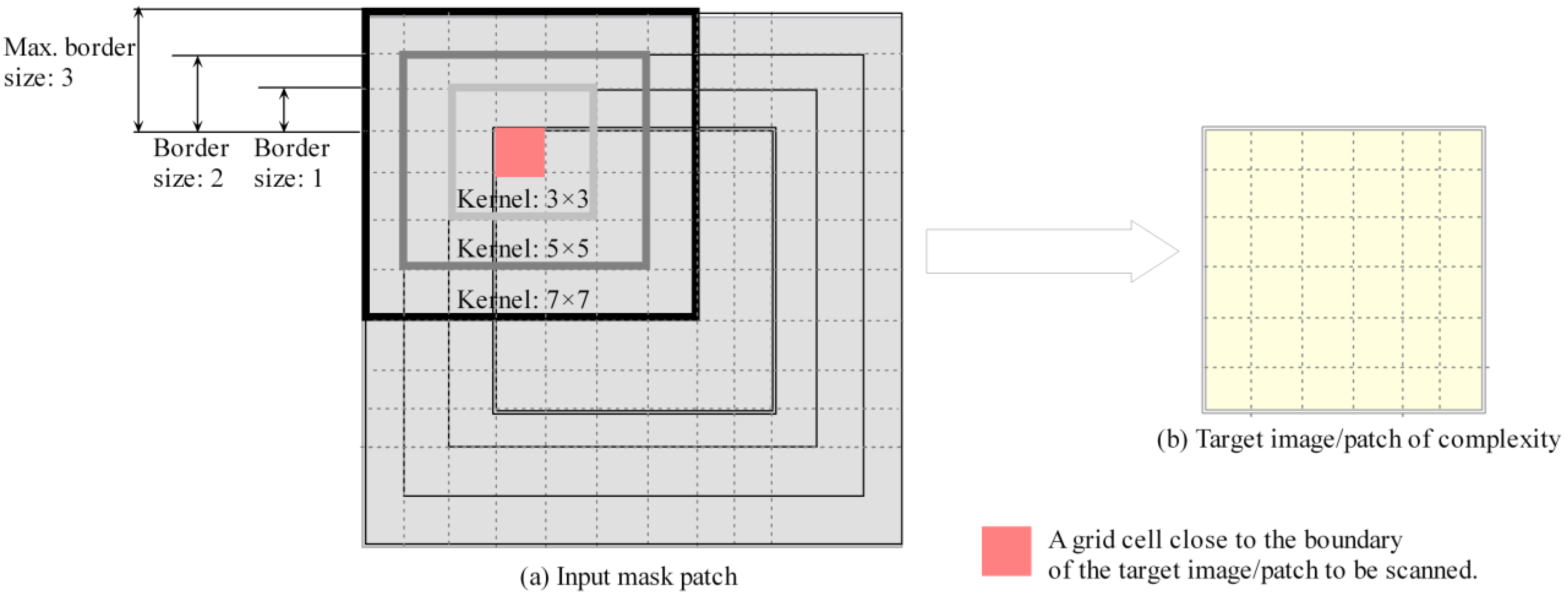
2.1. Definition and Extraction of Entropy-Based Multiscale Complexity
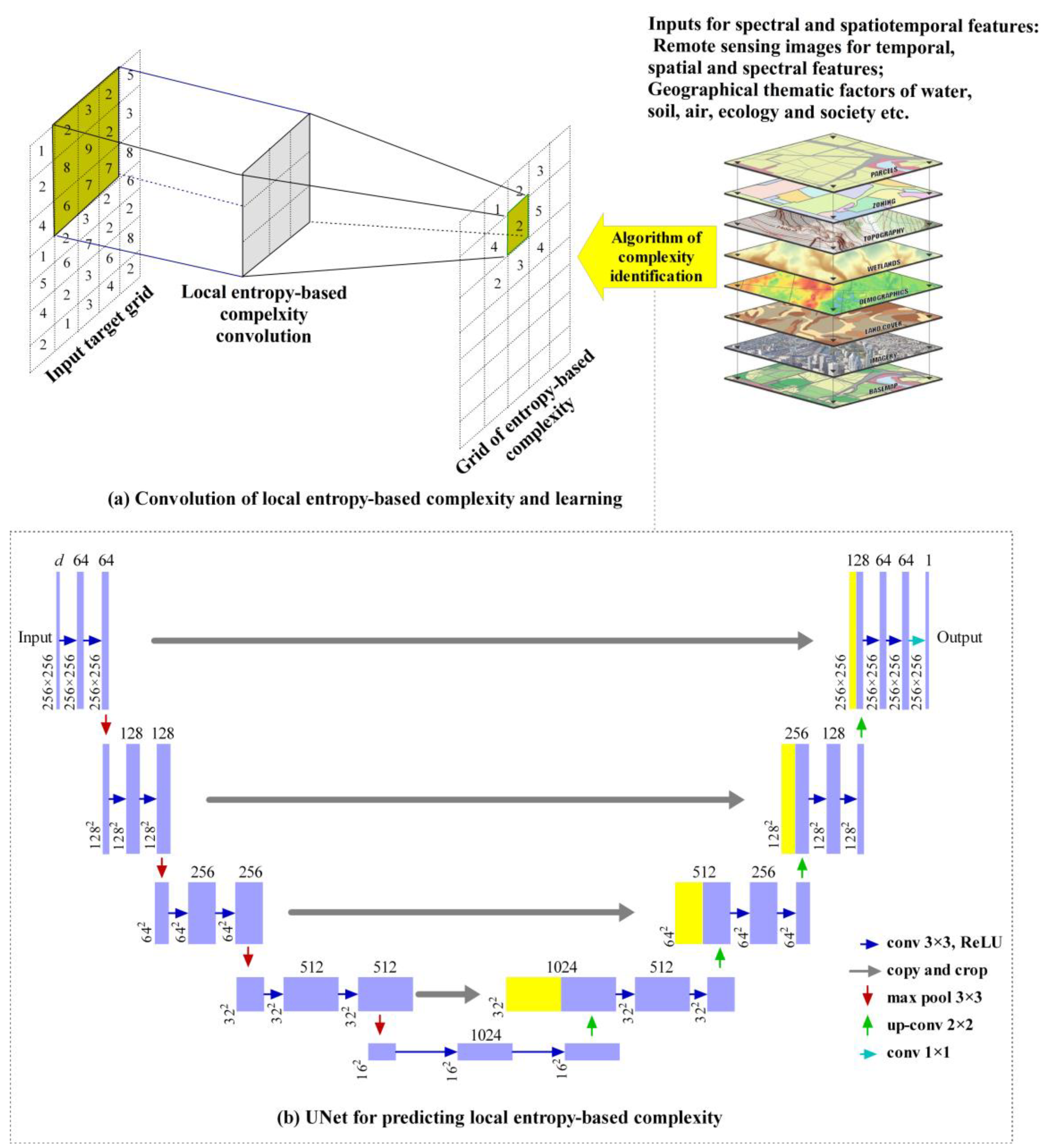
2.2. Learning Entropy-Based Multiscale Complexity
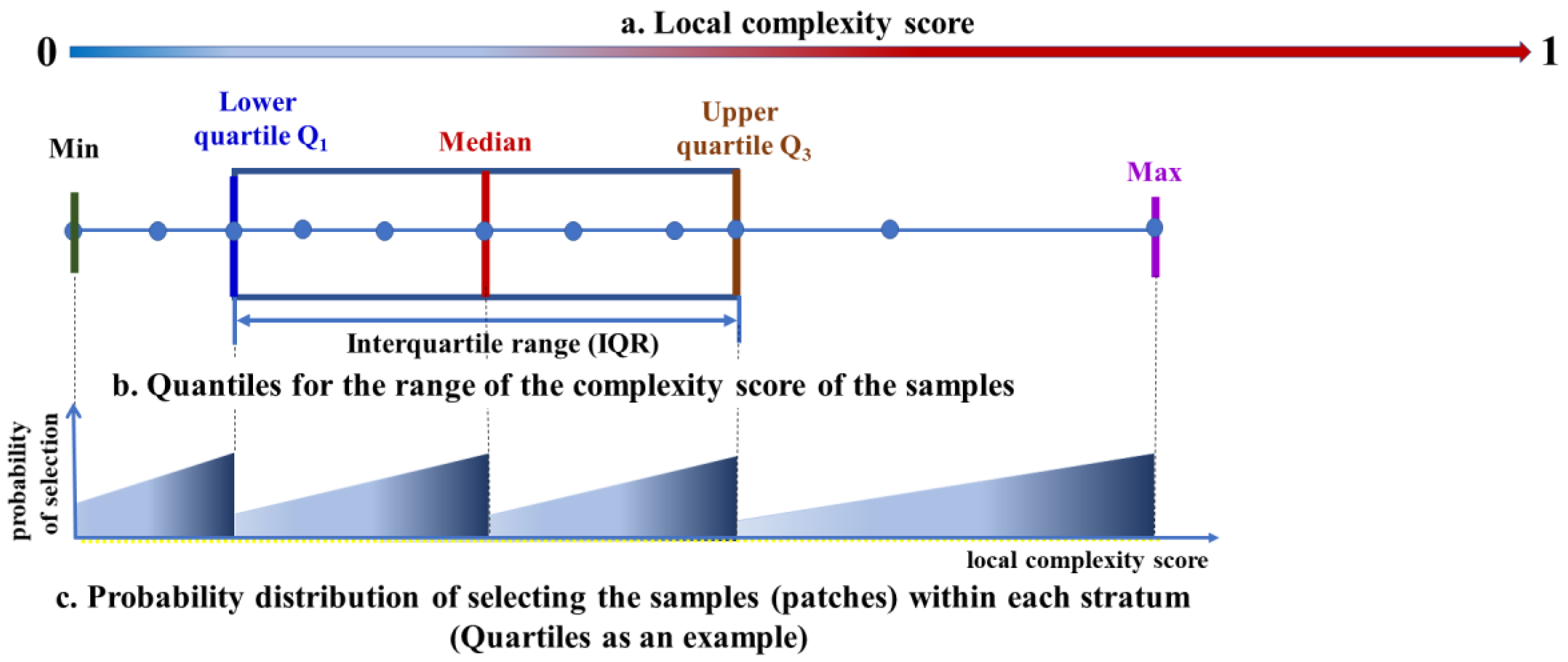
2.3. Complexity-Informed Optimal Sampling and Constrained Optimization
3. Experiments
3.1. Dataset
3.2. Experimental Detail
3.3. Training
3.4. Evaluation and Prediction
- (1)
- R2 can be defined as:where is the observed complexity computed from the ground truth data (binary mask), is the complexity estimated by the learned model, denotes the mean of the observed complexity, n is number of samples, TSS denotes the total sum of squares (=), RSS denotes the residual sum of squares (=), and ESS denotes the explained sum of squares ().
- (2)
- RMSE can be defined as:
4. Results
4.1. Quantification of Local Surface Complexity
4.2. Learning of Local Surface Complexity
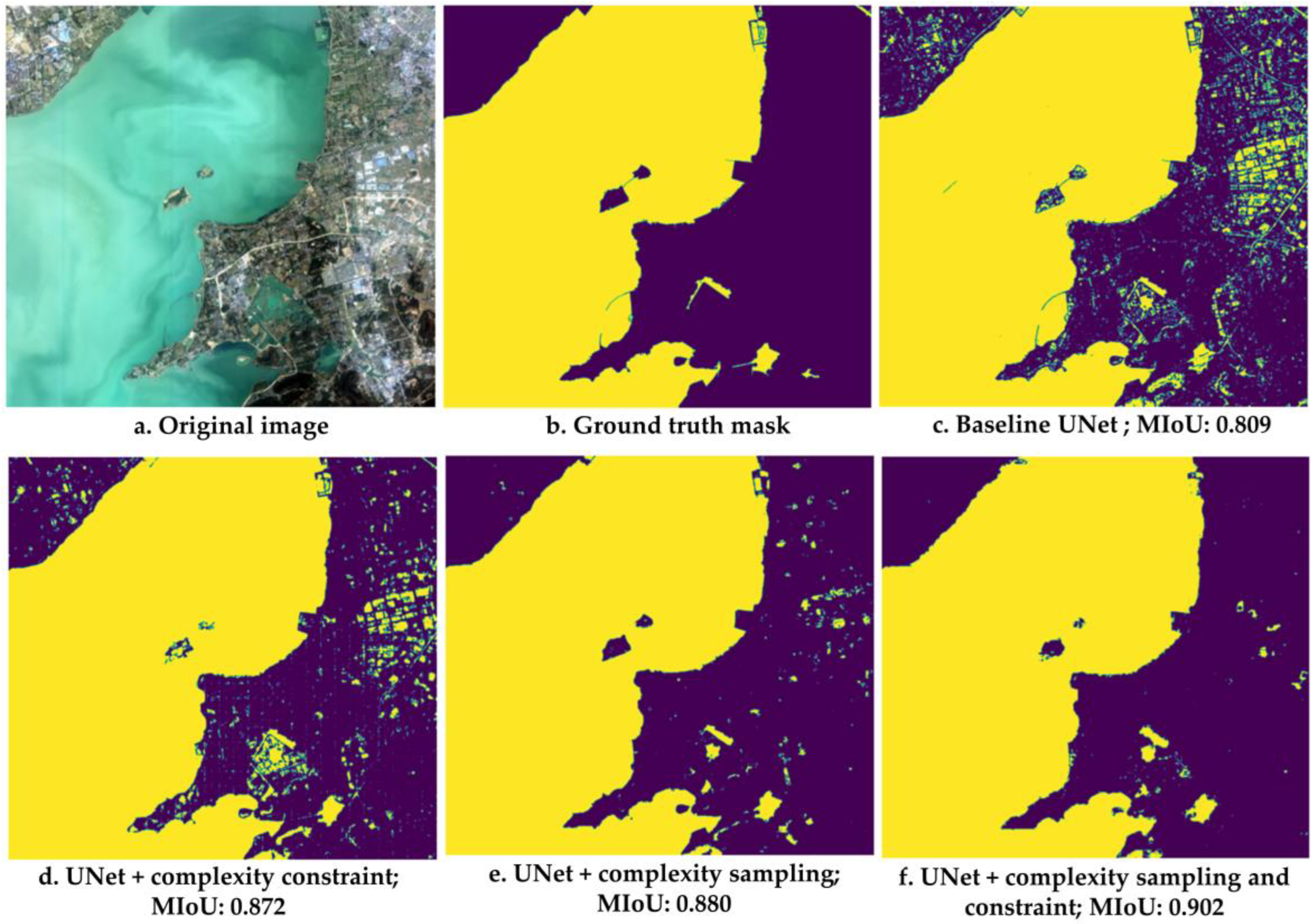
4.3. Optimal Sampling and Constraints for Land Cover Segmentations
5. Discussion
5.1. Optimal Sampling to Reduce Bias
5.2. Constrained Optimization to Reduce Overfitting
5.3. Combination of Optimal Sampling and Constrained Optimization
5.4. Limitations and Prospects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emery, B.; Camps, A. Introduction to Satellite Remote Sensing: Atmosphere, Ocean, Land and Cryosphere Applications; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Managi, S.; Wang, J.; Zhang, L. Research progress on monitoring and assessment of forestry area for improving forest management in China. For. Policy Econ. 2019, 1, 57–70. [Google Scholar] [CrossRef]
- Li, M. Dynamic monitoring algorithm of natural resources in scenic spots based on MODIS Remote Sensing technology. Earth Sci. Res. J. 2021, 25, 57–64. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.X.; Geng, G.N.; Zheng, B.; Jiang, X.J.; Zhang, Q.; He, K.B. Fusing Observational, Satellite Remote Sensing and Air Quality Model Simulated Data to Estimate Spatiotemporal Variations of PM2. 5 Exposure in China. Remote Sens. 2017, 9, 221. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Q.; Li, Y.; Liu, S.; Wang, Z.; Zhu, L.; Wang, Z. An overview of satellite remote sensing technology used in China’s environmental protection. Earth Sci. Inform. 2017, 10, 137–148. [Google Scholar] [CrossRef]
- Reba, M.; Seto, K.C. A systematic review and assessment of algorithms to detect, characterize, and monitor urban land change. Remote Sens. Environ. 2020, 242, 111739. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.L.; Ye, Y.X.; Yin, G.F.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Zhang, L.P.; Zhang, L.F.; Du, B. Deep Learning for Remote Sensing Data A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.C.; Xia, G.S.; Zhang, L.P.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, T.; Gao, G.; Ren, G.; Ma, Y.; Chanussot, J.; Jia, X. Multimodal hyperspectral remote sensing: An overview and perspective. Sci. China Inf. Sci. 2021, 64, 1–24. [Google Scholar] [CrossRef]
- Balsamo, G.; Agusti-Parareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Bousserez, N.; Boussetta, S.; Brown, A.; Buizza, R.; et al. Satellite and In Situ Observations for Advancing Global Earth Surface Modelling: A Review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
- Fisher, R.A.; Koven, C.D. Perspectives on the future of land surface models and the challenges of representing complex terrestrial systems. J. Adv. Model. Earth Syst. 2020, 12, e2018MS001453. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Monthly Analysis of Wetlands Dynamics Using Remote Sensing Data. ISPRS Int. J. Geo-Inf. 2018, 7, 411. [Google Scholar] [CrossRef]
- Wen, J.G.; Liu, Q.; Xiao, Q.; Liu, Q.H.; You, D.Q.; Hao, D.L.; Wu, S.B.; Lin, X.W. Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments. Remote Sens. 2018, 10, 370. [Google Scholar] [CrossRef]
- Xu, L.; Herold, M.; Tsendbazar, N.-E.; Masiliūnas, D.; Li, L.; Lesiv, M.; Fritz, S.; Verbesselt, J. Time series analysis for global land cover change monitoring: A comparison across sensors. Remote Sens. Environ. 2022, 271, 112905. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, R.; Shi, Z.; Zhang, N.; Zhu, X. Bayesian Constrained Energy Minimization for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8359–8372. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, M.; Li, Z.; Yu, Q.; Chen, B. Classification model for “same subject with different spectra” on complicated surface in Southern hilly areas. Remote Sens. Land Res. 2016, 28, 79–83. (In Chinese) [Google Scholar]
- Zhu, Q.; Liao, C.; Hu, H.; Mei, X.; Li, H. MAP-Net: Multiple attending path neural network for building footprint extraction from remote sensed imagery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6169–6181. [Google Scholar] [CrossRef]
- Alaei, N.; Mostafazadeh, R.; Esmali Ouri, A.; Hazbavi, Z.; Sharari, M.; Huang, G. Spatial Comparative Analysis of Landscape Fragmentation Metrics in a Watershed with Diverse Land Uses in Iran. Sustainability 2022, 14, 14876. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Huang, Q.; Zhao, A.G.; Lv, H.; Zhuang, S.B. Semantic Network-Based Impervious Surface Extraction Method for Rural-Urban Fringe From High Spatial Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4980–4998. [Google Scholar] [CrossRef]
- Lu, W.; Li, Y.C.; Zhao, R.K.; Wang, Y. Using Remote Sensing to Identify Urban Fringe Areas and Their Spatial Pattern of Educational Resources: A Case Study of the Chengdu-Chongqing Economic Circle. Remote Sens. 2022, 14, 3148. [Google Scholar] [CrossRef]
- Christiansen, E.H.; Hamblin, W.K. Dynamic Earth: An Introduction to Physical Geology; Jones & Bartlett Publishers: Burlington, MA, USA, 2014. [Google Scholar]
- Chen, X.; Fan, J. Opportunities for complexity science: The Nobel Prize in Physics. Physics 2022, 21, 1–9. (In Chinese) [Google Scholar]
- Ge, Y.; Jin, Y.; Stein, A.; Chen, Y.; Wang, J.; Wang, J.; Cheng, Q.; Bai, H.; Liu, M.; Atkinson, P.M. Principles and methods of scaling geospatial Earth science data. Earth Sci. Rev. 2019, 197, 102897. [Google Scholar] [CrossRef]
- Sadeghi, B.; Ghahremanloo, M.; Mousavinezhad, S.; Lops, Y.; Pouyaei, A.; Choi, Y. Contributions of meteorology to ozone variations: Application of deep learning and the Kolmogorov-Zurbenko filter. Environ. Pollut. 2022, 310, 119863. [Google Scholar] [CrossRef]
- Jiang, H.; Shihua, L.; Dong, Y. Multidimensional Meteorological Variables for Wind Speed Forecasting in Qinghai Region of China: A Novel Approach. Adv. Meteorol. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, W.; Lv, Z. Uncertainty assessment in multitemporal land use/cover mapping with classification system semantic heterogeneity. Remote Sens. 2019, 11, 2509. [Google Scholar] [CrossRef]
- Angelo, J.A. Satellites; Infobase Publishing: New York, NY, USA, 2014. [Google Scholar]
- Wang, X.H.; Qin, H.; Zhang, Z.; Li, F. Assessment of Land Surface Complexity In Relation To Information Capacity and the Fractal Dimension in Different Landform Regions Using Landsat Data. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Beijing, China, 22–26 April 2013; IOP Publishing: Bristol, UK, 2014; p. 012213. [Google Scholar]
- Li, J.; Peng, B.; Wei, Y.; Ye, H. Accurate extraction of surface water in complex environment based on Google Earth Engine and Sentinel-2. PLoS ONE 2021, 16, e0253209. [Google Scholar] [CrossRef]
- Sun, J. Exploring edge complexity in remote-sensing vegetation index imageries. J. Land Use Sci. 2014, 9, 165–177. [Google Scholar] [CrossRef]
- Wilson, R.; Complexity in Remote Sensing: A Literature Review, Synthesis and Position Paper. 2 June 2011. Available online: http://www.rtwilson.com/academic/downloads/RWilson_IRP.pdf (accessed on 1 July 2022).
- Li, H.; Li, Y.; Zhang, G.; Liu, R.; Huang, H.; Zhu, Q.; Tao, C. Global and local contrastive self-supervised learning for semantic segmentation of HR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Li, W.; Chen, K.; Chen, H.; Shi, Z. Geographical knowledge-driven representation learning for remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Swope, A.M.; Rudelis, X.H.; Story, K.T. Representation learning for remote sensing: An unsupervised sensor fusion approach. arXiv 2021, arXiv:2108.05094. [Google Scholar]
- Li, Y.; Kong, D.; Zhang, Y.; Chen, R.; Chen, J. Representation learning of remote sensing knowledge graph for zero-shot remote sensing image scene classification. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 1351–1354. [Google Scholar]
- Lin, D.; Fu, K.; Wang, Y.; Xu, G.; Sun, X. MARTA GANs: Unsupervised representation learning for remote sensing image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2092–2096. [Google Scholar] [CrossRef]
- Yan, C.; Fan, X.; Fan, J.; Wang, N. Improved U-Net remote sensing classification algorithm based on Multi-Feature Fusion Perception. Remote Sens. 2022, 14, 1118. [Google Scholar] [CrossRef]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-FCN: Object detection via region-based fully convolutional networks. In Advances in Neural Information Processing Systems; Curran Associates: Manila, Philippines, 2016; Volume 29. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3431–3440. [Google Scholar]
- Peng, C.; Zhang, X.; Yu, G.; Luo, G.; Sun, J. Large kernel matters—improve semantic segmentation by global convolutional network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4353–4361. [Google Scholar]
- Zhao, W.; Persello, C.; Stein, A. Extracting planar roof structures from very high resolution images using graph neural networks. ISPRS J. Photogramm. Remote Sens. 2022, 187, 34–45. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September, 2018; pp. 833–851. [Google Scholar]
- Aleissaee, A.A.; Kumar, A.; Anwer, R.M.; Khan, S.; Cholakkal, H.; Xia, G.-S. Transformers in remote sensing: A survey. arXiv 2022, arXiv:2209.01206. [Google Scholar] [CrossRef]
- Wang, W.; Yao, L.; Chen, L.; Lin, B.; Cai, D.; He, X.; Liu, W. CrossFormer: A versatile vision transformer hinging on cross-scale attention. arXiv 2021, arXiv:2108.00154. [Google Scholar]
- Chen, K.; Zou, Z.; Shi, Z. Building extraction from remote sensing images with sparse token transformers. Remote Sens. 2021, 13, 4441. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Zhao, J.; Zhang, D.; Yao, R.; Xue, Y. Swin transformer embedding UNet for remote sensing image semantic segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like transformer for efficient semantic segmentation of remote sensing urban scene imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Zorzi, S.; Bazrafkan, S.; Habenschuss, S.; Fraundorfer, F. Polyworld: Polygonal building extraction with graph neural networks in satellite images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 24 June 2022; pp. 1848–1857. [Google Scholar]
- Hu, Y.; Wang, Z.; Huang, Z.; Liu, Y. PolyBuilding: Polygon transformer for building extraction. ISPRS J. Photogramm. Remote Sens. 2023, 199, 15–27. [Google Scholar] [CrossRef]
- Li, C.; Ma, Z.; Wang, L.; Yu, W.; Tan, D.; Gao, B.; Feng, Q.; Guo, H.; Zhao, Y. Improving the accuracy of land cover mapping by distributing training samples. Remote Sens. 2021, 13, 4594. [Google Scholar] [CrossRef]
- Meng, X.-L. Statistical paradises and paradoxes in big data (I): Law of large populations, big data paradox, and the 2016 US presidential election. Ann. Appl. Stat. 2018, 12, 685–726. [Google Scholar] [CrossRef]
- Ghorbanian, A.; Kakooei, M.; Amani, M.; Mahdavi, S.; Mohammadzadeh, A.; Hasanlou, M. Improved land cover map of Iran using Sentinel imagery within Google Earth Engine and a novel automatic workflow for land cover classification using migrated training samples. ISPRS J. Photogramm. Remote Sens. 2020, 167, 276–288. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Wang, L.; Hu, L.; Gong, P. Comparison of classification algorithms and training sample sizes in urban land classification with Landsat thematic mapper imagery. Remote Sens. 2014, 6, 964–983. [Google Scholar] [CrossRef]
- Duan, X.; Yi, Y. System Complexity and Metrics. J. Natl. Univ. Def. Technol. 2019, 41, 191–198. (In Chinese) [Google Scholar]
- Wehrl, A. General Properties of Entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Frigg, R.; Werndl, C. Entropy—A Guide for the Perplexed. In Probabilities in Physics; Beisbart, C., Hartmann, S., Eds.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process Syst. 2019, 32, 8026–8037. [Google Scholar]
- Li, L.F. Deep Residual Autoencoder with Multiscaling for Semantic Segmentation of Land-Use Images. Remote Sens. 2019, 11, 2142. [Google Scholar] [CrossRef]
- Kendal, W.S.; Jørgensen, B. Taylor’s power law and fluctuation scaling explained by a central-limit-like convergence. Phys. Rev. E 2011, 83, 066115. [Google Scholar] [CrossRef]
- Berstad, T.J.D.; Riegler, M.; Espeland, H.; de Lange, T.; Smedsrud, P.H.; Pogorelov, K.; Stensland, H.K.; Halvorsen, P. Tradeoffs using binary and multiclass neural network classification for medical multidisease detection. In Proceedings of the 2018 IEEE International Symposium on Multimedia (ISM), Taichung, Taiwan, 10–12 December 2018; pp. 1–8. [Google Scholar]
- Phinzi, K.; Abriha, D.; Bertalan, L.; Holb, I.; Szabó, S. Machine learning for gully feature extraction based on a pan-sharpened multispectral image: Multiclass vs. Binary approach. ISPRS Int. J. Geo-Inf. 2020, 9, 252. [Google Scholar] [CrossRef]
- Rajagopal, S.; Hareesha, K.S.; Kundapur, P.P. Performance analysis of binary and multiclass models using azure machine learning. Int. J. Electr. Comput. Eng. 2020, 10, 978. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention– MICCAI 2015: 18th International Conference, Part III. Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Mu, X.H.; Hu, M.G.; Song, W.J.; Ruan, G.Y.; Ge, Y.; Wang, J.F.; Huang, S.; Yan, G.J. Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover. Remote Sens. 2015, 7, 16164–16182. [Google Scholar] [CrossRef]
- Feng, W.; Boukir, S.; Huang, W. Margin-based random forest for imbalanced land cover classification. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3085–3088. [Google Scholar]
- Yang, Y.; Sun, X.; Diao, W.; Yin, D.; Yang, Z.; Li, X. Statistical sample selection and multivariate knowledge mining for lightweight detectors in remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Jadon, S. A survey of loss functions for semantic segmentation. In Proceedings of the 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Viña del Mar, Chile, 27–29 October 2020; pp. 1–7. [Google Scholar]
- Tong, X.-Y.; Xia, G.-S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef]
- GB/T 21010-2017; Current land use classification. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China and Standardization Administration of the People’s Republic of China. 2017.
- Colditz, R.R. An evaluation of different training sample allocation schemes for discrete and continuous land cover classification using decision tree-based algorithms. Remote Sens. 2015, 7, 9655–9681. [Google Scholar] [CrossRef]
- Liu, Z.; Pontius, R.G., Jr. The total operating characteristic from stratified random sampling with an application to flood mapping. Remote Sens. 2021, 13, 3922. [Google Scholar] [CrossRef]
- Felicen, M.; De La Cruz, R.; Olfindo, N., Jr.; Borlongan, N.; Ebreo, D.; Perez, A. Validation points generation for LiDAR-extracted hydrologic features. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII, Edinburgh, UK, 26–28 September 2016; pp. 267–276. [Google Scholar]
- Jin, H.; Stehman, S.V.; Mountrakis, G. Assessing the impact of training sample selection on accuracy of an urban classification: A case study in Denver, Colorado. Int. J. Remote Sens. 2014, 35, 2067–2081. [Google Scholar] [CrossRef]
- Shetty, S.; Gupta, P.K.; Belgiu, M.; Srivastav, S. Assessing the effect of training sampling design on the performance of machine learning classifiers for land cover mapping using multi-temporal remote sensing data and google earth engine. Remote Sens. 2021, 13, 1433. [Google Scholar] [CrossRef]
- Kotary, J.; Fioretto, F.; Van Hentenryck, P.; Wilder, B. End-to-end constrained optimization learning: A survey. arXiv 2021, arXiv:2103.16378. [Google Scholar]
- Teng, W.; Wang, N.; Shi, H.; Liu, Y.; Wang, J. Classifier-constrained deep adversarial domain adaptation for cross-domain semisupervised classification in remote sensing images. IEEE Geosci. Remote. Sens. Lett. 2019, 17, 789–793. [Google Scholar] [CrossRef]
- Wang, C.; Li, L. Multi-scale residual deep network for semantic segmentation of buildings with regularizer of shape representation. Remote Sens. 2020, 12, 2932. [Google Scholar] [CrossRef]
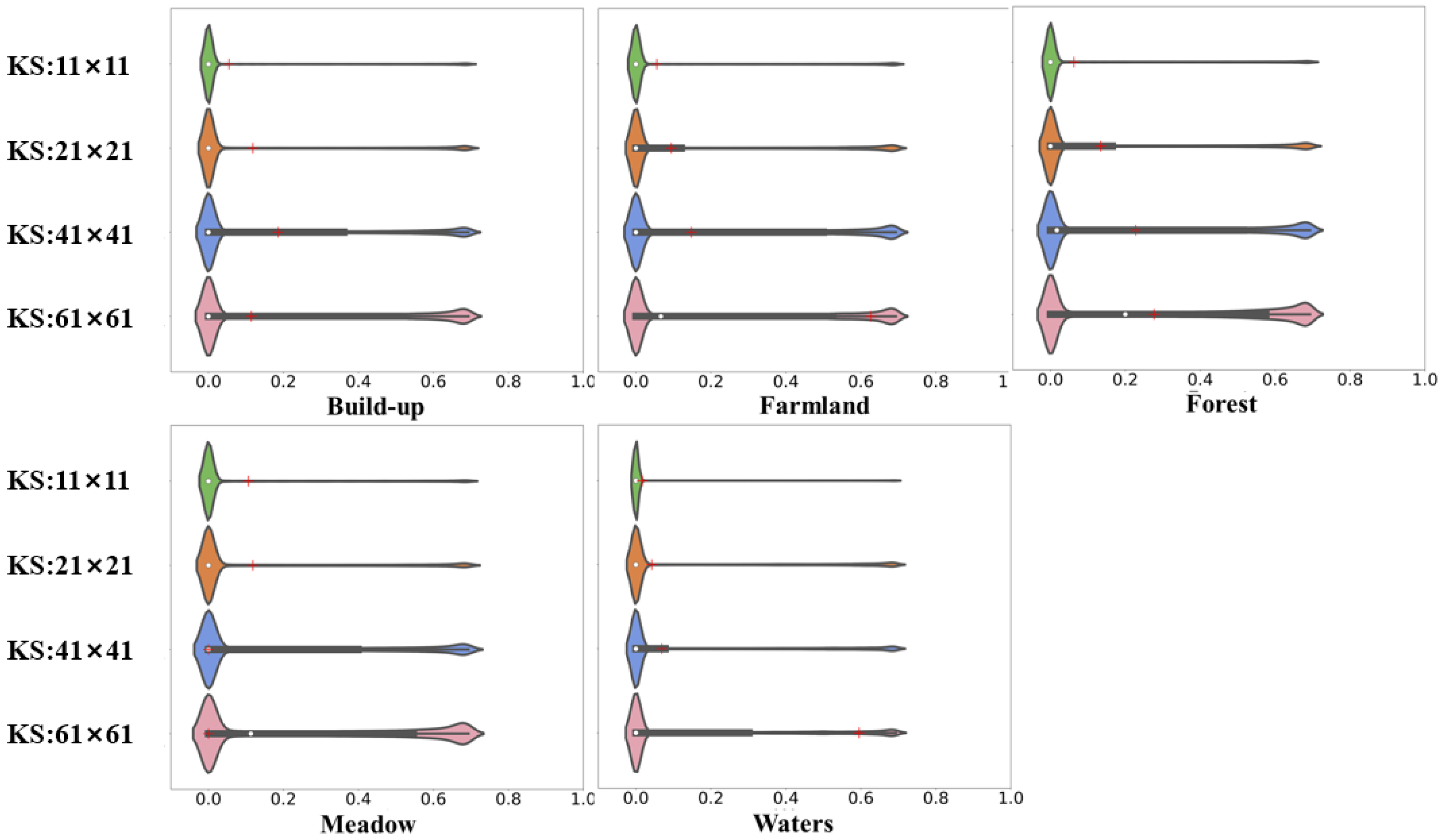





| Model | Upscale Size | Kernel Size | Build-Up | Farmland | Forest | Meadow | Waters | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | |||
| UNet | 4 × 4 m2 | 61 × 61 | 0.980 | 0.439 | 0.632 | 0.414 | 0.985 | 0.639 | 0.983 | 0.548 | 0.981 | 0.738 |
| 8 × 8 m2 | 41 × 41 | 0.995 | 0.876 | 0.984 | 0.560 | 0.997 | 0.895 | 0.996 | 0.826 | 0.989 | 0.895 | |
| 16 × 16 m2 | 21 × 21 | 0.992 | 0.925 | 0.991 | 0.714 | 0.995 | 0.935 | 0.996 | 0.933 | 0.995 | 0.966 | |
| 32 × 32 m2 | 11 × 11 | 0.990 | 0.941 | 0.982 | 0.751 | 0.989 | 0.947 | 0.990 | 0.925 | 0.993 | 0.969 | |
| XGBoost | 4 × 4 m2 | 61 × 61 | 0.032 | 0.021 | 0.052 | 0.048 | 0.105 | 0.102 | 0.079 | 0.076 | 0.233 | 0.225 |
| 8 × 8 m2 | 41 × 41 | 0.074 | 0.071 | 0.038 | 0.033 | 0.103 | 0.100 | 0.063 | 0.059 | 0.108 | 0.104 | |
| 16 × 16 m2 | 21 × 21 | 0.026 | 0.024 | 0.046 | 0.042 | 0.079 | 0.077 | 0.055 | 0.051 | 0.204 | 0.198 | |
| 32 × 32 m2 | 11 × 11 | 0.054 | 0.052 | 0.040 | 0.036 | 0.063 | 0.060 | 0.082 | 0.072 | 0.165 | 0.160 | |
| Random forest | 4 × 4 m2 | 61 × 61 | 0.071 | 0.096 | 0.130 | 0.050 | 0.153 | 0.109 | 0.136 | 0.112 | 0.402 | 0.283 |
| 8 × 8 m2 | 41 × 41 | 0.123 | 0.059 | 0.093 | 0.011 | 0.145 | 0.089 | 0.112 | 0.064 | 0.211 | 0.102 | |
| 16 × 16 m2 | 21 × 21 | 0.118 | 0.085 | 0.108 | 0.025 | 0.188 | 0.155 | 0.178 | 0.153 | 0.385 | 0.291 | |
| 32 × 32 m2 | 11 × 11 | 0.212 | 0.183 | 0.125 | 0.061 | 0.253 | 0.241 | 0.334 | 0.273 | 0.444 | 0.390 | |
| Model | Upscale Size | Kernel Size | Build-Up | Farmland | Forest | Meadow | Waters | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | |||
| UNet | 4 × 4 m2 | 61 × 61 | 0.036 | 0.195 | 0.149 | 0.189 | 0.028 | 0.139 | 0.027 | 0.137 | 0.013 | 0.049 |
| 8 × 8 m2 | 41 × 41 | 0.020 | 0.094 | 0.032 | 0.170 | 0.020 | 0.115 | 0.016 | 0.103 | 0.015 | 0.049 | |
| 16 × 16 m2 | 21 × 21 | 0.025 | 0.076 | 0.025 | 0.138 | 0.018 | 0.067 | 0.016 | 0.063 | 0.010 | 0.026 | |
| 32 × 32 m2 | 11 × 11 | 0.027 | 0.068 | 0.036 | 0.134 | 0.028 | 0.060 | 0.024 | 0.067 | 0.014 | 0.030 | |
| XGBoost | 4 × 4 m2 | 61 × 61 | 0.260 | 0.261 | 0.256 | 0.256 | 0.247 | 0.247 | 0.219 | 0.219 | 0.107 | 0.108 |
| 8 × 8 m2 | 41 × 41 | 0.262 | 0.263 | 0.261 | 0.262 | 0.211 | 0.211 | 0.216 | 0.217 | 0.143 | 0.144 | |
| 16 × 16 m2 | 21 × 21 | 0.273 | 0.274 | 0.257 | 0.258 | 0.257 | 0.257 | 0.236 | 0.237 | 0.131 | 0.132 | |
| 32 × 32 m2 | 11 × 11 | 0.271 | 0.271 | 0.263 | 0.264 | 0.257 | 0.258 | 0.236 | 0.238 | 0.150 | 0.151 | |
| Random forest | 4 × 4 m2 | 61 × 61 | 0.267 | 0.273 | 0.253 | 0.264 | 0.238 | 0.244 | 0.212 | 0.215 | 0.099 | 0.109 |
| 8 × 8 m2 | 41 × 41 | 0.257 | 0.265 | 0.254 | 0.265 | 0.211 | 0.218 | 0.216 | 0.217 | 0.140 | 0.150 | |
| 16 × 16 m2 | 21 × 21 | 0.260 | 0.265 | 0.249 | 0.260 | 0.240 | 0.249 | 0.220 | 0.224 | 0.114 | 0.122 | |
| 32 × 32 m2 | 11 × 11 | 0.258 | 0.264 | 0.251 | 0.260 | 0.230 | 0.229 | 0.202 | 0.209 | 0.122 | 0.132 | |
| Land Cover | Sampling | Complexity Constraint a | Training | Regular Testing | Independent Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PA | JI | MIoU | PA | JI | MIoU | PA | JI | MIoU | |||
| Build-up | Random b | No | 0.853 | 0.756 | 0.743 | 0.856 | 0.748 | 0.745 | 0.853 | 0.723 | 0.755 |
| Random | Yes | 0.878 | 0.794 | 0.785 | 0.872 | 0.772 | 0.782 | 0.872 | 0.744 | 0.778 | |
| Complexity c | No | 0.884 | 0.796 | 0.791 | 0.877 | 0.778 | 0.789 | 0.885 | 0.750 | 0.784 | |
| Complexity | Yes | 0.890 | 0.801 | 0.801 | 0.885 | 0.788 | 0.799 | 0.890 | 0.754 | 0.785 | |
| Farmland | Random | No | 0.862 | 0.788 | 0.755 | 0.845 | 0.783 | 0.747 | 0.832 | 0.724 | 0.696 |
| Random | Yes | 0.868 | 0.797 | 0.764 | 0.854 | 0.794 | 0.758 | 0.835 | 0.731 | 0.702 | |
| Complexity | No | 0.936 | 0.896 | 0.880 | 0.863 | 0.874 | 0.854 | 0.864 | 0.769 | 0.757 | |
| Complexity | Yes | 0.945 | 0.911 | 0.897 | 0.864 | 0.887 | 0.868 | 0.869 | 0.777 | 0.765 | |
| Forest | Random | No | 0.992 | 0.984 | 0.976 | 0.904 | 0.821 | 0.823 | 0.871 | 0.635 | 0.731 |
| Random | Yes | 0.991 | 0.983 | 0.983 | 0.912 | 0.834 | 0.830 | 0.866 | 0.631 | 0.726 | |
| Complexity | No | 0.990 | 0.980 | 0.975 | 0.903 | 0.812 | 0.809 | 0.869 | 0.634 | 0.730 | |
| Complexity | Yes | 0.994 | 0.988 | 0.988 | 0.921 | 0.844 | 0.842 | 0.879 | 0.652 | 0.744 | |
| Meadow | Random | No | 0.990 | 0.984 | 0.979 | 0.966 | 0.977 | 0.969 | 0.918 | 0.829 | 0.842 |
| Random | Yes | 0.996 | 0.994 | 0.991 | 0.972 | 0.986 | 0.981 | 0.930 | 0.851 | 0.864 | |
| Complexity | No | 0.996 | 0.994 | 0.991 | 0.969 | 0.985 | 0.979 | 0.925 | 0.843 | 0.856 | |
| Complexity | Yes | 0.997 | 0.996 | 0.994 | 0.969 | 0.987 | 0.982 | 0.932 | 0.855 | 0.867 | |
| Waters | Random | No | 0.986 | 0.982 | 0.960 | 0.985 | 0.982 | 0.959 | 0.902 | 0.824 | 0.809 |
| Random | Yes | 0.989 | 0.985 | 0.967 | 0.987 | 0.985 | 0.967 | 0.935 | 0.877 | 0.872 | |
| Complexity | No | 0.997 | 0.996 | 0.991 | 0.991 | 0.995 | 0.988 | 0.938 | 0.884 | 0.880 | |
| Complexity | Yes | 0.997 | 0.996 | 0.992 | 0.994 | 0.995 | 0.990 | 0.950 | 0.904 | 0.902 | |
| Land Cover | Landuse Type | Training | Regular Testing | Independent Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PA | JI | MIoU | PA | JI | MIoU | PA | JI | MIoU | ||
| Build-up | Crossformer | 0.871 | 0.775 | 0.775 | 0.870 | 0.765 | 0.773 | 0.863 | 0.722 | 0.742 |
| DeepLab V3+ | 0.870 | 0.765 | 0.765 | 0.870 | 0.748 | 0.762 | 0.850 | 0.710 | 0.724 | |
| Global CNN | 0.857 | 0.772 | 0.772 | 0.890 | 0.781 | 0.776 | 0.861 | 0.724 | 0.737 | |
| FCN-ResNet | 0.928 | 0.841 | 0.847 | 0.890 | 0.759 | 0.821 | 0.865 | 0.731 | 0.750 | |
| Complexity analysis a | 0.890 | 0.801 | 0.801 | 0.885 | 0.788 | 0.799 | 0.890 | 0.754 | 0.785 | |
| Farmland | Crossformer | 0.808 | 0.669 | 0.670 | 0.807 | 0.667 | 0.669 | 0.802 | 0.686 | 0.653 |
| DeepLab V3+ | 0.857 | 0.946 | 0.746 | 0.821 | 0.688 | 0.734 | 0.827 | 0.694 | 0.677 | |
| Global CNN | 0.828 | 0.721 | 0.721 | 0.826 | 0.683 | 0.714 | 0.827 | 0.722 | 0.694 | |
| FCN-ResNet | 0.949 | 0.903 | 0.903 | 0.826 | 0.689 | 0.857 | 0.825 | 0.720 | 0.692 | |
| Complexity analysis | 0.945 | 0.911 | 0.897 | 0.864 | 0.887 | 0.868 | 0.869 | 0.777 | 0.765 | |
| Forest | Crossformer | 0.870 | 0.772 | 0.773 | 0.880 | 0.773 | 0.773 | 0.796 | 0.497 | 0.593 |
| DeepLab V3+ | 0.961 | 0.926 | 0.926 | 0.898 | 0.816 | 0.903 | 0.848 | 0.586 | 0.689 | |
| Global CNN | 0.815 | 0.670 | 0.670 | 0.854 | 0.745 | 0.685 | 0.839 | 0.570 | 0.673 | |
| FCN-ResNet | 0.973 | 0.948 | 0.948 | 0.887 | 0.795 | 0.915 | 0.823 | 0.555 | 0.656 | |
| Complexity analysis | 0.994 | 0.988 | 0.988 | 0.921 | 0.844 | 0.842 | 0.879 | 0.652 | 0.744 | |
| Meadow | Crossformer | 0.881 | 0.768 | 0.768 | 0.877 | 0.762 | 0.767 | 0.820 | 0.665 | 0.666 |
| DeepLab V3+ | 0.984 | 0.965 | 0.966 | 0.952 | 0.895 | 0.951 | 0.909 | 0.811 | 0.825 | |
| Global CNN | 0.869 | 0.765 | 0.765 | 0.911 | 0.804 | 0.773 | 0.855 | 0.723 | 0.729 | |
| FCN-ResNet | 0.982 | 0.960 | 0.961 | 0.942 | 0.877 | 0.943 | 0.906 | 0.805 | 0.820 | |
| Complexity analysis | 0.997 | 0.996 | 0.994 | 0.969 | 0.987 | 0.982 | 0.932 | 0.855 | 0.867 | |
| Waters | Crossformer | 0.969 | 0.908 | 0.909 | 0.974 | 0.917 | 0.910 | 0.842 | 0.740 | 0.702 |
| DeepLab V3+ | 0.994 | 0.980 | 0.981 | 0.987 | 0.957 | 0.976 | 0.940 | 0.887 | 0.883 | |
| Global CNN | 0.887 | 0.733 | 0.734 | 0.969 | 0.902 | 0.763 | 0.914 | 0.824 | 0.811 | |
| FCN-ResNet | 0.994 | 0.983 | 0.983 | 0.979 | 0.938 | 0.973 | 0.970 | 0.940 | 0.940 | |
| Complexity analysis | 0.997 | 0.996 | 0.992 | 0.994 | 0.995 | 0.990 | 0.950 | 0.904 | 0.902 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhu, Z.; Wang, C. Multiscale Entropy-Based Surface Complexity Analysis for Land Cover Image Semantic Segmentation. Remote Sens. 2023, 15, 2192. https://doi.org/10.3390/rs15082192
Li L, Zhu Z, Wang C. Multiscale Entropy-Based Surface Complexity Analysis for Land Cover Image Semantic Segmentation. Remote Sensing. 2023; 15(8):2192. https://doi.org/10.3390/rs15082192
Chicago/Turabian StyleLi, Lianfa, Zhiping Zhu, and Chengyi Wang. 2023. "Multiscale Entropy-Based Surface Complexity Analysis for Land Cover Image Semantic Segmentation" Remote Sensing 15, no. 8: 2192. https://doi.org/10.3390/rs15082192
APA StyleLi, L., Zhu, Z., & Wang, C. (2023). Multiscale Entropy-Based Surface Complexity Analysis for Land Cover Image Semantic Segmentation. Remote Sensing, 15(8), 2192. https://doi.org/10.3390/rs15082192








