Multi-Dimensional Spread Target Detection with Across Range-Doppler Unit Phenomenon Based on Generalized Radon-Fourier Transform
Abstract
1. Introduction
- The EI-GRFT method is proposed and its theoretical principles and detection performance are analyzed. The relationship between detection threshold and false alarm probability is examined, and the analysis process of detection probability is presented.
- The DT-HGRFT method is proposed, and its theoretical principles are analyzed for double-threshold detection under sparse SC distribution, hybrid integration under echo decoherence, and sliding window detection under multi-dimensional spread.
- Based on different scenarios, we propose corresponding simplified methods based on DT-HGRFT. Specifically, we propose Double-Threshold based Generalized Radon-Fourier Transform (DT-GRFT) when each unit in the detection window contains SCs, and Energy Integration based Hybrid Generalized Radon-Fourier Transform (EI-HGRFT) when the echo remains completely coherent within the integration time.
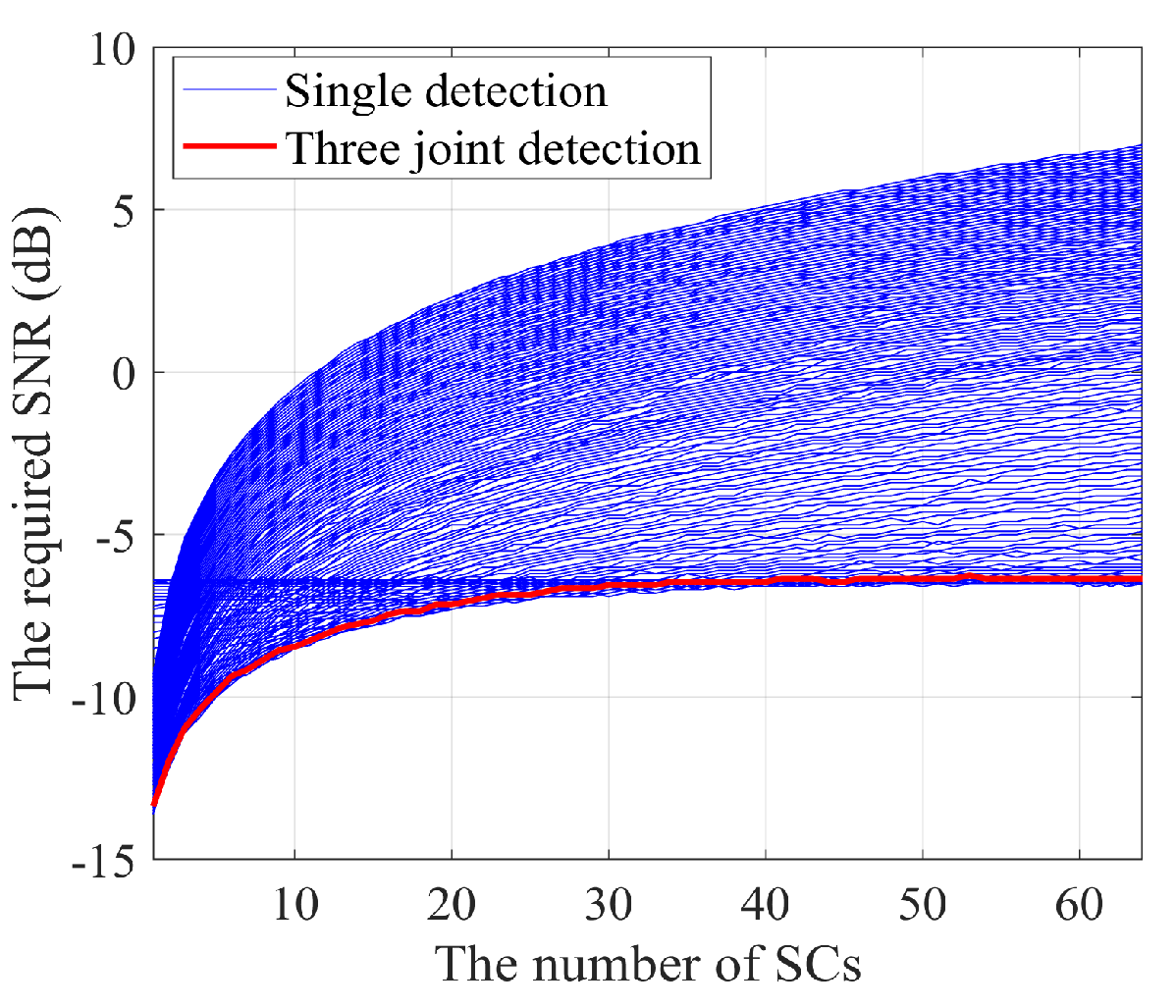
- The proposed multiple DT-HGRFT joint detection method can effectively address the challenge of setting an optimal first threshold when dealing with targets with a large distribution of SCs or when there is no prior information about the number of SCs.
- Extensive simulation and real data experiments are carried out to analyze the performance of the proposed methods and verify the effectiveness of the proposed methods.
2. Signal Model & Theoretical Analyses
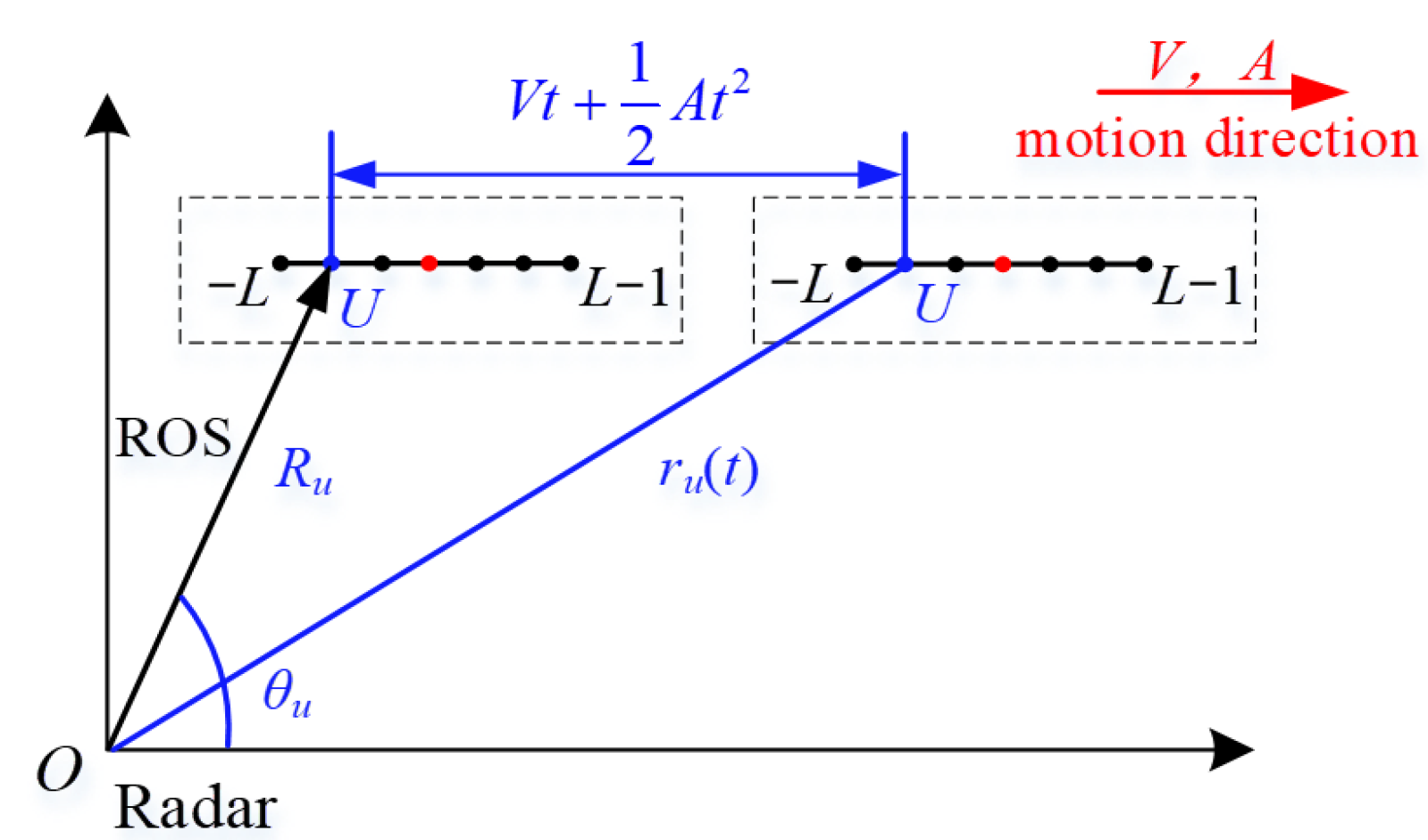
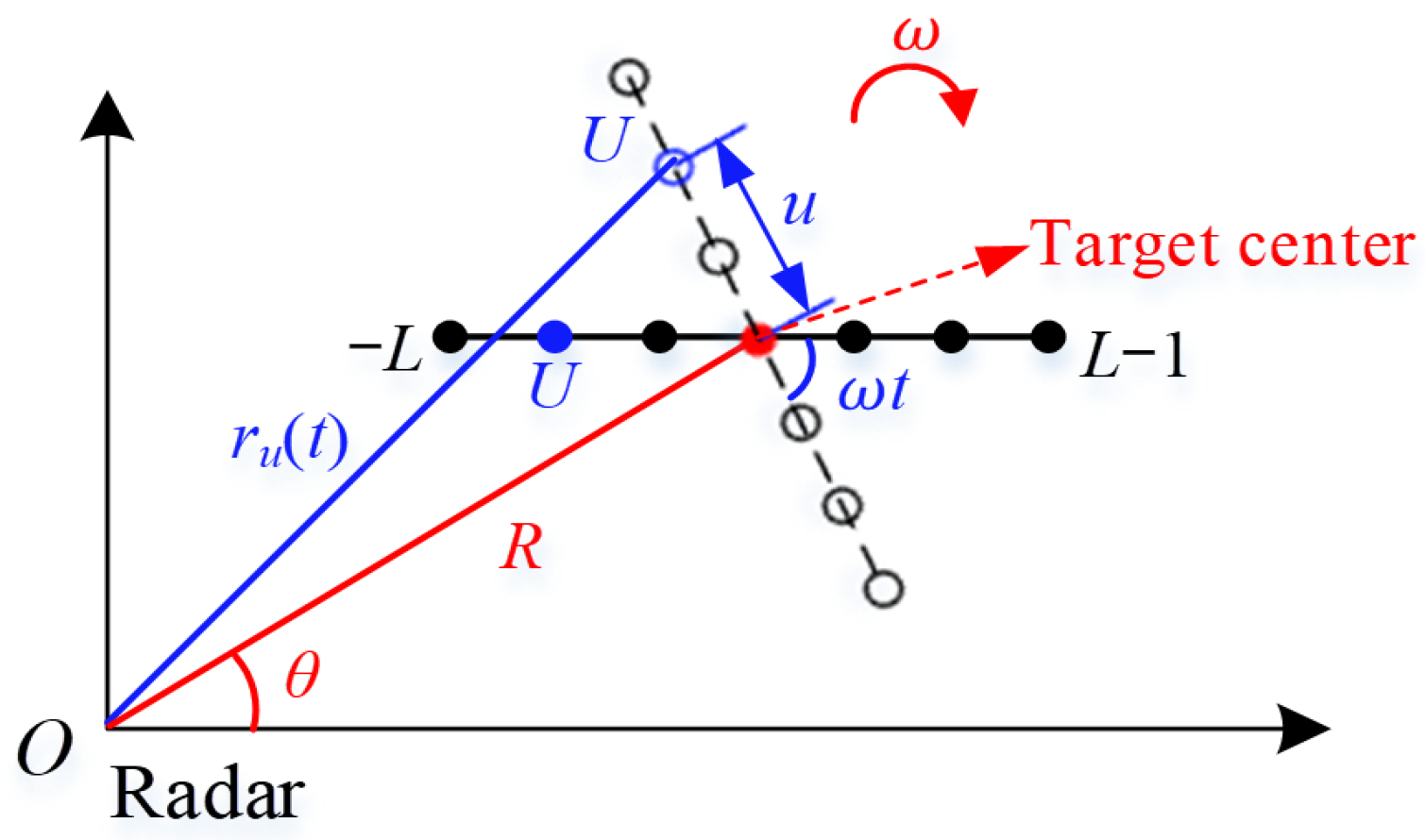
2.1. Echo Model
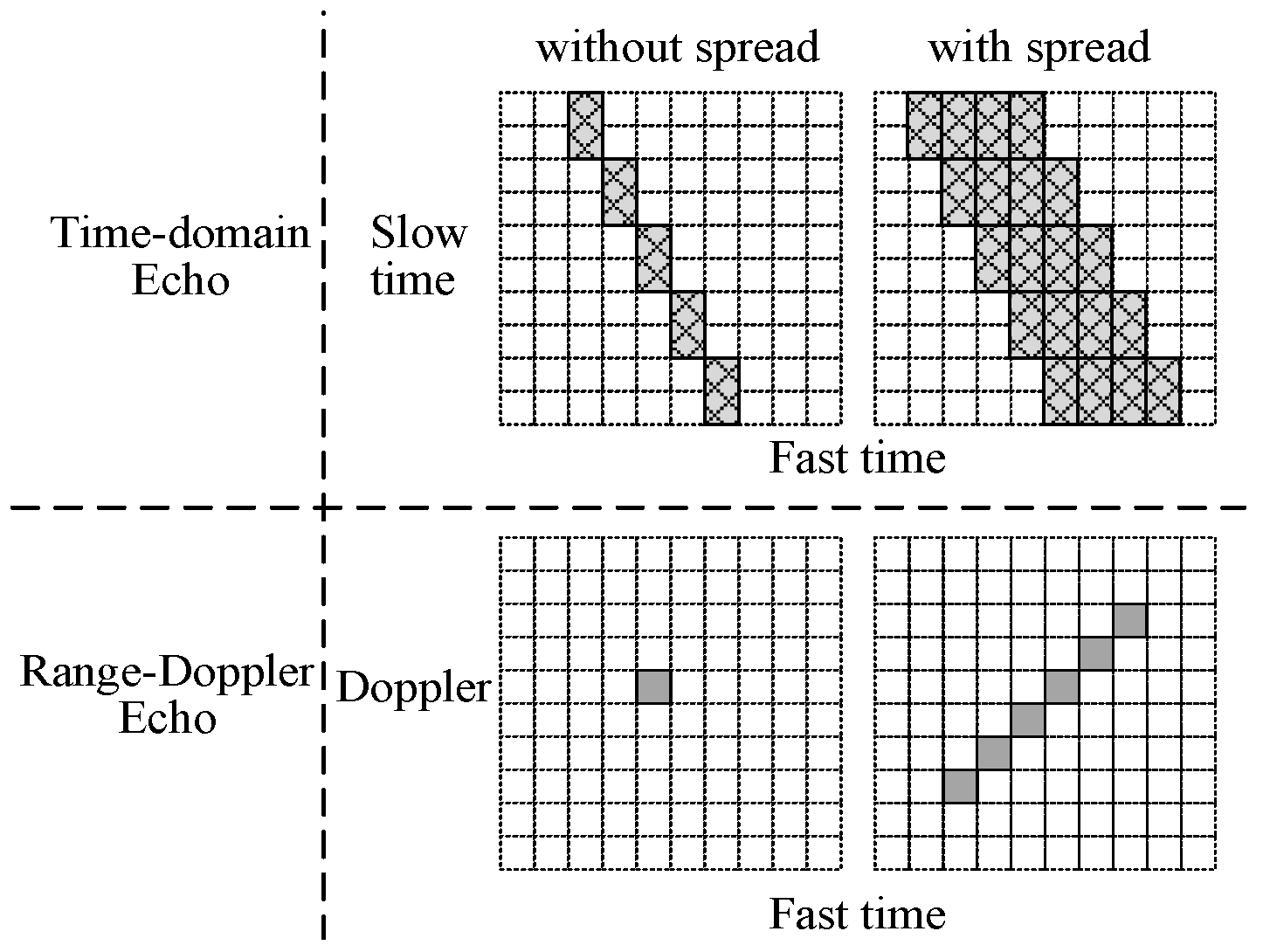
2.2. The Properties of Multi-Dimensional Spread Target
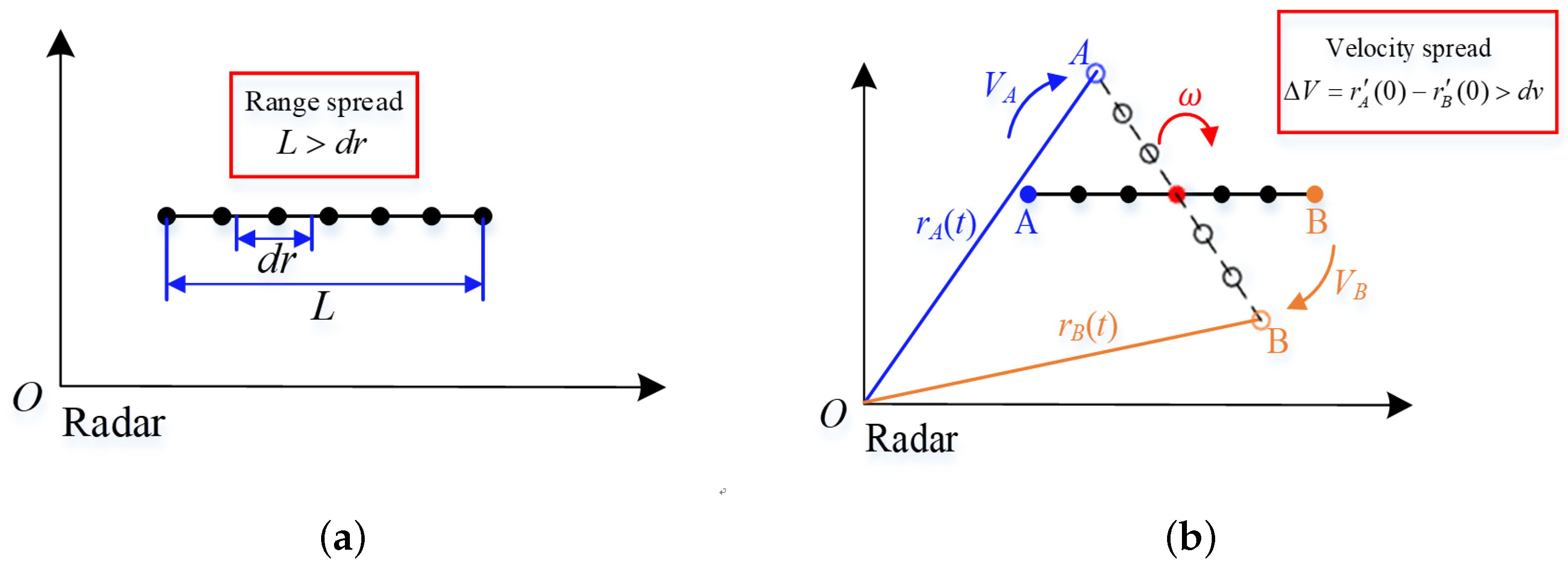
2.2.1. Analyses of the Property of Range Spread Target
2.2.2. Analyses of the Property of Multiple Motion Parameters
2.3. The Length of Coherent Times
3. The Proposed Energy-Integrated GRFT Method
3.1. Echo Model
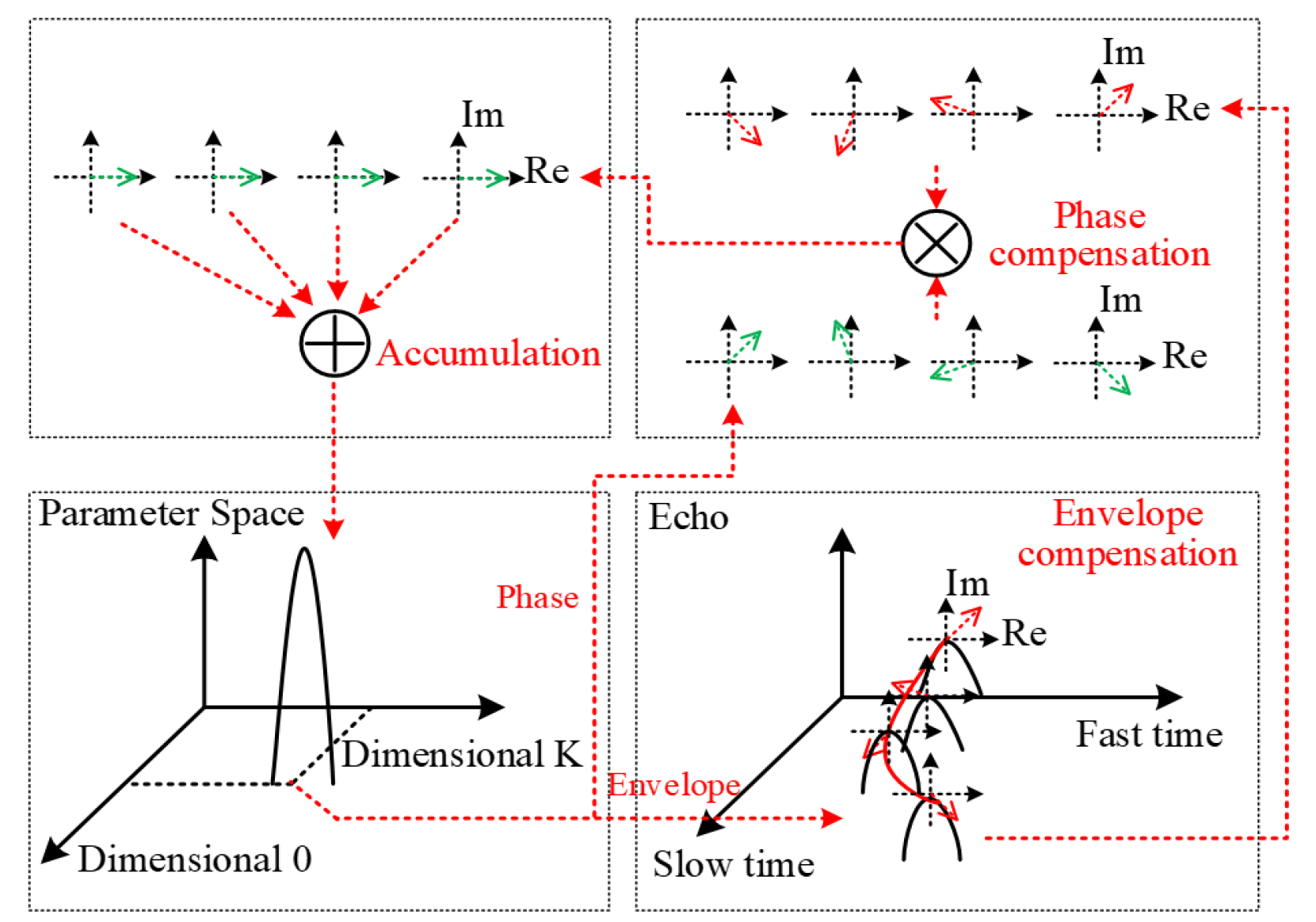
3.2. The Principle of Energy-Integrated GRFT
4. The Proposed Double-Threshold Hybrid GRFT Method
4.1. Brief Introduction for HGRFT
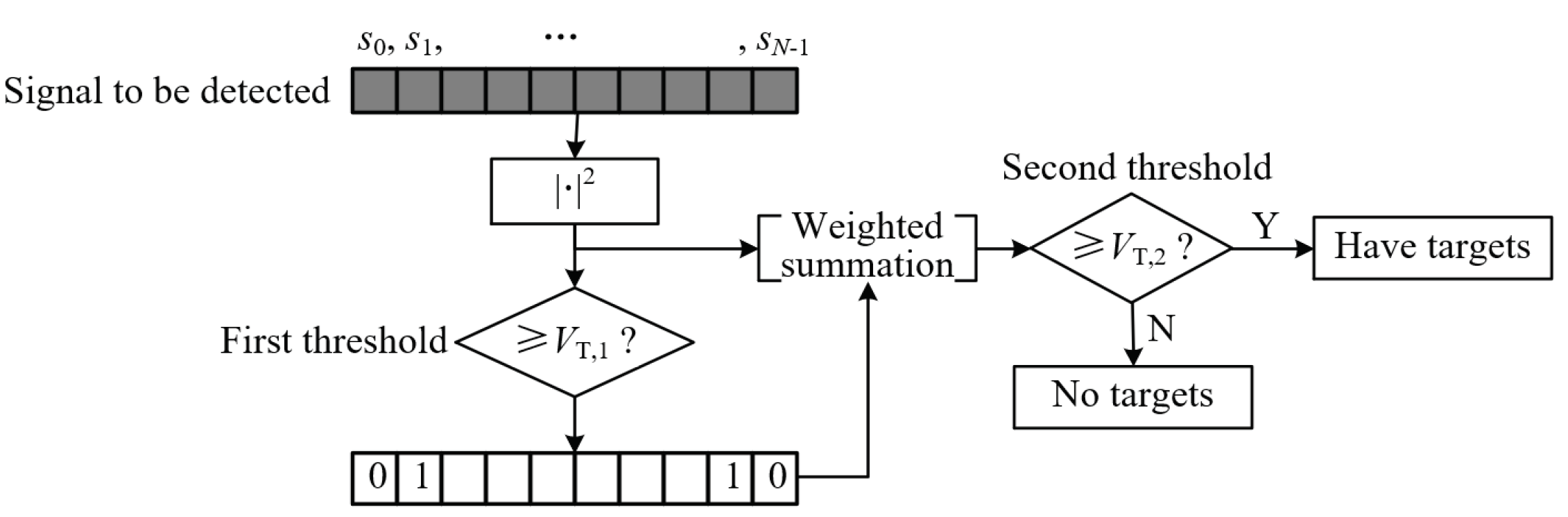
4.2. DT-HGRFT within Sparse Distribution of Scattering Centers
4.2.1. The Number of Scattering Centers Is Known
4.2.2. The Number of Scattering Center Is Unknown
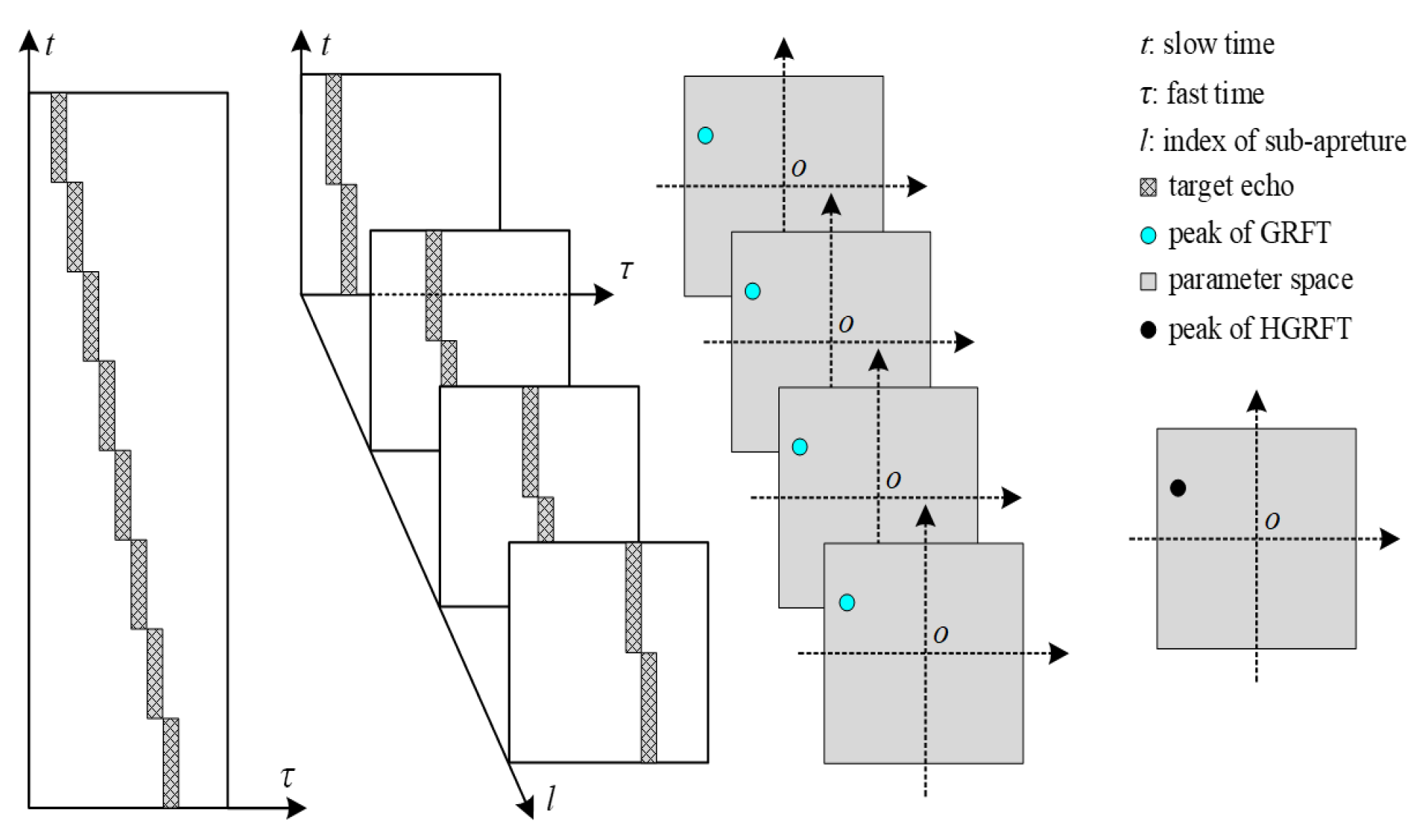
4.3. Hybrid Intergation under Echo Decorrelation
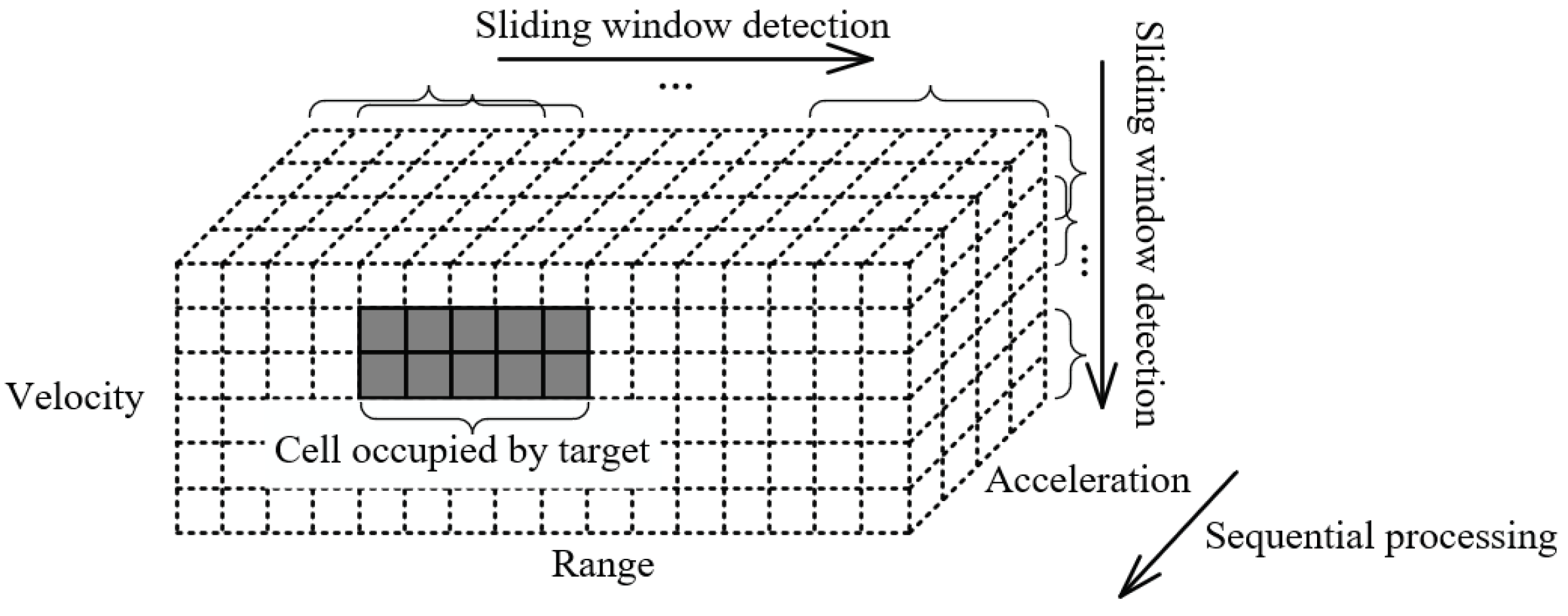
4.4. Sliding Window Detection under Multi-Dimensional Spread Conditions
4.5. DT-HGRFT & Its Relationship with GRFT and EI-GRFT
4.6. Joint Detection of Multiple DT-HGRFT
5. Theoretical Analyses of the EI-GRFT and DT-HGRFT
5.1. The Relationship between Threshold and False Alarm Probability of EI-GRFT
5.2. The Detection Probability Analyses of EI-GRFT
5.3. Analyses of the Second Thresholds of DT-GRFT and DT-HGRFT
5.3.1. The Second Threshold Setting of DT-HGRFT
5.3.2. The Second Threshold Setting of DT-GRFT
6. Numerical Simulations and Experimental Results
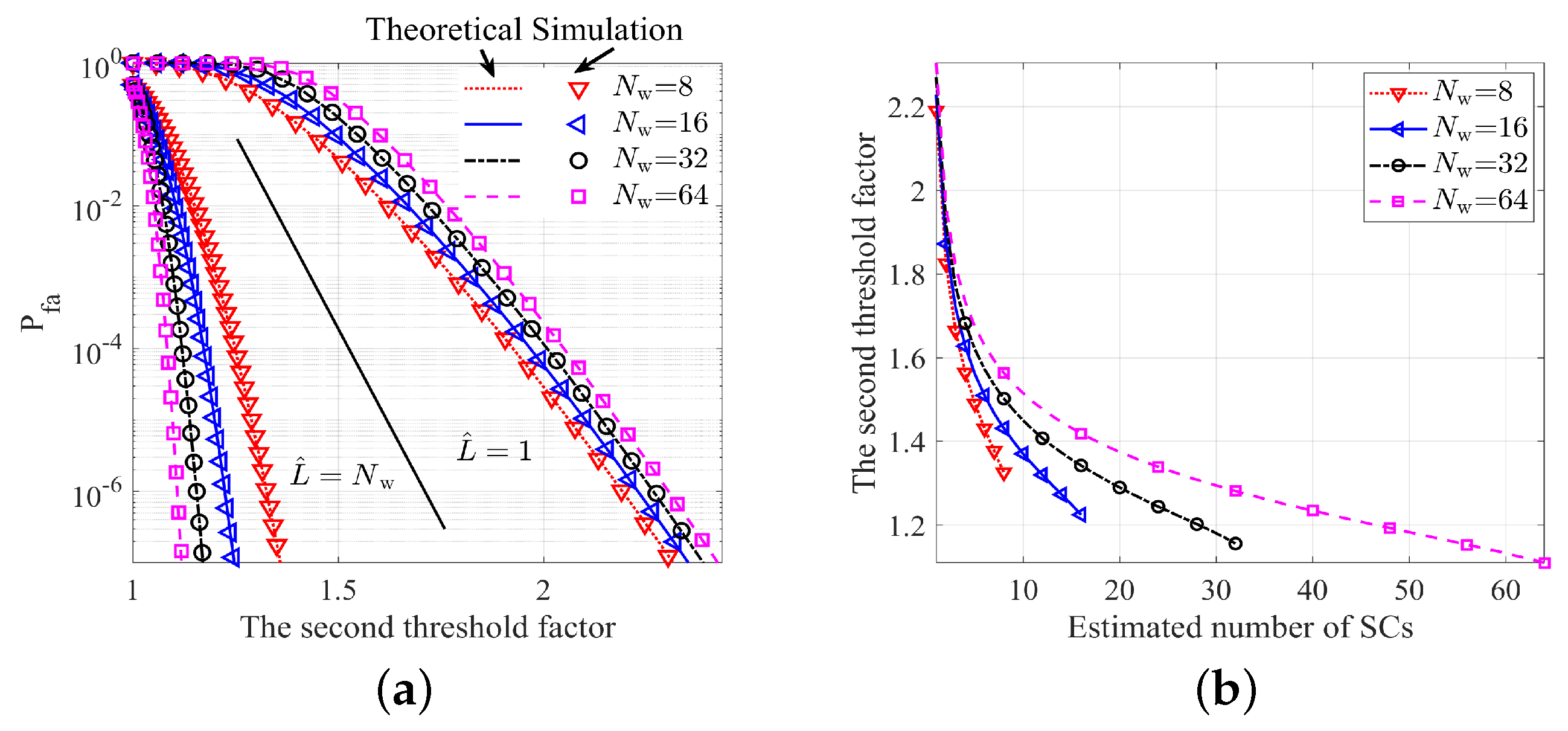
6.1. Simulation of the Influence of the First and Second Thresholds
The Influence of the Second Threshold on the False Alarm Probability
6.2. Simulation of the Influence of the First Threshold on Detection Performance
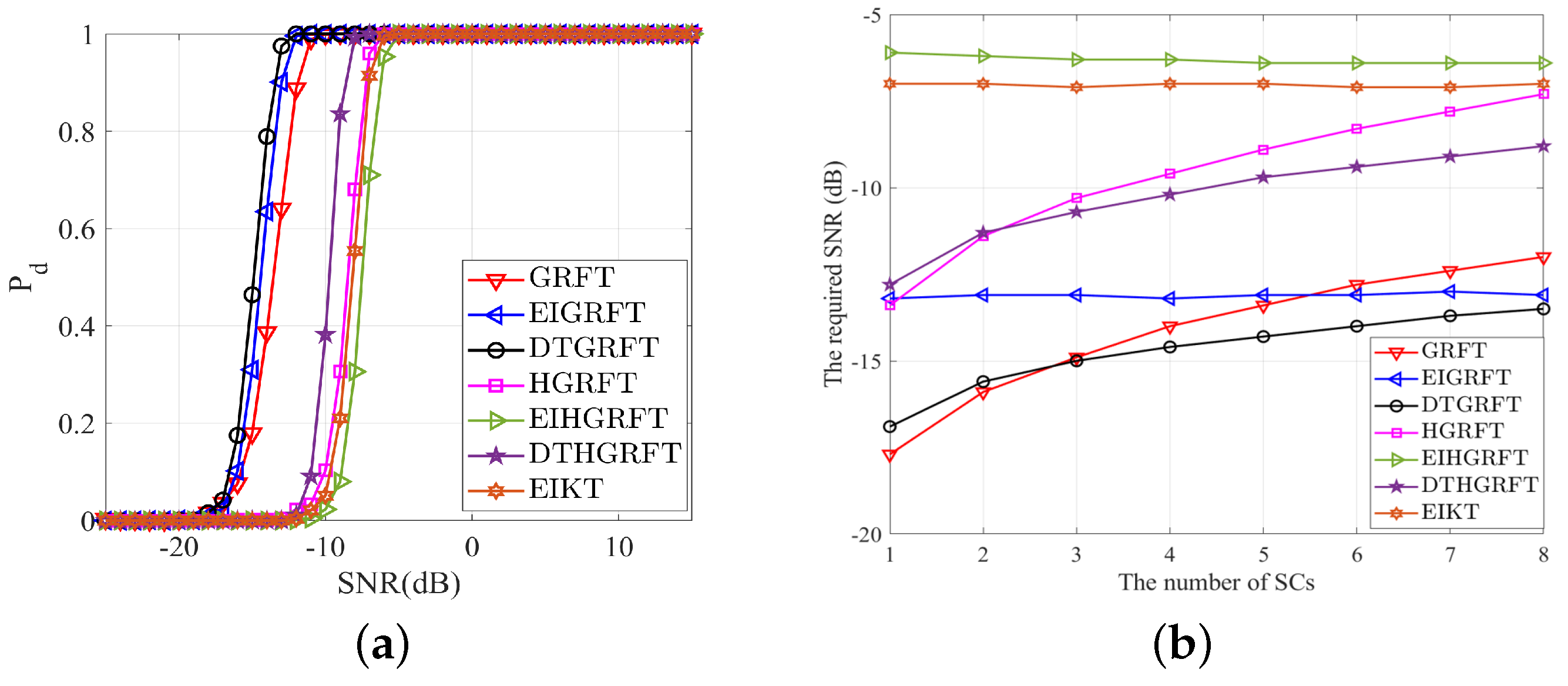
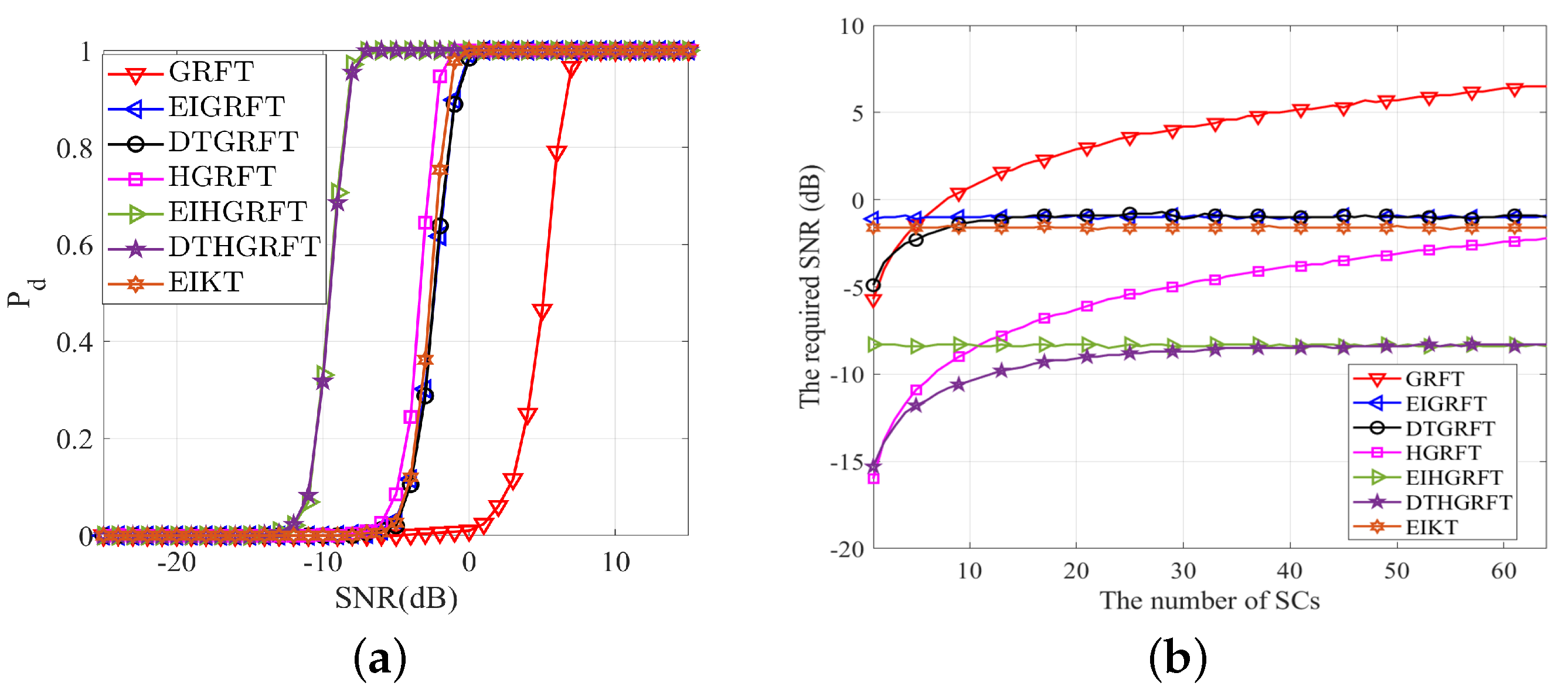
6.3. Simulation of Detection Performance
- When the number of SCs is very small, GRFT still has the best detection performance. As the number of SCs increases, the SNR requirements of GRFT continue to increase and the growth rate is faster than that of DT-GRFT, so the detection performance of DT-GRFT quickly outperforms GRFT. Even when the number of SCs is 8, only some units in the two-dimensional detection window contain SCs. At this time, the detection performance of EI-GRFT is inferior to that of DT-GRFT. Since the first threshold of DT-GRFT can more accurately extract the units with SCs, it will basically not accumulate additional noise.
- Due to the slow rotation of the target, the incident angle of the radar observation target changes very little, and the target echo is fully coherent during the entire integration time. Therefore, the detection performance of GRFT, EI-GRFT and DT-GRFT using full coherent integration between pulses is better than that of HGRFT, EI-HGRFT and DT-HGRFT using mixed integration.
- Although the target has a large acceleration, the projection in the slant-range direction is small, so that the defocusing phenomenon of the echo in the range-Doppler domain is not serious. Hence, the detection performance of EI-KT is slightly better than that of EI-HGRFT with too many non-coherent integration times between sub-apertures.
- The faster rotation of the target results in shorter echo dereferencing time, ence the detection performance of the three methods using hybrid integration between pulses is correspondingly better than that of the three methods using full coherent integration.
- The echo decoherence phenomenon causes the performance of EI-GRFT to be slightly worse than that of EI-KT which cannot compensate acceleration.
6.4. Real Data Experiments
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbols and Nomenclatures | Meaning |
|---|---|
| The carrier frequency | |
| M | The num of pulses |
| L | The num of scattering centers |
| The angular velocity | |
| The range of the l-th SC at the m-th pulse | |
| slow time | |
| fast time | |
| The power of complex Gaussian white noise | |
| The motion parameter vector contains all dimensions | |
| The echo at m-th pules and n-th range resolution unit | |
| G | Spectrum of 1-D range image of the range spread target |
| The false alarm probability | |
| ARDU | Across Range-Doppler Unit |
| CDF | Cumulative Distribution Function |
| DFT | Discrete Fourier Transform |
| DT-GRFT | Double Threshold based Generalized Radon-Fourier Transform |
| DT-HGRFT | Double Threshold based Hybrid Generalized Radon-Fourier Transform |
| EI-GRFT | Energy Integration based Generalized Radon-Fourier Transform |
| EI-HGRFT | Energy Integration based Hybrid Generalized Radon-Fourier Transform |
| GLRT | Generalized Likelihood Ratio Test |
| GRFT | Generalized Radon-Fourier Transform |
| HGRFT | Hybrid Generalized Radon-Fourier Transform |
| HT | Hough Transform |
| KT | Keystone Transform |
| LFM | Linear Frequency Modulation |
| MLE | Maximum Likelihood Estimation |
| Probability Density Function | |
| PRT | Pulse Repetition Time |
| RCS | Radar Cross Section |
| SAR | Synthetic Aperture Radar |
| SNR | Signal to Noise Ratio |
References
- Qian, L.C. Research on Radar Target Detection Algorithm Based on Long Time Coherent Integration. Ph.D. Thesis, Air Force Early Warning Academy, Wuhan, China, 2013. [Google Scholar]
- Zhou, X. Research on Key Technologies of Radar Detection for High-Speed and High-Mobility Stealth Targets. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2018. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; MCGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection (II): Blind Speed Sidelobe Suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection (III): Optimality and Fast Implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.N.; Xia, X.G.; Farina, A. Focus-before-detection radar signal processing: Part i—Challenges and methods. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 48–59. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.N.; Xia, X.G.; Long, T.; Mao, E.K. Focus-before-detection radar signal processing: Part ii–recent developments. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 34–49. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.N.; Xia, X.G.; Long, T.; Mao, E. Focus-before-detection Methods for Radar Detection of Near Space High-maneuvering Aircrafts. J. Radar 2017, 6, 230–238. [Google Scholar]
- Jia, X.; Xia, X.G.; Peng, S.B.; Ji, Y.; Peng, Y.N.; Qian, L.C. Radar Maneuvering Target Motion Estimation Based on Generalized Radon-Fourier Transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar] [CrossRef]
- Swerling, P. Probability of Detection for Fluctuating Targets. Inf. Theory IRE Trans. 1960, IT-6, 269–308. [Google Scholar] [CrossRef]
- Scholtz, R.A.; Kappl, J.J.; Nahi, N.E. The Detection of Moderately-Fluctuating Rayleigh Targets. IEEE Trans. Aerosp. Electron. Syst. 1976, AES-12, 117–126. [Google Scholar] [CrossRef]
- Zhou, X.; Qian, L.C.; Ding, Z.; Xu, J.; Liu, W.; You, P.J.; Long, T. Radar Detection of Moderately Fluctuating Target Based on Optimal Hybrid Integration Detector. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2408–2425. [Google Scholar] [CrossRef]
- Zyl, J.J.V.; Carande, R.E.; Lou, Y.; Miller, T.; Wheeler, K.B. The NASA/JPL Three-frequency Polarimetric Airsar System. In Proceedings of the IGARSS ’92 International Geoscience and Remote Sensing Symposium, Houston, TX, USA, 26–29 May 1992; Volume 1, pp. 649–651. [Google Scholar]
- Horn, R. The DLR airborne SAR project E-SAR. In Proceedings of the IGARSS ’96—1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; Volume 3, pp. 1624–1628. [Google Scholar]
- Born, G.H.; Dunne, J.A.; Lame, D.B. Seasat Mission Overview. Science 1979, 204, 1405–1406. [Google Scholar] [CrossRef]
- Attema, E.; Duchossois, G.; Kohlhammer, G. ERS-1/2 SAR land applications: Overview and main results. In Proceedings of the IGARSS ’98—Sensing and Managing the Environment, 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings, (Cat. No.98CH36174), Seattle, WA, USA, 6–10 July 1998; Volume 4, pp. 1796–1798. [Google Scholar]
- Desnos, Y.L.; Buck, C.; Guijarro, J.; Levrini, G.; Suchail, J.L.; Torres, R.; Laur, H.; Closa, J.; Rosich, B. The ENVISAT advanced synthetic aperture radar system. In Proceedings of the IGARSS 2000, IEEE 2000 International Geoscience and Remote Sensing Symposium, Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Proceedings (Cat. No.00CH37120), Honolulu, HI, USA, 24–28 July 2000; Volume 3, pp. 1171–1173. [Google Scholar]
- Rosenqvist, A.; Shimada, M.; Chapman, B.D.; McDonald, K.; Grandi, G.D.; Jonsson, H.; Williams, C.L.; Rauste, Y.; Nilsson, M.; Sango, D.; et al. An overview of the JERS-1 SAR Global Boreal Forest Mapping (GBFM) project. In Proceedings of the IGARSS 2004, 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 2, pp. 1033–1036. [Google Scholar]
- Mahmood, A. RADARSAT-1 Background Mission for a global SAR coverage. In Proceedings of the IGARSS’97. 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings, Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; Volume 3, pp. 1217–1219. [Google Scholar]
- Li, C.; Wang, W.; Wang, P.; Chen, J.; Xu, H.; Yang, W.; Yu, Z.; Sun, B.; Li, J. Status and development trend of spaceborne SAR technology. J. Electron. Inf. Technol. 2016, 38, 229–240. [Google Scholar]
- Avent, R.K.; Shelton, J.D.; Brown, P. The ALCOR C-band imaging radar. IEEE Antennas Propag. Mag. 1996, 38, 16–27. [Google Scholar] [CrossRef]
- Hall, T.D.; Duff, G.; Maciel, L.J. The Space Mission at Kwajalein. Linc. Lab. J. 2012, 19. [Google Scholar]
- Czerwinski, M.G.; Usoff, J.M. Development of the Haystack Ultrawideband Satellite Imaging Radar. Linc. Lab. J. 2014, 21, 28–44. [Google Scholar]
- Stambaugh, J.; Lee, R.; Cantrell, W.H. The 4 GHz Bandwidth Millimeter-Wave Radar. Linc. Lab. J. 2012, 19, 64–76. [Google Scholar]
- Stone, M.L.; Banner, G.P. Radars for the Detection and Tracking of Ballistic Missiles, Satellites, and Planets. Linc. Lab. J. 2000, 12, 217–244. [Google Scholar]
- Merz, K.; Banka, D.; Jehn, R.; Landgraf, M.; Rosebrock, J. Observations of interplanetary meteoroids with TIRA. Planet. Space Sci. 2005, 53, 1121–1134. [Google Scholar] [CrossRef]
- Slade, M.A.; Benner, L.A.M.; Silva, A. Goldstone Solar System Radar Observatory: Earth-Based Planetary Mission Support and Unique Science Results. Proc. IEEE 2011, 99, 757–769. [Google Scholar] [CrossRef]
- Harmon, J.K.; Nolan, M.C.; Husmann, D.I.; Campbell, B.A. Arecibo radar imagery of Mars: The major volcanic provinces. Icarus 2012, 220, 990–1030. [Google Scholar] [CrossRef]
- Harmon, J.K.; Nolan, M.C. Arecibo radar imagery of Mars: II. Chryse–Xanthe, polar caps, and other regions. Icarus 2017, 281, 162–199. [Google Scholar] [CrossRef]
- Harmon, J.K.; Slade, M.A.; Rice, M.S. Radar imagery of Mercury’s putative polar ice: 1999–2005 Arecibo results. Icarus 2011, 211, 37–50. [Google Scholar] [CrossRef]
- Slade, M.A.; Zohar, S.; Jurgens, R.F. Venus—Improved spin vector from Goldstone radar observations. Astron. J. 1990, 100, 1369–1374. [Google Scholar] [CrossRef]
- Nicholson, P.D.; French, R.G.; Campbell, D.B.; Margot, J.L.; Nolan, M.C.; Black, G.J.; Salo, H. Radar imaging of Saturn’s rings. Icarus 2005, 177, 32–62. [Google Scholar] [CrossRef]
- Thompson, T.W.; Campbell, B.A.; Bussey, D.B.J. 50 Years of Arecibo Lunar radar mapping. Ursi Radio Sci. Bull. 2017, 89, 23–35. [Google Scholar]
- Lawrence, K.J.; Benner, L.A.M.; Brozović, M.; Ostro, S.J.; Jao, J.S.; Giorgini, J.D.; Slade, M.A.; Jurgens, R.F.; Nolan, M.C.; Howell, E.S.; et al. Arecibo and Goldstone radar images of near-Earth Asteroid (469896) 2005 WC1. Icarus 2018, 300, 12–20. [Google Scholar] [CrossRef]
- Harmon, J.K.; Nolan, M.C.; Giorgini, J.D.; Howell, E.S. Radar observations of 8P/Tuttle: A contact-binary comet. Icarus 2010, 207, 499–502. [Google Scholar] [CrossRef]
- van der Spek, G.A. Detection of a Distributed Target. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 922–931. [Google Scholar] [CrossRef]
- Hughes, P.K. A High-Resolution Radar Detection Strategy. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 663–667. [Google Scholar] [CrossRef]
- Gerlach, K.; Steiner, M.J.; Lin, F.C. Detection of a spatially distributed target in white noise. IEEE Signal Process. Lett. 1997, 4, 198–200. [Google Scholar] [CrossRef]
- Meng, X.; Qu, D.; He, Y. CFAR detection of range-extended targets in Gaussian background. Syst. Eng. Electron. Technol. 2005, 27, 1012–1015. [Google Scholar]
- He, Y.; feng Gu, X.; Jian, T.; Zhang, B.; Li, B. A M out of n detector based on scattering density. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–4. [Google Scholar]
- Long, T.; Zheng, L.; Li, Y.; Yang, X. Improved Double Threshold Detector for Spatially Distributed Target. IEICE Trans. Commun. 2012, 95-B, 1475–1478. [Google Scholar] [CrossRef]
- Gu, X.; Jian, T.; He, Y. Dual-threshold CFAR detector for range-extended targets and its performance analysis. J. Electron. Inf. 2012, 34, 6. [Google Scholar]
- Wen, X.; Liu, H.; Wen, X.; Liu, H. Normal distribution test algorithm for range-extended target detection. J. Xidian Univ. 2013, 40, 31–35. [Google Scholar]
- Dai, F.; Liu, H.; Wu, S. A Range Extended Target Detector Based on Sequential Statistics. J. Electron. Inf. 2009. [Google Scholar]
- Mohammadi, M.; Moqiseh, A.; Gheidi, H.; Nayebi, M.M. Noncoherent integration of UWB RADAR signals using the Hough transform. In Proceedings of the 2008 European Radar Conference, Amsterdam, The Netherlands, 30–31 October 2008; pp. 9–12. [Google Scholar]
- sheng Zhang, S.; Zeng, T.; Long, T.; peng Yuan, H. Dim target detection based on keystone transform. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 889–894. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X. Detection of range spread target with coherent integration. In Proceedings of the IET International Radar Conference, Xi’an, China, 14–16 April 2013; pp. 1–4. [Google Scholar]
- Zhu, H.; Chen, Y.; Wang, N. A novel method of wideband radar signal detection. In Proceedings of the 2014 7th International Congress on Image and Signal Processing, Dalian, China, 14–16 October 2014; pp. 847–851. [Google Scholar]
- wen Xu, S.; Shui, P.; Yan, X.Y. CFAR detection of range-spread target in white Gaussian noise using waveform entropy. Electron. Lett. 2010, 46, 647–649. [Google Scholar]
- Liu, S.; Ding, Z.; Zhou, X.; You, P.J. A Novel Method for Abrupt Motion Change Radar Target Detection Based on Generalized Radon-Fourier Transform. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–5. [Google Scholar]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.; Shi, C.; Wang, X. Adaptive estimation of strong scattering points in range-extended target detection. J. Nav. Acad. Aeronaut. Eng. 2014, 29, 440–444. [Google Scholar]
- Guo, P.; Liu, Z.; Luo, D.; Li, J. Range extended target detection method based on online estimation of strong scattering points. J. Electron. Inf. 2020, 42, 910–916. [Google Scholar]
- He, Y.; Guan, J.; Meng, X. Radar Target Detection and Constant False Alarm Processing; Tsinghua University Press: Beijing, China, 2011. [Google Scholar]




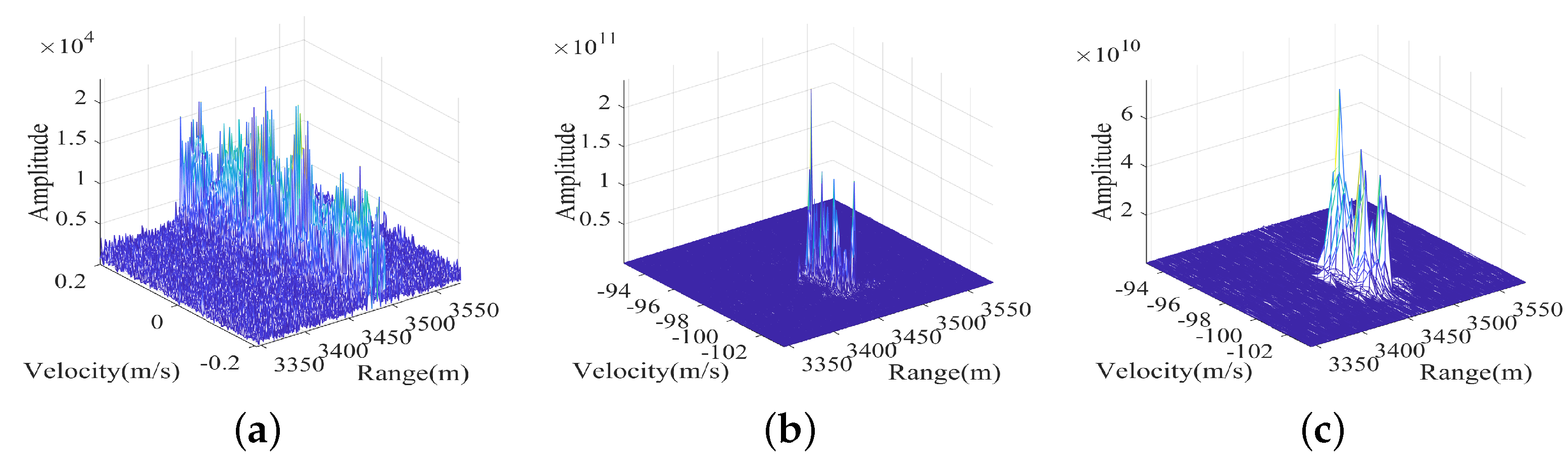

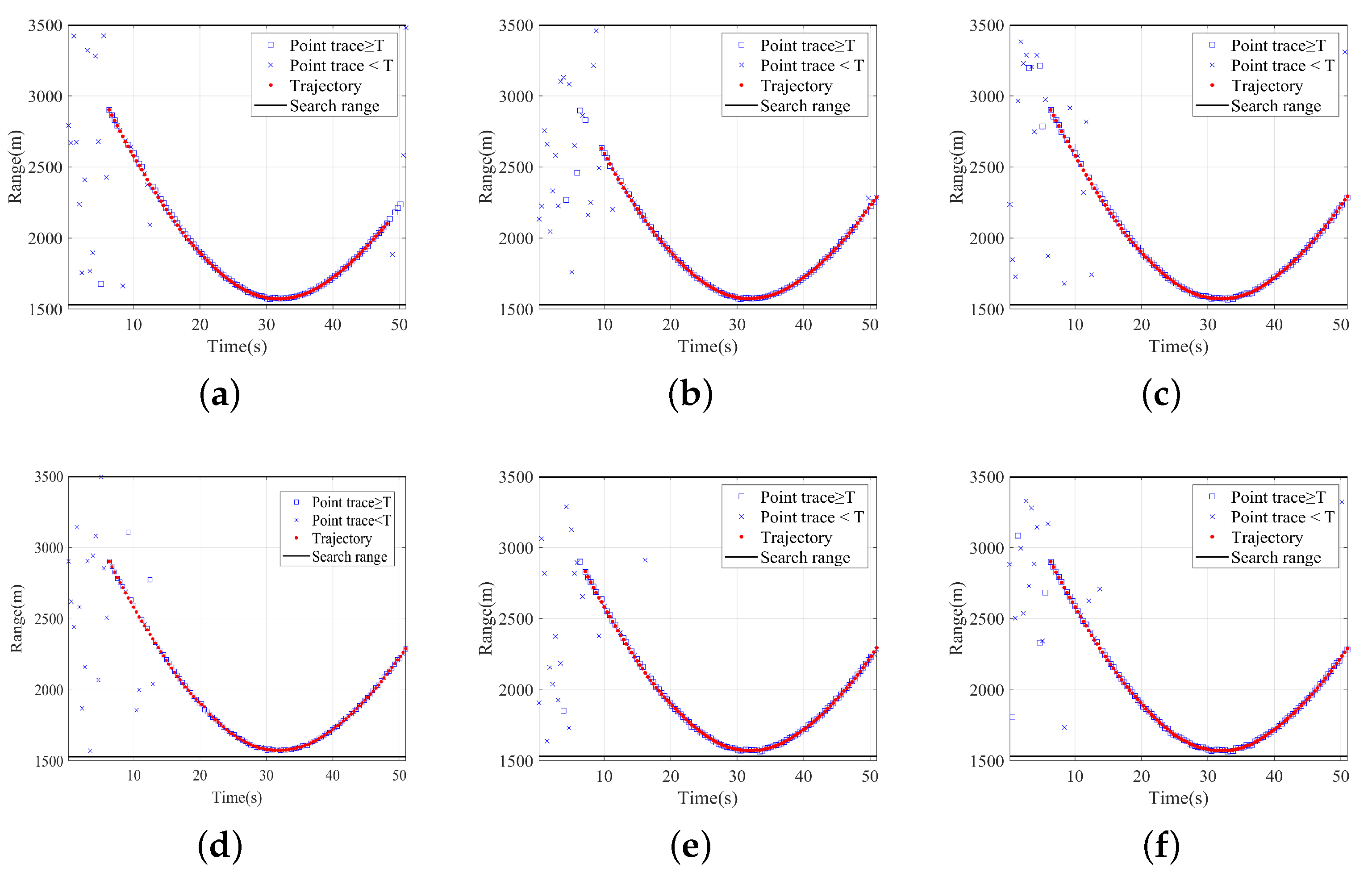
| Parameters | Values | Units |
|---|---|---|
| Carrier frequency | 3 | GHz |
| Sampling frequency | 500 | MHz |
| Bandwidth | 500 | MHz |
| Pulse repetition time (PRT) | 1 | ms |
| Integration time | 1.28 | s |
| Targets | No. 1 | No. 2 |
|---|---|---|
| Situations | Multi-dimensional spread target | Echo decoherence & range spread target |
| Initial distance of target center | 600 km | 600 km |
| Initial velocity of target center | 250 m/s | 250 m/s |
| Initial acceleration of target center | 30 | 30 |
| Target size | 19.2 m | 19.2 m × 19.2 m |
| Target rotate speed | 0.94/s | 3.73/s |
| Angle between motion direction and radar beam | 82.82 | 0 |
| Number of sub-apertures | 32 | 32 |
| Detection window size of EI/DT-(H)GRFT | ||
| Detection window size of EI-KT | ||
| False alarm probability ( ) | ||
| Simulation times | 1000 | 1000 |
| Method | Steps |
|---|---|
| Step 1: Confirm the motion model and the order of motion model Step 2: Taking uniformly accelerated motion as an example, divide the grid of search distance R, velocity V, and acceleration A; Step 3: Calculate ,for each distance, speed, and acceleration, where denotes fast time, t denotes slow time, T denotes the accumulation time and denotes the signal after range compression. | |
| EI-GRFT | Step 1: Calculate GRFT and square the modulus of the result; Step 2: The result obtained in Step 1 is convolutionally processed with a multi-dimensional rectangular window. |
| HGRFT | Step 1: Confirm the number of sub-apertures and divide sub-apertures; Step 2: Perform GRFT within each sub-aperture (zero time set to the center of the entire echo); Step 3: Conduct noncoherent accumulation between sub-apertures. |
| EI-HGRFT | Step 1: Calculate HGRFT Step 2: The result obtained in Step 1 is convolutionally processed with a multi-dimensional rectangular window. |
| DT-GRFT | Step 1: Calculate GRFT and square the modulus of the result; Step2: For the result obtained in Step 1, the original value that exceeds the first threshold is retained, and the value that does not exceed the first threshold is set to 0; Step3: The result obtained in Step 2 is convolutionally processed with a multi-dimensional rectangular window. |
| DT-HGRFT | Step1: Calculate HGRFT; Step 2: For the result obtained in Step 1, the original value that exceeds the first threshold is retained, and the value that does not exceed the first threshold is set to 0; Step 3: The result obtained in Step 2 is convolutionally processed with a multi-dimensional rectangular window. |
| EI-KT | Step1: Perform Fourier transform along the fast time dimension to transform the echo into the fast time frequency domain; Step2: Perform scale operation on each fast time frequency unit along the slow time dimension; Step3: Perform inverse Fourier transform along the fast time dimension to transform the echo into a two-dimensional time domain; Step4: Perform Fourier transform along the slow time dimension and take the modulus square; Step5: The result obtained in Step 4 is convolved with a two-dimensional rectangular window. |
| Parameters | Values |
|---|---|
| Waveband | S |
| Synthetic bandwidth | 320 MHz |
| Synthetic pulse repetition time | 4.096 ms |
| Integration time | 0.4096 s |
| Number of sub-apertures | 4 |
| Detection window size of EI/DT-GRFT | |
| Detection window size of EI/DT-HGRFT | |
| Detection window size of EI-KT | |
| The first threshold factor of DT-GRFT | 0.5 |
| The first threshold factor of DT-HGRFT | 0.6 |
| The first threshold factor of two DT-GRFT joint detection | 0, 1 |
| The first threshold factor of two DT-HGRFT joint detection | 0, 1.2 |
| Methods | Maximum Detection Range | Multiple of Improved Detection Range (GRFT Results Are Benchmarks) | Improved SNR | Total Calculation Time |
|---|---|---|---|---|
| GRFT | 1858 m | - | - | 9915 s |
| HGRFT | 1859 m | 1.00 | 0.01 | 659 s |
| EI-KT | 2369 m | 1.28 | 4.22 | 601 s |
| EI-GRFT | 2902 m | 1.56 | 7.75 | 12,983 s |
| EI-HGRFT | 2901 m | 1.42 | 6.04 | 13,819 s |
| DT-GRFT | 2901 m | 1.56 | 7.74 | 865 s |
| DT-HGRFT | 2902 m | 1.56 | 7.75 | 887 s |
| Two DT-GRFT joint detection | 2832 m | 1.52 | 7.32 | 22,217 s |
| Two DT-HGRFT joint detection | 2901 m | 1.56 | 7.74 | 1057 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Wei, Y.; Ding, Z.; You, P.; Liu, S.; Zhang, T. Multi-Dimensional Spread Target Detection with Across Range-Doppler Unit Phenomenon Based on Generalized Radon-Fourier Transform. Remote Sens. 2023, 15, 2158. https://doi.org/10.3390/rs15082158
Wang G, Wei Y, Ding Z, You P, Liu S, Zhang T. Multi-Dimensional Spread Target Detection with Across Range-Doppler Unit Phenomenon Based on Generalized Radon-Fourier Transform. Remote Sensing. 2023; 15(8):2158. https://doi.org/10.3390/rs15082158
Chicago/Turabian StyleWang, Guanxing, Yangkai Wei, Zegang Ding, Pengjie You, Siyuan Liu, and Tianyi Zhang. 2023. "Multi-Dimensional Spread Target Detection with Across Range-Doppler Unit Phenomenon Based on Generalized Radon-Fourier Transform" Remote Sensing 15, no. 8: 2158. https://doi.org/10.3390/rs15082158
APA StyleWang, G., Wei, Y., Ding, Z., You, P., Liu, S., & Zhang, T. (2023). Multi-Dimensional Spread Target Detection with Across Range-Doppler Unit Phenomenon Based on Generalized Radon-Fourier Transform. Remote Sensing, 15(8), 2158. https://doi.org/10.3390/rs15082158





