Abstract
With the rapid development of Earth system science, a new understanding of the complete Earth system has highlighted the crucial importance of integrated observations, especially in research involving large-scale geoscience phenomena. As an active sensor with all-time and all-weather capabilities, synthetic aperture radar (SAR) has been widely used in recent decades for Earth observation. However, the existing spaceborne, airborne, and ground-based SAR systems have difficulty providing temporally consistent and spatially continuous Earth observation data on a global scale. As Earth’s only natural satellite, the Moon is a very promising Earth observation platform. By deploying a transmitter on the Moon and a receiver on the high-orbit satellite, a Moon-based/spaceborne bistatic synthetic aperture radar (MS-BiSAR) can be formed. In this paper, the MS-BiSAR geometric model of Earth observation was established using ephemeris and orbit propagators with reference system transformations, and three different MS-BiSAR configurations were used to calculate and analyze their geometric characteristics and Earth observation coverage. The results show that with the advantage of wide swaths, continuous observation capabilities, and large coverage, such an MS-BiSAR could significantly contribute to monitoring and understanding large-scale geoscience phenomena.
1. Introduction
With the rapid development of Earth system science in recent years, scientists urgently need long-term Earth-observing data on a global scale. As a microwave sensor with all-time and all-weather capabilities, synthetic aperture radar has become increasingly important in Earth observation, especially in the fields of global change research, resource exploration, environmental monitoring, and disaster assessment [1,2]. However, the current SAR systems based on low-Earth-orbit satellites, aircraft, and ground-based platforms are limited by observation geometry, making it difficult to meet the demand for data that enable global spatiotemporal scale consistency and spatial continuity for Earth system science research [3].
In recent decades, geosynchronous Earth orbit (GSO) SAR has been discussed as a potential solution to the limited observation width of LEO SAR, as it offers the opportunity to map much wider image swaths. However, deploying high-power transmitters on satellite platforms and achieving continuous imaging over large areas of the Earth’s surface remains a challenge for engineering implementations. Additionally, high-power transmitters require frequent maintenance and calibration to maintain long-term consistency, which presents some challenges for satellite platforms. As a result, no GSO SAR systems are currently in operation [4,5]. Some papers have proposed a bistatic SAR system based on a GSO satellite transmitter and an airborne or low-Earth-orbit satellite receiver that can reduce the demand for transmitting power and provide higher imaging resolution, making it more feasible in engineering [6,7]. However, in the research on large-scale geoscience phenomena, Earth scientists prioritize high swath width more than the improvement of image resolution. As for GSO-BiSAR, the imaging swath width of this system is still limited by the altitude of the receiving platform. Moreover, the use of a GSO satellite transmitter is hampered by energy supply limitations that necessitate long idle periods for battery charging, resulting in a limited effective illumination time for regions of interest. All of these factors present difficulties for the continuous, large-scale monitoring of the Earth’s surface.
Therefore, we need a more effective Earth observation platform that can enable observations of larger-scale geoscience phenomena to deepen our understanding of the Earth system [8,9].
As the only natural and long-term stable satellite of the Earth, the Moon has gained attention from scientists over the past few decades. Especially after the 21st century, countries around the world, especially the United States and China, have successively launched lunar exploration programs [10,11,12,13]. Due to its unique advantage of Earth observation, the Moon is considered a potentially ideal platform for Earth observation. Compared to satellites, aircraft, and ground-based platforms used for Earth observations, the Moon-based Earth observatory has distinct characteristics and offers an opportunity to enhance our overall Earth observation system. The Moon-based observation platform has the following advantages [8,14,15]: First, due to tide locking, one side of the Moon is always pointing toward the Earth, so continuous Earth observation from the Moon is possible. Second, with a higher orbit, the Moon-based observation platform can simultaneously observe the Earth at the hemispheric scale, making it more suitable for the continuous observation of large-scale geoscience phenomena. Third, unlike the limitations of spaceborne platforms, Moon-based platforms can provide sufficient energy supply and space to deploy active sensors with high transmit power and large antennas. Fourth, as a permanent platform, the Moon-based observation platform can operate much longer than the spaceborne platform with proper maintenance, which makes it possible to provide long-term consistent calibrated observation data. Fifth, a Moon-based observation station can provide a unique and unparalleled perspective for observing phenomena such as oceanic and solid tides caused by the tidal force of the Moon.
Until now, various studies have been conducted on Moon-based Earth observations, and synthetic aperture radar is considered one of the primary sensors for the Moon-based platform [15,16,17,18,19]. However, the fixed lunar orbits and the viewing angles of Moon-based platforms not only limit the flexibility of interference baselines for Moon-based interferometric synthetic aperture radar (InSAR), but also make it difficult to avoid various electromagnetic interferences from the Earth. In addition, recent studies have suggested that more information can be derived from bistatic scattering than from backscattering [20], but Moon-based monostatic SAR can only receive the backscattered signal of the target’s scattering echo. Meanwhile, due to the lack of forward-looking imaging and nadir imaging capabilities, Moon-based monostatic SAR may have limitations in observing some regions of interest, making it difficult to meet the requirement of continuous monitoring over time for a given study area. Moreover, the long distance between the Moon and the Earth brings large propagation losses, requiring the radar system to produce hundreds of kilowatts of transmission power, which brings great challenges to engineering implementations.
In accordance with these problems, the MS-BiSAR with a Moon-based transmitter and a high-orbit satellite-based receiver for Earth observation is put forward in this paper. Figure 1 shows a conceptual illustration of MS-BiSAR Earth observation. Compared with Moon-based monostatic SAR, MS-BiSAR can achieve more flexible interferometric baselines to obtain three-dimensional surface information. A flexible position of the receiving satellite can also avoid interference signals from the Earth. At the same time, MS-BiSAR has the capability to receive bistatic scattering echoes, which expands the potential applications of surface parameter inversion. By designing the receiving satellite orbit, BiSAR can adjust the imaging area and achieve forward and subsatellite point imaging that cannot be achieved by monostatic SAR, which is beneficial for the continuous large-scale monitoring of a study area. Finally, the shorter propagation distance of MS-BiSAR can significantly reduce the demand for transmission power, and in some cases even reduce the transmission power by two orders of magnitude, compared to Moon-based monostatic SAR.
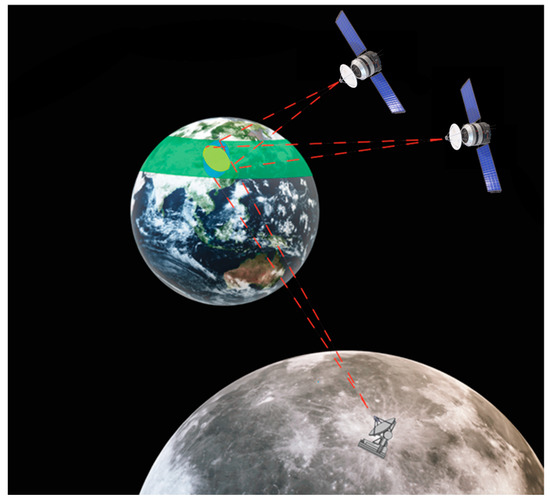
Figure 1.
A conceptual illustration of MS-BiSAR Earth observation.
To better understand the capability of MS-BiSAR for Earth observation, it is necessary to accurately calculate its monitoring capability on the Earth at different times with multiple configurations in order to obtain high-quality homogenized data on a global scale and support the analysis and prediction of complex geoscience phenomena, such as environmental changes and solid Earth motion. Therefore, analyzing the geometric characteristics and observation coverage of Earth observation systems is crucial for the acquisition of global Earth observation data and a better understanding of the Earth system. In this paper, three contributions are made. Firstly, we develop a reference systems transformation approach for MS-BiSAR Earth observation. Secondly, we establish the geometric model of MS SAR. Finally, we determine the conditions under which an area on Earth can be observed by MS-BiSAR and calculate as well as analyze the coverage for three configurations of MS-BiSAR Earth observation.
2. Data and Methods
To quantify the geometric characteristics and coverage of MS-BiSAR Earth observation, it is necessary to establish precise geometric relationships between the Moon, the satellite, and Earth. This can be achieved by utilizing ephemeris and Earth orientation parameters (EOP) to determine the attitude and position of both celestial bodies. Subsequently, the positions of the satellites in the three orbits can be calculated using an orbit propagator. Once the attitude and position are transformed into a unified reference system, we can proceed with the quantitative analysis. Figure 2 illustrates the main workflow of this process.
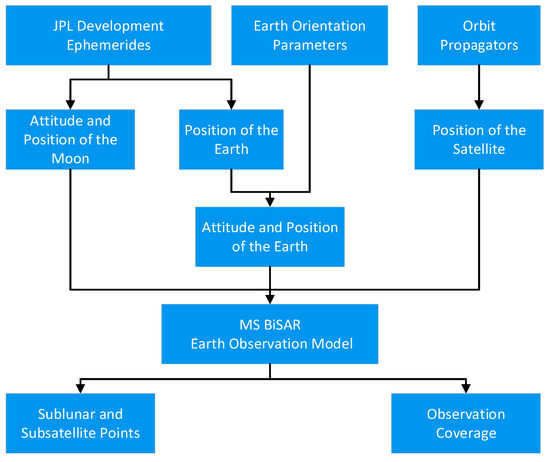
Figure 2.
The main work content and steps of this paper.
2.1. Ephemerides and Earth Orientation Parameters
To establish the precise geometric relationship between the Moon and the Earth, this paper utilizes two types of data: ephemeris and Earth orientation parameters.
The Development Ephemerides (DE) series, developed by NASA’s Jet Propulsion Laboratory, is one of the most widely used ephemerides in the international astronomical community. These ephemerides provide information on the positions, velocities, and accelerations of celestial bodies in the Solar System [21]. The coordinate and time systems used for DE430 are the International Celestial Reference System (ICRS) and Barycentric Dynamical Time (TDB), respectively. Since the 1960s, JPL has successively released DE200, DE403, DE421, DE430, DE432, DE436, DE438, and other versions of ephemeris products. DE430, which was released in 2013, is a general-purpose ephemeris generated by fitting numerically integrated orbits of the Moon and planets to observations, and it inherits the features of DE421 and those of its predecessor DE405. It provides the Moon’s state vectors from 1960 AD to 2650 AD, including the position, velocity, and orientation, stored as Chebyshev polynomial coefficients. Since more precise lunar nutation and vibration are considered in DE430, it was chosen for use in this paper.
The Earth Orientation Parameters are the parameters representing the rotational part of the transformation between the ICRS and the International Terrestrial Reference System (ITRS). It uses the UT1 time system as the reference time, which is based on the Earth’s rotation rate. Due to the gravitational influence of celestial bodies such as the Sun and the Moon, the rotation rate and spatial orientation of the Earth’s rotation axis experience irregularities, resulting in a variety of long-period and short-period changes, such as precession, nutation, and polar shift. To accurately transform the Geocentric Celestial Reference System (GCRS) into the ITRS, the EOPs are utilized to define these irregularities in the Earth’s rotation.
2.2. Satellite Orbit
The coverage of MS-BiSAR for Earth observation is mainly determined by the positions of both the transmitting and receiving platforms. Therefore, to meet the requirements for observing large-scale geoscience phenomena, a relatively high orbit altitude is necessary for the receiving satellite.
Figure 3 shows the observation geometry of the MS-BiSAR in the Earth-Centered Inertial Coordinate System (ECI) and the antenna coordinate system (ACS). It can be seen from the figure that different orbit parameters can have an impact on the satellite orbit, thereby affecting the Earth observation characteristics of MS-BiSAR.
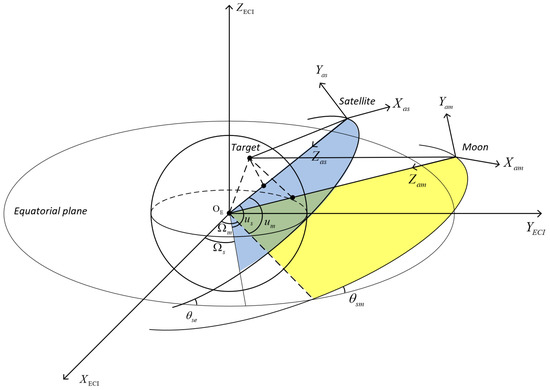
Figure 3.
Observation geometry of the MS-BiSAR in the ECI and ACS, where is the argument of latitude and and are the orbit inclination and right ascension node, respectively (not to scale for the sake of clarity).
This paper primarily considers two types of satellite orbits: geosynchronous orbit and highly elliptical orbit (HEO). The former provides continuous coverage of one-third of the Earth’s sphere, while the latter provides better coverage of the Earth’s high latitudes.
Geosynchronous orbit refers to the orbit of an anterograde satellite whose orbital period is equal to the rotation period of the Earth. Its orbital semi-major axis is approximately 42,000 km. Based on orbital inclination, GSO can be divided into geostationary orbit (GEO) and inclined geosynchronous orbit (IGSO). Satellites in GEO have an inclination of zero degrees and are stationary above the equator, providing continuous observation of a fixed coverage area. IGSO has a non-zero inclination and its nadir tracks across the northern and southern hemispheres, with the intersection point being on the equator. Satellites in such orbits provide better coverage at middle and high latitudes than GEO satellites. HEO is an elliptical orbit with a low perigee and an extremely high apogee. With a perigee of less than 1000 km and an apogee higher than 36,000 km, HEO satellites spend a long time passing through apogee and a short time passing through perigee, enabling them to cover the ground area below the apogee for more than 12 h. By adjusting orbit parameters appropriately, HEO satellites are suitable for long-term polar region observations. This paper utilizes Molniya orbits to conduct research on MS-BiSAR with an HEO configuration.
To simulate satellite orbits, an orbit propagator is required. This paper utilizes Simplified Deep-Space Perturbations-4 (SDP4) orbit propagators [22], which is a solver that calculates the position and velocity of an object whose motion is predominantly influenced by gravity from celestial bodies. By using SDP4 orbit propagators, the position and velocity of satellites with variant orbital parameters in ITRS at a given moment can be determined. Since the satellites discussed in this paper follow quasi-periodic orbits, accurately predicting their long-term orbits poses significant challenges. Therefore, an effective method has been employed in this study to reduce the errors of the long-term predictor by using SDP4 orbit propagators to predict the position and velocity of the satellite within a single orbital period, repeating this process to obtain the motion state of the satellite throughout the entire study period.
2.3. Reference Systems and Transformations
To analyze the observational geometry and Earth observation coverage in this study, it is necessary to describe the relative position and attitude of the Moon-based platform, satellite platform, and Earth, which are defined in different reference systems. As a result, reference system transformations are crucial.
The reference system comprises both coordinate and time systems. Therefore, in studying the geometric characteristics and coverage of MS-BiSAR, it is necessary to bring the Moon-based observatory, satellites, and Earth under a unified time system (UT1) and coordinate system (ITRS). Due to the abundance of reference materials available for time system transformations [23], this paper will not delve into them in detail; instead, this paper primarily focuses on coordinate system transformation.
To simplify the calculations and incorporate existing research on potential Moon base sites [18,24], this paper makes three assumptions, as follows:
- The Earth is a sphere with a radius of = 6378 km;
- The Moon is a sphere with a radius of = 1737 km;
- The Moon-based observatory is located at the center of the lunar near side (0°, 0°).
Three types of reference systems are introduced in this paper. The first type is the geodetic reference system, used to describe the positions of Moon-based observatories on the Moon and targets on the Earth. The geographic reference system (GRS) and the selenographic reference system (SRS) are examples of such reference systems in this paper. The second type is a reference system dealing with the parameters related to the celestial body surface, its origin is defined at the center of the celestial body, and its X-axis lies at the intersection of latitude 0° and longitude 0° degrees on the celestial surface, with its basic plane in the celestial equatorial plane forming a right-handed coordinate system. In this paper, such reference systems include the mean Earth/polar axis reference system (MERS), the principal axis lunar reference system (PALRS), and the ITRS. The third type is the celestial reference system (CRS), with an origin at the center of the celestial body, and its fundamental plane being the mean equator plane containing the celestial’s center of epoch J2000.0. Its principal X-axis is pointing to the mean vernal equinox of epoch J2000.0. In this paper, the GCRS with an origin at the center of the Earth and the selenocentric celestial reference system (SCRS) with an origin at the center of the Moon are involved. While some papers describe the methods of reference system transformation in detail, this paper briefly introduces them [25,26]. Figure 4 shows the key reference system transformation processes involved in this paper.
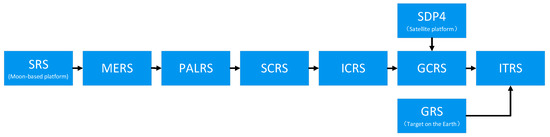
Figure 4.
Flowchart of reference systems transformation.
The reference systems transformations start from the Moon-based observatory’s coordinate, which is given by the latitude and longitude in SRS. It can be expressed as a Cartesian coordinate in the MERS.
Then, with the following transformation equation, it can be converted into the GCRS:
where and are the ICRS coordinates of the Moon and Earth, respectively. and are the rotation matrices for the coordinate transformation from MERS to PALRS and PALRS to ICRS, respectively. Since MERS and PALRS have the same origin, they are only slightly different in terms of rotation in axes, which is a fixed matrix. Meanwhile, DE430 could provide the at a given moment.
Now, the coordinates of the Moon-based observatory have been converted into the GCRS. The satellite orbits generated by SDP4 orbit propagators are also in the GCRS. The coordinate of the satellite is . To analyze the geometric properties of MS-BiSAR Earth observation, they are converted into the ITRS by rotation of the axis of the GCRS.
where , , , and are the rotation matrices that result from the Earth’s precession, nutation, rotation, and polar motion, respectively. These rotation matrices are realized using EOP data.
3. Results and Discussion
After completing the previous data preparation and determining the method of reference system transformation, an observation geometric model can be constructed, and relevant observation parameters can be calculated and analyzed. Among them, the results of substellar points and observational coverage are analyzed and discussed in detail.
3.1. Geometric Model
Since the lunar revolution period is equal to its rotation period, the Moon is always facing the Earth on the same side, which is referred to as tidal locking. Additionally, the nutation, libration, and precession of the Moon will also lead to changes in the relative position and attitude between the Moon and the Earth.
To better analyze the geometric characteristics of Earth observations, we established a simplified MS-BISAR Earth observation model in the ITRS, with the three assumptions mentioned earlier, as shown in Figure 5. In this model, the Earth is fixed, while the Moon and the satellite rotate around it. Parameters such as the position and velocity of the platform and targets on the Earth can be obtained by reference system transformation as introduced in the previous section.
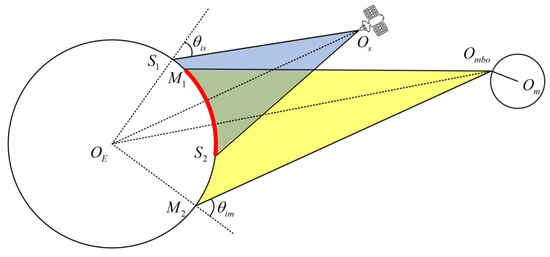
Figure 5.
Simplified MS-BiSAR Earth observation geometrical model. is the Moon-based observatory, is the selenocenter, is the geocenter, and is the satellite. and are the threshold for the incidence angle of transmitter and receiver, respectively. and are the boundaries of the observable area of the satellite receiver. Meanwhile, and are the boundaries of the observable area of the Moon-based observatory. The red area is defined as the observable area of MS-BiSAR (not to scale for the sake of clarity).
Based on the simplified MS-BiSAR Earth observation geometric model, we can derive several parameters, such as the nadir position and local incidence angle, for further analysis.
3.2. Nadir Points of the Moon-Based Observatory and Satellites on Earth
The nadir point is the point on the Earth’s surface directly beneath a satellite or celestial body at a given moment in time, while the nadir track refers to the path it follows as it orbits the Earth. By analyzing the nadir points and tracks, we can determine the relative position and attitude between the Moon-based observatory, the satellite, and the Earth, allowing for further analysis of the observation characteristics of different bistatic configurations for Earth observation.
Since the distance between the Moon and the Earth is significantly larger than the radius of the Moon, the difference between the nadir point of the Moon-based observatory and the Moon itself is negligible. Therefore, in this section, we refer to the nadir point of the Moon-based observatory as the sublunar point and the nadir point of the satellite platform as the subsatellite point.
3.2.1. Nadir Points Characteristics of Moon-Based Observatory
Figure 6 shows the latitude and longitude of the sublunar points at 00:00:00 daily from 1 January 1980 to 1 January 2023.
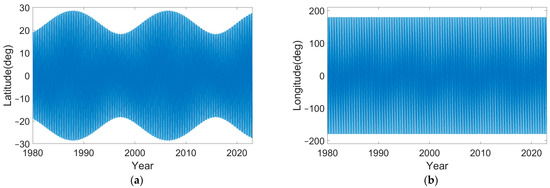
Figure 6.
Position of sublunar points from 19802022: (a) latitude; (b) longitude.
During this period, the longitude of the sublunar varies evenly between −180° and 180°. The maximum values of latitude fluctuate back and forth between 18.5° and 28.7° in the northern and southern hemispheres, respectively, and present a stable fluctuation period of 18.6 years, which corresponds to the variation period of the angle between the lunar orbital plane and the Earth’s equatorial plane.
Due to the regularity of lunar movement, we chose 1 January 2022 to 1 January 2023 as the research period and calculated the position of the sublunar point at 00:00 daily.
As can be seen from Figure 7, the latitude of the sublunar point, centered on the equator, fluctuates sinusoidal between −27.4° and 27.4° with a frequency of one sidereal month (27.3 days), resulting in a different coverage of the northern and southern hemispheres at different times.
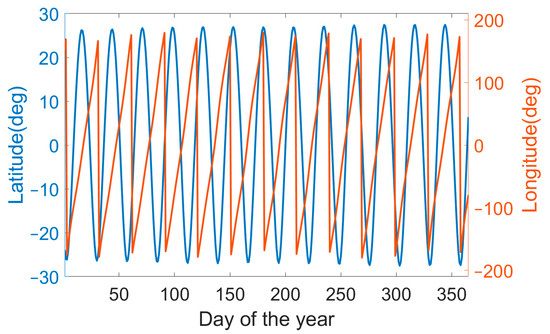
Figure 7.
Latitude and longitude of sublunar points over 2022.
Then, the positions of sublunar points with time steps of 10 min were calculated from 1 January 2022 to 28 January 2022 (one sidereal month). As can be seen from Figure 8, in a sidereal month, the latitude of the sublunar points fluctuates once between the maximum and minimum values, and the longitude position of the sublunar point fluctuates between −180° and 180°, with a cycle of once per day. The latitude of the sublunar points has a significant sine wave period variation within one sidereal month, which also reflects the temporal coverage of Moon-based Earth observation in middle- and high-latitude regions. This is also a key factor that we focus on when analyzing the observational performance of Moon-based Earth observation.
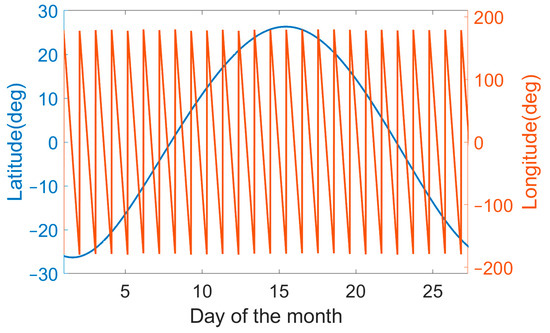
Figure 8.
Latitude and longitude of sublunar points over one orbital period.
3.2.2. Nadir Track Characteristics of Satellites and Moon
Since the period of GEO and IGSO is one day, while the HEO is half a day, we can select the nadir track of satellites with variant orbital parameters for analysis in one day. To clearly illustrate the tracks of subsatellite points, we have included them in the Robinson projection map. For comparison, we have also included the tracks of sublunar points.
Figure 9 shows the subsatellite points of GSO with an orbital inclination of 0° (GEO), 45° (IGSO), 75° (IGSO), and HEO. The density of the points reflects the duration of time that the satellite stays above this area.
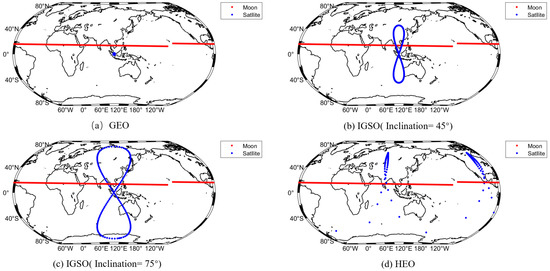
Figure 9.
Nadir track of satellites with variant orbital parameters and Moon-based observatory in one day.
It shows that the longitude and latitude of the subsatellite points of the GEO satellite do not change in one day, and it is stationary above a certain point on the Earth. As for IGSO, the maximum latitude variation of the subsatellite is equal to that of the orbital inclination, and the period of longitude and latitude change is one day. The subsatellite point of the highly elliptical orbit has the longest duration in the middle and high latitudes of the northern hemisphere (also could be the southern hemisphere with appropriate orbital parameters), but the duration is very short in other areas.
Here, we selected the subsatellite point of three common satellite orbits, GEO, IGSO, and HEO, for analysis. In fact, due to the high degree of freedom of the satellite orbital parameters, changes to them will lead to large changes in the nadir track. There are also some suitable orbits of satellites that can be discussed in the future.
3.3. Coverage Characteristic Analysis
Coverage characteristics are an important evaluation indicator for Earth observation. In order to simulate the coverage characteristics of the Earth’s surface of the MS-BiSAR, we used the observation geometric model for further analysis.
The observability of a region on Earth is determined by the position of the transmitter, the receiver, and the observation target. Only surface areas that are observable by both the transmitter and the receiver can be considered as areas covered by the MS-BiSAR.
Since the radar echo of the terrain becomes very weak with a large incidence angle, it can result in a low signal-to-noise ratio (SNR) of the image and may also be obstructed by the topography of the terrain. As a result, the incidence angle is usually set within a certain range. As for BiSAR, the incidence angles of the transmitter and the receiver are not the same. Thus, this research defined the coverage area of bistatic SAR for Earth observation based on the incidence angle of the transmitter and the receiver and set the threshold ( and ) for the incidence angle to 60°.
Then, we calculated whether the location of the given point on the Earth’s surface is observable. We defined the coordinates of the Moon-based observatory , the satellite , the target on the Earth , and the barycenter of the Earth .
The incidence angle of the transmitter and the receiver are as follows:
When and the target on the Earth is observable.
In order to calculate the accumulated coverage time of each area on the Earth, the Earth’s surface needs to be meshed first with an appropriate sampling grid. In this paper, we used a Fibonacci grid instead of altitude–longitude grid to achieve a more uniform sphere partitioning, and effectively reduce the calculation time and numerical errors [27].
Then, the Fibonacci grid was used to set 10,001 sampling points on the Earth’s surface (each point represents an area of about 50,000 ) and calculate the accumulated observable time of GEO, IGSO, HEO, and GEO constellation bistatic configurations in 2022 with the time step of 10 min.
As can be seen from Figure 10, all three MS configurations can achieve large coverage of the Earth, but the characteristics of coverage vary depending on the orbit of the satellite. For the GEO receiver configuration, it has good long-term coverage of middle and low latitudes within the longitude range of more than 100 degrees. For the IGSO receiver configuration, since its subsatellite point is not fixed, its accumulated observable coverage is larger than GEO, especially in middle and high latitudes. The coverage area of both configurations above is nearly equatorially symmetric. For the HEO receiver configuration, because most of its subsatellite points are concentrated in the middle and high latitudes, it has better coverage for high latitudes than the GEO and IGSO receiver configurations, so the HEO configuration will be more suitable for the continuous monitoring of polar regions. However, none of the three configurations above can achieve global coverage. The configuration of IGSO constellations can achieve good coverage of most of the Earth’s surface, and if the number of satellites in the constellation is increased, the coverage of Earth observation could be improved.
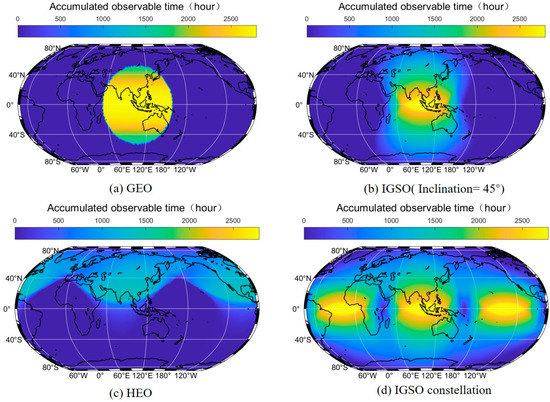
Figure 10.
The global accumulated observable time of MS-BiSAR (different configuration) over 2022.
Due to the unique properties of each orbit, the observation geometry will differ after the formation of MS-BiSAR. Therefore, when selecting the configuration of the platform, the specific requirements of the observation mission need to be taken into consideration.
We conducted calculations on the annual accumulated observable time of MS-BiSAR for Earth observation during a lunar nodal regression cycle (approximately 18.6 years) in the GEO configuration. The calculations were based on different latitude locations below the satellite’s ascending node longitude, and the results are presented in Table 1. It shows that there are differences in the annual accumulated observable time at different latitude positions due to the periodic changes in the lunar orbit and axis. By calculating the coefficient of variation (CV) for the annual accumulated observable time at different locations, we observe that low-latitude regions have minor annual variations in accumulated observable time. As latitude increases, the annual variability progressively increases, particularly for high-latitude areas where the CV can exceed 40%. Since the operational cycle of MS-BiSAR exceeds the lunar precession period, when designing the receiving satellite orbit for observation tasks in high-latitude regions it is necessary to consider the coverage capability over the entire lunar nodal regression cycle.

Table 1.
Annual accumulated observable time of MS-BiSAR (GEO configuration) for different locations in one lunar precession period.
It should be noted that this study is based on certain assumptions, which may result in slight errors when compared to actual situations. For example, we assumed that the Earth and Moon were ideal spheres, while in reality their irregularities could also impact their coverage characteristics. Additionally, as mentioned earlier, this paper assumes that the lunar-based observatory is located at the center of the near side of the Moon; however, some studies have suggested that the observatory’s location can affect the Earth observation coverage, which needs further analysis. Furthermore, although the ephemeris, EOP, and orbit propagators used in this research have been endorsed by experts in the field, these models still contain errors that contribute to the overall error in this research. Additionally, model and algorithm errors might occur during reference system transformations, with up to six transformations in this particular paper, resulting in a further magnification of their impact on simulation results. Moreover, the assessment of observable area in this section is solely based on observed geometry. Therefore, factors such as the bistatic electromagnetic scattering characteristics of the target, SNR, the angle between the range direction and azimuth direction, and imaging resolution need to be considered for a more comprehensive analysis.
Overall, while we have made efforts to minimize any potential errors, it is important to acknowledge the limitations resulting from the assumptions we made. Further investigation and verification are needed to verify our results.
4. Conclusions
In this paper, we propose the concept of using a Moon-based transmitter and a high-orbit satellite-based receiver to form a bistatic SAR for Earth observation, called MS-BiSAR, and analyze its geometric characteristics and observation coverage to meet the demand for temporally consistent and spatially continuous Earth observation data on a global scale in geoscience research.
A geometric model of the MS-BiSAR’s Earth observation was established using JPL ephemerides, Earth orientation parameters (EOP), and SDP4 orbit propagators with reference system transformations, and its geometric characteristics were analyzed. The motion of the Moon has both long-term (18.6 years) and short-term (27.3 days) periods. During these periodic motions, the nadir point of the Moon-based observatory moves across different latitudes, which affects the geometric characteristics of Earth observation. The changes in the nadir points of different satellite orbits vary, resulting in differences in the coverage capability of different satellites. For the GSO orbit, its nadir point always moves along a fixed longitude and latitude range on the Earth’s surface, and by increasing the orbit inclination, its latitude range can be expanded. For the HEO orbit, the subsatellite points are mainly distributed in the mid-to-high latitudes of one hemisphere throughout one orbital period, with a very short duration of time for other areas.
Based on the geometric model, the accumulated observable times of three different platform configurations within a year were calculated and analyzed. The results show that MS-BiSAR with GSO satellite can provide good coverage over a third of the Earth’s sphere, and its coverage can be increased at middle and high latitudes with higher orbital inclination. For the configuration of the HEO satellite platform and Moon-based platform, better coverage of polar regions can be achieved. However, none of these configurations can achieve complete coverage of the Earth. To achieve global observation, a receiving constellation consisting of multiple high-orbital satellites is needed. Finally, this paper took the IGSO satellite receiver as an example and calculated the accumulated observable time of MS-BiSAR for different latitude ground areas during one nodal regression cycle. The results show that there are significant variations in the observable times for high-latitude regions in different years, while the variations are relatively small for mid-to-low latitude regions.
In conclusion, with the advantage of wide swaths, continuous observation capabilities, and large coverage, the MS-BiSAR could provide temporally consistent and spatially continuous Earth observation data for large-scale geoscience phenomena, which will help us deepen our understanding of Earth system science. In future work, the precision of the observational geometry model established in this paper will be improved, and more optimized observation constraints will also be discussed. Meanwhile, other issues related to the MS-BiSAR, such as imaging spatial resolution, bistatic configuration, and Earth science phenomena suitable for MS-BiSAR observations, will be further considered.
Author Contributions
Conceptualization and summary H.G. and K.Z.; methodology, K.Z.; software, K.Z. and D.J.; writing—original draft preparation, K.Z.; writing—review and editing, C.H.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2022YFB3902100), the Innovative Research Program of the International Research Center of Big Data for Sustainable Development Goals (CBAS2022IRP02), and the National Natural Science Foundation of China (Grant No. 41590853).
Data Availability Statement
Not applicable.
Acknowledgments
We thank the IAU SOFA Collection for its use, copyright© International Astronomical Union Standards of Fundamental Astronomy (http://www.iausofa.org accessed on 27 August 2021). We thank the JPL for the free access to DE430 and the IERS for the free access to EOP data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, H.D. Theory and Application of Earth Observation by Radar; Science Press: Beijing, China, 2000. [Google Scholar]
- Huadong, G.; Wenjin, W.; Ke, Z.; Xinwu, L. New generation SAR for Earth environment observation. Acta Geod. Cartogr. Sin. 2022, 51, 862. [Google Scholar]
- Reid, W.V.; Chen, D.; Goldfarb, L.; Hackmann, H.; Lee, Y.-T.; Mokhele, K.; Ostrom, E.; Raivio, K.; Rockström, J.; Schellnhuber, H.J. Earth system science for global sustainability: Grand challenges. Science 2010, 330, 916–917. [Google Scholar] [CrossRef]
- Hobbs, S.; Mitchell, C.; Forte, B.; Holley, R.; Snapir, B.; Whittaker, P. System Design for Geosynchronous Synthetic Aperture Radar Missions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7750–7763. [Google Scholar] [CrossRef]
- Long, T.; Hu, C.; Ding, Z.; Dong, X.; Tian, W.; Zeng, T. Geosynchronous SAR: System and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Sun, Z.; Yen, G.G.; Wu, J.; Ren, H.; An, H.; Yang, J. Mission planning for energy-efficient passive UAV radar imaging system based on substage division collaborative search. IEEE Trans. Cybern. 2021, 53, 275–288. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Wu, J.; Pei, J.; Li, Z.; Huang, Y.; Yang, J. Inclined geosynchronous spaceborne–airborne bistatic SAR: Performance analysis and mission design. IEEE Trans. Geosci. Remote Sens. 2015, 54, 343–357. [Google Scholar] [CrossRef]
- Guo, H.D.; Ding, Y.X.; Liu, G. Moon-based Earth observation. Sci. Bull. 2022, 67, 2036–2039. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.Z.; Guo, H.D.; Liu, G.; Ye, H.L. Simulation Study of Geometric Characteristics and Coverage for Moon-Based Earth Observation in the Electro-Optical Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2431–2440. [Google Scholar] [CrossRef]
- Li, C.L.; Wang, C.; Wei, Y.; Lin, Y.T. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef]
- Zhao, W.J.; Wang, C. China’s lunar and deep space exploration: Touching the Moon and exploring the universe. Natl. Sci. Rev. 2019, 6, 1274–1278. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.; Craig, D.; Herrmann, N.; Mahoney, E.; Krezel, J.; McIntyre, N.; Goodliff, K. The Artemis Program: An Overview of NASA’s Activities to Return Humans to the Moon. In Proceedings of the 2020 IEEE Aerospace Conference (Aeroconf 2020), Big Sky, MT, USA, 7–14 March 2020. [Google Scholar]
- Wang, Q.; Liu, J.Z. A Chang’e-4 mission concept and vision of future Chinese lunar exploration activities. Acta Astronaut. 2016, 127, 678–683. [Google Scholar] [CrossRef]
- Guo, H.D. Earth system observation from space: From scientific satellite to Moon-based platform. J. Remote Sens. 2016, 20, 716–723. [Google Scholar]
- Guo, H.D.; Liu, G.; Ding, Y.X. Moon-based Earth observation: Scientific concept and potential applications. Int. J. Digit. Earth 2018, 11, 546–557. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, K.S. Effects of the Earth’s Curvature and Lunar Revolution on the Imaging Performance of the Moon-Based Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5868–5882. [Google Scholar] [CrossRef]
- Ding, Y.; Guo, H.; Liu, G.; Han, C.; Shang, H.; Ruan, Z.; Lv, M. Constructing a high-accuracy geometric model for Moon-based Earth observation. Remote Sens. 2019, 11, 2611. [Google Scholar] [CrossRef]
- Chen, G.; Guo, H.; Ding, Y.; Shang, H.; Lv, M.; Zhang, K. Influence of topography on the site selection of a Moon-based Earth observation station. Sensors 2021, 21, 7198. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.D.; Fu, W.X.; Liu, G. Development of Earth Observation Satellites. In Scientific Satellite and Moon-Based Earth Observation for Global Change; Springer: Singapore, 2019; pp. 31–49. [Google Scholar]
- Li, T.; Hajnsek, I.; Chen, K.-S. Sensitivity analysis of bistatic scattering for soil moisture retrieval. Remote Sens. 2021, 13, 188. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The planetary and lunar ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep. 2014, 196, 42–196. [Google Scholar]
- Hoots, F.R.; Roehrich, R.L. Models for Propagation of NORAD Element Sets; Aerospace Defense Command Peterson AFB CO Office of Astrodynamics: Fort Belvoir, VA, USA, 1980. [Google Scholar]
- Montenbruck, O.; Gill, E.; Lutze, F. Satellite orbits: Models, methods, and applications. Appl. Mech. Rev. 2002, 55, B27–B28. [Google Scholar] [CrossRef]
- Chen, G.; Guo, H.; Jiang, H.; Han, C.; Ding, Y.; Wu, K. Analysis of Comprehensive Multi-Factors on Station Selection for Moon-Based Earth Observation. Remote Sens. 2022, 14, 5404. [Google Scholar] [CrossRef]
- Sui, Y.; Guo, H.; Liu, G.; Ren, Y. Analysis of long-term Moon-based observation characteristics for Arctic and Antarctic. Remote Sens. 2019, 11, 2805. [Google Scholar] [CrossRef]
- Dong, J.L.; Shen, Q.; Jiang, L.M.; Jiang, H.J.; Li, D.W.; Wang, H.S.; Mao, S. An Analysis of Spatiotemporal Baseline and Effective Spatial Coverage for Lunar-Based SAR Repeat-Track Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3458–3469. [Google Scholar] [CrossRef]
- Gonzalez, A. Measurement of Area on a Sphere Using Fibonacci and Latitude-Longitude Lattices. Math. Geosci. 2010, 42, 49–64. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).