Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data
Abstract
1. Introduction
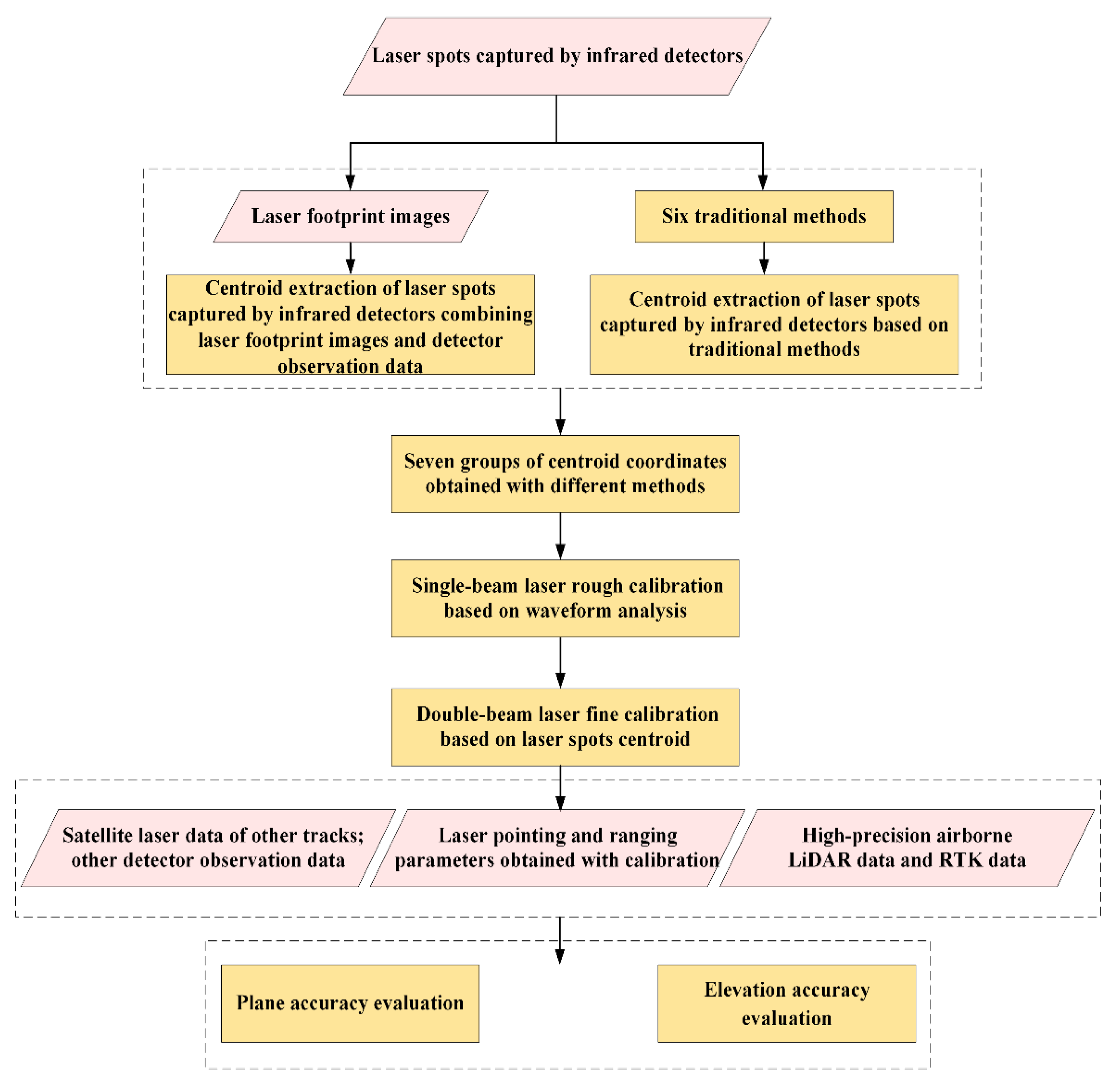
2. Materials and Methods
2.1. Study Areas and Data Sources
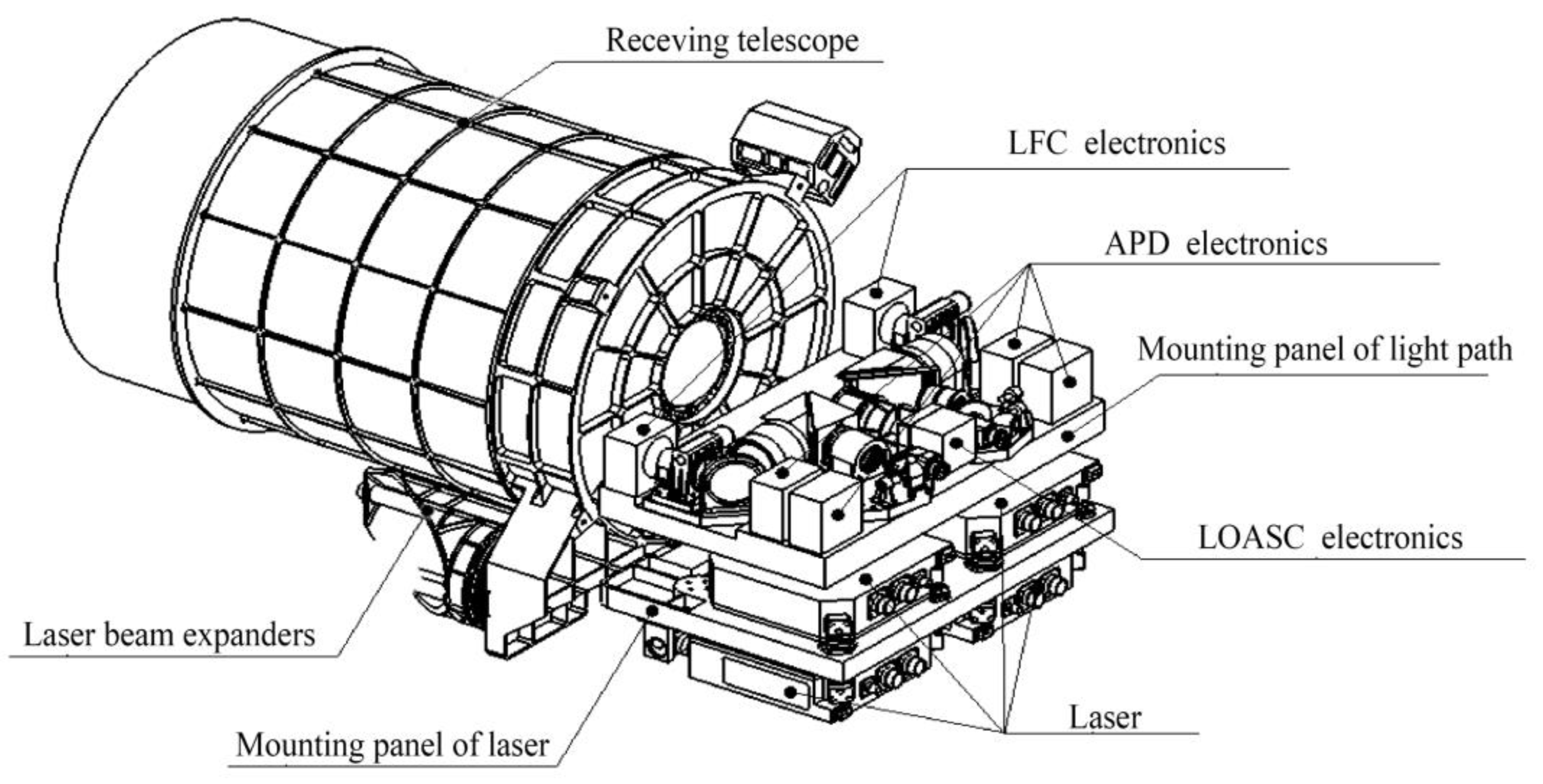
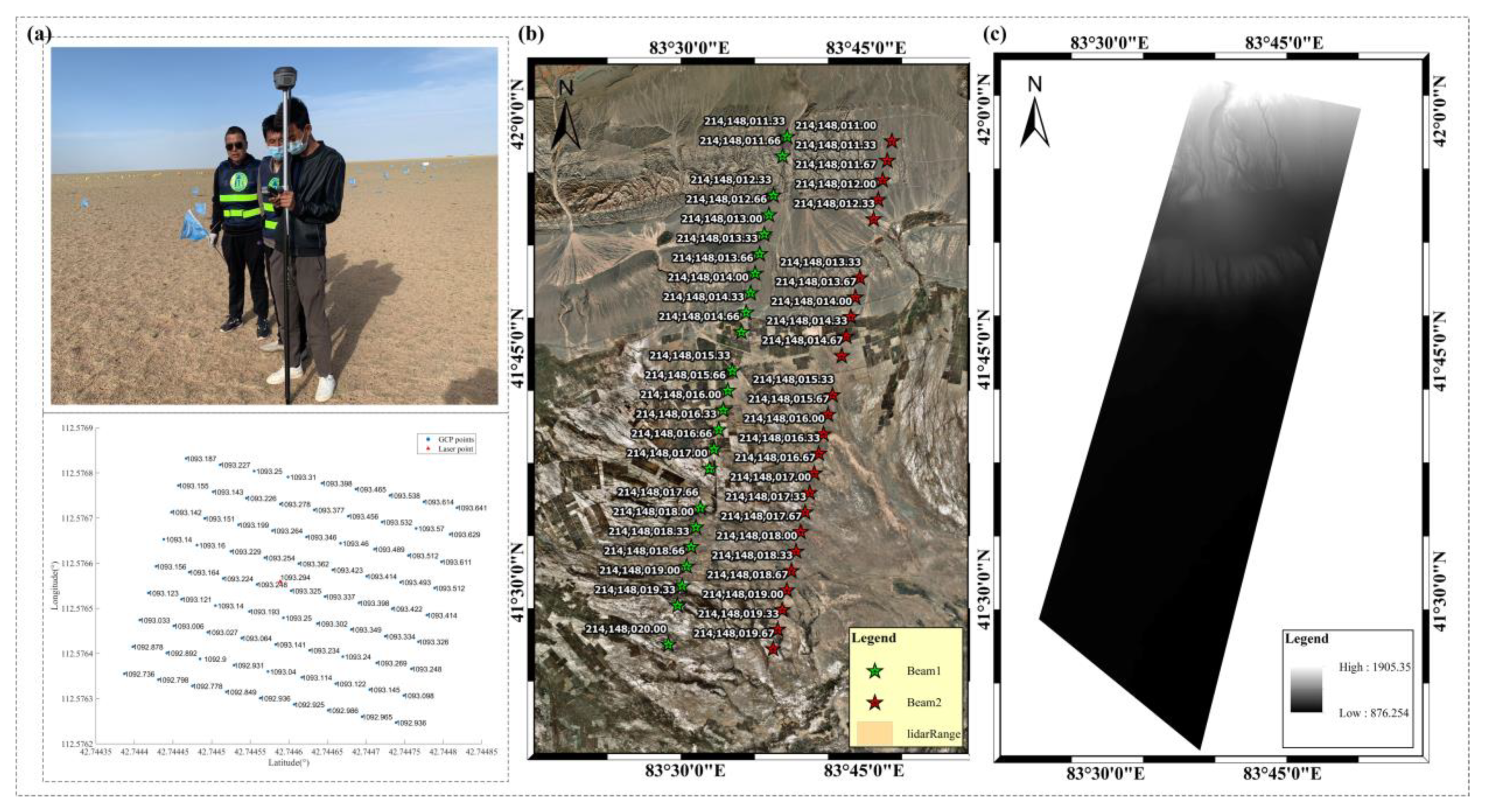
2.1.1. Experimental Data
2.1.2. Verification Data
2.2. Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data
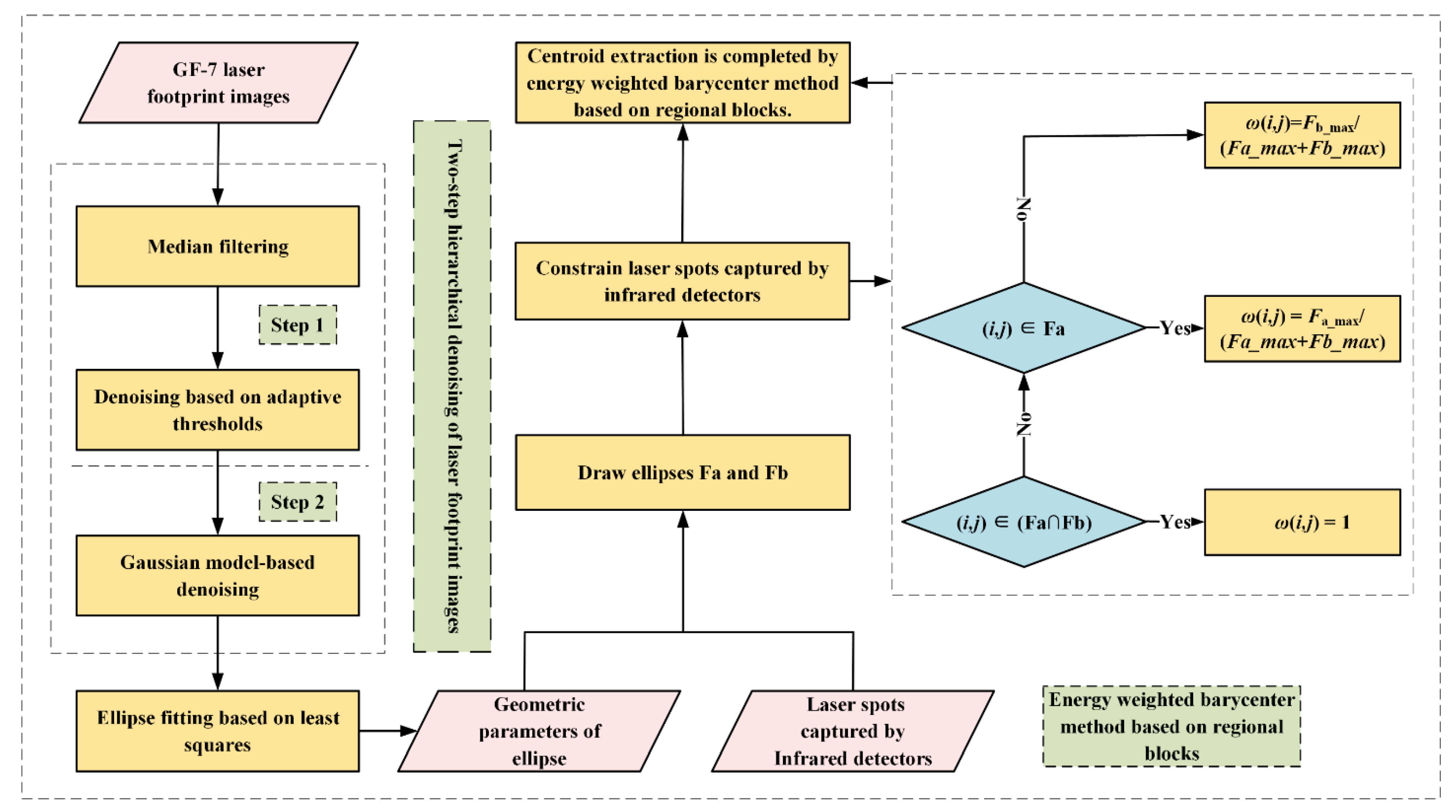
2.2.1. Hierarchical Denoising for Laser Footprint Images with Self-Adaptive “Two-Step Method”
- Coarse denoising:
- 2.
- Fine denoising:
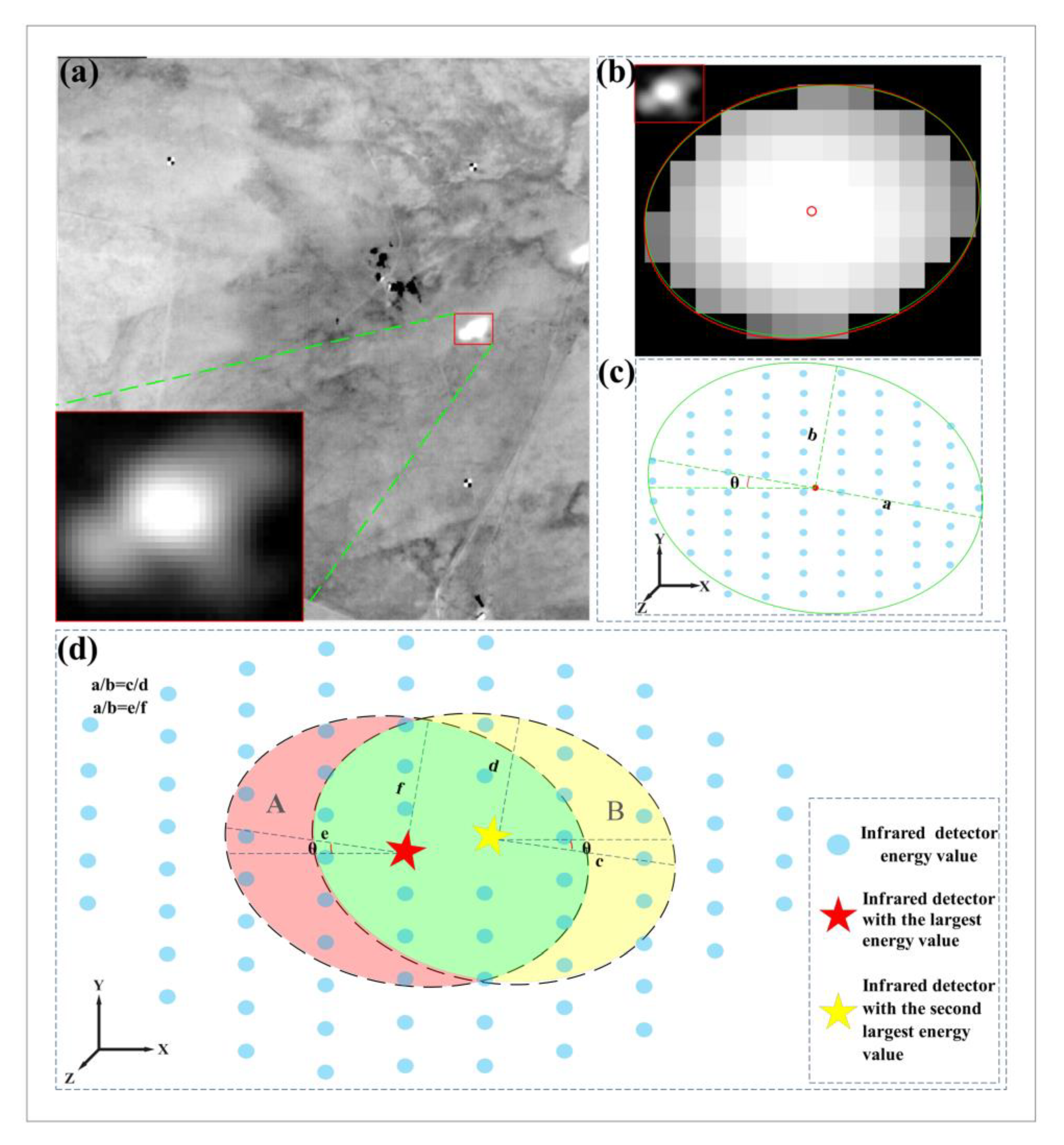
2.2.2. Geometric Parameters Extraction for Real Laser Footprints
2.2.3. After Constraining the Spot Captured by Detectors, the Centroid of the Spot Was Extracted by Energy Weighted Barycenter Method Based on Regional Blocks
2.3. Verification Based on Laser Footprint Positioning
2.3.1. Centroid Extraction of Spots Based on Infrared Detectors
- Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data:
- ➣
- The GF-7 satellite laser footprint images were denoised by the “two-step method” to obtain real laser footprints. Then, the geometric parameters, such as the ratio of the major axis to the minor axis and the inclination angle, were obtained by means of the least square ellipse fitting method;
- ➣
- Based on the obtained geometric parameters, ellipses were drawn in combination with the largest value and the second largest value of the spot energy to complete the division of the spot area;
- ➣
- The centroid of the spot was extracted using the energy weighted barycenter method based on regional blocks.
- Other traditional methods for centroid extraction of spots:
- ➣
- The centroids of spots were extracted using six traditional methods, such as the Gaussian surface fitting method.
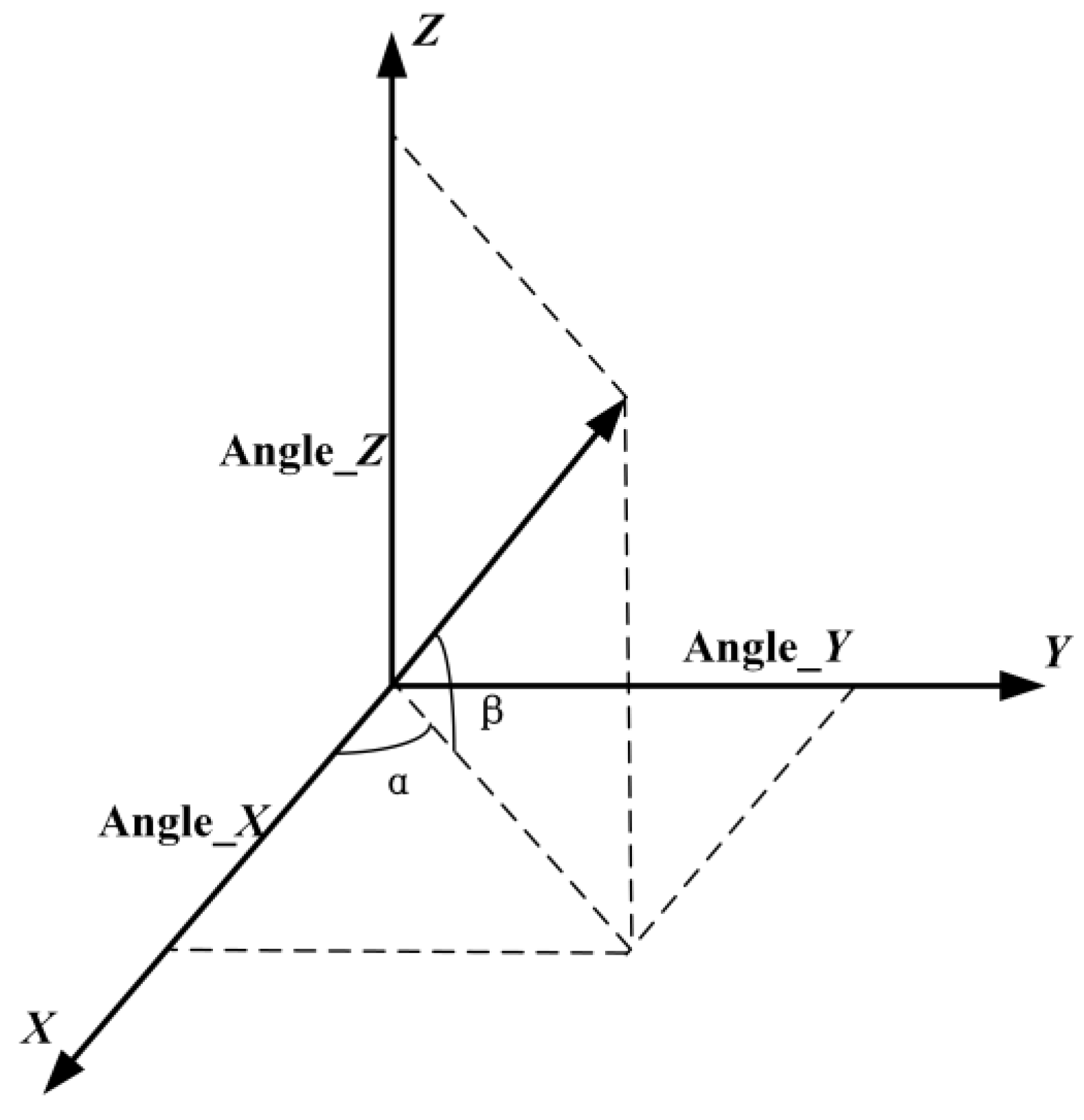
2.3.2. Calculation of Laser Pointing Angle and Ranging Parameters Based on the Single-Beam and Double-Beam Laser Calibration Models According to the Centroids Extracted
- Single-beam laser rough calibration:
- 2.
- Double-beam laser fine calibration:
2.3.3. Accuracy Evaluation of Spot Centroid Extraction Based on Infrared Detectors
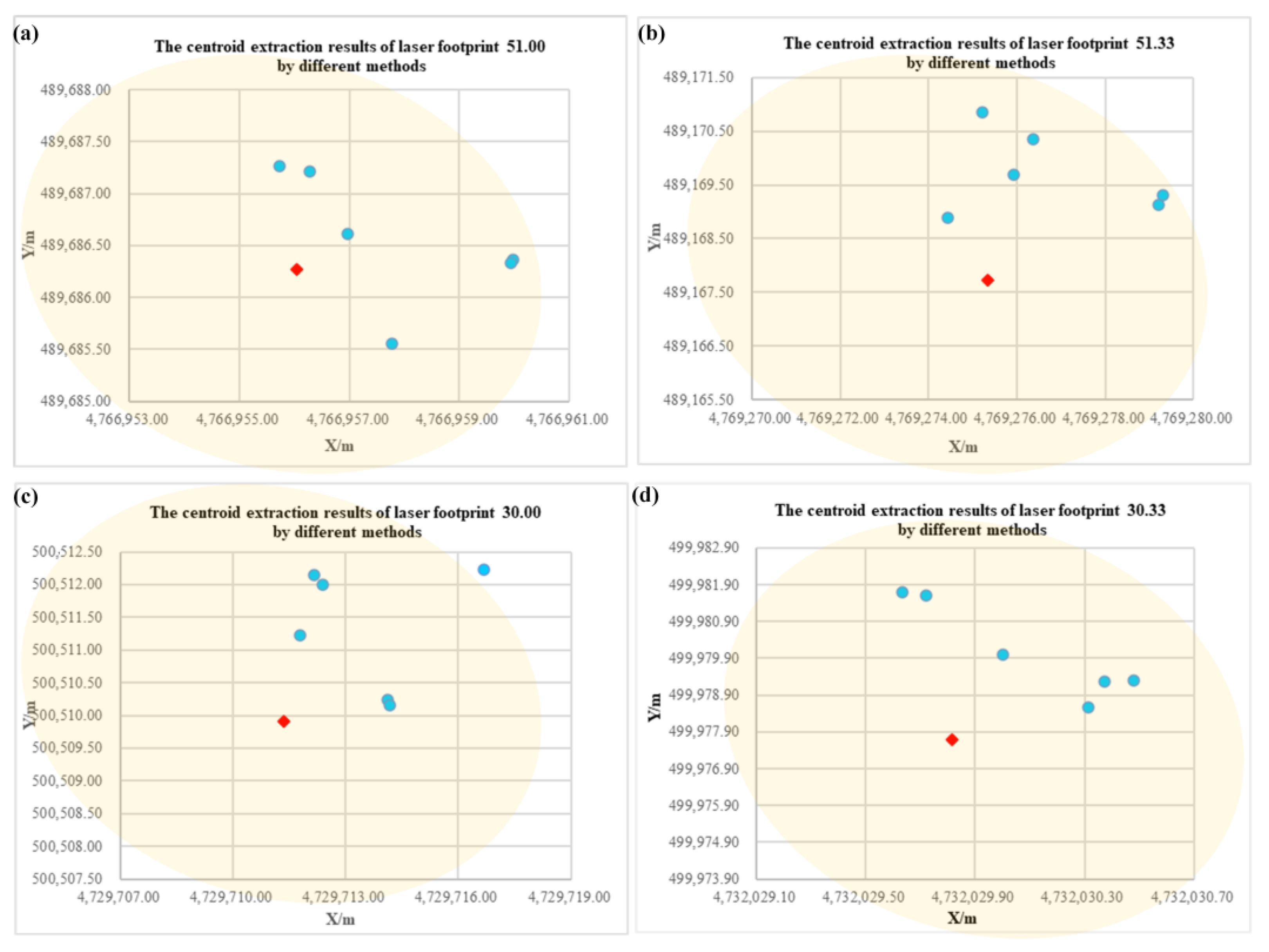
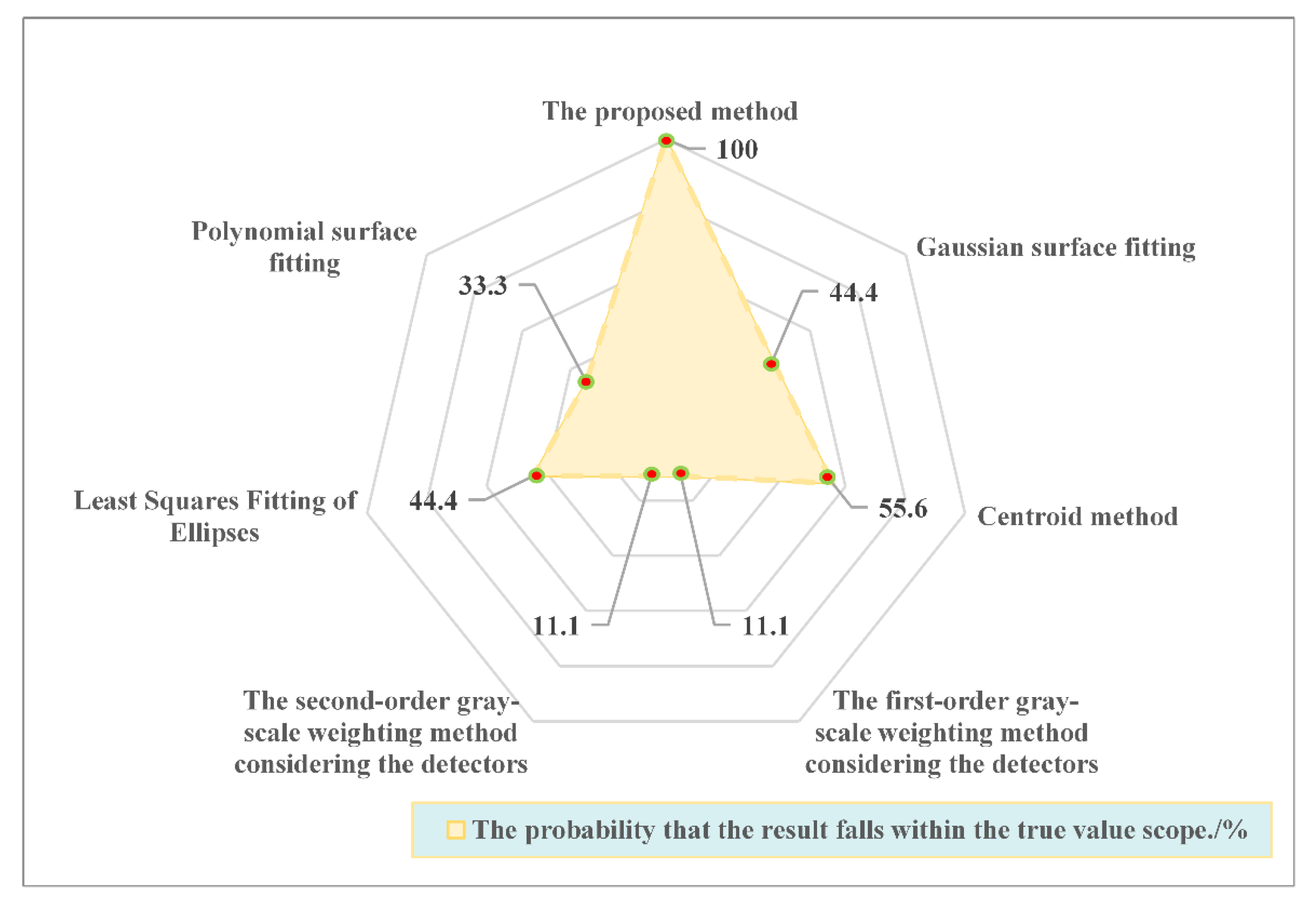
3. Results
4. Discussion
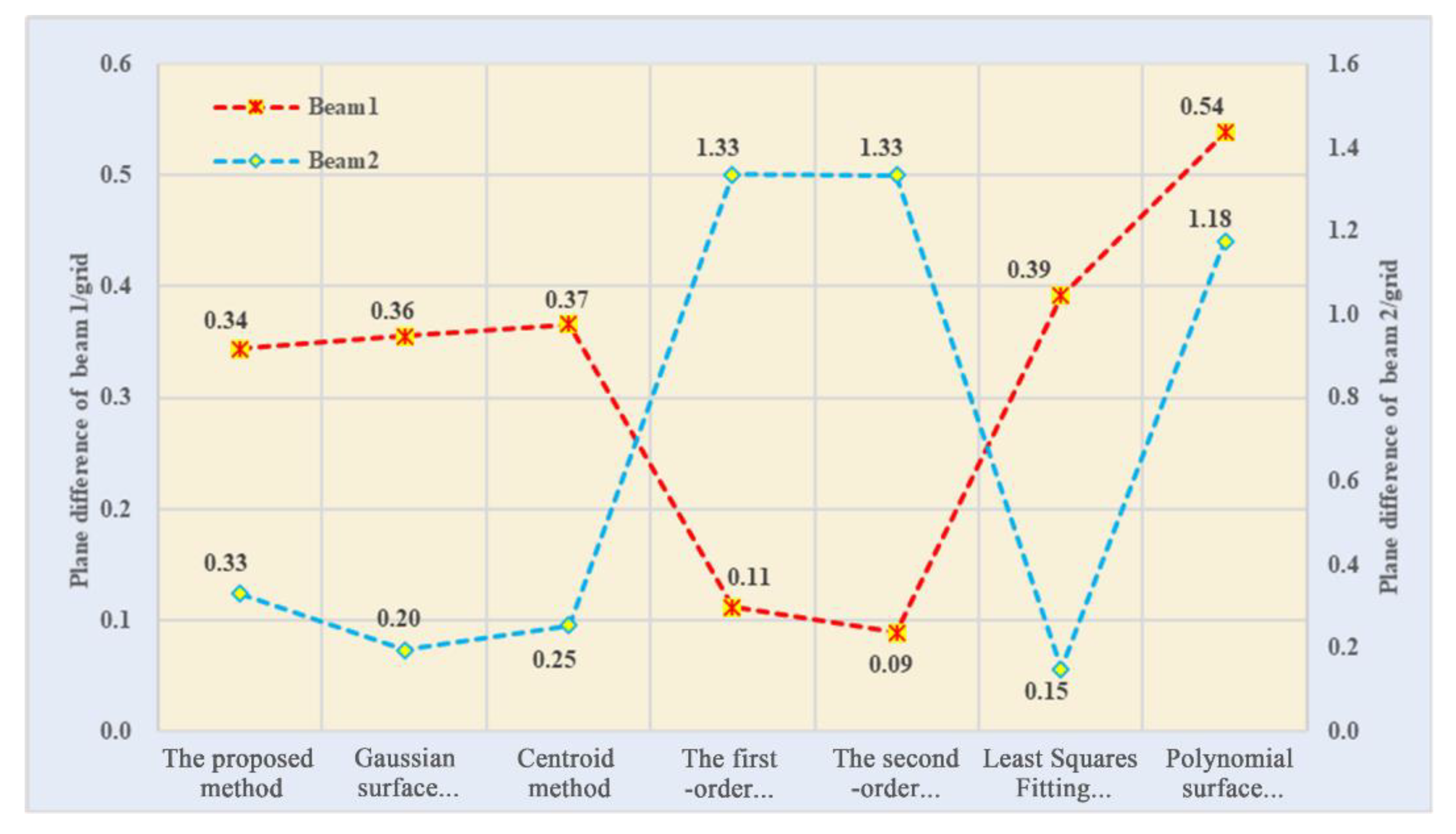
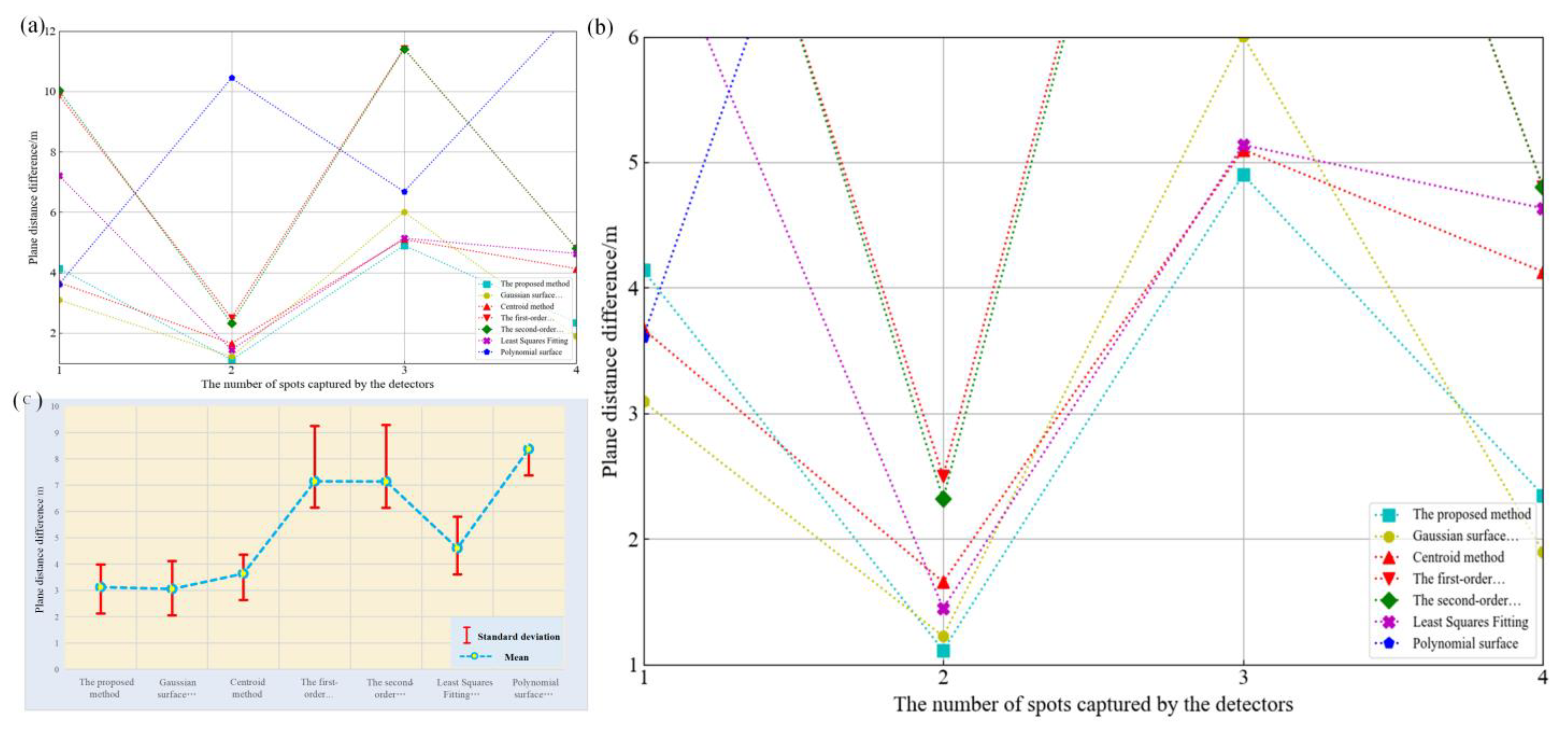
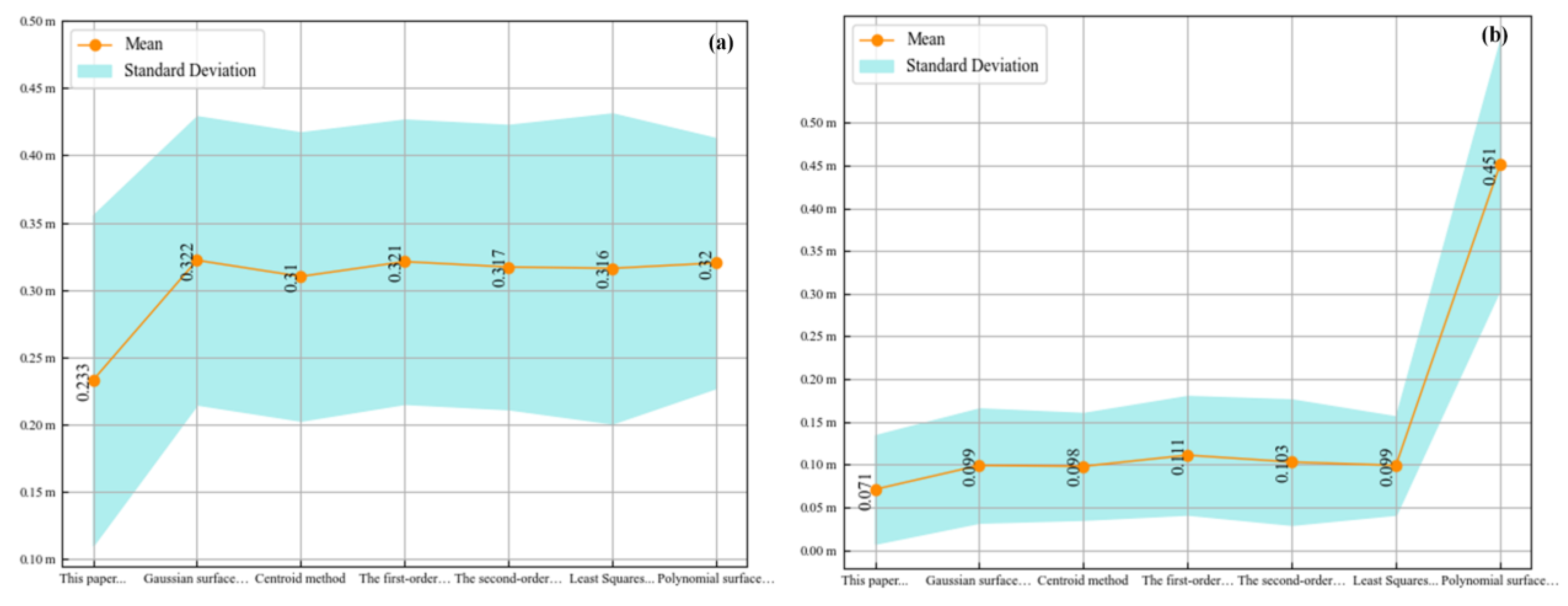
4.1. Verification of Relative Plane Accuracy
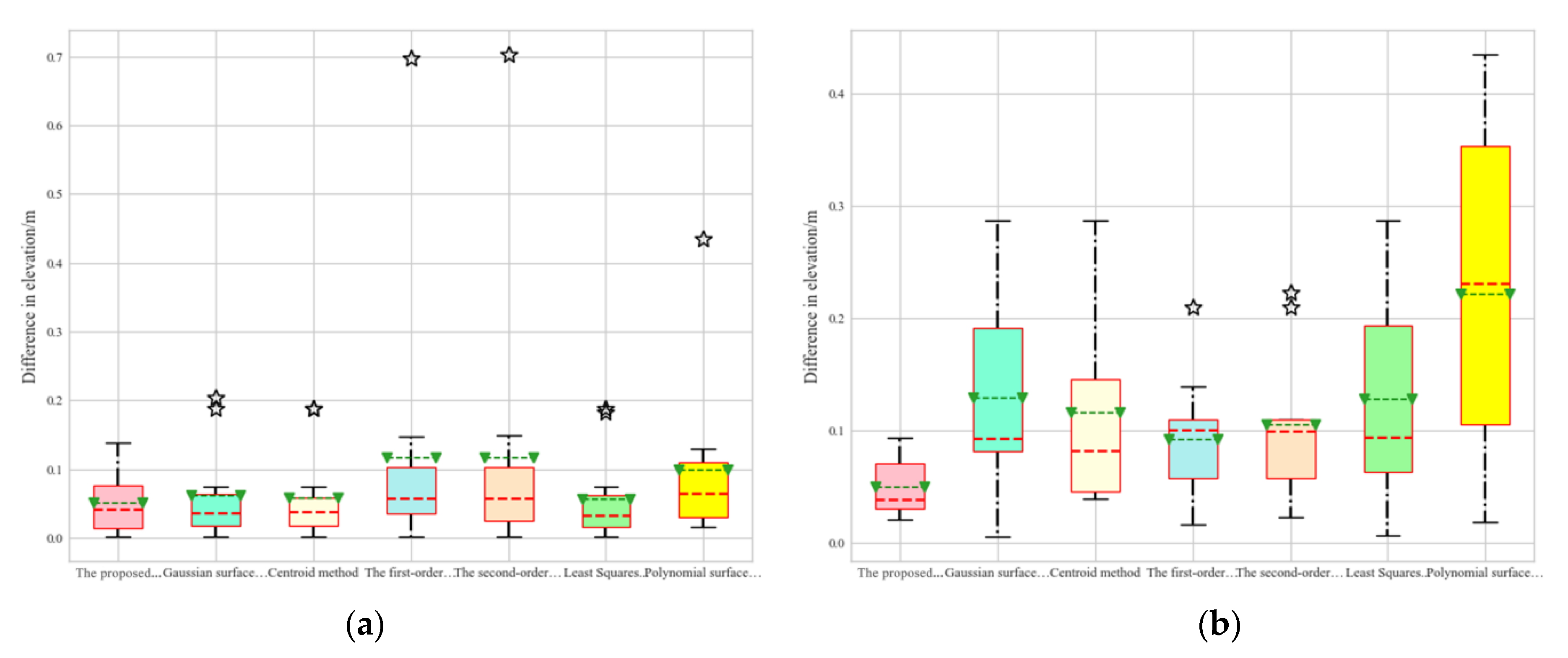
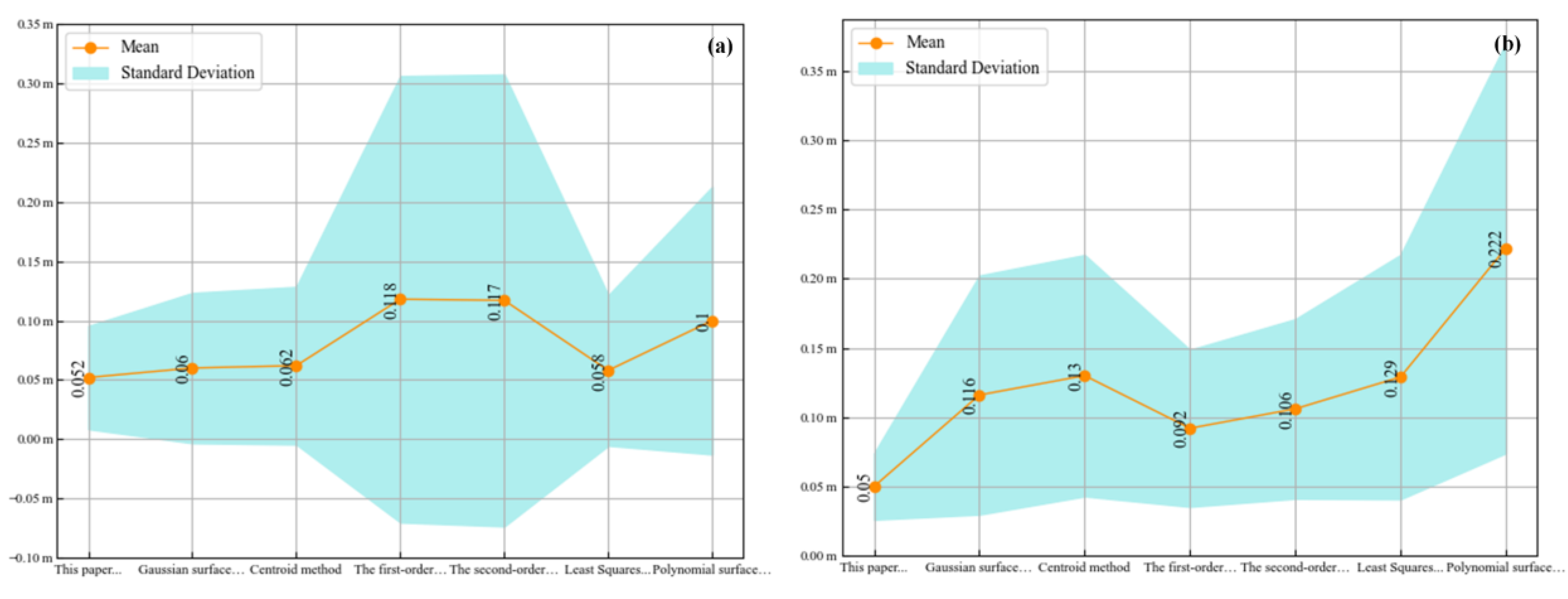
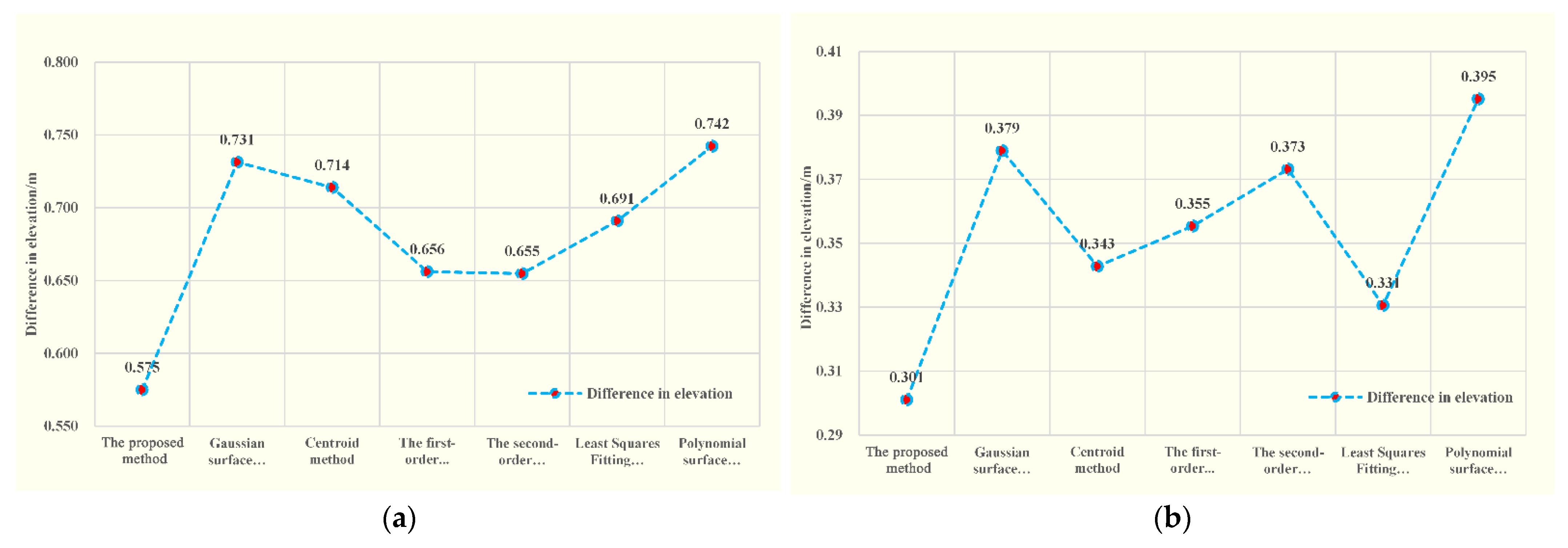
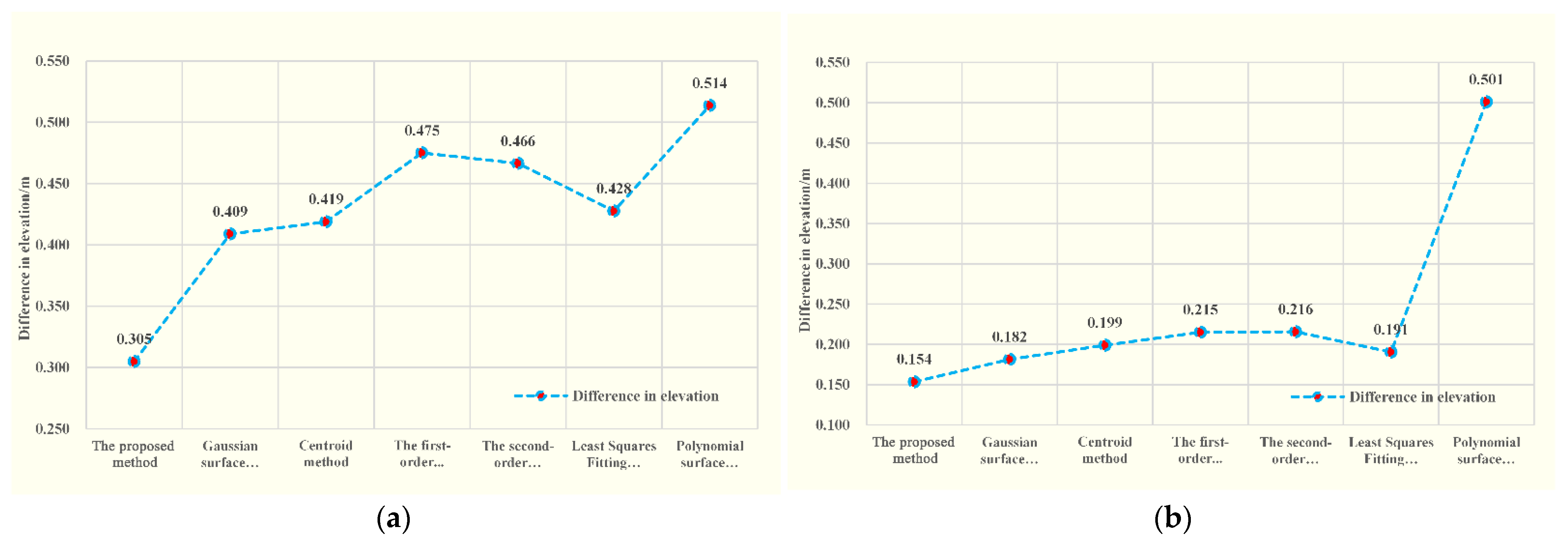
4.2. Verification of Elevation Accuracy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, X.; Xie, J.; Fu, X.; Mo, F.; Li, S.; Dou, X. ZY3-02 Laser Altimeter On-orbit Geometrical Calibration and Test. Acta Geod. Cartogr. Sin. 2017, 46, 714–723. [Google Scholar]
- Mattei, S.; Santovito, M.R.; Moccia, A. New rangefinder system for microsatellite. SPIE 2009, 41, 862. [Google Scholar]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, 97–116. [Google Scholar] [CrossRef]
- Abshire, J.B.; Sun, X.; Riris, H.; Sirota, J.M.; McGarry, J.F.; Palm, S.; Yi, D.; Liiva, P. Geoscience laser altimeter system (GLAS) on the ICESat mission: Pre-launch and on-orbit measurement performance. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1534–1542. [Google Scholar]
- Li, D. China’s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3. Acta Geod. Cartogr. Sin. 2012, 41, 317–322. [Google Scholar]
- Tang, X.; Xie, J.; Liu, R.; Huang, G.; Zhao, C.; Zhen, Y.; Tang, H.; Dou, X. Overview of the GF-7 laser altimeter system mission. Earth Space Sci. 2020, 7, 19–29. [Google Scholar] [CrossRef]
- Liu, R.; Xie, J.; Xu, C.; Zeng, J.; Mo, F.; Yang, X. A Separate Calibration Method of Laser Pointing and Ranging for the GF-7 Satellite Laser That Does Not Require Field Detectors. Remote Sens. 2022, 14, 5935. [Google Scholar] [CrossRef]
- Huang, G.; Ding, Y.; Wu, J.; Shu, R.; Wang, X.; Jiang, Z. Design and implementation of key technology of GF-7 satellite laser altimeter subsystem. Space Eng. 2020, 29, 68–73. [Google Scholar]
- Tang, X.; Xie, J.; Mo, F.; Dou, X.; Li, X.; Li, S.; Li, S.; Huang, G.; Fu, X.; Liu, R.; et al. GF-7 dual-beam laser altimeter on-orbit geometric calibration and test verification. Acta Geod. Cartogr. Sin. 2021, 50, 384–395. [Google Scholar]
- Xie, J.; Liu, R.; Wang, Z.; Mo, F.; Dou, X. In-orbit geometric calibration and accuracy evaluation of GaoFen-7 spaceborne laser altimeter. Infrared Laser Eng. 2021, 50, 20200396. [Google Scholar]
- Magruder, L.A.; Schutz, B.E.; Silverberg, E.C. Laser pointing angle and time of measurement verification of the ICESat laser altimeter using a ground-based electro-optical detection system. J. Geodesy. 2003, 77, 148–154. [Google Scholar] [CrossRef]
- Xie, J.; Tang, X.; Mo, F.; Tang, H.; Wang, Z.; Wang, X. In-orbit geometric calibration and experimental verification of the ZY3-02 laser altimeter. Photogramm. Rec. 2018, 33, 341–362. [Google Scholar] [CrossRef]
- Magruder, L.A.; Webb, C.E.; Urban, T.J.; Silverberg, E.C.; Schutz, B.E. ICESat Altimetry Data Product Verification at White Sands Space Harbor. IEEE Trans. Geosci. Remote Sens. 2006, 45, 147–155. [Google Scholar] [CrossRef]
- Waerbeke, L.V.; Mellier, V.; Erben, T.; Cuillandre, J.C.; Bernardeau, F.; Maoli, R.; Bertin, E.; Mc Cracken, H.G.; Le Fevre, O.; Fort, B.; et al. Detection of correlated galaxy ellipticities on CFHT data: First evidence for gravitational lensing by large-scale structures. arXiv 2000, arXiv:astro-ph/0002500. [Google Scholar]
- Zhan, Y.; Zheng, Y.; Zhang, C.; Ma, G.; Luo, Y. Image Centroid Algorithms for Sun Sensors with Super Wide Field of View. Acta Geod. Cartogr. Sin. 2015, 44, 1078–1084. [Google Scholar]
- Wang, H.; Zhou, W.; Lin, H.; Wang, X. Parameter estimation of Gaussian gray diffusion model of static image spot. Acta Opt. Sin. 2012, 32, 0323004. [Google Scholar] [CrossRef]
- Ren, S.; Tang, X.; Zhu, X.; Li, A.; Qu, D. A High-Precision Extraction Algorithm for Centroid of Laser Footprint Spot of GF-7 Satellite. Acta Opt. Sin. 2021, 41, 1012001. [Google Scholar]
- Yao, J.; Li, G.; Chen, J.; Zhou, X.; Guo, A.; Huang, G.; Tang, X.; Ai, B. Analysis on the change of GF-7 satellite laser altimeter spot centroid position. Infrared Laser Eng. 2021, 50, 20210539. [Google Scholar]
- Song, J.; Fan, D.; Ji, S.; Li, D.; Chu, G. Laser Spot Centroid Extraction of GF-7 Footprint Images. J. Geomat. Sci. Technol. 2021, 38, 507–513. [Google Scholar]
- Xie, J.; Liu, R.; Tang, X.; Yang, X.; Zeng, J.; Mo, F.; Mei, Y. A Geometric Calibration Method Without a Field Site of the GF-7 Satellite Laser Relying on a Surface Mathematical Model. IEEE Trans. Geosci. Remote Sens. 2022, 61, 1–14. [Google Scholar] [CrossRef]
- Senkal, E.; Kaplan, G.; Avdan, U. Accuracy assessment of digital surface models from unmanned aerial vehicles’ imagery on archaeological sites. Int. J. Eng. Sci. 2021, 6, 81–89. [Google Scholar] [CrossRef]
- Arasan, G.; Yılmaz, A.; Fırat, O.; Avşar, E.; Güner, H.; Ayğan, K.; Yüce, D. Accuracy assessments of Göktürk-1 satellite im agery. Int. J. Eng. Sci. 2020, 5, 160–168. [Google Scholar]
- Özcihan, B.; Özlü, L.D.; Karakap, M.İ.; Sürmeli, H.; Algancı, U.; Sertel, E. A comprehensive analysis of different geometric correction methods for the Pleiades -1A and Spot-6 satellite images. Int. J. Eng. Sci. 2023, 8, 146–153. [Google Scholar]
- Wu, Y.; Long, X.; Yang, J.; Han, Q.; Li, Q.; Li, S. Variation Law Analysis and Application of GaoFen-7 Laser Pointing. Acta Opt. Sin. 2021, 41, 2328003. [Google Scholar]
- Li, K.; Zhang, Y.; Meng, W. Point-Source-Target-Based Method for Space Remote Sensing Geometric Calibration and Positioning Accuracy Improvement. Acta Opt. Sin. 2020, 40, 1828003. [Google Scholar]
- Arthur, R.W.; Takis, K.; Brian, K. Adaptive median filter for the removal of periodic interference from an image. Phys. A 1994, 2238, 207–217. [Google Scholar]
- Xie, J.; Liu, R. Sliding window Gaussian fitting algorithm for ranging error suppression of full-waveform spaceborne laser. Acta Geod. Cartogr. Sin. 2021, 50, 1240–1250. [Google Scholar]
- Ren, S. Research on Laser Footprint Spot Assisted Laser Positioning of Gaofen-7 Satellite. Graduate. Degree Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2021. [Google Scholar]
- Tang, X.; Xie, J.; Wang, X.; Jiang, W. High-Precision Attitude Post-Processing and Initial Verification for the ZY-3 Satellite. Remote Sens. 2015, 7, 11–134. [Google Scholar] [CrossRef]
- Liang, B.; Zhu, H.; Zhang, T. Research status and development tendency of star tracker technique. Chin. Opt. 2016, 9, 16–29. [Google Scholar] [CrossRef]
- Fang, Y.; Jing, G.; Chao, Y. Research on Precise Orbit Determination Time Synchronization and Extended Application of LEO Constellation Based on GNSS. In Proceedings of the China Satellite Navigation Conference (CSNC 2022), Beijing, China, 25–27 May 2022; pp. 89–101. [Google Scholar]
- Yousif, H.; El-Rabbany, A. Assessment of several interpolation methods for precise GPS orbit. J. Navigat. 2007, 60, 443–455. [Google Scholar] [CrossRef]
- Maraş, E.E.; Nasery, N. Investigating the length, area and volume measurement accuracy of UAV-Based oblique photogrammetry models produced with and without ground control points. Int. J. Eng. Sci. 2023, 8, 32–51. [Google Scholar] [CrossRef]
- Liu, R.; Xie, J. Calibration of the laser pointing bias of the GaoFen-7 satellite based on simulation waveform matching. Opt. Express 2021, 29, 21844–21858. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Xie, J.; Gao, X.; Mo, F.; Feng, W.; Liu, R. The In-Orbit Calibration Method Based on Terrain Matching with Pyramid-Search for the Spaceborne Laser Altimeter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1053–1062. [Google Scholar] [CrossRef]



| Purpose | Data | Beam | Time | Filename | Timecode of Laser Footprint (s) |
|---|---|---|---|---|---|
| Calibration | GCPs | Beam 1 | 29 August 2021 | SYC-GF7-20210830-010119-0000011637_1 | 241,743,151.00, 241,743,151.33 |
| GCPs | Beam 2 | 13 September 2021 | MYC-GF7-20210914-010412-000011921_2 | 243,038,830.00, 243,038,830.33 | |
| Positioning verification (method one) | GCPs | Beam 1 | 29 August 2021 | SYC-GF7-20210830-010119-0000011637_1 | 241,743,151.00, 241,743,151.33 |
| GCPs | Beam 2 | 13 September 2021 | MYC-GF7-20210914-010412-000011921_2 | 243,038,830.00, 243,038,830.33 | |
| Positioning verification (method two) | CPs | Beam 1 | 14 June 2020 19 June 2020 24 June 2020 | SYC-GF7-20200614-003402-0000003397_1 SYC-GF7-20200619-003478-0000003529_1 KSC-GF7-20200624-003555-0000003615_1 | 203,600,254.00, 204,032,177.00, 204,464,095.00 |
| CPs | Beam 2 | 14 June 2020 19 June 2020 | SYC-GF7-20200614-003402-0000003397_1 SYC-GF7-20200619-003478-0000003529_1 | 203,600,253.33, 204,032,175.67 | |
| Elevation verification | RTK(CPs) | Beam 1 | 14 June 2020 19 June 2020 24 June 2020 29 August 2021 3 September 2021 13 September 2021 | SYC-GF7-20200614-003402-0000003397_1 SYC-GF7-20200619-003478-0000003529_1 KSC-GF7-20200624-003555-0000003615_1 SYC-GF7-20210830-010119-0000011637_1 MYC-GF7-20210903-010194-000011739_1 MYC-GF7-20210914-010412-000011921_1 | 203,600,253.67, 203,600,254.00, 204,032,175.67, 204,032,176.00, 204,032,176.33, 204,464,095.00, 204,464,097.33, 204,464,098.00, 241,743,149.00, 241,743,149.33, 241,743,149.66, 241,743,150.00, 241,743,150.33, 241,743,150.66, 243,038,830.33, 243,038,830.66, 242,175,040.66, 242,175,041.00. |
| Beam 2 | 14 June 2020 19 June 2020 24 June 2020 29 August 2021 13 September 2021 | SYC-GF7-20200614-003402-0000003397_2 SYC-GF7-20200619-003478-0000003529_2 KSC-GF7-20200624-003555-0000003615_2 SYC-GF7-20210830-010119-0000011637_2 MYC-GF7-20210914-0104120000011921_2 | 203,600,253.00, 203,600,253.33, 204,032,175.33 204,032,175.67, 204,032,176.00, 204,464,097.33 204,464,099.33, 204,464,099.67, 241,743,147.33, 241,743,148.00, 241,743,148.33, 241,743,154.00, 241,743,154.33, 243,038,830.67, 243,038,831.00, 243,038,831.67, 243,038,832.00, 243,038,832.33 | ||
| Laser Footprints | Beam 1 | 14 October 2020 | KRN-GF7-20201014-005278-0000005703_1 | 214,148,011.33, 214,148,011.66, 214,148,012.33, 214,148,012.66, 214,148,013.00, 214,148,013.33, 214,148,013.66, 214,148,014.00, 214,148,014.33, 214,148,014.66, 214,148,015.33, 214,148,015.66, 214,148,016.00, 214,148,016.33, 214,148,016.66, 214,148,017.00, 214,148,017.66, 214,148,018.00, 214,148,018.33, 214,148,018.66, 214,148,019.00, 214,148,019.33, 214,148,020.00. | |
| Beam 2 | 14 October 2020 | KRN-GF7-20201014-005278-0000005703_2 | 214,148,011.00, 214,148,011.33, 214,148,011.67, 214,148,012.00, 214,148,012.33, 214,148,013.33, 214,148,013.67, 214,148,014.00, 214,148,014.33, 214,148,014.67, 214,148,015.33, 214,148,015.67, 214,148,016.00, 214,148,016.33, 214,148,016.67, 214,148,017.00, 214,148,017.33, 214,148,017.67, 214,148,018.00, 214,148,018.33, 214,148,018.67, 214,148,019.00, 214,148,019.33, 214,148,019.67 | ||
| DSM | Beam 1/ Beam 2 | 10 October 2020 | High precision airborne LIDAR DSM | 214,148,011.33, 214,148,011.66, 214,148,012.33, 214,148,012.66, 214,148,013.00, 214,148,013.33, 214,148,013.66, 214,148,014.00, 214,148,014.33, 214,148,014.66, 214,148,015.33, 214,148,015.66, 214,148,016.00, 214,148,016.33, 214,148,016.66, 214,148,017.00, 214,148,017.66, 214,148,018.00, 214,148,018.33, 214,148,018.66, 214,148,019.00, 214,148,019.33, 214,148,020.00, 214,148,011.00, 214,148,011.33, 214,148,011.67, 214,148,012.00, 214,148,012.33, 214,148,013.33, 214,148,013.67, 214,148,014.00, 214,148,014.33, 214,148,014.67, 214,148,015.33, 214,148,015.67, 214,148,016.00, 214,148,016.33, 214,148,016.67, 214,148,017.00, 214,148,017.33, 214,148,017.67, 214,148,018.00, 214,148,018.33, 214,148,018.67, 214,148,019.00, 214,148,019.33, 214,148,019.67 |
| Centroid Extraction Methods | Beam 1 | Beam 2 | ||
|---|---|---|---|---|
| dα/(°) | dβ/(°) | dα/(°) | dβ/(°) | |
| The proposed method | 0.001464 | 0.002862 | 0.000223 | 0.001524 |
| Centroid method | 0.001465 | 0.002659 | 0.000206 | 0.001405 |
| Gaussian surface fitting | 0.001488 | 0.002694 | 0.000183 | 0.001312 |
| The first-order gray-scale weighting method considering the detectors | 0.001048 | 0.002672 | 0.000142 | 0.001264 |
| The second-order gray-scale weighting method considering the detectors | 0.001052 | 0.002685 | 0.000132 | 0.001273 |
| Least Squares Fitting of Ellipses | 0.00144 | 0.002649 | 0.000203 | 0.00131 |
| Polynomial surface fitting | 0.001484 | 0.002695 | −0.00095 | 0.00104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Xie, J.; Liu, R.; Mo, F.; Zeng, J. Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data. Remote Sens. 2023, 15, 2129. https://doi.org/10.3390/rs15082129
Yang X, Xie J, Liu R, Mo F, Zeng J. Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data. Remote Sensing. 2023; 15(8):2129. https://doi.org/10.3390/rs15082129
Chicago/Turabian StyleYang, Xiaomeng, Junfeng Xie, Ren Liu, Fan Mo, and Junze Zeng. 2023. "Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data" Remote Sensing 15, no. 8: 2129. https://doi.org/10.3390/rs15082129
APA StyleYang, X., Xie, J., Liu, R., Mo, F., & Zeng, J. (2023). Centroid Extraction of Laser Spots Captured by Infrared Detectors Combining Laser Footprint Images and Detector Observation Data. Remote Sensing, 15(8), 2129. https://doi.org/10.3390/rs15082129







