Next Article in Journal
Holistic Reduction to Compare and Create New Indices for Global Inter-Seasonal Monitoring: Case Study for High Resolution Surface Water Mapping
Previous Article in Journal
Reconstructing Digital Terrain Models from ArcticDEM and WorldView-2 Imagery in Livengood, Alaska
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 8
10.3390/rs15082064
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Systematic Evaluation of Four Satellite AOD Datasets for Estimating PM2.5 Using a Random Forest Approach

by
Jana Handschuh
*,
Thilo Erbertseder
and
Frank Baier
German Aerospace Center (DLR), German Remote Sensing, Data Center (DFD), 82234 Weßling, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(8), 2064; https://doi.org/10.3390/rs15082064
Submission received: 8 March 2023 / Revised: 3 April 2023 / Accepted: 11 April 2023 / Published: 13 April 2023
Browse Figures
Versions Notes

Abstract

:
The latest epidemiological studies have revealed that the adverse health effects of PM2.5 have impacts beyond respiratory and cardio-vascular diseases and also affect the development of the brain and metabolic diseases. The need for accurate and spatio-temporally resolved PM2.5 data has thus been substantiated. While the selective information provided by station measurements is mostly insufficient for area-wide monitoring, satellite data have been increasingly applied to comprehensively monitor PM2.5 distributions. Although the accuracy and reliability of satellite-based PM2.5 estimations have increased, most studies still rely on a single sensor. However, several datasets have become available in the meantime, which raises the need for a systematic analysis. This study presents the first systematic evaluation of four satellite-based AOD datasets obtained from different sensors and retrieval methodologies to derive ground-level PM2.5 concentrations. We apply a random forest approach and analyze the effect of the resolution and coverage of the satellite data and the impact of proxy data on the performance. We examine AOD data from the Moderate resolution Imaging spectroradiometer (MODIS) onboard Terra and Aqua satellites, including Dark Target (DT) algorithm products and the Multi-Angle Implementation of Atmospheric Correction (MAIAC) product. Additionally, we explore more recent datasets from the Sea and Land Surface Temperature Radiometer (SLSTR) onboard Sentinel-3a and from the Tropospheric Monitoring Instrument (TROPOMI) operating on the Sentinel-5 precursor (S5p). The method is demonstrated for Germany and the year 2018, where a dense in situ measurement network and relevant proxy data are available. Overall, the model performance is satisfactory for all four datasets with cross-validated R2 values ranging from 0.68 to 0.77 and excellent for MODIS AOD reaching correlations of almost 0.9. We find a strong dependency of the model performance on the coverage and resolution of the AOD training data. Feature importance rankings show that AOD has less weight compared to proxy data for SLSTR and TROPOMI.

Graphical Abstract

1. Introduction

According to the World Health Organization [1], almost the entire global population breathes air that is impaired with harmful substances. Fine particulate matter with particle sizes smaller than 2.5 μm (PM2.5) is one of the most harmful air pollutants causing serious health risks and premature deaths worldwide. PM2.5 is capable of entering the bloodstream, lungs and other organs, causing a wide range of diseases, such as asthma [2,3], lung cancer [4,5], other lung dysfunctions [6,7], cardiovascular diseases [8] or even brain damage [9] and diabetes [10]. It is further linked to influenza incidence [11] and the severity of COVID-19 [12]. In 2020, more than 96% of the population of the European Union (EU) lived in areas where the WHO guideline concentration of PM2.5 was exceeded, resulting in over 200.000 premature deaths [13]. Germany is located in the center of the EU and is suffering from both trans-boundary transport and local traffic, industrial and agricultural emissions. It is important to increase our understanding of processes leading to high surface PM concentrations and its distribution to appropriately assess the related health risks. Comprehensive monitoring and mapping are therefore essential and rely on data that can adequately reflect the temporal and spatial variability in ground-level PM2.5 concentrations.
Well-developed in situ station networks, providing accurate and frequent PM2.5 measurements, form an important basis for the investigation of temporal variations. However, they are not able to depict the spatial variability in the aerosol distribution between measurement sites. In contrast, satellite observations of the aerosol optical depth (AOD) have been effectively proven to be a complementary data source to obtain area-wide information on aerosol distributions [14]. AOD quantifies the aerosol load of the atmosphere by measuring the light extinction by particles in the atmospheric column.
A variety of methods have been developed to derive PM2.5 surface concentrations from satellite-based AOD observations in the last two decades, using different datasets and considering various study regions and time periods. A review can be found in the work of Chu et al. or Zhang et al. [15,16]. Most of the studies used observation-based approaches for PM2.5 estimations, including simple and multiple linear regression models [17,18,19], geographically and temporally weighted regression models [20,21] and mixed-effects models [22]. Other methods are based on chemical transport modeling [23,24] or empirical physical models [25,26].
The relationship between AOD and PM2.5 is complex and depends on several factors, most importantly meteorological conditions, but also on aerosol composition and the vertical particle distribution [27]. The mentioned methods are capable of predicting PM2.5 concentrations from AOD, but their accuracy is limited since they cannot adequately reproduce the spatial and temporal heterogeneity of these influencing factors [28]. In recent years, the application of machine learning (ML) approaches has increased drastically in the field of air quality and in particular in predicting PM2.5 from AOD [29]. ML methods have been proven to efficiently combine information on PM2.5, AOD and other spatial–temporal varying predictors. Several studies have compared the performance of different ML methods for PM2.5 predictions, such as simple decision trees, random forests, support vector machines or Gradient Boosting, and a majority of them found random forest (RF) to perform the best [30,31,32,33,34,35]. The RF models allow for the consideration of numerous parameters for very accurate PM2.5 predictions and provide importance measures to assess the influence of the respective parameters on the model’s accuracy.
Several studies using RF for AOD-based PM2.5 estimations were performed for Asia, including different parts of China [28,35,36,37,38], Thailand [34,39] and Iran [40]; fewer focused on the United States [41,42,43] and Europe, including Italy [44] and Great Britain [45].
All these studies show the very good performance of the RF approach to predict PM2.5 using satellite AOD and other input variables. Nevertheless, there are differences in the accuracies of the resulting PM2.5 concentrations. The performance of an RF model is highly dependent on the parameter selection for model training and the quality of the input data themselves. The quality of satellite AOD data as the most important predictor for ground-level PM2.5 concentrations is, for example, affected by cloud contamination, heterogeneous surface conditions and retrieval accuracies [46]. Furthermore, the data availability of satellite AOD data, which can be very limited, e.g., due to cloudiness, can highly influence the RF model performance. This holds not only for RF, but for most of the regression-based models. Individual studies combined different AOD datasets to enlarge the sample size for accurate PM2.5 predictions [25,47] or used model data to obtain full-coverage AOD datasets [41,44].
A variety of AOD datasets have previously been used for PM2.5 estimations using RF, with most of the studies using a single AOD dataset alone. The most commonly used AOD datasets for worldwide PM2.5 estimations are those from the Moderate Resolution Imaging Spectroradiometer (MODIS) onboard the NASA satellites Aqua and Terra [48]. Nowadays, several AOD products exist based on MODIS observations derived by different retrieval algorithms and with different spatial resolutions. For Europe and other vegetation-dominated regions, the Dark Target (DT) algorithm products in 10 km and 3 km spatial resolution are widely used. On the one hand, the 3 km product has the advantage of providing the spatial aerosol distribution in more detail; on the other hand, the data availability can be very limited over bright surfaces [49]. Hu et al. estimated PM2.5 concentrations with a random forest model for the US using Aqua/MODIS AOD in 3 km resolution (combined DT and Deep Blue—DB) and achieved a cross-validated R2 of 0.8 [41]. Zamani Joharestani et al. used the same dataset for PM2.5 estimations over Tehran, Iran, and achieved an R2 of 0.78 [40].
The most recently released MODIS-based AOD product is retrieved by means of the Multi-Angle Implementation of Atmospheric Correction (MAIAC) algorithm with a spatial resolution of 1 km. Due to improved cloud screening and an enhanced radiative transfer model for the retrieval [50], the MAIAC dataset is the one with the best coverage (sample size) and spatial detail compared to the DT products, and this makes it very attractive for regional air quality studies. For example, Di et al., Stafoggia et al. and Schneider et al. used MAIAC data to estimate PM2.5 concentrations based on RF for the US, Italy and Great Britain [43,44,45]. They achieved model accuracies of 0.85, 0.8 and 0.77, respectively.
However, the MODIS expected operation time is already exceeded [51]. In near-future next-generation satellite instruments such as the Visible Infrared Imaging Radiometer Suite (VIIRS) operating on Suomi NPP and NOAA-20 satellites, Sea and Land Surface Temperature Radiometer (SLSTR) onboard Sentinel-3a/b, the Ocean and Land Colour Instrument (OLCI), the Tropospheric Monitoring Instrument (TROPOMI) onboard Sentinel-5p or products obtained from geostationary satellites such as Sentinel-4, which will allow a continuation of the long-term aerosol data collection.
In this study, we present a first systematic evaluation of four AOD datasets as predictors for ground-level PM2.5 concentrations using the RF approach. We examine the performance of the individual AOD products for PM2.5 prediction and evaluate the impact of dataset characteristics such as resolution or coverage on the accuracy of the RF models. Furthermore, we perform a feature importance analysis to investigate the influence of several variables on the power of our random forest models. This study is the first to exploit TROPOMI AOD observations for ground-level PM2.5 estimation. We focus on central Europe as a target region, and in particular, Germany, which is a region with diverse land-use classes and thus strongly varying spatio-temporal aerosol distribution. Large clean air areas alternate with polluted ones suffering from the long-range transport of aerosol but also from local emissions. The network of in situ station measurements is well developed in central Europe, enabling a high-quality validation of the applied method. In addition, high-quality proxy data from satellite and atmospheric models are available for the target region. Finally, an RF-based derivation of the surface PM2.5 concentration for this most populated country in the European Union is still pending.
Section 2 gives an overview of the data used in this study and the development of RF models. The results are then shown in Section 3, followed by a detailed discussion in Section 4. In Section 5, we summarize the results and draw the main conclusions.

2. Materials and Methods

2.1. Study Region

Our target region is defined from 46°N to 56°N and 2°E to 16°E and covers Germany and parts of the surrounding countries of Poland, the Czech Republic, Austria, Switzerland, France, Belgium, Luxembourg and The Netherlands. The terrain height is generally sloping from the mountains of the Alps in the south to the North Sea in the northwest and the Baltic Sea in the northeast. The land use in Germany is very heterogenous. The west is dominated by industry, the north and east are more dominated by agriculture, and the south is covered by large forests. The biggest cities with over 1 Mio. inhabitants are the capital of Berlin in the east, Hamburg in the north, Munich in the south and Cologne in the west as part of the highly industrially polluted Ruhr region. The road and highway network are well developed and frequently used, causing a lot of country intern traffic emissions. According to the EEA, energy consumption is the principal source of PM2.5 in the EU, followed by industry and transport/traffic [52]. However, agricultural activity and, in particular, ammonia emissions from farming also contribute a significant proportion to PM pollution [53]. In Germany, high PM levels can be mainly linked to agricultural activity in the northwest, central and easterly areas, but also in the Rhine valley in the southwest. Agricultural emissions have a strong seasonal dependency and are more severe in spring and autumn when fertilization usually takes place.

2.2. Datasets

Multiple datasets, including in situ measurements, satellite data and atmospheric model data, were obtained and processed for the complete year 2018 and the study region described above. The year was chosen as it was a special year with high temperatures and little precipitation, resulting in very dry conditions in the second half of the year. In addition, the coverage with satellite data was better for 2018 compared to other years, at least in the summer period.

2.2.1. PM2.5 Station Data

In situ station measurements of PM2.5 concentrations are provided by the European Environment Agency (EEA) on their download platform [54]. We downloaded the E2a dataset which provides hourly data for almost all stations; otherwise, daily mean data are available. Our study region comprised 350 stations in Germany (175), Poland (3), the Czech Republic (32), Austria (24), Switzerland (1), France (54), Belgium (35), Luxembourg (4) and The Netherlands (24). We used every available station, disregarding the station type (background, industrial or traffic) or background (rural, urban or suburban). For all stations with hourly data, we calculated a daily mean value, requiring a minimum of six hourly measurements per day.

2.2.2. Satellite AOD Data

In this study, we used four different satellite AOD datasets. Their characteristics are listed in Table 1. Two of the datasets are based on observations by the MODIS instruments aboard the Terra and Aqua satellites and are retrieved by two different algorithms, MAIAC and DT (hereafter the MODIS-DT dataset). We retrieved the MAIAC combined Terra/Aqua AOD product (MCD19A2) from NASA’s LAADS DAAC download service [55] and the 3 km DT products for Terra (MOD04_3K) and Aqua (MYD04_3K). We combined the DT products, applying a regression procedure for accurate averaging of the datasets [25,56]. Therefore, we performed a linear regression on collocated pixel data from both products on a seasonal basis and used the obtained linear relationship to predict daily AOD values for pixels where one of the products had missing values. The combined AOD product thus contained averages from two values per day for each pixel.
Besides the MODIS-based AOD products, which are well-established in air quality research, we used more recent datasets from the Copernicus Missions Sentinel-3a (SLSTR instrument) and Sentinel-5p (TROPOMI instrument).
The most important differences between the datasets are the sensor characteristics, determining retrieval frequencies and spatio-temporal resolution, as well as the retrieval algorithms. The retrieval algorithms are the main sources of uncertainty in the AOD values. Retrieval accuracies depend on several factors including radiance calibration, the treatment of the underlying surface, cloud screening or the applied aerosol model for aerosol type classification [57]. In principle, all four algorithms work very similarly, utilizing a spectral difference between aerosol particles in the atmosphere and the Earth’s surface and computing AOD from these using look up tables based on radiative transfer models. However, they differ regarding the mentioned factors. For more detail, see the references given in Table 1.
The orbital AOD data (polygons) of each product were merged daily and resampled onto a fixed regular longitude–latitude grid at 0.01° spatial resolution, following the application of Müller et al. [58]. For the MODIS and SLSTR products, we did not apply any quality checks. This proved adequate in our previous study [25]. Regarding the TROPOMI data, we adhered to the highly recommended quality levels and neglected all data with a corresponding cloud fraction value higher than 0.1 (10% cloud cover) to avoid the cloud contamination of individual footprints.
Table
Table 1. Overview of the different AOD datasets with key references.
Table 1. Overview of the different AOD datasets with key references.
MODIS-DTMAIACSLSTRTROPOMI
SatelliteTerra/AquaTerra/AquaSentinel-3aSentinel-5p
Overpass time10:30/13:3010:30/13:3010:3013:30
InstrumentMODISMODISSLSTRTROPOMI
in operation since2000/20022000/200220172017
Instrument modeRadiometer
(Nadir-view)		Radiometer (Nadir-view)Dual-view
radiometer (Nadir/along-track)		Spectrometer
(Nadir-view)
Swath width2330 km2330 km1400 km/740 km2600 km
AOD RetrievalDark Target AlgorithmMulti-Angle Implementation of Atmospheric Correction AlgorithmSwansea University AlgorithmNASA TropOMAER Algorithm
ReferenceLevy et al. [59], Remer et al. [49]Lyapustin et al. [50]North and Heckel [60]Torres et al. [61]
Resolution3 km × 3 km1 km × 1 km10 km × 10 km5.5 km × 3.5 km
AOD wavelength550 nm550 nm550 nm500 nm

2.2.3. Meteorological Fields

Numerous meteorological parameters linked to horizontal and vertical aerosol distribution were considered in this study. Therefore, we used high-resolution forecast data provided by the European Centre for Medium-Range Weather Forecasts (ECMWF), and in particular, the Atmospheric High Resolution 10-day forecast (SetI—HRES) dataset. We applied daily atmospheric fields for a single timestep at 12 p.m. at 0.1° spatial resolution for a total of 13 parameters listed in Table 2. The horizontal wind components enabled us to calculate the wind speed. All the data were resampled to the same 0.01°-grid as the AOD data.

2.2.4. Additional Satellite Data

To possibly link surface variability and processes to aerosol variability, we considered additional satellite datasets for surface parameters such as the land surface temperature (LST) and the Normalized Difference Vegetation Index (NDVI). Both parameters were obtained from the MODIS sensor and were provided via the NASA data hub LAADS DAAC. We used daily LST data for both the Aqua and Terra MODIS instruments (MYD11A1, MOD11A1) with 1 km spatial resolution [65]. In order to have the best possible coverage for the model training, we first combined the daily Terra and Aqua MODIS data and then calculated the monthly mean LST fields. NDVI data are also available from both the Aqua and Terra MODIS instruments [66]. We used the combined monthly datasets MYD13A3 (Aqua) and MOD13A3 (Terra) with 1 km spatial resolutions. Both datasets were resampled to the joint 0.01°-grid.

2.3. Methods

2.3.1. Random Forest Models

Random forest is a machine learning method introduced by Breiman [67], allowing for high-accuracy predictions of a target variable using multiple independent predictor variables. In principle, the method consists of building an ensemble of decision trees based on different subsets of the training data. Output is an ensemble prediction of the target variable averaged over all decision trees. Each tree is grown using a randomly chosen bootstrap sample of the training data. Further sampling is carried out at each split of the tree by randomly selecting a subset of predictor variables that are available for the split. Due to the introduction of this randomness, the RF approach is not prone to overfitting as simpler regression methods are [38]. Compared to other machine learning algorithms, RF is user-friendly, it requires relatively small computing times, no normalization to scale the input variables is needed and it is straightforward to interpret. Another advantage of the RF algorithm is its ability to estimate feature importance by quantifying the increase in prediction error when the respective predictor variable is permuted. Once an RF model is built, no further data on the target variable are needed, and it can be applied for any set of predictor variables. This means for spatial data, it can be applied to any grid point that is covered by the predictor variables, and no interpolations need to be conducted.

2.3.2. Model Development

For this study, we developed RF models using in situ PM2.5 concentrations (in μg/m3) as target variables and a total of 24 parameters as (potential) predictor variables, which are listed in Table 2. In addition to the data described above, we used data for land cover, PM2.5 emissions, population density and some dummy variables to incorporate spatial–temporal dependencies (month, season, day of year, station elevation, longitude and latitude). We applied the open-source software R for model development (“randomForest” package) and data analysis [68]. First of all, the data were prepared for RF by spatially and temporarily collocating the spatial data with the station measurements. Therefore, we used a nearest-neighbor method, choosing the grid boxes closest to the station locations. The daily station-wise data for each variable were merged to one dataset. As R requires data frames without any missing values as input for the “randomForest” function, we read the dataset containing the station collocations to a data frame and removed all lines containing at least one missing value. To gain the maximum possible sample size for each dataset, this process was repeated for each of the four AOD datasets separately. Hence, the sample sizes for the model training differed depending on the AOD dataset considered. Initially, we trained the RF randomly using 75% of the sample including MAIAC-AOD and all other mentioned variables as training data with default settings for the “randomForest” function [68]. Next, we performed an empirical variable selection using the increased mean square error (IncMSE) as an importance measure and additional statistical indicators such as the coefficient of determination (R2), Pearson correlation coefficient (R) and the root mean square error (RMSE) to assess the model performance for the complete year depending on the incorporation of different variable combinations for the training. Space-related variables such as elevation or geographical coordinates, as well as surface-related variables such as albedo and land cover lowered the performance in terms of the mentioned statistical indicators and were eliminated after checking their individual influences on the model. All other variables with importance ranking in the lower third of absolute importance were tested for their effect on the model performance in the same way. Finally, a combination of 15 predictors was needed to attain maximum accuracy. These were AOD, boundary layer height (BLH) in meters, monthly LST (LSTm) in Kelvin, NDVI, relative humidity (RH) in %, temperature (T) in Kelvin, wind speed (W) in m/s, surface pressure (SP) in hPa, downward solar radiation at surface (SSR) in J/m2, downward thermal radiation at surface (STR) in J/m2, convective available potential energy (CAPE) in J/kg, dewpoint temperature (D) in Kelvin, direct solar radiation (DSR) in J/m2 and month and day of the year (DoY). With this final set of training variables, we tuned the RF model by finding the best configuration for the hyperparameters mtry (number of available variables for each split) and ntree (number of trees). The best performance was found for mtry between 3 and 6 and ntree ≥ 500. For convenience, we decided on the setting mtry = 5 and ntree = 1000 for the final model setup.
Importance values to determine the effects of the variables in the random forest models were obtained by the R “randomForest” function during the model training process [68]. Therefore, a permutation feature importance method was used, which calculates the increase in prediction error (MSE) when permuting the values of a variable. The “importance” function of the “randomForest” package provides importance values as increased MSE in %.

2.3.3. Cross-Validation and Final Model Setup

The final model settings were used to train four different RFs, one for each AOD dataset. Subsequently we performed a 10-fold cross-validation (CV) for each model to assess the model performance and accuracy in terms of R2, R, RMSE and the mean difference between predictions and observations (Bias). Therefore, the data were randomly split into 10 subsets; 9 of them were used for training and 1 for prediction/validation. This procedure was repeated 10 times. In this way, each subset was held out for validation once. CV statistics were then calculated using the predictions from all ten model runs.
For the final training of the RF models, we used all available PM2.5-AOD collocations. Lastly, these final models were applied to predict daily area-wide PM2.5 concentration maps for Germany and surrounding countries from the different AOD datasets.

3. Results

3.1. Model Performances

Four satellite AOD datasets were used to train RF models for ground-level PM2.5 prediction. These datasets have different characteristics such as observation time, observing geometry, spatial resolution and retrieval algorithms (see Table 1), leading to differences in AOD coverage and collocated AOD values. Table 3 gives some basic numbers on the datasets for an initial comparison. In total, all datasets covered nearly 100% of the study region, gathering all observations in 2018, but with rather low mean daily coverages between 5.5% (SLSTR) and 19% (MODIS-DT). The spatio-temporal AOD averages over the whole study region in 2018 ranged from a minimum value of 0.13 ± 0.06 for MAIAC to the maximum of 0.22 ± 0.06 for TROPOMI. The clearly higher AOD mean value for TROPOMI can be explained by the lower retrieval wavelength. Note that the number of collocations with station measurements available for the model training was less than 20% for all datasets. This means 80% of potential collocations were not available due to missing satellite observations.
Hereafter, our different RF models will be designated after the incorporated AOD datasets. The sets of all other variables were identical in each model, disregarding the deviating set of in situ samples depending on the exact collocations with station measurements.
Figure 1 and Table 4 show the overall cross-validation results and statistics of the different models for the entire study area and study period. All models performed very well in predicting ground-level PM2.5 concentrations in Germany, showing high correlations with in situ data between 0.84 and 0.88. The accuracy of the models is given in terms of R2. The highest accuracy could be achieved with MAIAC with an R2 of 0.77, followed by 0.74, 0.70 and 0.68 for MODIS-DT, TROPOMI and SLSTR, respectively. The errors of the predicted PM2.5 concentrations were rather low for all models. RMSE values ranged from 3.51 μg/m3 for TROPOMI to 4.36 μg/m3 for MODIS-DT. Biases were constantly positive but very low, indicating a minimal overestimation of the predicted PM2.5 concentrations. The lowest bias could be found for TROPOMI with 0.08 μg/m3 equating to 0.76%. The maximum bias of 0.13 μg/m3 (0.97%) was associated with the MAIAC predictions. The density scatter plots in Figure 1 further illustrate the good agreement between predicted and measured PM2.5 concentrations. The value ranges for SLSTR and TROPOMI were in general a bit lower than that of MAIAC and MODIS-DT, but distributions were very similar for all models with a majority of PM2.5 concentrations below 25 μg/m3. A slight overestimation by the models could be observed in the lower value range (<25 μg/m3), predicting higher PM2.5 values compared to in situ measurements. In higher value ranges (>25 μg/m3), the models slightly underestimated the actual concentrations.
The prediction accuracies of the models were relatively constant over the year, as there were only minor variations in all statistical parameters for the different seasons (see Table 4). The model performances were slightly better for winter and spring compared to summer and autumn. The maximum differences in R2 and correlation could be found between spring and summer for all models, with the highest values in summer. Biases ranged from 0.06 μg/m3 (0.4%) to 0.16 μg/m2 (1.2%), with both values related to the SLSTR model in spring and winter, respectively. The maximum RMSE was found for spring for the MODIS-DT predictions with a value of 4.38 μg/m3. In general, however, the seasonal variation in the model performance was almost negligible.
We also investigated the spatial variation in the model performances by considering station-wise CV statistics and found no striking variability. The range of R2 lay between 0.26 for SLSTR and 0.14 for MODIS-DT with maximum R2 values of 0.8 and 0.85, respectively. The higher the R2 range, the higher the spatial variation in model accuracy. Thus, MODIS-DT showed the lowest variation and thereby strongest spatial robustness for the study region, followed by MAIAC, TROPOMI and SLSTR. The same was true for correlations with ranges from 0.09 to 0.17 and RMSEs with ranges between 1.39 μg/m3 and 2.22 μg/m3.
The station-wise relative bias is shown in Figure 2, together with the final annual mean PM2.5 predictions. There were both positive and negative biases, but positive biases predominated. The bias range was again the largest for SLSTR with a value of 8.5%; the minimum range could be found for MAIAC with 4.7%. Still, the mean bias of all stations lay under 1% for all models. The spatial variation in the bias showed no significant pattern. There were both positive and negative biases, and one could not relate these to remarkable high or low mean PM2.5 concentrations or to certain geographical areas. All datasets showed similar patterns in the PM2.5 distribution, even though the value ranges differed. The spatial averages for MODIS-DT, MAIAC and SLSTR were in a very close range with 14.2 ± 4.7 μg/m3, 13.4 ± 4.7 μg/m3 and 14.2 ± 4.2 μg/m3, respectively. The lowest average was found for TROPOMI-PM2.5 with 11.2 ± 3.0 μg/m3.

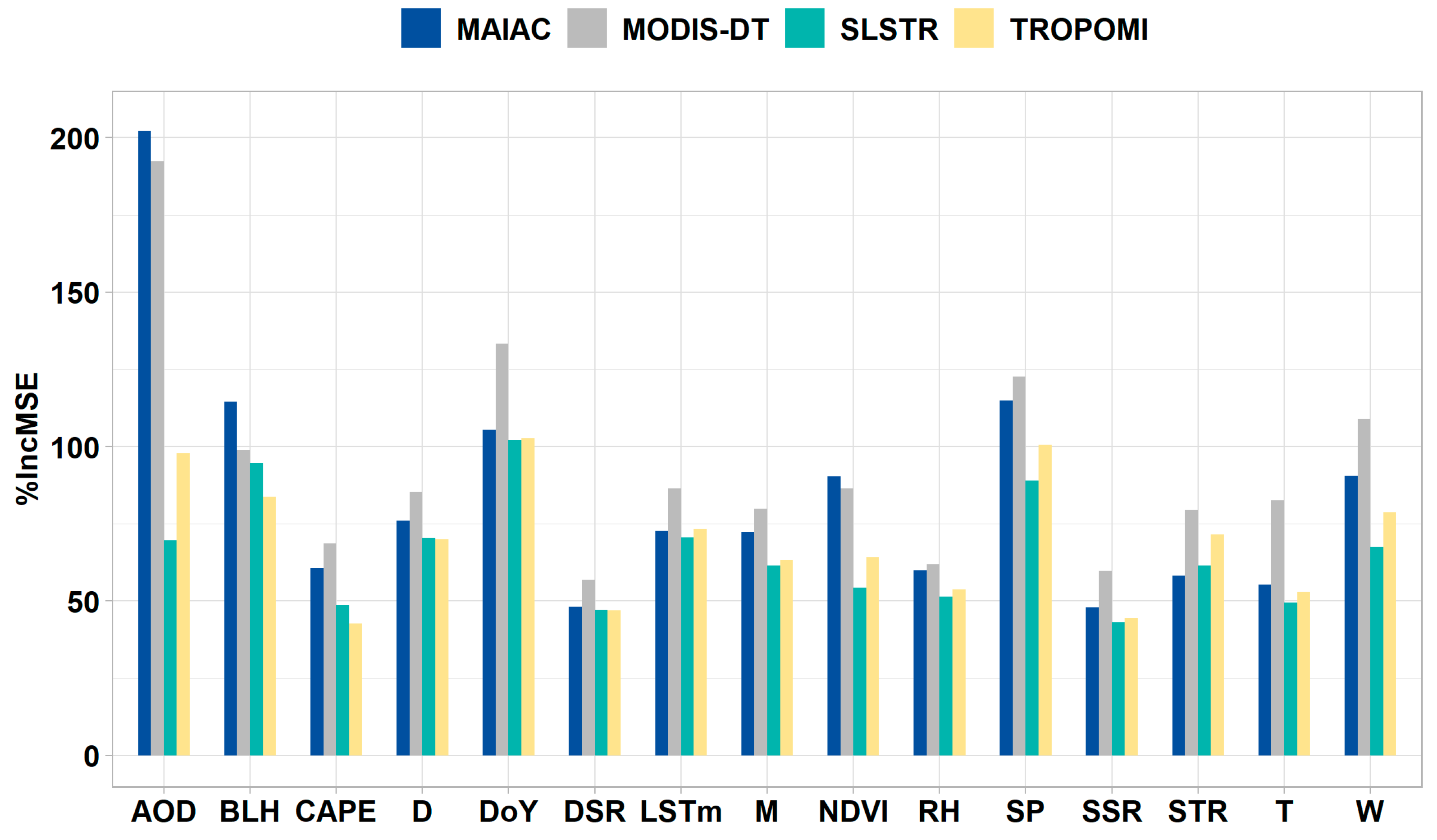
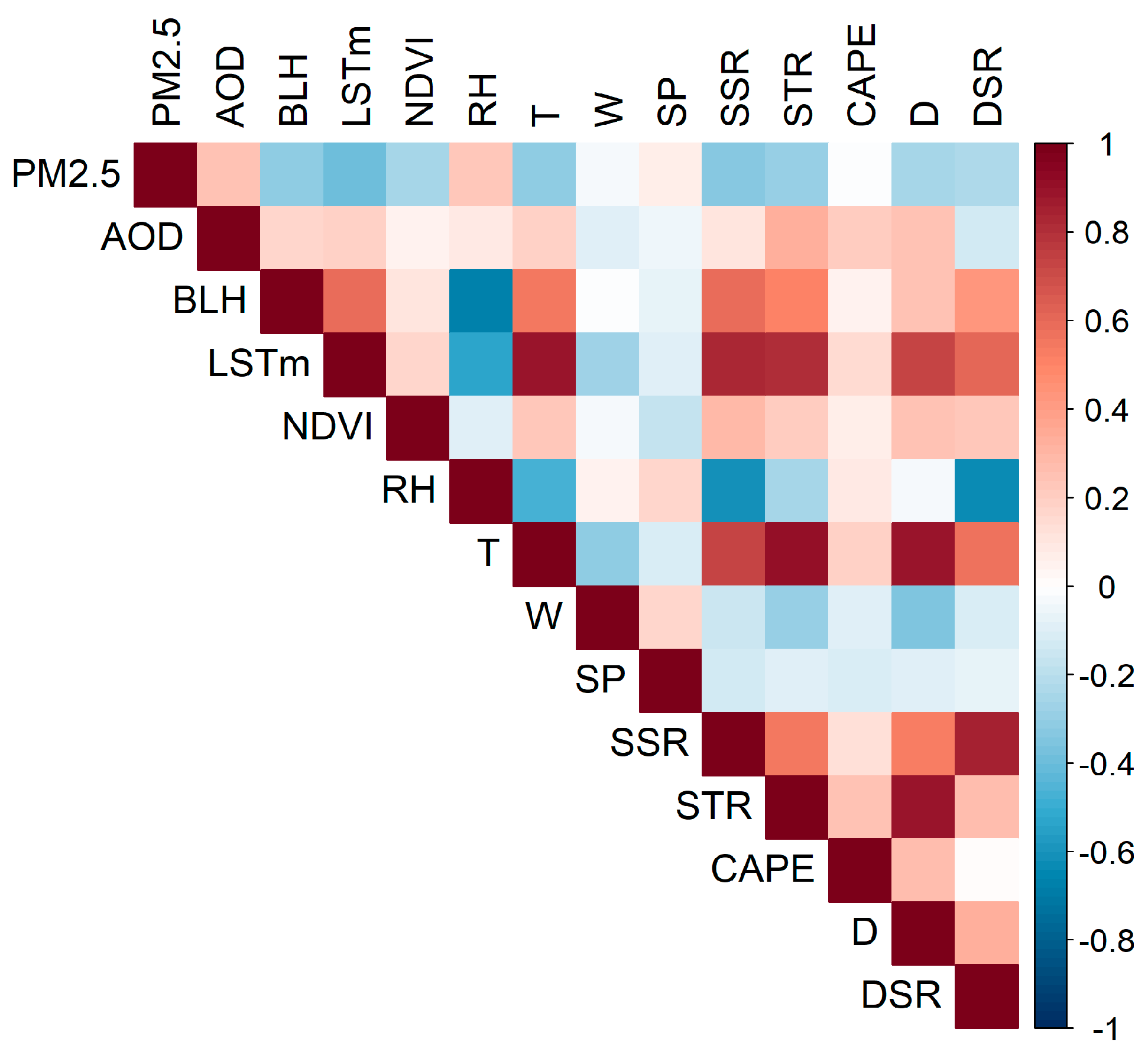
3.2. Feature Importance Analysis

Overall, we achieved very good performances with all our final models (R2 0.95 to 0.96), indicating that each of the AOD datasets is suitable as a PM2.5 predictor. Nevertheless, there were differences in the impact of the AOD as a predictor in the different models. Figure 3 shows the results of the feature importance assessment of all 15 predictor variables that were included in the final model. For all models, AOD, surface pressure, BLH and day of the year were under the six most important predictors. Interestingly, in the SLSTR and TROPOMI models AOD was not the most important variable, as was expected and was true for MAIAC and MODIS-DT. For the TROPOMI model, AOD only came in third place, and for SLSTR, it only came in sixth place in the importance ranking. Instead, for both TROPOMI and SLSTR, DoY was found to be the most important predictor variable. Higher rankings of wind speed, monthly LST, dewpoint and NDVI indicate the important influence of seasonality and degree of stagnation on the PM2.5 variability. Air temperature, relative humidity, CAPE and shortwave radiation parameters proved to be of lower importance in all models. Compared to the TROPOMI and SLSTR models, longwave thermal radiation showed lesser importance for MAIAC and MODIS-DT.
Cross-correlations between all predictor variables are illustrated in Figure 4. As the cross-correlations did not differ significantly among the different AOD dataset models, we only show one correlation plot (MAIAC) as a sample result. In general, PM2.5 indicated weak positive correlations with AOD and RH and was negatively correlated with LSTm and other meteorological and surface parameters. At the same time, AOD was one of the most important predictor variables, while RH proved less important. The strongest negative correlations were found for BLH, T, the monthly averaged LST and SSR, with values of 0.30, 0.32, 0.39 and 0.34, respectively. At the same time, BLH and LSTm proved to be two of the more important auxiliary variables, while T and SSR were two of the least important predictors. The most important positive correlations existed between the different temperature and radiation variables, while strong negative correlations were found between RH and BLH and also RH and DSR.

4. Discussion

4.1. Model Performances

We examined the performance of the random forest method to predict ground-level PM2.5 concentrations using satellite AOD data and additional variables. Four models were built, each incorporating a different AOD dataset, to analyze the effect of dataset characteristics on the model performance. In general, all models performed well and showed high predictabilities (R2), correlations and small errors compared to in situ measurements. Nevertheless, there were differences in the performance, likely due to the varying dataset characteristics.
The MAIAC-based RF performed the best, followed by MODIS-DT, TROPOMI and SLSTR. Obviously, there is a positive link/correlation between the resolution of the AOD datasets and the performance of the RF models. This could be explained by the collocation of AOD pixels with respect to the measurement sites. For reasons of representativity, with a higher spatial resolution, it is more likely to select a pixel value which is really close to the actual station measurement. With a coarse-resolution dataset, the pixel value may represent conditions that are too far away from the point observation. Thus, MAIAC with 1 km spatial resolution can reflect the measured aerosol amounts better than MODIS-DT, TROPOMI and SLSTR with 3 km, 5 km and 10 km resolution, respectively. To our knowledge, there have been no studies comparing different datasets for the estimation of PM2.5 concentrations using the RF approach and considering the influence of spatial resolution on model performances so far. However, Mei et al. studied the linear relationship between PM and AOD in the US using the different MODIS datasets and could conclude a positive effect on correlations with higher-resolution AODs [69]. Moreover, Li et al. compared MODIS-DT, -MAIAC and -DB AOD datasets by applying a mixed-effects model for PM2.5 retrieval [70]. They found better performance for MAIAC compared to the other datasets with 10 km spatial resolution.
Another reason for the performance differences could be the dependency of the RF method on the sample size used for model training and thereby on the coverage and overall availability of AOD data. The datasets differ significantly in the amount of data they provide. On one hand, this is due to changing weather conditions between the overpass times and differences in geometric sensor properties, such as the swath width. Other explanations can be found in the differing retrieval algorithms. The MODIS-DT algorithm, for example, has a weakness in retrieving AOD over bright surfaces as it relies on an optical contrast between particles and the surface, thus generating a large number of missing values over highly reflective ground such as urban areas [71]. The TROPOMI dataset suffers from the same limitation. In contrast, the new multi-angle MAIAC algorithm can deal with both dark and bright surfaces, producing a much larger number of retrievals than the DT algorithm [72,73]. The algorithm is capable of retrieving aerosols and bidirectional surface reflectance simultaneously by using observation-based multi-angle information [50]. As a dual view-instrument, the SLSTR product is also not affected by the brightness issue, since no a priori assumptions on surface reflectance are needed for an accurate retrieval [74]. However, as SLSTR has a comparably narrow swath width, it covers a much smaller area each day, making it the dataset with the lowest coverage and sample size in this study.
The limited sample size of AOD data can significantly affect the accuracy of PM2.5 prediction models, and in general, all satellite AOD products suffer from a missing data problem. To address this issue, some studies introduced gap-filling approaches by imputing missing values using external data sources such as simulations from chemical transport models [41,44,45], multi-stage prediction models [37] or by AOD data fusion methods [25,47,75]. However, AOD imputations may introduce systematic and static errors, which will be propagated to PM2.5 predictions, increasing their uncertainty [76].
SLSTR and TROPOMI AOD products display a generally lower coverage compared to the MODIS-based products. For SLSTR, this is mainly due to the relatively small swath width and daily covered area. In the case of TROPOMI, the smaller sample size is mainly due to cloud coverage. We applied a rather conservative quality check, skipping pixels with more than 10% cloud cover. Though the TROPOMI-based RF model showed a good performance and the predicted PM2.5 concentrations indicated strong agreement with station measurements, we noticed that the annual PM mean values were generally too low compared to the other products. We assume that, due to the recommended quality control, we eliminated too many valid high AOD values in the dataset, leading to low-biased mean PM2.5 values. Future work should further investigate the influence of cloud coverage and respective quality flags on results.
The overall quality and accuracy of the AOD retrievals can also affect the performance of PM2.5 estimations, thereby limiting their power as PM2.5 predictors. Cloud screening, for example, is a major source of uncertainty [57]. On the one hand, inaccurate and incautious cloud screening can lead to erroneous retrievals of very high AODs. On the other hand, with over-strict cloud screening, strong aerosol signals could be discarded, leading to systematically lower AODs. This can at least partly explain the low bias of TROPOMI PM2.5 and the weak impact of AOD. Among other factors, Lyapustin et al. attribute the higher accuracy of MAIAC AOD compared to MODIS-DT to the more effective cloud screening in the MAIAC algorithm [50]. Garrigues et al. compared the global model-based Copernicus Atmospheric Monitoring Service (CAMS) AOD product to AOD observations from different sensors [77]. They concluded that cloud contamination, aerosol model assumptions and radiometric calibration are among the main driving factors for the differences between the examined AOD products. In particular, performance may differ at high and low aerosol loads. In summer 2018, large parts of Germany were prone to a severe drought. This could have led to changes in albedo, vegetation and AOD due to dust events. For example, Reinermann et al. found a striking decrease in the MODIS Enhanced Vegetation Index [78]. The affected areas coincided with differences between MODIS, SLSTR and TROPOMI PM2.5.
With respect to the overall performance of the four different models, we compared the seasonal and spatial variability. The statistics proved to be rather stable over space and time, indicating that the RF models are robust and capable of depicting the influence of spatial and temporal variabilities well. With respect to season, all models were equally robust, with only very slight differences in the model performance. Spatially, MODIS-DT is the most robust model with the smallest variations In the station-wise CV statistics. In this respect, higher but still rather small variations were found for SLSTR. This could again be explained by the smaller sample size per station increasing uncertainties.
Compared to our previous study using a semi-empirical regression approach to estimate PM2.5 concentrations from AOD [25], we achieved much better results with the RF approach with an increase in maximum CV R2 from 0.57 to 0.77 and in R from 0.76 to 0.88. The consideration of multiple predictor variables is a great advantage of RF and substantiated that PM2.5 estimations benefit from adding proxy data other than only three variables (AOD, BLH and RH). We found that RF is able to compensate for minor issues in the AOD data, such as, for example, AOD overestimations over urban areas or coastlines due to retrieval limitations. In addition, RF seems to be independent from the AOD wavelength in some way, as we could achieve very good results with the TROPOMI AOD data with a wavelength difference of 50 nm compared to the classic AOD datasets. Physical-based approaches are stronger depending on wavelength, as they rely on assumptions regarding optical parameters. Other studies also compared RF to simpler regression methods and found better performances with RF for the respective study regions [35,36,79]. Reid et al., for example, showed that RF can also outperform other machine learning methods such as generalized boosting models or support vector machines [80].

4.2. Feature Importance

During the model development, we found that space-related variables such as geographical coordinates or elevation had no influence on model accuracies or even worsened them. The same applies for parameters linking to geographical factors such as land use/land cover or population density. This is contrary to expectations and other authors, e.g., [81]. Zamani Joharestani et al., found that longitude, latitude and elevation were some of the most important variables for their RF model to predict PM2.5 concentrations in Teheran and demonstrated that they could even replace other correlated variables [40]. Furthermore, Stafoggia et al. as well as Murugan and Palanichamy showed that spatial coordinates have high importance for the accuracy of their RF PM2.5 prediction models for Italy and Malaysia, respectively [30,44]. Hu et al., trained a PM2.5 prediction model for the US and found that land use and population density had a significant influence on model accuracy [41]. A possible explanation why LC did not improve our results is the aggregation over seasons which smooths out transient effects, e.g., impacts by local emissions, on shorter time scales. Compared to other regions, central Europe, and especially Germany, mostly exhibits a rather flat topography in areas with elevated PM2.5. This especially favors dynamic variables such as 10 m winds. We expect a stronger impact of static spatial variables when limiting the training of ML to more structured areas and shorter time scales.
Nevertheless, we and many other studies found that spatio-temporally varying variables such as meteorological parameters are more important for model performances than static ones. Regarding our study, the ranking of the variable importance differs from model to model, but we could identify some overall important variables. These are AOD, BLH, surface pressure, DoY, dewpoint and wind. This is in line with the findings of many other studies such as Wei et al., Chen et al., Yang et al., Gao et al., or Wei et al. [35,36,37,38,73]. Most of these studies also identified RH and temperature as important variables, which we cannot confirm with our results. RH was one of the least important variables in terms of MSE increase for all our models. We would have expected a higher importance of RH, as it is an indicator for the hygroscopic growth of aerosol and thus a very important parameter to depict the spatial–temporal variability in PM2.5. Zamani Joharestani et al. found that dependent, highly correlated variables can be predicted by other variables and can be used as substitutes for each other [40]. We suggest that the influence of RH might be represented by highly correlated variables such as BLH or LST and thus lose importance for model predictive power. This does not necessarily mean that RH has a negligible influence on the PM-AOD relationship, especially because leaving out RH as a predictor has downgraded the performance of our models. Strobel et al. pointed out that strong correlations between predictor variables can affect the importance measure [82]. This could also be an explanation for other unexpected low importance features in our models. Air temperature, for example, was expected to have a large effect on model accuracy, as this was shown by, e.g., Chen et al. or Gao et al. [36,38]. In our models, 2 m air temperature proved to be less important. It is not clear to what extent other highly correlated variables such as dewpoint or LST may already reflect their influence on PM2.5. Future studies should further investigate cross-correlations between predictor variables to avoid potential shading effects [41].
The variable importance assessment’s most striking finding was that AOD did not turn out to be the most crucial component for PM2.5 prediction for the SLSTR and TROPOMI models. This is in agreement with the study of Zamani Joharestani et al. using standard Aqua/MODIS AOD products [40]. They tested the impact of eliminating AOD as a predictor variable for PM2.5 estimation and found a positive effect on model accuracy. They explained this with the very small sample size due to missing AOD data and furthermore inferred that other features may act as substitutes for AOD to predict PM2.5. We assume that this is also a limiting factor in our models, because SLSTR and TROPOMI exhibited significantly worse coverage than MODIS. Other variables with better coverage and resolutions may replace AOD observations, decreasing the importance of AOD as a PM2.5 predictor. In the case of our SLSTR and TROPOMI model, the day of the year was the most important predictor. This may reflect the importance of changing weather situations during the year.

4.3. Limitations

The differences in feature importance highlight the different impacts of proxy variables on model performances given a certain AOD dataset. For each AOD dataset, different predictor variables should be chosen, and it could be of benefit to use additional variables to better depict the vertical atmospheric conditions or the settlement structure. Additionally, we believe that a separated model development for each AOD dataset could potentially improve the accuracy of the predictions. Furthermore, our feature selection and hyperparameter settings for the model training could be further improved.
There are other limitations in our study that should be acknowledged. First, one of the weaknesses of the RF algorithm is that the feature importance is not considered during the model building [83]. For each split in the decision trees, variables are randomly chosen from the total set, disregarding their importance for model accuracy. If variables are not well chosen and less important features act as predictors more often, this could negatively affect the model performance. Another drawback of RF is the algorithm’s inability to handle missing values. Training and predictions can only be made when all predictor variables are available. This is particularly problematic when applying satellite data, which have a quite high rate of missing values.
Other limitations are related to data matchups. The collocation of the pixel-based satellite and model data with the monitor locations brings uncertainties, as the pixel values do not necessarily represent the conditions at the ground site well. This issue becomes more severe with increasing pixel size. It is also worth mentioning the temporal mismatch between satellite, model and station data. The satellite overpasses are at 10:30 and 13:30 local time, for the model data the 12:00 timestep was used, matching the mean overpass times. The station data were considered as daily mean values.Additionally, the distribution of ground monitors should be mentioned as a limitation in our study. The number of monitors was considerably higher in residential, urban and industrial areas, resulting in an under-representation of rural conditions which could have led to bias in the PM2.5 predictions for the remote areas.
Furthermore, we used BLH as a proxy for the vertical aerosol distribution, assuming that aerosols are confined and homogeneously mixed within the boundary layer. This is a reasonable assumption, as most aerosols are emitted at ground level within the boundary layer, but it is not valid in the presence of elevated aerosol layers originated from remote sources. Tsai et al. investigated the effect of using BLH or aerosol layer height (ALH) for AOD normalization on correlations with ground-based PM2.5 measurements and found significant improvement in the correlations when using the ALH instead of BLH [84]. Nonetheless, BLH is an important parameter to predict PM2.5 from AOD, but the consideration of ALH could potentially provide more accurate estimates.

5. Conclusions

We applied a random forest approach to derive ground-level PM2.5 concentrations using satellite AOD data together with additional data layers. Unlike other studies that mostly rely on single-platformed satellite AOD products, we systematically evaluated four different AOD datasets in their performance as PM2.5 predictors. Besides the established AOD datasets from MODIS (DT and MAIAC), the study explored new SLSTR and TROPOMI data. We conclude that all datasets performed generally well as predictor variables, but with different prediction strengths. In the study region, which was Germany, as part of central Europe, we found a strong dependency on the coverage and resolution of the AOD datasets. Thus, the MAIAC and MODIS-DT models performed, best as they showed the highest numbers of collocations with in situ measurements. Performances based on TROPOMI and SLSTR datasets were lower, which can probably be attributed to retrieval uncertainties in these quite new AOD datasets. MODIS AOD retrievals, and in particular, the cloud screening procedure, have been optimized continuously for about 20 years, resulting in very mature datasets. As the TROPOMI and SLSTR instruments are quite new, it can be expected that the corresponding AOD results are potentially still more influenced by retrieval issues. Nevertheless, with convincing accuracies of 0.95 for the final models, we could substantiate that TROPOMI and SLSTR AODs are also able predictors for PM2.5 and that they have high potential to continue the global aerosol data collection once MODIS is out of service. With its high spectral resolution and O2A-band, TROPOMI can resolve the Aerosol Layer Height and advance on the general assumption of homogeneously mixed aerosols in the BL (at higher optical depths). In addition, a TROPOMI-like instrument will be mounted on the geostationary satellite Sentinel-4. The significantly improved temporal coverage will favor better results for the estimated PM2.5. Song et al. have already shown that AOD data from a geostationary satellite substantially improved performances on PM2.5 predictability compared to data from low Earth-orbiting satellites [85].
Although static predictor variables showed only a weak impact on the seasonal time scale, variables such as CLC should further improve the predictive power of RF models on shorter time scales. We furthermore suppose that the consideration of additional variables relating to population patterns and settlement structures as well as traffic patterns could be of added value in our RF models.
With our findings, we can produce reliable and high-resolution PM2.5 datasets for a longer time period to analyze and assess the spatio-temporal variability in PM2.5 pollution in Germany. They can be applied to investigate long- and short-term exposures and potential health effects on regional and urban scales in the most populous country in the European Union. In particular, the data will support cohort studies on the impact of environmental stressors with health insurance data [11]. In particular, the low bias and RMSE of the derived PM2.5 yearly averages with respect to in situ measurements makes them suitable for applications in air quality management and compliance monitoring. According to the EU air quality directive, from 1 January 2020, the PM2.5 annual mean values will no longer be allowed to exceed a value of 20 μg/m3. Thus, the data can support policy makers in delineating areas of exceedance, in evaluating the success of mitigation measures and in identifying the need for other restrictions regarding PM2.5 pollution.

Author Contributions

The authors’ contributions are as follows: conceptualization, J.H., T.E. and F.B.; methodology, J.H.; validation, J.H.; formal analysis, J.H.; investigation, J.H.; data curation, J.H.; writing—original draft preparation, J.H.; writing—review and editing, J.H., T.E. and F.B.; visualization, J.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the mFUND program of the Federal Ministry for Digital and Transport (BMDV) for the projects S-VELD (grant number 19F2065) and KLIPS (grant number 19F2134B).

Data Availability Statement

The data presented in this study are not publicly available as produced for internal use. They are available on request from the corresponding author.

Acknowledgments

We want to thank all data suppliers: NASA for providing MODIS and MAIAC data, Swansea University (Peter North and colleagues) for making SLSTR AOD data available, DLR (Diego Loyola and colleagues) who provided the TROPOMI AOD data, ECMWF for the appropriation of meteorological data and EEA for providing in situ measurements of PM2.5. Thanks to Martijn Schaap from TNO for promoting this work, as well as the review and editing.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. World Health Organization (WHO). Billions of People Still Breath Unhealthy Air: New WHO Data. Available online: https://www.who.int/news/item/04-04-2022-billions-of-people-still-breathe-unhealthy-air-new-who-data (accessed on 25 November 2022).
  2. Lee, S.; Ku, H.; Hyun, C.; Lee, M. Machine Learning-Based Analyses of the Effects of Various Types of Air Pollutants on Hospital Visits by Asthma Patients. Toxics 2022, 10, 644. [Google Scholar] [CrossRef] [PubMed]
  3. Samoli, E.; Nastos, P.T.; Paliatsos, A.G.; Katsouyanni, K.; Priftis, K.N. Acute effects of air pollution on pediatric asthma exacerbation: Evidence of association and effect modification. Environ. Res. 2011, 111, 418–424. [Google Scholar] [CrossRef] [PubMed]
  4. Lepeule, J.; Laden, F.; Dockery, D.; Schwartz, J. Chronic exposure to fine particles and mortality: An extended follow-up of the Harvard Six Cities study from 1974 to 2009. Environ. Health Perspect. 2012, 120, 965–970. [Google Scholar] [CrossRef]
  5. European Environment Agency (EEA). Air Pollution—Air Pollution and Cancer. Available online: https://www.eea.europa.eu/publications/environmental-burden-of-cancer/air-pollution (accessed on 9 January 2022).
  6. Muttoo, S. The Association of Ambient Nitrogen Dioxide and Particulate Matter Exposure on Infant Lung Function. Ph.D. Thesis, University of KwaZulu-Natal, Durban, South Africa, 2022. [Google Scholar]
  7. Ebersviller, S.; Lichtveld, K.; Sexton, K.G.; Zavala, J.; Lin, Y.H.; Jaspers, I.; Jeffries, H.E. Gaseous VOCs rapidly modify particulate matter and its biological effects—Part 1: Simple VOCs and model PM. Atmos. Chem. Phys. 2012, 12, 12277–12292. [Google Scholar] [CrossRef] [Green Version]
  8. Brook, R.D.; Rajagopalan, S. Particulate matter, air pollution, and blood pressure. J. Am. Soc. Hypertens. 2009, 3, 332–350. [Google Scholar] [CrossRef] [PubMed]
  9. Binter, A.C.; Kusters, M.S.; van den Dries, M.A.; Alonso, L.; Lubczyńska, M.J.; Hoek, G.; White, T.; Iñiguez, C.; Tiemeier, H.; Guxens, M. Air pollution, white matter microstructure, and brain volumes: Periods of susceptibility from pregnancy to preadolescence. Environ. Pollut. 2022, 313, 120109. [Google Scholar] [CrossRef]
  10. Bai, L.; Benmarhnia, T.; Chen, C.; Kwong, J.C.; Burnett, R.T.; van Donkelaar, A.; Martin, R.V.; Kim, J.; Kaufman, J.S.; Chen, H. Chronic Exposure to Fine Particulate Matter Increases Mortality through Pathways of Metabolic and Cardiovascular Disease: Insights from a Large Mediation Analysis. J. Am. Heart Assoc. 2022, 11, e026660. [Google Scholar] [CrossRef]
  11. Rittweger, J.; Gilardi, L.; Baltruweit, M.; Dally, S.; Erbertseder, T.; Mittag, U.; Naeem, M.; Schmid, M.; Schmitz, M.-T.; Wüst, S.; et al. Temperature and particulate matter as environmental factors associated with seasonality of influenza incidence—An approach using Earth observation-based modeling in a health insurance cohort study from Baden-Württemberg (Germany). Environ. Health 2022, 21, 131. [Google Scholar] [CrossRef]
  12. Mendy, A.; Wu, X.; Keller, J.L.; Fassler, C.S.; Apewokin, S.; Mersha, T.B.; Xie, C.; Pinney, S.M. Air pollution and the pandemic: Long-term PM2.5 exposure and disease severity in COVID-19 patients. Respirology 2021, 26, 1181–1187. [Google Scholar] [CrossRef]
  13. European Environment Agency (EEA). Air Quality in Europe 2022. Available online: https://www.eea.europa.eu//publications/air-quality-in-europe-2022 (accessed on 11 January 2023).
  14. Hoff, R.M.; Christopher, S.A. Remote sensing of particulate pollution from space: Have we reached the promised land? J. Air Waste Manag. Assoc. 2009, 59, 645–675. [Google Scholar] [CrossRef]
  15. Chu, Y.; Liu, Y.; Li, X.; Liu, Z.; Lu, H.; Lu, Y.; Mao, Z.; Chen, X.; Li, N.; Ren, M.; et al. A review on predicting ground PM2.5 concentration using satellite aerosol optical depth. Atmosphere 2016, 7, 129. [Google Scholar] [CrossRef] [Green Version]
  16. Zhang, Y.; Li, Z.; Bai, K.; Wei, Y.; Xie, Y.; Zhang, Y.; Ou, Y.; Cohen, J.; Zhang, Y.; Peng, Z.; et al. Satellite remote sensing of atmospheric particulate matter mass concentration: Advances, challenges, and perspectives. Fundam. Res. 2021, 1, 240–258. [Google Scholar] [CrossRef]
  17. Toth, T.D.; Zhang, J.; Campbell, J.R.; Hyer, E.J.; Reid, J.S.; Shi, Y.; Westphal, D.L. Impact of data quality and surface-to-column representativeness on the PM2.5/satellite AOD relationship for the contiguous United States. Atmos. Chem. Phys. 2014, 14, 6049–6062. [Google Scholar] [CrossRef] [Green Version]
  18. Schaap, M.; Apituley, A.; Timmermans, R.M.A.; Koelemeijer, R.B.A.; Leeuw, G.D. Exploring the relation between aerosol optical depth and PM2.5 at Cabauw, The Netherlands. Atmos. Chem. Phys. 2009, 9, 909–925. [Google Scholar] [CrossRef] [Green Version]
  19. Zhang, Y.; Li, Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
  20. Zou, B.; Pu, Q.; Bilal, M.; Weng, Q.; Zhai, L.; Nichol, J.E. High-resolution satellite mapping of fine particulates based on geographically weighted regression. IEEE Geosci. Remote Sens. Lett. 2016, 13, 495–499. [Google Scholar] [CrossRef]
  21. He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
  22. Beloconi, A.; Kamarianakis, Y.; Chrysoulakis, N. Estimating urban PM10 and PM2.5 concentrations, based on synergistic MERIS/AATSR aerosol observations, land cover and morphology data. Remote Sens. Environ. 2016, 172, 148–164. [Google Scholar] [CrossRef] [Green Version]
  23. Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef] [Green Version]
  24. Xu, J.W.; Martin, R.V.; Van Donkelaar, A.; Kim, J.; Choi, M.; Zhang, Q.; Geng, G.; Liu, Y.; Ma, Z.; Huang, L.; et al. Estimating ground-level PM2.5 in eastern China using aerosol optical depth determined from the GOCI satellite instrument. Atmos. Chem. Phys. 2015, 15, 13133–13144. [Google Scholar] [CrossRef] [Green Version]
  25. Handschuh, J.; Erbertseder, T.; Schaap, M.; Baier, F. Estimating PM2.5 surface concentrations from AOD: A combination of SLSTR and MODIS. Remote Sens. Appl. Soc. Environ. 2022, 26, 100716. [Google Scholar] [CrossRef]
  26. Lin, C.; Li, Y.; Yuan, Z.; Lau, A.K.H.; Li, C.; Fung, J.C.H. Using satellite remote sensing data to estimate the high-resolution distribution of ground-level PM2.5. Remote Sens. Environ. 2015, 156, 117–128. [Google Scholar] [CrossRef]
  27. Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Boys, B.L. Use of satellite observations for long-term exposure assessment of global concentrations of fine particulate matter. Environ. Health Perspect. 2015, 123, 135–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A.; et al. Improved 1 km resolution PM2.5 estimates across China using enhanced space–time extremely randomized trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef] [Green Version]
  29. Mehmood, K.; Bao, Y.; Cheng, W.; Khan, M.A.; Siddique, N.; Abrar, M.M.; Naidu, R. Predicting the quality of air with machine learning approaches: Current research priorities and future perspectives. J. Clean. Prod. 2022, 379, 134656. [Google Scholar] [CrossRef]
  30. Murugan, R.; Palanichamy, N. Smart City Air Quality Prediction using Machine Learning. In Proceedings of the 5th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 6–8 May 2021; pp. 1048–1054. [Google Scholar] [CrossRef]
  31. Maaloul, K.; Brahim, L. Comparative Analysis of Mashine Learning for Predicting Air Quality in Smart Cities. WSEAS Trandaction on Computers. 2022. Available online: https://wseas.com/journals/computers/2022/a605105-027(2022).pdf (accessed on 25 September 2022).
  32. Fernando, R.M.; Ilmini, W.M.K.S.; Vidanagama, D.U. Prediction of Air Quality Index in Colombo. Available online: http://ir.kdu.ac.lk/handle/345/5301 (accessed on 16 November 2022).
  33. Danesh Yazdi, M.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Lyapustin, A.; Katsouyanni, K.; Schwartz, J. Predicting fine particulate matter (PM2.5) in the greater London area: An ensemble approach using machine learning methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef] [Green Version]
  34. Aman, N.; Manomaiphiboon, K.; Inerb, M.; Devkota, B.; Kokkaew, E.; Wang, Y. A machine learning application for PM2.5 estimation over Greater Bangkok. In Proceedings of the 8th International Conference on Sustainable Energy and Environment (SEE 2022), Bangkok, Thailand, 7–9 November 2022. [Google Scholar]
  35. Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
  36. Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.A.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef] [PubMed]
  37. Yang, L.; Xu, H.; Yu, S. Estimating PM2.5 Concentrations in Contiguous Eastern Coastal Zone of China Using MODIS AOD and a Two-Stage Random Forest Model. J. Atmos. Ocean. Technol. 2021, 38, 2071–2080. [Google Scholar] [CrossRef]
  38. Gao, X.; Ruan, Z.; Liu, J.; Chen, Q.; Yuan, Y. Analysis of Atmospheric Pollutants and Meteorological Factors on PM2.5 Concentration and Temporal Variations in Harbin. Atmosphere 2022, 13, 1426. [Google Scholar] [CrossRef]
  39. Gupta, P.; Zhan, S.; Mishra, V.; Aekakkararungroj, A.; Markert, A.; Paibong, S.; Chishtie, F. Machine Learning Algorithm for Estimating Surface PM2.5 in Thailand. Aerosol Air Qual. Res. 2021, 21, 210105. [Google Scholar] [CrossRef]
  40. Zamani Joharestani, M.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 prediction based on random forest, XGBoost, and deep learning using multisource remote sensing data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef] [Green Version]
  41. Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]
  42. Brokamp, C.; Jandarov, R.; Rao, M.B.; LeMasters, G.; Ryan, P. Exposure assessment models for elemental components of particulate matter in an urban environment: A comparison of regression and random forest approaches. Atmos. Environ. 2017, 151, 1–11. [Google Scholar] [CrossRef] [Green Version]
  43. Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef] [PubMed]
  44. Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; De Hoogh, K.; De’Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013–2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef]
  45. Schneider, R.; Vicedo-Cabrera, A.M.; Sera, F.; Masselot, P.; Stafoggia, M.; de Hoogh, K.; Kloog, I.; Reis, S.; Vieno, M.; Gasparrini, A. A satellite-based spatio-temporal machine learning model to reconstruct daily PM2.5 concentrations across Great Britain. Remote Sens. 2020, 12, 3803. [Google Scholar] [CrossRef] [PubMed]
  46. Holzer-Popp, T.; Leeuw, G.D.; Griesfeller, J.; Martynenko, D.; Klüser, L.; Bevan, S.; Davies, W.; Ducos, F.; Deuzé, J.L.; Graigner, R.G.; et al. Aerosol retrieval experiments in the ESA Aerosol_cci project. Atmos. Meas. Tech. 2013, 6, 1919–1957. [Google Scholar] [CrossRef] [Green Version]
  47. Pu, Q.; Yoo, E.H. A gap-filling hybrid approach for hourly PM2.5 prediction at high spatial resolution from multi-sourced AOD data. Environ. Pollut. 2022, 315, 120419. [Google Scholar] [CrossRef]
  48. Levy, R.C.; Remer, L.A.; Mattoo, S.; Vermote, E.F.; Kaufman, Y.J. Second-generation operational algorithm: Retrieval of aerosol properties over land from inversion of Moderate Resolution Imaging Spectroradiometer spectral reflectance. J. Geophys. Res. Atmos. 2007, 112, 78141. [Google Scholar] [CrossRef] [Green Version]
  49. Remer, L.A.; Mattoo, S.; Levy, R.C.; Munchak, L.A. MODIS 3 km aerosol product: Algorithm and global perspective. Atmos. Meas. Tech. 2013, 6, 1829–1844. [Google Scholar] [CrossRef] [Green Version]
  50. Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef] [Green Version]
  51. Schneider, C.; Pelzer, M.; Toenges-Schuller, N.; Nacken, M.; Niederau, A. ArcGIS basierte Lösung zur detaillierten, deutschlandweiten Verteilung (Gridding) nationaler Emissionsjahreswerte auf Basis des Inventars zur Emissionsberichterstattung. Dessau. Roßlau Retrieved 2016, 27, 2019. [Google Scholar]
  52. Yao, F.; Si, M.; Li, W.; Wu, J. A multidimensional comparison between MODIS and VIIRS AOD in estimating ground-level PM2.5 concentrations over a heavily polluted region in China. Sci. Total Environ. 2018, 618, 819–828. [Google Scholar] [CrossRef]
  53. European Environment Agency (EEA). Air Quality in Europe 2021: Sources and Emissions of Air Pollutants in Europe. Available online: https://www.eea.europa.eu/publications/air-quality-in-europe-2021/sources-and-emissions-of-air (accessed on 9 January 2023).
  54. Timmermans, R.; van Pinxteren, D.; Kranenburg, R.; Hendriks, C.; Fomba, K.W.; Herrmann, H.; Schaap, M. Evaluation of modelled LOTOS-EUROS with observational based PM10 source attribution. Atmos. Environ. X 2022, 14, 100173. [Google Scholar] [CrossRef]
  55. European Environment Agency (EEA). Download of Air Quality Data. Available online: https://discomap.eea.europa.eu/map/fme/AirQualityExport.htm (accessed on 17 September 2020).
  56. LAADS DAAC. Available online: https://ladsweb.modaps.eosdis.nasa.gov/archive/allData/61/ (accessed on 17 September 2020).
  57. Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in China using satellite remote sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
  58. Li, Z.; Zhao, X.; Kahn, R.; Mishchenko, M.; Remer, L.; Lee, K.-H.; Wang, M.; Laszlo, I.; Nakajima, T.; Maring, H. Uncertainties in satellite remote sensing of aerosols and impact on monitoring its long-term trend: A review and perspective. Ann. Geo-Phys. 2009, 27, 2755–2770. [Google Scholar] [CrossRef]
  59. Müller, I.; Erbertseder, T.; Taubenbock, H. Tropospheric NO2: Explorative analyses of spatial variability and impact factors. Remote Sens. Environ. 2022, 270, 112839. [Google Scholar] [CrossRef]
  60. Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef] [Green Version]
  61. North, P.; Heckel, A. Algorithm Theoretical Basis Document—Annex C (SU-SLSTR). Copernicus Climate Change Service (C3S). Available online: http://datastore.copernicus-climate.eu/documents/satellite-aerosol-properties/C3S_D312b_Lot2.1.2.2_v1.1_201902_ATBD_AER_v1.1_and_annexes.zip (accessed on 13 May 2021).
  62. Torres, O.; Jethva, H.; Ahn, C.; Jaross, G.; Loyola, D.G. TROPOMI aerosol products: Evaluation and observations of synoptic-scale carbonaceous aerosol plumes during 2018–2020. Atmos. Meas. Tech. 2020, 13, 6789–6806. [Google Scholar] [CrossRef]
  63. Wan, Z. Collection-6 MODIS Land Surface Temperature Products Users’ Guide. ICESS, University of California, Santa Barbara. 2013. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD11_User_Guide_V61.pdf (accessed on 16 December 2022).
  64. Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Vegetation Index and Phenology Lab, The University of Arizona: Tucson, AZ, USA, 2015. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD13_User_Guide_V61.pdf (accessed on 16 December 2022).
  65. Weigand, M.; Staab, J.; Wurm, M.; Taubenböck, H. Spatial and semantic effects of LUCAS samples on fully automated land use/land cover classification in high-resolution Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102065. [Google Scholar] [CrossRef]
  66. Gallego, F.J. A population density grid of the European Union. Popul. Environ. 2010, 31, 460–473. [Google Scholar] [CrossRef]
  67. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  68. Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
  69. Mei, L.; Strandgren, J.; Rozanov, V.; Vountas, M.; Burrows, J.P.; Wang, Y. A study of the impact of spatial resolution on the estimation of particle matter concentration from the aerosol optical depth retrieved from satellite observations. Int. J. Remote Sens. 2019, 40, 7084–7112. [Google Scholar] [CrossRef]
  70. Li, R.; Mei, X.; Chen, L.; Wang, Z.; Jing, Y.; Wei, L. Influence of Spatial Resolution and Retrieval Frequency on Applicability of Satellite-Predicted PM2.5 in Northern China. Remote Sens. 2020, 12, 736. [Google Scholar] [CrossRef] [Green Version]
  71. Munchak, L.A.; Levy, R.C.; Mattoo, S.; Remer, L.A.; Holben, B.N.; Schafer, J.S.; Hostetler, C.A.; Ferrare, R.A. MODIS 3 km aerosol product: Applications over land in an urban/suburban region. Atmos. Meas. Tech. 2013, 6, 1747–1759. [Google Scholar] [CrossRef] [Green Version]
  72. Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res. Atmos. 2011, 116, 14986. [Google Scholar] [CrossRef]
  73. Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
  74. Popp, T.; C3S_312b_Lot2 Aerosol Team. Product User Guide and Specification—Aerosol Products. Copernicus Climate Change Service (C3S). Available online: http://datastore.copernicus-climate.eu/documents/satellite-aerosol-properties/C3S_D312b_Lot2.3.2.2_v1.1_201902_PUGS_AER_v1.1.pdf (accessed on 13 May 2021).
  75. Jing, Y.; Pan, L.; Sun, Y. Estimating PM2.5 concentrations in a central region of China using a three-stage model. Int. J. Digit. Earth 2023, 16, 578–592. [Google Scholar] [CrossRef]
  76. Pu, Q.; Yoo, E.-H. Ground PM2.5 prediction using imputed MAIAC AOD with uncertainty quantification. Environ. Pollut. 2021, 274, 116574. [Google Scholar] [CrossRef] [PubMed]
  77. Garrigues, S.; Remy, S.; Chimot, J.; Ades, M.; Inness, A.; Flemming, J.; Kipling, Z.; Laszlo, I.; Benedetti, A.; Ribas, R.; et al. Monitoring multiple satellite aerosol optical depth (AOD) products within the Copernicus Atmosphere Monitoring Service (CAMS) data assimilation system. Atmos. Chem. Phys. 2022, 22, 14657–14692. [Google Scholar] [CrossRef]
  78. Reinermann, S.; Gessner, U.; Asam, S.; Kuenzer, C.; Dech, S. The Effect of Droughts on Vegetation Condition in Germany: An Analysis Based on Two Decades of Satellite Earth Observation Time Series and Crop Yield Statistics. Remote Sens. 2019, 11, 1783. [Google Scholar] [CrossRef] [Green Version]
  79. Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting daily urban fine particulate matter concentrations using a random forest model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef]
  80. Reid, C.E.; Jerrett, M.; Petersen, M.L.; Pfister, G.G.; Morefield, P.E.; Tager, I.B.; Raffuse, S.M.; Balmes, J.R. Spatiotemporal prediction of fine particulate matter during the 2008 northern California wildfires using machine learning. Environ. Sci. Technol. 2015, 49, 3887–3896. [Google Scholar] [CrossRef]
  81. Yang, W.; Jiang, X. Evaluating the influence of land use and land cover change on fine particulate matter. Sci. Rep. 2021, 11, 17612. [Google Scholar] [CrossRef]
  82. Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  83. Rogers, J.; Gunn, S. Identifying Feature Relevance Using a Random Forest. Lect. Notes Comput. Sci. 2006, 3940, 173–184. [Google Scholar] [CrossRef]
  84. Tsai, T.-C.; Jeng, Y.-J.; Chu, D.A.; Chen, J.-P.; Chang, S.-C. Analysis of the relationship between MODIS aerosol optical depth and particulate matter from 2006 to 2008. Atmos. Environ. 2011, 45, 4777–4788. [Google Scholar] [CrossRef]
  85. Song, C.H.; Yu, J.; Lee, D.; Lee, S.; Kim, H.S.; Han, K.M.; Jeon, M.; Park, S.; Im, J.; Park, S.-Y.; et al. Synergistic combination of information from ground observations, geostationary satellite, and air quality modeling towards improved PM2.5 predictability. Preprint 2022. [Google Scholar] [CrossRef]
Remotesensing 15 02064 g001 550
Figure 1. Cross-validated PM2.5 predictions from the random forest models plotted against the observational PM2.5 data for all station–satellite collocations in 2018. Dotted red lines represent the regression lines.
Figure 1. Cross-validated PM2.5 predictions from the random forest models plotted against the observational PM2.5 data for all station–satellite collocations in 2018. Dotted red lines represent the regression lines.
Remotesensing 15 02064 g001
Remotesensing 15 02064 g002 550
Figure 2. Annual mean PM2.5 predictions (μg/m3) for 2018 from the different RF-models MAIAC, MODIS-DT, SLSTR and TROPOMI. The circles depict the bias in % as the difference between the annual mean predictions and observations at monitoring sites.
Figure 2. Annual mean PM2.5 predictions (μg/m3) for 2018 from the different RF-models MAIAC, MODIS-DT, SLSTR and TROPOMI. The circles depict the bias in % as the difference between the annual mean predictions and observations at monitoring sites.
Remotesensing 15 02064 g002
Remotesensing 15 02064 g003 550
Figure 3. Feature importance rankings for the different datasets, showing the increase in prediction error when permuting the respective variables in the random forests.
Figure 3. Feature importance rankings for the different datasets, showing the increase in prediction error when permuting the respective variables in the random forests.
Remotesensing 15 02064 g003
Remotesensing 15 02064 g004 550
Figure 4. Cross-correlations of the predictor variables used for the MAIAC random forest model.
Figure 4. Cross-correlations of the predictor variables used for the MAIAC random forest model.
Remotesensing 15 02064 g004
Table
Table 2. Overview of the datasets used as proxy data for RF models. (1) ECMWF—see Section 2.2.3; (2) EEA metadata—see Section 2.2.1; (3) European Union, Copernicus Land Monitoring Service, European Environment Agency; (4) Weigand et al. [62]; (5) MODIS—see Section 2.2.4; (6) Schneider et al. [63]; (7) Joint Research Centre (JRC)—Gallego [64].
Table 2. Overview of the datasets used as proxy data for RF models. (1) ECMWF—see Section 2.2.3; (2) EEA metadata—see Section 2.2.1; (3) European Union, Copernicus Land Monitoring Service, European Environment Agency; (4) Weigand et al. [62]; (5) MODIS—see Section 2.2.4; (6) Schneider et al. [63]; (7) Joint Research Centre (JRC)—Gallego [64].
Parameter NameAcronymLevelAggregation/
Timestep		SourceUsed
AlbedoA-daily 12 p.m.(1)no
Boundary Layer HeightBLH-daily 12 p.m.(1)yes
Convective Available Potential EnergyCAPE-daily 12 p.m.(1)yes
Coordinates (Lon/Lat)--static(2)no
Day of YearDoY-daily-yes
Dewpoint temperatureD2 mdaily 12 p.m.(1)yes
Direct Solar RadiationDSRsurfacedaily 12 p.m.(1)yes
Elevation--static(2)no
Land Cover (CORINE)CLC-static (2018)(1)no
Land Cover BSLC-static (2015–2017)(4)no
Land Surface TemperatureLSTsurfacedaily mean(5)no
Land Surface TemperatureLSTmsurfacemonthly mean(5)yes
MonthM-monthly-yes
Normalized Difference Vegetation IndexNDVI-monthly(5)yes
PM2.5 EmissionsEsurfacestatic (2018)(6)no
Population DensityPD-static (2018)(7)no
Relative HumidityRH1000 hPadaily 12 p.m.(1)yes
Season--seasonal-no
Surface PressureSPsurfacedaily 12 p.m.(1)yes
Surface Solar Radiation downwardSSRsurfacedaily 12 p.m.(1)yes
Surface Thermal Radiation downward STRsurfacedaily 12 p.m.(1)yes
Temperature T2 mdaily 12 p.m.(1)yes
Total Precipitation TPsurfacedaily 12 p.m.(1)no
Horizontal Wind ComponentsW10 mdaily 12 p.m.(1)yes
Table
Table 3. Some basic numbers on the different AOD datasets for the year 2018.
Table 3. Some basic numbers on the different AOD datasets for the year 2018.
MODIS-DTMAIACSLSTRTROPOMI
AOD mean0.17 ± 0.080.13 ± 0.060.17 ± 0.080.22 ± 0.06
AOD covered area of study region99.4%99.0%99.0%98.2%
mean daily coverage19.0%13.7%5.5%8.8%
mean pixel counts54463126
collocations with in situ measurements22,56019,200736011,430
percentage of total potential collocations18.6%15.8%6.1%9.4%
Table
Table 4. Overall and seasonal CV PM2.5 statistics for the different datasets including the number of samples (N), the coefficient of determination (R2), the Pearson correlation coefficient (R), root mean square error (RMSE) and mean bias.
Table 4. Overall and seasonal CV PM2.5 statistics for the different datasets including the number of samples (N), the coefficient of determination (R2), the Pearson correlation coefficient (R), root mean square error (RMSE) and mean bias.
DatasetPeriodNR2RRMSE
(μg/m3)		Bias
(μg/m3)
MODIS-DT201822,5600.740.874.360.11
Winter57080.750.874.360.12
Spring54610.750.874.380.08
Summer54140.730.864.350.14
Autumn59770.740.874.360.12
MAIAC201819,2000.770.884.100.13
Winter41320.770.894.120.16
Spring58060.780.894.090.10
Summer49310.760.884.100.14
Autumn43310.760.884.120.12
SLSTR201873600.680.844.200.10
Winter16220.690.844.170.16
Spring20320.700.854.180.06
Summer18110.670.834.210.09
Autumn18950.680.834.220.10
TROPOMI201811,4300.700.843.510.08
Winter26920.700.843.540.07
Spring26870.710.853.470.10
Summer30600.700.843.490.09
Autumn29910.690.843.530.07
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Handschuh, J.; Erbertseder, T.; Baier, F. Systematic Evaluation of Four Satellite AOD Datasets for Estimating PM2.5 Using a Random Forest Approach. Remote Sens. 2023, 15, 2064. https://doi.org/10.3390/rs15082064

AMA Style

Handschuh J, Erbertseder T, Baier F. Systematic Evaluation of Four Satellite AOD Datasets for Estimating PM2.5 Using a Random Forest Approach. Remote Sensing. 2023; 15(8):2064. https://doi.org/10.3390/rs15082064

Chicago/Turabian Style

Handschuh, Jana, Thilo Erbertseder, and Frank Baier. 2023. "Systematic Evaluation of Four Satellite AOD Datasets for Estimating PM2.5 Using a Random Forest Approach" Remote Sensing 15, no. 8: 2064. https://doi.org/10.3390/rs15082064

APA Style

Handschuh, J., Erbertseder, T., & Baier, F. (2023). Systematic Evaluation of Four Satellite AOD Datasets for Estimating PM2.5 Using a Random Forest Approach. Remote Sensing, 15(8), 2064. https://doi.org/10.3390/rs15082064

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop