Abstract
North Brazil Current (NBC) rings are believed to play a key role in the Atlantic Ocean circulation and climate. Here, we use a new collection of high-resolution in-situ observations acquired during the EURECA-OA field experiment together with satellite altimetry to define, with unprecedented detail, the structure and evolution of these eddies. In-situ observations reveal a more complex structure than previously documented. In particular, we highlight a measurable impact of the Amazon outflow in creating a barrier layer over a large portion of the eddies. We show that this unprecedented data set allows us to estimate the accuracy of satellite altimetry gridded fields. The geostrophic velocities derived from satellite altimetry turn out to be considerably lower (up to 50% in amplitude) than the values measured by current meters. However, eddy properties as detected by TOEddies, a newly developed algorithm show to be relatively precise. For example, the eddy center and maximum azimuthal velocity contour fall within 25 ± 5 km and 16 ± 9 km, respectively, from the in-situ observed values. We apply TOEddies to 27 years of satellite altimetry to investigate the generic NBC rings behavior. We found a mean generation rate of 4.5 ± 1.1 rings per year, and a strong seasonal cycle in all eddy properties.
1. Introduction
Mesoscale eddies are a common feature in the ocean and play a major role in ocean variability, as demonstrated in various studies [1,2,3]. These structures are believed to have a significant impact on the transport of heat, salt, mass, and biogeochemical properties throughout the World Ocean by advecting water masses over long distances and extended periods of time [4]. The circulation in the Western Tropical North Atlantic (WTNA) is very active and this results in complex patterns at all temporal scales (mean, seasonal cycle, and synoptic) [5,6]. In particular, it is dominated by the North Brazil Current (NBC) which is an intense western boundary current. It has sources in the equatorial region and in the South Atlantic. Near 6°–8°N, the NBC seasonally separates from the coast to feed the North Equatorial Counter Current (Figure 1) [6,7,8]. The NBC retroflection is more developed from June to February, while it is nearly absent from March to May [6].
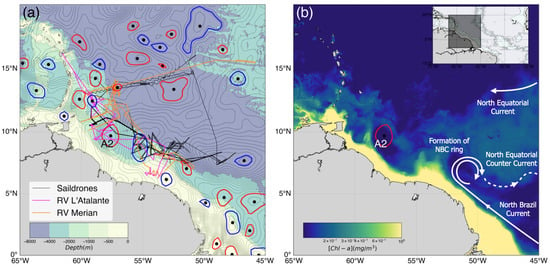
Figure 1.
(a) Bathymetry of the tropical Atlantic Ocean (from the ETOPO2 dataset). The region of interest is delineated by the shaded gray square in the upper right panel. The absolute dynamic topography (ADT) contours for 30 January 2020 are shown in gray. The anticyclonic and cyclonic eddies detected by TOEddies are shown as red and blue contours, respectively. The NBC A2 ring discussed in this work is highlighted. The thin lines indicate the trajectories of 2 research ships and 5 Saildrones ™deployed during the EURECA-OA campaign. (b) Schematic of major ocean currents in the western tropical Atlantic superimposed on the 30 January 2020 chlorophyll-a field using the GlobColour gap-free chlorophyll-a product (GlobColour data, accessed on 18 January 2023 (http://globcolour.info) developed, validated, and distributed by ACRI-ST, France). The A2 detected by TOEddies on the same day is shown as red contour.
Regularly, the NBC retroflection sheds large warm-core anticyclonic rings, dubbed NBC rings. They are characterized in the literature by a mean radius of 200 km [9]. Their vertical extent has been documented to vary from 200–300 m to 1000 m [9,10,11]. NBC rings clearly appear (at least the shallower variety that is intensified at the surface) in satellite altimetry maps as large sea level anomalies (SLAs) [12,13]. They translate northwestward along the South American continental slope with velocities ranging from 0.1 to 0.17 m/s (8–15 km/day) [9,11,12,14,15] before colliding with the Lesser Antilles where most of them break up and dissipate by interaction with the topography [9,15,16]. Yet, other studies suggest that NBC rings can enter the Gulf of Mexico, and impact the mesoscale dynamic in this basin [17]. The evolution and the fate of NBC Rings are important elements of the global ocean circulation and climate as they provide an essential part of the inter-hemispheric transport of mass, heat, salt, and many different biogeochemical ocean properties playing a key role in the Atlantic Meridional overturning Circulation (AMOC; [11]). Ref. [11] estimate that NBC rings transport 9.3 Sv (1 Sv = ms) on an annual average. They also contribute to the offshore advection and dispersal of fresh and nutrient-rich waters from the Amazon River (Figure 1) [7,10,18,19].
While satellite data provide access to the evolution of the surface properties of the shallower variant of NBC rings, hydrographic data give information on their vertical structure. Based on either one or the other, previous studies focused on the characterization of NBC rings, their structures, and associated dynamics [7,8,9,10,11,12,14,20,21,22,23,24,25,26]. Based on satellite Sea Surface Temperature (SST), Ref. [27] identified warm-core eddies for the first time in this region. Other studies on NBC rings identified them from velocity fields in numerical simulations, Ref. [15] or used SLA and empirical mode decomposition, Ref. [24] to focused on their propagation and decay. Although NBC rings were extensively studied since the inception of sea surface temperature or altimetry satellite missions, not many studies addressed statistics over the entire length of available satellite time series [15,24,25,26,28]. Recently, Ref. [25] applied for the first time the angular momentum eddy detection and tracking algorithm (AMEDA; [29]) to a 24-year long time series in the WTNA, and investigated the inter and intra-annual variability of NBC rings. However, in-situ observations describing the vertical structures and properties of the rings remain relatively rare, as do quantitative estimates of transport and other properties from satellite and in-situ observations.
In this framework, this work takes advantage of the high-resolution and large spatial extension of in-situ observations undertaken during the EURECA-OA field experiment, a project within the larger EURECA/ATOMIC (Elucidating the role of clouds circulation in climate/Atlantic Tradewind Ocean–Atmosphere Mesoscale Interaction Campaign) initiative [30] that took place in January–February 2020 in the WTNA, to qualify NBC rings detection and their properties evolution from altimetry satellite data. EURECA-OA aimed at studying small-scale (0.1–100 km) ocean processes and their impact on air-sea fluxes. In this experiment, four research vessels (RVs) from France, Germany, and the United States [31,32,33] and many different uncrewed platforms [30] provided numerous in-situ measurements of the ocean and atmosphere. Here we have identified and tracked in time ocean eddies and NBC rings in particular, from satellite altimetry by applying the recently developed Tracking Ocean Eddies (TOEddies) automatic detection algorithm [34,35,36] to Absolute Dynamic Topography (ADT) maps [37] to identify NWTA eddies, their trajectories, and associated parameters. TOEddies was also applied to Near Real Time ADT maps during the EURECA-OA field experiment to guide the in-situ sampling strategy [31].
This article focuses on a shallow NBC ring, dubbed as A2 in the following (see also [19]), that was crossed by different RVs close to its center 4 times. A2 vertical properties were measured by a suite of different devices, providing a robust and relatively complete dynamical description of the eddy. In the first part of this study, we use the acquired high-resolution in-situ observations to qualify the ability of satellite altimetry gridded maps and the TOEddies detection algorithm in defining the ring, providing also an error estimate for the algorithm in estimating the position of eddy center and eddy boundaries. We then discuss the comparison of in-situ velocities and surface geostrophic velocities derived from satellite altimetry products for ring A2, including an assessment of if in-situ observed ring velocities correlate vertically. In the second part of this study, we use TOEddies to provide a more comprehensive assessment (compared to the literature) of the spatio-temporal variability of NBC rings physical parameters. Our results are carefully compared with [25], as similar ring identification methods were used over a comparable period of time. The study is organized as follows: in Section 2 the data and methods we used are described. In Section 3, we define and describe the A2 NBC ring properties and define the ring boundaries, center, and azimuthal velocities from both, in-situ observations and the TOEddies algorithm. We then investigate the seasonal and inter-annual spatio-temporal variability of NBC rings parameters and trajectories, as well as their interactions with other eddies in the region. Our results are compared with previous studies. The summary and conclusions are presented in Section 4.
2. Materials and Methods
2.1. The EURECA-OA Cross-Calibrated Measurements
The EURECA-OA field experiment took place in the WNTA during January–February 2020 as part of the EURECA-ATOMIC initiative [30]. The complete ocean and atmosphere set of platforms deployed and measurements acquired during the experiment are described in Ref. [30]. In order to optimize the exploitation of the large array of ocean observations undertaken during the experiment (Figure 1), all vertical profiles measuring temperature, salinity, oxygen, and velocity, have been calibrated and cross-validated in reference to quality-controlled CTD (Conductivity - Temperature - Depth) profiles (see [38]). All the observations acquired by the different devices deployed along the same section are then concatenated together and associated with uncertainty. In this study, we present sections sampled by the R/Vs L’Atalante [31] and Maria S Merian [32]. These sections include CTD, uCTD (for underway CTD), and MVP (Moving Vessel Profiler) profiles. The upper-ocean velocity of the water column was acquired by Ocean Surveyor ADCPs (Acoustic Doppler Current Profiler) on two ships: the R/V L’Atalante was equipped with a 38 kHZ and a 150 kHz and surveyed a depth range from 20 m to below 1000 m, whereas the R/V Maria S Merian was equipped with a 38 kHZ and a 75 kHz, providing measurements from around 40 m to below 1000 m depth.
From these thermohaline and dynamical measurements performed at high vertical and horizontal resolutions, we derived density and velocity maps to estimate the Ertel Potential Vorticity (EPV) using the [39] equation. To remove any discrepancies linked to the gradient calculation on an irregular sampling, the measurements are linearly interpolated on a grid with a 1 km horizontal step and 0.5 dbar vertical resolution, then smoothed by applying a Butterworth filter with a cut-off frequency set at 10 km and 5 dbar in the horizontal and vertical, respectively. The anomaly of EPV, used to underline the presence of coherent vortices, is calculated from a mean state obtained by averaging together all the vertical profiles measured during the EURECA-OA experiment.
2.2. The Eddy Detection and Tracking Algorithm TOEddies
NBC Rings from the WTNA are identified and tracked in time by the TOEddies automatic detection algorithm [34,35,36]. This detection is applied over 27 years (01/01/1993 to 01/03/2020) of the “all-sat-merged” series [37] of delayed time daily Absolute Dynamical Topography (ADT) maps gridded at 1/4° (version DT-2018 of the altimetric product [40]) in the Tropical Atlantic Ocean [70°W–20°W; 10°S–20°N]. TOEddies was also applied to ad-hoc Near Real Time (NRT) ADT maps during the field experiment as well as later with the purpose of comparisons and assessments together with different gridded ADT maps that used a different interpolation distance. These products have been provided by Collecte Localisation Satellites (CLS) and have been computed with a Mean Dynamic Topography (MDT) at a higher resolution (1/8° instead of 1/4°) than the standard MDT product.
The TOEddies method is based on the algorithm proposed and developed by [41,42,43] and it has been used in studies analyzing various aspects of the Atlantic Ocean dynamics. Refs. [34,35,36] developed the new algorithm to detect and track the origin and evolution of Agulhas Current rings. In developing these studies, they included in TOEddies the co-location with Argo floats profiles. These are flagged according as falling within or outside cyclonic or anticyclonic eddies. Ref. [44] applied TOEddies to estimate the role of mesoscale eddies on the meridional transport and advection of water masses across the zonal South Atlantic GO-SHIP section at 34.5°S. Ref. [45] applied TOEddies to assess the cross-basing connectivity linked with mesoscale eddies generated within the largest Atlantic coastal upwelling systems. Ref. [46] applied TOEddies to evaluate the effect of mesoscale eddies on South Atlantic subtropical mode water formation and transport.
The TOEddies detection algorithm is a two-step process. During a first step, TOEddies identifies eddies as closed contours of ADT encompassing only one local extremum. The key assumption of the TOEddies algorithm is that mesoscale eddies satisfy the geostrophic balance. Therefore, the instantaneous eddy streamlines should coincide with the closed isolines of the daily ADT maps. Hence, ADT and not SLA represents the geostrophic stream function. Moreover, very often SLA and ADT closed contours do not coincide as SLA is very sensitive to large SSH gradients associated with intense currents and quasi-stationary meanders and eddies characterizing the MDT (see example in Ref. [47]). TOEddies identifies the local ADT extrema (maxima and minima). Then, it looks for the outermost closed ADT contour around each extremum. In addition to the outer closed ADT contour, TOEddies also identifies, using geostrophic velocities derived from ADT maps, the contour where the mean azimuthal velocity of the eddy is maximum. The equivalent radius corresponding to the area inside this contour, , is then derived alongside with , the mean radius corresponding to the area inside the outermost closed ADT contour. In the second step, TOEddies determine eddy trajectories. For this purpose, TOEddies uses an algorithm based on the overlapping of eddy contours at consecutive time steps [34,43]. The main advantage of the TOEddies tracking method is that it also captures eddy merging and splitting events.
In the present study we defined as NBC rings the anticyclonic eddies detected by TOEddies applied on ADT maps, firstly detected between 3°N and 9°N and between 52°W and 44°W and that crossed during their lifetime a meridional section at 55°W. Although such limits are larger than what is found in the literature, we observed that some rings detaching from the NBC retroflection were located further south-east than the usual geographical domains used to define NBC rings. Moreover, the mean position of the NBC retroflection lies between 6°N and 8°N, and 49°W and 50°W, and shows a large variability [5,14,20,48].
In this study, we computed and analyzed many eddy parameters introduced in Ref. [25], to provide a quantitative comparison with our results. They used AMEDA, a hybrid algorithm based on dynamic parameters and geometric properties of the velocity field. They applied AMEDA to the absolute sea surface height (SSH) and associated geostrophic current fields at 50 m depth provided by the “Global Observed Ocean Physics Temperature Salinity Heights and Currents Reprocessing”—ARMOR3D [49,50]. ARMOR3D is an observational-based product that combines statistical satellite SLA, SST, and sea surface salinity (SSS) data sets with in-situ vertical profiles of temperature and salinity to construct a weekly global 3D field of temperature, salinity, and geostrophic velocities at 1/4° spatial resolution. However, the accuracy of ARMOR3D in representing the vertical mesoscale structure of the ocean has not been fully evaluated, especially in the WNTA. The calculated parameters are eddy lifetime (weeks), maximum azimuthal velocity (m.s) and its associated radius (km), the amplitude (cm), the kinetic energy of the eddy EKE (cm.s), the Rossby number , the translational velocity (m.s), and the distance traveled (km). The NBC ring lifetime corresponds to the number of weeks between the first and last ring detection. The radius and the maximum azimuthal velocity is provided by the algorithm as described by [34,35]. The module of the ADT difference between the ADT extremum and the outermost closed ADT contour for a ring defines its amplitude. The rings EKE is computed as the mean EKE of all ADT maps grid points falling inside the ring maximum velocity contours. To compute the EKE fields, we followed the method of [51]: the geostrophic velocity associated with the ADT product is decomposed as the sum of a low-passed component U and anomaly u’ with respect to this low-passed component. Data are filtered with a 121-day moving median, as NBC rings have a mean lifetime of 3 to 4 months [9]. The eddies EKE is then computed from velocity anomalies as . The mean kinetic energy of the low-frequency currents is based on low-pass filtered velocities, and can be estimated as . We computed the EKE of the rings as well as the average EKE of all ADT map grid points located within the outer contours of the rings. The results are very similar, with the EKE calculated within the outer contours having values on average 2.9% higher than the EKE calculated within the maximum velocity contours. The vortex Rossby number represents a proxy to quantify the surface intensity of eddies and is defined as . The ring translating speed is computed as the velocity required by the structure to move from one detected position to the next one in time (at t + 1). Finally, the distance covered by the rings is computed by summing all distances between consecutive daily detection positions.
3. Results and Discussion
3.1. In-Situ and Satellite Observations of a North Brazil Current Ring
During the EURECA-OA experiment, the TOEddies algorithm was used to track mesoscale eddies in near real-time through the region and adapt the sampling strategy of all deployed observing platforms (ships and uncrewed devices) to center and measure eddies hydrographic properties. Among all structures sampled during the experiment, one NBC ring (eddy A2 in Figure 1) was crossed 4 different times by 2 R/Vs. This provided a set of high-resolved sections of eddy hydrographic properties acquired using CTD, uCTD, MVP, L-ADCP (Lower-ADCP), and S-ADCP (Ship-ADCP). We identified from satellite altimetry maps and measured with in-situ devices different eddies present in the region during the EURECA-OA field experiment. However, as A2 was sampled more than once and at different times during the field experiment, the present study takes advantage of this unique hydrographic description of this specific NBC ring to describe the eddy properties and evaluate the ability of TOEddies applied to satellite altimetry maps to detect the eddy and define its properties.
3.1.1. The A2 NBC Ring as Defined from Satellite Altimetry
A2 was first detected by TOEddies on 21 July 2019 when still inside the NBC retroflection, at 47.3°W and 4.9°N (see Supplementary Material Figure S1). It was last detected on 5 March 2020, west of Barbados, in the Tobago basin, at 60.3°W and 13.0°N. The estimated ring lifetime was 32.7 weeks, which is among the longest NBC rings lifetimes of all rings detected by TOEddies over the 27 years of altimetric data. This high-end value might be due to the fact that TOEddies defines eddies as closed contours of ADT. Therefore, if the detected eddies are embedded in the retroflection before being ejected, their lifetimes will tend to be longer than other estimates. The A2 ring was indeed detected within the NBC retroflection 3 months before being completely ejected. During these 3 months, the different properties of the ring increase in amplitude (Figure 2). When A2 is definitively ejected from the NBC retroflection, at the end of October 2019, its radius, azimuthal velocity, and Rossby number decrease steadily with time while moving northwestward, along the South American continental slope towards the Lesser Antilles (Figure 2a–c,f), whereas the evolution of the ring amplitude and EKE is more complex (Figure 2d,e). The four colored vertical lines in Figure 2 correspond to the dates when the 4 in-situ sections have been undertaken during the EURECA-OA field experiment. They are stacked together because they took place very close in time compared to the lifetime of A2. A video of the evolution of the A2 contour on the daily ADT fields that includes the tracks of the main observing platforms deployed during EURECA-OA is available in the supplementary files.
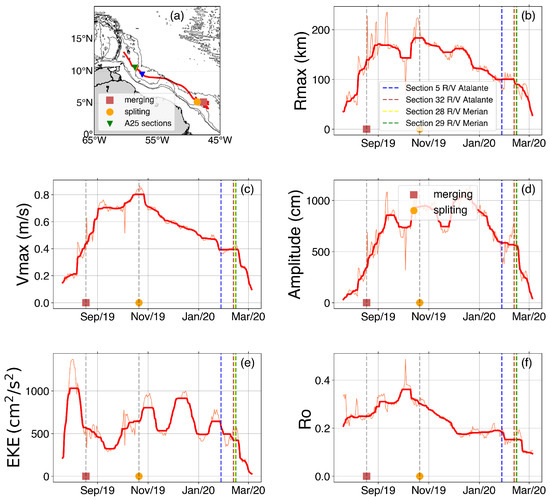
Figure 2.
(a) Bathymetry map (from the ETOPO2 data set [52]) showing the trajectory of NBC Ring A2, positions of splitting and merging events, and intersections with the 4 sections performed during the EURECA-OA experiment. Evolution of A2 parameters is shown in the other panels: (b) Radius of maximum velocity, (c) Azimuthal velocity maximum, (d) Amplitude, (e) EKE, (f) Rossby number. The colored vertical bars indicate the date of the four sections performed by R/V L’Atalante and R/V Maria S Merian.
3.1.2. The A2 NBC Ring In-Situ Observed Characteristics
From 27 to 29 January 2020, the R/V L’Atalante carried out an eastward zonal section of A2 at 9.4°N. It sampled A2 with S-ADCP, LADCPs CTD, uCTD, and MVP profilers (Figure 3a). From 12 to 13 February, the R/V L’Atalante crossed A2 again (Figure 3d), right before the R/V Maria S Merian sampled it on 14 February (Figure 3h), and then on the 15th (Figure 3k). These sections provided high-resolution observations of the ring.
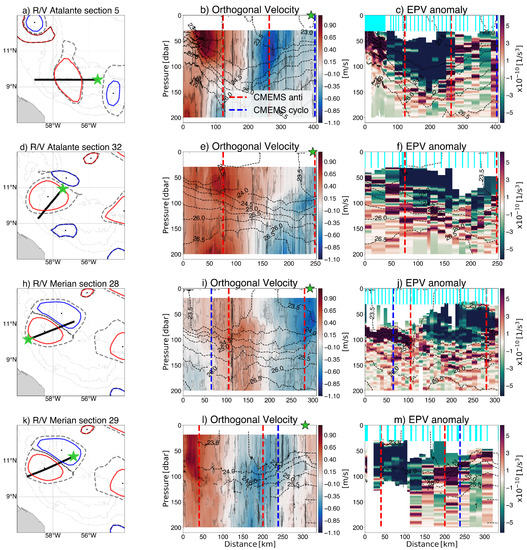
Figure 3.
Ring A2 sections performed by R/V L’Atalante and R/V Maria S Merian during the EURECA-OA experiment. The first to fourth rows correspond respectively to the Sections 5 and 32 of RV/ L’Atalante, and 28 and 29 of R/V Maria S Merian (in chronological order). For each of the four sections, the first panels show the trajectory of the R/V in black, with the green star indicating the end of the section. Red and blue contours are indicative of the anticyclones and cyclones, respectively, detected by TOEddies. The second panel is the velocity, orthogonal to the section, measured by the S-ADCP, and the last panel represents the Ertel potential vorticity anomaly (EPVa) (see Section 2.1 for computation). The dotted black lines are isopycnals, computed by combining cross-validated CTD, uCTD, and MVP devices (the profile positions are indicated by cyan bars on the EPVa sections). The pink line varying vertically indicates that below it, only CTD measurements are represented. The red and blue vertical lines stand for the maximum velocity contours provided by TOEddies. On those four different sections, the surface intensified ring A2 detected by TOEddies is visible in the first 200 m, while a subsurface intensified ring is detected below A2.
The observed velocity structure of ring A2 appears to be more complex than expected (Figure 3). This ring shows high azimuthal velocities close to the surface. A2 has a shallow vertical extension (about 120 m: Figure 3a), and corresponds to a surface intensified ring as described by [9,11,13]. A2 presents an asymmetry in its structure: the maximum azimuthal velocity at the western edge of the ring (left-hand side of the panels) is intenser and closer to the surface than on the eastern eddy side (right-hand side of the panels). This asymmetry is illustrated in Figure S1 and stands out in particular in Figure S4b, where the blue and red vertical velocity profiles correspond respectively to the eastern and western maximum of azimuthal velocity for the first R/V Atalante section. The maximum of velocity at the western edge of the eddy lies closer to the surface, (45 m depth), and shows a higher value (1.22 m/s) than the eastern eddy boundary where the maximum is deeper (75 m depth) and lower in intensity (1.02 m/s). This asymmetry in the A2 structure might be attributed, in part, to the presence of a subsurface anticyclonic eddy (that we dubbed ASUB1) located below the western end of A2. The presence of ASUB1 can explain the upward tilt of the isopycnals, inducing a compression of the water column and a lift in the position, and an increase in the intensity of the local A2 azimuthal velocity maximum. Another factor that might influence the asymmetry is the proximity of the western half of A2 to the upper continental slope. There, the interaction of A2 with the continental slope might also induce an increase and uplift of A2 velocity by compressing the water column. Figure 9a in Ref. [9] also shows this asymmetry for 3 different rings, with higher azimuthal velocity values in their inshore part, in the upper 100 m. This asymmetry was also observed by Ref. [13] for most of the rings, with a comparable difference of 30 cm/s between the two edges of their “ring 1”. Ref. [13] state that this effect is analogous to the well-known wind intensification in the northeast quadrant of tropical cyclones, and occurs because the forward (westward) motion of the ring adds to the clockwise swirl velocity on the southern side of the ring. From the 4 in-situ sections that have sampled A2 during different phases of the one-month EURECA-OA field experiment, we observe that A2 azimuthal velocities decrease with time. This change in azimuthal velocity is also shown by altimetry. This coincides with A2 starting to interact with the steep continental slope when approaching Barbados and the Tobago basin between the end of January and mid-February 2020 (see Figure 3a,d,h,k). On average, between the first and the last section carried out over the ring, the value of the maximum azimuthal velocity dropped by approximately 26%. At the same time, as A2 started to ascend the continental slope, a cyclonic structure developed, generating a modon-type dipole [53] that lived for 27 days during which A2 continued drifting northward, slowly detaching from this cyclonic eddy. This can be explained by the interaction between the ring and the rising continental slope, which engender cyclonic vorticity by water column compression [53,54,55].
The A2 observations carried out during the EURECA-OA experiment provide a precise description of the eddy thermohaline structure. A2 is characterized by salinity ranging from 35.5 psu (in the upper layers around its edges) to 36 psu within its core and a homogeneous temperature of 27 °C (Figure 4). These properties correspond to potential density varying between 23.2 kg.m where salinity is the freshest, to 25.3 kg.m. The lower limit of A2 is clearly revealed by the presence at depth (155 m at the eddy center) of a saltier layer (S = 37 psu), large values of the Brünt-Väisälä frequency (N), and the changing sign of EPV anomaly (the EPV anomaly is negative inside A2; Figure 4). Using the EPV anomaly to describe the volume of the ring, the A2 maximal radius extends to 125 km. Salinity values around 36 psu within the A2 density range are characteristic of water masses originating from the South Atlantic [11], composed here essentially of Tropical Surface Water [56]. However, Figure 4 reveals that a large fraction of the ring’s upper layers is influenced by the presence of fresher water spreading across the eddy boundaries. This lower salinity water is very likely a remnant of the interaction of A2 with the Amazon River plume that has been advected around the eddy when A2 was younger and closer to the Amazon River mouth, very much as described by [18,19,57]. These fresher waters have been translating solidly with A2 northwestward. Their presence has an important impact on the A2 mixing layer (shallower in the region where the water is fresher as this water acts as a barrier layer), masking the eddy imprint on the Sea Surface Temperature field and strongly affecting air-sea exchanges such as CO [19]. A2 has an influence that goes deeper than 155 m as it stretches and pushes down along its passage denser isopycnals (up to 26.5 kg.m and 200 m depth). In this density layer (25.3–26.5 kg.m), salinity values are larger than 37 psu and correspond to Subtropical Underwater, or Salinity Maximal Water [58]. At the periphery of the ring, this same water is found between 60 and 190 m depth and is characterized by salinity above 37.2 psu, with a similar pattern for the dissolved oxygen concentration. The in-situ observations acquired during the EURECA-OA experiment allow accurate comparisons with the detections and tracking of A2 by TOEddies enabling a validation and error estimation for the latter.
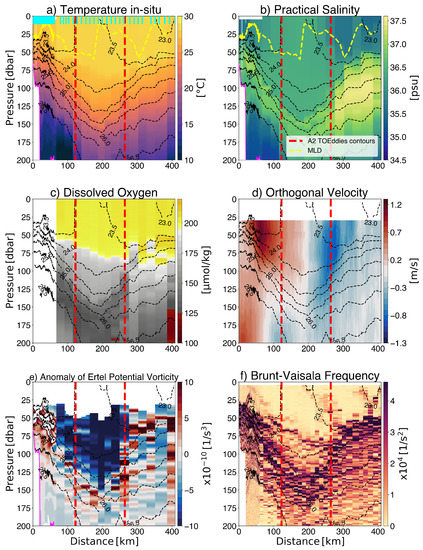
Figure 4.
Ring A2 section performed by R/V L’Atalante during the EURECA-OA experiment, between 27 and 29 January 2020. Red contours indicate the ring maximum velocity contours detected by TOEddies. The dotted black lines are isopycnals, computed by combining cross-validated CTD, uCTD, and MVP devices (the profile positions are indicated by cyan bars on the first panel). The magenta line varying vertically indicates that below it, only CTD measurements are represented. The yellow dashed line corresponds to the mixed layer depth (MLD).
From the available in-situ measurements, we estimated the volume of A2 and the associated mass, heat, and salt transport in the upper layer. The high-resolution data allowed us to derive the Ertel potential vorticity anomaly [39], or EPVa below. This quantity has been shown to characterize coherent eddies in the ocean well (as in [4,59,60,61]). We use it here to define the boundaries of the ring and its volume. By comparison between the EPVa and the potential density anomalies, we chose two isopycnals to define the upper and lower limits of A2: 23.2 kg.m and 25.3 kg.m. They correspond to the green lines in Figure 5. We defined the lateral boundary of the eddy as the limits where the EPVa changes sign, with negative values of EPVa corresponding to the A2 core. These boundaries are shown as a dark purple dashed line in Figure 5. Prior to the volume calculation, we interpolated the EPVa cross-section to a 0.5 dbar and 1 km grid, and performed smoothing using vertical and horizontal cutoff frequencies of 5 m and 10 km, respectively. We assumed that the eddy was axisymmetric. We calculated the volume and property transport for A2 along Section 5 of the R/V L’Atalante as the ship passed through the eddy closest to its center. Heat, salt, and oxygen contents were calculated by integrating the measurements along this section over the bounded volume. We obtained a volume of 4.51 × 10 m and a transport of 0.14 Sv. This value is lower than the CNB ring mass transports estimated previously. Ref. [11] estimated an average annualized transport of 0.8 Sv for surface-intensified NBC rings, and 1.7 Sv for subsurface-intensified rings. However, Ref. [11] focused his transport estimates on the South Atlantic waters for each ring, whereas we calculated the total volume and A2 transport. The A2 mass transport is associated with heat and salt transport of 0.016 PW and 5.3 Sv PSU, respectively (1 Sv PSU kg/s). For comparison, Ref. [26] reconstructed an average NBC ring from in situ measurements and found an average heat transport of 0.07 PW. [8] calculated ring transports ranging from 0.06 PW to 0.10 PW, and the estimated heat transports from the five rings presented in Ref. [21] is 0.036 PW. To allow for more comparisons, we also calculated the A2 volume using 2 additional methods (which are more widely used) to define the ring boundaries. The results are provided in Table 1. The first method is to consider the ring as a cylinder while for the second method we used the location of the maximum azimuthal velocity to define the horizontal boundaries of the eddy (this corresponds to the yellow dotted line in Figure 5). The values obtained exceed in both cases the volume and transport estimates we obtained by constraining the eddy volume with EPVa. This suggests that the published transport estimates may overestimate the transport of shallow NBC rings. For heat, salt, and oxygen contents, we calculated climatological anomalies for the different properties along Section 5 of the R/V L’Atalante using the World Ocean Atlas [62,63,64] as the reference climatology. All anomalies (heat and salt) are positive for A2, except for oxygen.
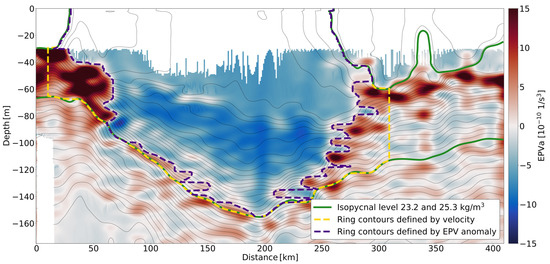
Figure 5.
Ertel potential vorticity anomaly for Section 5 of the R/V L’Atalante. The green isopycnals define the upper and lower limits of A2, while the blue and yellow dashed lines define its horizontal limits using two different methods.

Table 1.
A2 volume, heat, salt and oxygen content, content anomalies and transports for Section 5 of R/V L’Atalante, using 3 different methods.
3.1.3. Computation of TOEddies Error in Estimating the Ring Center
We applied the method described in [65,66], to estimate the A2 ring center from S-ADCP velocities of the 4 sections presented in Figure 3, and ADCP velocities from one of the Saildrones deployed during EURECA-OA when it crossed this ring. To estimate the center of the ring, we created a grid with a resolution of 1/8° around the velocity sections and calculated the tangential and radial velocity components centered at each grid point and at each vertical level from the surface to 90 m depth. The center of the eddy is then assessed by averaging this field vertically and looking for the minimal tangential velocity. This was done for each day when A2 was crossed, using estimated center by TOEddies for each day and corresponding available in-situ measurements (see Figure S2 for an illustration for 27 February 2020). The mean distance for those days, and standard deviation, between the estimated center by this method and by the TOEddies detection algorithm is 25.4 ± 5.0 km. This difference is reasonable, as it corresponds to less than 2 times the mean distance covered by NBC rings in a day. It also corresponds to the resolution of the ADT gridded maps that are used by TOEddies to detect the rings. Moreover, the accuracy of the center position estimation depends on how close the ship sections were carried out from the eddy center. Furthermore, ring A2 presents a shape that deviates slightly from a circle. For all these reasons, the error estimate has to be interpreted carefully. Finally, we also examined the satellite coverage of this ring to know how reliable was the interpolated L4 (gridded) ADT product compared to the L2 (along-track) one. From the 20th of January 2020 to the 17th of February, several tracks of at least 4 different satellites went over A2 providing confidence on ADT fields used by TOEddies to detect this ring.
3.1.4. Computation of TOEddies Error in Estimating the Contours of Maximum Velocity
The TOEddies algorithm is based on the geostrophic approximation and considers closed isocontours of ADT as streamlines. It was used operationally during the EURECA-OA field experiment. The acquired observations, and in particular ADCP measurements, can be used to evaluate the error of the algorithm in assessing the ring contours of maximum azimuthal velocity. The velocity norm averaged over the first 100 m of the water column is plotted as a function of the distance along the undertaken in-situ sections on Figure 6. The mean error, and the standard deviation, associated with the maximum velocity as observed in-situ and as computed from the altimetry geostrophic maps is 16 ± 9 km and varies from 31 km for R/V Atalante Section 5 (Figure 6a) to 7 km for the R/V Maria S Merian Section 28 (Figure 6c). For sections that lasted more than one day, the TOEddies contour used to calculate this error is the one that corresponds to the day the R/V entered or exited the ring. For each of the sections in Figure 6, the average error presented is the average of the error when the R/V entered the ring, and when it exited the ring. The large error associated with the first section might be linked to the particular synoptical situation described before (asymmetry between the velocity distribution at the western eddy edge compared to the eastern). If this ring did not satisfy completely the geostrophic approximation at this time of its lifetime, the algorithm might face issues in selecting a specific ADT contour corresponding to the ring velocity field. Moreover, we observe in Figure 2b that at the time of the first section (corresponding to the blue vertical line), the raw A2 radius decreased by 20 km for a few days before reaching its former value of about 100 km. Thus, the resolution and quality of the ADT fields used to estimate the contours play an important role in the error range. Overall, TOEddies performs well in estimating the maximum velocity contours, as the error estimate is close to or smaller than the ADT resolution (which is 25 km). Figure 6e show estimates of this error as a function of depth limit in averaging S-ADCP velocities. The error in estimating maximum velocity positions is 22 ± 11 km when compared with in-situ velocities at 31 m depth, and decreases as depth increases.
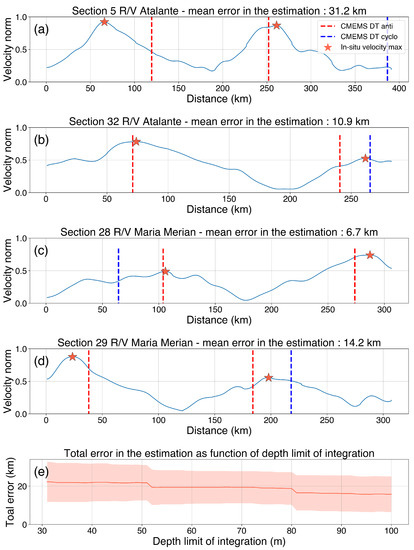
Figure 6.
Comparison of the azimuthal velocity maximum position estimated by TOEddies (vertical red/blue lines, for anticyclonic/cyclonic eddies) and by averaging S-ADCP velocities over the first 100 m (red stars). The error in the estimation for each sections of A2 is presented on the first 4 panels. (a) Section 5 R/V L’Atalante, (b) Section 32 R/V L’Atalante, (c) Section 28 R/V Maria S Merian, (d) Section 29 R/V Maria S Merian, (e) Mean error in the estimation of azimuthal velocity maximum position as a function of depth limit for S-ADCP data integration.
3.1.5. Comparison between In-Situ and Satellite-Derived Surface Geostrophic Velocities
One of the main uncertainties in applying the TOEddies algorithm lies in determining with precision the azimuthal velocity maximum associated with eddies. Applied to satellite altimetry, TOEddies takes as an input the surface geostrophic velocity fields derived from ADT. Here, we test how surface geostrophic velocity derived from ADT and the observed in-situ velocity compare with each other. Ref. [67] showed, using S-ADCP and neutrally buoyant RAFOS floats, that correlation coefficients between altimetry-derived geostrophic velocities and in-situ velocities decrease with depth. Figure 7 shows such a comparison for R/V L’Atalante Section 5. Figure 7a shows the average of the S-ADCP velocities for the upper 100 m in red arrows, for the upper 30 m in green and geostrophic velocities derived from satellite altimetry in blue. The in-situ averaged velocities are larger and follow a slightly different direction than geostrophic velocities derived from satellite ADT maps. Figure 7b presents the intensity of the in-situ velocity along the section at different depths. From 30 m to about 200 m depth (lines in shades of blue), the signal of the surface intensified ring A2 is discernible, whereas from 200 m to 500 m it disappears.
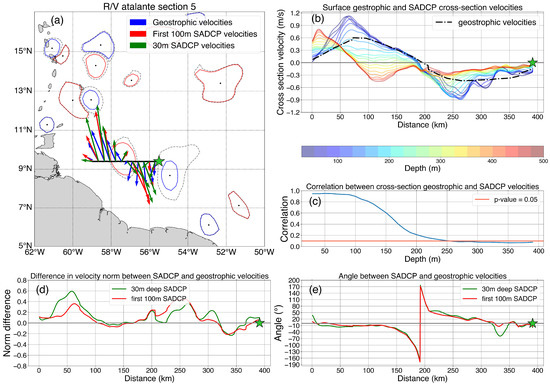
Figure 7.
Comparison between S-ADCP and surface geostrophic velocities derived from satellite altimetry for R/V L’Atante Section 5. (a) Ring A2 section, with maximum velocity contour in red (blue) for anticyclones (cyclones) and outermost contour in dotted black line. Surface geostrophic velocities are shown in blue arrows, the first 100 m averaged S-ADCP velocities are in red, and the 30 m depth velocities are in green. (b) Cross-section surface geostrophic velocities are shown in dotted black lines and cross-section S-ADCP at different depths are shown in jet colors. (c) Pearson coefficient correlation between Surface geostrophic and S-ADCP velocities plotted as a function of depth. (d) Difference in velocity norm between surface geostrophic and S-ADCP velocities at different depths. (e) Angle difference between surface geostrophic and S-ADCP velocities at different depths.
The Pearson correlation coefficient between geostrophic and S-ADCP velocities decreases with depth, and shows values of about 0.95 from 30 m to 90 m depth (Figure 7c). Although the two data sets are highly and significantly correlated, an important difference in velocity norm exists. For S-ADCP velocities averaged over the first 100 m, at the inshore and offshore azimuthal velocity maxima, the differences with surface geostrophic velocities derived from ADT maps are respectively 36 cm/s and 45 cm/s, whereas for S-ADCP velocities at 30 m depth, the differences are respectively 60 cm/s and 35 cm/s (Figure 7d). In terms of direction, the angle difference between geostrophic and S-ADCP velocity vectors remains small outside the ring. However, when approaching the ring center, the difference increases until it reaches ±180° and decreases again. Yet, this result is not significant, as this corresponds to a region close to the eddy center, where velocities are very small. For S-ADCP velocities averaged over the first 100 m, at the inshore and offshore azimuthal velocity maxima, the angle differences with altimetry derived surface geostrophic velocities are respectively −11° and 20°, whereas, for S-ADCP velocities at 30 m depth, the differences are respectively −15° and 25° (Figure 7e). Comparisons of S-ADCP velocities and satellite-derived surface geostrophic velocity for the other three sections undertaken by the R/Vs Atalante and Maria S Merian during EURECA-OA provide similar results (Figures S3–S5). We computed the difference in velocity norm and angle using all four sections and velocities down to 500 m depth. We plotted the results as a function of the S-ADCP velocity norm in Figure 8. At the scale of the EURECA-OA experiment, we observe that for S-ADCP velocity norms smaller than 0.1 m/s, surface geostrophic velocities derived from satellite ADT maps tend to overestimate the local velocity. The difference linearly increases with the S-ADCP velocity norm. These results indicate that ring velocity intensity is underestimated when using the geostrophic velocity computed from satellite altimetry, especially for high azimuthal velocity values, up to almost 50%. In-situ velocities at 30 m depth are, on average, larger than geostrophic velocities derived from satellite altimetry fields. The difference in terms of velocity direction is, on average, confined between –25° and 25°, and presents a large variability for small values of in-situ velocities. Statistics on this comparison, computed using all the R/V sections, and not only the ones crossing eddies, are presented in Table 2. Overall, the norm difference between velocities averaged over the first 100 m and geostrophic velocities is 0.05 ± 0.14 m/s while for S-ADCP velocities at 30 m depth it is 0.09 ± 0.16 m/s. These differences might be due to the fact that NBC rings do not necessarily satisfy entirely the geostrophic equilibrium, considering that their mean Rossby number is 0.17. In some cases, cyclostrophy might be important enough as discussed by [68,69].
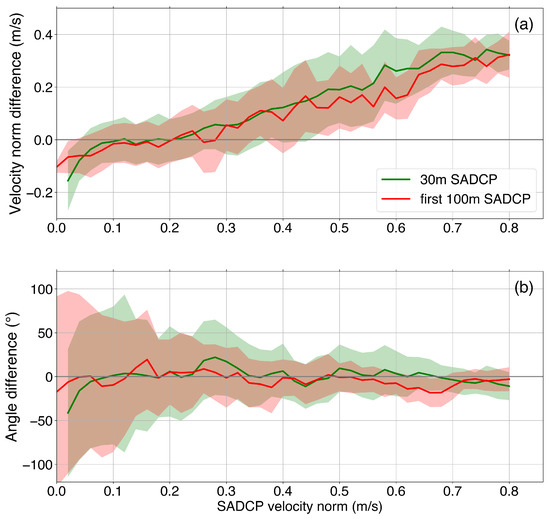
Figure 8.
Comparison between S-ADCP and surface geostrophic velocities, derived from satellite altimetry, using all the R/V L’Atalante and R/V Maria S Merian sections with S-ADCP data available until at least 500 m. S-ADCP velocities averaged over the first 100 m are represented in red while S-ADCP velocities at 30 m depth are shown in green. (a) Velocity norm difference (m/s) between S-ADCP and surface geostrophic velocities as a function of S-ADCP velocity norm. (b) Angle difference (°) between S-ADCP and surface geostrophic velocity vectors as a function of S-ADCP velocity norm. On average, the difference lies between −25° and 25°, with a larger variability for smaller values of in-situ velocities.

Table 2.
Statistics on the differences between norms and directions of surface geostrophic velocities derived from satellite altimetry and S-ADCP velocities, at 30 m deep and averaged over the first 100 m. Those values were computed using all the R/V L’Atalante and R/V Maria S Merian sections with S-ADCP data available.
3.2. Spatio-Temporal Variability of NBC Rings Parameters as Derived from TOEddies
The results of the previous section show the ability of TOEddies (within the limits of satellite altimetry to capture the complex, multi-scale dynamics of the ocean and the accuracy of the method and assumptions made) in detecting and tracking NBC rings when applied to the 1/4° ADT gridded maps. In this section, we apply TOEddies to investigate further the NBC rings life cycle and the spatio-temporal variability in their parameters. Although more in-depth statistical comparisons with other methods would be interesting, these are not included in this study and are beyond the scope of this manuscript.
3.2.1. Variability in NBC Rings Generation
During the 27 years period of the satellite altimetry time series (1993–2020), TOEddies found 122 anticyclonic eddies crossing 55°W that were defined, according to our criteria, as NBC rings. This corresponds to a mean generation rate of 4.5 ± 1.1 rings per year. The ring count for each year is shown in Figure 9. The shedding rate obtained varied from a maximum of 7 rings in 2005 and a minimum of 3 rings for several other years. Results from previous studies are summarized in Table 3. In comparison, Ref. [25] found a rate of 5 rings per year, ref. [16] evaluated an annual rate of 9 ± 3, and previous studies estimates vary between 2 and 9 rings per year, depending on the period and the method used to define them [7,8,11,14,15,24,28]. Recently, Ref. [26] used the META2.0 DT global dataset of eddy trajectories (distributed by AVISO—https://www.aviso.altimetry.fr/en/data/products/ (accessed on 1 January 2023)), based on SLA maps, and found 128 rings from 1993 to 2016, meaning a mean generation rate of 5.3 ± 1.5 rings/year. Although our results remain comparable, ref. [25,26] detected on average more rings than TOEddies between 1993 and 2016. Moreover, Ref. [22] defined 34 anticyclonic eddies formed in the NBC retroflection from October 1992 to December 1998, using the upper layer thickness computed from TOPEX/POSEIDON sea surface height anomalies (SSHa) combined with historical hydrographic data. During the exact same period of time, Ref. [25] identified 29 rings, whereas we detected 26 by applying TOEddies. Ref. [10], using SeaWifs ocean color imagery, identified 18 NBC rings from 1997 to 2000 as does TOEddies, whereas [25] found only 16 for the same period of time. Ref. [24] applied an empirical mode decomposition method to satellite altimetry maps over the period 1993–2015, and obtained a mean shedding rate of 5 rings per year, similar to our estimates. Ref. [7] used a 1 year mooring time series and found a potential generation rate of 7 rings per year, whereas [11] found a yearly rate of 6.5 rings, using almost 2 years of ship and mooring measurements. The underestimation of ring generation using satellite observations compared with the modeling study of [15] as well as subsurface observations detailed in [7,11] can be explained by the presence of subsurface intensified rings that do not generate a surface nor dynamic height signal, and therefore cannot be detected in the present study. Ref. [28] identified from drifting buoys, satellite imagery, and model outputs, 44 rings between 2001 and 2009, with a maximum shedding rate in 2005 and 2007, which is consistent with our and [25] results. Using surface drifters and subsurface floats data collected during the 1989–1992 period [20] suggest a generation rate of 3 rings/year, which can be considered now, in light of all previous studies, as the lower-limit value for NBC rings generation. Finally, Ref. [70] theorized that, for the retroflection on the beta-plane, the shedding period of NBC rings is 90 days, meaning 4 rings per year.
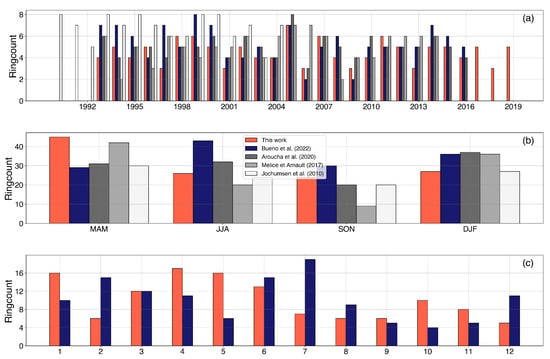
Figure 9.
(a) Number of North Brazil Current (NBC) rings generated per year. (b) Seasonal cycle in the generation of NBC rings. (c) Ring generation as a function of months. Comparison with other studies.

Table 3.
NBC ring generation rates and properties from previous studies.
Among the NBC rings defined by TOEddies, we analyzed those observed with in-situ devices and documented them in published studies. We were able to find all of the 13 surfaces intensified rings previously observed [11,72] and 1 out of 5 of those that were identified as subsurface intensified [11,72]. Despite the generation rates vary slightly among the different methods of eddy detection, our results do not diverge significantly from the others. This suggests that we can trust TOEddies as well as our definition of NBC rings.
The NBC rings time series provided by TOEddies show a clear interannual variability in their generation. The rate varies between 3 and 6 rings per year, except for 2005 during which 7 rings were spawned (Figure 9a). In the literature, the mechanism that drives the year-to-year variability remains unclear. Previous works pointed out possible causes. Ref. [8] proposed the penetration latitude of the NBC retroflection as a factor impacting NBC rings generation. Indeed, a ring is shed almost every time that the NBC retroflection reaches its northernmost position. Ref. [23] investigated the influence of large-scale transport processes in the Atlantic basin, and speculated a weak relationship between ring generation and the North Tropical Atlantic Index, as summed up by [25]. Ref. [28] suggested a biannual pattern in NBC ring generation rates, where alternate years present a distinct gap in ring formation during the late spring and early summer. They also suggest that processes linking the Intertropical Convergence Zone and trade winds are not the main factors influencing ring formation.
Figure 9b,c, show, respectively, the seasonal and monthly ring generation rate. We observe a maximum of ring formation during spring (March–April–May, MAM) and a lower and similar rate in the three other seasons, with a minimum during fall (September-October-November, SON). Rings generated in winter (December–January–February, DJF), MAM, summer (June–July–August, JJA), and SON represent respectively 22.1%, 36.9%, 21.3%, and 19.7%. We observed almost twice as much ring genesis during MAM than SON. Ref. [25] observed a generation maximum in DJF, with 31.4% of rings generation, and a minimum of 16.53% in SON. Ref. [22] used the TOPEX-POSEIDON altimeter data and obtained similar results as [25]. Ref. [26] found a maximum rate of generation in JJA while [10,15,24] obtained results consistent with our study, with a higher generation rate in MAM and lower in SON. It is important to highlight here that in our study, unlike in Ref. [25], we decided to take into account the first detection date of the rings by TOEddies as the generation date. Thus, most of the rings are initially defined inside the North Brazil Retroflection area. As Ref. [10] stated, this difference in methodology is most likely responsible for the differences shown. Also, Ref. [25] used the AMEDA algorithm which defines eddies from the horizontal geostrophic velocity field, applied to ARMOR 3D data, not on daily ADT fields. This might explain a part of the differences as well.
Regarding the monthly variability, we observe in Figure 9b a maximum of ring generation during April, followed by January and May, whereas [25] found a maximum in February, followed by March and June, Ref. [26] in July, June, and February, and [16] in July, August, and February. Ref. [22] presented December and January as months with the highest rate of ring formation, with a year-to-year variability in those months. Although December accounts for a low ring generation in the present study, results for January are consistent. From a model perspective, Ref. [21] showed a maximum modeled generation rate in February, April, and May. Moreover, all previously published works indicate that fall (SON) is the season with the lowest rate of ring generation. As stated by [16,25,28], the seasonality appears to be inconsistent between different years. Despite some differences, especially in terms of identified months with maximum generation rate for NBC rings, our results remain coherent with previous studies.
The NBC has a large annual cycle at this latitude, ranging from a maximum transport of 36 Sv in July–August to a minimum of 13 Sv in April–May, with an annual mean transport of approximately 26 Sv. The mean transport is dominated by flow in the upper 150 m, and the seasonal cycle is contained almost entirely in the top 300 m [6]. The NBC transport cycle is in good agreement with linear wind-driven models and appears to be in near-equilibrium with remote wind stress curl forcing across the tropical Atlantic for much of the year. The NBC retroflection occurs in a seasonal pattern. There is strong retroflection from late summer to early winter, and a weakened or no retroflection during other times of the year. Our results suggest that the seasonal NBC ring maximum generation rate occurs when the NBC transport is minimum and the retroflection is weaker (in spring, MAM) and the minimum rate takes place when the NBC retroflection is strongest, suggesting a direct dynamical (nonlinear) correlation between the intensity of the retroflection and the ring generation process.
3.2.2. Statistics of Physical NBC Characteristics Derived from Satellite Altimetry
To allow comparisons between our results and [25], we computed 8 parameters: the eddy lifetime, horizontal length , maximum azimuthal velocity , Rossby number , Eddy Kinetic Energy (EKE), amplitude, translation speed, and covered distance. The mean values of these parameters are shown in bins of 1°/1° in Figure 10. The spatial variability differs for each parameter. , , amplitude and EKE show higher amplitude near the NBC retroflection, at around 7°N and 50°W (Figure 10b–e). The translation speed tends to show weaker values closer to the coast, and higher when approaching the Lesser Antilles (Figure 10a). Ref. [28] also found higher translation speeds for rings separating completely from the shelf break to follow a more northwestward path. Here, very likely, the topographic-beta effect reduces the drifting speed of the rings located close to the continental slope. The translation speed close to the Lesser Antilles is difficult to estimate with accuracy because of the distortion in ring shape due to the interaction of the rings with the rising continental topography and islands [9]. The NBC rings Rossby number is characterized by a latitudinal gradient. Very likely, this is related to the latitudinal increase of the Coriolis parameter f (Figure 10f). The physical parameters’ standard deviations also show differences (Figure S6). , amplitude and EKE variability present high values northwestward of the retroflection region, at around 8°N and 52°W (Figure S6c–e), whereas the variability of the translation speed and remain relatively constant inside the regional box (Figure S6a,f). An area of high variability in and amplitude appears near 11°N and 57°W.
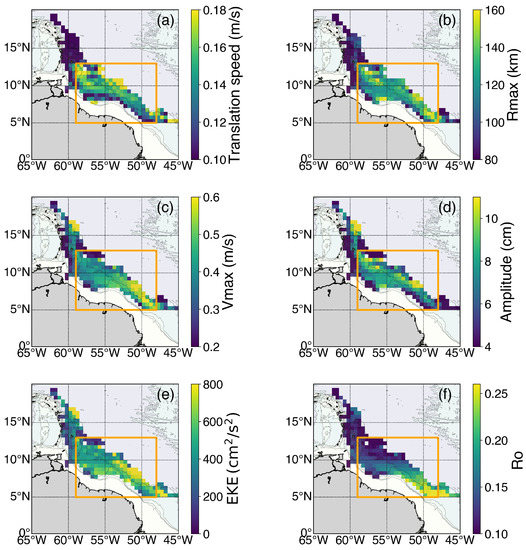
Figure 10.
NBC ring mean values for different parameters: (a) Translation speed, (b) Radius max, (c) Azimuthal velocity max, (d) Normalized Rossby number, (e) Kinetic energy and (f) Amplitude. The orange box defines the region where statistics were computed.
To further investigate NBC ring statistics, we focused on a region where, on average, rings are at their maximum intensity, and where the number of detected structures is sufficient for statistics to be reliable. This box is shown in Figure 10. We computed the global average parameters and statistics on the inter- and intra-annual variability for each ring during those time steps they were inside the box, in order to give the same weight to all the rings, whatever their lifetimes and time spent inside this box. The detected rings have an average lifetime of 17.5 (±7.4) weeks, with values ranging from a minimum of 5 weeks to a maximum of 38.6 weeks. These results are consistent with previous studies. Ref. [25] found an average lifetime of 15.3 (±5.4) weeks, but only selected anticyclonic eddies detected north of 5°N. In the present study, some rings that detached from the NBC retroflection were initially detected by TOEddies between 3°N and 5°N in the region south-east of the NBC retroflection, where the ADT field shows high variability. This variability, due to the proximity of both the equator and the coast, and the fact that it is a region highly dynamic, might explain that the rings detected within the retroflection region can take a couple of weeks before detaching from the NBC retroflection. This can affect the average ring lifetime. This is the case for 8 rings whose lifetimes were greater than 30 weeks. Using subsurface floats and surface drifters, Ref. [9] estimated an averaged lifetime of 13.2 (±5.2) weeks. This smaller value compared to our estimates might be explained by the fact that some of these drifting platforms might have remained within the ring cores during only a limited period of the eddies’ lifespan, and therefore they do not reflect reliably the life duration of NBC rings. Ref. [22] suggest a lifetime of 16 weeks on average, derived from the analysis of TOPEX-POSEIDON altimeter data. Ref. [20] estimate 12 weeks for while 6 rings sampled by looping surface drifters and SOFAR floats studied travel from the very north of the retroflection region to the Lesser Antilles southernmost point. Ref. [26] found a mean lifetime of 11.4 (±7.1) weeks.
TOEddies estimates for the NBC rings translation speed show that it varies from a minimum of 0.09 m/s to a maximum of 0.22 m/s, with an average value of 0.15 (±0.03) m/s. As a comparison, Refs. [8,10,14,22,24,26,28,73] respectively found translation speeds of 0.16, 0.15, 0.16 (±0.05), 0.15, 0.14, 0.17, 0.17 and 0.16 m/s with different methods. Our estimates show that the distance covered by the rings varies from a minimum of 503 km to a maximum of 2731 km, with an average covered distance of 1421 (±432) km.
The analyses of NBC ring radius provide an average value of 123.9 (±23.3) km, with a minimum of 65 km and a maximum of 179.8 km. Results from previous studies are summarized in Table 3. Ref. [25] detected bigger structures, with an average of 139.5 (±23.6) km, but performed their statistics at the time steps corresponding to the week of maximum SSHa for each ring, which might also correspond to a time step of high values. Ref. [26] found using an eddy detection and tracking algorithm an average radius of 138 (±43) km. Among other studies, values of range from 75 km to 200 km [10,14,15,20,21,23,71]. Rings structures with a radius of about 125 km were also detected from SSHa by [24] and from subsurface floats and drifters by [9].
The minimum and maximum values of the mean azimuthal velocities are respectively 0.21 m/s and 0.73 m/s, while the mean value for is 0.45 (±0.11) m/s. Results from previous studies are summarized in Table 3. While [25] found a mean azimuthal velocity of 0.27 (±0.08) m/s using the 50 m deep 1/4° velocity fields from ARMOR 3D, it seems that the geostrophic velocities fields provided by AVISO and used in this study give results closer to other studies. Indeed, azimuthal velocities computed from in-situ data range from 12 to 115 cm/s [9,11,20,21,71], while azimuthal velocities measured during the EURECA-OA campaign range from 50 to 110 cm/s. Azimuthal velocities in Ref. [25] might also be smaller because they performed their statistics during the week of maximum amplitude for each ring, when the swirl velocity might not always be maximum. It is important to be precise here to compute for each ring, we only have access to surface geostrophic velocity fields, while NBC rings possess complex vertical structures of velocity, with maximum of the azimuthal velocities not always located at the sea surface [9]. Ref. [14] also showed differences between geostrophic surface velocities derived from Geosat and from moored current meters at different depths, at time steps correlated to NBC rings presence. Moreover, we showed in a previous section that rings azimuthal velocities can be underestimated up to 50% by surface geostrophic velocities. Therefore, we expect to obtain underestimated values of , that can still be used and give information on their seasonal variations. We can note that ring azimuthal velocities are more than 2 times greater than translating speeds. This proves that NBC rings are coherent structures trapping and transporting water masses and the related properties along their trajectory [3,53].
The amplitude of the selected NBC rings varied from a minimum of 1.9 cm to a maximum of 15.8 cm, with an average amplitude of 7.2 (±2.7) cm. In comparison, Ref. [25] detected rings with a higher mean SSHa of 9.4 (±4.0). This divergence can be explained by the fact that they chose the week of maximum SSHa for each ring to perform their statistics, so high values of SSHa are expected. This also explains why they detected a higher SSHa maximum (24.0 cm) compared to our estimate. The results of the present study are consistent with those found in the literature. Ref. [26] detected rings with an average amplitude of 9 (±5) cm. Ref. [14] detected from Geosat tracks over a ring an SSHa maximum of 10 to 14 cm, and found a high-pass filtered SSH variability varying with seasons from 2 to 3 cm, while [22] found an average sea height residue of 8 (±1) cm. Based on field measurements and altimetry data, Ref. [11] estimated SSHa variations between 15 cm and 25 cm, and more recently [71] found SSHa values ranging from 20 to 30 cm. It is important to keep in mind here that our amplitude values are the averaged amplitude values for each ring over the time spent in the previously defined regional box. Without averaging the amplitude values for each ring, we detect a maximum value of 23.6 cm and a minimum of 3.0 cm.
In this study, NBC rings presented an average EKE of 509.3 (±216.6) cm/s, with minimum and maximum values of respectively 115.7 cm/s and 1308.6 cm/s. The important standard deviation indicates that the energy of NBC rings traveling through the regional box highly fluctuates from ring to ring. In comparison, [25] found a mean kinetic energy associated with the rings of 255.30 (±154.81) cm/s, also with a high standard deviation, and a maximum value of 789.93 cm/s. However, our methodologies differ: while we computed eddy kinetic energy inside each ring, they computed the total kinetic energy. Like for , it is also believed that the difference lies in the difference of velocity fields and the different time steps used to compute the eddy kinetic energy of the rings. In the present study, the estimates of the ring velocities are higher on average and as the kinetic energy depends on the square of the velocity in each grid point inside the eddy contour, EKE estimates are higher. Ref. [14] presented similar results as [25], with EKE values varying from 100 to 300 cm/s. Ref. [74] applied an eddy detection algorithm to the whole tropical Atlantic Ocean and found EKE values varying from 300 cm/s to 600 cm/s for all anticyclonic eddies in a box defined around the NBC retroflection, which is in agreement with our study.
Finally, the rings presented an average Rossby number of 0.17 (±0.03), with values ranging from a minimum of 0.08 to a maximum of 0.27. In order to obtain positive values, we used the absolute to compute the Rossby number. represents the ratio of inertial to Coriolis forces for a rotating fluid, and depends on the Coriolis parameter f which is small in this region close to the equator. As a result, the values of are higher compared to regions further away from the equator. Moreover, this explains the latitudinal gradient of on panel (f) of Figure S6. On average, Ref. [25] used the same method (vortex ) to compute and found a mean value of 0.08 (±0.04). The difference with the present study lies mostly in the difference of , which is on average almost 2 times higher for us. Other computation methods exist and were applied to NBC rings, based on the core angular velocity or the core vorticity. Using the same method as this study, Ref. [21] found absolute between 0.12 and 0.26 and [71] identified a mean of 0.33 (±0.07), with values ranging from 0.25 to 0.47. The Rossby numbers computed from the EURECA-OA measurements, at the depth of the maximum eddy velocity for the 4 previously discussed ring sections, range between 0.25 and 0.46 and are coherent with results from previous studies based on in-situ data. Those values are higher than the geostrophic estimates of Ro, as geostrophic velocities tend to underestimate NBC ring azimuthal velocities.
3.2.3. Inter-Annual and Intra-Annual Variability of Physical NBC Characteristics Derived from Satellite Altimetry
In order to investigate the inter-annual variability, the characteristics of the rings are plotted as a function of the years of generation in Figure 11. We observe alternating longer and shorter ring lifetimes from 2012 to 2019 (Figure 11a). Unlike [25], ring lifetime is not reduced in the last decade. We notice a large value for the eddy radius in 2009 as well as for 2017 and 2006 (Figure 11b). Ref. [28] also obtained higher annually averaged Ring size in 2006. 2006, 1997, 2009 and 2017 are, in order, the years with the highest azimuthal velocity (Figure 11c). We also observe high values of amplitude and EKE in 2009, followed by 2006 and 2017 (Figure 11d,e). Unlike [25], the NBC ring amplitude does not show an increasing trend for the last decade.
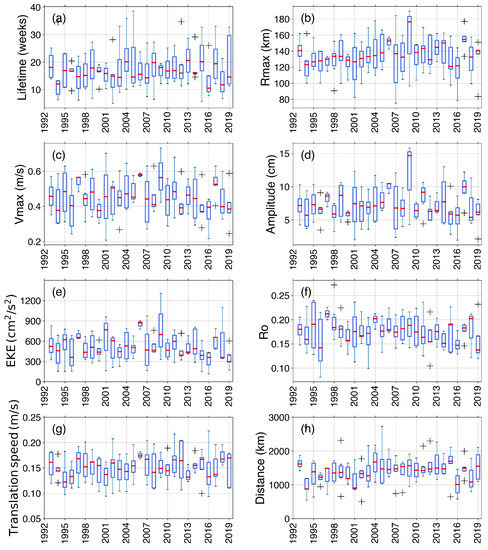
Figure 11.
Inter-annual variability of the NBC rings physical parameters during the 27 years of ADT fields. (a) Lifetime, (b) Radius max (c) Velocity max, (d) Rossby number, (e) Kinetic energy, (f) Amplitude, (g) Translation speed, (h) Distance covered. The box extends from the first to third quartile values, with a red line at the median. The whiskers extend from the edges of the box to show the extreme data points, and black crosses are outliers.
Using the same method as [25], we computed the annual climatological anomalies for the parameters of the ring over the 27-year period (Figure S7), and obtained strong positive anomalies of , , amplitude and EKE in 2009, 2006 and 2017. Although [25] performed their statistics on the week corresponding to the maximum of SSHa, they also pointed out a positive anomaly in 2009 for those parameters, but obtained very different results for 2006. They pointed out the combination of both increased NBC velocities and Amazon River runoff in 2009, which might explain the change in the NBC rings estimates during this year. We computed climatological anomalies associated with the Mean Kinetic Energy (MKE) in the region and found positive anomalies for those 3 years, suggesting an increased transport for the NBC. However, the evaluation of the processes driving the observed anomalies goes beyond the scope of the present study, and further work is needed to investigate those events. The lifetime, , the translation speed, and the covered distance climatological anomalies seem to be uncorrelated with the other parameters anomalies. The lifetime and distance anomalies seem to be evolving in phase: the greater the anomaly of covered distance is, the longer the rings live. However, the relation between the anomalies of translation speed and covered distance is less clear, as greater translation speeds do not systematically correspond to greater covered distance by the rings.
To study their seasonality, the variability of the physical parameters is plotted against the month of the ring formation in Figure 12. All parameters follow a similar seasonal cycle, with maximum values during summer (JJA) and in the middle of winter, except for the translation speed that presents the opposite cycle. NBC rings generated in winter show a shorter lifespan than those generated in summer, with rings shed in July living 2 times longer than the ones generated in February or April. For all parameters, spring (MAM) represent a trimester of minimum values. This cycle is believed to be directly linked with the seasonality of the NBC itself, weaker from April to May and stronger from August to September [6]. In spring, the NBC retroflection regains strength [6,8,48], and more kinetic energy is available, facilitating the development of a closed circulation and subsequent the formation of coherent and large NBC rings [28]. This increase of kinetic energy, visible in Figure 12e, enhances the NBC ring strength, and is correlated with an increase in ring lifetimes (Figure 12a), azimuthal velocities (Figure 12c), length scales (Figure 12b), amplitude (Figure 12d), (Figure 12f) and distance covered (Figure 12h). On the contrary, the translation speed of rings generated in summer is weaker than for the ones generated in other seasons (Figure 12g). August stands out as a month for which the median ring’s physical characteristics are weaker. This corresponds to the month where the NBC and the North Equatorial Counter Current velocities are maximum [6,75,76] and to the month of the northernmost position of the NBC retroflection. Using the algorithm AMEDA, Ref. [25] found no clear seasonal variability in and SSHa. This difference might be explained by their approach that focuses the statistical estimates on the week when the ring SSHa is maximum. Indeed, the ring amplitude maximum may be linked to other factors, that does not depend on the season of generation.
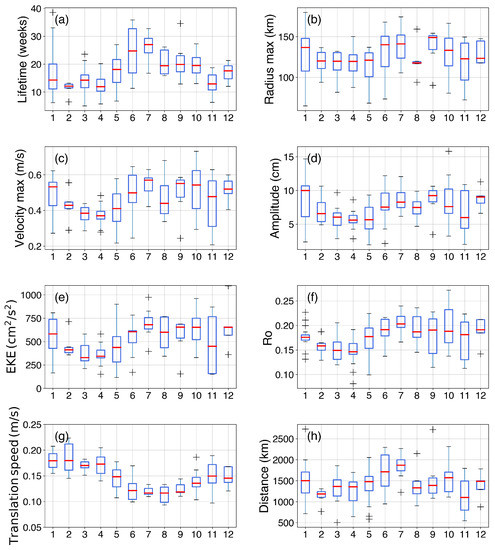
Figure 12.
Seasonal cycles of the NBC rings physical parameters during the 27 years of ADT fields. (a) Lifetime, (b) Radius max (c) Velocity max, (d) Rossby number, (e) Kinetic energy, (f) Amplitude, (g) Translation speed, (h) Distance covered. The box extends from the first to third quartile values, with a red line at the median. The whiskers extend from the edges of the box to show the extreme data points, and black crosses are outliers.
3.2.4. Normalized Ring Life Cycle
In order to describe NBC rings evolution with time, the mean temporal evolution of eddy properties during their life cycle is shown in Figure S8, where their variations are normalized against lifetime. In general, the rings present a growing phase during the first 20% of their lifetimes, during which the radius , the maximum azimuthal velocity , the EKE and their amplitude increases. A plateau is reached for and between 20% and 40 % of their lifetime, while it is reached a little later for EKE as well as for the amplitude (around and between 40% and 60% of the average ring lifetime). After this plateau, those four parameters slowly decrease until the ring reaches 80% of its lifetime. There, all parameters quickly drop in value. Concerning the translation speed, it quickly grows in the first 10% of the rings’ lifetimes and remains constant at 15 m/s until the last 10% of the life of the eddies, where it steeply decays. Finally, the mean Rossby number reaches a maximum of 0.26 in the ring early days, before decreasing constantly with the increasing Coriolis parameter f. The maximum values reached by , , EKE, and the amplitude during the ring lifetime are respectively 137 km, 0.52 m/s, 610 cm/s and 8.6 cm. Ref. [77] performed the same kind of analysis with an eddy detection algorithm applied to the AVISO daily mean SLA from 1993 to 2016. They reconstructed the normalized life cycle for anticyclonic eddies in the world oceans, taking into account the lifetime length, and showed that for medium-lived anticyclonic eddies (30 days to 1 year), the radius evolution is rather symmetric. Yet, in the present study, the radius tends to have an asymmetric structure. As for the amplitude and the EKE, it is expected that they present respectively a symmetric and an asymmetric growth. It is important to also point out the high variability of such parameters, especially for EKE. The seasonality in ring parameters can explain a part of this variability. Indeed, we previously showed that parameters of rings generated in spring have weaker values on average, and we would expect weaker values for such parameters during the whole ring lifespan. Our definition of NBC rings also explains a part of this variability. We chose to consider that anticyclonic eddies are considered NBC rings from their first detection date inside the NBC retroflection to their last detection, which increases the lifespan of eddies sometime by 2 weeks. For those rings, the parameters decaying phase starts after 20% of their life. Ring-eddy interactions, although not frequent, can also modify the ring parameters. Ref. [25] showed that 2 rings merging together could produce an increase of 22% in velocity and 52% in EKE.
After obtaining this seasonal cycle for the ring physical parameters in the previous section, we expect to find clear differences in those parameters during the life of rings generated in different seasons. The mean temporal evolution of eddy properties during their life cycle is shown in Figure 13, as a function of their generation season. Rings generated in spring show on average weaker values of , , EKE, and amplitude at any moment of their life, compared to rings generated in other seasons. They present a slightly smaller radius in their early days, and it decreases towards weaker values compared with other seasons. They show high constant translation speeds during their entire journey, traveling faster in the direction of the Lesser Antilles. On the contrary, rings generated in summer across the region with a relatively constant speed, almost 2 times weaker than for winter and spring. Their peaks before the first 20% of their life and slowly decays to reach a plateau and finally decreases until the last detection date. Regarding , and the amplitude, the growth shape does not change much with the season, and we obtain results are expected when comparing with the mean parameters seasonality. The maximum of EKE is reached at 30% of the life for rings shed in winter, 40% for autumn rings, and 50% for summer rings.
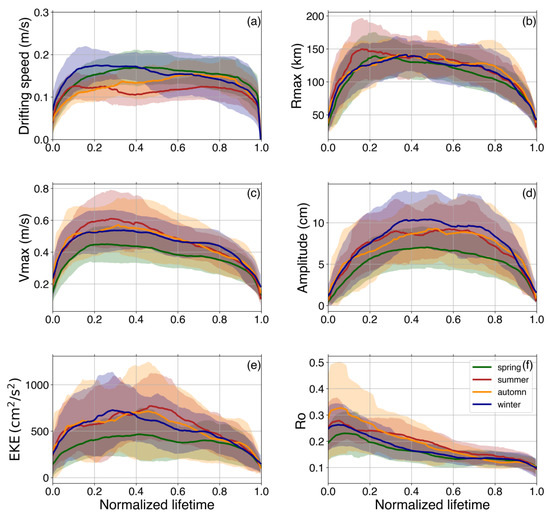
Figure 13.
Ensemble mean and standard deviation of NBC ring parameters for each season as a function of a normalized lifetime. (a) translation speed, (b) Radius max (c) Velocity max, (d) Amplitude, (e) Kinetic energy, (f) Rossby number.
Finally, we investigated the seasonality in NBC rings trajectories (Figure 14). Rings generated in winter take a more northern path, and present the trajectory the furthest away from the shelf, whereas summer rings travel closer to the continental slope. This seems to agree with the fact suggested by in-situ observations of a shallower structure for NBC rings in summer discussed by [11]. Shallower rings might move closer to the shelf than deeper rings, which are constrained to drift more offshore.
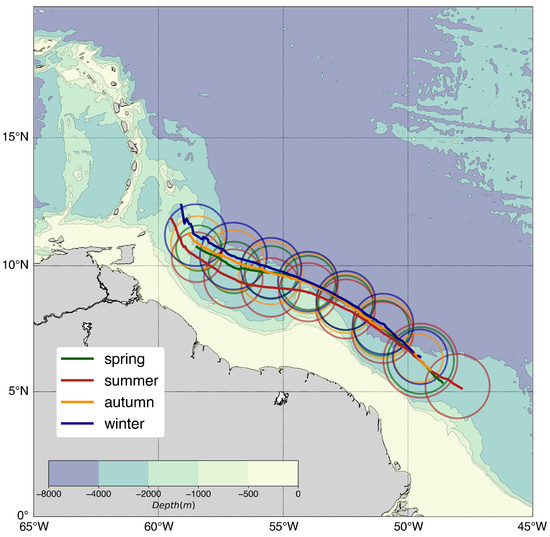
Figure 14.
Mean NBC rings trajectories seasonality and estimated contours based on the average radius for each different season (considering rings as circles). Green, red, orange, and blue respectively correspond to rings generated in spring, summer, autumn and winter.
3.2.5. NBC Rings Merging and Splitting: Spatial Distribution and Impact
Finally, the TOEddies algorithm allows the detection of eddy merging and splitting events. Figure 15 shows the number of anticyclonic eddies merging(splitting) with(from) rings. 57% of all detected interactions of anticyclonic eddies with rings were merging events. Interactions exist all along the ring pathways, but are more frequent in the NBC retroflection region. This is expected as many anticyclonic recirculations are detected in this dynamical region (that could not be considered as eddies, considering their short lifetimes, small scales, and proximity with the retroflection) increasing the number of detected interactions. Ref. [78] found that merging events tend to manifest as an intense eddy (in terms of EKE) merging with a weaker one. We verified this hypothesis for the NBC rings. The results show that the mean EKE of rings merging with other eddies is, on average, 3.4 times higher than that of those eddies. During the 27 years study period, we detected 10 rings merging with another ring, while [25] found only four. 10 rings were also detected to split in the NBC retroflection region.
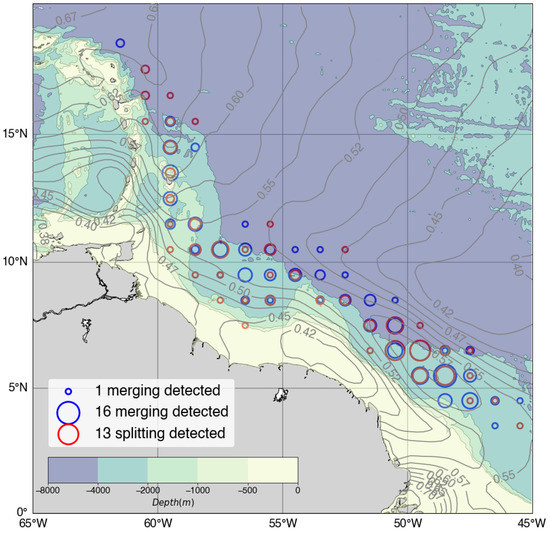
Figure 15.
Number of merging (in red) and splitting (in blue) events, with or from NBC rings, in bins of 1° by 1°. The contours of mean dynamic topography are in gray.
The detection and tracking of eddy merging and splitting in the region allows us to reconstruct the eddy network as defined by [34] (Figure 16) associated with the rings. This provides information on the origins of the eddies involved in merging with NBC rings, as well as the fate of the rings that split. In Figure 16, the eddy trajectories colors depend on the order of the reconstruction: eddies that merged(split) with(from) rings are order 1 trajectories, while eddies that merged(split) with(from) an eddy that previously split from a ring are considered order 2, etc. Our results suggest that a connection might exist between eddies coming from the middle of the Tropical Atlantic Ocean and NBC rings. Eddies originating from 10°N and 20°N might also end up merging with rings or eddies that previously split from rings. Finally, no ring was detected crossing the Lesser Antilles, but several anticyclonic eddies detected inside the Caribbean Sea are considered by TOEddies as linked with ring-splitting events. Although TOEddies finds this connection, the island chain acts as a topographic barrier preventing NBC rings to enter the Caribbean Sea, and it is very unlikely that those direct connections are real. As a matter of fact, Ref. [16] stated, using a geodesic eddy detection method, that NBC rings do not connect the tropical Atlantic and the Gulf of Mexico as coherent material vortices. However, water trapped inside rings can leak in the Caribbean basin through the islands. As a comparison, Ref. [26] used an eddy detection algorithm and detected 2 rings going through the Island chain.
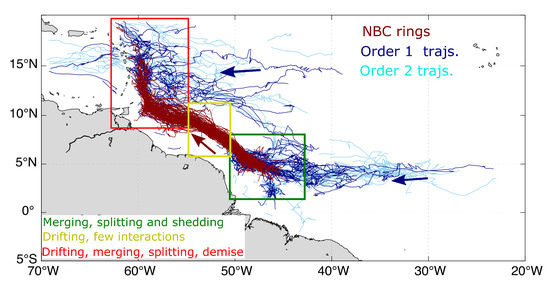
Figure 16.
Network associated with NBC rings (in dark red). Order 1 trajectories are in dark blue and represent eddies that merged (split) with (from) NBC rings. Order 2 trajectories are in cyan and represent eddies that merged (split) with (from) eddies that interacted directly with NBC rings.
4. Summary and Conclusions
The January–February 2020 EUREC4A-OA field experiment provides unprecedented high-resolution in-situ observations to investigate the vertical structure and evolution of an NBC ring and to qualify how the eddy detection and tracking algorithm TOEddies performs. During the cruise we crossed A2, one surface intensified NBC ring, four times. This allowed us to characterize, at high-resolution, its thermohaline and dynamic properties that reveal a more complex structure than previously documented for the observed ring. In particular, despite the relatively low Amazon River outflow in winter, a band of relatively fresh waters encircled and capped the upper layers of the ring over its wide boundaries, masking the eddy core upper-layer temperature and salinity. This is important in terms of freshwater budget for the area [18] and in shaping air-sea fluxes [19].
Comparisons between the ring properties derived from in-situ observations and TOEddies demonstrate the high performance of the algorithm within the limits of satellite altimetry in observing the entire spectrum of the upper-ocean dynamics and the accuracy of the method. In particular, the positions of the maximum azimuthal velocities of the ring and the centers of the ring are accurately assessed. Based on S-ADCP velocity measurements, we found a deviation of 25 ± 5 km for the center and of 16 ± 9 km for the maximum velocity contour estimates. These are reasonable numbers considering the resolution of the gridded altimetry products (1/4°) and the spatio-temporal interpolation of the altimetry L4 product. ADCP measurements show that the ring does not satisfy entirely the geostrophic approximation. They reveal a sensible difference (up to 50% in intensity) from the estimates of surface geostrophic velocities derived from satellite altimetry. This difference increases for velocities closer to the surface.
Using the 27 years of the TOEddies database, we produced new NBC rings statistics. We identified a mean generation rate of 4.5 ± 1.1 rings per year, with more rings shed in boreal spring, and less in boreal autumn. Our estimates compare well, albeit they somewhat differ, with previous estimates from satellite altimetry and ocean color. By comparing TOEddies ring detections with EUREC4A-OA and published in-situ data, we show that only the surface-intensified variety of rings can be identified in a robust way from satellite altimetry to allow for statistics. NBC rings radius, azimuthal velocities, amplitudes, and EKE have their highest values near the generation region, the NBC retroflection. Based on those spatial statistics, we defined a region in which to compute average ring parameters. The average ring lifetime is 17.5 (±7.5) weeks, they cover an average distance of 1421 (±432) km, and their mean translation speed is 0.15 (±0.03) m/s. Their mean radius is 123.9 (±23.3) km, they have a mean azimuthal velocity of 0.45 (±0.11) m/s, an average amplitude of 7.2 (±2.7) cm, an average EKE of 509.3 (±216.6) cm/s and a mean Rossby number of 0.17 (±0.03). By using the Ertel Potential Vorticity anomaly as the limits of the core of the eddy, we obtained a volume of 4.51 × 10 m, a transport of 0.14 Sv, and a heat transport of 0.016 PW, respectively. These values are less than published studies, essentially because of how we defined the eddy boundaries. It suggests that existing estimates may overestimate the transport of shallow NBC rings.
NBC rings characteristics show a clear seasonal cycle. Weaker rings are generated in spring (compared to the other seasons), with, on average, a smaller radius, a weaker amplitude, a shorter lifetime, a weaker azimuthal velocity. They move faster and cover a shorter distance. The opposite is true for summer. For example, in summer, NBC ring lifetime is, on average, 2 times longer. 2006, 2009, and 2017 stand out as years of anomalously large ring radius, azimuthal velocities, amplitude, and EKE. By studying the evolution of ring properties along their trajectories, we identified 3 phases: a sharp increase in their properties during the first 20% of their lifetime, a plateau, and a decrease in the last 60% of their trajectories. Summer ring trajectories follow the continental slope closer to the coast than rings generated in other seasons, probably because in that season they are shallower than in other periods of the year. TOEddies also reveal possible connections between NBC rings and anticyclonic eddies moving into the area from the open ocean near the retroflection (very likely in connection with Tropical Instability Waves) as well as north of 10°N. Our statistics have been compared with previously published works.
In the present study, we combined unprecedented high-resolution in-situ measurements and the TOEddies algorithm, applied to satellite altimetry to guide ships measurements as well as to analyze in-situ observations and derive eddy statistical properties. The approach showed to be a successful strategy in providing new insights into these types of eddies’ properties and evolutions. The TOEddies proves to be a robust method for defining and tracking eddies whose presence is detectable in satellite altimetry. NBC rings are shown to be more complex structures than previously thought and further analyses of the EUREC4A-OA in-situ observations will provide new elements to improve the dynamical understanding of the region as well as of the role of these eddies in the large-scale circulation of the ocean, air-sea interactions, and climate change.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15071897/s1, Figure S1: Section 5 of R/V L’Atalante. (a) Ring A25 orthogonal velocity section with the position of the two vertical velocity profiles located close from the maximum. (b) Absolute velocity profiles corresponding to the panel (a). Ring A25 shows an asymmetry in its velocity structure.; Figure S2: Section 5 of R/V L’Atalante. A2 maximum velocity contour detected by TOEddies on 27 February 2020 is in red, with the estimated center for that day. Geostrophic velocities interpolated along the R/V trajectory are in blue. Nencioli contours estimated using S-ADCP measurements are shown in dashed black lines.; Figure S3: Comparison between SADCP and surface geostrophic velocities derived from satellite altimetry for R/V L’Atante section 32. (a) Ring A25 section, with maximum velocity contour in red(blue) for anticyclones (cyclones) and outermost contour in dotted black line. Surface geostrophic velocities are shown in blue arrows, the first 100m averaged SADCP velocities in red and the 30m depth velocities in green. (b) Cross-section surface geostrophic velocities are shown in dotted black line and cross-section SADCP at different depth are shown in jet colors. (c) Pearson coefficient correlation between Surface geostrophic and SADCP velocities plotted as a function of depth. (d) Difference in velocity norm between surface geostrophic and SADCP velocities at different depths. (e) Angle difference between surface geostrophic and SADCP velocities at different depths. Figure S4: Same as Figure S3 but for section 28 from the R/V Maria S. Merian. Figure S5: Same as Figure S3 but for section 29 from the R/V Maria S. Merian. Figure S6: NBC ring standard deviation values for different parameters: (a) translation speed, (b) Radius max, (c) Azimuthal velocity max, (d) Normalized Rossby number, (e) Kinetic energy and (f) Amplitude. Figure S7: Average climatological anomaly of NBC rings physical parameters over the 27 years of ADT fields. (a) Lifetime, (b) Radius max (c) Velocity max, (d) Normalized Rossby number, (e) Kinetic energy, (f) Amplitude, (g) Translation speed, (h) Distance covered. Figure S8: Ensemble mean and standard deviation of NBC rings parameters as a function of normalized lifetime. (a) translation speed, (b) Radius max (c) Velocity max, (d) Amplitude, (e) Kinetic energy, (f) Rossby number. Video S1: Evolution of the A2 contour detected on the daily ADT fields, with tracks of the main observing platforms deployed during EURECA-OA.
Author Contributions
S.S., X.C. and J.K. conceptualized the project. All authors conducted fieldwork and carried out the measurements and data analysis. S.S., X.C., C.S., P.L. and R.L. contributed to the interpretation of the results. C.S., P.L. and S.S. wrote the manuscript with input from all co-authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the European Union’s Horizon 2020 research and innovation program under grant agreements no. 817578 (TRIATLAS), the Centre National d’Etudes Spatiales through the TOEddies and EUREC4A-OA projects, the French national program LEFE INSU, the IFREMER, the French vessel research fleet, the French research infrastructures AERIS and ODATIS, IPSL, the Chaire Chanel program of the Geosciences Department at ENS, and the EUREC4A-OA JPI Ocean and Climate program and by TRIATLAS H2020 EU program.
Data Availability Statement
We benefited from numerous data sets made freely available and listed here: the ADT produced by Ssalto/Duacs distributed by CMEMS, accessed on 19 January 2021 (https://resources.marine.copernicus.eu), the chl-a and SST maps produced by CLS (https://datastore.cls.fr/catalogues/chlorophyll-high-resolution-daily, accessed on 14 April 2021, and https://datastore.cls.fr/catalogues/sea-surface-temperature-infra-red-high-resolution-daily accessed on 15 April 2021), the SMOS L2Q field produced by CATDS (CATDS, 2019), accessed on 20 April 2021 (https://doi.org/10.12770/12dba510-cd71-4d4f-9fc1-9cc027d128b0), the SMAP maps produced by Remote Sensing System (RSS v4 40 km) and the CCI+SSS maps produced in the frame of the ESA CCI+SSS project, accessed on 25 April 2021 (https://doi.org/10.5285/5920a2c77e3c45339477acd31ce62c3c). The concatenated RVs Atalante and Maria S Merian hydrographic data are available on the SEANOE website: https://www.seanoe.org/data/00809/92071/, accessed on 15 March 2021.
Acknowledgments
This research has been supported by the European Union’s Horizon 2020 research and innovation program under grant agreements no. 817578 (TRIATLAS), the Centre National d’Etudes Spatiales through the TOEddies and EUREC4A-OA projects, the French national program LEFE INSU, the IFREMER, the French vessel research fleet, the French research infrastructures AERIS and ODATIS, IPSL, the Chaire Chanel program of the Geosciences Department at ENS, and the EUREC4A-OA JPI Ocean and Climate program and by TRIATLAS H2020 EU programme. We also warmly thank the captain and crew of RVs Atalante and Maria S. Merian.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Stammer, D. Global characteristics of ocean variability estimated from regional TOPEX/POSEIDON altimeter measurements. J. Phys. Oceanogr. 1997, 27, 1743–1769. [Google Scholar] [CrossRef]
- Stammer, D.; Wunsch, C. Temporal changes in eddy energy of the oceans. Deep Sea Res. Part II Top. Stud. Oceanogr. 1999, 46, 77–108. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale, coherent vortices in the ocean. Rev. Geophys. 1985, 23, 165–182. [Google Scholar] [CrossRef]
- Schott, F.A.; Fischer, J.; Stramma, L. Transports and pathways of the upper-layer circulation in the western tropical Atlantic. J. Phys. Oceanogr. 1998, 28, 1904–1928. [Google Scholar] [CrossRef]
- Johns, W.E.; Lee, T.; Beardsley, R.; Candela, J.; Limeburner, R.; Castro, B. Annual cycle and variability of the North Brazil Current. J. Phys. Oceanogr. 1998, 28, 103–128. [Google Scholar] [CrossRef]
- Johns, W.E.; Lee, T.N.; Schott, F.A.; Zantopp, R.J.; Evans, R.H. The North Brazil Current retroflection: Seasonal structure and eddy variability. J. Geophys. Res. Ocean. 1990, 95, 22103–22120. [Google Scholar] [CrossRef]
- Garzoli, S.L.; Ffield, A.; Yao, Q. North Brazil Current rings and the variability in the latitude of retroflection. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 357–373. [Google Scholar]
- Fratantoni, D.M.; Richardson, P.L. The evolution and demise of North Brazil Current rings. J. Phys. Oceanogr. 2006, 36, 1241–1264. [Google Scholar] [CrossRef]
- Fratantoni, D.M.; Glickson, D.A. North Brazil Current ring generation and evolution observed with SeaWiFS. J. Phys. Oceanogr. 2002, 32, 1058–1074. [Google Scholar] [CrossRef]
- Johns, W.E.; Zantopp, R.J.; Goni, G.J. Cross-gyre transport by North Brazil Current rings. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 411–441. [Google Scholar]
- Garraffo, Z.D.; Johns, W.E.; Chassignet, E.P.; Goni, G.J. North Brazil Current rings and transport of southern waters in a high resolution numerical simulation of the North Atlantic. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 375–409. [Google Scholar]
- Wilson, W.D.; Johns, W.E.; Garzoli, S.L. Velocity structure of North Brazil current rings. Geophys. Res. Lett. 2002, 29, 114-1–114-4. [Google Scholar] [CrossRef]
- Didden, N.; Schott, F. Eddies in the North Brazil Current retroflection region observed by Geosat altimetry. J. Geophys. Res. Ocean. 1993, 98, 20121–20131. [Google Scholar] [CrossRef]
- Jochumsen, K.; Rhein, M.; Hüttl-Kabus, S.; Böning, C.W. On the propagation and decay of North Brazil Current rings. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Andrade-Canto, F.; Beron-Vera, F. Do eddies connect the tropical Atlantic Ocean and the Gulf of Mexico? Geophys. Res. Lett. 2022, 49, e2022GL099637. [Google Scholar] [CrossRef]
- Huang, M.; Liang, X.; Zhu, Y.; Liu, Y.; Weisberg, R.H. Eddies connect the tropical Atlantic Ocean and the Gulf of Mexico. Geophys. Res. Lett. 2021, 48, e2020GL091277. [Google Scholar] [CrossRef]
- Reverdin, G.; Olivier, L.; Foltz, G.; Speich, S.; Karstensen, J.; Horstmann, J.; Zhang, D.; Laxenaire, R.; Carton, X.; Branger, H.; et al. Formation and evolution of a freshwater plume in the northwestern tropical Atlantic in February 2020. J. Geophys. Res. Ocean. 2021, 126, e2020JC016981. [Google Scholar] [CrossRef]
- Olivier, L.; Boutin, J.; Reverdin, G.; Lefèvre, N.; Landschützer, P.; Speich, S.; Karstensen, J.; Labaste, M.; Noisel, C.; Ritschel, M.; et al. Wintertime process study of the North Brazil Current rings reveals the region as a larger sink for CO2 than expected. Biogeosciences 2022, 19, 2969–2988. [Google Scholar] [CrossRef]
- Richardson, P.; Hufford, G.; Limeburner, R.; Brown, W. North Brazil current retroflection eddies. J. Geophys. Res. Ocean. 1994, 99, 5081–5093. [Google Scholar] [CrossRef]
- Fratantoni, D.M.; Johns, W.E.; Townsend, T.L. Rings of the North Brazil Current: Their structure and behavior inferred from observations and a numerical simulation. J. Geophys. Res. Ocean. 1995, 100, 10633–10654. [Google Scholar] [CrossRef]
- Goni, G.J.; Johns, W.E. A census of North Brazil Current rings observed from TOPEX/POSEIDON altimetry: 1992–1998. Geophys. Res. Lett. 2001, 28, 1–4. [Google Scholar] [CrossRef]
- Goni, G.J.; Johns, W.E. Synoptic study of warm rings in the North Brazil Current retroflection region using satellite altimetry. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 335–356. [Google Scholar]
- Mélice, J.L.; Arnault, S. Investigation of the Intra-Annual Variability of the North Equatorial Countercurrent/North Brazil Current Eddies and of the Instability Waves of the North Tropical Atlantic Ocean Using Satellite Altimetry and Empirical Mode Decomposition. J. Atmos. Ocean. Technol. 2017, 34, 2295–2310. [Google Scholar] [CrossRef]
- Aroucha, L.; Veleda, D.; Lopes, F.; Tyaquiçã, P.; Lefèvre, N.; Araujo, M. Intra-and Inter-Annual Variability of North Brazil Current Rings Using Angular Momentum Eddy Detection and Tracking Algorithm: Observations From 1993 to 2016. J. Geophys. Res. Ocean. 2020, 125, e2019JC015921. [Google Scholar] [CrossRef]
- Bueno, L.F.; Costa, V.S.; Mill, G.N.; Paiva, A.M. Volume and Heat Transports by North Brazil Current Rings. Front. Mar. Sci. 2022, 1053. [Google Scholar] [CrossRef]
- Legeckis, R.; Gordon, A.L. Satellite observations of the Brazil and Falkland currents—1975 1976 and 1978. Deep Sea Res. Part A Oceanogr. Res. Pap. 1982, 29, 375–401. [Google Scholar] [CrossRef]
- Sharma, N.; Anderson, S.P.; Brickley, P.; Nobre, C.; Cadwallader, M.L. Quantifying the seasonal and interannual variability of the formation and migration pattern of North Brazil Current Rings. In Proceedings of the OCEANS 2009, Biloxi, MS, USA, 26–29 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–7. [Google Scholar]
- Le Vu, B.; Stegner, A.; Arsouze, T. Angular Momentum Eddy Detection and tracking Algorithm (AMEDA) and its application to coastal eddy formation. J. Atmos. Ocean. Technol. 2018, 35, 739–762. [Google Scholar] [CrossRef]
- Stevens, B.; Bony, S.; Farrell, D.; Ament, F.; Blyth, A.; Fairall, C.; Karstensen, J.; Quinn, P.K.; Speich, S.; Acquistapace, C.; et al. EUREC 4 a. Earth Syst. Sci. Data 2021, 13, 4067–4119. [Google Scholar] [CrossRef]
- Speich, S.; Embarked Science Team. EUREC4A-OA. Cruise Report. 19 January–19 February 2020. Vessel: L’ATALANTE 2021. Available online: https://archimer.ifremer.fr/doc/00689/80129/ (accessed on 1 January 2023).
- Karstensen, J.; Lavik, G.; Kopp, A.; Mehlmann, M.; Boeck, T.; Ribbe, J.; Guettler, J.; Nordsiek, F.; Philippi, M.; Bodenschatz, E.; et al. EUREC4A Campaign, Cruise No. MSM89, 17 January–20 February 2020, Bridgetown Barbados–Bridgetown Barbados, The Ocean Mesoscale Component in the EUREC4A++ Field Study, MARIA S. MERIAN-Berichte, 2020. Available online: https://oceanrep.geomar.de/id/eprint/56445/1/msm89_cruise_report.pdf (accessed on 1 January 2023).
- Quinn, P.K.; Thompson, E.J.; Coffman, D.J.; Baidar, S.; Bariteau, L.; Bates, T.S.; Bigorre, S.; Brewer, A.; De Boer, G.; De Szoeke, S.P.; et al. Measurements from the RV Ronald H. Brown and related platforms as part of the Atlantic Tradewind Ocean-Atmosphere Mesoscale Interaction Campaign (ATOMIC). Earth Syst. Sci. Data 2021, 13, 1759–1790. [Google Scholar] [CrossRef]
- Laxenaire, R.; Speich, S.; Blanke, B.; Chaigneau, A.; Pegliasco, C.; Stegner, A. Anticyclonic eddies connecting the western boundaries of Indian and Atlantic Oceans. J. Geophys. Res. Ocean. 2018, 123, 7651–7677. [Google Scholar] [CrossRef]
- Laxenaire, R.; Speich, S.; Stegner, A. Evolution of the thermohaline structure of one Agulhas ring reconstructed from satellite altimetry and Argo floats. J. Geophys. Res. Ocean. 2019, 124, 8969–9003. [Google Scholar] [CrossRef]
- Laxenaire, R.; Speich, S.; Stegner, A. Agulhas Ring Heat Content and Transport in the South Atlantic Estimated by Combining Satellite Altimetry and Argo Profiling Floats Data. J. Geophys. Res. Ocean. 2020, 125, e2019JC015511. [Google Scholar] [CrossRef]
- Taburet, G.; Sanchez-Roman, A.; Ballarotta, M.; Pujol, M.I.; Legeais, J.F.; Fournier, F.; Faugere, Y.; Dibarboure, G. DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 2019, 15, 1207–1224. [Google Scholar] [CrossRef]
- L’Hégaret, P.; Schütte, F.; Speich, S.; Reverdin, G.; Baranowski, D.B.; Czeschel, R.; Fischer, T.; Foltz, G.R.; Heywood, K.J.; Krahmann, G.; et al. Ocean cross-validated observations from the R/Vs L’Atalante, Maria S. Merian and Meteor and related platforms as part of the EUREC 4 A-OA/ATOMIC campaign. Earth Syst. Sci. Data Discuss. 2022, 1–39. [Google Scholar] [CrossRef]
- Müller, P. Ertel’s potential vorticity theorem in physical oceanography. Rev. Geophys. 1995, 33, 67–97. [Google Scholar] [CrossRef]
- Ballarotta, M.; Ubelmann, C.; Pujol, M.I.; Taburet, G.; Fournier, F.; Legeais, J.F.; Faugère, Y.; Delepoulle, A.; Chelton, D.; Dibarboure, G.; et al. On the resolutions of ocean altimetry maps. Ocean Sci. 2019, 15, 1091–1109. [Google Scholar] [CrossRef]
- Chaigneau, A.; Gizolme, A.; Grados, C. Mesoscale eddies off Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 2008, 79, 106–119. [Google Scholar] [CrossRef]
- Chaigneau, A.; Eldin, G.; Dewitte, B. Eddy activity in the four major upwelling systems from satellite altimetry (1992–2007). Prog. Oceanogr. 2009, 83, 117–123. [Google Scholar] [CrossRef]
- Pegliasco, C.; Chaigneau, A.; Morrow, R. Main eddy vertical structures observed in the four major Eastern Boundary Upwelling Systems. J. Geophys. Res. Ocean. 2015, 120, 6008–6033. [Google Scholar] [CrossRef]
- Manta, G.; Speich, S.; Karstensen, J.; Hummels, R.; Kersalé, M.; Laxenaire, R.; Piola, A.; Chidichimo, M.; Sato, O.; Cotrim da Cunha, L.; et al. The South Atlantic Meridional Overturning Circulation and Mesoscale Eddies in the First GO-SHIP Section at 34.5°S. J. Geophys. Res. Ocean. 2021, 126, e2020JC016962. [Google Scholar] [CrossRef]
- Ioannou, A.; Speich, S.; Laxenaire, R. Mesoscale Eddy Connectivity in the Atlantic Ocean. In Proceedings of the AGU Fall Meeting Abstracts, Online, 1–17 December 2020; Volume 2020, p. OS017-06. [Google Scholar]
- Chen, Y.; Speich, S.; Laxenaire, R. Formation and Transport of the South Atlantic Subtropical Mode Water in Eddy-Permitting Observations. J. Geophys. Res. Ocean. 2022, 127, e2021JC017767. [Google Scholar] [CrossRef]
- Pegliasco, C.; Chaigneau, A.; Morrow, R.; Dumas, F. Detection and tracking of mesoscale eddies in the Mediterranean Sea: A comparison between the Sea Level Anomaly and the Absolute Dynamic Topography fields. Adv. Space Res. 2021, 68, 401–419. [Google Scholar] [CrossRef]
- Garzoli, S.L.; Ffield, A.; Johns, W.E.; Yao, Q. North Brazil Current retroflection and transports. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Guinehut, S.; Dhomps, A.L.; Larnicol, G.; Le Traon, P.Y. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef]
- Mulet, S.; Rio, M.H.; Mignot, A.; Guinehut, S.; Morrow, R. A new estimate of the global 3D geostrophic ocean circulation based on satellite data and in-situ measurements. Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 70–81. [Google Scholar] [CrossRef]
- Jouanno, J.; Sheinbaum, J.; Barnier, B.; Molines, J.M.; Candela, J. Seasonal and interannual modulation of the eddy kinetic energy in the Caribbean Sea. J. Phys. Oceanogr. 2012, 42, 2041–2055. [Google Scholar] [CrossRef]
- Smith, W.H.; Sandwell, D.T. Global sea floor topography from satellite altimetry and ship depth soundings. Science 1997, 277, 1956–1962. [Google Scholar] [CrossRef]
- Flierl, G.R. Particle motions in large-amplitude wave fields. Geophys. Astrophys. Fluid Dyn. 1981, 18, 39–74. [Google Scholar] [CrossRef]
- De Marez, C.; Carton, X.; Morvan, M.; Reinaud, J.N. The interaction of two surface vortices near a topographic slope in a stratified ocean. Fluids 2017, 2, 57. [Google Scholar] [CrossRef]
- Morvan, M.; l’Hégaret, P.; Carton, X.; Gula, J.; Vic, C.; de Marez, C.; Sokolovskiy, M.; Koshel, K. The life cycle of submesoscale eddies generated by topographic interactions. Ocean Sci. 2019, 15, 1531–1543. [Google Scholar]
- Stramma, L.; Fischer, J.; Brandt, P.; Schott, F. Circulation, variability and near-equatorial meridional flow in the central tropical Atlantic. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 1–22. [Google Scholar]
- Coles, V.J.; Brooks, M.T.; Hopkins, J.; Stukel, M.R.; Yager, P.L.; Hood, R.R. The pathways and properties of the Amazon River Plume in the tropical North Atlantic Ocean. J. Geophys. Res. Ocean. 2013, 118, 6894–6913. [Google Scholar] [CrossRef]
- Stramma, L.; Rhein, M.; Brandt, P.; Dengler, M.; Böning, C.; Walter, M. Upper ocean circulation in the western tropical Atlantic in boreal fall 2000. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 221–240. [Google Scholar] [CrossRef]
- Doglioli, A.; Blanke, B.; Speich, S.; Lapeyre, G. Tracking coherent structures in a regional ocean model with wavelet analysis: Application to Cape Basin eddies. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Meunier, T.; Tenreiro, M.; Pallàs-Sanz, E.; Ochoa, J.; Ruiz-Angulo, A.; Portela, E.; Cusí, S.; Damien, P.; Carton, X. Intrathermocline eddies embedded within an anticyclonic vortex ring. Geophys. Res. Lett. 2018, 45, 7624–7633. [Google Scholar] [CrossRef]
- Meunier, T.; Pallás Sanz, E.; de Marez, C.; Pérez, J.; Tenreiro, M.; Ruiz Angulo, A.; Bower, A. The dynamical structure of a warm core ring as inferred from glider observations and along-track altimetry. Remote Sens. 2021, 13, 2456. [Google Scholar] [CrossRef]
- Garcia, H.E.; Weathers, K.W.; Paver, C.R.; Smolyar, I.; Boyer, T.P.; Locarnini, M.M.; Zweng, M.M.; Mishonov, A.V.; Baranova, O.K.; Seidov, D.; et al. World Ocean Atlas 2018, Volume 3: Dissolved Oxygen, Apparent Oxygen Utilization, and Dissolved Oxygen Saturation. Available online: https://archimer.ifremer.fr/doc/00651/76337/ (accessed on 1 January 2023).
- Locarnini, M.M.; Mishonov, A.V.; Baranova, O.K.; Boyer, T.P.; Zweng, M.M.; Garcia, H.E.; Seidov, D.; Weathers, K.; Paver, C.; Smolyar, I.; et al. World Ocean Atlas 2018, Volume 1: Temperature. Available online: https://archimer.ifremer.fr/doc/00651/76338/ (accessed on 1 January 2023).
- World Ocean Atlas 2018, Volume 2: Salinity. Available online: https://archimer.ifremer.fr/doc/00651/76339/ (accessed on 1 January 2023).
- Nencioli, F.; Kuwahara, V.S.; Dickey, T.D.; Rii, Y.M.; Bidigare, R.R. Physical dynamics and biological implications of a mesoscale eddy in the lee of Hawai’i: Cyclone Opal observations during E-Flux III. Deep Sea Res. Part II Top. Stud. Oceanogr. 2008, 55, 1252–1274. [Google Scholar] [CrossRef]
- Kersale, M.; Petrenko, A.; Doglioli, A.M.; Dekeyser, I.; Nencioli, F. Physical characteristics and dynamics of the coastal Latex09 Eddy derived from in situ data and numerical modeling. J. Geophys. Res. Ocean. 2013, 118, 399–409. [Google Scholar] [CrossRef]
- Boebel, O.; Barron, C. A comparison of in-situ float velocities with altimeter derived geostrophic velocities. Deep Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 119–139. [Google Scholar] [CrossRef]
- Ioannou, A.; Stegner, A.; Tuel, A.; LeVu, B.; Dumas, F.; Speich, S. Cyclostrophic corrections of AVISO/DUACS surface velocities and its application to mesoscale eddies in the Mediterranean Sea. J. Geophys. Res. Ocean. 2019, 124, 8913–8932. [Google Scholar] [CrossRef]
- Cao, Y.; Dong, C.; Stegner, A.; Bethel, B.J.; Li, C.; Dong, J.; Lü, H.; Yang, J. Global Sea Surface Cyclogeostrophic Currents Derived from Satellite Altimetry Data. J. Geophys. Res. Ocean. 2023, 128, e2022JC019357. [Google Scholar] [CrossRef]
- Nof, D.; Pichevin, T. The retroflection paradox. J. Phys. Oceanogr. 1996, 26, 2344–2358. [Google Scholar] [CrossRef]
- Castelão, G.; Johns, W. Sea surface structure of North Brazil Current rings derived from shipboard and moored acoustic Doppler current profiler observations. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Silva, A.; Bourlès, B.; Araujo, M. Circulation of the thermocline salinity maximum waters off the Northern Brazil as inferred from in situ measurements and numerical results. In Annales Geophysicae; Copernicus GmbH: Göttingen, Germany, 2009; Volume 27, pp. 1861–1873. [Google Scholar]
- Nof, D. On the β-induced movement of isolated baroclinic eddies. J. Phys. Oceanogr. 1981, 11, 1662–1672. [Google Scholar] [CrossRef]
- Aguedjou, H.; Dadou, I.; Chaigneau, A.; Morel, Y.; Alory, G. Eddies in the Tropical Atlantic Ocean and their seasonal variability. Geophys. Res. Lett. 2019, 46, 12156–12164. [Google Scholar] [CrossRef]
- Richardson, P.L.; Walsh, D. Mapping climatological seasonal variations of surface currents in the tropical Atlantic using ship drifts. J. Geophys. Res. Ocean. 1986, 91, 10537–10550. [Google Scholar] [CrossRef]
- Richardson, P.L.; Arnault, S.; Garzoli, S.; Bruce, J.G. Annual cycle of the Atlantic north equatorial countercurrent. Deep Sea Res. Part A Oceanogr. Res. Pap. 1992, 39, 997–1014. [Google Scholar] [CrossRef]
- Chen, G.; Han, G. Contrasting short-lived with long-lived mesoscale eddies in the global ocean. J. Geophys. Res. Ocean. 2019, 124, 3149–3167. [Google Scholar] [CrossRef]
- Cui, W.; Wang, W.; Zhang, J.; Yang, J. Multicore structures and the splitting and merging of eddies in global oceans from satellite altimeter data. Ocean Sci. 2019, 15, 413–430. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).