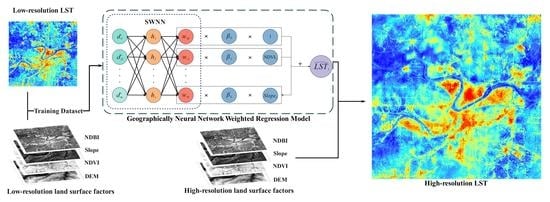
A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression
Abstract
1. Introduction
2. Materials
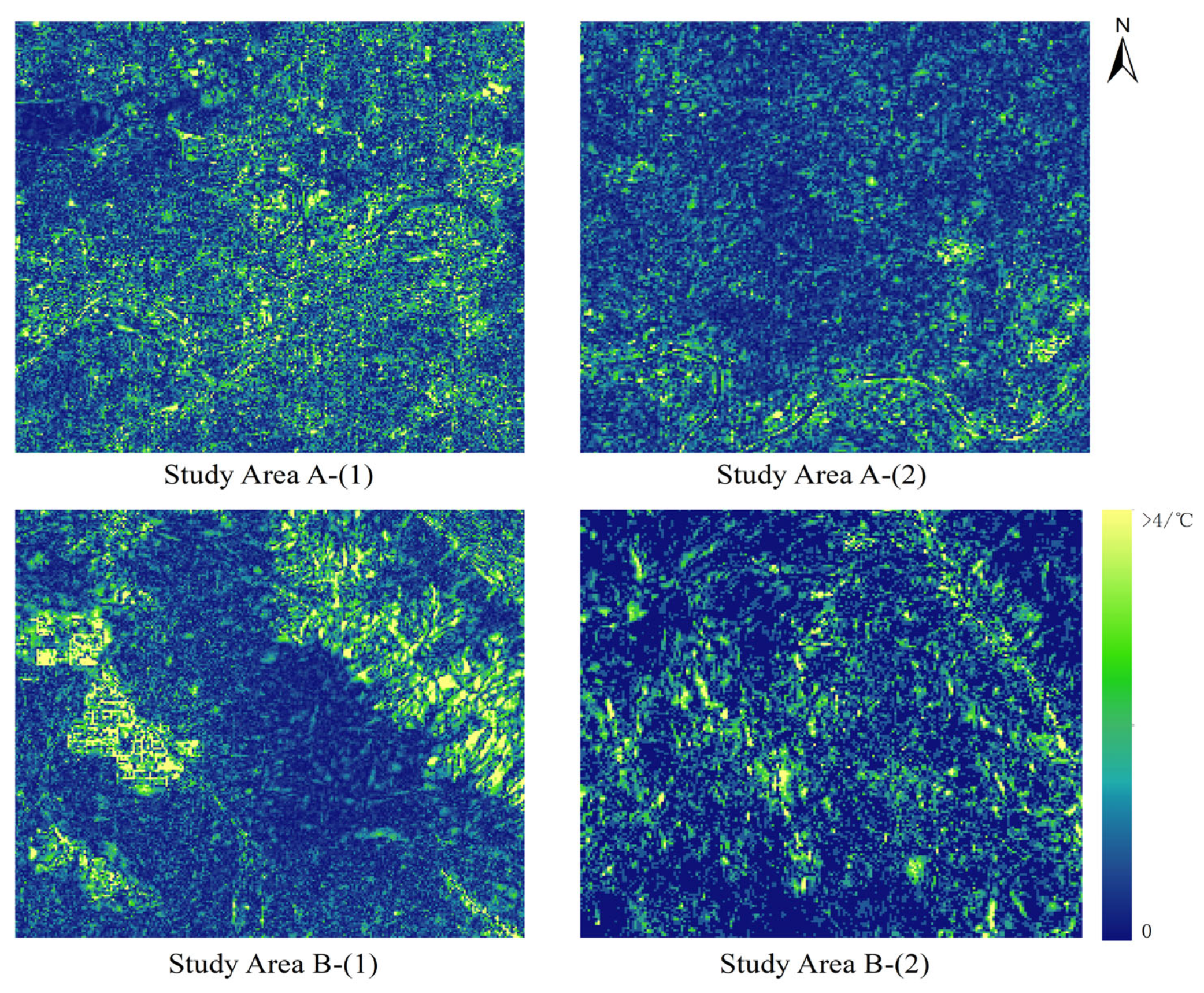
2.1. Study Area
2.2. Data
- (1)
- NDVI is sensitive to vegetation cover, with a value range of [−1, 1], indicating the presence of vegetation cover and increasing with the coverage degree. In this study, it was calculated from the Landsat 8 red band (R) and near-infrared band (NIR). The calculation formula is as follows:
- (2)
- NDBI is sensitive to impervious surfaces and has a value range of [−1, 1]. It can accurately reflect information on built-up land, with higher values indicating higher proportions and densities of built-up land. In this study, NDBI was calculated using Landsat 8 Near Infrared (NIR) and Shortwave Infrared 1 (SWIR1) bands.
- (3)
- DEM. Obtained by clipping NASA DEM data.
- (4)
- Slope. Obtained by using ArcGIS default slope analysis, with DEM data as the input raster.
- (5)
- Land surface temperature. Obtained from Landsat 8 thermal infrared band 10-TIRS using the mono-window algorithm proposed by Qin [38].where T represents LST (°C), Ts represents the brightness temperature (/K) of the sensor, Ta represents the average atmospheric temperature (/K), and a and b are reference coefficients. When the LST is between 0 and 70 °C, the values of a and b are −67.355351 and 0.458606, respectively. C and D are intermediate variables, which are calculated using the following formula:where is the emissivity of the surface, which is obtained according to Qin’s empirical formula, and is the total atmospheric transmittance from the ground to the sensor, provided by NASA.
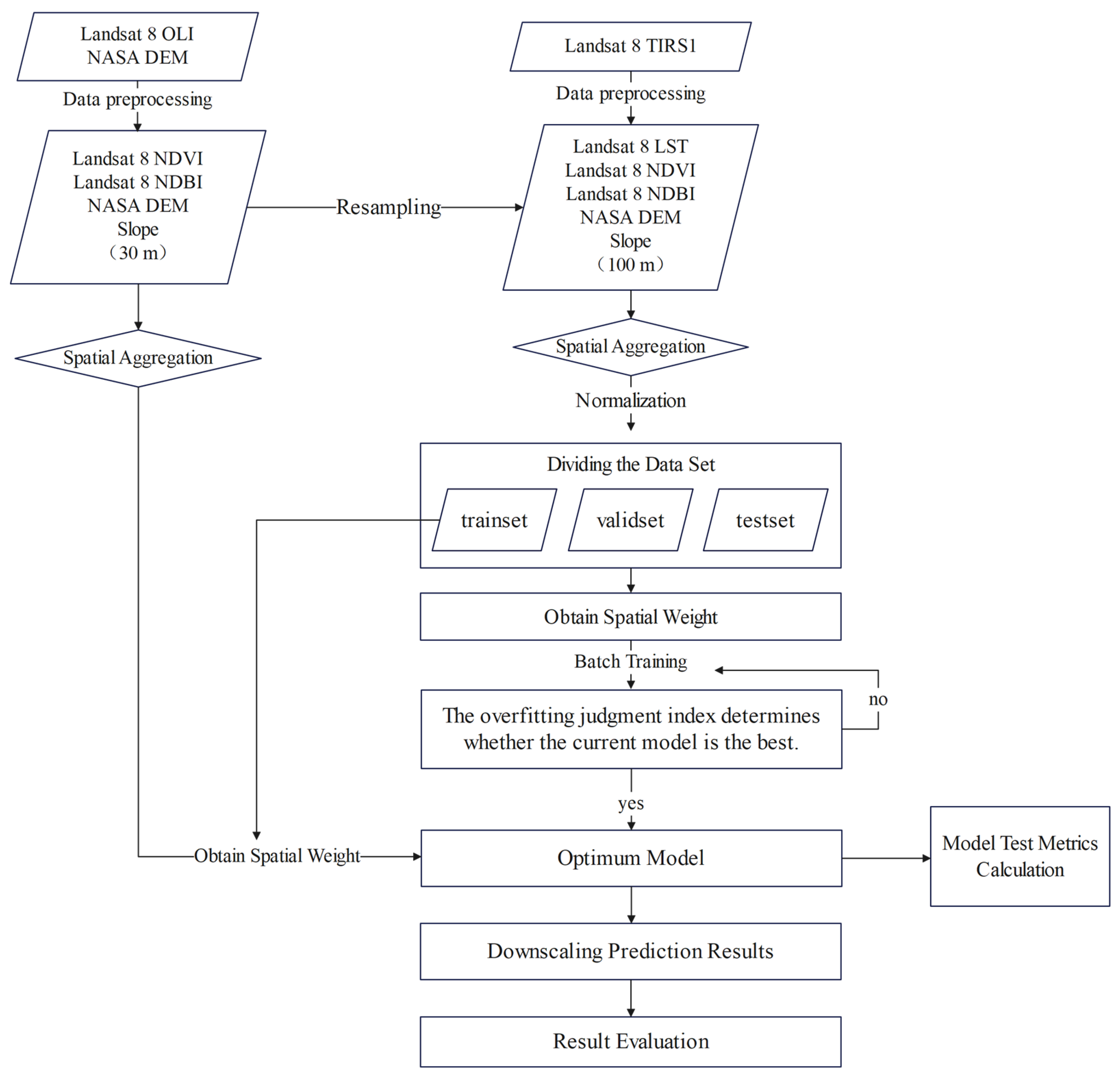
3. Methods
3.1. Land Surface Temperature Downscaling Model Based on GNNWR
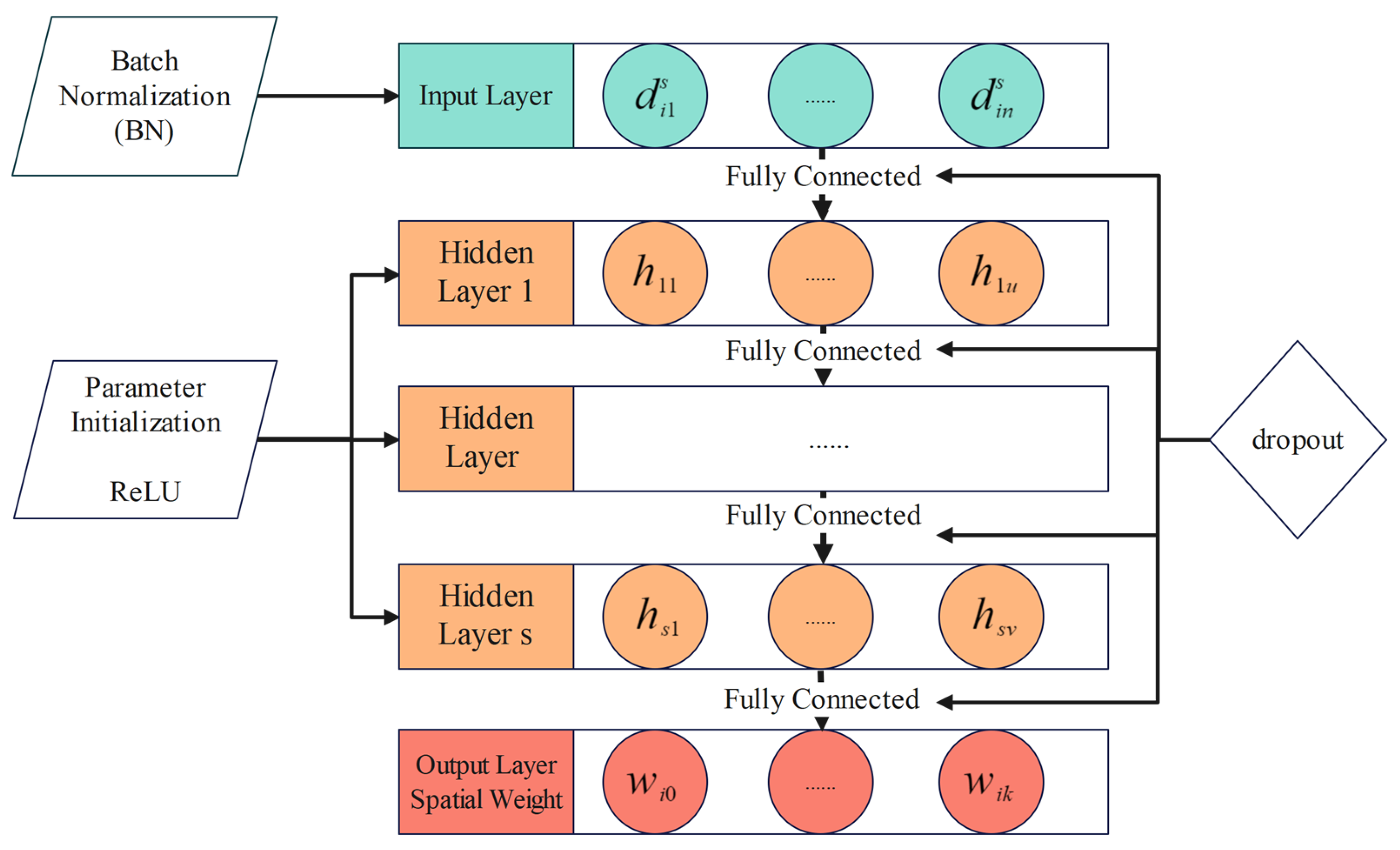
3.2. Model Design and Implementation
3.3. Model Evaluation
4. Results
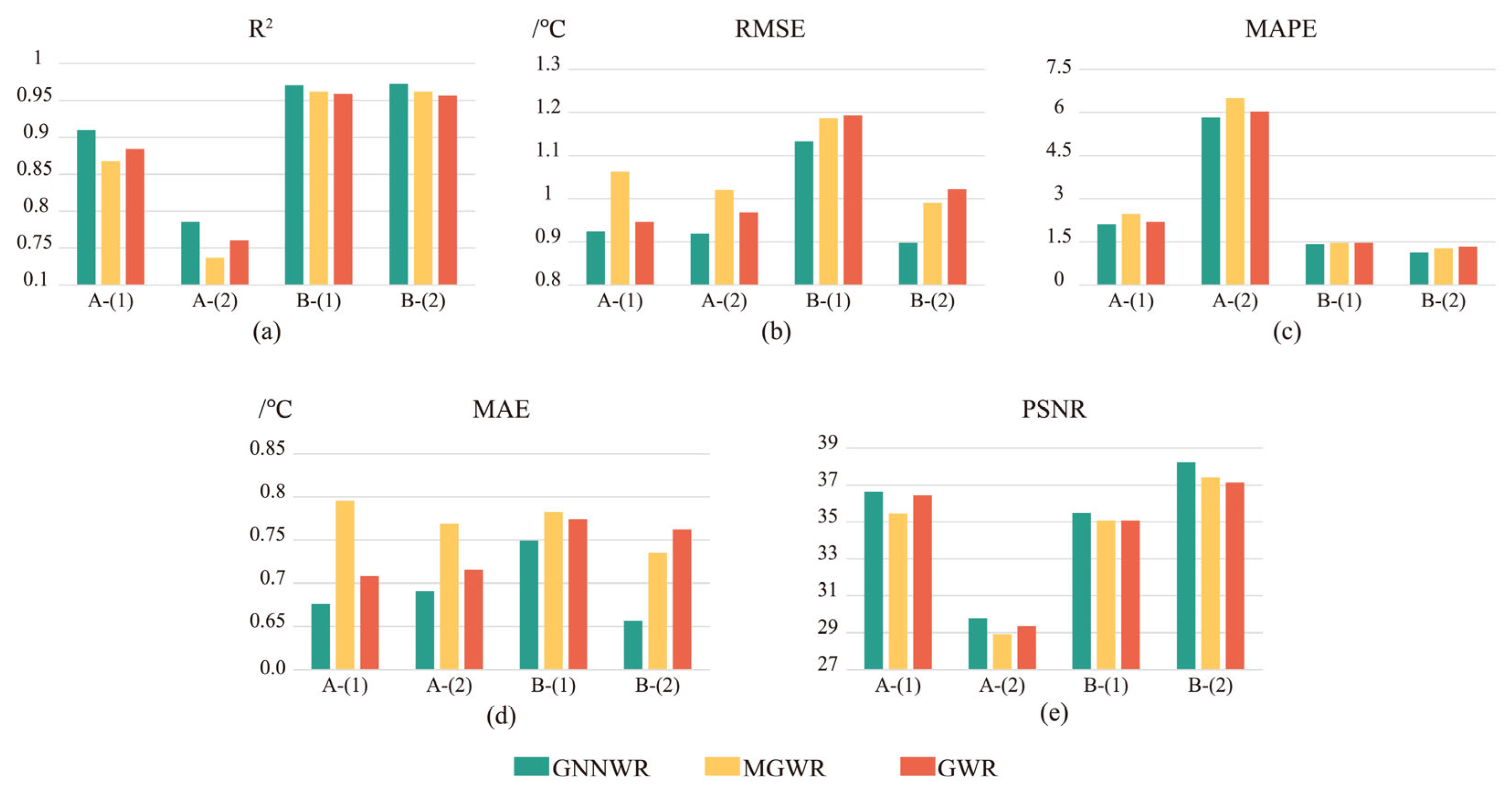
4.1. Comparison and Analysis of Model Performance
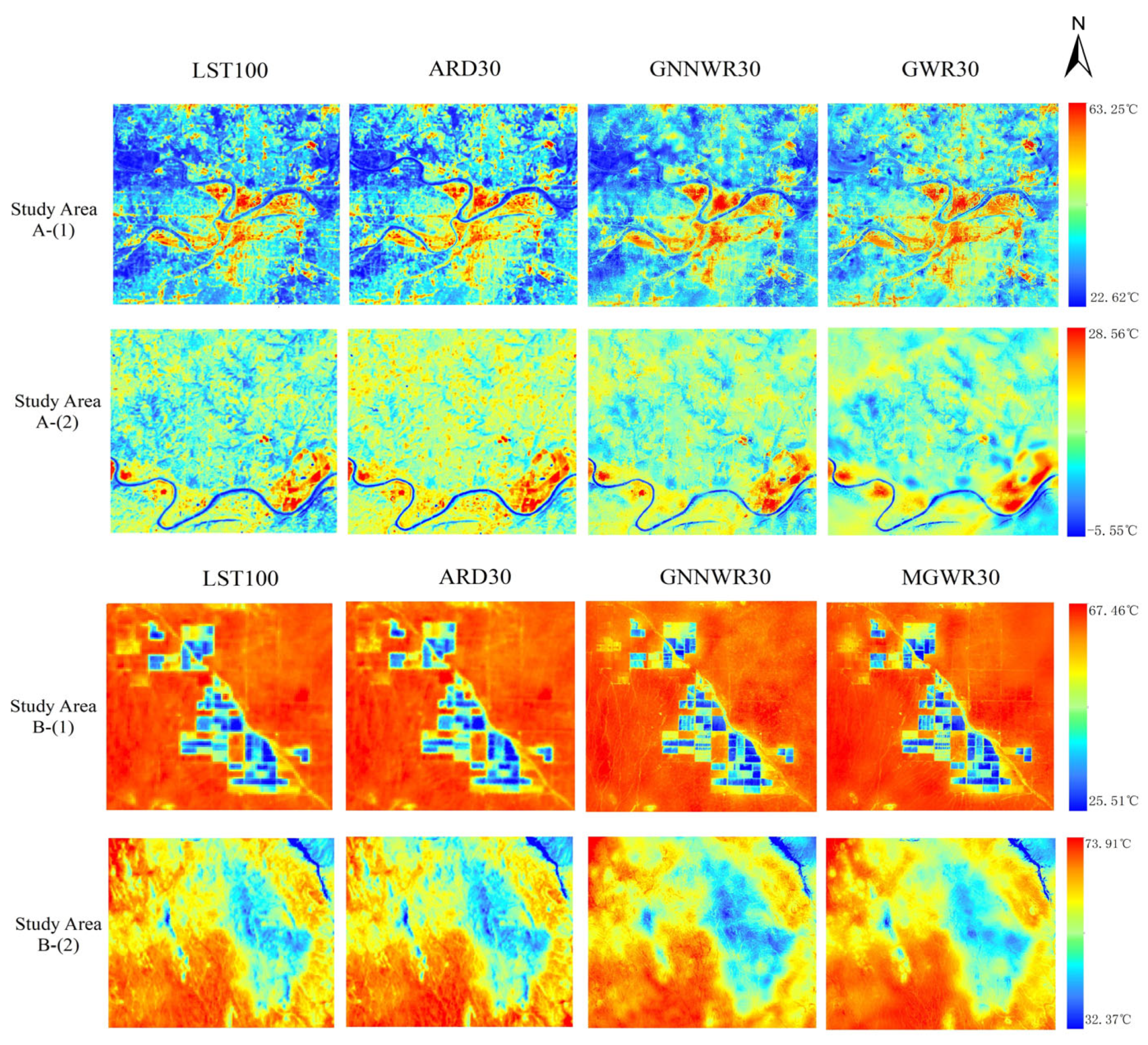
4.2. Spatial Distribution of High-Resolution Land Surface Temperature
5. Discussion
5.1. Availability and Advantages of the GNNWR Model
5.2. Veracity and Reasonability of LST Mappings
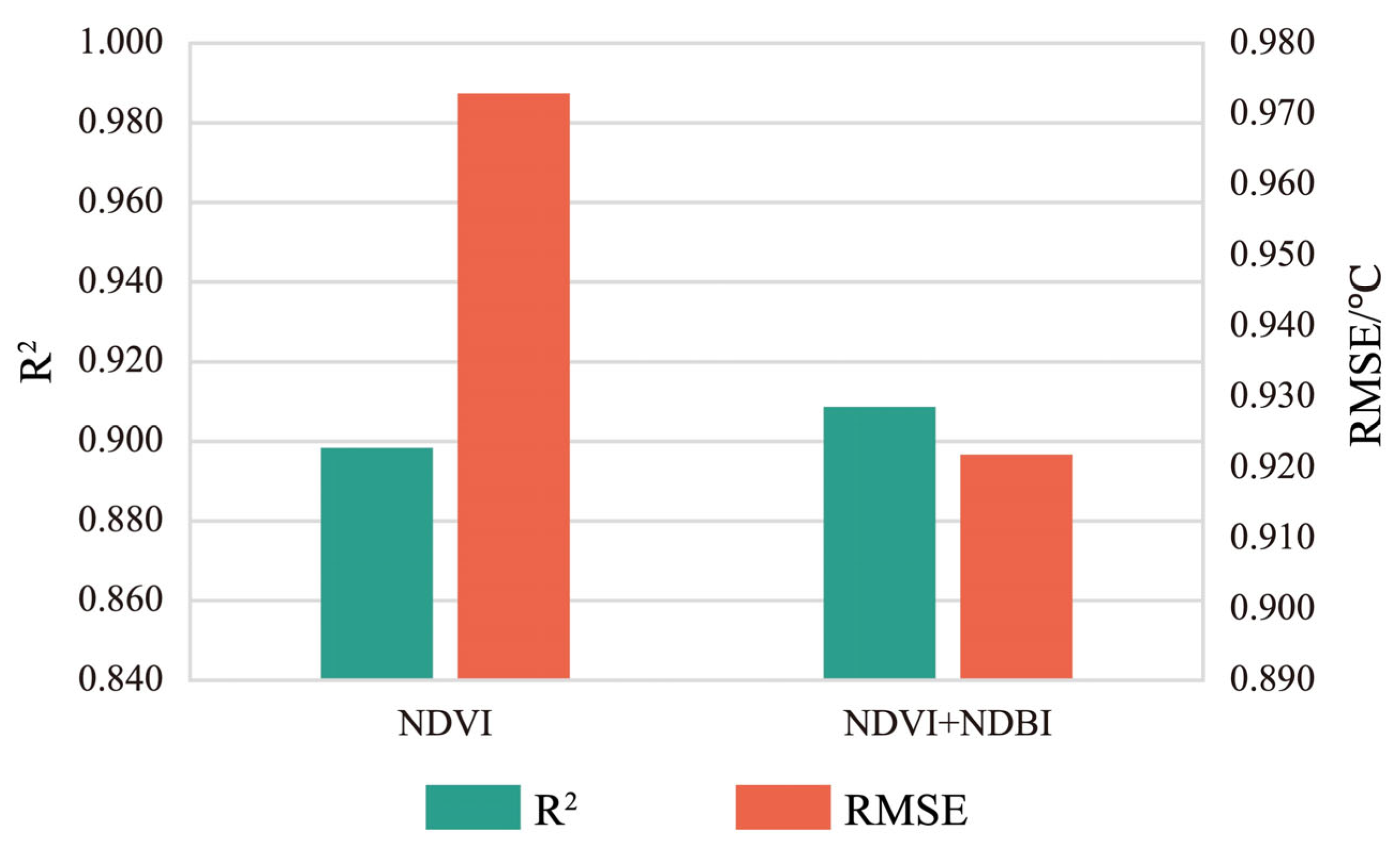
5.3. Model Applicability of Different Factors and Sensors
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Eleftheriou, D.; Kiachidis, K.; Kalmintzis, G.; Kalea, A.; Bantasis, C.; Koumadoraki, P.; Spathara, M.E.; Tsolaki, A.; Tzampazidou, M.I.; Gemitzi, A. Determination of annual and seasonal daytime and nighttime trends of MODIS LST over Greece—Climate change implications. Sci. Total Environ. 2018, 616, 937–947. [Google Scholar] [CrossRef] [PubMed]
- Gillies, R.R.; Carlson, T.N. Thermal remote-sensing of surface soil-water content with partial vegetation cover for incorporation into climate-models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL)—1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Mattar, C.; Sobrino, J.A.; Malhi, Y. Digital thermal monitoring of the Amazon forest: An intercomparison of satellite and reanalysis products. Int. J. Digit. Earth 2016, 9, 477–498. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and Land Surface Temperature for Drought Assessment: Merits and Limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Christensen, P.R.; Bandfield, J.L.; Hamilton, V.E.; Howard, D.A.; Lane, M.D.; Piatek, J.L.; Ruff, S.W.; Stefanov, W.L. A thermal emission spectral library of rock-forming minerals. J. Geophys. Res. Planets 2000, 105, 9735–9739. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, W.; Zhang, Z.; Wang, S.; Zhang, B.; Cheema, M.J.M.; Shalamzari, M.J. Reconstructing high-resolution gridded precipitation data using an improved downscaling approach over the high altitude mountain regions of Upper Indus Basin (UIB). Sci. Total Environ. 2021, 784, 147140. [Google Scholar] [CrossRef]
- Noor, R.; Arshad, A.; Shafeeque, M.; Liu, J.; Baig, A.; Ali, S.; Maqsood, A.; Pham, Q.B.; Dilawar, A.; Khan, S.N.; et al. Combining APHRODITE Rain Gauges-Based Precipitation with Downscaled-TRMM Data to Translate High-Resolution Precipitation Estimates in the Indus Basin. Remote Sens. 2023, 15, 318. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, S.; Li, J. A Self-Calibration Variance-Component Model for Spatial Downscaling of GRACE Observations Using Land Surface Model Outputs. Water Resour. Res. 2021, 57, e2020WR028944. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Milewski, A.M.; Thomas, M.B.; Seyoum, W.M.; Rasmussen, T.C. Spatial downscaling of GRACE TWSA data to identify spatiotemporal groundwater level trends in the upper Floridan aquifer, Georgia, USA. Remote Sens. 2019, 11, 2756. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Zhang, G.; Zhang, J. Improving the spatial resolution of grace-derived terrestrial water storage changes in small areas using the machine learning spatial downscaling method. Remote Sens. 2021, 13, 4760. [Google Scholar] [CrossRef]
- Arshad, A.; Mirchi, A.; Samimi, M.; Ahmad, B. Combining downscaled-GRACE data with SWAT to improve the estimation of groundwater storage and depletion variations in the Irrigated Indus Basin (IIB). Sci. Total Environ. 2022, 838, R713–R715. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pal, S.C.; Arshad, A.; Pham, Q.B.; Zhang, L. Constructing high-resolution groundwater drought at spatio-temporal scale using GRACE satellite data based on machine learning in the Indus Basin. J. Hydrol. 2022, 612, 128295. [Google Scholar] [CrossRef]
- Li, X.; Zhang, G.; Zhu, S.; Xu, Y. Step-By-Step Downscaling of Land Surface Temperature Considering Urban Spatial Morphological Parameters. Remote Sens. 2022, 14, 3038. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Q.; Yin, K.; He, G.; Zhang, Z.; Wang, G.; Wen, M.; Zhang, N. Spatial downscaling of land surface temperature based on a multi-factor geographically weighted machine learning model. Remote Sens. 2021, 13, 1186. [Google Scholar] [CrossRef]
- Li, W.; Niu, L.; Chen, H.; Wu, H. Robust Downscaling Method of Land Surface Temperature by Using Random Forest Algorithm. J. Geo-Inf. Sci. 2020, 22, 1666–1678. [Google Scholar]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Sharpening of very high resolution images with spectral distortion minimization. In Proceedings of the 23rd International Geoscience and Remote Sensing Symposium (IGARSS 2003), Toulouse, France, 21–25 July 2003; pp. 458–460. [Google Scholar]
- Pardo-Iguzquiza, E.; Chica-Olmo, M.; Atkinson, P.M. Downscaling cokriging for image sharpening. Remote Sens. Environ. 2006, 102, 86–98. [Google Scholar] [CrossRef]
- Fasbender, D.; Tuia, D.; Bogaert, P.; Kanevski, M. Support-Based Implementation of Bayesian Data Fusion for Spatial Enhancement: Applications to ASTER Thermal Images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 598–602. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A Data Mining Approach for Sharpening Thermal Satellite Imagery over Land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L. Spatial Downscaling of MODIS Land Surface Temperatures Using Geographically Weighted Regression: Case Study in Northern China. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Zhu, X.; Song, X.; Leng, P.; Hu, R. Spatial downscaling of land surface temperature with the multi-scale geographically weighted regression. Natl. Remote Sens. Bull. 2021, 25, 1749–1766. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Li, J.; Jin, M.; Li, H. Exploring Spatial Influence of Remotely Sensed PM2.5 Concentration Using a Developed Deep Convolutional Neural Network Model. Int. J. Environ. Res. Public Health 2019, 16, 454. [Google Scholar] [CrossRef] [PubMed]
- Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]
- Du, Z.; Wang, Z.; Wu, S.; Zhang, F.; Liu, R. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. Int. J. Geogr. Inf. Sci. 2020, 34, 1353–1377. [Google Scholar] [CrossRef]
- Du, Z.; Qi, J.; Wu, S.; Zhang, F.; Liu, R. A spatially weighted neural network based water quality assessment method for large-scale coastal areas. Environ. Sci. Technol. 2021, 55, 2553–2563. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Wang, Y.; Zhang, F.; Liu, R.; Du, Z. Satellite-based mapping of high-resolution ground-level pm2.5 with viirs ip aod in china through spatially neural network weighted regression. Remote Sens. 2021, 13, 1979. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Wu, S. House Price Valuation Model Based on Geographically Neural Network Weighted Regression: The Case Study of Shenzhen, China. ISPRS Int. J. Geo-Inf. 2022, 11, 450. [Google Scholar] [CrossRef]
- Jianliang, N.I.E.; Jianjun, W.U.; Xi, Y.; Ming, L.I.U.; Jie, Z.; Lei, Z. Downscaling land surface temperature based on relationship between surface temperature and vegetation index. Acta Ecol. Sin. 2011, 31, 4961–4969. [Google Scholar]
- Wang, S.M.; Luo, X.B.; Peng, Y.D. Spatial Downscaling of MODIS Land Surface Temperature Based on Geographically Weighted Autoregressive Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2532–2546. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Dai, Z.; Wu, S.; Wang, Y.; Zhou, H.; Zhang, F.; Huang, B.; Du, Z. Geographically convolutional neural network weighted regression: A method for modeling spatially non-stationary relationships based on a global spatial proximity grid. Int. J. Geogr. Inf. Sci. 2022, 36, 2248–2269. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Du, Z.; Wu, S.; Wang, Z.; Wang, Y.; Zhang, F.; Liu, R. Estimating Ground-Level PM_(2.5)Concentrations Across China Using Geographically Neural Network Weighted Regression. J. Geo-Inf. Sci. 2020, 22, 122–135. [Google Scholar]
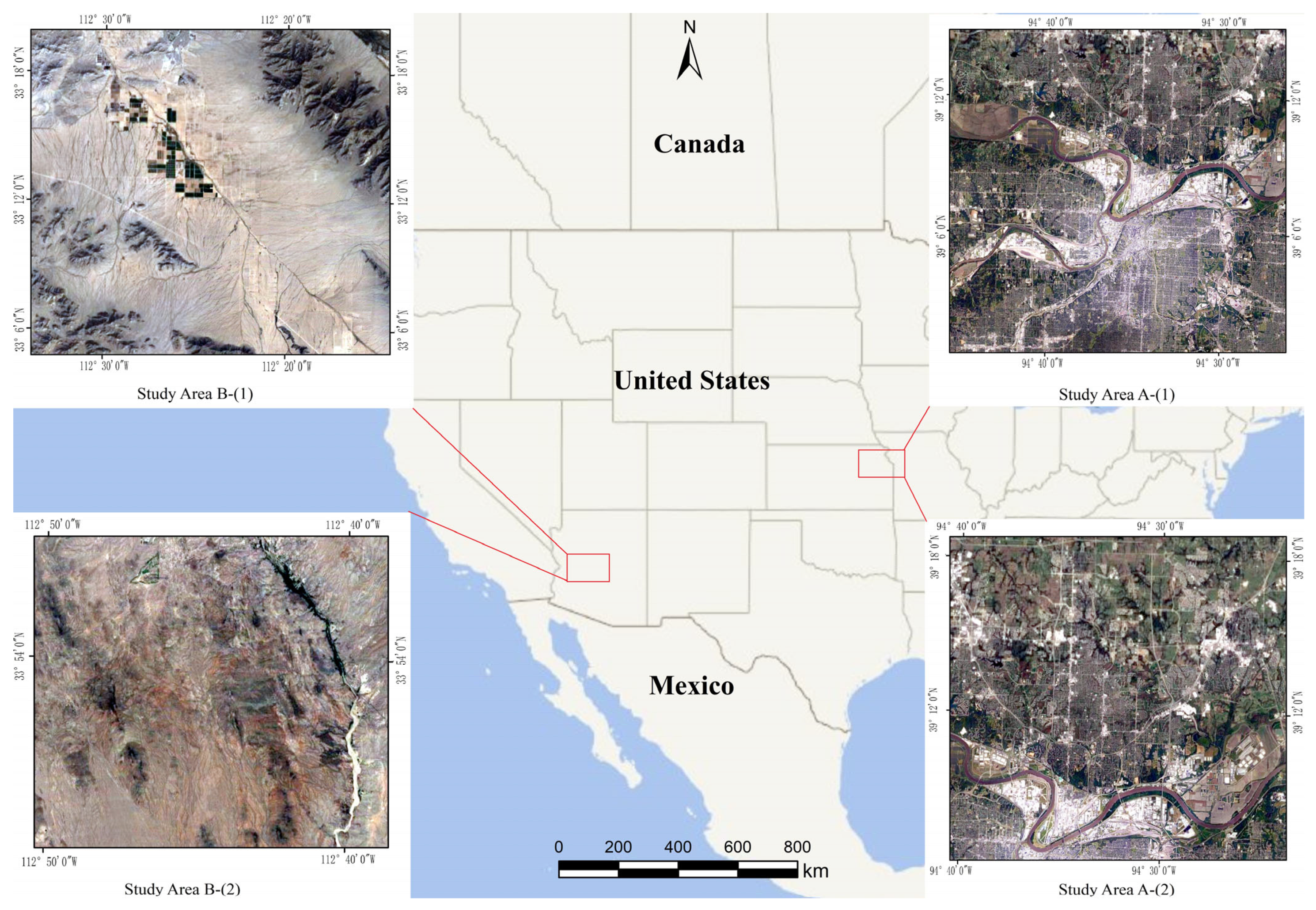


| Study Area | Alias | Area Code | Acquisition Time | Main Geomorphological Features |
|---|---|---|---|---|
| Kansas City, USA | Study area A | A-(1) | 25 July 2017 | Complex landforms |
| A-(2) | 15 February 2017 | Complex landforms | ||
| Phoenix City, USA | Study area B | B-(1) | 15 July 2017 | Bare flatland |
| B-(2) | 15 July 2017 | Bare soil mountainous area |
| Area Code | Regional Average LST/°C | Regional Maximum LST/°C | Regional Minimum LST/°C |
|---|---|---|---|
| A-(1) | 32.303 | 50.013 | 27.114 |
| A-(2) | 12.586 | 24.620 | −4.914 |
| B-(1) | 58.557 | 70.267 | 29.084 |
| B-(2) | 59.732 | 73.911 | 33.112 |
| Factor Name | Variable Name | Spatial Resolution | Data Source |
|---|---|---|---|
| Normalized difference vegetation index | NDVI | 30 m | Landsat8 band4 R Landsat8 band5 NIR |
| Normalized difference built-up index | NDBI | 30 m | Landsat8 band4 SWIR1 Landsat8 band5 NIR |
| Digital Elevation Model | DEM | 30 m | NASA DEM |
| Slope | Slope | 30 m | NASA DEM |
| Land Surface Temperature | LST | 100 m | Landsat8 band10 TIRS1 |
| Input Layer | Hidden Layer 1 | Hidden Layer 2 | Hidden Layer 3 | Hidden Layer 4 | Hidden Layer 5 | Output Layer |
|---|---|---|---|---|---|---|
| 8192 | 2048 | 1024 | 256 | 128 | 32 | 5 |
| Maximum epoch | Learning Rate | Dropout | Batch Maximum | Optimizer | ||
| 1000 | 0.001 | 0.8 | 512 | Adam | ||
| Area Code | Model | Regression Evaluation Metrics | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE/°C | MAPE | MAE/°C | PSNR | ||
| A-(1) | GNNWR | 0.909 | 0.922 | 2.066 | 0.675 | 36.729 |
| MGWR | 0.868 | 1.058 | 2.422 | 0.793 | 35.534 | |
| GWR | 0.884 | 0.944 | 2.165 | 0.707 | 36.523 | |
| RF | 0.802 | 1.351 | 3.220 | 1.046 | 33.408 | |
| TsHARP | 0.639 | 1.842 | 4.230 | 1.384 | 30.713 | |
| A-(2) | GNNWR | 0.789 | 0.918 | 5.734 | 0.690 | 29.857 |
| MGWR | 0.737 | 1.016 | 6.401 | 0.767 | 28.980 | |
| GWR | 0.760 | 0.966 | 5.941 | 0.714 | 29.419 | |
| RF | 0.672 | 1.147 | 6.985 | 0.876 | 27.924 | |
| TsHARP | 0.285 | 1.692 | 10.381 | 1.236 | 24.547 | |
| B-(1) | GNNWR | 0.971 | 1.127 | 1.389 | 0.749 | 35.566 |
| MGWR | 0.962 | 1.180 | 1.457 | 0.780 | 35.166 | |
| GWR | 0.959 | 1.185 | 1.449 | 0.771 | 35.129 | |
| RF | 0.898 | 2.079 | 2.789 | 1.514 | 30.247 | |
| TsHARP | 0.298 | 5.442 | 7.621 | 4.096 | 21.899 | |
| B-(2) | GNNWR | 0.974 | 0.896 | 1.123 | 0.656 | 38.327 |
| MGWR | 0.962 | 0.988 | 1.258 | 0.734 | 37.480 | |
| GWR | 0.957 | 1.018 | 1.305 | 0.760 | 37.220 | |
| RF | 0.407 | 4.233 | 5.582 | 3.298 | 24.841 | |
| TsHARP | 0.171 | 5.298 | 7.332 | 4.201 | 22.892 | |
| Study Area | 0–1 °C | 1–2 °C | 2–3 °C | 3–4 °C | >4 °C |
|---|---|---|---|---|---|
| Study area A-(1) | 60.48 | 26.86 | 8.44 | 2.92 | 1.30 |
| Study area A-(2) | 74.33 | 20.38 | 3.94 | 0.85 | 0.51 |
| Study area B-(1) | 64.61 | 21.95 | 7.10 | 3.46 | 2.88 |
| Study area B-(2) | 59.25 | 26.21 | 9.34 | 3.19 | 2.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, M.; Zhang, L.; Wu, S.; Zhu, Y.; Dai, Z.; Wang, Y.; Qi, J.; Chen, Y.; Du, Z. A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression. Remote Sens. 2023, 15, 1740. https://doi.org/10.3390/rs15071740
Liang M, Zhang L, Wu S, Zhu Y, Dai Z, Wang Y, Qi J, Chen Y, Du Z. A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression. Remote Sensing. 2023; 15(7):1740. https://doi.org/10.3390/rs15071740
Chicago/Turabian StyleLiang, Minggao, Laifu Zhang, Sensen Wu, Yilin Zhu, Zhen Dai, Yuanyuan Wang, Jin Qi, Yijun Chen, and Zhenhong Du. 2023. "A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression" Remote Sensing 15, no. 7: 1740. https://doi.org/10.3390/rs15071740
APA StyleLiang, M., Zhang, L., Wu, S., Zhu, Y., Dai, Z., Wang, Y., Qi, J., Chen, Y., & Du, Z. (2023). A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression. Remote Sensing, 15(7), 1740. https://doi.org/10.3390/rs15071740