Abstract
Autonomous navigation (AN) and manoeuvring are increasingly important in distributed satellite systems (DSS) in order to avoid potential collisions with space debris and other resident space objects (RSO). In order to accomplish collision avoidance manoeuvres, tracking and characterization of RSO is crucial. At present, RSO are tracked and catalogued using ground-based observations, but space-based space surveillance (SBSS) represents a valid alternative (or complementary asset) due to its ability to offer enhanced performances in terms of sensor resolution, tracking accuracy, and weather independence. This paper proposes a particle swarm optimization (PSO) algorithm for DSS AN and manoeuvring, specifically addressing RSO tracking and collision avoidance requirements as an integral part of the overall system design. More specifically, a DSS architecture employing hyperspectral sensors for Earth observation is considered, and passive electro-optical sensors are used, in conjunction with suitable mathematical algorithms, to accomplish autonomous RSO tracking and classification. Simulation case studies are performed to investigate the tracking and system collision avoidance capabilities in both space-based and ground-based tracking scenarios. Results corroborate the effectiveness of the proposed AN technique and highlight its potential to supplement either conventional (ground-based) or SBSS tracking methods.
1. Introduction
Despite growing awareness of the orbital debris problem, recent developments such as launch ride-sharing, growth in the availability of small launch vehicles, and particularly large-scale satellite constellation deployments are dramatically increasing the orbital congestion. According to space environment statistics recently published by ESA [1] the current space environment situation is alarming. Figure 1a,b, illustrate the current space situation in terms of number of launches and debris population in space. Further exacerbating the space situation are an unfortunate series of events such as anti-satellite weapons (ASAT) tests, on orbit collisions, and satellite breakups. Further, several commercial entities have made plans to launch larger constellations (700–5000 spacecraft each) in the coming months. Currently, the space domain usage is unsustainable. If this continues, the population of space debris will increase multifold, ceasing space activities in the near future. An increase in space objects will increase the probability of collisions, which can, in- turn, lead to Kessler Syndrome [2].
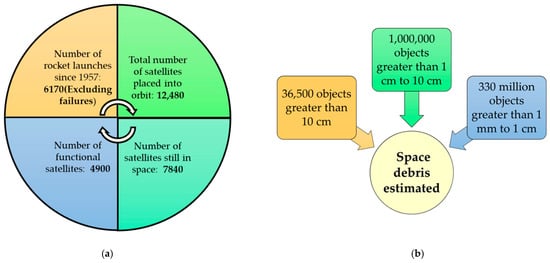
Figure 1.
(a) Space environment statistics by ESA; (b) Space debris population estimation by ESA.
Spacecraft operators must become more aware of the potential threats posed by the existing resident space objects (RSO) in order to prevent further collisions in Earth orbit. This includes not only tracking the total objects in space but also continuously estimating the probability of other accidental collisions. Unfortunately, neither of these tasks are trivial and require considerable tracking resources (optical telescopes and radar), computing power, and sophisticated software to calculate numerous satellite–satellite or satellite–debris conjunctions on a daily basis. The above tasks are referred to as ‘space situational awareness’ (SSA) or space domain awareness (SDA). Traditionally, these tasks are accomplished by a network of ground-based observation facilities known as the Space Surveillance Network (SSN), owned and operated by the US Department of Defence (DoD) [3]. Besides this, various other ground-based telescopes and space surveillance systems contribute to SSA. Different SSA systems in current use are briefly described in [4]. Table 1 provides a summary of major ground-based systems and the time frames during which they were introduced. Although these ground-based radars, laser, and telescope systems continue to play a pivotal role in providing situational awareness in the space environment, whether or not these systems can effectively achieve the goal in the future, adapting to the evolving space domain, is still a question. This is due to the following reasons.

Table 1.
Main ground-based SSA systems.
- Most of the ground-based systems are able to perform regional surveillance and then randomly look at other areas.
- They lack persistency in surveillance. In order to achieve true surveillance, it is necessary to monitor objects or regions for extended periods of time.
- Due to space perturbations, there is an on-orbit change in the RSO position. This will decrease the revisit frequency of the RSO within the field of view of the sensors on ground.
- Weather conditions are still a significant concern for ground-based systems. In typical ground-based observation sites, weather restricts visibility more than half the time, with some sites having a visibility of no more than 25% [4].
- For optical sensors on the ground, daylight observations represent a significant challenge because the passage of objects between the Earth and the Sun is almost always difficult to monitor.
1.1. Space-Based Space Surveillance (SBSS)
The gaps associated with ground-based measurements pave a path for tracking RSO by exploiting space borne measurements [5,6]. This type of approach is termed space-based space surveillance (SBSS). SBSS is an effective approach due to its capability to offer enhanced performances in terms of tracking accuracy and weather independence, allowing space-borne measurements to provide a broader range of useful observations [7]. In addition, space-based observation systems are not prone to atmospheric scattering, diffraction, turbulence, and aberrations [8]. Historically, radar sensors have been explored for space-borne measurements; however, the challenges associated with size and power consumption have shifted the focus towards optical sensors. Technological developments in optical sensor principles (e.g., coupled charged device (CCD)) [9], complementary metal–oxide–semiconductor (CMOS), and photon counting sensors [7,10]) have significantly enhanced optical detection performance, demonstrating the ability to track a 3 cm diameter object at a 3000 km range [7,9].
The precision in state information of the RSO will continue to be pivotal for the future space traffic management (STM) applications. These estimations can be provided using two approaches. Cooperative surveillance relies on state estimates from on-board time and space position information (TSPI)/navigation systems (e.g., GNSS, INS) and on the collaborative exchange of information among all other vehicles in the course of a potential collision. Whereas non-cooperative surveillance is typically carried out by ground or space-based radar or electro-optical sensors that do not require communication with the observed object. These systems are prone to errors caused by physical phenomena or by the mathematical extrapolation itself. In other words, a non-cooperative scenario is described as an encounter between a host platform and a RSO or possibly a non-cooperative spacecraft, in which only the host spacecraft is capable of preventing a potential collision. On the other hand, a cooperative scenario is described as a scenario in which all the potentially colliding RSO are capable of communicating position data and, if necessary, they can perform manoeuvres to avoid a collision [11].
SBSS has already been attempted in the past; [12] describes various SBSS missions and Figure 2 summarizes different attempts made by different countries for debris tracking. The current space-based SSA systems face issues such as latency and limited coverage, making them unreliable for the future to come. Hence, there is a need for a reliable and sustainable SSA system to fill the gaps in the present.
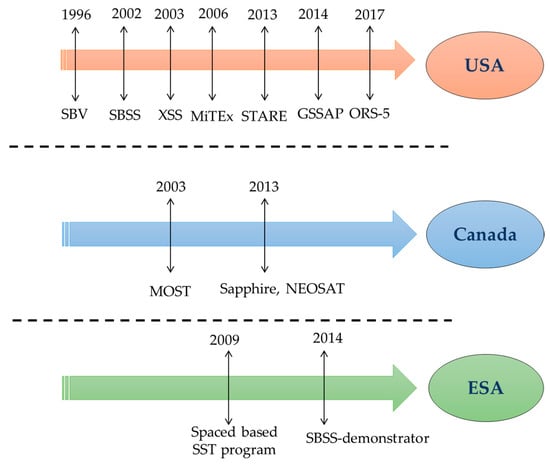
Figure 2.
Various SBSS missions during their respective timelines.
In 1996, the space-based visible instrument (SBV) onboard the mid-course space experiment led to the first SBSS mission [13,14,15]. This was followed by the United States Air Force’s SBSS mission, also known as the SBSS block 10 satellite. The SBSS constellation aimed to detect and track all space resident objects in orbit around the Earth in real-time [16]. A similar space surveillance mission was conducted by Sapphire, a Canadian satellite for US SSN. It was able to provide accurate measurements in rate track or sidereal track modes [17]. Furthermore, the ORS-5 demonstrator, also known as Sensor-Sat, was launched by the United States with an objective to demonstrate technologies for geosynchronous SSA. The success of the above-mentioned technological demonstrations paved a path to create new evolutionary frameworks for SBSS and to create new profitable pathways for accurate RSO tracking for various commercial actors and orbital startup companies [18]. The overall business of SDA faces formidable challenges. Most objects are extremely difficult to observe when they pass between the Earth and the Sun. Although space-based sensors can provide observations much closer to the Sun, they have limitations when the target positioned between Sun and the sensor [19].
Recent technological advances have led to the concept of multiple spacecraft operating in optimal coordination to accomplish desired mission goals [20]. Considering this, distributed satellite systems (DSS) is a promising concept for the future of SSA and STM. DSS mission architectures move away from the monolith system concept to adopt multiple elements that interact, cooperate, and communicate with each other [21,22,23], resulting in new systematic properties and/or emerging functions. Different types of DSS have been proposed to date, including constellations [24], clusters, swarms, trains, fractionated spacecraft, and federated satellites [25,26,27,28]. From the system architecture point of view, these concepts vary across different verticals, such as the number of assets, homogeneity of the assets, physical separation between the assets, and so forth [29]. For better understanding of various DSS configurations, the reader is referred to references [30,31,32,33,34,35,36].
In contrast to the conventional ground-based systems whose observations are conducted from accurately surveyed locations, SBSS platforms are subjected to positional errors and tracking errors caused by onboard TSPI/Navigation systems and tracking sensors, respectively. These errors can be represented geometrically in the form of ellipsoids which can be combined to form the total uncertainty volume that determines the total uncertainty in the tracking estimates [37] to support separation assurance (SA) and collision avoidance (CA) between the RSO, which is followed by the application of relevant collision avoidance manoeuvres. There exists a duality to the approach mentioned previously. On one hand, for the existing DSS constellation, optimized manoeuvres can be performed to avoid collisions with RSO. Alternatively, the design of the astrionics onboard could be optimized to mitigate errors and achieve mission objectives. In this paper, a non-cooperative SBSS scenario is analysed, in which DSS spacecraft collaboratively track the RSO subject to specific errors in tracking and navigation systems for positioning that will ultimately determine the uncertainty volume or a confidence region around the detected RSO.
1.2. Aim and Structure of the Article
This article proposes a unified approach that combines RSO tracking and AN/manoeuvring algorithms with an aim to realize trusted autonomy in heterogenous DSS platforms for SA and CA. The remainder of the article is structured as follows. Section 2 presents an overview of various RSO tracking approaches and the equations corresponding to the proposed tracking algorithm. Section 3 summarises autonomous navigation (AN) and various trajectory optimization approaches for spaceflight applications and the equations for PSO algorithm. Verification case studies carried out in various scenarios are defined in Section 4. The results obtained from the case studies are discussed in Section 5. Section 6 comprises the conclusions and scope for future research.
2. Tracking Algorithms Overview
A single angles-only sensor is not sufficient for accurate RSO tracking. In contrast, using two angles-only sensors allows one to determine the range, and thus the 3D location, of an object via simple triangulation [38,39,40,41]. Typically, an error in the sensor measurement always prevails because the sensors do not exactly point towards the RSO, making it necessary to find the most probable RSO position. Without the error in measurement, the triangulation becomes trivial. In [42,43] a ground-based optical system was proposed, consisting of two ground-based optical sensors located at two different sites to track the debris using simultaneous optical measurements.
Several algorithms are proposed in the literature to solve this problem. For instance, in [44], the proposed algorithm estimates the most probable position of the RSO as the midpoint of the shortest line joining the two lines of sight. In [45], the most probable RSO position is estimated as a point on the shortest line between the two lines of sight that subtends an equal angle with respect to the observation sites. Although numerical solutions are proposed to calculate position errors in the triangulation solution, relating the measurement errors with the experimental parameters is a huge challenge. In [46], the analytical expressions for the position error for tracking an RSO in space for several observation-station configurations is presented. The current work deals with AN and tracking through simultaneous optical measurements performed by multiple heterogenous platforms that constitute a DSS architecture. In order to justify the aim of the current work, a suitable tracking algorithm with high position accuracy is tested in different operating scenarios (ground-based tracking, space-based tracking).
2.1. Triangulation Problem
This section introduces a suitable tracking algorithm and the corresponding equations required to estimate the position of the RSO, and the errors associated with the measurements. Attention is then turned towards the uncertainty quantification of navigation and tracking errors in the form of a covariance matrix to generate an overall uncertainty volume. Figure 3 and Figure 4 illustrate the tracking problem in both ground-based and space-based scenarios respectively.
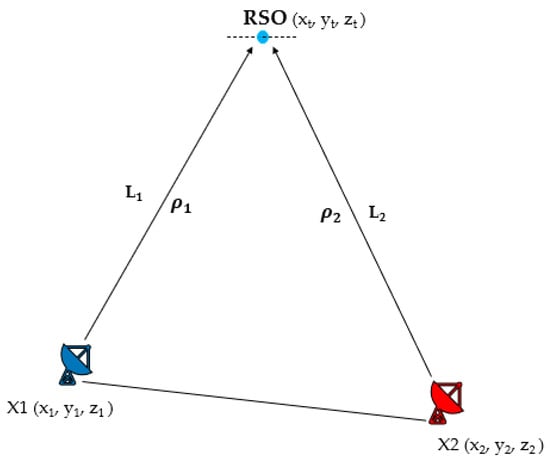
Figure 3.
Simplified conceptual illustration for ground-based scenario.
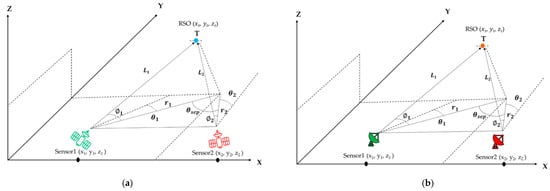
Figure 4.
(a) Multi sensor RSO tracking for space-based scenario, (b) Multi sensor RSO tracking for ground-based scenario.
2.2. Tracking Algorithm
In order to compute the RSO position estimate, it is necessary to know the location of each sensor , as well as the line of sight (LOS) azimuth and elevation pointing angles from each sensor to the target. An inaccuracy in determining these 10 parameters will result in an error in the target position estimate. Furthermore, the relationship between the measurement error and the errors in the estimated target location is a function of the sensor–target–sensor geometry, where a sensor–target–sensor separation of 90° results in the lowest error sensitivity, while a sensor separation of or results in impossible solutions (as seen from the target). To define the triangulation problem, we need to define the positions of the sensors and the RSO in a right-handed coordinate system as illustrated in Figure 4.
The and axes form the horizontal plane, and the axis points out of plane vertically. and are the azimuth angles of the corresponding sensors measured clockwise from positive y axis towards positive axis. The corresponding elevation angles are denoted by and which increase from in the plane to pointing vertically. The separation angle is measured from sensor through the RSO to sensor . The sensor positions and the LOS from sensor to target allows the 3D target position computation.
The equations to calculate the position estimates are defined below [47]:
where:
- (xt,yt,zt) = target RSO position coordinates,
- (xi,yi,zi) = corresponding sensor position coordinates
- ri = horizontal ranges from the x − y components of the corresponding sensor to the x and y components of the RSO,
- φi = corresponding sensor to RSO elevation angle,
- θi = corresponding sensor to RSO azimuth angle.
- i = 1, 2 (number of sensors used to perform triangulation)
These equations relate the target location to measurements of the sensor position and LOS from the sensors to the target, aiding the target position estimation. The error propagation equations corresponding to the respective position coordinates are derived in [48], with a key assumption that the error generated by each sensor follows a Gaussian distribution. The sigmas for each are the sums of various partial derivatives that are simplified as [49]:
The various c’s mentioned in the equations are the error coefficients that are functions of the sensor-to-sensor separation angle [48,49]. The error coefficients describe the dependence of target position estimates ) on errors in each of the sensor position coordinates . For instance, the indicates the error coefficient for the coordinate of the target position. corresponds to error coefficient for azimuth error in . Equations (5)–(8) relate the target position uncertainties to the standard deviations of measurement errors: for position; for the azimuth; and for elevation measurements.
Equation (8) refers to the error in measurement of from a single sensor. However, since the measurements performed during triangulation involve two sensors, we can compute the error estimates from:
2.3. Uncertainty Quantification
In multi-sensor platforms, the uncertainty position of the RSO is influenced by the accuracy of the sensor positions and the sensor to target LOS. It is crucial to know each sensor location (), () and the corresponding LOS vector’s azimuth and elevation (and), respectively. The tracked RSO position can be analysed by combining the tracking and the navigation uncertainty using the proposed mathematical framework. To obtain the covariance matrix corresponding to the navigation error, the reader is directed to [37] in which the steps are described in detail. Therefore, navigation measurements are assumed to be provided by an on-board GNSS system, and the corresponding uncertainty values are derived from a literature LEO GPS accuracy experiment [50]. The uncertainty in the tracking measurements can be expressed in terms of the covariances as follows:
where , and are obtained using Equations (5), (6) and (8a).
To determine the total covariance matrix Gauss–Helmert formulation, [51,52] are used in order to relate the sensor measurement errors to the final RSO position (). We define the vectors of estimated observations and estimated parameters, respectively:
The total covariance matrix can then be expressed as:
where is the covariance matrix of the observations which can be written as a 10·10 diagonal matrix with elements [. For matrix B, we first define the function as:
Then, matrix is defined as and, therefore, has a 3 × 10 dimension.
2.4. Covariance Matrix to Ellipsoid
It is crucial to understand the influence of a single term of the covariance matrix on the size and orientation of the ellipsoid. The principle component analysis (PCA) framework [11,53] describes the relationship between the covariance matrix and the rotated ellipsoid as follows:
where the correlation coefficient is expressed as:
A convenient way to express the ellipsoid equation is to use the covariance matrix :
where is a vector expressed in Cartesian coordinates. can be written as:
where:
Hence, the rotated ellipsoid equation can be written as:
Equation (20) expresses the contribution of the individual terms of the covariance matrix to the overall ellipsoid shape and size:
where:
Hence, the ellipsoid equation in (17) can be modified as:
where:
- is a vector in the Cartesian coordinates about the nominal position (origin), of the ellipsoid.
- R = rotation matrix,
- A = diagonal eigenvalues matrix respectively, which are derived from Q.
Given a pair of angles the corresponding radial distance from the centre of the ellipse, this can be calculated using:
where
3. Trajectory Optimization Techniques Overview
Spacecraft trajectory optimization is of paramount importance due to its direct influence on the system performance [54]. It is one of the highly studied problems in the field of aerospace engineering [55,56]. An optimal trajectory for a spacecraft can be defined as the one that meets some criteria, including initial and final conditions. The first serious attempt to classify these approaches was conducted back in 1998 by Betts [57], known as the direct and indirect methods. Both branches aim to minimize cost functions and constraint through discrete approximations. The direct methods transcribe the continuous optimal control problem into an optimization problem [58] adopting the state-space representation. The system equations are satisfied by integrating them implicitly or explicitly within a finite interval, thereby converting it into a non-linear programming problem (NLP) [59]. Although the solution obtained from direct methods is not necessarily optimal, its simple implementation, reduced problem size, and larger domain of convergence makes this method a widely used one [60]. One of the direct methods is referred to as the shape based method [61,62]. In the method, the state variables are interpolated, and the control variables are taken in the objective function. This is followed by a gradient-based technique or metaheuristic to minimize the cost by varying the state variables. The most popular technique among the direct methods is the Fourier series, specifically for low-thrust trajectory optimization applications [63,64,65]. The solution obtained by the shape-based method satisfies the equation of motion and the boundary conditions. Moreover, the solution obtained from the shape-based method can serve as a very good guess for other optimization approaches.
Gradient-based methods such as NLP appear to be the most popular computational techniques for addressing trajectory optimization problems. The NLP uses the gradient information and is often capable of quick convergence and accurate results, leading to its popularity. However, the most noticeable limitation of gradient-based methods is that the analyst must have some a priori knowledge of the optimal trajectory. In other words, the initial guess should be near to the global optimal solution. Failing to do so will lead to a non-global optimal solution or the optimization routine will become extremely slow.
An entirely different class of optimization approaches are referred to as metaheuristics, an alternative approach that addresses the issues faced by gradient-based methods. Essentially, a metaheuristic is an iterative approach to exploring and exploiting the search space that intelligently combines different concepts that are inspired by phenomena occurring in nature for guiding a subordinate heuristic [66]. These algorithms belong to a special class of artificial intelligence (AI) techniques, which also include evolutionary algorithms such as genetic algorithms (GA), PSO, and other insect/swarm inspired algorithms [67]. The metaheuristic approaches are classified into two types, single solution algorithms and population based algorithms, the latter are often used for spacecraft trajectory optimization problems [68,69]. The second branch of optimization approaches is that of indirect methods. Indirect methods consider the dualized form of the equations, including the states and co-states within the discretized time frame [65]. Although the indirect methods are better than direct methods in terms of accuracy, they have certain limitations, such as:
- The necessary conditions, including the co-state differential equations, the Hamiltonian, and the optimality conditions, must be expressed analytically.
- Due to discretization of co-states, the problem size becomes large.
- The analyst must guess certain aspects of the solution, such as portions of the time domain containing constrained or unconstrained control arcs.
- The domain of convergence decreases due to the requirement of the initial guess being close to optimal solution.
The feasibility of performing the on-board optimization routine depends on computation time and cost. Hence, the PSO technique is chosen as a primary optimization routine due to its capability for global convergence and its robustness to solve highly non-linear problems with greater computational efficiency. Moreover, this technique is used widely to solve diverse spacecraft trajectory optimization problems, and its on-board implementation was verified, through various case studies, for adequate convergence time and low computation cost [70].
4. Case Studies
4.1. SBSS Scenario
Globally, the UAE is classified as a country with a high vulnerability to climate change, adversely affecting the infrastructure, human health, and natural habitat, which in turn impacts various sectors and policies including socioeconomic, health, and environment [79]. Adding on to the problem of climate change are intermittent events of oil spills that have a long term effect on eco-systems and economies. An Earth observation constellation comprising 40 satellites evenly spaced across four orbital planes with RAAN distributed between 0 degrees and 360 degrees (i.e., 0, 90, 180, 360) as illustrated in Figure 5 is hypothesized to detect oil spills, monitor climate change, and track RSOs simultaneously for SA and CA. The spacecraft in the DSS constellation are assumed to be placed in nearly circular arrangement (eccentricity = 0.001) at an altitude of 500 km at an inclination of 99 degrees, and are equipped with a hyperspectral payload with artificial intelligence (AI) to process the data on-board of the satellite for oil spill detection and climate change analysis [80,81,82]. The characteristics of the on-board payload are listed in Table 2. To ensure the safety of DSS assets, the DSS constellation performs RSO tracking and establishes a collaborative exchange of tracking information through inter-satellite links to accomplish AN (AN) for CA [83,84]. The DSS constellation also acts as a service provider for other operational satellites or sub-orbital vehicles by establishing a data exchange using inter-satellite links so that they can perform AN for CA, as illustrated in Figure 6.
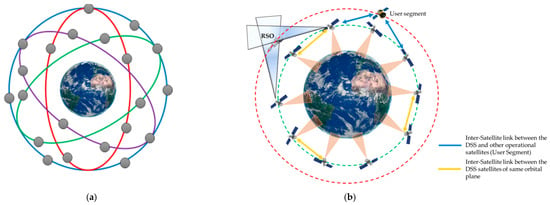
Figure 5.
(a) Proposed DSS constellation with 4 orbital planes (not to scale); (b) Simplified DSS system architecture for a single orbital plane.

Table 2.
Hyperspectral payload specifications.
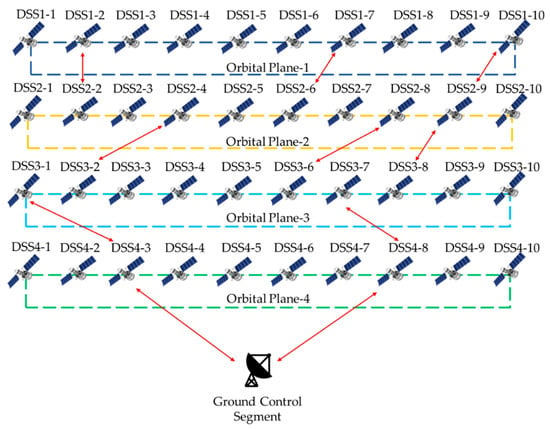
Figure 6.
Inter-Satellite links between the DSS assets.
In recent studies, star trackers have been investigated as an alternative sensor for debris surveillance [85]. The participating spacecraft in the constellation are equipped with star trackers for attitude determination and RSO tracking. The spacecraft are assumed to simultaneously perform Earth observation operations along with AN for CA. RSO tracking and detection are performed using optical sensors and star trackers due to [86]:
- The passage of the RSO across the sensor’s field of view [10].
- The exploitation of brightness, angular velocity, and other threshold parameters for RSO travelling across the FOV of the sensor [87].
The major focus is to come up with a suitable mission architecture that accomplishes Earth observation and SSA mission objectives expeditiously. The requirements of the mission architecture are as follows:
- The system configuration must be feasible for multiple applications. For instance, AN for CA (current interest), SBSS for STM, multi-domain traffic management (MDTM) [88], and point-to-point sub orbital space transport, which are envisioned in the longer term.
- The satellites in the DSS architecture should complement each other and form ad-hoc or optional teams to make autonomous decisions and maximize mission objectives without involving the ground control segment, making them distinct compared to conventional satellite systems.
As mentioned earlier, the on-board payload for Earth observation is HyperScout-2, as specified in Table 2, whereas, for RSO tracking, the DSS assets are equipped with an MAI-SS star tracker, which has the specifications tabulated in Table 3. The two payloads are illustrated in Figure 7.

Table 3.
Star tracker payload specifications.

Figure 7.
(a) HyperScout-2; (b) MAI-SS star tracker, Adcole Maryland Aerospace [89,90].
For the proposed SBSS mission architecture, the following assumptions are critical:
- The star trackers on board track the RSOs with the stars in the background.
- The participating spacecraft are equipped with state-of-the-art GPS for positioning and navigation that provide a full set of navigation data.
- The RSO position is estimated by simultaneous optical measurements obtained from two different spacecraft.
- The participating spacecraft share their position information and the estimated RSO position through a network.
- Mutual separation between the spacecraft belonging to the DSS constellation is guaranteed using intersatellite links and continuous monitoring from the ground stations.
The proposed AN system comprises the following components. Figure 8 illustrates the system architecture and its individual components:
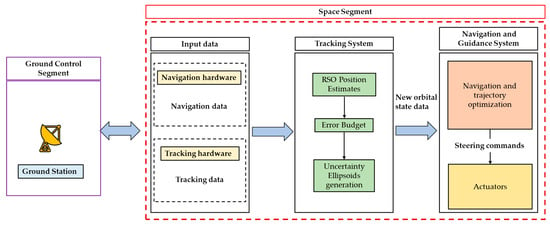
Figure 8.
AN system architecture for SBSS.
- Navigation hardware comprises the state-of-the-art GPS to obtain a full set of navigation data comprising the DSS satellite positions, velocities, and attitude rates.
- Tracking hardware comprises star trackers that track the RSO.
- The obtained data from the hardware is used as inputs by the on-board Tracking System to obtain the RSO position estimates, error measurement budget, and to generate the uncertainty ellipsoids.
- The navigation and guidance system exploits the data generated by the tracking system for trajectory optimization and AN/manoeuvring to generate the steering commands.
- Actuators use the steering commands to perform the collision avoidance manoeuvres in order to avoid a collision with the RSO.
4.2. Case Study 2—Ground-Based Surveillance
The ground-based surveillance system comprises two electro-optical (EO) sensors that are located at two different observation sites, as illustrated in Figure 9. As illustrated in Figure 4b, two ground-based EO sensors track the RSO simultaneously and share the estimated RSO position data with a distributed satellite system (DSS) constellation through a network [24,81,82,91]. For the ground-based tracking scenario, the following assumptions are adopted [92]:
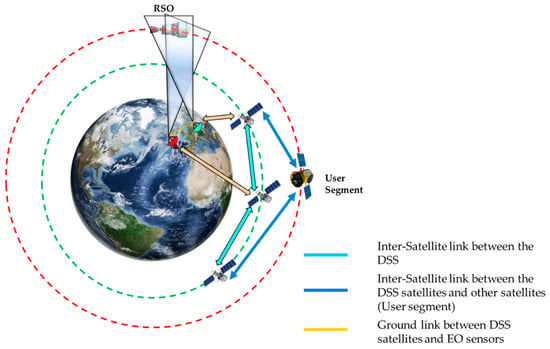
Figure 9.
Ground-based surveillance scenario.
- The DSS assets are placed in a nearly circular low earth orbit (LEO) at an altitude of 500 km to carry out Earth observation activities.
- The participating spacecraft are equipped with sophisticated GPS for positioning and navigation that provide a full set of navigation data.
- The estimated RSO position from ground-based sensors is uplinked to the DSS assets to ensure their safety.
- The participating spacecraft share their position information and the RSO position estimates with other satellites using inter-satellite links (ISL).
- The ground-based EO sensors assumed in this scenario are similar to the sensors used in [93] and operate in the infra-red (IR) region between the wavelengths of 3–12 µm.
The proposed AN system comprises the following components:
- Navigation hardware comprises the state of the art GPS to obtain a full set of navigation data comprising the DSS satellite positions, velocities, and attitude rates.
- Tracking hardware comprises ground-based EO sensors that track the RSO by simultaneous optical measurements.
- The obtained data from the hardware are used as inputs by the On-Board System (OBS) to obtain the RSO position estimates, error measurement budget, and to generate the uncertainty ellipsoids.
- The navigation and guidance system exploits the data generated by the OBS for trajectory planning and optimization to generate the steering commands.
- Actuators use the steering commands to perform the collision avoidance manoeuvres in order to avoid a collision with the RSO.
Figure 10 illustrates the individual segments of the tracking system architecture.
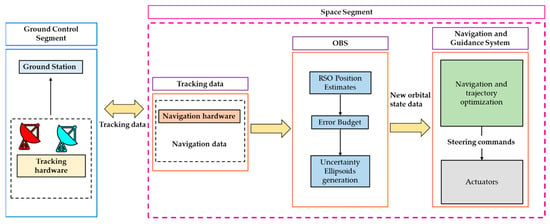
Figure 10.
AN system architecture for ground-based tracking scenario.
5. Results and Discussions
Simulation case studies were performed in both space-based and ground-based tracking scenarios. The results obtained are presented and discussed in the following sections. However, it has to be noted that the current work focuses on estimating the RSO position and the associated errors. Assuming that the tracked RSO moves in a circular orbit, the equations used to estimate RSO velocity from position estimates are defined in [94]. Assuming that the RSO is moving freely in a circular orbit, then its motion can be governed by classic orbital dynamics, as:
where:
- rt = the position vector of the RSO in ECI frame,
- fi = orbital perturbations that take into account J2 perturbations and drag.
- The velocity of the RSO can be calculated by integrating Equation (60).
5.1. Space-Based Tracking Scenario
To estimate the target position using the algorithm defined in Section 2.2, we define the satellite orbital elements in the ECI frame and the Cartesian frame (Table 4). The values of the corresponding error coefficients must be computed to calculate the errors in target position estimates. The error coefficients are sums of partial derivatives that are mentioned in [48]. The sigmas for each are calculated using Equations (5)–(8) with the corresponding azimuth angles = 27 deg and = 315 deg, and elevation angles =58 deg and = 62 deg. Assuming that the state-of-the-art star trackers can provide the RSO sigma position = 0.5 m and sensor angular error = 0.0022 degrees, running the algorithm allows us to obtain the sigmas listed in Table 5.

Table 4.
Sensor orbital state elements.

Table 5.
RSO position estimates and errors.
Using the mathematical framework presented in Section 2.2 and Section 2.3, the covariance matrix corresponding to the navigation errors, tracking errors, and total error can be presented in the form of an uncertainty ellipsoid, illustrated in Figure 11.
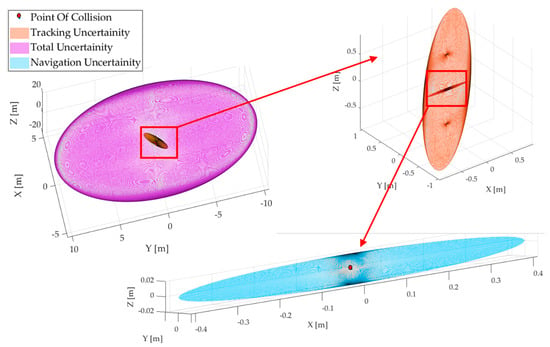
Figure 11.
Uncertainty volumes around the tracked RSO in space-based scenario.
5.2. Ground-Based Tracking Scenario
To track the RSO using the ground-based optical sensors, it is crucial to define the sensor positions in the Cartesian frame. For this particular scenario, two ground-based sensors are assumed to be located in Goldstone, California and Canberra, Australia. The geocentric coordinates of these two sites are converted to a Cartesian frame and the sensor positions are tabulated in Table 6.

Table 6.
Ground-based sensor positions.
The sensor positions in Table 6 are used as inputs in the tracking algorithm to calculate the RSO position estimates and the corresponding errors listed in Table 7.

Table 7.
RSO position estimates and the corresponding errors.
An uncertainty ellipsoid, as shown in Figure 12, can be generated using the mathematical framework presented in Section 2.2 and Section 2.3 to represent the navigation errors, tracking errors, and total error for the ground-based tracking scenario.
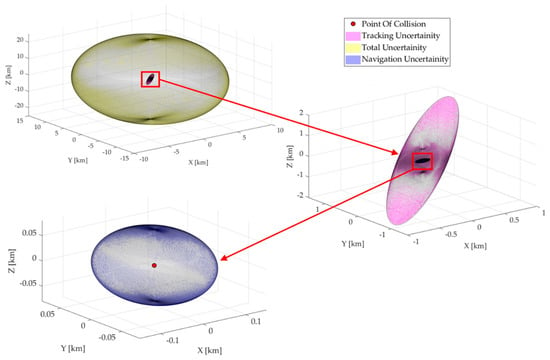
Figure 12.
Uncertainty volumes around the tracked RSO in ground-based scenario.
5.3. Trajectory Optimization for Collision Avoidance
It is assumed that a user segment satellite (Figure 5b) is present in an orbit that intercepts the orbit of the tracked RSO that was tracked in both the tracking scenarios, indicating a possible collision event. In order to avoid the total uncertainty volume, the spacecraft performs a collision avoidance manoeuvre based on the values obtained from Table 5 and Table 7 to reorient its initial orbit to a new orbit with a semimajor axis increased to 4.7 km in the SBSS scenario and 5.4 km in the ground-based tracking scenario (in-plane); failing to do so may result in a collision. It is assumed that the spacecraft that performs the orbit-raising manoeuvre is equipped with Nano Avionics EPSSC1 [95], which can generate a thrust of 1 N with a specific impulse of 213 seconds. An orbit raising manoeuvre (in-plane) is preferred over the out-of-plane manoeuvre (inclination change) due to its optimality in terms cost and manoeuvre time. Table 8 tabulates the orbital parameters of the spacecraft before and after the manoeuvre.

Table 8.
Initial and final orbital parameters of the spacecraft after collision avoidance manoeuvres.
The control parameters for the constant thrust directions are tabulated in Table 9 for both ground-based and space-based tracking scenarios.

Table 9.
Generated control parameters for thrust directions.
The total manoeuvre time is higher for the ground-based scenario than the space-based scenario, as the variation in the semimajor axis is greater in comparison. The solution converged after 465,000 iterations with a total run time of 4255.9 s on an Intel Core generation processor in a MATLAB environment. The change in thrust vector angles with respect to time in both the tracking scenarios is illustrated in Figure 13 and Figure 14.
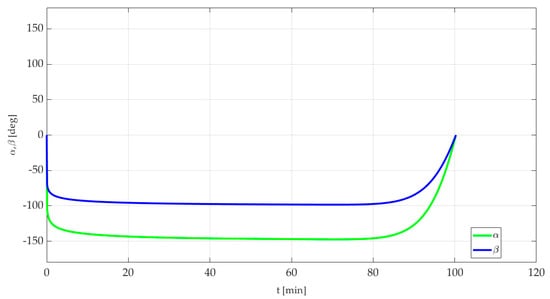
Figure 13.
Change in thrust control angles in time (SBSS scenario).
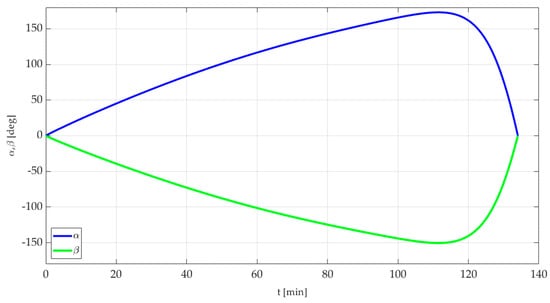
Figure 14.
Change in thrust control angles over time (ground-based scenario).
According to the results illustrated in Figure 13 and Figure 14, the total reorientation time in the SBSS and the ground-based scenarios is 100 min and 130 min, respectively. It can be observed that the thrust vector angles start from at time t = 0 and return to at the reorientation time, indicating the end of the orbit raising manoeuvre. The trajectory change from the initial trajectory to the final optimal trajectory is illustrated in Figure 15 and Figure 16.
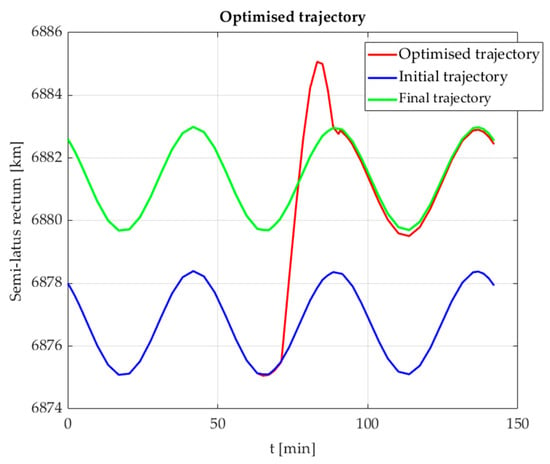
Figure 15.
Change in semimajor axis from initial to final trajectory (SBSS).
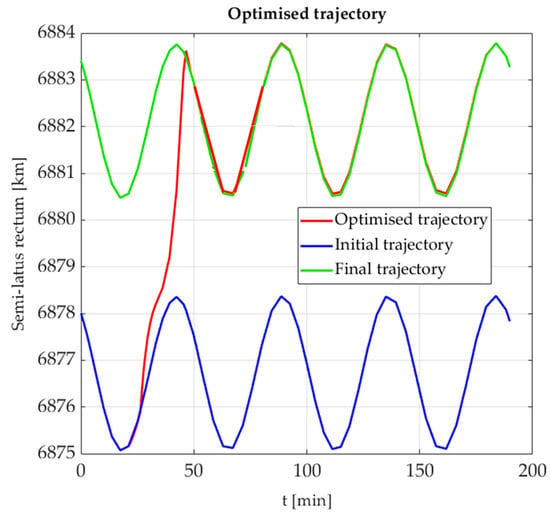
Figure 16.
Change in semimajor axis from initial to final trajectory (ground-based scenario).
The proposed approach results in orbit raising manoeuvres that require minimum and manoeuvre time taking into account actual conditions, all modelled perturbations, and any chosen thrust profile, thereby granting the spacecraft with responsive trajectory planning and navigation capabilities.
6. Conclusions and Future Work
Over the past decade, space debris has caused an increased congestion of the orbital domain. Fragments of past space endeavours are trapped in orbit around Earth, posing a threat to the sustainability of the space sector. As space debris accumulates over time, it poses an increasingly higher risk to the satellites that are currently operational and to future space missions. This paper proposes an autonomous navigation (AN) and tracking framework for separation assurance (SA) in the low earth orbit (LEO) region. A suitable tracking algorithm was tested in both ground-based and space-based scenarios to accomplish AN/manoeuvring for avoidance of collisions with debris and other resident space objects (RSO). Particle swarm optimization (PSO) algorithms were developed to implement autonomous on-board trajectory generation and manoeuvre planning for RSO avoidance. Simulation case studies were performed in the presence of both ground-based surveillance and space-based space surveillance (SBSS), demonstrating the validity of the proposed techniques and the complementarity of ground-based and space-based tracking techniques to support DSS AN for RSO collision avoidance. Current research is addressing the optimal fusion of SBSS and ground-based sensors (using both conventional and AI-based techniques) to enhance the tracking accuracy, coverage, and timeliness of AN tasks in complex mission scenarios. By incorporating suitable AI techniques, trusted autonomous satellite operations (TASO) can be achieved using optimal combinations of SBSS and ground-based tracking data.
Author Contributions
Conceptualisation, K.F.H. and R.S.; methodology, K.F.H. and R.S.; software, K.F.H. and K.T.; validation, K.F.H., K.T., A.G. and R.S.; writing—original draft preparation, K.F.H. and K.T.; writing—review and editing, A.G. and R.S.; visualisation, K.F.H., K.T. and R.S.; supervision, A.G. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the SmartSat Cooperative Research Centre (CRC) for their partial support through the collaborative research project No. 2.13s.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Space Environment Statistics Space Debris User Portal. Available online: https://sdup.esoc.esa.int/discosweb/statistics/ (accessed on 16 July 2022).
- Kessler, D.; Johnson, N.; Liou, J.-C.; Matney, M. The Kessler Syndrome: Implications to Future Space operations. Adv. Astronaut. Sci. 2010, 137, 2010. [Google Scholar]
- Hilton, S.; Sabatini, R.; Gardi, A.; Ogawa, H.; Teofilatto, P. Space traffic management: Towards safe and unsegregated space transport operations. Prog. Aerosp. Sci. 2019, 105, 98–125. [Google Scholar] [CrossRef]
- Ackermann, M.R.; Kiziah, R.; Zimmer, P.C.; McGraw, J.; Cox, D. A systematic examination of ground-based and space-based approaches to optical detection and tracking of satellites. In Proceedings of the 31st Space Symposium, Technical Track, Colorado Springs, CO, USA, 13–17 April 2015. [Google Scholar]
- Flohrer, T.; Krag, H.; Klinkrad, H.; Schildknecht, T. Feasibility of performing space surveillance tasks with a proposed space-based optical architecture. Adv. Space Res. 2011, 47, 1029–1042. [Google Scholar] [CrossRef]
- Utzmann, J.; Wagner, A. SBSS Demonstrator: A Space-Based Telescope for Space Surveillance and Tracking; International Astronautical Federation: Paris, France, 2015. [Google Scholar]
- Felicetti, L.; Emami, M.R. A multi-spacecraft formation approach to space debris surveillance. Acta Astronaut. 2016, 127, 491–504. [Google Scholar] [CrossRef]
- Vanwijck, X.; Flohrer, T. Possible contribution of space-based assets for space situational awareness. In Proceedings of the 59th International Astronautical Congress, Glasgow, Scotland, 29 September–3 October 2008; pp. 2466–2472. [Google Scholar]
- Utzmann, J.; Wagner, A.; Silha, J.; Schildknecht, T.; Willemsen, P.; Teston, F.; Flohrer, T. Space-Based Space Surveillance and Tracking Demonstrator: Mission and System Design; International Astronautical Federation: Paris, France; p. 7.
- Gruntman, M. Passive optical detection of submillimeter and millimeter size space debris in low Earth orbit. Acta Astronaut. 2014, 105, 156–170. [Google Scholar] [CrossRef]
- Sabatini, R.; Battipede, M.; Cairola, F. Innovative Techniques for Spacecraft Separation Assurance and Debris Collision Avoidance. Master’s Thesis, RMIT University, Melbourne, VIC, Australia, 2020. [Google Scholar]
- Yunpeng, H.; Kebo, L.; Yan’gang, L.; Lei, C. Review on strategies of space-based optical space situational awareness. J. Syst. Eng. Electron. 2021, 32, 1152–1166. [Google Scholar] [CrossRef]
- Gaposchkin, E.M.; von Braun, C.; Sharma, J. Space-Based Space Surveillance with the Space-Based Visible. J. Guid. Control Dyn. 2000, 23, 148–152. [Google Scholar] [CrossRef]
- Sharma, J. Space-Based Visible Space Surveillance Performance. J. Guid. Control Dyn. 2000, 23, 153–158. [Google Scholar] [CrossRef]
- Stokes, G.; Vo, C.; Sridharan, R.; Sharma, J. The space-based visible program. In Proceedings of the Space 2000 Conference and Exposition, Long Beach, CA, USA, 19–21 September 2000; p. 5334. [Google Scholar]
- Space Based Space Surveillance (SBSS). Available online: https://www.globalsecurity.org/space/systems/sbss.htm (accessed on 13 July 2022).
- Maskell, P.; Oram, L. Sapphire: Canada’s answer to space-based surveillance of orbital objects. In Proceedings of the Advanced Maui Optical and Space Surveillance Conference, Maui, HI, USA, 16–19 September 2008. [Google Scholar]
- Steve Wozniak and Alex Fielding’s Startup Privateer Aims to be the Google Maps of Space. TechCrunch. Available online: https://social.techcrunch.com/2021/10/12/steve-wozniak-privateer-space-company/ (accessed on 16 July 2022).
- Liu, M.; Wang, H.; Yi, H.; Xue, Y.; Wen, D.; Wang, F.; Shen, Y.; Pan, Y. Space Debris Detection and Positioning Technology Based on Multiple Star Trackers. Appl. Sci. 2022, 12, 3593. [Google Scholar] [CrossRef]
- Hussain, K.F.; Thangavel, K.; Gardi, A.; Sabatini, R. Autonomous Optical Sensing for Space-Based Space Surveillance. Presented at the IEEE Aerospace conference, Big Sky, MT, USA, 23. In Proceedings of the Presented at the IEEE Aerospace Conference, Big Sky, MT, USA, March 2023. [Google Scholar]
- Araguz, C.; Bou-Balust, E.; Alarcón, E. Applying autonomy to distributed satellite systems: Trends, challenges, and future prospects. Syst. Eng. 2018, 21, 401–416. [Google Scholar] [CrossRef]
- Le Moigne, J.; Adams, J.C.; Nag, S. A New Taxonomy for Distributed Spacecraft Missions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 872–883. [Google Scholar] [CrossRef]
- Brown, O.; Eremenko, P. The Value Proposition for Fractionated Space Architectures. In Space 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar] [CrossRef]
- Hussain, K.; Hussain, K.; Carletta, S.; Teofilatto, P. Deployment of a microsatellite constellation around the Moon using chaotic multi body dynamics. In Proceedings of the 71st International Astronautical Congress (IAC), Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Golkar, A.; Cruz, I.L.I. The Federated Satellite Systems paradigm: Concept and business case evaluation. Acta Astronaut. 2015, 111, 230–248. [Google Scholar] [CrossRef]
- Graziano, M.D. Overview of Distributed Missions. In Distributed Space Missions for Earth System Monitoring; D’Errico, M., Ed.; Springer: New York, NY, USA, 2013; pp. 375–386. [Google Scholar] [CrossRef]
- von Maurich, O.; Golkar, A. Data authentication, integrity and confidentiality mechanisms for federated satellite systems. Acta Astronaut. 2018, 149, 61–76. [Google Scholar] [CrossRef]
- Ben-Larbi, M.K.; Pozo, K.F.; Haylok, T.; Choi, M.; Grzesik, B.; Haas, A.; Krupke, D.; Konstanski, H.; Schaus, V.; Fekete, S.P.; et al. Towards the automated operations of large distributed satellite systems. Part 1: Review and paradigm shifts. Adv. Space Res. 2021, 67, 3598–3619. [Google Scholar] [CrossRef]
- Selva, D.; Golkar, A.; Korobova, O.; Cruz, I.L.I.; Collopy, P.; de Weck, O.L. Distributed Earth Satellite Systems: What Is Needed to Move Forward? J. Aerosp. Inf. Syst. 2017, 14, 412–438. [Google Scholar] [CrossRef]
- Yaglioglu, B. A fractionated spacecraft architecture for Earth observation missions. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2011. [Google Scholar]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.; Illingworth, A.J.; O’connor, E.J.; Rossow, W.B.; Durden, S.L.; et al. The CloudSat mission and the A-Train: A new dimension of space-based observations of clouds and precipitation. Bull. Am. Meteorol. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Cluster—Satellite Missions—eoPortal Directory. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/content/-/article/cluster (accessed on 16 July 2022).
- Fang, W.; An, Y.; He, K.; Li, J.; Wang, B.; Li, J.; Wang, Q.; Guo, Q. Energy-Efficient Network Transmission between Satellite Swarms and Earth Stations Based on Lyapunov Optimization Techniques. Math. Probl. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Golkar, A. Federated satellite systems (FSS): A vision towards an innovation in space systems design. In Proceedings of the IAA Symposium on Small Satellites for Earth Observation, Berlin, Germany, 6–10 May 2013. [Google Scholar]
- Poghosyana, A.; Llucha, I.; Matevosyana, H.; Lamba, A.; Morenoa, C.A.; Taylora, C.; Golkara, A.; Coteb, J.; Mathieub, S.; Pierottib, S.; et al. Unified classification for distributed satellite systems. In Proceedings of the 4th International Federated and Fractionated Satellite Systems Workshop, Rome, Italy, 10 October 2016. [Google Scholar]
- Hilton, S.; Gardi, A.; Sabatini, R.; Ezer, N.; Desai, S. Human-Machine System Design for Autonomous Distributed Satellite Operations. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 1–8 October 2020. [Google Scholar] [CrossRef]
- Hilton, S.; Cairola, F.; Gardi, A.; Sabatini, R.; Pongsakornsathien, N.; Ezer, N. Uncertainty quantification for space situational awareness and traffic management. Sensors 2019, 19, 4361. [Google Scholar] [CrossRef]
- Sanders-Reed, J.N. Vehicle real-time attitude-estimation system (VRAES). In Acquisition, Tracking, and Pointing X.; SPIE: Bellingham, WA, USA, 1996; Volume 2739, pp. 266–277. [Google Scholar] [CrossRef]
- Walton, J.S. Image-based motion measurement: New technology, new applications. In Proceedings of the 21st International Congress on: High-Speed Photography and Photonics, Taejon, Republic of Korea, 30 May 1995; Volume 2513, pp. 862–880. [Google Scholar] [CrossRef]
- Guezennec, Y.G.; Brodkey, R.S.; Trigui, N.; Kent, J.C. Algorithms for fully automated three-dimensional particle tracking velocimetry. Exp. Fluids 1994, 17, 209–219. [Google Scholar] [CrossRef]
- Adamczyk, A.A.; Rimai, L. Reconstruction of a 3-dimensional flow field from orthogonal views of seed track video images. Exp. Fluids 1988, 6, 380–386. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Kurosaki, H.; Oda, H.; Tagawa, M. Ground-based optical observation system for LEO objects. Adv. Space Res. 2015, 56, 414–420. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Li, Z.; Kang, Z. A New Triangulation Algorithm for Positioning Space Debris. Remote Sens. 2021, 13, 4878. [Google Scholar] [CrossRef]
- Lloyd, K.H. Concise Method for Photogrammetry of Objects in the Sky; Weapons Research Establishment: Salisbury, Australia, 1971. [Google Scholar]
- Powers, J.W. Range Trilateration Error Analysis; IEEE: Piscataway, NJ, USA, 1966; pp. 572–585. [Google Scholar] [CrossRef]
- Long, S.A.T. Analytical Expressions for Position Error in Triangulation Solution of Point in Space for Several Station Configurations. L–9235, June 1974. Available online: https://ntrs.nasa.gov/citations/19740020173 (accessed on 18 July 2022).
- Sanders-Reed, J.N. Impact of tracking system knowledge on multisensor 3D triangulation. In Acquisition, Tracking, and Pointing XVI.; SPIE: Bellingham, WA, USA, 2002; Volume 4714, pp. 33–41. [Google Scholar]
- Sanders-Reed, J.N. Error propagation in two-sensor three-dimensional position estimation. Opt. Eng. 2001, 40, 627–636. [Google Scholar] [CrossRef]
- Sanders-Reed, J.N. Triangulation Position Error Analysis for Closely Spaced Imagers; SAE International: Warrendale, PA, USA. [CrossRef]
- Hauschild, A.; Markgraf, M.; Montenbruck, O. GPS receiver performance on board a LEO satellite. Gnss 2014, 9, 47–57. [Google Scholar]
- Curry, G.R. Radar System Performance Modeling, Artech House; Inc. Ed.: Norwood, MA, USA, 2005. [Google Scholar]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Wijewickrema, S.N.; Papliński, A.P. Principal component analysis for the approximation of an image as an ellipse. In Proceedings of the 13th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Plzen, Czech Republic, 31 January–4 March 2005. [Google Scholar]
- Behdinan, K.; Perez, R.E.; Liu, H.T. Multidisciplinary design optimization of aerospace systems. In Proceedings of the Canadian Design Engineering Network (CDEN) Conference, Kaninaskis, AB, USA, 18–20 July 2005. [Google Scholar] [CrossRef]
- Carrington, C.K.; Junkins, J.L. Optimal nonlinear feedback control for spacecraft attitude maneuvers. J. Guid. Control Dyn. 1986, 9, 99–107. [Google Scholar] [CrossRef]
- Bilimoria, K.D.; Wie, B. Time-optimal three-axis reorientation of a rigid spacecraft. J. Guid. Control Dyn. 1993, 16, 446–452. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Polovinkin, E.S. Pontryagin’s Direct Method for Optimization Problems with Differential Inclusion. In Proceedings of the Steklov Institute of Mathematics; Pleiades Publishing, Ltd.: Moscow, Russia, 2019; Volume 304, pp. 241–256. [Google Scholar] [CrossRef]
- Ben-Asher, J.Z. Optimal Control Theory with Aerospace Applications; The American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010. [Google Scholar]
- Conway, B.A. Spacecraft Trajectory Optimization; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gondelach, D.J.; Noomen, R. Hodographic-Shaping Method for Low-Thrust Interplanetary Trajectory Design. J. Spacecr. Rockets 2015, 52, 728–738. [Google Scholar] [CrossRef]
- Vasile, M.; De Pascale, P.; Casotto, S. On the optimality of a shape-based approach based on pseudo-equinoctial elements. Acta Astronaut. 2007, 61, 286–297. [Google Scholar] [CrossRef]
- Taheri, E.; Abdelkhalik, O. Initial three-dimensional low-thrust trajectory design. Adv. Space Res. 2016, 57, 889–903. [Google Scholar] [CrossRef]
- Taheri, E.; Abdelkhalik, O. Shape Based Approximation of Constrained Low-Thrust Space Trajectories using Fourier Series. J. Spacecr. Rockets 2012, 49, 535–546. [Google Scholar] [CrossRef]
- Shirazi, A.; Ceberio, J.; Lozano, J.A. Spacecraft trajectory optimization: A review of models, objectives, approaches and solutions. Prog. Aerosp. Sci. 2018, 102, 76–98. [Google Scholar] [CrossRef]
- Voß, S.; Martello, S.; Osman, I.H.; Roucairol, C. (Eds.) Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization; Springer: Boston, MA, USA, 1998. [Google Scholar] [CrossRef]
- Câmara, D. 4—Swarm Intelligence (SI). In Bio-Inspired Networking; Câmara, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 81–102. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. CSUR 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Xiong, N.; Molina, D.; Leon, M.; Herrera, F. A Walk into Metaheuristics for Engineering Optimization: Principles, Methods and Recent Trends. Int. J. Comput. Intell. Syst. 2015, 8, 606–636. [Google Scholar] [CrossRef]
- Leboucher, C.; Shin, H.-S.; Siarry, P.; Le Ménec, S.; Chelouah, R.; Tsourdos, A. Convergence proof of an enhanced Particle Swarm Optimisation method integrated with Evolutionary Game Theory. Inf. Sci. 2016, 346, 389–411. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95—International Conference on Neural Networks; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Lin, M.; Zhang, Z.-H.; Zhou, H.; Shui, Y. Multiconstrained Ascent Trajectory Optimization Using an Improved Particle Swarm Optimization Method. Int. J. Aerosp. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Rahimi, A.; Kumar, K.D.; Alighanbari, H. Particle Swarm Optimization Applied to Spacecraft Reentry Trajectory. J. Guid. Control Dyn. 2013, 36, 307–310. [Google Scholar] [CrossRef]
- Huang, P.; Xu, Y. PSO-Based Time-Optimal Trajectory Planning for Space Robot with Dynamic Constraints. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1402–1407. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar] [CrossRef]
- Baù, G.; Hernando-Ayuso, J.; Bombardelli, C. A generalization of the equinoctial orbital elements. Celest. Mech. Dyn. Astron. 2021, 133, 1–29. [Google Scholar] [CrossRef]
- Stuart, E. Applied Nonsingular Astrodynamics: Optimal Low-Thrust Orbit Transfer JA Kéchichian Cambridge University Press, University Printing House, Shaftesbury Road, Cambridge CB2 8BS, UK. 2018. xvii; 461 pp. Illustrated.£ 89.99. ISBN 978-1-108-47236-4. Aeronaut. J. 2020, 124, 2036–2037. [Google Scholar]
- Rajendra, P.P.; Kuga, H.K. An evaluation of Jacchia and MSIS 90 atmospheric models with CBERS data. Acta Astronaut. 2001, 48, 579–588. [Google Scholar] [CrossRef]
- Climate change—The Official Portal of the UAE Government. Available online: https://u.ae/en/information-and-services/environment-and-energy/climate-change/climate-change (accessed on 24 December 2022).
- Thangavel, K.; Spiller, D.; Sabatini, R.; Marzocca, P. On-board Data Processing of Earth Observation Data Using 1-D CNN. In Proceedings of the SmartSat CRC Conference 2022, Sydney, Australia, 12–13 September 2022. [Google Scholar] [CrossRef]
- Thangavel, K.; Spiller, D.; Sabatini, R.; Marzocca, P.; Esposito, M. Near Real-time Wildfire Management Using Distributed Satellite System. IEEE Geosci. Remote Sens. Lett. 2022, 20, 1–5. [Google Scholar] [CrossRef]
- Thangavel, K.; Spiller, D.; Sabatini, R.; Amici, S.; Sasidharan, S.T.; Fayek, H.; Marzocca, P. Autonomous Satellite Wildfire Detection Using Hyperspectral Imagery and Neural Networks: A Case Study on Australian Wildfire. Remote Sens. 2023, 15, 720. [Google Scholar] [CrossRef]
- Spiller, D.; Thangavel, K.; Sasidharan, S.T.; Amici, S.; Ansalone, L.; Sabatini, R. Wildfire segmentation analysis from edge computing for on-board real-time alerts using hyperspectral imagery. In Proceedings of the 2022 IEEE International Conference on Metrology for Extended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), Rome, Italy, 25–27 October 2022; pp. 725–730. [Google Scholar] [CrossRef]
- Thangavel, K.; Servidia, P.; Sabatini, R.; Marzocca, P.; Fayek, H.; Spiller, D. Distributed Satellite System for Maritime Domain Awareness. In Proceedings of the 20th Australian International Aerospace Congress (AIAC20), Melbourne, VIC, Australia, 27–28 February 2023. [Google Scholar]
- Ettouati, I.; Mortari, D.; Pollock, T. Space surveillance using star trackers. Part I: Simulations. Pap. AAS 2006, 06-231. [Google Scholar]
- Lagona, E.; Hilton, S.; Afful, A.; Gardi, A.; Sabatini, R. Autonomous Trajectory Optimisation for Intelligent Satellite Systems and Space Traffic Management. Acta Astronaut. 2022, 194, 185–201. [Google Scholar] [CrossRef]
- Flohrer, T.; Peltonen, J.; Kramer, A.; Eronen, T.; Kuusela, J.; Riihonen, E.; Schildknecht, T.; Stöveken, E.; Valtonen, E.; Wokke, F.; et al. Space-Based Optical Observations of Space Debris. In Proceedings of the 4th European Conference on Space Debris, Darmstadt, Germany, 18–20 April 2005; p. 165. [Google Scholar]
- Thangavela, K.; Gardia, A.; Hiltona, S.; Affula, A.M.; Sabatinib, R. Towards Multi-Domain Traffic Management. Structure 2021, 1, 2. [Google Scholar]
- HyperScout-2|InCubed. Available online: https://incubed.esa.int/portfolio/hyperscout-2/ (accessed on 24 December 2022).
- MAI-SS—Star Tracker|SatCatalog. Available online: https://www.satcatalog.com/component/mai-ss/ (accessed on 25 December 2022).
- Thangavel, K.; Spiller, D.; Sabatini, R.; Servidia, P.; Marzocca, P.; Fayek, H.; Hussain, K.; Gardi, A. Trusted Autonomous Distributed Satellite System Operations for Earth Observation. In Proceedings of the 17th International Conference on Space Operations, Dubai, United Arab Emirates, 6–10 March 2023. [Google Scholar] [CrossRef]
- Hussain, K.F.; Thangavel, K.; Gardi, A.; Sabatini, R. Autonomous tracking of Resident Space Objects using multiple ground-based Electro-Optical sensors. In Proceedings of the 17th International Conference on Space Operations, Dubai, United Arab Emirates, 6–10 March 2023. [Google Scholar]
- Infrared Detectors for Space Application. Vigo USA. Available online: https://vigophotonics.com/us/applications/infrared-detectors-for-space-application/ (accessed on 31 January 2023).
- Zhai, G.; Zhang, J.; Zhou, Z. On-orbit target tracking and inspection by satellite formation. J. Syst. Eng. Electron. 2013, 24, 879–888. [Google Scholar] [CrossRef]
- CubeSat Propulsion System EPSS, NanoAvionics. Available online: https://nanoavionics.com/cubesat-components/cubesat-propulsion-system-epss/ (accessed 2 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).