Exploring the Potential of vis-NIR Spectroscopy as a Covariate in Soil Organic Matter Mapping
Abstract
1. Introduction
2. Materials and Methods
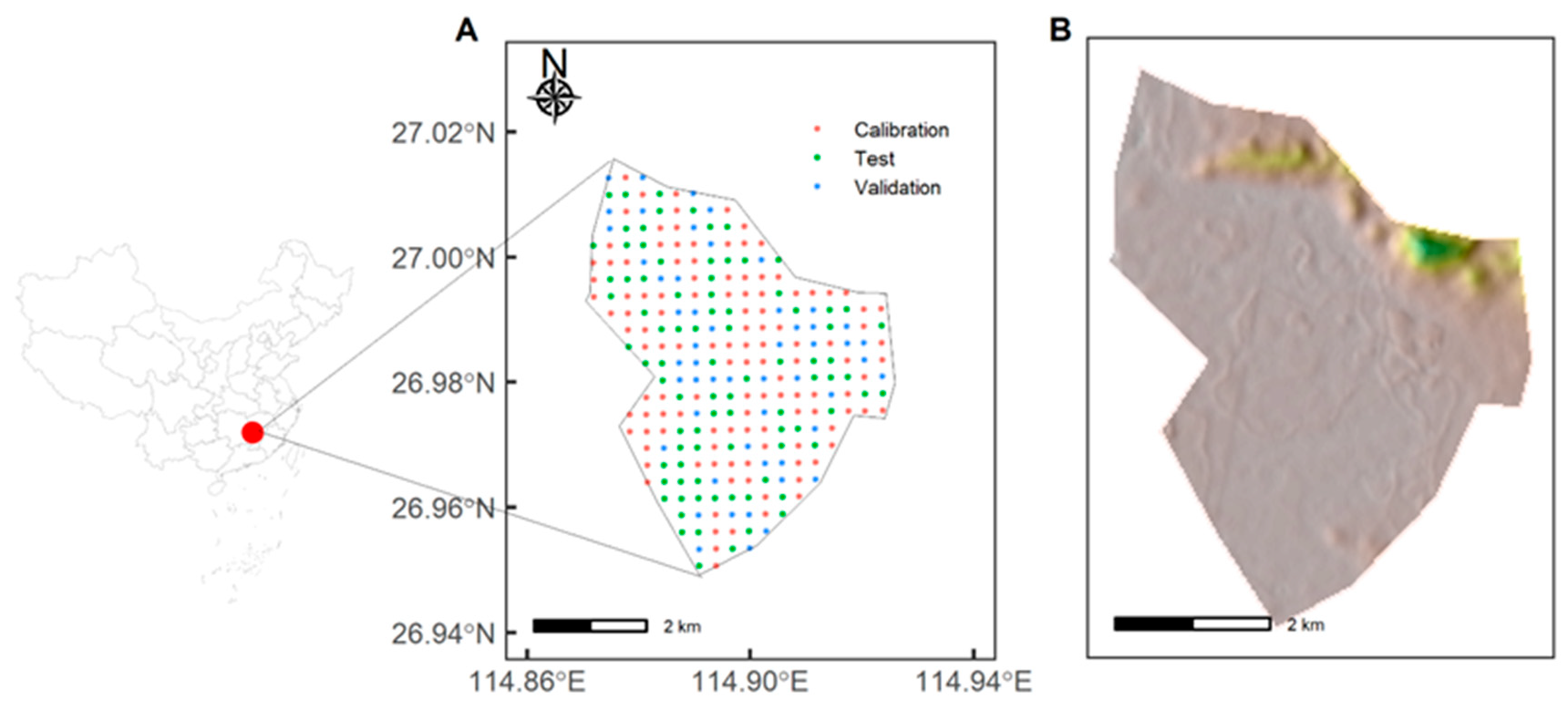
2.1. Study Area and Soil Sampling
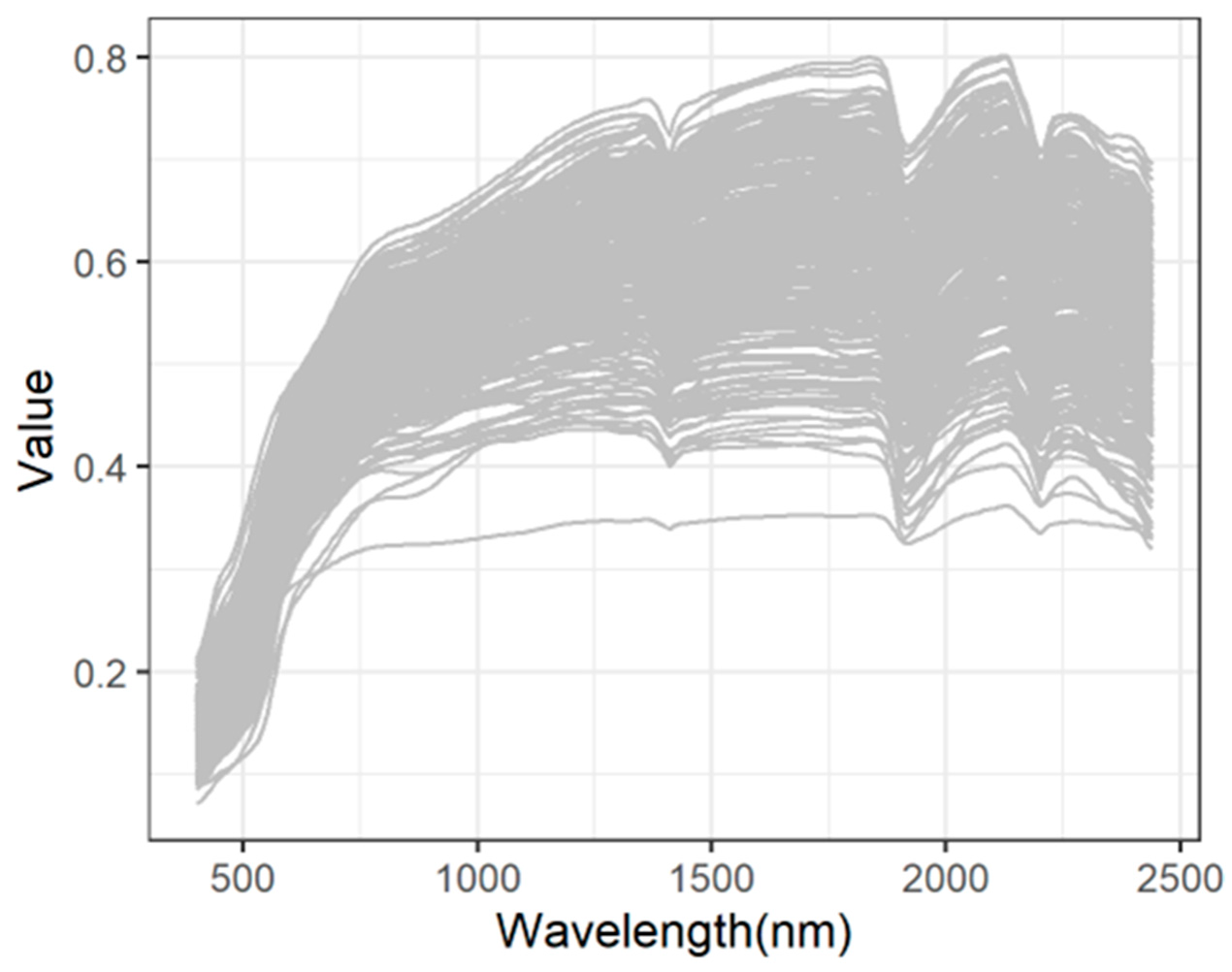
2.2. Measurement and Processing of vis-NIR Spectra
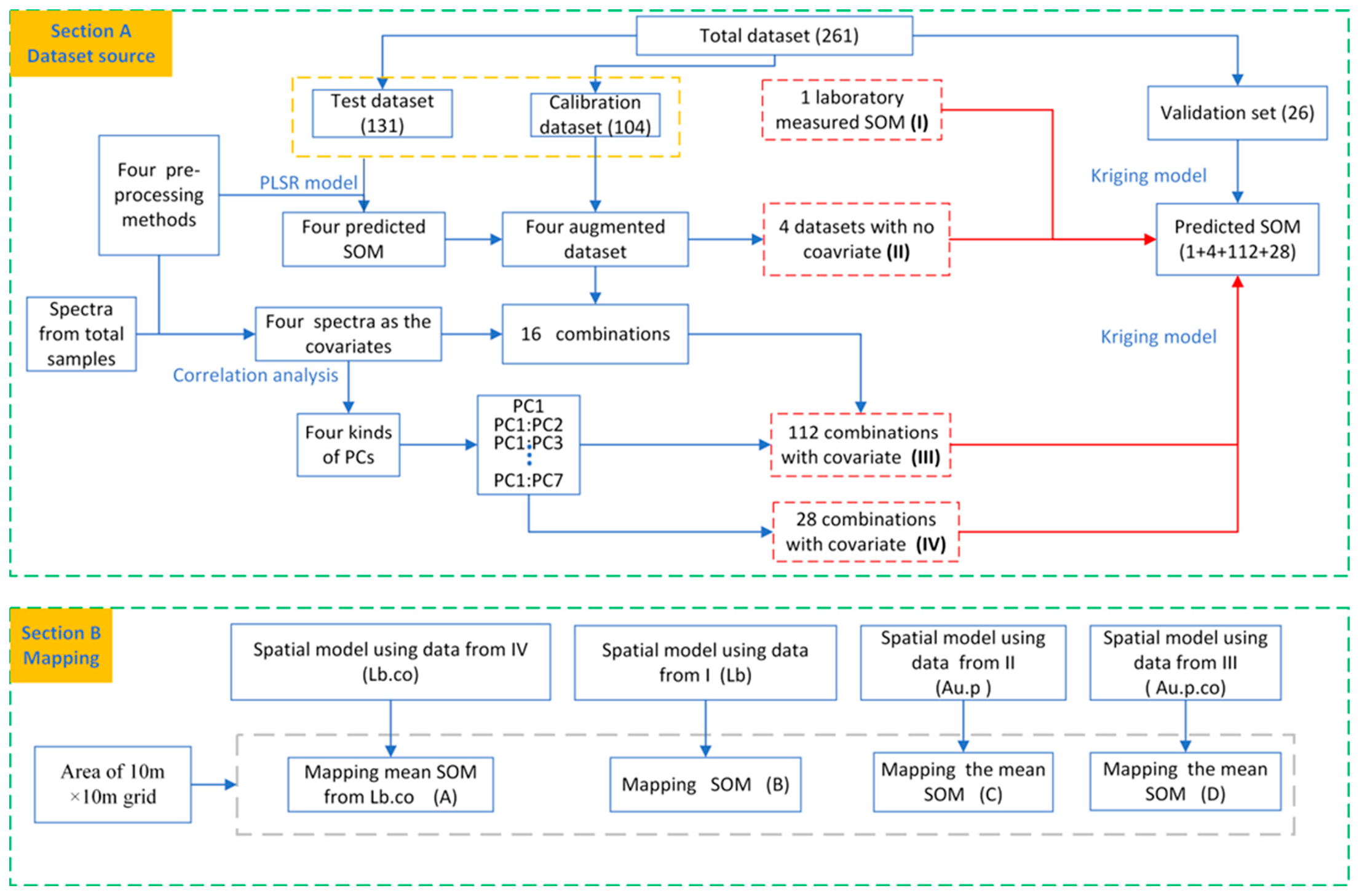
2.3. Spectroscopic Model and Augmented Data
2.4. Laboratory Analyses of Soil Organic Matter (SOM)
2.5. Selection of Covariates
2.6. Spatial Modeling, Performance Estimation, and SOM Mapping
3. Results
3.1. SOM and vis-NIR Spectra
3.2. Prediction of PLSR
3.3. Correlation Analysis
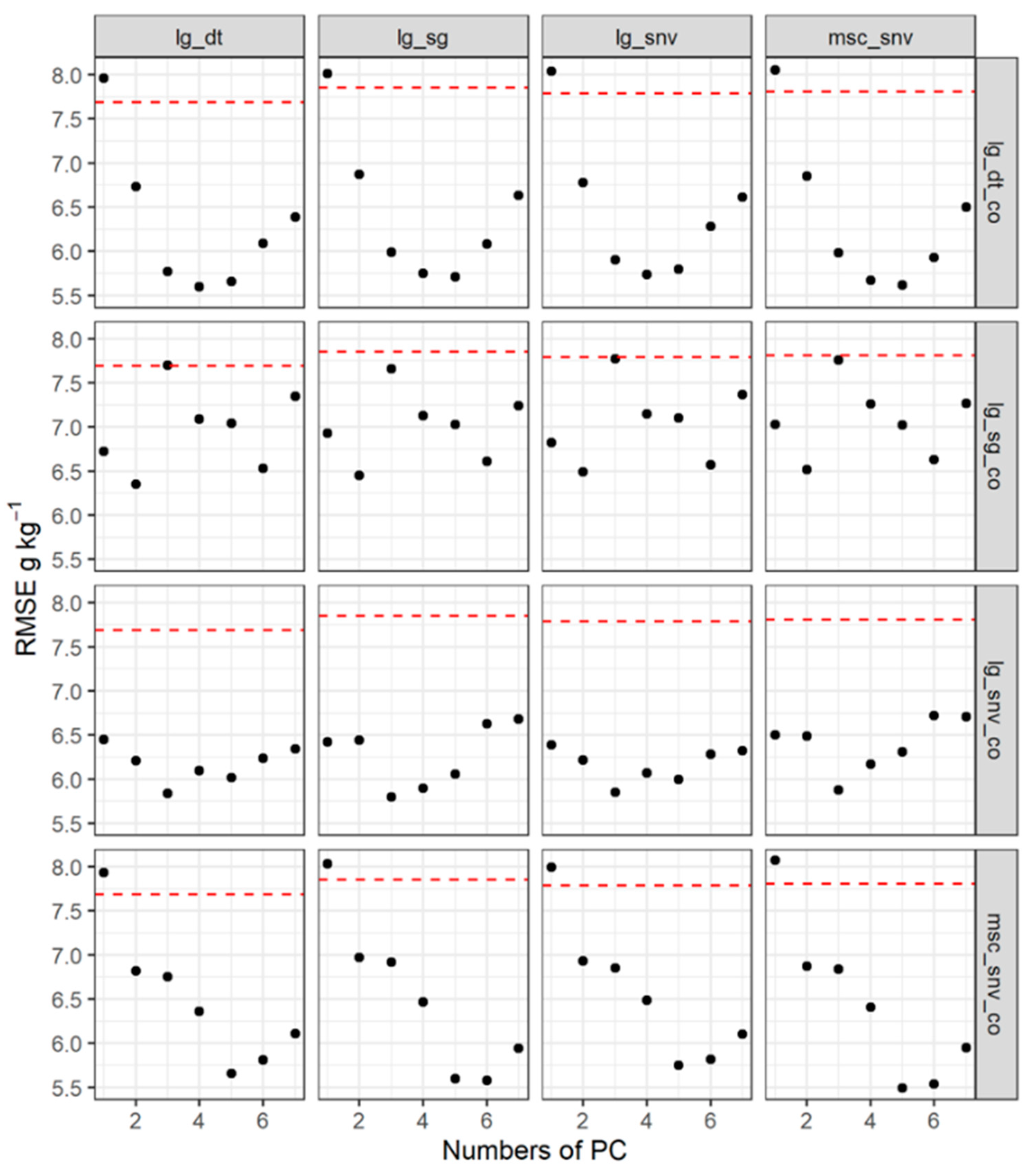
3.4. The Prediction from the Spatial Model with Spectra as the Covariate
3.5. Spatial Analysis and SOM Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Camargo, L.A.; Júnior, J.M.; Barrón, V.; Alleoni LR, F.; Barbosa, R.S.; Pereira, G.T. Mapping of clay, iron oxide and adsorbed phosphate in Oxisols using diffuse reflectance spectroscopy. Geoderma 2015, 251, 124–132. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Heller, D.; Chudnovsky, A. A Novel Method of Classifying Soil Profiles in the Field using Optical Means. Soil Sci. Soc. Am. J. 2008, 72, 1113–1123. [Google Scholar] [CrossRef]
- Van Zijl, G. Digital soil mapping approaches to address real world problems in southern Africa. Geoderma 2019, 337, 1301–1308. [Google Scholar] [CrossRef]
- Leenen, M.; Pätzold, S.; Tóth, G.; Welp, G. A LUCAS-based mid-infrared soil spectral library: Its usefulness for soil survey and precision agriculture. J. Plant Nutr. Soil Sci. 2022, 185, 370–383. [Google Scholar] [CrossRef]
- Brevik, E.C.; Calzolari, C.; Miller, B.A.; Pereira, P.; Kabala, C.; Baumgarten, A.; Jordán, A. Soil mapping, classification, and pedologic modeling: History and future directions. Geoderma 2016, 264, 256–274. [Google Scholar] [CrossRef]
- Brus, D. Sampling for digital soil mapping: A tutorial supported by R scripts. Geoderma 2019, 338, 464–480. [Google Scholar] [CrossRef]
- Li, N.; Arshad, M.; Zhao, D.; Sefton, M.; Triantafilis, J. Determining optimal digital soil mapping components for exchangeable calcium and magnesium across a sugarcane field. Catena 2019, 181, 104054. [Google Scholar] [CrossRef]
- Mirzaeitalarposhti, R.; Demyan, M.S.; Rasche, F.; Cadisch, G.; Müller, T. Mid-infrared spectroscopy to support regional-scale digital soil mapping on selected croplands of South-West Germany. Catena 2017, 149, 283–293. [Google Scholar] [CrossRef]
- Lopo, M.; dos Santos, C.A.T.; Páscoa, R.N.M.J.; Graça, A.R.; Lopes, J.A. Near infrared spectroscopy as a tool for intensive mapping of vineyards soil. Precis. Agric. 2017, 19, 445–462. [Google Scholar] [CrossRef]
- Páscoa, R.; Lopo, M.; dos Santos, C.T.; Graça, A.; Lopes, J. Exploratory study on vineyards soil mapping by visible/near-infrared spectroscopy of grapevine leaves. Comput. Electron. Agric. 2016, 127, 15–25. [Google Scholar] [CrossRef]
- Paz-Kagan, T.; Zaady, E.; Salbach, C.; Schmidt, A.; Lausch, A.; Zacharias, S.; Notesco, G.; Ben-Dor, E.; Karnieli, A. Mapping the Spectral Soil Quality Index (SSQI) Using Airborne Imaging Spectroscopy. Remote Sens. 2015, 7, 15748–15781. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Walvoort, D.; Mcbratney, A.; Janik, L.J.; Skjemstad, J. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Yang, M.; Chen, S.; Li, H.; Zhao, X.; Shi, Z. Effectiveness of different approaches for in situ measurements of organic carbon using visible and near infrared spectrometry in the Poyang Lake basin area. Land Degrad. Dev. 2021, 32, 1301–1311. [Google Scholar] [CrossRef]
- Vasques, G.; Grunwald, S.; Sickman, J. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar] [CrossRef]
- Samson, M.; Deutsch, C. The Sill of the Variogram. Geostatistics Lessons. Available online: https://geostatisticslessons.com/lessons/sillofvariogram (accessed on 25 February 2021).
- Rosin, N.A.; Demattê, J.A.M.; Poppiel, R.R.; Silvero, N.E.Q.; Rodriguez-Albarracin, H.S.; Rosas, J.T.F.; Greschuk, L.T.; Bellinaso, H.; Minasny, B.; Gomez, C.; et al. Mapping Brazilian soil mineralogy using proximal and remote sensing data. Geoderma 2023, 432. [Google Scholar] [CrossRef]
- Zhang, Y.; Saurette, D.D.; Easher, T.H.; Ji, W.; Adamchuk, V.I.; Biswas, A. Comparison of sampling designs for calibrating digital soil maps at multiple depths. Pedosphere 2022, 32, 588–601. [Google Scholar] [CrossRef]
- Yu, D.; Ramsey, R.D.; Zhao, X.-M.; Fu, Y.-Q.; Sun, C.-K. Feasible conversion degree of dryland to paddy field in Jinxian County, Jiangxi province, China. Geocarto Int. 2019, 34, 1042–1053. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Barnes, R.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Ru, R.S. Soil Physical and Chemical Analysis; Shanghai Science and Technology Publishing House: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Klingenfuß, C.; Roßkopf, N.; Walter, J.; Heller, C.; Zeitz, J. Soil organic matter to soil organic carbon ratios of peatland soil substrates. Geoderma 2014, 235, 410–417. [Google Scholar] [CrossRef]
- Yang, M.; Mouazen, A.; Zhao, X.; Guo, X. Assessment of a soil fertility index using visible and near-infrared spectroscopy in the rice paddy region of southern China. Eur. J. Soil Sci. 2020, 71, 615–626. [Google Scholar] [CrossRef]
- Steinberg, A.; Chabrillat, S.; Stevens, A.; Segl, K.; Foerster, S. Prediction of Common Surface Soil Properties Based on Vis-NIR Airborne and Simulated EnMAP Imaging Spectroscopy Data: Prediction Accuracy and Influence of Spatial Resolution. Remote Sens. 2016, 8, 613. [Google Scholar] [CrossRef]
- Yang, M.; Xu, D.; Chen, S.; Li, H.; Shi, Z. Evaluation of Machine Learning Approaches to Predict Soil Organic Matter and pH Using vis-NIR Spectra. Sensors 2019, 19, 263. [Google Scholar] [CrossRef] [PubMed]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Rizzo, R.; Demattê, J.A.M.; Lepsch, I.F.; Gallo, B.C.; Fongaro, C.T. Digital soil mapping at local scale using a multi-depth Vis–NIR spectral library and terrain attributes. Geoderma 2016, 274, 18–27. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Wadoux, A.C.; Franceschini, M.H.; Terra, F.; Marques, K.P.P.; Sayão, V.M.; Demattê, J.A.M. Robust soil mapping at the farm scale with vis–NIR spectroscopy. Eur. J. Soil Sci. 2019, 70, 378–393. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Webster, R.; Bui, E.N.; Baldock, J.A. Baseline map of organic carbon in Australian soil to support national carbon accounting and monitoring under climate change. Glob. Chang. Biol. 2014, 20, 2953–2970. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Chen, C.; Grundy, M.; Searle, R.; Clifford, D.; Campbell, P. The Australian three-dimensional soil grid: Australia’s contribution to the GlobalSoilMap project. Soil Res. 2015, 53, 845–864. [Google Scholar] [CrossRef]
- Somarathna, P.; Minasny, B.; Malone, B.P.; Stockmann, U.; McBratney, A. Accounting for the measurement error of spectroscopically inferred soil carbon data for improved precision of spatial predictions. Sci. Total. Environ. 2018, 631-632, 377–389. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B.; Söderström, M. The use of near infrared (NIR) spectroscopy to improve soil mapping at the farm scale. Precis. Agric. 2008, 9, 57–69. [Google Scholar] [CrossRef]
- De Oliveira, J.F.; Brossard, M.; Corazza, E.J.; De Fátima Guimarães, M.; Marchão, R.L. Field-scale spatial correlation between soil and Vis-NIR spectra in the Cerrado biome of Central Brazil. Geoderma Reg. 2022, 30, e00532. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]


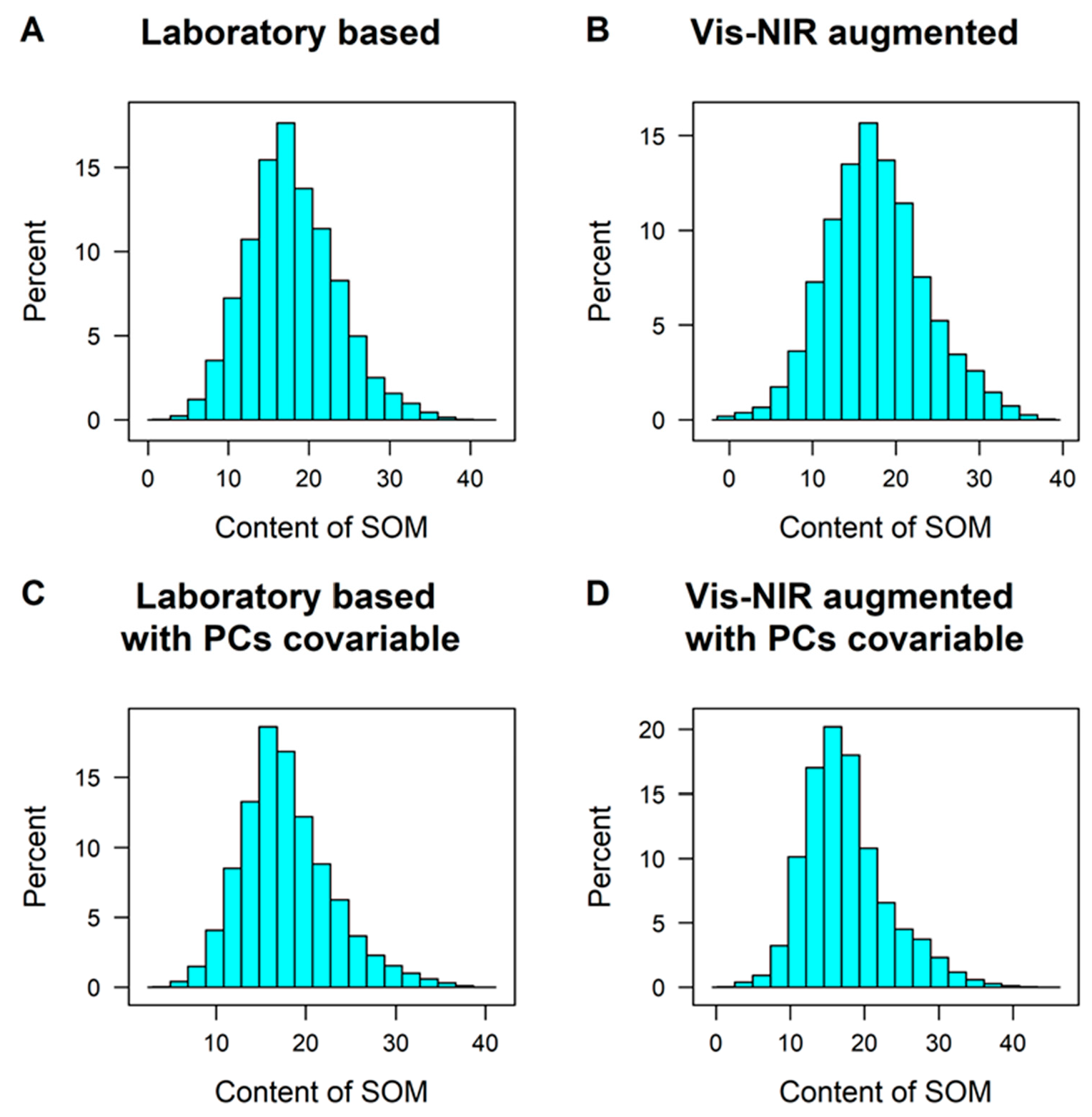
| N | Mean | SD | Skew | Min. | 1st Qu. | Median | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|---|---|---|
| Calibration /g kg−1 | 104 | 18.92 | 8.87 | 0.61 | 2.31 | 12.08 | 18.72 | 23.55 | 49.68 |
| Test/g kg−1 | 131 | 18.32 | 6.57 | 0.31 | 2.06 | 14.37 | 16.99 | 23.31 | 35.58 |
| Validation /g kg−1 | 26 | 17.63 | 7.36 | 0.31 | 4.96 | 12.22 | 17.59 | 23.26 | 37.09 |
| Transformation | Validation Dataset | Test Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RPIQ | Bias | R2 | RMSE | RPIQ | Bias | R2 | |
| lg.sg | 6.11 | 1.51 | 0.11 | 0.56 | 4.32 | 2.17 | 0.39 | 0.69 |
| msc.snv | 5.40 | 1.71 | 0.09 | 0.66 | 4.61 | 2.03 | 0.20 | 0.64 |
| lg.snv | 5.74 | 1.61 | 0.71 | 0.63 | 4.19 | 2.23 | 0.31 | 0.71 |
| lg.dt | 5.48 | 1.68 | 0.63 | 0.65 | 4.07 | 2.30 | −0.04 | 0.72 |
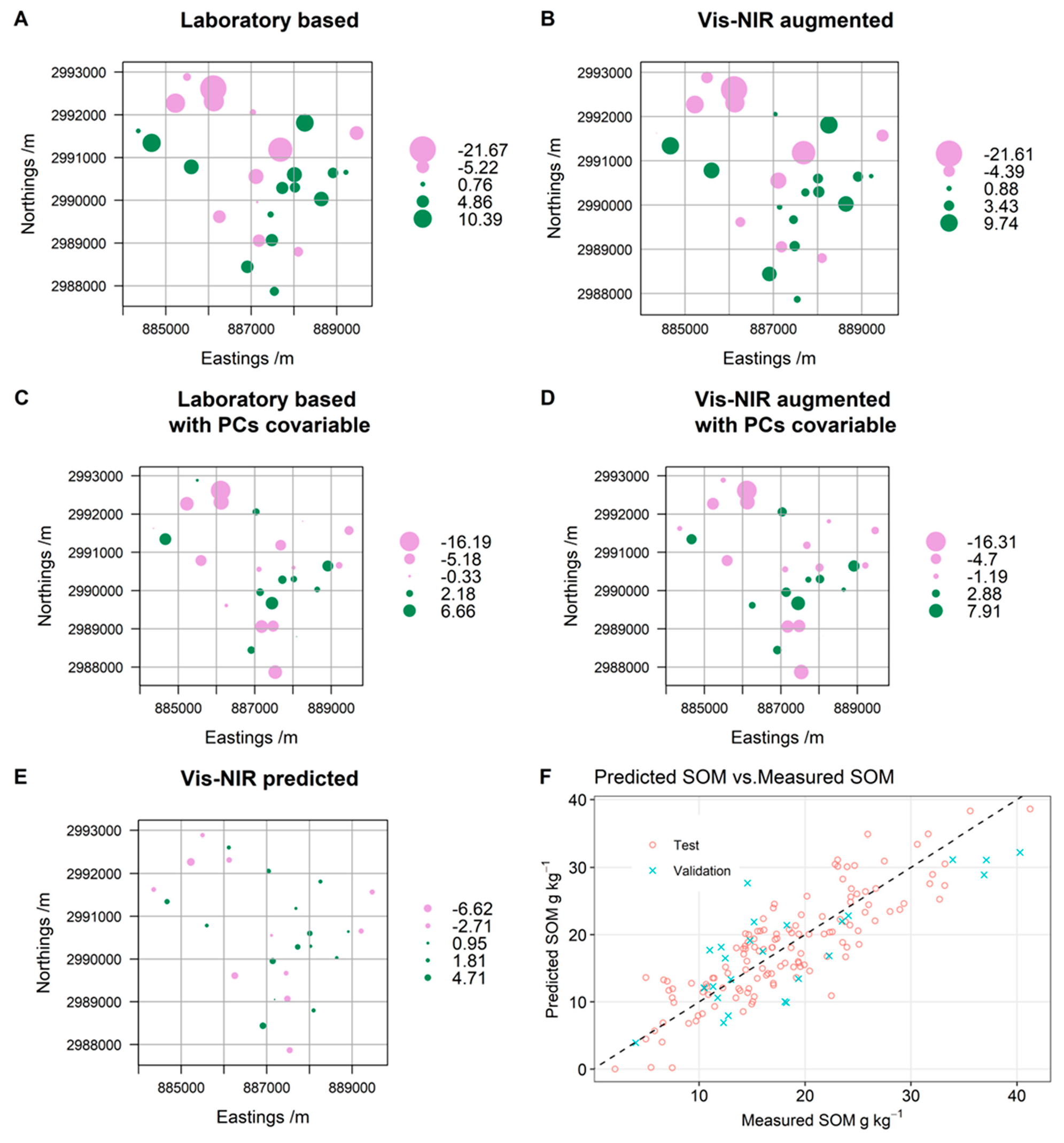
| LVs | Cross-Validation | Validation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE /g kg−1 | RPIQ | ME /g kg−1 | R2 | RMSE/g kg−1 | RPIQ | ME /g kg−1 | ||
| Lb | 4 | 0.18 | 6.83 | 1.54 | 1.01 | 0.27 | 7.12 | 1.27 | 1.04 |
| Au.p | 6 | 0.18 | 6.74 | 1.56 | 0.68 | 0.35 | 7.69 | 1.20 | 0.97 |
| Lb.co | 7 | 0.50 | 5.36 | 2.08 | 0.17 | 0.58 | 5.51 | 1.64 | 0.74 |
| Au.p.co | 8 | 0.47 | 5.46 | 1.86 | 0.34 | 0.66 | 5.66 | 1.65 | 1.37 |
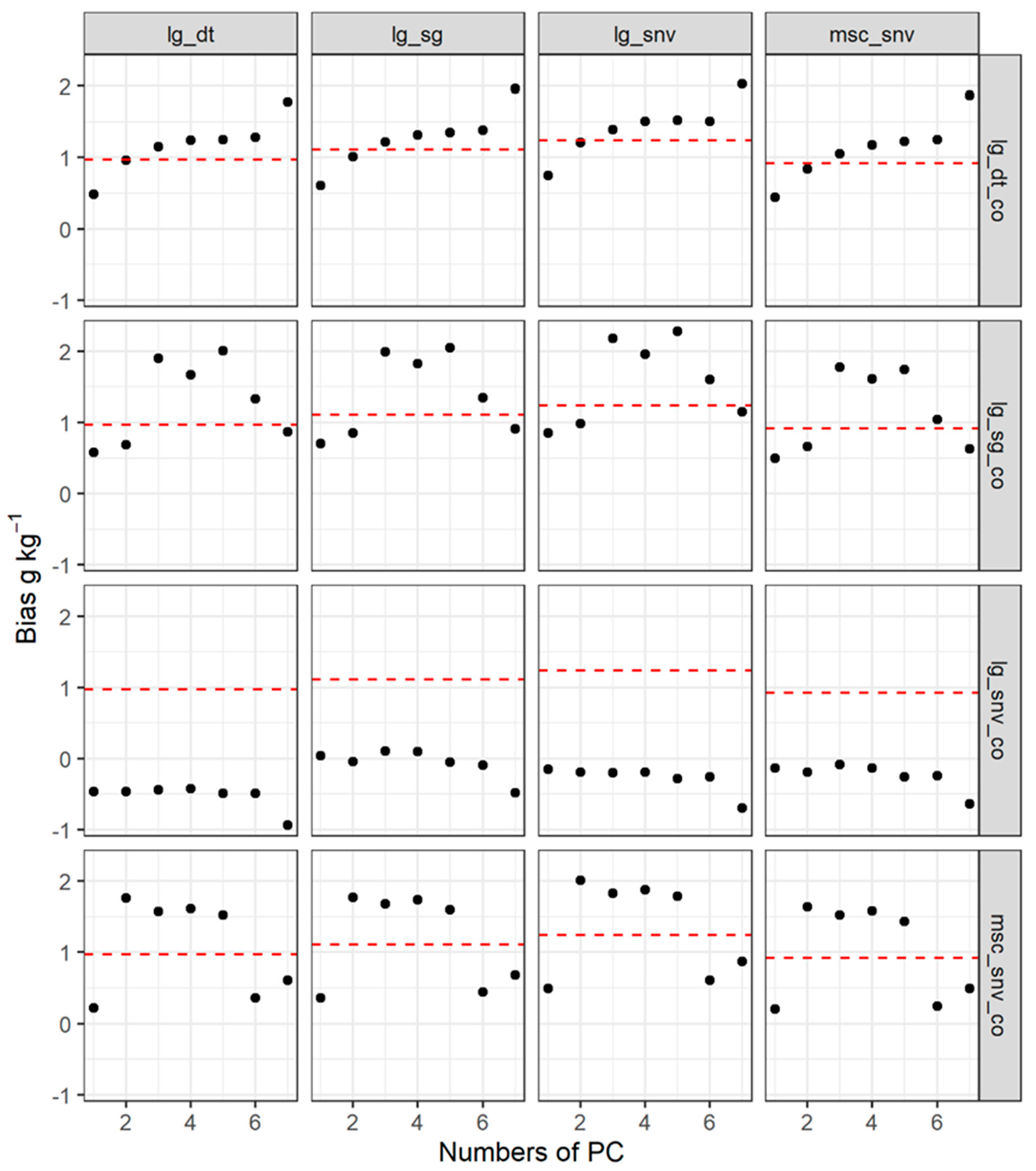
| PCs | Pre-Processing | RMSE | RPIQ | Bias | R2 | RMSE | RPIQ | Bias | R2 | RMSE | RPIQ | Bias | R2 | RMSE | RPIQ | Bias | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lg.sg | msc.snv | lg.snv | lg.dt | ||||||||||||||
| 1 | lg.sg | 6.93 | 1.33 | 0.7 | 0.45 | 7.03 | 1.31 | 0.5 | 0.42 | 6.82 | 1.35 | 0.85 | 0.47 | 6.72 | 1.37 | 0.58 | 0.48 |
| msc.snv | 8.03 | 1.15 | 0.36 | 0.24 | 8.07 | 1.14 | 0.2 | 0.23 | 7.99 | 1.15 | 0.49 | 0.24 | 7.93 | 1.16 | 0.22 | 0.25 | |
| lg.snv | 6.42 | 1.44 | 0.04 | 0.52 | 6.5 | 1.42 | −0.13 | 0.51 | 6.39 | 1.44 | −0.15 | 0.52 | 6.45 | 1.43 | −0.46 | 0.51 | |
| lg.dt | 8.01 | 1.15 | 0.61 | 0.25 | 8.05 | 1.15 | 0.44 | 0.24 | 8.04 | 1.15 | 0.75 | 0.24 | 7.96 | 1.16 | 0.48 | 0.25 | |
| 2 | lg.sg | 6.45 | 1.43 | 0.85 | 0.54 | 6.52 | 1.42 | 0.66 | 0.52 | 6.49 | 1.42 | 0.98 | 0.53 | 6.35 | 1.45 | 0.69 | 0.54 |
| msc.snv | 6.97 | 1.32 | 1.77 | 0.46 | 6.87 | 1.34 | 1.64 | 0.47 | 6.93 | 1.33 | 2.01 | 0.48 | 6.82 | 1.35 | 1.76 | 0.49 | |
| lg.snv | 6.44 | 1.43 | −0.04 | 0.56 | 6.49 | 1.42 | −0.19 | 0.55 | 6.22 | 1.48 | −0.19 | 0.55 | 6.21 | 1.49 | −0.46 | 0.55 | |
| lg.dt | 6.87 | 1.34 | 1.01 | 0.47 | 6.85 | 1.35 | 0.84 | 0.47 | 6.78 | 1.36 | 1.21 | 0.49 | 6.73 | 1.37 | 0.96 | 0.49 | |
| 3 | lg.sg | 7.66 | 1.2 | 1.99 | 0.36 | 7.76 | 1.19 | 1.78 | 0.34 | 7.77 | 1.19 | 2.18 | 0.36 | 7.7 | 1.2 | 1.9 | 0.36 |
| msc.snv | 6.92 | 1.33 | 1.68 | 0.46 | 6.84 | 1.35 | 1.52 | 0.47 | 6.85 | 1.35 | 1.83 | 0.48 | 6.75 | 1.37 | 1.57 | 0.49 | |
| lg.snv | 5.8 | 1.59 | 0.11 | 0.64 | 5.88 | 1.57 | −0.08 | 0.63 | 5.85 | 1.58 | −0.2 | 0.59 | 5.84 | 1.58 | −0.44 | 0.6 | |
| lg.dt | 5.99 | 1.54 | 1.22 | 0.59 | 5.98 | 1.54 | 1.05 | 0.59 | 5.9 | 1.56 | 1.39 | 0.61 | 5.77 | 1.6 | 1.15 | 0.62 | |
| 4 | lg.sg | 7.13 | 1.29 | 1.83 | 0.45 | 7.26 | 1.27 | 1.61 | 0.43 | 7.15 | 1.29 | 1.96 | 0.47 | 7.09 | 1.3 | 1.67 | 0.47 |
| msc.snv | 6.47 | 1.42 | 1.74 | 0.54 | 6.41 | 1.44 | 1.58 | 0.54 | 6.49 | 1.42 | 1.88 | 0.55 | 6.36 | 1.45 | 1.61 | 0.55 | |
| lg.snv | 5.9 | 1.56 | 0.1 | 0.6 | 6.17 | 1.5 | −0.13 | 0.55 | 6.07 | 1.52 | −0.19 | 0.56 | 6.1 | 1.51 | −0.42 | 0.56 | |
| lg.dt | 5.75 | 1.6 | 1.32 | 0.63 | 5.67 | 1.63 | 1.18 | 0.63 | 5.74 | 1.61 | 1.51 | 0.64 | 5.6 | 1.65 | 1.24 | 0.65 | |
| 5 | lg.sg | 7.03 | 1.31 | 2.05 | 0.47 | 7.02 | 1.31 | 1.74 | 0.46 | 7.1 | 1.3 | 2.28 | 0.47 | 7.04 | 1.31 | 2.01 | 0.47 |
| msc.snv | 5.6 | 1.65 | 1.6 | 0.66 | 5.49 | 1.68 | 1.43 | 0.67 | 5.75 | 1.6 | 1.79 | 0.65 | 5.66 | 1.63 | 1.52 | 0.65 | |
| lg.snv | 6.06 | 1.52 | −0.05 | 0.58 | 6.31 | 1.46 | −0.26 | 0.54 | 6 | 1.54 | −0.28 | 0.57 | 6.02 | 1.53 | −0.49 | 0.57 | |
| lg.dt | 5.71 | 1.62 | 1.35 | 0.64 | 5.62 | 1.64 | 1.23 | 0.64 | 5.8 | 1.59 | 1.52 | 0.64 | 5.66 | 1.63 | 1.25 | 0.65 | |
| 6 | lg.sg | 6.61 | 1.4 | 1.35 | 0.52 | 6.63 | 1.39 | 1.04 | 0.51 | 6.57 | 1.4 | 1.6 | 0.54 | 6.53 | 1.41 | 1.33 | 0.55 |
| msc.snv | 5.58 | 1.65 | 0.44 | 0.64 | 5.54 | 1.66 | 0.24 | 0.64 | 5.82 | 1.59 | 0.61 | 0.62 | 5.81 | 1.59 | 0.36 | 0.62 | |
| lg.snv | 6.63 | 1.39 | −0.09 | 0.5 | 6.72 | 1.37 | −0.24 | 0.48 | 6.28 | 1.47 | −0.26 | 0.54 | 6.24 | 1.48 | −0.49 | 0.55 | |
| lg.dt | 6.08 | 1.52 | 1.38 | 0.59 | 5.93 | 1.56 | 1.25 | 0.6 | 6.28 | 1.47 | 1.51 | 0.57 | 6.09 | 1.51 | 1.28 | 0.59 | |
| 7 | lg.sg | 7.24 | 1.27 | 0.91 | 0.46 | 7.27 | 1.27 | 0.63 | 0.46 | 7.37 | 1.25 | 1.15 | 0.46 | 7.35 | 1.26 | 0.87 | 0.46 |
| msc.snv | 5.94 | 1.55 | 0.68 | 0.59 | 5.95 | 1.55 | 0.49 | 0.59 | 6.1 | 1.51 | 0.87 | 0.59 | 6.11 | 1.51 | 0.61 | 0.58 | |
| lg.snv | 6.68 | 1.38 | −0.48 | 0.48 | 6.71 | 1.38 | −0.64 | 0.48 | 6.32 | 1.46 | −0.69 | 0.54 | 6.34 | 1.45 | −0.93 | 0.54 | |
| lg.dt | 6.63 | 1.39 | 1.96 | 0.54 | 6.5 | 1.42 | 1.87 | 0.54 | 6.61 | 1.4 | 2.03 | 0.56 | 6.39 | 1.44 | 1.78 | 0.57 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Chen, S.; Guo, X.; Shi, Z.; Zhao, X. Exploring the Potential of vis-NIR Spectroscopy as a Covariate in Soil Organic Matter Mapping. Remote Sens. 2023, 15, 1617. https://doi.org/10.3390/rs15061617
Yang M, Chen S, Guo X, Shi Z, Zhao X. Exploring the Potential of vis-NIR Spectroscopy as a Covariate in Soil Organic Matter Mapping. Remote Sensing. 2023; 15(6):1617. https://doi.org/10.3390/rs15061617
Chicago/Turabian StyleYang, Meihua, Songchao Chen, Xi Guo, Zhou Shi, and Xiaomin Zhao. 2023. "Exploring the Potential of vis-NIR Spectroscopy as a Covariate in Soil Organic Matter Mapping" Remote Sensing 15, no. 6: 1617. https://doi.org/10.3390/rs15061617
APA StyleYang, M., Chen, S., Guo, X., Shi, Z., & Zhao, X. (2023). Exploring the Potential of vis-NIR Spectroscopy as a Covariate in Soil Organic Matter Mapping. Remote Sensing, 15(6), 1617. https://doi.org/10.3390/rs15061617







