Credible Remote Sensing Scene Classification Using Evidential Fusion on Aerial-Ground Dual-View Images
Abstract
1. Introduction
- A Theory of Evidence Based Sample Uncertainty Quantification (TEB-SUQ) approach is used in both views of aerial and ground images to measure the decision-making risk during their fusion.
- An Evidential Fusion strategy is proposed to fuse aerial-ground dual-view images at decision-level for remote sensing scene classification. Unlike other existing decision-level fusion methods, the proposed strategy focuses the results not only on the classification probability but also on the decision-making risk of each view. Thus, the final result will depend more on the view with lower decision-making risk.
- A more concise loss function, namely Reciprocal Loss is designed to simultaneously constrain the uncertainty of individual view and of their fusion. It can be used not only to train an end-to-end aerial-ground dual-view remote sensing scene classification model, but also to train a fusion classifier without feature extraction.
2. Data and Methodology
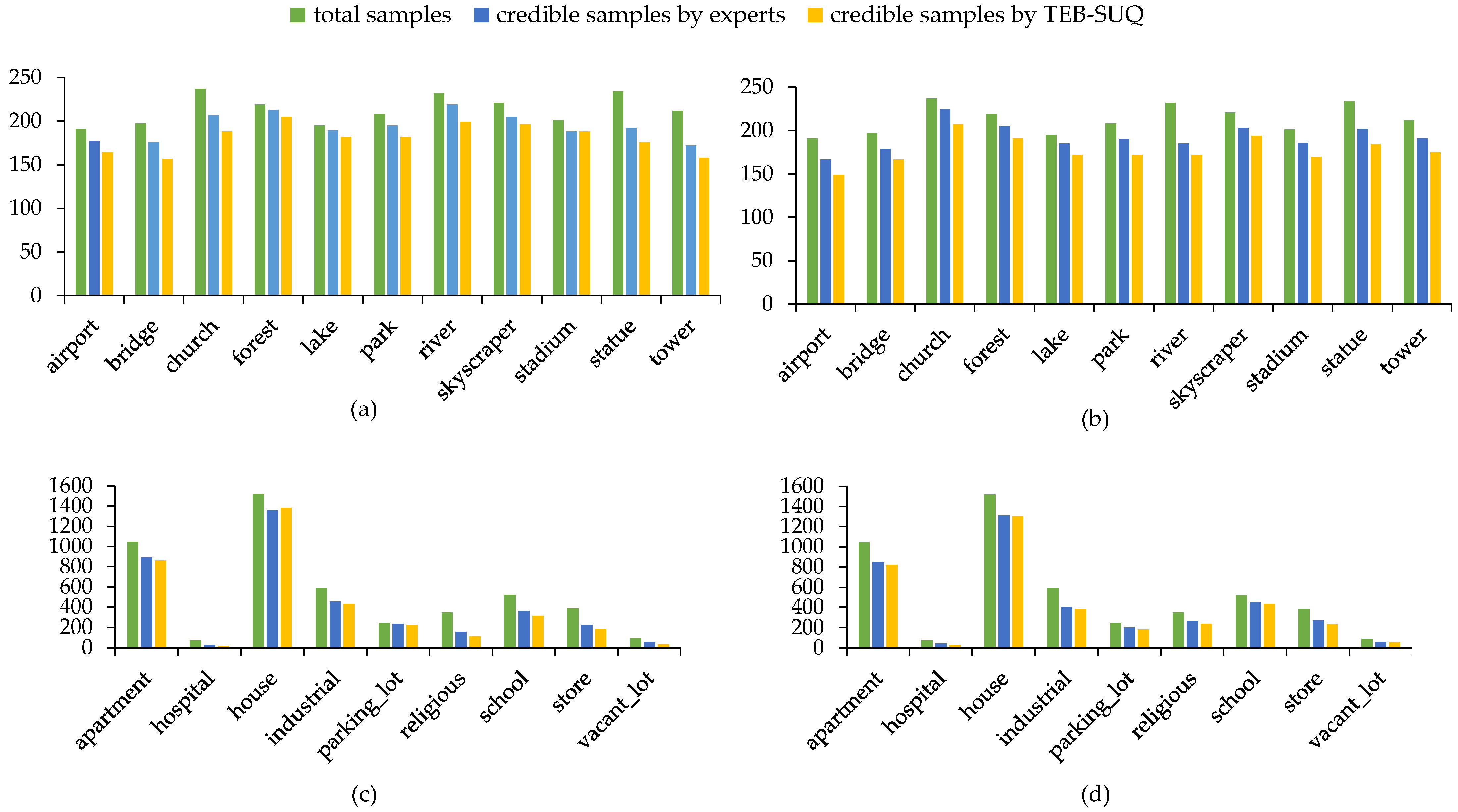
2.1. Datasets Description
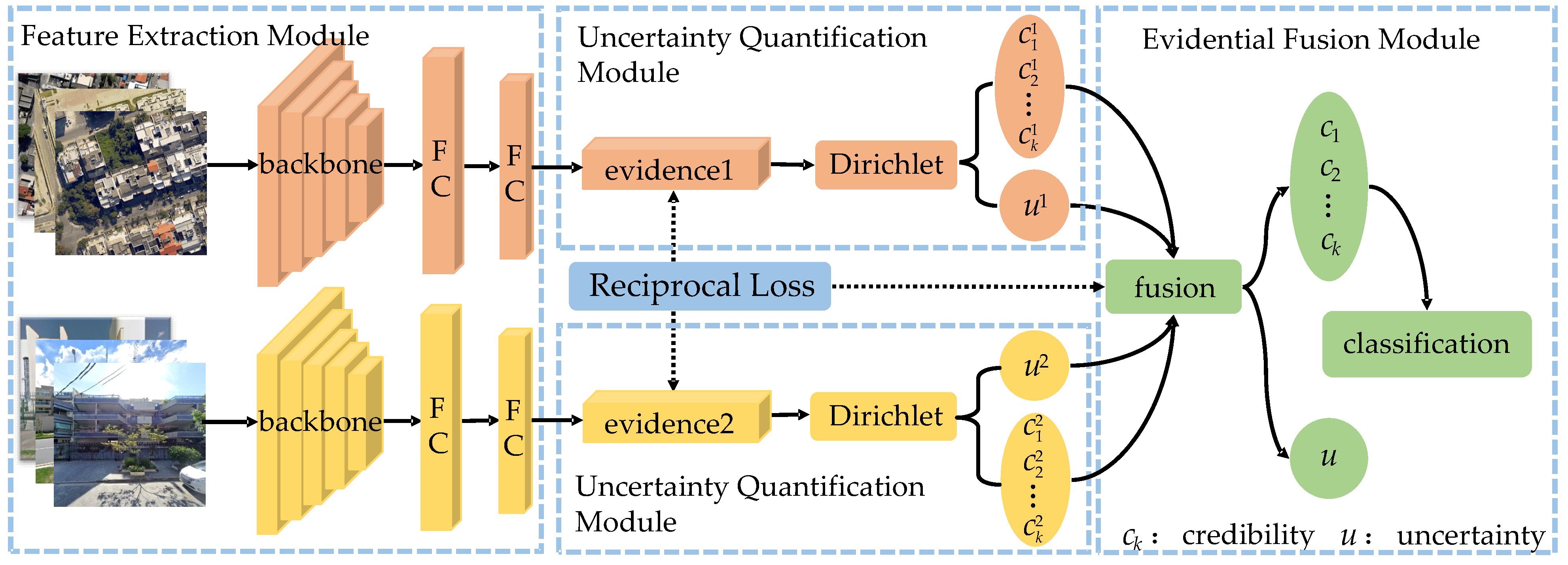
2.2. Overview
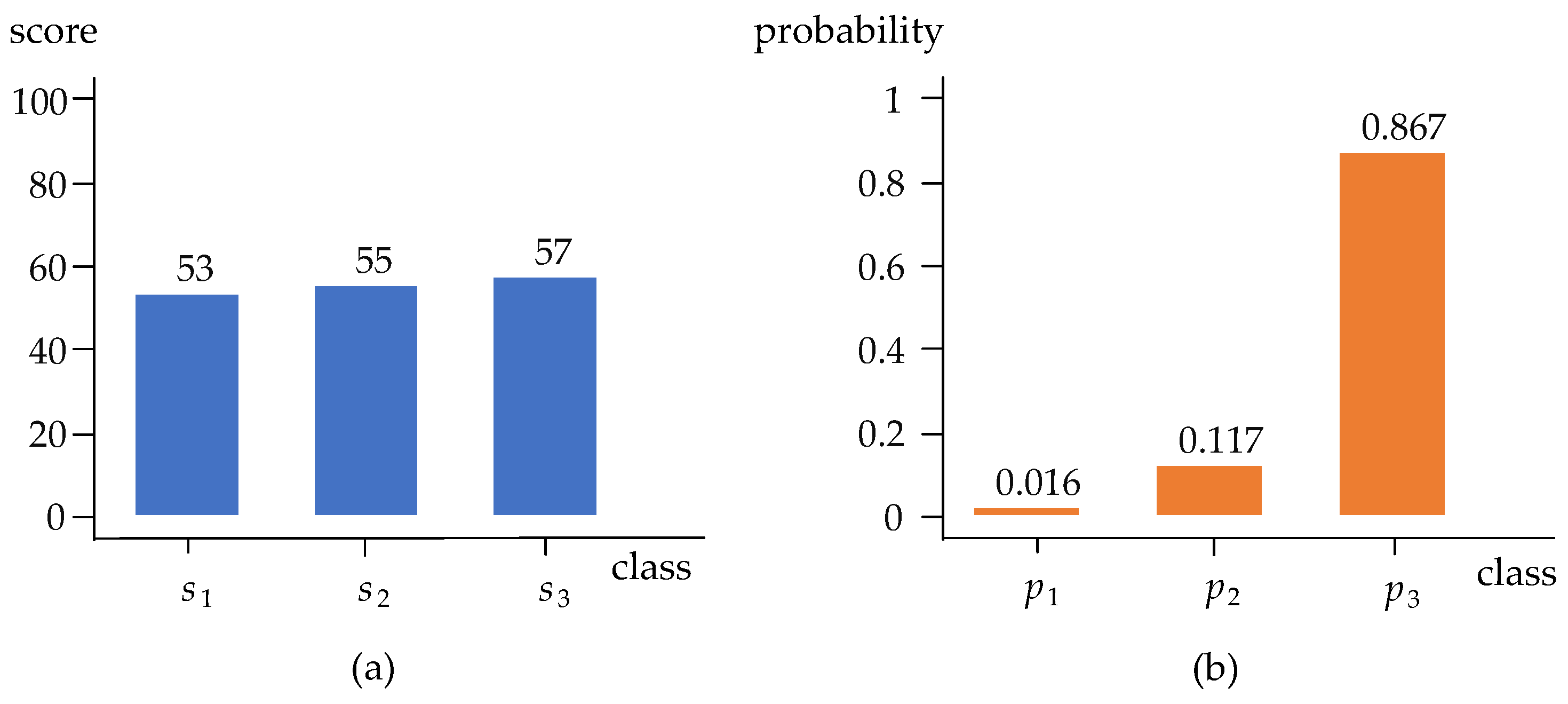
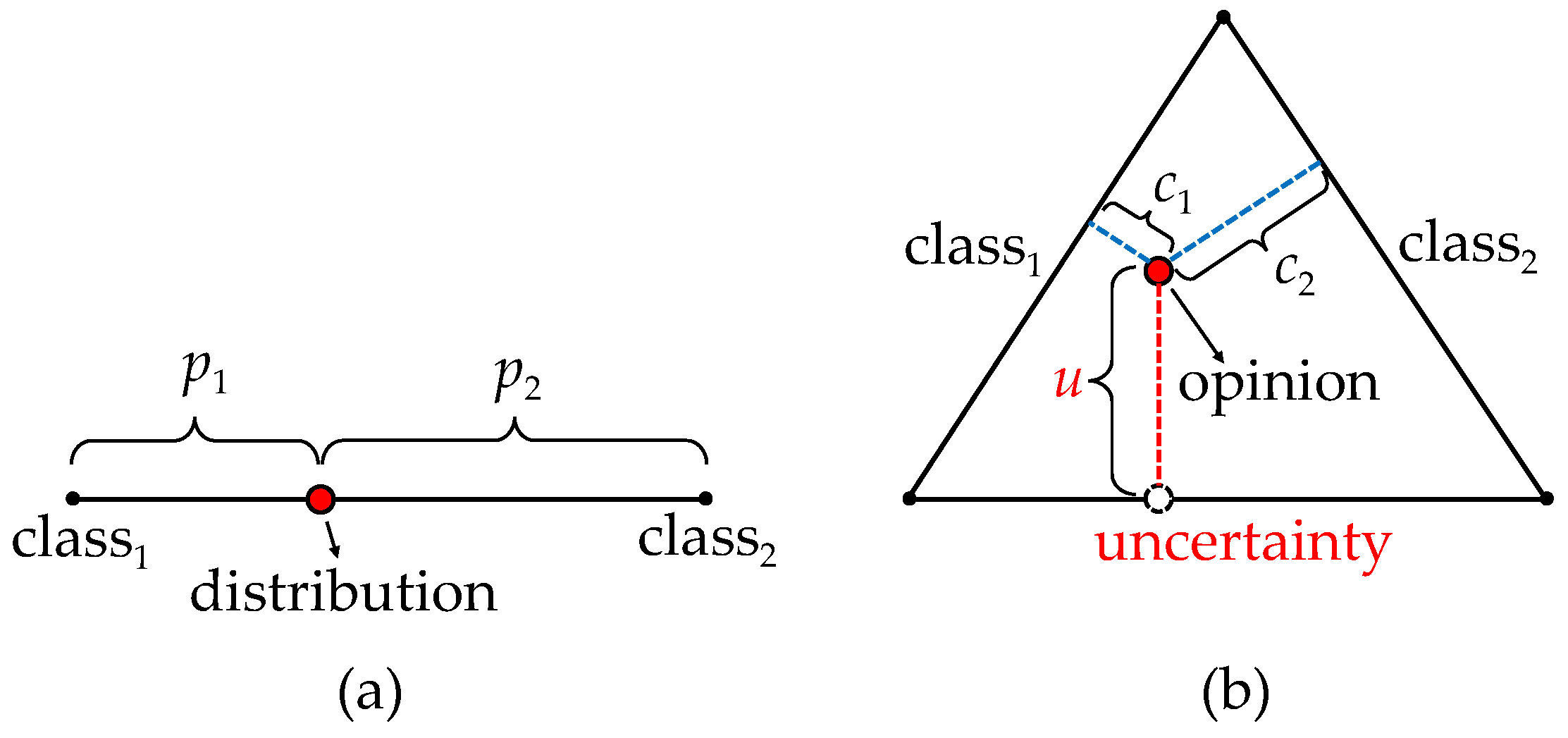
2.3. Uncertainty Estimation Based on Evidential Learning
2.4. Evidential Fusion
2.5. Reciprocal Loss
3. Results
3.1. Experimental Setup
3.2. Ablation Study
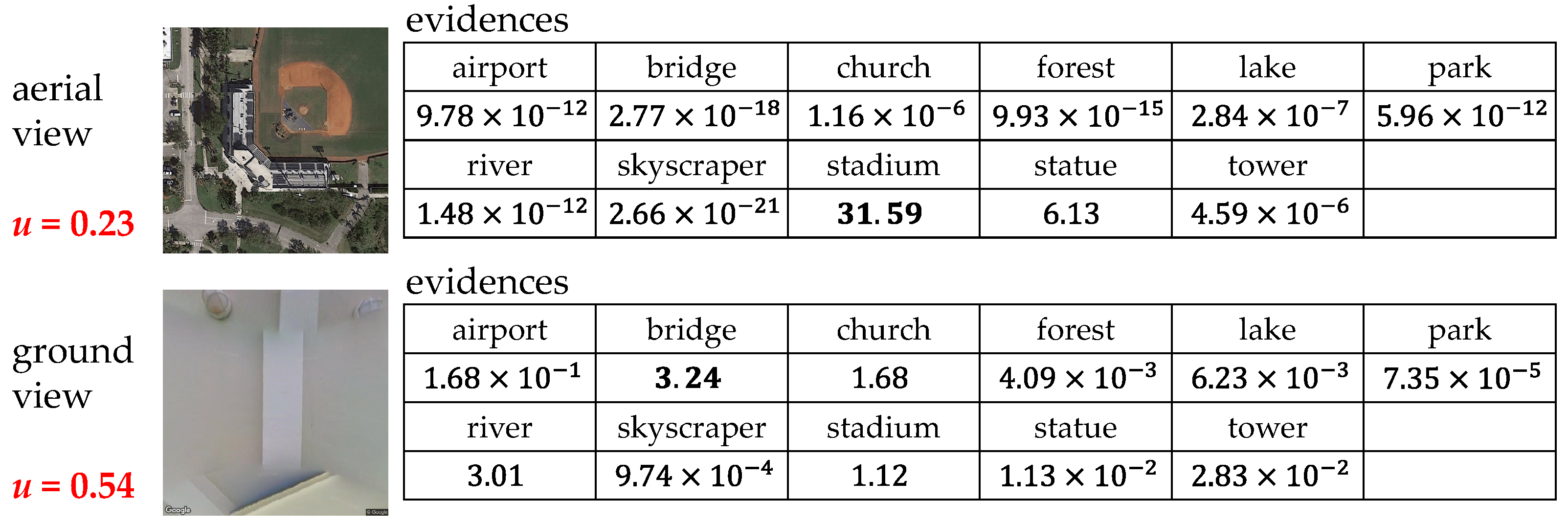
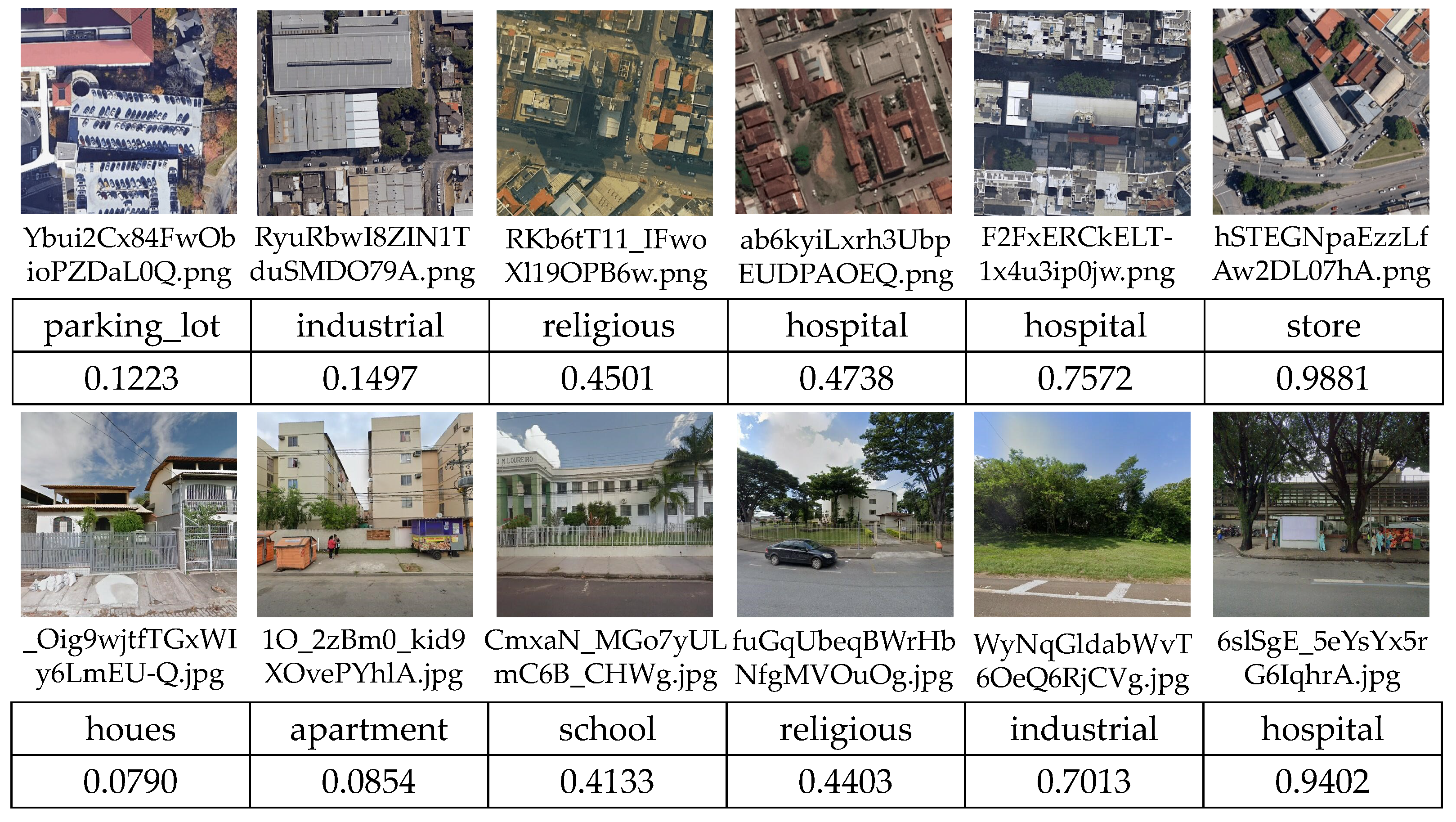
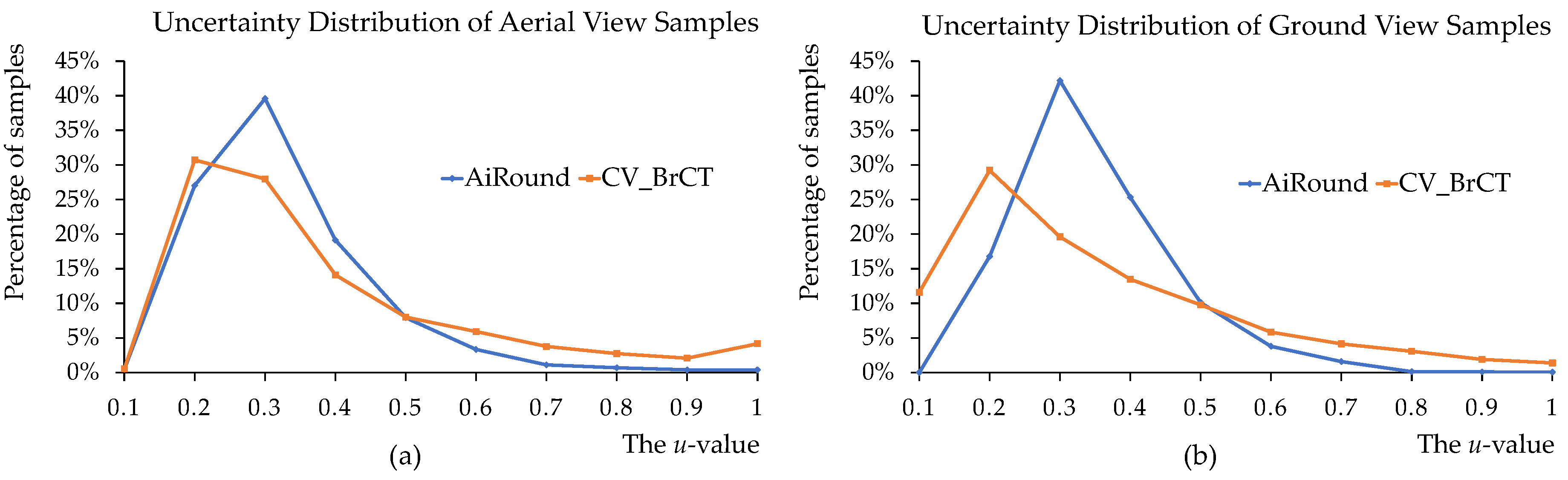
3.2.1. Validation for the Effectiveness of Uncertainty Estimation
3.2.2. Validation for the Effectiveness of the Reciprocal Loss
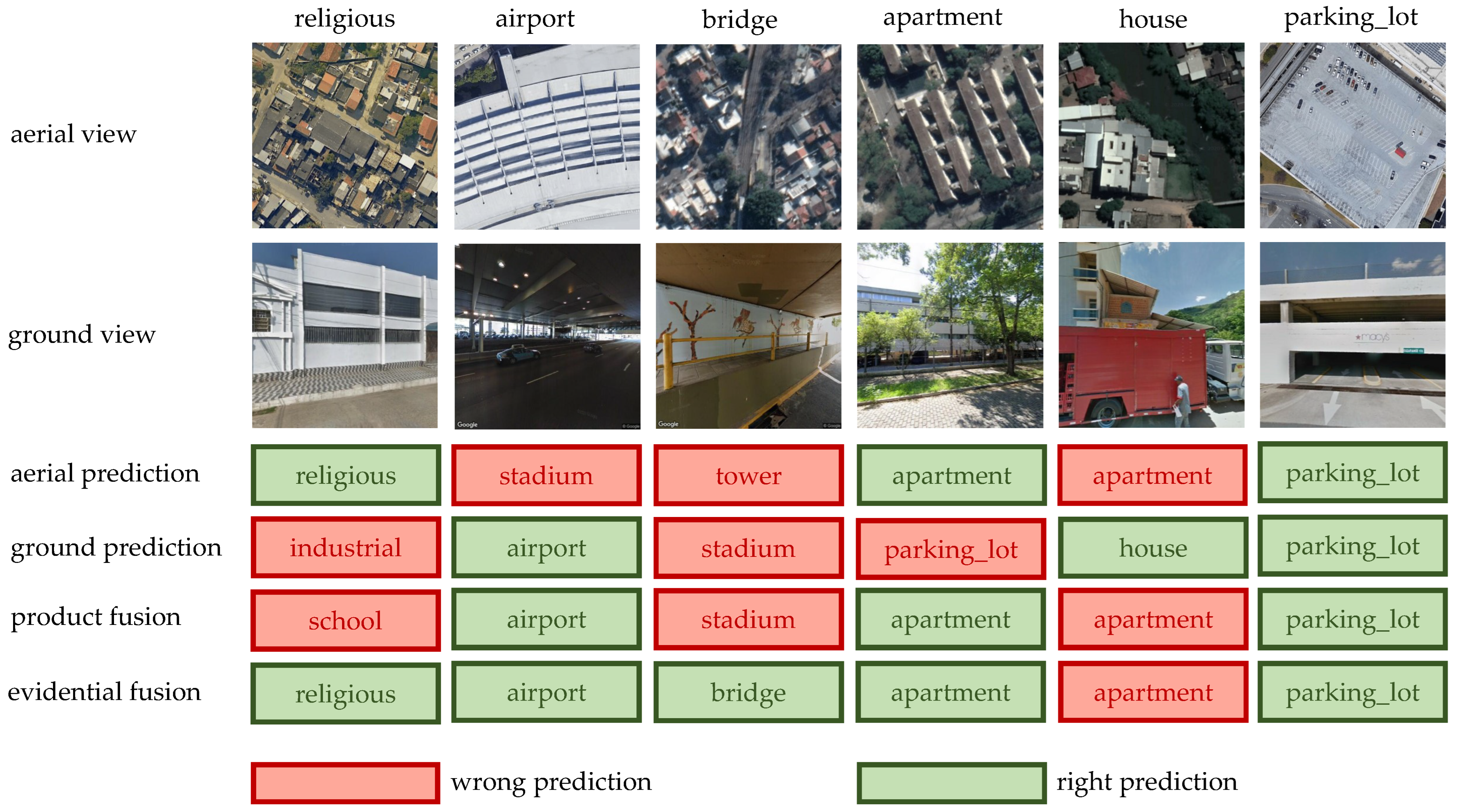
3.2.3. Validation for the Effectiveness of the Evidential Fusion Strategy
3.3. Comparison Experiment with Different Fusion Approaches at Data-Level, Feature-Level and Decision-Level
- Six-channel [42]: This method concatenates the RGB channels of the paired aerial view and ground view images into a six-channel image as the input of a CNN.
- Feature concatenation [31]: A Siamese-like CNN is used to concatenate the intermediate feature tensors before the first convolution layer that doubles its amount of kernels.
- CILM [43]: The loss function of contrast learning is combined with CE Loss in this method, allowing the features extracted by the two subnetworks to be fused without sharing any weight.
- Maximum [31]: Each view employs an independent DNN to obtain its prediction result, which consists of a class label and its probability. The final prediction is the class label corresponding to the maximum of the class probabilities predicted by each view.
- Minimum [31]: Each view employs an independent DNN to obtain its prediction result, which consists of a class label and its probability. The final prediction is the class label corresponding to the minimum of the class probabilities predicted by each view.
- Sum [31]: Each view employs an independent DNN to generate a vector containing probabilities for each class. The fused vector is the sum of single view vectors. The final prediction result is the class label corresponding to the largest element in the fused vector.
- Product [31]: Each view employs an independent DNN to generate a vector containing probabilities for each class. An elementwise multiplication is performed between single view vectors to obtain the fused vector. The final prediction result is the class label corresponding to the largest element in the fused vector.
- SFWS (Softmax Feature Weighted Strategy) [44]: Each view employs an independent DNN to obtain a vector containing probabilities for each class. Then, the matrix nuclear norm of the vector is computed as the weight of the fusion. The final prediction result is the class label corresponding to the largest element in the fused vector.
4. Discussion
4.1. Discussion on Uncertainty Estimation
4.2. Discussion on Loss Functions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Cheng, G.; Xie, X.; Han, J.; Guo, L.; Xia, G.S. Remote Sensing Image Scene Classification Meets Deep Learning: Challenges, Methods, Benchmarks, and Opportunities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3735–3756. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, P.; Liu, N.; Yin, Q.; Zhang, F. Graph-Embedding Balanced Transfer Subspace Learning for Hyperspectral Cross-Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2944–2955. [Google Scholar] [CrossRef]
- Chen, L.; Cui, X.; Li, Z.; Yuan, Z.; Xing, J.; Xing, X.; Jia, Z. A New Deep Learning Algorithm for SAR Scene Classification Based on Spatial Statistical Modeling and Features Re-Calibration. Sensors 2019, 19, 2479. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, S.; Chanussot, J.; Li, X. Scene Classification With Recurrent Attention of VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1155–1167. [Google Scholar] [CrossRef]
- Li, B.; Guo, Y.; Yang, J.; Wang, L.; Wang, Y.; An, W. Gated Recurrent Multiattention Network for VHR Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Qiao, Z.; Yuan, X. Urban land-use analysis using proximate sensing imagery: A survey. Int. J. Geogr. Inf. Sci. 2021, 35, 2129–2148. [Google Scholar] [CrossRef]
- Baltrušaitis, T.; Ahuja, C.; Morency, L.P. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 423–443. [Google Scholar] [CrossRef]
- Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1204–1211. [Google Scholar] [CrossRef]
- Amolins, K.; Zhang, Y.; Dare, P. Wavelet based image fusion techniques—An introduction, review and comparison. ISPRS J. Photogramm. Remote Sens. 2007, 62, 249–263. [Google Scholar] [CrossRef]
- Lin, T.Y.; Belongie, S.; Hays, J. Cross-View Image Geolocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 891–898. [Google Scholar]
- Lin, T.Y.; Cui, Y.; Belongie, S.; Hays, J. Learning Deep Representations for Ground-to-Aerial Geolocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5007–5015. [Google Scholar]
- Zhang, X.; Du, S.; Wang, Q. Hierarchical semantic cognition for urban functional zones with VHR satellite images and POI data. ISPRS J. Photogramm. Remote Sens. 2017, 132, 170–184. [Google Scholar] [CrossRef]
- Workman, S.; Zhai, M.; Crandall, D.J.; Jacobs, N. A Unified Model for Near and Remote Sensing. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2688–2697. [Google Scholar]
- Zhang, W.; Li, W.; Zhang, C.; Hanink, D.M.; Li, X.; Wang, W. Parcel-based urban land use classification in megacity using airborne LiDAR, high resolution orthoimagery, and Google Street View. Comput. Environ. Urban Syst. 2017, 64, 215–228. [Google Scholar] [CrossRef]
- Deng, Z.; Sun, H.; Zhou, S. Semi-Supervised Ground-to-Aerial Adaptation with Heterogeneous Features Learning for Scene Classification. ISPRS Int. J. Geo-Inf. 2018, 7, 182. [Google Scholar] [CrossRef]
- Cao, R.; Zhu, J.; Tu, W.; Li, Q.; Cao, J.; Liu, B.; Zhang, Q.; Qiu, G. Integrating Aerial and Street View Images for Urban Land Use Classification. Remote Sens. 2018, 10, 1553. [Google Scholar] [CrossRef]
- Hoffmann, E.J.; Wang, Y.; Werner, M.; Kang, J.; Zhu, X.X. Model Fusion for Building Type Classification from Aerial and Street View Images. Remote Sens. 2019, 11, 1259. [Google Scholar] [CrossRef]
- Srivastava, S.; Vargas-Muñoz, J.E.; Tuia, D. Understanding urban landuse from the above and ground perspectives: A deep learning, multimodal solution. Remote Sens. Environ. 2019, 228, 129–143. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. CoSpace: Common Subspace Learning From Hyperspectral-Multispectral Correspondences. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4349–4359. [Google Scholar] [CrossRef]
- Wang, X.; Feng, Y.; Song, R.; Mu, Z.; Song, C. Multi-attentive hierarchical dense fusion net for fusion classification of hyperspectral and LiDAR data. Inf. Fusion 2022, 82, 1–18. [Google Scholar] [CrossRef]
- Fan, R.; Li, J.; Song, W.; Han, W.; Yan, J.; Wang, L. Urban informal settlements classification via a transformer-based spatial-temporal fusion network using multimodal remote sensing and time-series human activity data. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102831. [Google Scholar] [CrossRef]
- Hu, T.; Yang, J.; Li, X.; Gong, P. Mapping Urban Land Use by Using Landsat Images and Open Social Data. Remote Sens. 2016, 8, 151. [Google Scholar] [CrossRef]
- Liu, X.; He, J.; Yao, Y.; Zhang, J.; Liang, H.; Wang, H.; Hong, Y. Classifying urban land use by integrating remote sensing and social media data. Int. J. Geogr. Inf. Sci. 2017, 31, 1675–1696. [Google Scholar] [CrossRef]
- Jia, Y.; Ge, Y.; Ling, F.; Guo, X.; Wang, J.; Wang, L.; Chen, Y.; Li, X. Urban Land Use Mapping by Combining Remote Sensing Imagery and Mobile Phone Positioning Data. Remote Sens. 2018, 10, 446. [Google Scholar] [CrossRef]
- Tu, W.; Hu, Z.; Li, L.; Cao, J.; Jiang, J.; Li, Q.; Li, Q. Portraying Urban Functional Zones by Coupling Remote Sensing Imagery and Human Sensing Data. Remote Sens. 2018, 10, 141. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L. Scene Classification via a Gradient Boosting Random Convolutional Network Framework. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1793–1802. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, F. Aerial Scene Classification via Multilevel Fusion Based on Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 287–291. [Google Scholar] [CrossRef]
- Yang, N.; Tang, H.; Sun, H.; Yang, X. DropBand: A Simple and Effective Method for Promoting the Scene Classification Accuracy of Convolutional Neural Networks for VHR Remote Sensing Imagery. IEEE Geosci. Remote Sens. Lett. 2018, 15, 257–261. [Google Scholar] [CrossRef]
- Vargas-Munoz, J.E.; Srivastava, S.; Tuia, D.; Falcão, A.X. OpenStreetMap: Challenges and Opportunities in Machine Learning and Remote Sensing. IEEE Geosci. Remote Sens. Mag. 2021, 9, 184–199. [Google Scholar] [CrossRef]
- Machado, G.; Ferreira, E.; Nogueira, K.; Oliveira, H.; Brito, M.; Gama, P.H.T.; Santos, J.A.d. AiRound and CV-BrCT: Novel Multiview Datasets for Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 488–503. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, C.; Fu, H.; Zhou, J.T. Trusted Multi-View Classification. In Proceedings of the International Conference on Learning Representations (ICLR), Online, 3–7 May 2021. [Google Scholar]
- Sensoy, M.; Kaplan, L.; Kandemir, M. Evidential Deep Learning to Quantify Classification Uncertainty. In Proceedings of the International Conference on Neural Information Processing Systems (NeurIPS), Montréal, QC, Canada, 3–8 December 2018; pp. 3183–3193. [Google Scholar]
- Moon, J.; Kim, J.; Shin, Y.; Hwang, S. Confidence-Aware Learning for Deep Neural Networks. In Proceedings of the PMLR International Conference on Machine Learning (ICML), Online, 13–18 July 2020; Volume 119, pp. 7034–7044. [Google Scholar]
- Van Amersfoort, J.; Smith, L.; Teh, Y.W.; Gal, Y. Uncertainty Estimation Using a Single Deep Deterministic Neural Network. In Proceedings of the PMLR International Conference on Machine Learning (ICML), Online, 13–18 July 2020; Volume 119, pp. 9690–9700. [Google Scholar]
- Yager, R.R.; Liu, L. Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Jøsang, A. Subjective Logic: A Formalism for Reasoning under Uncertainty; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Lin, J. On The Dirichlet Distribution. Master’s Thesis, Queen’s University, Kingston, ON, Canada, 2016; pp. 10–11. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vo, N.N.; Hays, J. Localizing and Orienting Street Views Using Overhead Imagery. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 494–509. [Google Scholar]
- Geng, W.; Zhou, W.; Jin, S. Multi-View Urban Scene Classification with a Complementary-Information Learning Model. Photogramm. Eng. Remote Sens. 2022, 88, 65–72. [Google Scholar] [CrossRef]
- Zhou, M.; Xu, X.; Zhang, Y. An Attention-based Multi-Scale Feature Learning Network for Multimodal Medical Image Fusion. arXiv 2022, arXiv:2212.04661. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the EEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Ju, Y.; Jian, M.; Guo, S.; Wang, Y.; Zhou, H.; Dong, J. Incorporating lambertian priors into surface normals measurement. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Ju, Y.; Shi, B.; Jian, M.; Qi, L.; Dong, J.; Lam, K.M. NormAttention-PSN: A High-frequency Region Enhanced Photometric Stereo Network with Normalized Attention. Int. J. Comput. Vis. 2022, 130, 3014–3034. [Google Scholar] [CrossRef]
- Liang, W.; Tadesse, G.A.; Ho, D.; Fei-Fei, L.; Zaharia, M.; Zhang, C.; Zou, J. Advances, challenges and opportunities in creating data for trustworthy AI. Nat. Mach. Intell. 2022, 4, 669–677. [Google Scholar] [CrossRef]

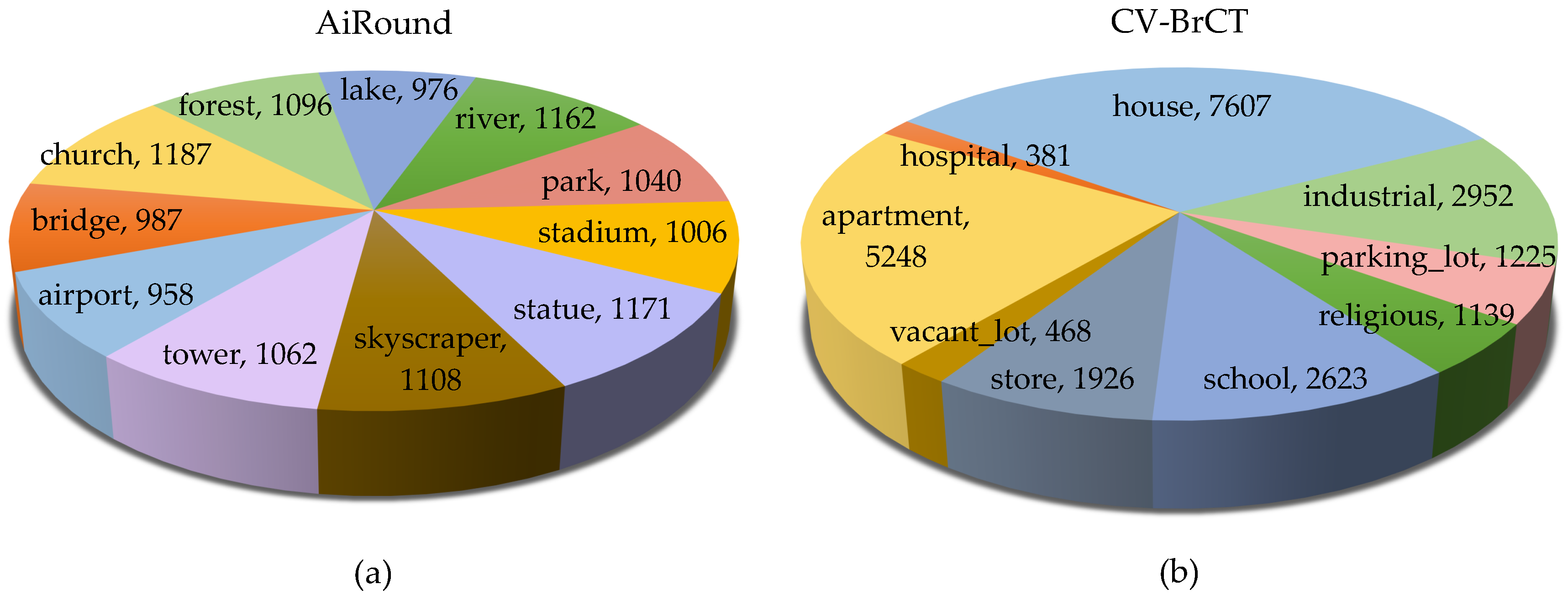



| Views * | A-AiRound | G-AiRound | A-CV-BrCT | G-CV-BrCT |
|---|---|---|---|---|
| 0.065 | 0.078 | 0.183 | 0.090 |
| Loss Functions | AiRound | CV-BrCT | ||
|---|---|---|---|---|
| Acc | F1 | Acc | F1 | |
| EDL-CE Loss [33] | 90.23 ± 0.32 | 90.64 ± 0.29 | 86.98 ± 0.17 | 81.56 ± 0.34 |
| EDL-MSE Loss [33] | 90.44 ± 0.03 | 91.02 ± 0.02 | 86.24 ± 0.02 | 80.89 ± 0.01 |
| Reciprocal Loss | 92.16 ± 0.31 | 92.49 ± 0.25 | 88.21 ± 0.26 | 83.57 ± 0.29 |
| Views | AlexNet [40] | VGG-11 [39] | ResNet-18 [41] | |
|---|---|---|---|---|
| Single Views | Aerial-s | 76.96 | 82.75 | 80.93 |
| (softmax) | Ground-s | 71.35 | 77.10 | 76.68 |
| Single Views | Aerial-e | 76.04 | 82.64 | 80.83 |
| (evidential) | Ground-e | 70.96 | 76.99 | 76.36 |
| Decision- | Sum [31] | 84.02 | 87.75 | 88.02 |
| Level Fusion | Product [31] | 86.74 | 90.41 | 89.56 |
| Strategies | Proposed | 88.12 ± 0.23 | 92.16 ± 0.31 | 91.02 ± 0.35 |
| Views | AlexNet [40] | VGG-11 [39] | ResNet-18 [41] | |
|---|---|---|---|---|
| Single Views | Aerial-s | 84.63 | 87.11 | 86.74 |
| (softmax) | Ground-s | 68.01 | 71.43 | 70.96 |
| Single Views | Aerial-e | 84.37 | 87.06 | 86.18 |
| (evidential) | Ground-e | 66.36 | 70.15 | 70.86 |
| Decision- | Sum [31] | 85.26 | 86.70 | 85.59 |
| Level Fusion | Product [31] | 86.52 | 87.21 | 86.83 |
| Strategies | Proposed | 88.02 ± 0.28 | 88.21 ± 0.26 | 87.95 ± 0.19 |
| Methods | AlexNet [40] | VGG-11 [39] | Inception [45] | ResNet-18 [41] | DenseNet [46] |
|---|---|---|---|---|---|
| Six-Ch. [42] | 70.19 | 72.34 | 71.76 | 71.29 | 71.57 |
| Concat. [31] | 82.52 | 84.69 | 83.91 | 83.56 | 83.72 |
| CILM [43] | 83.49 | 85.72 | 85.05 | 84.72 | 84.91 |
| Max. [31] | 84.86 | 88.17 | 88.39 | 88.21 | 89.96 |
| Min. [31] | 85.52 | 89.56 | 89.12 | 88.42 | 90.41 |
| Sum [31] | 84.02 | 87.75 | 88.05 | 88.02 | 89.88 |
| Product [31] | 86.74 | 90.41 | 90.02 | 89.56 | 91.16 |
| SFWS [44] | 85.94 | 89.61 | 89.18 | 88.95 | 90.05 |
| Proposed | 88.12 ± 0.23 | 92.16 ± 0.31 | 91.41 ± 0.18 | 91.02 ± 0.35 | 92.16 ± 0.19 |
| Methods | AlexNet [40] | VGG-11 [39] | Inception [45] | ResNet-18 [41] | DenseNet [46] |
|---|---|---|---|---|---|
| Six-Ch. [42] | 71.92 | 73.46 | 75.26 | 73.25 | 74.19 |
| Concat. [31] | 81.86 | 83.25 | 84.65 | 83.28 | 84.24 |
| CILM [43] | 83.10 | 84.32 | 85.22 | 84.31 | 85.19 |
| Max. [31] | 85.52 | 86.74 | 86.70 | 85.84 | 86.95 |
| Min. [31] | 86.02 | 86.95 | 86.95 | 86.24 | 87.02 |
| Sum [31] | 85.26 | 86.70 | 86.24 | 85.59 | 86.85 |
| Product [31] | 86.52 | 87.21 | 87.02 | 86.83 | 87.54 |
| SFWS [44] | 86.21 | 86.95 | 86.73 | 86.52 | 87.21 |
| Proposed | 88.02 ± 0.28 | 88.21 ± 0.26 | 88.21 ± 0.23 | 87.95 ± 0.19 | 88.34 ± 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Gao, Q.; Hao, S.; Sun, J.; Zhou, L. Credible Remote Sensing Scene Classification Using Evidential Fusion on Aerial-Ground Dual-View Images. Remote Sens. 2023, 15, 1546. https://doi.org/10.3390/rs15061546
Zhao K, Gao Q, Hao S, Sun J, Zhou L. Credible Remote Sensing Scene Classification Using Evidential Fusion on Aerial-Ground Dual-View Images. Remote Sensing. 2023; 15(6):1546. https://doi.org/10.3390/rs15061546
Chicago/Turabian StyleZhao, Kun, Qian Gao, Siyuan Hao, Jie Sun, and Lijian Zhou. 2023. "Credible Remote Sensing Scene Classification Using Evidential Fusion on Aerial-Ground Dual-View Images" Remote Sensing 15, no. 6: 1546. https://doi.org/10.3390/rs15061546
APA StyleZhao, K., Gao, Q., Hao, S., Sun, J., & Zhou, L. (2023). Credible Remote Sensing Scene Classification Using Evidential Fusion on Aerial-Ground Dual-View Images. Remote Sensing, 15(6), 1546. https://doi.org/10.3390/rs15061546






