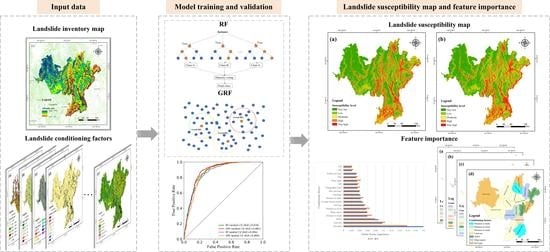
Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China
Abstract
1. Introduction
2. Study Area and Materials
2.1. Study Area
2.2. Preparation of Sample Dataset
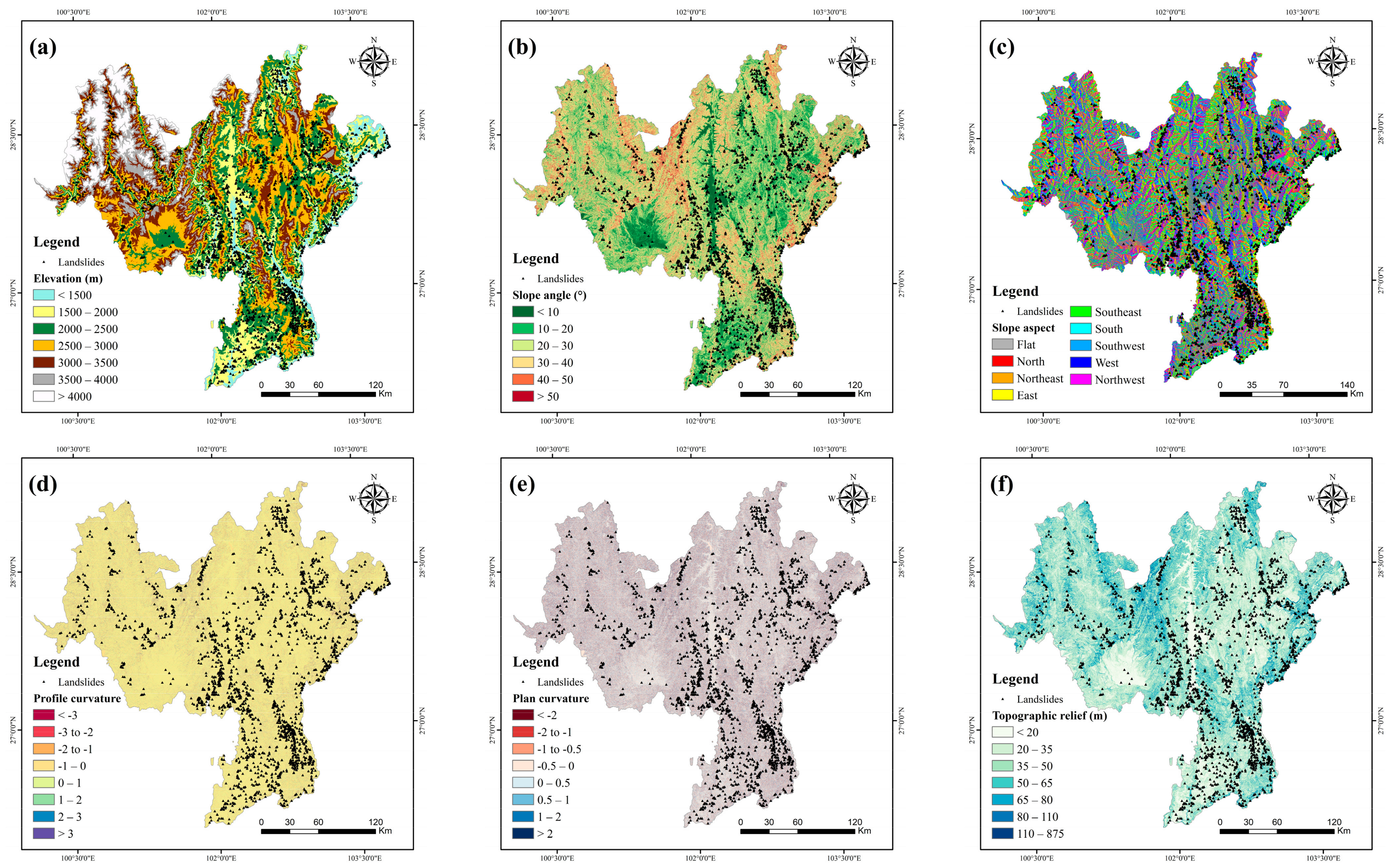
2.3. Landslide Conditioning Factors
2.3.1. Topography Factors
2.3.2. Geology Factors
2.3.3. Ecology Factors
2.3.4. Hydrology and Meteorology Factors
2.3.5. Human Activity Factors
3. Methodology
3.1. Feature Screening Method
3.2. Machine Learning Models
3.2.1. Random Forest
3.2.2. Geographical Random Forest
3.3. Model Evaluation Metrics and Validation Methods
4. Results
4.1. Multicollinearity Diagnosis
4.2. Model Performance Evaluation
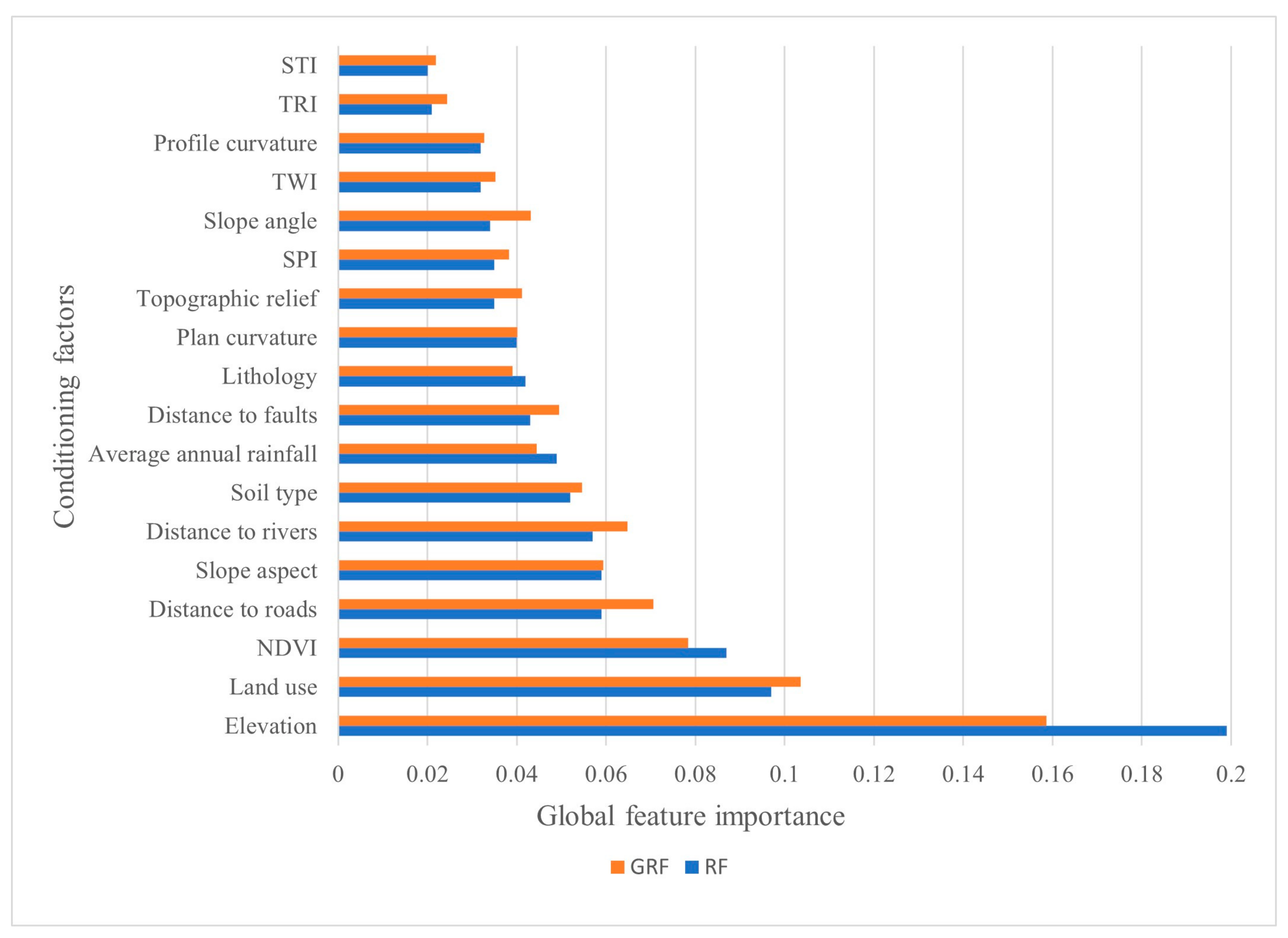
4.3. Global Feature Importance Comparison
4.4. Landslide Susceptibility Maps
5. Discussion
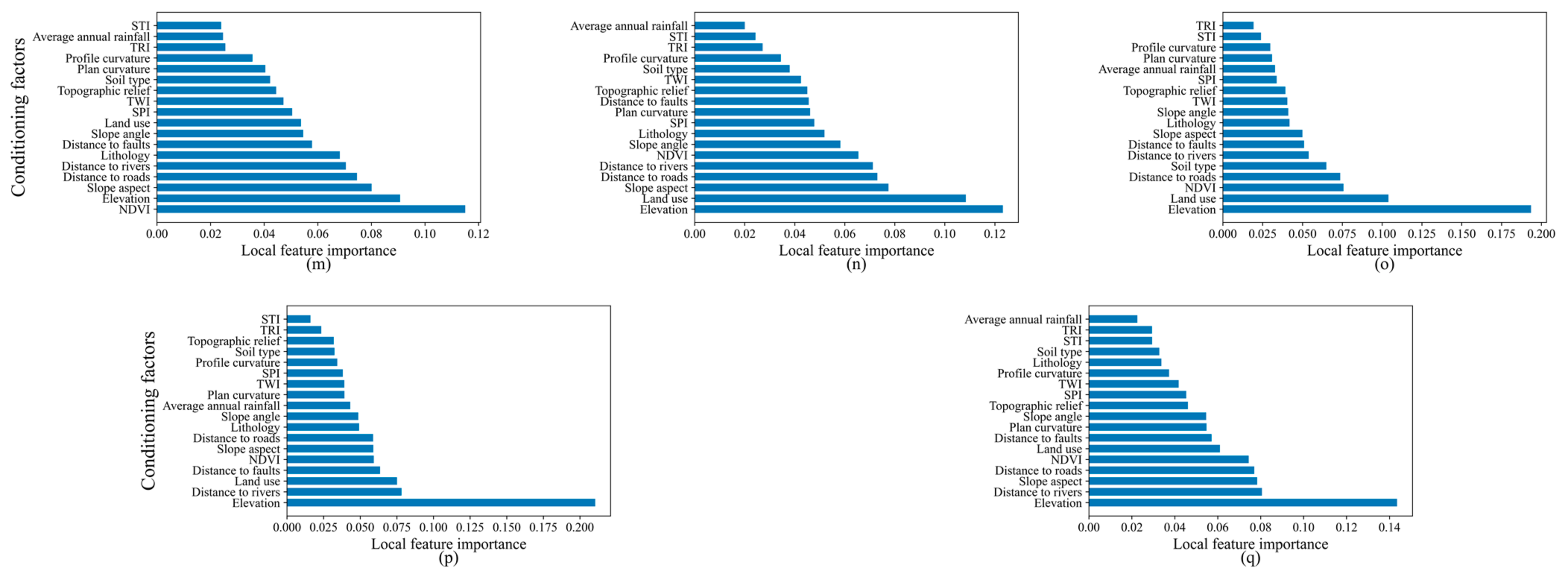
5.1. Local Feature Importance
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rotaru, A.; Oajdea, D.; Răileanu, P. Analysis of the Landslide Movements. Int. J. Geol. 2007, 1, 70–79. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide Risk Assessment and Management: An Overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Niu, C.; Zhang, H.; Liu, W.; Li, R.; Hu, T. Using a Fully Polarimetric SAR to Detect Landslide in Complex Surroundings: Case Study of 2015 Shenzhen Landslide. ISPRS J. Photogramm. Remote Sens. 2021, 174, 56–67. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A Comparative Study of Heterogeneous Ensemble-Learning Techniques for Landslide Susceptibility Mapping. Int. J. Geogr. Inf. Sci. 2021, 35, 321–347. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance Evaluation of the GIS-Based Data Mining Techniques of Best-First Decision Tree, Random Forest, and Naïve Bayes Tree for Landslide Susceptibility Modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of Deep Learning Algorithms for National Scale Landslide Susceptibility Mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Kjekstad, O.; Highland, L. Economic and Social Impacts of Landslides. In Landslides—Disaster Risk Reduction; Sassa, K., Canuti, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 573–587. ISBN 978-3-540-69970-5. [Google Scholar]
- Yong, C.; Jinlong, D.; Fei, G.; Bin, T.; Tao, Z.; Hao, F.; Li, W.; Qinghua, Z. Review of Landslide Susceptibility Assessment Based on Knowledge Mapping. Stoch. Environ. Res. Risk Assess. 2022, 36, 2399–2417. [Google Scholar] [CrossRef]
- Lima, P.; Steger, S.; Glade, T.; Murillo-García, F.G. Literature Review and Bibliometric Analysis on Data-Driven Assessment of Landslide Susceptibility. J. Mt. Sci. 2022, 19, 1670–1698. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-Based Landslide Susceptibility Models Using Frequency Ratio, Logistic Regression, and Artificial Neural Network in a Tertiary Region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Riaz, M.T.; Basharat, M.; Brunetti, M.T. Assessing the Effectiveness of Alternative Landslide Partitioning in Machine Learning Methods for Landslide Prediction in the Complex Himalayan Terrain. Prog. Phys. Geogr. Earth Environ. 2022, 03091333221113660. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling Susceptibility to Landslides Using the Weight of Evidence Approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Quevedo, R.P.; Maciel, D.A.; Uehara, T.D.T.; Vojtek, M.; Rennó, C.D.; Pradhan, B.; Vojteková, J.; Pham, Q.B. Consideration of Spatial Heterogeneity in Landslide Susceptibility Mapping Using Geographical Random Forest Model. Geocarto Int. 2021, 37, 1–24. [Google Scholar] [CrossRef]
- Zeng, H.; Zhu, Q.; Ding, Y.; Hu, H.; Chen, L.; Xie, X.; Chen, M.; Yao, Y. Graph Neural Networks with Constraints of Environmental Consistency for Landslide Susceptibility Evaluation. Int. J. Geogr. Inf. Sci. 2022, 36, 1–26. [Google Scholar] [CrossRef]
- Stamatopoulos, C.A.; Di, B. Analytical and Approximate Expressions Predicting Post-Failure Landslide Displacement Using the Multi-Block Model and Energy Methods. Landslides 2015, 12, 1207–1213. [Google Scholar] [CrossRef]
- Chen, T.; Niu, R.; Jia, X. A Comparison of Information Value and Logistic Regression Models in Landslide Susceptibility Mapping by Using GIS. Environ. Earth Sci. 2016, 75, 867. [Google Scholar] [CrossRef]
- Vakhshoori, V.; Zare, M. Landslide Susceptibility Mapping by Comparing Weight of Evidence, Fuzzy Logic, and Frequency Ratio Methods. Geomat. Nat. Hazards Risk 2016, 7, 1731–1752. [Google Scholar] [CrossRef]
- Li, L.; Lan, H.; Guo, C.; Zhang, Y.; Li, Q.; Wu, Y. A Modified Frequency Ratio Method for Landslide Susceptibility Assessment. Landslides 2017, 14, 727–741. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating Machine Learning and Statistical Prediction Techniques for Landslide Susceptibility Modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the Landslide Susceptibility: Which Algorithm, Which Precision? CATENA 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Riaz, M.T.; Basharat, M.; Pham, Q.B.; Sarfraz, Y.; Shahzad, A.; Ahmed, K.S.; Ikram, N.; Waseem, M.H. Improvement of the Predictive Performance of Landslide Mapping Models in Mountainous Terrains Using Cluster Sampling. Geocarto Int. 2022, 37, 12294–12337. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of Heuristic, General Statistical and Machine Learning Models for Landslide Susceptibility Prediction and Mapping. CATENA 2020, 191, 104580. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of Advanced Random Forest and Decision Tree Algorithms for Modeling Rainfall-Induced Landslide Susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Shi, S.; Wen, H.; Xu, J.; Zhou, X.; Wu, J. A Hybrid Optimization Method of Factor Screening Predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 2021, 379, 107623. [Google Scholar] [CrossRef]
- Cheng, J.; Dai, X.; Wang, Z.; Li, J.; Qu, G.; Li, W.; She, J.; Wang, Y. Landslide Susceptibility Assessment Model Construction Using Typical Machine Learning for the Three Gorges Reservoir Area in China. Remote Sens. 2022, 14, 2257. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y.; et al. Landslide Spatial Modelling Using Novel Bivariate Statistical Based Naïve Bayes, RBF Classifier, and RBF Network Machine Learning Algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial Prediction Models for Shallow Landslide Hazards: A Comparative Assessment of the Efficacy of Support Vector Machines, Artificial Neural Networks, Kernel Logistic Regression, and Logistic Model Tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Predictive Performances of Ensemble Machine Learning Algorithms in Landslide Susceptibility Mapping Using Random Forest, Extreme Gradient Boosting (XGBoost) and Natural Gradient Boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
- Yang, W.; Deng, M.; Tang, J.; Luo, L. Geographically Weighted Regression with the Integration of Machine Learning for Spatial Prediction. J. Geogr. Syst. 2022, 1–24. [Google Scholar] [CrossRef]
- Gu, T.; Li, J.; Wang, M.; Duan, P. Landslide Susceptibility Assessment in Zhenxiong County of China Based on Geographically Weighted Logistic Regression Model. Geocarto Int. 2022, 37, 4952–4973. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Xu, C.; Xu, C.; Song, C. Local-Scale Landslide Susceptibility Mapping Using the B-GeoSVC Model. Landslides 2019, 16, 1301–1312. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical Random Forests: A Spatial Extension of the Random Forest Algorithm to Address Spatial Heterogeneity in Remote Sensing and Population Modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Grekousis, G.; Feng, Z.; Marakakis, I.; Lu, Y.; Wang, R. Ranking the Importance of Demographic, Socioeconomic, and Underlying Health Factors on US COVID-19 Deaths: A Geographical Random Forest Approach. Health Place 2022, 74, 102744. [Google Scholar] [CrossRef] [PubMed]
- Quiñones, S.; Goyal, A.; Ahmed, Z.U. Geographically Weighted Machine Learning Model for Untangling Spatial Heterogeneity of Type 2 Diabetes Mellitus (T2D) Prevalence in the USA. Sci. Rep. 2021, 11, 6955. [Google Scholar] [CrossRef]
- Aguirre-Gutiérrez, J.; Rifai, S.; Shenkin, A.; Oliveras, I.; Bentley, L.P.; Svátek, M.; Girardin, C.A.J.; Both, S.; Riutta, T.; Berenguer, E.; et al. Pantropical Modelling of Canopy Functional Traits Using Sentinel-2 Remote Sensing Data. Remote Sens. Environ. 2021, 252, 112122. [Google Scholar] [CrossRef]
- Santos, F.; Graw, V.; Bonilla, S. A Geographically Weighted Random Forest Approach for Evaluate Forest Change Drivers in the Northern Ecuadorian Amazon. PLoS ONE 2019, 14, e0226224. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-Validation Strategies for Data with Temporal, Spatial, Hierarchical, or Phylogenetic Structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
- Xiang, X.; Xiao, D. Socioeconomic Development Evaluation for Chinese Poverty-Stricken Counties Using Indices Derived from Remotely Sensed Data. Eur. J. Remote Sens. 2021, 54, 226–239. [Google Scholar] [CrossRef]
- Liu, B.; Cao, W.; Liu, S.; Tao, H.; Shi, Z.; Guo, S. Land Resources Assessment Model for Mountainous Areas Based on GIS: A Case Study of Liangshan Yizu Autonomous Prefecture, Sichuan Province. Acta Geogr. Sin. 2011, 66, 1131. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zhang, J.; Liu, H.; Huang, H.; Zhang, T.; Huang, Y. Classification of Soil Parent Materials in Mountain Areas of Southwest China Based on Geological Formations: A Case Study of Daliangshan Region. Geol. Surv. China 2021, 8, 50–62. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Wei, F.Q.; Zhang, J.H.; Deng, B.; Xu, A.S. Debris Flow and Landslide Forecast Based on Gis and Doppler Weather Radar in Liangshan Prefecture. Ital. J. Eng. Geol. Environ. 2011, 903–911. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Li, S.; Ren, F.; Du, Q. A Hybrid Model Considering Spatial Heterogeneity for Landslide Susceptibility Mapping in Zhejiang Province, China. CATENA 2020, 188, 104425. [Google Scholar] [CrossRef]
- Wei, A.; Yu, K.; Dai, F.; Gu, F.; Zhang, W.; Liu, Y. Application of Tree-Based Ensemble Models to Landslide Susceptibility Mapping: A Comparative Study. Sustainability 2022, 14, 6330. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, J.; Mu, J.; Zheng, J.; Zhan, J.; Wang, J.; Fu, Y. Evaluation of Landslide Susceptibility of the Ya’an–Linzhi Section of the Sichuan–Tibet Railway Based on Deep Learning. Environ. Earth Sci. 2022, 81, 250. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide Susceptibility Mapping Using Hybrid Random Forest with GeoDetector and RFE for Factor Optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Yao, K.; Yang, S.; Wu, S.; Tong, B. Landslide Susceptibility Assessment Considering Spatial Agglomeration and Dispersion Characteristics: A Case Study of Bijie City in Guizhou Province, China. ISPRS Int. J. Geo-Inf. 2022, 11, 269. [Google Scholar] [CrossRef]
- Yuan, R.; Chen, J. A Hybrid Deep Learning Method for Landslide Susceptibility Analysis with the Application of InSAR Data. Nat. Hazards 2022, 2, 1393–1426. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Xu, J.; Zhang, Y.; Wang, D.; Zhang, J. Improving Geospatial Agreement by Hybrid Optimization in Logistic Regression-Based Landslide Susceptibility Modelling. Front. Earth Sci. 2021, 9, 686. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, W.; Xu, X.; Zhang, Z.; Wu, X. Evaluation of Neural Network Models for Landslide Susceptibility Assessment. Int. J. Digit. Earth 2022, 15, 934–953. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. GIS-Based Landslide Susceptibility Assessment Using Optimized Hybrid Machine Learning Methods. CATENA 2021, 196, 104833. [Google Scholar] [CrossRef]
- Erener, A.; Düzgün, H.S.B. Landslide Susceptibility Assessment: What Are the Effects of Mapping Unit and Mapping Method? Environ. Earth Sci. 2012, 66, 859–877. [Google Scholar] [CrossRef]
- Wang, F.; Xu, P.; Wang, C.; Wang, N.; Jiang, N. Application of a GIS-Based Slope Unit Method for Landslide Susceptibility Mapping along the Longzi River, Southeastern Tibetan Plateau, China. ISPRS Int. J. Geo-Inf. 2017, 6, 172. [Google Scholar] [CrossRef]
- Xie, J.; Uchimura, T.; Chen, P.; Liu, J.; Xie, C.; Shen, Q. A Relationship between Displacement and Tilting Angle of the Slope Surface in Shallow Landslides. Landslides 2019, 16, 1243–1251. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide Susceptibility Assessment in Lianhua County (China): A Comparison between a Random Forest Data Mining Technique and Bivariate and Multivariate Statistical Models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of Convolutional Neural Networks for Landslide Susceptibility Mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of Alternating Decision Tree with AdaBoost and Bagging Ensembles for Landslide Susceptibility Mapping. CATENA 2020, 187, 104396. [Google Scholar] [CrossRef]
- Yuanbo, L.I.U.; Ruiqing, N.I.U.; Xianyu, Y.U.; Kaixiang, Z. Application of the Rotation Forest Model in Landslide Susceptibility Assessment. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 959–964. [Google Scholar] [CrossRef]
- Liao, M.; Wen, H.; Yang, L. Identifying the Essential Conditioning Factors of Landslide Susceptibility Models under Different Grid Resolutions Using Hybrid Machine Learning: A Case of Wushan and Wuxi Counties, China. CATENA 2022, 217, 106428. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, A.; Huang, Z.; Sun, L.; Han, X. Discussion on the Tree-Based Machine Learning Model in the Study of Landslide Susceptibility. Nat. Hazards 2022, 113, 887–911. [Google Scholar] [CrossRef]
- Hamedi, H.; Alesheikh, A.A.; Panahi, M.; Lee, S. Landslide Susceptibility Mapping Using Deep Learning Models in Ardabil Province, Iran. Stoch. Environ. Res. Risk Assess. 2022, 12, 4287–4310. [Google Scholar] [CrossRef]
- Saleem, N.; Huq, M.E.; Twumasi, N.Y.D.; Javed, A.; Sajjad, A. Parameters Derived from and/or Used with Digital Elevation Models (DEMs) for Landslide Susceptibility Mapping and Landslide Risk Assessment: A Review. ISPRS Int. J. Geo-Inf. 2019, 8, 545. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, R.; Jiang, Y.; Liu, H.; Wei, Z. GIS-Based Logistic Regression for Rainfall-Induced Landslide Susceptibility Mapping under Different Grid Sizes in Yueqing, Southeastern China. Eng. Geol. 2019, 259, 105147. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, Y.; Wang, S.; Wang, F. Machine Learning and Fractal Theory Models for Landslide Susceptibility Mapping: Case Study from the Jinsha River Basin. Geomorphology 2020, 351, 106975. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kornejady, A.; Kerle, N.; Shabani, F. Investigating the Effects of Different Landslide Positioning Techniques, Landslide Partitioning Approaches, and Presence-Absence Balances on Landslide Susceptibility Mapping. CATENA 2020, 187, 104364. [Google Scholar] [CrossRef]
- Saha, A.; Pal, S.C.; Santosh, M.; Janizadeh, S.; Chowdhuri, I.; Norouzi, A.; Roy, P.; Chakrabortty, R. Modelling Multi-Hazard Threats to Cultural Heritage Sites and Environmental Sustainability: The Present and Future Scenarios. J. Clean. Prod. 2021, 320, 128713. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Merghadi, A.; Shirzadi, A.; Nguyen, H.; Hussain, Y.; Avtar, R.; Chen, Y.; Pham, B.T.; Yamagishi, H. Different Sampling Strategies for Predicting Landslide Susceptibilities Are Deemed Less Consequential with Deep Learning. Sci. Total Environ. 2020, 720, 137320. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Stewart, K.; Fan, J. Incorporating Space and Time into Random Forest Models for Analyzing Geospatial Patterns of Drug-Related Crime Incidents in a Major, U.S. Metropolitan Area. Comput. Environ. Urban Syst. 2021, 87, 101599. [Google Scholar] [CrossRef]
- Kohestani, V.R.; Hassanlourad, M.; Ardakani, A. Evaluation of Liquefaction Potential Based on CPT Data Using Random Forest. Nat. Hazards 2015, 79, 1079–1089. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: New York, NY, USA, 2003; ISBN 978-0-470-85525-6. [Google Scholar]
- Bradley, A.P. The Use of the Area under the ROC Curve in the Evaluation of Machine Learning Algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Lombardo, L.; Opitz, T.; Ardizzone, F.; Guzzetti, F.; Huser, R. Space-Time Landslide Predictive Modelling. Earth-Sci. Rev. 2020, 209, 103318. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Rotation Forest Fuzzy Rule-Based Classifier Ensemble for Spatial Prediction of Landslides Using GIS. Nat. Hazards 2016, 83, 97–127. [Google Scholar] [CrossRef]
- Lin, Q.; Lima, P.; Steger, S.; Glade, T.; Jiang, T.; Zhang, J.; Liu, T.; Wang, Y. National-Scale Data-Driven Rainfall Induced Landslide Susceptibility Mapping for China by Accounting for Incomplete Landslide Data. Geosci. Front. 2021, 12, 101248. [Google Scholar] [CrossRef]
- Lima, P.; Steger, S.; Glade, T. Counteracting Flawed Landslide Data in Statistically Based Landslide Susceptibility Modelling for Very Large Areas: A National-Scale Assessment for Austria. Landslides 2021, 18, 3531–3546. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Glade, T. The Influence of Systematically Incomplete Shallow Landslide Inventories on Statistical Susceptibility Models and Suggestions for Improvements. Landslides 2017, 14, 1767–1781. [Google Scholar] [CrossRef]







| Category | Subcategories | Applicable Scale |
|---|---|---|
| Knowledge-driven methods | - | Small (<1:250,000), Medium (1:250,000–1:25,000) |
| Data-driven methods | Deterministic methods | Large (1:25,000–1:5000), Detailed (<1:5000) |
| Traditional statistical methods | Medium (1:250,000–1:25,000), Large (1:25,000–1:5000), Detailed (<1:5000) | |
| Machine learning methods | Large (1:25,000–1:5000), Detailed (<1:5000) |
| Category | Conditioning Factor | Data Name | Data Source | Data Type | Precision |
|---|---|---|---|---|---|
| Topography factors | Elevation | DEM | Geospatial Data Cloud | Grid | 30 m |
| Slope angle | |||||
| Slope aspect | |||||
| Profile curvature | |||||
| Plan curvature | |||||
| Topographic relief | |||||
| Topographic roughness index | |||||
| Geology factors | Lithology | Geologic map | RESDC | Vector | 1:200,000 |
| Distance to faults | |||||
| Ecology factors | Soil type | Soil map | Grid | 30 m | |
| Normalized difference vegetation index | Landsat8 | United States Geological Survey | Grid | 30 m | |
| Hydrology and meteorology factors | Topographic wetness index | DEM | Geospatial Data Cloud | Grid | 30 m |
| Stream power index | |||||
| Sediment transport index | |||||
| Distance to rivers | River map | National Basic Geographical Database (NBGD) | Vector | 1:250,000 | |
| Average annual rainfall | Rainfall monitoring data | China Meteorological Data Network | Tabular | - | |
| Human activity factors | Distance to roads | Road map | NBGD | Vector | 1:250,000 |
| Land use | Land use map | RESDC | Grid | 30 m |
| Category | Factor | Classification Scheme |
|---|---|---|
| Topography factors | Elevation (m) | 1. <1500; 2. 1500–2000; 3. 2000–2500; 4. 2500–3000; 5. 3000–3500; 6. 3500–4000; 7. >4000 |
| Slope angle (°) | 1. <10; 2. 10–20; 3. 20–30; 4. 30–40; 5. 40–50; 6. >50 | |
| Slope aspect | 1. flat; 2. north; 3. northeast; 4. east; 5. southeast; 6. south; 7. southwest; 8. west; 9. northwest | |
| Profile curvature | 1. <−3; 2. −3 to −2; 3. −2 to −1; 4. −1 to 0; 5. 0 to 1; 6. 1 to 2; 7. 2 to 3; 8. >3 | |
| Plan curvature | 1. <−2; 2. −2 to −1; 3. −1 to −0.5; 4. −0.5 to 0; 5. 0 to 0.5; 6. 0.5 to 1; 7. 1 to 2; 8. >2 | |
| Topographic relief (m) | 1. <20; 2. 20–35; 3. 35–50; 4. 50–65; 5. 65–80; 6. 80–110; 7. >110 | |
| Topographic roughness index | 1. <1.05; 2. 1.05–1.25; 3. 1.25–1.5; 4. 1.5–2; 5. >2 | |
| Geology factors | Lithology | 1. extremely soft rock; 2. soft rock; 3. soft–hard combined rock; 4. hard rock; 5. extremely hard rock |
| Distance to faults (m) | 1. <500; 2. 500–1000; 3. 1000–1500; 4. 1500–2000; 5. 2000–2500; 6. 2500–3000; 7. >3000 | |
| Ecology factors | Soil type | 1. semi-leaching soil; 2. semi-hydraulic soil; 3. primary soil; 4. alpine soil; 5. lake and water; 6. leaching soil; 7. anthropogenic soil; 8. water-forming soil; 9. iron-bauxite; 10. rock |
| Normalized difference vegetation index | 1. <0; 2. 0–0.2; 3. 0.2–0.4; 4. 0.4–0.6; 5. 0.6–0.8; 6. >0.8 | |
| Hydrology and meteorology factors | Topographic wetness index | 1. <4; 2. 4–6; 3. 6–8; 4. 8–11; 5. 11–15; 6. 15–21; 7. >21 |
| Stream power index | 1. <15; 2. 15–30; 3. 30–45; 4. 45–60; 5. 60–100; 6. 100–1000; 7. >1000 | |
| Sediment transport index | 1. <20; 2. 20–40; 3. 40–70; 4. 70–100; 5.100–200; 6. >200 | |
| Distance to rivers (m) | 1. <200; 2. 200–400; 3. 400–600; 4. 600–800; 5. 800–1000; 6. 1000–1200; 7. >1200 | |
| Average annual rainfall (mm) | 1. <785; 2. 785–843; 3. 843–892; 4. 892–928; 5. 928–971; 6. 971–1053; 7. >1053 | |
| Human activity factors | Distance to roads (m) | 1. <200; 2. 200–400; 3. 400–600; 4. 600–800; 5. 800–1000; 6. 1000–1200; 7. >1200 |
| Land use | 1. cropland; 2. forest land 3. grassland; 4. water area; 5. construction land; 6. unused land |
| Conditioning Factors | TOL | VIF | Conditioning Factors | TOL | VIF |
|---|---|---|---|---|---|
| Elevation | 0.59 | 1.70 | Soil type | 0.82 | 1.23 |
| Slope angle | 0.15 | 6.56 | NDVI | 0.87 | 1.16 |
| Slope aspect | 0.99 | 1.01 | TWI | 0.49 | 2.06 |
| Profile curvature | 0.77 | 1.30 | SPI | 0.31 | 3.26 |
| Plan curvature | 0.60 | 1.67 | STI | 0.35 | 2.83 |
| Topographic relief | 0.17 | 5.74 | Distance to rivers | 0.86 | 1.16 |
| TRI | 0.23 | 4.31 | Average annual rainfall | 0.80 | 1.25 |
| Lithology | 0.91 | 1.10 | Distance to roads | 0.87 | 1.14 |
| Distance to faults | 0.95 | 1.05 | Land use | 0.94 | 1.06 |
| Model | Cross-Validation Method | Accuracy | Precision | Recall | F-Score | AUC |
|---|---|---|---|---|---|---|
| RF | Random CV | 0.806 | 0.781 | 0.852 | 0.815 | 0.876 |
| GRF | 0.829 | 0.801 | 0.879 | 0.838 | 0.881 | |
| RF | Spatial CV | 0.789 | 0.766 | 0.833 | 0.798 | 0.856 |
| GRF | 0.798 | 0.767 | 0.858 | 0.810 | 0.860 |
| Models | Susceptibility Level | Area (km2) | Percentage of Area (%) | Number of Landslides | Percentage of Landslides (%) | Landslide Density |
|---|---|---|---|---|---|---|
| RF | Very Low | 26,450.31 | 43.86 | 12 | 0.52 | 0.01 |
| Low | 10,132.89 | 16.80 | 61 | 2.64 | 0.16 | |
| Moderate | 8327.19 | 13.81 | 184 | 7.96 | 0.58 | |
| High | 8239.20 | 13.66 | 469 | 20.29 | 1.48 | |
| Very High | 7154.91 | 11.86 | 1586 | 68.60 | 5.78 | |
| GRF | Very Low | 24,289.59 | 40.28 | 8 | 0.35 | 0.01 |
| Low | 11,706.39 | 19.41 | 31 | 1.34 | 0.07 | |
| Moderate | 8964.90 | 14.87 | 138 | 5.97 | 0.40 | |
| High | 8349.93 | 13.85 | 411 | 17.78 | 1.28 | |
| Very High | 6993.69 | 11.60 | 1724 | 74.57 | 6.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Zhu, Y.; Sun, K.; Zou, Q.; Zhao, S.; Li, W.; Hu, L.; Wang, S. Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China. Remote Sens. 2023, 15, 1513. https://doi.org/10.3390/rs15061513
Dai X, Zhu Y, Sun K, Zou Q, Zhao S, Li W, Hu L, Wang S. Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China. Remote Sensing. 2023; 15(6):1513. https://doi.org/10.3390/rs15061513
Chicago/Turabian StyleDai, Xiaoliang, Yunqiang Zhu, Kai Sun, Qiang Zou, Shen Zhao, Weirong Li, Lei Hu, and Shu Wang. 2023. "Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China" Remote Sensing 15, no. 6: 1513. https://doi.org/10.3390/rs15061513
APA StyleDai, X., Zhu, Y., Sun, K., Zou, Q., Zhao, S., Li, W., Hu, L., & Wang, S. (2023). Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China. Remote Sensing, 15(6), 1513. https://doi.org/10.3390/rs15061513