Next Article in Journal
Development and Application of Predictive Models to Distinguish Seepage Slicks from Oil Spills on Sea Surfaces Employing SAR Sensors and Artificial Intelligence: Geometric Patterns Recognition under a Transfer Learning Approach
Previous Article in Journal
Spatio-Temporal Heterogeneity and Cumulative Ecological Impacts of Coastal Reclamation in Coastal Waters
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 6
10.3390/rs15061497
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

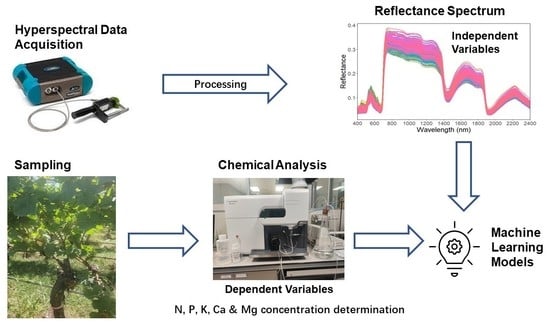
Assessing the Leaf Blade Nutrient Status of Pinot Noir Using Hyperspectral Reflectance and Machine Learning Models

by
Hongyi Lyu
1,
Miles Grafton
1,*,
Thiagarajah Ramilan
1,
Matthew Irwin
1 and
Eduardo Sandoval
2
1
School of Agriculture and Environment, Massey University, Palmerston North 4410, New Zealand
2
Massey Agri-Food (MAF) Digital Lab., Massey University, Palmerston North 4410, New Zealand
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(6), 1497; https://doi.org/10.3390/rs15061497
Submission received: 31 January 2023 / Revised: 4 March 2023 / Accepted: 6 March 2023 / Published: 8 March 2023
(This article belongs to the Section Biogeosciences Remote Sensing)
Browse Figures
Review Reports Versions Notes

Abstract

:
Monitoring grape nutrient status, from flowering to veraison, is important for viticulturists when implementing vineyard management strategies, in order to produce quality wines. However, traditional methods for measuring nutrient elements incur high labour costs. The aim of this study is to explore the potential of predicting grapevine leaf blade nutrient concentration based on hyperspectral data. Leaf blades were collected at two Pinot Noir commercial vineyards at Martinborough, New Zealand. The leaf blade spectral data were obtained with a handheld spectroradiometer, to evaluate surface reflectance and derivative spectra in the spectrum range between 400 and 2400 nm. Afterwards, leaf blades nutrient concentrations (N, P, K, Ca, and Mg) were measured, and their relationships with the hyperspectral data were modelled by machine learning models; partial least squares regression (PLSR), random forest regression (RFR), and support vector regression (SVR) were used. Pearson correlation and recursive feature elimination, based on cross-validation, were used as feature selection methods for RFR and SVR, to improve the model’s performance. The variable importance score of PLSR, and permutation variable importance of RFR and SVR, were used to determine the most sensitive wavelengths, or spectral regions related to each biochemical variable. The results showed that the best predictive performance for leaf blade N concentration was based on PLSR to raw reflectance data (R2 = 0.66; RMSE = 0.15%). The combination of support vector regression with the Pearson correlation selected method and second derivative reflectance provided a high accuracy for K and Ca modelling (R2 = 0.7; RMSE = 0.06%; R2 = 0.62; RMSE = 0.11%, respectively). However, the modelling performance for P and Mg, by different feature groups and variable selection methods, was poor (R2 = 0.15; RMSE = 0.02%; R2 = 0.43; RMSE = 0.43%, respectively). Thus, a larger dataset is needed for improving the prediction of P and Mg. The results indicated that for Pinot Noir leaf blades, raw reflectance data had potential for the prediction of N concentration, while the second-derivative spectra were more suitable to predict K and Ca. This study led to the provision of rapid and non-destructive measurements of grapevine leaf nutrient status.

Graphical Abstract

1. Introduction

Wine grapes are a major horticultural crop in New Zealand, grown on over 41,000 ha [1]. Compared to most other horticultural crops, grapevines require lower nutrient input during the growing stage [2]. However, inadequate nutrient inputs have a significant effect on vine vigour and fruit set [3]. Nutrients play essential roles in the development of grapevine photosynthesis processes and metabolic pathways [4]. Grapevines require sixteen essential nutrients for healthy growth and performance. These are classified as macro-, and micronutrients based on the quantity of the nutrient required by the crop. Macro-nutrients include nitrogen (N), phosphorous (P), potassium (K), calcium (Ca), and magnesium (Mg), and are essential elements that affect vine vigour, grape yield, and quality [2,4,5]. For example, insufficient N results in low vigour and poor production, while too much N results in the reduction of fruit set and bud fertility. Vines deficient in P generally display low vigour, poor bud initiation, and fruit set [6]. Deficiency of K in vines has a negative effect on berry colour development for red varieties. In addition, excessive P and K may limit the uptake of other elements, such as calcium, magnesium, and zinc [4]. Hence, maintaining these essential elements within a specific range is important to vine growth and berry quality management [3,7].
A previous study has shown that grapevine nutrient status varies spatially in a single block [8], which leads to variability in grape yield and quality across the vineyard. Currently, the common methods of measuring grapevine nutrients are plant tissue (e.g., leaf blade) or soil analysis [9]. The vine canopy uptake rate of each nutrient varies in time throughout different growing stages [2,10]. The canopy uptake rate of each nutrient is normally at its peak during flowering. Thus, the test laboratories in New Zealand recommend that growers collect tissue samples at flowering, or just before flowering, to correct possible nutritional problems for the current crop. However, tissue analysis in chemical laboratories is expensive and time consuming. It is important to explore the possibility of using remote sensors for monitor grapevine nutrients in a rapid and non-destructive way. The current methods require growers to collect a large number of leaves or soil samples for destructive tissue analysis, or chemical analysis, which is time consuming [11,12]. Most vineyards in New Zealand use uniform drip irrigation, which causes variations in soil moisture, root growth, and nutrient concentration [9]. Thus, soil analysis cannot give an accurate indication of the nutrient status of an individual vine [9,13]. Typically, growers manually collect many leaf blades and petioles from many vines and send them to a laboratory for analysis, to represent the nutrient status of the entire vineyard block at both flowering and veraison. This standard measurement cannot directly reflect the nutritional variability status of the crop. During the flowering stage, the nutrients of grapes change rapidly, but normal laboratory analysis can take two or three days. Thus, vineyard managers do not have a direct and quick understanding of the state of grape nutrient status, and may miss the best time to add fertilizers. In addition, the results of laboratory analysis are inadequate to effectively map the spatial and temporal distribution of nutrient deficiencies, especially in vineyard areas with high variations in soil or vine vigour [3]. This measurement provides growers a reference to help guide their fertilizer management of the entire vineyard. However, this strategy, which is based on such sparse data, may result in suboptimal growth, and unnecessary leaching and runoff of nutrients [3]. In this context, sensors, specifically proximal sensors, can provide a potentially promising method to monitor vine nutrient status in a non-destructive and timely way.
Studies on remote sensing for monitoring plant and leaf nutritional status have made significant advances, especially in estimating leaf N concentration [3,12,14]. Many studies utilized wavelengths in the visible (VIS) and near-infrared (NIR) regions related to chlorophyll absorption, in order to estimate leaf nitrogen (N) status [15,16]. However, these studies did not utilize the nitrogen absorption features of the shortwave infrared (SWIR) regions. Reflectance responses of N in the SWIR spectrum are partially associated with C-H, O-H, and N-H stretch [17]. Identifying the absorption features from the full spectrum (350–2500 nm) may improve leaf N content predictions [14,18].
In addition, only a few systematic research reports on the monitoring of nutrients other than N are published [12]. For example, phosphorus (P) is an important element for plant growth, since it is related to photosynthesis, cell formation, division of living cells, nucleic acids, and various enzymes [19]. One study found important associations between the spectral regions of 540, 720, 740, and 850 nm with maize leaf P content during the vegetation production and flowering stages [20]. However, in the VIS region, water absorption can interfere with sensor response, which makes it difficult to determine the most sensitive band for detection of leaf P [19]. The use of spectral reflectance at NIR and SWIR regions to predict P can reduce the effect of water absorption and common aerosols [21].
Most studies on the estimation of plant P status by remote sensing mainly apply to grasslands [19,22], field crops [20,21,23,24], and trees [25], while few studies have used remote sensing to evaluate the leaf nutritional status of grapevine [3,5]. A recent study focused on evaluating a large group of macronutrients (N, P, K, Ca, and Mg) and one micronutrient (Boron), and found the optimal wavelengths to estimate grapevine leaf nutrient content to be the spectral region between 400 and 2500 nm. Their method did not return satisfactory results for these nutrients (leave-one-out cross-validation R2 < 0.50) [3]. They used canopy-level spectra from an unmanned aerial system (UAS) hyperspectral imagery. The reflectance response at this stage was influenced by the structural trait, atmosphere, soil, and cover crop [26]. In addition, it is difficult to identify the weaker spectral responses of nutrients at the canopy scale, compared to the leaf scale spectra [27]. It is important to explore the possibility of using a handheld spectroradiometer to predict grapevine leaf nutrient status at the leaf-level.
Potassium (K) is another key element for plant growth and performance, since it affects cell electrochemical balance, osmotic adjustment, starch synthesis, sucrose translocation, and the activity of many enzymes [28]. Some studies have evaluated the spectral response of plant K changes, including studies of wheat [21,24], rice [29], and grasslands [30]. Many studies indicated that the spectral reflectance at the SWIR region is significant, and is associated with crop canopy K status [24,30]. Some studies have also found that the spectral region which most closely relates to crop K content at the leaf scale is at the NIR (780–1300 nm) region [31]. For the study on grapevine potassium change based on hyperspectral data, one study found that K deficiency in grapevine leaves can be effectively evaluated based on the variation index at the NIR region [5].
There is a gap in the knowledge, in terms of macronutrient (N, P, K, Ca, and Mg) prediction by handheld spectrometers at the grapevine leaf-level, that needs to be explored by new research. Few research studies have been conducted to examine the possibilities of achieving this outcome. Handheld full spectrum (350–2500 nm) spectroradiometers provide a more comprehensive relationship between spectral information and target parameters, than multi spectral sensors and vegetative indices. The aim of this study is (a) to build regression models from the different hyperspectral data (raw and derivative pre-processing reflectance), in order to model different biochemical variables based on the models’ accuracy, and (b) to determine the sensitive bands or spectral regions related to each biochemical variable.

2. Methodology

2.1. Research Sites

The data were collected from two commercial vineyards located in Martinborough, in the middle of New Zealand (Figure 1). The vineyards are owned by the Palliser Estate, and are named Wharekauhau and Pencarrow. The experimental sites in these two vineyards are 3.31 and 7.51 ha, with the grape variety of Pinot Noir grafted on rootstock 101-14 in 1998 and 2000, respectively. The row and vine spacings were 2.2 and 1.7 m for Wharekauhau, and 2.2 and 1.8 m for Pencarrow, respectively (Figure 2). The vines used in this study were trained with two-cane vertical shoot positioning. The topsoil and subsoil of both vineyards contain silt and clay textures, which have moderate soil water holding capacity. The trials reported in this study took place a week before flowering (at the end of November) to match the vineyard nutrient management strategy.

2.2. Sampling Plan and Chemical Analysis

Data were collected from 274 individual vines in the study area, consisting of 118 vines from Wharekauhau and 156 vines from Pencarrow, shown in Figure 2. For each vine, two leaves were collected opposite the basal cluster on each fruiting shoot [9]. Once leaves had been collected, the leaf blades were separated from the petiole immediately and placed in a labelled paper bag. When all the blades were collected, they were immediately sent to Massey University’s Analytical Chemistry Laboratory, and were frozen at −18 °C until they were subjected to the laboratory analysis.
Immediately after hyperspectral reflectance data were recorded, leaf blades were oven dried at 60 °C until the sample weight stabilized, and then ground through a 1 mm sieve. The dried samples were analysed at the Massey University’s Analytical Chemistry Laboratory for standard tissue nutrient content (N, P, K, Ca, and Mg). Due to time and resource constraints, only 85 vines were measured for K, Ca, and Mg concentration.

2.3. Acquisition of Spectral Data

After two days of sampling (unfortunately the sampling data is Friday, the hyperspectral measurements of the leaf blades can only be made on the following Monday), hyperspectral data measurements from two collected leaf blades were taken from each study vine. The measurements were conducted in the Massey Agri-Food Digital lab using an ASD FieldSpec 4 Hi-Res NG Spectroradiometer (Malvern Panalytical Ltd., Malvern, UK). The spectroradiometer provides controlled illumination by a leaf clip and contact probe. The spectroradiometer is warmed up for 30 min prior to measurements. During the measurement, a white panel ceramic referencing tile is used to calibrate and provide a reference spectrum, after each of the three measurements are made on each leaf. The ratio of the optical energy of the sample to that of the reference panel is used to calculate reflectance. The sensor has a spectral range from 350 to 2500 nm, and has a sampling interval of 1.4 nm between 350 and 1000 nm, and 1.1 nm between 1001 and 2500 nm. The spectral data were interpolated to 1 nm spectral resolution, and included 2151 bands between 350 and 2500 nm. The left and right sides of the adaxial surface of each leaf blade were measured separately. Each point was measured three times, with a total of six readings collected per leaf blade. The reflectance data in the regions less than 400 nm and greater than 2400 nm were removed due to the signal noise. The remaining data were then exported as ASCII text files for each spectral measurement using ViewSpec Pro 6.2 software (Analytical Spectral Devices, Inc., Boulder, CO, USA), and were then averaged to obtain the mean spectral wavelength for each sampling vine.

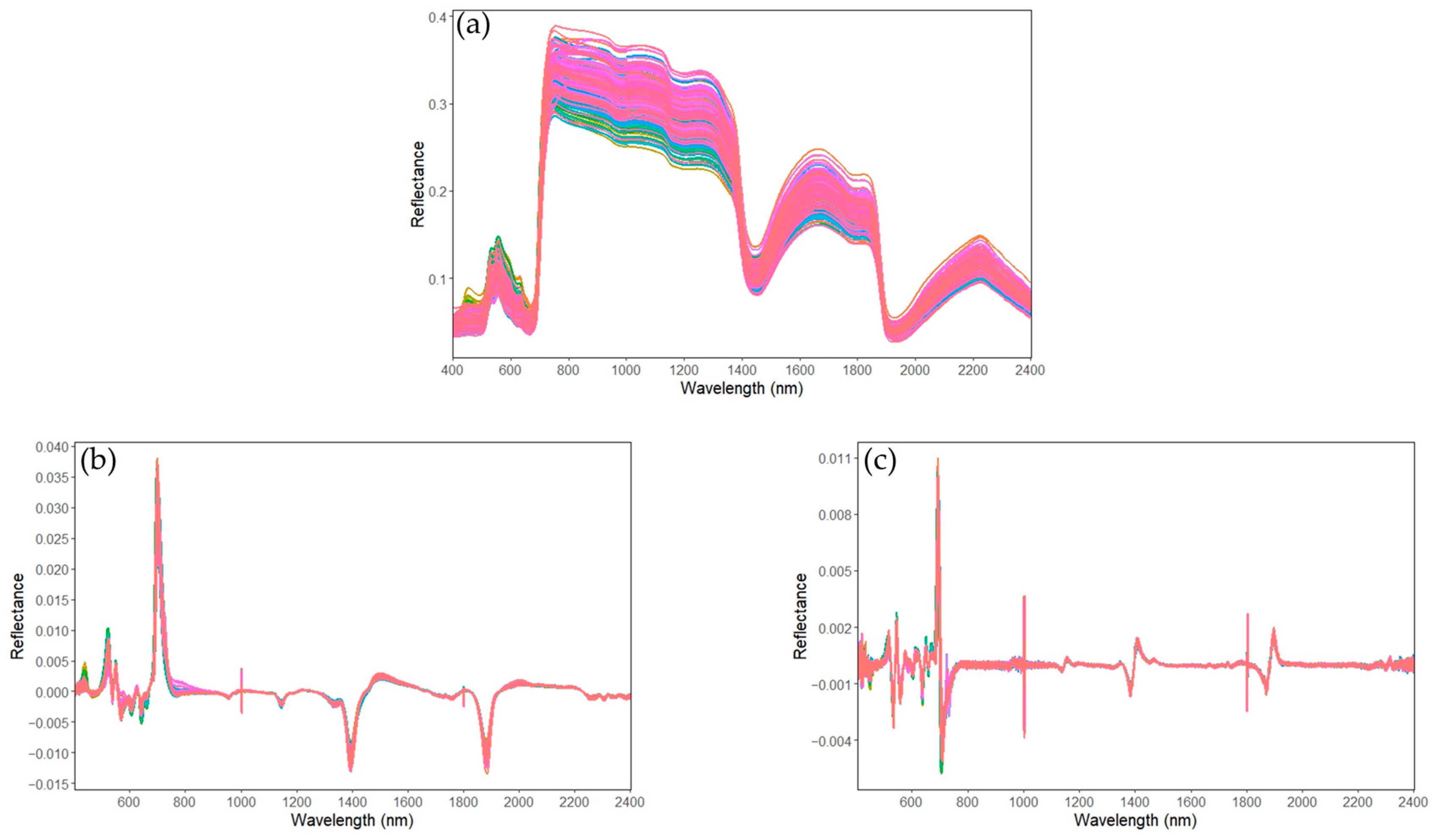
2.4. Spectral Pre-Treatments

The raw reflectance data were transformed to first derivative (1D), second derivative (2D), and vegetation indices (VI), which aims to reduce noise and eliminate insignificant signals in the spectra. The derivative pre-processing is a common method for modelling spectral data, as it can enhance the absorption features over the spectrum, and eliminate the signal noise. Many studies have discussed the promising results of predicting leaf nutrient status based on a spectral derivative pre-processing technique [32,33]. These pre-processing procedures were conducted using the “prospectr” package in R statistical software (R Core Team, version 4.2.2), with a derivative gap of 3 [34].
Vegetation indices are widely used in predicting leaf nutrient content. These indices are computed using the reflectance at certain wavelengths, which are sensitive to target parameters. However, these indices, which are calibrated from various datasets, utilize only specific regions of the spectrum, and may not be suitable for all datasets. The common vegetation indices used for leaf nutrient prediction are shown in Table 1. These indices are calculated for the purpose of comparing vine leaf nutrient estimation fitted with multivariable hyperspectral data, and univariable vegetation indices. The raw reflectance and derivative transformation data are used as inputs in machine learning models, including partial least square regression, random forest regression, and support vector regression, and the VIs are used as univariable input based on ordinary linear regression.

2.5. Data Analysis

A summary statistical analysis, of minimum, maximum, mean, standard deviation (SD), and coefficient of variation (CV), was calculated for different biochemical variables from the laboratory chemical analysis of the leaf blades. This was important to explore the nutritional conditions of Pinot Noir leaf blades during the study period, and the possible methods for analysis.
The dataset is divided into training and test sets, for measuring prediction accuracy. The training set consists of 70% of the data for training and optimizing model hyperparameters. The test set consists of the remaining 30% of the data for estimating the model prediction accuracy and error. In this study, the dataset was stratified and split based on the distribution of each variable, to ensure that both training and test sets were adequately represented within the whole sample population for each measurement. The splitting process was undertaken using the “rsample” package in R statistical software (R Core Team, version 4.2.2) [35]. Tenfold cross-validation for hyperparameter tuning was implemented in the training sets. The training sets were randomly divided into ten subsets of equal size for each iteration. In this context, 90% of the training set made up the new training set to tune the hyperparameters, while the remaining set served as the validation set to evaluate performance and compute the root mean squared error (RMSE). Subsequently, calculating the average performance of the algorithm, and then the suitable hyperparameter is chosen. The test dataset was only used to evaluate model performance. The prediction metrics to evaluate the model performance were the coefficient of determination (R2) and root mean squared error (RMSE). Then, a scatter plot was constructed to ascertain the relationship between the test data and the predicted data.
Table
Table 1. The common vegetation indices used in predicting plant nutrient status.
Table 1. The common vegetation indices used in predicting plant nutrient status.
Vegetation IndicesAcronymFormulaReference
Normalized difference vegetation indexNDVI(R860 − R650)/(R860 + R650)[36]
Modified Normalized Difference Vegetation IndexmNDVI(R775 − R670)/(R775 + R670)[37]
Renormalized Difference Vegetation IndexRDVI(R800 − R670)/((R800 + R670) × 0.5[38]
Green Normalized Difference Vegetation IndexGNDVI(R860 − R550)/(R860 + R550)[39]
Chlorophyll Absorption Reflectance IndexCARI[(R700 − R670) − 0.2 × (R700 − R550)][40]
Chlorophyll IndicesClgreen(R730/R530) – 1[41]
Normalized Difference Red-EdgeNDRE(R790 − R720)/(R790 + R720)[40]
Plant cell density indexPCDR860/R650[42]
Normalized index (870, 1450)N_870_1450(R870 – R1450)/(R870 + R1450)[24]
Normalized index (1645, 1715)N_1645_1715(R1645 – R1715)/(R1645 + R1715)[24]
Modified anthocyanin reflectance indexmARI(1/R550 − 1/R700) × R780[43]
Carotenoid reflectance indexCRI-1(1/R515 − 1/R565) × R790[43]
Photochemical reflectance indexPRI(R531 − R570)/(R531 + R570)[44]
Normalized difference lignin indexNDLI(log(1/R1754)) − log(1/R1680))/(log(1/R1754) + log(1/R1680))[45]

2.6. Variable Selection

The hyperspectral reflectance data in this study is a high dimensional data set. Using the full set may result in overfitting and low accuracy of the machine learning model. In this study, hierarchical clustering, Pearson correlation, and recursive feature elimination based on cross-validation were chosen for variable selection of raw and derivative reflectance spectrum data.

2.6.1. Hierarchical Clustering

Hierarchical clustering was chosen in this study because it can reduce the number of redundant features, and mitigate the multicollinearity. In this study, the cluster was based on Euclidean distance using complete linkage clustering. The predictor variables were chosen, taking one variable from each cluster. The height of the cut to the dendrogram was set to 25. This reduced the number of bands for subsequent use in the variable selection method. In order to compare the influence of hierarchical clustering on regression model performance, the full set of predictor variables was also used in the following variable selection method.

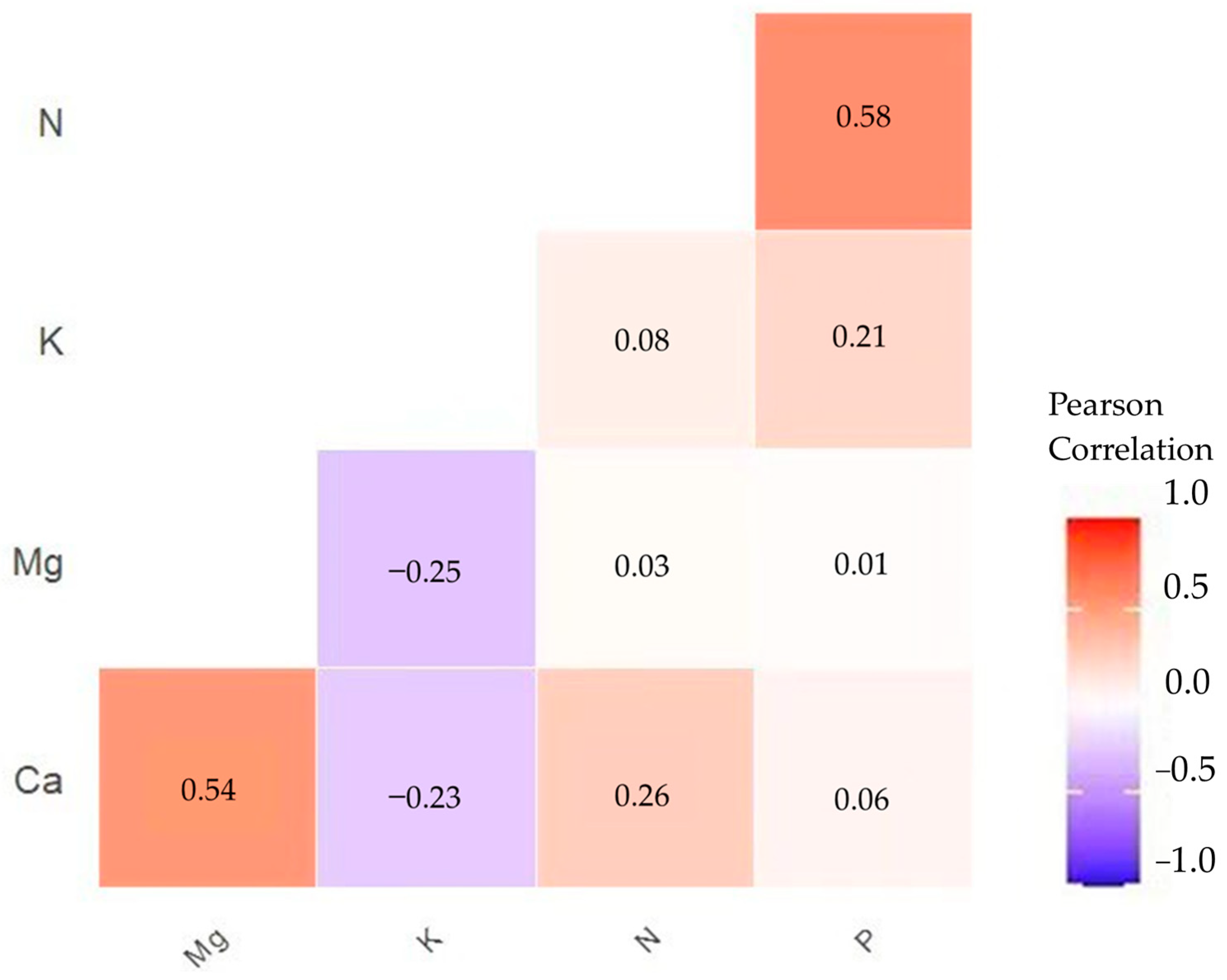
2.6.2. Pearson Correlation

Pearson correlation is a measure of the linear relationship of 2 or more variables. In this study, it was used to determine the correlation between responses (N, P, K, Ca, and Mg) and predictor variables (the reflectance at each wavelength). Pearson correlation required the variables to have a normal distribution. The values of Pearson correlation coefficients range from +1 to −1. The closer to ±1, the stronger the linear relationship. Correlations between N and predictor variables with Pearson coefficients smaller than 0.4 were discarded. Furthermore, due to the low correlation between P, K, Ca, and Mg and predictor variables, Pearson coefficients higher than 0.2 were selected as input variables to predict other biochemical variables. This correlation was implemented using the “HiClimR” package in R statistical software (R Core Team, version 4.2.2) [46].

2.6.3. Recursive Feature Elimination Based on Cross-Validation (RFECV)

RFECV is a wrapper feature selection method, and aims to select features by recursively considering smaller and smaller sets of features. In each iteration, it identifies the weakest feature, and the model is reconstructed using the remaining variables, until the specified number of features is reached. To determine the optimal number of features, 10-fold cross-validation is used with RFE to select the best number of variables, according to the Root Mean Square Error (RMSE). Due to the computational capacity, the number of features that should be retained in the updated model was set to 1:5, 10, 20, 40, 80, 160, 320, 640, 1280, and 2000 features. This step was implemented using the “caret” package in R statistical software (R Core Team, version 4.2.2) for RFR and SVR.

2.7. Machine Learning Models

To estimate different biochemical variables from hyperspectral reflectance, the following standard machine learning algorithms were applied: partial least squares regression (PLSR), random forest regression (RFR), and support vector regression (SVR). The regression modelling analysis was implemented using the “pls” and “caret” packages in R statistical software (R Core Team, version 4.2.2) [47,48]. In respect to the configuration of each algorithm, the tuned hyperparameters of the methods used were set to the package default values, except those described in Table 2. The hyperparameter tuning was based on the 10-fold cross-validation method. The optimized hyperparameters resulted in the models with the lowest RMSE values. These parameters were then used for later evaluation of model performance on the test set. In addition, the contribution of each spectral wavelength to the best performance machine learning model was computed by variable importance score for PLSR, and permutation variable importance for RFR and SVR.

3. Results

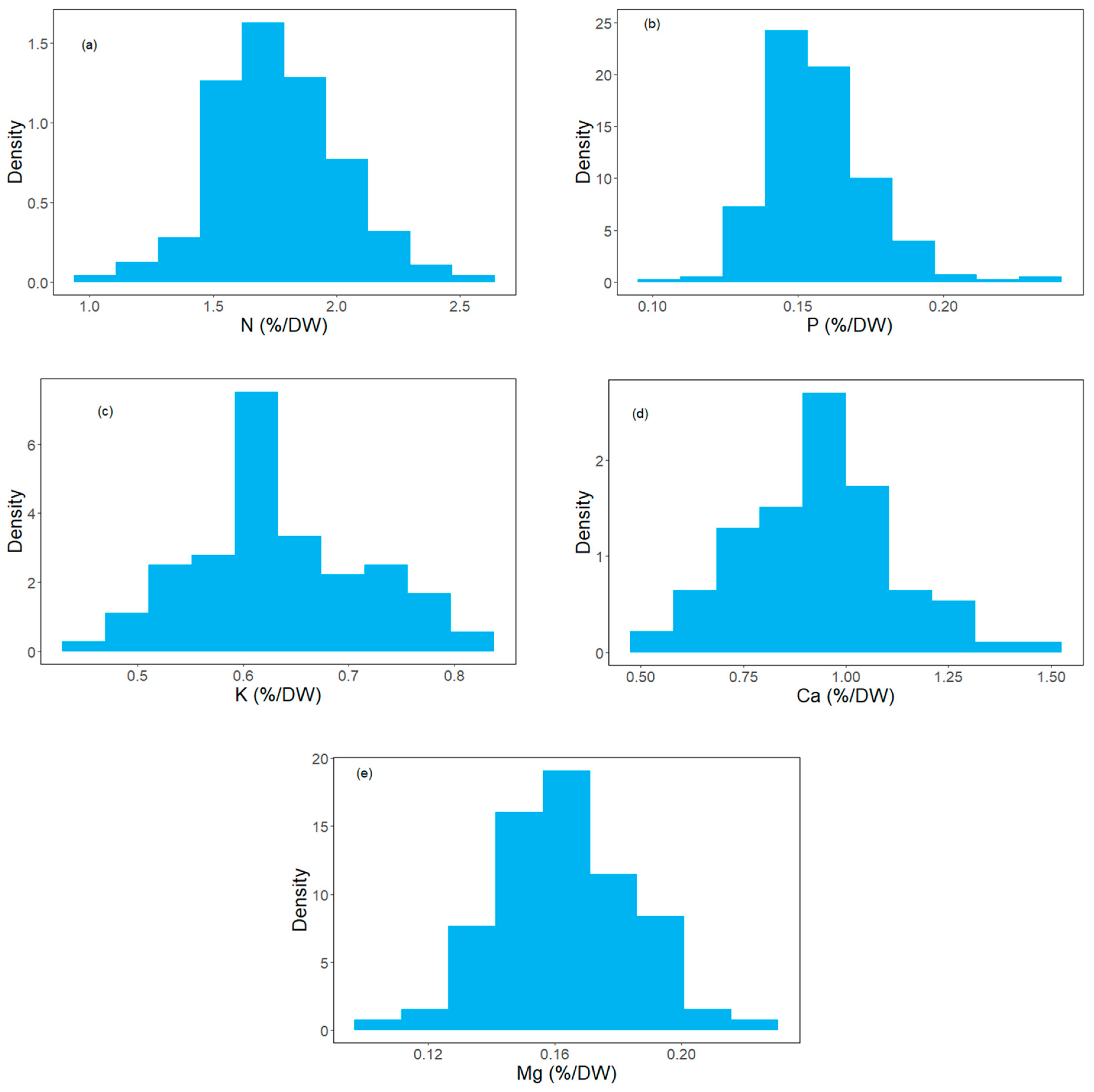
3.1. Biochemical Variables

The descriptive statistics of the measured biochemical variables for the dataset (vine leaf mineral content before flowering) stage are presented in Table 3. The data of biochemical variables were measured separately for each vine leaf in the laboratory, after recording spectral data. The vine nutrient concentration ranged from 0.97 to 2.5% for N, 0.11 to 0.23% for P, 0.45 to 0.82% for K, 0.53 to 1.45% for Ca, and 0.1 to 0.22% for Mg. The concentration of Ca in collected leaf samples differed greatly, with a coefficient of variation (CV) of 19.14%. Lower variations of N, P, K, and Mg occurred in collected samples, with CV values of 14.12, 12.5, 12.7, and 12.5%, respectively. Analysis has shown that N P, K, Ca, and Mg presented a uniform distribution. The density histogram in Figure 3 shows the distribution of vine leaf nutrient concentrations values, and the class number was determined by the square root of the total sample number.
The correlation between biochemical variables is shown Figure 4. Concentrations of N and P correlated significantly and positively (r = 0.58, p < 0.01). Mg concentration was significantly positive with Ca concentration (r = 0.54, p < 0.01). Lower correlation coefficient values between other biochemical variables are favourable for isolating the nutrient from the sensitive wavelengths [21].

3.2. Spectral Analysis

Figure 5 shows the raw reflectance spectra of the typical spectral reflectance curve of grapevines. Strong absorption regions at 450 (blue) and 670 nm (red) are from strong chlorophyll absorption and moderate reflectance in green light, strong reflectance between 700 and 1300 nm (NIR region) is due to the healthy internal structure of plant leaves, and strong absorption at around 1450 and 1900 nm (SWIR region) is due to water absorption. Differences in reflectance and absorption between collected samples at specific wavelengths across VIS, NIR, and SWIR regions will have the potential to predict different biochemical variables for each observation. The numeric derivative pre-processing reflectance spectra may also be potentially related to the vine nutrient status. For example, 400–800, 1000, 1300–1500, and 1700–1900 nm for the first derivative reflectance, as well as 400–700, 1000–1200, 1300–1500, and 1800–2000 nm for the second derivative reflectance (Figure 5b,c).

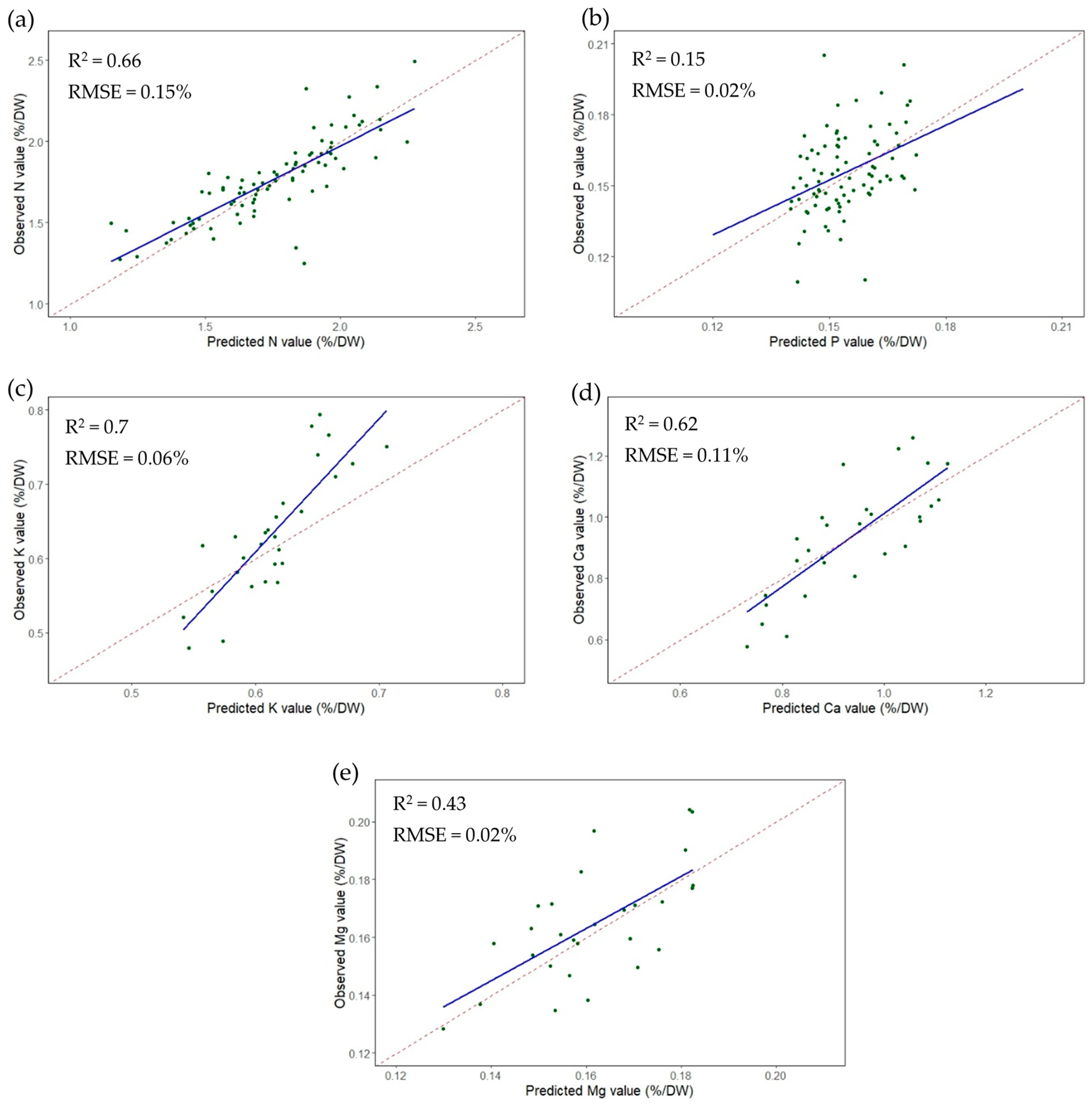
3.3. Prediction Accuracy

The best results of the machine learning algorithms, between the different feature groups and variable selection methods, are shown in Table 4. The prediction accuracy evaluation of test datasets is based on R2 and RMSE. The model with the highest value of R2, along with the lowest value of RMSE, was chosen as the best performance model. The best modelling performance of N is PLSR trained with raw reflectance data, with the highest R2 (0.66) and lowest RMSE (0.15%). The modelling performance of P and Mg by different feature groups and variable selection methods is poor, as no model returns a high R2 (R2 = 0.15; R2 = 0.43, respectively). The highest values of R2 between laboratory measured values and predicted values of K concentration occur from SVR, based on the Pearson correlation selection variable and second derivative data (R2 = 0.7, RMSE = 0.06%). SVR trained with the second derivative data based on the Pearson correlation selection method also results in the best performance of predicting Ca (R2 = 0.62, RMSE = 0.11%). Compared with the raw reflectance data, the derivative pre-processing can improve the model performance. Excluding N, the modelling accuracy of other biochemical variables by vegetation index is poor, as most of the vegetation indices resulted in modelling with R2 of less than 0.5 (Table 4). To ascertain the relationship between the best predicted values and the actual values, their regression values are plotted (Figure 6). Most biochemical variables, including N, P, Ca, and Mg, show a closer resemblance with a 1:1 relationship. However, Figure 6c only shows moderate agreement of the predicted K concentration with the actual concentration.

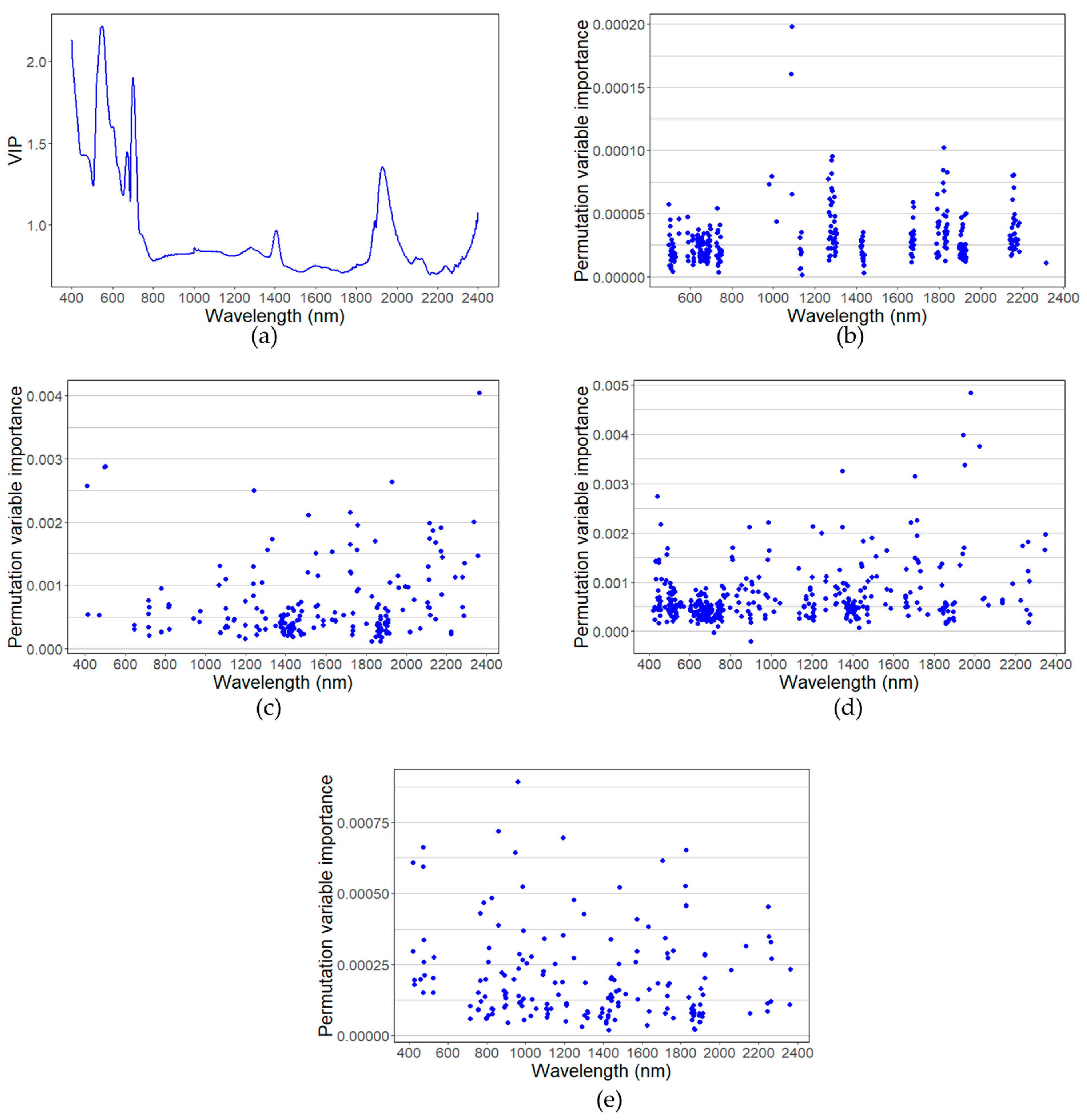
3.4. Contribution of Each Wavelength to the Algorithm

Figure 7 presents the variable importance for the best predicted model with the highest accuracy on the test set. PLSR uses a variable importance score. RFR and SVR use permutation variables for importance. This used PLSR to compute variable importance for N for raw reflectance, and used SVR to compute permutation variable importance for the remaining biochemical variables, with Pearson correlation selected variables from derivative reflectance data. This computation was based on the training set, and it can show the contribution of each wavelength to the algorithms’ performance.
The variable importance (VIP) value for the PLSR model for N shows that the electromagnetic spectrum contributed more at around 400–440, 515–615, 690–720, and 1890–1990 nm (Figure 7a). The permutation importance of the SVR model, in respect to P, with Pearson correlation selected variables from first derivative reflectance data, concentrated at around 980–1010, 1260–1290, 1675, 1790–1820, and 2150–2180 nm (Figure 7b). The important regions of K, computed by SVR with Pearson correlation selected variables from second derivative reflectance data, are at around 410, 490–500, 1235–1240, 1500, 1700–1750, 1900–1950, 2130–2150, 2175–2180, 2330, and 2360 nm (Figure 7c). The important second derivative Pearson correlation selected variables, computed based on SVR for Ca, show high values at around 410–460, 800, 870, 960–980, 1200–1250, 1340–1350, 1650–1700, 1930–1950, 1970, and 2030 nm (Figure 7d). With SVR for Mg, the permutation importance value with Pearson correlation selected variables from second derivative reflectance was high at around 420, 470, 860–880, 930–960, 1180, 1720, and 1820–1840 nm (Figure 7e).

4. Discussion

A small dataset of essential grape nutrient concentrations (274 samples for N and P; 88 samples for K, Ca, and Mg) from Pinot Noir cultivars, under uniform commercial vineyard management strategy, were presented in this study. The study presents the capability of non-destructive prediction of vine leaf biochemical variables using a handheld hyperspectral spectroradiometer. In this study, in order for the training dataset to have enough samples to train the regression model, the data of two vineyards are combined to divide the training set and the test set. In future studies, data from more seasons and more vineyards should be collected, to increase the size of the dataset and separate out independent test sets, to make the machine learning models more compelling.
In this study, raw reflectance and their derivative transformations were used to predict biochemical variables by machine learning models. The results showed good performance in predicting levels of N, K, and Ca, with an R2 of 0.66, 0.7, and 0.62, respectively. Levels of P and Mg were poorly represented, with an R2 of 0.15 and 0.43, respectively. A previous study at grape canopy level demonstrated poor prediction performances for N (R2 = 0.44), P (R2 = 0.34), K (R2 = 0.26), Ca (R2 = 0.33), Mg (R2 = 0.23), and Boron (R2 = 0.46) using UAS hyperspectral imaging in the spectral region of 400–2500 nm [3]. It is more complex and impractical to identify leaf nutrients at the canopy level using hyperspectral aerial images [26], due to the effect on data of the atmosphere and inter-row vegetation. One leaf-level study showed that macro- and micronutrient levels (N, P, K, Ca, Mg, S, Cu, Fe, Mn, and Zn) in Valencia orange leaves can be successfully predicted using handheld hyperspectral spectroradiometers in the spectral region of 380–1020 nm, with R2 above 0.6 for all nutrients [12]. In addition, previous leaf-level studies demonstrated that using visible and near-infrared data can successfully predict winter wheat [49] and paddy rice [32] leaf N status (R2 > 0.75), rice leaf K status (R2 = 0. 74) [50], cacao leaf Ca, P, and N status (R2 > 0.73) [11], and citrus tree leaf N, K, Ca, Mg, Fe, and Zn status (R2 > 0.76) [51]. This study failed to predict P and Mg in grapevine leaf blades. This might be attributed to the fact that there was less variability of P and Mg concentrations in this experiment than in other studies. Although the variability of K concentration was very low, a good predictive ability for K was found using second derivative transformation data. The value range of K concentrations was larger than that of P and Mg, which might explain the high prediction performance. In addition, the high correlation between N–P, and Ca–Mg may also affect the model performance. The higher cross-correlation between biochemical variables makes it hard to isolate the impact of the biochemical variables on the evaluated wavelengths [24]. As a result, multiple correlated nutrient deficiencies may result in the similarity in the spectral responses, and thus reduce the correlation between an individual biochemical variable and the relevant spectral regions.
Previous studies have demonstrated that the visible and near-infrared spectrum is most suitable for plant nutrient status estimation. Two studies have successfully predicted the grape vine nutrient status, including chlorophyll content and nitrogen, using VIs from remote sensing imagery [52,53]. This study suggested good performance by using the entire spectrum to predict different nutrient elements by machine learning techniques, rather than that of using VIs calculated from only two or three wavelengths (Table 4). Wei et al. [54], who stated that regression models that use the entire wavelength spectrum to predict grapevine water content are better than models that use vegetation indices, calculated from reflectance at two or three wavelengths. However, this experiment did not explore all the vegetation indices. In future studies, more combinations of vegetation indices, including normalised index and simple ratio, should be selected to explore the relationship between them and leaf nutrient concentration.
Spectral pre-processing can improve the regression modelling performance when predicting leaf nutrient status [12,33,55,56]. In this study, the model fitted using the derivative transformation spectra data outperformed those regressed with the raw reflectance data (Table 4). Derivative transformation is an important spectral pre-processing method, as it allows for highlighted absorption features of the primary spectra to reduce the random noise effect [55]. This study demonstrated a better relation of K and Ca when linked to the SVR with second derivative reflectance, which can be related to the results reported in the previous study [56]. The first derivative of the dataset was evaluated, but it does not improve the modelling accuracy compared to models trained with raw reflectance data. Thus, we suggest further research should continue to investigate the impact of other spectral pre-processing methods, including first derivative transformation on predicting biochemical variables.
Due to the high dimensionality of a hyperspectral dataset, the irrelevant information in the dataset has a negative impact on the accuracy of prediction. Thus, the removal of less informative variables is an important step to improve model performance [57]. The study showed that Pearson correlation works better, using second derivative reflectance as an input variable in RFR and SVR models, to predict K and Ca. Compared with the Pearson correlation selection method, RFECV does not improve the accuracy of the prediction. One possible reason for the poor performance of the RFECV-based regression model is that the number of features that should be retained in the updated regression model does not continuously cover all input variables. Thus, the RFECV variable selection method needs to be run on a computer with high computational capacity to improve the model performance. Although hierarchical clustering reduces the multicollinearity of the data, it does not improve the accuracy of most prediction models. The regression model based on predictor variables, without hierarchical clustering, returns a good performance for K and Ca. Multicollinearity has a negative impact on the interpretation of permutation variable importance. Future studies should continue to explore more efficient solutions to mitigate multicollinearity.
The machine learning models that were implemented in this study demonstrated good performance for predicting levels of N, K, and Ca, but not for P and Mg. SVR is known to handle high dimensionality data, and performed better in the dataset used when compared with RF and PLSR in predicting P, K, Ca, and Mg [58]. SVR is a kernel-based method used for modelling data in a non-linear manner. It has shown good performance in predicting Mg and Na concentration for mangrove foliage [59]. PLSR can also reduce the high dimensionality and multicollinearity down to a few independent variables. In this study, PLSR has been shown to outperform SVR and RFR in predicting N, using the full spectrum of untransformed variables. This is attributed to a linear relationship between N and reflectance data. However, the performance of the PLSR model to predict other biochemical variables was poorer than RFR and SVR. This is possibly due to the non-linear relationship between input variables and biochemical variables. RFR was reported to show robustness in predicting plant nutrients, by using high-dimensional hyperspectral data [12,60]. However, in this study it had a low accuracy in the used dataset, compared with SVR. Regardless, a framework with different machine learning algorithms is recommended when predicting different biochemical variables, as no algorithm is universally applicable to different tasks.
The variable importance identifies the wavelengths and spectral regions which contributed the most to predict each biochemical variable. This study suggests that the visible and near-infrared spectrum provides the most important information for quantifying grapevine N status during flowering, since the important raw reflectance wavebands occurred between 400–440 nm, 515–615 nm, and 690–720 nm based on the VIP score (Figure 7a). The wavelengths around these regions are generally associated with strong absorption by chlorophyll-a, chlorophyll-b, and carotenoids. Previous studies have found that using the chlorophyll absorption spectrum region can estimate the leaf nitrogen content, since N is the most important biochemical variable in chlorophylls [15,16]. In addition, the important bands in the SWIR spectrum are 1890–1990 nm. Reflectance responses in this SWIR spectrum are partially associated with O-H stretch, which are the prominent bonds in starch [17,61]. The crop’s N status can affect the activities of starch metabolizing enzymes [62]. However, this region overlaps with the water absorption band regions. If using remote airborne or satellite spectra to predict leaf N status in the field, the reflectance at 1890–1990 nm would be meaningless. When solar energy is used as a source illumination, the radiance is largely absorbed by atmospheric water vapor before reaching the surface of the plant.
The most sensitive bands for P data are determined to be between 1080 and 1090 nm. This is similar to the findings of Mahajan et al. [21], who proposed a new normalised vegetation index, calculated from 1080 and 1480 nm wavelengths, to predict wheat P status (Figure 7b). However, the low accuracy of the model predicting P in this paper may lead to the removal of sensitive bands related to P. Future studies should consider reducing the lower cross-correlation between biochemical variables, by designing different nutrient treatments. For grapevine leaf K estimation, wavelengths of 410, 490–500, 1242, 1929, and 2362 nm are found to perform best in this study (Figure 7c). The 410 and 490–500 nm bands correspond to the blue band, which is related to photosynthesis. K plays a key role in the process of photosynthesis and the tissue composition of plants [63]. It is also important to consider that the strong water absorption of wavebands at 1242 nm and 1929 nm may affect the ability to predict K when using these bands in field measurements [64]. However, previous studies show that the spectral bands in rice, that are sensitive to leaf K status, are mainly in the SWIR region (1300–2000 nm) [24,50]. They attributed this finding to the effect of K ions on leaf water content. A previous study, which used hyperspectral data to predict the grape water status (GWS) in the same vineyard of this study, showed that the sensitive bands for GWS in the SWIR spectrum include 2050–2370 nm [54]. This study also shows that this region contributed the most in predicting leaf K concentration.
For leaf Ca estimation in grapevines, wavelengths of 440, 458, 893, 984, 1204, 1246, and 1350 nm are found to perform best (Figure 7d). For leaf Mg estimation in grapevine, wavelengths of 421, 470, 859, 947, 961, 984, 1193, 1483, 1706, and 1820–1830 nm are found to perform best (Figure 7e). The sensitive spectral regions selected for the Ca and Mg models coincide highly in the visible and near-infrared region. This could be attributed to the high cross-relationship between Ca and Mg in this study. In the SWIR spectrum, the sensitive bands in this study coincide with the water absorption bands (1400 and 1940 nm). The effects of atmospheric absorption and water absorption at this band should also be considered when using unmanned aerial vehicles or satellite measurements in the field for these elements. It is worth noting that in this study, spectral measurement of the leaf blades was carried out after they were frozen, which may affect the hyperspectral reflectance spectrum [65]. Freezing temperatures may change the pigment contents of the leaf and leaf surface structure, thus affecting leaf optical features. Further study should continue to explore the relationship between grapevine leaf nutrients and the spectra response at the leaf-level, based on in-field hyperspectral measurement.

5. Conclusions

This paper explores the relationship between biochemical variables and hyperspectral reflectance (400–2400 nm) at the leaf-level, collected before flowering, from two commercial vineyards, using machine learning techniques. The PLSR method was able to return good predictions (R2 = 0.66; RMSE = 0.15%) for the N variable. The SVR method provided good model performance for K and Ca (R2 = 0.7; RMSE = 0.06%; R2 = 0.62; RMSE = 0.11%, respectively). However, the regression model performance for P and Mg were relatively low (R2 = 0.15; RMSE =0.02%; R2 = 0.43; RMSE = 0.43%, respectively), thus indicating that a larger dataset or alternative methods are necessary in future studies. In addition, the result revealed that the machine learning models based on raw reflectance or derivative transformation data outperform linear regression using traditional vegetation indices. Another result showed that the Pearson correlation selected method, with derivative pre-processing spectral data, was more suitable to model most nutrients. This study also identified the sensitive bands most responsible for the prediction. Further study should be explored with new data collected from different growing stages and years, to validate these informative bands for grapevine nutrient monitoring. This study has proven the potential for a rapid and non-destructive determination of biochemicals in grapevine using a hand-held spectroradiometer.

Author Contributions

Conceptualization, H.L. and M.G.; methodology, H.L., T.R., M.G. and M.I.; software, H.L., M.I. and E.S.; validation, H.L., T.R., M.I. and E.S.; formal analysis, H.L.; investigation, H.L., E.S., T.R. and M.I.; resources, M.G. and E.S.; data curation, H.L., M.I. and E.S.; writing—original draft preparation, H.L.; writing—review and editing, M.G. and T.R.; visualization, H.L. and M.I.; supervision, M.G., T.R. and M.I.; project administration, M.G.; funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors sincerely thank the Palliser Estate for providing the vineyards as study fields, as well as Guy McMaster (chief viticulturist of the Palliser Estate).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. New Zealand Winegrowers. Vineyard Report 2022 New Zealand Winegrowers; New Zealand Winegrowers: Auckland, New Zealand, 2022; pp. 1–22. [Google Scholar]
  2. Schreiner, R.P.; Scagel, C.F.; Baham, J. Nutrient Uptake and Distribution in a Mature “Pinot Noir” Vineyard. HortScience 2006, 41, 336–345. [Google Scholar] [CrossRef] [Green Version]
  3. Chancia, R.; Bates, T.; Vanden Heuvel, J.; van Aardt, J. Assessing Grapevine Nutrient Status from Unmanned Aerial System (UAS) Hyperspectral Imagery. Remote Sens. 2021, 13, 4489. [Google Scholar] [CrossRef]
  4. Ashley, R. Grapevine Nutrition-an Australian Perspective; Foster’s Wine Estates Americas: Melbourne, Australia, 2011; Volume 1000. [Google Scholar]
  5. Debnath, S.; Paul, M.; Rahaman, D.M.; Debnath, T.; Zheng, L.; Baby, T.; Schmidtke, L.M.; Rogiers, S.Y. Identifying Individual Nutrient Deficiencies of Grapevine Leaves Using Hyperspectral Imaging. Remote Sens. 2021, 13, 3317. [Google Scholar] [CrossRef]
  6. Schreiner, R.P.; Osborne, J. Defining Phosphorus Requirements for Pinot Noir Grapevines. Am. J. Enol. Vitic. 2018, 69, 351–359. [Google Scholar] [CrossRef]
  7. Padilla, F.M.; Gallardo, M.; Peña-Fleitas, M.T.; De Souza, R.; Thompson, R.B. Proximal Optical Sensors for Nitrogen Management of Vegetable Crops: A Review. Sensors 2018, 18, 2083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. King, P.D.; Smart, R.E.; McClellan, D.J. Within-vineyard Variability in Vine Vegetative Growth, Yield, and Fruit and Wine Composition of Cabernet Sauvignon in Hawke’s Bay, New Zealand. Aust. J. Grape Wine Res. 2014, 20, 234–246. [Google Scholar] [CrossRef]
  9. Moyer, M.; Singer, S.D.; Davenport, J.R.; Hoheisel, G.-A. Vineyard Nutrient Management in Washington State; Washington State University Extension: Pullman, WA, USA, 2018. [Google Scholar]
  10. Schreiner, R.P. Nutrient Uptake and Distribution in Young Pinot Noir Grapevines over Two Seasons. Am. J. Enol. Vitic. 2016, 67, 436–448. [Google Scholar] [CrossRef]
  11. Malmir, M.; Tahmasbian, I.; Xu, Z.; Farrar, M.B.; Bai, S.H. Prediction of Macronutrients in Plant Leaves Using Chemometric Analysis and Wavelength Selection. J. Soils Sediments 2020, 20, 249–259. [Google Scholar] [CrossRef]
  12. Osco, L.P.; Ramos, A.P.M.; Faita Pinheiro, M.M.; Moriya, É.A.S.; Imai, N.N.; Estrabis, N.; Ianczyk, F.; Araújo, F.F.; Liesenberg, V.; Jorge, L.A.D.C. A Machine Learning Framework to Predict Nutrient Content in Valencia-Orange Leaf Hyperspectral Measurements. Remote Sens. 2020, 12, 906. [Google Scholar] [CrossRef] [Green Version]
  13. Christensen, P.; Kearney, U.C. Use of Tissue Analysis in Viticulture. In Cooperative Extension Pub. NG10-00; University of California: Visalia, CA, USA, 2005. [Google Scholar]
  14. Ye, X.; Abe, S.; Zhang, S. Estimation and Mapping of Nitrogen Content in Apple Trees at Leaf and Canopy Levels Using Hyperspectral Imaging. Precis. Agric. 2020, 21, 198–225. [Google Scholar] [CrossRef]
  15. Fu, Y.; Yang, G.; Pu, R.; Li, Z.; Li, H.; Xu, X.; Song, X.; Yang, X.; Zhao, C. An Overview of Crop Nitrogen Status Assessment Using Hyperspectral Remote Sensing: Current Status and Perspectives. Eur. J. Agron. 2021, 124, 126241. [Google Scholar] [CrossRef]
  16. Berger, K.; Verrelst, J.; Feret, J.-B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop Nitrogen Monitoring: Recent Progress and Principal Developments in the Context of Imaging Spectroscopy Missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef] [PubMed]
  17. Bruning, B.; Liu, H.; Brien, C.; Berger, B.; Lewis, M.; Garnett, T. The Development of Hyperspectral Distribution Maps to Predict the Content and Distribution of Nitrogen and Water in Wheat (Triticum aestivum). Front. Plant Sci. 2019, 10, 1380. [Google Scholar] [CrossRef] [PubMed]
  18. Camino, C.; González-Dugo, V.; Hernández, P.; Sillero, J.C.; Zarco-Tejada, P.J. Improved Nitrogen Retrievals with Airborne-Derived Fluorescence and Plant Traits Quantified from VNIR-SWIR Hyperspectral Imagery in the Context of Precision Agriculture. Int. J. Appl. Earth Obs. Geoinf. 2018, 70, 105–117. [Google Scholar] [CrossRef]
  19. Peng, Y.; Zhang, M.; Xu, Z.; Yang, T.; Su, Y.; Zhou, T.; Wang, H.; Wang, Y.; Lin, Y. Estimation of Leaf Nutrition Status in Degraded Vegetation Based on Field Survey and Hyperspectral Data. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [Green Version]
  20. Oppelt, N.; Mauser, W. Hyperspectral Monitoring of Physiological Parameters of Wheat during a Vegetation Period Using AVIS Data. Int. J. Remote Sens. 2004, 25, 145–159. [Google Scholar] [CrossRef]
  21. Mahajan, G.R.; Sahoo, R.N.; Pandey, R.N.; Gupta, V.K.; Kumar, D. Using Hyperspectral Remote Sensing Techniques to Monitor Nitrogen, Phosphorus, Sulphur and Potassium in Wheat (Triticum aestivum L.). Precis. Agric. 2014, 15, 499–522. [Google Scholar] [CrossRef]
  22. Wijesingha, J.; Astor, T.; Schulze-Brüninghoff, D.; Wengert, M.; Wachendorf, M. Predicting Forage Quality of Grasslands Using UAV-Borne Imaging Spectroscopy. Remote Sens. 2020, 12, 126. [Google Scholar] [CrossRef] [Green Version]
  23. Mahajan, G.R.; Pandey, R.N.; Sahoo, R.N.; Gupta, V.K.; Datta, S.C.; Kumar, D. Monitoring Nitrogen, Phosphorus and Sulphur in Hybrid Rice (Oryza sativa L.) Using Hyperspectral Remote Sensing. Precis. Agric. 2017, 18, 736–761. [Google Scholar] [CrossRef]
  24. Pimstein, A.; Karnieli, A.; Bansal, S.K.; Bonfil, D.J. Exploring Remotely Sensed Technologies for Monitoring Wheat Potassium and Phosphorus Using Field Spectroscopy. Field Crops Res. 2011, 121, 125–135. [Google Scholar] [CrossRef]
  25. Skidmore, A.K.; Ferwerda, J.G.; Mutanga, O.; Van Wieren, S.E.; Peel, M.; Grant, R.C.; Prins, H.H.; Balcik, F.B.; Venus, V. Forage Quality of Savannas—Simultaneously Mapping Foliar Protein and Polyphenols for Trees and Grass Using Hyperspectral Imagery. Remote Sens. Environ. 2010, 114, 64–72. [Google Scholar] [CrossRef]
  26. Kumar, L.; Schmidt, K.; Dury, S.; Skidmore, A. Imaging Spectrometry and Vegetation Science. In Imaging Spectrometry; Springer: Berlin/Heidelberg, Germany, 2001; pp. 111–155. ISBN 978-0-306-47578-8. [Google Scholar]
  27. Kokaly, R.F.; Clark, R.N. Spectroscopic Determination of Leaf Biochemistry Using Band-Depth Analysis of Absorption Features and Stepwise Multiple Linear Regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
  28. Schreiner, R.P.; Osborne, J. Potassium Requirements for Pinot Noir Grapevines. Am. J. Enol. Vitic. 2020, 71, 33–43. [Google Scholar] [CrossRef]
  29. Chen, L.; Lin, L.; Cai, G.; Sun, Y.; Huang, T.; Wang, K.; Deng, J. Identification of Nitrogen, Phosphorus, and Potassium Deficiencies in Rice Based on Static Scanning Technology and Hierarchical Identification Method. PloS ONE 2014, 9, e113200. [Google Scholar] [CrossRef] [PubMed]
  30. Mutanga, O.; Odindi, J. Exploring the Potential of Hyperspectral Data and Multivariate Techniques in Discriminating Different Fertilizer Treatments in Grasslands. J. Appl. Remote Sens. 2015, 9, 096033. [Google Scholar]
  31. Ponzoni, F.J.; De, J.L.; Goncalves, M. Spectral Features Associated with Nitrogen, Phosphorus, and Potassium Deficiencies in Eucalyptus saligna Seedling Leaves. Int. J. Remote Sens. 1999, 20, 2249–2264. [Google Scholar] [CrossRef]
  32. Yang, J.; Du, L.; Gong, W.; Shi, S.; Sun, J.; Chen, B. Analyzing the Performance of the First-Derivative Fluorescence Spectrum for Estimating Leaf Nitrogen Concentration. Opt. Express 2019, 27, 3978–3990. [Google Scholar] [CrossRef]
  33. Yang, J.; Cheng, Y.; Du, L.; Gong, W.; Shi, S.; Sun, J.; Chen, B. Selection of the Optimal Bands of First-Derivative Fluorescence Characteristics for Leaf Nitrogen Concentration Estimation. Appl. Opt. 2019, 58, 5720–5727. [Google Scholar] [CrossRef]
  34. Stevens, A.; Ramirez-Lopez, L.; Hans, G. Miscellaneous Functions for Processing and Sample Selection of Spectroscopic Data. 2022. Available online: https://cran.r-project.org/web/packages/prospectr/index.html (accessed on 5 March 2023).
  35. Frick, H.; Chow, F.; Kuhn, M.; Mahoney, M.; Silge, J.; Wickham, H. General Resampling Infrastructure. 2022. Available online: https://cran.r-project.org/web/packages/rsample/index.html (accessed on 5 March 2023).
  36. Rouse Jr, J.W.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NTRS: Chicago, IL, USA, 1974; pp. 1–120. [Google Scholar]
  37. Jurgens, C. The Modified Normalized Difference Vegetation Index (MNDVI) a New Index to Determine Frost Damages in Agriculture Based on Landsat TM Data. Int. J. Remote Sens. 1997, 18, 3583–3594. [Google Scholar] [CrossRef]
  38. Roujean, J.-L.; Breon, F.-M. Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
  39. Gitelson, A.A.; Merzlyak, M.N. Remote Sensing of Chlorophyll Concentration in Higher Plant Leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
  40. Sellami, M.H.; Albrizio, R.; Čolović, M.; Hamze, M.; Cantore, V.; Todorovic, M.; Piscitelli, L.; Stellacci, A.M. Selection of Hyperspectral Vegetation Indices for Monitoring Yield and Physiological Response in Sweet Maize under Different Water and Nitrogen Availability. Agronomy 2022, 12, 489. [Google Scholar] [CrossRef]
  41. Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-Destructive Chlorophyll Assessment in Higher Plant Leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
  42. Arnó Satorra, J.; Martínez Casasnovas, J.A.; Ribes Dasi, M.; Rosell Polo, J.R. Precision Viticulture. Research Topics, Challenges and Opportunities in Site-Specific Vineyard Management. Span. J. Agric. Res. 2009, 7, 779–790. [Google Scholar] [CrossRef] [Green Version]
  43. Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band Model for Noninvasive Estimation of Chlorophyll, Carotenoids, and Anthocyanin Contents in Higher Plant Leaves. Geophys. Res. Lett. 2006, 33, 6457. [Google Scholar] [CrossRef] [Green Version]
  44. Gamon, J.A.; Penuelas, J.; Field, C.B. A Narrow-Waveband Spectral Index That Tracks Diurnal Changes in Photosynthetic Efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
  45. Serrano, L.; Penuelas, J.; Ustin, S.L. Remote Sensing of Nitrogen and Lignin in Mediterranean Vegetation from AVIRIS Data: Decomposing Biochemical from Structural Signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
  46. Badr, H.; Zaitchik, B.; Dezfuli, A. Hierarchical Climate Regionalization. Authorea Preprints. 2022. Available online: https://cran.r-project.org/web/packages/HiClimR/index.html (accessed on 5 March 2023).
  47. Liland, K.H.; Mevik, B.H.; Wehrens, R. Paul Hiemstra Partial Least Squares and Principal Component Regression. 2022. Available online: https://cran.r-project.org/web/packages/HiClimR/index.html (accessed on 5 March 2023).
  48. Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, R.C. Classification and Regression Training. R J. 2022, 223. Available online: https://cran.r-project.org/web/packages/pls/index.html (accessed on 5 March 2023).
  49. Li, Z.; Jin, X.; Yang, G.; Drummond, J.; Yang, H.; Clark, B.; Li, Z.; Zhao, C. Remote Sensing of Leaf and Canopy Nitrogen Status in Winter Wheat (Triticum aestivum L.) Based on N-PROSAIL Model. Remote Sens. 2018, 10, 1463. [Google Scholar] [CrossRef] [Green Version]
  50. Lu, J.; Yang, T.; Su, X.; Qi, H.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Monitoring Leaf Potassium Content Using Hyperspectral Vegetation Indices in Rice Leaves. Precis. Agric. 2020, 21, 324–348. [Google Scholar] [CrossRef]
  51. Galvez-Sola, L.; García-Sánchez, F.; Pérez-Pérez, J.G.; Gimeno, V.; Navarro, J.M.; Moral, R.; Martínez-Nicolás, J.J.; Nieves, M. Rapid Estimation of Nutritional Elements on Citrus Leaves by near Infrared Reflectance Spectroscopy. Front. Plant Sci. 2015, 6, 571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  52. Retzlaff, R.; Molitor, D.; Behr, M.; Bossung, C.; Rock, G.; Hoffmann, L.; Evers, D.; Udelhoven, T. UAS-Based Multi-Angular Remote Sensing of the Effects of Soil Management Strategies on Grapevine. OENO One 2015, 49, 85–102. [Google Scholar] [CrossRef] [Green Version]
  53. Gil-Pérez, B.; Zarco-Tejada, P.J.; Correa-Guimaraes, A.; Relea-Gangas, E.; Navas-Gracia, L.M.; Hernández-Navarro, S.; Sanz-Requena, J.F.; Berjón, A.; Martín-Gil, J. Remote Sensing Detection of Nutrient Uptake in Vineyards Using Narrow-Band Hyperspectral Imagery. Vitis 2010, 49, 167–173. [Google Scholar]
  54. Wei, H.-E.; Grafton, M.; Bretherton, M.; Irwin, M.; Sandoval, E. Evaluation of Point Hyperspectral Reflectance and Multivariate Regression Models for Grapevine Water Status Estimation. Remote Sens. 2021, 13, 3198. [Google Scholar] [CrossRef]
  55. Wu, D.; Sun, D.-W. Advanced Applications of Hyperspectral Imaging Technology for Food Quality and Safety Analysis and Assessment: A Review—Part I: Fundamentals. Innov. Food Sci. Emerg. Technol. 2013, 19, 1–14. [Google Scholar] [CrossRef]
  56. Hu, N.; Li, W.; Du, C.; Zhang, Z.; Gao, Y.; Sun, Z.; Yang, L.; Yu, K.; Zhang, Y.; Wang, Z. Predicting Micronutrients of Wheat Using Hyperspectral Imaging. Food Chem. 2021, 343, 128473. [Google Scholar] [CrossRef]
  57. Xiaobo, Z.; Jiewen, Z.; Povey, M.J.; Holmes, M.; Hanpin, M. Variables Selection Methods in Near-Infrared Spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef]
  58. Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep Learning in Remote Sensing Applications: A Meta-Analysis and Review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
  59. Axelsson, C.; Skidmore, A.K.; Schlerf, M.; Fauzi, A.; Verhoef, W. Hyperspectral Analysis of Mangrove Foliar Chemistry Using PLSR and Support Vector Regression. Int. J. Remote Sens. 2013, 34, 1724–1743. [Google Scholar] [CrossRef]
  60. Prado Osco, L.; Marques Ramos, A.P.; Roberto Pereira, D.; Akemi Saito Moriya, É.; Nobuhiro Imai, N.; Takashi Matsubara, E.; Estrabis, N.; de Souza, M.; Marcato Junior, J.; Gonçalves, W.N. Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery. Remote Sens. 2019, 11, 2925. [Google Scholar] [CrossRef] [Green Version]
  61. Curran, P.J. Remote Sensing of Foliar Chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
  62. Li, G.; Hu, Q.; Shi, Y.; Cui, K.; Nie, L.; Huang, J.; Peng, S. Low Nitrogen Application Enhances Starch-Metabolizing Enzyme Activity and Improves Accumulation and Translocation of Non-Structural Carbohydrates in Rice Stems. Front. Plant Sci. 2018, 9, 1128. [Google Scholar] [CrossRef] [PubMed]
  63. Tränkner, M.; Tavakol, E.; Jákli, B. Functioning of Potassium and Magnesium in Photosynthesis, Photosynthate Translocation and Photoprotection. Physiol. Plant. 2018, 163, 414–431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Murphy, R.J.; Whelan, B.; Chlingaryan, A.; Sukkarieh, S. Quantifying Leaf-Scale Variations in Water Absorption in Lettuce from Hyperspectral Imagery: A Laboratory Study with Implications for Measuring Leaf Water Content in the Context of Precision Agriculture. Precis. Agric. 2019, 20, 767–787. [Google Scholar] [CrossRef]
  65. Solanki, T.; García Plazaola, J.I.; Robson, T.M.; Fernández Marín, B. Freezing Induces an Increase in Leaf Spectral Transmittance of Forest Understorey and Alpine Forbs. Photochem. Photobiol. Sci. 2022, 21, 997–1009. [Google Scholar] [CrossRef]
Remotesensing 15 01497 g001 550
Figure 1. Location of study vineyards.
Figure 1. Location of study vineyards.
Remotesensing 15 01497 g001
Remotesensing 15 01497 g002 550
Figure 2. Distribution of sampling points in Wharekauhau (a) and Pencarrow (b). (N, P, K, Ca, and Mg were measured at red points; only N and P were measured at blue points).
Figure 2. Distribution of sampling points in Wharekauhau (a) and Pencarrow (b). (N, P, K, Ca, and Mg were measured at red points; only N and P were measured at blue points).
Remotesensing 15 01497 g002
Remotesensing 15 01497 g003 550
Figure 3. Histograms of N concentration (a), P concentration (b), K concentration (c), Ca concentration (d), and Mg concentration (e).
Figure 3. Histograms of N concentration (a), P concentration (b), K concentration (c), Ca concentration (d), and Mg concentration (e).
Remotesensing 15 01497 g003
Remotesensing 15 01497 g004 550
Figure 4. Pearson’s correlation between individual nutrients in the grapevine leaf samples.
Figure 4. Pearson’s correlation between individual nutrients in the grapevine leaf samples.
Remotesensing 15 01497 g004
Remotesensing 15 01497 g005 550
Figure 5. The spectral wavelength of raw reflectance (a), first derivative reflectance (b), and second derivative reflectance (c). Each color represents an individual sample spectrum.
Figure 5. The spectral wavelength of raw reflectance (a), first derivative reflectance (b), and second derivative reflectance (c). Each color represents an individual sample spectrum.
Remotesensing 15 01497 g005
Remotesensing 15 01497 g006 550
Figure 6. Biochemical variable prediction comparison against laboratory chemical measurement for the best algorithm’s results of N based on the PLSR model with the raw reflectance (a), P based on the SVR model with Pearson correlation selected from 1D variables (b), K based on the SVR model with Pearson correlation selected from 2D variables (c), Ca based on the SVR model with Pearson correlation selected from 2D variables (d), and Mg based on the SVR model with Pearson correlation selected from 2D variables (e). The blue line is the regression line, whilst the dotted line is the 1–1 line.
Figure 6. Biochemical variable prediction comparison against laboratory chemical measurement for the best algorithm’s results of N based on the PLSR model with the raw reflectance (a), P based on the SVR model with Pearson correlation selected from 1D variables (b), K based on the SVR model with Pearson correlation selected from 2D variables (c), Ca based on the SVR model with Pearson correlation selected from 2D variables (d), and Mg based on the SVR model with Pearson correlation selected from 2D variables (e). The blue line is the regression line, whilst the dotted line is the 1–1 line.
Remotesensing 15 01497 g006
Remotesensing 15 01497 g007 550
Figure 7. The variable importance for N based on the PLSR model with the raw reflectance (a), P based on the SVR model with Pearson correlation selected from 1D variables (b), K based on the SVR model with Pearson correlation selected from 2D variables (c), Ca based on the SVR model with Pearson correlation selected from 2D variables (d), and Mg based on the SVR model with Pearson correlation selected from 2D variables (e).
Figure 7. The variable importance for N based on the PLSR model with the raw reflectance (a), P based on the SVR model with Pearson correlation selected from 1D variables (b), K based on the SVR model with Pearson correlation selected from 2D variables (c), Ca based on the SVR model with Pearson correlation selected from 2D variables (d), and Mg based on the SVR model with Pearson correlation selected from 2D variables (e).
Remotesensing 15 01497 g007
Table
Table 2. The tuned hyperparameters and their criteria for each regression model.
Table 2. The tuned hyperparameters and their criteria for each regression model.
AlgorithmHyperparameterCriteria
Patrial least squares regressionNumber of components1:20
Random forest regressionNumber of trees250, 500, 750, 1000
Number of variables to be considered for the best split0.05, 0.15, 0.25, 0.33, 0.4 × feature numbers
Number of depths of the tree1, 3, 5, 10
Support vector regressionKernel functionRadial basis kernel
Table
Table 3. Descriptive statistics of vine leaf nutrient concentration.
Table 3. Descriptive statistics of vine leaf nutrient concentration.
Biochemical VariablesMinimum-MaximumMean ± SDCV
N (%/DW)0.97–2.51.77 ± 0.2514.12
P (%/DW)0.11–0.230.16 ± 0.0212.5
K (%/DW)0.45–0.820.63 ± 0.0812.7
Ca (%/DW)0.53–1.450.94 ± 0.1819.14
Mg (%/DW)0.1–0.220.16 ± 0.0212.5
Notes: “DW” refers to the dry weight; “CV” refers to coefficient of variation; “SD” refers to standard deviation.
Table
Table 4. Best modelling performance on the test dataset between different spectral data transformation methods.
Table 4. Best modelling performance on the test dataset between different spectral data transformation methods.
MethodN (n = 274)P (n = 274)K (n = 88)Ca (n = 88)Mg (n = 88)
PLSR
R20.660.120.060.380.07
RMSE0.150.020.10.140.02
Data typeRaw reflectanceRaw reflectanceSecond derivative reflectanceFirst derivative reflectanceFirst derivative reflectance
Variable sourceFull setFull setFull setFull setFull set
RFR
R20.60.130.350.510.26
RMSE0.170.020.070.140.02
Data typeFull setFirst derivative reflectanceSecond derivative reflectanceSecond derivative reflectanceSecond derivative reflectance
Variable sourceRFECV based on hierarchical clusteringRFECVPearson correlationPearson correlation based on hierarchical clusteringPearson correlation
SVR
R20.620.150.70.620.43
RMSE0.160.020.060.110.02
Data typeFull setFirst derivative reflectanceSecond derivative reflectanceSecond derivative reflectanceSecond derivative reflectance
Variable sourceRFECV based on hierarchical clusteringPearson correlationPearson correlationPearson correlationPearson correlation
Linear regression
R20.580.130.20.20.19
RMSE0.150.020.080.140.02
Variable sourceCARINDREGNDVIGNDVIN_1645_1715
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lyu, H.; Grafton, M.; Ramilan, T.; Irwin, M.; Sandoval, E. Assessing the Leaf Blade Nutrient Status of Pinot Noir Using Hyperspectral Reflectance and Machine Learning Models. Remote Sens. 2023, 15, 1497. https://doi.org/10.3390/rs15061497

AMA Style

Lyu H, Grafton M, Ramilan T, Irwin M, Sandoval E. Assessing the Leaf Blade Nutrient Status of Pinot Noir Using Hyperspectral Reflectance and Machine Learning Models. Remote Sensing. 2023; 15(6):1497. https://doi.org/10.3390/rs15061497

Chicago/Turabian Style

Lyu, Hongyi, Miles Grafton, Thiagarajah Ramilan, Matthew Irwin, and Eduardo Sandoval. 2023. "Assessing the Leaf Blade Nutrient Status of Pinot Noir Using Hyperspectral Reflectance and Machine Learning Models" Remote Sensing 15, no. 6: 1497. https://doi.org/10.3390/rs15061497

APA Style

Lyu, H., Grafton, M., Ramilan, T., Irwin, M., & Sandoval, E. (2023). Assessing the Leaf Blade Nutrient Status of Pinot Noir Using Hyperspectral Reflectance and Machine Learning Models. Remote Sensing, 15(6), 1497. https://doi.org/10.3390/rs15061497

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop