Tree-Species Classification and Individual-Tree-Biomass Model Construction Based on Hyperspectral and LiDAR Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. Airborne-Laser-Scanning Data
2.2.2. Remotely Sensed Optical Image
2.2.3. Field-Measured Data
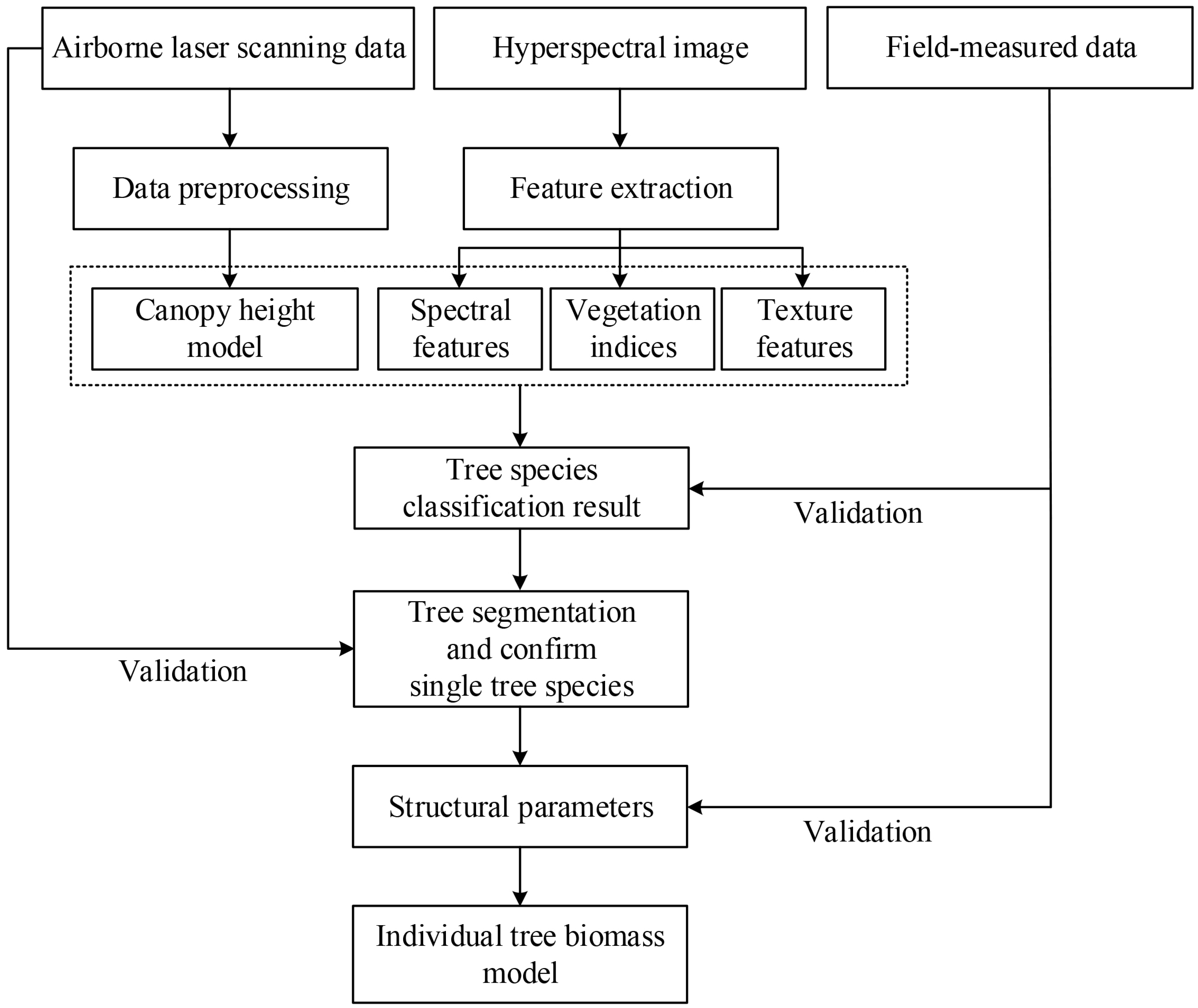
2.3. Overall Work
2.4. Data Preprocessing
2.5. Tree-Species Classification
2.5.1. Feature Extraction
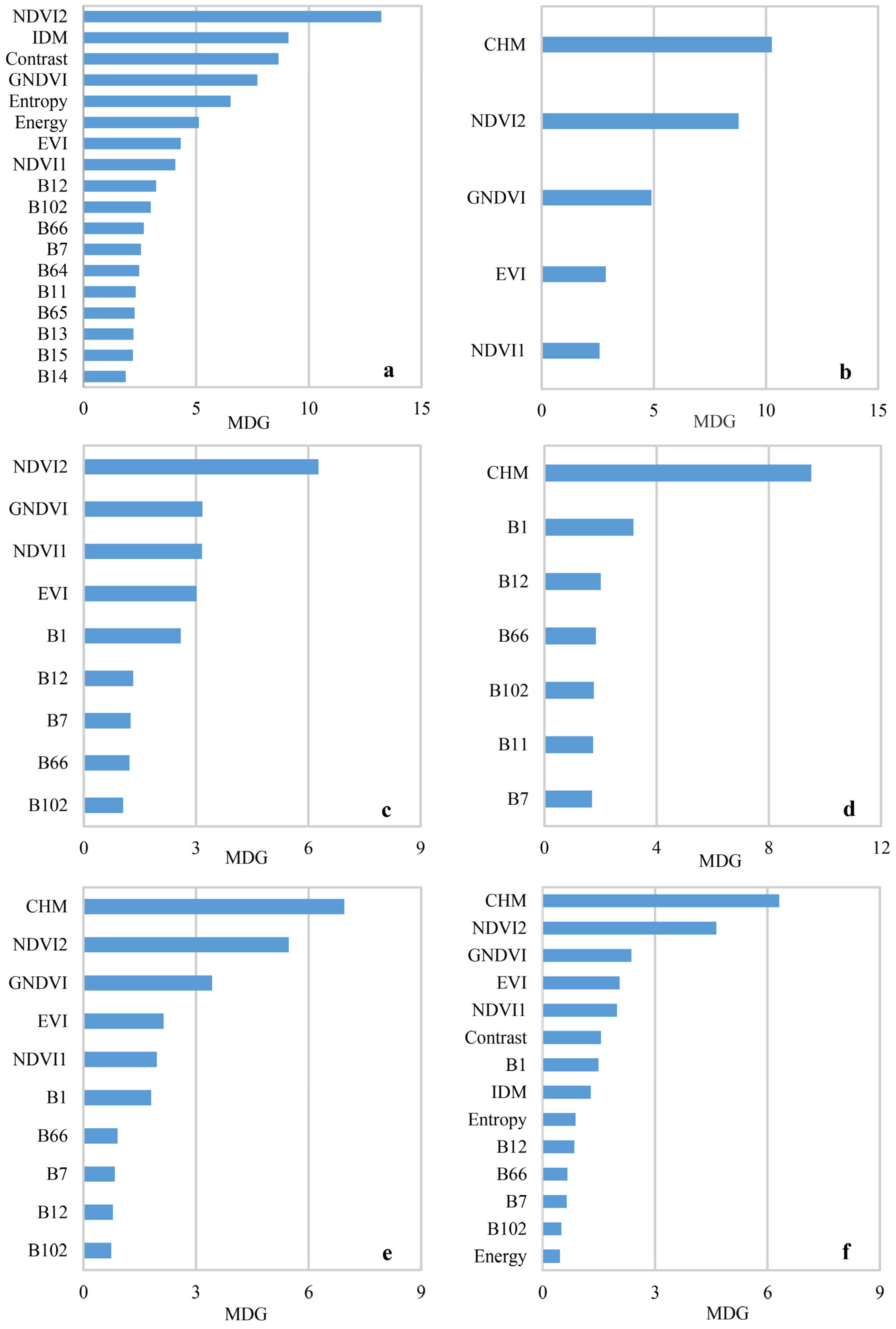
2.5.2. Optimal Variable Selection
2.6. Individual-Tree Biomass Model
2.6.1. Tree Segmentation
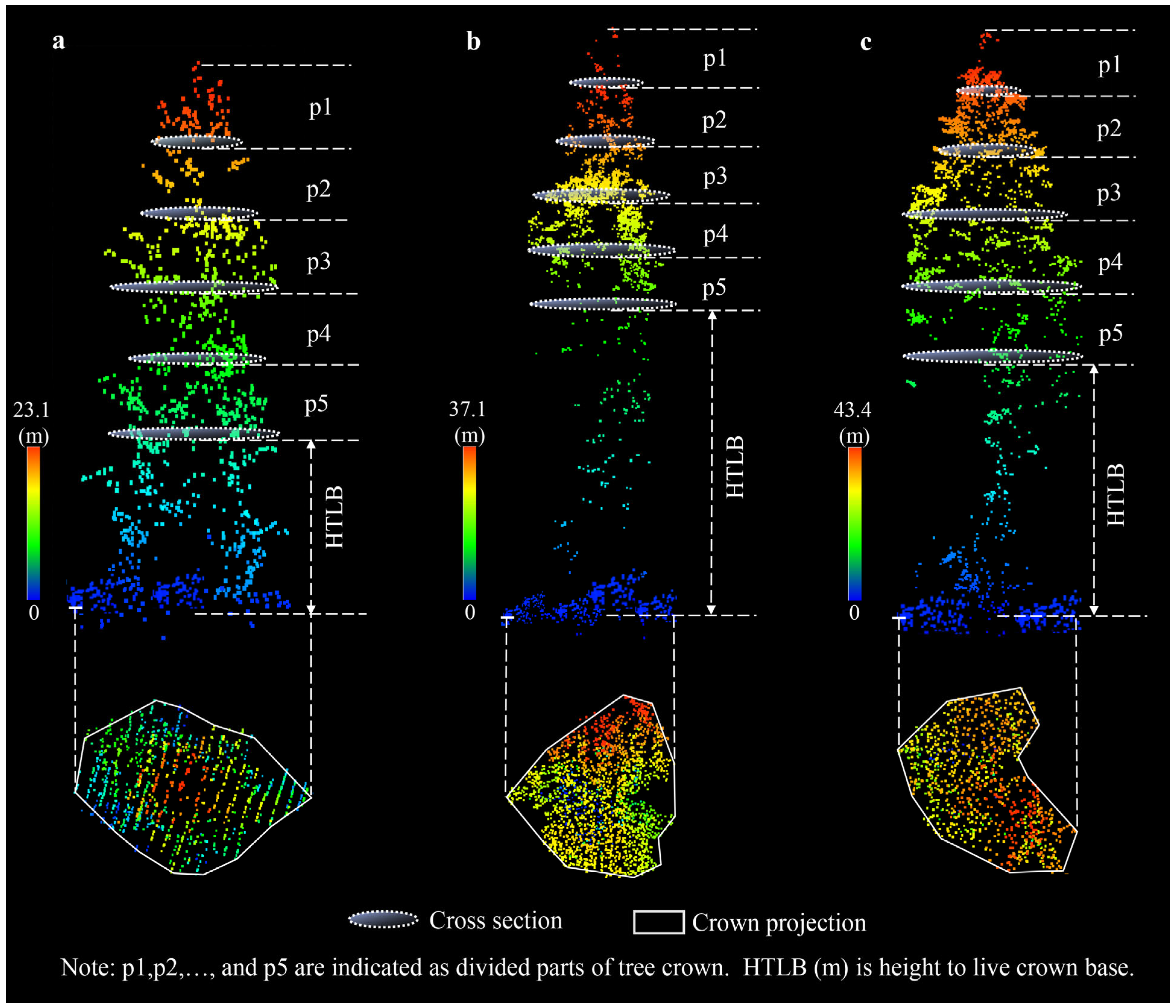
2.6.2. Crown Parameter Extraction
2.6.3. Multivariate Nonlinear Fitting
2.7. Accuracy Assessment
3. Results
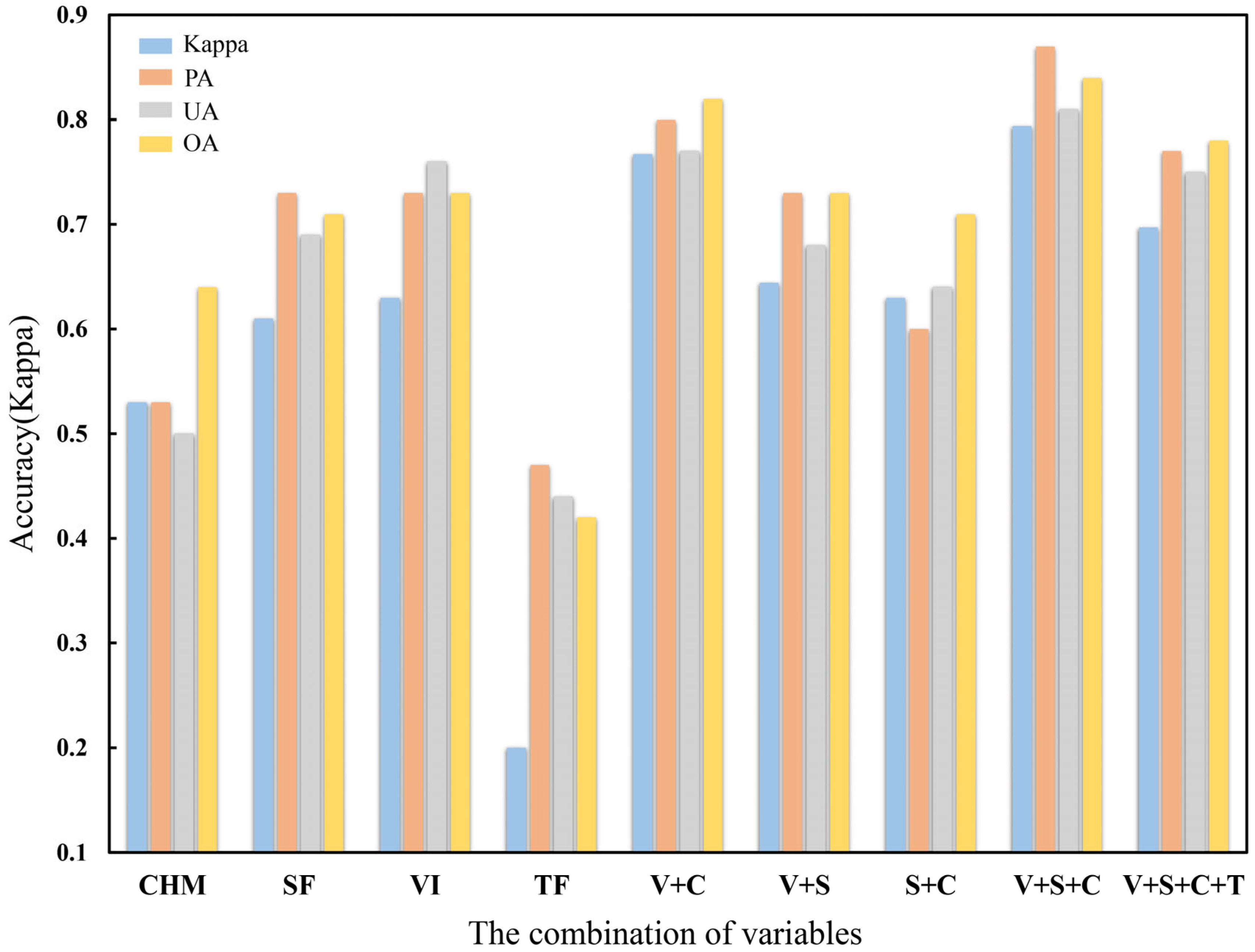
3.1. Results of Optimal Variable Selection
3.2. Tree Segmentation and Validation
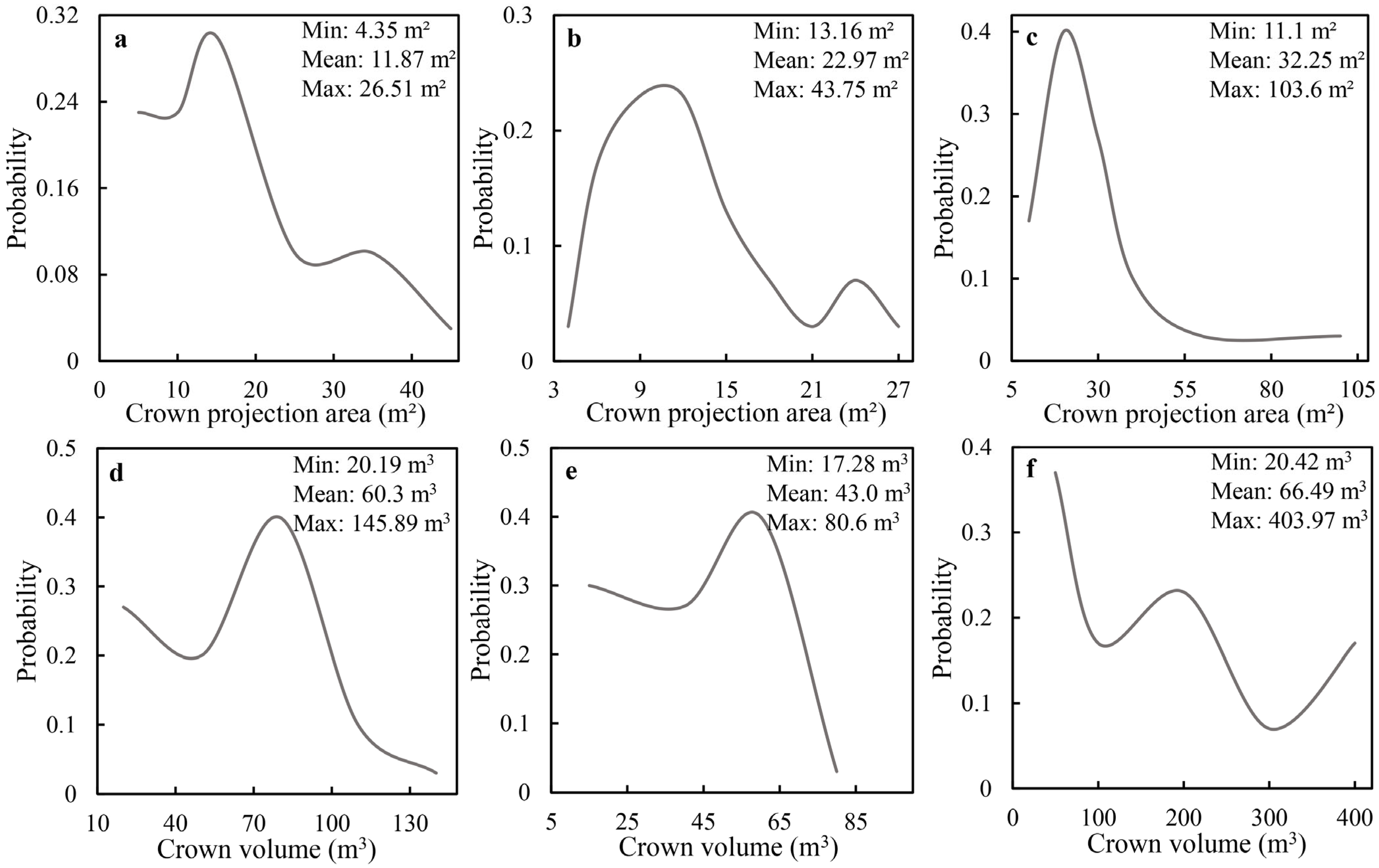
3.3. Results of the Tree-Crown-Parameter Extraction
3.4. Results of Individual-Tree-Biomass Model
4. Discussion
4.1. Feature Determination
4.2. Tree-Segmentation Accuracy Analysis
4.3. Effects of Crown Parameters on Biomass Models
5. Conclusions
- The selection of classification variables was critical for tree-species classification. The type and number of variables would affect classification results, and more variables have not produced better results. Variables could be selected based on the realities of the study area and the characteristics of trees.
- The tree height and crown size extracted by the algorithm were compared with the measured tree height and the results of visual interpretation. We found that they were consistent with the actual situation of trees in PC. The individual-tree parameters measured by ALS in this study could be used as variables in the biomass model.
- When tree height, crown size, projected area, and volume were introduced as variables into the biomass model, the fitting effects of the three tree species were all optimal. Thus, the introduction of crown parameters into biomass model construction was a feasible method to improve the estimation accuracy of forest individual-tree biomass.
Author Contributions
Funding
Conflicts of Interest
References
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.N.; et al. Individual Tree Detection and Classification with UAV-Based Photogrammetric Point Clouds and Hyperspectral Imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Yang, J.; Cooper, D.J.; Li, Z.; Song, W.; Zhang, Y.; Zhao, B.; Han, S.; Wang, X. Differences in Tree and Shrub Growth Responses to Climate Change in a Boreal Forest in China. Dendrochronologia 2020, 63, 125744. [Google Scholar] [CrossRef]
- Sarker, L.R.; Nichol, J.E. Improved Forest Biomass Estimates Using ALOS AVNIR-2 Texture Indices. Remote Sens. Environ. 2011, 115, 968–977. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest Biomass Estimation from Airborne LiDAR Data Using Machine Learning Approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban Tree Species Mapping Using Hyperspectral and LiDAR Data Fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Knapp, D.E.; Tupayachi, R.; Anderson, C.; Carranza, L.; Martinez, P.; Houcheime, M.; Sinca, F.; Weiss, P. Spectroscopy of Canopy Chemicals in Humid Tropical Forests. Remote Sens. Environ. 2011, 115, 3587–3598. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree Species Classification in the Southern Alps Based on the Fusion of Very High Geometrical Resolution Multispectral/Hyperspectral Images and LiDAR Data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Tan, B.; Li, Z.; Chen, E.; Pang, Y.; Wu, H. Research Advance in Forest Information Extraction from Hyperspectral Remote Sensing Data. For. Res. 2008, 21, 105–111. [Google Scholar]
- Zhang, W.; Li, X.; Dou, Y.; Zhao, L. A Geometry-Based Band Selection Approach for Hyperspectral Image Analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4318–4333. [Google Scholar] [CrossRef]
- Koukoulas, S.; Blackburn, G.A. Mapping Individual Tree Location, Height and Species in Broadleaved Deciduous Forest Using Airborne LiDAR and Multi-spectral Remotely Sensed Data. Int. J. Remote Sens. 2005, 26, 431–455. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating Individual Trees in a Savanna Woodland Using Small Footprint LiDAR Data. Photogramm. Eng. Remote Sens. J. Am. Soc. Photogramm. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Pang, Y.; Zhao, F.; Li, Z.; Zhou, S.; Deng, G.; Liu, Z.; Chen, E. Forest Height Inversion Using Airborne LiDAR Technology. Natl. Remote Sens. Bull. 2008, 12, 152–158. [Google Scholar]
- He, Q.; Chen, E.; Cao, C.; Liu, Q.; Pang, Y. A Study of Forest Parameters Mapping Technique Using Airborne LiDAR Data. Adv. Earth Sci. 2009, 24, 748–755. [Google Scholar]
- Liu, L.; Pang, Y.; Fan, W.; Li, Z.; Zhang, D.; Li, M. Fused Airborne LiDAR and Hyperspectral Data for Tree Species Identification in a Natural Temperate Forest. Natl. Remote Sens. Bull. 2013, 17, 679–695. [Google Scholar]
- Liu, J.; Wu, Z.; Li, J.; Plaza, A.; Yuan, Y. Probabilistic-Kernel Collaborative Representation for Spatial–Spectral Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2371–2384. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual Tree Biomass Estimation Using Terrestrial Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Usol’Tsev, V.A.; Shobairi, S.; Chasovskikh, V. Additive Allometric Models of Single-tree Biomass of Two-needled Pines as a Basis of Regional Mensuration Standards for Eurasia. Plant Arch. 2018, 18, 2752–2758. [Google Scholar]
- Feng, Z. Some Problems and Perfect Approaches of Research on Forest Biomass. World For. Res. 2005, 18, 25–28. [Google Scholar]
- Liu, H.; Fan, W.; Xu, Y.; Lin, W. Single Tree Biomass Estimation Based on UAV LiDAR Point Cloud. J. Cent. South Univ. For. Technol. 2021, 41, 92–99. [Google Scholar]
- Xu, H. A Comparison between CAR and VAR Biomass Models. J. Sourthwest For. Univ. 2003, 23, 36–39. [Google Scholar]
- Feng, Z.; Luo, X.; Ma, Q.; Hao, X.; Chen, X.; Zhao, L. An Estimation of Tree Canopy Biomass Based on 3D Laser Scanning Imaging System. J. Beijing For. Univ. 2007, 29, 52–56. [Google Scholar]
- Wang, X.; Zheng, G.; Yun, Z.; Xu, Z.; Moskal, L.M.; Tian, Q. Characterizing the Spatial Variations of Forest Sunlit and Shaded Components Using Discrete Aerial Lidar. Remote Sens. 2020, 12, 1071. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Individual Tree Segmentation and Tree Species Classification in Subtropical Broadleaf Forests Using UAV-based LiDAR, Hyperspectral, and Ultrahigh-resolution RGB Data. Remote Sens. Environ. 2022, 280, 113143. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Li, G. Above-ground Biomass Estimation Using Airborne Discrete-return and Full-waveform LiDAR Data in a Coniferous Forest. Ecol. Indic. 2017, 78, 221–228. [Google Scholar] [CrossRef]
- Li, H.; Hu, B.; Li, Q.; Jing, L. CNN-Based Individual Tree Species Classification Using High-Resolution Satellite Imagery and Airborne LiDAR Data. Forests 2021, 12, 1697. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Daloye, A.M.; Erkbol, H.; Fritschi, F.B. Crop Monitoring Using Satellite/UAV Data Fusion and Machine Learning. Remote Sens. 2020, 12, 1357. [Google Scholar] [CrossRef]
- Omer, G.; Mutanga, O.; Abdel-Rahman, E.M.; Adam, E. Empirical Prediction of Leaf Area Index (LAI) of Endangered Tree Species in Intact and Fragmented Indigenous Forests Ecosystems Using WorldView-2 Data and Two Robust Machine Learning Algorithms. Remote Sens. 2016, 8, 324. [Google Scholar] [CrossRef]
- Nouri, H.; Beecham, S.; Anderson, S.; Nagler, P. High Spatial Resolution WorldView-2 Imagery for Mapping NDVI and Its Relationship to Temporal Urban Landscape Evapotranspiration Factors. Remote Sens. 2014, 6, 580–602. [Google Scholar] [CrossRef]
- Pu, R. Mapping Urban Forest Tree Species Using IKONOS Imagery: Preliminary Results. Environ. Monit. Assess. 2011, 172, 199–214. [Google Scholar] [CrossRef]
- Pu, R.; Landry, S. A Comparative Analysis of High Spatial Resolution IKONOS and WorldView-2 Imagery for Mapping Urban Tree Species. Remote Sens. Environ. 2012, 124, 516–533. [Google Scholar] [CrossRef]
- Liu, L.; Kuang, G. Overview of Image Textural Feature Extraction Methods. J. Image Graph. 2009, 14, 622–635. [Google Scholar]
- Chen, D.; Stow, D.; Gong, P. Examining the Effect of Spatial Resolution and Texture Window Size on Classification Accuracy: An Urban Environment Case. Int. J. Remote Sens. 2004, 25, 2177–2192. [Google Scholar] [CrossRef]
- Pan, C.; Lin, Y.; Chen, Y. Decision Tree Classification of Remote Sensing Images Based on Multi-feature. J. Optoelectron. Laser 2010, 21, 731–736. [Google Scholar]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, G.; Moskal, L.M. Stratifying Forest Overstory for Improving Effective LAI Estimation Based on Aerial Imagery and Discrete Laser Scanning Data. Remote Sens. 2020, 12, 2126. [Google Scholar] [CrossRef]
- Gong, Y.; He, C.; Feng, Z.; Li, W.; Yan, F. Amended Delaunay Algorithm for Single Tree Factor Extraction Using 3-D Crown Modeling. Trans. Chin. Soc. Agric. Mach. 2013, 44, 192–199. [Google Scholar]
- Yu, D.; Feng, Z. Tree Crown Volume Measurement Method Based on Oblique Aerial Images of UAV. Trans. Chin. Soc. Agric. Eng. 2019, 35, 90–97. [Google Scholar]
- Gonzalez-Benecke, C.A.; Flamenco, H.N.; Wightman, M.G. Effect of Vegetation Management and Site Conditions on Volume, Biomass and Leaf Area Allometry of Four Coniferous Species in the Pacific Northwest United States. Forests 2018, 9, 581. [Google Scholar] [CrossRef]
- Poudel, K.P.; Temesgen, H. Developing Biomass Equations for Western Hemlock and Red Alder Trees in Western Oregon Forests. Forests 2016, 7, 88. [Google Scholar] [CrossRef]
- Peterson, E.B.; Peterson, N.M.; Comeau, P.; Thomas, K.D. Bigleaf Maple Managers’ Handbook for British Columbia; British Columbia, Ministry of Forests Research Program: Terrace, BC, Canada, 1999. Available online: https://www.for.gov.bc.ca/hfd/pubs/Docs/Mr/Mr090.htm (accessed on 13 December 2022).
- Xu, H. A Biomass Model Compatible with Volume. J. Beijing For. Univ. 1999, 21, 32–36. [Google Scholar]
- Ly, A.; Marsman, M.; Wagenmakers, E.-J. Analytic Posteriors for Pearson’s Correlation Coefficient. Stat. Neerl. 2018, 72, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Hollaus, M.; Wagner, W.; Eberhöfer, C.; Karel, W. Accuracy of Large-scale Canopy Heights Derived from LiDAR Data Under Operational Constraints in a Complex Alpine Environment. ISPRS J. Photogramm. Remote Sens. 2006, 60, 323–338. [Google Scholar] [CrossRef]
- Zhao, D.; Pang, Y.; Li, Z.; Sun, G. Filling Invalid Values in a LiDAR-derived Canopy Height Model with Morphological Crown Control. Int. J. Remote Sens. 2013, 34, 4636–4654. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of Personal Laser Scanning in Forestry Inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef] [PubMed]
- Buddenbaum, H.; Schlerf, M.; Hill, J. Classification of Coniferous Tree Species and Age Classes Using Hyperspectral Data and Geostatistical Methods. Int. J. Remote Sens. 2005, 26, 5453–5465. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X. Object-oriented Tree Species Classification with Multi-scale Texture Features Based on Airborne Hyperspectral Images. J. Beijing For. Univ. 2020, 42, 91–101. [Google Scholar]
- Wang, X.; Zheng, G.; Yun, Z.; Moskal, L.M. Characterizing Tree Spatial Distribution Patterns Using Discrete Aerial Lidar Data. Remote Sens. 2020, 12, 712. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. A Robust Approach for Tree Segmentation in Deciduous Forests Using Small-footprint Airborne LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 532–541. [Google Scholar] [CrossRef]
- Zheng, G.; Ma, L.; Eitel, J.U.H.; He, W.; Magney, T.S.; Moskal, L.M.; Li, M. Retrieving Directional Gap Fraction, Extinction Coefficient, and Effective Leaf Area Index by Incorporating Scan Angle Information From Discrete Aerial Lidar Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 577–590. [Google Scholar] [CrossRef]
- Nelson, R.; Swift, R.; Krabill, W. Using Airborne Lasers to Estimate Forest Canopy and Stand Characteristics. J. For. 1988, 86, 31–38. [Google Scholar]
- Pang, Y.; Li, Z.; Chen, E.; Sun, G. LiDAR Remote Sensing Technology and Its Application in Forestry. Sci. Silvae Sin. 2005, 41, 129–136. [Google Scholar]
- Zhang, Z.; Cao, L.; She, G. Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree Species Classification and Estimation of Stem Volume and DBH Based on Single Tree Extraction by Exploiting Airborne Full-waveform LiDAR Data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]




| Category | Parameter | Name and Value |
|---|---|---|
| ALS data | Sensor | Leica ALS60 |
| Field of view (°) | 28 | |
| Flight height (m) | 900 | |
| Pulse rate (kHz) | 105 | |
| Accuracy (m) | 0.03 | |
| Overlap | 100% (50% side-lap) | |
| Average point density (points/m2) | 20 | |
| Hyperspectral data | Sensor | HyMap |
| Spectral range (nm) | 400~2500 | |
| Spectral resolution (nm) | 15~16 | |
| Spatial resolution (m) | 2.9 | |
| Field of view (°) | 61.3 |
| Plot | Tree Number | Forest Type | Mean DBH (cm) | Mean Height (m) | Mean HTLB (m) |
|---|---|---|---|---|---|
| PC-1 | 65 | C | 13.85 | 9.88 | 1.19 |
| PC-2 | 44 | M | 10.38 | 7.43 | 1.37 |
| PC-3 | 43 | M | 20.27 | 17.36 | 9.94 |
| PC-4 | 43 | C | 29.56 | 25.14 | 13.56 |
| PC-5 | 28 | M | 31.19 | 25.65 | 15.99 |
| PC-6 | 78 | M | 16.04 | 7.34 | 5.86 |
| PC-7 | 31 | M | 40.82 | 27.56 | 17.47 |
| PC-8 | 38 | M | 31.52 | 21.13 | 11.94 |
| PC-9 | 45 | M | 29.95 | 24.41 | 15.60 |
| PC-10 | 46 | M | 39.42 | 26.93 | 16.39 |
| PC-11 | 50 | C | 27.67 | 21.61 | 14.60 |
| PC-12 | 73 | C | 6.66 | 5.23 | 0.02 |
| PC-13 | 22 | B | 44.00 | 23.50 | 13.97 |
| PC-14 | 43 | M | 24.16 | 20.96 | 12.28 |
| PC-15 | 60 | B | 18.01 | 17.80 | 10.26 |
| PC-16 | 49 | M | 21.88 | 13.60 | 7.79 |
| PC-17 | 68 | M | 26.84 | 25.20 | 19.06 |
| PC-18 | 73 | M | 18.99 | 17.26 | 9.63 |
| PC-19 | 121 | M | 15.65 | 14.82 | 8.05 |
| Mean | 54 | - | 24.57 | 18.57 | 10.79 |
| Parameter Category | Index | Formula | Name and Description |
|---|---|---|---|
| Vegetation indices | NDVI1 | (NIR1 − RED)/(NIR1 + RED) | Normalized Difference Vegetation Index-NIR1. |
| NDVI2 | (NIR2 − RED)/(NIR2 + RED) | Normalized Difference Vegetation Index-NIR2. | |
| GNDVI | (NIR1 − GREEN)/(NIR1 + GREEN) | Green Normalized Difference Vegetation Index. | |
| EVI | 2.5 (NIR1 − RED)/(NIR1 + 6 RED − 7.5 BLUE + 1) | Enhanced Vegetation Index. | |
| Texture features | Energy | A measure of the stability of grayscale changes. | |
| Entropy | Randomness measures the amount of information contained in an image. | ||
| Contrast | Grooves that reflect the clarity and texture of the image. | ||
| IDM | Reflect the homogeneity of the image texture and measure the local changes in the image texture. |
| Tree Species | Allometric Equation |
|---|---|
| Douglas fir (Genus Pseudotsuga) | |
| Red alder (Alnus rubra) | |
| Bigleaf maple (Acer macrophyllum Pursh) | |
| Plot ID | Density | Tree | Forest Type | Segmented Tree | Tree- Detection Rate | Tree Location RMSE (m) | Crown Radius RMSE (m) |
|---|---|---|---|---|---|---|---|
| PC-MC | Medium | 181 | C | 167 | 90% | 0.72 | 1.88 |
| PC-HC | High | 50 | C | 46 | 87% | 1.52 | 2.3 |
| PC-LB | Low | 22 | B | 18 | 89% | 1.47 | 1.77 |
| PC-HB | High | 60 | B | 50 | 90% | 1.95 | 1.83 |
| PC-LM | Low | 72 | M | 66 | 92% | 1.32 | 1.65 |
| PC-MM | Medium | 78 | M | 56 | 89% | 1.40 | 1.2 |
| PC-HM | High | 557 | M | 468 | 84% | 2.65 | 1.73 |
| Tree Species | Biomass Models | Parameter Estimation | Goodness of Fit | |||||
|---|---|---|---|---|---|---|---|---|
| a1 | a2 | a3 | a4 | a5 | R2 | RMSE (kg·Plant−1) | ||
| Douglas fir | 1 | 0.923 | 1.576 | 0.134 | - | - | 0.84 | 6.472 |
| 2 | 0.78 | 1.607 | 0.105 | 0.055 | - | 0.843 | 6.083 | |
| 3 | 0.962 | 1.206 | 0.157 | 0.191 | - | 0.871 | 5.514 | |
| 4 | 0.888 | 1.232 | 0.141 | 0.185 | 0.027 | 0.871 | 5.477 | |
| Red alder | 1 | 1.835 | 1.523 | 0.336 | - | - | 0.637 | 9.06 |
| 2 | 2.52 | 1.412 | 0.355 | −0.065 | - | 0.654 | 9 | |
| 3 | 1.119 | 1.706 | 0.208 | 0.127 | - | 0.68 | 8.8 | |
| 4 | 0.028 | 1.559 | 0.165 | 0.182 | 1.241 | 0.709 | 8.11 | |
| Bigleaf maple | 1 | 16.058 | −0.094 | 0.787 | - | - | 0.496 | 29.26 |
| 2 | 6.453 | 0.002 | 0.336 | 0.422 | - | 0.601 | 27.71 | |
| 3 | 0.184 | 0.144 | 0.318 | 1.062 | - | 0.724 | 19.1 | |
| 4 | 0.008 | −0.383 | 0.075 | −0.038 | 2.184 | 0.790 | 18.05 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Y.; Zheng, G.; Du, Z.; Ma, X.; Li, J.; Moskal, L.M. Tree-Species Classification and Individual-Tree-Biomass Model Construction Based on Hyperspectral and LiDAR Data. Remote Sens. 2023, 15, 1341. https://doi.org/10.3390/rs15051341
Qiao Y, Zheng G, Du Z, Ma X, Li J, Moskal LM. Tree-Species Classification and Individual-Tree-Biomass Model Construction Based on Hyperspectral and LiDAR Data. Remote Sensing. 2023; 15(5):1341. https://doi.org/10.3390/rs15051341
Chicago/Turabian StyleQiao, Yifan, Guang Zheng, Zihan Du, Xiao Ma, Jiarui Li, and L. Monika Moskal. 2023. "Tree-Species Classification and Individual-Tree-Biomass Model Construction Based on Hyperspectral and LiDAR Data" Remote Sensing 15, no. 5: 1341. https://doi.org/10.3390/rs15051341
APA StyleQiao, Y., Zheng, G., Du, Z., Ma, X., Li, J., & Moskal, L. M. (2023). Tree-Species Classification and Individual-Tree-Biomass Model Construction Based on Hyperspectral and LiDAR Data. Remote Sensing, 15(5), 1341. https://doi.org/10.3390/rs15051341







