Adaptive-Attention Completing Network for Remote Sensing Image
Abstract
1. Introduction
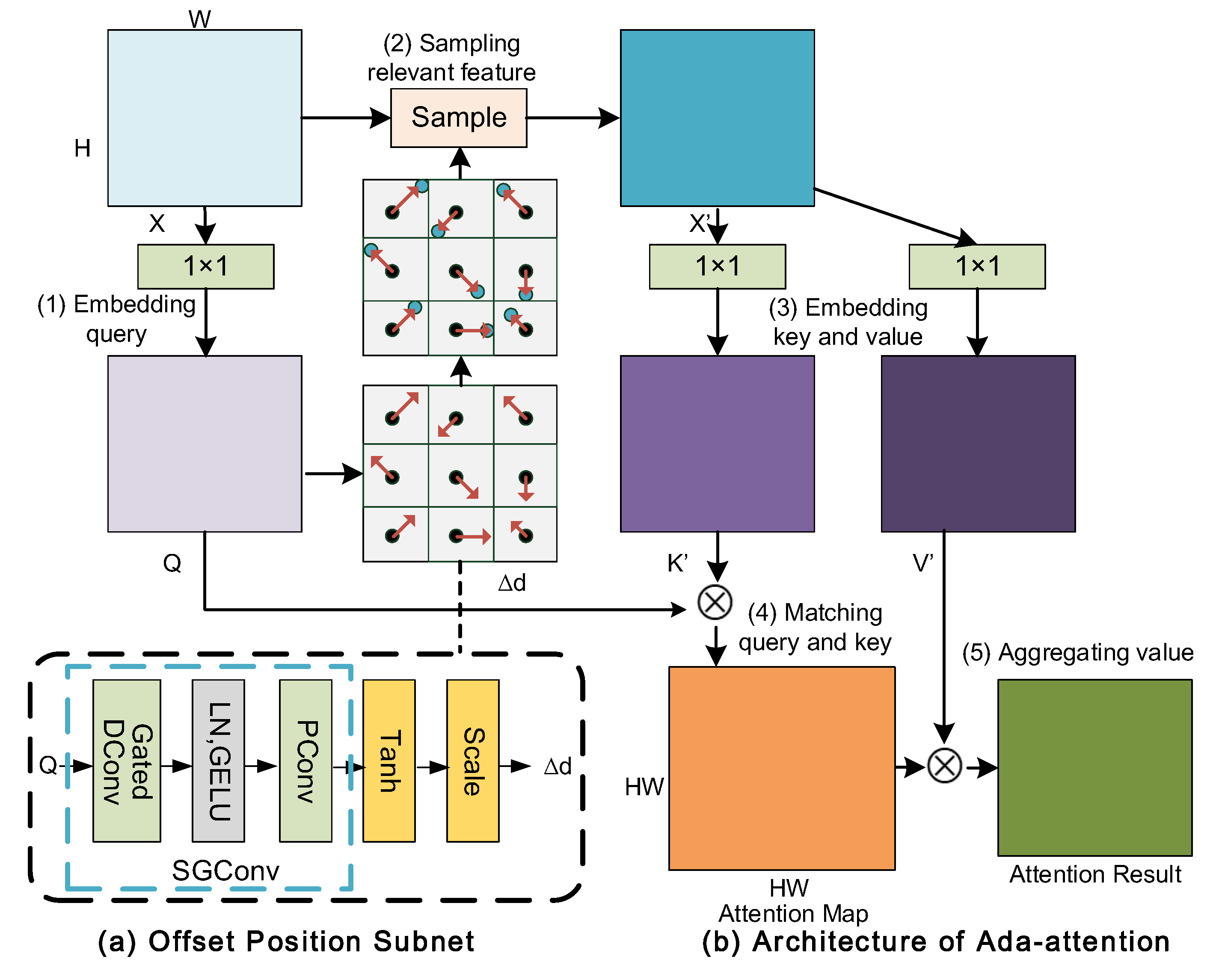
- We proposed an Adaptive Attention (Ada-attention) that utilizes an offset position subnet to dynamically select more relevant keys and values and enhance the attention capacity when modeling more informative long-term dependencies.
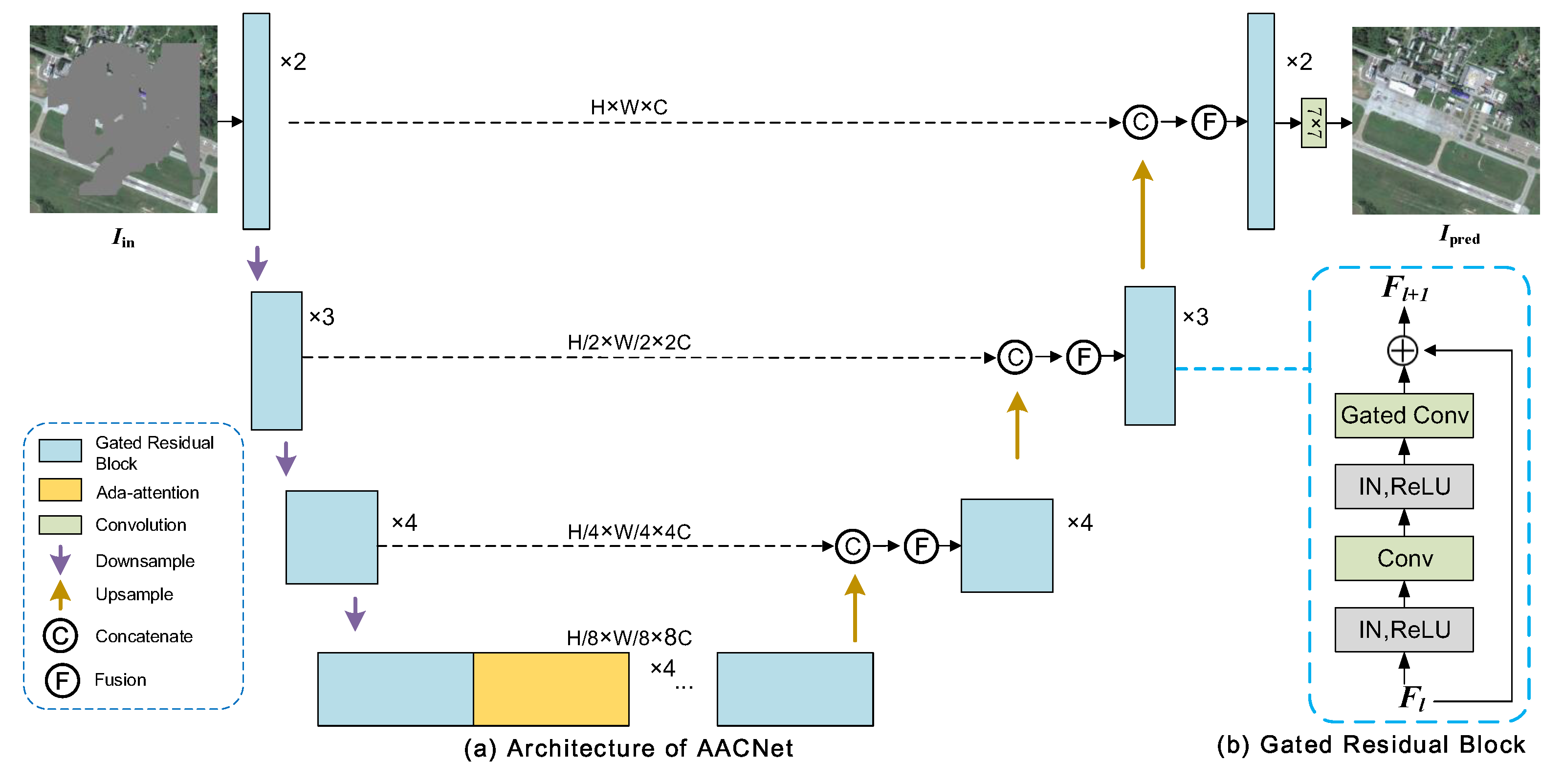
- We customized a U-shaped Adaptive-attention Completing Network (AACNet) for remote sensing images that stack gated residual blocks and our proposed Ada-attention modules.
- Extensive experiments were conducted on multiple datasets, and the results demonstrated that the proposed attention focused on more informative global features than standard self-attention, and our AACNet reconstruction results outperformed the state-of-the-art baselines.
2. Related Work
2.1. Missing Information Reconstruction of Remote Sensing Images
2.2. Learning-Based Image Inpainting
2.3. Attention Mechanism
3. Methodology
3.1. Network Architecture
3.1.1. Encoder
3.1.2. Decoder
3.1.3. Gated Residual Block
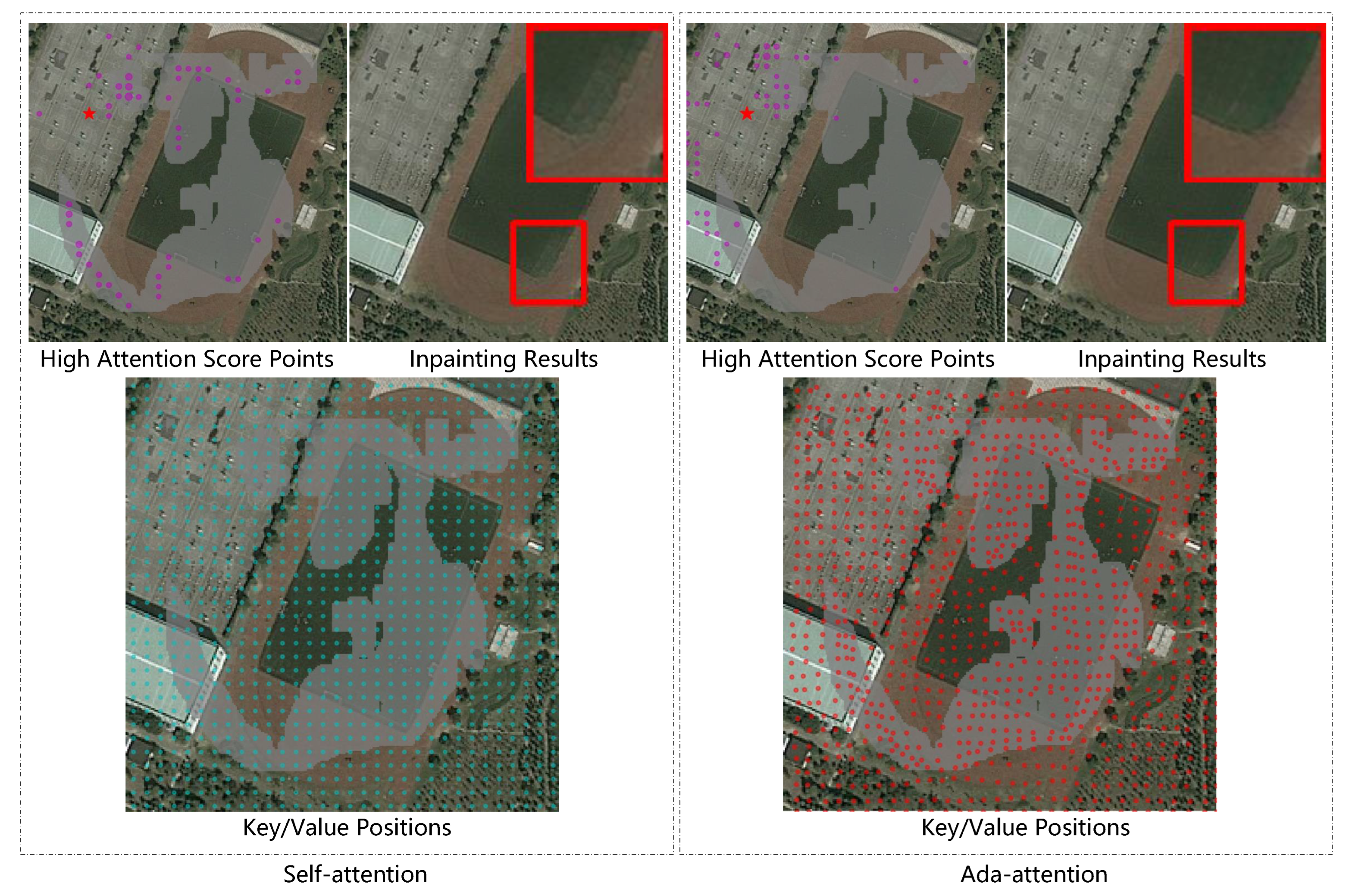
3.2. Adaptive Attention (Ada-Attention)
3.2.1. Self-Attention
3.2.2. Single Head Ada-Attention
3.2.3. Multi-Group Multi-Head Ada-Attention
| Algorithm 1 Pseudo-code for multi-group multi-head Ada-attention |
| Input:X, a feature map of shape (batch size, channel, height, width); , number of heads; G, number of groups Output: out, result of multi-group multi-head Ada-attention with shape .
|
3.2.4. Complexity Analysis
3.3. Inpainting Loss
4. Experiments
4.1. Experiments Details
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.1.3. Implementation Details
4.2. Performance of AACNet
4.2.1. Comparison Baselines
- DSN [5]. This adopts the deformable convolution and regional composite normalization into a parallel U-Net model to dynamically select features and normalization styles to outperform completion images.
- LaMa [44]. This uses fast Fourier convolutions to capture broad receptive fields on large training masks with lower parameter and time costs and achieves an excellent performance.
- InRSI [2]. Based on single source data, this adopts the two-stage generator with gated convolutions and attentions. It also introduces local and global patch-GAN to jointly generate better contents for the RS image.
- BC [43]. This proposes a bilateral convolution to generate useful features from known data and utilizes multi-range window attention to capture wide dependencies and reconstruct missing data in the RS image.
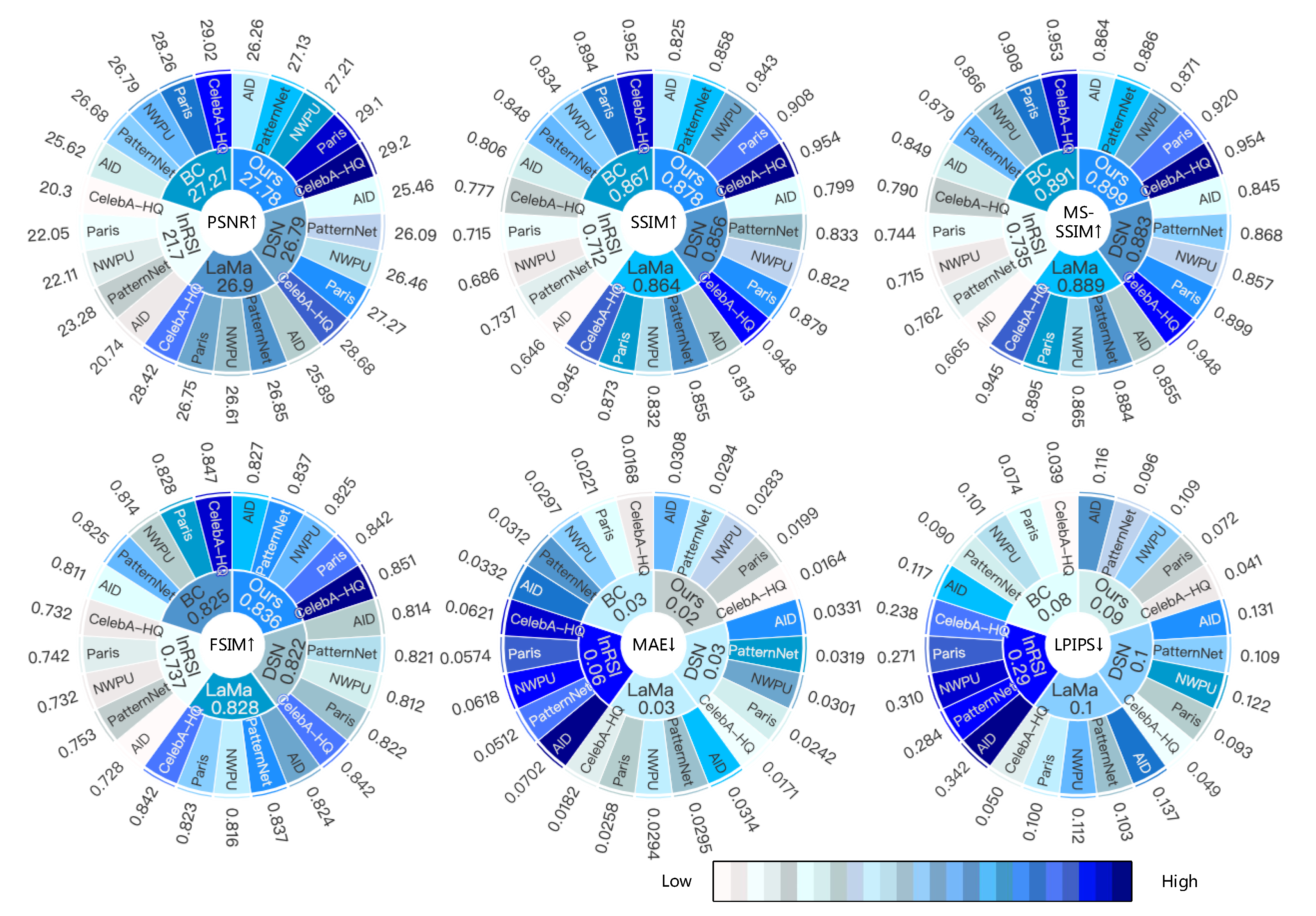
4.2.2. Quantiative Comparison with Baselines
4.2.3. Qualitative Comparison with Baselines
4.3. Real Data Experiment
4.4. Ablation Study
4.4.1. Effectiveness of Our Ada-Attention
4.4.2. Attention-Focusing Ability Analysis
4.4.3. Attention Module Position Analysis
4.4.4. Parameter Efficiency
4.4.5. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RS | remote sensing |
| AACNet | adaptive-attention completing network |
| Ada-attention | adaptive attention |
| SGConv | separable gated convolution |
| MHSA | multi-head self-attention |
| CNNs | convolutional neural networks |
| NLP | natural language processing |
| SLC | scan line corrector |
| MODIS | moderate-resolution imaging spectroradiometer |
| PC | partial convolution |
| GC | gated convolution |
| RN | region normalization |
| DSN | dynamic selection network |
| RFR | recurrent feature reasoning network |
| BC | bilateral convolution |
| LaMa | large mask inpainting |
| InRSI | inpainting-on-RSI |
| IN | instance normalization |
| ReLU | rectified linear unit |
| GELU | gaussian error linear unit |
| LN | layer normalization |
| GAN | generative adversarial network |
| PSNR | peak signal-to-noise ratio |
| SSIM | structural similarity index measure |
| MAE | mean absolute error |
References
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Shao, M.; Wang, C.; Wu, T.; Meng, D.; Luo, J. Context-based multiscale unified network for missing data reconstruction in remote sensing images. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context Encoders: Feature Learning by Inpainting. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. ACM Trans. Graph. (ToG) 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Y.; Zhang, L. Dynamic selection network for image inpainting. IEEE Trans. Image Process. 2021, 30, 1784–1798. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative Image Inpainting with Contextual Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zeng, Y.; Fu, J.; Chao, H.; Guo, B. Learning Pyramid-Context Encoder Network for High-Quality Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Li, X.; Shen, H.; Zhang, L.; Zhang, H.; Yuan, Q. Dead pixel completion of aqua MODIS band 6 using a robust M-estimator multiregression. IEEE Geosci. Remote Sens. Lett. 2013, 11, 768–772. [Google Scholar]
- Wang, Q.; Wang, L.; Li, Z.; Tong, X.; Atkinson, P.M. Spatial–spectral radial basis function-based interpolation for Landsat ETM+ SLC-off image gap filling. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7901–7917. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhang, L. Recovering missing pixels for Landsat ETM+ SLC-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing data reconstruction in remote sensing image with a unified spatial–temporal–spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Zhang, L.; Tao, D.; Zeng, C. Compressed sensing-based inpainting of aqua moderate resolution imaging spectroradiometer band 6 using adaptive spectrum-weighted sparse Bayesian dictionary learning. IEEE Trans. Geosci. Remote Sens. 2013, 52, 894–906. [Google Scholar] [CrossRef]
- Scaramuzza, P.; Barsi, J. Landsat 7 scan line corrector-off gap-filled product development. In Proceedings of the Pecora, Sioux Falls, SD, USA, 23–27 October 2005; Volume 16, pp. 23–27. [Google Scholar]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Li, H.; Zhang, L. Patch matching-based multitemporal group sparse representation for the missing information reconstruction of remote-sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3629–3641. [Google Scholar] [CrossRef]
- Cheng, Q.; Shen, H.; Zhang, L.; Yuan, Q.; Zeng, C. Cloud removal for remotely sensed images by similar pixel replacement guided with a spatio-temporal MRF model. ISPRS J. Photogramm. Remote Sens. 2014, 92, 54–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C.; Wu, Y.; Luo, J. Remote sensing image cloud removal by deep image prior with a multitemporal constraint. Opt. Contin. 2022, 1, 215–226. [Google Scholar] [CrossRef]
- Ji, T.Y.; Yokoya, N.; Zhu, X.X.; Huang, T.Z. Nonlocal tensor completion for multitemporal remotely sensed images’ inpainting. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3047–3061. [Google Scholar] [CrossRef]
- Ng, M.K.P.; Yuan, Q.; Yan, L.; Sun, J. An adaptive weighted tensor completion method for the recovery of remote sensing images with missing data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3367–3381. [Google Scholar] [CrossRef]
- Yu, C.; Chen, L.; Su, L.; Fan, M.; Li, S. Kriging interpolation method and its application in retrieval of MODIS aerosol optical depth. In Proceedings of the 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–6. [Google Scholar]
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image inpainting. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 417–424. [Google Scholar]
- Barcelos, C.A.Z.; Batista, M.A. Image inpainting and denoising by nonlinear partial differential equations. In Proceedings of the 16th Brazilian Symposium on Computer Graphics and Image Processing, Sao Carlos, Brazil, 12–15 October 2003; pp. 287–293. [Google Scholar]
- Criminisi, A.; Perez, P.; Toyama, K. Region Filling and Object Removal by Exemplar-Based Image Inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef]
- Barnes, C.; Shechtman, E.; Finkelstein, A.; Goldman, D.B. PatchMatch: A randomized correspondence algorithm for structural image editing. ACM Trans. Graph. 2009, 28, 24–35. [Google Scholar] [CrossRef]
- Singh, P.; Komodakis, N. Cloud-gan: Cloud removal for sentinel-2 imagery using a cyclic consistent generative adversarial networks. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1772–1775. [Google Scholar]
- Shao, M.; Wang, C.; Zuo, W.; Meng, D. Efficient Pyramidal GAN for Versatile Missing Data Reconstruction in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Pan, H. Cloud removal for remote sensing imagery via spatial attention generative adversarial network. arXiv 2020, arXiv:2009.13015. [Google Scholar]
- Meraner, A.; Ebel, P.; Zhu, X.X.; Schmitt, M. Cloud removal in Sentinel-2 imagery using a deep residual neural network and SAR-optical data fusion. ISPRS J. Photogramm. Remote Sens. 2020, 166, 333–346. [Google Scholar] [CrossRef]
- Nazeri, K.; Ng, E.; Joseph, T.; Qureshi, F.; Ebrahimi, M. Edgeconnect: Structure guided image inpainting using edge prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Ren, Y.; Yu, X.; Zhang, R.; Li, T.H.; Li, G. StructureFlow: Image Inpainting via Structure-aware Appearance Flow. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Xiong, W.; Yu, J.; Lin, Z.; Yang, J.; Lu, X.; Barnes, C.; Luo, J. Foreground-Aware Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Peng, J.; Liu, D.; Xu, S.; Li, H. Generating Diverse Structure for Image Inpainting With Hierarchical VQ-VAE. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 19–25 June 2021. [Google Scholar]
- Liu, H.; Wan, Z.; Huang, W.; Song, Y.; Han, X.; Liao, J. PD-GAN: Probabilistic Diverse GAN for Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 19–25 June 2021; pp. 9371–9381. [Google Scholar]
- Liu, Q.; Tan, Z.; Chen, D.; Chu, Q.; Dai, X.; Chen, Y.; Liu, M.; Yuan, L.; Yu, N. Reduce Information Loss in Transformers for Pluralistic Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2022; pp. 11347–11357. [Google Scholar]
- Du, Y.; He, J.; Huang, Q.; Sheng, Q.; Tian, G. A Coarse-to-Fine Deep Generative Model with Spatial Semantic Attention for High-Resolution Remote Sensing Image Inpainting. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Wang, N.; Zhang, L.; Du, B.; Tao, D. Recurrent Feature Reasoning for Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zhang, H.; Hu, Z.; Luo, C.; Zuo, W.; Wang, M. Semantic image inpainting with progressive generative networks. In Proceedings of the 26th ACM international conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; pp. 1939–1947. [Google Scholar]
- Wang, W.; Zhang, J.; Niu, L.; Ling, H.; Yang, X.; Zhang, L. Parallel multi-resolution fusion network for image inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 14559–14568. [Google Scholar]
- Guo, X.; Yang, H.; Huang, D. Image Inpainting via Conditional Texture and Structure Dual Generation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 14134–14143. [Google Scholar]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.C.; Tao, A.; Catanzaro, B. Image Inpainting for Irregular Holes Using Partial Convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 85–100. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Free-form image inpainting with gated convolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 4471–4480. [Google Scholar]
- Huang, W.; Deng, Y.; Hui, S.; Wang, J. Image Inpainting with Bilateral Convolution. Remote Sens. 2022, 14, 6140. [Google Scholar] [CrossRef]
- Suvorov, R.; Logacheva, E.; Mashikhin, A.; Remizova, A.; Ashukha, A.; Silvestrov, A.; Kong, N.; Goka, H.; Park, K.; Lempitsky, V. Resolution-robust large mask inpainting with fourier convolutions. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2022; pp. 2149–2159. [Google Scholar]
- Yu, T.; Guo, Z.; Jin, X.; Wu, S.; Chen, Z.; Li, W.; Zhang, Z.; Liu, S. Region normalization for image inpainting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12733–12740. [Google Scholar]
- Ma, X.; Zhou, X.; Huang, H.; Chai, Z.; Wei, X.; He, R. Free-form image inpainting via contrastive attention network. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 9242–9249. [Google Scholar]
- Qin, J.; Bai, H.; Zhao, Y. Multi-scale attention network for image inpainting. Comput. Vis. Image Underst. 2021, 204, 103155. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, B.; Xiao, Y.; Yang, C. Coherent semantic attention for image inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27–28 October 2019; pp. 4170–4179. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable DETR: Deformable transformers for end-to-end object detection. In Proceedings of the 9th International Conference on Learning Representations (ICLR), Virtual Event, Austria, 3–7 May 2021. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Child, R.; Gray, S.; Radford, A.; Sutskever, I. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Roy, A.; Saffar, M.; Vaswani, A.; Grangier, D. Efficient content-based sparse attention with routing transformers. Trans. Assoc. Comput. Linguist. 2021, 9, 53–68. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance normalization: The missing ingredient for fast stylization. arXiv 2016, arXiv:1607.08022. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Bridging nonlinearities and stochastic regularizers with gaussian error linear units. CoRR 2016, arXiv:abs/1606.08415. [Google Scholar]
- Kirkland, E.J. Bilinear interpolation. In Advanced Computing in Electron Microscopy; Springer: Berlin/Heidelberg, Germany, 2010; pp. 261–263. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11-–14 October 2016. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Drineas, P.; Mahoney, M.W.; Cristianini, N. On the Nyström Method for Approximating a Gram Matrix for Improved Kernel-Based Learning. J. Mach. Learn. Res. 2005, 6, 2153–2175. [Google Scholar]
- Huang, W.; Deng, Y.; Hui, S.; Wang, J. Multi-receptions and multi-gradients discriminator for Image Inpainting. IEEE Access 2022, 10, 131579–131591. [Google Scholar] [CrossRef]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. PatternNet: A benchmark dataset for performance evaluation of remote sensing image retrieval. ISPRS J. Photogramm. Remote Sens. 2018, 145, 197–209. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Doersch, C.; Singh, S.; Gupta, A.; Sivic, J.; Efros, A. What makes paris look like paris? Commun. ACM 2015, 58, 103–110. [Google Scholar] [CrossRef]
- Lee, C.H.; Liu, Z.; Wu, L.; Luo, P. MaskGAN: Towards Diverse and Interactive Facial Image Manipulation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Lin, D.; Xu, G.; Wang, X.; Wang, Y.; Sun, X.; Fu, K. A remote sensing image dataset for cloud removal. arXiv 2019, arXiv:1901.00600. [Google Scholar]
- Ebel, P.; Meraner, A.; Schmitt, M.; Zhu, X.X. Multisensor data fusion for cloud removal in global and all-season sentinel-2 imagery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5866–5878. [Google Scholar] [CrossRef]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3730–3738. [Google Scholar]
- Korhonen, J.; You, J. Peak signal-to-noise ratio revisited: Is simple beautiful? In Proceedings of the 2012 Fourth International Workshop on Quality of Multimedia Experience, Melbourne, Australia, 5–7 July 2012; pp. 37–38. [Google Scholar]
- Hassan, M.; Bhagvati, C. Structural similarity measure for color images. Int. J. Comput. Appl. 2012, 43, 7–12. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thirty-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]









| Module | Computation | Parameter |
|---|---|---|
| Self-attention [49] | ||
| Ada-attention |
| Name | Description | Training Images | Test Images | Release Organization |
|---|---|---|---|---|
| AID [72] | This contains 30 scene categories of RS aerial RGB images. | 9500 | 500 | Wuhan University |
| PatternNet [73] | This contains 45 scene categories of RS digital images. | 30,000 | 400 | Wuhan University |
| NWPU-RESISC45 [74] | This contains 38 scene categories of RS digital images. | 31,000 | 500 | Northwestern Polytechnical University |
| Paris StreetView [75] | This contains buildings of Paris of natural digital images. | 14,900 | 100 | Carnegie Mellon University |
| CelebA-HQ [76] | This contains celebrity face digital images for face restoration or synthesis. | 28,000 | 2000 | NVIDIA |
| RICE-II [77] | This contains cloud removal digital images with cloud, mask, and ground truth. | 630 | 106 | Chinese Academy of Sciences |
| SEN12MS-CR [78] | This contains cloud and cloud-free Sentinel-2 multispectral optical images and Sentinel-1 SAR images for the cloud removal task. | 101,615 | 7899 | Technical University of Munich |
| Stage Name | Operator | Input_Size | Output_Size | Kernel_Size | Stride |
|---|---|---|---|---|---|
| Encoder 1 | GRes Block ∗ 2 | 256 × 256 × 4 | 256 × 256 × C | 5, 3 | 1 |
| Downsample 1 | Conv | 256 × 256 × C | 128 × 128 × 2C | 3 | 2 |
| Encoder 2 | GRes Block ∗ 3 | 128 × 128 × 2C | 128 × 128 × 2C | 3 | 1 |
| Downsample 2 | Conv | 128 × 128 × 2C | 64 × 64 × 4C | 3 | 2 |
| Encoder 3 | GRes Block ∗ 4 | 64 × 64 × 4C | 64 × 64 × 4C | 3 | 1 |
| Downsample 3 | Conv | 64 × 64 × 4C | 32 × 32 × 8C | 3 | 2 |
| Encoder 4 | [GRes Block, ASC_Attent] ∗ 4, GRes Block ∗ 1 | 32 × 32 × 8C | 32 × 32 × 8C | [3, 5] ∗ 4, 3 | 1 |
| Upsample 3 | interpolation 2 times, Conv | 32 × 32 × 8C | 64 × 64 × 4C | 3 | 1 |
| Fuse 3 | Concat(Upsample 3, Encoder 3), Conv | 64 × 64 × 8C | 64 × 64 × 4C | 1 | 1 |
| Decoder 3 | GRes Block ∗ 4 | 64 × 64 × 4C | 64 × 64 × 4C | 3 | 1 |
| Upsample 2 | interpolation 2 times, Conv | 64 × 64 × 4C | 128 × 128 × 2C | 3 | 1 |
| Fuse 2 | Concat(Upsample 2, Encoder 2), Conv | 128 × 128 × 4C | 128 × 128 × 2C | 1 | 1 |
| Decoder 2 | GRes Block ∗ 3 | 128 × 128 × 2C | 128 × 128 × 2C | 3 | 1 |
| Upsample 1 | interpolation 2 times, Conv | 128 × 128 × 2C | 256 × 256 × C | 3 | 1 |
| Fuse 1 | Concat(Upsample 1, Encoder 1), Conv | 256 × 256 × 2C | 256 × 256 × C | 1 | 1 |
| Decoder 1 | GRes Block ∗ 2 | 256 × 256 × C | 256 × 256 × C | 3 | 1 |
| Conv | Conv | 256 × 256 × C | 256 × 256 × 3 | 7 | 1 |
| Output | Tanh | 256 × 256 × 3 | 256 × 256 × 3 | - | - |
| DataSet | AID | PatternNet | NWPU-RESISC45 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | Mask Ratio | DSN | LaMa | InRSI | BC | Ours | DSN | LaMa | InRSI | BC | Ours | DSN | LaMa | InRSI | BC | Ours |
| PSNR↑ | 10–30% | 27.50 | 28.01 | 24.80 | 27.66 | 28.24 | 28.33 | 29.09 | 25.53 | 28.92 | 29.28 | 28.66 | 28.85 | 25.01 | 28.98 | 29.32 |
| 30–50% | 23.42 | 23.77 | 16.68 | 23.58 | 24.28 | 23.85 | 24.61 | 21.02 | 24.43 | 24.97 | 24.25 | 24.36 | 19.21 | 24.61 | 25.10 | |
| AVG | 25.46 | 25.89 | 20.74 | 25.62 | 26.26 | 26.09 | 26.85 | 23.28 | 26.68 | 27.13 | 26.46 | 26.61 | 22.11 | 26.79 | 27.21 | |
| SSIM↑ | 10–30% | 0.881 | 0.892 | 0.817 | 0.886 | 0.896 | 0.904 | 0.918 | 0.844 | 0.913 | 0.919 | 0.899 | 0.906 | 0.816 | 0.906 | 0.911 |
| 30–50% | 0.717 | 0.734 | 0.476 | 0.727 | 0.753 | 0.761 | 0.792 | 0.630 | 0.782 | 0.798 | 0.745 | 0.758 | 0.556 | 0.762 | 0.775 | |
| AVG | 0.799 | 0.813 | 0.646 | 0.806 | 0.825 | 0.833 | 0.855 | 0.737 | 0.848 | 0.858 | 0.822 | 0.832 | 0.686 | 0.834 | 0.843 | |
| MS-SSIM↑ | 10–30% | 0.912 | 0.920 | 0.833 | 0.915 | 0.924 | 0.927 | 0.936 | 0.862 | 0.933 | 0.937 | 0.922 | 0.927 | 0.835 | 0.927 | 0.929 |
| 30–50% | 0.777 | 0.790 | 0.498 | 0.783 | 0.804 | 0.809 | 0.831 | 0.662 | 0.825 | 0.834 | 0.793 | 0.803 | 0.595 | 0.806 | 0.813 | |
| AVG | 0.845 | 0.855 | 0.665 | 0.849 | 0.864 | 0.868 | 0.884 | 0.762 | 0.879 | 0.886 | 0.857 | 0.865 | 0.715 | 0.866 | 0.871 | |
| FSIM↑ | 10–30% | 0.871 | 0.880 | 0.818 | 0.869 | 0.879 | 0.880 | 0.891 | 0.823 | 0.882 | 0.888 | 0.872 | 0.876 | 0.808 | 0.873 | 0.879 |
| 30–50% | 0.757 | 0.769 | 0.637 | 0.754 | 0.775 | 0.762 | 0.783 | 0.684 | 0.768 | 0.785 | 0.752 | 0.757 | 0.657 | 0.755 | 0.771 | |
| AVG | 0.814 | 0.824 | 0.728 | 0.811 | 0.827 | 0.821 | 0.837 | 0.753 | 0.825 | 0.837 | 0.812 | 0.816 | 0.732 | 0.814 | 0.825 | |
| MAE↓ | 10–30% | 2.08% | 1.93% | 3.09% | 2.10% | 1.97% | 1.96% | 1.79% | 3.02% | 1.94% | 1.85% | 1.85% | 1.78% | 3.33% | 1.84% | 1.77% |
| 30–50% | 4.54% | 4.35% | 10.96% | 4.54% | 4.19% | 4.42% | 4.11% | 7.22% | 4.30% | 4.02% | 4.17% | 4.11% | 9.03% | 4.10% | 3.88% | |
| AVG | 3.31% | 3.14% | 7.02% | 3.32% | 3.08% | 3.19% | 2.95% | 5.12% | 3.12% | 2.94% | 3.01% | 2.94% | 6.18% | 2.97% | 2.83% | |
| LPIPS↓ | 10–30% | 0.085 | 0.087 | 0.230 | 0.075 | 0.072 | 0.070 | 0.064 | 0.195 | 0.057 | 0.059 | 0.078 | 0.070 | 0.217 | 0.063 | 0.066 |
| 30–50% | 0.178 | 0.186 | 0.454 | 0.159 | 0.160 | 0.149 | 0.142 | 0.374 | 0.124 | 0.134 | 0.165 | 0.155 | 0.404 | 0.139 | 0.152 | |
| AVG | 0.131 | 0.137 | 0.342 | 0.117 | 0.116 | 0.109 | 0.103 | 0.284 | 0.090 | 0.096 | 0.122 | 0.112 | 0.310 | 0.101 | 0.109 | |
| DataSet | Paris StreetView | CelebA-HQ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | Mask Ratio | DSN | LaMa | InRSI | BC | Ours | DSN | LaMa | InRSI | BC | Ours |
| PSNR↑ | 10–30% | 29.56 | 28.95 | 25.02 | 30.66 | 31.45 | 31.12 | 30.91 | 23.26 | 31.53 | 31.65 |
| 30–50% | 24.99 | 24.55 | 19.09 | 25.87 | 26.75 | 26.24 | 25.93 | 17.34 | 26.52 | 26.75 | |
| AVG | 27.27 | 26.75 | 22.05 | 28.26 | 29.10 | 28.68 | 28.42 | 20.30 | 29.02 | 29.20 | |
| SSIM↑ | 10–30% | 0.933 | 0.929 | 0.840 | 0.943 | 0.951 | 0.972 | 0.970 | 0.875 | 0.974 | 0.975 |
| 30–50% | 0.825 | 0.817 | 0.590 | 0.844 | 0.865 | 0.924 | 0.919 | 0.679 | 0.930 | 0.933 | |
| AVG | 0.879 | 0.873 | 0.715 | 0.894 | 0.908 | 0.948 | 0.945 | 0.777 | 0.952 | 0.954 | |
| MS-SSIM↑ | 10–30% | 0.946 | 0.943 | 0.855 | 0.952 | 0.958 | 0.972 | 0.970 | 0.880 | 0.975 | 0.975 |
| 30–50% | 0.852 | 0.847 | 0.633 | 0.865 | 0.881 | 0.925 | 0.919 | 0.699 | 0.930 | 0.932 | |
| AVG | 0.899 | 0.895 | 0.744 | 0.908 | 0.920 | 0.948 | 0.945 | 0.790 | 0.953 | 0.954 | |
| FSIM↑ | 10–30% | 0.880 | 0.880 | 0.814 | 0.885 | 0.894 | 0.895 | 0.896 | 0.809 | 0.898 | 0.900 |
| 30–50% | 0.764 | 0.766 | 0.670 | 0.772 | 0.791 | 0.790 | 0.789 | 0.654 | 0.796 | 0.802 | |
| AVG | 0.822 | 0.823 | 0.742 | 0.828 | 0.842 | 0.842 | 0.842 | 0.732 | 0.847 | 0.851 | |
| MAE↓ | 10–30% | 1.47% | 1.58% | 3.14% | 1.33% | 1.21% | 1.03% | 1.08% | 3.49% | 1.00% | 0.98% |
| 30–50% | 3.36% | 3.58% | 8.33% | 3.10% | 2.78% | 2.40% | 2.57% | 8.93% | 2.36% | 2.29% | |
| AVG | 2.42% | 2.58% | 5.74% | 2.21% | 1.99% | 1.71% | 1.82% | 6.21% | 1.68% | 1.64% | |
| LPIPS↓ | 10–30% | 0.058 | 0.060 | 0.181 | 0.044 | 0.042 | 0.031 | 0.030 | 0.157 | 0.023 | 0.024 |
| 30–50% | 0.127 | 0.139 | 0.361 | 0.104 | 0.101 | 0.067 | 0.070 | 0.319 | 0.056 | 0.058 | |
| AVG | 0.093 | 0.100 | 0.271 | 0.074 | 0.072 | 0.049 | 0.050 | 0.238 | 0.039 | 0.041 | |
| RICE-II | SEN12MS-CR | ||||||
|---|---|---|---|---|---|---|---|
| Models | PSNR↑ | SSIM↑ | MAE↓ | Models | PSNR↑ | SSIM↑ | MAE↓ |
| SpA-GAN [28] | 29.74 | 0.731 | 4.42% | DSen2-CR [29] | 28.43 | 0.882 | 2.86% |
| BC [43] | 30.97 | 0.789 | 4.26% | ||||
| Ours | 32.42 | 0.795 | 3.50% | Ours | 28.96 | 0.881 | 2.72% |
| Metrics | PSNR↑ | SSIM↑ | MAE↓ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mask Ratio | Base | W/MHSA | Ours | Base | W/MHSA | Ours | Base | W/MHSA | Ours |
| 10–30% | 27.74 | 28.06 | 28.24 | 0.888 | 0.893 | 0.896 | 2.09% | 2.01% | 1.97% |
| 30–50% | 23.85 | 24.12 | 24.28 | 0.734 | 0.746 | 0.753 | 4.42% | 4.27% | 4.19% |
| AVG | 25.79 | 26.09 | 26.26 | 0.811 | 0.819 | 0.825 | 3.26% | 3.14% | 3.08% |
| Metrics | PSNR↑ | SSIM↑ | MAE↓ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mask Ratio | Edge | Inter | Ours | Edge | Inter | Ours | Edge | Inter | Ours |
| 10–30% | 28.26 | 28.19 | 28.24 | 0.897 | 0.896 | 0.896 | 1.96% | 1.98% | 1.97% |
| 30–50% | 24.29 | 24.25 | 24.28 | 0.753 | 0.751 | 0.753 | 4.18% | 4.21% | 4.19% |
| AVG | 26.27 | 26.22 | 26.26 | 0.825 | 0.823 | 0.825 | 3.07% | 3.09% | 3.08% |
| Image Resolution | MAC (G) | PSNR↑ | SSIM↑ | MAE↓ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10–30% | 30–50% | AVG | 10–30% | 30–50% | AVG | 10–30% | 30–50% | AVG | ||
| 384 × 384 | 266.24 | 30.66 | 25.92 | 28.29 | 0.923 | 0.794 | 0.859 | 1.41% | 3.34% | 2.37% |
| 256 × 256 | 113.66 | 28.24 | 24.28 | 26.26 | 0.896 | 0.753 | 0.825 | 1.97% | 4.19% | 3.08% |
| 128× 128 | 27.185 | 29.33 | 25.37 | 27.35 | 0.903 | 0.771 | 0.837 | 1.86% | 3.87% | 2.87% |
| 64 × 64 | 6.756 | 24.03 | 21.02 | 22.53 | 0.763 | 0.625 | 0.694 | 4.67% | 8.02% | 6.34% |
| 32 × 32 | 1.687 | 15.55 | 14.04 | 14.8 | 0.404 | 0.254 | 0.329 | 11.97% | 16.82% | 14.40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Deng, Y.; Hui, S.; Wang, J. Adaptive-Attention Completing Network for Remote Sensing Image. Remote Sens. 2023, 15, 1321. https://doi.org/10.3390/rs15051321
Huang W, Deng Y, Hui S, Wang J. Adaptive-Attention Completing Network for Remote Sensing Image. Remote Sensing. 2023; 15(5):1321. https://doi.org/10.3390/rs15051321
Chicago/Turabian StyleHuang, Wenli, Ye Deng, Siqi Hui, and Jinjun Wang. 2023. "Adaptive-Attention Completing Network for Remote Sensing Image" Remote Sensing 15, no. 5: 1321. https://doi.org/10.3390/rs15051321
APA StyleHuang, W., Deng, Y., Hui, S., & Wang, J. (2023). Adaptive-Attention Completing Network for Remote Sensing Image. Remote Sensing, 15(5), 1321. https://doi.org/10.3390/rs15051321












