Abstract
The Calibration Microwave Radiometer (CMR) is a three-band radiometer deployed on the HY-2C satellite in a near-Earth orbit, and since it launched, there are few studies presented on the performance of CMR to date. Therefore, this paper focuses on providing an assessment of HY-2C CMR brightness temperature and wet troposphere correction (WTC). CMR works at 18.7 GHz, 23.8 GHz and 37 GHz in a nadir-viewing direction, aligned with the HY-2C radar altimeter. The wet troposphere path delay of the radar altimeter signal caused by water vapour and cloud liquid water content can be monitored and corrected by CMR. In this paper, guided by the concept of antenna pattern correction algorithm and a purely statistical method, we directly establish the function between the CMR antenna temperature and the model-derived WTC calculated by the European Centre from Medium-Range Weather Forecasting (ECMWF) Reanalysis data, which can obtain the brightness temperature and the WTC of CMR simultaneously. Firstly, the algorithm principle of CMR to establish the function between the antenna temperature and the model-derived WTC is introduced, and then the brightness temperature of CMR is evaluated using reference brightness temperatures of the Advanced Microwave Radiometer 2 (AMR-2) on Jason-3 satellite at crossover points. Furthermore, the performance of the CMR WTC is validated in three ways: (1) directly comparing with the colocated WTC measured by Jason-3 AMR-2, (2) directly comparing with model-derived WTC from ECMWF, which allows a rapid check at a global scale, (3) comparing the standard deviation of the Sea Surface Height (SSH) difference at crossover points using different WTC retrieval methods. The linear fit with Jason-3 brightness temperature and WTC in all non-precipitation conditions demonstrated a good agreement with Jason-3. In addition, the WTC of CMR has an obvious decrease in the standard deviation of the SSH difference compared with model-derived WTC, indicating the CMR can significantly improve the accuracy of the HY-2C SSH measurements. All the assessments indicate that the CMR performances are satisfying the expectations and fulfilling the mission requirements.
1. Introduction
The rise of the global mean sea level caused by global warming will have a great impact on the human living environment and economic development. Since the 1990s, radar altimeters have proven to be superb tools for monitoring global mean sea levels. The radar altimeter measures the precise distance between the satellite and the ocean surface by sending a radar pulse to see how long it takes to return. While, the water vapour and cloud liquid water content in the troposphere would slow the propagation velocity of the radar pulse due to the refraction effect, which leads to the delay of the radar signal return time and results in 3~50 cm uncertainty error for sea level measurements with radar altimetry [1]. Therefore, the wet troposphere path delay is a major error source in radar altimetry applications [2].
At present, there are three main methods to correct the wet path delay for radar altimeters. The first one is using an onboard passive microwave radiometer, the second one is by means of the Global Navigation Satellite Systems (GNSS), and the third one is based on the Numerical Weather Model (NWM) method. With the high variability of water vapour and cloud liquid water content both in space and time over the ocean, the onboard passive microwave radiometer has been recognized as the most accurate means to measure the wet troposphere correction (WTC) in most altimetric missions, such as the Earth Remote Sensing (ERS) series satellites [3,4], the Jason series satellites [5,6], the Sentinel series satellites [7,8,9] and the HY series satellites [10]. While the measurements of microwave radiometers are invalid when the satellites are close to coastal, inland and polar zones due to the contamination of other surfaces present in the microwave radiometer footprint [11]. Hence, the WTC derived from GNSS are developed to solve this altimetry issue [12]. In the absence of microwave radiometer measurements, some satellites, like the Gryosat series or as an independent reference to evaluate the long-term stability of the radiometer corrections, or when the satellite is close to coastal or ice-covered areas, the model-derived WTC from the European Center for Medium-Range Weather Forecasts (ECMWF) or the National Centers for Environmental Prediction (NCEP) are recommended [13,14,15]. Although the accuracy of the model-derived WTC is worse than that of a microwave radiometer, with the quality improvements of assimilated data, the reanalysis data product from ECMWF has been used to establish the WTC retrieval algorithm [16,17,18].
HY-2C is the third ocean dynamic environment monitoring satellite of the China National Space Administration (CNSA), and was successfully launched from Jiuquan Satellite Launch Center on September 21, 2020. One of the main payloads of HY-2C is the Calibration Microwave Radiometer (CMR) deployed for conducting the WTC of the microwave radar altimeter. The nadir-viewing CMR is a three-frequency radiometer operating at 18.7 GHz, 23.8 GHz and 37 GHz. The 23.8 GHz channel is the primary channel for monitoring water vapour, which signifies that the higher the water vapour concentration the larger the brightness temperature of the 23.8 GHz channel. The 37 GHz and 18.7 GHz channels which are insensitive to water vapour, are utilized to remove the influences of cloud liquid water and excess ocean surface emissivity caused by wind. By combining the measured brightness temperature at each frequency, the water vapour and liquid water signals can be extracted [10].
Generally, the data processing of the microwave radiometer measured brightness temperatures into the radar altimeter WTC can be broken into three distinct procedures. The initial procedure is the calibration of antenna temperatures, in which raw digital counts proportional to measure voltage are converted into antenna temperatures. The second procedure is the calibration of brightness temperatures (TB). The antenna temperature is not the physical temperature of the antenna but represents the brightness temperature of the scene in the field of the antenna, which is factored by the main lobe and the side lobe of the antenna. Therefore, the brightness temperature calibration aims at converting the antenna temperature into the main lobe’s brightness temperature (measured brightness temperature), which is the desired scene radiance by using the antenna pattern correction algorithm. The final procedure converts the main lobe’s brightness temperature at different channels into WTC by a retrieval algorithm [19].
As for the last procedure of the above data processing chain, statistical methods such as log-linear parametric algorithms or neural networks have been widely adopted to retrieve WTC, and comprise the semi-empirical method and the purely empirical method [20]. The semi-empirical statistical algorithm applied on ERS-1, ERS-2 and Envisat microwave radiometers is usually established in two steps: (1) establish the function between the model-derived WTC and the corresponding collocated simulated brightness temperatures. The model-derived WTC is computed using the NWM analyses and the simulated brightness temperature for each channel is calculated using a radiative transfer model. 2) establish a valid transfer function between the measured brightness temperature and the simulated ones. Picard et al. [18], points out that the uncertainty of this semi-empirical method derives from the transfer function and the radiative transfer model, therefore, they adopt the purely empirical method, using the measured brightness temperature instead of the simulated ones to establish the functional relationship with the model-derived WTC. In the purely empirical method, there is no bias and errors introduced by the deviation between the measured and the simulated brightness temperatures, and the corresponding performance is close to what was expected with the semi-empirical approach [18].
Consequently, accurate WTC retrieval demands well-calibrated brightness temperatures [20]. Simulated brightness temperature derived from radiosonde or atmospheric reanalysis data can be used as a reference for calibration. Since the radiosonde or the reanalysis data do not provide the brightness temperature directly, it requires interpolating the relevant atmospheric parameters along the satellite track and then bringing them into the radiative transfer model to generate the corresponding simulated brightness temperature for each channel. The uncertainty of this operation comes from the data itself and the radiative transfer model. Hence, to reduce the transfer error between the antenna temperature and the measured brightness temperature, guided by the concept of the antenna pattern correction (APC) algorithm and the purely empirical method, we directly establish the function between antenna temperature and model-derived WTC, which do not use the simulated brightness temperature as a reference, just via the APC formula and the model-derived WTC to obtain the brightness temperature and the WTC of CMR simultaneously.
Section 2 presents the algorithm theory of HY-2C CMR to establish the function between the antenna temperature and the model-derived WTC. Section 3 presents the validation results of the HY-2C CMR brightness temperatures for each channel by comparing them with the corresponding brightness temperature of Jason-3 AMR-2 and the simulated brightness temperature. Section 4 provides a relatively comprehensive validation of the HY-2C CMR WTC by comparing with (1) the WTC of Jason-3 AMR-2; (2) the model-derived WTC from ECMWF; (3) the standard deviation of the sea surface height (SSH) at crossover points. Finally, conclusions are presented in Section 5.
2. Principle from Antenna Temperature to Model-Derived WTC
To establish the function between antenna temperature and the model-derived WTC, we divided this objective into two processes: (1) use the APC algorithm to construct the relationship between the antenna temperature and the main-lobe brightness temperature, and (2) find the relationship between the main-lobe brightness temperature and the model-derived WTC. Combine the above two processes, and the coefficients in the function are determined by model-derived WTC.
2.1. From Antenna Temperature to Main-Lobe Brightness Temperature
The three frequency signals of HY-2C CMR share a common 90 cm offset parabolic reflector, which focuses the collected multi-frequency microwave signals on the feed horn. In the antenna temperature calibration stage, the large reflector is trivial to install, thus the antenna reflector was dismounted and the feed horn was used to view the calibrator target directly. At this moment, it can be assumed that the emissivity of the reflector is 0. While the on-orbit reflector is unfolded, the emissivity of the CMR aluminium reflector is not 0, and a compromise between antenna size and spatial resolution makes the CMR have a significant side lobe. Thus, the reflector losses must be taken into account and the side-lobe contribution has to be removed as much as possible. In other words, any brightness temperatures outside the main lobe should be removed.
The antenna temperature consists of two parts: the main-lobe brightness temperature Tml and the side-lobe brightness temperature Tsl. The side-lobe contributions come from several parts: from the Earth, from the cold sky, from the sun and from the satellite itself. In the scope of this work, we mainly take the contributions from the Earth and the cold sky into account. Thus, the antenna temperature TA is expressed as follows:
where Tref is the physical temperature of the antenna parabolic reflector. ηref is the transmission coefficient of the reflector which is hard to measure accurately. The range of ηref is estimated about 0.977 to 0.933 (where the corresponding loss is about 0.1 dB and 0.3 dB). ηml and ηsl are ratios of the antenna to the main lobe and side-lobe, among them, the ηsl can divide into ηe and ηc which are ratios of the Earth and the cold sky, respectively, and with measurement error in the pre-launch stage. Te is the effective side-lobe brightness temperature of the Earth, and Tsky is the cosmic background brightness temperature of 2.73 K.
Equation (1) can be inverted to obtain Tml:
The contribution of the Earth varies with latitude and seasons. The antenna temperature also varies with latitude and seasons and has a strong correlation with the sea surface temperature. Therefore, similarly to the side-lobe correction of Jason microwave radiometer, the effective Earth side-lobe brightness temperatures for each channel of CMR are determined at every observation point by a quadratic function of antenna temperature itself [21], given by:
where d1 and d2 are fixed values for each frequency (f), and d0 is a coefficient related to latitude (lat).
2.2. From Antenna Temperature to Model-Derived WTC
As mentioned in Section 1, compared with the semi-empirical method whose uncertainty derives from the radiative transfer model and transfer function, the purely empirical method has no bias and errors introduced by the deviation between the measured and the simulated brightness temperature. Here, the purely empirical method to establish the function between measured brightness temperature and model-derived WTC has been adopted.
Due to their global coverage and multi-variable meteorological reanalysis, the Numerical Weather Model data have been widely used to calculate the model-derived WTC. ECMWF has released the fifth atmospheric reanalysis (ERA-5) model of the global climate and weather data, providing hourly parameters of atmospheric, land surface and ocean climate. In this paper, we use ERA-5 data from four cycles distributed in the four seasons of a year, from 15 October 2020, to 24 October 2020, 21 January 2021, to 31 January 2021, 21 April 2021, to 30 April 2021, and from 19 July 2021, to 28 July 2021 (cycle003, cycle013, cycle022 and cycle031 of HY-2C CMR) to calculate the model-derived WTC. The temporal and spatial resolution of ERA-5 data used in this paper is 1 h and 0.25° × 0.25°, and these data are freely available in the Copernicus Climate Data Store.
The model-derived WTC can be obtained from a numerical integration of temperature and specific humidity on 37 pressure levels, according to Equation (4). This numerical integration is performed from the level at the top of the atmosphere (TOA) down to the level at the surface [22,23]. The model-derived WTC is shown as the following equation:
where PTOA and Psurf are the top of the atmosphere and the surface pressure given in hPa, q represents the specific humidity in kg.kg−1, which means the mass of cloud liquid water content per kilogram of the moist air. T is the temperature in Kelvin, φ is the latitude and the EC_WTC is in meters.
Next, the model-derived WTC for each HY-2C CMR along-track position is derived by bi-linear interpolation of the two nearest grid points in space and time. The ERA-5 data used to interpolate has to be filtrated, and the concrete filter criteria are: (1) the quality flags of antenna temperature TA18.7, TA23.8 and TA37 should be equal to zero (valid measurements), (2) the surface type is open ocean, (3) to avoid land contamination, the observation points are at a distance from coast larger than 50 km, (4) the observation points can not be contaminated by sea ice, (5) the latitude range should be between 60°N~60°S [24]. The final database contains a total of 1,580,531 geophysical situations to ensure a good distribution in time and geography. Two-thirds of the data are randomly selected as the algorithm database to derive the measured brightness temperature and the WTC of CMR, and the remaining one-third of the data is used as the retrieval database to evaluate.
The general expression of the log-linear parametric algorithm establishing the function between simulated brightness temperature and model-derived WTC is given by [16,25]:
where pdv is the retrieved WTC in meter, the brightness temperature TB18.7, TB23.8 and TB37 are the simulated brightness temperature in Kelvin. It has been demonstrated that the performance of this log-linear algorithm is inferior to the basic back propagation (BP) neural network [16], to increase the non-linearity processing ability of the log-linear model, we use an improved version of the log-linear algorithm, the expression is as follows:
where the CMR_WTC is the along-track model-based WTC from HY-2C CMR, TB18.7, TB23.8 and TB37 are the main-lobe brightness temperatures of CMR for each channel.
Regard the EC_WTC as the true value and combine Equations (2), (3) and (6), the relationship between model-derived WTC and antenna temperature can be established, which is done by adjusting a set of coefficients. The set of coefficients includes: (1) the emissivity of the reflector which is hard to measure accurately due to the size. (2) the efficiencies of the antenna to the Earth, the cold sky and the main lobe, which are measured with measurement error. (3) the coefficients in the effective Earth side-lobe brightness temperature for each channel. (4) the coefficients in the WTC retrieval process.
3. Assessment of HY-2C CMR Brightness Temperatures
Through the analysis of Section 2, we can obtain the measured brightness temperature of HY-2C CMR. The major difficulty in evaluating the measured brightness temperature is to find a reference and the usage of crossover points from a pair of sensors is a common practice. The three-channel Jason-3 AMR-2 that operates at 18.7 GHz, 23.8 GHz and 34 GHz is generally regarded as an important reference for its high accuracy measurement of brightness temperatures, which has been fully calibrated. Thus, the quantitative evaluation of the measured brightness temperature of HY-2C CMR is performed by directly comparing it with the brightness temperatures of Jason-3 AMR-2.
Jason-3 was successfully launched on January 17, 2016, and the orbital altitude is 1336 km. The revisit period of Jason-3 is around 10 days with 254 passes for each cycle, and the latitude range is between 66.15°S to 66.15°N. Jason-3 products consist of three families: Geophysical Data Record (GDR), Interim Geophysical Data Record (IGDR) and Operational Geophysical Data Record (OGDR) [26]. The major differences in these products are their quality and latency, among them, although the GDR products have the longest product latency around 60 days, it also has the best quality.
In the scope of this paper, we adopt version “F” of Jason-3 GDR products from 1 November 2020, to 1 August 2021, for comparison, and these data are distributed by the Archiving, Validation and Interpretation of Satellite Oceanographic (AVISO). Before comparison, some invalid crossover points have to be removed: (1) the radiometer surface type, if not the open ocean, (2) the crossover points are at a distance from the coast less than 50 km, which were removed using a land mask map with a resolution of 9865 × 9865 pixels, (3) the points are contaminated by sea ice, (4) cloud liquid water content greater than 1 kg/m2, (5) the latitude is outside 60°N~60°S. For the comparison with Jason-3, crossover points between Jason-3 AMR-2 and HY-2C CMR with the time window ΔT < 30 min and the distance window ΔD < 30 km are chosen.
The final number of crossover points in that period is 12,788, and Figure 1 shows the crossover points spatial distribution of each channel. The corresponding brightness temperature and the mean values for each channel are: TB18.7 ranges from 123.7 K–191.4 K (mean 144.5 K); TB23.8 ranges from 137.8 K–235.6 K (mean 180.2 K); TB37 ranges from 152.7 K–227.6 K (mean 172.2 K).
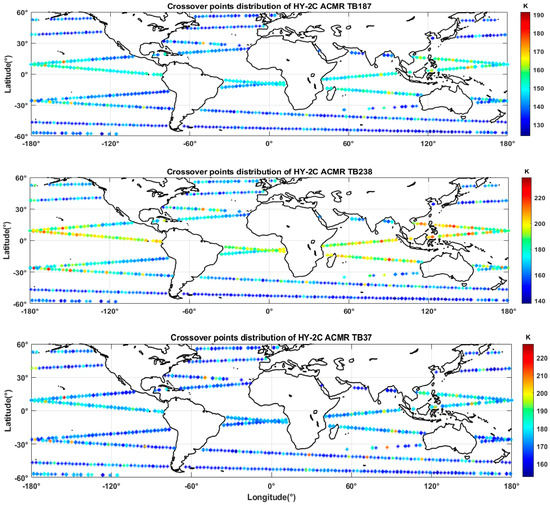
Figure 1.
Crossover points spatial distribution of TB18.7 in K (top panel), TB23.8 (middle panel) and TB37 (bottom panel).
The left panel of Figure 2 shows the scatter diagram of the brightness temperature of HY-2C CMR against the one from Jason-3 AMR-2, while the right panel shows the corresponding scatter diagram against the brightness temperature differences between HY-2C CMR and Jason-3 AMR-2. It should be noted that due to the different frequency selections of CMR and AMR-2 on the cloud liquid water channel (37 GHz vs. 34 GHz), the brightness temperature of CMR 37 GHz is not compared with AMR-2 in this study.
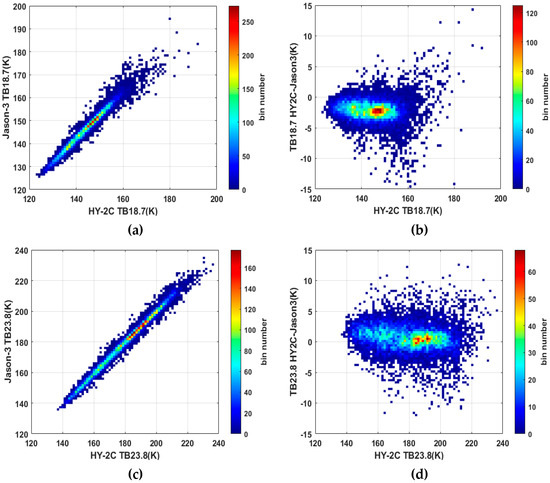
Figure 2.
(a): HY-2C TB versus Jason-3 TB 18.7, in K; (b): HY-2C TB versus brightness temperature difference between HY-2C and Jason-3, in K; (c): HY-2C TB versus Jason-3 TB 23.8, in K; (d): HY-2C TB versus brightness temperature difference between HY-2C and Jason-3, in K.
Using crossover points between HY-2C CMR and Jason-3 AMR-2, we have calculated the mean deviation (HY-2C minus Jason-3), the standard deviation (STD), the correlation coefficient and the linear fitting coefficient between HY-2C brightness temperature and the corresponding ones of Jason-2. They are summarized in Table 1.

Table 1.
Statistical characteristics for the comparison between TBs from HY-2C and Jason-3.
The brightness temperature mean deviation between HY-2C and Jason-3 for corresponding channels are −2.20 K and 0.62 K. The standard deviations are 1.64 K and 2.03 K. The linear regression and correlation coefficient demonstrated that the scaling factors are approximate to 1 and with small offsets, indicating that the brightness temperatures of HY-2C CMR have a good agreement with Jason-3 AMR-2.
4. Assessment of HY-2C CMR Wet Troposphere Corrections
To give a comprehensive assessment of the accuracy of HY-2C CMR retrieval WTC, three ways have been performed, namely: (1) direct comparisons with the WTC from Jason-3 AMR-2 at crossover points, (2) direct comparisons with the model-derived WTC from ECMWF at interpolation points, (3) compared the decrease of the standard deviation of the SSH difference at crossover points between different WTC retrieval methods.
4.1. Comparison with the WTC of Jason-3 AMR-2
As mentioned in Section 3, the WTC measurement accuracy of Jason-3 AMR-2 (hereafter Jason-3 WTC) is also relatively high, therefore, to evaluate the retrieval WTC accuracy of HY-2C CMR, we continue to adopt the WTC of Jason-3 AMR-2 as a reference. The filter criteria for the valid crossover points are the same as in Section 3. Figure 3 shows the WTC differences (HY-2C minus Jason-3) spatial coverage of the 9-month period crossover points between HY-2C and Jason-3. The colour scale means WTC differences between HY-2C and Jason-3 are in cm. The blue colour indicates that the value of HY-2C WTC is smaller than the one of Jason-3, in other words, drier measurements of HY-2C, while red indicates the opposite.
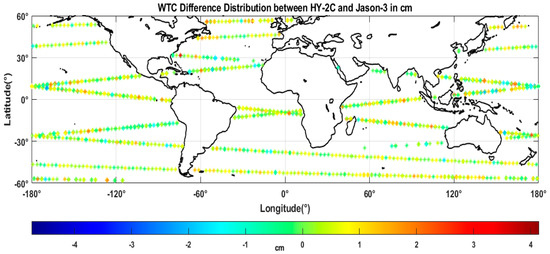
Figure 3.
WTC differences in the spatial distribution of crossover points between HY-2C and Jason-3 with ΔT < 30 min and ΔD < 30 km (~12,788 points). The colour scale indicates WTC differences in cm.
Figure 4 shows the scatter diagram of HY-2C WTC versus Jason-3 WTC, computed over open ocean from 1 November 2020, to 1 August 2021 (left) as well as against the WTC difference between HY-2C and Jason-3 (right). Based on the crossover points, we also calculated the main statistical characteristics such as mean deviation, root mean square error (RMSE), correlation coefficient and linear fitting coefficient between HY-2C WTC and the corresponding one of Jason-3. They are summarized in Table 2.
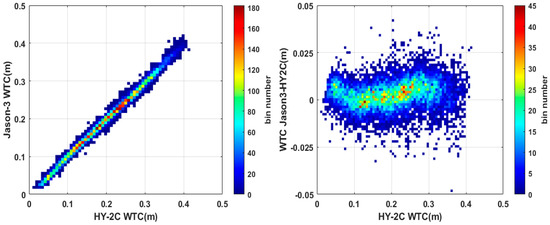
Figure 4.
(Left panel) WTC of HY-2C versus WTC of Jason-3; (Right panel) WTC of HY-2C versus WTC differences between HY-2C and Jason-3.

Table 2.
Statistical characteristics of comparison between HY-2C WTC and other WTC methods.
The overall mean deviation and root mean square error between HY-2C WTC and the one Jason-3 are 0.27 cm and 0.76 cm respectively. The scale factor and the offset are 0.99 and 0.01 cm, respectively. And the correlation coefficient is 0.99, and they all demonstrate a good overall WTC agreement with Jason-3. Both Figure 3 and Figure 4 indicate that HY-2C measures relatively wetter than Jason-3 by about 0.27 cm.
4.2. Comparison with Model-Derived WTC from ECMWF
Comparing the model-derived WTC from ECMWF and WTC of radiometer has been demonstrated to be an effective method to indicate any abnormal behaviour of the microwave radiometer [27]. Although with its poor temporal sampling, the model-derived WTC from ERA-5 can still be used as a supplementary way to execute a statistical comparison, which conducts a fast examination of the HY-2C CMR behaviour on a global scale.
As mentioned in Section 2.2, we mainly adopt specific humidity (q) and temperature at each grid at various pressure levels from the algorithm database and retrieval database for the estimation of model-derived WTC. The model-derived WTC from ECMWF for each HY-2C CMR along-track is derived by bi-linear interpolation of the two nearest grid points in space and time. And the valid interpolation points filter criteria are the same as the ones in Section 2.2. The number of algorithm database and retrieval database are 1,053,687 and 526,844, respectively.
The left panel of Figure 5 shows the scatter diagram of HY-2C WTC against the model-derived WTC from ERA-5 in meters (top: algorithm database, bottom: retrieval database), while the right panel shows the corresponding scatter diagram against the WTC difference between HY-2C and ERA-5. The statistical characteristics are also summarized in Table 2. The comparison with model-derived WTC from ERA-5 shows that on average HY-2C measures wetter by about 0.07 cm, and the RMSE of the differences is within 1.13–1.14 cm. The scale factor is within 0.9947–0.9949, the positive offset is 0.01 cm and the correlation coefficient is about 0.99. All the statistical characteristic shows a good agreement of WTC between HY-2C and ERA-5, since, the WTC of HY-2C has been obtained using this model-derived WTC from ERA-5.
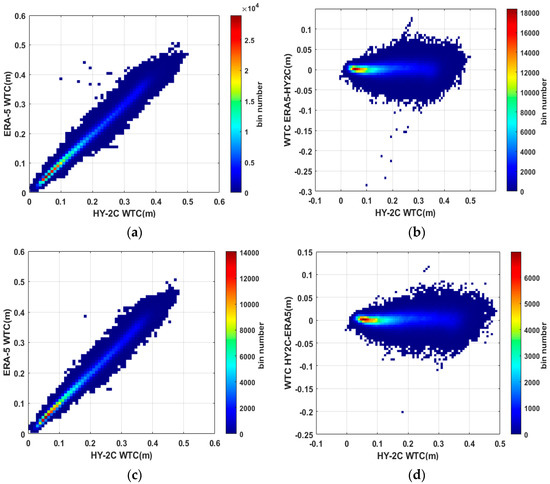
Figure 5.
(a): HY-2C WTC versus ERA-5 WTC in algorithm database; (b): HY-2C WTC versus WTC difference between HY-2C and ERA-5 in algorithm database; (c): HY-2C WTC versus ERA-5 WTC in retrieval database; (d): HY-2C WTC versus WTC difference between HY-2C and ERA-5 in retrieval database.
4.3. Comparison of the Standard Deviation of the SSH Difference at Crossover Points
The SSH obtained from the altimeter can be used to observe the global sea level and its changes with time. The final measurement of SSH requires several corrections, the SSH calculation method of HY-2C is shown as follows:
where H is the HY-2C orbital height above a reference ellipsoid; Rtr is the raw measured range between HY-2C and sea surface; ΔRcorr represents the sum of the range corrections and the geophysical corrections. The range corrections ΔRrange include: retracking correction ΔRepoch, Doppler correction ΔRDoppler, system bias correction ΔRsystem_bias and modeled instrumental correction ΔRmodel. The geophysical corrections ΔRgeo include the dry troposphere correction ΔRdry, the wet troposphere correction ΔRwet, the ionosphere correction ΔRiono, the sea state bias correction ΔRssb, the geocentric ocean tide correction ΔRocean, the pole tide correction ΔRsolid, the pole tide correction ΔRpole and the dynamical atmospheric correction ΔRDAC [28,29].
It is obvious that the accuracy of the SSH has a direct relationship with the accuracy of the WTC adopted to acquire the SSH [29]. Ideally, the change of SSH is negligible within a short period window, which means that the SSH differences derived at crossover points between the ascending and descending passes of a satellite would be approximately 0, any observed variability of SSH is caused by corrections. Thus, the standard deviation of the SSH differences at crossover points can be applied as a global metric for comparing different WTC retrieval methods. The main advantage of this method is that it does not require any other references and can evaluate the overall performance of the altimeter system. When comparing two WTC retrieval methods, the smaller standard deviation of SSH difference at crossover points indicates the better one.
To reduce the oceanic variability impact, the maximum time difference is within 3 days and the SSH differences at crossover points are smaller than 0.2 m. For keeping the regions where the signal will be stronger, additional filter criteria are performed to remove high latitudes (ranges larger than 50°S and 50°N) and remove shallow water (bathymetry smaller than −1000 m) [29,30,31].
In this work, to have a point for comparison, we used the retrieved WTC of HY-2C CMR and model-derived WTC, to evaluate the standard deviation of the SSH difference of HY-2C at crossover points. The HY-2C IGDR data span from 1 October 2020, to 1 April 2021, and these data are provided by the National Satellite Ocean Application Service (NSOAS), Ministry of Natural Resources, China.
To compare the WTC of HY-2C and model-derived WTC, the SSH of the ascending and descending passes at crossover points for each method are first computed, respectively. Then, both the standard deviation of SSH (STD (SSH_MO) and STD (SSH_CMR)) at crossover points have been computed. Figure 6 and Figure 7 demonstrate the SSH differences histogram of the crossover points for HY-2C applying the model-derived WTC and the retrieved WTC of CMR, respectively. The STD (SSH_MO) is around 4.79 cm, and the STD (SSH_CMR) is around 4.51 cm. Therefore, the WTC of CMR significantly improved the accuracy of HY-2C SSH measurements with regard to the model-derived WTC.
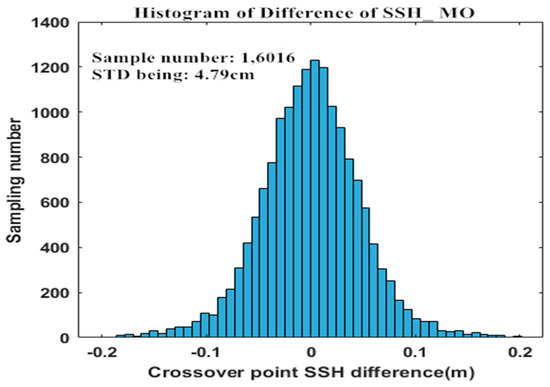
Figure 6.
SSH differences histogram of crossover points for HY-2C using model-derived WTC.
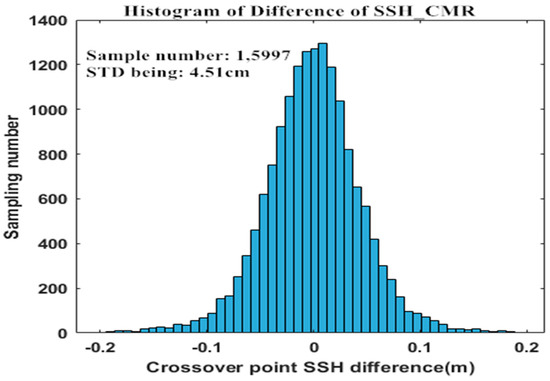
Figure 7.
SSH differences histogram of crossover points for HY-2C using CMR_WTC.
Figure 8 demonstrates the crossover points distribution of SSH differences for HY-2C using WYC of CMR. It can be seen that there is no apparent geographical correlation and as a result, the system consistencies between the ascending and descending passes of HY-2C have a high quality.
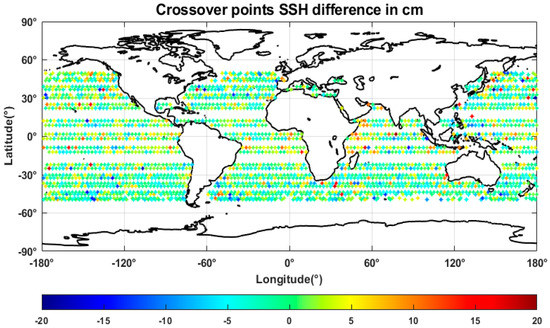
Figure 8.
Distribution of the crossover points SSH difference for HY-2C using CMR_WTC.
5. Conclusions
To accurately assess the sea level changes derived from HY-2C, the accuracy and stability constraints of WTC derived from CMR are particularly strict. The HY-2C CMR has been working in its orbit for 2 years, but few studies have been presented on the performance of CMR to date. Therefore, this paper focuses on presenting an assessment of the HY-2C CMR.
Usually, the in-orbit calibration of the microwave radiometer is regarded as the first step to ensure the good quality of the brightness temperature products and the good behaviour of the retrieval WTC. And then continue to establish the function between the brightness temperatures and retrieval WTC. In this paper, we establish the function between the antenna temperature and model-derived WTC, which can obtain the measured brightness temperature and the retrieved WTC simultaneously.
The results of measured brightness temperature for different channels of HY-2C CMR are directly compared with the ones of Jason-3 AMR-2. The statistical characteristics like mean deviation, standard deviation, correlation coefficient and linear regression coefficients demonstrate that the measured brightness temperatures for each channel of CMR are well calibrated.
The results of retrieved WTC of HY-2C CMR are assessed comprehensively by three methods. During the comparison with Jason-3 WTC and model-derived WTC, it is shown that the retrieved WTC of CMR has a good agreement with Jason-3 WTC and model-derived WTC. The standard deviation of SSH differences at ascending and descending crossover points for HY-2C using the WTC of CMR and model-derived WTC have been compared with each other. The HY-2C SSH measurement performances by WTC of CMR have obviously improved with regard to the SSH measurements with model-derived WTC. All the above assessments indicate that the CMR performances are satisfying the expectations and fulfilling the mission requirements.
Author Contributions
Methodology, X.Z. and J.Z.; Software, X.Z. and M.J.; Validation, X.Z., J.Z. and M.J.; Writing—original draft, X.Z.; Writing—review and editing, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are not publicly avaliable due to privacy.
Acknowledgments
The Jason-3 GDR-F data are obtained from Archiving, Validation and Interpretation of Satellite Oceanographic Data (AVISO). The temperature and specific humidity used to derive the model-based WTC from ECMWF are downloaded from ECMWF reanalysis project ERA5. The HY-2C IGDR data are provided by the National Satellite Ocean Application Service (NSOAS), Ministry of Natural Resources, China. The authors are grateful to AVISO, ECMWF and NSOAS for providing data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, X.; Liu, X.Y.; Zhu, J.; Chen, C.; Wang, H.; Zhai, W. Intercomparison and Anomaly Analysis of WET Tropospheric Corrections from Jason-3 and Saral. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Vieira, E.; Lázaro, C.; Fernandes, J. Spatio-temporal variability of the wet component of the troposphere Application to satellite altimetry. Adv. Space Res. 2019, 63, 1737–1753. [Google Scholar] [CrossRef]
- Bennartz, R.; Höschen, H.; Picard, B.; Schröder, M.; Stengel, M.; Sus, O.; Bojkov, B.; Casadio, S.; Diedrich, H.; Eliasson, S.; et al. An intercalibrated dataset of total column water vapour and wet tropospheric correction based on MWR on board ERS-1, ERS-2, and Envisat. Atmos. Meas. Tech. 2017, 10, 1387–1402. [Google Scholar] [CrossRef]
- Eymard, L.; Obligis, E. The Altimetric Wet Tropospheric Correction: Progress since the ERS-1 Mission. Proc. Symp. Years Prog. Radar Altimetry 2006, 614, 1387–2017. [Google Scholar]
- Brown, S.T.; Desai, S.; Lu, W.; Tanner, A. On the Long-Term Stability of Microwave Radiometers Using Noise Diodes for Calibration. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 1908–1920. [Google Scholar] [CrossRef]
- Maiwald, F.; Montes, O.; Padmanabhan, S.; Michaels, D.; Iyakara, A.K.; Jarnot, R.; Brown, S.T.; Dawson, D.; Wu, A.; Hatch, W.; et al. Reliable and Stable Radiometers for Jason-3. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 9, 2754–2762. [Google Scholar] [CrossRef]
- Lázaro, M.Á.P.; Pujades, M.B.; Sola, R.G.; Coto, A.G.; Fernández, J.L.G.; Camacho, Y. Design, development and calibration of the MWR microwave radiometer on board Sentinel-3. In Proceedings of the 2014 44th European Microwave Conference, Rome, Italy, 6–9 October 2014; pp. 1671–1674. [Google Scholar] [CrossRef]
- Frery, M.-L.; Siméon, M.; Goldstein, C.; Féménias, P.; Borde, F.; Houpert, A.; Garcia, A.O. Sentinel-3 Microwave Radiometers: Instrument Description, Calibration and Geophysical Products Performances. Remote. Sens. 2020, 12, 2590. [Google Scholar] [CrossRef]
- Donlon, C.J.; Cullen, R.; Giulicchi, L.; Vuilleumier, P.; Francis, C.R.; Kuschnerus, M.; Simpson, W.; Bouridah, A.; Caleno, M.; Bertoni, R.; et al. The Copernicus Sentinel-6 mission: Enhanced continuity of satellite sea level measurements from space. Remote. Sens. Environ. 2021, 258, 112395. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, D.; Li, Y.; Zhao, J. Prelaunch calibration and primary results from in-orbit calibration of the atmospheric correction microwave radiometer (ACMR) on the HY-2A satellite of China. Int. J. Remote. Sens. 2014, 35, 4496–4514. [Google Scholar] [CrossRef]
- Vieira, T.; Fernandes, M.J.; Lazaro, C. Independent Assessment of on-Board Microwave Radiometer Measurements in Coastal Zones Using Tropospheric Delays From GNSS. IEEE Trans. Geosci. Remote. Sens. 2018, 57, 1804–1816. [Google Scholar] [CrossRef]
- Lázaro, C.; Fernandes, M.J.; Vieira, T.; Vieira, E. A coastally improved global dataset of wet tropospheric corrections for satellite altimetry. Earth Syst. Sci. Data 2020, 12, 3205–3228. [Google Scholar] [CrossRef]
- Brown, S. A Novel Near-Land Radiometer Wet Path-Delay Retrieval Algorithm: Application to the Jason-2/OSTM Advanced Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1986–1992. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Lázaro, C.; Vieira, T. On the role of the troposphere in satellite altimetry. Remote. Sens. Environ. 2021, 252, 112149. [Google Scholar] [CrossRef]
- Vieira, T.; Fernandes, M.J.; Lázaro, C. Analysis and retrieval of tropospheric corrections for CryoSat-2 over inland waters. Adv. Space Res. 2018, 62, 1479–1496. [Google Scholar] [CrossRef]
- Obligis, E.; Eymard, L.; Tran, N.; Labroue, S.; Femenias, P. First three years of the microwave radiometer aboard Envisat: In-flight calibration, processing, and validation of the geophysical products. J. Atmos. Ocean. Technol. 2006, 23, 802–814. [Google Scholar] [CrossRef]
- Obligis, E.; Rahmani, A.; Eymard, L.; Labroue, S.; Bronner, E. An Improved Retrieval Algorithm for Water Vapor Retrieval: Application to the Envisat Microwave Radiometer. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 3057–3064. [Google Scholar] [CrossRef]
- Picard, B.; Frery, M.-L.; Obligis, E.; Eymard, L.; Steunou, N.; Picot, N. SARAL/AltiKa Wet Tropospheric Correction: In-Flight Calibration, Retrieval Strategies and Performances. Mar. Geodesy 2015, 38, 277–296. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, D.; Wang, Z.; Li, Y. The Validation of HY-2A ACMR retrieval algorithms and product. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGASS), Beijing, China, 10–15 July 2016. [Google Scholar] [CrossRef]
- Vieira, T.; Fernandes, M.J.; Lázaro, C. An enhanced retrieval of the wet tropospheric correction for Sentinel-3 using dynamic inputs from ERA5. J. Geodesy 2022, 96, 28. [Google Scholar] [CrossRef]
- Obligis, E.; Eymard, L.; Tran, N. A New Sidelobe Correction Algorithm for Microwave Radiometers: Application to the Envisat Instrument. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 602–612. [Google Scholar] [CrossRef]
- Vieira, T.; Fernandes, M.J.; Lázaro, C. Modelling the Altitude Dependence of the Wet Path Delay for Coastal Altimetry Using 3-D Fields from ERA5. Remote. Sens. 2019, 11, 2973. [Google Scholar] [CrossRef]
- Collecte Localisation Satellites (CLS). Surface Topography Mission (STM) SRAL/MWR L2 Algorithm Definition, Accuracy and Specification; Ramonville St-Agne, France, 2011. Available online: https://www.eumetsat.int/media/38625 (accessed on 1 February 2023).
- Fernandes, M.J.; Lázaro, C. Independent assessment of Sentinel-3A wet tropospheric correction over the open and coastal ocean. Remote. Sens. 2018, 10, 484. [Google Scholar] [CrossRef]
- Thao, S.; Eymard, L.; Obligis, E.; Picard, B. Comparison of Regression Algorithms for the Retrieval of the Wet Tropospheric Path. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 4302–4314. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, Z. Evaluating the Accuracy of Jason-3 Water Vapor Product Using PWV Data from Global Radiosonde and GNSS Stations. IEEE Trans. Geosci. Remote. Sens. 2021, 59, 4008–4017. [Google Scholar] [CrossRef]
- Obligis, E.; Tran, N.; Eymard, L. An Assessment of Jason-1 Microwave Radiometer Measurement and Products. Mar. Geodesy 2004, 27, 255–277. [Google Scholar] [CrossRef]
- Wang, J.; Xu, H.; Yang, L.; Song, Q.; Ma, C. Cross-Calibrations of the HY-2B Altimeter Using Jason-3Satellite During the Period of April2019–September 2020. Front. Earth Sci. 2021, 9, 647583. [Google Scholar] [CrossRef]
- Jiang, M.; Xu, K.; Liu, Y.; Zhao, J.; Wang, L. Assessment of reprocessed sea surface height measurements derived from HY-2A radar altimeter and its application to the observation of 2015–2016 El Niño. Acta Oceanol. Sin. 2018, 37, 115–129. [Google Scholar] [CrossRef]
- Bao, L.; Gao, P.; Peng, H.; Jia, Y.; Shum, C.K.; Lin, M.; Guo, Q. First accuracy assessment of the HY-2A altimeter sea surface height observations: Cross-calibration results. Adv. Space Res. 2015, 55, 90–105. [Google Scholar] [CrossRef]
- Legeais, J.-F.; Ablain, M.; Thao, S. Evaluation of wet troposphere path delays from atmospheric reanalyses and radiometers and their impact on the altimeter sea level. Ocean Sci. 2014, 10, 893–905. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).