Abstract
The widespread use of mobile devices has resulted in the generation of vast amounts of spatial data. The availability of such large-scale spatial data facilitates the development of data-driven approaches to address real-life problems. This paper introduces the max coverage region (MCR) problem in road networks and provides efficient solutions. Given a set of spatial objects and a coverage radius, the MCR problem aims to identify a location from the road network, so that we can reach as many spatial objects as possible within the given coverage radius from the location. This problem is fundamental to supporting many real-world applications. Given a road network and a set of sensors, this problem can be used to find the best location for a sensor maintenance station. This problem can also be applied in medical research, such as in a protein–protein interaction network, where the nodes represent proteins, the edges represent their interactions, and the weight of an edge represents confidence. We can use the MCR problem to find the set of interacting proteins with a confidence budget. We propose an efficient exact solution to solve the problem, where we reduce the MCR problem to an equivalent problem named the most overlapped interval and design an edge-level upper bound estimation method to reduce the search space. Furthermore, we propose two approximate solutions that sacrifice a little accuracy for much better efficiency. Our experimental study on real-road network datasets demonstrates the effectiveness and superiority of the proposed approaches.
1. Introduction
With the proliferation of GPS-enabled mobile devices, users can access various location-based services, such as Foursquare and Google Maps. Therefore, massive volumes of spatial data are being generated rapidly every day. The availability of such large-scale spatial data facilitates the development of data-driven approaches to address problems in real scenarios, such as urban planning. Consider the following example.
Example 1.
Suppose that the government has already placed a set of sensors along the road network. In order to collect data from the sensors and guarantee the sensors work properly, the government would desire to set up a maintenance station to host engineers. Intuitively, a good location for the station should reach as many sensors as possible within a reasonable distance. Where should the station be set up?
In this paper, we generalize the motivating example and formulate the max coverage region (MCR) problem. Informally, given a set of spatial objects in the road network, we wish to find a location, such that the objects within its coverage are maximized. Here, we assume that an object is in the coverage of a location if the road network distance between the object and the location is no larger than a given threshold.
Example 2.
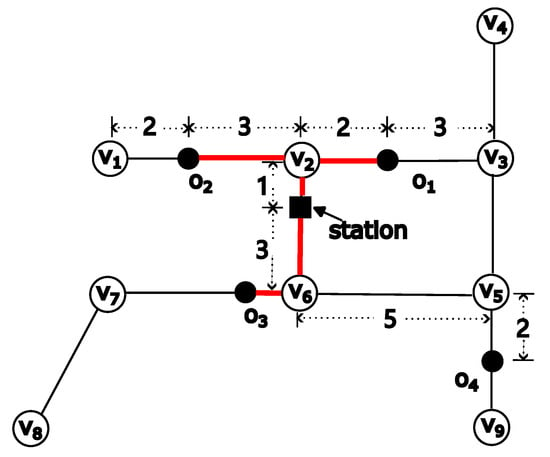
Consider the example in Figure 1. The road network consists of nine nodes and nine edges. The black dots represent four spatial objects. Assume the coverage radius is 4. When the station is placed at the black square, it covers , , and . The shortest path between the station and each covered object is highlighted in red. As no other location can cover more than three spatial objects, the black square is the result that the MCR problem aims to return.

Figure 1.
An example of a road network. The numbers on the edge indicates the length of the road segments.
It is non-trivial to solve the MCR problem. In the road network, there are infinite candidate locations and it is prohibitively expensive to consider all these locations in the search of the max coverage region. Moreover, in order to determine whether the region at a location has the maximum coverage, it is required to compute the network distance between the location and many objects, which is also expensive. Thus, these demand techniques that can efficiently identify the optimal location over very large volumes of spatial objects.
To address the aforementioned challenges, we first propose the most overlapped interval (MOI) problem. Instead of searching for the optimal location from the infinite set of candidate locations, we construct an equivalent MOI problem and design an effective algorithm based on a linear scan to solve it. This reduction greatly reduces the search space. However, even if we can search an edge efficiently, it becomes prohibitively expensive if we search every edge. Therefore, we propose an edge-level upper-bound estimation method. By acquiring the upper bounds for every edge, we search the edges in a greedy manner and terminate immediately when the upper bound of the remaining edges is worse than the current known optimal location. In some scenarios, it is acceptable to sacrifice a little accuracy for much better efficiency. Motivated by this, we further propose two highly efficient solutions that find results with comparable quality. According to our experiments, the runtimes of the approximate solutions are only of the exact solutions. To demonstrate the superiority of our proposed solutions, we conducted extensive experiments on five real-world road network datasets. The experiments show that our solutions are capable of handling large-scale datasets and could find satisfying results.
Our paper is related to the community search/detection problem, the best region search problem, and the location selection problem. We will elaborate on these three problems in turn.
Best region search problem. The best region search problem aims to find the location of a given-size rectangular region such that the score of the region is maximized. This kind of problem is first proposed and investigated as the maximizing range sum (MaxRS) problem [1,2] in the computational geometry community. The score of a region in the MaxRS problem is the number of spatial objects inside the region. Imai et al. [2] developed an efficient algorithm to find the position of the rectangle of the given size enclosing the maximum number of spatial objects. The algorithm’s complexity is , where n is the number of spatial objects. Nandy and Bhattacharya [1] reduced the MaxRS problem to a rectangle overlapping problem and then designed a sweep-line-based algorithm with the same time complexity . Choi et al. [3] thoroughly investigated the MaxRS problem. They assumed that the scalability of the spatial object was too large to be placed in memory. They proposed an external memory algorithm based on the in-memory algorithm. Tao et al. [4] proposed sacrificing some accuracy for better efficiency. They proposed a -approximate algorithm for addressing the MaxRS problem efficiently. Feng et al. [5] generalized the MaxRS problem to propose the best region search problem, where the score of a region was generalized from the SUM to a user-defined submodular monotone function. Mostafiz et al. [6] extended the MaxRS problem by taking the types of spatial objects into account. Users can issue constraints on the types of spatial objects while searching for the region with the maximum total weight. Feng et al. [7] next proposed an attribute-aware similar function to evaluate the similarity between regions. Users can issue a query region to search for regions that have similar attribute distributions. Moreover, researchers proposed the use of a semantic window [8] and searchlight [9] to investigate the region search problem in an interactive data exploration manner for multidimensional data. All of this work focuses on finding the location of a rectangular region in the Euclidean space. In this paper, we aim to find the optimal location for a station whose coverage is defined as a subgraph on the road network. In addition, the aforementioned region search problems require users to specify the width and the height of the rectangular region, which is difficult to set. In contrast, in this paper, we eliminate the shape-related parameter and only let the users specify the radius of the coverage, which is intuitive and straightforward. Thus, the aforementioned studies are different from our problem.
The length-constrained maximum-sum region (LCMSR) query [10] is the most relevant to our work. Given a spatial network and a set of query keywords, the LCMSR query returns a subgraph from the road network such that (1) the distance between any pair of nodes in the subgraph is no larger than a threshold, and (2) the total textual relevance between the keywords on each node in the subgraph and the query keywords is maximized. The LCMSR problem differs from our problem in the following aspects: (1) The LCMSR problem imposes a length constraint on the pairwise distance to control the shape of the region, making the LCMSR problem NP-hard. In contrast, in our paper, we assume the coverage of a station is a subgraph centered at a location in the road network. As we will show in Section 2.2, our proposed problem can be solved in polynomial time. (2) The LCMSR problem only considers the nodes in the spatial network; however, in this paper, we assume that spatial objects can be located at any location on any edge in the road network. Therefore, the techniques proposed for LCMSR cannot be applied to solve our problem.
Location selection problem. Our MCR problem is related to the location selection problem. The location selection problem aims to find the location for a new facility, such that a certain objective function is optimized. As input, the min-dist optimal-location query [11] uses a set S of sites, a set O of weighted objects, and a spatial region Q. It returns a location in Q, which, if a new site is built there, minimizes the average distance from each object to its closest site. Xiao et al. [12] extended the location selection problem to road networks, as movements between spatial locations are usually confined by the underlying road network in practice. Chen et al. [13] also investigated the location selection problem in road networks, but they considered minimizing the maximum distance between any client and the site that served him/her. Another class of studies aimed to find the location for a new server to maximize its influence. For instance, Du et al. [14] assumed that the influence of a new site is the total weight of its reverse nearest neighbors, i.e., the total weight of objects that are closer to this site than the others. They consider this problem in the L1-norm space. Moreover, Cabello et al. [15] studied this problem in the L2-norm space and a very efficient algorithm was proposed [16]. Choudhury et al. [17] incorporated textual information into this problem and only considered the reverse k-nearest neighbors that were textual relevant to the query keywords. Zhou et al. [18] and Yan et al. [19] also considered the problem with different definitions of influence, respectively. Moreover, many works [20,21,22] investigated the problem of selecting the top-k locations. The location selection problem differs from the MCR problem, as it cares about the reverse nearest neighbors of the new site. In other words, the new site has to compete with other sites to affect more objects. In our paper, the location of the station is independent. We only need to find the optimal location to cover as many objects as possible without considering the effect of other competing stations.
The contributions of this paper are summarized as follows:
- We formulated the max coverage region (MCR) problem. To reduce the search space, we propose a most overlapped interval (MOI) problem and prove that it is equivalent to solving the MOI problem. This idea greatly reduces the search space from infinite candidate locations to intervals.
- To address the MCR problem, we developed an edge-level upper-bound estimation method. This enabled us to search the road network in a greedy manner.
- We propose two approximate solutions. They are highly efficient and return results with comparable quality.
- Extensive experiments were conducted on five real-road network datasets. The results demonstrate the efficiency and effectiveness of our proposed solutions.
2. Method
2.1. Problem Definition
In this subsection, we first present the max coverage region (MCR) problem.
Definition 1
(Road Network Graph). A road network consists of a set of nodes V, a set of undirected edges , and a distance function . Each node is a spatial location , where are its coordinates.
A set O of data objects resides on the road network. Each data object is a point on an edge .
The road network graph models the roads in real life, where each node represents a road junction, and each edge represents a road segment. Data objects can be the locations of vehicles or pedestrians.
Consider the example in Figure 1, where the road network consists of nine nodes and nine edges. There are four data objects , , , and . The four data objects are located on edges , , and , respectively.
Remark 1.
Note that in this paper, we assume that the spatial objects are located on the edges of the road network. At first glance, it may seem that we can treat the spatial objects as nodes and build a new graph. However, this is not appropriate due to the following reasons: (1) In real-life scenarios, the spatial objects are usually used to represent points of interest, user check-ins, and GPS locations. Compared with the road network, such spatial objects may change rapidly. If we transform these spatial objects in the nodes in the network, we may need to frequently update the network when these spatial objects change, which would be very inefficient. (2) As we treat the spatial objects separately, we can store and manage the set of spatial objects on each edge together and build an efficient index. This enables us to access spatial objects efficiently.
Definition 2
(Coverage). Let p be a location in the road network. Given a threshold γ, a data object (o) is in p’s coverage if the road network distance between p and o is no larger than γ, i.e., .
In Figure 1, the shortest paths between the station and , , and are highlighted in red. In Figure 1, the distances between the station and , , and are 3, 4.
Definition 3
(The MCR Problem). Consider a road network graph G. Given a set (O) of data objects that reside on the road network and a threshold γ, and given a road network graph and a set of data objects that reside on the road network, the MCR problem aims to find the optimal location for a station, such that the number of data objects that are covered by the station is maximized.
2.2. An Exact Solution
The MCR problem requires selecting the best location for a station to cover as much as spatial objects as possible. Intuitively, the optimal location can be located at any point in the road network. Apparently, it is prohibitively expensive to enumerate all points, which is infinite. To tackle this challenge, we first present an effective exact method for the MCR problem. To this end, we first introduce how to select the best point on a given edge that covers the maximum number of spatial objects.
2.2.1. Searching an Edge for the Optimal Location
To search for the point that covers the maximum number of spatial objects of an edge, a naive idea is to evaluate the number of objects that are covered by each point on this edge. For instance, take Figure 2a as an example, where the blue point p is a point on the edge . For the blue point p on the edge , we explore close objects within the given radius by expanding from p. The coverage of p is highlighted in red. As can be seen from the figure, objects and are covered by p. By repeating this procedure for every point on the edge , we can find the optimal location on this edge. Unfortunately, as there is an infinite number of points, this idea is prohibitively expensive.
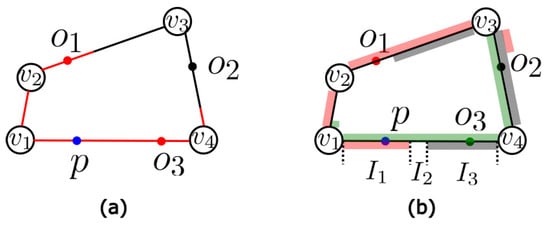
Figure 2.
In (a), the coverage of point p is highlighted in red. Point p covers spatial objects and . In (b), the coverage of , and are highlighted in red, grey and green, respectively. Point p is in the coverage of and .
To address the above issue, we propose the most overlapped interval (MOI) problem. We then show that we can reduce the problem of searching for the optimal point on the edge to solve the most overlapped interval problem, which can be solved efficiently. We next give the formal definition of the MOI problem and illustrate how to perform the reduction with a detailed example.
Definition 4
(Most Overlapped Interval). Given an edge , a segment is a part of the edge bounded by two endpoints and on the edge. Let be a set of segments on the edge. The most overlapped interval problem aims to find the interval , , such that overlaps with the maximum number of segments.
Example 3.
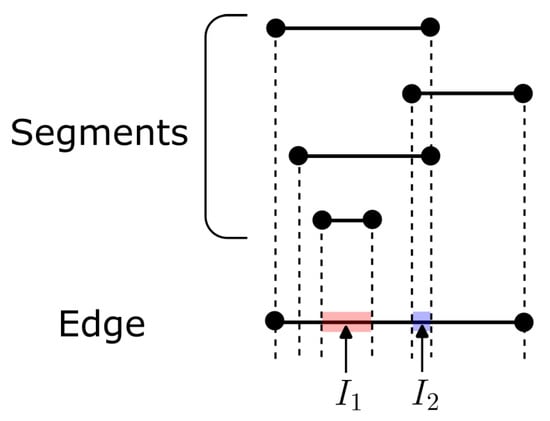
Consider the example in Figure 3, where there is one edge and four segments. The endpoints of the segments divide the edge into six intervals. We notice that intervals and overlap with three segments, which is more than other intervals. Thus, both and are the most overlapped intervals on the edge.

Figure 3.
Most overlapped interval problem.
To explain how we can reduce the problem of searching for the optimal point on the edge of the MOI problem, we first present the following observation. Consider edge in the example in Figure 2a. We observe that spatial object is in the coverage of point p (highlighted in red). Inversely, if we draw the coverage of , we notice that point p is located at the interval , which is the overlap between ’s coverage and the edge . In fact, any point on the interval can cover . Motivated by this observation, a natural idea to identify the overlap between and every spatial object’s coverage. Each overlap corresponds to a segment on the edge . We can then find the most overlapped interval. Any point on this interval is an optimal location on the edge that covers the maximum number of spatial objects. The following example demonstrates the reduction from Figure 2a.
Example 4.
There are three spatial objects (, , and ) in Figure 2a. For each spatial object, we draw the coverage of , , and , which are highlighted in red, gray, and green, respectively. Each object’s coverage overlaps with edge and the resulting segments divide the edge into three different intervals, denoted as , , and . Interval overlaps with the red and the green segments, while overlaps with the green and the gray segments. Thus, and are the most overlapped intervals. We can pick a point p from and return it to users as a result.
We showed how to reduce the problem of searching an edge for the optimal point to the most overlapped interval problem. Two questions are to be answered: (1) Which spatial objects should we consider to compute the overlap between the edge and their coverage so that we can generate the segments for the MOI problem? (2) How do we address the MOI problem efficiently? We next elaborate on the two questions in turn.
- Identifying valid spatial objects.
As we demonstrated above, the input of the reduced MOI problem is the set of segments, each of which is the overlap between a spatial object’s coverage and the edge. Some spatial objects are very far from the edge, such that any point on the edge cannot reach the object. It is unnecessary to consider such spatial objects while we are generating the overlapped segments for the MOI problem. Thus, to identify the valid spatial objects to generate segments for the reduced MOI problem on the edge , we can divide the spatial objects into three classes as follows:
Case 1: Irrelevant objects. A spatial object (o) is an irrelevant object to the edge if no point on can reach o within the radius . As a result, we do not need to consider such objects when searching for the most overlapped interval. We can easily derive the following lemma to verify whether a spatial object is irrelevant.
Lemma 1.
If and , then o is an irrelevant object to .
Proof.
For any point p on , its distance to o is . Since , , it is obvious that . Thus, o is an irrelevant object. □
Case 2: Fully-covered objects. A spatial object (o) is a fully-covered object to edge if any point on can reach o within the radius . Thus, it is unnecessary to consider o anymore when searching the edge for the most overlapped interval. We derive the following lemma to verify whether o is a fully-covered object.
Lemma 2.
An object (o) is a fully-covered object toif at least one of the following conditions holds:
- 1.
- ;
- 2.
- ;
- 3.
- .
Proof.
It is obvious that o is a fully-covered object when the first two conditions hold. For the third condition, consider a point p on the edge . We
Since , we , i.e., any point can reach o within the radius . □
Case 3: Partially covered objects. A spatial object (o) is a partially covered object to edge if some points on can reach o within the radius, while the other points cannot. Therefore, to search for the optimal point on the edge , we need to find all partially covered objects and determine the most influenced interval. To verify whether an object is a partially covered object to , we present the following lemma.
Lemma 3.
An object (o) is a partially covered object if the following two conditions hold:
- 1.
- 2.
- , or
Proof.
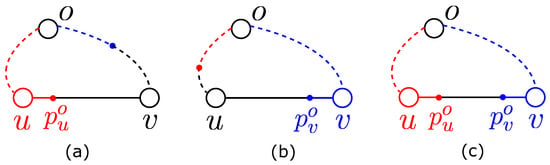
According to the definition of partially covered objects, we consider the following three cases: (1) As shown in Figure 4a, only the points on the interval can reach o within through node u; (2) only the points on the interval can reach o within through v; and (3) points on both intervals and can reach o within through u and v, respectively. By considering the three cases, we can easily derive the inequalities in the lemma. □

Figure 4.
Three cases of partially covered objects. In (a), object o can be reached from edge through u. In (b), object o can be reached from through v. In (c), object o can be reached from through either u and v.
The above three cases indicate that we only need to consider the segments concerning the intersection between the partially covered object’s coverage and the edge .
- Solve the MOIproblem
We showed how to identify the set of spatial objects whose coverage on the edge should be considered in the MOI problem. With the MOI problem constructed, how can one efficiently find the most overlapped interval? To answer this question, one straightforward idea is to maintain a counter for each interval and iterate over all segments to update the counter of every overlapped interval. We refer to this algorithm as the MOIEnumerate algorithm.
MOIEnumerate Algorithm. Algorithm 1 shows the pseudocode of the straightforward idea. The algorithm takes as input a set of segments on the edge and outputs the most overlapped interval . The algorithm first collects the endpoints from all segments (lines 1–3) and sorts the endpoints (line 4). It computes all intervals bounded by every two consecutive endpoints (line 5). Next, the algorithm iterates over all segments (lines 6–8). For each segment, it computes the overlapped intervals (line 7) and increases the associated counters by 1 (line 8). When all segments are processed, we choose the interval with the largest counter (line 9) and return it to the user as the final result.
| Algorithm 1: MOIEnumerate |
 |
Complexity Analysis. It takes to sort the endpoints of all segments, where is the number of segments. The endpoints divide the edge into intervals. Then, for each segment, we need to locate the intervals that are covered by the segment and update the counter for each interval. Thus, it takes time to process one segment, and there are segments to be processed. Therefore, the total complexity of Algorithm 1 is .
The MOIEnumerate algorithm is easy to implement. However, an expensive operation in the algorithm is the counter-updating operation, i.e., for each segment, we need to identify the overlapped intervals and update their counters in turn. The number of overlapping intervals is ; thus, the MOIEnumerate algorithm scales poorly with respect to the number of segments.
MOILinearScan Algorithm. To tackle this efficiency issue of the MOIEnumerate algorithm, we next analyze the MOI problem and design an efficient linear scan-based algorithm, named MOILinearScan. We use the following example to explain the intuition behind the algorithm.
Example 5.
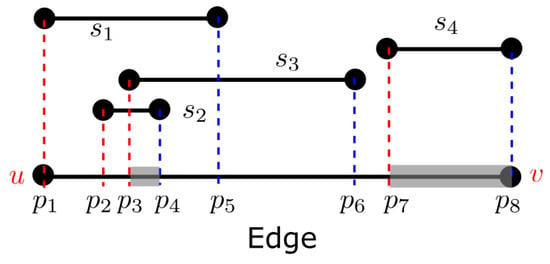
Consider the example in Figure 5. The endpoints of the segments divide the edge into several disjoint intervals. In the example, , …, are the endpoints of four segments. We mark the left endpoints in red and the right endpoints in blue.

Figure 5.
Property analysis of the MOI problem. The red dashed lines correspond to the left endpoints of intervals, while the blue dashed lines correspond to the right endpoints of intervals.
Assume we move a sweep point from u to v (from left to right). The sweep point first meets the left endpoint of segment . From now on, the sweep point overlaps with segment . We keep moving the sweep point until it meets the left endpoint of segment . The sweep point overlaps with and now. Similarly, when the sweep point meets the left endpoint of segment , the sweep point overlaps with segments , , and . Then, the next endpoint the sweep point meets is , which is the right endpoint of segment . After that, the sweep point only overlaps with and . We keep moving the sweep point until it reaches the end of this edge, i.e., v.
Assume a sweep point is moving from left to right. From the above example, we can observe the following properties:
Property 1.
When the sweep point meets a left endpoint of any segment, the next interval is overlapped with this segment.
Property 2.
When the sweep point meets the right endpoint of any segment, the next interval is no longer overlapped with this segment.
The two properties tell the status of consecutive intervals. Recall that each interval is bounded by two endpoints. If the endpoints do not overlap with each other, the difference between the number of overlapped segments of two consecutive intervals is 1. For instance, overlap with one segment, while overlap with two segments. Similarly, overlap with three segments, while overlap with two segments.
From the two properties, we derive the following lemma, which is the key to the MOILinearScan algorithm.
Lemma 4.
Among all intervals on the edge , the interval between a left endpoint and a right endpoint has the maximal number of overlapped segments, compared to its adjacent intervals.
Proof.
The two properties indicate the set of overlapped segments of such an interval and its adjacent intervals. Thus, the lemma is easily proved. □
This inspired us to use a design a sweep point-based method to search for the most overlapped interval. Specifically, we use a sweep point to scan the edge from left to right. During the sweeping, we maintain a counter to record the number of overlapped segments, keeping in mind the type of the recently passed endpoint, i.e., whether it is a left endpoint or a right endpoint of a segment. If we encounter an interval bounded by a left endpoint and a right endpoint consecutively, it is a maximal interval, which means the overlapped segments of this interval are larger than the adjacent intervals. We refer to this algorithm as MOILinearScan.
Algorithm 2 shows the pseudocode of MOILinearScan. The algorithm takes (as input) a set of segments on the edge , and outputs the most overlapped interval . Initially, the algorithm collects the left and right endpoints of all segments and stores them in lists L and R, respectively (lines 2–3). Both lists are sorted in ascending order (line 4). The variable is initialized as , representing the last endpoint the sweep point has encountered, and counter (lines 5–6). Next, it iteratively pops endpoints from L and R, representing moving the sweep point from left to right (lines 7–15). In each iteration, if , it means the sweep point meets a left endpoint, and the following interval’s counter will be increased by 1 (lines 8–10). Otherwise, it means the sweep point meets the right endpoint and the current interval’s counter is larger than its adjacent intervals. If the current interval’s counter is larger than the record , we record the interval and its counter with and . When all left endpoints are processed, we can terminate the iteration (lines 16–17) and return to users.
Example 6.
Consider the example in Figure 5. The two lists are sorted as , . The variable is initialized as , and is initialized as 1. In the first iteration, is ‘popped’ from L, as . We update , . In the second iteration, is ‘popped’ from L, and , . In the third iteration, is ‘popped’ from R. In this case, the interval is a maximal interval. We use and to record this interval. By repeating this process, we can know the counter for every interval. Since interval has the maximum counter, we return it to the user as the final result.
Complexity Analysis. It takes time to sort the left/right endpoints of the segments. We next process an endpoint from either L or R in every iteration, and there are iterations. Putting these together, the total complexity of Algorithm 2 is .
| Algorithm 2: MOILinearScan. |
 |
2.2.2. Searching the Whole Road Network for the Optimal Location
In the previous subsection, we demonstrated how to search an edge for the optimal location, such that a station placed on that location covered the maximum number of spatial objects. Thus, in order to search the whole road network for the optimal point, the natural idea is to repeat the previous procedure on every edge of the road network. For instance, for every edge, we identify the partially covered objects and construct the corresponding MOI problem and invoke Algorithm 2 to solve it. Unfortunately, this idea involves many redundant operations, and it is unnecessary to examine every edge. In this subsection, we present a method to estimate an upper bound for every edge to show the maximum number of objects that a station on the edge can cover. With the upper bound, we can examine the edges in a greedy manner, which greatly reduces the search space.
- Estimating Upper Bounds for Edges
The upper bound of an edge tells us what is the maximum number of covered objects if we place a station on the edge. A straightforward idea to define the upper bound is based on partially covered objects and fully-covered objects that we introduced in Section 2.2.1. Recall that fully-covered objects are the set of spatial objects that any point on the edge can reach within the radius, while partially covered objects are the set of spatial objects that only a part of points on the edge can reach within the radius. Therefore, The total number of fully-covered and partially covered objects is an upper bound for the maximum covered objects if we place a station on this edge. However, the spatial objects in the road network are usually very large and could emerge rapidly. It would be expensive to check every spatial object’s status. In contrast, the road network is relatively small and seldom changes. As a result, we propose computing the upper bounds on the edge level.
To this end, a key question to be answered is: what is the upper bound of the distance between two points and , where and are from two different edges? To answer this question, we use the example in Figure 6 to explain. In the example, and are two edges, and and are two points on the two edges, respectively. We can easily derive the distance between and as
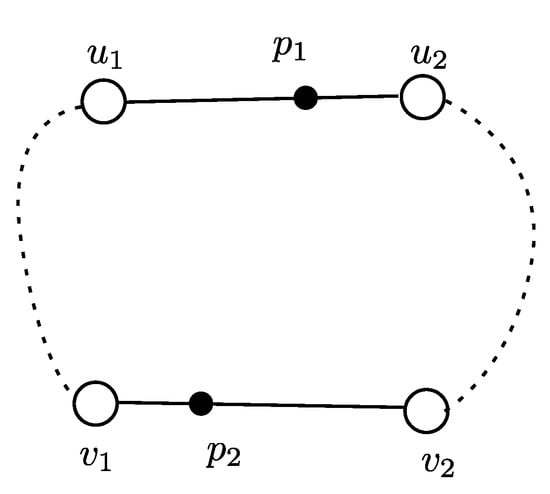
Figure 6.
An example of analyzing the relationship between edges.
As it is obvious that , , , , where / is the length of edge /. We define the function as follows
We can easily derive that
The computation of function only relies on the edge length ( and ) and node pair distances (, , , ), which means they can be efficiently computed. Moreover, as they give an upper bound for the maximum point distances between two edges, they can be used to estimate the coverage number upper bound on an edge. Specifically, given an edge e, we identify the set of candidate edges, such that for each edge , we . Apparently, if an edge , it means no matter which location in e is the station placed, it cannot cover the spatial objects in , as their distance would be larger than . We can simply add up the number of spatial objects in every as the coverage number upper bound.
- The Searching Algorithm
With the upper bound defined, we can search the graph in a greedy manner. The edges with higher upper bounds are searched first. The search is terminated if the upper bounds of the remaining edges are less than the coverage number of the current optimal point. Algorithm 3 shows the pseudocode for searching the whole graph. It takes as input the road network and a radius , and outputs the station location that covers the maximum number of spatial objects. It uses a priority queue h to keep the edges and their coverage number upper bound and h is initialized as empty (line 1). Initially, for each edge e, it computes the coverage number upper bound and pushes it into the priority queue (lines 2–5). Specifically, it first identifies the set of edges such that the distance upper bound does not exceed for every (line 3). Then it computes the coverage number upper bound by adding up the number of objects on every edge in (line 4). With all upper bounds computed and pushed into h, it starts searching greedily (lines 7–14). It uses to record the currently known optimal location and to record its coverage number. In each iteration, it pops edge e with the maximum upper bound from h (line 8). If the upper bound is less than , it is unnecessary to examine the remaining edges and the search is terminated (liens 9–10). Otherwise, it constructs the corresponding MOI problem on the edge e by generating the segments on e from the objects on (line 11). Then it invokes Algorithm 2 to solve the MOI problem and find the optimal point p and its coverage number on the edge e (line 12). The current optimal point is updated accordingly if (lines 13–14). When the search is finished, it returns and to the users as the final result.
Remark 2.
In Algorithm 3, in order to compute the coverage number upper bound for each edge, we need to identify the edge set (line 3). For each edge , we compute , which involves many node pair distance computations. As an edge can only be added into if , we do need to compute all pair-wise distances in the road network. In contrast, we only need to perform a length-constrained Dijkstra algorithm for each node, i.e., compute the set of nodes whose distance is less than γ. This is much more efficient.
| Algorithm 3: MCRExact. |
 |
Complexity. To compute the coverage upper bound, we need to perform a length-constrained Dijkstra algorithm for every node. Let be the average complexity for such a length-constrained Dijkstra algorithm. It takes to initialize the priority queue h. During the search, we need to compute the segments on the edge and invoke Algorithm 2 to solve the constructed MOI problem. Let be the number of generated segments. It takes to finish one iteration. Let k be the number of iterations that we need to search. The total time complexity is .
2.3. An Approximate Solution
In the previous section, we demonstrated an exact solution to the MCR problem. We notice that the complexity of the exact solution increases when the radius becomes larger, as we visit more nodes in the length-constrained Dijkstra algorithm. In some scenarios, people may focus more on efficiency than accuracy. They may intend to sacrifice a little accuracy for much better efficiency. As a result, in this section, we present two approximate solutions. Though they may not always return the exact result, they can still find satisfactory results and are highly efficient.
Before we present the approximate solutions, we first analyze the search space of the exact algorithm MCRExact. Recall that we computed the upper bound for each edge in the network. The edges are searched in a greedy manner until the upper bound of the remaining edges is smaller than the current result. As shown in Figure 7a, the edges that are searched are marked in red. Apparently, it takes most of the runtime to search the edges. There are infinite candidate locations on each edge. Even though we constructed a corresponding MOI problem and reduce the search space from infinity to , it is still inefficient when there are many spatial objects. Moreover, when the network consists of many edges, the total runtime will be much longer. Thus, to achieve better efficiency, we propose two approaches, namely NodeApprox and EdgeApprox, which will be elaborated on next.
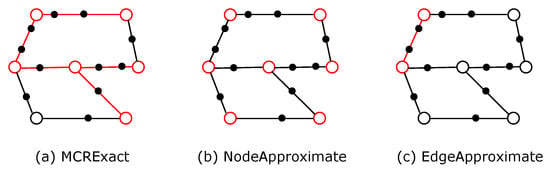
Figure 7.
The high-level idea of the exact approach and the two approximate approaches. The search space of each approach is highlighted in red.
The NodeApprox approach. Instead of searching the edges in a greedy manner, the NodeApprox approach adopts a totally different idea. Specifically, it only considers the nodes in the network as the candidate locations, i.e., the station can only be placed on a node in the road network. As shown in Figure 7b, only the nodes in the road network are marked in red, which means we will only examine every node and find the node that covers the maximum number of spatial objects. To examine a node, we can invoke a length-constrained Dijkstra algorithm to obtain the number of covered spatial objects.
The complexity of this approach is , where is the average complexity for the length-constrained Dijkstra search, and is the number of nodes in the road network.
The EdgeApprox Approach. The NodeApprox approach only considers the nodes in the road network as candidate station locations. It totally disregards the candidate locations on the edges, which makes it difficult to find satisfactory results in some scenarios. To tackle this issue, we design EdgeApprox with the following ideas: We first apply a length-constrained Dijkstra search for each node in the road network. Let be the coverage number of node v, i.e., the number of spatial objects that v can reach within the radius. For each edge , we compute its score as . Intuitively, if the two nodes have large scores, it is likely that the edge connecting the two nodes will contain a satisfactory location for the station. We pick the edge with the maximum score and construct a MOI problem on this edge. We invoke Algorithm 2 to solve the constructed MOI problem and return the best point on this edge to the user as the approximate result.
The complexity of this approach is , where is the number of nodes, is the average complexity for the length-constrained Dijkstra search, and s is the number of segments in the constructed MOI problem.
3. Results and Discussion
3.1. Experimental Setup
Datasets. In this paper, we use five real-world public datasets, namely NY, BAY, COL, FLA, and NW (http://www.diag.uniroma1.it//challenge9/download.shtml (accessed on 31 January 2023)). These datasets are the road networks in New York City, San Francisco Bay Area, Colorado, Florida, and Northwest USA, respectively. In the road network, each edge represents a road segment and its weight is the physical distance of the road. For each dataset, we randomly generate spatial objects and place them on the road network. Specifically, the number of spatial objects on an edge is proportional to , where / is the degree of node u/v, and is the length of the edge. Informally, if an edge is connected to nodes with a higher degree, or if the edge is longer, it is likely to hold more spatial objects. Each edge holds about 15.2 spatial objects on average. The details of the five datasets are reported in Table 1. We illustrate the distribution of edge lengths in each dataset in Figure 8. As can be observed from the figure, the lengths of most of the edges are smaller than 6000.

Table 1.
Details of the datasets. # nodes, # edges, and # objects represent the numbers of nodes, edges, and objects, respectively.
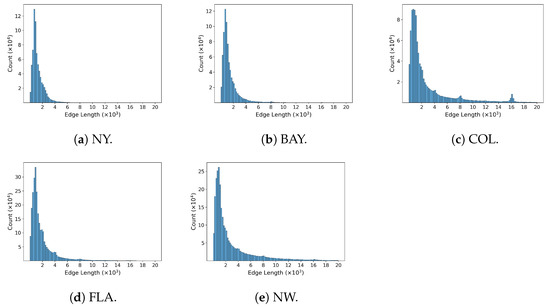
Figure 8.
Distribution of edge length in each dataset.
Evaluated Algorithms. We evaluate the following algorithms. (a) MCRExact, the exact algorithm for the MCR problem; (b) NodeApprox, the method that only considers nodes in the road network as the candidate locations for the station; (c) EdgeApprox, the method that only search the most promising edge.
Query Radius. Recall that the proposed approach involves many length-constrained Dijkstra searches. Apparently, the edge length in the road network influences the efficiency of the algorithm. Thus, it is not a good idea to use the same query radius on different datasets. To consider the effect of edge length, we set as the unit query radius, where avg. edge length is the average edge length of the road network. We set the query radius as . We can change the query radius by using different values for k.
Performance Measure. We consider the following performance measures: (1) the runtime of each algorithm and (2) the coverage number, i.e., the number of spatial objects that can be covered if the station is placed at the location returned by the algorithm.
All algorithms were implemented in Python 3.9.7. All experiments were run on a Windows desktop with AMD Ryzen 7 5800H CPU and 16 GB memory.
3.2. Experimental Results
The efficiency of the proposed approaches. In this set of experiments, we evaluated the efficiency of the proposed approaches on different datasets by varying the query radius. The runtimes of the evaluated algorithms are reported in Table 2. From the table, we can see that the proposed approximate solutions are much more efficient than the exact solution, especially when the radius is small. This is because when the radius is large, the coverage of a station is more likely to cover complete edges, which makes the upper bound more tight. With a tighter upper bound, more edges can be pruned. In some cases, the runtimes of the approximate solutions are about of that of the exact solution. This illustrates that the proposed approximate approaches are much more efficient than the exact algorithm.

Table 2.
Runtime of the proposed approach vs. query radius (seconds).
Quality of Results of the Approximate Solutions. We will now investigate the quality of results of the approximate solutions. We vary the coverage radius and report the number of covered spatial objects when the station is placed at the location returned by the solution in Table 3. We observe that the approximate solutions return a comparative result as the exact solution. For instance, in most datasets, the results of the two approximate algorithms are about 98% of the results of the exact algorithm. In addition, we notice that when the radius is larger, the gap between the quality of results of the approximate solution and the exact solution is smaller.

Table 3.
Result Quality of the approximate approach vs. query radius.
Effectiveness of upper bound. Recall that in the exact solution, we design an upper bound for each edge so that we can search the edges in the graph in a greedy manner. In this set of experiments, we investigate the effectiveness of the upper bound.
Firstly, Table 4 reports the number of edges that are searched in the road network and its ratio to the total number of edges. A smaller value means that many edges are pruned by their upper bounds. We observe that only a small ratio of edges are searched. In most cases, less than 1% of edges are searched. This demonstrates the effectiveness of our proposed pruning technique. In addition, as can be observed from the table, the ratio of the edges that are searched decreases as the radius increases. This is because more complete edges are fully covered when the radius is large. Recall that in the upper bound computation, we consider all spatial objects on both fully-covered edges and partially covered edges. When there are more fully-covered edges, the upper bound is tighter, which means we can prune more edges.

Table 4.
Effectiveness of the pruning technique based on the upper bound. The table reports the number of edges that are searched, and the ratio to the total number of edges.
Secondly, we compare the runtime of the exact solution when the upper bound-based pruning technique is removed, i.e., we do not terminate the algorithm early and keep searching until all edges have been examined. Figure 9 reports the runtime of the exact solution with and without the upper bound-based pruning. As can be observed from the figure, when there is no pruning, the runtime increases as the radius increases. The gap becomes more obvious when the radius is large. When the radius is 2000, the exact algorithm with pruning is about an order of magnitude faster than the counterpart without pruning. This demonstrates the effectiveness of the upper bound.
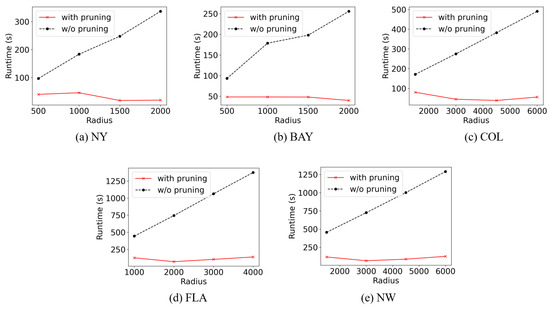
Figure 9.
The effect of upper-bound-based pruning on runtime.
The efficiency of MOIEnumerate and MOILinearScan. Recall that in order to solve the constructed MOI problem, we designed two algorithms, namely MOIEnumerate and MOILinearScan. In this set of experiments, we investigated the efficiency of the two algorithms. Specifically, we randomly generated segments on an edge to obtain two types of instances of the MOI problem: (1) In the first type, the segments were generated by following the uniform distribution, i.e., the endpoints of the segments were randomly drawn from uniform distribution independently. Thus, the segment length was not fixed. (2) In the second type, the length of the segments was fixed. The center of each segment was randomly drawn from a normal distribution. Figure 10 reports the runtimes of MOIEnumerate and MOILinearScan w.r.t. the number of segments. From the figure, we observe that (1) the runtime of MOIEnumerate increases rapidly as the number of segments increases. This is consistent with its complexity, which is , where is the number of segments in the MOI problem. (2) MOILinearScan scales well and is almost linear w.r.t. the number of segments. The results show that the proposed Algorithm 2 is highly efficient.
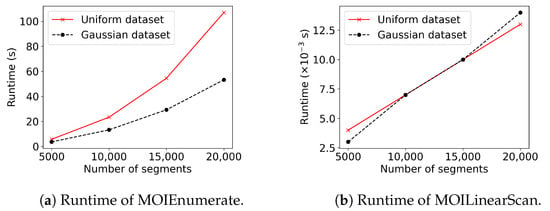
Figure 10.
Runtime of MOIEnumerate and MOILinearScan vs. the number of segments.
Scalability. Finally, in this set of experiments, we evaluated the scalability of the three proposed approaches. We used the largest road network NW and increased the number of spatial objects in the road network from 2,200,849 to 107,215,000. We used a fixed query radius of 1500 and report the runtime of the three approaches in Figure 11. As can be seen from the figure, all three approaches scaled well with respect to the number of spatial objects. This demonstrates the superiority of our proposed approaches.
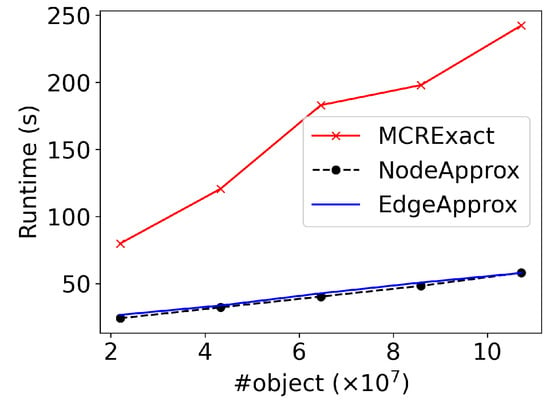
Figure 11.
Scalability.
4. Conclusions
In this paper, we propose a novel problem named max coverage region (MCR). The problem aims to select the optimal location for a station in the road network, such that the station can cover as many spatial objects as possible. There are an infinite set of candidate locations in the road network. To tackle this challenge, we propose the most overlapped interval (MOI) problem and show that we can solve the MCR problem by solving the MOI problem. With this reduction, we propose a linear scan-based algorithm to efficiently solve MOI in time. We further propose an edge-level upper bound estimation method to prune unnecessary edges to improve the efficiency. In addition to the exact solution, we propose approximate solutions to sacrifice a little accuracy for much better efficiency. We conducted extensive experiments on five real-world road networks and demonstrate the effectiveness and efficiency of the proposed solutions.
Author Contributions
Conceptualization, L.F. and Y.Z. (Yudong Zhang); methodology, L.F., G.Y.Y. and Y.Z. (Yudong Zhang); software, L.F.; validation, L.F., Z.K., Y.Z. (Yuzhang Zhou) and Y.Z. (Yudong Zhang); formal analysis, L.F., Z.K., Y.Z. (Yuzhang Zhou) and Y.Z. (Yudong Zhang); investigation, L.F.; resources, L.F., Z.K., Y.Z. (Yuzhang Zhou) and Y.Z. (Yudong Zhang); data curation, L.F., Z.K., Y.Z. (Yuzhang Zhou) and Y.Z. (Yudong Zhang); writing—original draft preparation, L.F.; writing—review and editing, L.F., G.Y.Y. and Y.Z. (Yudong Zhang); visualization, L.F., Z.K., Y.Z. (Yuzhang Zhou) and Y.Z. (Yudong Zhang); supervision, L.F.; project administration, L.F.; funding acquisition, Y.Z. (Yudong Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 61906039), Youth Scholar Program of SEU, and the Fundamental Research Funds for the Central Universities (grant no. 2242022k30007), Medical Research Council Confidence in Concept Award, UK (MC_PC_17171); Royal Society International Exchanges Cost Share Award, UK (RP202G0230); British Heart Foundation Accelerator Award, UK (AA/18/3/34220); Hope Foundation for Cancer Research, UK (RM60G0680); Global Challenges Research Fund (GCRF), UK (P202PF11); Sino-UK Industrial Fund, UK (RP202G0289); LIAS Pioneering Partnerships award, UK (P202ED10); Data Science Enhancement Fund, UK (P202RE237); Fight for Sight, UK (24NN201); Sino-UK Education Fund, UK (OP202006); Biotechnology and Biological Sciences Research Council (BBSRC), UK (RM32G0178B8).
Data Availability Statement
The five real-world road network datasets (NY, BAY, COL, FLA, and NW) comes from https://www.diag.uniroma1.it/challenge9/download.shtml (accessed on 12 May 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nandy, S.C.; Bhattacharya, B.B. A unified algorithm for finding maximum and minimum object enclosing rectangles and cuboids. Comput. Math. Appl. 1995, 29, 45–61. [Google Scholar] [CrossRef]
- Imai, H.; Asano, T. Finding the connected components and a maximum clique of an intersection graph of rectangles in the plane. J. Algorithms 1983, 4, 310–323. [Google Scholar] [CrossRef]
- Choi, D.W.; Chung, C.W.; Tao, Y. A scalable algorithm for maximizing range sum in spatial databases. arXiv 2012, arXiv:1208.0073. [Google Scholar] [CrossRef]
- Tao, Y.; Hu, X.; Choi, D.W.; Chung, C.W. Approximate MaxRS in spatial databases. In Proceedings of the 39th International Conference on Very Large Data Bases 2013, (VLDB 2013), Riva del Garda, Italy, 26–30 August 2013; Volume 6, pp. 1546–1557. [Google Scholar]
- Feng, K.; Cong, G.; Bhowmick, S.S.; Peng, W.C.; Miao, C. Towards best region search for data exploration. In Proceedings of the 2016 International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 1055–1070. [Google Scholar]
- Mostafiz, M.I.; Mahmud, S.F.; Hussain, M.M.U.; Ali, M.E.; Trajcevski, G. Class-based conditional MaxRs query in spatial data streams. In Proceedings of the 29th International Conference on Scientific and Statistical Database Management, Chicago, IL, USA, 27–29 June 2017; pp. 1–12. [Google Scholar]
- Feng, K.; Cong, G.; Jensen, C.S.; Guo, T. Finding attribute-aware similar region for data analysis. Proc. VLDB Endow. 2019, 12, 1414–1426. [Google Scholar] [CrossRef]
- Kalinin, A.; Cetintemel, U.; Zdonik, S. Interactive data exploration using semantic windows. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, Snowbird, UT, USA, 22–27 June 2014; pp. 505–516. [Google Scholar]
- Kalinin, A.; Cetintemel, U.; Zdonik, S. Searchlight: Enabling integrated search and exploration over large multidimensional data. Proc. VLDB Endow. 2015, 8, 1094–1105. [Google Scholar] [CrossRef]
- Cao, X.; Cong, G.; Jensen, C.S.; Yiu, M.L. Retrieving regions of interest for user exploration. Proc. VLDB Endow. 2014, 7, 733–744. [Google Scholar] [CrossRef]
- Zhang, D.; Du, Y.; Xia, T.; Tao, Y. Progressive computation of the min-dist optimal-location query. In Proceedings of the 32nd International Conference on Very Large Data Bases, Seoul, Republic of Korea, 12–15 September 2006; pp. 643–654. [Google Scholar]
- Xiao, X.; Yao, B.; Li, F. Optimal location queries in road network databases. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 804–815. [Google Scholar]
- Chen, Z.; Liu, Y.; Wong, R.C.W.; Xiong, J.; Mai, G.; Long, C. Efficient algorithms for optimal location queries in road networks. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, Snowbird, UT, USA, 22–27 June 2014; pp. 123–134. [Google Scholar]
- Du, Y.; Zhang, D.; Xia, T. The optimal-location query. In Proceedings of the International Symposium on Spatial and Temporal Databases, Angra dos Reis, Brazil, 22–24 August 2005; pp. 163–180. [Google Scholar]
- Cabello, S.; Díaz-Báñez, J.M.; Langerman, S.; Seara, C.; Ventura, I. Reverse Facility Location Problems; Citeseer: Princeton, NJ, USA, 2006. [Google Scholar]
- Wong, R.C.W.; Özsu, M.T.; Yu, P.S.; Fu, A.W.C.; Liu, L. Efficient method for maximizing bichromatic reverse nearest neighbor. Proc. VLDB Endow. 2009, 2, 1126–1137. [Google Scholar] [CrossRef]
- Choudhury, F.M.; Culpepper, J.S.; Sellis, T.; Cao, X. Maximizing bichromatic reverse spatial and textual k nearest neighbor queries. Proc. VLDB Endow. 2016, 9, 456–467. [Google Scholar] [CrossRef]
- Zhou, Z.; Wu, W.; Li, X.; Lee, M.L.; Hsu, W. Maxfirst for maxbrknn. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 828–839. [Google Scholar]
- Yan, D.; Wong, R.C.W.; Ng, W. Efficient methods for finding influential locations with adaptive grids. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 1475–1484. [Google Scholar]
- Huang, J.; Wen, Z.; Qi, J.; Zhang, R.; Chen, J.; He, Z. Top-k most influential locations selection. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 2377–2380. [Google Scholar]
- Xia, T.; Zhang, D.; Kanoulas, E.; Du, Y. On computing top-t most influential spatial sites. In Proceedings of the 31st International Conference on Very Large Data Bases, Trondheim, Norway, 30 August–2 September 2005; pp. 946–957. [Google Scholar]
- Zhan, L.; Zhang, Y.; Zhang, W.; Lin, X. Finding top k most influential spatial facilities over uncertain objects. In Proceedings of the the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 922–931. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).