Retrieval of TP Concentration from UAV Multispectral Images Using IOA-ML Models in Small Inland Waterbodies
Abstract
1. Introduction
2. Materials and Methods
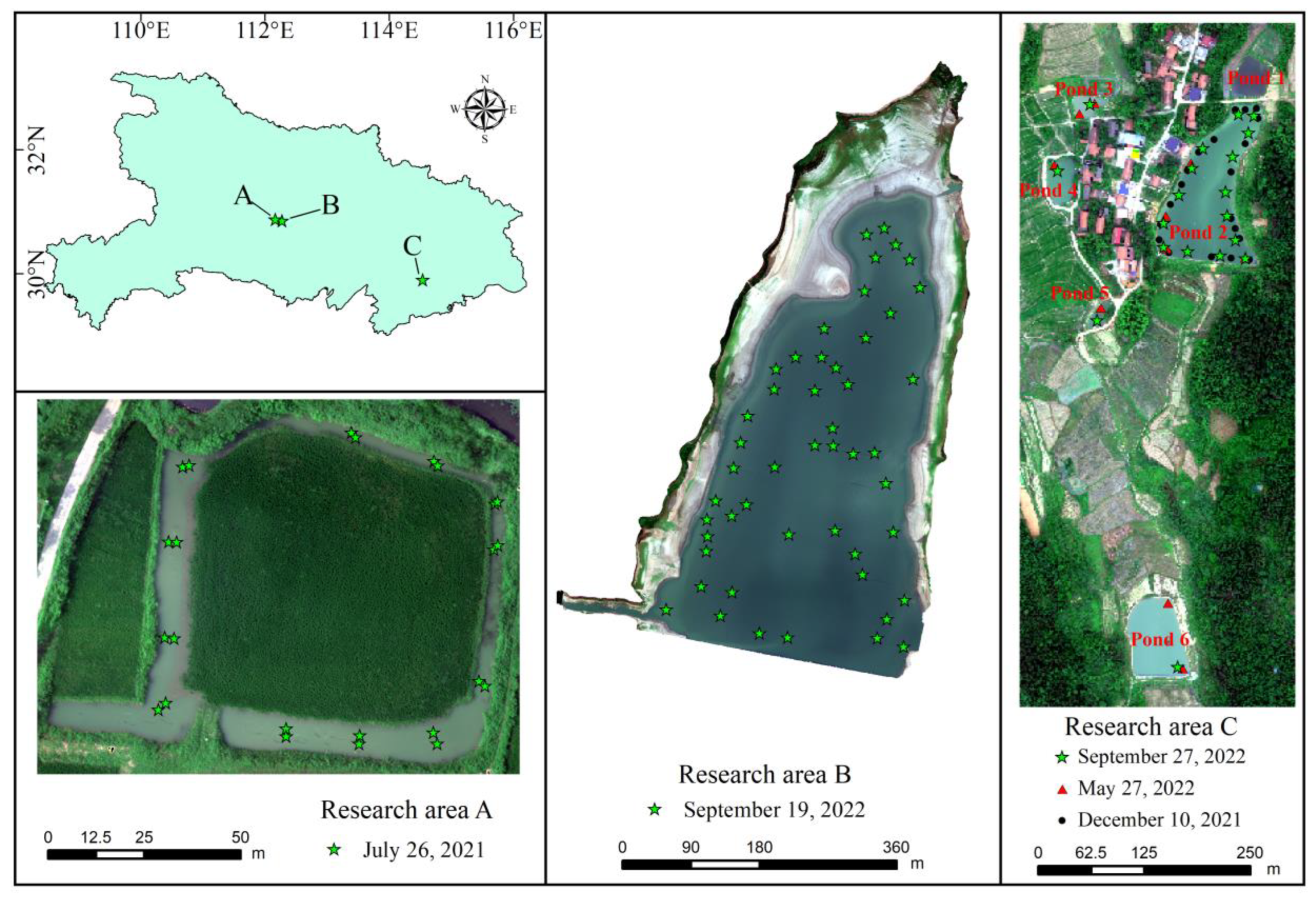
2.1. Study Area
2.2. Data Processing
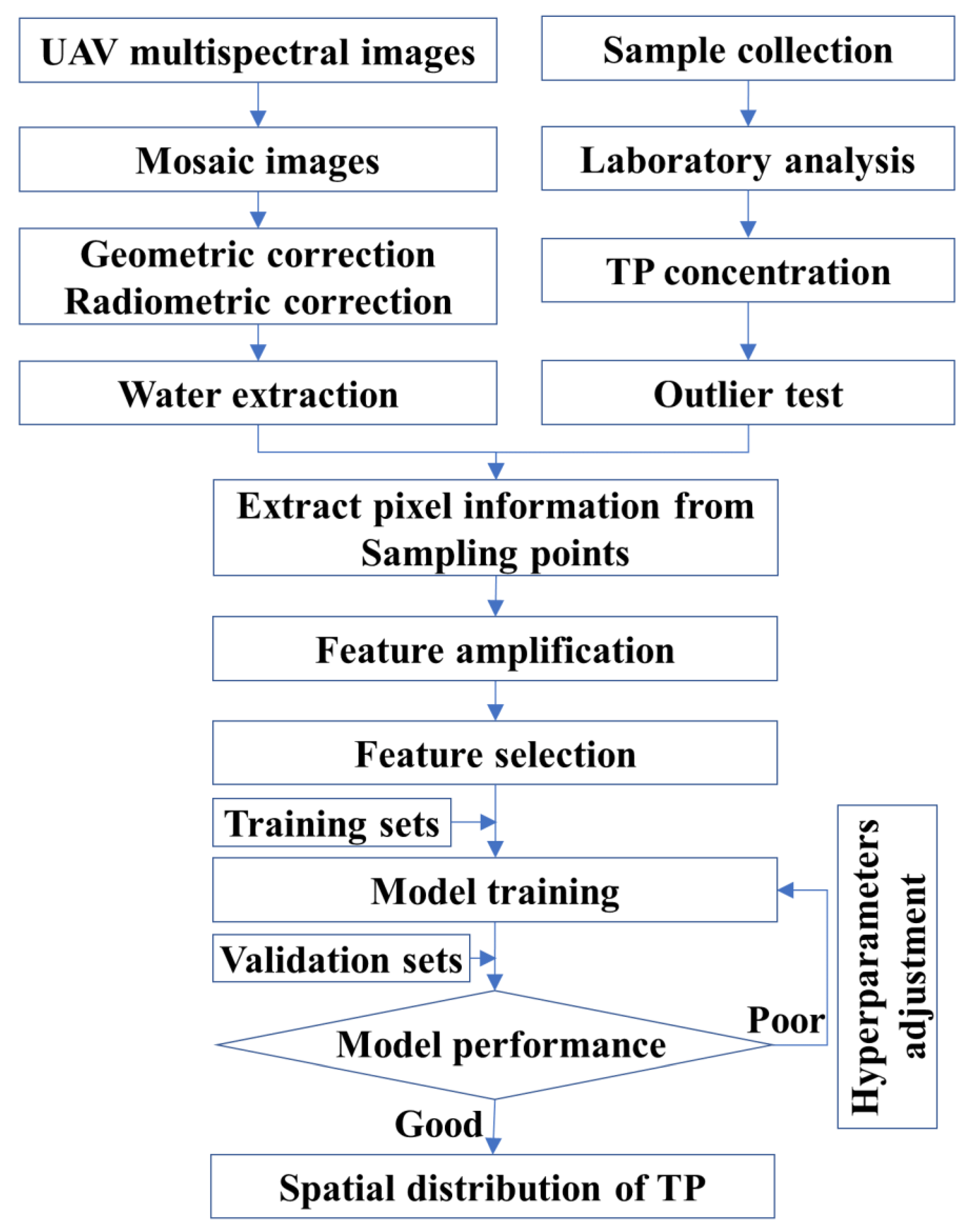
2.2.1. UAV Data and Preprocessing
2.2.2. Field Data and Preprocessing
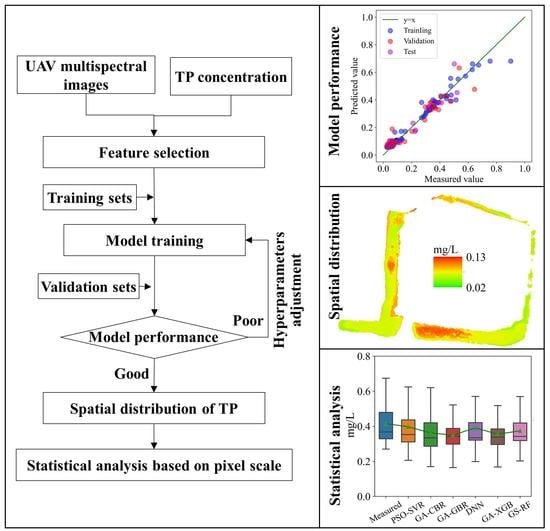
2.3. Model Development
2.3.1. Modeling Sets Construction
2.3.2. Feature Selection
- Step 1: find the feature that has the highest r (Pearson’s correlation coefficient) value with the target variable and the feature is the first variable of the feature subset.
- Step 2: select the feature that maximizes Merits calculated by Equation (2) and add the selected feature to the feature subset.
- Step 3: repeat step 2 until the value of Merits does not increase.
2.3.3. IOA-ML Models
2.3.4. Model Accuracy Assessment
3. Results
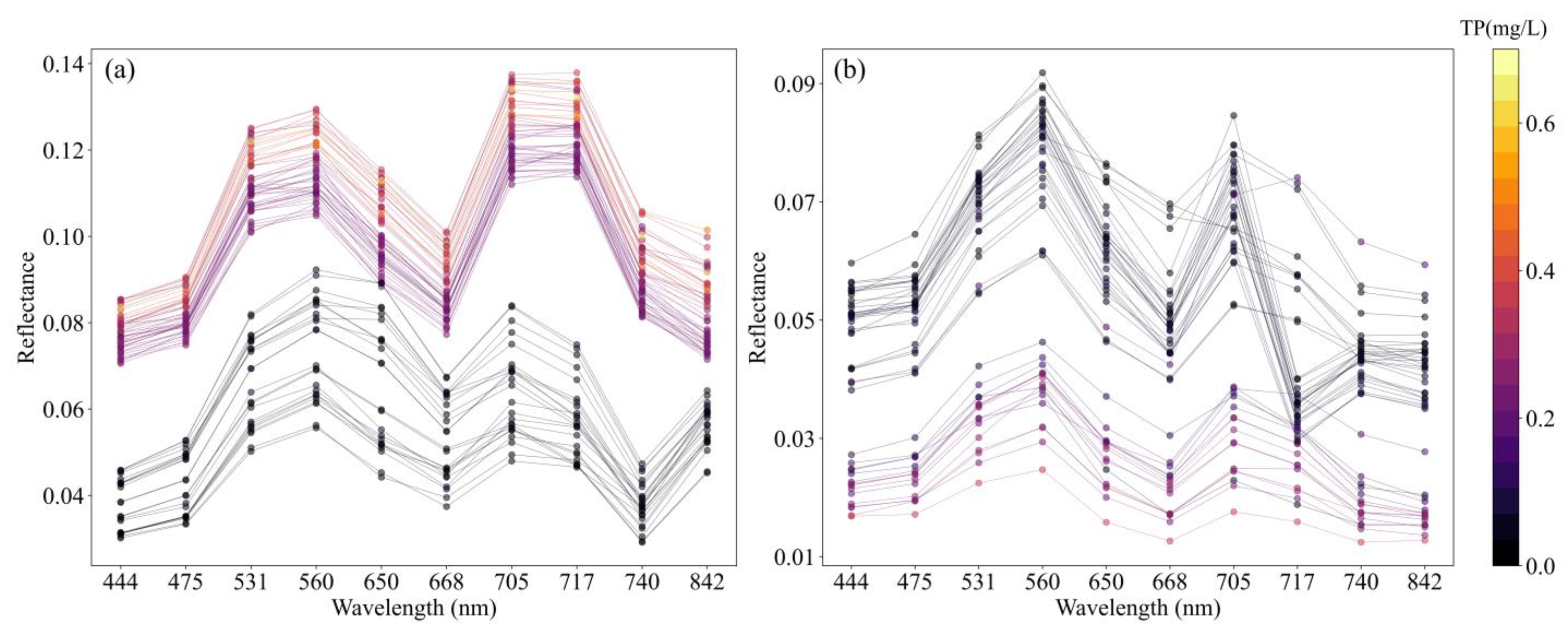
3.1. Spectral Response to TP Concentration
3.2. Selection of Band Combinations
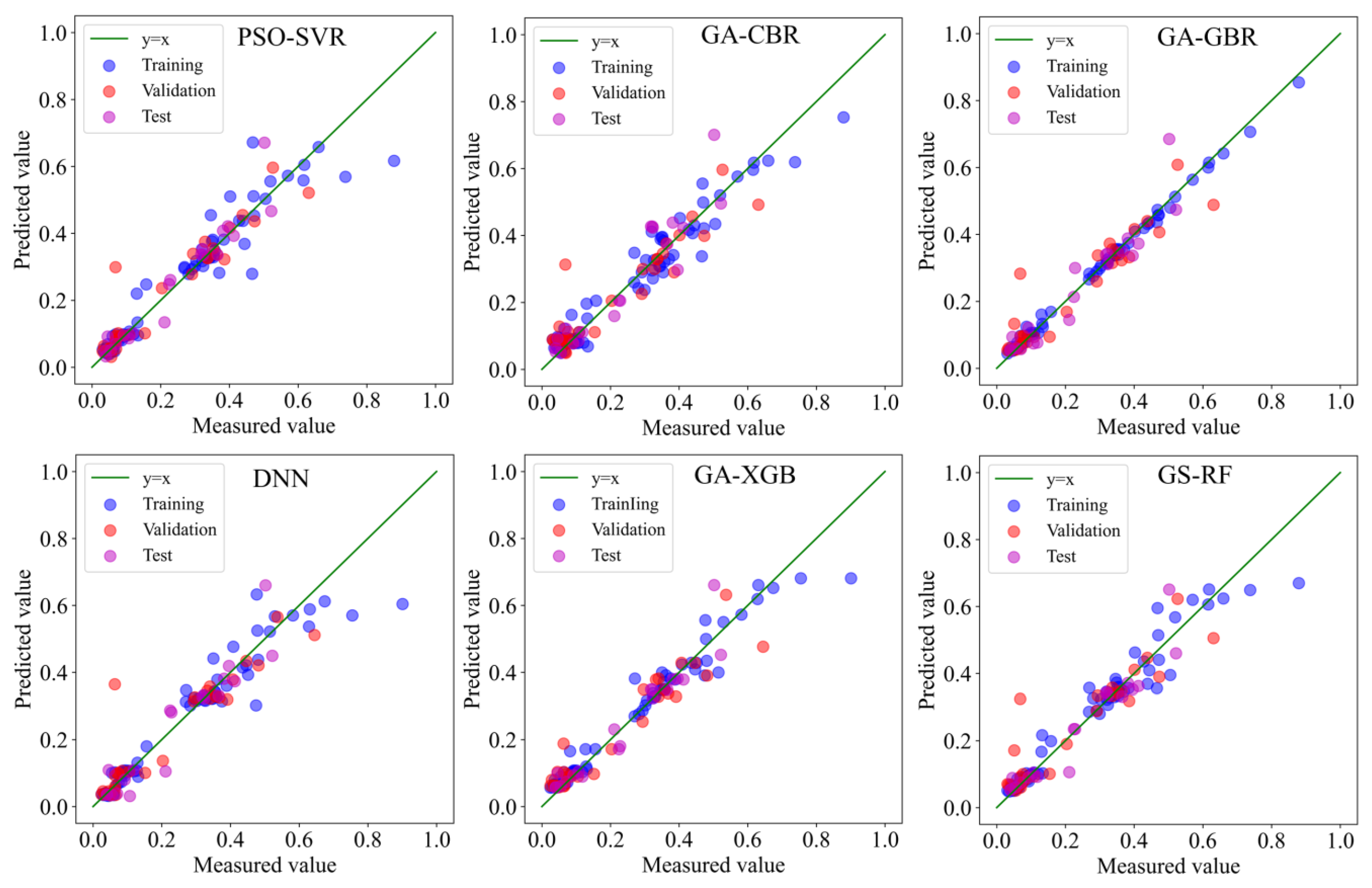
3.3. Evaluation of IOA-ML Models
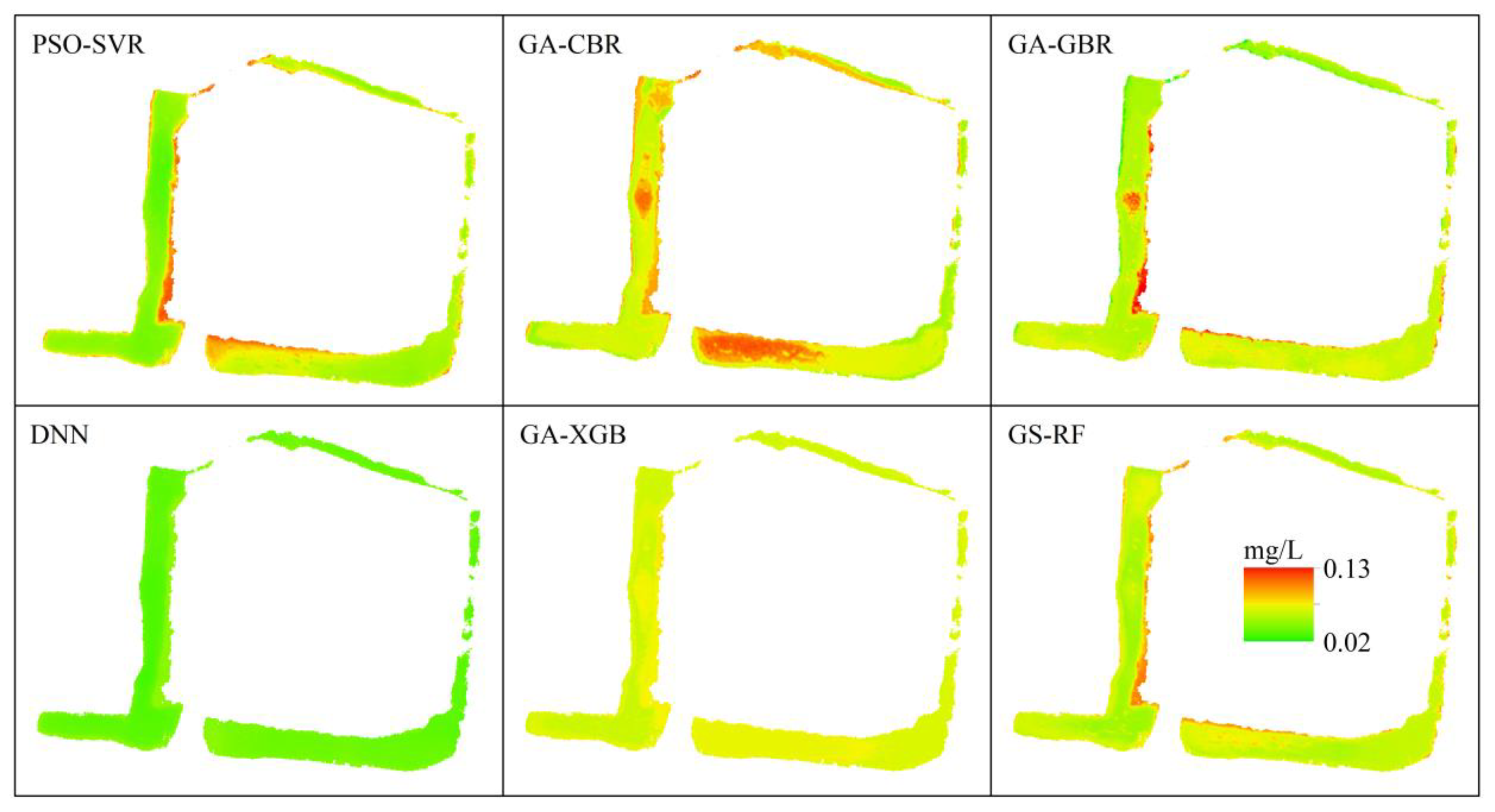
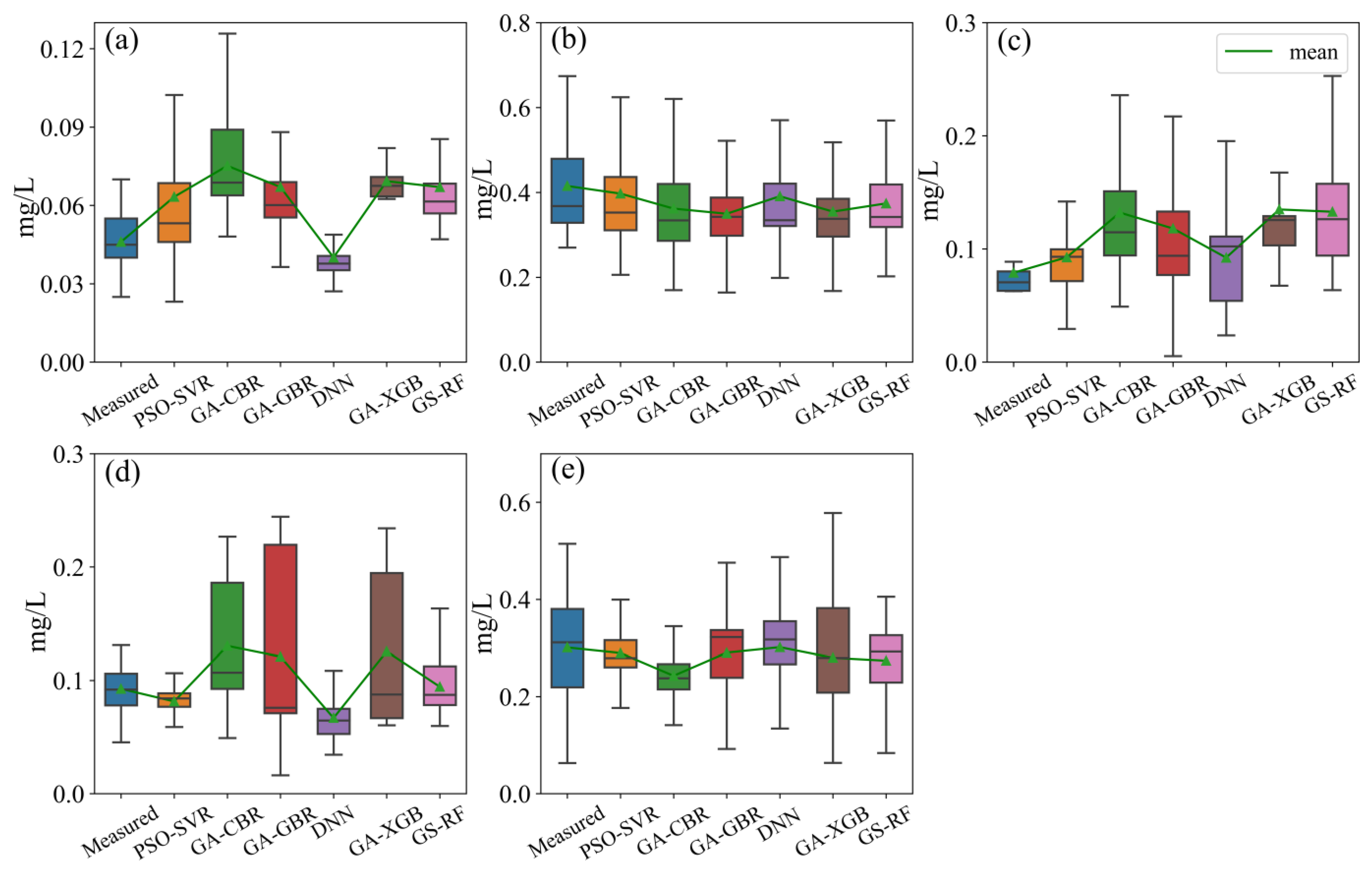
3.4. Spatial Distribution of TP Concentration
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tian, S.; Guo, H.; Xu, W.; Zhu, X.; Wang, B.; Zeng, Q.; Mai, Y.; Huang, J.J. Remote sensing retrieval of inland water quality parameters using sentinel-2 and multiple machine learning algorithms. Environ. Sci. Pollut. Res. 2022, 30, 18617–18630. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Spyrakos, E.; Tyler, A.N.; Shen, Q.; Zhang, F.; Kutser, T.; Lehmann, M.K.; Wu, Y.; et al. Trophic state assessment of global inland waters using a modis-derived forel-ule index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef]
- Du, C.; Wang, Q.; Li, Y.; Lyu, H.; Zhu, L.; Zheng, Z.; Wen, S.; Liu, G.; Guo, Y. Estimation of total phosphorus concentration using a water classification method in inland water. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 29–42. [Google Scholar] [CrossRef]
- Liu, J.; Gu, W.; Liu, Y.; Zhang, C.; Li, W.; Shao, D. Dynamic characteristics of net anthropogenic phosphorus input and legacy phosphorus reserves under high human activity—A case study in the Jianghan plain. Sci. Total Environ. 2022, 836, 155287. [Google Scholar] [CrossRef] [PubMed]
- Ji, P.; Xu, H.; Zhan, X.; Zhu, G.; Kang, L. Spatial-temporal variations and driving of nitrogen and phosphorus ratios in lakes in the middle and lower reaches of Yangtze River. Environ. Sci. 2020, 41, 4030–4041. [Google Scholar]
- Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV multispectral image-based urban river water quality monitoring using stacked ensemble machine learning algorithms—A case study of the Zhanghe river, China. Remote Sens. 2022, 14, 3272. [Google Scholar] [CrossRef]
- Chawla, I.; Karthikeyan, L.; Mishra, A.K. A review of remote sensing applications for water security: Quantity, quality, and extremes. J. Hydrol. 2020, 585, 124826. [Google Scholar] [CrossRef]
- Fichot, C.G.; Downing, B.D.; Bergamaschi, B.A.; Windham-Myers, L.; Marvin-Dipasquale, M.; Thompson, D.R.; Gierach, M.M. High-resolution remote sensing of water quality in the San Francisco bay–delta estuary. Environ. Sci. Technol. 2016, 50, 573–583. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Ha, N. Seamless retrievals of chlorophyll-a from sentinel-2 (MSI) and sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Wang, S.; Shen, M.; Liu, W.; Ma, Y.; Shi, H.; Zhang, J.; Liu, D. Developing remote sensing methods for monitoring water quality of alpine rivers on the Tibetan Plateau. GIScience Remote Sens. 2022, 59, 1384–1405. [Google Scholar] [CrossRef]
- Hu, M.; Ma, R.; Xiong, J.; Wang, M.; Cao, Z.; Xue, K. Eutrophication state in the eastern China based on landsat 35-year observations. Remote Sens. Environ. 2022, 277, 1130577. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, X. A machine learning approach to estimate chlorophyll-a from landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Liu, Y.; Sun, M.; Chen, H.; Wang, X. Inversion of river and lake water quality parameters by UAV hyperspectral imaging technology. Yangtze River 2020, 51, 205–212. [Google Scholar]
- Su, T.; Chou, H. Application of multispectral sensors carried on unmanned aerial vehicle (UAV) to trophic state mapping of small reservoirs: A case study of Tain-pu reservoir in Kinmen, Taiwan. Remote Sens. 2015, 7, 10078–10097. [Google Scholar] [CrossRef]
- Wang, L.; Yue, X.; Wang, H.; Ling, K.; Liu, Y.; Wang, J.; Hong, J.; Pen, W.; Song, H. Dynamic inversion of inland aquaculture water quality based on UAVs-WSN spectral analysis. Remote Sens. 2020, 12, 402. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, K.; Feng, H.; Fang, Y. Inversion of water quality elements in small and micro-size water region using multispectral image by UAV. Acta Sci. Circumstantiae 2019, 39, 1241–1249. [Google Scholar]
- Xiong, J.; Lin, C.; Cao, Z.; Hu, M.; Xue, K.; Chen, X.; Ma, R. Development of remote sensing algorithm for total phosphorus concentration in eutrophic lakes: Conventional or machine learning? Water Res. 2022, 215, 118213. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Du, C.; Li, Y.; Wang, Q.; Zhu, L.; Lü, H. Inversion model and daily variation of total phosphorus concentrations in Taihu Lake based on GOCI data. Environ. Sci. 2016, 37, 862–872. [Google Scholar]
- Zhang, B.; Li, J.; Shen, Q.; Chen, D. A bio-optical model based method of estimating total suspended matter of lake Taihu from near-infrared remote sensing reflectance. Environ. Monit. Assess. 2008, 145, 339–347. [Google Scholar] [CrossRef]
- Fan, D.; He, H.; Wang, R.; Zeng, Y.; Fu, B.; Xiong, Y.; Liu, L.; Xu, Y.; Gao, E. Chlnet: A novel hybrid 1D CNN-SVR algorithm for estimating ocean surface chlorophyll-a. Front. Mar. Sci. 2022, 9, 1555. [Google Scholar] [CrossRef]
- Zhang, H.; Xue, B.; Wang, G.; Zhang, X.; Zhang, Q. Deep learning-based water quality retrieval in an impounded lake using landsat 8 imagery: An application in Dongping lake. Remote Sens. 2022, 14, 4505. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Deng, L.; Ouyang, B. Retrieval of water quality parameters from hyperspectral images using a hybrid feedback deep factorization machine model. Water Res. 2021, 204, 117618. [Google Scholar] [CrossRef] [PubMed]
- Chang, N.; Xuan, Z.; Yang, Y. Exploring spatiotemporal patterns of phosphorus concentrations in a coastal bay with MODIS images and machine learning models. Remote Sens. Environ. 2013, 134, 100–110. [Google Scholar] [CrossRef]
- Chen, B.; Mu, X.; Chen, P.; Wang, B.; Choi, J.; Park, H.; Xu, S.; Wu, Y.; Yang, H. Machine learning-based inversion of water quality parameters in typical reach of the urban river by UAV multispectral data. Ecol. Indic. 2021, 133, 108434. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, C.; Akbar, A.; Xue, Y.; Zhou, Y. Spectral and spatial feature integrated ensemble learning method for grading urban river network water quality. Remote Sens. 2021, 13, 4591. [Google Scholar] [CrossRef]
- Zhu, T.; Tao, C.; Cheng, H.; Cong, H. Versatile in silico modelling of microplastics adsorption capacity in aqueous environment based on molecular descriptor and machine learning. Sci. Total Environ. 2022, 846, 157455. [Google Scholar] [CrossRef]
- Brewer, K.; Clulow, A.; Sibanda, M.; Gokool, S.; Odindi, J.; Mutanga, O.; Naiken, V.; Vimbayi, G.P.C.; Mabhaudhi, T. Estimation of maize foliar temperature and stomatal conductance as indicators of water stress based on optical and thermal imagery acquired using an unmanned aerial vehicle (UAV) platform. Drones 2022, 6, 169. [Google Scholar] [CrossRef]
- Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of water quality from UAV-borne hyperspectral imagery: A comparative study of machine learning algorithms. Remote Sens. 2021, 13, 3928. [Google Scholar] [CrossRef]
- Farahani, G. Feature selection based on cross-correlation for the intrusion detection system. Secur. Commun. Netw. 2020, 2020, 8875404. [Google Scholar] [CrossRef]
- Rafael, G.M.; Tomáš, H.; Ricardo, C.; Joaquin, V.; Andre, C. Hyper-parameter tuning of a decision tree induction algorithm. In Proceedings of the Conference on Intelligent Systems (BRACIS 2016), Recife, Brazil, 9–12 October 2016. [Google Scholar]
- Bazi, Y.; Melgani, F. Semisupervised PSO-SVM regression for biophysical parameter estimation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1887–1895. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of catboost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Qian, J.; Liu, H.; Qian, L.; Bauer, J.; Xue, X.; Yu, G.; He, Q.; Zhou, Q.; Bi, Y.; Norra, S. Water quality monitoring and assessment based on cruise monitoring, remote sensing, and deep learning: A case study of Qingcaosha reservoir. Front. Environ. Sci. 2022, 10, 979133. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chang, C.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy-principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Song, M.; Li, E.; Chang, C.; Wang, Y.; Yu, C. Spectral characteristics of nitrogen and phosphorus in water. In Proceedings of the 7th International Conference on Communications, Signal Processing, and Systems, Dalian, China, 14–16 July 2018; Volume 516, pp. 569–578. [Google Scholar]
- Yang, Z.; Gong, C.; Ji, T.; Hu, Y.; Li, L. Water quality retrieval from ZY1-02D hyperspectral imagery in urban water bodies and comparison with sentinel-2. Remote Sens. 2022, 14, 5029. [Google Scholar] [CrossRef]
- Jang, M.T.G.; Alcantara, E.; Rodrigues, T.; Park, E.; Ogashawara, I.; Marengo, J.A. Increased chlorophyll-a concentration in Barra Bonita reservoir during extreme drought periods. Sci. Total Environ. 2022, 843, 157106. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Huang, T.; Zeng, M.; Shi, J.; Cao, Z.H.; Zhou, S. Abnormal increase of Mn and TP concentrations in a temperate reservoir during fall overturn due to drought-induced drawdown. Sci. Total Environ. 2017, 575, 996–1004. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, H.; Huang, J.J.; Tian, S.; Xu, W.; Mai, Y. An ensemble machine learning model for water quality estimation in coastal area based on remote sensing imagery. J. Environ. Manag. 2022, 323, 116187. [Google Scholar] [CrossRef]
- Al-Shaibah, B.; Liu, X.; Zhang, J.; Tong, Z.; Zhang, M.; El-Zeiny, A.; Faichia, C.; Hussain, M.; Tayyab, M. Modeling water quality parameters using landsat multispectral images: A case study of Erlong lake, northeast China. Remote Sens. 2021, 13, 1603. [Google Scholar] [CrossRef]
- Singh, S.; Singh, A.K. Web-spam features selection using CFS-PSO. Proc. Comput. Sci. 2018, 125, 568–575. [Google Scholar] [CrossRef]
- Mireei, S.A.; Amini-Pozveh, S.; Nazeri, M. Selecting optimal wavelengths for detection of insect infested tomatoes based on SIMCA-aided CFS algorithm. Postharvest Biol. Technol. 2017, 123, 22–32. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, Q.; Liu, G.; Jacinthe, P.; Wang, X.; Lyu, L.; Tao, H.; Ma, Y.; Duan, H.; Shang, Y. Remote sensing of total suspended matter concentration in lakes across China using Landsat images and Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2022, 187, 61–78. [Google Scholar] [CrossRef]
- Politi, E.; Cutler, M.E.J.; Rowan, J.S. Evaluating the spatial transferability and temporal repeatability of remote-sensing-based lake water quality retrieval algorithms at the European scale: A meta-analysis approach. Int. J. Remote Sens. 2015, 36, 2995–3023. [Google Scholar] [CrossRef]
- Jensen, D.; Simard, M.; Cavanaugh, K.; Sheng, Y.; Twilley, R. Improving the transferability of suspended solid estimation in wetland and Deltaic waters with an empirical hyperspectral approach. Remote Sens. 2019, 11, 1629. [Google Scholar] [CrossRef]


| Item | Parameters |
|---|---|
| Diagonal wheelbases | 895 mm |
| Empty weight | 6.3 kg |
| Maximum takeoff weight | 9 kg |
| No load endurance | 55 min |
| Maximum flight/ascending/descending speed | 23 m/s/6 m/s/5 m/s |
| Maximum wind resistance level | 15 m/s |
| RedEdge-MX | Blue475 | Green560 | Red668 | Red edge717 | Nir842 |
| Wavelength range (nm) | 475 ± 16 | 560 ± 13.5 | 668 ± 7 | 717 ± 6 | 842 ± 28.5 |
| RedEdge-MX Blue | Blue444 | Green531 | Red650 | Red edge705 | Red edge740 |
| Wavelength range (nm) | 444 ± 14 | 531 ± 7 | 650 ± 8 | 705 ± 5 | 740 ± 9 |
| Time | Area | Height | Resolution | Number of Photos | Sampling Number |
|---|---|---|---|---|---|
| 26 July 2021 | Research area A | 50 m | 3.67 cm | 1820 | 24 |
| 19 September 2022 | Research area B | 200 m | 14.4 cm | 3210 | 48 |
| 10 December 2021 | Research area C | 100 m | 7.7 cm | 6460 | 20 (all in pond 2) |
| 27 May 2022 | Research area C | 200 m | 14.3 cm | 2760 | 10 (4 in pond 2, 2 in pond 3, 1 in pond 4, 1 in pond 5, 2 in pond 6) |
| 27 September 2022 | Research area C | 200 m | 14.4 cm | 2560 | 19 (15 in pond 2, 1 in pond 3, 1 in pond 4, 1 in pond 5, 1 in pond 6) |
| Selection Order | Feature | Merits |
|---|---|---|
| 1 | rededge740 × rededge714 × rededge705 × nir842 | 0.8329 |
| 2 | (blue444 − red668 − nir842) ÷ rededge714 | 0.8796 |
| 3 | rededge740 × red668 × red650 × nir842 | 0.8952 |
| 4 | red668 ÷ green560 ÷ green531 ÷ rededge714 | 0.923 |
| 5 | rededge740 × rededge714 × red650 × nir842 | 0.9394 |
| Model | R2 | RMSE (mg/L) | RPD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Validation | Test | Training | Validation | Test | Training | Validation | Test | |
| PSO-SVR | 0.9015 | 0.8929 | 0.9045 | 0.0649 | 0.0583 | 0.0486 | 3.1859 | 3.0561 | 3.2351 |
| GA-CBR | 0.9506 | 0.8148 | 0.7462 | 0.0445 | 0.0742 | 0.0792 | 4.5 | 2.3234 | 1.9849 |
| GA-GBR | 0.984 | 0.8458 | 0.8281 | 0.0253 | 0.0677 | 0.0651 | 7.9153 | 2.5466 | 2.4125 |
| DNN | 0.8856 | 0.8054 | 0.8143 | 0.0699 | 0.0786 | 0.0677 | 2.9565 | 2.2667 | 2.3206 |
| GA-XGB | 0.9584 | 0.9082 | 0.9124 | 0.0422 | 0.054 | 0.047 | 4.906 | 3.3005 | 3.379 |
| GS-RF | 0.9534 | 0.8579 | 0.8624 | 0.0447 | 0.0672 | 0.0583 | 4.6304 | 2.6528 | 2.6962 |
| Model | R2 | RMSE (mg/L) | RPD | |||
|---|---|---|---|---|---|---|
| Validation | Test | Validation | Test | Validation | Test | |
| PSO-SVR | 1.18% | 0.20% | −8.77% | −1.04% | 5.11% | 0.95% |
| GA-CBR | 5.61% | 7.29% | −16.30% | −14.12% | 14.07% | 12.32% |
| GA-GBR | 4.84% | 6.07% | −17.74% | −20.33% | 15.07% | 16.97% |
| DNN | 6.62% | 6.65% | −18.91% | −20.46% | 15.96% | 17.09% |
| GA-XGB | 2.53% | 6.65% | −11.85% | −30.11% | 10.57% | 23.15% |
| GS-RF | 0.49% | 4.72% | −5.00% | −20.45% | 1.50% | 16.93% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W.; Liu, J.; Wang, H.; Miao, D.; Shao, D.; Gu, W. Retrieval of TP Concentration from UAV Multispectral Images Using IOA-ML Models in Small Inland Waterbodies. Remote Sens. 2023, 15, 1250. https://doi.org/10.3390/rs15051250
Hu W, Liu J, Wang H, Miao D, Shao D, Gu W. Retrieval of TP Concentration from UAV Multispectral Images Using IOA-ML Models in Small Inland Waterbodies. Remote Sensing. 2023; 15(5):1250. https://doi.org/10.3390/rs15051250
Chicago/Turabian StyleHu, Wentong, Jie Liu, He Wang, Donghao Miao, Dongguo Shao, and Wenquan Gu. 2023. "Retrieval of TP Concentration from UAV Multispectral Images Using IOA-ML Models in Small Inland Waterbodies" Remote Sensing 15, no. 5: 1250. https://doi.org/10.3390/rs15051250
APA StyleHu, W., Liu, J., Wang, H., Miao, D., Shao, D., & Gu, W. (2023). Retrieval of TP Concentration from UAV Multispectral Images Using IOA-ML Models in Small Inland Waterbodies. Remote Sensing, 15(5), 1250. https://doi.org/10.3390/rs15051250