Thick Cloud Removal in Multi-Temporal Remote Sensing Images via Frequency Spectrum-Modulated Tensor Completion
Abstract
1. Introduction
- Different orthogonal decompositions are performed on spatial and temporal dimensions of the tensor. The spatial–temporal tensor for each band is transformed to a spatial–frequential tensor by FT. Singular-value decomposition is performed in low-rank matrix completion in the spatial dimension. Through the frequency spectrum-modulating spatial matrix, joint spatial–temporal low-rank information is achieved, and the effects of different spatial–temporal low-rank properties are avoided. Meanwhile, using the property of conjugated symmetry of FT can also reduce the computation cost during the iteration.
- Gaussian low-pass filtering is applied in the frequency spectrum, and spatial low-rank adaptive weights are calculated according to the frequency characteristics of the time domain. Thus, the difficulty in selecting appropriate weights is solved. This scheme can maintain the low-frequency land features and weaken the high-frequency noise caused by clouds.
2. Methodology
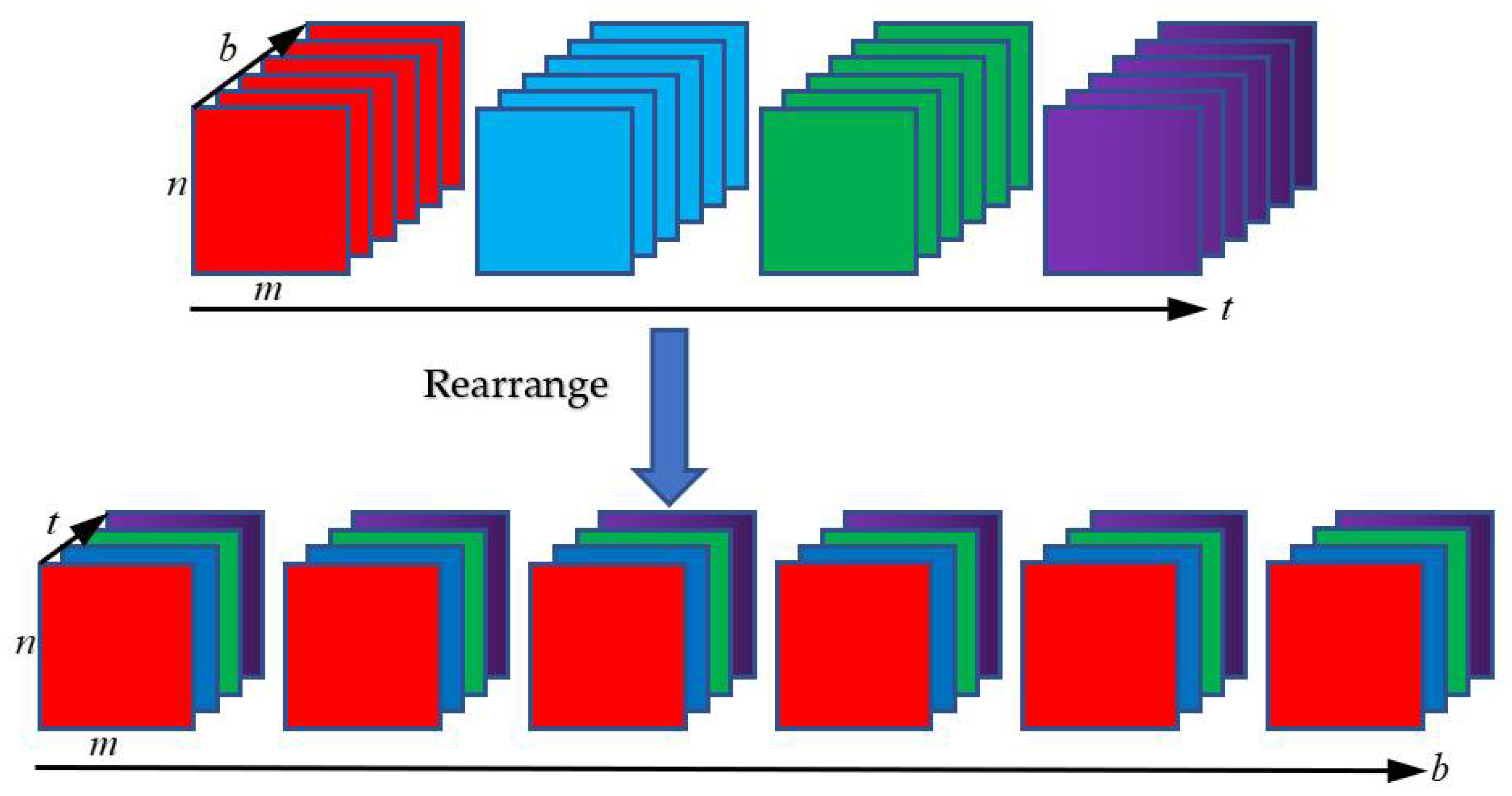
2.1. Spatial–Temporal Low-Rank Tensor Rearrangement
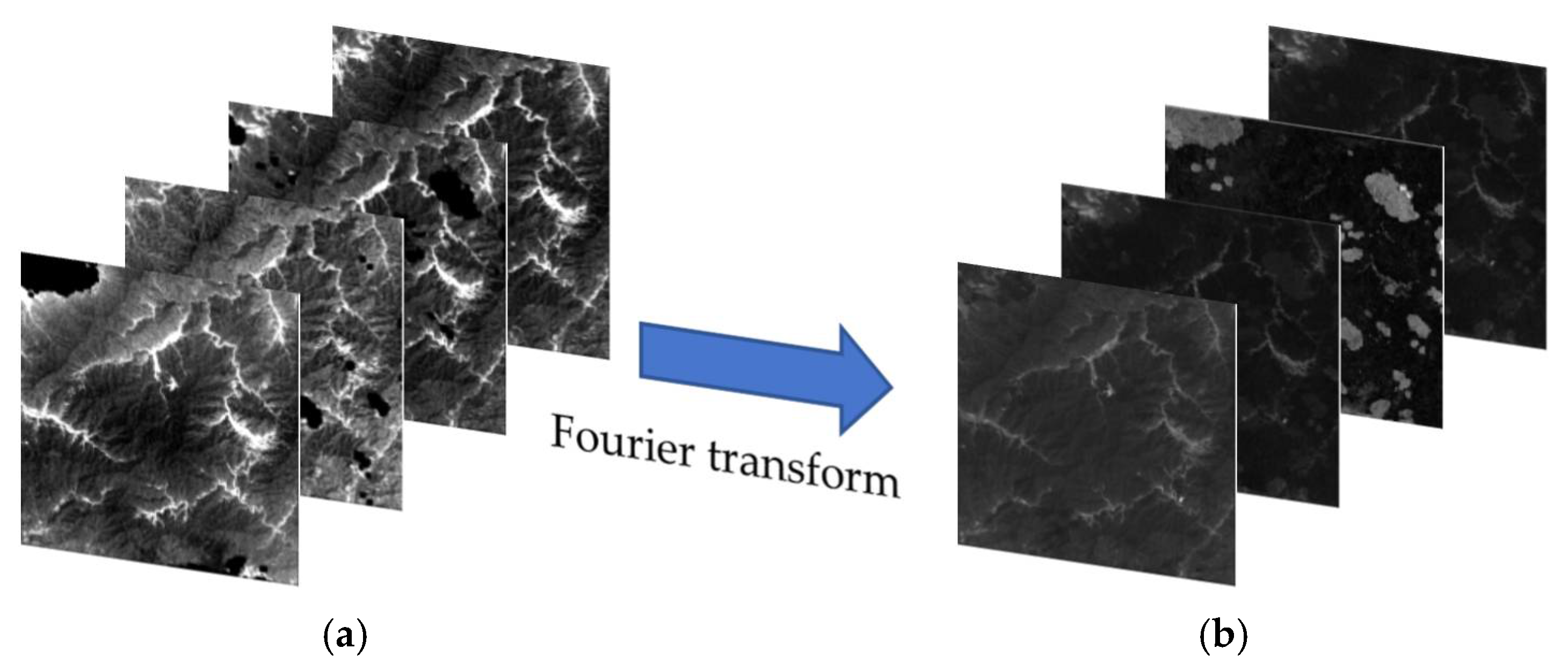
2.2. Frequency Spectrum-Modulated Tensor Completion
2.3. Model Optimization
| Algorithm 1 Optimization of the FMTC method |
| Input: Original remote sensing data , parameter . |
| Initialize: . fortodo Obtain the rearranged spatial–temporal tensor for each band. for to do |
| Update by Equation (10); |
| Update by Equation (11); |
| Update by Equation (12); |
| end for; |
| repeat until convergence; |
| end for; |
| Output: Reconstructed image data . |
3. Experimental Results
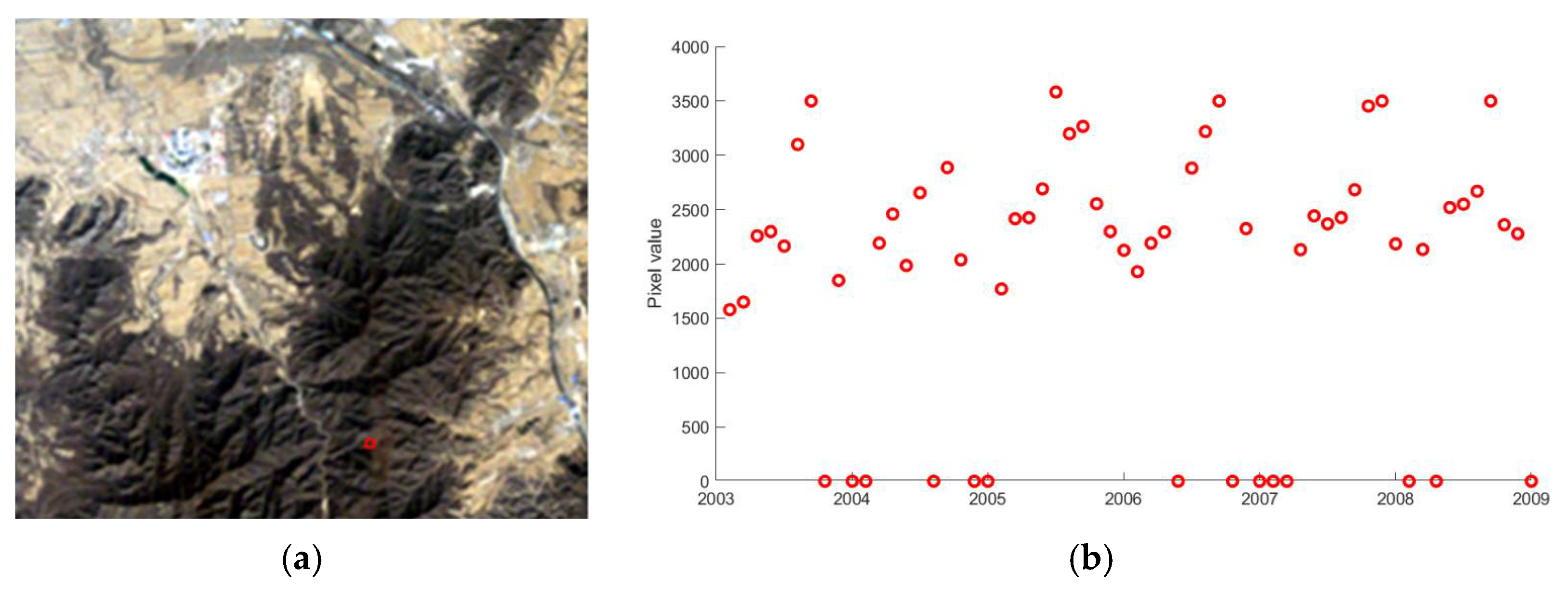
3.1. Experimental Data
3.2. Evaluation Indicators
3.3. Simulated Data Experiments
3.3.1. The Experiment Based on Different Land-Cover Types
3.3.2. The Experiment with Different Missing Sizes
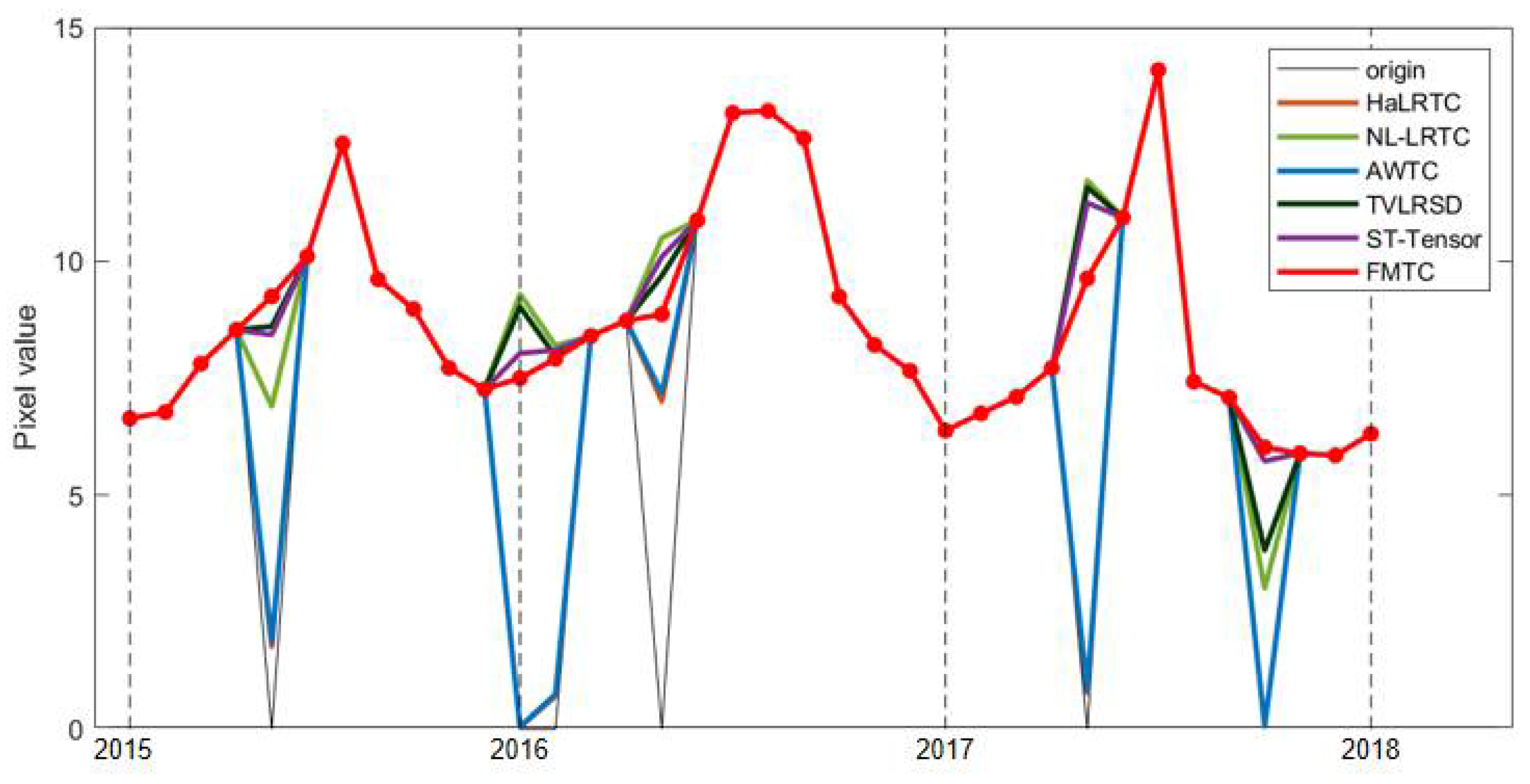
3.4. Real Data Experiments
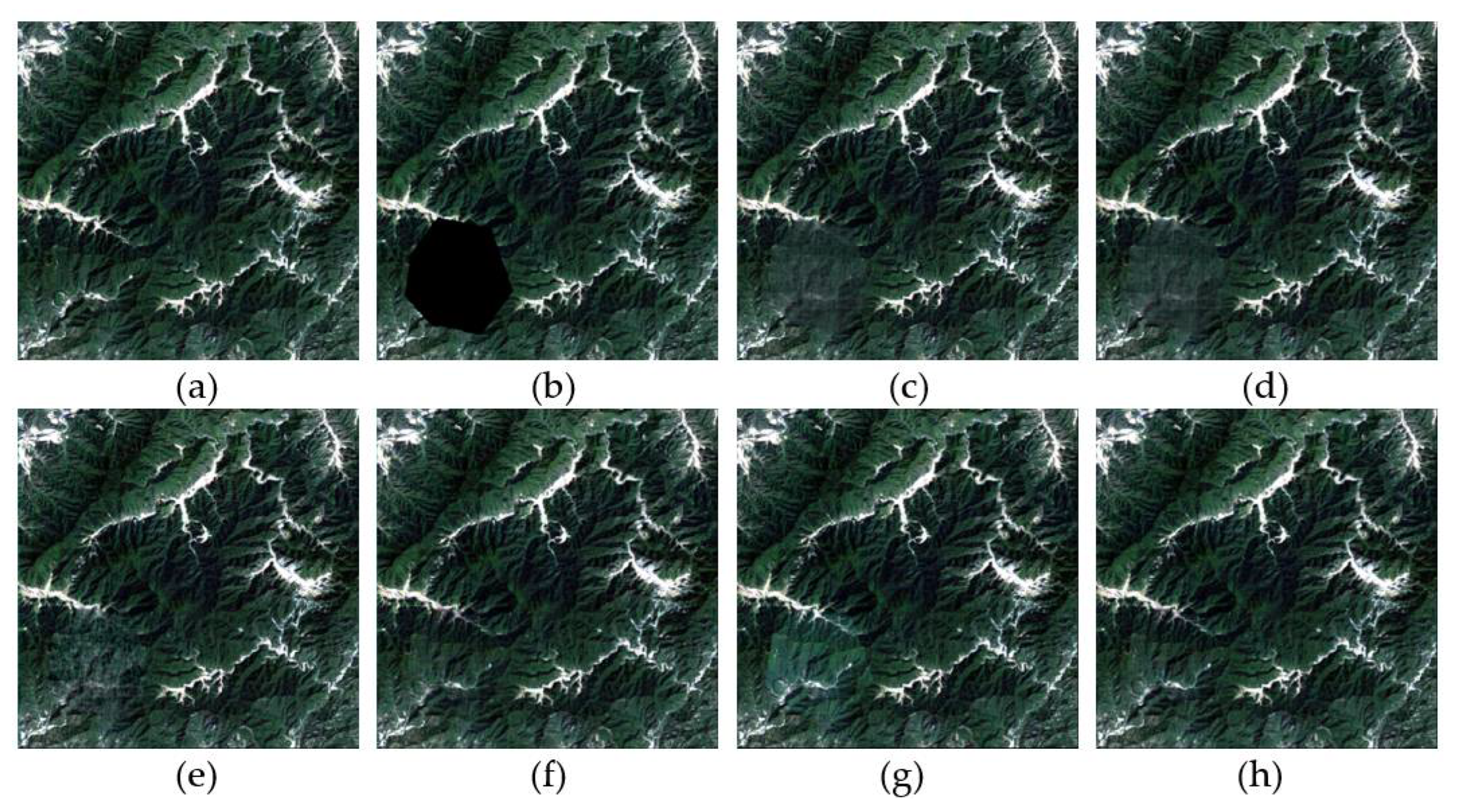
3.4.1. Real Data Experiment 1
3.4.2. Real Data Experiment 2
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leh, M.; Bajwa, S.; Chaubey, I. Impact of Land Use Change on Erosion Risk: An Integrated Remote Sensing, Geographic Information System and Modeling Methodology. Land Degrad. Dev. 2011, 24, 409–421. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef]
- Shahzad, M.; Zhu, X.X. Automatic Detection and Reconstruction of 2-D/3-D Building Shapes from Spaceborne TomoSAR Point Clouds. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1292–1310. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral Target Detection: An Overview of Current and Future Challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised Spectral–Spatial Feature Learning via Deep Residual Conv–Deconv Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 391–406. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM- and MRF-Based Method for Accurate Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Li, S.; Yin, H.; Fang, L. Remote Sensing Image Fusion via Sparse Representations Over Learned Dictionaries. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4779–4789. [Google Scholar] [CrossRef]
- Xie, D.; Gao, F.; Sun, L.; Anderson, M. Improving Spatial–temporal Data Fusion by Choosing Optimal Input Image Pairs. Remote Sens. 2018, 10, 1142. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Siu, W.C.; Hung, K.W. Review of image interpolation and super-resolution. In Proceedings of the Signal & Information Processing Association Summit & Conference, Hollywood, CA, USA, 3–6 December 2012. [Google Scholar]
- Chao, Y.; Chen, L.; Lin, S.; Meng, F.; Li, S. Kriging interpolation method and its application in retrieval of MODIS aerosol optical depth. In Proceedings of the International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–6. [Google Scholar]
- Lorenz, L.; Melgant, F.; Merrier, G. Multiresolution inpainting for reconstruction of missing data in VHR images. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Kitchener, M.A.; Bouzerdoum, A.; Phung, S.L. A Compressive Sensing Approach to Image Restoration. In Proceedings of the 2010 International Conference on Digital Image Computing: Techniques and Applications, Sydney, Australia, 1–3 December 2010; pp. 111–115. [Google Scholar]
- Zhang, J.; Zhao, D.; Gao, W. Group-based sparse representation for image restoration. IEEE Trans. Image Process. 2014, 23, 3336–3351. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-Based Algorithm for Destriping and Inpainting of Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Cheng, Q.; Shen, H.; Zhang, L.; Li, P. Inpainting for Remotely Sensed Images with a Multichannel Nonlocal Total Variation Model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 175–187. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Restoration of Aqua MODIS Band 6 Using Histogram Matching and Local Least Squares Fitting. IEEE Trans. Geosci. Remote Sens. 2009, 47, 613–627. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Zhang, J.; Jin, J.; Liang, J.; Liao, M.; Yan, K.; Peng, Q. A new cloud removal algorithm for multi-spectral images. In Proceedings of the MIPPR 2005: SAR and Multispectral Image Processing, Wuhan, China, 31 October–2 November 2005. [Google Scholar]
- Feng, C.; Ma, J.W.; Dai, Q.; Chen, X. An improved method for cloud removal in ASTER data change detection. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar]
- Zhang, Y.; Guindon, B.; Cihlar, J. An image transform to characterize and compensate for spatial variations in thin cloud contamination of Landsat images. Remote Sens. Environ. 2002, 82, 173–187. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, Q.; Li, J.; Luo, W.; Liu, X.; Lei, B.; Yang, J.; Zhang, B. Information reconstruction in the cloud removing area based on multi-temporal CHRIS images. In Proceedings of the MIPPR 2007: Remote Sensing and GIS Data Processing and Applications; and Innovative Multispectral Technology and Applications, Wuhan, China, 15–17 November 2007. [Google Scholar]
- Melgani, F. Contextual reconstruction of cloud-contaminated multitemporal multispectral images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 442–455. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, F.; Qin, Y. Study on the Thick Cloud Removal Method Based on Multi-Temporal Remote Sensing Images. In Proceedings of the 2010 International Conference on Multimedia Technology, Ningbo, China, 29–31 October 2010. [Google Scholar]
- Lin, C.-H.; Tsai, P.-H.; Lai, K.-H.; Chen, J.-Y. Cloud Removal from Multitemporal Satellite Images Using Information Cloning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 232–241. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Zhang, L.; Zhang, H.; Yuan, Q.; Yang, G. Recovering Quantitative Remote Sensing Products Contaminated by Thick Clouds and Shadows Using Multitemporal Dictionary Learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7086–7098. [Google Scholar]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Ng, M.K.-P.; Yuan, Q.; Yan, L.; Sun, J. An Adaptive Weighted Tensor Completion Method for the Recovery of Remote Sensing Images with Missing Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3367–3381. [Google Scholar] [CrossRef]
- Ji, T.Y.; Yokoya, N.; Zhu, X.X.; Huang, T.Z. Nonlocal tensor completion for multitemporal remotely sensed images’ inpainting. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3047–3061. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.-Z. Blind cloud and cloud shadow removal of multitemporal images based on total variation regularized low-rank sparsity decomposition. ISPRS J. Photogramm. Remote Sens. 2019, 157, 93–107. [Google Scholar] [CrossRef]
- Chu, D.; Shen, H.; Guan, X.; Chen, J.M.; Li, X.; Li, J.; Zhang, L. Long time-series NDVI reconstruction in cloud-prone regions via spatial–temporal tensor completion. Remote Sens. Environ. 2021, 264, 112632. [Google Scholar] [CrossRef]
- Duan, C.; Pan, J.; Li, R. Thick Cloud Removal of Remote Sensing Images Using Temporal Smoothness and Sparsity Regularized Tensor Optimization. Remote Sens. 2020, 12, 3446. [Google Scholar] [CrossRef]
- Lin, J.; Huang, T.-Z.; Zhao, X.-L.; Chen, Y.; Zhang, Q.; Yuan, Q. Robust Thick Cloud Removal for Multitemporal Remote Sensing Images Using Coupled Tensor Factorization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Liu, N.; Li, W.; Wang, Y.; Tao, R.; Du, Q.; Chanussot, J. A Survey on Hyperspectral Image Restoration: From the View of Low-Rank Tensor Approximation. arXiv 2022, arXiv:2205.08839. [Google Scholar]
- Liu, N.; Li, W.; Tao, R.; Du, Q.; Chanussot, J. Multigraph-Based Low-Rank Tensor Approximation for Hyperspectral Image Restoration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Kurucz, M.; Benczúr, A.; Csalogány, K. Methods for large scale SVD with missing values. In Proceedings of the KDD Cup and Workshop, San Jose, CA, USA, 12 August 2007. [Google Scholar]
- Cai, J.-F.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis with a New Tensor Nuclear Norm. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 925–938. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Shen, H.; Li, X.; Zhang, L.; Tao, D.; Zeng, C. Compressed Sensing-Based Inpainting of Aqua Moderate Resolution Imaging Spectroradiometer Band 6 Using Adaptive Spectrum-Weighted Sparse Bayesian Dictionary Learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 894–906. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Ferraro, M.; Boccignone, G.; Caelli, T. Entropy-based representation of image information. Pattern Recognit. Lett. 2002, 23, 1391–1398. [Google Scholar] [CrossRef]
- Li, Z.; Jing, Z.; Yang, X.; Sun, S. Color transfer based remote sensing image fusion using non-separable wavelet box transform. Pattern Recognit. Lett. 2005, 26, 2006–2014. [Google Scholar] [CrossRef]
















| Source | Duration | Resolution | Band | Size |
|---|---|---|---|---|
| Landsat-5 | 2003–2011 | 30 m | 1–6 | |
| Landsat-8 | 2013–2018 | 30 m | 1–7 |
| Dataset | Location | Land-Cover Types | Mask Date | Source |
|---|---|---|---|---|
| Dataset 1 | Beijing City Center | Impervious | 17 May 2009 | Landsat-5 |
| Dataset 2 | Yanqing, Beijing | Soil | 26 April 2007 | Landsat-5 |
| Dataset 3 | Huairou, Beijing | Vegetation | 2 June 2009 | Landsat-5 |
| Dataset 4 | Miyun, Beijing | Water | 7 May 2011 | Landsat-5 |
| Dataset 5 | Pinggu, Beijing | Vegetation/Soil/Impervious | 18 May 2015 | Landsat-8 |
| Land-Cover Type | Indicator | HaLRTC | AWTC | NL-LRTC | TVLRSD | ST-Tensor | FMTC |
|---|---|---|---|---|---|---|---|
| Impervious | PSNR | 51.024 | 51.954 | 52.325 | 53.490 | 55.201 | 55.021 |
| SSIM | 0.9926 | 0.9935 | 0.9941 | 0.9958 | 0.9992 | 0.9990 | |
| SAM | 0.0767 | 0.0782 | 0.6989 | 0.0603 | 0.0533 | 0.0530 | |
| Time(s) | 161.59 | 426.37 | 649.48 | 592.94 | 839.64 | 269.19 | |
| Soil | PSNR | 38.839 | 39.235 | 40.865 | 41.876 | 41.914 | 41.975 |
| SSIM | 0.9941 | 0.9951 | 0.9971 | 0.9983 | 0.9984 | 0.9987 | |
| SAM | 0.0437 | 0.0421 | 0.0326 | 0.0295 | 0.0289 | 0.0271 | |
| Time(s) | 186.13 | 438.46 | 659.46 | 526.35 | 837.09 | 294.14 | |
| Vegetation | PSNR | 38.681 | 39.024 | 40.216 | 43.453 | 43.477 | 43.492 |
| SSIM | 0.9985 | 0.9992 | 0.9993 | 0.9995 | 0.9996 | 0.9997 | |
| Time(s) | 168.38 | 362.47 | 0.0457 | 461.96 | 710.46 | 352.98 | |
| SAM | 0.0591 | 0.0588 | 574.18 | 0.0376 | 0.0374 | 0.0358 | |
| Water | PSNR | 32.076 | 32.705 | 38.783 | 41.684 | 42.926 | 43.003 |
| SSIM | 0.9664 | 0.9696 | 0.9762 | 0.9826 | 0.9874 | 0.9901 | |
| SAM | 0.0402 | 0.01386 | 0.0364 | 0.0358 | 0.0327 | 0.0321 | |
| Time(s) | 390.34 | 822.65 | 776.04 | 768.35 | 910.67 | 431.76 |
| Missing Size | Indicator | HaLRTC | AWTC | NL-LRTC | TVLRSD | ST-Tensor | FMTC |
|---|---|---|---|---|---|---|---|
| 6.01% | PSNR | 39.658 | 40.675 | 45.319 | 48.355 | 49.521 | 49.531 |
| SSIM | 0.9927 | 0.9941 | 0.9973 | 0.9984 | 0.9999 | 0.9998 | |
| SAM | 0.0863 | 0.0852 | 0.7126 | 0.0664 | 0.0635 | 0.0625 | |
| Time(s) | 191.19 | 483.61 | 593.45 | 563.95 | 784.55 | 277.23 | |
| 19.26% | PSNR | 26.208 | 26.783 | 37.634 | 43.639 | 44.022 | 44.083 |
| SSIM | 0.9240 | 0.9336 | 0.9736 | 0.9959 | 0.9980 | 0.9979 | |
| SAM | 0.0924 | 0.0911 | 0.6089 | 0.0477 | 0.0446 | 0.0440 | |
| Time(s) | 326.74 | 684.39 | 715.64 | 706.97 | 936.21 | 386.42 | |
| 32.48% | PSNR | 25.785 | 26.199 | 37.599 | 40.868 | 42.815 | 42.844 |
| SSIM | 0.8343 | 0.8482 | 0.9157 | 0.9945 | 0.9962 | 0.9964 | |
| SAM | 0.1018 | 0.0993 | 0.6943 | 0.0401 | 0.0374 | 0.0366 | |
| Time(s) | 403.51 | 704.62 | 903.49 | 873.56 | 1017.55 | 464.57 |
| Dataset | Location | Duration | Mask Date | Source | Land Cover Type |
|---|---|---|---|---|---|
| Dataset 6 | Changpin, Beijing | 2003–2011 | 22 May 2005 | Landsat-5 | impervious/vegetation/soil |
| Dataset 7 | Mentougou, Beijing | 2013–2018 | 21 April 2017 | Landsat-8 | vegetation/impervious/soil |
| Indicator | HaLRTC | AWTC | NL-LRTC | TVLRSD | ST-Tensor | FMTC |
|---|---|---|---|---|---|---|
| IE | 6.8669 | 6.8756 | 6.9317 | 6.9653 | 6.9470 | 6.9955 |
| AG | 0.0425 | 0.0438 | 0.0465 | 0.0469 | 0.0464 | 0.0476 |
| Indicator | HaLRTC | AWTC | NL-LRTC | TVLRSD | ST-Tensor | FMTC |
|---|---|---|---|---|---|---|
| IE | 6.6871 | 6.6871 | 6.6881 | 6.6899 | 6.6910 | 6.6913 |
| AG | 0.0301 | 0.0312 | 0.0325 | 0.0336 | 0.0341 | 0.0341 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhang, P.; Zhang, Y.; Xu, X.; Ji, L.; Tang, H. Thick Cloud Removal in Multi-Temporal Remote Sensing Images via Frequency Spectrum-Modulated Tensor Completion. Remote Sens. 2023, 15, 1230. https://doi.org/10.3390/rs15051230
Chen Z, Zhang P, Zhang Y, Xu X, Ji L, Tang H. Thick Cloud Removal in Multi-Temporal Remote Sensing Images via Frequency Spectrum-Modulated Tensor Completion. Remote Sensing. 2023; 15(5):1230. https://doi.org/10.3390/rs15051230
Chicago/Turabian StyleChen, Zhihong, Peng Zhang, Yu Zhang, Xunpeng Xu, Luyan Ji, and Hairong Tang. 2023. "Thick Cloud Removal in Multi-Temporal Remote Sensing Images via Frequency Spectrum-Modulated Tensor Completion" Remote Sensing 15, no. 5: 1230. https://doi.org/10.3390/rs15051230
APA StyleChen, Z., Zhang, P., Zhang, Y., Xu, X., Ji, L., & Tang, H. (2023). Thick Cloud Removal in Multi-Temporal Remote Sensing Images via Frequency Spectrum-Modulated Tensor Completion. Remote Sensing, 15(5), 1230. https://doi.org/10.3390/rs15051230









