Semantic Segmentation of Remote Sensing Imagery Based on Multiscale Deformable CNN and DenseCRF
Abstract
1. Introduction
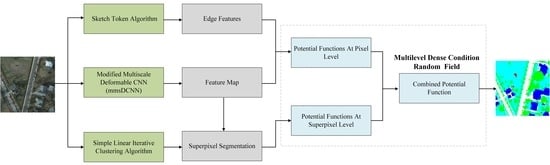
- A framework of the mmsDCNN-DenseCRF combined model for the semantic segmentation of remote sensing images is proposed.
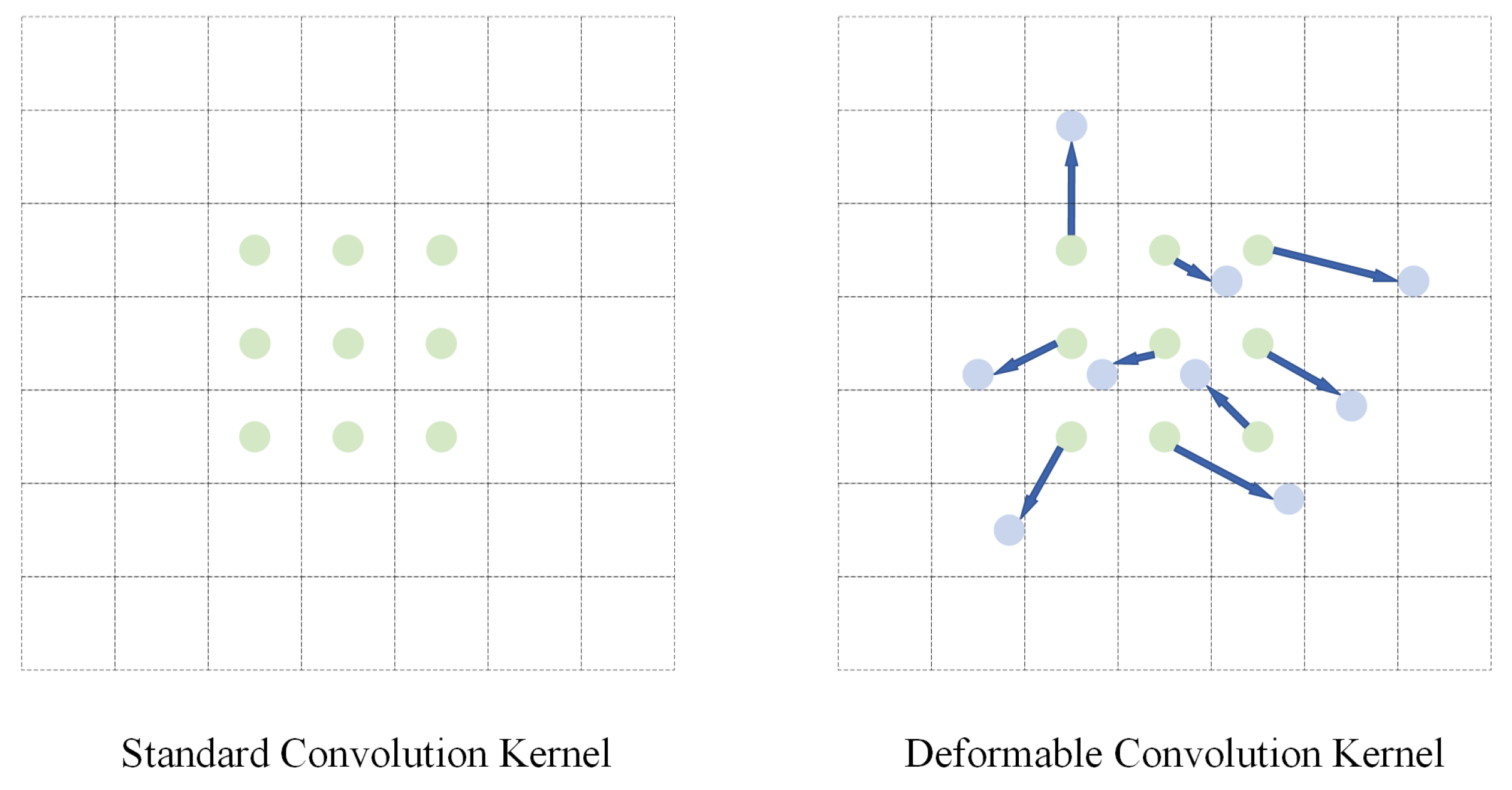
- We designed a lightweight mmsDCNN model, which incorporates deformable convolution into the mmsCNN proposed in our previous work [45]. Notably, the mmsDCNN adds an offset to the sampling position of the mmsCNN convolution, which enables the convolutional kernel to adaptively determine the receptive field size. Compared with the mmsCNN, the mmsDCNN can achieve a satisfactory performance improvement with only a tiny increase in the computational complexity.
- The multi-level DenseCRF model based on the superpixel level and pixel level is proposed. We combined the pixel-level potential function with the superpixel-based potential function to obtain the final Gaussian potential function, which enables our model to consider features of various scales and the context information of the image and prevents poor superpixel segmentation results from affecting the final result.
- To solve the problem of blurring edge categories or segmentation errors in the semantic segmentation task of DenseCRF, we utilized a Sketch token edge detection algorithm to extract the edge contour features of the image and integrated them into the Gaussian potential function of the DenseCRF model.
2. Methodology
2.1. mmsDCNN
2.2. The Multi-Level DenseCRF Model
2.2.1. Edge Constraint
2.2.2. Combined Multilevel Potential Function
3. Experiment
3.1. Datasets
3.2. Setting of the Experiments and Evaluation Metrics
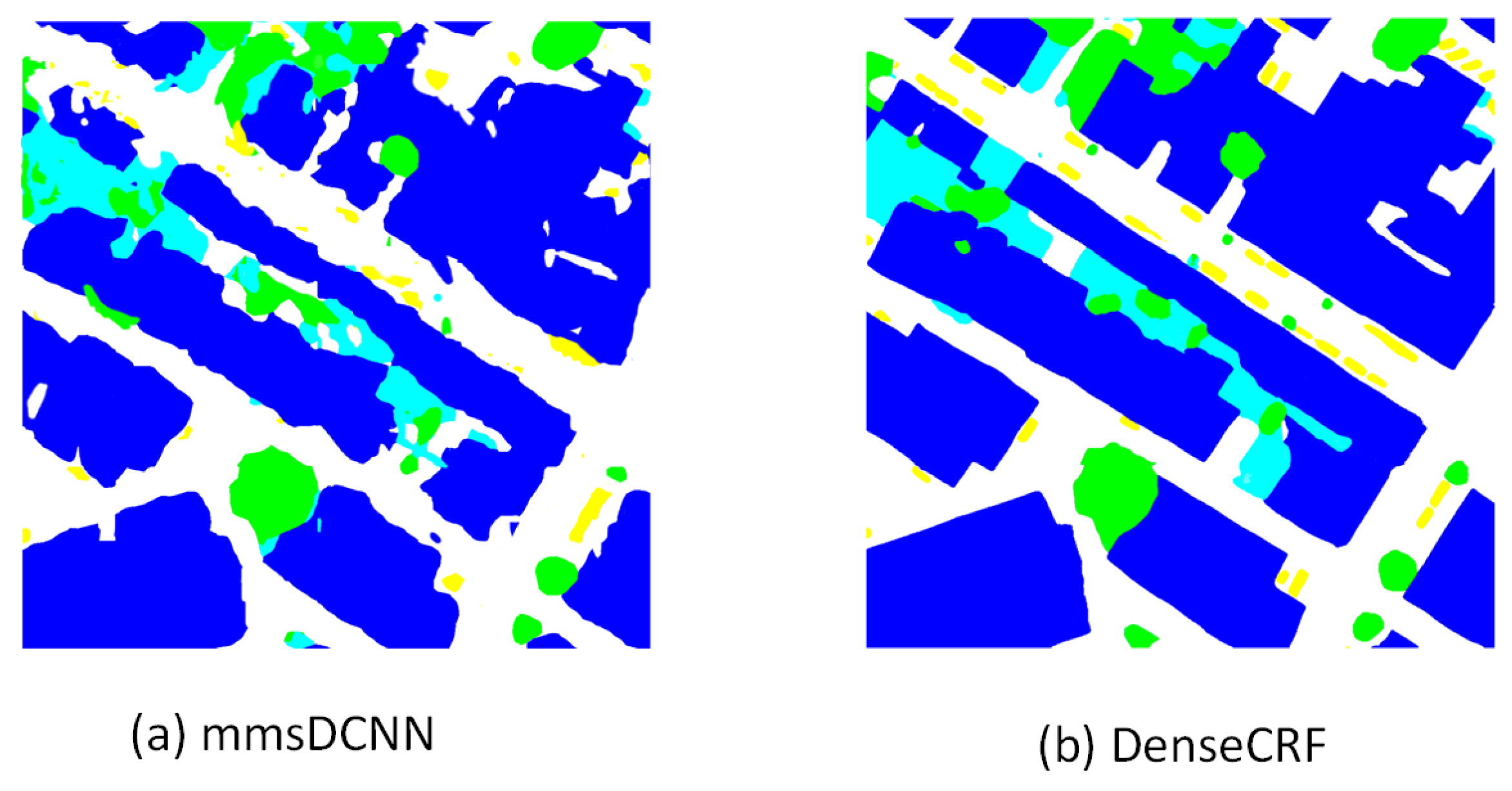
3.3. Experimental Results
3.3.1. Experimental Results on the Potsdam Dataset
3.3.2. Experimental Results on the Vaihingen Dataset
3.4. Robustness Verification
4. Discussion
4.1. Complexity Analysis
4.2. Improvements and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Csurka, G.; Perronnin, F. An efficient approach to semantic segmentation. Int. J. Comput. Vis. 2011, 95, 198–212. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Li, Y.; Tao, C.; Tan, Y.; Shang, K.; Tian, J. Unsupervised multilayer feature learning for satellite image scene classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 157–161. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Zhang, Y. Image retrieval from remote sensing big data: A survey. Inf. Fusion 2021, 67, 94–115. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. Isprs J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Zhang, Y.; Tao, C.; Xiao, R.; Tan, Y. Accurate cloud detection in high-resolution remote sensing imagery by weakly supervised deep learning. Remote Sens. Environ. 2020, 250, 112045. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Yuille, A.L. Deep networks under scene-level supervision for multi-class geospatial object detection from remote sensing images. Isprs J. Photogramm. Remote Sens. 2018, 146, 182–196. [Google Scholar] [CrossRef]
- Gu, W.; Bai, S.; Kong, L. A review on 2D instance segmentation based on deep neural networks. Image Vis. Comput. 2022, 120, 104401. [Google Scholar] [CrossRef]
- Elharrouss, O.; Al-Maadeed, S.; Subramanian, N.; Ottakath, N.; Almaadeed, N.; Himeur, Y. Panoptic segmentation: A review. arXiv 2021, arXiv:2111.10250. [Google Scholar]
- Hafiz, A.M.; Bhat, G.M. A survey on instance segmentation: State of the art. Int. J. Multimed. Inf. Retr. 2020, 9, 171–189. [Google Scholar] [CrossRef]
- Bolya, D.; Zhou, C.; Xiao, F.; Lee, Y.J. Yolact: Real-time instance segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9157–9166. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H. Conditional convolutions for instance segmentation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part I 16. Springer: Berlin, Germany, 2020; pp. 282–298. [Google Scholar]
- Kirillov, A.; He, K.; Girshick, R.; Rother, C.; Dollár, P. Panoptic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9404–9413. [Google Scholar]
- Li, X.; Chen, D. A survey on deep learning-based panoptic segmentation. Digit. Signal Process. 2022, 120, 103283. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Zhu, Z.; Xie, L.; Huang, G.; Du, D.; Wang, X. Attention-guided unified network for panoptic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7026–7035. [Google Scholar]
- Tasar, O.; Tarabalka, Y.; Alliez, P. Incremental learning for semantic segmentation of large-scale remote sensing data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3524–3537. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, W.; Zhang, T.; Li, J. HRCNet: High-resolution context extraction network for semantic segmentation of remote sensing images. Remote Sens. 2020, 13, 71. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: New York, NY, USA, 2011; pp. 2564–2571. [Google Scholar]
- Pietikäinen, M. Local binary patterns. Scholarpedia 2010, 5, 9775. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Dietz, K.; Gail, M.; Klein, M.; Klein, M. Logistic Regression; Springer: Berlin, Germany, 2002. [Google Scholar]
- Han, K.; Guo, J.; Zhang, C.; Zhu, M. Attribute-aware attention model for fine-grained representation learning. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; pp. 2040–2048. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Affonso, C.; Rossi, A.L.D.; Vieira, F.H.A.; de Leon Ferreira, A.C.P. Deep learning for biological image classification. Expert Syst. Appl. 2017, 85, 114–122. [Google Scholar] [CrossRef]
- Oprea, S.; Martinez-Gonzalez, P.; Garcia-Garcia, A.; Castro-Vargas, J.A.; Orts-Escolano, S.; Garcia-Rodriguez, J.; Argyros, A. A review on deep learning techniques for video prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2806–2826. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.; Guo, X.; Lee, H.; Lewis, R.L.; Singh, S. Action-conditional video prediction using deep networks in atari games. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef]
- Khan, S.; Rahmani, H.; Shah, S.A.A.; Bennamoun, M. A guide to convolutional neural networks for computer vision. Synth. Lect. Comput. Vis. 2018, 8, 1–207. [Google Scholar]
- Liu, Z.; Yeoh, J.K.; Gu, X.; Dong, Q.; Chen, Y.; Wu, W.; Wang, L.; Wang, D. Automatic pixel-level detection of vertical cracks in asphalt pavement based on GPR investigation and improved mask R-CNN. Autom. Constr. 2023, 146, 104689. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, H.; Yang, Z.; Jin, Q.; Wu, Y.; Xia, P.; Meng, L. Fast Tailings Pond Mapping Exploiting Large Scene Remote Sensing Images by Coupling Scene Classification and Sematic Segmentation Models. Remote Sens. 2023, 15, 327. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, W.; Feng, Y.; Song, R. TSCNet: Topological Structure Coupling Network for Change Detection of Heterogeneous Remote Sensing Images. Remote Sens. 2023, 15, 621. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Qiao, P.; Lv, X.; Li, J.; Du, T.; Cai, Y. Image Registration Algorithm for Remote Sensing Images Based on Pixel Location Information. Remote Sens. 2023, 15, 436. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Z.; Gu, X.; Wu, W.; Chen, Y.; Wang, L. Automatic detection of pothole distress in asphalt pavement using improved convolutional neural networks. Remote Sens. 2022, 14, 3892. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, J.; Bruzzone, L. Semantic segmentation of large-size VHR remote sensing images using a two-stage multiscale training architecture. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5367–5376. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. Isprs J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Chen, J.; Wang, D.; Chen, Y.; Wang, L. Automatic recognition of pavement cracks from combined GPR B-scan and C-scan images using multiscale feature fusion deep neural networks. Autom. Constr. 2023, 146, 104698. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Takikawa, T.; Acuna, D.; Jampani, V.; Fidler, S. Gated-scnn: Gated shape cnns for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: New York, NY, USA; pp. 5229–5238. [Google Scholar]
- Li, R.; Zheng, S.; Zhang, C.; Duan, C.; Su, J.; Wang, L.; Atkinson, P.M. Multiattention network for semantic segmentation of fine-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Klein, L.; Amar, C.B.; Audebert, N.; Lefèvre, S. Deep learning for semantic segmentation of remote sensing images with rich spectral content. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 2569–2572. [Google Scholar]
- Cheng, X.; Lei, H. Remote sensing scene image classification based on mmsCNN–HMM with stacking ensemble model. Remote Sens. 2022, 14, 4423. [Google Scholar] [CrossRef]
- Krähenbühl, P.; Koltun, V. Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials. In Proceedings of the Neural Information Processing Systems, Granada, Spain, 12–15 December 2011. [Google Scholar]
- Lim, J.J.; Zitnick, C.L.; Dollár, P. Sketch tokens: A learned mid-level representation for contour and object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3158–3165. [Google Scholar]
- Konecny, G. The International Society for Photogrammetry and Remote Sensing (ISPRS) study on the status of mapping in the world. In Proceedings of the International Workshop on “Global Geospatial Information”, Novosibirsk, Russia, 25 April 2013; Citeseer: Novosibirsk, Russian, 2013; pp. 4–24. [Google Scholar]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Scaling up your kernels to 31x31: Revisiting large kernel design in cnns. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11963–11975. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Dollár, P.; Zitnick, L.C. Structured Forests for Fast Edge Detection. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Xiaofeng, R.; Bo, L. Discriminatively trained sparse code gradients for contour detection. Adv. Neural Inf. Process. Syst. 2012, 25, 584–592. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Kohli, P.; Ladický, L.U.; Torr, P.H. Robust higher order potentials for enforcing label consistency. Int. J. Comput. Vis. 2009, 82, 302–324. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, S.; Ding, L.; Bruzzone, L. Multi-scale context aggregation for semantic segmentation of remote sensing images. Remote Sens. 2020, 12, 701. [Google Scholar] [CrossRef]
- Mousavi Kahaki, S.M.; Nordin, M.J.; Ashtari, A.H.; Zahra, S.J. Invariant feature matching for image registration application based on new dissimilarity of spatial features. PLoS ONE 2016, 11, e0149710. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Nekrasov, V.; Dharmasiri, T.; Spek, A.; Drummond, T.; Shen, C.; Reid, I. Real-time joint semantic segmentation and depth estimation using asymmetric annotations. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: New York, NY, USA, 2019; p. 7101. [Google Scholar]


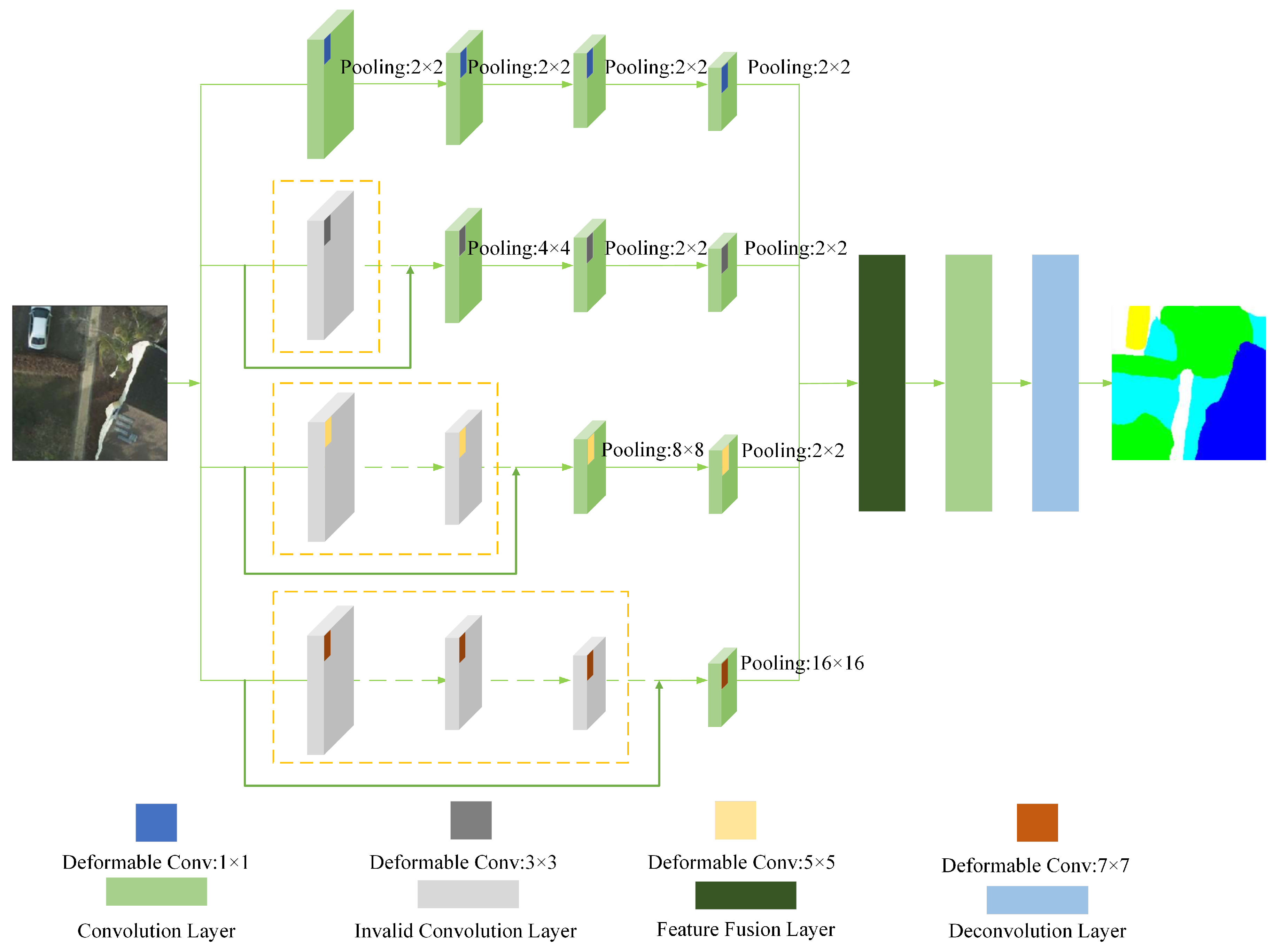




| Type | Number | Filter Size | Pad | Stride |
|---|---|---|---|---|
| Conv1 + ReLU | 32 | 0 | 1 | |
| Max Pooling | − | 0 | 2 | |
| Conv2 + ReLU | 64 | 1 | ||
| Max Pooling | − | 0 | ||
| Conv3 + ReLU | 128 | 1 | ||
| Max Pooling | − | 0 | ||
| Conv4 + ReLU | 256 | 1 | ||
| Max Pooling | − | 0 | ||
| Conv5 + ReLU | 6 | 0 | 1 | |
| Deconv Layer | 6 | 8 | 16 |
| Item | Potsdam Training | Potsdam Testing | Vaihingen Training | Vaihingen Testing |
|---|---|---|---|---|
| size (pixel) | ||||
| number | 6931 | 13454 | 654 | 2219 |
| overlap pixels | 72 | 192 | 72 | 192 |
| p pixels | 72 | 192 | 72 | 192 |
| The Experimental Environment | Experimental Configuration |
|---|---|
| Processor | |
| GPU | |
| Memory | |
| Operating system | |
| Compiler |
| Model | Recall (%) | Precision (%) | F1 Score (%) | OA (%) |
|---|---|---|---|---|
| FCN [59] | ||||
| PSPNet [40] | ||||
| FPN [60] | ||||
| UNet [39] | ||||
| DeepLabv3 [61] | ||||
| DANet [62] | ||||
| LWRefineNet [63] | ||||
| HRCNet-W48 [18] | ||||
| The proposed model |
| Model | ImSurface | Building | Low Vegetation | Tree | Car | mIoU (%) |
|---|---|---|---|---|---|---|
| FCN [59] | ||||||
| PSPNet [40] | ||||||
| FPN [60] | ||||||
| UNet [39] | ||||||
| DeepLabv3 [61] | ||||||
| DANet [62] | ||||||
| LWRefineNet [63] | ||||||
| HRCNet-W48 [18] | ||||||
| The proposed model |
| Model | Recall (%) | Precision (%) | F1 Score (%) | OA (%) |
|---|---|---|---|---|
| FCN [59] | ||||
| PSPNet [40] | ||||
| FPN [60] | ||||
| UNet [39] | ||||
| DeepLabv3 [61] | ||||
| DANet [62] | ||||
| LWRefineNet [63] | ||||
| HRCNet-W48 [18] | ||||
| The proposed model |
| Model | ImSurface | Building | Low Vegetation | Tree | Car | mIoU (%) |
|---|---|---|---|---|---|---|
| FCN [59] | ||||||
| PSPNet [40] | ||||||
| FPN [60] | ||||||
| UNet [39] | ||||||
| DeepLabv3 [61] | ||||||
| DANet [62] | ||||||
| LWRefineNet [63] | ||||||
| HRCNet-W48 [18] | ||||||
| The proposed model |
| Model | mIoU (%) | Precision (%) | F1 Score (%) | OA (%) |
|---|---|---|---|---|
| Proposed model | ||||
| Proposed model (salt-and-pepper noise) | ||||
| Proposed model (Gaussian noise) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Lei, H. Semantic Segmentation of Remote Sensing Imagery Based on Multiscale Deformable CNN and DenseCRF. Remote Sens. 2023, 15, 1229. https://doi.org/10.3390/rs15051229
Cheng X, Lei H. Semantic Segmentation of Remote Sensing Imagery Based on Multiscale Deformable CNN and DenseCRF. Remote Sensing. 2023; 15(5):1229. https://doi.org/10.3390/rs15051229
Chicago/Turabian StyleCheng, Xiang, and Hong Lei. 2023. "Semantic Segmentation of Remote Sensing Imagery Based on Multiscale Deformable CNN and DenseCRF" Remote Sensing 15, no. 5: 1229. https://doi.org/10.3390/rs15051229
APA StyleCheng, X., & Lei, H. (2023). Semantic Segmentation of Remote Sensing Imagery Based on Multiscale Deformable CNN and DenseCRF. Remote Sensing, 15(5), 1229. https://doi.org/10.3390/rs15051229