SquconvNet: Deep Sequencer Convolutional Network for Hyperspectral Image Classification
Abstract
1. Introduction
- (1)
- We introduce the BiLSTM2D layer and Sequencer module for the first time, and combine them with CNN to compensate for CNN’s shortcomings and improve the performance of HSI classification.
- (2)
- A supplementary classification module comprised of two convolutional layers and a fully connected layer is proposed, with the dual purpose of decreasing the network parameters and assisting the network in classification.
- (3)
- Using three typical baseline datasets, we performed qualitative and quantitative evaluation studies (IP, UP, SA). The experimental findings show that, in terms of classification accuracy and stability, our proposed model verifies its superiority.
2. Materials and Methods
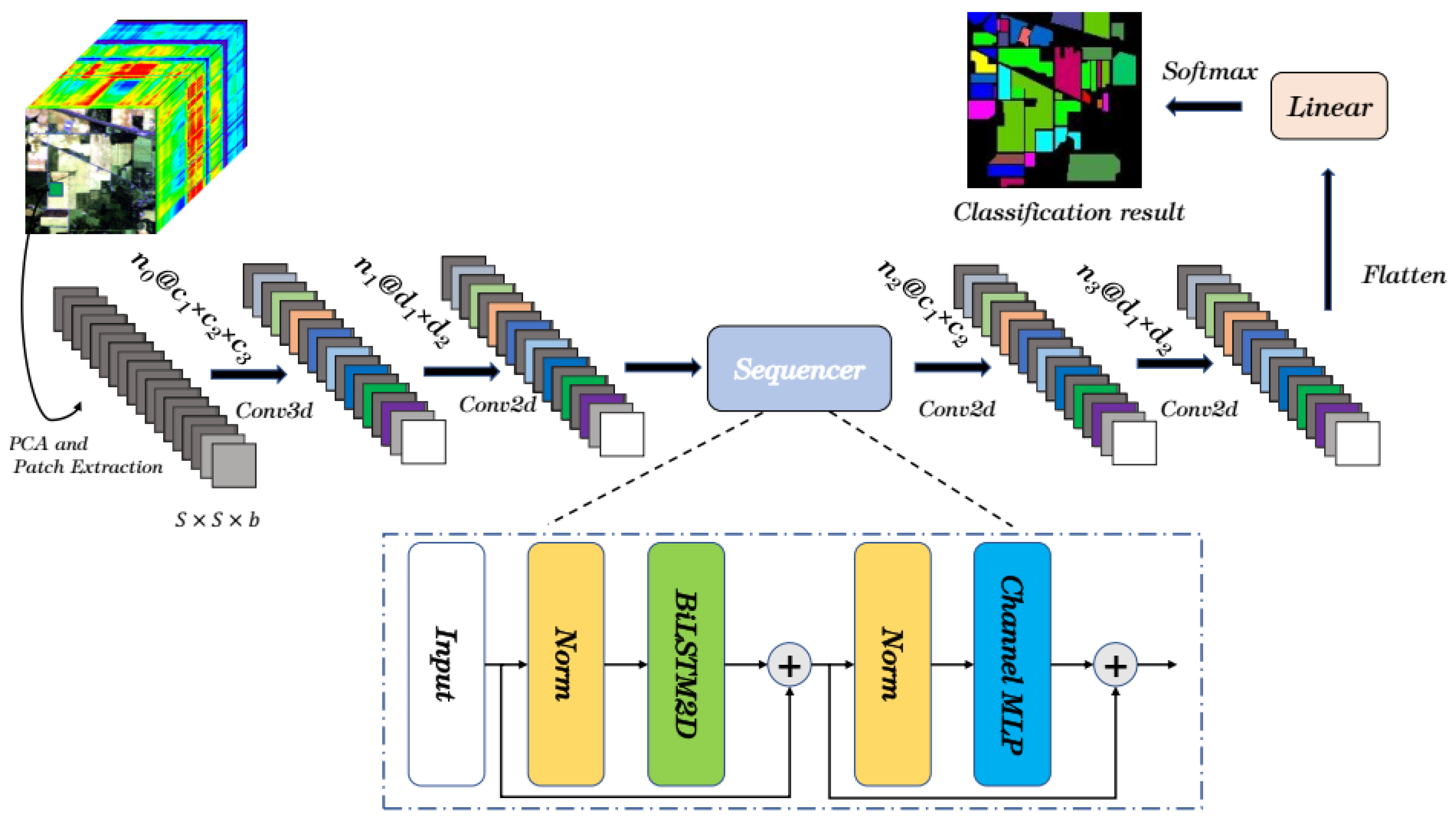
2.1. Overview of SquconvNet
2.2. Spectral-Spatial Feature Extraction Module
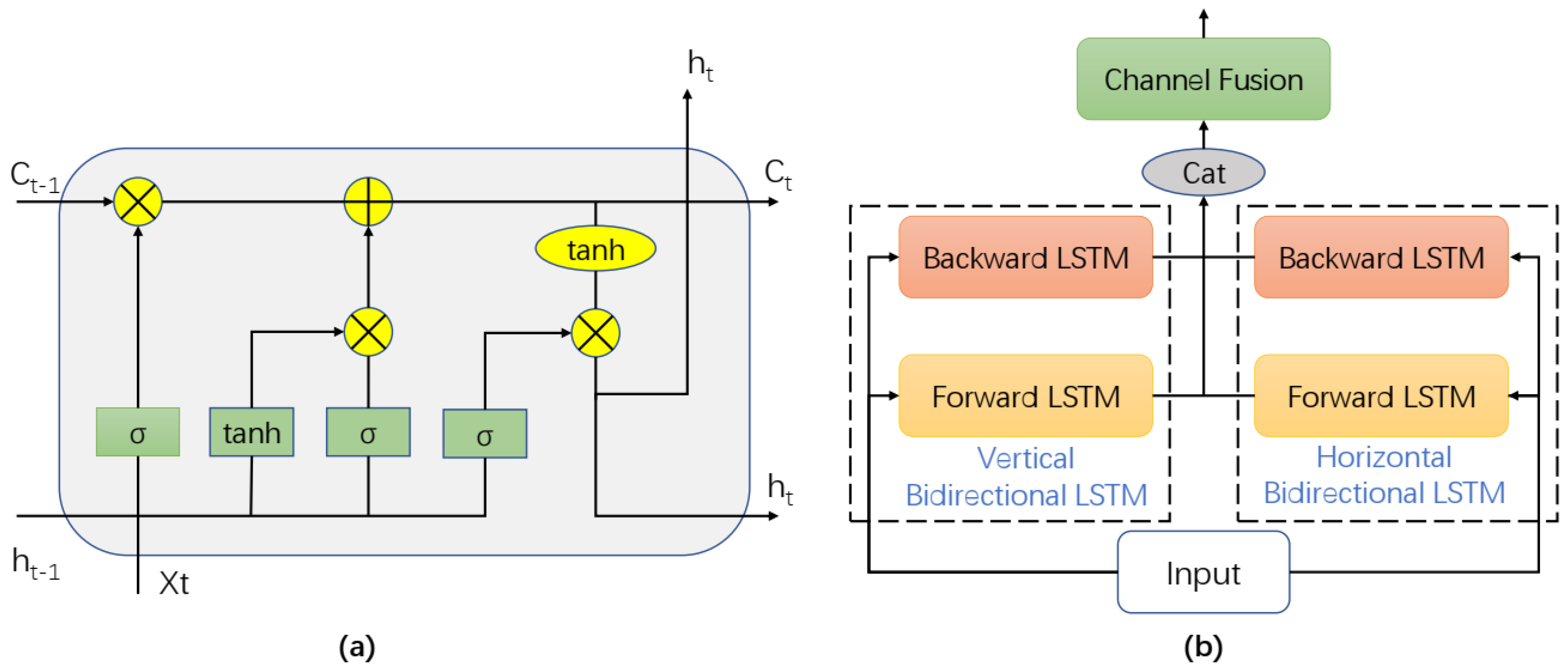
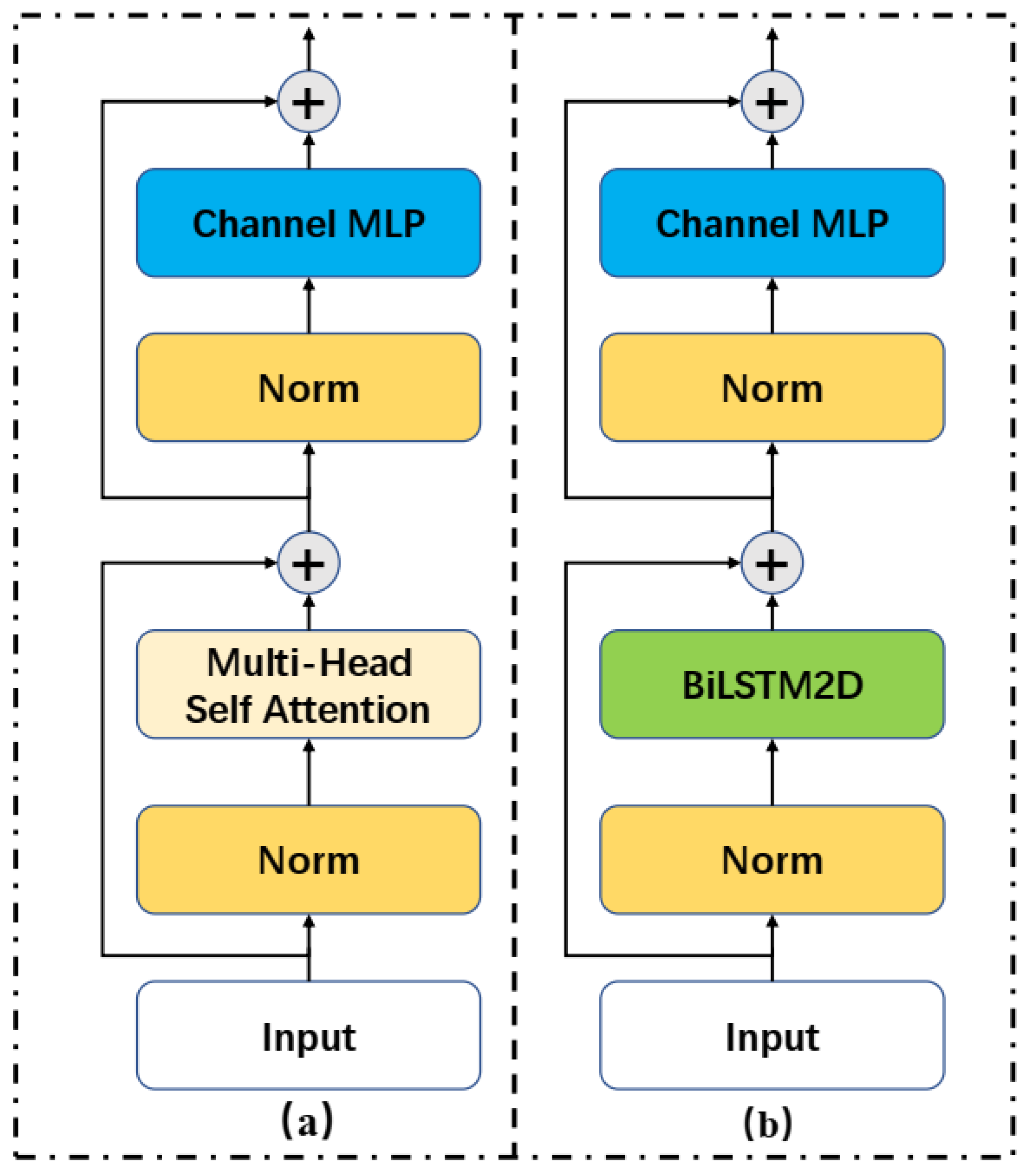
2.3. Sequencer Module
2.4. Auxiliary Classification Module
3. Experiment and Analysis
3.1. Hyperspectral Image Datasets Description
3.1.1. Indian Pines Dataset (IP)
3.1.2. University of Pavia Dataset (UP)
3.1.3. Salians Scene Dataset (SA)
3.2. Experimental Settings
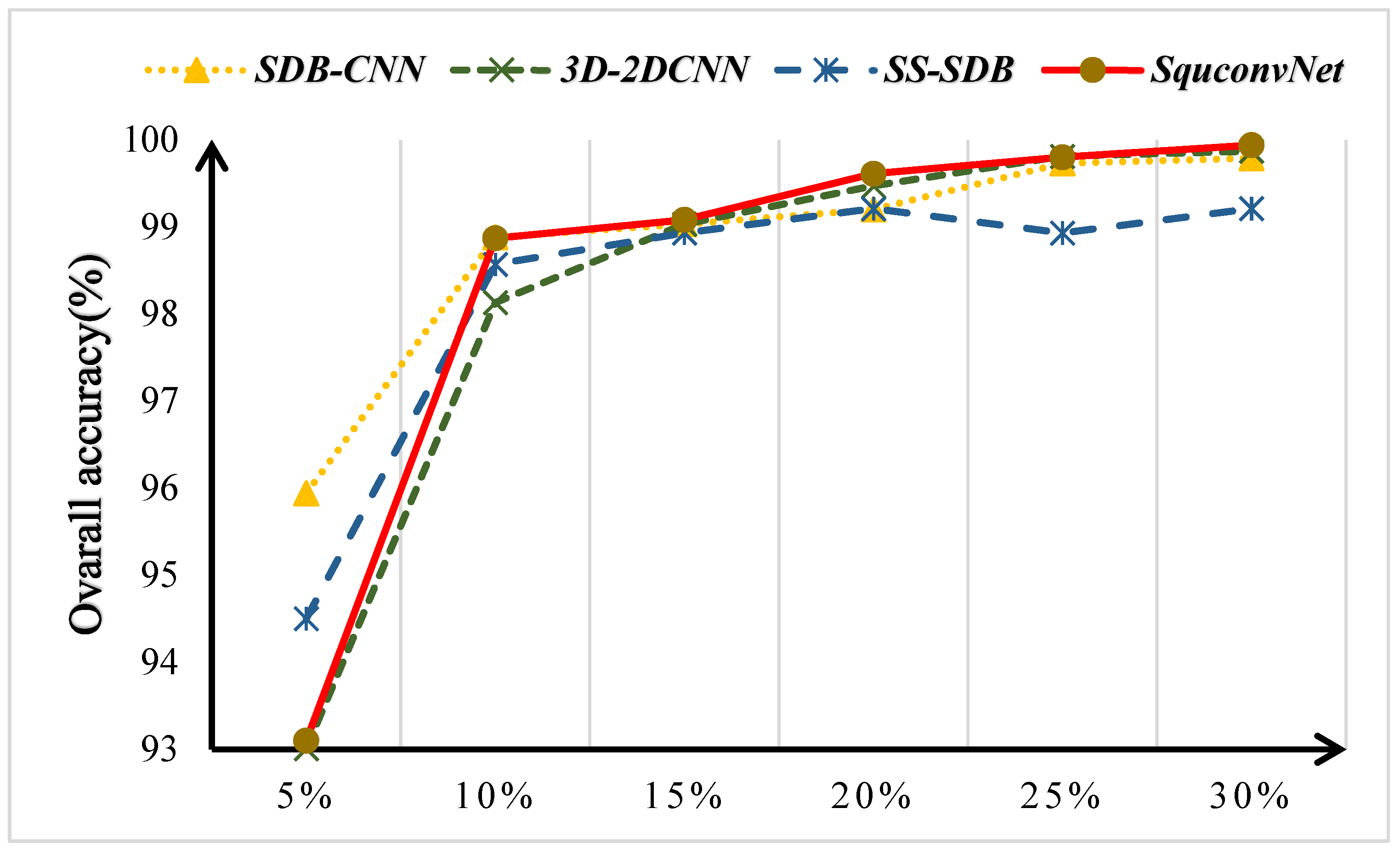
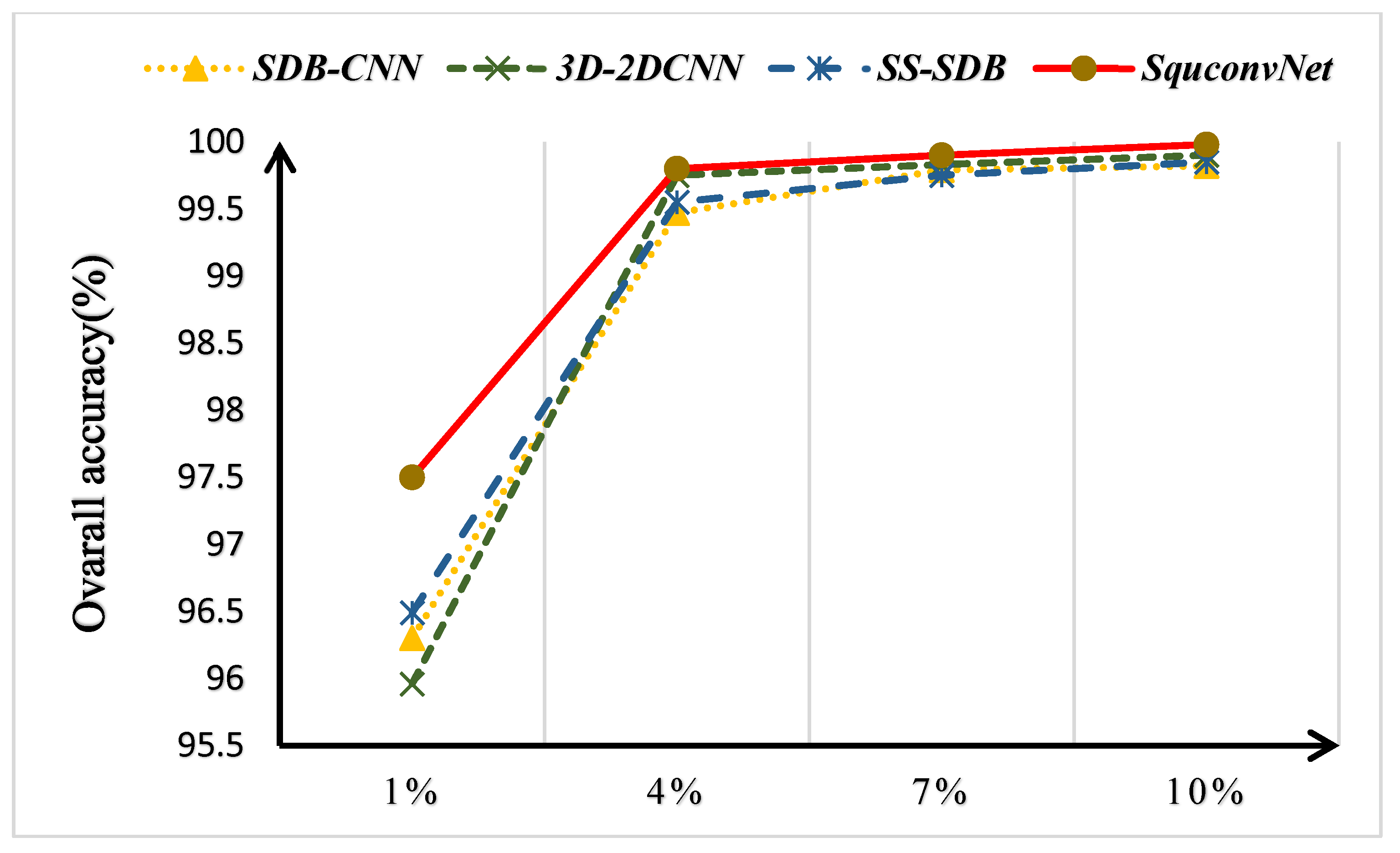
3.3. Experimental and Evaluation on Three Datasets
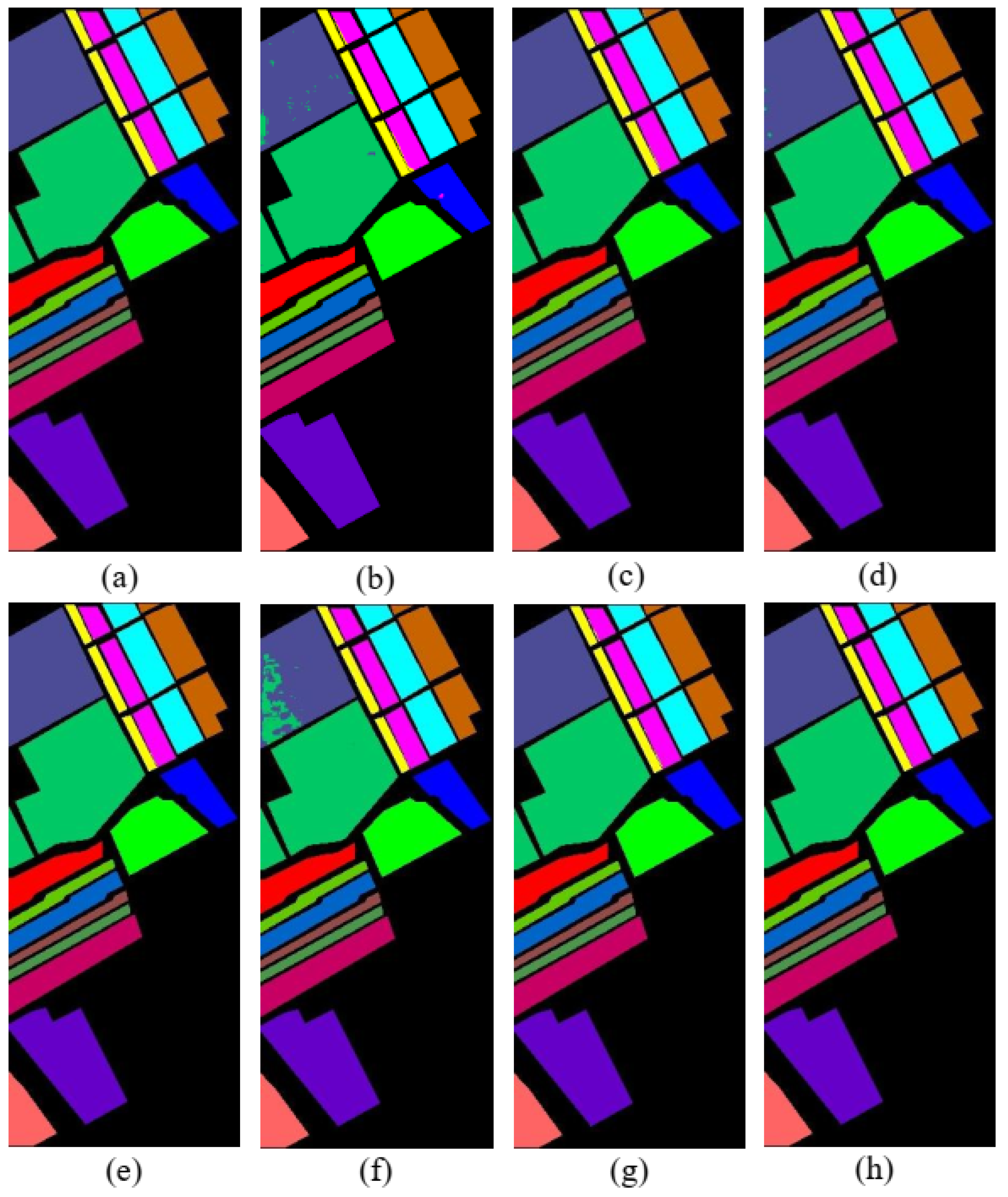
3.3.1. Experiment on IP Dataset
3.3.2. Experimental on UP Dataset
3.3.3. Experiment on SA Dataset
3.4. Learning Rate Experiment
4. Discussion
4.1. Discussion on the Ablation Experiment
4.2. Discussion on the Time Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prasad, S.; Bruce, L.M. Limitations of Principal Components Analysis for Hyperspectral Target Recognition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Piiroinen, R.; Heiskanen, J.; Maeda, E.; Viinikka, A.; Pellikka, P. Classification of Tree Species in a Diverse African Agroforestry Landscape Using Imaging Spectroscopy and Laser Scanning. Remote Sens. 2017, 9, 875. [Google Scholar] [CrossRef]
- Chen, S.Y.; Lin, C.S.; Tai, C.H.; Chuang, S.J. Adaptive Window-Based Constrained Energy Minimization for Detection of Newly Grown Tree Leaves. Remote Sens. 2018, 10, 96. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Chen, Z.C.; Huang, Z.H. Vicarious Radiometric Calibration of the Hyperspectral Imaging Microsatellites SPARK-01 and-02 over Dunhuang, China. Remote Sens. 2018, 10, 120. [Google Scholar] [CrossRef]
- Tane, Z.; Roberts, D.; Veraverbeke, S.; Casas, A.; Ramirez, C.; Ustin, S. Evaluating Endmember and Band Selection Techniques for Multiple Endmember Spectral Mixture Analysis using Post-Fire Imaging Spectroscopy. Remote Sens. 2018, 10, 389. [Google Scholar] [CrossRef]
- Ni, L.; Wub, H. Mineral Identification and Classification by Combining Use of Hyperspectral VNIR/SWIR and Multispectral TIR Remotely Sensed Data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3317–3320. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral-Spatial Classification of Hyperspectral Data Using Loopy Belief Propagation and Active Learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 844–856. [Google Scholar] [CrossRef]
- Zhang, L.; Zhong, Y.; Huang, B.; Gong, J.; Li, P. Dimensionality reduction based on clonal selection for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4172–4186. [Google Scholar] [CrossRef]
- Brown, A.J.; Sutter, B.; Dunagan, S. The MARTE VNIR Imaging Spectrometer Experiment: Design and Analysis. Astrobiology 2008, 8, 1001–1011. [Google Scholar] [CrossRef]
- Brown, A.J.; Hook, S.J.; Baldridge, A.M.; Crowley, J.K.; Bridges, N.T.; Thomson, B.J.; Marion, G.M.; de Souza, C.R.; Bishop, J.L. Hydrothermal formation of Clay-Carbonate alteration assemblages in the Nil Fossae region of Mars. Earth Planet. Sci. Lett. 2010, 297, 174–182. [Google Scholar] [CrossRef]
- Zhu, J.S.; Hu, J.; Jia, S.; Jia, X.P.; Li, Q.Q. Multiple 3-D Feature Fusion Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1873–1886. [Google Scholar] [CrossRef]
- Chen, Y.S.; Lin, Z.H.; Zhao, X.; Wang, G.; Gu, Y.F. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Lavanya, A.; Sanjeevi, S. An Improved Band Selection Technique for Hyperspectral Data Using Factor Analysis. J. Indian Soc. Remote Sens. 2013, 41, 199–211. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images With Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Ye, Q.; Yang, J.; Liu, F.; Zhao, C.; Ye, N.; Yin, T. L1-Norm Distance Linear Discriminant Analysis Based on an Effective Iterative Algorithm. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 114–129. [Google Scholar] [CrossRef]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Independent Component Discriminant Analysis for hyperspectral image classification. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral Image Classification With Independent Component Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.; Plaza, J.; Plaza, A. Cloud implementation of the K-means algorithm for hyperspectral image analysis. J. Supercomput. 2017, 73, 514–529. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM- and MRF-Based Method for Accurate Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Zhang, Y. Classification of hyperspectral image based on deep belief networks. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5132–5136. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep Pyramidal Residual Networks for Spectral–Spatial Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 740–754. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Li, J.J.; Zhao, X.; Li, Y.S.; Du, Q.; Xi, B.B.; Hu, J. Classification of Hyperspectral Imagery Using a New Fully Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 292–296. [Google Scholar] [CrossRef]
- Tun, N.L.; Gavrilov, A.; Tun, N.M.; Trieu, D.M.; Aung, H. Hyperspectral Remote Sensing Images Classification Using Fully Convolutional Neural Network. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg, Moscow, 26–29 January 2021; pp. 2166–2170. [Google Scholar]
- Bi, X.J.; Zhou, Z.Y. Hyperspectral Image Classification Algorithm Based on Two-Channel Generative Adversarial Network. Acta Opt. Sin. 2019, 39, 1028002. [Google Scholar] [CrossRef]
- Xue, Z.X. Semi-supervised convolutional generative adversarial network for hyperspectral image classification. IET Image Process. 2020, 14, 709–719. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- He, X.; Chen, Y.S.; Lin, Z.H. Spatial-Spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Qing, Y.H.; Liu, W.Y.; Feng, L.Y.; Gao, W.J. Improved Transformer Net for Hyperspectral Image Classification. Remote Sens. 2021, 13, 2216. [Google Scholar] [CrossRef]
- Hong, D.F.; Han, Z.; Yao, J.; Gao, L.R.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification With Transformers. Ieee Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Zhu, J.; Fang, L.; Ghamisi, P. Deformable convolutional neural networks for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1254–1258. [Google Scholar] [CrossRef]
- Tatsunami, Y.; Taki, M. Sequencer: Deep LSTM for Image Classification. arXiv 2022, arXiv:2205.01972. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, X.; Shang, S.; Tang, X.; Feng, J.; Jiao, L. Spectral Partitioning Residual Network With Spatial Attention Mechanism for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5507714. [Google Scholar] [CrossRef]







| Description | Datasets | ||
|---|---|---|---|
| IP | UP | SA | |
| Spatial Size | |||
| Spectral Band | 224 | 103 | 204 |
| No of Classes | 16 | 9 | 16 |
| Total sample pixels | 10,249 | 42,776 | 54,129 |
| Sensor | AVIRIS | ROSIS | AVIRIS |
| Spatial Resolution (m) | 20 | 1.3 | 3.7 |
| Category | Category Name | Training Samples | Test Samples | Number of Samples per Category |
|---|---|---|---|---|
| 1 | Alfalfa | 14 | 32 | 46 |
| 2 | Corn-notill | 431 | 997 | 1428 |
| 3 | Corn-mintill | 250 | 580 | 830 |
| 4 | Corn | 71 | 166 | 237 |
| 5 | Grass-pasture | 145 | 338 | 483 |
| 6 | Grass-trees | 219 | 511 | 730 |
| 7 | Grass-pasture-mowed | 8 | 20 | 28 |
| 8 | Hay-windrowed | 143 | 335 | 478 |
| 9 | Oats | 6 | 14 | 20 |
| 10 | Soybean-nottill | 292 | 680 | 972 |
| 11 | Soybean-mintill | 736 | 1719 | 2455 |
| 12 | Soybean-clean | 178 | 415 | 593 |
| 13 | Wheat | 62 | 143 | 205 |
| 14 | Woods | 381 | 884 | 1265 |
| 15 | Building-Grass-Trees-Drives | 117 | 269 | 386 |
| 16 | Stone-Steel-Towers | 28 | 65 | 93 |
| Total. | 3081 | 7168 | 10,249 |
| Category | Category Name | Training Samples | Test Samples | Number of Samples per Category |
|---|---|---|---|---|
| 1 | Asphalt | 663 | 5968 | 6631 |
| 2 | Meadows | 1865 | 16,784 | 18,649 |
| 3 | Gravel | 210 | 1889 | 2099 |
| 4 | Trees | 306 | 2758 | 3064 |
| 5 | Painted metal sheets | 134 | 1211 | 1345 |
| 6 | Bare Soil | 503 | 4526 | 5029 |
| 7 | Bitumen | 133 | 1197 | 1330 |
| 8 | Self-Blocking Bricks | 368 | 3314 | 3682 |
| 9 | Shadows | 95 | 852 | 947 |
| Total. | 4277 | 38,499 | 42,776 |
| Category | Category Name | Training Samples | Test Samples | Number of Samples per Category |
|---|---|---|---|---|
| 1 | Brocoli_green_weeds_1 | 201 | 1808 | 2009 |
| 2 | Brocoli_green_weeds_2 | 372 | 3354 | 3726 |
| 3 | Fallow | 197 | 1779 | 1976 |
| 4 | Fallow_rough_plow | 139 | 1255 | 1394 |
| 5 | Fallow_smooth | 268 | 2410 | 2678 |
| 6 | Stubble | 396 | 3563 | 3959 |
| 7 | Celery | 358 | 3221 | 3579 |
| 8 | Grapes_untrained | 1127 | 10,144 | 11,271 |
| 9 | Soil_vineyard_develop | 620 | 5583 | 6203 |
| 10 | Corn_senesced_green_weeds | 328 | 2950 | 3278 |
| 11 | Lettuce_romaine_4wk | 107 | 961 | 1068 |
| 12 | Lettuce_romaine_5wk | 193 | 1734 | 1927 |
| 13 | Lettuce_romaine_6wk | 91 | 825 | 916 |
| 14 | Lettuce_romaine_7wk | 107 | 963 | 1070 |
| 15 | Vineyard_untrained | 727 | 6541 | 7268 |
| 16 | Vineyard_vertical_trellis | 181 | 1626 | 1807 |
| Total. | 5412 | 48,717 | 54,129 |
| NO. | Resnet | 3D-CNN | SSRN | HybridSN | SPRN | SSFTT | Proposed |
|---|---|---|---|---|---|---|---|
| 1 | 99.69 0.936 | 100 0 | 99.69 0.936 | 99.69 0.936 | 97.5 6.527 | 99.38 1.248 | 100 |
| 2 | 99.23 0.237 | 99.16 0.398 | 95.54 12.69 | 99.64 0.237 | 79.56 33.04 | 99.32 0.496 | 99.87 0.11 |
| 3 | 99.8 0.168 | 99.72 0.520 | 98.24 4.936 | 99.64 0.598 | 87.77 29.73 | 98.86 0.712 | 100 0 |
| 4 | 99.32 0.351 | 100 0 | 100 0 | 100 0 | 91.08 22.41 | 99.31 0.728 | 100 |
| 5 | 99.76 0.553 | 99.70 0.400 | 99.67 0.362 | 99.67 0.598 | 98.25 0.018 | 97.62 3.56 | 99.94 0.12 |
| 6 | 99.32 0.351 | 99.86 0.197 | 99.90 0.158 | 99.98 0.06 | 97.04 7.517 | 99.65 0.325 | 100 |
| 7 | 98.5 2.29 | 100 0 | 99 2 | 99.5 1.5 | 94.5 11.5 | 99.85 0.447 | 100 |
| 8 | 100 0 | 100 0 | 100 0 | 99.91 0.27 | 96.63 6.803 | 74.76 17.73 | 100 |
| 9 | 94.29 4.286 | 99.29 2.142 | 97.86 4.574 | 93.57 7.458 | 80.71 38.61 | 98.79 0.746 | 99.29 2.142 |
| 10 | 99.63 0.165 | 99.57 0.309 | 99.50 0.466 | 99.84 0.364 | 88.44 29.58 | 98.79 0.746 | 99.62 0.256 |
| 11 | 99.76 0.099 | 99.92 0.118 | 91.83 21.039 | 99.78 0.18 | 86.95 19.72 | 99.56 0.37 | 99.92 0.063 |
| 12 | 98.22 0.763 | 98.91 0.500 | 98.91 0.571 | 99.69 0.241 | 95.25 11.66 | 97.73 1.876 | 99.11 0.343 |
| 13 | 99.51 0.77 | 99.65 0.472 | 99.86 0.28 | 100 0 | 97.48 6.64 | 99.2 0.94 | 100 0 |
| 14 | 100 0 | 100 0 | 99.98 0.069 | 99.94 0.117 | 99.82 0.543 | 99.83 0.192 | 100 |
| 15 | 99.96 0.111 | 99.85 0.342 | 99.18 1.835 | 99.63 0.409 | 92.89 10.91 | 98.38 2.313 | 100 0 |
| 16 | 99.23 1.033 | 98.31 2.790 | 99.38 0.754 | 99.08 1.411 | 96.31 6.123 | 94.58 6.193 | 100 0 |
| OA (%) | 99.6 0.05 | 99.69 0.083 | 97.09 7.261 | 99.77 0.095 | 90.57 12.81 | 99.09 0.434 | 99.87 0.034 |
| AA (%) | 99.22 0.287 | 99.62 0.182 | 98.66 2.481 | 99.35 0.459 | 92.51 10.77 | 96.94 1.566 | 99.86 0.125 |
| k × 100 | 99.54 0.064 | 99.64 0.095 | 96.77 8.027 | 99.74 0.111 | 89.35 14.46 | 98.96 0.496 | 99.85 0.041 |
| NO. | Resnet | 3D-CNN | SSRN | HybridSN | SPRN | SSFTT | Proposed |
|---|---|---|---|---|---|---|---|
| 1 | 99.42 0.558 | 99.81 0.160 | 99.91 0.190 | 99.98 0.023 | 99.5 0.948 | 99.61 0.298 | 99.99 0.006 |
| 2 | 99.75 0.177 | 99.99 0.003 | 99.98 0.252 | 99.99 0.005 | 96.14 10.36 | 99.94 0.121 | 100 0 |
| 3 | 98.39 1.395 | 99.32 0.484 | 99.30 0.395 | 99.15 0.798 | 91.71 22.28 | 98.98 0.644 | 99.48 0.266 |
| 4 | 99.41 0.277 | 98.77 0.260 | 100 0 | 98.95 1.052 | 99.99 0.024 | 98.73 0.542 | 99.80 0.128 |
| 5 | 99.92 0.105 | 99.92 0.154 | 100 0 | 99.65 0.624 | 96.96 7.054 | 99.37 0.677 | 100 0 |
| 6 | 99.77 0.471 | 99.99 0.012 | 99.9 0.203 | 100 0 | 96.96 7.054 | 99.98 0.024 | 100 0 |
| 7 | 96.3 3.819 | 99.89 0.129 | 98.33 3.506 | 99.48 0.773 | 94.55 10.92 | 99.63 0.531 | 99.99 0.024 |
| 8 | 96.94 4.011 | 98.99 0.420 | 99.97 0.742 | 98.81 0.659 | 92.05 14.43 | 98.66 0.995 | 99.71 0.158 |
| 9 | 96.44 1.714 | 95.56 1.967 | 99.79 0.321 | 94.52 3.216 | 98.78 0.44 | 97.46 0.007 | 99.85 0.211 |
| OA (%) | 99.19 0.574 | 99.64 0.069 | 99.69 0.437 | 99.58 0.165 | 96.55 7.78 | 99.57 0.129 | 99.93 0.026 |
| AA (%) | 98.93 0.763 | 99.09 0.200 | 99.69 0.402 | 98.88 0.395 | 98.56 1.431 | 99.15 0.183 | 99.86 0.049 |
| k × 100 | 98.93 0.763 | 99.53 0.090 | 99.72 0.438 | 99.44 0.219 | 95.61 9.772 | 99.43 0.172 | 99.90 0.031 |
| NO. | Resnet | 3D-CNN | SSRN | HybridSN | SPRN | SSFTT | Proposed |
|---|---|---|---|---|---|---|---|
| 1 | 99.13 2.41 | 100 0 | 100 0 | 100 0 | 100 0 | 100 0 | 100 0 |
| 2 | 99.76 0.695 | 99.99 0.009 | 100 0 | 100 0 | 100 0 | 99.99 0.009 | 100 0 |
| 3 | 99.14 1.068 | 100 0 | 100 0 | 100 | 97.51 7.252 | 99.93 0.185 | 100 0 |
| 4 | 99.39 1.116 | 100 0 | 99.95 0.069 | 99.97 0.096 | 99.41 0.842 | 99.31 1.131 | 100 0 |
| 5 | 99.40 0.905 | 99.32 0.39 | 99.73 0.216 | 99.78 0.111 | 98.11 0.525 | 99.42 0.621 | 99.93 0.070 |
| 6 | 100 0 | 100 0 | 100 0 | 100 0 | 100 0 | 99.88 0.149 | 100 0 |
| 7 | 99.91 0.107 | 99.95 0.056 | 99.99 0.020 | 99.99 0.009 | 100 0 | 99.91 0.021 | 100 0 |
| 8 | 84.2 30.68 | 100 0 | 99.98 0.021 | 99.98 0.032 | 92.8 11.17 | 99.89 0.148 | .003 |
| 9 | 99.95 0.112 | 100 0 | 100 0 | 100 0 | 98.45 0.046 | 99.99 0.021 | 100 0 |
| 10 | 99.78 0.499 | 100 0 | 99.93 0.054 | 99.98 0.028 | 99.92 0.151 | 99.89 0.148 | 99.96 0.060 |
| 11 | 99.69 0.299 | 99.88 0.278 | 99.92 0.205 | 99.32 1.005 | 99.99 0.03 | 99.73 0.403 | 100 0 |
| 12 | 99.84 0.276 | 100 0 | 100 0 | 100 0 | 99.93 0.188 | 99.94 0.124 | 100 0 |
| 13 | 99.77 0.536 | 99.92 0.121 | 100 0 | 100 0 | 100 0 | 99.21 0.884 | 100 0 |
| 14 | 99.92 0.146 | 99.95 0.095 | 99.95 0.139 | 99.97 0.067 | 99.8 0.384 | 99.5 0.594 | 99.99 0.030 |
| 15 | 99.26 0.86 | 99.98 0.020 | 99.74 0.151 | 99.98 0.060 | 95.1 9.154 | 99.96 0.025 | 99.99 0.006 |
| 16 | 99.94 0.186 | 100 0 | 100 0 | 100 0 | 100 0 | 99.72 0.731 | 100 0 |
| OA (%) | 96.44 6.513 | 99.95 0.022 | 99.94 0.026 | 99.97 0.028 | 97.46 2.178 | 99.88 0.038 | 99.99 0.007 |
| AA (%) | 98.69 2.198 | 99.94 0.033 | 99.95 0.026 | 99.94 0.071 | 98.81 0.825 | 99.77 0.099 | 99.99 0.009 |
| k × 100 | 96.082 7.15 | 99.95 0.025 | 99.93 0.710 | 99.96 0.0297 | 97.17 2.411 | 99.87 0.044 | 99.99 0.007 |
| Method | SSFE | SDB | AC | OA | AA | Kappa |
|---|---|---|---|---|---|---|
| SDB-CNN | √ | √ | 99.79 | 99.81 | 99.76 | |
| 3D-2DCNN | √ | √ | 99.87 | 99.91 | 99.86 | |
| SS-SDB | √ | √ | 99.69 | 99.75 | 99.65 | |
| SquconvNet | √ | √ | √ | 99.94 | 99.96 | 99.94 |
| Method | 3D-CNN | SSRN | HybridSN | SSFTT | SquconvNet | |
|---|---|---|---|---|---|---|
| IP | Train(s) | 174.3 | 498.4 | 318.6 | 38.2 | 35.1 |
| Test(s) | 1.80 | 1.67 | 3.4 | 0.32 | 0.37 | |
| Params. | 144 k | 364 k | 5122 k | 427 k | 878 k | |
| UP | Train(s) | 120.2 | 495.5 | 106.7 | 52.6 | 35.24 |
| Test(s) | 4.48 | 6.0 | 3.97 | 1.75 | 1.33 | |
| Params. | 135 k | 217 k | 4845 k | 427 k | 807 k | |
| SA | Train(s) | 143.7 | 555.8 | 136.5 | 67.0 | 46.5 |
| Test(s) | 5.41 | 7.76 | 4.98 | 2.24 | 1.71 | |
| Params. | 136 k | 370 k | 4846 k | 427 k | 809 k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Wang, Q.-W.; Liang, J.-H.; Zhu, E.-Z.; Zhou, R.-Q. SquconvNet: Deep Sequencer Convolutional Network for Hyperspectral Image Classification. Remote Sens. 2023, 15, 983. https://doi.org/10.3390/rs15040983
Li B, Wang Q-W, Liang J-H, Zhu E-Z, Zhou R-Q. SquconvNet: Deep Sequencer Convolutional Network for Hyperspectral Image Classification. Remote Sensing. 2023; 15(4):983. https://doi.org/10.3390/rs15040983
Chicago/Turabian StyleLi, Bing, Qi-Wen Wang, Jia-Hong Liang, En-Ze Zhu, and Rong-Qian Zhou. 2023. "SquconvNet: Deep Sequencer Convolutional Network for Hyperspectral Image Classification" Remote Sensing 15, no. 4: 983. https://doi.org/10.3390/rs15040983
APA StyleLi, B., Wang, Q.-W., Liang, J.-H., Zhu, E.-Z., & Zhou, R.-Q. (2023). SquconvNet: Deep Sequencer Convolutional Network for Hyperspectral Image Classification. Remote Sensing, 15(4), 983. https://doi.org/10.3390/rs15040983






