Abstract
Haze, generated by floaters (semitransparent clouds, fog, snow, etc.) in the atmosphere, can significantly degrade the utilization of remote sensing images (RSIs). However, the existing techniques for single image dehazing rarely consider that the haze is superimposed by floaters and shadow, and they often aggravate the degree of the haze shadow and dark region. In this paper, a single RSI dehazing method based on robust light-dark prior (RLDP) is proposed, which utilizes the proposed hybrid model and is robust to outlier pixels. In the proposed RLDP method, the haze is first removed by a robust dark channel prior (RDCP). Then, the shadow is removed with a robust light channel prior (RLCP). Further, a cube root mean enhancement (CRME)-based stable state search criterion is proposed for solving the difficult problem of patch size setting. The experiment results on benchmark and Landsat 8 RSIs demonstrate that the RLDP method could effectively remove haze.
1. Introduction
Haze affects the visibility of an optical remote sensing image (RSI), thereby, increasing the difficulty of many geographic monitoring procedures such as resource survey, environmental monitoring, and disaster analysis. As an example, semitransparent clouds are polymers formed by a mixture of small water droplets or small ice crystals that reflect and diffuse light in the air, thereby reducing the visibility of ground objects []. Haze is caused when the light reaching the optical camera is attenuated, while shadow is conversely caused when the light reaching ground is attenuated. Therefore, it is necessary to remove both haze and shadow from RSIs in advance to improve image clarity and provide assurance for subsequent tasks.
Optical RSI dehazing is considerably different from traditional image dehazing, in that there is a large distance between the optical sensor and the ground objects, irregular haze intensity, and absence of sky regions []. Additionally, optical RSIs take ground objects from a top-down perspective, and the presence of haze will also cause shadow. To solve the problems existing in prior-based methods, we propose an RLDP-based single RSI dehazing method which can simultaneously remove haze and shadow. At the same time, the patch size parameter can be adaptively searched according to the image contrast. The experiment results on benchmark RSIs and Landsat 8 RSIs demonstrate that RLDP can simultaneously remove haze and shadow.
The main contributions are as follows:
- For the regularity of satellite imaging, a semitransparent cloud was taken as an example, and a shadowing model and corresponding hybrid model were proposed. Then, a two-stage dehazing algorithm was proposed based on the haze hybrid model;
- An RLDP-based single RSI dehazing method which removes haze based on the robust dark channel prior (RDCP) and removes shadow with the robust light channel prior (RLCP) was proposed. A statistical-based criterion is also used to improve the robustness of RLDP;
- In order to solve the patch size setting problem, a CRME-based appropriate patch size search criterion was proposed. This method can adaptively adjust the patch size according to the contrast measure of a single image.
2. State of the Art
Researchers have developed various methods of computer vision to achieve image dehazing. Among such methods, prior-based and data-driven methods are the most popular [,].
The prior-based approaches are based on the atmosphere scattering model [], which can be expressed as follows:
where is the observed hazy image, is the haze-free image to be recovered, x is the position of any pixel, A is the global atmospheric light, and is the transmission map, with being the atmospheric scattering parameter and being the scene depth. The prior-based methods estimate the ill-posed parameters and A by prior assumptions. They then use Equation (1) to reconstruct the haze-free image to achieve image dehazing. He et al. [] pioneered an efficient dark channel prior to approximate model parameters. Salazar et al. [] presented a fast restoration method based on the prior proposed by He and morphological reconstruction. In addition, some other techniques learn the distributions of different parts scattering models [,]. Liu et al. [] added a boundary constraint to Equation (1). They then applied a non-local total variation regularization to solve the color distortion when the patch size is small. Nishino et al. [] constructed the statistical image model using a factorial Markov random field. They then estimated the parameters using a joint estimation algorithm. Berman et al. [] estimated initial transmission using the deviation of haze-lines in the hazy images, which is based on a global image color space distribution prior assumption. Bui et al. [] estimated transmission by a novel color ellipsoid prior to statistically fitting haze color pixel clusters. Berman et al. [] proposed a robust optimization scheme based on the previous haze-line model, which can achieve faster and better dehazing effects. Wang et al. [] proposed a fast algorithm to solve the linear assumption model based on dark channel. Zhu et al. [] offered a pixel-wise fusion weight map to guide multi-exposure image fusion, which improves the performance and robustness of dehazing. Han et al. [] proposed a muti-scale guided filtering method. Their method could dehaze well by fusing dehazing layer and detail enhancement layer at two scales. Li et al. [] used bright and dark channel priors for dehazing the segmented sky and non-sky regions separately and proposed a weighting method to fuse the parameters. Such methods are simple and easy to implement, but still suffer with the problems of easy distortion of image color, aggravation of shadow degree, and difficulty in parameter setting.
Data-driven methods are based on large datasets and try to learn the mapping of hazy-clear image pairs [,,,]. Li et al. [] pioneered a direct image dehazing network, which is designed using a re-formulated Equation (1) to learn the model parameters jointly. Li et al. [] presented a conditional GAN including an autoencoder structure for better dehazing. Qu et al. [] gave an enhanced Pix2pix dehazing network using a GAN to reconstruct a clear image and an enhancer to improve the reconstructing effect. Li et al. [] presented a multi-stage hybrid dehazing network using the autoencoder and RNN structure. Chen et al. [] defined a pixel-wise patch map to enhance DCP and presented a bi-attentive GAN to learn the patch map adaptively. Zhao et al. [] proposed a novel dehazing framework that fuses DCP and GAN. Their framework can be trained on unpaired datasets to improve the restoring visibility and result’s realness. Compared to the methods based on paired synthetic datasets, Chen et al. [,] proposed two unpaired dehazing methods with PDR-GAN and MO-GAN, which also achieved good results. Song et al. [] introduced the Swin Transformer and designed an improved multiple variants of DehazeFormer for dehazing, which earned a superior effect. Such methods are capable of removing opaque clouds (completely occluding ground objects) in RSIs, but have the following problems: (1) increasingly complex neural networks are used to improve the dehazing effect without considering the resource occupation. (2) in satellite remote sensing systems, it is infeasible to obtain multiple real-world training image pairs of the same location at once. Due to the forementioned issues, the focus of the paper study is on the prior-based single image dehazing method.
Researchers have proposed various methods to address the problem of optical RSI dehazing in recent years. Sun et al. [] presented a cloud removal network, which first used the RNN to segment cloud regions. They then used the autoencoder to reconstruct cloud-free RSI. Li et al. [] presented a first-coarse-then-fine network, which first extracts coarse features using autoencoder, and then, extracts detailed features using a subnet. Chen et al. [] presented a hybrid high-resolution learning framework to achieve single RSI dehazing with fine spatial details. Ding et al. [] proposed an extended image formation model and divided RSI dehazing into scene depth fusion and adaptive color constancy. Wen et al. [] presented a Wasserstein GAN-based thin cloud removal network, which effectively reduces both exposure and dark region. Chen et al. [] gave a memory-oriented GAN for recording haze distribution patterns of single RSI dehazing in an unpaired manner. Bie et al. [] proposed an RSI dehazing network including feature extraction based on a global attention mechanism and autoencoder with a Gaussian process. Zhou et al. [] presented a distortion coding and composite loss-based GAN, which can effectively remove thick clouds, as well as thin clouds.
3. Robust Light-Dark Prior
The proposed shadowing model and hybrid model of optical RSI are explored in detail with the semitransparent cloud as an example. Then, the RLDP and corresponding parameter estimation method is presented.
3.1. Haze Hybrid Model
The process of original atmosphere scattering model [] is shown in Figure 1a. As shown in Equation (1), the actual light that reaches the satellite camera consists of two components: direct attenuation and airlight. Direct attenuation is the light reflected from ground object that passes through the cloud and is attenuated by the cloud [], while airlight is the light reflected from the cloud particles to the satellite camera.
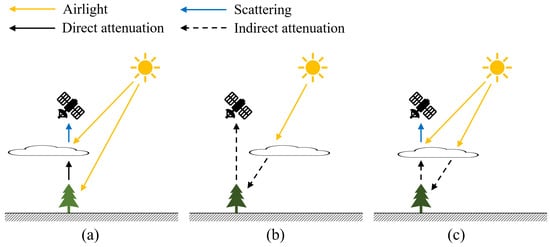
Figure 1.
The physical model of three different atmosphere scattering models. (a) Original atmosphere scattering model. (b) Shadowing model. (c) Haze hybrid model.
The shadow of the semitransparent cloud deepened the color of ground objects captured by the satellite camera, as shown in Figure 1b. Such findings could be attributed to the actual light received by the satellite camera being the indirect attenuation reflected after being attenuated by the cloud. The main differences between Figure 1a,b are: first, the cloud is suspended between the ground object and the camera in the atmosphere scattering model, while the cloud is suspended between the airlight and object in the shadowing model. Second, the cloud particles reflect airlight into the camera in the atmosphere scattering model, while the cloud particles form shadow on the ground object in the shadowing model. Thus, the proposed shadowing model can be expressed as follows:
where represents the observed haze-free but shadowing image, denotes the shadow-free image to be recovered, and is the shadow transmission map, with , , and being the atmospheric scattering parameter, the cloud transparency and bias, respectively. There are two differences between Equation (16) and Equation (1): first, the cloud particles do not reflect light into the camera, and, therefore, do not superimpose airlight; second, the bias is introduced, indicating that the transparency of cloud at x is bias from the position of cloud, being mainly related to the height of cloud and the angle of airlight.
A more complex haze hybrid model, as shown in Figure 1c, is the final target. In the model, the cloud is suspended between the airlight and the ground object. It is also between the ground object and the satellite camera. The light emanates from the source, attenuates for the first time when passing through the cloud, and then attenuates for the second time when reflected by the object passing through the cloud. The light entering the camera consists of the indirect-direct attenuated light and the airlight. Indirect attenuated light represents the light that passes through the clouds twice. As such, the proposed hybrid model can be expressed as follows:
In Equation (3), , A, and are all unknown; so, restoring the original image from Equation (3) seems more difficult. However, the restoration of the original image can be decomposed into two steps: haze removal and shadow removal. In the haze removal stage, any existing dehazing method can be used to estimate the dehazing parameters, such as DCP [] and CEP []. In the shadow removal stage, a shadow transmission estimating method based on the assumption of RLCP is presented.
3.2. Robust Light-Dark Prior
The initial prior-based method can be described as selecting a prior vector close to 0 or very low from the pixels in local patches. Recent methods enhance this prior, such as dark channel prior [], color-lines [], haze-lines [], and color ellipsoid prior []. Symmetrically, the initial light channel prior (LCP) can be calculated as follows:
where denotes a color channel c of image S at a pixel j and is a local patch centered at i. If we directly solve for the global maximum, it is vulnerable to outlier pixels; we equivalently convert Equation (4) as follows:
As the vectors from shadowing image signals are more dense and normally distributed, it is assumed that the pixel values of each channel in obey Gaussian distribution i.e.,
where
mean:
variance:
Based on the criterion of general Gaussian distribution [], the probability of data within exceeds . Therefore, to exclude the interference of outlier pixel values in the local patches and improve the robustness of the algorithm, we set the maximum value of the patch to , i.e.,
Similarly, we improve the dark channel prior using the criterion, and the proposed robust dark channel prior (RDCP) is formed as follows:
Our final robust light-dark prior (RLDP) is based on RLCP and RDCP while satisfying both observations and . The former is based on the observation that at least one color channel has some pixels whose intensity is very high and close to the minimum of channel maximums in most RGB patches.
3.3. Haze Removal Based on RLDP
Robust atmospheric light estimation: Atmospheric light is usually estimated by the brightest pixels (most haze-opaque pixels), but is easily confused by bright ground objects (especially glaciers, snow, etc.) in RSIs. To address this issue, we use the criterion when estimating A and use the top pixel max of the robust dark channel. The robust atmospheric light estimation method is as follows:
Referring to [], the robust transmission map can be estimated as follows:
where is a constant parameter used to bring the estimation of t closer to the RLCP observation. The value of can be determined by the specific application and can be empirically set to 0.95 in this paper.
Robust shadow transmission map estimation: RLCP satisfies the observation and Equations (8) and (16); thus,
In Figure 2, a pseudo-color composite image of Landsat 8 is shown on the right side. The red box marks a glacier patch (special ground object), and its statistical distribution is depicted in the lower left corner. The green box marks an additional patch, and its statistical distribution is depicted in the upper left corner. The g, b channel values of the glacier patch are too high and do not meet the RLDP assumption. Therefore, to eliminate the confusion of glaciers, we take the minimum of the maximum of three channels (). It can also be seen from the statistics that there are some outliers far from most of the pixels in the two patches. We can eliminate the interference of these outliers through the criterion when calculating the RLDP.
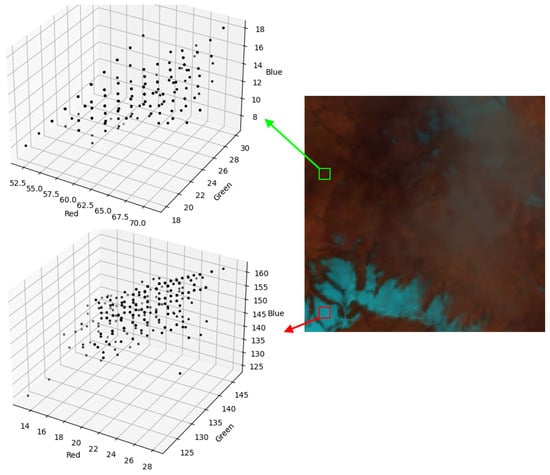
Figure 2.
Statistical color constructions of ground and glacier patches.
Therefore, the shadow transmission map can be estimated as follows:
where is a constant used to bring the estimation of s closer to the RLDP observation. Parameter s can usually be determined by the specific application. Otherwise, it can be determined by the component of the shadow vector, which is the robust average dark channel of the brightest area:
The fast RLDP implementation of the pseudocode is shown in Algorithm 1. This algorithm first assesses the global atmospheric light A by Equations (10) and (15), and then, estimates the and of each pixel i by Equations (12) and (14). Finally, the image dehazing is completed through two stages: recovering the haze-free image J and restoring shadow-free image I.
| Algorithm 1 RLDP-based dehazing method. |
Input: Haze and shadow image S, Patch size Output: Clear image S
|
3.4. CRME-Based Appropriate Patch Size Search Criterion
As with other priori-based methods, the proposed RLDP requires a pre-set parameter of patch size . As shown in Figure 3, a hazy RSI is shown on the left, and two sets of RLDP dehazing results with different patch sizes (using six patch size values at intervals between 1 and 120) are shown on the right. The upper set (green box) is the dehazing result of the less hazy area, while the lower set (red box) is the dehazing result of the dense hazy area. When setting the patch size to be too small, the image contrast is too high and the color is distorted after dehazing. Instead, when setting the patch size to be too large, the details become blurred and the dehazing effect becomes poor. Moreover, areas in one RSI with different hazy degrees are affected to varying degrees according to the patch size setting. Therefore, determining how to set a global patch size or a local adaptive patch size is an urgent problem.

Figure 3.
A hazy RSI and its 2 sets of RLDP dehazing resluts with different patch size (using 6 patch size values at intervals between 1 and 120) in different areas. The upper set is the dehazing result of the less hazy area and the lower set is the dehazing result of the dense hazy area.
To solve the patch size setting problem, most of the priori-based methods are set a fixed value based on historical experience to avoid a patch size that is too high or too low. In recent years, several adaptive approaches have been proposed. Chen et al. [] designed a CNN-based patch size selection model, which can adaptively and automatically select the patch size corresponding to each pixel. Chen et al. [] defined a pixel-wise patch map and presented a bi-attentive GAN for adaptively learning it by minimizing the error function for each pixel. By analyzing the test results on 50 hazy images, Hong et al. [] set the patch size to the value when the contrast metric tended to be maximum.
In order to find an appropriate patch size, there is a trade-off in contrast. Inspired by [], a high Color/Cube RME (CRME), which is an index that measures the relative difference of the patch center and all the neighbors in the patch, indicates a high image contrast. Unlike [], a stable CRME formula was proposed to search for an appropriate patch size in the shortest possible time. Appropriate patch size () is defined as the search step (where patch size is monotonically increased from 20 to 120) when CRME reaches a stable state for the first time.
where is a tiny constant (fixed to 0.001 in this paper) used to measure the stable state of CRME. Generally, the larger value, the easier it is to reach a stable state, corresponding to a smaller patch size, and vice versa, corresponding to a larger patch size.
4. Experiments
4.1. Experimental Setup
Quantitative experiments were conducted on an open-source: Remote sensing Image Cloud rEmoving dataset 1 (RICE1) [], which included 108 alpine images, 118 flat images, 110 sandy images, 54 mountainous images, and 110 sea images. Overall, RICE1 contained 500 semitransparent cloud and clear RSI pairs collected from Google Earth, all of which were 512 × 512 in size. Subsequently, several 652-band pseudo-color composite images of Landsat 8 images were selected. The study area is a plateau high-altitude area located at row 138, column 37, containing large glaciers. All experiments were performed on an Intel(R) Core (TM) i7-11700 @ 2.50 GHz and 32.0 GB RAM hardware environment with Python 3.9.
In order to quantitatively verify the dehazing performance of RLDP on RSI pairs, three image quality evaluation indicators, peak signal to noise ratio (PSNR), structural similarity (SSIM), and Commission Internationale de l’Eclairage difference evaluation 2000 (CIEDE2000) were used to evaluate the image quality. PSNR measures the quality of image dehazing, with higher values indicating lower distortion and better results. SSIM measures the similarity between the dehazed image and clear image in terms of brightness, contrast and structure. The closer the value is to 1, the more similar and the better results. Compared with the above two indicators, CIEDE2000 is more in line with subjective visual perception, and the lower the value, the smaller the color difference.
We empirically fixed the shadow parameter at 100 and patch size at , which is computed adaptively for each image by the proposed CRME-based appropriate patch size search criterion. Eventually, we compared the dehazing effect of RLDP with DCP 2010 [], CL 2014 [], CEP 2017 [], HL 2018 [], CEEF-TMM 2021 [], UNTV 2021 [], and ACT 2022 [].
4.2. Quantitative Evaluations
As shown in Table 1, the average SSIMs on flat, sandy, mountainous, and overall images of the proposed RLDP exceeded other comparison methods, demonstrating that RLDP could perform better dehazing in terms of brightness, contrast, and structure. The average PSNRs on flat, sandy, and overall images of the proposed RLDP exceeded other comparison methods, emanating that there is less distortion in recovered images using RLDP. The average CIEDE2000 of the proposed method wins on alpine, flat, sandy, sea, and overall, indicating that RLDP restores images with higher color quality. RLDP is less effective on alpine and sea, due to the color distribution of the images being narrow. This does not meet the observation of the robust prior, resulting in low and brighter restored images. Such issues can be remedied by combining a threshold with other methods.

Table 1.
Average SSIM/PSNR/CIEDE2000 on specific RICE1 RSIs.
4.3. Qualitative Evaluations
Figure 4 and Figure 5 show the dehazing effect on five benchmark RSIs and six Landsat 8 images (to show the details more clearly, the images were cropped to the size of 512 × 512). The DCP and CEEF-TMM could remove semitransparent clouds well, but the recovered images were dark overall. The CL could better restore the original color, but the dehazing effect on some images is poor, particularly for the second images. The CEP had the optimal dehazing effect, but made the image significantly distorted, with the bright areas exposed and the dark areas darkened. The images recovered by the HL had better visibility, but serious exposure could be seen. The UNTV is mainly used for underwater image dehazing, and the color distortion was serious during the present RSI image dehazing. The ACT worked better on the fourth image, ’Sea’, but there were slight exposure and color deviation problems in other images. The proposed RLDP method can inherit a better dehazing effect of DCP and can solve the problem that the DCP method makes images darker. In addition, RLDP can make the details clearer in cloud shadow and dark regions of the images. Despite such advantages, the inhomogeneous fog removal effect still needs to be improved due to the bias in the parameter estimation, especially in the atmospheric light estimation (as shown in the fifth and eighth images).

Figure 4.
Visual comparisons on benchmark RSIs. (a) Cloud image. (b) Clear image. (c) DCP. (d) CL. (e) CEP. (f) HL. (g) CEEF-TMM. (h) UNTV. (i) ACT. (j) RLDP.

Figure 5.
Visual comparisons on real-world RSIs. (a) Cloud image. (b) DCP. (c) CL. (d) CEP. (e) HL. (f) CEEF-TMM. (g) UNTV. (h) ACT. (i) RLDP.
The aforementioned experiments show that RLDP can solve the problem of dark region aggravation of existing dehazing methods and can reduce the shadow caused by semitransparent cloud. RLDP is able to increase the visibility of the details in cloud shadow and dark region, and can therefore achieve a better image dehazing quality.
5. Conclusions
In this paper, an RLDP-based method for single RSI dehazing was proposed. The proposed hybrid model is utilized to estimate parameters, the criterion is used to improve robustness, and the appropriate patch size search criterion is adopted to improve adaptability. RLDP assumes that the robust dark channel prior or the robust light channel prior is satisfied in most RGB patches. The results of qualitative and quantitative experiments demonstrate the better performance of RLDP. The prior-based approaches become ineffective in the presence of opaque clouds, and thus, further efforts will be made in future research to apply deep learning methods and study complex scenes with the coexistence of semitransparent clouds, opaque clouds, and shadow.
Author Contributions
Conceptualization, J.N.; Methodology, J.N.; Software, Y.Z.; Validation, B.D.; Supervision, B.D.; Project administration, B.D.; Funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported partially by the Sichuan Science and Technology Program (No. 22ZDYF2836, 2022YFQ0017).
Acknowledgments
The authors wish to thank the anonymous reviewers for their thorough review and highly appreciate their useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Després, V.; Huffman, J.A.; Burrows, S.M.; Hoose, C.; Safatov, A.; Buryak, G.; Elbert, W.; Andreae, M.O.; Pöschl, U.; Jaenicke, R.; et al. Primary biological aerosol particles in the atmosphere: A review. Tellus B Chem. Phys. Meteorol. 2012, 64, 15598. [Google Scholar] [CrossRef]
- Han, J.; Zhang, S.; Fan, N.; Ye, Z. Local Patchwise Minimal and Maximal Values Prior for Single Optical Remote Sensing Image Dehazing. Inf. Sci. 2022, 606, 173–193. [Google Scholar] [CrossRef]
- Qin, X.; Wang, Z.; Bai, Y.; Xie, X.; Jia, H. FFA-Net: Feature fusion attention network for single image dehazing. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 11908–11915. [Google Scholar]
- Fu, M.; Liu, H.; Yu, Y.; Chen, J.; Wang, K. DW-GAN: A Discrete Wavelet Transform GAN for NonHomogeneous Dehazing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 203–212. [Google Scholar]
- Liu, Q.; Gao, X.; He, L.; Lu, W. Single image dehazing with depth-aware non-local total variation regularization. IEEE Trans. Image Process. 2018, 27, 5178–5191. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar] [PubMed]
- Salazar-Colores, S.; Cabal-Yepez, E.; Ramos-Arreguin, J.M.; Botella, G.; Ledesma-Carrillo, L.M.; Ledesma, S. A fast image dehazing algorithm using morphological reconstruction. IEEE Trans. Image Process. 2018, 28, 2357–2366. [Google Scholar] [CrossRef]
- Nishino, K.; Kratz, L.; Lombardi, S. Bayesian defogging. Int. J. Comput. Vis. 2012, 98, 263–278. [Google Scholar] [CrossRef]
- Berman, D.; Avidan, S. Non-local image dehazing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1674–1682. [Google Scholar]
- Bui, T.M.; Kim, W. Single image dehazing using color ellipsoid prior. IEEE Trans. Image Process. 2017, 27, 999–1009. [Google Scholar] [CrossRef]
- Berman, D.; Treibitz, T.; Avidan, S. Single image dehazing using haze-lines. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 720–734. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, X.; Wu, X.; Liu, Y. Fast image dehazing method based on linear transformation. IEEE Trans. Multimed. 2017, 19, 1142–1155. [Google Scholar] [CrossRef]
- Zhu, Z.; Wei, H.; Hu, G.; Li, Y.; Qi, G.; Mazur, N. A novel fast single image dehazing algorithm based on artificial multiexposure image fusion. IEEE Trans. Instrum. Meas. 2020, 70, 1–23. [Google Scholar] [CrossRef]
- Han, Y.; Yin, M.; Duan, P.; Ghamisi, P. Edge-preserving filtering-based dehazing for remote sensing images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Li, C.; Yuan, C.; Pan, H.; Yang, Y.; Wang, Z.; Zhou, H.; Xiong, H. Single-Image Dehazing Based on Improved Bright Channel Prior and Dark Channel Prior. Electronics 2023, 12, 299. [Google Scholar] [CrossRef]
- Ullah, H.; Muhammad, K.; Irfan, M.; Anwar, S.; Sajjad, M.; Imran, A.S.; de Albuquerque, V.H.C. Light-DehazeNet: A Novel Lightweight CNN Architecture for Single Image Dehazing. IEEE Trans. Image Process. 2021, 30, 8968–8982. [Google Scholar] [CrossRef]
- Jia, T.; Li, J.; Zhuo, L.; Li, G. Effective Meta-Attention Dehazing Networks for Vision-Based Outdoor Industrial Systems. IEEE Trans. Ind. Inform. 2021, 18, 1511–1520. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, H.; Fu, M.; Chen, J.; Wang, X.; Wang, K. A two-branch neural network for non-homogeneous dehazing via ensemble learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 193–202. [Google Scholar]
- Kan, S.; Zhang, Y.; Zhang, F.; Cen, Y. A GAN-based input-size flexibility model for single image dehazing. Signal Process. Image Commun. 2022, 102, 116599. [Google Scholar] [CrossRef]
- Li, B.; Peng, X.; Wang, Z.; Xu, J.; Feng, D. Aod-net: All-in-one dehazing network. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4770–4778. [Google Scholar]
- Li, R.; Pan, J.; Li, Z.; Tang, J. Single image dehazing via conditional generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8202–8211. [Google Scholar]
- Qu, Y.; Chen, Y.; Huang, J.; Xie, Y. Enhanced pix2pix dehazing network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 8160–8168. [Google Scholar]
- Li, R.; Pan, J.; He, M.; Li, Z.; Tang, J. Task-oriented network for image dehazing. IEEE Trans. Image Process. 2020, 29, 6523–6534. [Google Scholar] [CrossRef]
- Chen, W.T.; Fang, H.Y.; Ding, J.J.; Kuo, S.Y. PMHLD: Patch map-based hybrid learning DehazeNet for single image haze removal. IEEE Trans. Image Process. 2020, 29, 6773–6788. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Shen, Y.; Zhou, Y. RefineDNet: A weakly supervised refinement framework for single image dehazing. IEEE Trans. Image Process. 2021, 30, 3391–3404. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Kong, C.; Dai, L. Unpaired Image Dehazing With Physical-Guided Restoration and Depth-Guided Refinement. IEEE Signal Process. Lett. 2022, 29, 587–591. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Y. Memory-Oriented Unpaired Learning for Single Remote Sensing Image Dehazing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Song, Y.; He, Z.; Qian, H.; Du, X. Vision Transformers for Single Image Dehazing. arXiv 2022, arXiv:2204.03883. [Google Scholar]
- Sun, L.; Zhang, Y.; Chang, X.; Wang, Y.; Xu, J. Cloud-aware generative network: Removing cloud from optical remote sensing images. IEEE Geosci. Remote Sens. Lett. 2019, 17, 691–695. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X. A coarse-to-fine two-stage attentive network for haze removal of remote sensing images. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1751–1755. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Dai, L.; Kong, C. Hybrid high-resolution learning for single remote sensing satellite image Dehazing. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Y.; Fu, X. An Image Dehazing Approach with Adaptive Color Constancy for Poor Visible Conditions. IEEE Geosci. Remote Sens. Lett. 2021, 19. [Google Scholar] [CrossRef]
- Wen, X.; Pan, Z.; Hu, Y.; Liu, J. Generative adversarial learning in YUV color space for thin cloud removal on satellite imagery. Remote Sens. 2021, 13, 1079. [Google Scholar] [CrossRef]
- Bie, Y.; Yang, S.; Huang, Y. Single Remote Sensing Image Dehazing using Gaussian and Physics-Guided Process. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhou, J.; Luo, X.; Rong, W.; Xu, H. Cloud Removal for Optical Remote Sensing Imagery Using Distortion Coding Network Combined with Compound Loss Functions. Remote Sens. 2022, 14, 3452. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, D.; Yan, Y.; Kwong, S.; Chen, J.; Duan, L.Y. IDeRs: Iterative dehazing method for single remote sensing image. Inf. Sci. 2019, 489, 50–62. [Google Scholar] [CrossRef]
- Guo, X.; Yang, Y.; Wang, C.; Ma, J. Image dehazing via enhancement, restoration, and fusion: A survey. Inf. Fusion 2022, 86, 146–170. [Google Scholar] [CrossRef]
- Fattal, R. Dehazing using color-lines. ACM Trans. Graph. (TOG) 2014, 34, 1–14. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Chen, W.T.; Ding, J.J.; Kuo, S.Y. PMS-net: Robust haze removal based on patch map for single images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11681–11689. [Google Scholar]
- Hong, S.; Kang, M.G. Single image dehazing based on pixel-wise transmission estimation with estimated radiance patches. Neurocomputing 2022, 492, 545–560. [Google Scholar] [CrossRef]
- Lin, D.; Xu, G.; Wang, X.; Wang, Y.; Sun, X.; Fu, K. A remote sensing image dataset for cloud removal. arXiv 2019, arXiv:1901.00600. [Google Scholar]
- Liu, X.; Li, H.; Zhu, C. Joint contrast enhancement and exposure fusion for real-world image dehazing. IEEE Trans. Multimed. 2021, 24, 3934–3946. [Google Scholar] [CrossRef]
- Xie, J.; Hou, G.; Wang, G.; Pan, Z. A variational framework for underwater image dehazing and deblurring. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 3514–3526. [Google Scholar] [CrossRef]
- Kumar, B.P.; Kumar, A.; Pandey, R. Region-based adaptive single image dehazing, detail enhancement and pre-processing using auto-colour transfer method. Signal Process. Image Commun. 2022, 100, 116532. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).