Estimation of Geopotential Value W0 for the Geoid and Local Vertical Datum Parameters
Abstract
:1. Introduction
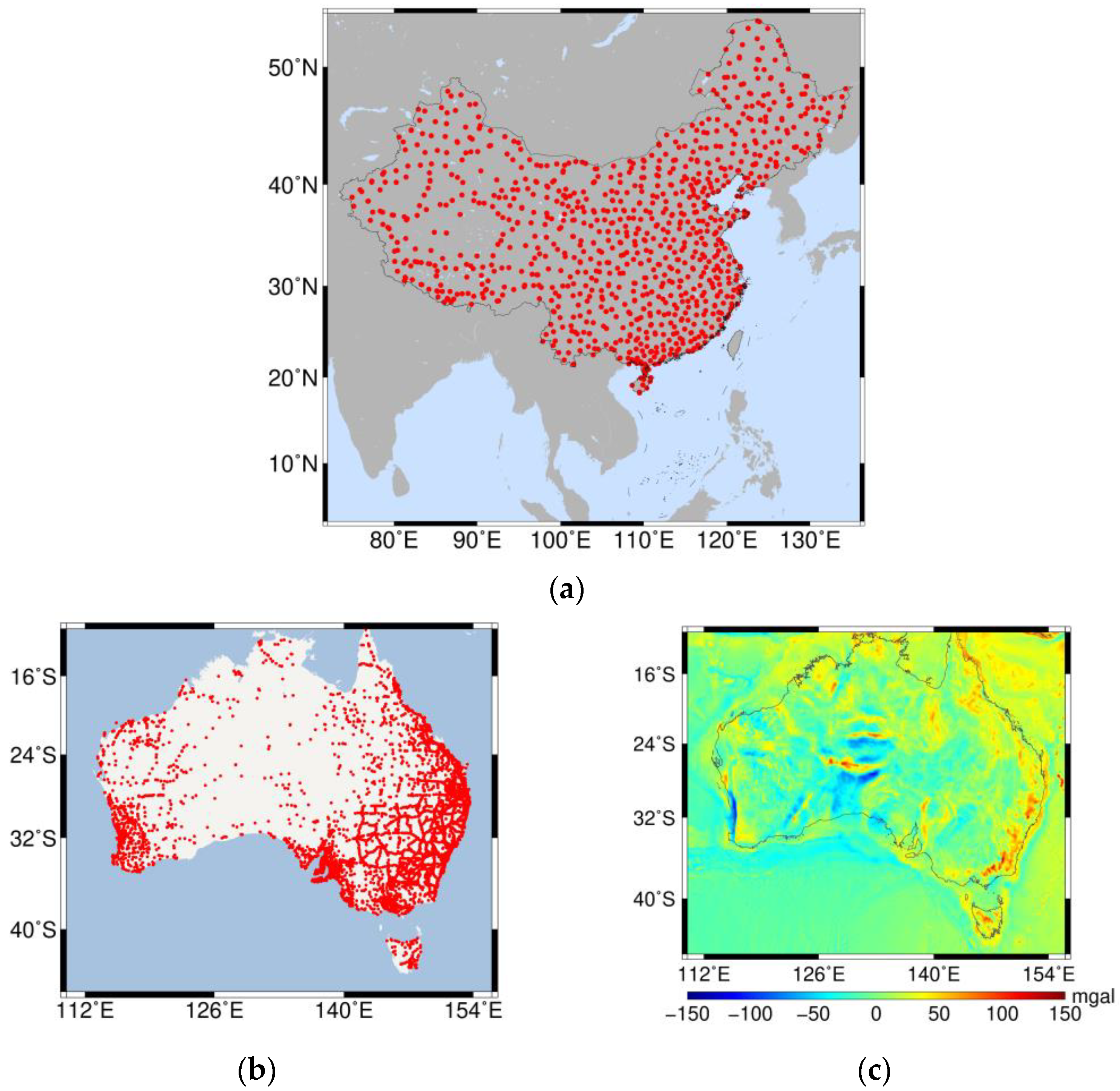
2. Data Sources
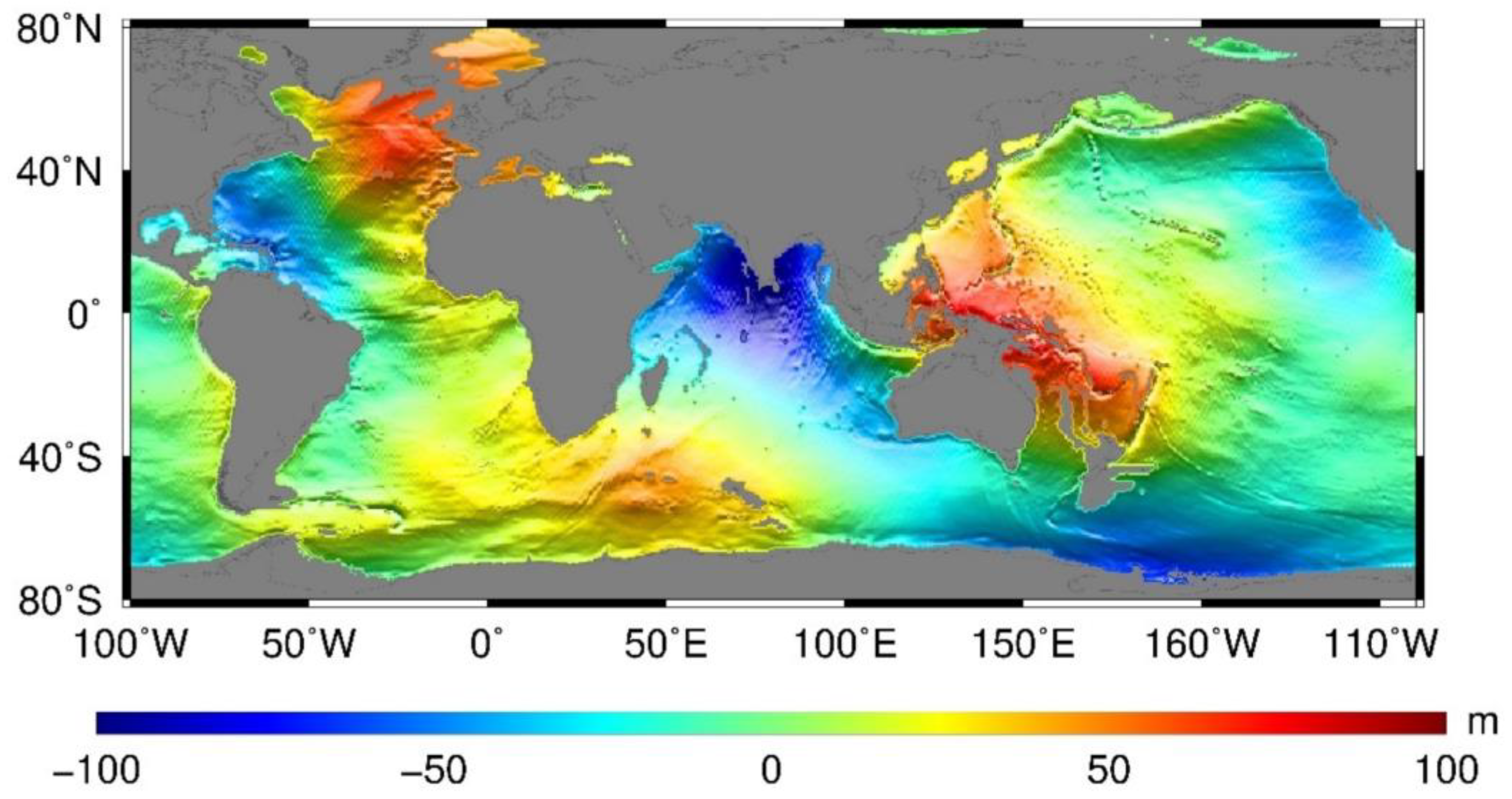
2.1. Satellite Altimetry Data
2.2. GNSS/Leveling Data
2.3. Gravity Data
3. Methods
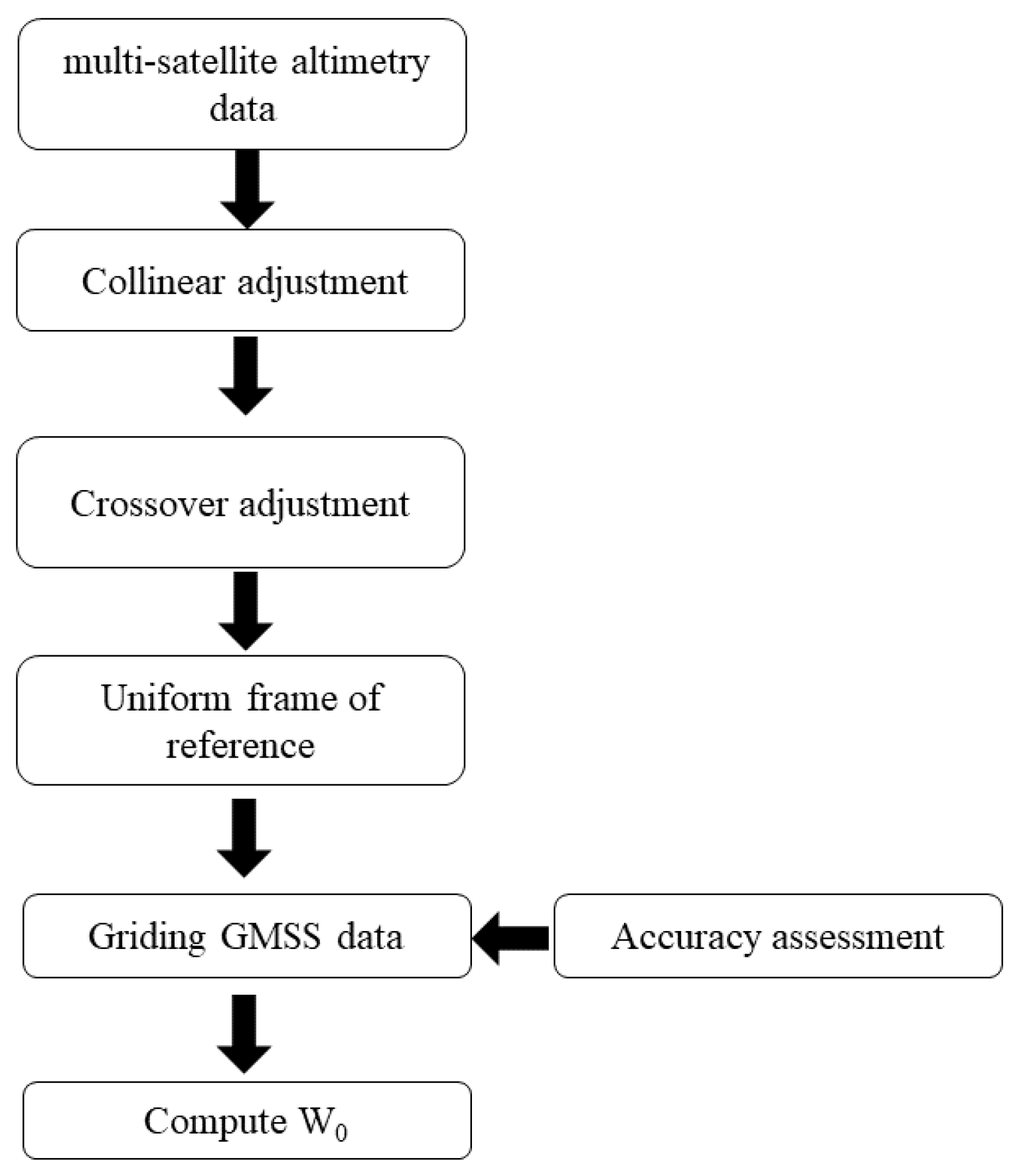
3.1. Adjustment Approaches for Altimetry Satellite Data and the Approach to Calculate W0
3.1.1. The Collinear Adjustment Approach
3.1.2. The Crossover Adjustment Approach
3.1.3. The Uniform Reference Frame Approach
3.1.4. Direct Determination of W0 from MSS Data and the GGM
3.2. Approaches for the Unification of the Global Vertical Datum
3.2.1. The Geopotential Difference Approach
3.2.2. The Geodetic Boundary Value Problem Approach
3.2.3. Adjustment Method for Systematic Error
4. Results
4.1. Determination of W0 Based on the Altimetry Data
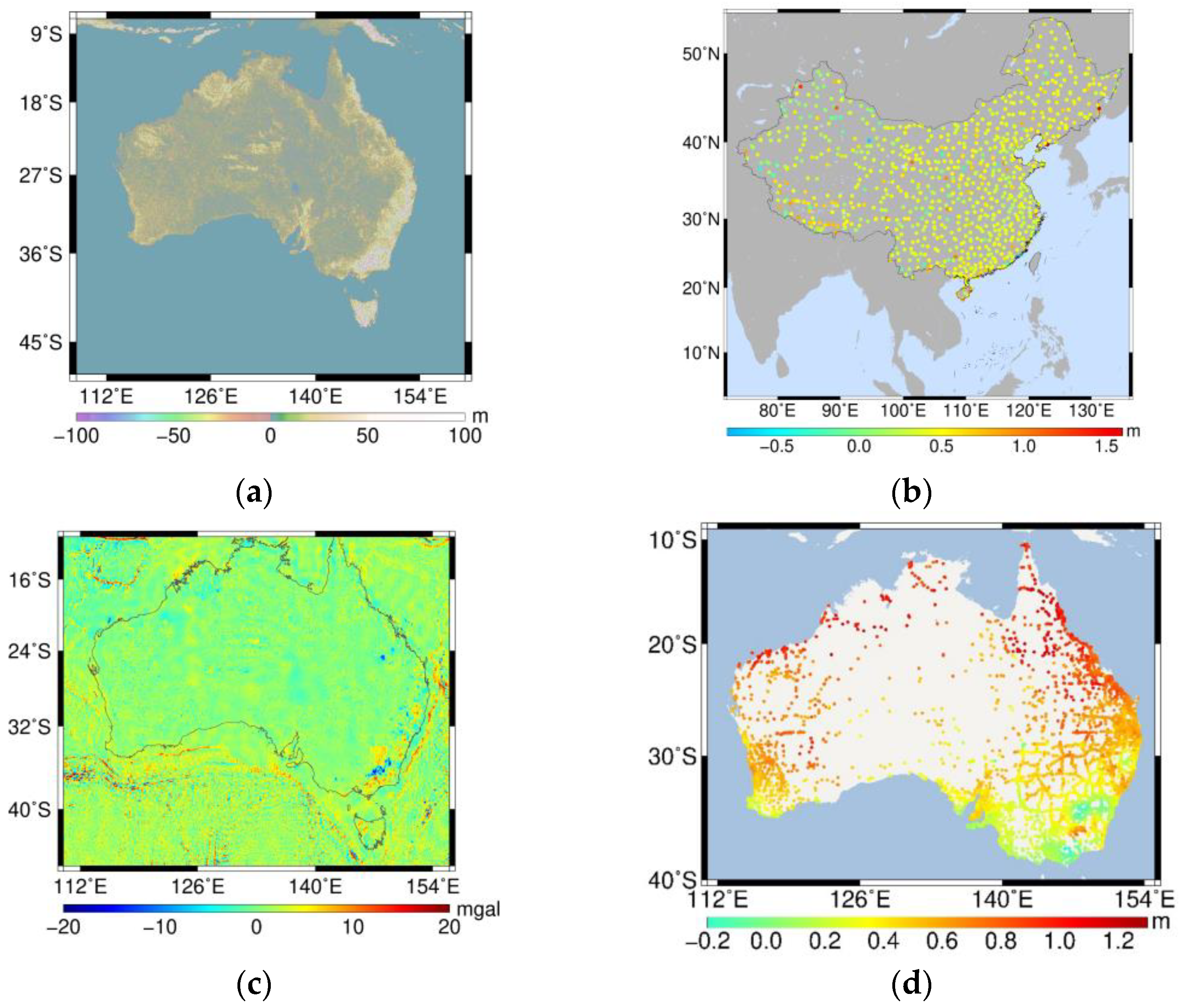
4.2. Determination of the Chinese Height Datum Parameters Based on the Geopotential Difference Approach
4.3. Determination of the Australian Height Datum Parameters Based on the Geodetic Boundary Value Problem Approach
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayden, T. Geopotential of the Geoid-Based North American Vertical Datum. Master’s Thesis, Graduate Studies, University of Calgary, Calgary, AB, Canada, 2013. [Google Scholar]
- Zhang, C. The role of global vertical benchmarks in global change research. Geosci. Front. 2002, 9, 393–400. [Google Scholar]
- Zhang, L.; Li, F.; Chen, W.; Zhang, C. Height datum unification between Shenzhen and Hong Kong using the solution of the linearized fixed-gravimetric boundary value problem. J. Geod. 2009, 83, 411–417. [Google Scholar] [CrossRef]
- Li, J.; Chu, Y.; Xu, X. Determination of regional and global elevation datum differences. J. Surv. Mapp. 2017, 46, 12. [Google Scholar]
- Meyer, T.H.; Roman, D.R.; Zilkoski, D.B. What does height really mean? Part III: Height Systems. Surv. Land Inf. Sci. 2006, 66, 149–160. [Google Scholar]
- Gauss, C.F. Bestimmung des Breitenunterschiedes Zwischen den Sternwarten von Göttingen und Altona: Durch Beobachtungen am Ramsdenschen Zenithsector; Bei Vandenhoeck und Ruprecht: Göttingen, Germany, 1828. [Google Scholar]
- Chen, J.; Tapley, B.; Save, H.; Tamisiea, M.E.; Bettadpur, S.; Ries, J. Quantification of ocean mass change using gravity recovery and climate experiment, satellite altimeter, and Argo floats observations. J. Geophys. Res. Solid Earth 2018, 123, 10,212–10,215. [Google Scholar] [CrossRef]
- Sánchez, L.; Čunderlík, R.; Mikula, K.; Minarechová, Z.; Dayoub, N.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. A conventional value for the geoid reference potential W0. In Proceedings of the Unified Analysis Workshop, Paris, France, 10–12 July 2017. [Google Scholar]
- Sanchez, L. Definition and realisation of the SIRGAS vertical reference system within a globally unified height system. In Proceedings of the Dynamic Planet, Cairns, Australia, 22–26 August 2005; pp. 638–645. [Google Scholar]
- Amin, H.; Sjöberg, L.E.; Bagherbandi, M. A global vertical datum defined by the conventional geoid potential and the Earth ellipsoid parameters. J. Geod. 2019, 93, 1943–1961. [Google Scholar] [CrossRef]
- Yuan, J.; Guo, J.; Zhu, C.; Li, Z.; Liu, X.; Gao, J. SDUST2020 MSS: A global 1′ × 1′ mean sea surface model determined from multi-satellite altimetry data. Earth Syst. Sci. Data Discuss. 2022, 15, 155–169. [Google Scholar] [CrossRef]
- Schaeffer, P.; Faugére, Y.; Legeais, J.; Ollivier, A.; Guinle, T.; Picot, N. The CNES_CLS11 global mean sea surface computed from 16 years of satellite altimeter data. Mar. Geod. 2012, 35, 3–19. [Google Scholar] [CrossRef]
- Jin, T.; Li, J.; Jiang, W. The global mean sea surface model WHU2013. Geod. Geodyn. 2016, 7, 202–209. [Google Scholar] [CrossRef]
- Chu, Y.; Li, J. Combine the global gravity field model and the sea surface height model to determine the mean sea surface position constant. Geod. Geodyn. 2012, 32, 5. [Google Scholar]
- Dayoub, N.; Edwards, S.J.; Moore, P. The Gauss–Listing geopotential value W0 and its rate from altimetric mean sea level and GRACE. J. Geod. 2012, 86, 681–694. [Google Scholar] [CrossRef]
- Yuan, J.; Guo, J.; Liu, X.; Zhu, C.; Niu, Y.; Li, Z.; Ji, B.; Ouyang, Y. Mean sea surface model over China seas and its adjacent ocean established with the 19-year moving average method from multi-satellite altimeter data. Cont. Shelf Res. 2020, 192, 104009. [Google Scholar] [CrossRef]
- Burša, M.; Kenyon, S.; Kouba, J.; Raděj, K.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. Dimension of the Earth’s general ellipsoid. Earth Moon Planets 2002, 91, 31–41. [Google Scholar] [CrossRef]
- Bao, L.; Peng, G.; Peng, H.; Jia, Y.; Qi, G. First accuracy assessment of the HY-2A altimeter sea surface height observations: Cross-calibration results. Adv. Space Res. 2015, 55, 90–105. [Google Scholar] [CrossRef]
- Beckley, B.D.; Zelensky, N.P.; Holmes, S.A.; Holmes, S.A. Assessment of the Jason-2 extension to the TOPEX/Poseidon, Jason-1 sea-surface height time series for global mean sea level monitoring. Mar. Geod. 2010, 33, 447–471. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Zhang, J.; Cui, W. Global data quality assessment based on Jason-3 satellite altimeter alignment with Jason-2 data. Acta Oceanol. Sin. 2020, 42, 11. [Google Scholar]
- Andersen, O.; Knudsen, P.; Stenseng, L. A new DTU18 MSS mean sea surface–Improvement from SAR altimetry. In Proceedings of the 25 Years of Progress in Radar Altimetry Symposium, Ponta Delgada, Portugal, 24–29 September 2018. [Google Scholar]
- CNES. Along-Track Level-2+ (L2P) SLA Product Handbook. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_L2P_all_missions_except_S3.pdf (accessed on 25 November 2022).
- Ebadi, A.; Ardalan, A.A.; Karimi, R. The Iranian height datum offset from the GBVP solution and spirit-leveling/gravimetry data. J. Geod. 2019, 93, 1207–1225. [Google Scholar] [CrossRef]
- Gerlach, C.; Rummel, R. Global height system unification with GOCE: A simulation study on the indirect bias term in the GBVP approach. J. Geod. 2013, 87, 57–67. [Google Scholar] [CrossRef]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S.; Bui, L.K.; Balmino, G. Determination of the geopotential value on the permanent GNSS stations in Vietnam based on the Geodetic Boundary Value Problem approach. Geophys. J. Int. 2021, 226, 1206–1219. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Yuan, J.; Guo, J.; Zhu, C.; Hwang, C.; Yu, D.; Sun, M.; Mu, D. High-resolution sea level change around China seas revealed through multi-satellite altimeter data. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102433. [Google Scholar] [CrossRef]
- Sanchez, B.V.; Pavlis, N.K. Estimation of main tidal constituents from TOPEX altimetry using a Proudman function expansion. J. Geophys. Res. Ocean. 1995, 100, 25229–25248. [Google Scholar] [CrossRef]
- Huang, M.; Wang, R.; Chai, G.; Ouyang, Y. Multi-generation satellite altimetry data combined adjustment and gravity field inversion. J. Wuhan Univ. (Inf. Sci. Ed.) 2007, 11, 988–993. [Google Scholar]
- Wagner, C.A. Radial variations of a satellite orbit due to gravitational errors: Implications for satellite altimetry. J. Geophys. Res. Solid Earth 1985, 90, 3027–3036. [Google Scholar] [CrossRef]
- Rummel, R. Principle of satellite altimetry and elimination of radial orbit errors. In Satellite Altimetry in Geodesy and Oceanography; Rummel, R., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 190–241. [Google Scholar]
- Jin, T.; Li, J.; Xing, L.; Chu, Y. Unified study of multi-source satellite altimetry data benchmark. Geod. Geodyn. 2008, 28, 5. [Google Scholar]
- Zhang, P.; Bao, L.; Guo, D.; Wu, L.; Li, Q.; Liu, H.; Xue, Z.; Li, Z. Estimation of vertical datum parameters using the GBVP approach based on the combined global geopotential models. Remote Sens. 2020, 12, 4137. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. Corrections to “The gravitational potential and its derivatives for the prism”. J. Geod. 2002, 76, 475. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Hirt, C.; Featherstone, W.; Marti, U. Combining EGM2008 and SRTM/DTM2006. 0 residual terrain model data to improve quasigeoid computations in mountainous areas devoid of gravity data. J. Geod. 2010, 84, 557–567. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Z.; Bao, L.; Zhang, P.; Wang, Y.; Wu, L.; Wang, Y. The Refined Gravity Field Models for Height System Unification in China. Remote Sens. 2022, 14, 1437. [Google Scholar] [CrossRef]
- Beckley, B.D.; Zelensky, N.P.; Luthcke, S.B.; Luthcke, S.B. Towards a seamless transition from TOPEX/Poseidon to Jason-1. Mar. Geod. 2004, 27, 373–389. [Google Scholar] [CrossRef]
- Sánchez, L.; Čunderlík, R.; Dayoub, N.; Mikula, K.; Minarechová, Z.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. A conventional value for the geoid reference potential W0. J. Geod. 2016, 90, 815–835. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS 2010 conventions. In IERS Technical Note; Bundesamt für Kartographie und Geodäasie: Frankfurt, Germany, 2010; p. 179. [Google Scholar]
- Čunderlík, R.; Mikula, K. Numerical solution of the fixed altimetry-gravimetry BVP using the direct BEM formulation. In the Observing Our Changing Earth; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 133, pp. 229–236. [Google Scholar]
- Burša, M.; Kenyon, S.; Kouba, J.; Šíma, Z.; Vatrt, V.; Vítek, V.; Vojtíšková, M. The geopotential value W 0 for specifying the relativistic atomic time scale and a global vertical reference system. J. Geod. 2007, 81, 103–110. [Google Scholar] [CrossRef]
- Burša, M.; Kouba, J.; Raděj, K.; True, S.A.; Vatrt, V.; Vojtíšková, M. Monitoring geoidal potential on the basis of TOPEX/POSEIDON altimeter data and EGM96. In Geodesy on the Move; Springer: Berlin/Heidelberg, Germany, 1998; pp. 352–358. [Google Scholar]
- Rapp, R. Equatorial radius estimates from Topex altimeter data. In Festschrift to E; Groten, M., Becker, G., Hein, R.R., Eds.; Institute of Geodesy and Navigation, Univ. FAF: Munich, Germany, 1995. [Google Scholar]
| Mission | Timespan | Cycles |
|---|---|---|
| T/P | 1 October 1997~15 January 2002 | 186~343 |
| Jason-1 | 15 January 2002~26 January 2009 | 1~259 |
| Jason-2 | 26 January 2009~2 October 2016 | 21~303 |
| Jason-3 | 2 October 2016~10 August 2020 | 24~165 |
| T/P Interleaved | 14 August 2004~16 August 2005 | 439~475 |
| ERS-2 | 3 June 1996~15 September 2003 | 12~88 |
| Envisat | 11 July 2005~5 July 2010 | 39~90 |
| HY-2A | 12 April 2014~27 February 2016 | 67~115 |
| GFO | 4 August 2004~10 August 2008 | 135~220 |
| Mission | Before Collinear Adjustment | After Collinear Adjustment | ||
|---|---|---|---|---|
| Mean (m) | STD (m) | Mean (m) | STD (m) | |
| T/P, Jason-1, Jason-2, Jason-3 | −0.0005 | 0.1031 | −0.00018 | 0.0173 |
| ERS-2 | 0.0004 | 0.1442 | 0.0001 | 0.0384 |
| Envisat | 0.0013 | 0.1312 | −0.0005 | 0.0420 |
| T/P Interleaved | −0.0018 | 0.1188 | 0.0004 | 0.0284 |
| GFO | 0.0026 | 0.1285 | 0.0018 | 0.0315 |
| HY-2A | −0.0030 | 0.1745 | 0.0025 | 0.0378 |
| Mission | Before Crossover Adjustment | After Crossover Adjustment | ||
|---|---|---|---|---|
| Mean (m) | STD (m) | Mean (m) | STD (m) | |
| T/P, Jason-1, Jason-2, Jason-3 | −0.00018 | 0.0173 | 0.000002 | 0.0002 |
| ERS-2 | 0.0001 | 0.0384 | 0.000013 | 0.0013 |
| Envisat | −0.0005 | 0.0420 | 0.000017 | 0.0024 |
| T/P Interleaved | 0.0004 | 0.0284 | −0.000038 | 0.0008 |
| GFO | 0.0018 | 0.0315 | 0.000047 | 0.0010 |
| HY-2A | 0.0025 | 0.0378 | −0.00007 | 0.0004 |
| ERS-2 | −0.0402 | 0.0229 | 0.0628 | 55.14 |
| Envisat | −0.0128 | −0.0267 | 0.0013 | −18.15 |
| T/P Interleaved | −0.0753 | −0.0214 | −0.0452 | −16.96 |
| GFO | −0.0538 | 0.0621 | 0.0772 | −16.17 |
| HY-2A | 0.0345 | 0.0015 | −0.0005 | −2.16 |
| MSS Model | Mean (m) | STD (m) |
|---|---|---|
| CSL15 | −0.1202 | 0.0611 |
| DTU18 | −0.1139 | 0.0605 |
| SDUST2020 | −0.1555 | 0.0608 |
| MSS Data | GGM Model | W0 (m2s−2) | |
|---|---|---|---|
| This study | GMSS data | EIGEN-6C4 | 62,636,856.8200 |
| Sánchez et al. (2016) [39] | DTU10 | EGM2008 | 62,636,853.4000 |
| Chu et al. (2012) [14] | CNES_CLS10, CLS01, WHU2009, DNSC08 | EGM2008 EGM96 | 62,636,858.3333 |
| Dayoub et al. (2012) [15] | DNSC08 | EGM2008 | 62,636,854.2000 |
| IERS Standards. (2010) [40] | / | / | 62,636,856.0000 |
| Čunderlík et al. (2009) [41] | CLS01 | EIGEN-GC03 | 62,636,857.9500 |
| Sánchez et al. (2007) [9] | KMS04 | EGM96 | 62,636,854.4000 |
| Bursa et al. (2007) [42] | T/P | EGM96 | 62,636,854.6000 |
| Bursa et al. (1998) [43] | T/P (1993~1996) | EGM96 | 62,636,855.6100 |
| Rapp et al. (1995) [44] | T/P | / | 62,636,856.8800 |
| Offset | East–West Tilt (m/°) | North–South Tilt (m/°) | |
|---|---|---|---|
| CHD | 0.3939 | 0.0019 | −0.0019 |
| AHD | 0.4885 | −0.0005 | 0.0388 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, S.; Yuan, J.; Fan, D.; Tan, X. Estimation of Geopotential Value W0 for the Geoid and Local Vertical Datum Parameters. Remote Sens. 2023, 15, 912. https://doi.org/10.3390/rs15040912
Liu X, Li S, Yuan J, Fan D, Tan X. Estimation of Geopotential Value W0 for the Geoid and Local Vertical Datum Parameters. Remote Sensing. 2023; 15(4):912. https://doi.org/10.3390/rs15040912
Chicago/Turabian StyleLiu, Xinyu, Shanshan Li, Jiajia Yuan, Diao Fan, and Xuli Tan. 2023. "Estimation of Geopotential Value W0 for the Geoid and Local Vertical Datum Parameters" Remote Sensing 15, no. 4: 912. https://doi.org/10.3390/rs15040912
APA StyleLiu, X., Li, S., Yuan, J., Fan, D., & Tan, X. (2023). Estimation of Geopotential Value W0 for the Geoid and Local Vertical Datum Parameters. Remote Sensing, 15(4), 912. https://doi.org/10.3390/rs15040912








