PSSA: PCA-Domain Superpixelwise Singular Spectral Analysis for Unsupervised Hyperspectral Image Classification
Abstract
1. Introduction
2. Related Works
2.1. Notation
2.2. Superpixel Image Segmentation
2.3. Brief of the 2D-SSA
2.4. The Anchor-Based Graph Clustering (AGC)
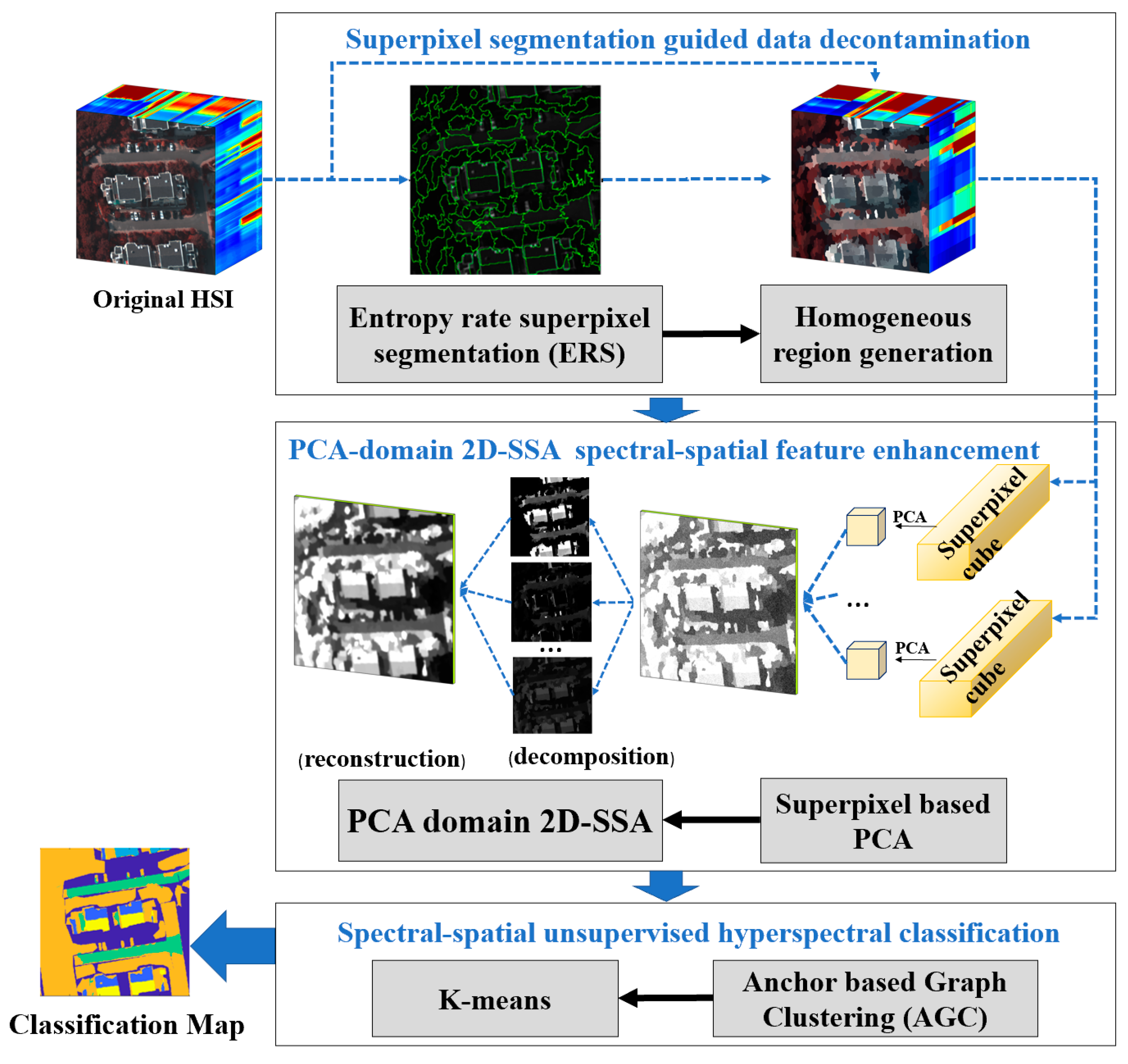
3. The Proposed Algorithm
3.1. Superpixel Segmentation Guided Data Decontamination
3.2. PCA-Domain 2D-SSA Spectral-Spatial Feature Enhancement
3.3. Spectral-Spatial Unsupervised HSI Classification
| Algorithm 1: Proposed unsupervised HSI classification |
| Input: Hyperspectral image datasets . Output: Indicator matrices and clustering result . Decontaminate to according to Equation (9); Input to data optimization with 2D-SSA for according Equations (11) and (12) Choose m samples in for AGC construction Calculate the matrix according to Ref. [27] while iterations do Update and with by and Update the indicator matrix according to Equation (7) End Input Y to the K-means to get the clustering result . |
4. Datasets and Experimental Settings
4.1. Introduction to the Datasets
4.2. Evaluation Metrics
4.3. Implementation Details
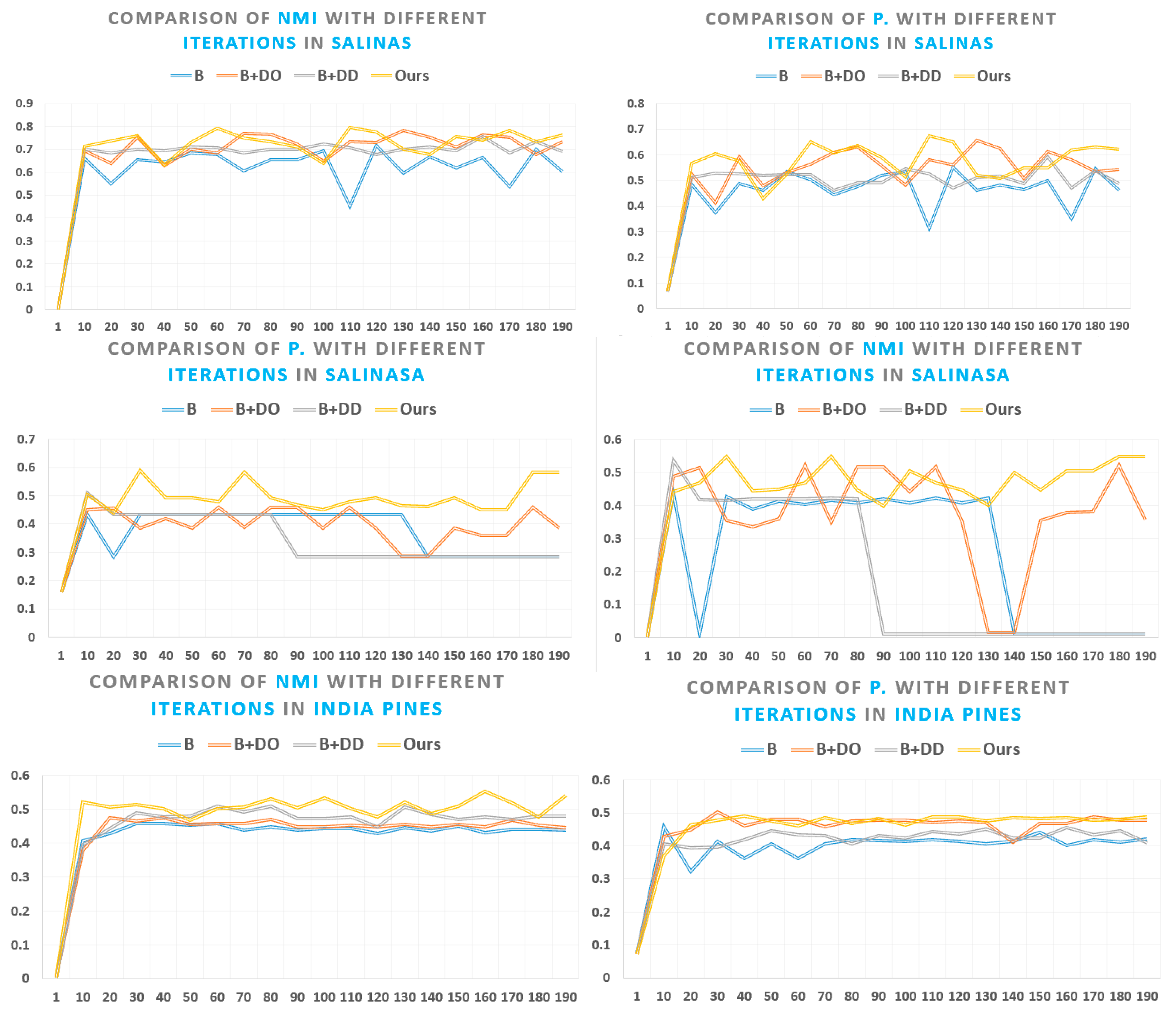
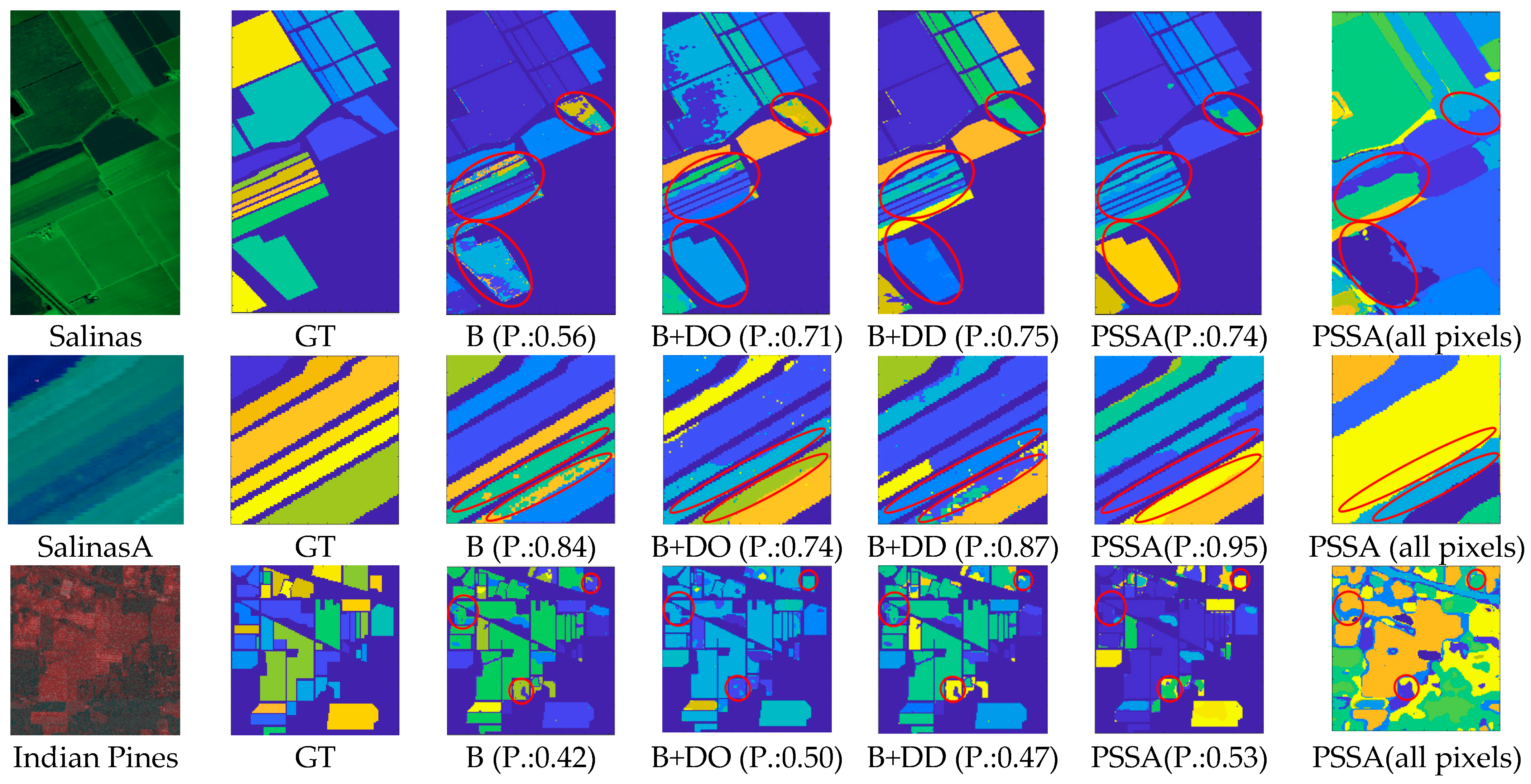
5. Experimental Results and Discussion
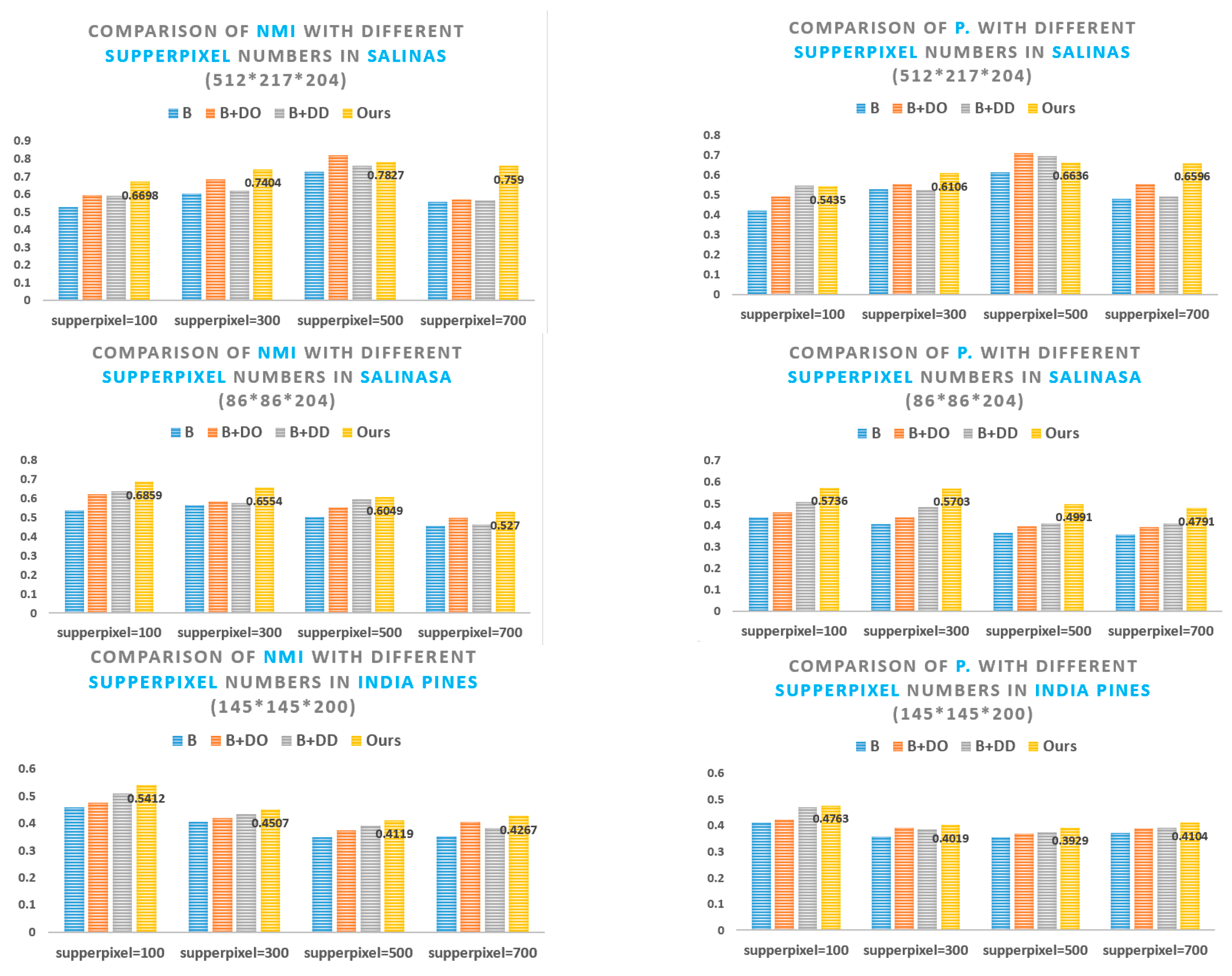
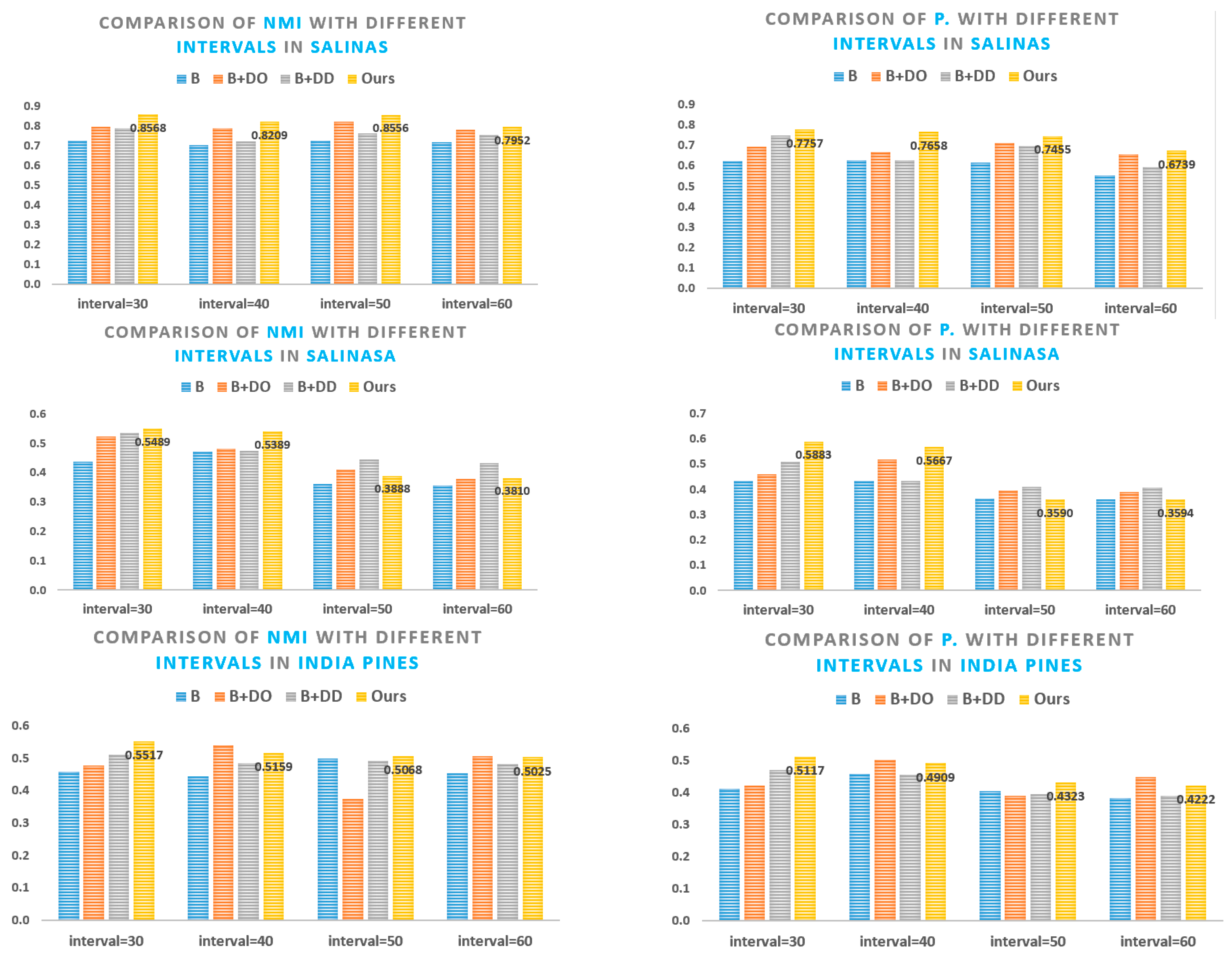
5.1. Superpixel Segmentation Analysis
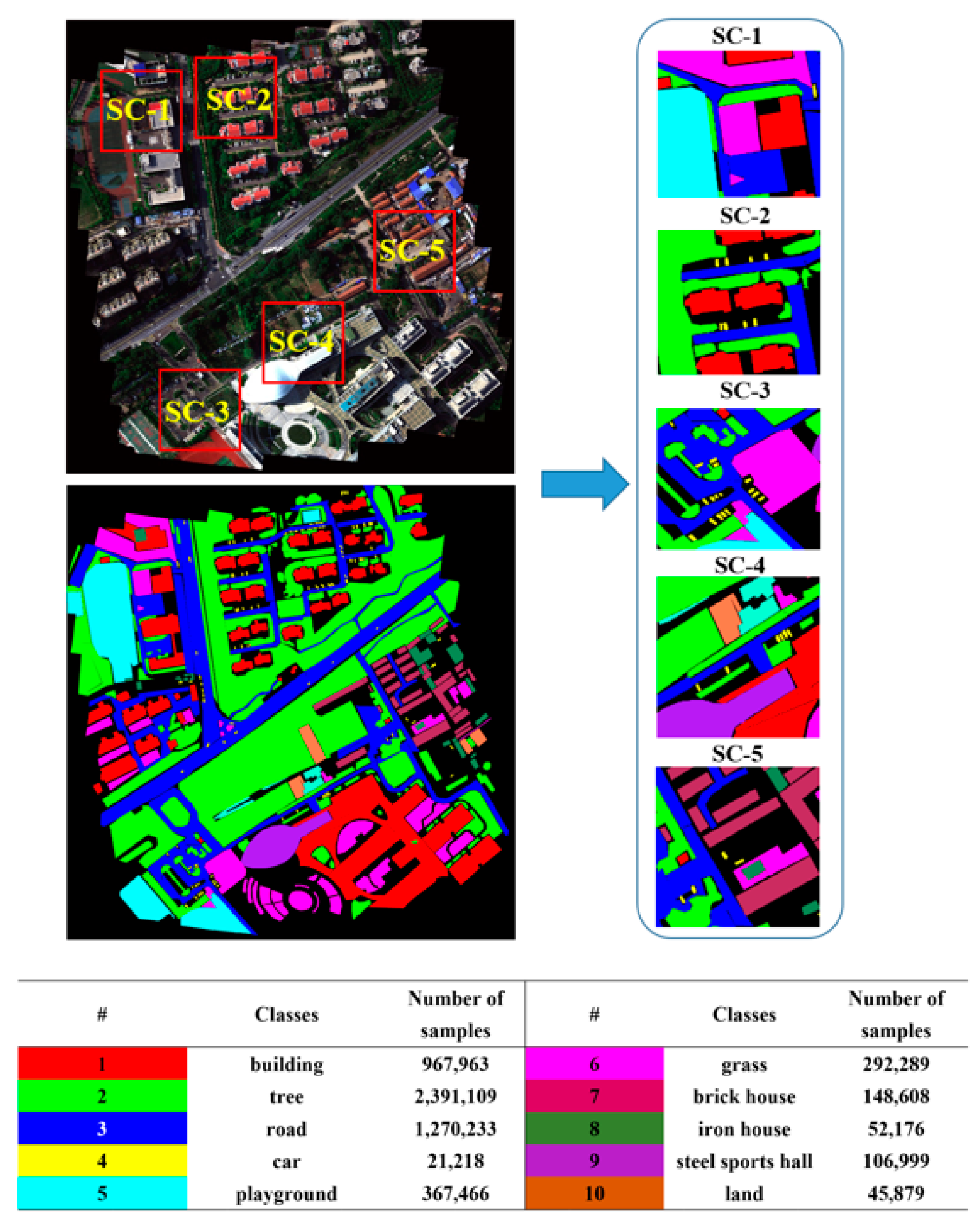
5.2. Experimental Results on the Self-Collected Dataset
5.3. Experimental Results on Publicly Available Datasets
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tiwari, K.; Arora, M.; Singh, D. An assessment of independent component analysis for detection of military targets from hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 730–740. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hyperspectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Magaz. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Jiao, Q.; Zhang, B.; Liu, J.; Liu, L. A novel two-step method for winter wheat-leaf chlorophyll content estimation using a hyperspectral vegetation index. Int. J. Remote Sens. 2014, 35, 7363–7375. [Google Scholar] [CrossRef]
- David, G.; David, B. Hyperspectral forest monitoring and imaging implications. In Spectral Imaging Sensor Technologies: Innovation Driving Advanced Application Capabilities; Spie-Int Soc Optical Engineering: Baltimore, MD, USA, 2014; Volume 9104, pp. 1–9. [Google Scholar]
- Xu, S.; Ren, J.; Lu, H.; Wang, X.; Sun, X.; Liang, X. Nondestructive detection and grading of flesh translucency in pineapples with visible and near-infrared spectroscopy. Postharvest Biol. Technol. 2022, 192, 112029. [Google Scholar] [CrossRef]
- Yan, Y.; Ren, J.; Zhao, H.; Windmill, J.F.C.; Ijomah, W.; de Wit, J.; von Freeden, J. Non-Destructive Testing of Composite Fiber Materials with Hyperspectral Imaging—Evaluative Studies in the EU H2020 FibreEUse Project. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Ge, X.; Ding, J.; Jin, X.; Wang, J.; Chen, X.; Li, X.; Liu, J.; Xie, B. Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sens. 2021, 13, 1562. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of Spectral—Temporal Response Surfaces by Combining Multispectral Satellite and Hyperspectral UAV Imagery for Precision Agriculture Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Tang, J.; García-Haro, F.J.; Suomalainen, J.; Kooistra, L. Combining hyperspectral UAV and multispectral Formosat-2 imagery for precision agriculture applications. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 24–27 June 2014; pp. 1–4. [Google Scholar]
- Zhang, H.; Zhai, H.; Zhang, L.; Li, P. Spectral–Spatial Sparse Subspace Clustering for Hyperspectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3672–3684. [Google Scholar] [CrossRef]
- Nemhauser, G.L.; Wolsey, L.A.; Fisher, M.L. Ananalysis of the approximations for maximizing submodular set functions. Math. Program. 1978, 14, 265–294. [Google Scholar] [CrossRef]
- Wang, R.; Nie, F.; Yu, W. Fast Spectral Clustering with Anchor Graph for Large Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2003–2007. [Google Scholar] [CrossRef]
- Xu, J.; Fowler, J.E.; Xiao, L. Hypergraph-Regularized Low-Rank Subspace Clustering Using Superpixels for Unsupervised Spatial–Spectral Hyperspectral Classification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 871–875. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy K-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 2012, 15, 580–585. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B.; You, J.; Tao, D. Hyperspectral image unsupervised classification by robust manifold matrix factorization. Inf. Sci. 2019, 485, 154–169. [Google Scholar] [CrossRef]
- Sun, G.; Fu, H.; Ren, J.; Zhang, A.; Zabalza, J.; Jia, X.; Zhao, H. SpaSSA: Superpixelwise Adaptive SSA for Unsupervised Spatial–Spectral Feature Extraction in Hyperspectral Image. IEEE Trans. Cybern. 2022, 52, 6158–6169. [Google Scholar] [CrossRef] [PubMed]
- Hinojosa, C.; Vera, E.; Arguello, H. A Fast and Accurate Similarity-Constrained Subspace Clustering Algorithm for Hyperspectral Image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10773–10783. [Google Scholar] [CrossRef]
- Yue, J.; Fang, L.; Rahmani, H.; Ghamisi, P. Self-Supervised Learning with Adaptive Distillation for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501813. [Google Scholar] [CrossRef]
- Zhu, M.; Fan, J.; Yang, Q.; Chen, T. SC-EADNet: A Self-Supervised Contrastive Efficient Asymmetric Dilated Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Anindya, I.C.; Kantarcioglu, M. Adversarial anomaly detection using centroid-based clustering. In Proceedings of the 2018 IEEE International Conference on Information Reuse and Integration (IRI), Lake City, UT, USA, 6–9 July 2018; pp. 1–8. [Google Scholar]
- Zhong, Y.; Zhang, L.; Huang, B.; Li, P. An unsupervised artificial immune classifier for multi/hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 420–431. [Google Scholar] [CrossRef]
- Chen, W.-Y.; Song, Y.; Bai, H.; Lin, C.-J.; Chang, E.Y. Parallel Spectral Clustering in Distributed Systems. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 568–586. [Google Scholar] [CrossRef]
- Nie, F.; Wang, X.; Jordan, M.; Huang, H. The constrained Laplacian rank algorithm for graph-based clustering. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 12–17. [Google Scholar]
- Yang, T.-N.; Lee, C.-J.; Yen, S.-J. Fuzzy objective functions for robust pattern recognition. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju Island, Republic of Korea, 20–24 August 2009; pp. 2057–2062. [Google Scholar]
- Zhong, Y.; Zhang, L.; Gong, W. Unsupervised remote sensing image classification using an artificial immune network. Int. J. Remote Sens. 2011, 32, 5461–5483. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, S.; Zhang, L. Automatic Fuzzy Clustering Based on Adaptive Multi-Objective Differential Evolution for Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2290–2301. [Google Scholar] [CrossRef]
- Zhang, L.; You, J. A spectral clustering based method for hyperspectral urban image. In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, United Arab Emirates, 6–8 March 2017; pp. 1–3. [Google Scholar]
- Zhao, Y.; Yuan, Y.; Nie, F.; Wang, Q. Spectral clustering based on iterative optimization for large-scale and high-dimensional data. Neurocomputing 2018, 318, 227–235. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, Z.; Nie, F.; Li, X. Spectral Embedded Adaptive Neighbors Clustering. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 1265–1271. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Yuan, Y.; Wang, Q. Fast Spectral Clustering for Unsupervised Hyperspectral Image Classification. Remote Sens. 2019, 11, 399. [Google Scholar] [CrossRef]
- Tang, X.; Jiao, L.; Emery, W.J.; Liu, F.; Zhang, D. Two-Stage Reranking for Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5798–5817. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Bergh, M.V.D.; Boix, X.; Roig, G.; de Capitani, B.; Van Gool, L. SEEDS: Superpixels Extracted via Energy-Driven Sampling. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Li, Z.; Chen, J. Superpixel segmentation using linear spectral clustering. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1356–1363. [Google Scholar]
- Tang, Y.; Zhao, L.; Ren, L. Different Versions of Entropy Rate Superpixel Segmentation for Hyperspectral Image. In Proceedings of the International Conference on Signal and Image Processing, Wuxi, China, 19–21 July 2019; pp. 1050–1054. [Google Scholar]
- Zabalza, J.; Ren, J.; Zheng, J.; Han, J.; Zhao, H.; Li, S.; Marshall, S. Novel Two-Dimensional Singular Spectrum Analysis for Effective Feature Extraction and Data Classification in Hyperspectral Imaging. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4418–4433. [Google Scholar] [CrossRef]
- Fu, H.; Sun, G.; Ren, J.; Zhang, A.; Jia, X. Fusion of PCA and Segmented-PCA Domain Multiscale 2-D-SSA for Effective Spectral-Spatial Feature Extraction and Data Classification in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Ma, P.; Ren, J.; Zhao, H.; Sun, G.; Murray, P.; Zheng, J. Multiscale 2-D Singular Spectrum Analysis and Principal Component Analysis for Spatial–Spectral Noise-Robust Feature Extraction and Classification of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1233–1245. [Google Scholar] [CrossRef]
- Rodríguez-Aragón, L.J.; Zhigljavsky, A. Singular spectrum analysis for image processing. Stat. Its Interface 2010, 3, 419–426. [Google Scholar] [CrossRef]
- Türkmen, A.C. A review of nonnegative matrix factorization methods for clustering. Comput. Sci. 2015, 1, 405–408. [Google Scholar]
- Huang, Z.; Fang, L.; Li, S. Subpixel-Pixel-Superpixel Guided Fusion for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5998–6007. [Google Scholar] [CrossRef]
- Hyperspectral Remote Sensing Scenes. Available online: http://www.ehu.es/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes (accessed on 12 July 2021).
- Li, F.; Zhang, P.; Huchuan, L. Unsupervised Band Selection of Hyperspectral Images via Multi-Dictionary Sparse Representation. IEEE Access 2018, 6, 71632–71643. [Google Scholar] [CrossRef]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Xie, F.; Lei, C.; Jin, C.; An, N. A Novel Spectral–Spatial Classification Method for Hyperspectral Image at Superpixel Level. Appl. Sci. 2020, 10, 463. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2007, 2, 1–27. [Google Scholar] [CrossRef]

| weighted undirected graph | |
| Vertices | |
| Edges | |
| Subset of edges | |
| Binary map | |
| Trajectory matrix | |
| Pixels | |
| Eigenvalues | |
| Eigenvectors | |
| Cluster indicator matrix | |
| Cluster indicator | |
| Similarity matrix | |
| Laplacian matrix | |
| Hyperspectral image | |
| Superpixel |
| Indian Pines | SalinasA | Salinas | ||||
|---|---|---|---|---|---|---|
| NMI | P | NMI | P | NMI | P | |
| LSC | 0.574 | 0.497 | 0.773 | 0.705 | 0.691 | 0.672 |
| EEDS | 0.575 | 0.522 | 0.803 | 0.773 | 0.517 | 0.444 |
| SLIC | 0.524 | 0.507 | 0.867 | 0.851 | 0.736 | 0683 |
| ERS | 0.59 | 0.53 | 0.95 | 0.90 | 0.86 | 0.74 |
| Datasets | Metrics | Unsupervised | Supervised | ||||
|---|---|---|---|---|---|---|---|
| SC | NEC | AGC | PSSA | KNN | SVM | ||
| SC-1 | OA | NaN | 0.27 | 0.36 | 0.51 | 0.82 | 0.87 |
| AA | NaN | 0.17 | 0.31 | 0.49 | 0.57 | 0.88 | |
| Kappa | NaN | 0.10 | 0.21 | 0.39 | 0.77 | 0.83 | |
| NMI | NaN | 0.27 | 0.28 | 0.38 | - | - | |
| P. | NaN | 0.46 | 0.51 | 0.53 | - | - | |
| SC-2 | OA | NaN | 0.57 | 0.56 | 0.82 | 0.91 | 0.94 |
| AA | NaN | 0.46 | 0.43 | 0.72 | 0.58 | 0.86 | |
| Kappa | NaN | 0.38 | 0.36 | 0.70 | 0.86 | 0.90 | |
| NMI | NaN | 0.40 | 0.38 | 0.50 | - | - | |
| P. | NaN | 0.72 | 0.59 | 0.74 | - | - | |
| SC-3 | OA | NaN | 0.46 | 0.43 | 0.77 | 0.80 | 0.81 |
| AA | NaN | 0.31 | 0.32 | 0.61 | 0.53 | 0.84 | |
| Kappa | NaN | 0.33 | 0.26 | 0.67 | 0.76 | 0.82 | |
| NMI | NaN | 0.35 | 0.43 | 0.52 | - | - | |
| P. | NaN | 0.44 | 0.51 | 0.73 | - | - | |
| SC-4 | OA | NaN | 0.40 | 0.43 | 0.64 | 0.79 | 0.82 |
| AA | NaN | 0.28 | 0.30 | 0.48 | 0.50 | 0.74 | |
| Kappa | NaN | 0.27 | 0.33 | 0.57 | 0.67 | 0.76 | |
| NMI | NaN | 0.37 | 0.41 | 0.56 | - | - | |
| P. | NaN | 0.43 | 0.49 | 0.57 | - | - | |
| SC-5 | OA | NaN | 0.36 | 0.40 | 0.57 | 0.80 | 0.87 |
| AA | NaN | 0.15 | 0.35 | 0.48 | 0.49 | 0.80 | |
| Kappa | NaN | 0.10 | 0.26 | 0.44 | 0.72 | 0.81 | |
| NMI | NaN | 0.22 | 0.34 | 0.44 | - | - | |
| P. | NaN | 0.38 | 0.46 | 0.64 | - | - | |
| Datasets | Metrics | Unsupervised | Supervised | ||||
|---|---|---|---|---|---|---|---|
| SC | NEC | AGC | PSSA | KNN | SVM | ||
| Salinas | OA | NaN | 0.51 | 0.46 | 0.71 | 0.82 | 0.92 |
| AA | NaN | 0.46 | 0.42 | 0.63 | 0.84 | 0.96 | |
| Kappa | NaN | 0.46 | 0.44 | 0.67 | 0.80 | 0.91 | |
| NMI | NaN | 0.72 | 0.71 | 0.86 | - | - | |
| P. | NaN | 0.60 | 0.56 | 0.74 | - | - | |
| SalinasA | OA | 0.74 | 0.72 | 0.65 | 0.82 | 0.94 | 0.98 |
| AA | 0.72 | 0.69 | 0.61 | 0.84 | 0.81 | 0.98 | |
| Kappa | 0.68 | 0.65 | 0.56 | 0.77 | 0.94 | 0.98 | |
| NMI | 0.80 | 0.77 | 0.81 | 0.90 | - | - | |
| P. | 0.81 | 0.78 | 0.84 | 0.95 | - | - | |
| Indian Pines | OA | 0.40 | 0.37 | 0.42 | 0.49 | 0.52 | 0.73 |
| AA | 0.41 | 0.32 | 0.23 | 0.33 | 0.44 | 0.62 | |
| Kappa | 0.32 | 0.29 | 0.30 | 0.38 | 0.44 | 0.69 | |
| NMI | 0.44 | 0.45 | 0.46 | 0.59 | - | - | |
| P. | 0.36 | 0.43 | 0.42 | 0.53 | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Xue, D.; Tang, Y.; Zhao, Y.; Ren, J.; Sun, H. PSSA: PCA-Domain Superpixelwise Singular Spectral Analysis for Unsupervised Hyperspectral Image Classification. Remote Sens. 2023, 15, 890. https://doi.org/10.3390/rs15040890
Liu Q, Xue D, Tang Y, Zhao Y, Ren J, Sun H. PSSA: PCA-Domain Superpixelwise Singular Spectral Analysis for Unsupervised Hyperspectral Image Classification. Remote Sensing. 2023; 15(4):890. https://doi.org/10.3390/rs15040890
Chicago/Turabian StyleLiu, Qiaoyuan, Donglin Xue, Yanhui Tang, Yongxian Zhao, Jinchang Ren, and Haijiang Sun. 2023. "PSSA: PCA-Domain Superpixelwise Singular Spectral Analysis for Unsupervised Hyperspectral Image Classification" Remote Sensing 15, no. 4: 890. https://doi.org/10.3390/rs15040890
APA StyleLiu, Q., Xue, D., Tang, Y., Zhao, Y., Ren, J., & Sun, H. (2023). PSSA: PCA-Domain Superpixelwise Singular Spectral Analysis for Unsupervised Hyperspectral Image Classification. Remote Sensing, 15(4), 890. https://doi.org/10.3390/rs15040890









