Volcanic Cloud Detection and Retrieval Using Satellite Multisensor Observations
Abstract
1. Introduction
2. Methods
2.1. Satellite Data
2.2. Volcanic Cloud Detection
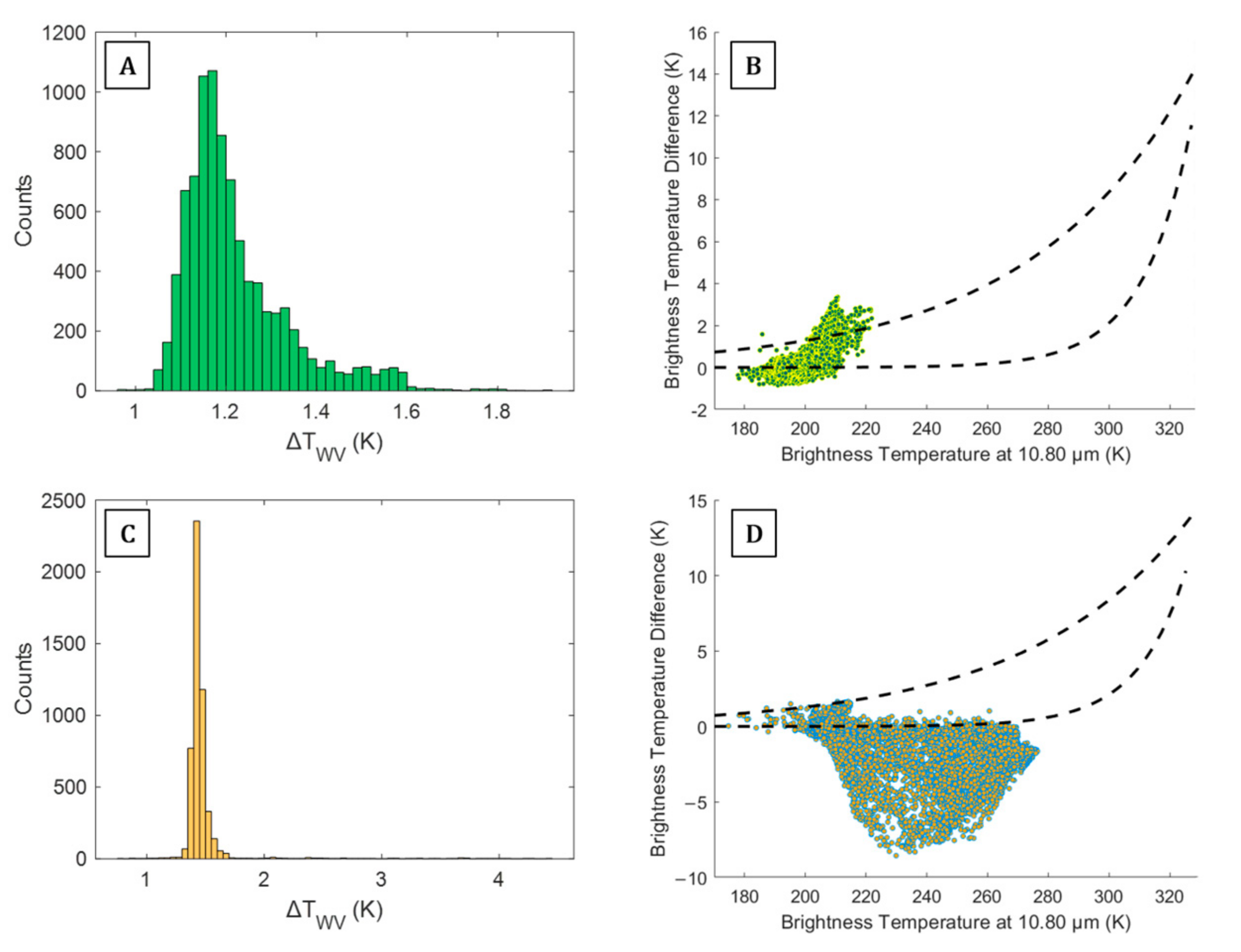
2.2.1. Multi-Spectral Brightness Temperature Difference
2.2.2. Random Forest Classification Technique
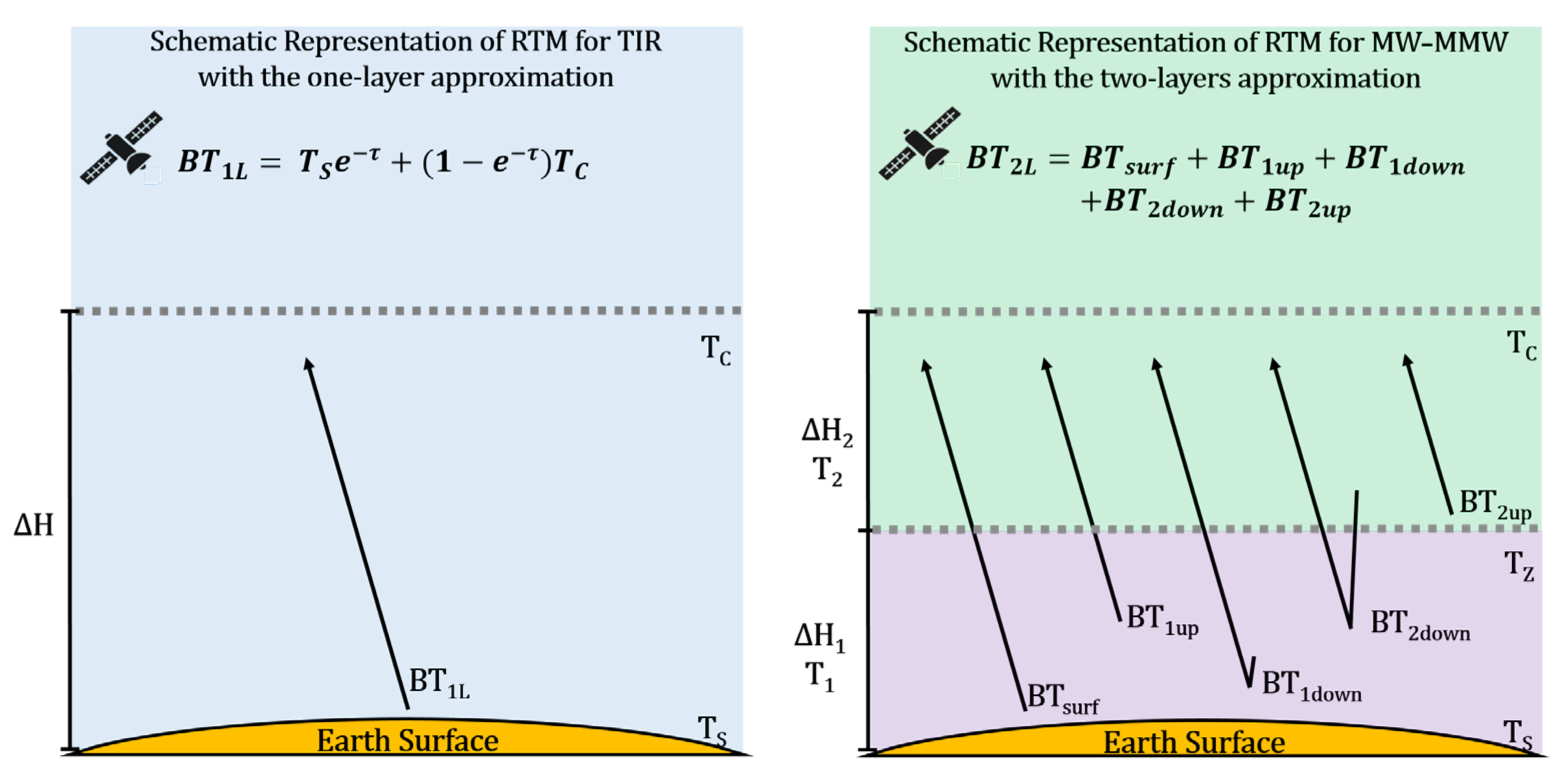
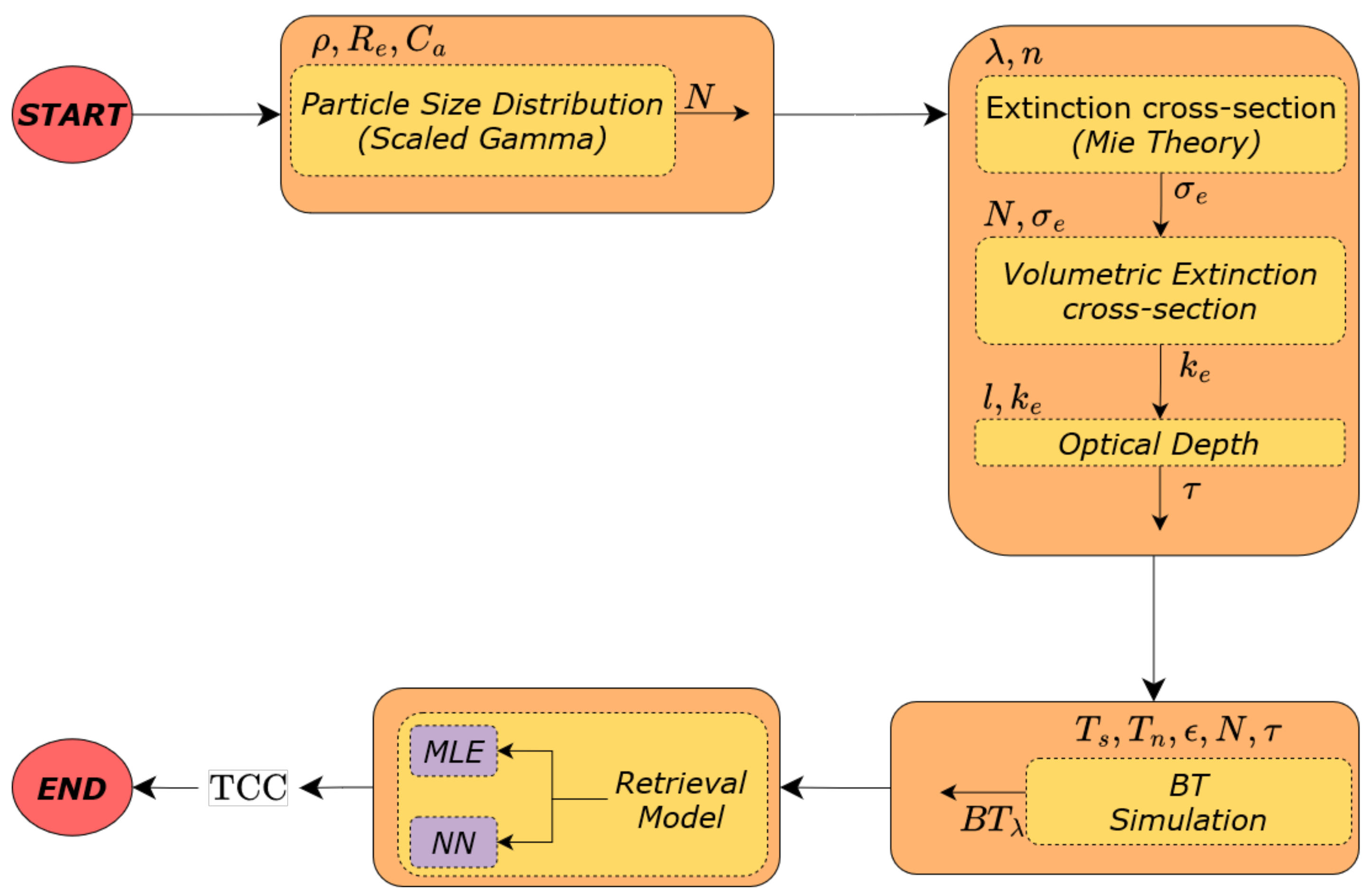
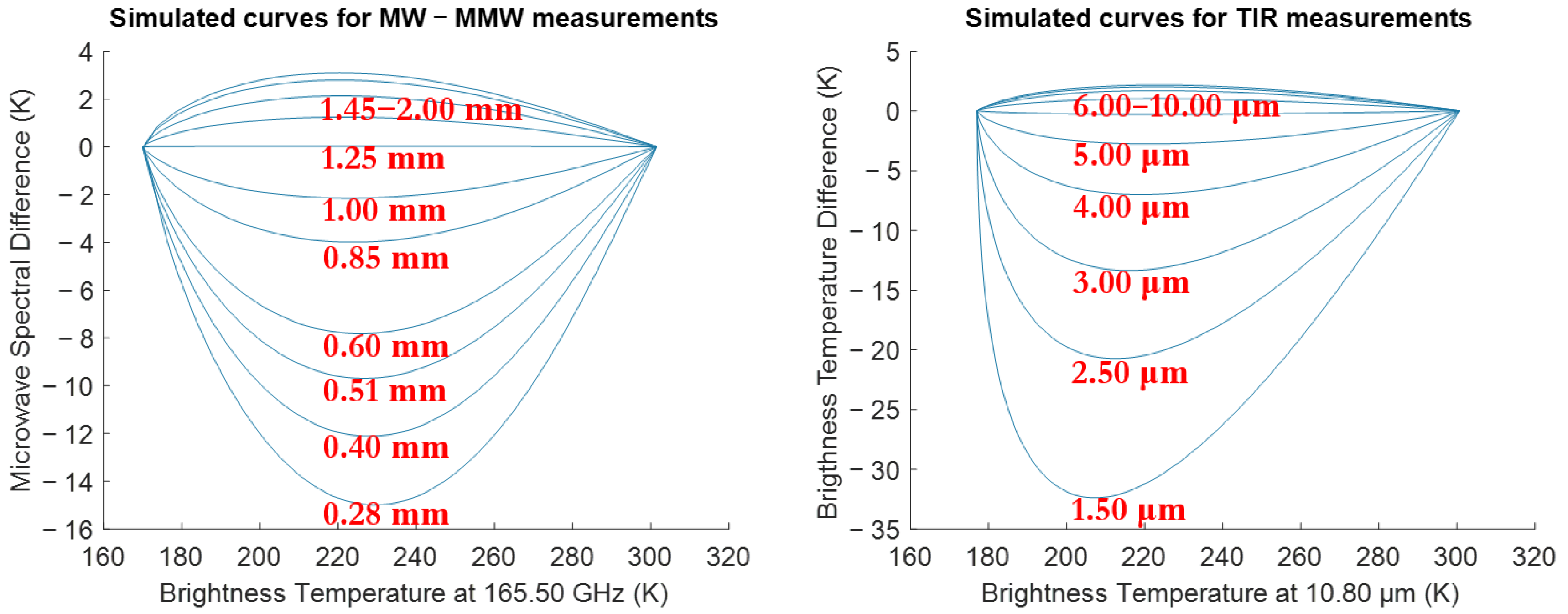
2.3. Radiative Transfer Modelling
2.4. The Empirical Parametric Retrieval (EPR) Method
3. Test Cases
3.1. The Kelud Eruption in 2014
3.2. The Calbuco Eruption in 2015
4. Results
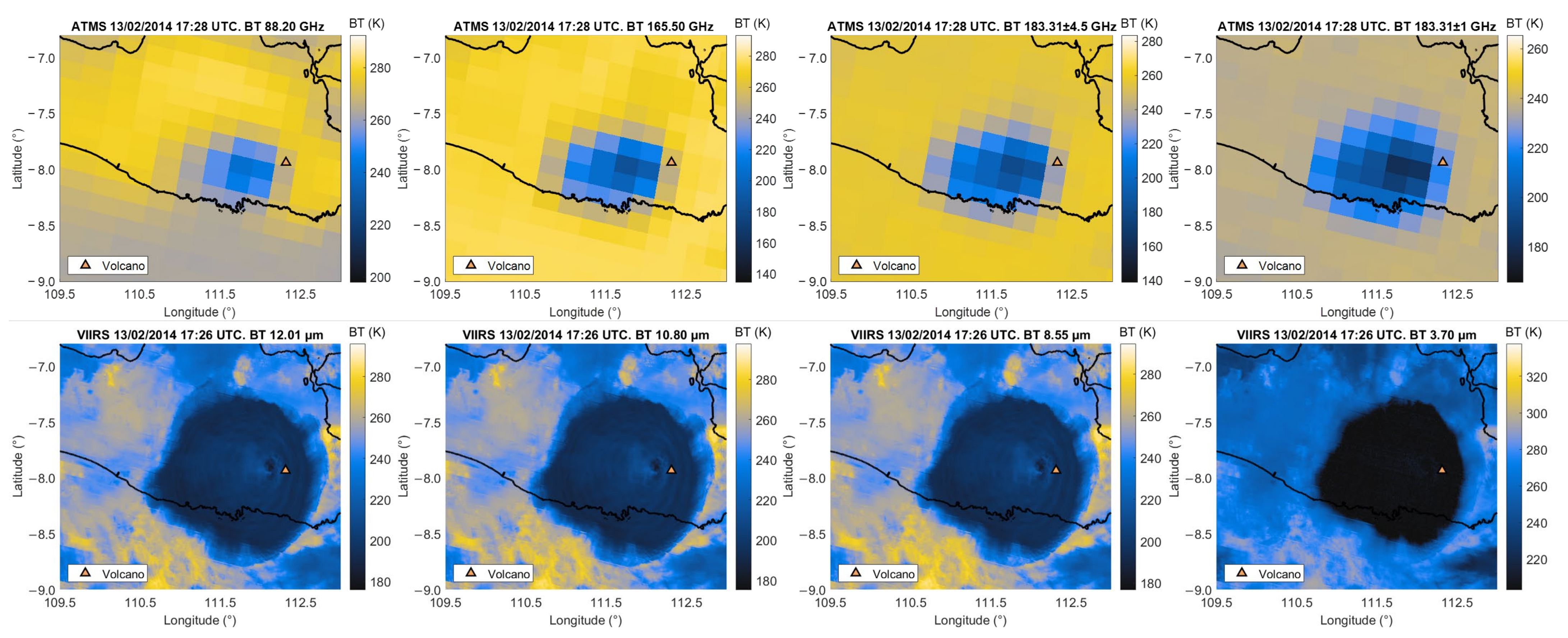
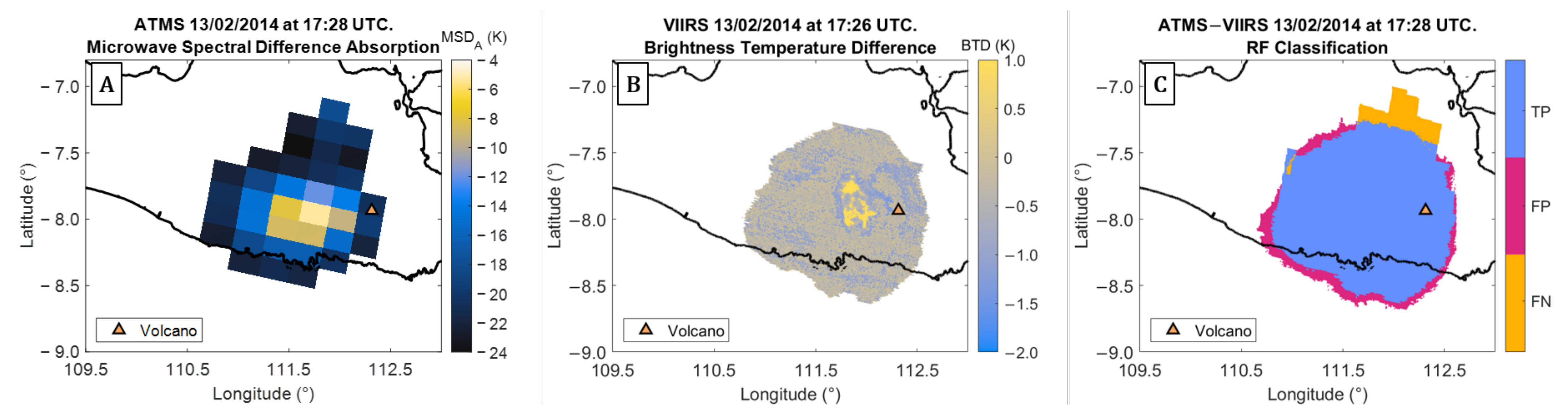
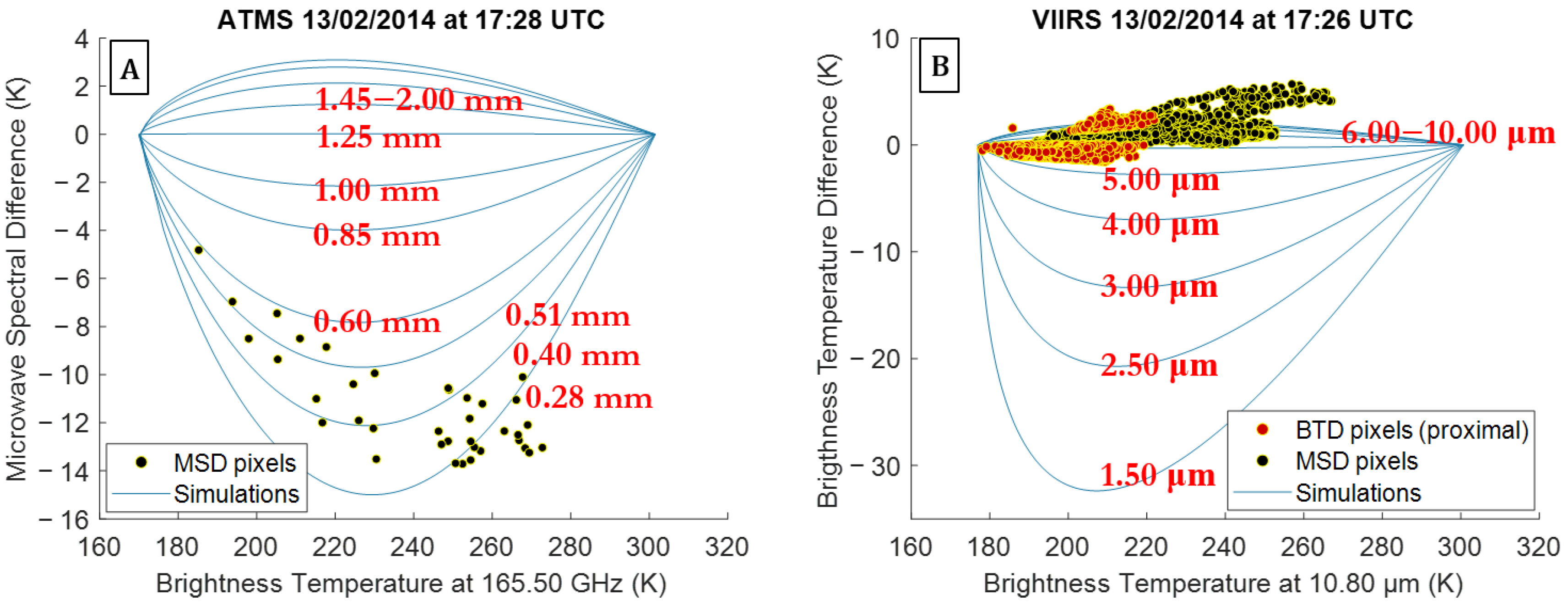
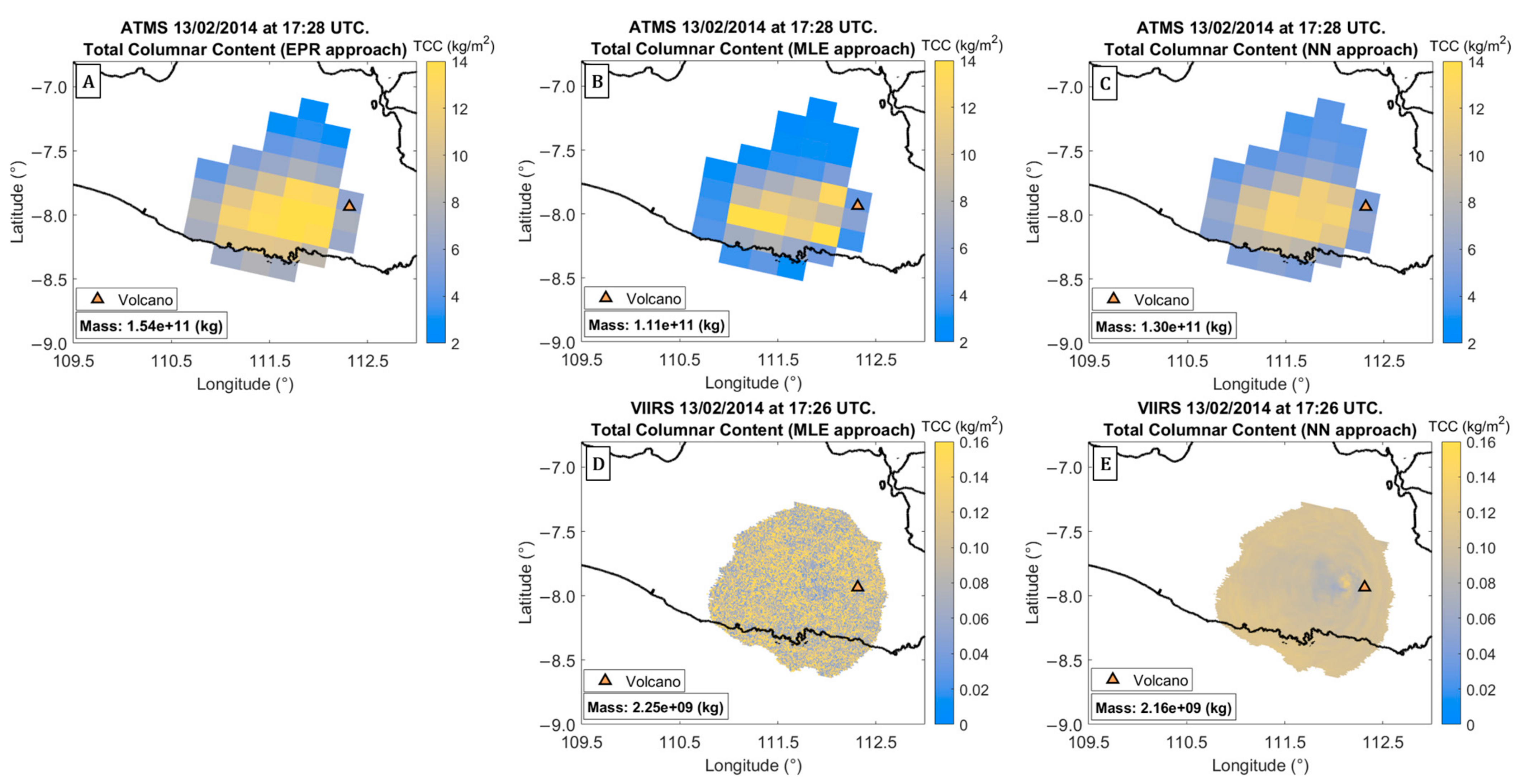
4.1. Kelud: Detection and Retrieval
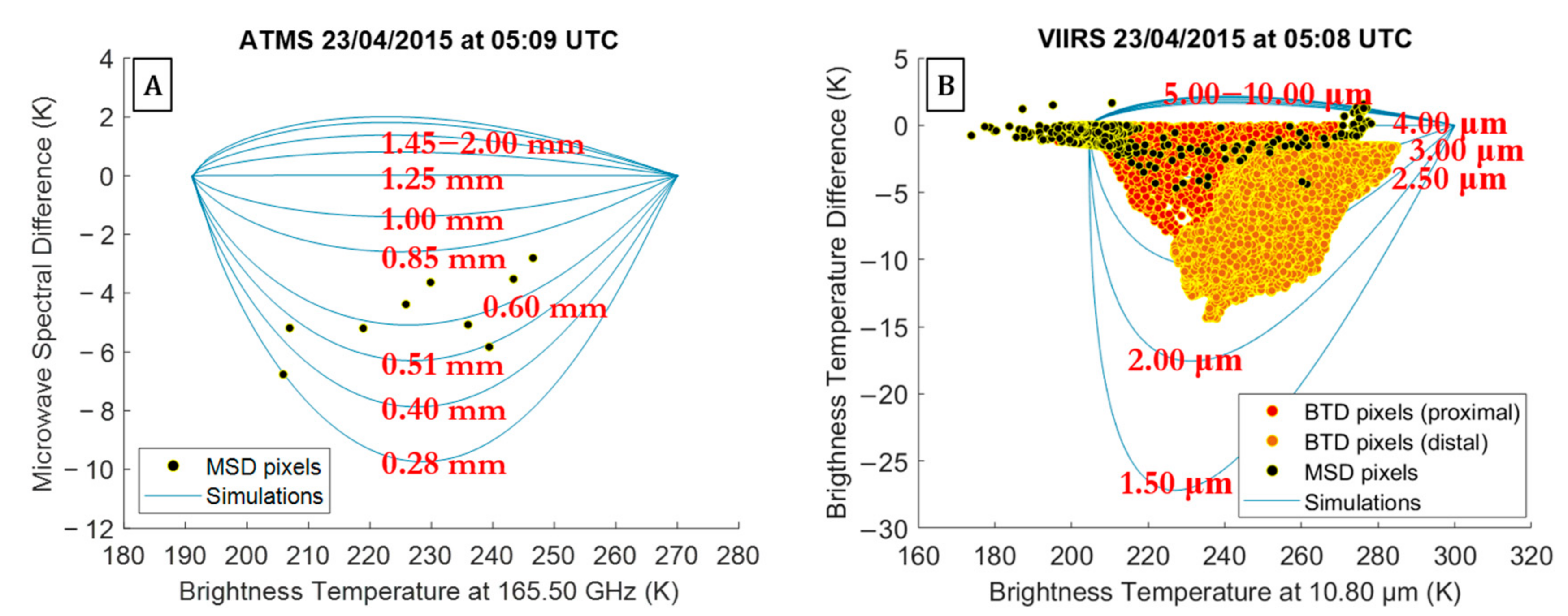
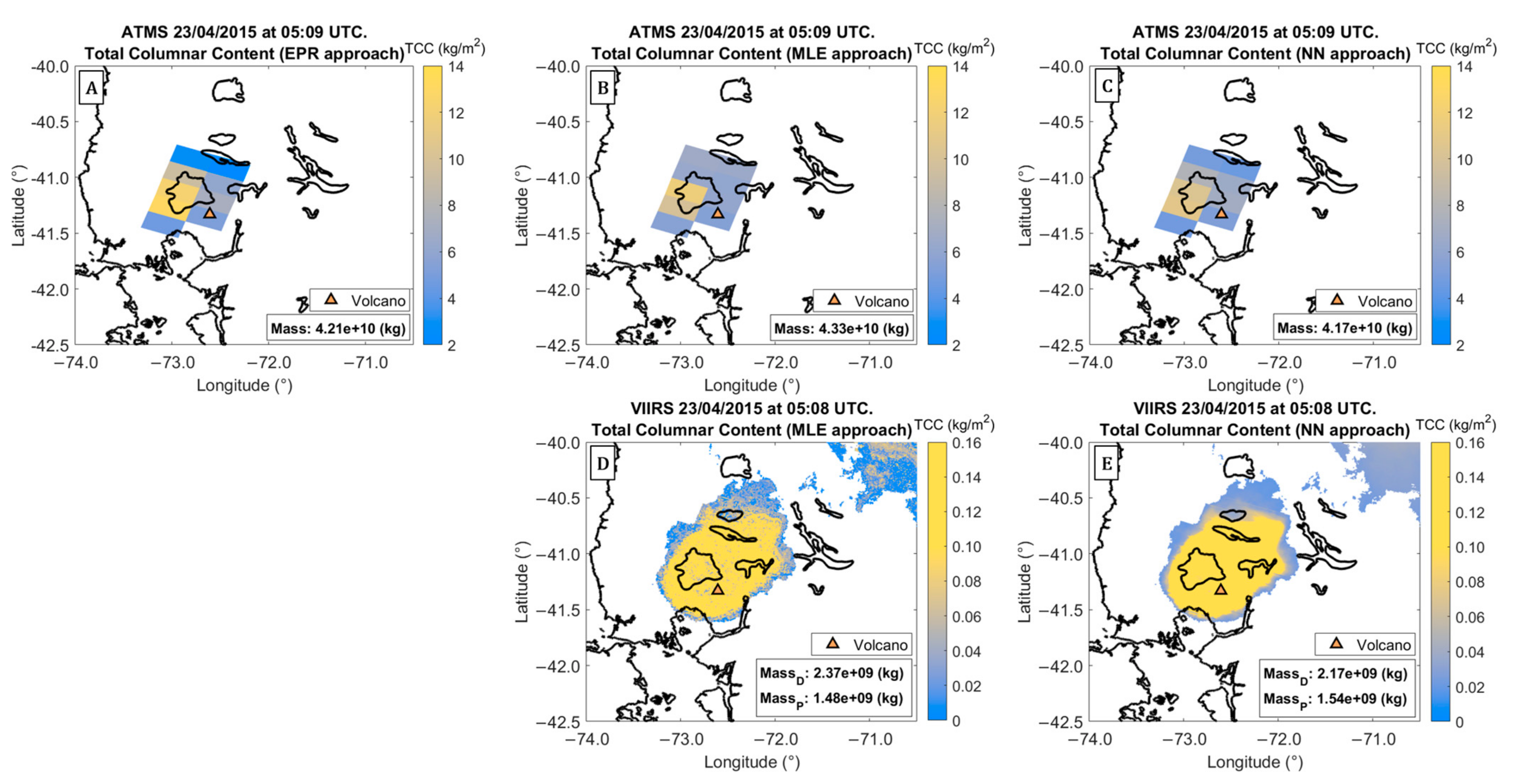
4.2. Calbuco: Detection and Retrieval
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Acronyms | Full Name |
| ADAM | Adaptive Moment Estimation |
| ARIA | Aerosol Refractive Index Archive |
| ATMS | Advanced Technology Microwave Sounder |
| AVHRR | Advanced Very High-Resolution Radiometer |
| BT | Brightness Temperature |
| BTD | Brightness Temperature Difference |
| CV | Cross-Validation |
| EPR | Empirical Parametric Retrieval |
| FA | Fine Ash |
| FN | False Negatives |
| FP | False Positives |
| GEO | Geosynchronous Earth Orbit |
| LEO | Low Earth Orbit |
| MAP | Maximum a Posteriori Probability |
| MassD | Mass Distal |
| MassP | Mass Proximal |
| MHS | Microwave Humidity Sounder |
| MLE | Maximum Likelihood Estimation |
| MMW | Millimetre-wave |
| MSD | Microwave Spectral Difference |
| MSDA | Microwave Spectral Difference Absorption |
| MSDW | Microwave Spectral Difference Window |
| MSE | Mean Squared Error |
| MW | Microwave |
| NN | Neural Network |
| NOAA | National Oceanic and Atmospheric Administration |
| PSD | Particle Size Distribution |
| ReLu | Rectified Linear unit |
| RMSE | Root Mean Squared Error |
| RTM | Radiative Transfer Model |
| RTMA | Radiative Transfer Model Algorithm |
| SL | Small Lapilli |
| S-NPP | Suomi-National Polar-orbiting Partnership |
| TCC | Total Columnar Content |
| TIR | Thermal-InfraRed |
| TP | True Positives |
| VIIRS | Visible Infrared Imaging Radiometer Suite |
Appendix A
References
- Marzano, F.S.; Corradini, S.; Mereu, L.; Kylling, A.; Montopoli, M.; Cimini, D.; Merucci, L.; Stelitano, D. Multi-satellite Multi-sensor Observations of a Sub-Plinian Volcanic Eruption: The 2015 Calbuco Explosive Event in Chile. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2597–2612. [Google Scholar] [CrossRef]
- Mereu, L.; Scollo, S.; Mori, S.; Boselli, A.; Leto, G.; Marzano, F.S. Maximum-likelihood retrieval of volcanic ash concentration and particle size from ground-based scanning lidar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5824. [Google Scholar] [CrossRef]
- Prata, A.J. Satellite detection of hazardous volcanic clouds and the risk to global air traffic. Nat. Hazards 2009, 51, 303–324. [Google Scholar] [CrossRef]
- Thomas, H.E.; Watson, I.M.; Carn, S.A.; Prata, A.J.; Realmuto, V.J. A comparison of AIRS, MODIS and OMI sulphur dioxide retrievals in volcanic clouds. Geomatics Nat. Hazards Risk 2011, 2, 217–232. [Google Scholar] [CrossRef]
- Corradini, S.; Guerrieri, L.; Brenot, H.; Clarisse, L.; Merucci, L.; Pardini, F.; Prata, A.J.; Realmuto, V.J.; Stelitano, D.; Theys, N. Tropospheric Volcanic SO2 Mass and Flux Retrievals from Satellite. The Etna December 2018 Eruption. Remote Sens. 2021, 13, 2225. [Google Scholar] [CrossRef]
- Corradini, S.; Montopoli, M.; Guerrieri, L.; Ricci, M.; Scollo, S.; Merucci, L.; Marzano, F.S.; Pugnaghi, S.; Prestifilippo, M.; Ventress, L.J.; et al. A Multi-Sensor Approach for Volcanic Ash Cloud Retrieval and Eruption Characterization: The 23 November 2013 Etna Lava Fountain. Remote Sens. 2016, 8, 58. [Google Scholar] [CrossRef]
- Delene, D.J.; Rose, W.I.; Grody, N.C. Remote sensing of volcanic ash clouds using special sensor microwave imager data. J. Geophys. Res. Solid Earth 1996, 101, 11579. [Google Scholar] [CrossRef]
- Larson, K.M. A new way to detect volcanic plumes. Geophys. Res. Lett. 2013, 40, 2657–2660. [Google Scholar] [CrossRef]
- Rainville, N.; Palo, S.; Larson, K.M. Modeling GPS signal propagation through volcanic plumes. J. Geophys. Res. Atmos. 2021, 126, e2020JD034526. [Google Scholar] [CrossRef]
- Harper, J.S.M.; Cimarelli, C.; Dufek, J.; Gaudin, D.; Thomas, R.J. Inferring Compressible Fluid Dynamics From Vent Discharges During Volcanic Eruptions. Geophys. Res. Lett. 2018, 45, 7226–7235. [Google Scholar] [CrossRef]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaä, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics: Understanding Why and How; Springer: London, UK, 2005; Volume 488. [Google Scholar]
- Larry, W. All of Statistics: A Concise Course in Statistical Inference; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Miura, K. An introduction to maximum likelihood estimation and information geometry. Interdiscip. Inf. Sci. 2011, 17, 155–174. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer series in statistics New York: New York, NY, USA, 2001. [Google Scholar]
- Amari, S.I. Information geometry of the EM and em algorithms for neural networks. Neural Netw. 1995, 8, 1379–1408. [Google Scholar] [CrossRef]
- Moldovan, A.; Cataron, A.; Andonie, R. Learning in Feedforward Neural Networks Accelerated by Transfer Entropy. Entropy 2020, 22, 102. [Google Scholar] [CrossRef]
- Norton, P. Understanding the NEΔT of tactical infrared focal plane arrays. Opto-Electronics Rev. 2012, 20, 275–278. [Google Scholar] [CrossRef]
- Monarrez, R.; Hearty, T.; Lambrigsten, B.; Schreier, M.; Tkatcheva, I.; Manning, E.; Zong, J.; Iredell, L. Nasa Advanced Technology Microwave Sounder (atms) Level 1b Product User Guide. (2019), 70. Available online: https://docserver.gesdisc.eosdis.nasa.gov/public/project/JPSS-1/SNDRJ1ATMSL1B.2.Readme.12AUG2019.pdf (accessed on 4 April 2022).
- Weng, F.; Yang, H.; Zou, X. On convertibility from antenna to sensor brightness temperature for atms. IEEE Geosci. Remote Sens. Lett. 2012, 10, 771. [Google Scholar] [CrossRef]
- Cao, C.; Xiong, X.; Wolfe, R.; DeLuccia, F.; Liu, Q.; Blonski, S.; Lin, G.; Nishihama, M.; Pogorzala, D.; Oudrari, H.; et al. Visible Infrared Imaging Radiometer Suite (VIIRS) Sensor Data Record (SDR) User’s Guide. (2017), 51. Available online: https://ncc.nesdis.noaa.gov/documents/documentation/viirs-users-guide-tech-report-142a-v1.3.pdf (accessed on 12 December 2022).
- Tschudi, M.; Riggs, G.; Hall, D.; Roman, M.O. Suomi Npp VIIRS Ice Surface Temperature Algorithm Theoretical Basis Document (ATBD). 2016, 17. Available online: https://nsidc.org/sites/nsidc.org/files/technical-references/VIIRS_IST_ATBD_V1.pdf (accessed on 12 December 2022).
- Eumetsat. Mhs Level 1 Product Format Specification. 2013. Volume 56. Available online: https://www.eumetsat.int/media/38679 (accessed on 12 December 2022).
- Eumetsat. Avhrr Level 1b Product Guide. 2011. Volume 98. Available online: https://www.eumetsat.int/media/15351 (accessed on 12 December 2022).
- Wen, S.; Rose, W.I. Retrieval of sizes and total masses of particles in volcanic clouds using AVHRR bands 4 and 5. J. Geophys. Res. Atmos. 1994, 99, 5421. [Google Scholar] [CrossRef]
- Prata, A.; Grant, I. Retrieval of microphysical and morphological properties of volcanic ash plumes from satellite data: Application to Mt Ruapehu, New Zealand. Q. J. R. Meteorol. Soc. 2001, 127, 2153. [Google Scholar] [CrossRef]
- Yu, T.; Prata, A.J.; Rose, W.I. Atmospheric correction for satellite-based volcanic ash mapping and retrievals using “split window” IR data from GOES and AVHRR. J. Geophys. Res. Atmos. 2002, 107, AAC 10-1–AAC 10-19. [Google Scholar] [CrossRef]
- Prata, A. Observations of volcanic ash clouds in the 10–12 μm window using avhrr/2 data. Int. J. Remote Sens. 1989, 10, 751. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Marzano, F.S.; Pierdicca, N. Modeling Microwave Fully Polarimetric Passive Observations of the Sea Surface: A Neural Network Approach. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2098. [Google Scholar] [CrossRef]
- Marzano, F.S.; Lamantea, M.; Montopoli, M.; Herzog, M.; Graf, H.; Cimini, D. Microwave remote sensing of the 2011 Plinian eruption of the Grímsvötn Icelandic volcano. Remote. Sens. Environ. 2013, 129, 168. [Google Scholar] [CrossRef]
- Prata, F.; Lynch, M. Passive Earth Observations of Volcanic Clouds in the Atmosphere. Atmosphere 2019, 10, 199. [Google Scholar] [CrossRef]
- Picchiani, M.; Chini, M.; Corradini, S.; Merucci, L.; Piscini, A.; Del Frate, F. Neural network multispectral satellite images classification of volcanic ash plumes in a cloudy scenario. Ann. Geophys. 2014, 57. section letters. [Google Scholar] [CrossRef]
- Torrisi, F. Automatic detection of volcanic ash clouds using MSG-SEVIRI satellite data and machine learning techniques. Il Nuovo Cim. C 2022, 45, 1–10. [Google Scholar]
- Torrisi, F.; Amato, E.; Corradino, C.; Mangiagli, S.; Del Negro, C. Characterization of Volcanic Cloud Components Using Machine Learning Techniques and SEVIRI Infrared Images. Sensors 2022, 22, 7712. [Google Scholar] [CrossRef]
- Petracca, I.; De Santis, D.; Picchiani, M.; Corradini, S.; Guerrieri, L.; Prata, F.; Merucci, L.; Stelitano, D.; Del Frate, F.; Salvucci, G.; et al. Volcanic cloud detection using Sentinel-3 satellite data by means of neural networks: The Raikoke 2019 eruption test case. Atmospheric Meas. Tech. Discuss. 2022, 15, 7195–7210. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Hao, J.; Ho, T.K. Machine Learning Made Easy: A Review of Scikit-learn Package in Python Programming Language. J. Educ. Behav. Stat. 2019, 44, 348–361. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sun, X.; Zhou, T.; Li, G.; Hu, J.; Yang, H.; Li, B. An empirical study on real bugs for machine learning programs. In 2017 24th Asia-Pacific Software Engineering Conference (APSEC), Nanjing, China, 4–8 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 348–357. [Google Scholar]
- Haley, S.; Behnke, S.; Edens, H.; Thomas, R. Observations Show Charge Density of Volcanic Plumes is Higher Than Thunderstorms. J. Geophys. Res. Atmos. 2021, 126, e2021JD035404. [Google Scholar] [CrossRef]
- Montopoli, M.; Cimini, D.; Lamantea, M.; Herzog, M.; Graf, H.F.; Marzano, F.S. Microwave Radiometric Remote Sensing of Volcanic Ash Clouds From Space: Model and Data Analysis. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4678–4691. [Google Scholar] [CrossRef]
- Ulaby, F.; Long, D. Microwave Radar and Radiometric Remote Sensing; Artech House: Boston, MA, USA, 2014. [Google Scholar]
- Solimini, D. Understanding Earth Observation; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the Icml, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Du, X.; Xiao, G.; Sui, Y. Fault triggers in the tensorflow framework: An experience report. In Proceedings of the 2020 IEEE 31st International Symposium on Software Reliability Engineering (ISSRE), Coimbra, Portugal, 12–15 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–12. [Google Scholar]
- Kristiansen, N.I.; Prata, A.J.; Stohl, A.; Carn, S.A. Stratospheric volcanic ash emissions from the 13 February 2014 Kelut eruption. Geophys. Res. Lett. 2015, 42, 588. [Google Scholar] [CrossRef]
- Maeno, F.; Nakada, S.; Yoshimoto, M.; Shimano, T.; Hokanishi, N.; Zaennudin, A.; Iguchi, M. A sequence of a plinian eruption preceded by dome destruction at Kelud volcano, Indonesia, on February 13, 2014, revealed from tephra fallout and pyroclastic density current deposits. J. Volcanol. Geotherm. Res. 2019, 382, 24. [Google Scholar] [CrossRef]
- Romero, J.; Morgavi, D.; Arzilli, F.; Daga, R.; Caselli, A.; Reckziegel, F.; Viramonte, J.; Díaz-Alvarado, J.; Polacci, M.; Burton, M.; et al. Eruption dynamics of the 22–23 April 2015 Calbuco Volcano (Southern Chile): Analyses of tephra fall deposits. J. Volcanol. Geotherm. Res. 2016, 317, 15. [Google Scholar] [CrossRef]
- Suzuki, Y.; Iguchi, M. Determination of the mass eruption rate for the 2014 Mount Kelud eruption using three-dimensional numerical simulations of volcanic plumes. J. Volcanol. Geotherm. Res. 2019, 382, 42–49. [Google Scholar] [CrossRef]
- Subasilar, B. Analytical approaches to the delta-Eddington model of the radiative transfer through vertically inhomogeneous optical depths. Appl. Math. Model. 2008, 32, 514. [Google Scholar] [CrossRef]
- Drossart, P. A statistical model for the scattering by irregular particles. Astrophys. J. 1990, 361, L29. [Google Scholar] [CrossRef]
- Marzano, F.S.; Marchiotto, S.; Textor, C.; Schneider, D.J. Model-Based Weather Radar Remote Sensing of Explosive Volcanic Ash Eruption. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3591–3607. [Google Scholar] [CrossRef]
- Kylling, A.; Kahnert, M.; Lindqvist, H.; Nousiainen, T. Volcanic ash infrared signature: Porous non-spherical ash particle shapes compared to homogeneous spherical ash particles. Atmospheric Meas. Tech. 2014, 7, 919–929. [Google Scholar] [CrossRef]
- Heifetz, A.; Chien, H.; Liao, S.; Gopalsami, N.; Raptis, A. Millimeter-wave scattering from neutral and charged water droplets. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2550–2557. [Google Scholar] [CrossRef]
- Kocifaj, M.; Kómar, L.; Kundracik, F.; Markoš, P.; Petržala, J.; Videen, G. The Nature, Amplitude and Control of Microwave Attenuation in the Atmosphere. J. Geophys. Res. Atmos. 2021, 126, e2021JD034978. [Google Scholar] [CrossRef]
- Corradini, S.; Spinetti, C.; Carboni, E.; Tirelli, C.; Buongiorno, M.F.; Pugnaghi, S.; Gangale, G. Mt. Etna tropospheric ash retrieval and sensitivity analysis using Moderate Resolution Imaging Spectroradiometer measurements. J. Appl. Remote Sens. 2008, 2, 023550. [Google Scholar] [CrossRef]



| Date | Start Time UTC | End Time UTC | Sensor | Application |
|---|---|---|---|---|
| 13 February 2014 | 18:08 | 18:19 | MHS | Training |
| 13 February 2014 | 18:11 | 18:15 | MHS | Training |
| 13 February 2014 | 17:18 | 19:04 | AVHRR | Training |
| 23 April 2015 | 06:54 | 06:58 | MHS | Training |
| 23 April 2015 | 06:54 | 07:03 | MHS | Training |
| 23 April 2015 | 06:16 | 08:08 | AVHRR | Training |
| 13 February 2014 | 17:28 | 17:36 | ATMS | Prediction |
| 13 February 2014 | 17:26 | 17:32 | VIIRS | Prediction |
| 23 April 2015 | 05:09 | 05:17 | ATMS | Prediction |
| 23 April 2015 | 05:08 | 05:13 | VIIRS | Prediction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romeo, F.; Mereu, L.; Scollo, S.; Papa, M.; Corradini, S.; Merucci, L.; Marzano, F.S. Volcanic Cloud Detection and Retrieval Using Satellite Multisensor Observations. Remote Sens. 2023, 15, 888. https://doi.org/10.3390/rs15040888
Romeo F, Mereu L, Scollo S, Papa M, Corradini S, Merucci L, Marzano FS. Volcanic Cloud Detection and Retrieval Using Satellite Multisensor Observations. Remote Sensing. 2023; 15(4):888. https://doi.org/10.3390/rs15040888
Chicago/Turabian StyleRomeo, Francesco, Luigi Mereu, Simona Scollo, Mario Papa, Stefano Corradini, Luca Merucci, and Frank Silvio Marzano. 2023. "Volcanic Cloud Detection and Retrieval Using Satellite Multisensor Observations" Remote Sensing 15, no. 4: 888. https://doi.org/10.3390/rs15040888
APA StyleRomeo, F., Mereu, L., Scollo, S., Papa, M., Corradini, S., Merucci, L., & Marzano, F. S. (2023). Volcanic Cloud Detection and Retrieval Using Satellite Multisensor Observations. Remote Sensing, 15(4), 888. https://doi.org/10.3390/rs15040888







