Abstract
Single image super-resolution (SISR) is to reconstruct a high-resolution (HR) image from a corresponding low-resolution (LR) input. It is an effective way to solve the problem that infrared remote sensing images are usually suffering low resolution due to hardware limitations. Most previous learning-based SISR methods just use synthetic HR-LR image pairs (obtained by bicubic kernels) to learn the mapping from LR images to HR images. However, the underlying degradation in the real world is often different from the synthetic method, i.e., the real LR images are obtained through a more complex degradation kernel, which leads to the adaptation problem and poor SR performance. To handle this problem, we propose a novel closed-loop framework that can not only make full use of the learning ability of the channel attention module but also introduce the information of real images as much as possible through a closed-loop structure. Our network includes two independent generative networks for down-sampling and super-resolution, respectively, and they are connected to each other to get more information from real images. We make a comprehensive analysis of the training data, resolution level and imaging spectrum to validate the performance of our network for infrared remote sensing image super-resolution. Experiments on real infrared remote sensing images show that our method achieves superior performance in various training strategies of supervised learning, weakly supervised learning and unsupervised learning. Especially, our peak signal-to-noise ratio (PSNR) is 0.9 dB better than the second-best unsupervised super-resolution model on PROBA-V dataset.
1. Introduction
Infrared remote sensing has strong anti-interference ability and penetration ability for cloud cover compared with visible remote sensing. Even in a dark environment, it can obtain available images through infrared radiation radiated by objects. Thus, infrared remote sensing technology is widely used owing to these advantages. However, due to hardware limitations in the processing design of infrared detection elements, the spatial resolution of infrared remote sensing images is usually low, which has a great impact on the interpretation tasks that rely on high-quality images. Updating infrared remote sensing hardware is difficult, costly and time-consuming. Therefore, it becomes an ideal solution to improve the spatial resolution of infrared remote sensing images through super-resolution reconstruction algorithms [1]. Super-resolution (SR) is to recover the natural and sharp detailed high-resolution (HR) counterparts from low-resolution (LR) images. It can not only improve the visual quality of the image itself, but also help to improve the performance of image classification [2,3], target detection, target tracking [4,5] and other tasks [6,7,8,9] that are limited by the spatial resolution. Hence, the super-resolution algorithm can effectively make up for the defects of infrared remote sensing imaging, and encourage it to play a greater role in application [10]. The SR algorithms can be divided into multiple images super-resolution (MISR) [11,12] and single image super-resolution (SISR) [13] according to the number of LR images used. MISR needs multiple images of the same scene, which is not practicable in the field of infrared remote sensing. SISR requires only a single image of the target scene to recover the corresponding HR image, which has wide applicability and practical value [14,15]. Therefore, in this paper, we focus on SISR for infrared remote sensing.
The research of SR algorithms starts from the methods based on the frequency domain [16] and gradually develops into the spatial domains [17,18]. Traditional SR algorithms in spatial domains can be divided into methods based on interpolation [17,18] and reconstruction [19]. Interpolation-based algorithms, such as nearest, bilinear, bicubic [18], etc., do not essentially generate missing high-frequency information, but simply weight the adjacent pixels. Therefore, the blur and aliasing effect in the reconstructed images are usually obvious. The reconstruction-based methods introduce prior information and establish a reasonable model to obtain the final HR images through iterative calculation. The representative methods are iterative back-projection (IBP) [20], maximum a posterior (MAP) [21], and projections onto convex sets (POCS) [22]. The reconstruction quality is better than interpolation-based methods, but these reconstruction-based methods have high computational complexity, slow convergence speed, and poor practicability. The methods based on sparse representation [23,24] get significant improvement compared with interpolation-based and reconstruction-based methods, but their modeling capability and expression ability are limited. Thus, recently, SR methods based on sparse representation gradually have been replaced by deep learning based methods [25,26,27].
Most deep-learning-based SR methods rely on paired training data to learn the mapping between LR images and HR images. Since the real HR-LR image pairs are difficult to obtain, they usually use HR images and their corresponding bicubic-degraded LR counterparts. However, the real-world data does not necessarily have the same distribution as the LR image obtained by a specific degradation method. Therefore, even if the SR method can obtain good results on artificially synthesized LR images, it is very challenging to learn a good model for real-world applications [28]. To alleviate this problem caused by degradation in the real world, we propose a more practical framework, i.e., closed-loop network. It contains not only a network for super-resolution, but also a network for down-sampling. These two networks have independent functions, facilitating the use of excellent super-resolution network structure. Most importantly, connecting these two networks can make full use of the information of real LR images during the training process to learn the real causes of degradation, so as to improve the performance of the SR network on real LR data. We compare and analyze the network training modes with full supervision, weak supervision and non-supervision, respectively. Furthermore, according to the characteristics of infrared remote sensing images with fixed resolution and multi-band imaging, the resolution adaptability and band adaptability are explored and evaluated for the proposed method. To summarize, the main contributions of this paper can be highlighted as follows.
- We proposed a novel closed-loop framework to better super-resolve infrared remote sensing LR images in real world. Since our closed-loop network can work with LR input only, i.e., in unsupervised manner, our method has better practical utility.
- We provided reasonable training suggestions about how to train our network in the ways of supervised learning, weakly supervised learning and unsupervised learning.
- We experimentally studied the resolution level adaptability and spectrum adaptability of our proposed infrared remote sensing image SR method. Such analyses are especially needed for infrared remote sensing, but usually neglected in natural image super-resolution.
The remainder of this paper is organized as follows. Section 2 presents an overview of learning-based SISR methods and their limitations. Section 3 describes details of our closed-loop framework. Section 4 and Section 5 show experimental results to validate the proposed approach and explore the resolution and band adaptability of infrared remote image super-resolution. Conclusions are given in Section 6.
2. Related Works
Generally, learning-based SISR algorithms can be categorized into three different groups, i.e., supervised learning, unsupervised learning and weakly supervised learning. Thus, we summarize related previous works from these three aspects in this section.
2.1. Supervised Learning
Supervised learning methods aim at learning the relationship between the LR domain and HR domain with an external training set containing HR images and corresponding LR images. In the past few years, many supervised learning-based methods have succeeded in SR tasks, including sparse coding [23,24], neighborhood embedding [29] and mapping functions [30,31].
The supervised learning-based methods get better performance than reconstruction-based methods with the help of training sets. However, the training data is also the reason for the shortcomings of this kind of method. Because real HR-LR image pairs are extremely difficult to obtain. In general, the remote sensing satellites will not set two different resolutions for the same load. Thus, LR images are generally captured by down-sampling from HR images with a degradation kernel, which is inconsistent with the degradation of real LR data. As a result, although the SR model based on supervised learning can achieve good performance on the down-sampled data, it can not meet expectations when applied in real LR images [32].
2.2. Unsupervised Learning
Unsupervised learning methods only rely on LR images to perform super-resolution. In a single image, the repeated appearance of small image patches has been proved to be a very strong characteristic of natural images [33]. Natural images follow the rule of perspective projection, where the near scene is large and the distant scene is small. It has laid the foundation for many unsupervised image enhancement methods, including super-resolution [34]. The early unsupervised learning methods are mainly based on the above characteristic, also known as self-similarity. Huang et al. [35] proposed a compositional model which can simultaneously handle perspective distortion and affine transformation to expand the internal patch space. Shocher et al. [36] exploited the internal recurrence of information inside the test image, and then trained a light convolutional neural network (CNN) to reconstruct the corresponding HR image. These algorithms work well for images with multi-scale similar structures. However, due to the far imaging distance in satellite remote sensing, the influence of the depth of field on imaging is negligible. Remote sensing images are mostly like the results of parallel projection. Compared with natural images, remote sensing images have poor self-similarity, so such methods may not achieve good performance.
Besides, there are other unsupervised methods in the remote sensing community. Haut et al. [37] proposed a deep generative network that used random noise to generate HR images. In [37], HR images were updated by minimizing mean square error (MSE) loss of the down-sampled version of the output HR image and the real LR image. Sheikholeslami et al. [38] took the LR image directly as input and simplified the network structure to further improve efficiency. Both methods down-sampled the output image to solve the problem of lacking ground-truth HR image. However, the fixed down-sampling function used in these methods may also cause the problem of inconsistent degenerate kernels, similar to supervised learning methods.
2.3. Weakly Supervised Learning
CycleGAN (Cycle-consistent Generative Adversarial Network) [39] is a pioneering work of unpaired training mode for image-to-image translation. Inspired by it, Yuan et al. [40] firstly proposed CinCGAN (Cycle-in-Cycle Generative Adversarial Network) for image super-resolution. It contains two cycle GAN structures, and discriminate the domain of generated images with a discriminator instead of matching HR constraints. Bulat et al. [41] learned the HR-to-LR degradation model from unpaired images, and then used HR image and the LR image generated by the degradation model to train the SR model. Wang et al. [42,43] proposed Cycle-CNN, using two cycles in different directions to make full use of the information of real high and low-resolution data, making it more suitable for SR task of real remote sensing images. Guo et al. [44] proposed a dual regression network using paired synthetic data and additional unpaired LR data for training. The above methods are obviously not fully supervised, since no matched HR-LR pairs are used for supervised training. However, they are not strictly unsupervised either, because there are HR images in the target domain used in training. In this paper, we prefer to regard these methods using unpaired training data as weakly supervised learning SR methods. These weakly supervised learning methods aim to make the SR algorithm more practical on real LR images by using unpaired HR images at target resolution. They have used various methods to solve the impact of the artificial down-sampling kernel of supervised learning, but real LR and HR images are both needed, still facing data acquisition difficulty in remote sensing applications.
Although the above-mentioned learning-based methods have their own limitations, single-image super-resolution is indeed an ill-posed problem and hard to solve perfectly. Therefore, inspired by supervised learning and unpaired training mode, we try to propose a flexible framework that can generally adapt the training mode in the case of supervised learning, unsupervised learning and weakly supervised learning. Such an SISR model can make full use of the mapping constraints of supervised learning, and can also introduce the characteristics of real images to reduce the negative impact caused by the difference between the synthetic degradation kernel and the real degradation kernel, so as to get better SR results for real LR images.
3. Method
3.1. Framework
Our framework contains two networks, one for super-resolution (denoted as S) and one for down-sampling (denoted as D). Because of the opposite function, connecting these two networks can form a closed-loop and perform self-supervision without matching ground truth. As shown in Figure 1, there are two possible basic types of connections. The forward loop refers to the way that the image passes through the super-resolution network S first and then the down-sampling network D. Starting from the LR image , the super-resolution network can obtain its HR version and the down-sampling network takes the HR output as input to get the low-resolution image of the same size as the original input in the end of the loop. The input and final output can be constrained by loss functions. The backward loop refers to the opposite process. The HR image is used as the input of down-sampling network first, then the super-resolution network performs SR on the obtained LR image . As a result, we get a high-resolution image which is of the same size as the original input . The double loop is the combination of forward loop and backward loop. It is worth noting that the LR and HR image in each loop is relative concepts. The super-resolution network S learns how to reconstruct during training and helps us get final results during testing. The closed-loop structure adjusts S more suitable to reconstruct LR images in real world by taking the real images as self-supervision input. Our experimental results in Section 4.1 also demonstrate the effectiveness of the closed-loop structure in learning the true causes of degradation.

Figure 1.
The cycle structure of our closed-loop framework. Our framework consists of two generative networks for super-resolution (S) and down-sampling (D), respectively. The left subfigure starting with the LR image is denoted as a forward loop, the center one starting with the HR image is denoted as a backward loop, and the right one is a double loop. and are loss functions denoted in Equations (1) and (2) separately.
We design the structure of the down-sampling network D according to Cycle-CNN [42]. As shown in Figure 2, it first downscales the feature maps using an average-pooling layer, and the resblock in D is much simpler, including only two convolution layers and a rectified linear unit (ReLU) [45] layer, which is determined by the difficulty of the task.
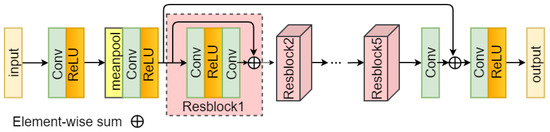
Figure 2.
The down-sampling network of our closed-loop framework.
The structure of super-resolution network S is similar to RCAN (Residual Channel Attention Networks) [46], and its function is opposite to D. We adjust the number of modules in the network according to our SR task. The overview of super-resolution network S is shown in Figure 3. Specially, we use five residual modules as the main body, and each residual module contains five stacked blocks with a convolution layer at the end. Each block contains two convolution layers, a ReLU layer and channel attention (CA) module [47]. Multiple levels of skip connections are all over the network. Sub-pixel layer [48] is selected to up-sample feature maps to a larger size. Finally, the output image is obtained through a convolution layer. It should be noticed that the CA module used in this paper is to further tap the learning ability of convolutional neural networks. Its overall structure is shown in the lower right corner of Figure 3. The global pooling layer simplifies each channel of the previously extracted feature map to a single value, i.e., the average value of each channel. Then the number of channels is first reduced by a convolution layer and then restored to the original number by another convolution layer. The sigmoid activation function maps the value of each channel to the range of as the weight of each channel feature map. The original feature map multiplies its weight to get the final feature map with channel attention. Through such a simple process, the channel attention module further enhances the nonlinear mapping ability of the convolutional neural network.
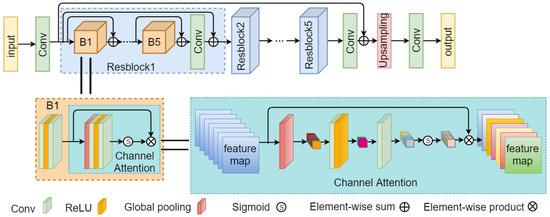
Figure 3.
The super-resolution network of our closed-loop framework.
3.2. Loss Functions
A network is connected to the task through the loss function. As suggested by [47], we take mean square error (MSE) as the loss function. In our closed-loop framework in Figure 1, there are two ways to connect the SR network and down-sampling network, and we can choose one or both. Therefore, the self-supervised loss without matching ground truth has the following three forms, i.e.,
where N is the batch-size, indicates the unpaired loss, and f, b and d represent forward loop, backward loop and double loop, respectively. and are the linear combination weights of and in .
These loss functions can make the input and output of the closed-loop tend to be consistent, but there is not an effective way to ensure the performance of the SR network. Therefore, we need an additional loss function to constrain the SR network. In order to ensure that the HR images generated by the SR network maintain a high degree of consistency in content with the input LR images, HR-LR image pairs are still required. In general, LR images paired with HR images are obtained by down-sampling HR images using bicubic kernels, and we denote them as . Then, the loss of paired data is as
In this way, the paired loss makes the SR network more stable, and the unpaired losses and make use of real data and the closed-loop structure in order to make the network more adaptable to real data.
3.3. Datasets for Study
We use two datasets in our research, i.e., PROBA-V dataset and Landsat-8 dataset.
3.3.1. PROBA-V Dataset
The full name of PROBA-V satellite [49] is Project for On-Board Autonomy-Vegetation, which is mainly used for vegetable monitoring. There are multiple payloads on the satellite that can be used to obtain images of different resolution levels. The data used in our paper comes from the PROBA-V Super-Resolution competition [50] (https://kelvins.esa.int/proba-v-super-resolution/data/ accessed on 20 November 2019). We can download the near-infrared (NIR) dataset with 566 different scenes. Each data-point consists of one 100 m resolution image and several 300 m resolution images from the same scene. The 300 m resolution data is delivered as 128 × 128 gray-scale images, while the 100 m resolution data is delivered as 384 × 384 gray-scale images. Different from the original task of multi-image super-resolution using PROBA-V data, we reorganize the dataset for our single image super-resolution task by selecting the one with the best quality from the 300 m data as the LR image in each scene according to the attached quality map. The total 566 scenes in the PROBA-V dataset are split into 500 scenes for training, 6 scenes for validating and 60 scenes for testing. The specific information of the PROBA-V dataset is shown in Table 1. It is worth noting that the HR and LR images in PROBA-V dataset are real and matched.

Table 1.
The information of PROBA-V dataset used in this paper.
3.3.2. Landsat-8 Dataset
The Landsat-8 satellite carries two sensors, namely the Operational Land Imager (OLI) and the Thermal Infrared Sensor (TIRS). Landsat-8 can provide multiple infrared spectrum images, which is convenient for us to study the influence of different imaging bands on the performance of super-resolution. In addition, since the resolution of the Landsat-8 infrared image is 30m, which is different from the resolution of PROBA-V, the impact of the resolution of training data can also be explored. To solve the problem of resolution adaptability, we collect 566 near infrared images from Landsat-8 website [51] (https://earthexplorer.usgs.gov/ accessed on 20 November 2019), and divide the dataset according to the same ratio as PROBA-V. As for the issue of spectrum adaptability, we choose, in total, five bands to construct the dataset separately, including the near-infrared band (B5), short-wave infrared band 1 (B6), short-wave infrared band 2 (B7), thermal infrared band 1 (B10) and thermal infrared band 2 (B11). For each band, we collect eight remote sensing scenes, crop them into 2005 images in the size of 384 × 384, and split 2000 images for training and 5 for validating. Considering the practicability of remote sensing image super-resolution, we directly choose two complete infrared remote sensing scenes of each band as a testing set instead of cropped data. Detailed information on the Landsat-8 dataset used in our paper is shown in Table 2.

Table 2.
The information of Landsat-8 dataset used in this paper.
3.4. Training Mode
Corresponding to the three different closed-loops in Figure 1 and the three unpaired losses in Section 3.2, there could be three training modes. The proposed training process of these three modes is summarized in Algorithm 1. For clear description in a unified form, we use and to represent the paired LR data and HR data, respectively. is the input of the forward loop and is the input of the backward loop. Our goal is to get a well-trained super-resolution network S and a down-sampling network D. and represent the parameters of these two networks, respectively. Different training modes are selected by setting the weight parameters of each loss function. In practice, we can select the training mode first to reduce unnecessary operations.
| Algorithm 1 Pseudo-codes of our framework in three training modes. |
| Require: Infrared remote sensing training images , , , , |
| Goal The well-trained S and D |
| 1: Initialize , |
| 2: repeat |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: Choose training mode: |
| 12: forward loop: |
| 13: backward loop: |
| 14: double loop: |
| 15: ADAM-optimizer (, variable )) |
| 16: until Reach maximum iteration of minibatch updating |
| 17: |
| 18: function test () |
| 19: |
| 20: return |
| 21: end function |
Supervised, weakly supervised and unsupervised data situations could happen in all three different training modes in Algorithm 1. Table 3 summarizes these possible combinations. The supervised data includes paired HR-LR images donated as and . Weakly supervised data includes unpaired HR and LR images donated as and , where are matched with their down-sampling version . The unsupervised case only contains LR images donated as , which are matched with down-sampled lower-resolution images .

Table 3.
The training data of different training modes at different data situation. (— means not used.)
To detailed show how to select the training mode in various data situations, we give an example experimental setting on real LR images of the PROBA-V dataset. As shown in Table 4, the training data corresponding to supervised learning, weakly supervised learning, and unsupervised learning are real paired HR-LR images, unpaired HR-LR images, and LR images, respectively. Training details are described as follows.

Table 4.
Correspondence table of training data in different training modes on the PROBA-V dataset. (— means not used.)
- Supervised learning: The real HR data and LR data in the PROBA-V dataset are represented by and , respectively. In order to prove the superiority of our framework, we also separately train the super-resolution network S for comparison in addition to three different training modes. When the super-resolution network is trained separately, the paired loss in Algorithm 1 is used as the total loss.
- Weakly supervised learning: The real unpaired HR-LR data can be obtained by shuffling the order of PROBA-V data. In order to distinguish from the data for supervised learning, the unpaired HR and LR data are represented by and , respectively. For the purpose of calculating paired loss, we need to down-sample the 100m HR data to obtain the matching LR data .
- Unsupervised learning: In most cases, the super-resolution task is carried out with only LR images. We use the real LR data from the PROBA-V dataset and denote it as and down-sample it to get paired data .
4. Experimental Results
4.1. Training Mode Selection
We first explore the training mode under different data situations on real LR images of the PROBA-V dataset as shown in Table 4. We use peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) as evaluation indicators like many other related studies. We train 12 SR models and test them using real LR images in the testing set of the PROBA-V dataset. Experimental results are shown in Table 5.

Table 5.
Results of different training modes under different data situations on the PROBA-V dataset. The best results are marked in red.
First of all, regardless of the data situation, simply training a super-resolution network S cannot achieve the best performance. It is due to the fact that S only uses the information of paired data. When the dataset does not contain real HR-LR image pairs, it introduces too much influence of the down-sampling kernel of the synthetic data on SR model.
When using real paired HR and LR data to train the SR model, the forward loop and backward loop simultaneously achieve the best results, and the double loop does not seem to be so effective. When the dataset contains real unpaired HR-LR data, the overall performance is reduced, but the advantage of the backward loop is comparatively obvious among the three training modes. It indicates that when the data is not matched, the data of the target resolution has a greater effect. The double loop mode does not superimpose the advantages of a forward loop and backward loop, and increases the computation complexity of the model. This indicates that the double loop mode may be too complicated for the SR task with the data used in this paper.
It should be noticed that when we perform unsupervised learning, the input of the forward loop is , not the with relatively lower resolution, because the original intention of the closed-loop structure is to introduce the information of real data. The input of the backward loop is also , because there is no higher-resolution data in our dataset. The forward loop and the backward loop achieve the same SSIM performance on the testing set, while the forward loop achieves better PSNR performance. The reason may be the training process of the forward loop is more consistent with the testing process.
4.2. Comparison with Learning Based SR Methods
We compare with some state-of-the-art SR methods on the PROBA-V dataset, including supervised learning, weakly supervised learning and unsupervised learning. The results are shown in Table 6. In the case of supervised learning, our closed-loop framework performs PSNR of 40.3701dB, while the SR network S only obtains 40.0677dB, which has approved the effectiveness of our closed-loop structure. Since the PROBA-V dataset contains real paired HR-LR data, EDSR [52] and SRFBN [53] also achieve good results in supervised learning experiments. As for the cases of weakly supervised learning and unsupervised learning, our method achieves the best PSNR and the second-best SSIM. The visual comparison of each unsupervised method is shown in Figure 4. It can be shown in Table 6 that UGSR [37] and EUSR [38] do not always get satisfactory results for infrared remote sensing images with relatively low pixel values and low contrast. We separately show some results of UGSR and EUSR in Figure 5. UGSR reconstructs the HR image from random noise while EUSR does this from LR image directly. EUSR performs relatively better and sometimes could get good results such as subfigure (h) of Figure 5.

Figure 4.
Visual results of our method and other unsupervised methods (BDB [33], IBP [20], FSR [55], GPR [56], and ZSSR [36]) on the PROBA-V dataset. Since the pixel value of the infrared HR image is relatively low as shown in (e), histogram equalization (histequal) has been performed on other images in this figure for better visualization. Noting that infrared lights are not visible to human eyes, we show a single channel of infrared remote sensing image in gray-scale. The yellow circle in each image is the result of a local enlargement. In addition, we ignore the geographical locations in the figure since SR focuses on image quality improvement. Such visualization setting is also applied in other figures of this paper.

Figure 5.
Visual results of UGSR [37] and EUSR [38] on the PROBA-V dataset. Since the pixel value of the infrared HR images is relatively low as shown in (a) and (e), histogram equalization (histequal) has been performed on other images in this figure for better visualization.

Table 6.
Comparison between our method and other advanced SR algorithms on PROBA-V dataset. The best results are marked in red.
Table 6.
Comparison between our method and other advanced SR algorithms on PROBA-V dataset. The best results are marked in red.
| SR Type | Method | PSNR(dB) | SSIM |
|---|---|---|---|
| Supervised learning | S | 40.0677 | 0.9671 |
| Ours | 40.3701 | 0.9675 | |
| RDN [54] | 33.5486 | 0.9187 | |
| EDSR [52] | 40.5574 | 0.9675 | |
| SRFBN [53] | 40.6953 | 0.9679 | |
| Weakly supervised learning | Ours | 39.9832 | 0.9645 |
| Cycle-CNN [42] | 39.9691 | 0.9646 | |
| S | 39.1031 | 0.9635 | |
| RDN [54] | 33.8350 | 0.9527 | |
| EDSR [52] | 39.1036 | 0.9636 | |
| SRFBN [53] | 39.0796 | 0.9635 | |
| Unsupervised learning | Ours | 40.1415 | 0.9645 |
| IBP [20] | 39.1382 | 0.9643 | |
| BDB [33] | 37.3865 | 0.9348 | |
| FSR [55] | 39.2305 | 0.9674 | |
| GPR [56] | 37.5735 | 0.9631 | |
| UGSR [37] | 35.4371 | 0.9255 | |
| EUSR [38] | 23.6012 | 0.4987 | |
| ZSSR [36] | 38.1762 | 0.9597 | |
| MZSR [57] | 38.0026 | 0.8942 | |
| dSRVAE [58] | 38.3937 | 0.9486 | |
| DASR [59] | 39.7955 | 0.9637 |
4.3. Ablation Study of Attention Mechanism
To prove the effectiveness of our proposed closed-loop structure, we choose one SR model with channel attention (CA) module [47] as our S network and compare itself with closed-loop structure as shown in the supervised learning part of Table 6. In order to analyze the effect of different attention modules, we compare them with another attention module named convolutional block attention module (CBAM) [60]. Results in Table 7 show that CBAM has better performance than CA, and achieves the best SR performance compared with other supervised SR methods. It can be seen that a more powerful attention module can improve the SR performance, indicating that our closed-loop network has the potential to get better SR performance by updating the basic modules.

Table 7.
Comparison of different attention modules in supervised manner on PROBA-V dataset. The best results are marked in red.
4.4. Resolution Adaptability Analysis
Since remote sensing images have clear resolution levels, it is valuable to study the SR performance of testing data with different resolution levels from the training data. Therefore, we conduct a cross-comparison experiment in this subsection by training different SR models of scale and testing LR images with different spatial resolutions. Since Landsat-8-NIR does not contain real 90 m resolution data, the LR data used in supervised training is obtained by down-sampling from PROBA-V and Landsat-8 datasets (i.e., and ), denoted as and . We adapt the backward loop mode and train two models using PROBA-V and Landsat-8-NIR data, respectively, in a supervised way. As for the unsupervised mode with only LR images, we use the forward loop mode for training. The lower-resolution data paired with and are further down-sampled and represented by and , respectively. In order to keep the experimental condition as consistent as possible, we also use down-sampled LR data during the testing process of all trained models, namely and , respectively. The experimental results are listed in Table 8. It can be seen that a SR model trained for super-resolving the data from 90m to 30m does not perform well for the task of super-resolving the data from 300 m to 100 m, and vice versa. The situation is more obvious in unsupervised learning. However, the performance gap on is relatively smaller than . This may indicate that data with higher resolution is more sensitive to the resolution of training data.

Table 8.
Results of resolution adaptability (PSNR(dB)/SSIM). The best results under each data situation are marked in red.
4.5. Spectrum Adaptability Analysis
The spectrum is also an important factor affecting SR performance. In this subsection, we explore whether the SR model trained with a certain band is applicable to other infrared bands. The Landsat-8 dataset is used since it has multiple infrared spectrum bands with the same spatial resolution. The 30m data of Landsat-8 is regarded as HR data. LR data for training is down-sampled from HR data. As for supervised training, we train SR models with , and scales for bands B5, B6, B7, B10 and B11, respectively. Besides, we only train the unsupervised model on scale , to avoid large-scale down-sampling during the training process. Experimental results are shown in Table 9 and Table 10.

Table 9.
Results of spectrum adaptability for supervised learning (PSNR(dB)/SSIM). The best results of every spectrum are marked in red.

Table 10.
Results of spectrum adaptability for unsupervised learning (PSNR(dB)/SSIM). The best results of every spectrum are marked in red.
We can see that although they are all infrared remote sensing data with the same resolution, the difference in the spectrum of the training data will also have a great impact on the performance, which is more obvious in the PSNR index. In most cases, the SR model achieves the best results when testing images have the same spectrum as the training data. Sometimes, an SR model trained by a similar spectrum performs better than the model trained by its corresponding spectrum, and the gap between them is usually small. Such gap can be clearly shown in Figure 6, where we use the results obtained by the model trained by the same spectrum as the performance benchmark for each band and show the difference of each model with its benchmark. It can be seen that for bands B5, B6, and B7, the models trained by B5, B6, and B7 usually perform well. The models trained by B10 and B11 always achieve better SRs of B10 and B11. B5 maintains the rule that the benchmark result is the best, and the training data cannot be replaced by other spectra. Figure 7 shows a partial image of B5 testing set. It can be seen that the model trained by B10 and B11 has a poor recovery effect on the small lines. Compared with other bands, B10 and B11 have less volatility and better band adaptability. However, when the scale factor is 4, the band adaptability is extremely reduced, and the best performance can be obtained only when the data matches.
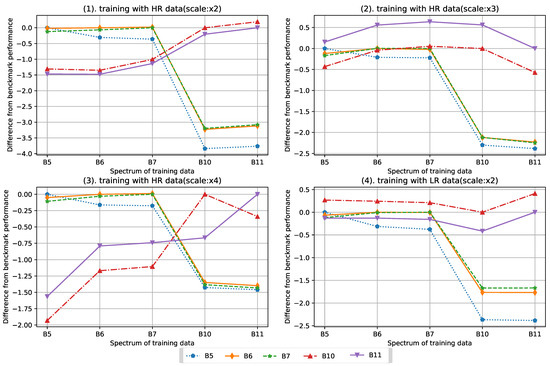
Figure 6.
PSNR performance difference between each band and their benchmark result. The benchmark of each band refers to the result obtained by the model trained with the same band.

Figure 7.
Visual results of B5 testing set. The titles of subfigures (b–f) represent the training set of SR models.
5. Discussions
5.1. Training Mode Selection
Our framework can derive a variety of training modes, and can be trained in supervised, weakly supervised or unsupervised ways. Therefore, there should be an optimal choice corresponding to different data situations. Based on the experimental analysis in Section 4.1, we can draw the following conclusion. First, when using real paired HR-LR images to train the SR model, a single loop is sufficient. Second, when there are HR images in the training set, the backward loop can achieve better SR performance on the real LR data. We even do not need to consider whether we have the unpaired real LR images, because they are not needed in the backward mode. The last and most important point is that when there is only LR training data, i.e., the SR model is trained in an unsupervised manner, the forward loop mode is the best choice.
5.2. Advantages and Limitations
Our proposed closed-loop framework is designed to super-resolve infrared remote-sensing LR images in the real world. It can be trained in the ways of supervised learning, weakly supervised learning and unsupervised learning. Especially, training with LR input only in an unsupervised manner gives our method better practical utility. However, given real paired HR-LR data, the supervised methods EDSR [52] and SRFBN [53] may perform better than ours. However, for more general situations when supervised methods cannot work, i.e., weakly supervised learning and unsupervised learning, our method has obvious advantages. It should be noticed that the way to train an unsupervised network by a single image may be unstable due to relatively low pixel values and low contrast of infrared remote sensing images, e.g., UGSR [37] and EUSR [38]. Such unstableness of SR results makes UGSR and EUSR face difficulties in the practice of infrared remote sensing image super-resolution. While owing to the design of the closed-loops, our framework can achieve stable and comprehensively optimal SR results.
5.3. Adaptability of Resolution and Spectrum
Remote sensing images and natural images are quite different. Due to the long imaging distance, the spatial resolution of each part of the remote sensing image tends to be consistent. However, the spatial resolution in different areas of natural images often differs due to the different distances between the imaging object and the lens, resulting in blocks of different resolutions on the same image. Therefore, the super-resolution reconstruction of natural images does not need to explain and study the specific resolution of the image, but only super-resolve the input image for a certain up-scaling factor. Since remote sensing images have clear resolution levels, it is valuable to study the SR performance of testing data with different resolution levels from the training data. In addition, the spectrum is also an important factor for infrared remote sensing. Typical satellites with infrared sensors like Landsat-8 usually have multiple bands of sensing spectrum. Such resolution adaptability and spectrum adaptability analyses are especially needed for infrared remote sensing, but usually neglected in natural image super-resolution. According to our experimental study in Section 4.4 and Section 4.5, data with the higher spatial resolution is more sensitive to the resolution of training data, and SR network for the same up-scaling factor is still recommended to be re-trained with the data of targeting spatial resolution. Besides, as a summary of the experimental analysis of multiple infrared bands of Landsat-8 data, the short-wave infrared bands B6 and B7 are relatively similar in SR performance. We can replace or merge the training set to deal with the lack of training data. It is the same for B10 and B11.
6. Conclusions
In this paper, we have proposed a novel closed-loop framework for super-resolution of infrared remote sensing images. It contains two networks and can flexibly implement multiple closed-loop training modes. Experimental results demonstrate our framework can achieve good super-resolution performance in supervised, weakly supervised and unsupervised situations, and effectively alleviate the impact of synthetic data. In view of the characteristics of infrared remote sensing images, we have conducted research on resolution adaptability and band adaptability, and done comprehensive analysis and discussion. The PSNR result of our method on the PROBA-V dataset is 0.9dB better than the second-best unsupervised super-resolution model. Our method shows outstanding advantages in super-resolution reconstruction of real remote sensing images, which means that our method has great application value in the tasks affected by the spatial resolution of infrared remote sensing data, such as object detection and recognition. Codes and data of this paper will be released to the public at https://github.com/haopzhang/CLN4SR (accessed on 31 January 2023) to accelerate the following related researches.
Author Contributions
Conceptualization, H.Z. and C.Z.; methodology, C.Z. and H.Z.; software, C.Z.; validation, C.Z., H.Z. and F.X.; formal analysis, C.Z.; investigation, C.Z.; resources, H.Z. and Z.J.; data curation, H.Z. and C.Z.; writing—original draft preparation, C.Z.; writing—review and editing, H.Z., F.X. and Z.J.; visualization, C.Z.; supervision, H.Z. and Z.J.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 62271017 and 62271018), and the Fundamental Research Funds for the Central Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Fernandezbeltran, R.; Latorrecarmona, P.; Pla, F. Single-frame super-resolution in remote sensing: A practical overview. Int. J. Remote Sens. 2017, 38, 314–354. [Google Scholar] [CrossRef]
- Pham, M.; Aptoula, E.; Lefevre, S. Feature Profiles from Attribute Filtering for Classification of Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 249–256. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Lin, H.; Shi, Z.; Zou, Z. Fully Convolutional Network With Task Partitioning for Inshore Ship Detection in Optical Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1665–1669. [Google Scholar] [CrossRef]
- Wu, T.; Luo, J.; Fang, J.; Ma, J.; Song, X. Unsupervised Object-Based Change Detection via a Weibull Mixture Model-Based Binarization for High-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 63–67. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Y.; Ding, M.; Ghanem, B. SOD-MTGAN: Small Object Detection via Multi-Task Generative Adversarial Network. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2018; pp. 210–226. [Google Scholar]
- Tatem, A.J.; Lewis, H.G.; Atkinson, P.M.; Nixon, M.S. Super-resolution target identification from remotely sensed images using a Hopfield neural network. IEEE Trans. Geosci. Remote Sens. 2001, 39, 781–796. [Google Scholar] [CrossRef]
- Dai, D.; Wang, Y.; Chen, Y.; Van Gool, L. Is image super-resolution helpful for other vision tasks? In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Lake Placid, NY, USA, 7–10 March 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Zanotta, D.C.; Ferreira, M.P.; Zorte, M.; Shimabukuro, Y. A statistical approach for simultaneous segmentation and classification. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4899–4901. [Google Scholar] [CrossRef]
- Hou, B.; Zhou, K.; Jiao, L. Adaptive Super-Resolution for Remote Sensing Images Based on Sparse Representation with Global Joint Dictionary Model. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2312–2327. [Google Scholar] [CrossRef]
- Liao, R.; Tao, X.; Li, R.; Ma, Z.; Jia, J. Video Super-Resolution via Deep Draft-Ensemble Learning. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 531–539. [Google Scholar] [CrossRef]
- Xu, J.; Liang, Y.; Liu, J.; Huang, Z. Multi-Frame Super-Resolution of Gaofen-4 Remote Sensing Images. Sensors 2017, 17, 2142. [Google Scholar] [CrossRef]
- Yang, C.; Ma, C.; Yang, M. Single-Image Super-Resolution: A Benchmark. In Proceedings of the Europeon Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 372–386. [Google Scholar]
- Yang, D.; Li, Z.; Xia, Y.; Chen, Z. Remote sensing image super-resolution: Challenges and approaches. In Proceedings of the IEEE International Conference on Digital Signal Processing, Singapore, 21–24 July 2015; pp. 196–200. [Google Scholar]
- Pohl, C.; Genderen, J.V. Remote Sensing Image Fusion. In Encyclopedia of Image Processing; Laplante, P.A., Ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 627–640. [Google Scholar]
- Harris, J.L. Diffraction and Resolving Power. J. Opt. Soc. Am. 1964, 54, 931–936. [Google Scholar] [CrossRef]
- Turkowski, K. Filters for common resampling tasks. In Graphics Gems; Glassner, A.S., Ed.; Morgan Kaufmann: San Diego, CA, USA, 1990; pp. 147–165. [Google Scholar]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Nasrollahi, K.; Moeslund, T. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef]
- Irani, M.; Peleg, S. Improving resolution by image registration. Graph. Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Schultz, R.R.; Stevenson, R.L. Extraction of high-resolution frames from video sequences. IEEE Trans. Image Process. 1996, 5, 996–1011. [Google Scholar] [CrossRef] [PubMed]
- Stark, H.; Oskoui, P. High-resolution image recovery from image-plane arrays, using convex projections. J. Opt. Soc. Am. A 1989, 6, 1715–1726. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Syrris, V.; Ferri, S.; Ehrlich, D.; Pesaresi, M. Image Enhancement and Feature Extraction Based on Low-Resolution Satellite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1986–1995. [Google Scholar] [CrossRef]
- Timofte, R.; De, V.; Gool, L.V. Anchored Neighborhood Regression for Fast Example-Based Super-Resolution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1920–1927. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Polatkan, G.; Zhou, M.; Carin, L.; Blei, D.M.; Daubechies, I. A Bayesian Nonparametric Approach to Image Super-Resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 346–358. [Google Scholar] [CrossRef]
- Efrat, N.; Glasner, D.; Apartsin, A.; Nadler, B.; Levin, A. Accurate Blur Models vs. Image Priors in Single Image Super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2832–2839. [Google Scholar] [CrossRef]
- Michaeli, T.; Irani, M. Blind Deblurring Using Internal Patch Recurrence. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 783–798. [Google Scholar]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 349–356. [Google Scholar]
- Huang, J.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Shocher, A.; Cohen, N.; Irani, M. “Zero-Shot” Super-Resolution Using Deep Internal Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Haut, J.M.; Fernandezbeltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A New Deep Generative Network for Unsupervised Remote Sensing Single-Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Sheikholeslami, M.M.; Nadi, S.; Naeini, A.A.; Ghamisi, P. An Efficient Deep Unsupervised Superresolution Model for Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1937–1945. [Google Scholar] [CrossRef]
- Zhu, J.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, S.; Zhang, J.; Zhang, Y.; Dong, C.; Lin, L. Unsupervised Image Super-Resolution Using Cycle-in-Cycle Generative Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 814–81409. [Google Scholar] [CrossRef]
- Ferrari, V.; Hebert, M.; Sminchisescu, C.; Weiss, Y. (Eds.) To Learn Image Super-Resolution, Use a GAN to Learn How to Do Image Degradation First; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Wang, P.; Zhang, H.; Zhou, F.; Jiang, Z. Unsupervised Remote Sensing Image Super-Resolution Using Cycle CNN. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3117–3120. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, P.; Jiang, Z. Nonpairwise-Trained Cycle Convolutional Neural Network for Single Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4250–4261. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, J.; Wang, J.; Chen, Q.; Cao, J.; Deng, Z.; Xu, Y.; Tan, M. Closed-Loop Matters: Dual Regression Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5406–5415. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 294–310. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Märtens, M.; Izzo, D.; Krzic, A.; Cox, D. Super-resolution of PROBA-V images using convolutional neural networks. Astrodynamics 2019, 3, 387–402. [Google Scholar] [CrossRef]
- Kelvins-PROBA-V Super Resolution—Data. Available online: https://kelvins.esa.int/proba-v-super-resolution/data/ (accessed on 20 November 2019).
- Earth Explorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 20 November 2019).
- Zhang, Y.; He, X.; Jing, M.; Fan, Y.; Zeng, X. Enhanced Recursive Residual Network for Single Image Super-Resolution. In Proceedings of the 2019 IEEE 13th International Conference on ASIC, Chongqing, China, 29 October–1 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3862–3871. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Zhao, N.; Wei, Q.; Basarab, A.; Dobigeon, N.; Kouame, D.; Tourneret, J. Fast Single Image Super-Resolution Using a New Analytical Solution for ℓ2 – ℓ2 Problems. IEEE Trans. Image Process. 2016, 25, 3683–3697. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Siu, W. Single image super-resolution using Gaussian process regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CL, USA, 20–25 June 2011; pp. 449–456. [Google Scholar]
- Soh, J.W.; Cho, S.; Cho, N.I. Meta-Transfer Learning for Zero-Shot Super-Resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3513–3522. [Google Scholar] [CrossRef]
- Liu, Z.S.; Siu, W.C.; Wang, L.W.; Li, C.T.; Cani, M.P.; Chan, Y.L. Unsupervised Real Image Super-Resolution via Generative Variational AutoEncoder. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 1788–1797. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Dong, X.; Xu, Q.; Yang, J.; An, W.; Guo, Y. Unsupervised Degradation Representation Learning for Blind Super-Resolution. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 10576–10585. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
