Superpixel Generation for Polarimetric SAR Images with Adaptive Size Estimation and Determinant Ratio Test Distance
Abstract
1. Introduction
- The adaptive size estimation of the initial superpixel via the structural complexity is proposed for PolSAR image superpixel generation for the first time.
- The DRT distance, with superior similarity measurement ability and computational efficiency compared to other distance measurements for PolSAR images, is utilized to generate compact superpixels.
- Extensive experiments conducted on five real-world PolSAR data sets effectively demonstrate that the proposed CEN can adaptively estimate . Our proposed method can provide better computational performance with higher boundary adherence than six competitive superpixel generation methods.
2. Determinant Ratio Test Distance
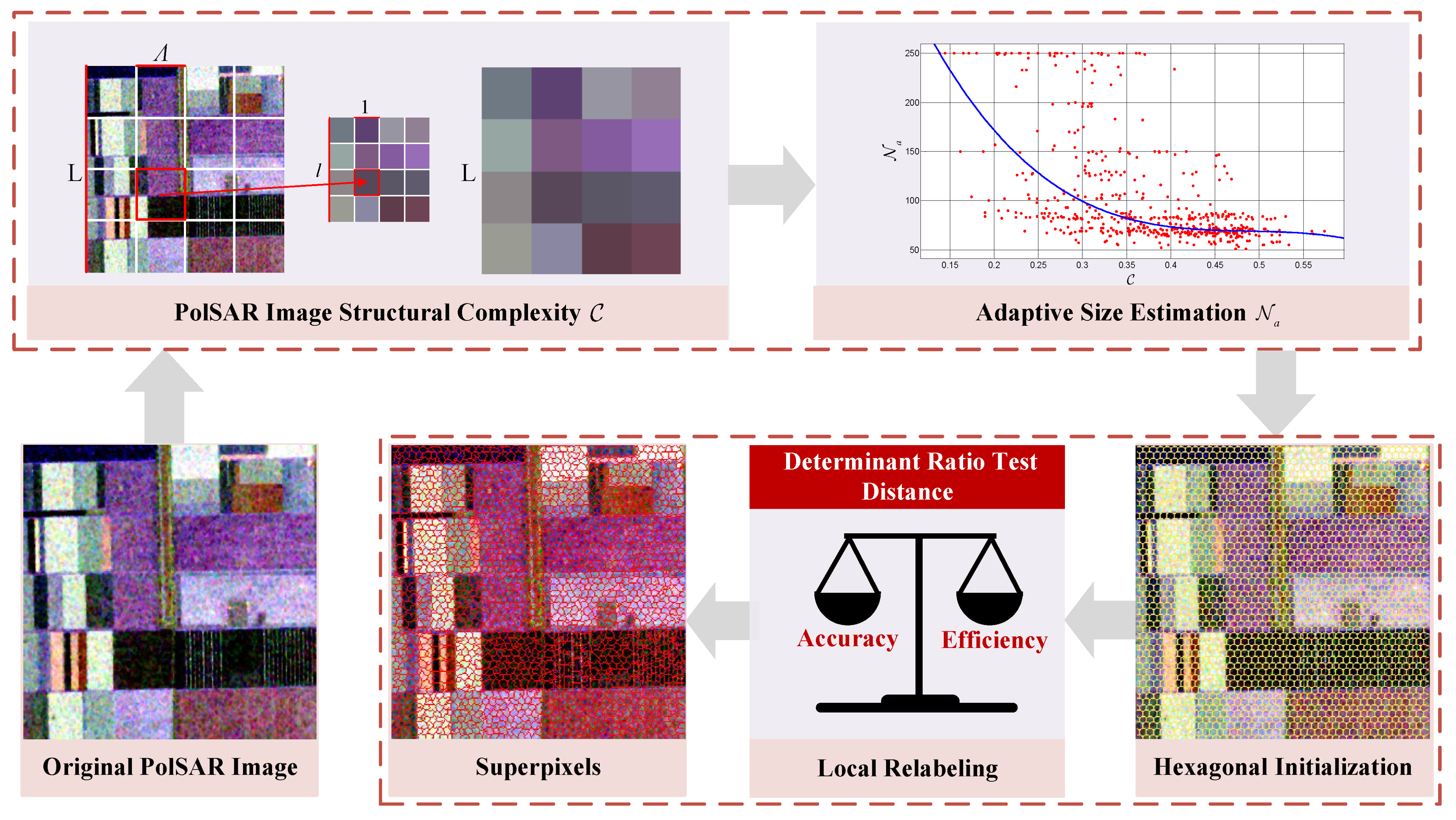
3. Materials and Methods
3.1. PolSAR Image Structural Complexity
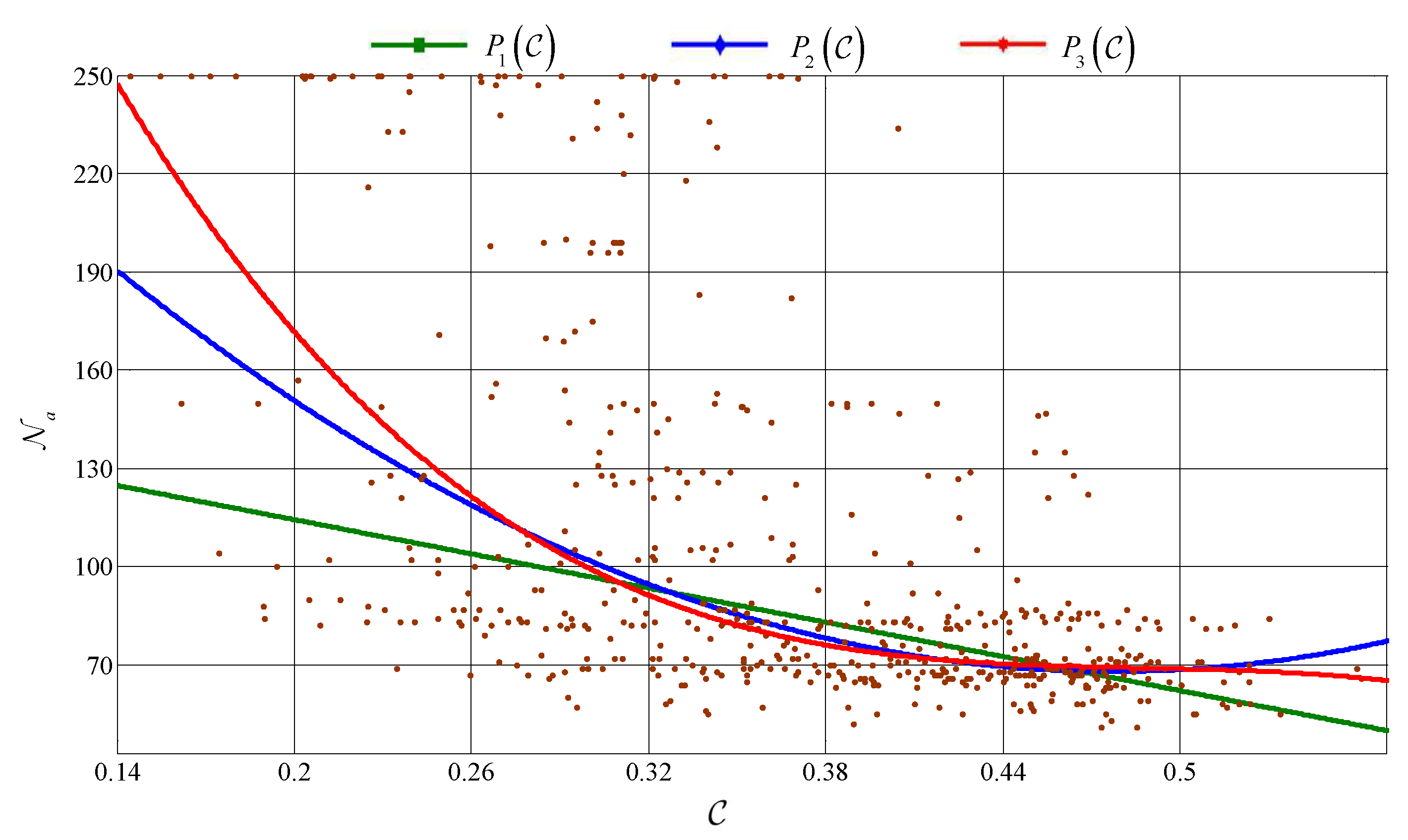
3.2. Estimation of the Adaptive Initial Superpixel Size
- (1)
- Parameter initialization. Input a PolSAR image. Set values of the patch size, the presupposed difference between the patches , and a predefined threshold .
- (2)
- Pseudo-cropping. Crop the input PolSAR image to get pseudo-patches with uniform steps. Calculate .
- (3)
- Real cropping. The total number of real-patches of the input PolSAR image is .
- (4)
- Calculate . Obtain real patches with uniform steps. Calculate .
- (5)
- Superpixel generation. Superpixel generation for patch is ; let the input traverse the range . Record the of of the patch .
- (6)
- Calculate differences. Sort the from highest to lowest , and calculate the difference , where .
- (7)
- Calculate . Select the corresponding values of , and sort the corresponding from highest to lowest. Therefore, .
- (8)
- Calculate sample points . Repeat step (5) to step (7) to obtain of patches for the input PolSAR image, and sample points .
3.3. Superpixel Generation Based on the DRT Distance
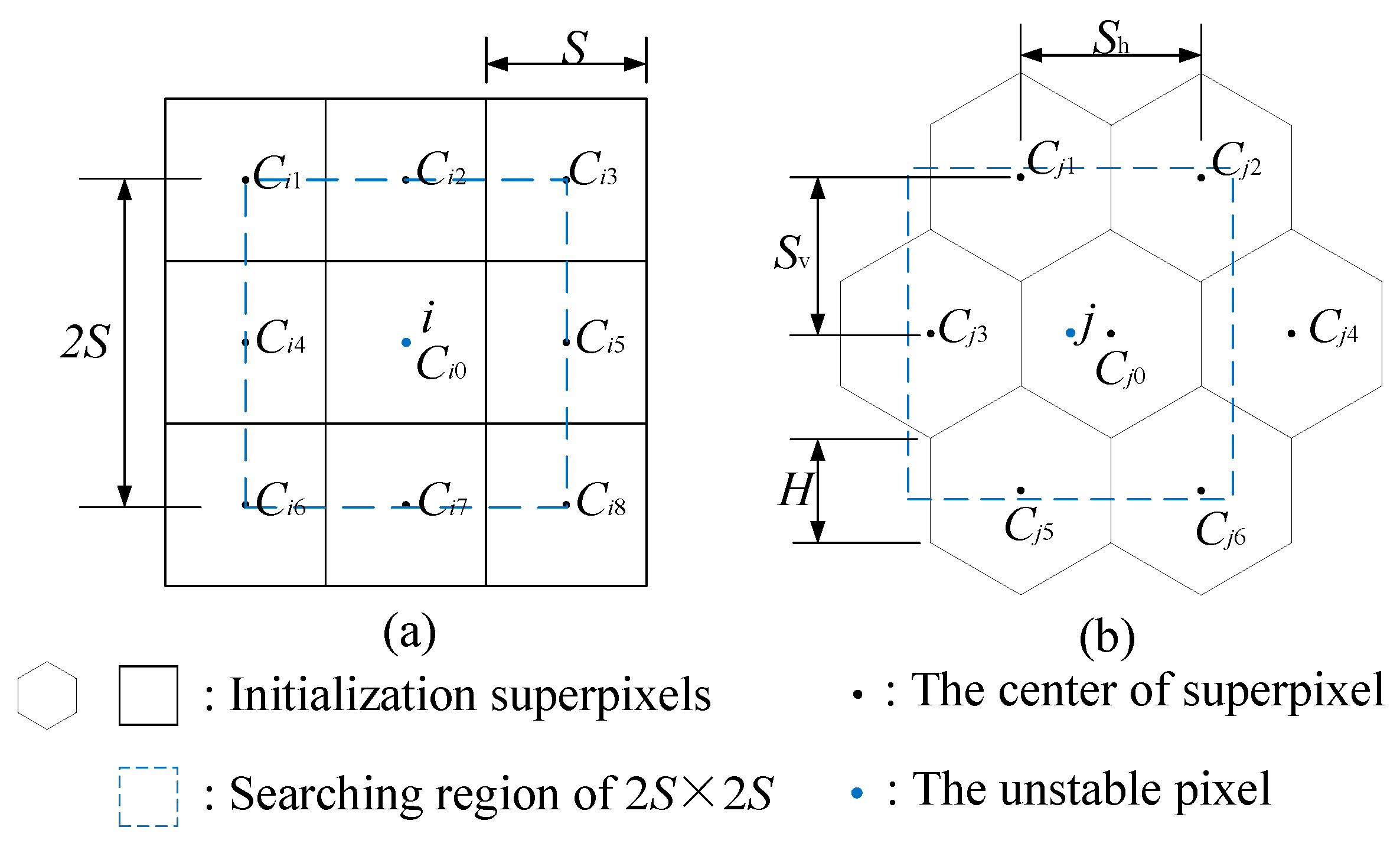
3.3.1. Initialization
3.3.2. Local Relabeling and Postprocessing
- (1)
- Initialization. Initialize the input PolSAR image as a hexagonal distribution by utilizing via the proposed CEN. Set the iteration index .
- (2)
- Local relabeling. If or the unstable pixel set is empty, then the algorithm ends and proceeds to (4). Otherwise, Equation (14) is adopted to relabel all unstable pixels with the searching area.
- (3)
- Updating. Update the superpixel models and the unstable pixel set. Set and return to (2).
- (4)
- Postprocessing. Locate the superpixels with sizes smaller than and merge them with the predefined criterion.
4. Results and Discussion
4.1. Data Sets
4.2. Experimental Setup of the Proposed CEN
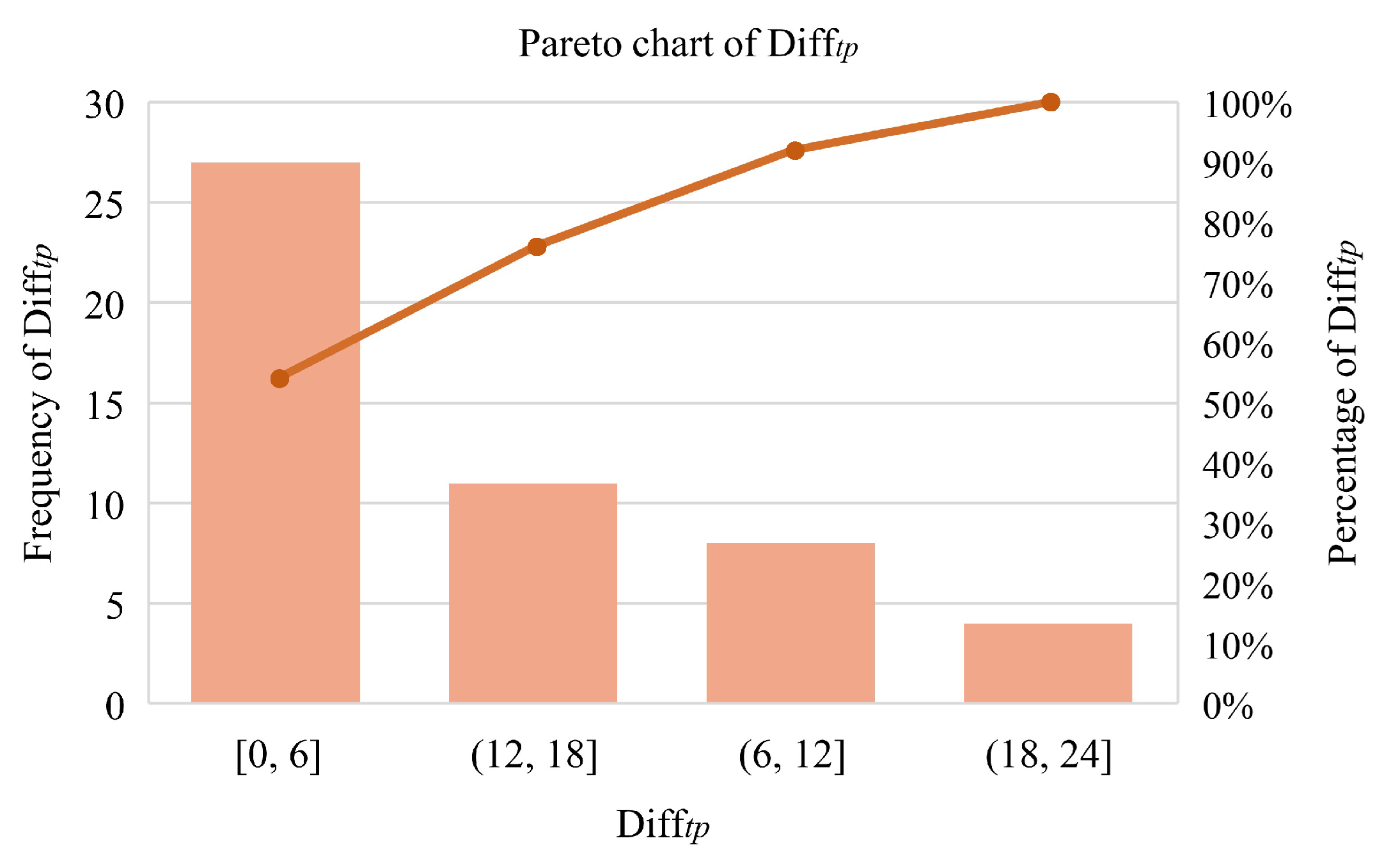
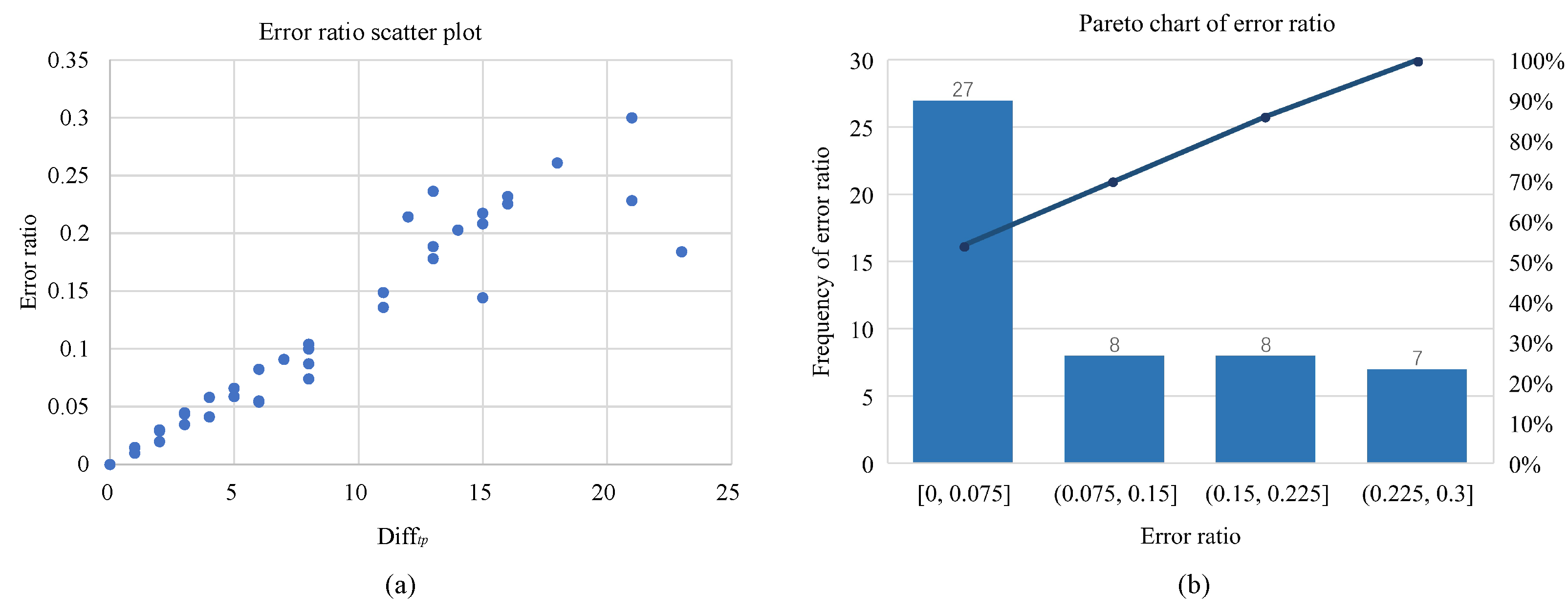
4.3. Curve Effectiveness Evaluation
- (1)
- Input. Input a PolSAR image and the number of test patches .
- (2)
- Generate test patches. Randomly generate the size of the current test patch , and , .
- (3)
- Calculate the optimal value of . Perform steps (5) to (7) of the algorithm details in Section 3.2 to obtain the of patch .
- (4)
- Calculate the estimated value of . Calculate the of patch , and then put this value into Equation (16) to obtain the estimated adaptive .
- (5)
- Calculate the . Calculate the absolute value of the difference between the optimal value and estimated value of the patch . Repeat steps (3) to (5), and calculate the of the patches of the input PolSAR image.
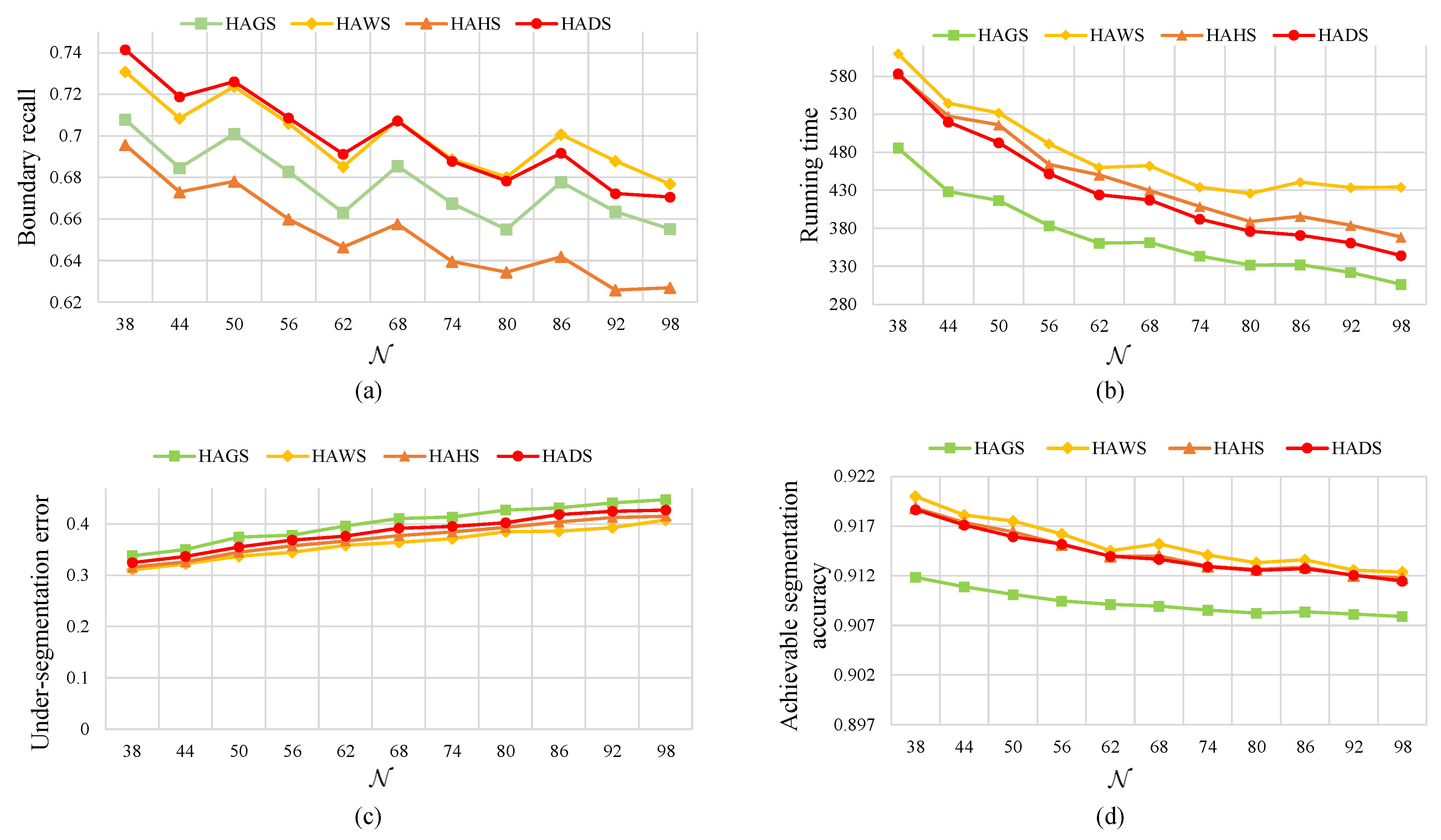
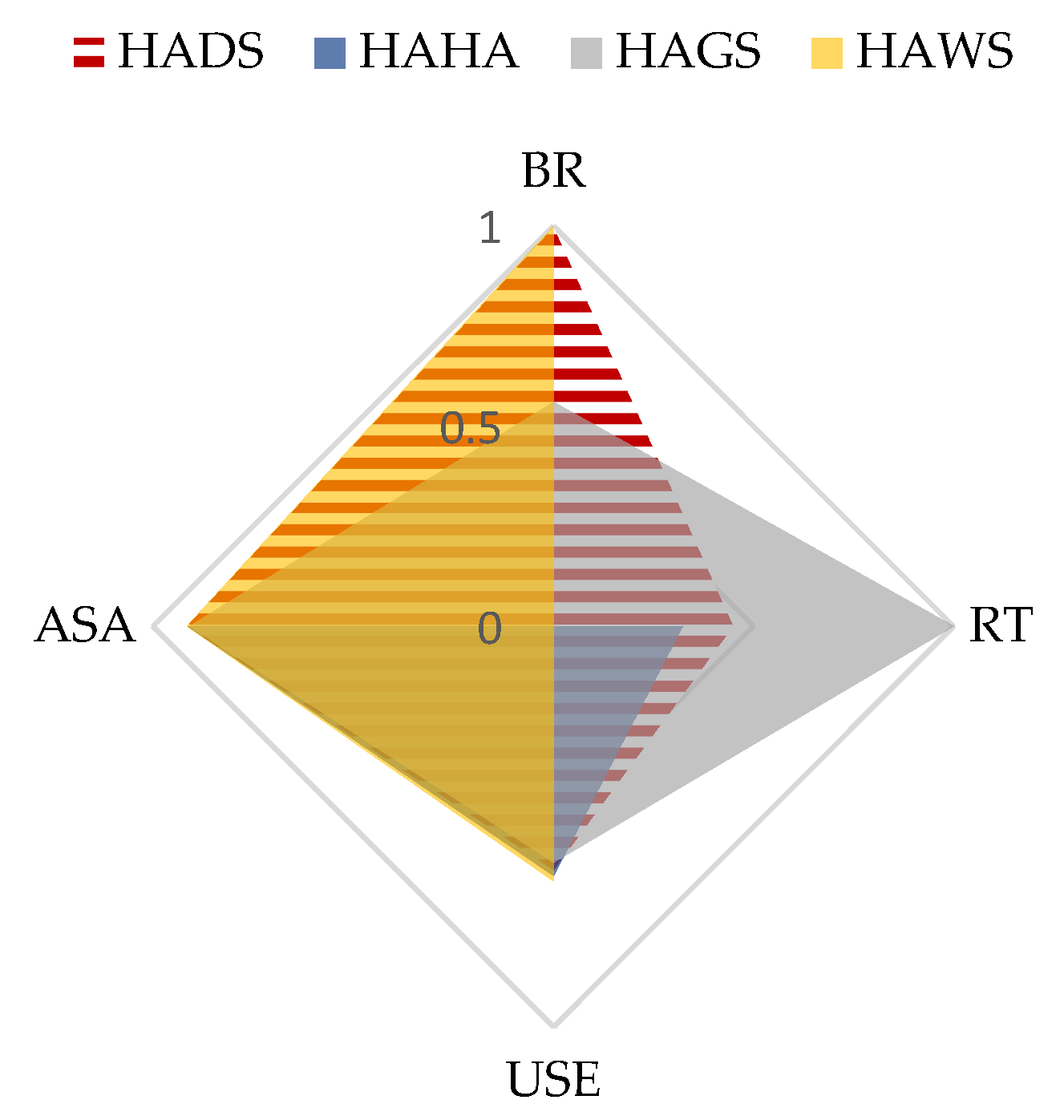
4.4. Superpixel Generation Results on Data Set 1
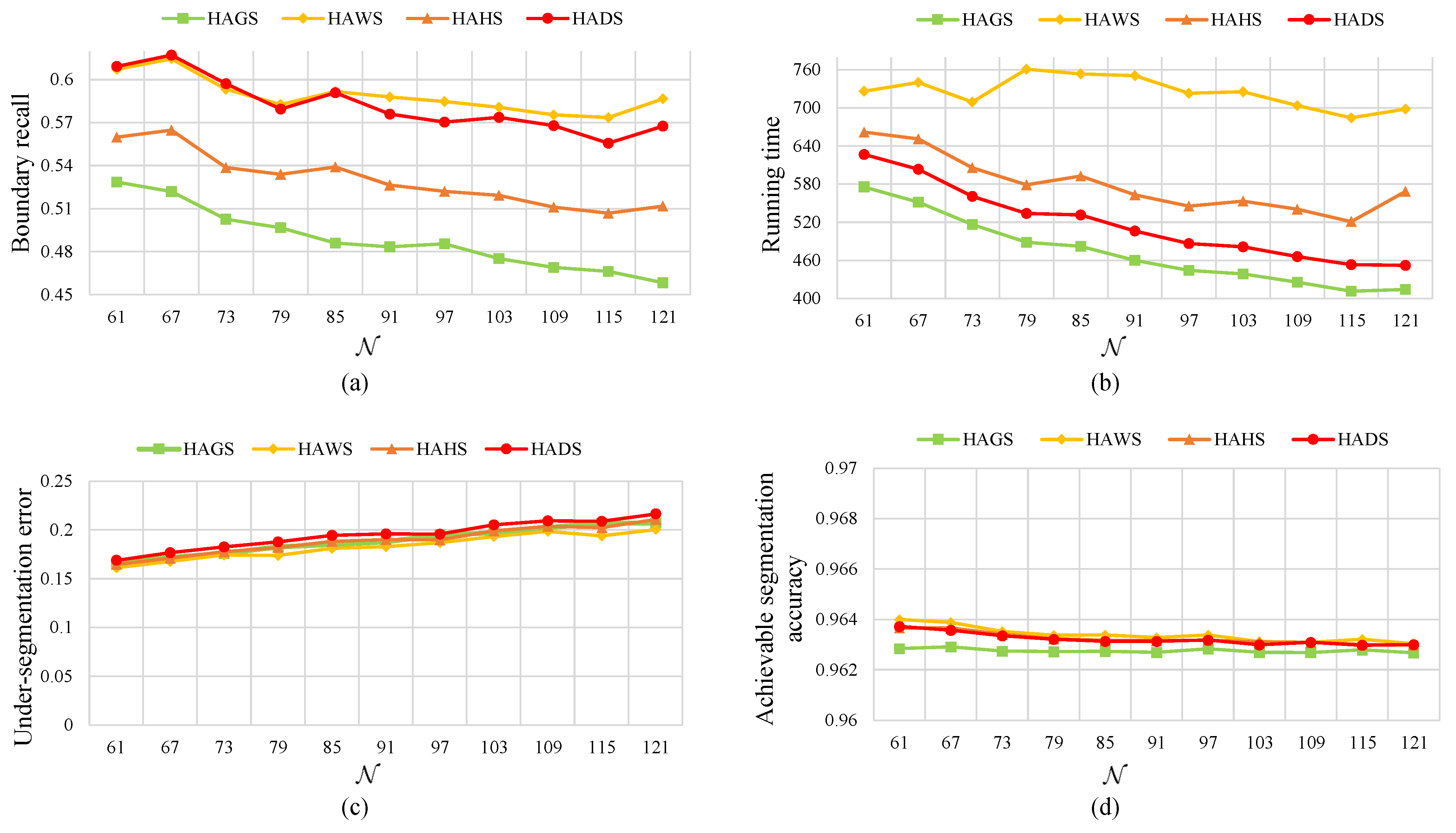
4.5. Superpixel Generation Results on Data Set 5
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, S.; Zhou, F. Semi-Supervised Classification for PolSAR Data With Multi-Scale Evolving Weighted Graph Convolutional Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2911–2927. [Google Scholar] [CrossRef]
- Zhang, T.; Du, Y.; Yang, Z.; Quan, S.; Liu, T.; Xue, F.; Chen, Z.; Yang, J. PolSAR Ship Detection Using the Superpixel-Based Neighborhood Polarimetric Covariance Matrices. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Gadhiya, T.; Roy, A.K. Superpixel-Driven Optimized Wishart Network for Fast PolSAR Image Classification Using Global k-Means Algorithm. IEEE Trans. Geosci. Remote Sens. 2019, 58, 97–109. [Google Scholar] [CrossRef]
- Bi, H.; Sun, J.; Xu, Z. A Graph-Based Semisupervised Deep Learning Model for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2116–2132. [Google Scholar] [CrossRef]
- Tan, W.; Sun, B.; Xiao, C.; Huang, P.; Yang, W. A Novel Unsupervised Classification Method for Sandy Land Using Fully Polarimetric SAR Data. Remote Sens. 2021, 13, 355. [Google Scholar] [CrossRef]
- Meilin, L.; Huanxin, Z.; Qian, M.; Jiachi, S.; Xu, C.; Xianxiang, Q. Unsupervised classification of PolSAR image based on tensor product graph diffusion. Proc. SPIE 2019, 11198, 1–6. [Google Scholar]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vis. Image Underst. CVIU 2018, 166, 1–27. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Sstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Quan, S.; Xiang, D.; Wang, W.; Xiong, B.; Kuang, G. Scattering Feature-Driven Superpixel Segmentation for Polarimetric SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2173–2183. [Google Scholar] [CrossRef]
- Yin, J.; Wang, T.; Du, Y.; Liu, X.; Zhou, L.; Yang, J. SLIC Superpixel Segmentation for Polarimetric SAR Images. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Xiang, D.; Wang, W.; Tang, T.; Guan, D.; Quan, S.; Liu, T.; Su, Y. Adaptive Statistical Superpixel Merging With Edge Penalty for PolSAR Image Segmentation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2412–2429. [Google Scholar] [CrossRef]
- Gao, H.; Wang, C.; Xiang, D.; Ye, J.; Wang, G. TSPol-ASLIC: Adaptive Superpixel Generation With Local Iterative Clustering for Time-Series Quad- and Dual-Polarization SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift analysis and applications. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 3–6 December 2002. [Google Scholar]
- Tuzel, M.; Ramalingam, O.; Liu, M.; Tuzel, O.; Ramalingam, S. Entropy rate superpixel segmentation. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Zhang, Y.; Hartley, R.; Mashford, J.; Burn, S. Superpixels via pseudo-Boolean optimization. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 1387–1394. [Google Scholar]
- Levinshtein, A.; Stere, A.; Kutulakos, K.N.; Fleet, D.J.; Siddiqi, K. TurboPixels: Fast Superpixels Using Geometric Flows. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2290–2297. [Google Scholar] [CrossRef]
- Nock, R.; Nielsen, F. Statistical region merging. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1452. [Google Scholar] [CrossRef]
- Yang, S.; Yuan, X.; Liu, X.; Chen, Q. Superpixel generation for polarimetric SAR using Hierarchical Energy maximization. Comput. Geosci. 2019, 135. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J. Superpixel segmentation using Linear Spectral Clustering. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Liu, B.; Hu, H.; Wang, H.; Wang, K.; Liu, X.; Yu, W. Superpixel-Based Classification With an Adaptive Number of Classes for Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 907–924. [Google Scholar] [CrossRef]
- Wang, W.; Xiang, D.; Ban, Y.; Zhang, J.; Wan, J. Superpixel Segmentation of Polarimetric SAR Data Based on Integrated Distance Measure and Entropy Rate Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4045–4058. [Google Scholar] [CrossRef]
- Lang, F.; Yang, J.; Li, D.; Shi, L.; Wei, J. Mean-Shift-Based Speckle Filtering of Polarimetric SAR Data. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 4440–4454. [Google Scholar] [CrossRef]
- Fengkai, L.; Jie, Y.; Shiyong, Y.; Fachao, Q. Superpixel Segmentation of Polarimetric Synthetic Aperture Radar (SAR) Images Based on Generalized Mean Shift. Remote Sens. 2018, 10, 1592. [Google Scholar]
- Hu, H.; Liu, B.; Zhang, Z.; Guo, W.; Yu, W. Superpixel generation for synthetic aperture radar imagery using edge-dominated local clustering. J. Appl. Remote Sens. 2018, 12, 045006. [Google Scholar] [CrossRef]
- Bagrov, A.A.; Iakovlev, I.A.; Iliasov, A.A.; Katsnelson, M.I.; Mazurenko, V.V. Multiscale structural complexity of natural patterns. Proc. Natl. Acad. Sci. USA 2020, 117, 30241–30251. [Google Scholar] [CrossRef]
- Feng, J.; Cao, Z.; Pi, Y. Polarimetric Contextual Classification of PolSAR Images Using Sparse Representation and Superpixels. Remote Sens. 2014, 6, 7158–7181. [Google Scholar] [CrossRef]
- Qin, F.; Guo, J.; Lang, F. Superpixel Segmentation for Polarimetric SAR Imagery Using Local Iterative Clustering. IEEE Geosci. Remote Sens. Lett. 2017, 12, 13–17. [Google Scholar]
- Yue, Z.; Zou, H.; Luo, T.; Qin, X.; Zhou, S.; Ji, K. A Fast Superpixel Segmentation Algorithm for PolSAR Images Based on Edge Refinement and Revised Wishart Distance. Sensors 2016, 16, 1687. [Google Scholar]
- Zhu, S.; Cao, D.; Jiang, S.; Wu, Y.; Hu, P. Fast superpixel segmentation by iterative edge refinement. Electron. Lett. 2015, 51, 230–232. [Google Scholar] [CrossRef]
- Li, M.; Zou, H.; Ma, Q.; Sun, J.; Qin, X. Superpixel Segmentation for PolSAR Images Based on Hexagon Initialization and Edge Refinement. In Proceedings of the ISPRS Archives, Virtual Event, 7–8 October 2020. [Google Scholar]
- Ratha, D.; De, S.; Celik, T.; Bhattacharya, A. Change Detection in Polarimetric SAR Images Using a Geodesic Distance Between Scattering Mechanisms. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1040–1066. [Google Scholar] [CrossRef]
- Akbari, V.; Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T.; Moser, G.; Serpico, S.B. Polarimetric SAR Change Detection With the Complex Hotelling–Lawley Trace Statistic. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3953–3966. [Google Scholar] [CrossRef]
- Bouhlel, N.; Akbari, V.; Méric, S. Change Detection in Multilook Polarimetric SAR Imagery With Determinant Ratio Test Statistic. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Qin, X.; Zou, H.; Yu, W.; Wang, P. Superpixel-Oriented Classification of PolSAR Images Using Complex-Valued Convolutional Neural Network Driven by Hybrid Data. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10094–10111. [Google Scholar] [CrossRef]
- Goodman, N.R. Statistical Analysis Based on a Certain Multivariate Complex Gaussian Distribution. Ann. Math. Stat. 1963, 34, 152–177. [Google Scholar] [CrossRef]
- Li, M.; Zou, H.; Qin, X.; Dong, Z.; Sun, L.; Wei, J. Efficient Superpixel Generation for Polarimetric SAR Images with Cross-Iteration and Hexagonal Initialization. Remote Sens. 2022, 14, 2914. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, T.; Sun, Z.; Nie, W.; Fang, Z. Middle- and Long-Term UT1-UTC Prediction Based on Constrained Polynomial Curve Fitting, Weighted Least Squares and Autoregressive Combination Model. Remote Sens. 2022, 14, 3252. [Google Scholar] [CrossRef]
- Ai, J.; Wang, F.; Mao, Y.; Luo, Q.; Yao, B.; Yan, H.; Xing, M.; Wu, Y. A Fine PolSAR Terrain Classification Algorithm Using the Texture Feature Fusion-Based Improved Convolutional Autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Yommy, A.S.; Liu, R.; Wu, A.S. SAR Image Despeckling Using Refined Lee Filter. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2015. [Google Scholar]















| Description | Data Set 1 | Data Set 2 | Data Set 3 | Data Set 4 | Data Set 5 |
|---|---|---|---|---|---|
| Organization | NASA/JPL | NASA/JPL | NASA/JPL | DLR | CASC |
| System | AIRSAR | AIRSAR | AIRSAR | ESAR | Gaofen-3 |
| Location | Flevoland | Flevoland | San Francisco | Oberpfaffenhofen | Changsha |
| Imaging year | 1991 | 1989 | - | 1999 | 2017 |
| Band | L | L | C | L | C |
| Resolution | ∼ 12 × 6 m | - | - | - | 8 m |
| Size | 750 × 1024 | 768 × 1024 | 900 × 1024 | 1300 × 1200 | 1000 × 1000 |
| Data Sets | Patch Size | Number of Patches | Number of Superpixel Generation | |||
|---|---|---|---|---|---|---|
| Data set 1 | 512 × 512 256 × 256 | 0.066 0.207 | 0.003 | 21 63 | 21 × 226 63 × 226 | |
| Data set 2 | 512 × 512 256 × 256 | 0.080 0.208 | 0.003 | 28 63 | 28 × 226 63 × 226 | |
| Data set 3 | 512 × 512 256 × 256 | 0.187 0.305 | 0.003 | 63 99 | 63 × 226 99 × 226 | |
| Data set 4 | 512 × 512 256 × 256 | 0.286 0.384 | 0.003 | 90 132 | 90 × 226 132 × 226 |
| n | ER | EA () | EA () | |||
|---|---|---|---|---|---|---|
| 65 | 0.5216 | 1 2 | 58 70 | 0.10 0.08 | 13% 49% | 76% 78% |
| Methods | POL-SLIC | POL-LSC | POL-HLT | HAGS | HAWS | HAHS | HADS | |
|---|---|---|---|---|---|---|---|---|
| Criteria | ||||||||
| BR | 0.51 | 0.61 | 0.67 | 0.69 | 0.71 | 0.66 | 0.71 | |
| RT(s) | 831.50 | 203.44 | 603.19 | 361.41 | 462.35 | 429.69 | 417.08 | |
| USE | 0.37 | 0.37 | 0.38 | 0.41 | 0.36 | 0.38 | 0.39 | |
| ASA | 0.91 | 0.91 | 0.91 | 0.91 | 0.92 | 0.91 | 0.91 | |
| n | ER | EA () | EA () | |||
|---|---|---|---|---|---|---|
| 87 | 0.3213 | 1 2 | 93 94 | 0.07 0.09 | 13% 48% | 77% 79% |
| Methods | POL-SLIC | POL-LSC | POL-HLT | HAGS | HAWS | HAHS | HADS | |
|---|---|---|---|---|---|---|---|---|
| Criteria | ||||||||
| BR | 0.37 | 0.52 | 0.54 | 0.48 | 0.59 | 0.53 | 0.58 | |
| RT(s) | 1085.21 | 255.90 | 752.99 | 460.02 | 750.68 | 562.82 | 506.24 | |
| USE | 0.23 | 0.20 | 0.20 | 0.19 | 0.18 | 0.19 | 0.20 | |
| ASA | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zou, H.; Qin, X.; Dong, Z.; Sun, L.; Wei, J. Superpixel Generation for Polarimetric SAR Images with Adaptive Size Estimation and Determinant Ratio Test Distance. Remote Sens. 2023, 15, 1123. https://doi.org/10.3390/rs15041123
Li M, Zou H, Qin X, Dong Z, Sun L, Wei J. Superpixel Generation for Polarimetric SAR Images with Adaptive Size Estimation and Determinant Ratio Test Distance. Remote Sensing. 2023; 15(4):1123. https://doi.org/10.3390/rs15041123
Chicago/Turabian StyleLi, Meilin, Huanxin Zou, Xianxiang Qin, Zhen Dong, Li Sun, and Juan Wei. 2023. "Superpixel Generation for Polarimetric SAR Images with Adaptive Size Estimation and Determinant Ratio Test Distance" Remote Sensing 15, no. 4: 1123. https://doi.org/10.3390/rs15041123
APA StyleLi, M., Zou, H., Qin, X., Dong, Z., Sun, L., & Wei, J. (2023). Superpixel Generation for Polarimetric SAR Images with Adaptive Size Estimation and Determinant Ratio Test Distance. Remote Sensing, 15(4), 1123. https://doi.org/10.3390/rs15041123







