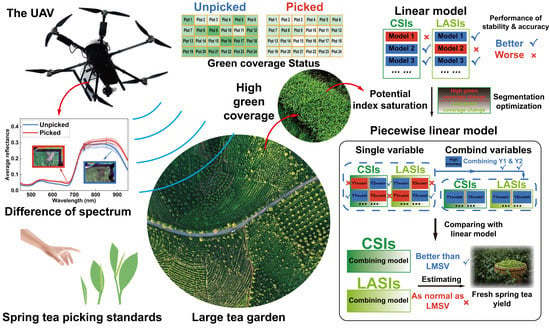
Fresh Yield Estimation of Spring Tea via Spectral Differences in UAV Hyperspectral Images from Unpicked and Picked Canopies
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Research Subject and Test Plot Design
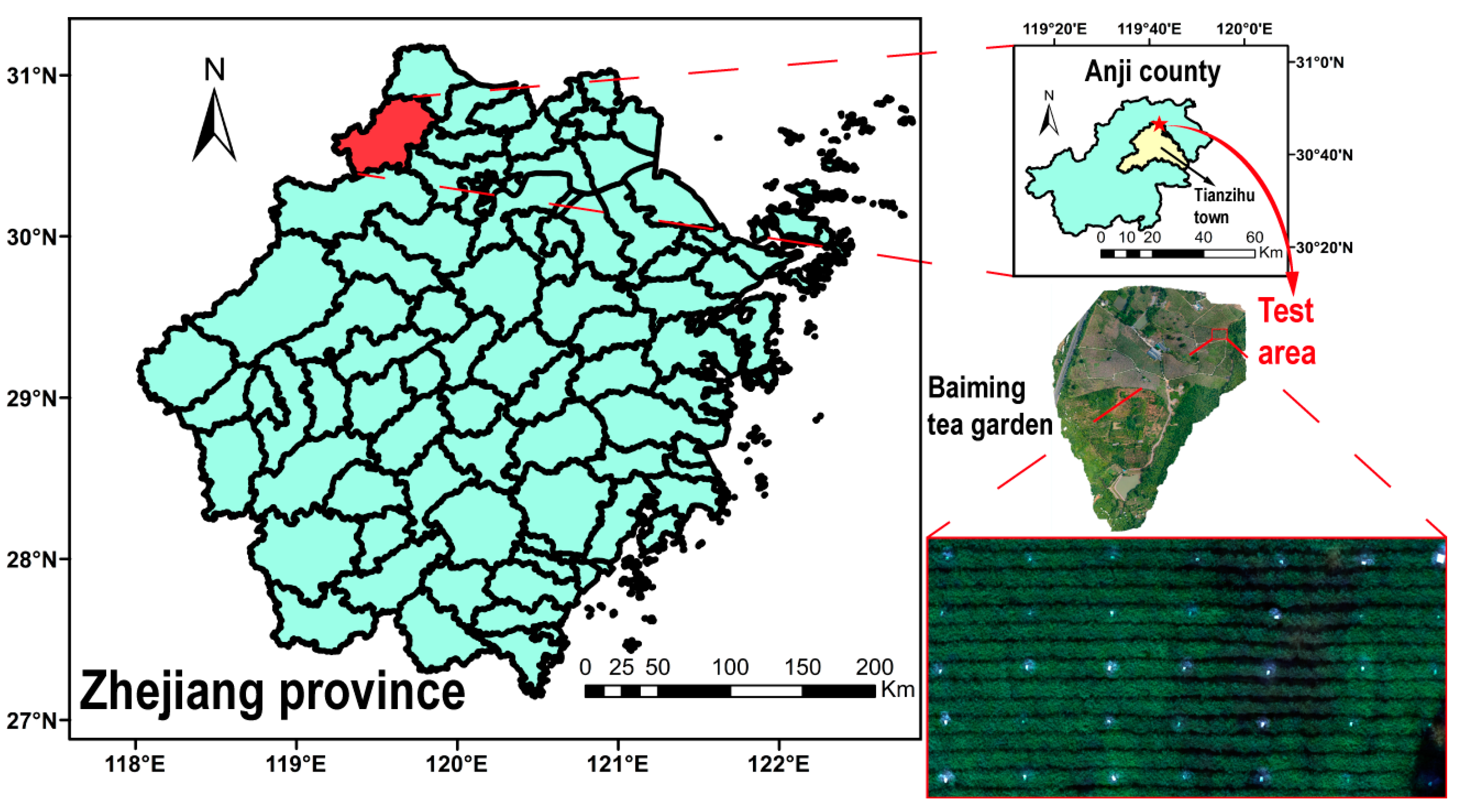
2.1.2. Hyperspectral Data Collection and Preprocessing
2.1.3. Spring Tea Yield Data Collecting and Preprocessing
2.1.4. Auxiliary Data Acquisition
- (1)
- Chlorophyll ratio and spectra between fresh tea and mature leaf measurements
- (2)
- Area measurement/determination of fresh tea components
- (3)
- Green coverage change acquired via unpicked and picked tea tree canopy data

2.2. Methods
2.2.1. Research Technical Framework
2.2.2. Fresh Yield Estimation Method for Spring Tea by Heperspectral Remote Sensing Data
- (1)
- Vegetation index selection for suitable spring tea fresh yield estimation
- (2)
- LMSV modeling and validation
- (3)
- PLMSV modeling and validation
- (4)
- PLMCV modeling and validation

3. Results and Analysis
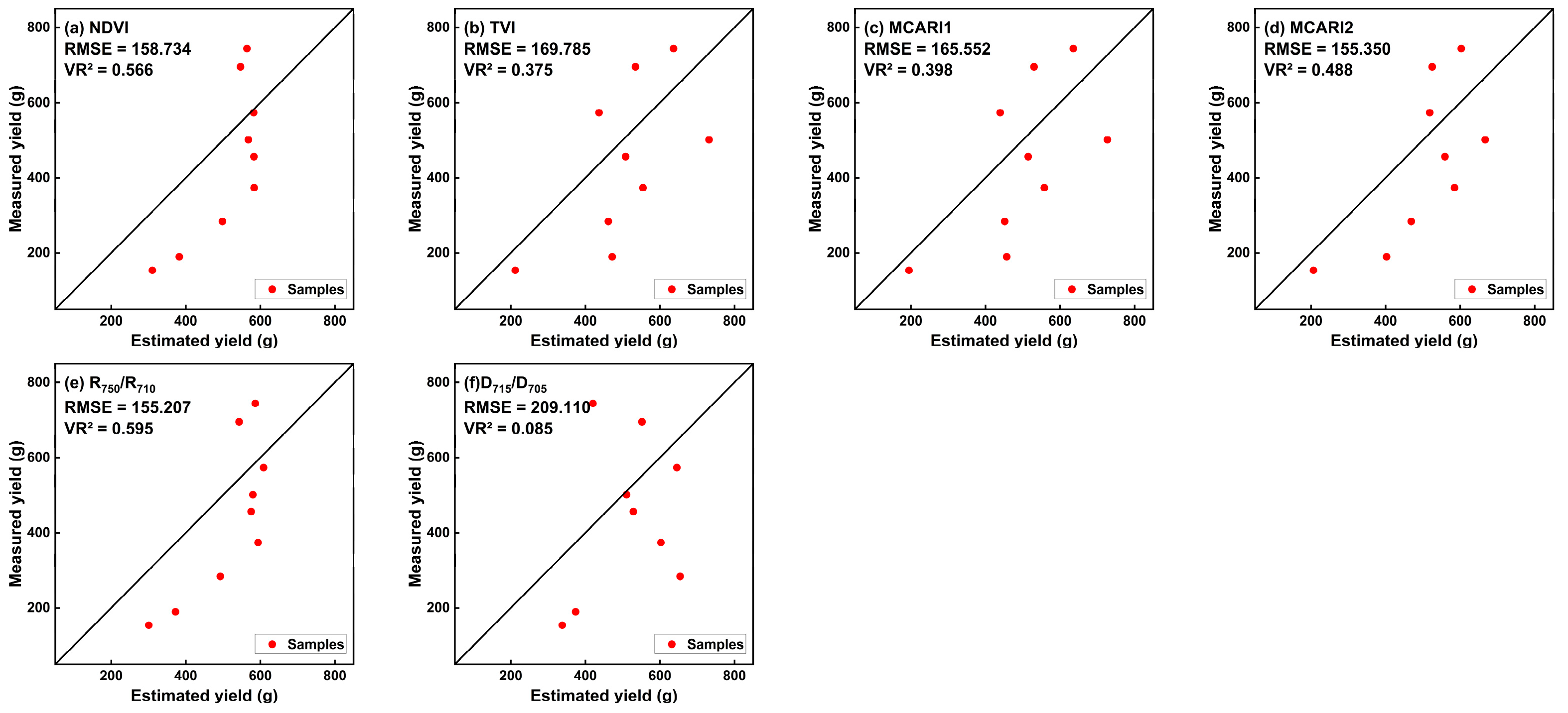
3.1. Vegetation Index Selection for Suitable Spring Tea Fresh Yield Estimation
3.2. LMSV Establishment and Validation for Spring Tea Fresh Yield Estimation
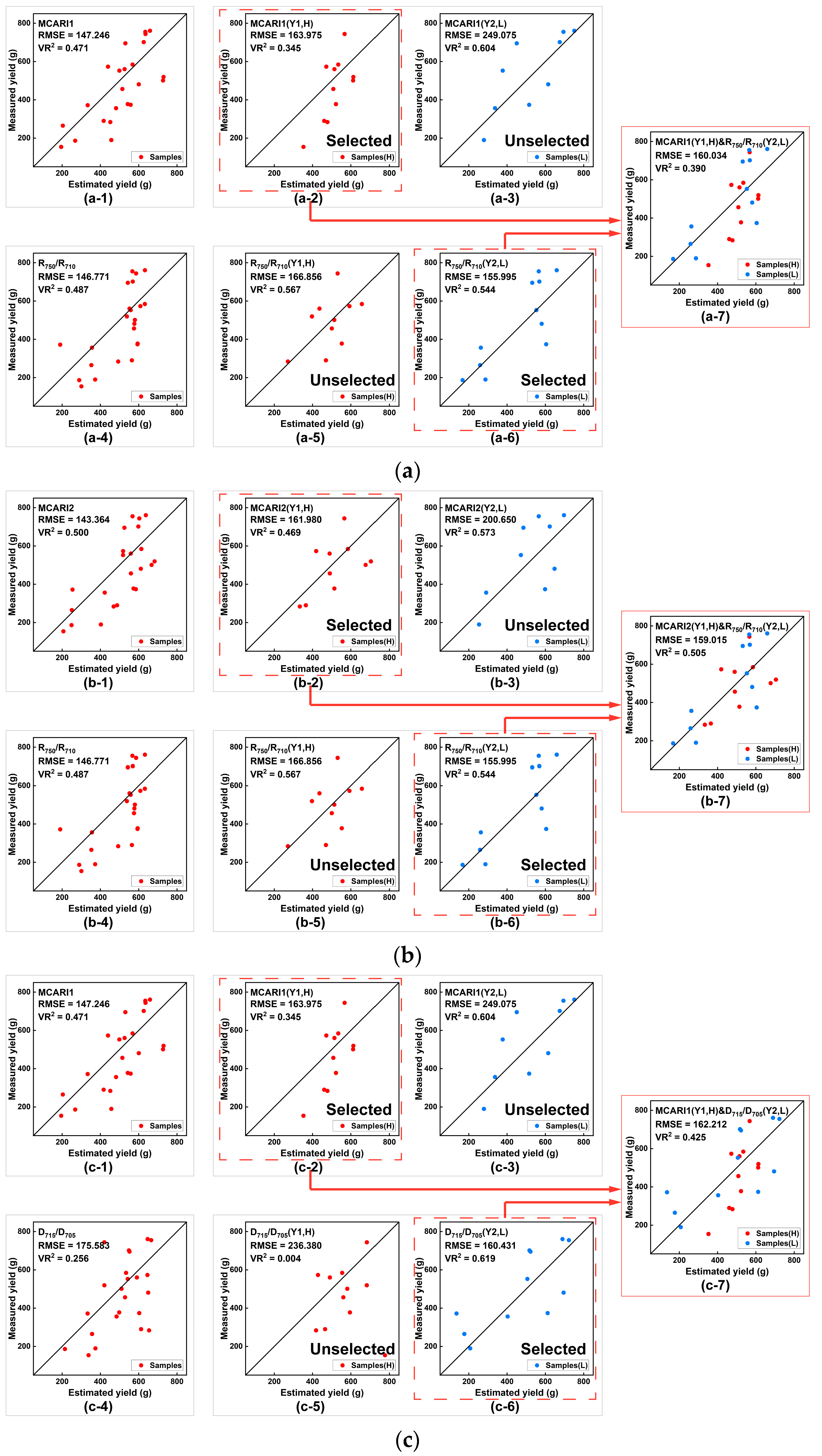
3.3. PLMSV Establishment and Validation for Spring Tea Fresh Yield Estimation
| Type | dVI | Modeling (n = 12) | Validation (m = 12) | ||
|---|---|---|---|---|---|
| Yield Estimation Model | M-R2 | RMSE (g) | V-R2 | ||
| dCSI | GNDVI | Y1 = −32,856dVI − 68.367 | 0.788 ** | 441.949 | 0.460 |
| Y2 = −12,356dVI + 409.49 | 0.452 | 247.639 | 0.443 | ||
| CUR | Y1 = −10,275dVI − 257.67 | 0.394 | 85.067 | 0.884 *** | |
| Y2 = −10,704dVI − 266.59 | 0.567 * | 126.369 | 0.777 ** | ||
| RDVI | Y1 = −9228.1dVI + 154.7 | 0.166 | 135.433 | 0.611 * | |
| Y2 = −15,582dVI − 48.019 | 0.724 ** | 337.852 | 0.733 ** | ||
| GI | Y1 = −1372.9dVI + 425.16 | 0.656 ** | 161.194 | 0.524 * | |
| Y2 = −846.11dVI + 520.87 | 0.551 * | 171.231 | 0.436 | ||
| PSSRa | Y1 = −206.55dVI + 328.4 | 0.73 ** | 163.665 | 0.508 * | |
| Y2 = −126.42dVI + 471.25 | 0.519 * | 179.242 | 0.399 | ||
| PSSRb | Y1 = −270.69dVI + 438.66 | 0.74 ** | 178.225 | 0.468 | |
| Y2 = −163.05dVI + 555.57 | 0.479 | 183.634 | 0.373 | ||
| PSNDa | Y1 = −9862.2dVI + 366.51 | 0.635 ** | 311.933 | 0.496 | |
| Y2 = −4258.5dVI + 529.34 | 0.554 * | 208.107 | 0.476 | ||
| PSNDb | Y1 = −11,273dVI + 479.93 | 0.657 ** | 319.173 | 0.485 | |
| Y2 = −4813.9dVI + 579.56 | 0.555 * | 215.554 | 0.465 | ||
| RARSa | Y1 = −1001.3dVI + 811.07 | 0.677 ** | 203.564 | 0.354 | |
| Y2 = −605.13dVI + 792.27 | 0.404 | 195.751 | 0.263 | ||
| RARSb | Y1 = −342.43dVI + 399.32 | 0.718 ** | 187.745 | 0.459 | |
| Y2 = −200.47dVI + 532.14 | 0.488 | 182.858 | 0.403 | ||
| PSRI | Y1 = 19,446dVI + 403.79 | 0.464 | 245.478 | 0.557 * | |
| Y2 = 9270.7dVI + 529.21 | 0.602 * | 203.659 | 0.514 * | ||
| PRVI | Y1 = −1201.6dVI − 35.5 | 0.775 ** | 252.182 | 0.472 | |
| Y2 = −684.55dVI + 305.65 | 0.499 | 229.277 | 0.432 | ||
| RVI | Y1 = −198.29dVI + 402.67 | 0.743 ** | 169.981 | 0.470 | |
| Y2 = −123.63dVI + 526.68 | 0.482 | 181.704 | 0.369 | ||
| dLASI | NDVI | Y1 = −10,003dVI + 451.51 | 0.645 ** | 316.014 | 0.487 |
| Y2 = −4312.8dVI + 566.44 | 0.555 * | 211.729 | 0.473 | ||
| TVI | Y1 = −22.706dVI + 481.47 | 0.005 | 183.798 | 0.601 * | |
| Y2 = −383.43dVI − 320.9 | 0.717 ** | 359.583 | 0.775 ** | ||
| MCARI1 | Y1 = −2692.6dVI + 343.05 | 0.047 | 142.381 | 0.609 * | |
| Y2 = −12,929dVI − 380.41 | 0.755 ** | 337.802 | 0.770 ** | ||
| MCARI2 | Y1 = −6573.7dVI + 112.36 | 0.325 | 169.586 | 0.614 * | |
| Y2 = −7170.4dVI + 137.65 | 0.69 ** | 260.667 | 0.684 ** | ||
| R750/R710 | Y1 = −4439.1dVI − 187.19 | 0.681 ** | 210.868 | 0.560 * | |
| Y2 = −2293.6dVI + 222.19 | 0.593 * | 179.265 | 0.585 * | ||
| D715/D705 | Y1 = 6982.1dVI + 272.99 | 0.103 | 283.262 | 0.023 | |
| Y2 = −10,886dVI + 929.84 | 0.587 * | 186.288 | 0.746 * | ||
3.4. PLMCV Validation for Spring Tea Fresh Yield Estimation
| Index Type | dVI | LMSV (m = 24) | PLMSV (Y1,H, n = 12) | PLMSV (Y2, L, n = 12) | PLMCV Y1 (H)&Y2 (L) (m = 24) | ||
|---|---|---|---|---|---|---|---|
| RMSE | VR2 | RMSE | VR2 | ||||
| CSI | CUR | 132.017 | 0.618 *** | Y1 = −10,275dVI − 257.67 | — | 124.602 | 0.625 *** |
| CUR | 132.017 | 0.618 *** | — | Y2 = −10,704dVI − 266.59 | |||
| GI | 149.045 | 0.461 *** | Y1 = −1372.9dVI + 425.16 | — | 133.838 | 0.617 *** | |
| CUR | 132.017 | 0.618 *** | — | Y2 = −10,704dVI − 266.59 | |||
| PSSRa | 151.298 | 0.444 *** | Y1 = −206.55dVI + 328.4 | — | 132.143 | 0.630 *** | |
| CUR | 132.017 | 0.618 *** | — | Y2 = −10,704dVI − 266.59 | |||
| PSSRb | 155.832 | 0.411 *** | Y1 = −270.69dVI + 438.66 | — | 136.439 | 0.617 *** | |
| CUR | 132.017 | 0.618 *** | — | Y2 = −10,704dVI − 266.59 | |||
| RVI | 154.562 | 0.419 *** | Y1 = −198.29dVI + 402.67 | — | 133.704 | 0.623 *** | |
| CUR | 132.017 | 0.618 *** | — | Y2 = −10,704dVI − 266.59 | |||
| CUR | 132.017 | 0.618 *** | Y1 = −10,275dVI − 257.67 | — | 137.928 | 0.527 *** | |
| GI | 149.045 | 0.461 *** | — | Y2 = −846.11dVI + 520.87 | |||
| GI | 149.045 | 0.461 *** | Y1 = −1372.9dVI + 425.16 | — | 146.325 | 0.515 *** | |
| GI | 149.045 | 0.461 *** | — | Y2 = −846.11dVI + 520.87 | |||
| PSSRa | 151.298 | 0.444 *** | Y1 = −206.55dVI + 328.4 | — | 144.777 | 0.529 *** | |
| GI | 149.045 | 0.461 *** | — | Y2 = −846.11dVI + 520.87 | |||
| PSSRb | 155.832 | 0.411 *** | Y1 = −270.69dVI + 438.66 | — | 148.708 | 0.516 *** | |
| GI | 149.045 | 0.461 *** | — | Y2 = −846.11dVI + 520.87 | |||
| RVI | 154.562 | 0.419 *** | Y1 = −198.29dVI + 402.67 | — | 146.203 | 0.522 *** | |
| GI | 149.045 | 0.461 *** | — | Y2 = −846.11dVI + 520.87 | |||
| LASI | MCARI1 | 147.246 | 0.471 *** | Y1 = −2692.6dVI + 343.05 | — | 160.034 | 0.390 *** |
| R750/R710 | 146.771 | 0.487 *** | — | Y2 = −2293.6dVI + 222.19 | |||
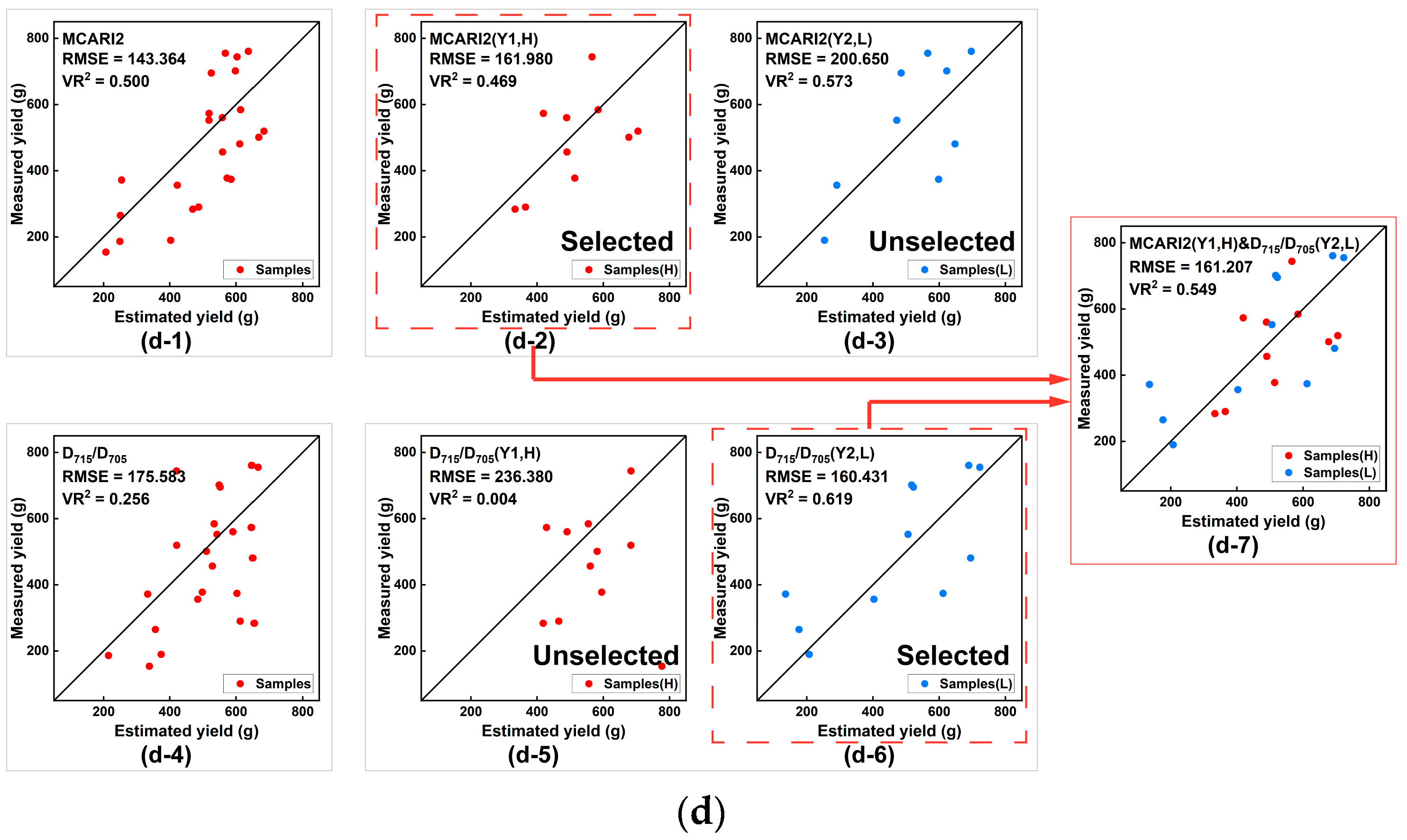
| MCARI2 | 143.364 | 0.500 *** | Y1 = −6573.7dVI + 112.36 | — | 159.015 | 0.505 *** | |
| R750/R710 | 146.771 | 0.487 *** | — | Y2 = −2293.6dVI + 222.19 | |||
| MCARI1 | 147.246 | 0.471 *** | Y1 = −2692.6dVI + 343.05 | — | 162.212 | 0.425 *** | |
| D715/D705 | 175.583 | 0.256 ** | — | Y2 = −10,886dVI + 929.84 | |||
| MCARI2 | 143.364 | 0.500 *** | Y1 = −6573.7dVI + 112.36 | — | 161.207 | 0.549 *** | |
| D715/D705 | 175.583 | 0.256 ** | — | Y2 = −10,886dVI + 929.84 | |||
4. Discussion
4.1. Spectral Difference for Spring Tea Fresh Yield Estimation
4.2. Reducing Saturation of Vegetation Index in High Coverage at Tea Tree Canopy
5. Conclusions
- (1)
- The correlation between 13 dCSIs, 6 dLASIs, and the yield was a linear correlation coefficient over 0.5 and a significance test at the 0.05 level, and the spectral difference determined by using hyperspectral remote sensing can provide the potential ability to estimate the fresh yield of spring tea.
- (2)
- Without considering the saturation of the vegetation index (LMSV), the performance of the selected CSIs for establishing the spring tea fresh yield estimation model was better than that of the selected LASIs. The best performance of these models was based on the CUR and had an encouraging MR2 (0.611) and a 0.01 significance test level, and with good accuracy (RMSE = 146.247 g; VR2 = 0.88).
- (3)
- Considering the saturation of vegetation index (PLMSVs or PLMCVs), the range of the evaluation metrics (RMSE and VR2) of the model estimation yield models from the selected dCSIs and dLASIs were amplified by taking PLMSVs, and the values of RMSE and VR2 of some vegetation index models were optimized. These results show that the PLMSVs could reduce saturation, such as in the CUR model with an ideal RMSE (124.602 g) and VR2 (0.625 at the 0.01 level from the significant test), or in the GI model with a good RMSE (146.325) and VR2 (0.515 at the 0.01 level from the significant test). These vegetation index models showed an obvious improvement when compared with those based on LMSV. In addition, for PLMCVs, the performance of the combined models, including the combination of PSSRa and GI, PSSRb and GI, and RVI and GI, could be improved when compared with that of any corresponding PLMSVs. These results show that PLMSVs and PLMCVs could improve spring tea fresh yield estimation ability and reduce vegetation index saturation in a high-coverage tea tree canopy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B



Appendix C




References
- China Tea Marketing Association. Report on 2020 World Tea Production and Marketing Situation. Available online: https://www.ctma.com.cn/index/index/zybg/id/6/ (accessed on 10 February 2022).
- China Tea Marketing Association. Report on 2021 Chinese Spring Tea Production and Marketing Situation. Available online: https://www.ctma.com.cn/index/index/zybg/id/3/ (accessed on 14 May 2021).
- Pádua, L.; Hruka, J.; Bessa, J.; Ado, T.; Martins, L.M.; Gonalves, J.A.; Peres, E.; Sousa, A.M.R.; Castro, J.P.; Sousa, J.J. Multi-Temporal Analysis of Forestry and Coastal Environments Using UASs. Remote Sens. 2018, 10, 24. [Google Scholar] [CrossRef]
- Tucker, C.J. A critical review of remote sensing and other methods for non-destructive estimation of standing crop biomass. Grass Forage Sci. 2010, 35, 177–182. [Google Scholar] [CrossRef]
- Cheng, T.; Yang, Z.; Inoue, Y.; Zhu, Y.; Cao, W. Preface: Recent Advances in Remote Sensing for Crop Growth Monitoring. Remote Sens. 2016, 8, 116. [Google Scholar] [CrossRef]
- Xu, X.; Wu, B.; Meng, J.; Li, Q.; Huang, W.; Liu, L.; Wang, J. Research advances in crop yield estimation models based on remote sensing. Trans. Chin. Soc. Agric. Eng. 2008, 24, 290–298. [Google Scholar]
- Swain, K.C.; Thomson, S.J.; Jayasuriya, H. Adoption of an Unmanned Helicopter for Low-Altitude Remote Sensing to Estimate Yield and Total Biomass of a Rice Crop. Trans. ASABE 2010, 53, 21–27. [Google Scholar] [CrossRef]
- Tennakoon, S.B.; Murty, V.V.N.; Eiumnoh, A. Estimation of cropped area and grain yield of rice using remote sensing data. Int. J. Remote Sens. 1992, 13, 427–439. [Google Scholar] [CrossRef]
- Feng, H.; Tao, H.; Fan, Y.; Liu, Y.; Li, Z.; Yang, G.; Zhao, C. Comparison of Winter Wheat Yield Estimation Based on Near-Surface Hyperspectral and UAV Hyperspectral Remote Sensing Data. Remote Sens. 2022, 14, 4158. [Google Scholar] [CrossRef]
- Tao, H.; Feng, H.; Yang, G.; Yang, X.; Miao, M.; Wu, Z.; Zhai, L. Comparison of winter wheat yields estimated with UAV digital image and hyperspectral data. Trans. Chin. Soc. Agric. Eng. 2019, 35, 111–118. [Google Scholar]
- Zhu, W.; Li, S.; Zhang, X.; Li, Y.; Sun, Z. Estimation of winter wheat yield using optimal vegetation indices from unmanned aerial vehicle remote sensing. Trans. Chin. Soc. Agric. Eng. 2018, 34, 78–86. [Google Scholar]
- Huang, J.; Tang, S.; Abou-Ismail, O.; Wang, R. Rice yield estimation using remote sensing and simulation model. J. Zhejiang Univ.-Sci. A 2002, 3, 461–466. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the AquaCrop model. Agric. Water Manag. 2020, 227, 105846. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Zhang, L.; Han, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. 2020, 162, 161–172. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, G.; Liu, J.; Zhang, X.; Xu, B.; Wang, Y.; Zhao, C.; Gai, J. Estimation of soybean breeding yield based on optimization of spatial scale of UAV hyperspectral image. Trans. Chin. Soc. Agric. Eng. 2017, 33, 110–116. [Google Scholar]
- Kim, J.H.; Jun, B.; Sugiyama, K.; Torao, K.; Arai, M. A method of yield and quality estimation for tea-plant using on-site remote sensing. J. Jpn. Agric. Syst. Soc. 2010, 26, 1–8. [Google Scholar]
- Phan, P.; Chen, N.; Xu, L.; Chen, Z. Using Multi-Temporal MODIS NDVI Data to Monitor Tea Status and Forecast Yield: A Case Study at Tanuyen, Laichau, Vietnam. Remote Sens. 2020, 12, 1814. [Google Scholar] [CrossRef]
- Jui, S.J.J.; Ahmed, A.A.M.; Bose, A.; Raj, N.; Sharma, E.; Soar, J.; Chowdhury, M.W.I. Spatiotemporal Hybrid Random Forest Model for Tea Yield Prediction Using Satellite-Derived Variables. Remote Sens. 2022, 14, 805. [Google Scholar] [CrossRef]
- Bahrami, H.; McNairn, H.; Mahdianpari, M.; Homayouni, S. A Meta-Analysis of Remote Sensing Technologies and Methodologies for Crop Characterization. Remote Sens. 2022, 14, 5633. [Google Scholar] [CrossRef]
- Hatfield, J.L. Remote sensing estimators of potential and actual crop yield. Remote Sens. Environ. 1983, 13, 301–311. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, K.; Ouyang, Q.; Chen, Q. Measurement of Chlorophyll Content and Distribution in Tea Plant’s Leaf Using Hyperspectral Imaging Technique. Spectrosc. Spectral Anal. 2011, 31, 512–525. [Google Scholar]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crop. Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Rehman, T.H.; Lundy, M.E.; Linquist, B.A. Comparative Sensitivity of Vegetation Indices Measured via Proximal and Aerial Sensors for Assessing N Status and Predicting Grain Yield in Rice Cropping Systems. Remote Sens. 2022, 14, 2770. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; Pauw, E.D. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Xiang, G.; Huete, A.R.; Ni, W.; Miura, T. Optical-Biophysical Relationships of Vegetation Spectra without Background Contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar]
- Padilla, F.M.; De Souza, R.; Peña-Fleitas, M.T.; Gallardo, M.; Giménez, C.; Thompson, R.B. Different Responses of Various Chlorophyll Meters to Increasing Nitrogen Supply in Sweet Pepper. Front. Plant Sci. 2018, 9, 1752. [Google Scholar] [CrossRef]
- Novichonok, E.V.; Novichonok, A.O.; Kurbatova, J.A.; Markovskaya, E.F. Use of the atLEAF+ chlorophyll meter for a nondestructive estimate of chlorophyll content. Photosynthetica. 2016, 54, 130–137. [Google Scholar] [CrossRef]
- Luo, Y. Tea Cultivation, 4th ed.; China Agriculture Press: Beijing, China, 2008; pp. 253–286, 342. [Google Scholar]
- Langat, J.K. Photosynthetically Active Radiation to Total Solar Radiation Top Canopy Ratio in Tea (Camellia sinensis [L.] O. Kuntze) Genotypes in the Kenyan Highlands. Int. J. Sci. Adv. Res. Eng. 2018, 4, 118–128. [Google Scholar]
- Anthony, N.R.; Anatoly, G.; Yi, P.; Andrés, V.; Timothy, A.; Donald, R. Green Leaf Area Index Estimation in Maize and Soybean: Combining Vegetation Indices to Achieve Maximal Sensitivity. Agron. J. 2012, 104, 1336. [Google Scholar]
- Gu, Y.; Wylie, B.K.; Howard, D.M.; Phuyal, K.P.; Lei, J. Ndvi saturation adjustment: A new approach for improving cropland performance estimates in the Greater Platte River Basin, USA. Ecol. Indic. 2013, 30, 1–6. [Google Scholar] [CrossRef]
- Daughtry, C.; Walthall, C.L.; Kim, M.S.; Colstoun, E.; Iii, M.M. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Chen, L.; Xu, B.; Zhao, C.; Duan, D.; Cao, Q.; Wang, F. Application of Multispectral Camera in Monitoring the Quality Parameters of Fresh Tea Leaves. Remote Sens. 2021, 13, 3719. [Google Scholar] [CrossRef]
- Benedetti, R.; Rossini, P. On the use of NDVI profiles as a tool for agricultural statistics: The case study of wheat yield estimate and forecast in Emilia Romagna. Remote Sens. Environ. 1993, 45, 311–326. [Google Scholar] [CrossRef]
- Yang, P.; van der Tol, C.; Campbell, P.K.E.; Middleton, E.M. Fluorescence Correction Vegetation Index (FCVI): A physically based reflectance index to separate physiological and non-physiological information in far-red sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2020, 240, 111676. [Google Scholar] [CrossRef]
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using Terra and Aqua MODIS reflectance data. Remote Sens. Environ. 2007, 106, 39–58. [Google Scholar] [CrossRef]
- Watt, M.S.; Buddenbaum, H.; Leonardo, E.M.C.; Estarija, H.J.; Bown, H.E.; Gomez-Gallego, M.; Hartley, R.J.L.; Pearse, G.D.; Massam, P.; Wright, L. Monitoring biochemical limitations to photosynthesis in N and P-limited radiata pine using plant functional traits quantified from hyperspectral imagery. Remote Sens. Environ. 2020, 248, 112003. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P. Microwave vegetation indexes for detecting biomass and water conditions of agricultural crops. Remote Sens. Environ. 1992, 40, 15–26. [Google Scholar] [CrossRef]
- Wu, B.; Huang, W.; Ye, H.; Luo, P.; Ren, Y.; Kong, W. Using Multi-Angular Hyperspectral Data to Estimate the Vertical Distribution of Leaf Chlorophyll Content in Wheat. Remote Sens. 2021, 13, 1501. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Rodriguez, D.; O’Leary, G. Measuring and predicting canopy nitrogen nutrition in wheat using a spectral index—The canopy chlorophyll content index (CCCI). Field Crops Res. 2010, 116, 318–324. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, L.; Yao, M.; Chen, L.; Yang, Y. Preliminary Study on Gene Expression Differences between Normal Leaves and Albino Leaves of Anji Baicha (Camellia sinensis cv. Baiye1). J. Tea Sci. 2008, 28, 50–55. [Google Scholar]
- Wu, B.; Li, Y.; Jin, Z. The Classification and Analysis of Disastrous Weather A fecting the Yield and Quality of Anji White Tea. Chin. Agric. Sci. Bull. 2018, 34, 137–143. [Google Scholar]
- Song, M.; Zhou, T.; Dai, J.; Zhang, J.; Kang, Z.; Jian, Z. Environmental Geochemistry of The Producing Area of The Anji White Tea, Zhejiang Province. Geophys. Geochem. Explor. 2009, 33, 444–447. [Google Scholar]
- Lu, W.; Qian, W.; Lai, J.; Ze, G.; Lou, L. Preliminary Studies for the Climate Causes on Quality Characteristics of Anji-baicha. Tea Sci. Technol. 2012, 3, 37–39. [Google Scholar]
- Li, D.; Chen, J.M.; Zhang, X.; Yan, Y.; Zhu, J.; Zheng, H.; Zhou, K.; Yao, X.; Tian, Y.; Zhu, Y.; et al. Improved estimation of leaf chlorophyll content of row crops from canopy reflectance spectra through minimizing canopy structural effects and optimizing off-noon observation time. Remote Sens. Environ. 2020, 248, 111985. [Google Scholar] [CrossRef]
- Jebur, A.; Abed, F.M.; Mohammed, M.U. Assessing the performance of commercial Agisoft photoScan software to deliver reliable data for accurate 3D modelling. MATEC Web Conf. 2020, 162, 03022. [Google Scholar] [CrossRef]
- Andalibi, L.; Ghorbani, A.; Moameri, M.; Hazbavi, Z.; Dadjou, F. Leaf Area Index Variations in Ecoregions of Ardabil Province, Iran. Remote Sens. 2021, 13, 2879. [Google Scholar] [CrossRef]
- Luo, Y.; Tang, M.; Cai, W.; Wen, D.; Wen, Z. Study on the Optimum Machine-plucking Period for High Quality Tea. J. Tea Sci. 2008, 28, 9–13. [Google Scholar]
- Hogood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties Experiment 93; Joint Research Centre of the European Commission, Institute for Remote Sensing Applications: Luxembourg, 1995; pp. 75–91. [Google Scholar]
- Buchaillot, M.L.; Soba, D.; Shu, T.; Liu, J.; Aranjuelo, I.; Araus, J.L.; Runion, G.B.; Prior, S.A.; Kefauver, S.C.; Sanz-Saez, A. Estimating peanut and soybean photosynthetic traits using leaf spectral reflectance and advance regression models. Planta 2022, 255, 93. [Google Scholar] [CrossRef]
- Delalieux, S.; Somers, B.; Hereijgers, S.; Verstraeten, W.W.; Coppin, P. A near-infrared narrow-waveband ratio to determine Leaf Area Index in orchards. Remote Sens. Environ. 2008, 112, 3762–3772. [Google Scholar] [CrossRef]
- Ma, S.; Ma, H.; Xu, Y.; Li, S.; Lv, C.; Zhu, M. A Low-Light Sensor Image Enhancement Algorithm Based on HSI Color Model. Sensors 2018, 18, 3583. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wen, Y.; Sun, H.; Li, M.; Zhao, Y.; Zhang, Y. Detection of crop growth index based on image segmentation. In Proceedings of the 2015 ASABE Annual International Meeting, New Orleans, LA, USA, 26–29 July 2015. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Solomon, C.A.; Breckon, T.B. Morphological Processing; John Wiley & Sons, Ltd.: New York, NY, USA, 2011; pp. 197–234. [Google Scholar]
- Qiao, K.; Zhu, W.; Xie, Z.; Li, P. Estimating the Seasonal Dynamics of the Leaf Area Index Using Piecewise LAI-VI Relationships Based on Phenophases. Remote Sens. 2019, 11, 689. [Google Scholar] [CrossRef]
- Mitchell, J.E.; Popovich, S.J. Effectiveness of basal area for estimating canopy cover of ponderosa pine. Forest Ecol. Manag. 1997, 95, 45–51. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007; pp. 355–408. [Google Scholar]
- Kim, M.S.; Daughtry, C.; Chappelle, E.W.; Mcmurtrey, J.E.; Walthall, C.L. The use of high spectral resolution bands for estimating absorbed photosynthetically active radiation (A par). In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, CNES, Val D’Isere, France, 17–24 January 1994. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J. Vegetation stress detection through chlorophyll a + b estimation and fluorescence effects on hyperspectral imagery. J. Environ. Qual. 2002, 31, 1433–1441. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Jean-Louis, R.; Francois-Marie, B. Estimating par absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 275–384. [Google Scholar]
- Simth, R.C.G.; Adams, J.; Stephens, D.J.; Hick, P.T. Forecasting Wheat Yield in a Mediterranean- type Environment from the NOAA Satellite. Aust. J. Agric. Res. 1995, 46, 113–125. [Google Scholar] [CrossRef]
- Blackburn, G.A. Quantifying Chlorophylls and Caroteniods at Leaf and Canopy Scales: An Evaluation of Some Hyperspectral Approaches. Remote Sens. Environ. 1998, 66, 273–285. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of Productivity of the Shortgrass Prairie. In Proceedings of the Remote sensing of Environment, VIII, Ann Arbor, MI, USA, 2–6 October 1972. [Google Scholar]
- Chappelle, E.W.; Kim, M.S.; McMurtrey, J.E. Ratio analysis of reflectance spectra (RARS): An algorithm for the remote estimation of the concentrations of chlorophyll A, chlorophyll B, and carotenoids in soybean leaves. Remote Sens. Environ. 1992, 39, 239–247. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plantarum. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Lacava, T.; Calice, G.; Coviello, I.; Mazzeo, G.; Tramutoli, V. Advanced multi-temporal passive microwave data analysis for soil wetness monitoring and flood risk forecast. Geosci. Remote Sens. Symp. 2010, 3, 490–493. [Google Scholar]
- Moore, D.S.; Mccabe, G.P.; Craig, B.A. Introduction to the Practice of SATISTICS, 7th ed.; W. H. Freeman: New York, NY, USA, 2012; p. 401. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation. In Proceedings of the 3rd ERTS Symposium, Washington, DC, USA, 10–14 December 1973; pp. 309–317. [Google Scholar]
- Eitel, J.U.H.; Long, D.S.; Gessler, P.E.; Smith, A.M.S. Using in-situ measurements to evaluate the new RapidEye™ satellite series for prediction of wheat nitrogen status. Int. J. Remote. Sens. 2007, 28, 4183–4190. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Naumann, J.C.; Rubis, K.; Young, D.R. Fusing chlorophyll fluorescence and plant canopy reflectance to detect TNT contamination in soils. Proc. SPIE-Int. Soc. Opt. Eng. 2010, 7664, 76641L-1. [Google Scholar]
- Naumann, J.C.; Anderson, J.E.; Young, D.R. Remote detection of plant physiological responses to TNT soil contamination. Plant Soil 2010, 329, 239–248. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Noland, T.L.; Mohammed, G.H.; Sampson, P.H. Scaling-up and model inversion methods with narrowband optical indices for chlorophyll content estimation in closed forest canopies with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1491–1507. [Google Scholar] [CrossRef]
- Huang, J.; Wang, F.; Wang, X. Hyperspectral Experiment for Paddy Rice Remote Sensing, 1st ed.; Zhejiang University Press: Hangzhou, China, 2010; pp. 26–31. [Google Scholar]
- Davenport, J.R.; Lang, N.S.; Perry, E.M.; Robert, P.C.; Rust, R.H.; Larson, W.E. Leaf spectral reflectance for early detection of disorders in model annual and perennial crops. In Proceedings of the 5th International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Xu, J.; Quackenbush, L.J.; Volk, T.A.; Im, J. Forest and Crop Leaf Area Index Estimation Using Remote Sensing: Research Trends and Future Directions. Remote Sens. 2020, 12, 2934. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Q.; Wu, W.; Xia, T.; Tang, H. Estimating the crop leaf area index using hyperspectral remote sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar] [CrossRef]
- Xing, N.; Huang, W.; Ye, H.; Ren, Y.; Xie, Q. Joint Retrieval of Winter Wheat Leaf Area Index and Canopy Chlorophyll Density Using Hyperspectral Vegetation Indices. Remote Sens. 2021, 13, 3175. [Google Scholar] [CrossRef]






| dCSIs | Name | Characteristics & Functions | Expression | Correlation |
|---|---|---|---|---|
| CARI [64] | Chlorophyll Absorption Ratio index | Estimate chlorophyll concentration | ; | 0.117 |
| GNDVI [65] | Green Normalized Difference Vegetative Index | Estimate photosynthetic activity | −0.588 *** | |
| CUR [66] | Curvature Index | Estimate biochemical constituents | −0.786 *** | |
| CI [67] | Chlorophyll Index | Estimate Chls content in broadleaf tree leaves | −0.05 | |
| RDVI [68] | Renormalized Difference Vegetation Index | Quantify variation of multi-chemical in vegetation | −0.693 *** | |
| GI [69] | Greenness Index | Estimate biochemical constituents at the leaf and canopy levels | −0.679 *** | |
| PSSRa [70] | Pigment Specific Simple Ratio of Chl a | Exhibited excellent predictive relationships for Chl a at canopy levels | −0.666 *** | |
| PSSRb [70] | Pigment Specific Simple Ratio of Chl b | Exhibited excellent predictive relationships for Chl b at canopy levels | −0.641 *** | |
| PSNDa [70] | Pigment Specific Normalized Difference in Chl a | Estimate excellent predictive relationships for Chl a at canopy levels | −0.637 *** | |
| PSNDb [70] | Pigment Specific Normalized Difference in Chl b | Estimate chlorophyll b at canopy | −0.632 *** | |
| RVI [71] | Ratio Vegetation Index | Estimate canopy chlorophyll density | −0.647 *** | |
| RARSa [72] | Ratio Analysis of Reflectance Spectra of Chl a | Estiamte chlorophyll a at canopy | −0.572 *** | |
| RARSb [72] | Ratio Analysis of Reflectance Spectra of Chl b | Estiamte chlorophyll b at canopy | −0.642 *** | |
| PSRI [73] | Plant Senescence Reflectance Index | To quantitatively analyze leaf senescence and fruit maturity. | 0.656 *** | |
| PRVI [74] | Polarization Ratio Variation Index | Estimate biochemical constituents | −0.625 *** |
| dLASIs | Name | Characteristics & Functions | Expression | Correlation |
|---|---|---|---|---|
| NDVI [76] | Normalized Difference Vegetation Index | Effective for quantifying green vegetation. Positively correlated with vegetation greenness. | −0.636 *** | |
| MCARI [77] | Modified Chlorophyll Absorption Ratio Index | Respond to chlorophyll changes and estimate chlorophyll absorption. | −0.447 ** | |
| TVI [78] | Triangular Vegetation Index | Estimate biochemical constituents | −0.655 *** | |
| MCARI1 [79] | Modified Chlorophyll Absorption Ratio Index 1 | Lower the sensitivity to chlorophyll effects, and the integration of a near-infrared wavelength increases the sensitivity to LAI changes. | −0.686 *** | |
| MCARI2 [79] | Modified Chlorophyll Absorption Ratio Index Improved | Keep the sensitivity to LAI and be less affected by chlorophyll. | −0.707 *** | |
| R740/R850 [80] | Simple Ratio R740/R850 | Estimate biochemical constituents, Response to contamination stress | −0.149 | |
| R761/R757 [81] | Simple Ratio R761/R757 | Estimate biochemical constituents, responses to contamination stress | −0.217 | |
| R750/R710 [82] | Simple Ratio R750/R710 | good indicators for Estimate biochemical constituents | −0.698 *** | |
| D705/D722 [66] | Derivative Indices D705/D722 | Estimate biochemical constituents at the canopy, map vegetation stress effects | 0.497 ** | |
| D730/D706 [82] | Derivative Indices D730/D706 | Estimate biochemical constituents | −0.262 | |
| Dmax/D720 [83] | Derivative Indices Dmax/D720 | Estimate leaf area index, Estimated yield of food crops | 0.273 | |
| Dmax/D745 [83] | Derivative Indices Dmax/D745 | Estimate leaf area index, Estimated yield of food crops | 0.0002 | |
| D715/D705 [82] | Derivative Indices D715/D705 | Estimate biochemical constituents with less influence | −0.506 ** |
| Type | dVI | Modeling (n = 15) | Validation (m = 9) | ||
|---|---|---|---|---|---|
| Yield Estimation Model | MR2 | RMSE (g) | VR2 | ||
| dCSI | GNDVI | Y = −6007.3dVI + 472.77 | 0.34 ** | 173.218 | 0.465 ** |
| CUR | Y = −8870.4dVI − 103.25 | 0.611 *** | 146.247 | 0.880 *** | |
| RDVI | Y = −6796.6dVI + 302.08 | 0.514 *** | 160.626 | 0.456 ** | |
| GI | Y = −675.09dVI + 523.28 | 0.425 *** | 148.821 | 0.554 ** | |
| PSSRa | Y = −98.101dVI + 484.46 | 0.426 *** | 154.844 | 0.511 ** | |
| PSSRb | Y = −116.91dVI + 542.22 | 0.389 ** | 159.135 | 0.492 ** | |
| PSNDa | Y = −2465.5dVI + 532.76 | 0.365 ** | 158.271 | 0.573 ** | |
| PSNDb | Y = −2712.2dVI + 560.91 | 0.361 ** | 159.488 | 0.562 ** | |
| RARSa | Y = −387.73dVI + 683.32 | 0.291 ** | 166.791 | 0.414 * | |
| RARSb | Y = −141.18dVI + 527.64 | 0.39 ** | 159.315 | 0.500 ** | |
| PSRI | Y = 5346.7dVI + 533.89 | 0.367 ** | 152.974 | 0.683 *** | |
| PRVI | Y = −383.47dVI + 406.15 | 0.396 ** | 167.388 | 0.444 ** | |
| RVI | Y = −92.724dVI + 522.78 | 0.403 ** | 158.607 | 0.483 ** | |
| dLASI | NDVI | Y = −2466.7dVI + 554.07 | 0.364 ** | 158.734 | 0.566 ** |
| TVI | Y = −147.08dVI + 236.36 | 0.479 *** | 169.785 | 0.375 * | |
| MCARI1 | Y = −5524.3dVI + 175.38 | 0.529 *** | 165.552 | 0.398 * | |
| MCARI2 | Y = −3787.9dVI + 341.73 | 0.525 *** | 155.350 | 0.488 ** | |
| R750/R710 | Y = −1602.2dVI + 327.25 | 0.483 *** | 155.207 | 0.595 ** | |
| D715/D705 | Y = −6158.4dVI + 782.57 | 0.404 ** | 209.110 | 0.085 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wu, K.; Wang, F.; Jin, L.; Zhang, R.; Tian, S.; Wu, W.; He, Y.; Huang, R.; Yuan, L.; et al. Fresh Yield Estimation of Spring Tea via Spectral Differences in UAV Hyperspectral Images from Unpicked and Picked Canopies. Remote Sens. 2023, 15, 1100. https://doi.org/10.3390/rs15041100
He Z, Wu K, Wang F, Jin L, Zhang R, Tian S, Wu W, He Y, Huang R, Yuan L, et al. Fresh Yield Estimation of Spring Tea via Spectral Differences in UAV Hyperspectral Images from Unpicked and Picked Canopies. Remote Sensing. 2023; 15(4):1100. https://doi.org/10.3390/rs15041100
Chicago/Turabian StyleHe, Zongtai, Kaihua Wu, Fumin Wang, Lisong Jin, Rongxu Zhang, Shoupeng Tian, Weizhi Wu, Yadong He, Ran Huang, Lin Yuan, and et al. 2023. "Fresh Yield Estimation of Spring Tea via Spectral Differences in UAV Hyperspectral Images from Unpicked and Picked Canopies" Remote Sensing 15, no. 4: 1100. https://doi.org/10.3390/rs15041100
APA StyleHe, Z., Wu, K., Wang, F., Jin, L., Zhang, R., Tian, S., Wu, W., He, Y., Huang, R., Yuan, L., & Zhang, Y. (2023). Fresh Yield Estimation of Spring Tea via Spectral Differences in UAV Hyperspectral Images from Unpicked and Picked Canopies. Remote Sensing, 15(4), 1100. https://doi.org/10.3390/rs15041100