Next Article in Journal
Soil Moisture Retrieval from Multi-GNSS Reflectometry on FY-3E GNOS-II by Land Cover Classification
Previous Article in Journal
Changes in Sea Surface Temperature and Sea Ice Concentration in the Arctic Ocean over the Past Two Decades
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 4
10.3390/rs15041096
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Proposed Ensemble Feature Selection Method for Estimating Forest Aboveground Biomass from Multiple Satellite Data

by
Yuzhen Zhang
1,*,
Jingjing Liu
1,
Wenhao Li
1 and
Shunlin Liang
2
1
Beijing Engineering Research Center of Industrial Spectrum Imaging, School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China
2
Department of Geography, The University of Hong Kong, Hong Kong
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(4), 1096; https://doi.org/10.3390/rs15041096
Submission received: 23 January 2023 / Revised: 11 February 2023 / Accepted: 14 February 2023 / Published: 17 February 2023
Browse Figures
Versions Notes

Abstract

:
Feature selection (FS) can increase the accuracy of forest aboveground biomass (AGB) prediction from multiple satellite data and identify important predictors, but the role of FS in AGB estimation has not received sufficient attention. Here, we aimed to quantify the degree to which FS can benefit forest AGB prediction. To this end, we extracted a series of features from Landsat, Phased Array L-band Synthetic Aperture Radar (PALSAR), and climatic and topographical information, and evaluated the performance of four state-of-the-art FS methods in selecting predictive features and improving the estimation accuracy with selected features. We then proposed an ensemble FS method that takes inro account the stability of an individual FS algorithm with respect to different training datasets used; the heterogeneity or diversity of different FS methods; the correlations between features and forest AGB; and the multicollinearity between the selected features. We further investigated the performance of the proposed stability-heterogeneity-correlation-based ensemble (SHCE) method for AGB estimation. The results showed that selected features by SHCE provided a more accurate prediction of forest AGB than existing state-of-the-art FS methods, with R2 = 0.66 ± 0.01, RMSE = 14.35 ± 0.12 Mg ha−1, MAE = 9.34 ± 0.09 Mg ha−1, and bias = 1.67 ± 0.11 Mg ha−1 at 90 m resolution. Boruta yielded comparable prediction accuracy of forest AGB, but could not identify the importance of features, which led to a slightly greater bias than the proposed SHCE method. SHCE not only ranked selected features by importance but provided feature subsets that enabled accurate AGB prediction. Moreover, SHCE provides a flexible framework to combine FS results, which will be crucial in many scenarios, particularly the wide-area mapping of land-surface parameters from various satellite datasets.

Graphical Abstract

1. Introduction

The estimation of forest aboveground biomass (AGB) is crucial to understanding the activity of the global carbon cycle, predicting changes in the climate system, providing guidance for sustainable forest management, and improving forest conservation services [1,2,3]. In recent decades, numerous studies have attempted to quantify forest AGB and its spatial patterns using a combination of field measurements and multiple remotely sensed data at local or global scales [4,5]. Some studies have focused on determining promising predictors from optical imagery, synthetic aperture radar (SAR), and lidar data. The results of these studies suggested that surface reflectance [6,7]; vegetation indices [8,9]; texture information [10]; canopy height and height of the median energy extracted from lidar data [11,12]; and SAR backscatter and relative height metrics [13,14], are important for AGB estimation. To further improve prediction accuracy, an increasing number of variables have been used to estimate forest AGB with the aid of machine learning and deep learning methods [15,16,17,18].
In many research fields, such as bioinformatics [19,20], image analysis [21], anomaly detection [22,23], and natural language processing [24], feature selection (FS), also known as variable selection, is often carried out before training a model since it can improve the prediction accuracy, speed up the training process, and facilitate data interpretation [25]. The inclusion of some unimportant or redundant variables often leads to poor prediction accuracy and high computational cost [26,27]. It is thus essential to perform feature selection for accurate estimation rather than use as many predictors as possible. However, published studies have confirmed and systematically explored the role of sample size, sensor type, and prediction methods in forest biomass estimation [28,29] but have largely ignored the role of feature selection in improving the prediction performance of forest AGB. Therefore, in this study, we aimed to explore the impacts of FS in AGB estimation.
According to the relationship with learning models, FS methods can be categorized into three types: filter, wrapper, and embedded algorithms [30]. Filter algorithms do not associate with a specific learning model and can be considered as a pre-processing step that ranks variables by importance or selects subsets of variables using some criterion (e.g., correlation or similarity measure). They are fast and intuitive but usually cannot provide optimal features for subsequent modelling [31]. Wrapper algorithms depend on the predictions of a learning model. They determine the subset of features that minimizes the generalization error of the learning model used. For this reason, wrapper methods enable more accurate estimations than filter methods in most cases [32], but they are computationally intensive and greatly dependent on the learning model used. Embedded methods, such as the least absolute shrinkage and selection operator (LASSO) technique and decision tree algorithms, select features as a part of the learning or model creation process [33,34]. There are also some hybrid algorithms that combine the merits of various FS algorithms [26,35,36,37,38]. Most of these are combinations of filter and wrapper methods and adopt a two-step strategy in which a filter algorithm is first employed to select features based on a specific criterion, and then a wrapper algorithm is applied to the selected features for further feature selection [39]. A hybrid feature-selection method can reduce computational complexity by removing unimportant features. However, it may also decrease prediction accuracy since the features removed by the filter algorithm might provide complementary information to the final selected feature set.
Although various FS algorithms have been proposed in different fields, each algorithm has its strength and weakness, and how to select the most appropriate approach for a given task remains an issue to be solved [40]. This study aimed to devise suitable solutions for forest AGB estimation. Specifically, our contributions include: (1) systematically evaluating the extent to which state-of-the-art FS algorithms improved the FS outcome and the prediction accuracy of forest AGB; and (2) developing an ensemble FS algorithm to rank predictors and produce an optimal feature subset that are stable and enable accurate estimation of forest AGB.

2. Data and Methods

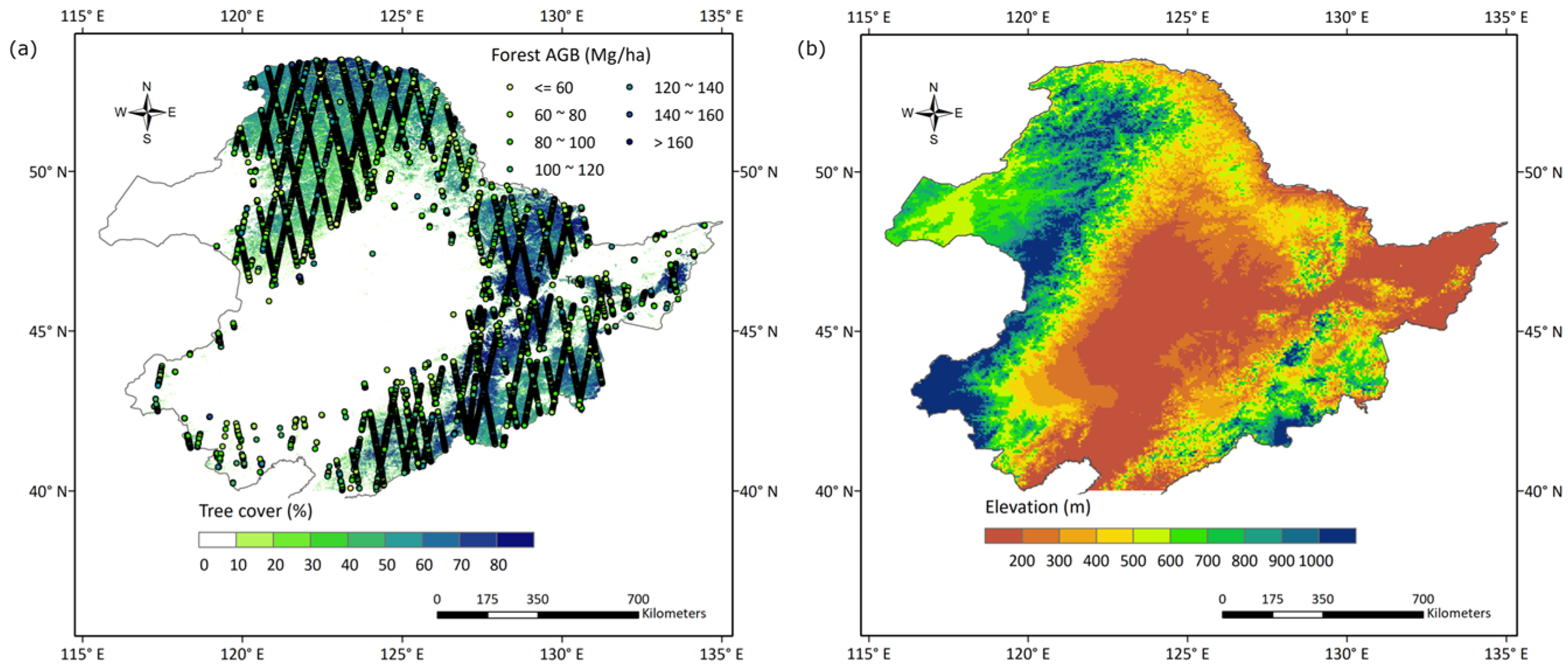
2.1. Study Area

The research area of this paper is northeast China, which includes Heilongjiang Province, Jilin Province, Liaoning Province, as well as the eastern part of the Inner Mongolia Autonomous Region [41]. The region is vast, and extends from 115°32′E to 135°09′E and from 38°42′N to 53°35′N. The study area has a temperate monsoon climate. The temperature in northeast China gradually decreases from south to north, and annual average temperature is between −4~11.5 °C. Annual precipitation decreases from east to west, is generally between 300 mm and 1000 mm, and the precipitation is mainly concentrated from June to August [42].
Northeast China is the largest natural forest region in China, with a forest area of about 50.5 million hectares [43]. The majority of forests in northeast China are warm temperate deciduous broadleaf forests, temperate coniferous and broadleaf mixed forests, and boreal forests from south to north [41,44]. They are mainly distributed over three forest regions, the Daxinganling Mountains, Xiaoxinganling Mountains, and Changbai Mountains, with forest land areas of 15.0, 6.0, and 13.6 million ha, respectively [45].

2.2. Forest AGB Data

Field measurements were taken at the Geoscience Laser Altimeter System (GLAS) footprints in the Tahe and Changbai Mountain forest regions of Northeast China in 2006 and 2007 (Figure 1). A total of 86 field plots were used [45]. For each field plot, the height and the diameter at breast height (DBH) of all the trees with a DBH larger than 5 cm were measured, and tree biomass was computed using the allometric equation [46,47,48]. Plot-level AGB were obtained by summing up all the tree biomass and then dividing by the area.
To obtain more training samples for AGB modelling with satellite data, the labor-intensive field measurements and the corresponding GLAS-derived metrics were used to develop AGB models which were further used for estimating AGB at GLAS footprints located in the study area [49]. Four GLAS metrics were extracted from GLAS waveform data, including the 25th percentile of canopy-reflection heights (CRH25), leading edge extent (Lead), quadratic mean-canopy height (QMCH), and the 75th percentile of height (TH75). The support-vector regression (SVR) algorithm was included to build the relationships between field AGB and GLAS-derived metrics. Four GLAS-derived metrics and the SVR algorithm were selected because one of our previous studies revealed that they could enable accurate AGB predictions [49].
GLAS data are greatly affected by clouds and system noise. Only cloudless waveforms (FRir_qa_flag = 15) that did not show any sign of saturation (SatNdx = 0) were included in this study [48]. To exclude possible cloud cover, GLAS waveforms, where the difference between DEM elevation and GLAS elevation (i_elev in GLA14) was >85 m, were eliminated [50]. Moreover, we only retained GLAS data with at least two Gaussian peaks to ensure that GLAS waveforms were reflected from the forest canopy rather than bare ground [51].
Here, we developed 100 SVR models by splitting the plot-level AGB into five folds, which was repeated 20 times, and then used the developed models to predict forest AGB at GLAS footprints. The average of 100 predictions was taken as the reference data (Figure 1). To reduce the possible impacts of unbalanced data distribution of reference AGB on subsequent modelling with satellite data, resampling was conducted by SMOGN, which combines random undersampling with a synthetic minority oversampling technique for regression (SMOTER), and the use of Gaussian noise techniques [52].

2.3. Landsat Data

The Landsat Collection 1 Level 1 Precision and Terrain (L1TP) corrected data have the highest geometric and radiometric quality [53,54]. The Landsat 5 L1TP data from May to September were used. For each growing season between 2007 to 2010, Landsat 5 thematic mapping (TM) images were composited into one image using the greenest NDVI (normalized difference vegetation index) method and Google Earth engine (GEE) [55,56]. Landsat data for 2007–2010 were selected, to be consistent with the PALSAR data in Section 2.4. The composite images were reprojected from the original universal transverse Mercator (UTM) projection to the WGS84 coordinate system. To reduce the spatial mismatch between Landsat and GLAS-derived biomass data, a 3 × 3 window was applied to the surface reflectance data, and the mean values of Landsat TM surface reflectance at the green, red, near-infrared, and shortwave bands were computed and used as predictors of forest AGB [57,58,59]. In addition to TM surface reflectance, various vegetation indices were used to estimate forest AGB [60,61,62], including NDVI; enhanced vegetation index (EVI); soil-adjusted vegetation index (SAVI); structural index (SI); normalized difference moisture index (NDMI); normalized burn ratio (NBR); and tasseled cap (TC) components that included TC brightness (TCB), TC greenness (TCG), TC wetness (TCW), TC distance (TCD), TC angle (TCA) and TC disturbance index (TCDI). The formulas to derive these metrics are shown in Table 1.
Some studies have suggested that the inclusion of texture information increases the accuracy of AGB prediction [63,64,65]. The gray level co-occurrence matrix (GLCM) texture measures associated with four TM bands including mean, variance (VAR), correlation (COR) and homogeneity (HOM), were thus extracted. All GLCM texture measures were calculated using 64 gray level quantization to reduce computational effort and avoid generating sparse GLCMs [66,67]. We conducted an experiment with two window sizes (3 × 3 and 5 × 5) to determine GLCM texture measures and found that GLCM texture measures using a 5 × 5 pixel window had stronger correlations with forest biomass [63], which were then used in this study.
We aggregated the forest cover data at 30 m spatial resolution [68] to 90 m resolution through averaging. Pixels with a forest cover >10% were considered as forests and non-forest pixels were excluded [4,45].

2.4. PALSAR Data

The ALOS PALSAR mosaics at 25 m resolution provided by the Japan Aerospace Exploration Agency (JAXA) were available for 2007–2010 [69,70] and downloaded from https://www.eorc.jaxa.jp/ALOS/en/palsar_fnf/fnf_index.htm (accessed on 14 March 2022). We converted digital values of original PALSAR HH and HV polarizations to normalized gamma nought radar backscatter coefficients γ0 using (1).
γ 0 = 10 × log 10 [ DN 2 ] − 83.0   dB
An improved adaptive Lee filter with a window size of 5 × 5 pixels was used to reduce salt and pepper noise. In addition to HH and HV, their difference (HH−HV) and ratio (HH/HV) were included as predictors of forest AGB [71,72]. Four GLCM texture measures were applied to HH and HV backscatter coefficients, generating an additional eight predictors. To be consistent with other datasets, PALSAR-derived metrics were averaged to the 90 m resolution.

2.5. Topographical Data

Elevation data were from the Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) and downloaded from https://srtm.csi.cgiar.org/ (accessed on 31 December 2021) [73]. The mean aggregation algorithm was used within 3 × 3 windows to generate the elevation data at 90 m resolution. Slope was calculated using ENVI software based on the elevation data at 90 m resolution.
Table
Table 1. Descriptions and equations for predictor variables.
Table 1. Descriptions and equations for predictor variables.
VariablesDescriptionsReferences
Green, Red, NIR, SWIR2Four spectral metrics extracted from Landsat TM 5 band 2, band 3, band 4, and band 6.
NDVI(TM4 − TM3)/(TM4 + TM3)[74]
EVI2.5 × (TM4 − TM3)/(TM4 + 6 × TM3 − 7.5 × TM1 + 1)[75]
SAVI1.5 × (TM4 − TM3)/(TM4 + TM3 + 0.5)[76]
NDMI(TM4 – TM5)/(TM4 + TM5)[77,78]
SITM4/TM5[79]
NBR(TM4 – TM7)/(TM4 + TM7)[80]
TCBB × [TM1, TM2, TM3, TM4, TM5, TM7, 1]T[81]
TCGG × [TM1, TM2, TM3, TM4, TM5, TM7, 1]T[81]
TCWW × [TM1, TM2, TM3, TM4, TM5, TM7, 1]T[81]
TCD TCB 2 + TCG 2 [82]
TCAartan(TCG/TCB)[83]
TM texture Four GLCM texture measures (mean, variance, correlation, homogeneity) extracted from each spectral band.[84]
FVCThe metrics were extracted from the global tree cover data published by Hansen.[68]
HH, HVPALSAR backscatter coefficients.
HH−HV, HH/HVThe difference and ratio values between HH and HV.[71]
PALSAR textureGLCM texture measure associated with HH and HV.
Elevation, SlopeTopographical predictors.
Note: B = [0.2909, 0.2493, 0.4806, 0.5568, 0.4438, 0.1706, 10.3695], G = [−0.2728, −0.2174, −0.5508, 0.7221, 0.0733, −0.1648, −0.7310], and W = [0.1446, 0.1761, 0.3322, 0.3396, −0.6210, −0.4186, −3.3828].

2.6. FS Methods

Four FS methods, including Boruta, nonlinear joint mutual information maximization (JMIM), recursive feature elimination (RFE), and mean decrease accuracy (MDA) were considered in this study. Random forests (RF) was the learner of the wrapper FS method.
The flowchart (Figure 2) illustrates the procedures to evaluate FS in the estimation of AGB from multiple satellite data. A 10-fold cross-validation (CV) was performed on the GLAS-derived forest AGB and the predictor variables extracted from multiple satellite data, which was iterated five times, generating 50 training datasets and 50 test datasets. Four FS methods were used to select variables based on 50 training datasets. We examined the stability of each FS method with respect to different training datasets, the heterogeneity or diversity of different FS methods, and the correlations between selected features. A novel ensemble FS algorithm was proposed considering the stability, heterogeneity, and correlation (SHC). The SHC ensemble (SHCE) method selected features according to the ranking scores of all features and determined the number of top features finally selected for AGB estimation using Akaike information criterion (AIC). FS outcomes generated by each FS method served the inputs of RF and XGBoost model to estimate forest AGB.

2.6.1. Boruta

Boruta measures the importance of features by comparing them with those of shadow variables [85]. Previous studies have suggested that Boruta outperformed Vita, the permutation approach and its variant Altmann, and RFE, and was robust for both high-dimensional and low-dimensional data analysis [86]. The Boruta procedure is summarized as follows. Create a shadow variable for each predictor variable by shuffling values of the original feature across samples to remove any possible correlations with the response variable and add the shadow variables into the original features; run the RF model to obtain an internal estimate of variable importance; label the features that have lower importance than the maximum importance of the shadow variables (MVSA) as unimportant and those that have greater importance than MVSA as important; remove the unimportant features; repeat the above procedures until the importance of all features has been determined.

2.6.2. JMIM

Information theory has been widely used in filter-based FS algorithms, in which the relevance and redundancy of features are measured by mutual information (MI), interaction information, conditional MI, or joint MI [87,88]. We used the nonlinear JMIM algorithm, which takes both the relevance of each feature and target variable together with the redundancy between features into consideration using MI and a maximum-of-the-minimum criterion [89]. The MI between forest AGB and each predictor variable was calculated, and the feature that had the maximum MI for AGB estimation was first selected. Candidate features with a larger minimum value of joint MI than all the other features that had not been included in the subset of already selected features were considered as the most relevant with forest AGB in the context of selected features and then added to the selected subset. This greedy search process was repeated until the MI that a selected variable shared with forest AGB no longer increased [89]. A K-nearest neighbors (KNN)-based estimation method was used to calculate MI for continuous variables, and the number of samples used for estimating kernel density was set to 5 [90].

2.6.3. RFE

Recursive feature elimination (RFE) was first proposed by Guyon et al. [91] for gene selection using support vector machines and later introduced into RF processes [92]. RFE aims to find an optimal feature subset that gives the best prediction performance based on a backward elimination strategy. The RFE procedure is as follows. Train the RF model with all features; compute the importance criterion; eliminate the least important feature; and train the RF model with the remaining features. These steps are repeated until a single input variable remains. RFE ranks the features in order of elimination. We used a five-fold CV to select the top k variables based on their ranking.

2.6.4. MDA

MDA quantifies feature importance based on the out-of-bag (OOB) error of a model when it was trained [93]. In this study, the importance of each variable was calculated by the difference averaged over all trees of RF between the mean square error of OOB prediction in which features were randomly permutated and that of the original OOB prediction [94]. If a variable is important, the associated change in the OOB prediction error caused by random permuting is large. According to the importance of each variable, a feature importance ranking was obtained. Similar to the RFE algorithm, a five-fold CV was conducted to select the top k features.

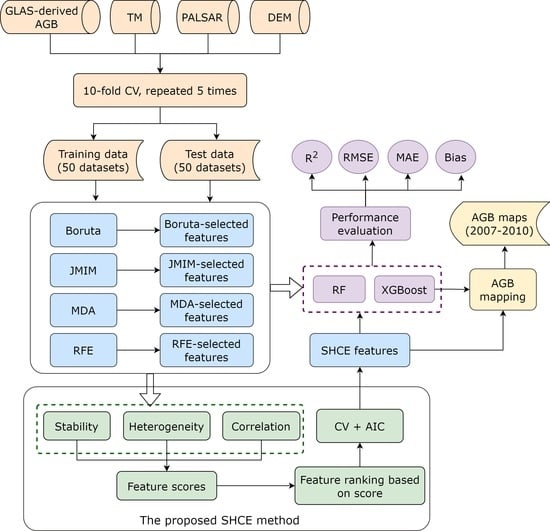
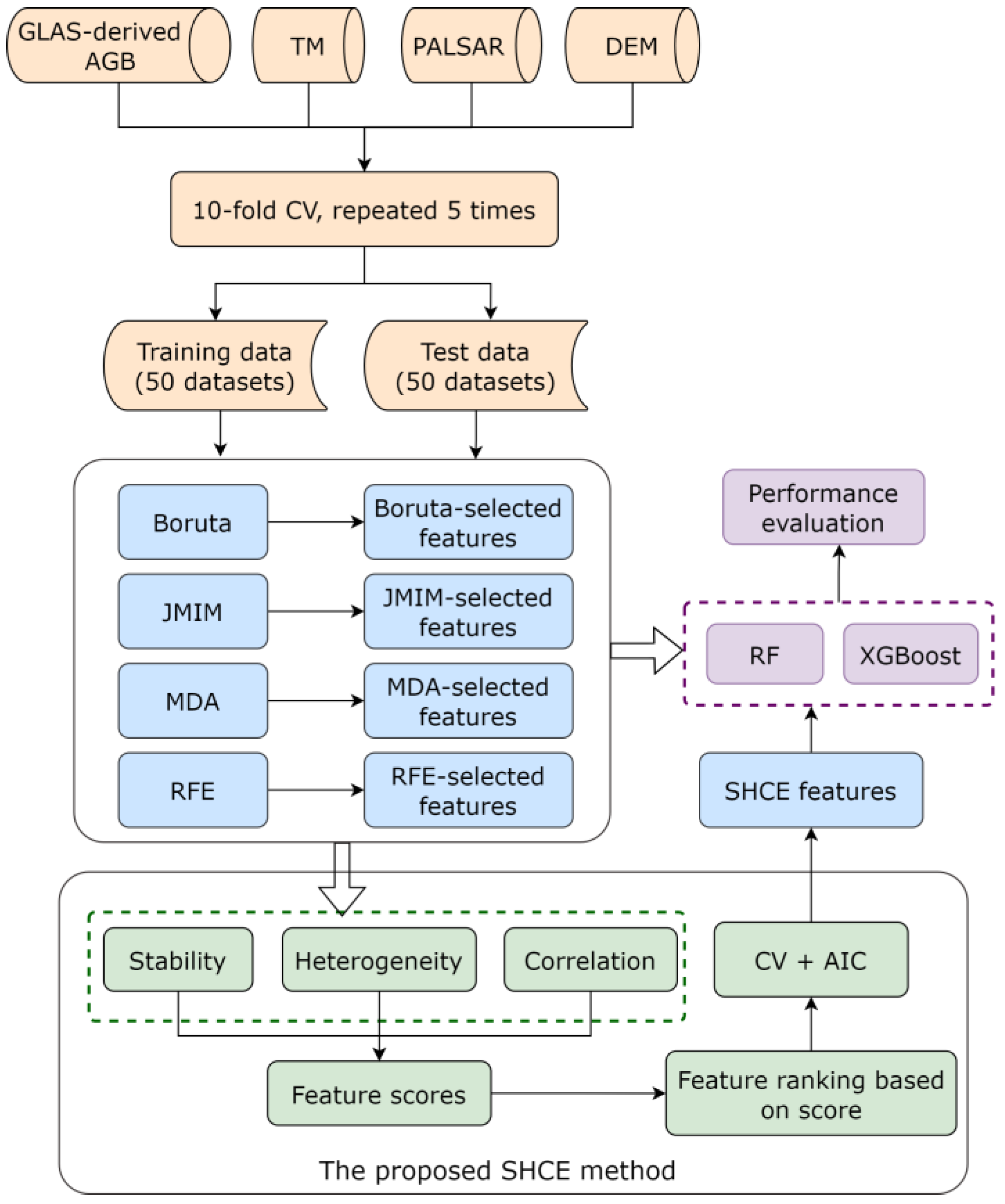
2.6.5. Proposed Ensemble FS Algorithm

An ensemble algorithm aggregates the outputs of multiple variable selectors and thus produced more robust and more stable FS results than a single FS algorithm [95,96,97]. We developed an ensemble FS algorithm that combined the results from JMIM, MDA, RFE and Boruta, taking into account the stability of each individual FS algorithm, the heterogeneity or diversity between the different FS algorithms, as well as the correlations between selected features. For simplicity, the stability-heterogeneity-correlation-based ensemble method was abbreviated as SHCE in this study.
Stability quantifies the consistency of FS results from different datasets produced by an individual FS algorithm. It is calculated by:
S T A i = ∑ j = 1 , j ≠ i N S ( f i , f j ) N − 1
where STAi is the stability score of feature subset i, N is the number of feature subsets produced by the FS algorithm, and S(fi,fj) is the similarity between feature subset i and feature subset j, which is calculated by:
S ( f i , f j ) = c − k i k j n min ( k i , k j ) − k i k j n
where ki is the number of features in feature subset fi, kj is the number of features in feature subset fj, c is the number of features common to fi and fj, and n is the total number of features [40,98]. A greater stability score suggests better stability of the FS result.
The heterogeneity score was introduced as a measure of the difference between FS results produced by the four different FS algorithms when trained with the same dataset. It is calculated by:
H E T i = ∑ j = 1 , j ≠ i M k i + k j − 2 c n M − 1
where HETi is the heterogeneity score of FS result i, and M is the number of feature selectors used in the ensemble algorithm. A greater heterogeneity score indicated that the FS results were diverse and could complement with each other.
The correlation score was originally derived from the correlation-based feature selection (CFS) algorithms, which selected features that had a high correlation with the target feature but with low multicollinearity between variables [99]. We calculated the CFS of FS result i using (5):
C F S i = k r x y ¯ k + k ( k − 1 ) r x x ¯
where r x y ¯ is the average of the coefficients of correlation between each feature within the feature subset and the corresponding target feature (forest AGB in this study); r x x ¯ is the average of the coefficients of correlation between pairs of features within the feature subset; and k is the number of features in the feature subset.
After computing the STA, HET and CFS scores for each FS result, data were rescaled using min–max normalization to eliminate dimensional differences between indicators. The average of the normalized STA, HET and CFS scores was used as the weight of each feature subset, and the importance of feature i in subset i was calculated by:
S c o r e i = ∑ i = 1 N u m W i F i N u m
where: Wi is the weight of feature subset Fi; and Num is the number of all feature subsets and was 200 (50 for each of the four FS algorithms).
All features were ranked according to their importance scores. Single features were selected sequentially for use by the RF model in AGB prediction. AIC was used to determine the number of features.

2.7. AGB Modelling

RF algorithms have been widely used in several fields because of their accuracy and their robustness against noise in the training data [100,101,102]. We selected RF as the learner to select features extracted multiple remote sensing data. However, the use of an RF algorithm for AGB estimation with selected features might bias the prediction results. To reduce the impacts on the accuracy assessment, we included XGBoost for the prediction of forest AGB using the features selected by Boruta, JMIM, MDA, RFE and SHCE as an alternative algorithm to RF. XGBoost is a boosting algorithm which transforms weak learners into strong learners by increasing the weights of samples misclassified or with large errors in subsequent iterations [15,103]. XGBoost implements parallel preprocessing at the node level, making it faster than a gradient boosting machine.
In this study, we evaluated and compared the AGB predictions obtained by RF and XGBoost, and the algorithm with a better prediction accuracy was adopted for forest AGB mapping for the study area.

2.8. Evaluation Metrics

The prediction accuracy was assessed in terms of the coefficient of determination (R2), root mean square error (RMSE), mean absolute error (MAE), and bias [104]. We calculated these metrics of AGB estimates achieved by RF and XGBoost models with selected features from Boruta, JMIM, MDA, RFE, and SHCE, respectively.

3. Results

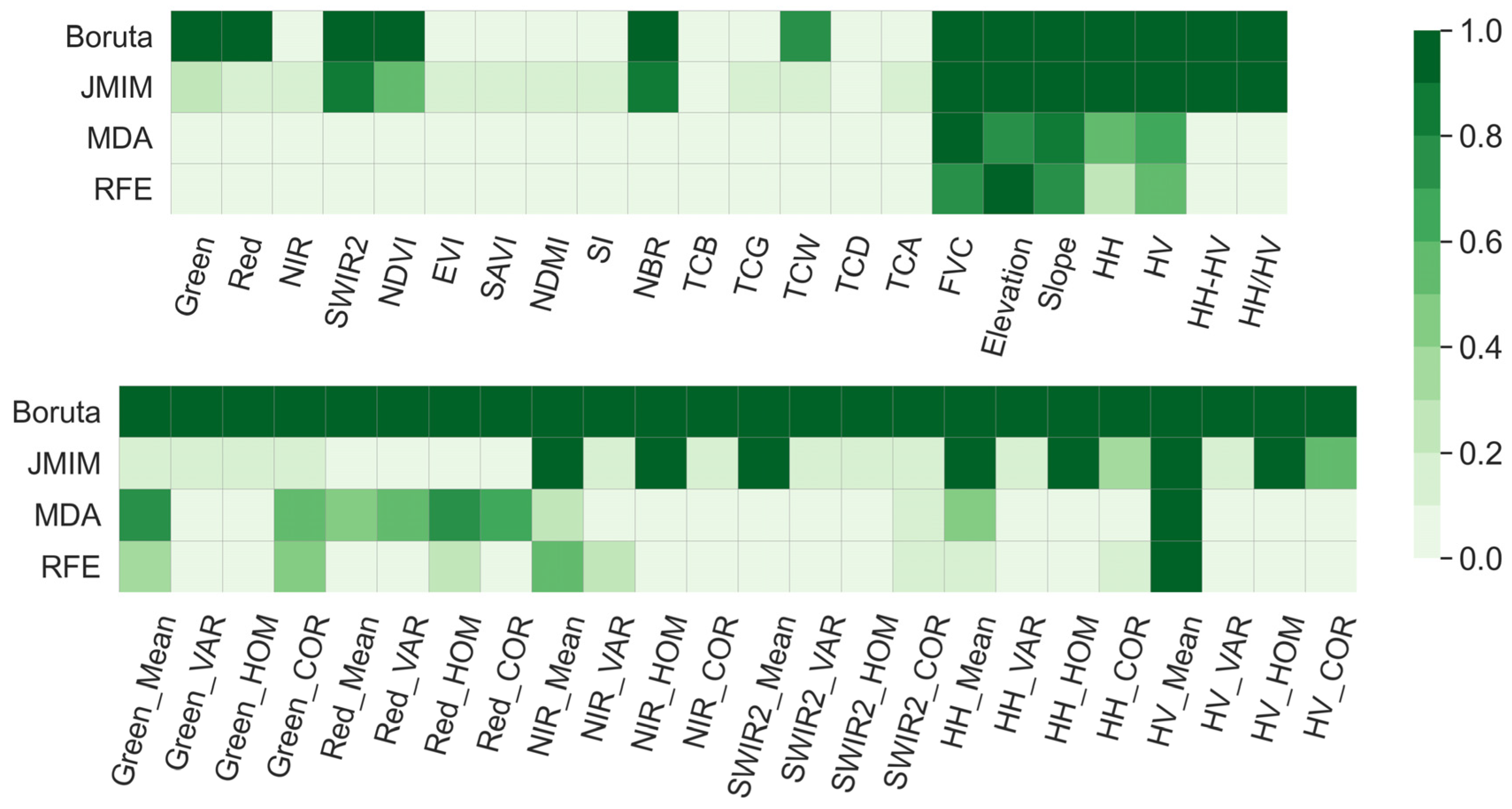
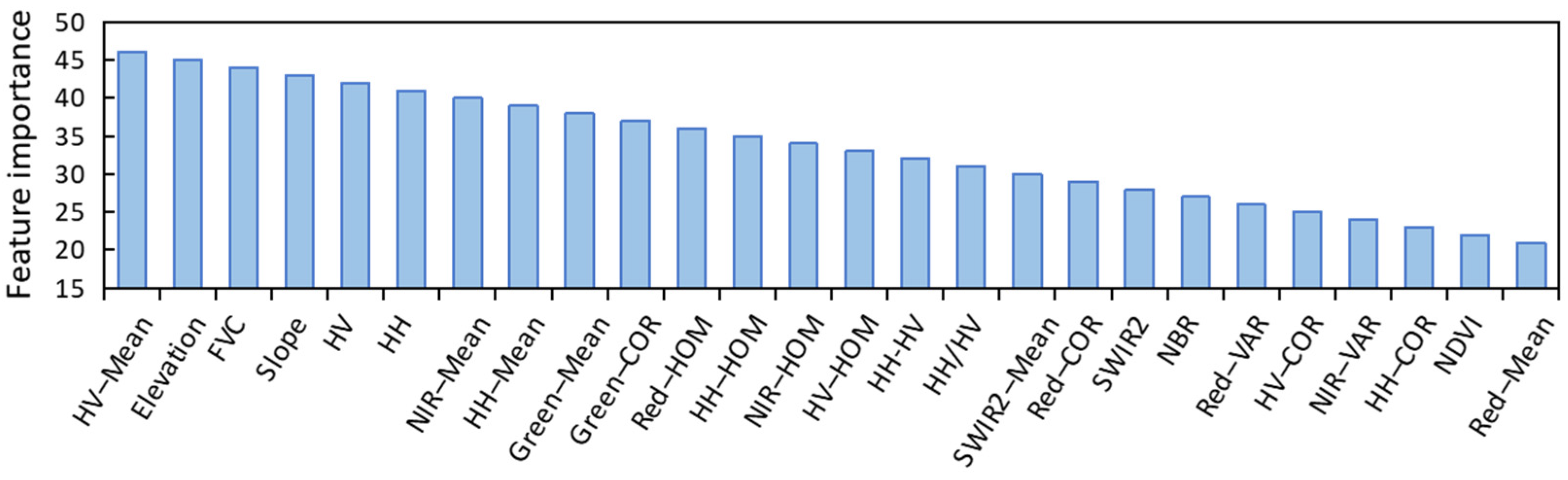
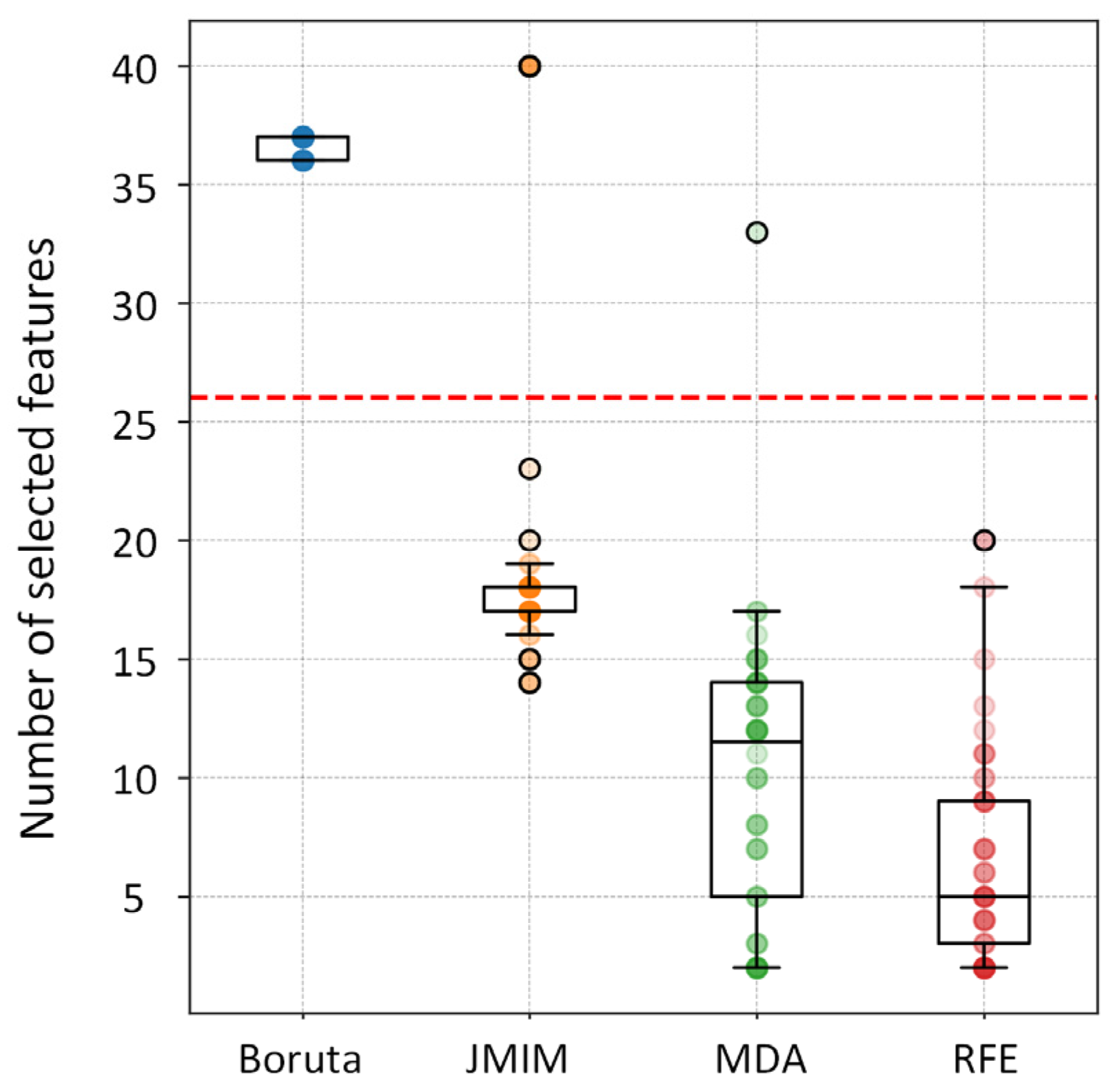
3.1. Important Features Identified for Forest AGB Prediction

In total, 46 features were extracted from Landsat TM, PALSAR and DEM data. FVC, elevation, slope, HV and HV-Mean were the features most frequently identified by Boruta, JMIM, RFE and MDA (Figure 3). The proposed SHCE algorithm ranked HV-Mean as the most important feature, followed by elevation, FVC, slope, HV and HH (Figure 4), which suggested that the features derived from PALSAR data were most relevant for AGB estimation, consistent with results from previous studies [105,106,107,108]. All the FS algorithms confirmed the importance of topographical information and tree cover data in the prediction of forest AGB [109,110,111,112]. The two most important variables for MDA were FVC and HV-Mean, and for RFE they were elevation and HV-Mean.
The features NBR and SWIR2 were selected as important features from Landsat surface reflectance and the derived vegetation indexes by Boruta, JMIM and SHCE. However, they were outweighed by texture information such as NIR-HOM, NIR-Mean, and Red-HOM. Results from all five FS algorithms showed that surface reflectance at the red, green, and near-infrared bands provided limited information for AGB prediction, but the GLCM textures applied on these bands could be important (Figure 3 and Figure 4). The results also suggested that TC-related variables were not as important as previous studies have suggested [60], and they contributed less to AGB prediction than other types of variables such as PALSAR-derived variables or texture metrics.
Results of Boruta were relatively stable, in contrast to the results of other FS algorithms, and 36 variables were selected (Figure 3 and Figure 5). Nine variables, including NIR, EVI, SAVI, NDMI, SI, TCB, TCG, TCD and TCA, were excluded in all 50 results by Boruta (Figure 3). The other FS methods produced subsets with overall smaller numbers of features, but they were more sensitive to the training datasets used, in particular MDA, and RFE (Figure 5).

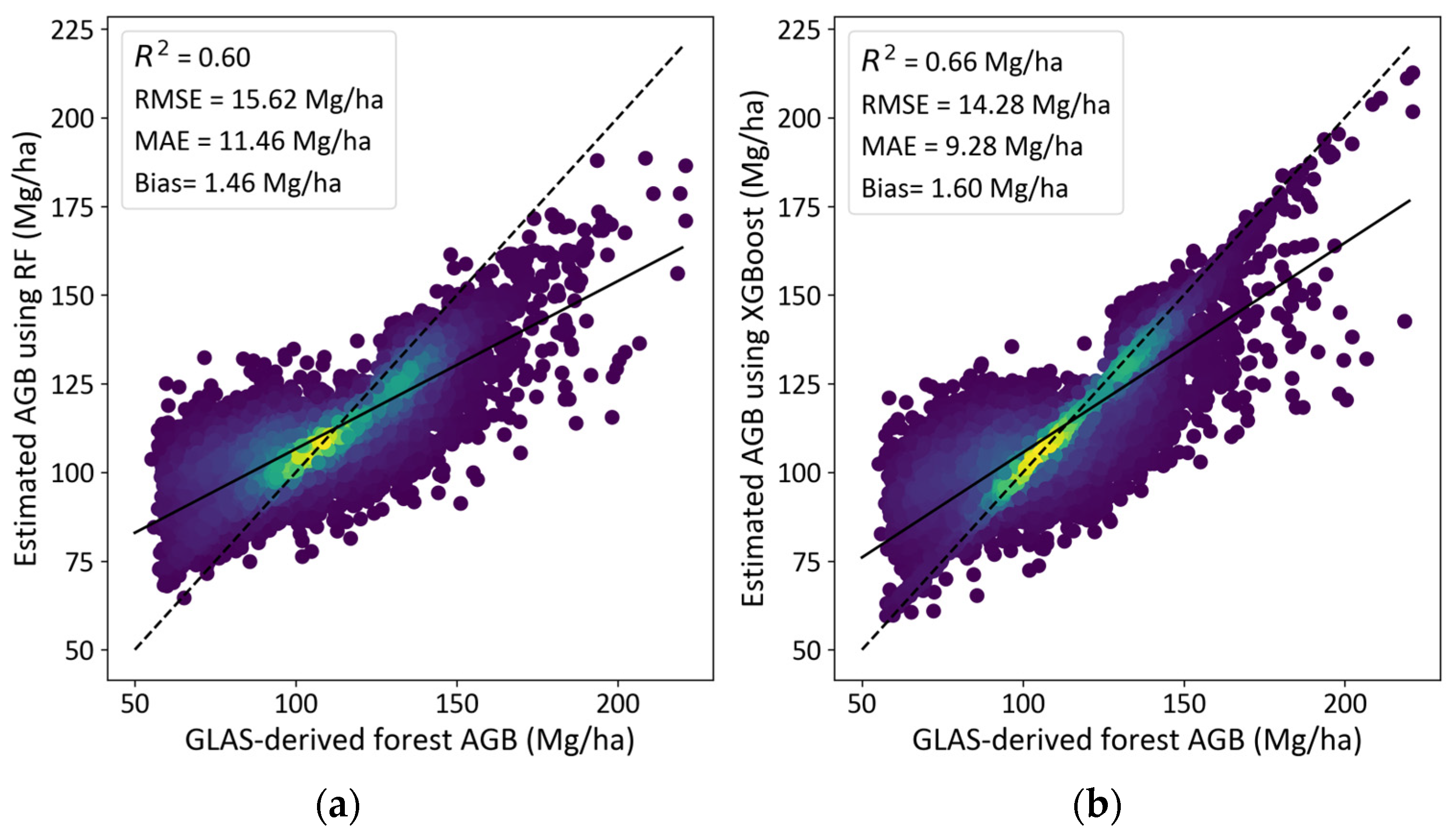
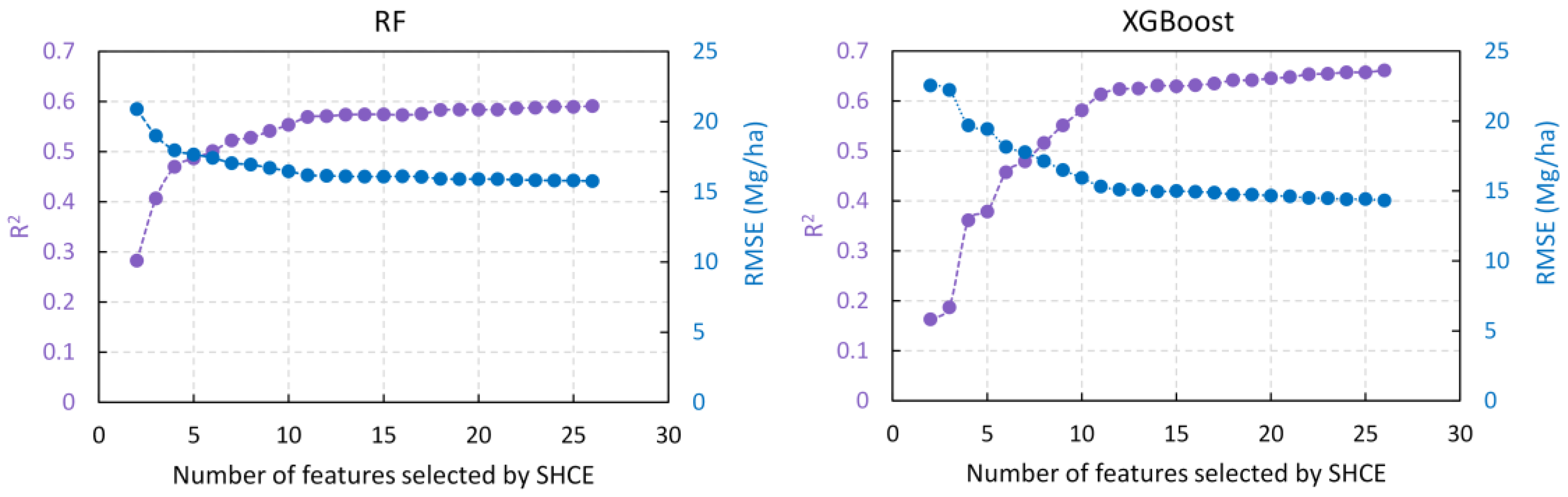
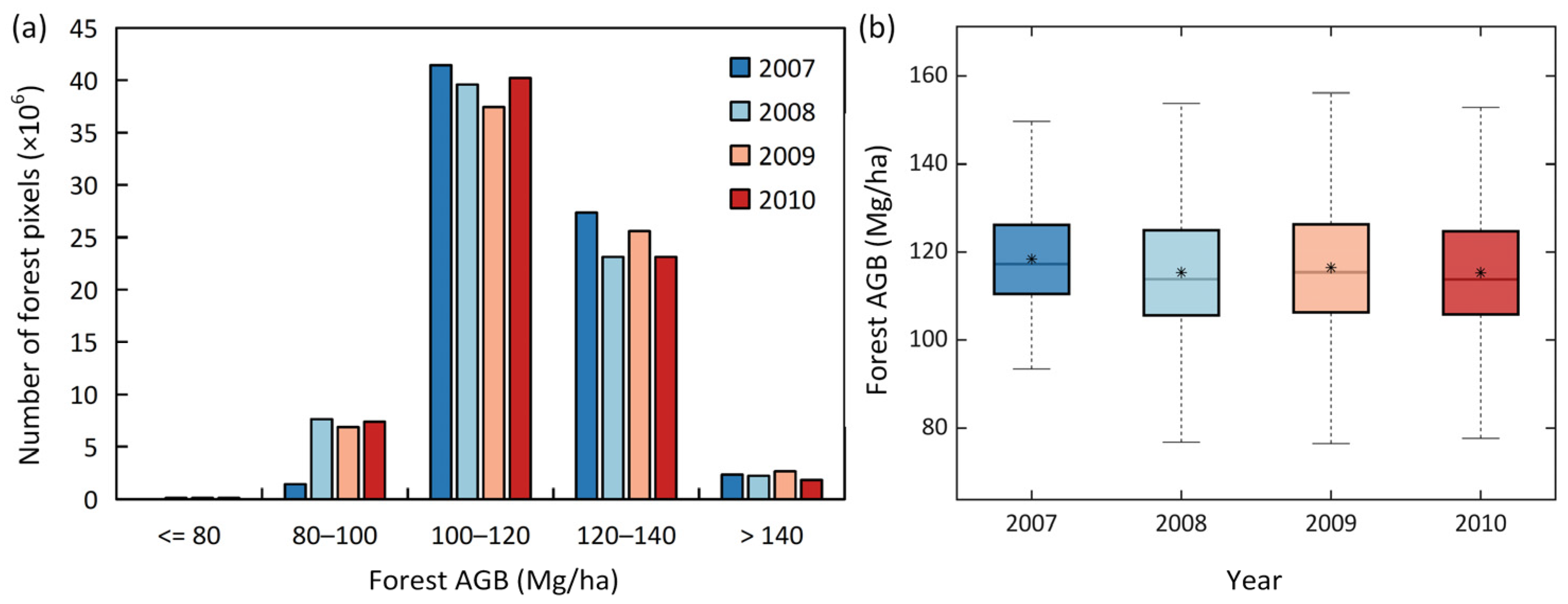
3.2. Accuracy of Forest AGB Prediction Based on Selected Features

We used RF and XGBoost with each of the feature sets selected by Boruta, JMIM, MDA, RFE and SHCE to assess the accuracy of AGB prediction. The results showed that the features selected by MDA and RFE provided less accurate AGB predictions. Both algorithms identified fewer features as being important than the other algorithms, and the features selected were highly unstable, which suggests the two algorithms did not properly detect variables important for AGB prediction (Figure 5 and Figure 6). JMIM selected slightly more features than RFE or MDA, but less than Boruta. AGB predictions using the JMIM features varied within a narrower range than those from RFE and MDA, which suggests that JMIM performed better than those two algorithms in identifying important features.
The features selected by Boruta, and the features selected by SHCE, provided more accurate forest AGB predictions when using RF (Figure 6), with respective indicator values R2 = 0.60 ± 0.01 and 0.59 ± 0.01, RMSE = 15.65 ± 0.12 and 15.76 ± 0.11 Mg ha−1, MAE = 11.52 ± 0.11 and 11.52 ± 0.08 Mg ha−1, and bias = 1.55 ± 0.09 and 1.51 ± 0.09 Mg ha−1. The XGBoost algorithm generally improved on RF AGB predictions. Similar to the results of RF, features selected by Boruta produced the greatest value of R2 = 0.68 ± 0.01, while for SHCE, R2 = 0.66 ± 0.01; features selected by SHCE produced AGB predictions with lower bias than features selected by Boruta, with bias = 1.84 ± 0.11 Mg ha−1 for Boruta and bias = 1.67 ± 0.11 Mg ha−1 for SHCE (Figure 6 and Figure 7). XGBoost with SHCE selected features gave RMSE = 14.35 ± 0.12 Mg ha−1 and MAE = 9.34 ± 0.09 Mg ha−1.
Forest AGB predictions using SHCE selected features were highly correlated with ground truth forest AGB produced using field measurements and GLAS data, particularly when using XGBoost, when many points were around the 1:1 line (Figure 8). Using features selected by Boruta provided similar results in terms of prediction accuracy. However, Boruta did not determine which were the key parameters for AGB prediction because it provided a feature subset rather than a feature ranking. The proposed SHCE accurately predicted forest AGB and also identified crucial features in the prediction (Figure 4 and Figure 6). Use of AIC enabled us to select 26 of 46 features for further analysis. Figure 9 shows that prediction accuracy increased with the inclusion of variables ranked as more important by SHCE. At least ten features were indispensable for accurate AGB estimation, including HH, HV, HH-Mean, HV-Mean, FVC, Slope, Elevation, NIR-Mean, Green-Mean and Green-COR (Figure 4 and Figure 9). Using only the ten most important features, predicted AGB accuracy was indicated by R2 = 0.57 and RMSE = 16.16 Mg ha−1 using the RF model and by R2 = 0.61 and RMSE = 15.32 Mg ha−1 using the XGBoost model. These indicators showed that prediction accuracy increased slightly as more variables were introduced until all 26 selected variables were included.

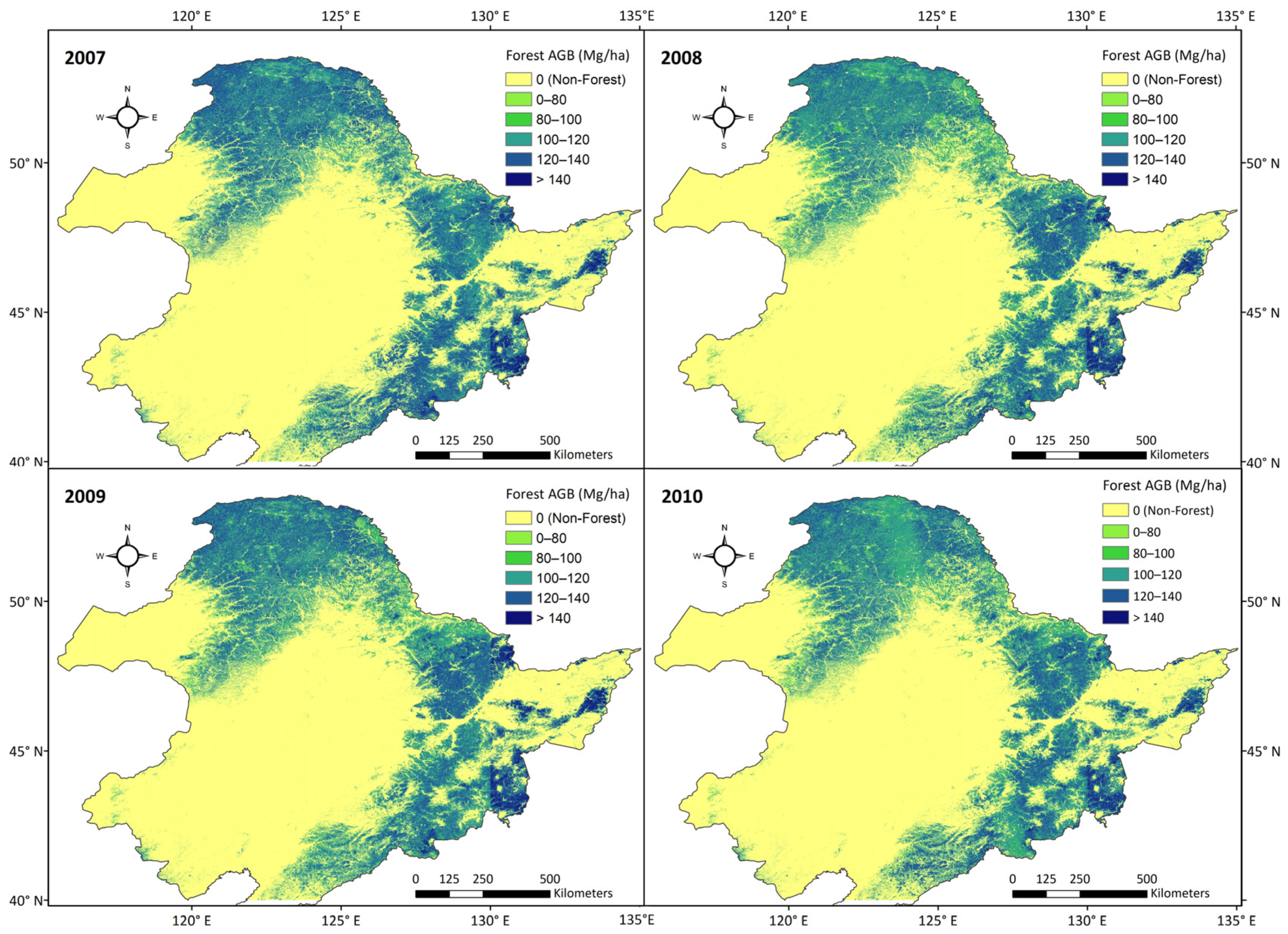
3.3. Forest AGB Maps at 90 m Resolution

We used XGBoost to generate forest AGB maps for 2007–2010 at 90 m resolution (Figure 10) using SHCE selected variables from the Landsat, PALSAR, and DEM data. The results showed that high AGB values tended to be found in regions covered by dense forest (Figure 1). Most forest AGB predictions were in the range 80–140 Mg ha−1, with slight interannual variation (Figure 10 and Figure 11). Statistical analysis of the forest AGB maps showed that predicted AGB values were 118.42 ± 10.60 Mg ha−1 for 2007, 115.38 ± 12.74 Mg ha−1 for 2008, 116.43 ± 12.92 Mg ha−1 for 2009 and 115.34 ± 12.54 Mg ha−1 for 2010. The predicted AGB values were greater than those found in a previous study that used MODIS data [45]. This difference is partly attributable to differences in spatial resolution and the inclusion of PALSAR data. In this study, GLAS-derived AGB samples were aggregated to 90 m rather than to the MODIS resolution to provide more samples with larger AGB values for further model training. In addition, Landsat captures more spatially distributed data than coarse resolution data, and PALSAR data contributes significantly to AGB estimates, and this may reduce the severity of saturation which has often hampered forest AGB prediction. For the year 2009, about 2.66 million forest pixels had AGB values > 140 Mg ha−1 at the spatial resolution of 90 m.

4. Discussion

4.1. The Significance of SHCE in Predicting Forest AGB

In this study, we used four state-of-the-art feature selection methods (Boruta, JMIM, RFE and MDA) and an innovative ensemble FS algorithm, SHCE, to select important predictive features from Landsat, PALSAR and DEM data. We analyzed their performance in forest AGB prediction. The results showed that MDA and RFE were highly dependent on the training data used, and both lacked the capacity to identify key variables. Overall, they produced inaccurate predictions of AGB. Boruta and the proposed SHCE algorithm produced relatively accurate predictions of forest AGB. Boruta used more variables than SHCE, which suggests that there is redundancy in the features selected by Boruta. This would account for the slight increase in bias shown in Figure 7.
SHCE is a flexible framework that can be used to combine different FS results. It ranked variables by importance and provided feature subsets to facilitate accurate prediction. We used SHCE to combine features selected from different training datasets by Boruta, JMIM, RFE and MDA. These four FS algorithms were chosen because our initial examination of FS algorithms, which included the genetic algorithm [97], the least absolute shrinkage and selection operator algorithm [113], sequential forward selection [114] and RReliefF [115,116], showed that Boruta, JMIM, RFE and MDA performed better than other algorithms in terms of stability and prediction accuracy [95].
Previous studies have shown that feature selection reduces overfitting, thus increasing generalizability, thereby allowing the SHCE model to be used in locations for which field measurements are unavailable [117]. This study is the first known attempt to identify key predictive features in order to increase prediction accuracy and increase our understanding of their influence on forest AGB. Autonomous aerial vehicles and hyperspectral techniques have both been increasingly used to inventory forests and observe forest dynamics [118,119,120]; these techniques have provided abundant information for AGB prediction but with feature redundancy. The identification and extraction of key features from data recorded by these recent techniques are thus becoming more important in increasing our understanding of their underlying relationships with forest AGB and in increasing prediction accuracy. SHCE can also be used in other scenarios, such as the prediction of forest AGB at different spatial resolutions or identifying features from other land surface parameters from several remote sensing datasets. These possibilities merit further investigation in future studies.

4.2. Identified Important Features for Forest AGB Prediction

A total of 46 variables were extracted from Landsat, PALSAR and DEM data. Elevation, slope, FVC, HV and HH were identified by almost all the FS algorithms, which implied their importance in forest AGB prediction. Previous studies have shown that PALSAR-derived variables were crucial to forest AGB prediction [105,106,107,108]. Our results confirmed the importance of elevation, slope, and tree cover, in addition to HV and HH, indicating that it is necessary to include topographical data and tree cover data in forest AGB prediction and mapping [109,110,111,112].
Fewer Landsat-derived variables were selected as predictor features than PALSAR-derived variables. Among the spectral reflectance and vegetation indices, SWIR2, NDVI, and NBR were identified as features that were relevant to forest AGB prediction by Boruta, JMIM and SHCE. Some studies have shown that NIR and NDVI could be used in forest AGB prediction [121,122,123]. Our results showed that SWIR2 bands were highly correlated with AGB, consistent with previous studies [124]. NBR has been used in predictions of burned areas and vegetation disturbance and recovery [125,126] and we found it to be a predictor of forest AGB. Some studies have found that forest disturbance and recovery indicators that were extracted from time-series data as predictor variables significantly increased the accuracy of AGB prediction [127,128]. However, we did not investigate the temporal information embedded in Landsat data, so the contribution of NBR to forest AGB prediction was thus different from that which would be found in analyzing vegetation disturbance and recovery.
Some GLCM textures, such as NIR_Mean, Green_Mean and Green_COR, were identified as key features and were assigned a higher priority than SWIR2, NBR and NDVI by SHCE. This suggested that spatial information or texture metrics contributed more to AGB prediction than spectral information. Only four GLCM texture measures, including mean, variance, correlation, and homogeneity were used in this study. Four other measures were examined (contrast, dissimilarity, entropy and angular second moment), but it was found that they provided limited information for AGB prediction, and variables related to these four measures were excluded from the final analysis and were not shown in this study.
Primary predictor variables derived from optical imagery were the Landsat surface reflectance and multiple vegetation indexes. Some biophysical parameters, such as leaf area index, canopy height and net primary production, which have been increasingly considered in mapping forest AGB [129,130,131,132], were not included due to lack of data availability. With the current development of high-resolution remotely sensed vegetation data products, more datasets will become publicly available, and the use of these variables in AGB predictions with GLCM texture measures applied should be fully explored in future studies.

4.3. Comparison of Forest AGB Maps with Other Studies

Forest AGB maps were generated from GLAS, Landsat and PALSAR remote sensing data with a spatial resolution of 90 m. To the best of our knowledge, there are no forest AGB maps of northeastern China with a finer resolution. Zhang et al. [133] found that most forest AGB maps covering the study area were generated from GLAS and MODIS data using tree-based modeling approaches or spatial downscaling algorithms, and all had spatial resolutions coarser than 500 m. Zhang et al. [45] used GLAS and MODIS data and predicted average forest AGB of 83.50 Mg ha−1 for 2005, which was lower than the predictions of this study. Tan et al. [134] used GIMMS NDVI and field inventory data and found that most forests had an AGB density of 90–110 Mg ha−1 carbon for the period 1982–1999 and about 30% of the forests had a carbon density of 70–90 Mg ha−1. The results of this study showed that mean forest AGB for the years 2007–2010 was about 115 Mg ha−1, slightly greater than was found by Tan et al. [134]. This difference may be partly due to the overall increase in forest AGB from 2000 to 2010 [135].
Surface reflectance and vegetation indexes were widely used predictors in published studies, but other variables that have been found to contribute significantly to AGB predictions have been largely ignored in the mapping of forest AGB across northeastern China. In this study, we extracted several features from different remote sensing datasets and so incorporated important features into AGB mapping. Previous studies suggested that forest AGB across northeastern China was strongly influenced by forest height [136]. The inclusion of forest height information will probably further increase the accuracy of forest AGB prediction in terms of both magnitude and spatial distribution. We did not include forest height as a predictor due to the lack of high-resolution forest height maps. In future studies, it may be necessary to map both forest height and AGB using multistage estimation methods [137,138].

4.4. Limitations of This Study

An FS wrapper algorithm is associated with a specific learning model, and the features selected are thus dependent on the learning model used. We used RF as the learning model for FS. Changing from RF to another learning model could affect the accuracy of forest AGB predictions. To reduce uncertainty in the predictions, we predicted AGB using both RF and XGBoost with the features selected by the five FS methods. Both RF and XGBoost produced consistent predictions for each set of features, and XGBoost made more accurate predictions. This indicates the robustness of our assessment of the five FS algorithms.
Forest AGB values used for calibration of satellite data and in AGB modeling were derived from field measurements and GLAS data. Cross-validation results suggested that forest AGB was accurate, with R2 of approximately 0.60 [49], which could be increased by using smaller footprint data or by increasing the number of field measurements [28]. However, taking these steps would surely increase the cost of predicting AGB. Landsat, PALSAR and GLAS data were the main input datasets in this study. Some recent studies have used GEDI and Sentinel data for AGB prediction [13,139,140], and the use of data from these advanced sensors may increase the spatial resolution and accuracy of AGB predictions. Field measurements that would correspond to GEDI and Sentinel data would have to be made, but high-resolution AGB maps with a spatial resolution of about 30 m could be generated in the future.

5. Conclusions

We proposed the SHCE feature selection algorithm and investigated the stability of individual FS algorithms, the heterogeneity or diversity of selected features, and correlations between features, and predicted forest AGB as well as multicollinearity between selected features in determining key predictors of forest AGB from several remote sensing datasets (Landsat, PALSAR and SRTM DEM). The results suggested that SHCE selected the important predictors and so produced an accurate prediction of forest AGB. The features HH, HV, HH-Mean, HV-Mean, FVC, slope, elevation, NIR-Mean, green-mean and green-COR contributed significantly to the AGB predictions. A comparison between results showed that XGBoost predictions of AGB were more accurate than RF predictions for all selected sets of features. We generated the first forest AGB maps at 90 m resolution for 2007–2010 using XGBoost with the feature set selected by SHCE.
The proposed SHCE method can be used as a framework in similar studies because it ranks predictor variables and generates an optimal subset for AGB prediction. Developments in remote-sensing techniques coupled with an effective FS method, such as SHCE, will increase our understanding of the relationships between the several features that influence forest AGB and facilitate the production of regional AGB maps at several spatial scales.

Author Contributions

Y.Z. conceived the study; Y.Z., J.L. and W.L. performed the data analysis; Y.Z., J.L., W.L. and S.L. contributed to writing the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 41801347) and the National Key Research and Development Program of China (2018YFC1407103).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef] [Green Version]
  2. Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Jackson, R.B. The Structure, Distribution, and Biomass of the World’s Forests. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 593–622. [Google Scholar] [CrossRef] [Green Version]
  3. Mitchard, E.T.A. The tropical forest carbon cycle and climate change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Quegan, S.; Toan, T.L.; Chave, J.; Dall, J.; Williams, M. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef] [Green Version]
  6. Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using ASTER satellite data. Int. J. Remote Sens. 2006, 27, 1135–1158. [Google Scholar] [CrossRef]
  7. Sun, Z.; Peng, S.; Li, X.; Guo, Z.; Piao, S. Changes in forest biomass over China during the 2000s and implications for management. For. Ecol. Manag. 2015, 357, 76–83. [Google Scholar] [CrossRef]
  8. Motlagh, M.G.; Kafaky, S.B.; Mataji, A.; Akhavan, R. Estimating and mapping forest biomass using regression models and Spot-6 images (case study: Hyrcanian forests of north of Iran). Environ. Monit. Assess. 2018, 190, 352. [Google Scholar] [CrossRef]
  9. Poulain, M.; Pena, M.; Schmidt, A.; Schmidt, H.; Schulte, A. Relationships between forest variables and remote sensing data in a Nothofagus pumilio forest. Geocarto Int. 2010, 25, 25–43. [Google Scholar] [CrossRef]
  10. Meng, S.; Pang, Y.; Zhang, Z.; Jia, W.; Li, Z. Mapping Aboveground Biomass using Texture Indices from Aerial Photos in a Temperate Forest of Northeastern China. Remote Sens. 2016, 8, 230. [Google Scholar] [CrossRef] [Green Version]
  11. Zhuang, W.; Mountrakis, G.; Wiley, J.J.; Beier, C.M. Estimation of above-ground forest biomass using metrics based on Gaussian decomposition of waveform lidar data. Int. J. Remote Sens. 2015, 36, 1871–1889. [Google Scholar] [CrossRef]
  12. Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite lidar vs. small footprint airborne lidar: Comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar] [CrossRef]
  13. Debastiani, A.B.; Sanquetta, C.R.; Dalla Corte, A.P.; Rex, F.E.; Pinto, N.S. Evaluating SAR-optical sensor fusion for aboveground biomass estimation in a Brazilian tropical forest. Ann. For. Res. 2019, 62, 109–122. [Google Scholar] [CrossRef]
  14. Yu, H.; Zhang, Z. The Performance of Relative Height Metrics for Estimation of Forest Above-Ground Biomass Using L- and X-Bands TomoSAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1857–1871. [Google Scholar] [CrossRef]
  15. Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An Evaluation of Eight Machine Learning Regression Algorithms for Forest Aboveground Biomass Estimation from Multiple Satellite Data Products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
  16. Gleason, C.J.; Im, J. Forest biomass estimation from airborne LiDAR data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
  17. Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
  18. Shao, Z.; Zhang, L.; Wang, L. Stacked Sparse Autoencoder Modeling Using the Synergy of Airborne LiDAR and Satellite Optical and SAR Data to Map Forest Above-Ground Biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
  19. Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [Green Version]
  20. Wang, L.; Wang, Y.; Chang, Q. Feature selection methods for big data bioinformatics: A survey from the search perspective. Methods 2016, 111, 21–31. [Google Scholar] [CrossRef]
  21. Bolón-Canedo, V.; Remeseiro, B. Feature selection in image analysis: A survey. Artif. Intell. Rev. 2020, 53, 2905–2931. [Google Scholar] [CrossRef]
  22. Huang, L.; Ran, J.; Wang, W.; Yang, T.; Xiang, Y. A multi-channel anomaly detection method with feature selection and multi-scale analysis. Comput. Netw. 2021, 185, 107645. [Google Scholar] [CrossRef]
  23. Teh, H.Y.; Wang, K.I.K.; Kempa-Liehr, A.W. Expect the Unexpected: Unsupervised Feature Selection for Automated Sensor Anomaly Detection. IEEE Sens. J. 2021, 21, 18033–18046. [Google Scholar] [CrossRef]
  24. Abualigah, L.M.; Khader, A.T. Unsupervised text feature selection technique based on hybrid particle swarm optimization algorithm with genetic operators for the text clustering. J. Supercomput. 2017, 73, 4773–4795. [Google Scholar] [CrossRef]
  25. Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
  26. Hsu, H.-H.; Hsieh, C.-W.; Lu, M.-D. Hybrid feature selection by combining filters and wrappers. Expert Syst. Appl. 2011, 38, 8144–8150. [Google Scholar] [CrossRef]
  27. Huang, N.; Li, R.; Lin, L.; Yu, Z.; Cai, G. Low Redundancy Feature Selection of Short Term Solar Irradiance Prediction Using Conditional Mutual Information and Gauss Process Regression. Sustainability 2018, 10, 2889. [Google Scholar] [CrossRef] [Green Version]
  28. Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
  29. Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernandez, J.; Corvalan, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
  30. Cai, J.; Luo, J.W.; Wang, S.L.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
  31. Archibald, R.; Fann, G. Feature selection and classification of hyperspectral images, with support vector machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
  32. Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
  33. Liu, H.; Zhou, M.; Liu, Q. An embedded feature selection method for imbalanced data classification. IEEE/CAA J. Autom. Sin. 2019, 6, 703–715. [Google Scholar] [CrossRef]
  34. Xie, Z.; Xu, Y. Sparse group LASSO based uncertain feature selection. Int. J. Mach. Learn. Cybern. 2014, 5, 201–210. [Google Scholar] [CrossRef]
  35. Hancer, E.; Xue, B.; Zhang, M.J. Differential evolution for filter feature selection based on information theory and feature ranking. Knowl.-Based Syst. 2018, 140, 103–119. [Google Scholar] [CrossRef]
  36. Moradi, P.; Gholampour, M. A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy. Appl. Soft Comput. 2016, 43, 117–130. [Google Scholar] [CrossRef]
  37. Zorarpacı, E.; Özel, S.A. A hybrid approach of differential evolution and artificial bee colony for feature selection. Expert Syst. Appl. 2016, 62, 91–103. [Google Scholar] [CrossRef]
  38. Got, A.; Moussaoui, A.; Zouache, D. Hybrid filter-wrapper feature selection using whale optimization algorithm: A multi-objective approach. Expert Syst. Appl. 2021, 183, 115312. [Google Scholar] [CrossRef]
  39. Chuang, L.-Y.; Yang, C.-H.; Wu, K.-C.; Yang, C.-H. A hybrid feature selection method for DNA microarray data. Comput. Biol. Med. 2011, 41, 228–237. [Google Scholar] [CrossRef] [PubMed]
  40. Pes, B.; Dessì, N.; Angioni, M. Exploiting the ensemble paradigm for stable feature selection: A case study on high-dimensional genomic data. Inf. Fusion 2017, 35, 132–147. [Google Scholar] [CrossRef]
  41. Wang, X.P.; Fang, J.Y.; Zhu, B. Forest biomass and root-shoot allocation in northeast China. For. Ecol. Manag. 2008, 255, 4007–4020. [Google Scholar] [CrossRef]
  42. Yao, Y.; Wang, X.; Li, Y.; Wang, T.; Shen, M.; Du, M.; He, H.; Li, Y.; Luo, W.; Ma, M.; et al. Spatiotemporal pattern of gross primary productivity and its covariation with climate in China over the last thirty years. Glob. Chang. Biol. 2017, 24, 184–196. [Google Scholar] [CrossRef] [PubMed]
  43. Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Zhou, Y.L. Geography of the Vegetation in Northeast China; Science Press: Beijing, China, 1997. [Google Scholar]
  45. Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of Northeastern China Using GLAS and MODIS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
  46. Sun, G.; Ranson, K.J.; Masek, J.; Guo, Z.; Pang, Y.; Fu, A.; Wang, D. Estimation of Tree Height and Forest Biomass from GLAS Data. J. For. Plan. 2008, 13, 157–164. [Google Scholar]
  47. Pang, Y.; Lefsky, M.; Sun, G.; Miller, M.E.; Li, Z. Temperate forest height estimation performance using ICESat GLAS data from different observation periods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 777–782. [Google Scholar]
  48. Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef] [Green Version]
  49. Zhang, Y.; Li, W.; Liang, S. New Metrics and the Combinations for Estimating Forest Biomass from GLAS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7830–7839. [Google Scholar] [CrossRef]
  50. Lee, S.; Ni-Meister, W.; Yang, W.; Qi, C. Physically based vertical vegetation structure retrieval from ICESat data: Validation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sens. Environ. 2011, 115, 2776–2785. [Google Scholar] [CrossRef]
  51. Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116, G04021. [Google Scholar] [CrossRef] [Green Version]
  52. Branco, P.; Torgo, L.; Ribeiro, R.P. SMOGN: A Pre-processing Approach for Imbalanced Regression. In Proceedings of the First International Workshop on Learning with Imbalanced Domains: Theory and Applications, Skopje, Macedonia, 22 September 2017; Paula Branco Luís, T., Nuno, M., Eds.; PMLR: London, UK, 2017; pp. 36–50. [Google Scholar]
  53. Dwyer, J.L.; Roy, D.P.; Sauer, B.; Jenkerson, C.B.; Lymburner, L. Analysis Ready Data: Enabling Analysis of the Landsat Archive. Remote Sens. 2018, 10, 1363. [Google Scholar] [CrossRef]
  54. Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
  55. Amani, M.; Ghorbanian, A.; Ahmadi, S.A.; Kakooei, M.; Moghimi, A.; Mirmazloumi, S.M.; Moghaddam, S.H.A.; Mahdavi, S.; Ghahremanloo, M.; Parsian, S.; et al. Google Earth Engine Cloud Computing Platform for Remote Sensing Big Data Applications: A Comprehensive Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5326–5350. [Google Scholar] [CrossRef]
  56. Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
  57. Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of feature selection and catboost for prediction: The first application to the estimation of aboveground biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
  58. Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
  59. Wu, C.; Shen, H.; Shen, A.; Deng, J.; Gan, M.; Zhu, J.; Xu, H.; Wang, K. Comparison of machine-learning methods for above-ground biomass estimation based on Landsat imagery. J. Appl. Remote Sens. 2016, 10, 035010. [Google Scholar] [CrossRef]
  60. Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Kennedy, R. Characterization of aboveground biomass in an unmanaged boreal forest using Landsat temporal segmentation metrics. ISPRS J. Photogramm. Remote Sens. 2014, 92, 137–146. [Google Scholar] [CrossRef]
  61. Gomez, C.; White, J.C.; Wulder, M.A.; Alejandro, P. Historical forest biomass dynamics modelled with Landsat spectral trajectories. ISPRS J. Photogramm. Remote Sens. 2014, 93, 14–28. [Google Scholar] [CrossRef] [Green Version]
  62. Zald, H.S.J.; Wulder, M.A.; White, J.C.; Hilker, T.; Hermosilla, T.; Hobart, G.W.; Coops, N.C. Integrating Landsat pixel composites and change metrics with lidar plots to predictively map forest structure and aboveground biomass in Saskatchewan, Canada. Remote Sens. Environ. 2016, 176, 188–201. [Google Scholar] [CrossRef] [Green Version]
  63. Lu, D.; Batistella, M. Exploring TM image texture and its relationships with biomass estimation in Rondônia, Brazilian Amazon. Acta Amaz. 2005, 35, 249–257. [Google Scholar] [CrossRef]
  64. Liao, Z.; He, B.; Quan, X. Potential of texture from SAR tomographic images for forest aboveground biomass estimation. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102049. [Google Scholar] [CrossRef]
  65. Eckert, S. Improved Forest Biomass and Carbon Estimations Using Texture Measures from WorldView-2 Satellite Data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef] [Green Version]
  66. Kelsey, K.C.; Neff, J.C. Estimates of Aboveground Biomass from Texture Analysis of Landsat Imagery. Remote Sens. 2014, 6, 6407–6422. [Google Scholar] [CrossRef] [Green Version]
  67. Clausi, D.A. An analysis of co-occurrence texture statistics as a function of grey level quantization. Can. J. Remote Sens. 2002, 28, 45–62. [Google Scholar] [CrossRef]
  68. Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  69. Shimada, M.; Ohtaki, T. Generating Large-Scale High-Quality SAR Mosaic Datasets: Application to PALSAR Data for Global Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 637–656. [Google Scholar] [CrossRef]
  70. Shimada, M.; Itoh, T.; Motooka, T.; Watanabe, M.; Shiraishi, T.; Thapa, R.; Lucas, R. New global forest/non-forest maps from ALOS PALSAR data (2007–2010). Remote Sens. Environ. 2014, 155, 13–31. [Google Scholar] [CrossRef]
  71. Shen, W.; Li, M.; Huang, C.; Tao, X.; Wei, A. Annual forest aboveground biomass changes mapped using ICESat/GLAS measurements, historical inventory data, and time-series optical and radar imagery for Guangdong province, China. Agric. For. Meteorol. 2018, 259, 23–38. [Google Scholar] [CrossRef] [Green Version]
  72. Zhang, Y.; Ling, F.; Foody, G.M.; Ge, Y.; Boyd, D.S.; Li, X.; Du, Y.; Atkinson, P.M. Mapping annual forest cover by fusing PALSAR/PALSAR-2 and MODIS NDVI during 2007–2016. Remote Sens. Environ. 2019, 224, 74–91. [Google Scholar] [CrossRef] [Green Version]
  73. Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-filled SRTM for the globe Version 4. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 31 December 2021).
  74. Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
  75. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  76. Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
  77. Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
  78. Hardisky, M.A.; Klemas, V.; Smart, R.M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina Alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 48, 77–84. [Google Scholar]
  79. Fiorella, M.; Ripple, W.J. Determining successional stage of temperate coniferous forests with Landsat satellite data. Photogramm. Eng. Remote Sens. 1993, 59, 239–246. [Google Scholar]
  80. López García, M.J.; Caselles, V. Mapping burns and natural reforestation using thematic Mapper data. Geocarto Int. 1991, 6, 31–37. [Google Scholar] [CrossRef]
  81. Crist, E.P. A TM Tasseled Cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
  82. Duane, M.V.; Cohen, W.B.; Campbell, J.L.; Hudiburg, T.; Turner, D.P.; Weyermann, D.L. Implications of Alternative Field-Sampling Designs on Landsat-Based Mapping of Stand Age and Carbon Stocks in Oregon Forests. For. Sci. 2010, 56, 405–416. [Google Scholar]
  83. Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
  84. Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
  85. Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 13. [Google Scholar] [CrossRef] [Green Version]
  86. Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of variable selection methods for random forests and omics data sets. Brief. Bioinform. 2017, 20, 492–503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  87. Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  88. Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
  89. Bennasar, M.; Hicks, Y.; Setchi, R. Feature selection using Joint Mutual Information Maximisation. Expert Syst. Appl. 2015, 42, 8520–8532. [Google Scholar] [CrossRef] [Green Version]
  90. Ross, B.C. Mutual Information between Discrete and Continuous Data Sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef]
  91. Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
  92. Rasel, S.M.M.; Chang, H.C.; Ralph, T.J.; Saintilan, N.; Diti, I.J. Application of feature selection methods and machine learning algorithms for saltmarsh biomass estimation using Worldview-2 imagery. Geocarto Int. 2021, 36, 1075–1099. [Google Scholar] [CrossRef]
  93. Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less is more: Optimizing classification performance through feature selection in a very-high-resolution remote sensing object-based urban application. GIScience Remote Sens. 2018, 55, 221–242. [Google Scholar] [CrossRef]
  94. Chrysafis, I.; Mallinis, G.; Gitas, I.; Tsakiri-Strati, M. Estimating Mediterranean forest parameters using multi seasonal Landsat 8 OLI imagery and an ensemble learning method. Remote Sens. Environ. 2017, 199, 154–166. [Google Scholar] [CrossRef]
  95. Saeys, Y.; Abeel, T.; Van de Peer, Y. Robust Feature Selection Using Ensemble Feature Selection Techniques. In Proceedings of the Machine Learning and Knowledge Discovery in Databases, European Conference, ECML PKDD 2008, Antwerp, Belgium, 15–19 September 2008; Daelemans, W., Goethals, B., Morik, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 313–325. [Google Scholar]
  96. Tsai, C.-F.; Sung, Y.-T. Ensemble feature selection in high dimension, low sample size datasets: Parallel and serial combination approaches. Knowl.-Based Syst. 2020, 203, 106097. [Google Scholar] [CrossRef]
  97. Wang, H.; He, C.; Li, Z. A new ensemble feature selection approach based on genetic algorithm. Soft Comput. 2020, 24, 15811–15820. [Google Scholar] [CrossRef]
  98. Kuncheva, L.I. A stability index for feature selection. In Proceedings of the IASTED International Conference on Artificial Intelligence and Applications, Innsbruck, Austria, 12–14 February 2007. [Google Scholar]
  99. Hall, M.A. Correlation-Based Feature Selection for Machine Learning, in Department of Computer Science; University of Waikato: Hamilton, New Zealand, 1999. [Google Scholar]
  100. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  101. Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114 (Suppl. C), 24–31. [Google Scholar] [CrossRef]
  102. Zhang, Y.; Liu, J.; Shen, W. A Review of Ensemble Learning Algorithms Used in Remote Sensing Applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
  103. Buhlmann, P.; Hothorn, T. Boosting Algorithms: Regularization, Prediction and Model Fitting. Statist. Sci. 2007, 22, 477–505. [Google Scholar]
  104. Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
  105. Endres, A.; Endres, A.; Mountrakis, G.; Jin, H.; Zhuang, W.; Manakos, I.; Wiley, J.J.; Beier, C.M. Relative importance analysis of Landsat, waveform LIDAR and PALSAR inputs for deciduous biomass estimation. Eur. J. Remote Sens. 2016, 49, 795–807. [Google Scholar] [CrossRef] [Green Version]
  106. Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S.; Das, A.K.; Mohan, S. Developing synergy regression models with space-borne ALOS PALSAR and Landsat TM sensors for retrieving tropical forest biomass. J. Earth Syst. Sci. 2016, 125, 725–735. [Google Scholar] [CrossRef] [Green Version]
  107. Baghdadi, N.; Le Maire, G.; Bailly, J.S.; Ose, K.; Nouvellon, Y.; Zribi, M.; Lemos, C.; Hakamada, R. Evaluation of ALOS/PALSAR L-Band Data for the Estimation of Eucalyptus Plantations Aboveground Biomass in Brazil. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3802–3811. [Google Scholar] [CrossRef] [Green Version]
  108. Rodríguez-Veiga, P.; Saatchi, S.; Tansey, K.; Balzter, H. Magnitude, spatial distribution and uncertainty of forest biomass stocks in Mexico. Remote Sens. Environ. 2016, 183, 265–281. [Google Scholar] [CrossRef] [Green Version]
  109. Yang, C.; Huang, H.; Wang, S. Estimation of tropical forest biomass using Landsat TM imagery and permanent plot data in Xishuangbanna, China. Int. J. Remote Sens. 2011, 32, 5741–5756. [Google Scholar] [CrossRef]
  110. Baccini, A.; Friedl, M.A.; Woodcock, C.E.; Warbington, R. Forest biomass estimation over regional scales using multisource data. Geophys. Res. Lett. 2004, 31, L10501. [Google Scholar] [CrossRef] [Green Version]
  111. Yang, L.; Liang, S.; Zhang, Y. A New Method for Generating a Global Forest Aboveground Biomass Map from Multiple High-Level Satellite Products and Ancillary Information. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2587–2597. [Google Scholar] [CrossRef]
  112. Zhang, Y.; Liang, S. Fusion of Multiple Gridded Biomass Datasets for Generating a Global Forest Aboveground Biomass Map. Remote Sens. 2020, 12, 2559. [Google Scholar] [CrossRef]
  113. Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011, 73, 273–282. [Google Scholar] [CrossRef]
  114. Gheyas, I.A.; Smith, L.S. Feature subset selection in large dimensionality domains. Pattern Recognit. 2010, 43, 5–13. [Google Scholar] [CrossRef] [Green Version]
  115. Li, B.; Xu, X.; Zhang, L.; Han, J.; Bian, C.; Li, G.; Liu, J.; Jin, L. Above-ground biomass estimation and yield prediction in potato by using UAV-based RGB and hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2020, 162, 161–172. [Google Scholar] [CrossRef]
  116. Robnik-Šikonja, M.; Kononenko, I. Theoretical and Empirical Analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef] [Green Version]
  117. Yu, H.; Wu, Y.; Niu, L.; Chai, Y.; Feng, Q.; Wang, W.; Liang, T. A method to avoid spatial overfitting in estimation of grassland above-ground biomass on the Tibetan Plateau. Ecol. Indic. 2021, 125, 107450. [Google Scholar] [CrossRef]
  118. Johansen, K.; Morton, M.; Malbeteau, Y.; Aragon, B.; Al-Mashharawi, S.; Ziliani, M.G.; Angel, Y.; Fiene, G.; Negrao, S.; Mousa, M.; et al. Predicting Biomass and Yield in a Tomato Phenotyping Experiment Using UAV Imagery and Random Forest. Front. Artif. Intell. 2020, 3, 28. [Google Scholar] [CrossRef] [PubMed]
  119. Lu, J.; Wang, H.; Qin, S.; Cao, L.; Pu, R.; Li, G.; Sun, J. Estimation of aboveground biomass of Robinia pseudoacacia forest in the Yellow River Delta based on UAV and Backpack LiDAR point clouds. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102014. [Google Scholar] [CrossRef]
  120. Laurin, G.V.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del Frate, F.; Guerriero, L.; Pirotti, F.; Valenti, R. Above ground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
  121. Pandit, S.; Tsuyuki, S.; Dube, T. Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data. Remote Sens. 2018, 10, 1848. [Google Scholar] [CrossRef] [Green Version]
  122. Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
  123. Wang, X.; Shao, G.; Chen, H.; Lewis, B.J.; Qi, G.; Yu, D.; Zhou, L.; Dai, L. An Application of Remote Sensing Data in Mapping Landscape-Level Forest Biomass for Monitoring the Effectiveness of Forest Policies in Northeastern China. Environ. Manag. 2013, 52, 612–620. [Google Scholar] [CrossRef]
  124. Otgonbayar, M.; Atzberger, C.; Chambers, J.; Damdinsuren, A. Mapping pasture biomass in Mongolia using Partial Least Squares, Random Forest regression and Landsat 8 imagery. Int. J. Remote Sens. 2019, 40, 3204–3226. [Google Scholar] [CrossRef]
  125. Meng, Q.; Meentemeyer, R.K. Modeling of multi-strata forest fire severity using Landsat TM Data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 120–126. [Google Scholar] [CrossRef]
  126. Wulder, M.A.; White, J.C.; Alvarez, F.; Han, T.; Rogan, J.; Hawkes, B. Characterizing boreal forest wildfire with multi-temporal Landsat and LIDAR data. Remote Sens. Environ. 2009, 113, 1540–1555. [Google Scholar] [CrossRef]
  127. Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E.; Yang, Z. Using Landsat-derived disturbance and recovery history and lidar to map forest biomass dynamics. Remote Sens. Environ. 2014, 151, 124–137. [Google Scholar] [CrossRef]
  128. Nguyen, T.H.; Jones, S.; Soto-Berelov, M.; Haywood, A.; Hislop, S. Landsat Time-Series for Estimating Forest Aboveground Biomass and Its Dynamics across Space and Time: A Review. Remote Sens. 2020, 12, 98. [Google Scholar] [CrossRef] [Green Version]
  129. Keeling, H.C.; Phillips, O.L. The global relationship between forest productivity and biomass. Glob. Ecol. Biogeogr. 2007, 16, 618–631. [Google Scholar] [CrossRef]
  130. Zhang, X.; Kondragunta, S. Estimating forest biomass in the USA using generalized allometric models and MODIS land products. Geophys. Res. Lett. 2006, 33, L09402. [Google Scholar] [CrossRef] [Green Version]
  131. Liang, S.L.; Cheng, J.; Jia, K.; Jiang, B.; Liu, Q.; Xiao, Z.Q.; Yao, Y.J.; Yuan, W.P.; Zhang, X.T.; Zhao, X.; et al. The Global Land Surface Satellite (GLASS) Product Suite. Bull. Am. Meteorol. Soc. 2021, 102, E323–E337. [Google Scholar] [CrossRef]
  132. Joetzjer, E.; Pillet, M.; Ciais, P.; Barbier, N.; Chave, J.; Schlund, M.; Maignan, F.; Barichivich, J.; Luyssaert, S.; Herault, B.; et al. Assimilating satellite-based canopy height within an ecosystem model to estimate aboveground forest biomass. Geophys. Res. Lett. 2017, 44, 6823–6832. [Google Scholar] [CrossRef] [Green Version]
  133. Zhang, Y.; Liang, S.; Yang, L. A review of regional and global gridded forest biomass datasets. Remote Sens. 2019, 11, 2744. [Google Scholar] [CrossRef] [Green Version]
  134. Tan, K.; Piao, S.; Peng, C.; Fang, J. Satellite-based estimation of biomass carbon stocks for northeast China’s forests between 1982 and 1999. For. Ecol. Manag. 2007, 240, 114–121. [Google Scholar] [CrossRef]
  135. Zhang, Y.; Liang, S. Changes in forest biomass and linkage to climate and forest disturbances over Northeastern China. Glob. Chang. Biol. 2014, 20, 2596–2606. [Google Scholar] [CrossRef]
  136. Wang, X.P.; Ouyang, S.; Sun, O.J.; Fang, J.Y. Forest biomass patterns across northeast China are strongly shaped by forest height. For. Ecol. Manag. 2013, 293, 149–160. [Google Scholar] [CrossRef]
  137. Nandy, S.; Srinet, R.; Padalia, H. Mapping Forest Height and Aboveground Biomass by Integrating ICESat-2, Sentinel-1 and Sentinel-2 Data Using Random Forest Algorithm in Northwest Himalayan Foothills of India. Geophys. Res. Lett. 2021, 48, e2021GL093799. [Google Scholar] [CrossRef]
  138. Solberg, S.; Nasset, E.; Gobakken, T.; Bollandsas, O.M. Forest biomass change estimated from height change in interferometric SAR height models. Carbon Balance Manag. 2014, 9, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  139. Chen, L.; Ren, C.Y.; Bao, G.D.; Zhang, B.; Wang, Z.M.; Liu, M.Y.; Man, W.D.; Liu, J.F. Improved Object-Based Estimation of Forest Aboveground Biomass by Integrating LiDAR Data from GEDI and ICESat-2 with Multi-Sensor Images in a Heterogeneous Mountainous Region. Remote Sens. 2022, 14, 2743. [Google Scholar] [CrossRef]
  140. Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass estimation from simulated GEDI, ICESat-2 and NISAR across environmental gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
Remotesensing 15 01096 g001 550
Figure 1. The study area: (a) the red triangles showed the field measurements in the Tahe county and Changbai Mountain region, and the points showed the GLAS footprints located in the forest region of the study area as well as their AGB values. The background map shows the spatial distribution of tree cover; and (b) shows the elevation map of the study area.
Figure 1. The study area: (a) the red triangles showed the field measurements in the Tahe county and Changbai Mountain region, and the points showed the GLAS footprints located in the forest region of the study area as well as their AGB values. The background map shows the spatial distribution of tree cover; and (b) shows the elevation map of the study area.
Remotesensing 15 01096 g001
Remotesensing 15 01096 g002 550
Figure 2. Flowchart illustrating feature selection for forest AGB estimation.
Figure 2. Flowchart illustrating feature selection for forest AGB estimation.
Remotesensing 15 01096 g002
Remotesensing 15 01096 g003 550
Figure 3. Frequency of features contained in the 50 feature subsets produced by Boruta, JMIM, MDA and RFE.
Figure 3. Frequency of features contained in the 50 feature subsets produced by Boruta, JMIM, MDA and RFE.
Remotesensing 15 01096 g003
Remotesensing 15 01096 g004 550
Figure 4. Feature importance ranked by the SHCE feature selection algorithm. The importance of each of the selected 26 features was obtained by subtracting 47 from its ranking order.
Figure 4. Feature importance ranked by the SHCE feature selection algorithm. The importance of each of the selected 26 features was obtained by subtracting 47 from its ranking order.
Remotesensing 15 01096 g004
Remotesensing 15 01096 g005 550
Figure 5. The number of feature subsets generated by each FS method based on 50 training datasets; the red dashed line shows the SHCE results.
Figure 5. The number of feature subsets generated by each FS method based on 50 training datasets; the red dashed line shows the SHCE results.
Remotesensing 15 01096 g005
Remotesensing 15 01096 g006 550
Figure 6. Boxplots showing forest AGB prediction accuracy using features selected by each FS algorithm for both RF and XGBoost models.
Figure 6. Boxplots showing forest AGB prediction accuracy using features selected by each FS algorithm for both RF and XGBoost models.
Remotesensing 15 01096 g006
Remotesensing 15 01096 g007 550
Figure 7. Forest AGB prediction accuracy using Boruta selected subsets and SHCE selected subsets as indicated by R2 and bias for comparison.
Figure 7. Forest AGB prediction accuracy using Boruta selected subsets and SHCE selected subsets as indicated by R2 and bias for comparison.
Remotesensing 15 01096 g007
Remotesensing 15 01096 g008 550
Figure 8. Density scatterplots of GLAS-derived forest AGB and predicted AGB using SHCE selected features from Landsat, PALSAR and DEM data using: (a) RF; and (b) XGBoost. The dashed line represents the 1:1 line.
Figure 8. Density scatterplots of GLAS-derived forest AGB and predicted AGB using SHCE selected features from Landsat, PALSAR and DEM data using: (a) RF; and (b) XGBoost. The dashed line represents the 1:1 line.
Remotesensing 15 01096 g008
Remotesensing 15 01096 g009 550
Figure 9. Prediction accuracy using different numbers of important predictors selected by the proposed SHCE algorithm.
Figure 9. Prediction accuracy using different numbers of important predictors selected by the proposed SHCE algorithm.
Remotesensing 15 01096 g009
Remotesensing 15 01096 g010 550
Figure 10. Forest AGB maps for 2007–2010 at 90 m spatial resolution generated using SCHE selected features and the XGBoost algorithm.
Figure 10. Forest AGB maps for 2007–2010 at 90 m spatial resolution generated using SCHE selected features and the XGBoost algorithm.
Remotesensing 15 01096 g010
Remotesensing 15 01096 g011 550
Figure 11. Distributions of AGB predictions for 2007–2010: (a) shows the number of forest pixels that had AGB values within each bin; and (b) shows AGB for each year, and * indicates the mean AGB for each year.
Figure 11. Distributions of AGB predictions for 2007–2010: (a) shows the number of forest pixels that had AGB values within each bin; and (b) shows AGB for each year, and * indicates the mean AGB for each year.
Remotesensing 15 01096 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, Y.; Liu, J.; Li, W.; Liang, S. A Proposed Ensemble Feature Selection Method for Estimating Forest Aboveground Biomass from Multiple Satellite Data. Remote Sens. 2023, 15, 1096. https://doi.org/10.3390/rs15041096

AMA Style

Zhang Y, Liu J, Li W, Liang S. A Proposed Ensemble Feature Selection Method for Estimating Forest Aboveground Biomass from Multiple Satellite Data. Remote Sensing. 2023; 15(4):1096. https://doi.org/10.3390/rs15041096

Chicago/Turabian Style

Zhang, Yuzhen, Jingjing Liu, Wenhao Li, and Shunlin Liang. 2023. "A Proposed Ensemble Feature Selection Method for Estimating Forest Aboveground Biomass from Multiple Satellite Data" Remote Sensing 15, no. 4: 1096. https://doi.org/10.3390/rs15041096

APA Style

Zhang, Y., Liu, J., Li, W., & Liang, S. (2023). A Proposed Ensemble Feature Selection Method for Estimating Forest Aboveground Biomass from Multiple Satellite Data. Remote Sensing, 15(4), 1096. https://doi.org/10.3390/rs15041096

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop