An Advanced Data Processing Algorithm for Extraction of Polarimetric Radar Signatures of Moving Automotive Vehicles Using the H/A/α Decomposition Technique
Abstract
1. Introduction
2. Materials and Methods
2.1. Fully Polarimetric Radar
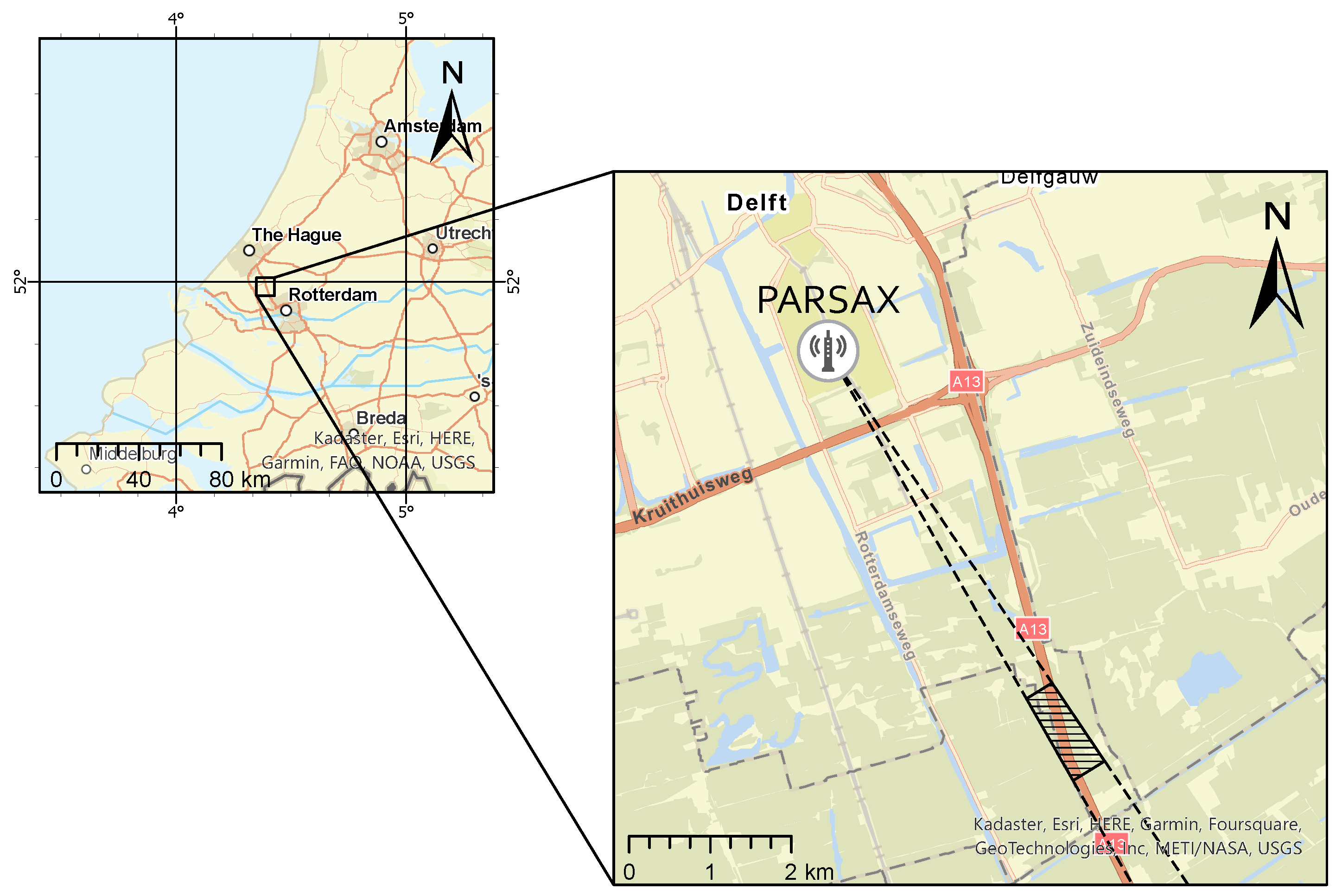
2.2. Data Acquisition
2.3. Signal and Data Processing Chain
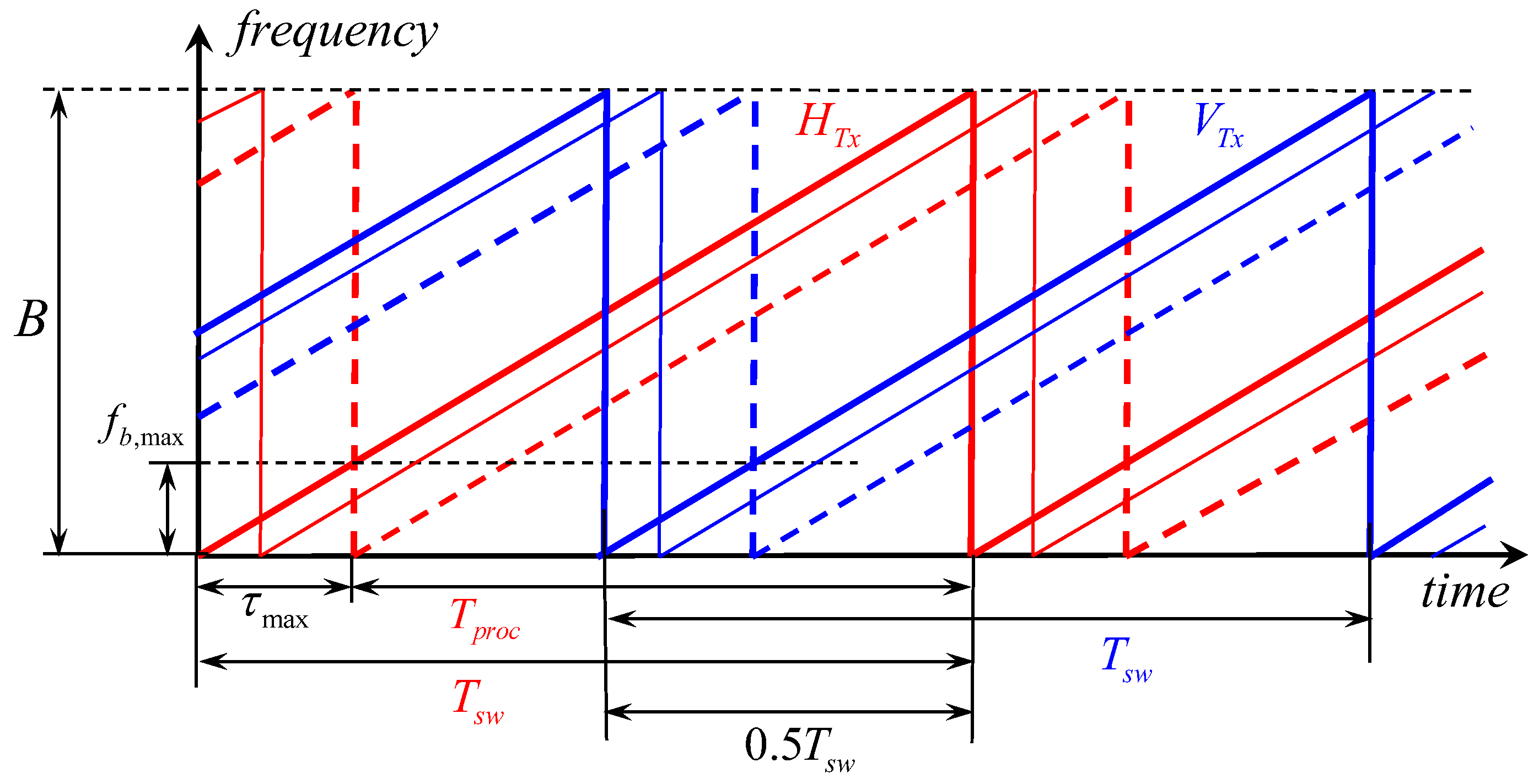
2.3.1. Range-Doppler Processing
2.3.2. Polarimetric Data Fusion
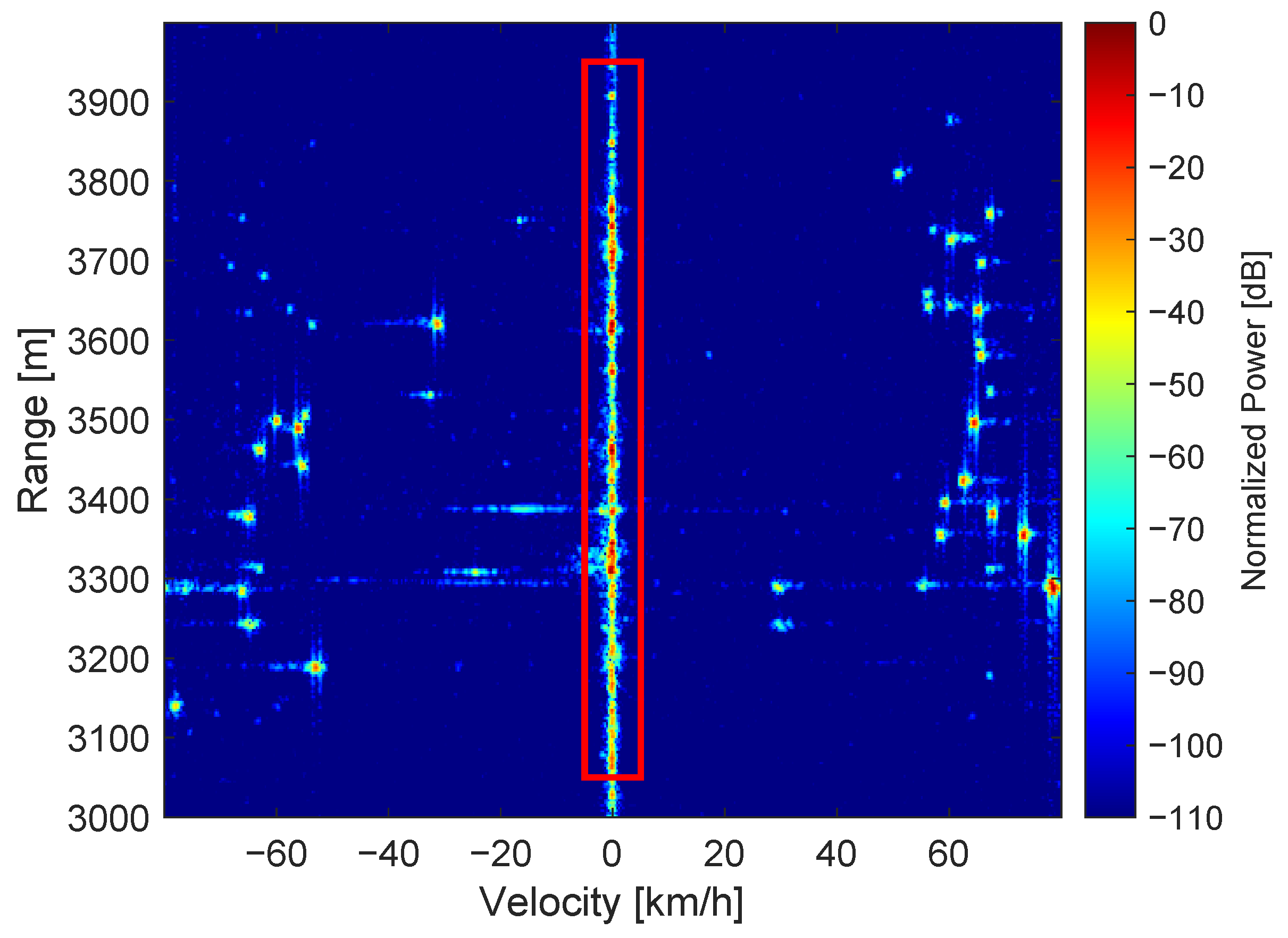
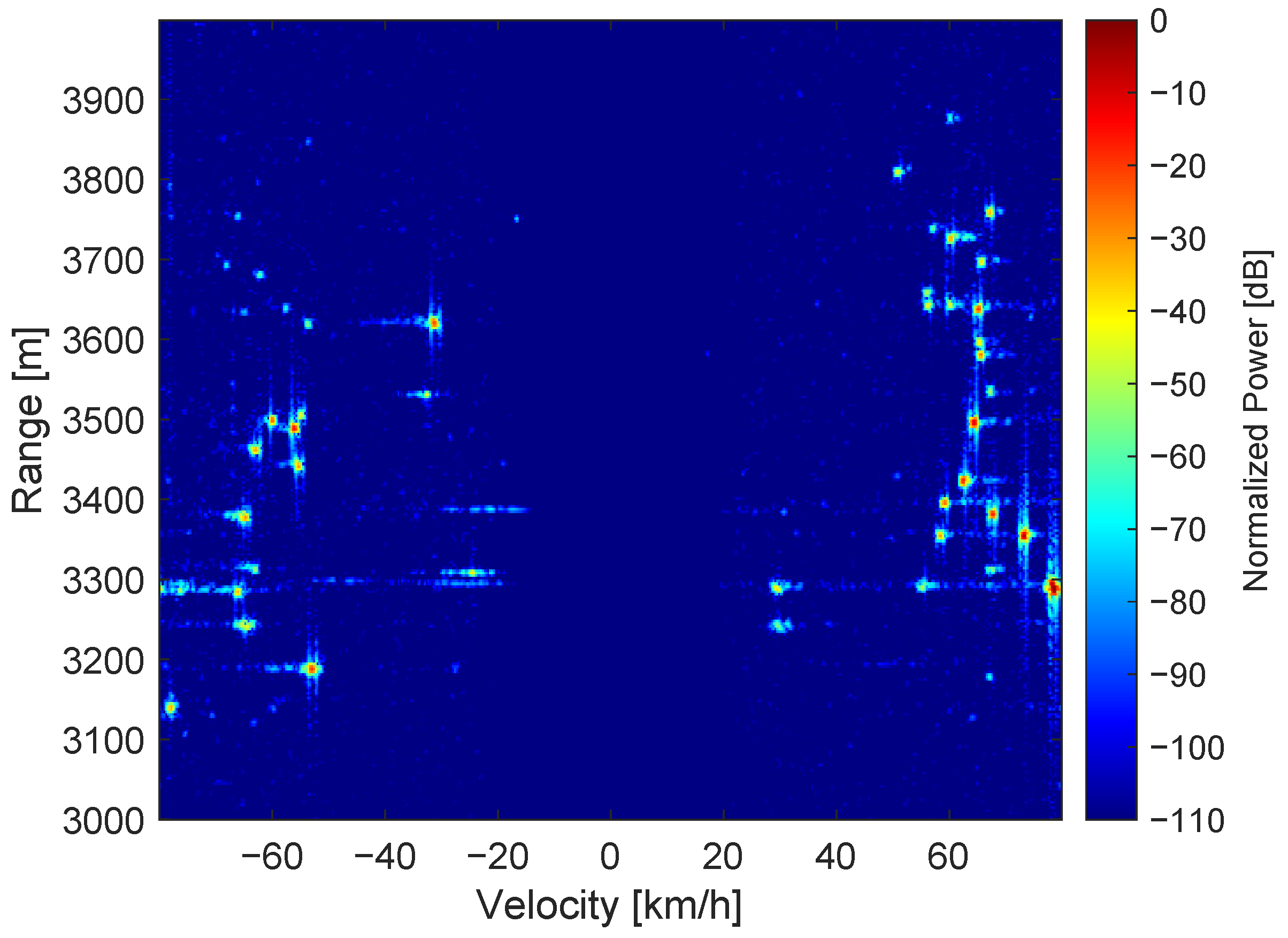
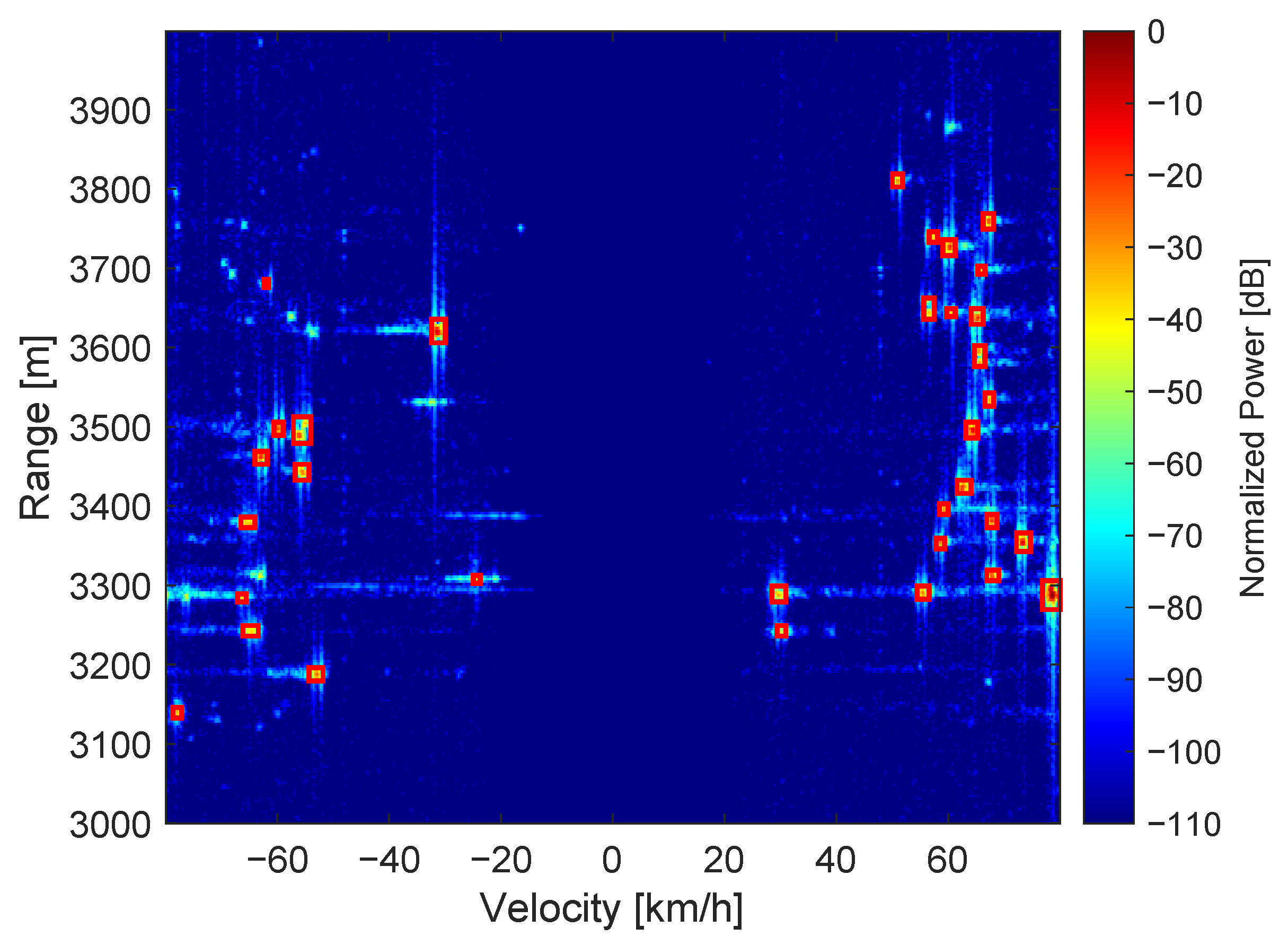
2.3.3. Target Detection and Clustering
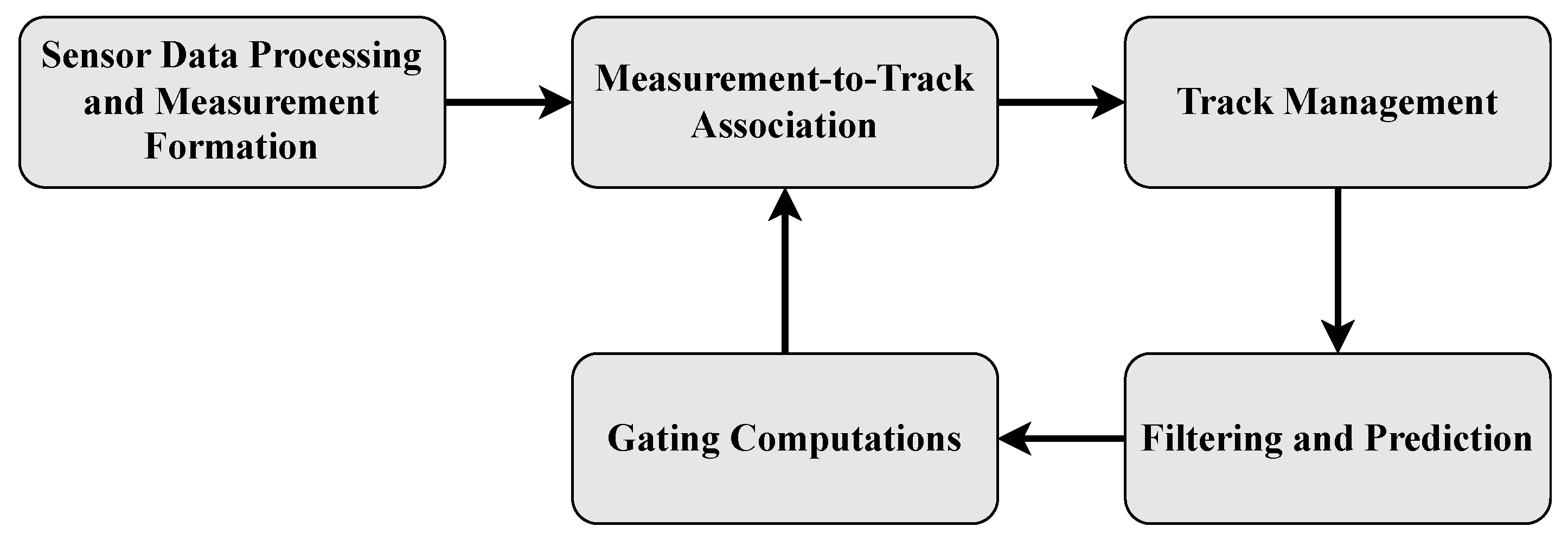
2.3.4. Multi-Target Tracking
2.4. H/A/α Decomposition
3. Results
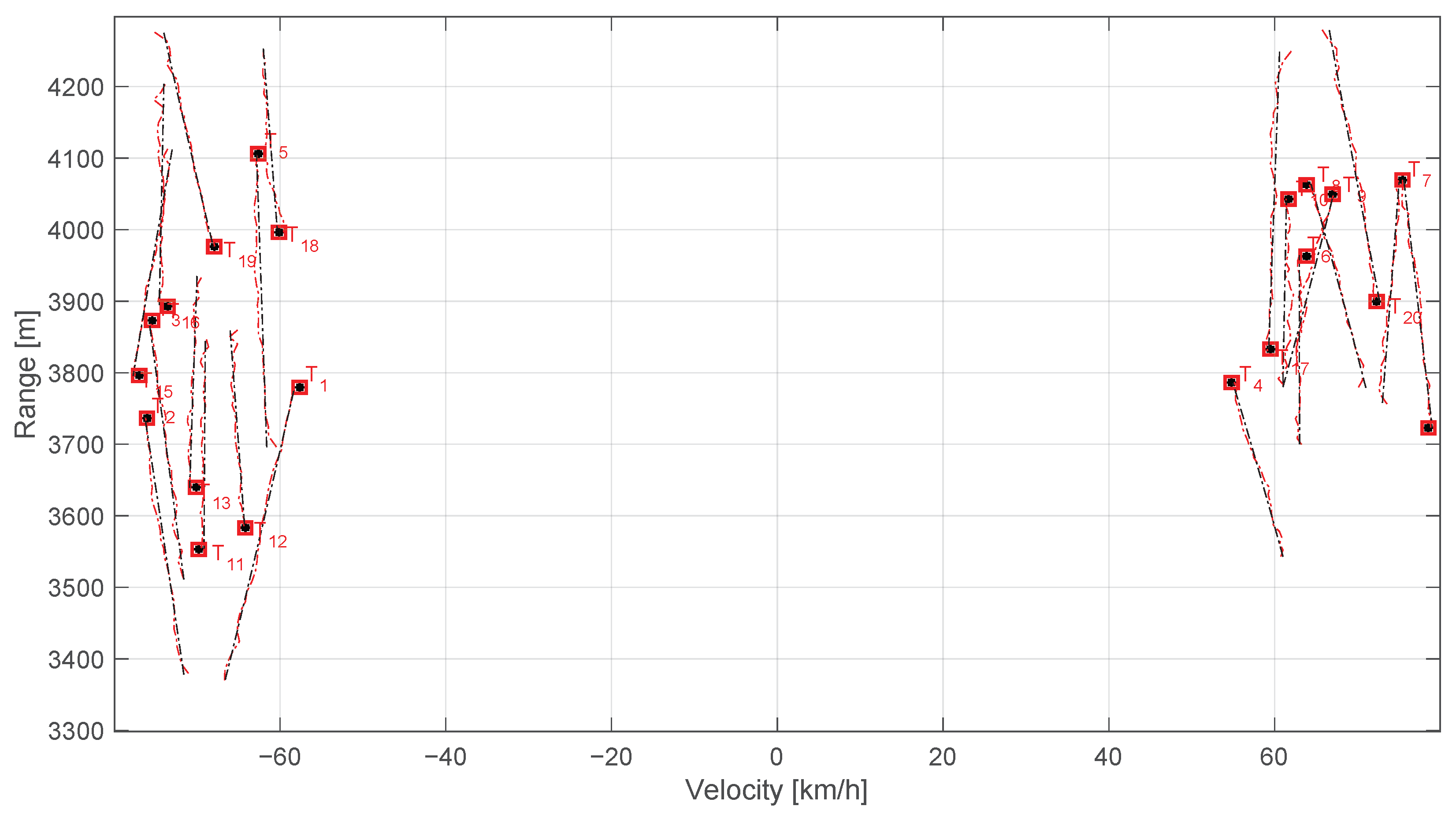
3.1. Tracking Performance
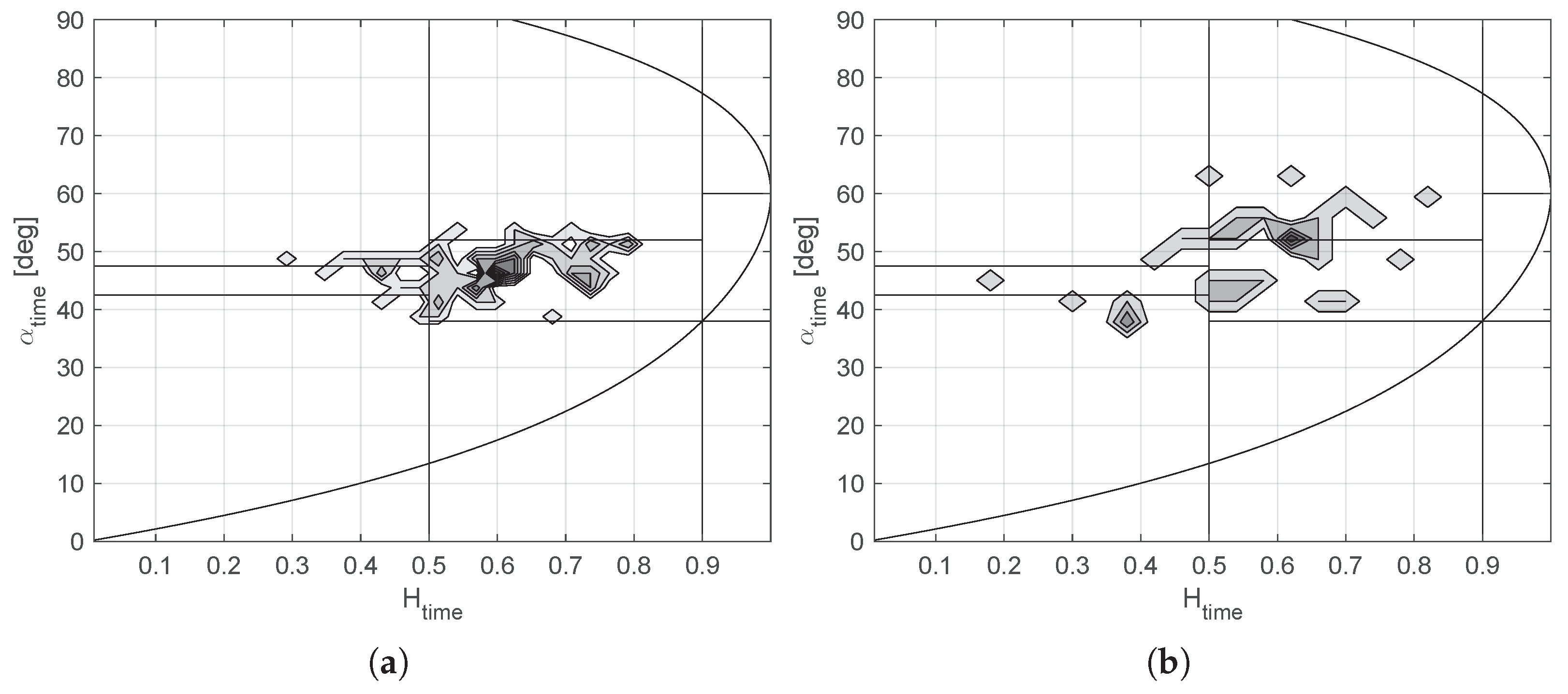
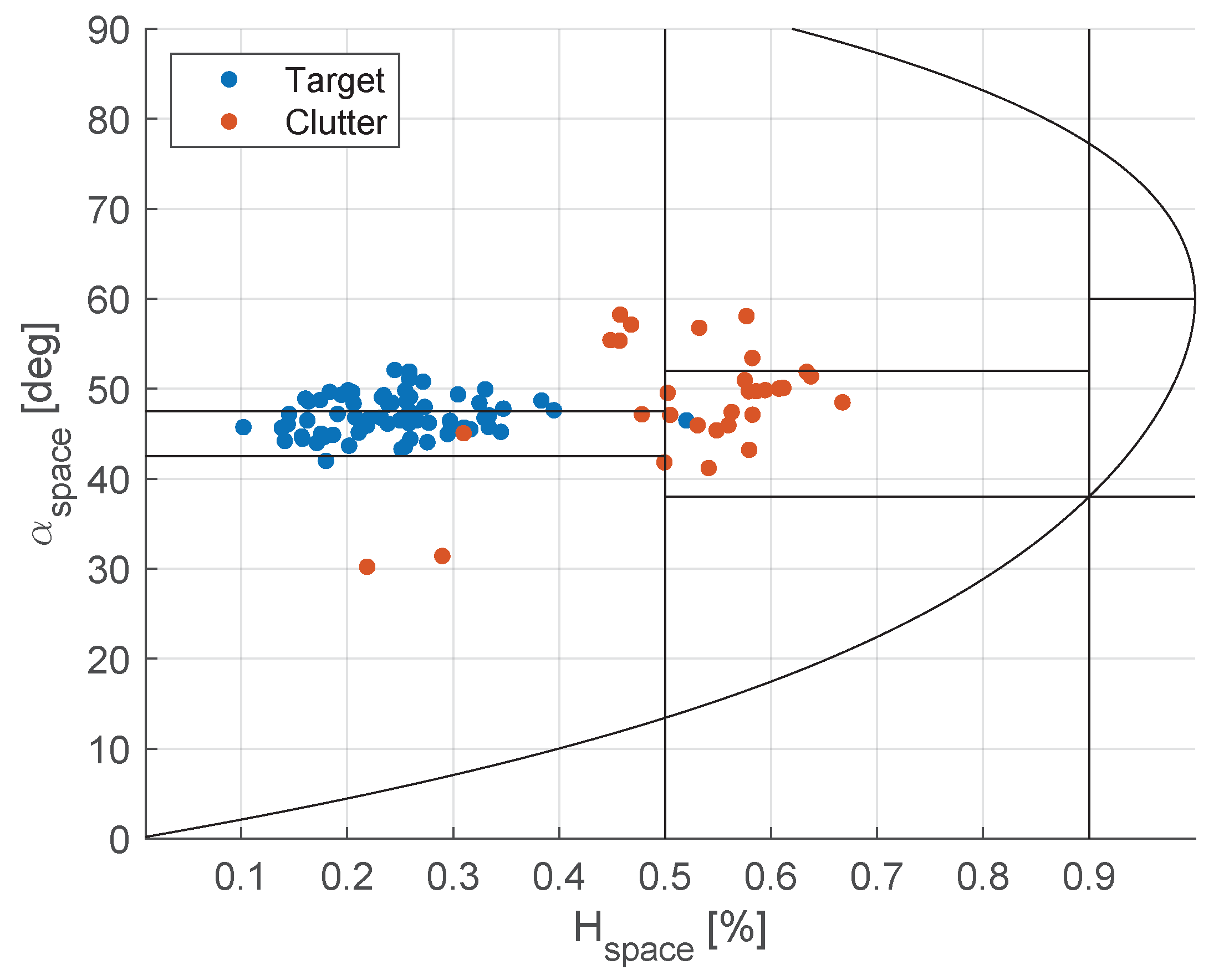
3.2. Analysis of Polarimetric Signatures
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CA-CFAR | Cell averaging CFAR |
| CFAR | Constant false alarm rate |
| DBSCAN | Density-based spatial clustering of applications with noise |
| FFT | Fast Fourier transform |
| FMCW | Frequency-modulated continuous-wave |
| FPGA | Field-programmable gate array |
| GOCA-CFAR | Greatest of cell averaging CFAR |
| GNN | Global nearest neighbor |
| HPF | High-pass filter |
| LFM | Linear frequency modulated |
| LRT | Likelihood ratio test |
| MHT | Multiple hypothesis tracking |
| MTT | Multi-target tracking |
| OPD | Optimal polarimetric detector |
| OS-CFAR | Ordered statistics CFAR |
| PMF | Polarimetric matched filter |
| PMSD | Polarimetric maximization synthesis detector |
| PSM | Polarization scattering matrix |
| PWF | Polarization whitening filter |
| RCS | Radar cross-section |
| RMSE | Root mean square error |
| SAR | Synthetic aperture radar |
| SD | Span detector |
| SNR | Signal-to-noise ratio |
| SOCA-CFAR | Smallest of cell averaging CFAR |
References
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Wiesbeck, W.; Sit, L. Radar 2020—The future of radar systems. In Proceedings of the International Radar Conference 2014, Lille, France, 13–17 October 2014; IEEE: Lille, France, 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Bosma, D.A.; Krasnov, O.A.; Yarovoy, A. Polarimetric Signatures of Moving Automotive Vehicles Based on H/A/a-decomposition: Preliminary Results with PARSAX Radar Data. In Proceedings of the 23rd International Radar Symposium (IRS), Gdansk, Poland, 12–14 September 2022; IEEE: Gdansk, Poland, 2022; pp. 414–419. [Google Scholar] [CrossRef]
- Wanielik, G.; Appenrodt, N.; Neef, H.; Schneider, R.; Wenger, J. Polarimetric millimeter wave imaging radar and traffic scene interpretation. In Proceedings of the IEE Colloquium on Automotive Radar and Navigation Techniques (Ref. No. 1998/230), London, UK, 9 February 1998; pp. 1–4. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Kay, J.H.; Orchard, B.J.; Whiting, R.H. Feature-aided tracking of moving ground vehicles. Algorithms Synth. Aperture Radar Imag. IX 2002, 4727, 234–245. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging—From Basics to Applications, 1st ed.; CRC Press LLC: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Copeland, J. Radar Target Classification by Polarization Properties. Proc. IRE 1960, 48, 1290–1296. [Google Scholar] [CrossRef]
- Kuhl, F.; Covelli, R. Object identification by multiple observations of the scattering matrix. Proc. IEEE 1965, 53, 1110–1115. [Google Scholar] [CrossRef]
- Lowenschuss, O. Scattering matrix application. Proc. IEEE 1965, 53, 988–992. [Google Scholar] [CrossRef]
- Huynen, J.R. Measurement of the target scattering matrix. Proc. IEEE 1965, 53, 936–946. [Google Scholar] [CrossRef]
- Huynen, J.R. Phenomenological Theory of Radar Targets. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1970. [Google Scholar]
- Boerner, W.M.; El-Arini, M.; Chan, C.; Saatchi, S.; Ip, W.; Mastoris, P.; Foo, B. Polarization Utilization in Radar Target Reconstruction; Technical Report; University of Illinois at Chicago Circle: Chicago, IL, USA, 1981. [Google Scholar]
- Boerner, W.M. Basic Concepts of Radar Polarimetry and Its Applications to Target Discrimination, Classification, Imaging and Identification; Technical Report; University of Illinois: Chicago, IL, USA, 1982. [Google Scholar]
- Boerner, W.M.; Kostinski, A.B.; James, B.D. On the concept of the polarimetric matched filter in high resolution radar imaging: An alternative for speckle radiation. Remote Sens. Mov. Towards 21st Century 1988, 1, 69–72. [Google Scholar]
- Boerner, W.M.; Yan, W.L.; Xi, A.Q.; Yamaguchi, Y. On the basic principles of radar polarimetry: The target characteristic polarization state theory of Kennaugh, Huynen’s polarization fork concept, and its extension to the partially polarized case. Proc. IEEE 1991, 79, 1538–1550. [Google Scholar] [CrossRef]
- Giuli, D. Polarization diversity in radars. Proc. IEEE 1986, 74, 245–269. [Google Scholar] [CrossRef]
- Pierce, L.; Ulaby, F.T.; Sarabandi, K.; Dobson, M.C. Knowledge-Based Classification of Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1081–1086. [Google Scholar] [CrossRef]
- Chen, K.S.; Huang, W.P.; Tsay, D.H.; Amar, F. Classification of multifrequency polarimetric SAR imagery using a dynamic learning neural network. IEEE Trans. Geosci. Remote Sens. 1996, 34, 814–820. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Bennett, A.; Currie, A. The stability of polarimetric features for target classification from SAR imagery. In Proceedings of the RADAR, Edinburgh, UK, 15–17 October 2002; IET: Edinburgh, UK, 2002; Volume 490, pp. 395–399. [Google Scholar] [CrossRef]
- Burns, J.; Herrick, D.; Ricoy, M. Wideband ISAR signatures of ground vehicles at UHF frequencies. In Proceedings of the IEEE Antennas and Propagation Society International Symposium 1992 (Digest), Chicago, IL, USA, 18–25 June 1992; IEEE: Chicago, IL, USA, 1992; pp. 1136–1140. [Google Scholar] [CrossRef]
- Kees, N.; Detlefsen, J. Road surface classification by using a polarimetric coherent radar module at millimeter waves. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, San Diego, CA, USA, 23–27 May 1994; IEEE: San Diego, CA, USA, 1994; pp. 1675–1678. [Google Scholar] [CrossRef]
- Finkele, R.; Schreck, A.; Wanielik, G. Polarimetric road condition classification and data visualisation. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Firenze, Italy, 10–14 July 1995; IEEE: Firenze, Italy, 1995; pp. 1786–1788. [Google Scholar] [CrossRef]
- Finkele, R. Detection of ice layers on road surfaces using a polarimetric millimetre wave sensor at 76 GHz. Electron. Lett. 1997, 33, 1153–1154. [Google Scholar] [CrossRef]
- Sarabandi, K.; Li, E.S. Polarimetric characterization of debris and faults in the highway environment at millimeter-wave frequencies. IEEE Trans. Antennas Propag. 2000, 48, 1756–1768. [Google Scholar] [CrossRef]
- Schipper, T.; Fortuny-Guasch, J.; Tarchi, D.; Reichardt, L.; Zwick, T. RCS measurement results for automotive related objects at 23–27 GHz. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011; IEEE: Rome, Italy, 2011; pp. 683–686. [Google Scholar]
- Geary, K.; Colburn, J.S.; Bekaryan, A.; Zeng, S.; Litkouhi, B. Characterization of automotive radar targets from 22 to 29 GHz. In Proceedings of the IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; IEEE: Atlanta, GA, USA, 2012; pp. 79–84. [Google Scholar] [CrossRef]
- Geary, K.; Colburn, J.S.; Bekaryan, A.; Zeng, S.; Litkouhi, B.; Murad, M. Automotive radar target characterization from 22 to 29 GHz and 76 to 81 GHz. In Proceedings of the IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013; IEEE: Ottawa, ON, Canada, 2013. [Google Scholar] [CrossRef]
- Alaqeel, A.A.; Ibrahim, A.A.; Nashashibi, A.Y.; Sarabandi, K.; Shaman, H.N. The phenomenology of radar backscattering response of vehicles at 222 GHz. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: Fort Worth, TX, USA, 2017; pp. 350–352. [Google Scholar] [CrossRef]
- Visentin, T. Polarimetric Radar for Automotive Applications. Ph.D. Thesis, Karlsruher Institut fur Technologie, Karlsruhe, Germany, 2018. [Google Scholar]
- Trummer, S.; Hamberger, G.F.; Koerber, R.; Siart, U.; Eibert, T.F. Performance analysis of 79 GHz polarimetric radar sensors for autonomous driving. In Proceedings of the European Microwave Week (EuMW)—14th European Radar Conference (EuRAD), Nuremberg, Germany, 11–13 October 2017; IEEE: Nuremberg, Germany, 2017; pp. 41–44. [Google Scholar] [CrossRef]
- Tilly, J.F.; Weishaupt, F.; Schumann, O.; Klappstein, J.; Dickmann, J.; Wanielik, G. Polarimetric signatures of a passenger car. In Proceedings of the Kleinheubach Conference (KHB), Miltenberg, Germany, 23–25 September 2019; IEEE: Miltenberg, Germany, 2019; pp. 6–9. [Google Scholar]
- Tilly, J.F.; Weishaupt, F.; Schumann, O.; Dickmann, J.; Wanielik, G. Road user classification with polarimetric radars. In Proceedings of the European Microwave Week (EuMW)—17th European Radar Conference (EuRAD) 2020, Utrecht, The Netherlands, 10–15 January 2021; IEEE: Utrecht, The Netherlands, 2021; pp. 112–115. [Google Scholar] [CrossRef]
- Krasnov, O.A.; Ligthart, L.P. Radar polarimetry using sounding signals with dual orthogonality—PARSAX approach. In Proceedings of the European Microwave Week (EuMW)—7th European Radar Conference (EuRAD), Paris, France, 30 September–1 October 2010; IEEE: Paris, France, 2010; pp. 121–124. [Google Scholar]
- Cloude, S.R.; Pettier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Krasnov, O.A.; Ligthart, L.P.; Li, Z.; Lys, P.; van der Zwan, F. The PARSAX—Full polarimetric FMCW radar with dual-orthogonal signals. In Proceedings of the European Microwave Week (EuMW)—5th European Radar Conference (EuRAD), Amsterdam, The Netherlands, 30–31 October 2008; IEEE: Amsterdam, The Netherlands, 2008; pp. 84–87. [Google Scholar]
- Babur, G.P.; Krasnov, O.A.; Ligthart, L.P. Quasi-simultaneous measurements of scattering matrix elements in polarimetric radar with continuous waveforms providing high-level isolation in radar channels. In Proceedings of the European Microwave Week (EuMW)—6th European Radar Conference (EuRAD), Rome, Italy, 30 September–2 October 2009; IEEE: Rome, Italy, 2009; pp. 1–4. [Google Scholar]
- Li, Z.; Lu, W.; Ligthart, L.P.; Van Der Zwan, F.; Huang, P.; Krasnov, O.A. A novel approach applied for the internal and semi-external calibration of the PARSAX dual-channel polarimetric agile radar system. In Proceedings of the 18th International Conference on Microwaves, Radar and Wireless Communications (MIKON 2010), Vilnius, Lithuania, 14–16 June 2010; IEEE: Vilnius, Lithuania, 2010. [Google Scholar]
- Li, Z.; Ligthart, L.P.; Huang, P.; Lu, W.; Van Der Zwan, F.; Krasnov, O.A.; Yarovoy, A.; Zhu, W. External calibration of the PARSAX dual-channel FMCW polarimetric agile radar system. In Proceedings of the European Microwave Week (EuMW)—9th European Radar Conference (EuRAD), Amsterdam, The Netherlands, 31 October–2 November 2012; IEEE: Amsterdam, The Netherlands, 2012; pp. 158–161. [Google Scholar]
- Cadzow, J.A. Generalized digital matched filtering. In Proceedings of the 12th Southeastern Symposium on System Theory, Virginia Beach, VA, USA, 19–20 May 1980; pp. 307–312. [Google Scholar]
- Kong, J.A.; Swartz, A.A.; Yueh, H.A.; Novak, L.M.; Shin, R.T. Identification of Terrain Cover Using the Optimum Polarimetric Classifier. J. Electromagn. Waves Appl. 1987, 2, 171–194. [Google Scholar] [CrossRef]
- Novak, L.M.; Burl, M.C. Optimal Speckle Reduction in Polarimetric SAR Imagery. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 293–305. [Google Scholar] [CrossRef]
- Novak, L.M.; Seciitin, M.B.; Cardullo, M.J. Studies of target detection algorithms that use polarimetric radar data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 150–165. [Google Scholar] [CrossRef]
- Finn, H.; Johnson, R.S. Adaptive detection mode with threshold control as a function of spatially sampled clutter level estimates. RCA Rev. 1968, 29, 414–464. [Google Scholar]
- Rohling, H. New CFAR-processor based on an ordered statistic. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 5–9 May 1985; IEEE: Arlington, VA, USA, 1985; pp. 271–275. [Google Scholar]
- Weiss, M. Analysis of Some Modified Cell-Averaging CFAR Processors in Multiple-Target Situations. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 102–114. [Google Scholar] [CrossRef]
- Petrov, N.; Le Chevalier, F.; Yarovoy, A.G. Detection of Range Migrating Targets in Compound-Gaussian Clutter. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 37–50. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis—Principles and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; AAAI Press: Portland, OR, USA, 1996; pp. 226–231. [Google Scholar]
- Blackman, S.S.; Popoli, R. Desing and Analysis of Modern Track Systems; Artech House: Norwood, MA, USA, 1999. [Google Scholar]
- Li, K.; Habtemariam, B.; Tharmarasa, R.; Pelletier, M.; Kirubarjan, T. Multitarget tracking with Doppler ambiguity. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2640–2656. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple Target Tracking with Radar Application; Artech House: Norwood, MA, USA, 1986. [Google Scholar]
- Ferrentino, E.; Nunziata, F.; Migliaccio, M.; Vicari, A. A sensitivity analysis of dual-polarization features to damage due to the 2016 Central-Italy earthquake. Int. J. Remote Sens. 2018, 39, 6846–6863. [Google Scholar] [CrossRef]
- Ferrentino, E.; Marino, A.; Nunziata, F.; Migliaccio, M. A dual–polarimetric approach to earthquake damage assessment. Int. J. Remote Sens. 2019, 40, 197–217. [Google Scholar] [CrossRef]
- Migliaccio, M.; Nunziata, F.; Montuori, A.; Brown, C.E. Marine added-value products using RADARSAT-2 fine quad-polarization. Can. J. Remote Sens. 2012, 37, 443–451. [Google Scholar] [CrossRef]




| Category | Parameter | Value |
|---|---|---|
| System characteristics | Center frequency () | GHz |
| Modulation bandwidth (B) | up to 50 MHz | |
| Sweep time () | 1 | |
| Effective bandwidth () | up to 45 MHz | |
| Range resolution () | up to 3.3 m | |
| Power characteristics | Maximum power per channel | 100 W |
| Transmitter attenuation | up to 80 dB | |
| Transmitter parabolic antenna | Antenna diameter | m |
| Antenna beamwidth | 1.8° | |
| Antenna gain | dB | |
| Receiver parabolic antenna | Antenna diameter | m |
| Antenna beamwidth | 4.6° | |
| Antenna gain | dB | |
| TX-RX isolation | HH-polarized | dB |
| VV-polarized | dB | |
| ADC characteristics | Maximum sampling frequency | 400 MHz |
| ADC resolution | 14-bit | |
| Spur-free dynamic range | ≥70 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosma, D.A.; Krasnov, O.A.; Yarovoy, A. An Advanced Data Processing Algorithm for Extraction of Polarimetric Radar Signatures of Moving Automotive Vehicles Using the H/A/α Decomposition Technique. Remote Sens. 2023, 15, 1060. https://doi.org/10.3390/rs15041060
Bosma DA, Krasnov OA, Yarovoy A. An Advanced Data Processing Algorithm for Extraction of Polarimetric Radar Signatures of Moving Automotive Vehicles Using the H/A/α Decomposition Technique. Remote Sensing. 2023; 15(4):1060. https://doi.org/10.3390/rs15041060
Chicago/Turabian StyleBosma, Detmer A., Oleg A. Krasnov, and Alexander Yarovoy. 2023. "An Advanced Data Processing Algorithm for Extraction of Polarimetric Radar Signatures of Moving Automotive Vehicles Using the H/A/α Decomposition Technique" Remote Sensing 15, no. 4: 1060. https://doi.org/10.3390/rs15041060
APA StyleBosma, D. A., Krasnov, O. A., & Yarovoy, A. (2023). An Advanced Data Processing Algorithm for Extraction of Polarimetric Radar Signatures of Moving Automotive Vehicles Using the H/A/α Decomposition Technique. Remote Sensing, 15(4), 1060. https://doi.org/10.3390/rs15041060









