Abstract
A new realization of the international terrestrial reference frame, a combination of four different space geodetic techniques, was released in 2022. Each geodetic solution should be combined carefully based on the local tie information at the co-located site. Although many approaches have been successfully applied to connect different geodetic sensors, to date, there has been no unified mathematical representation for the target motions. Herein, a unified conical model was developed to estimate the invariant points of geodetic sensors using a more robust and consistent approach. It modeled the motion of targets, in either the horizontal or vertical axis, as cones; thus, homogeneous modeling was implemented. In addition to its simplicity, the model simultaneously estimated the tilting of the vertical axis and horizontal offset. The mathematical relationship and normality of the normal vector were modeled as a Gauss–Markov model with fixed constraints. The pre-computed initial coordinates of the pillars and targets were adjusted simultaneously to calculate the correlation information for the local tie vector. The complete model was successfully applied to the co-located site, which was transformed into a global reference frame via the Helmert transformation based on the global navigation satellite system campaign. The results showed that the proposed method is more efficient in terms of the number of parameters for invariant points of geodetic sensors (only 13% compared to the 3D circle fitting type conventional approach). In addition, the reliability of the estimated solution can be increased by avoiding an ill-conditioned linear system through the conical model.
1. Introduction
The International Earth Rotation Service (IERS) plays a crucial role in establishing and maintaining the international terrestrial reference frame (ITRF) by analyzing data from four space geodetic systems as follows: global navigation satellite system (GNSS), satellite laser ranging (SLR), very long baseline interferometry (VLBI), and Doppler orbitography and radiopositioning integrated by satellites [1,2,3,4,5,6,7,8]. The IERS network is defined using space geodetic instruments installed on the sites, and many of the stations have more than two geodetic instruments located very close to each other [9]. The “co-located site” is the station where more than one instrument is in operation simultaneously. It is recommended to link the reference points of instruments using a local tie vector that represents a 3D baseline vector between the reference points of two space geodesy instruments [10,11]. Therefore, it is necessary to estimate a local tie vector with high accuracy to establish and maintain the geodetic reference frame, i.e., ITRF.
The reference point (or invariant point, IVP) of geodetic instruments, such as the VLBI telescope and SLR transmitter, is defined as the projection point of the secondary (elevation, EL) axis onto the primary (azimuth, AZ) axis of rotation [12]. Generally, the IVP of an instrument is located inside it and is thus not accessible. Therefore, the indirect method is frequently used to determine the location of the IVP [13,14,15] and involves a terrestrial ground survey by observing the reflective targets attached to the surface of the instrument. Subsequently, the trace of each target created by the rotational motions of the primary and secondary axes is modeled as a 3D circle in space [10,11,13,14,16,17,18,19,20]. Various types of 3D circle fitting algorithms (called “conventional” methods) have been proposed to compute the location of the IVP using terrestrial ground survey techniques. However, only a partial arc, instead of a full circle, can be obtained from the rotational sequences of the elevation axis because of the limited rotational motion of the elevation axis. This leads to an ill-conditioned linear system; consequently, the quality of the estimated IVP is degraded. To overcome this, modeling an incomplete arc as a part of the cone, i.e., its base, has been attempted. This approach significantly reduces the number of estimated parameters and increases the estimability of the linear system solved using the least-squares method [21]. However, the cone-shape model can only be applied to arcs generated from the rotational motion about the elevation axis and has a limitation in the estimation of the possible offset between the azimuth and elevation axes and the tilt angle between the azimuth axis and zenith direction.
In this study, the conical model is applied not only to the arcs from the rotational motion about the elevation axis but also to circles from the rotational motion about the azimuth axis. The conical model approach has the following advantages: (1) immaculate consistency in setting up the mathematical functions for both arcs from the rotational motions and (2) flexibility in the modeling, although tilting of the azimuth axis may exist. As mentioned earlier, IVP is defined as the point at which the elevation axis is projected onto the azimuth axis when an offset exists between the two axes. Hence, the mathematical model was fully extended to describe the possible offset between the azimuth and elevation axes. Once the complete mathematical model is constructed to connect the parameters with measurements from terrestrial ground surveying, adjustment computation is performed to obtain the least-squares solution. The new conical model provides consistency and efficiency in terms of geometric relationship for the IVP and numerical stability of the parameters with the corresponding covariance information.
In the following sections, detailed descriptions of the measurements from terrestrial ground surveying techniques are introduced. Then, a mathematical model to accommodate the tilting of the azimuth axis and offset between the axes and an adjustment model for the least-squares solution is proposed. Subsequently, the numerical test results and conclusions are presented.
2. Local Tie Strategy
Recently, a new realization of the international terrestrial reference system (known as ITRF2020) was announced by combining the individual solutions of space geodetic techniques [2]. To combine different solutions, the relative positions between the reference points should be represented together at the co-located sites. Because the reference points cannot be accessed directly, a special procedure for estimating the IVPs and the corresponding correlation information is required [22].
One of the co-located sites is operational in Korea (Sejong station), of which VLBI and GNSS are maintained by the National Geographic Information Institute, while SLR is operated by the Korea Astronomy and Space Science Institute. The diameter of the VLBI antenna is 22 m, and the GNSS station (4-char site name SEJN) is one of the international GNSS service (IGS) continuously operating reference stations (CORS). As shown in Figure 1, the two sensors are approximately 200 m apart and surrounded by pillars (five pillars for VLBI and three for SLR). The ground surveying to connect these sensors is accomplished by measuring the slant distances, the horizontal/vertical angles, and the height differences by spirit leveling; however, only two VLBI pillars are involved because of the obstruction by the nearby trees. Thus, the geometric condition of the connecting two areas is weak in rotation parameters.
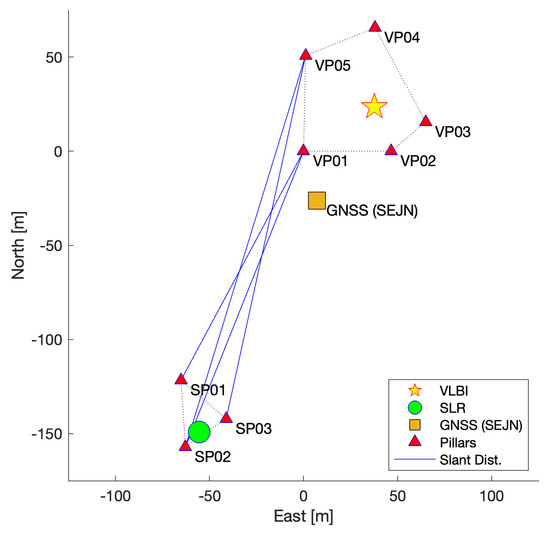
Figure 1.
Project site map at Sejong station in the local reference frame. VLBI and SLR are surrounded by the pillars, and the GNSS antenna is located closer to the VLBI area than the SLR site. The ground surveying to connect both sites was conducted for only two VLBI pillars owing to the limited clearance of the line of sight.
The observations can be divided into two surveying operations as follows: (1) conventional surveying in local frames, such as slant distances, horizontal and vertical angles, and height differences, and (2) GNSS campaign in the global reference frame. For local surveying, a total station was installed on the pillars, except at the GNSS station, with the origin defined at VP01 (VP02 is defined on the -axis or east direction). A 7-day GNSS campaign for all nine pillars, including the GNSS station, was conducted to calculate the coordinates of the global reference frame. The collected GNSS data were processed simultaneously with the IGS core stations to align with the global reference frame.
The local tie vectors (GNSS to IVPs), along with their covariance matrices, are estimated in the local reference frame; thus, they should be transformed into the global frame. The Helmert transformation is generally applied to estimate the parameters (translation, rotation, and scale) between the reference frames, assuming small rotation angles [23].
The developed mathematical model is based on two types of targets, either horizontal or vertical, although several of the targets are involved in both motions, depending on the attached location. Both VLBI and SLR have their own azimuthal systems that are not identical to the local geodetic reference frame. It should be mentioned here that we aim at the azimuth-elevation (AZ-EL) type, which is the most common mount among several types of VLBI antennas [24].
Note that the rotational axes for both motions are independent of each other. More specifically, the horizontal rotation ranges from to in (its own) azimuthal system, with a zenith angle of at all times, whereas the vertical motion covers only (i.e., a quarter circle), as shown in Figure 2. Therefore, the geometric condition should be reflected by considering the characteristics of the motion, as described in the following section. Detailed target location and ground survey information can be found in [21].
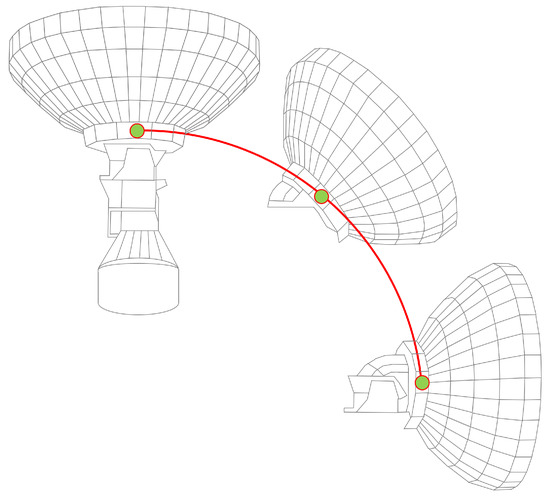
Figure 2.
Vertical motion of the VLBI antenna ( at the zenith to facing the front, resulting in a quarter circle of the target). All targets are attached to the supporting structure under the antenna dish (the vertical targets are located in the bending area).
3. The Conical Model
The sphero-conical model was successfully applied to estimate the VLBI IVP [21]. However, the horizontal and vertical motions, i.e., the circles in 3D space (horizontal targets) and the cones with the apex at the IVP (vertical targets), respectively, were modeled differently. Therefore, this model is insufficient for universal applications and has some limitations in that the -component of the IVP is not involved in the horizontal motion of the targets. Furthermore, if the vertical axis is tilted by chance, the angle cannot be readily calculated using the sphero-conical model.
Instead of separately modeling both motions, the model was modified to apply a homogeneous geometrical relationship (i.e., cones traced by targets). In addition to the target motions, we extended the model to explain not only the horizontal offset of the vertical axis but also the tilting of the reference axis. The Gauss–Markov model with fixed constraints was adopted for the parameters to be tightly constrained, obtaining a robust and universal mathematical relationship. It minimizes the number of parameters required to estimate the IVPs, which makes the model numerically efficient and stable.
3.1. Parameterization of the IVPs
Because it is necessary to obtain the correlation information between the co-located GNSS CORS and the IVPs, we conducted a simultaneous estimation for the primary unknowns (i.e., both IVPs), coordinates of pillars, and targets based on the mathematical relationship. The ground observations were combined with two constraints: (1) the partial minimum norm least-squares solution (PMINOLESS) [25] on the pillars and (2) the fixed constraints on the target motions. The second constraint for both the horizontal and vertical targets were similarly modeled as cones (a homogeneous “conical model”).
On a preferential basis, the Gauss–Markov model with fixed constraints is represented by [22,25,26]:
where A is the design matrix, and are the observation vector, and the corresponding error vector, respectively, along with the cofactor matrix and the unitless variance component of . The matrix K and the vector are the coefficient matrix and constant vector, respectively, for the constraints from the geometric relationship of the cones. The explicit solution of the model (given in Equation (1)), along with the corresponding dispersion matrix, can be found in many references, as given by [21,25]
where and . The unknown parameters can be described more clearly as follows:
where and represent the IVP parameters for the VLBI antenna and the SLR telescope, respectively, and is related to the coordinates. The VLBI parameters can be further subdivided to denote each unknown individual:
where are the coordinates of the IVP. The elements in and (that is, and ) are the slant heights of the cones, which will be explained in more detail in Section 3.2. is the number of targets on the VLBI antenna for azimuthal (horizontal) rotation, is the number of targets related to the vertical motion, and h is the horizontal offset from the vertical reference axis. The unit vector represents the (actual) vertical axis of horizontal rotation and the (common) normal vector for the planes comprised of the rotation. is the distance to the horizontal plane (or base of the cone) from the apex of the cone, which is composed of the horizontal target k. The antenna-related parameters and are described, in detail, in Section 3.3. The same structure applies to the IVP parameters of the SLR telescope ().
The coordinate parameter denotes the increment to the initial values for the pillars () and targets ( and for VLBI and SLR, respectively). As briefly explained above, the initial coordinates of the pillars and targets were calculated from the PMINOLESS approach beforehand, which were re-estimated during the IVP estimation process, with the mathematical models as constraints. The PMINOLESS approach is represented by the minimization problem [25].
where S is the appropriate selection matrix (a diagonal matrix with 1 for the selected elements and 0 for the rest of elements). In this experiment, the components corresponding to the pillars were selected. N and are the normal matrix and the corresponding vector, respectively.
The ground observations consisted of the slope distances, horizontal/vertical angles, and height differences. Therefore, the design matrix in Equation (1a) is represented as follows:
where ✓ symbol represents the nonzero elements of the submatrices. The first row of A corresponds to ground observations related to VLBI targets, whereas the second row corresponds to the SLR targets. The third row covers the ground observations between pillars (VLBI/SLR/GNSS), including the height differences. The third column corresponds to the pillars mentioned above; thus, it is related to all types of observations. In contrast, the fourth and fifth columns of A correspond to the VLBI and SLR targets, respectively.
3.2. Fixed Constraints
As mentioned above, the three-dimensional trace of the targets on the VLBI antenna and SLR telescope can be described by two motions: azimuthal rotation ( a full circle) and rotation in elevation ( a quarter circle). These motions are similarly represented by the “sphero-conical” model [21]; however, a homogeneous conical model was applied to both motions in this study. By omitting the argument list of the coordinates for compactness, the conical models can be represented by two equations and [22] as below:
where are again the coordinates of the IVP, which are the primary unknowns; and () and () are the slant heights of cones traced by the azimuthal rotation (target k) and the motion in elevation (target l), respectively, both from the apex at the IVP.
The whole fixed constraints can be represented by
where the elements of the matrix represent the geometric relationship between the IVP and the targets for VLBI ( and ) or SLR ( and ). The detailed expressions for and are shown in Appendix A as Equations (A3) and (A4), respectively.
3.3. Antenna Offset and Tilting
The vertical axis of the antenna (or the telescope) may have an offset from the reference axis (i.e., a horizontal offset from the (ideal) vertical axis). Because the horizontal offset is identical for any azimuthal direction, the offset at 0 in its own azimuth system is parameterized for both the VLBI and SLR, minimizing the number of unknowns. To estimate the horizontal offset, the mathematical model of the constraints must be modified accordingly. However, even if there is an offset on the vertical axis, it does not affect the apex of the azimuthal rotation. Therefore, the horizontal offset is exclusively related to vertical motion, and one parameter is sufficient for the entire antenna rotation.
Let be the local coordinates of the IVP with offset, which can be represented as follows:
where h is the horizontal offset of the vertical axis at an azimuth angle of , and represents the azimuth of the VLBI antenna (see Figure 3). Note that the bias of its azimuth system, which will be absorbed in the final Helmert transformation into the ITRF, is neglected.
where .
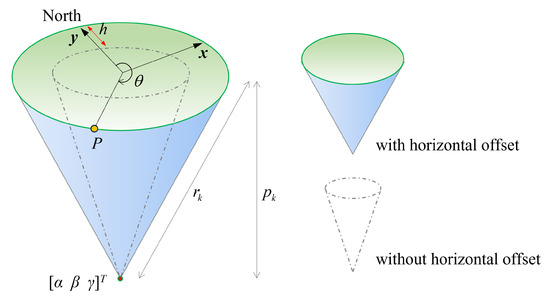
Figure 3.
Horizontal offset (h) of target k from the vertical reference axis. Regardless of the horizontal offset, the apex of the cone remains unchanged. The terms (east) and (north) represent the horizontal axes in the local coordinates system, and represents the (local) azimuth angle from north to the target point P (clockwise). All other terms () are the same as Equation (5).
However, the vertical axes of the space geodetic sensors might have tilted from the plumbline. Only the horizontal offset has been calculated by many researchers [11,27], but not surprisingly, the tilting of the axis was not modeled. Even if the vertical axis is tilted, the angle is generally very small. The horizontal targets rotate with respect to the assumed vertical axis by azimuthal rotation; thus, each horizontal plane shares the common normal vector with its plane.
The tilting of the vertical axis can be modeled using a planar equation comprising the horizontal rotation of the targets. We added three elements for the normal vector, along with the distance to the plane from the apex of the cone (i.e., IVP), to explain the tilting of the vertical axis (see Figure 4).
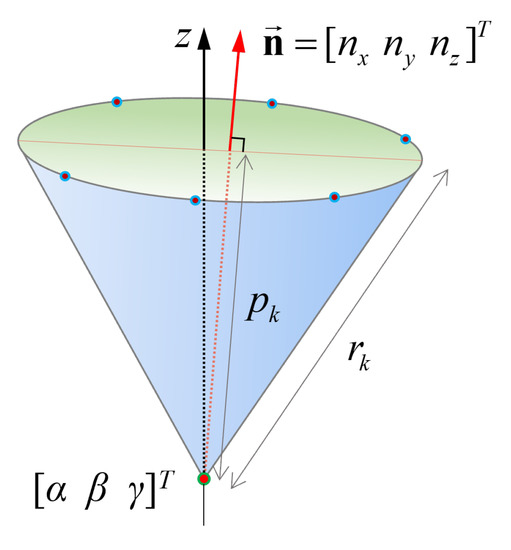
Figure 4.
The normal vector () common to all planes by the horizontal targets. The distance to the plane (or base of the cone) () is estimated to be positive for targets located above the IVP at (of course, negative for lower targets). The -axis represents the (ideal) vertical axis in the local coordinates system, and represents the slant height of the cone traced by the horizontal target k.
Assuming that a common normal vector of all planes comprised of the horizontal targets is , then all horizontal target points can be reduced to a single plane in 3D space using the vertical distance () of the cone. The planar equation for each target ) can be represented by
where represent the coordinates of the IVP. Figure 5 shows the overall schematic diagram of vertical movement of targets at azimuth () under horizontal offset (h).
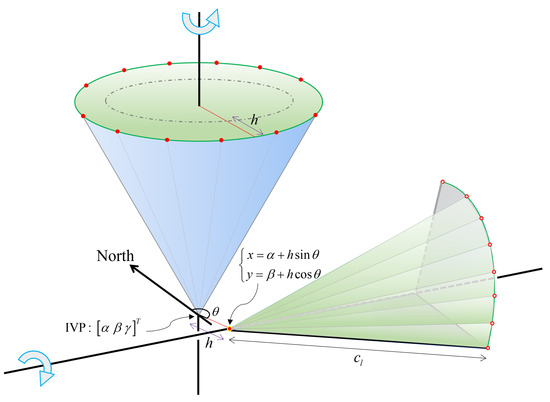
Figure 5.
Vertical movement of targets with horizontal offset (h) in the direction of the azimuth (). The apex of the horizontal rotation is at the IVP, whereas that of the vertical motion is away from the IVP by the offset (h).
To secure the relationship of the horizontal planes, the normal vector should be a unit vector, as represented by
Since the direction of the normal vector can be either upward or downward, we applied the additional constraint of with appropriate stochastic uncertainty to avoid the potential singularity (i.e., the direction of the normal vector to be upward). As a result, the distance to the plane () is estimated to be negative when the target is located below the IVP.
The complete model for estimating the IVPs is summarized in Appendix A in linearized form.
4. Results and Discussion
4.1. Estimation of the IVP Parameters
The main concern of IVP estimation at co-located stations is obtaining the full variance-covariance matrix for the local tie vector between the geodetic sensors, along with the primary unknowns, that is, the coordinates of the IVPs. Hence, the coordinates of the pillars and targets should be estimated simultaneously with IVPs.
Table 1 shows the number of unknowns for each IVP, pillar, and target coordinates. A total of 55 unknowns modeled both IVPs (38 for VLBI and 17 for SLR), which are classified according to their types, that is, the slant and vertical distances of the cones and the normal vector of the horizontal planes.

Table 1.
Number of unknowns for each IVP, coordinates of the pillars, and targets.
Table 2 shows the total number of parameters required for the conventional and the newly proposed conical methods, respectively. For example, the conventional method requires up to 286 unknowns under the assumption that the same in-situ measurements presented in Table 1 are used for the VLBI IVP estimation (i.e., , , and due to the azimuth rotational sequences with 30 increment). However, only 38 unknowns in total are necessary for the conical model (only about 13% compared to that of the conventional method). On top of the reduced parameters, the conical model is independent of the number of azimuth rotational sequences of the EL axis; we can increase the number of measurements without compromising the stability of the estimation process.

Table 2.
The number of required parameters with respect to the conventional 3D circle fitting type approach (k is the number of targets for AZ rotational axis, l is the number of targets for EL rotational axis, and m is the azimuth rotational sequences of EL axis).
Table 3 summarizes the overall statistics on the adjustment process in this study, including the number of observations and convergence criteria. The GNSS campaign was conducted on nine pillars with Trimble R8 receivers, including the GNSS (SEJN) station, on GPS week 2116 to 2117 (DOY 213 to 219) in 2020. The ground surveying (slant distances, horizontal/vertical angles, and height differences) was carried out from 28 September through 16 October using Trimble S8 total stations. All ground measurements () were used to estimate the 6673 unknowns, with convergence criteria of 5.00 mm for the norm of the correction on the entire unknowns and 0.50 mm for the primary IVPs only.

Table 3.
Overall statistics of the adjustment processed in this study.
The detailed status of the iteration process is represented in Table 4, showing the primary unknowns IVPs, norm of the parameter correction, and estimated variance component. Convergence was almost complete after two iterations, although corrections to the SLR IVP oscillated at approximately the mm level. In addition to the primary unknowns, all other parameters, including the estimated variance component, converged in a similar pattern.

Table 4.
Status of each iteration process (primary unknowns only). All units are meters except the unitless .
Table 5 shows the final estimated values and corresponding precision for both the IVPs and related parameters. The slant heights were estimated with similar precision, regardless of the horizontal () or vertical targets (). The horizontal offset was determined to be mm and mm for VLBI and SLR, respectively. As mentioned earlier, the horizontal offset is basically a constant value; thus, only one parameter was set up in a specific direction ( of the azimuth angle in its own local frame) to reduce the number of parameters (or to avoid duplication).

Table 5.
The final estimated parameters based on the Gauss–Markov model with fixed constraints and the corresponding precision. The IVP coordinates are given in the local coordinates system ().
The common normal vector of the horizontal planes for each geodetic sensor was estimated with a precision of (no units). The magnitude of the unit vectors was 1.0, owing to the fixed constraints on the parameters (see Equation (13)). Parameter is the height of the cones that correspond to the distance to the (horizontal) plane from the apex at the IVP. As shown in the table, the distances for horizontal targets to were estimated to have negative values (marked in bold). This implies that the horizontal planes are formed in the opposite direction of the normal vector. In other words, when the antenna faces the zenith (elevation angle or zenith angle ), the corresponding targets are located under the IVP on the local vertical axis. Thus, the targets can be grouped by their heights, as seen in the VLBI target locations (, , and ) [22].
Finally, the simultaneously estimated coordinates of the pillars and targets are summarized in Table 6, showing only a small portion of the entire coordinates (9 pillars, 924 targets for VLBI, 1273 targets for SLR, and a total of 6618 unknowns). The precision of the estimated coordinates ranges from the half-millimeter level (pillars) to several millimeters (targets), depending on the number of observations and the geometric relationship. The initial coordinates were predetermined using PMINOLESS, with a selection matrix for the pillars (VLBI/SLR/GNSS). They were estimated again using the fixed constraints of the conical models. Notably, the GNSS CORS (SEJN) has relatively large sigma values because of the lack of ground survey measurements (and no distance observations).

Table 6.
Estimated coordinates of IVPs, pillars, and targets with corresponding standard deviations. Only a small portion of the total targets is displayed for the sake of simplicity.
4.2. Helmert Transformation to ITRF2014
The estimated IVPs and corresponding correlation information should be provided to the IERS in the global reference frame (e.g., ITRF2014). Thus, it is necessary to transform the estimated local tie vectors into ITRF2014, based on the GNSS processing results on the pillars. Considering numerical stability, it would be better to estimate the transformation parameters in the north-east-up (neu) frame by referring to the GNSS CORS as its origin.
A well-known relationship between reference frames ( to ) can be found in the IERS webpage and/or other textbooks in geodesy [1,22,23,28,29], whereas the velocity components are neglected in this experiment.
where T denotes the translation, s denotes the scale, and R denotes the rotation angle between frames.
As pointed out by [21], generally, the coordinates both from and to frames have intrinsic errors. However, the conventional least-squares adjustment only deals with errors in one frame. Thus, it is more plausible to adopt the total least-squares within the Gauss–Helmert model approach to account for the errors in both frames [22,26,30,31]. The estimated parameters and corresponding precision are listed in Table 7, and the residuals in both frames after transformation are summarized in Table 8.

Table 7.
Helmert transformation parameters and summary of the estimation model (local frame to ITRF2014, both expressed in local east()-north()-up() frame).

Table 8.
Residuals in both frames after Helmert transformation (both in the local east()-north()-up() frame).
The equation for the Helmert transformation provided by the IERS assumes very small rotation angles between the frames. However, the local azimuthal frame at Sejong station is not fully aligned to the local geodetic frame at the GNSS and is approximately rotated by about the -axis. Thus, the equation should not be directly applied in this case. Consequently, a preliminary rotation was used in advance. Thus, the corresponding error propagation should be applied to the variance-covariance matrix.
As a byproduct of the IVP estimation, hypothesis testing of the estimated variance component can be performed to statistically determine the existence of the horizontal offset and/or tilting of the vertical axis. Because the offset and tilting of the axis were modeled as fixed constraints, the following hypothesis can be easily applied [25,32]:
where an appropriate (: significance level) can be used as a test statistic.
5. Conclusions
A new conical model was proposed and developed in this study to estimate the IVPs of space geodetic sensors. The targets’ horizontal and vertical motions were homogeneously modeled as the bases of cones as the apex at the invariant point, resulting in a simple, robust, and immaculate model. The slant heights of the cones, except for the IVPs, were the primary parameters to be estimated within the conical model. More importantly, the horizontal offset and tilting of the vertical axis were estimated simultaneously, which makes the proposed method more consistent and applicable than the conventional approach for various IVP estimation purposes.
The estimation process began with ground surveying, followed by the IVP estimation and Helmert transformation of IVPs and the corresponding correlation information into the global reference frame. The tilting of the vertical axis was estimated by setting up a common normal vector for all planes comprising the horizontal targets. The normality of the vector was secured using a fixed constraint, and the direction of the vector was constrained stochastically to avoid singularity. Thus, regardless of the location of the targets, i.e., either above or below the IVP, the distance parameters to the planes (or bottom of the cones) were estimated with numerical stability.
The proposed model and procedure were successfully applied to the commonly used AZ-EL type antenna with in situ measurements. The test results showed that the coordinates of VLBI/SLR IVPs were estimated with the submillimeter levels of accuracy in each component. The full variance-covariance of the estimated coordinates was simultaneously determined, which makes the local tie vector combine with the ITRF solution. Furthermore, the ratio of the number of parameters in the conical model to that of the conventional one was only 13%, which is a huge advantage in terms of the numerical stability of the estimation process.
Finally, the conical model makes it possible to efficiently determine not only the IVPs of VLBI and SLR but the tilting angle of the azimuth axis and the offset between the axes with sufficient accuracy. In addition, it can provide reliable solutions by avoiding an ill-conditioned linear system caused by the limited motion of the EL axis. The applicability to other types of antennas and/or telescopes should be investigated further.
Author Contributions
Conceptualization, T.-S.B. and C.-K.H.; methodology, T.-S.B.; software, T.-S.B.; validation, T.-S.B. and C.-K.H.; formal analysis, T.-S.B. and C.-K.H.; investigation, T.-S.B. and C.-K.H.; resources, T.-S.B. and C.-K.H.; data curation, T.-S.B.; writing—original draft preparation, T.-S.B. and C.-K.H.; writing—review and editing, T.-S.B. and C.-K.H.; visualization, T.-S.B.; supervision, T.-S.B.; project administration, T.-S.B.; funding acquisition, T.-S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant from National R&D Project ”Development of ground-based centimeter-level maritime precise PNT technologies” funded by the Ministry of Oceans and Fisheries (1525012253).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the National Geographic Information Institute of Korea for providing the observation data used in this experiment.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VLBI | Very Long Baseline Interferometry |
| SLR | Satellite Laser Ranging |
| GNSS | Global Navigation Satellite System |
| IVP | InVariant Point |
Appendix A. Linearization of the Model
The linearized form of the fixed constraints (see Equations (8a) and (8b)) can be represented by the total derivatives, as follows:
Therefore, the fixed constraints can be summarized in the matrix form as below (VLBI case with no antenna offset and horizontal plane parameters in Equation (5)):
Matrix denotes the geometric relation between the IVP and the targets and can thus be further partitioned to be matched with as
where corresponds to the IVP parameters , and and are related to unknowns and , respectively. represents the constraints for the horizontal offset (h) from the (ideal) vertical axis. The last element () models the horizontal planes, comprising the horizontal targets. The same relationship applies to the SLR parameters, and .
Similarly, the submatrix ( as well) can also be described more explicitly by partitioning the targets according to their motions as below:
where corresponds to the targets related to the azimuthal rotation, and represents the targets of motion in elevation (see Equation (A2)).
References
- IERS. Available online: https://www.iers.org/IERS/EN/Science/Techniques/techniques.html (accessed on 26 November 2022).
- ITRF. International Terrestrial Reference Frame 2020. Available online: https://itrf.ign.fr/en/solutions/ITRF2020 (accessed on 26 November 2022).
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the international terrestrial reference frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Métivier, L.; Altamimi, Z.; Rouby, H. Past and present ITRF solutions from geophysical perspectives. Adv. Space Res. 2020, 65, 2711–2722. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar]
- Pearlman, M.R.; Noll, C.E.; Pavlis, E.C.; Lemoine, F.G.; Combrink, L.; Degnan, J.J.; Kirchner, G.; Schreiber, U. The ILRS: Approaching 20 years and planning for the future. J. Geod. 2019, 93, 2161–2180. [Google Scholar] [CrossRef]
- Nothnagel, A.; Artz, T.; Behrend, D.; Malkin, Z. International VLBI Service for Geodesy and Astrometry – Delivering high-quality products and embarking on observations of the next generation. J. Geod. 2019, 91, 711–721. [Google Scholar] [CrossRef]
- Willis, P.; Lemoine, F.G.; Moreaux, G.; Soudarin, L.; Ferrage, P.; Ries, J.; Otten, M.; Saunier, J.; Noll, C.; Biancale, R.; et al. The International DORIS Service (IDS), recent developments in preparation for ITRF2013. IAG Symp. Ser. 2016, 143, 631–639. [Google Scholar]
- IERS. Available online: https://itrf.ign.fr/en/network (accessed on 26 November 2022).
- Sarti, P.; Sillard, P.; Vittuari, L. Surveying co-located space-geodetic instruments for ITRF computation. J. Geod. 2004, 78, 210–222. [Google Scholar] [CrossRef]
- Dawson, J.; Sarti, P.; Johnston, G.M.; Vittuari, L. Indirect approach to invariant point determination for SLR and VLBI systems: An assessment. J. Geod. 2007, 81, 433–441. [Google Scholar] [CrossRef]
- Lösler, M. Reference point determination with a new mathematical model at the 20 m VLBI radio telescope in Wettzell. J. Appl. Geod. 2008, 2, 233–238. [Google Scholar] [CrossRef]
- Dawson, J.; Johnston, G.; Twilley, B. he Determination of Telescope and Antenna Invariant Point (IVP). IERS Technical Note No. 33. In Proceedings of the IERS Workshop on Site Co-Location, Matera, Italy, 23–24 October 2003. [Google Scholar]
- Leinen, S.; Becker, M.; Dow, J.; Feltens, J.; Sauermann, K. Geodetic determination of radio telescope antenna reference point and rotation axis parameters. J. Surv. Eng. 2007, 133, 41–51. [Google Scholar] [CrossRef]
- Ning, T.; Haas, R.; Elgered, G. Determination of the local tie vector between the VLBI and GNSS reference points at Onsala using GPS measurements. J. Geod. 2015, 89, 711–723. [Google Scholar] [CrossRef]
- Johnston, G.; Dawson, J.; Naebkhil, S. The 2003 Mount Stromlo Local Tie Survey; Record 2004/20; Geoscicence Australia: Canberra, ACT, Australia, 2004; 26p. [Google Scholar]
- Johnston, G.; Dawson, J. The 2002 Mount Pleasant (Hobart) Radio Telescope Local Tie Survey; Record 2004/21; Geoscicence Australia: Canberra, ACT, Australia, 2004; 21p. [Google Scholar]
- Woods, A.R. Tidbinbilla Local Tie Survey; Record 2007/XX; Geoscicence Australia: Canberra, ACT, Australia, 2007; 23p. [Google Scholar]
- Shen, Y.; You, X.; Wang, J.; Wu, B.; Chen, J.; Ma, X.; Gong, X. Mathematical model for computing precise local tie vectors for CMONOC co-located GNSS/VLBI/SLR stations. Stud Geophys. Geod. 2015, 6, 1–6. [Google Scholar] [CrossRef]
- Ma, X.; Yu, K.; Montillet, J.; He, X. One-step solution to local tie vector determination at co-located GNSS/VLBI sites. J. Geod. 2018, 62, 535–561. [Google Scholar] [CrossRef]
- Bae, T.S.; Hong, C.K. Sphero-conical modeling for the estimation of very long baseline interferometry invariant point. Sensors 2022, 22, 7937. [Google Scholar] [CrossRef] [PubMed]
- Bae, T.-S.; Hong, C.-K.; Lim, S.-H. Total least-squares (TLS) within Gauss-Helmert model: 3D planar fitting and Helmert transformation of geodetic reference frames. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2022, 40, 315–324. [Google Scholar]
- Geometric Reference Systems in Geodesy. Available online: https://kb.osu.edu/bitstream/handle/1811/77986/Geom_Ref_Sys_Geodesy_2016.pdf?sequence=1&isAllowed=y (accessed on 16 July 2022).
- Nothnagel, A. Very Long Baseline Interferometry. In Handbuch der Geodäsie; Freeden, W., Rummel, R., Eds.; Springer Reference Naturwissenschaften Book Series; Springer Spektrum: Berlin/Heidelberg, Germany, 2019; pp. 1–58. [Google Scholar]
- Snow, K. Applications of Parameter Estimation and Hypothesis Testing to GPS Network Adjustments. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2002. [Google Scholar]
- Snow, K. Topics in Total Least-Squares Adjustment within the Errors-In-Variables Model: Singular Cofactor Matrices and Prior Information. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2012. [Google Scholar]
- Yoo, S.-M.; Jung, T.; Lee, S.-M.; Yoon, H.S.; Park, H.-E.; Chung, J.-K.; Wi, S.O.; Cho, J.; Byun, D.-Y. Determination of the invariant point of Korean VLBI network (KVN) radio telescopes: First results at KVN Ulsan and Tamna observatories. J. Korean Astron. Soc. 2018, 51, 143–153. [Google Scholar]
- Watson, G.A. Computing Helmert transformations. J. Comput. Appl. Math. 2006, 197, 387–394. [Google Scholar] [CrossRef]
- Ioannidou, S.; Pantazis, G. Helmert transformation problem. From Euler angles method to quaternion algebra. Int. J.-Geo-Inf. 2020, 9, 494. [Google Scholar] [CrossRef]
- Fang, X. Weighted total least squares: Necessary and sufficient conditions, fixed and random parameters. J. Geod. 2013, 87, 733–749. [Google Scholar] [CrossRef]
- Fang, X. Weighted total least-squares with constraints: A universal formula for geodetic symmetrical transformations. J. Geod. 2015, 89, 459–469. [Google Scholar] [CrossRef]
- Ghilani, C.D.; Wolf, P.R. Adjustment Computations: Spatial Data Analysis, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).