A Multi-Level Distributed Computing Approach to XDraw Viewshed Analysis Using Apache Spark
Abstract
1. Introduction
- (1)
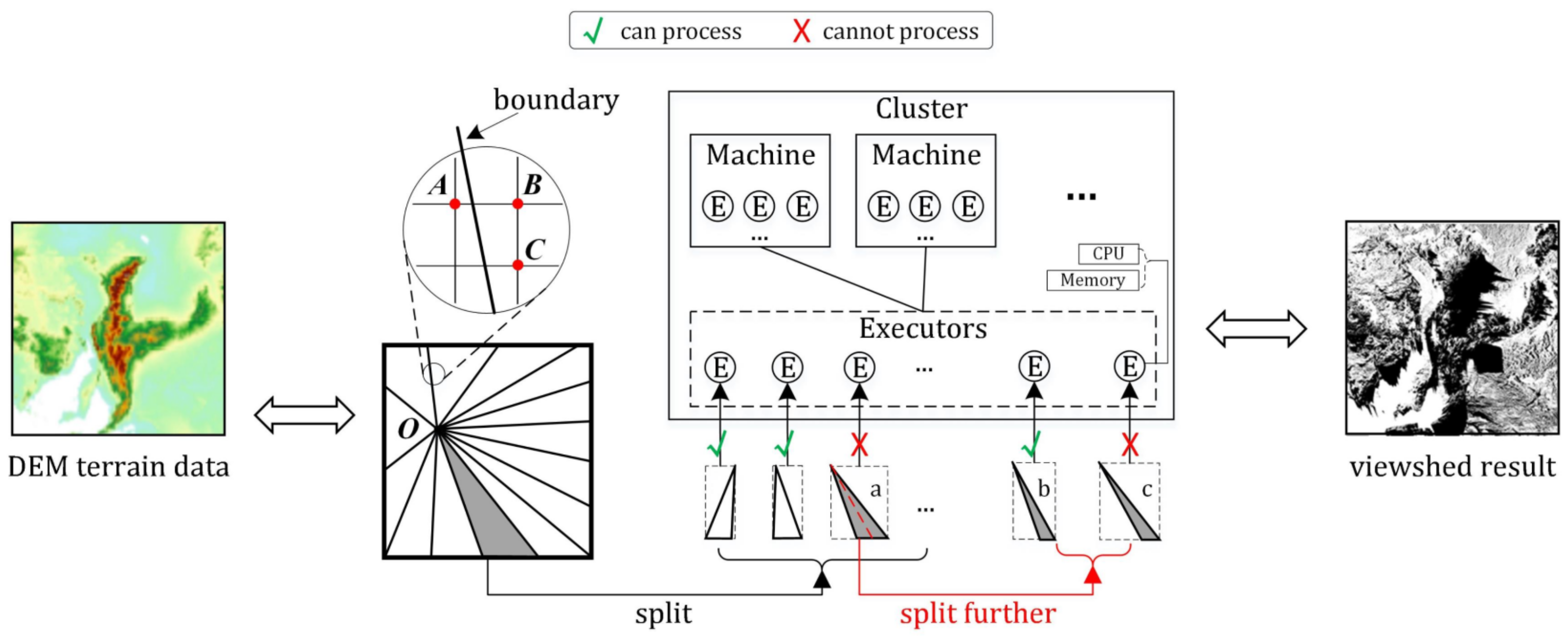
- The calculating bottleneck problem of the cluster’s executor is that a single executor in the cluster cannot easily hold the decomposed data in limited memory and process. The hardware resources such as CPU and memory in the Spark cluster are divided finely and wrapped into executors. The usual distributed approach divides the DEM grid into multiple triangles, and then multiple executors in cluster read and process the data in triangles’ MBR (Minimum Bounding Rectangle) in parallel. However, the MBR amplifies the data size of its corresponding triangle, which may not be easily read by a single executor all at once with limited hardware resources. More importantly, the large triangle may not be split further to reduce its MBR’s size. As an example shown in Figure 1, the data in both the triangle a and its further split part triangle c may not be processed all at once by a single executor.
- (2)
- The precision loss problem in calculation near the boundary is that the visibility results of grid points near the boundary may not be calculated. In Figure 1, the visibility calculation of point C near the boundary depends on the visibility results of A and B. However, unfortunately, the machine holding point C cannot obtain the calculation result of another machine holding point A, so its visibility cannot be calculated.
- (1)
- An improved approach named multi-level distributed XDraw (ML-XDraw) algorithm is designed to process viewshed analysis of large DEM data with Spark.
- (2)
- A multi-level data decomposition strategy is introduced to solve the calculating bottleneck problem of the cluster’s executor.
- (3)
- A boundary approximate calculation strategy is proposed to solve the precision loss problem in calculation near the boundary.
- (1)
- Dividing the DEM grid into multiple levels each holding further divided raster fragments by the multi-level data decomposition strategy.
- (2)
- Calculating each raster fragment’s visibility result by the raster fragment-based XDraw algorithm, whose implementation is based on the boundary approximate calculation strategy.
- (3)
- Organizing the total calculation process into a multi-level distributed algorithm using Apache Spark.
2. Methods
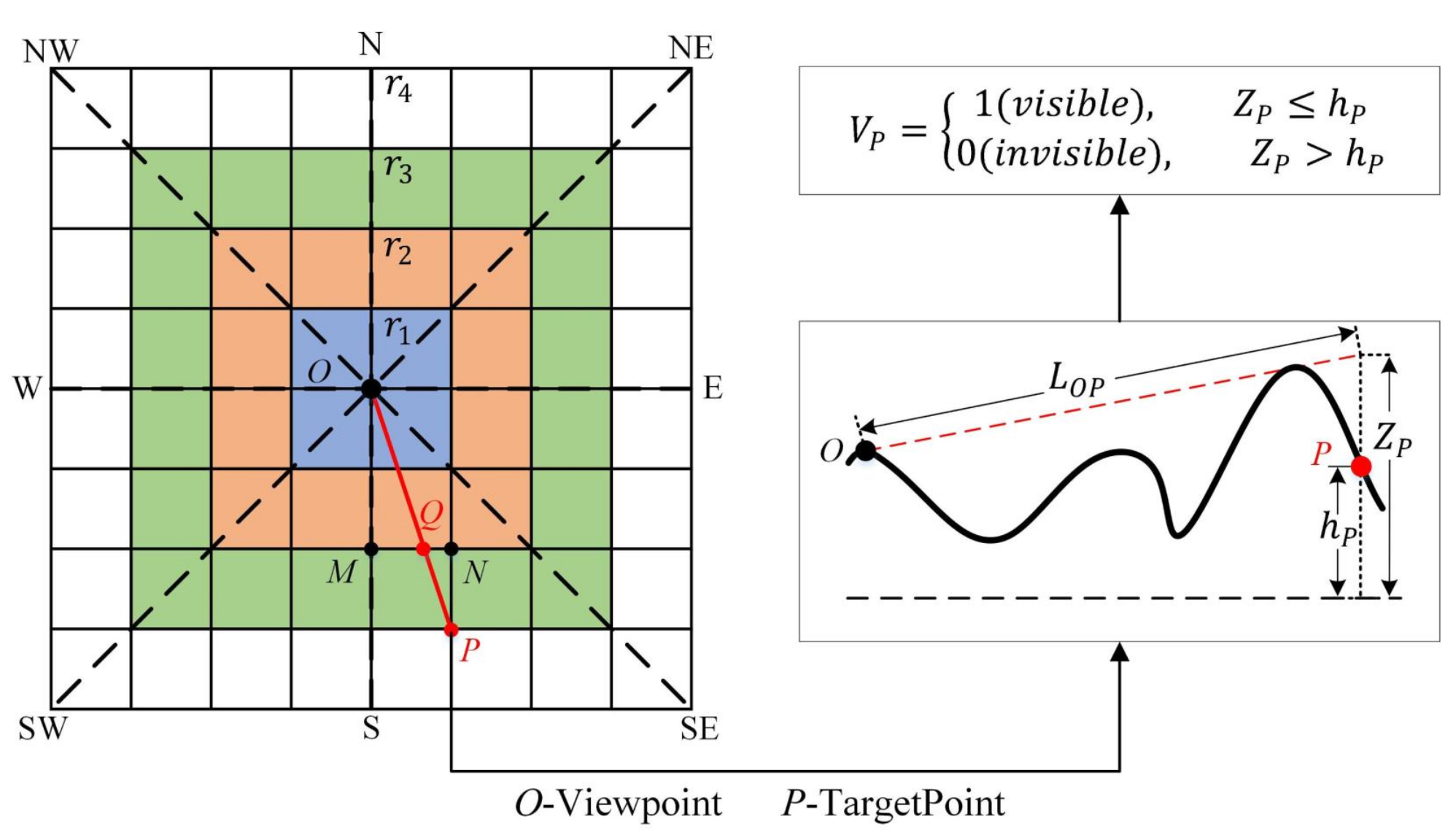
2.1. Serial XDraw Algorithm
2.2. Principle of Multi-Level Distributed XDraw Algorithm
2.2.1. Overview of the Improved Algorithm
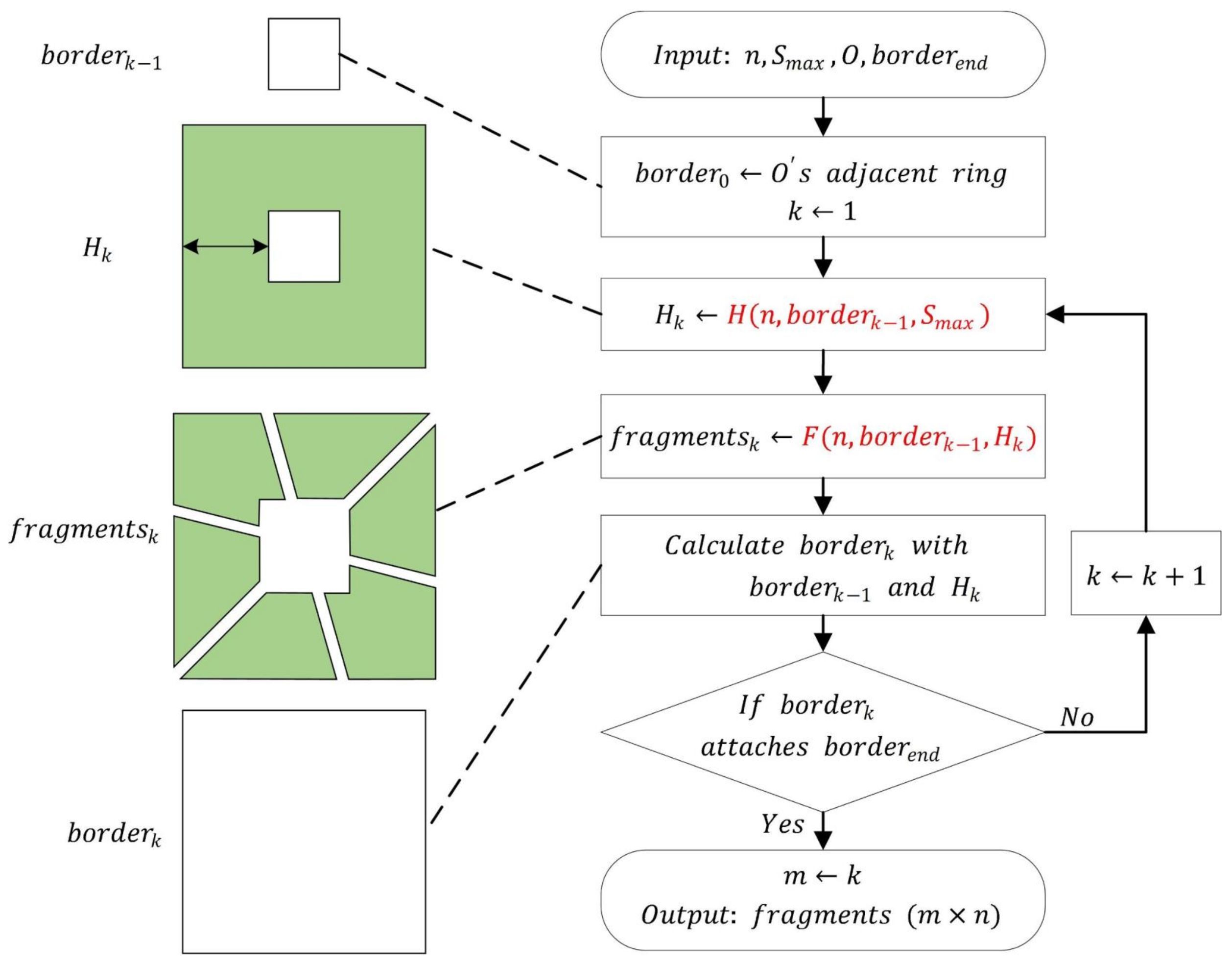
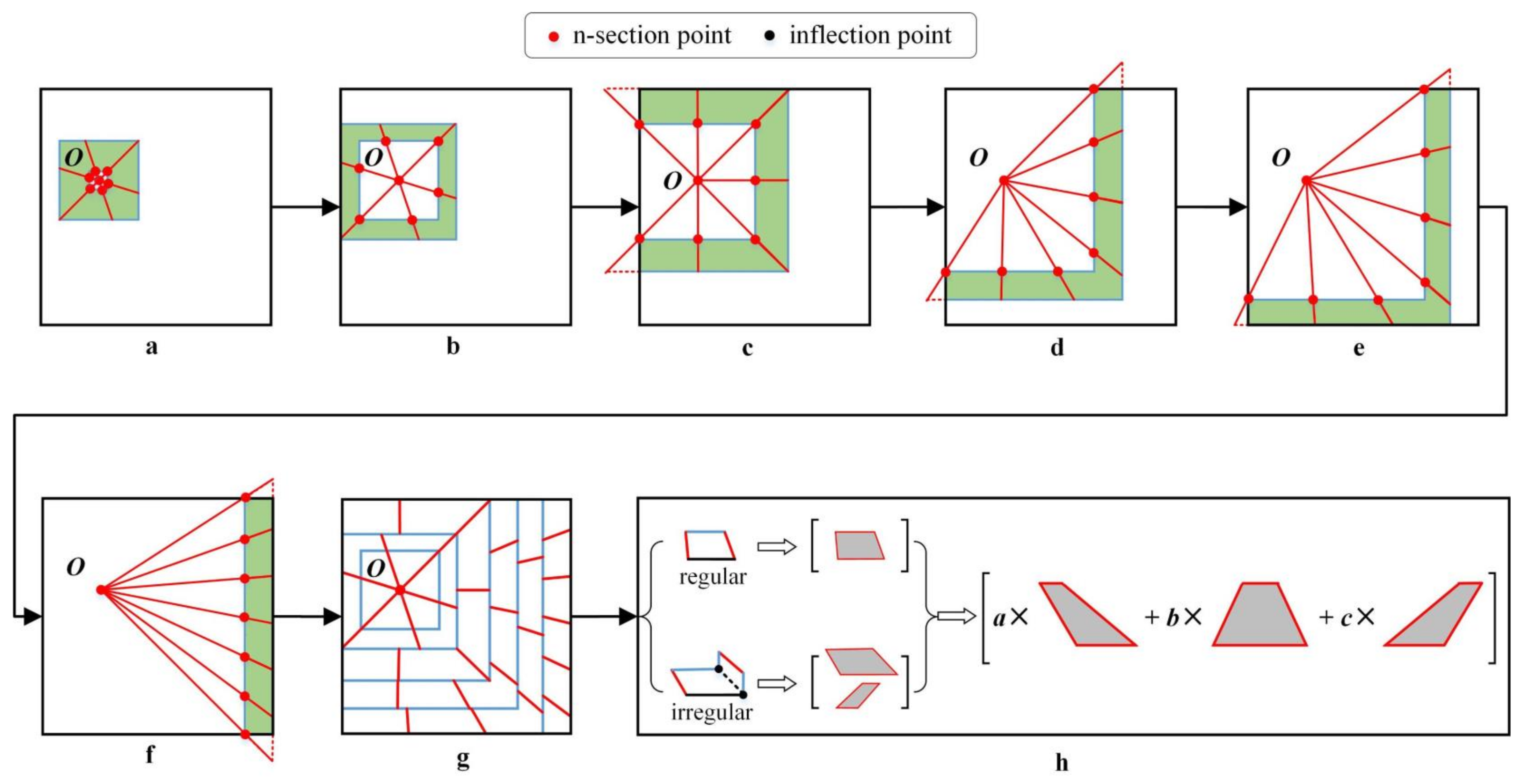
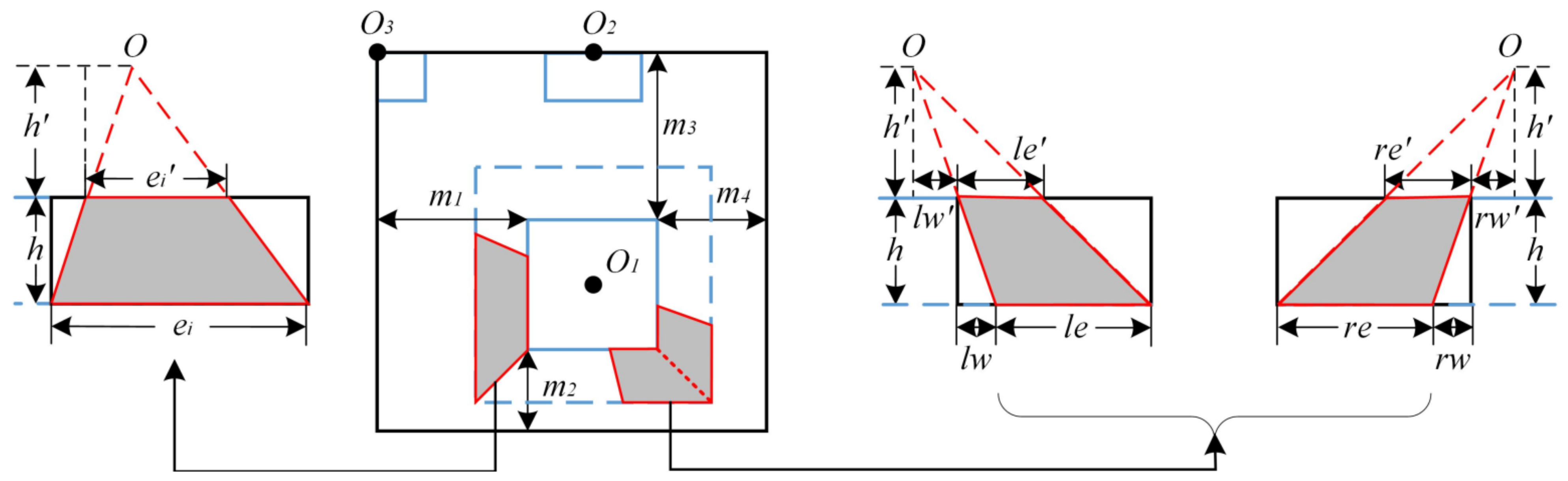
2.2.2. Multi-Level Data Decomposition Strategy
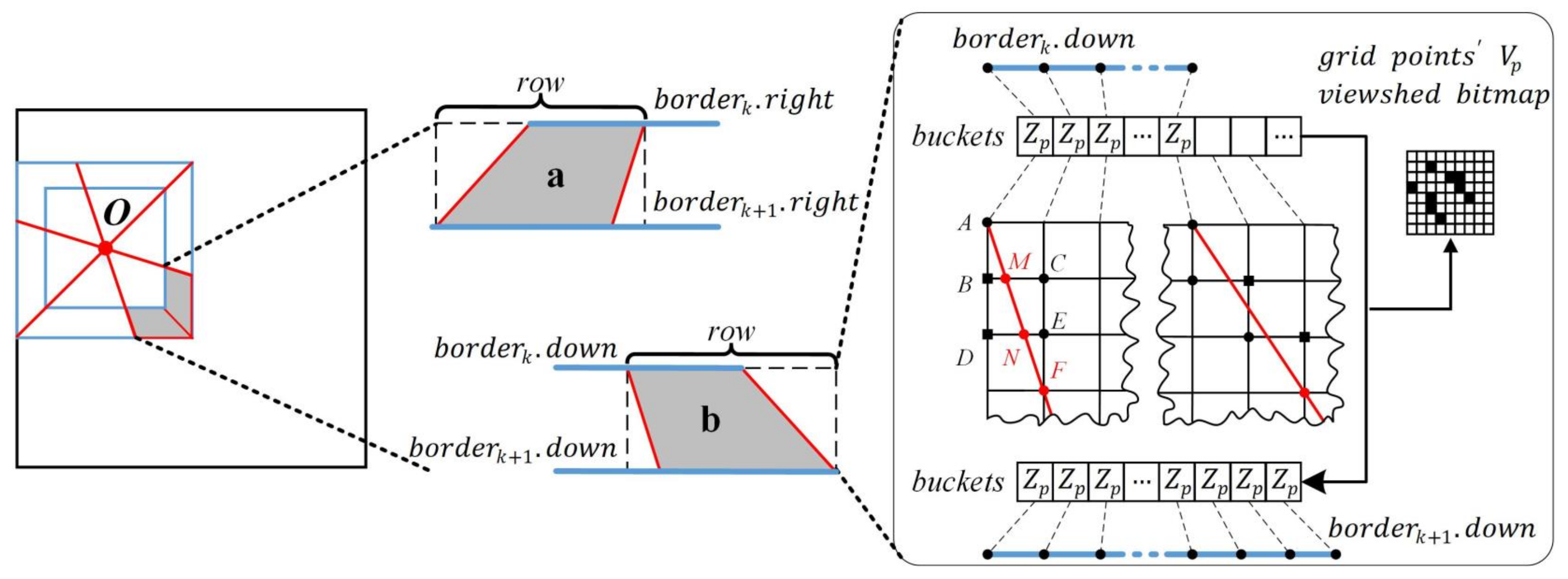
2.2.3. Boundary Approximate Calculation Strategy
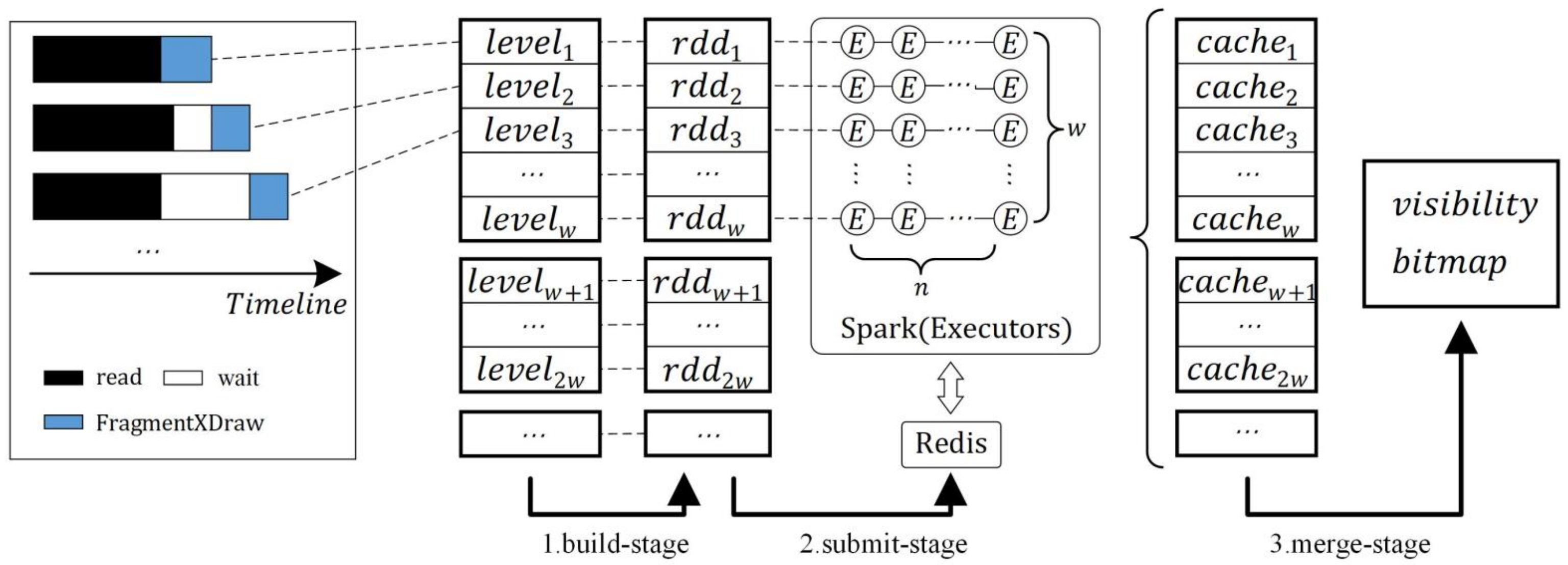
2.3. Algorithms Implementation Based on Spark
2.3.1. Spark-Based ML-XDraw Algorithm
| Algorithm 1: Spark-based ML-XDraw algorithm |
 |
2.3.2. Raster Fragment-Based XDraw Algorithm
| Algorithm 2: FragmentXDraw |
 |
| Algorithm 3: SectorXDraw |
 |
3. Experiments and Results
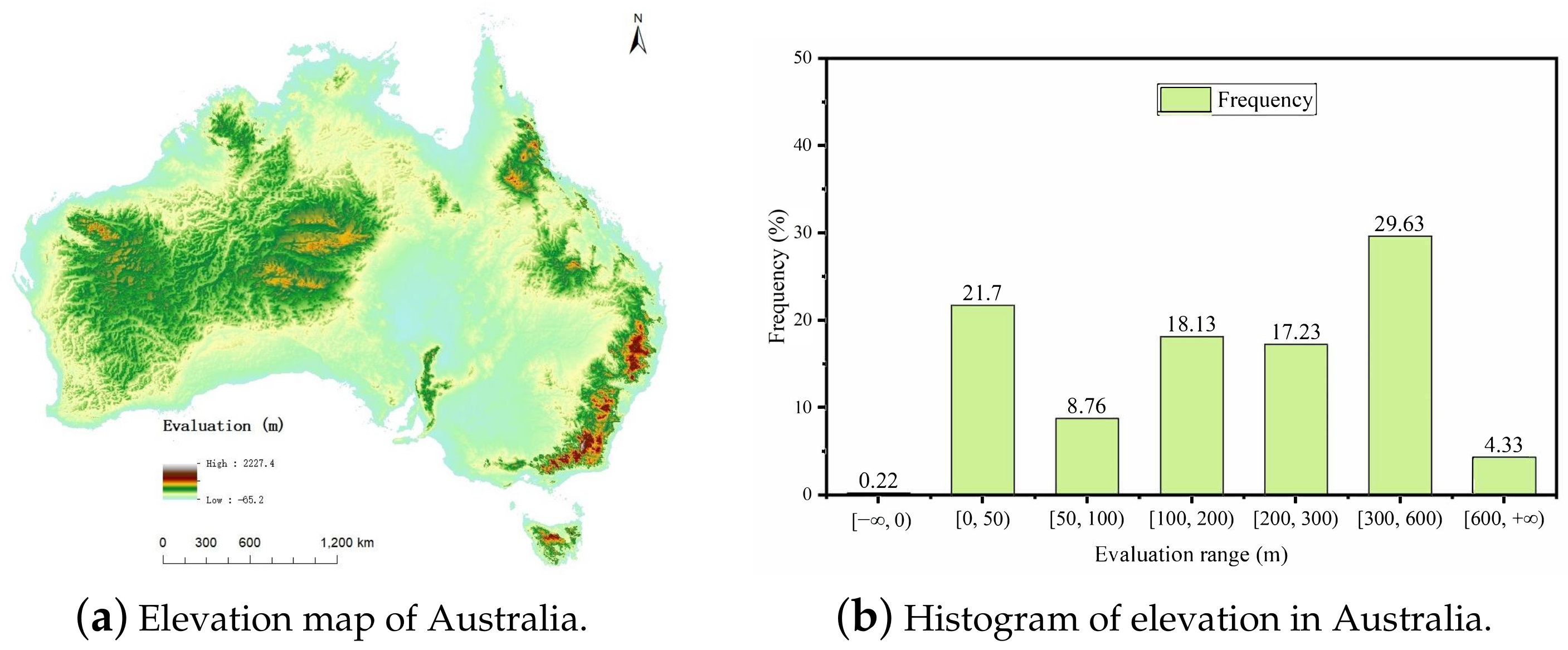
3.1. Datasets
3.2. Hardware Environment
3.3. Experimental Designs
3.4. Performance Evaluation
3.5. Results
4. Discussions
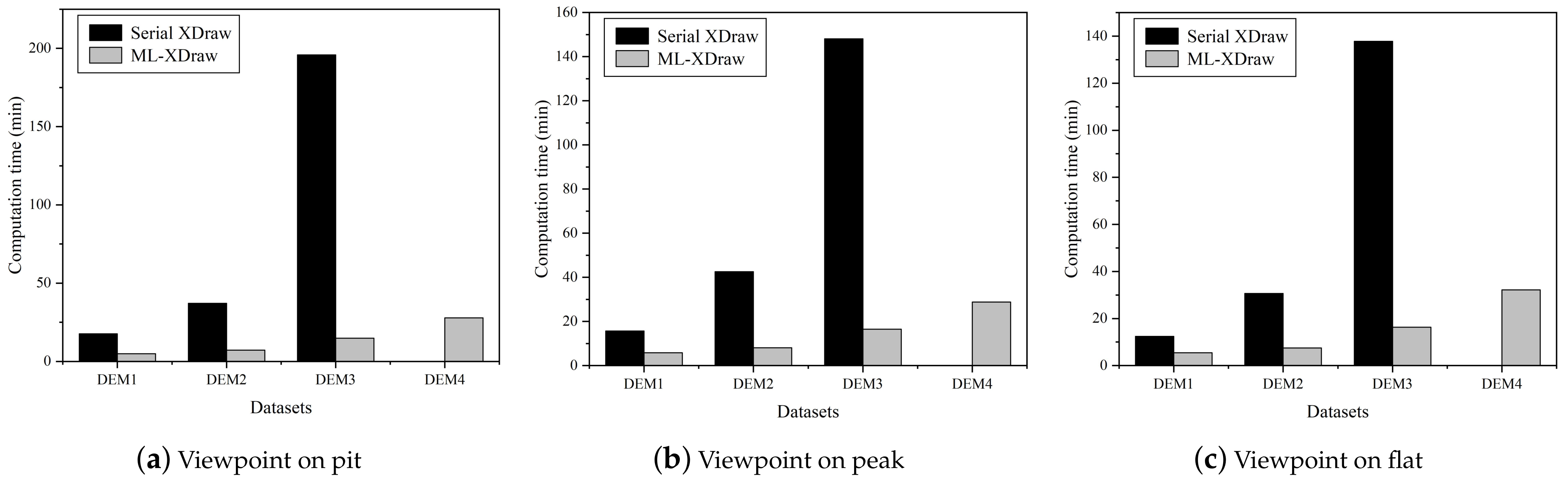
4.1. Effectiveness of the Approach on Parallel Performance
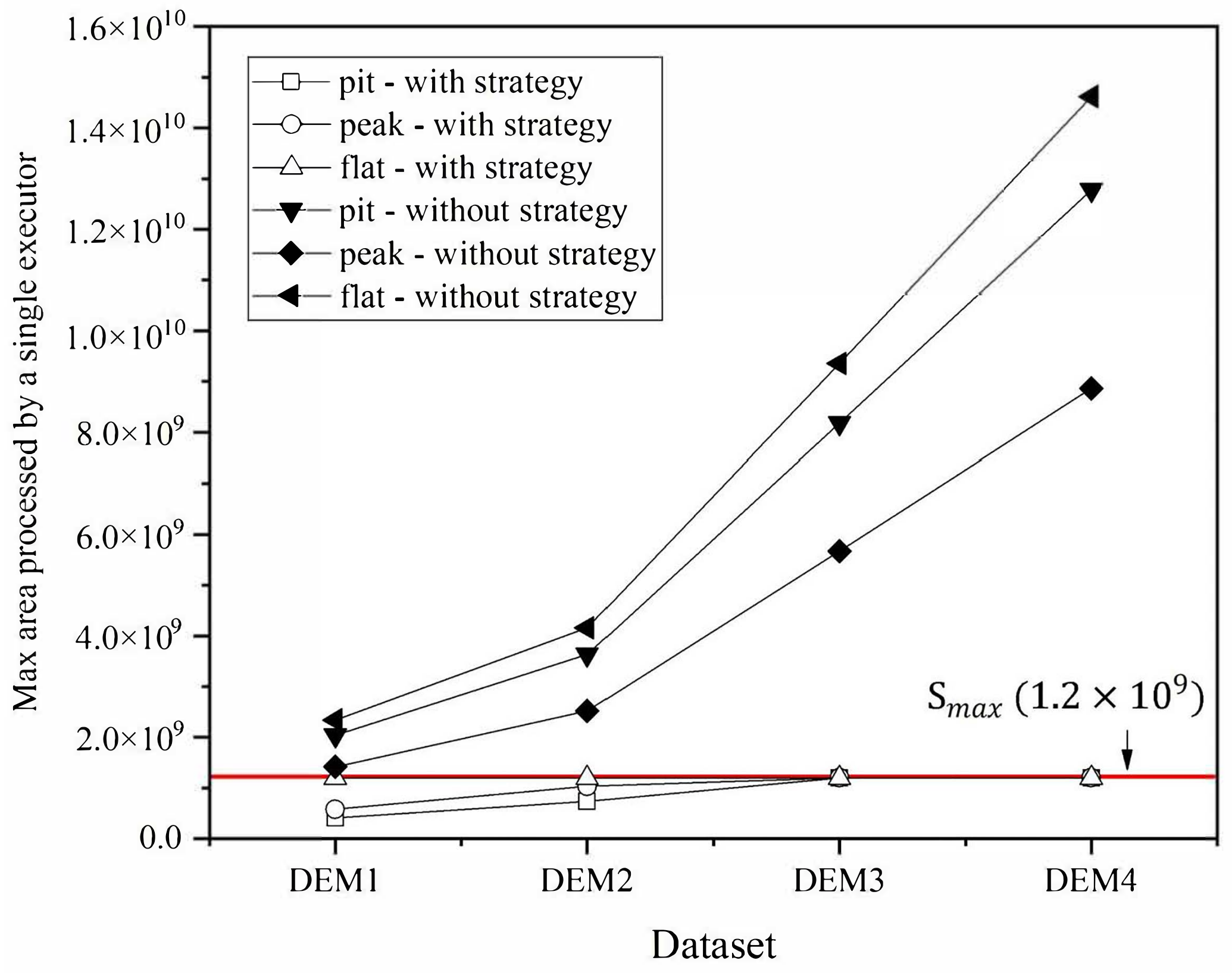
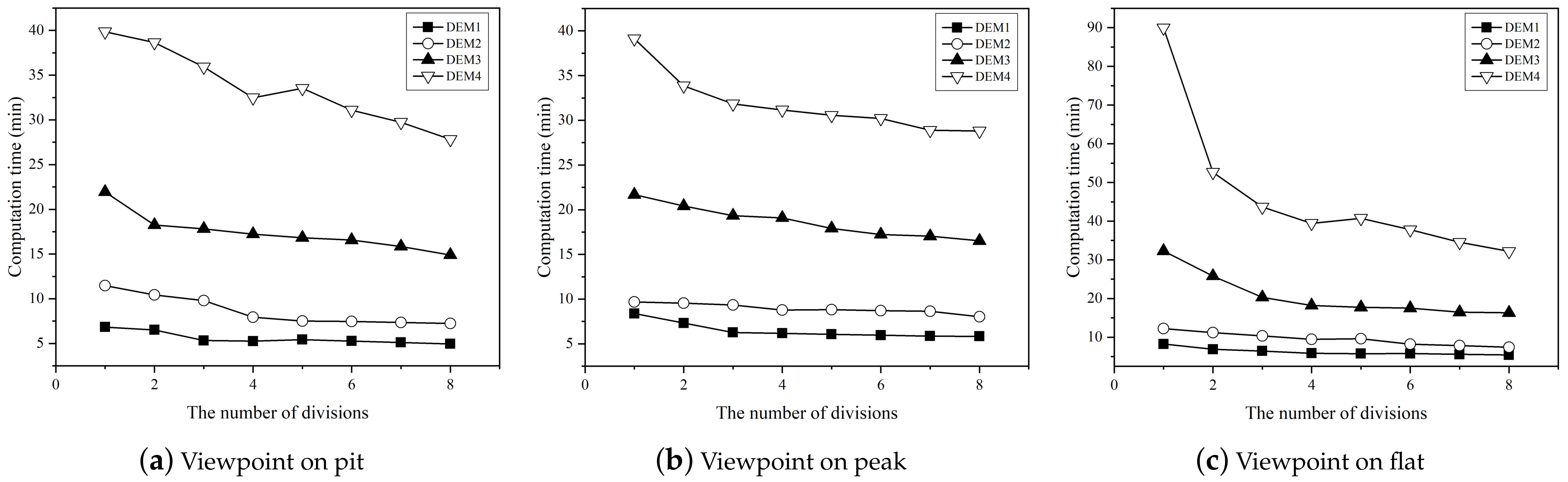
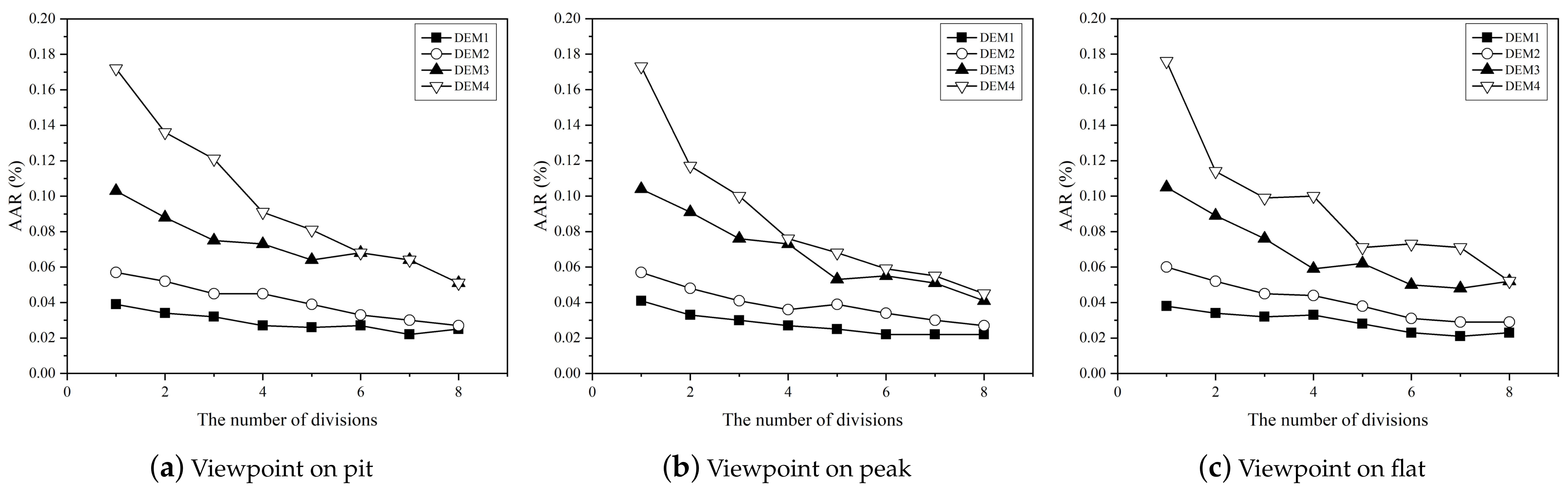
4.2. Effectiveness of Data Decomposition Strategy
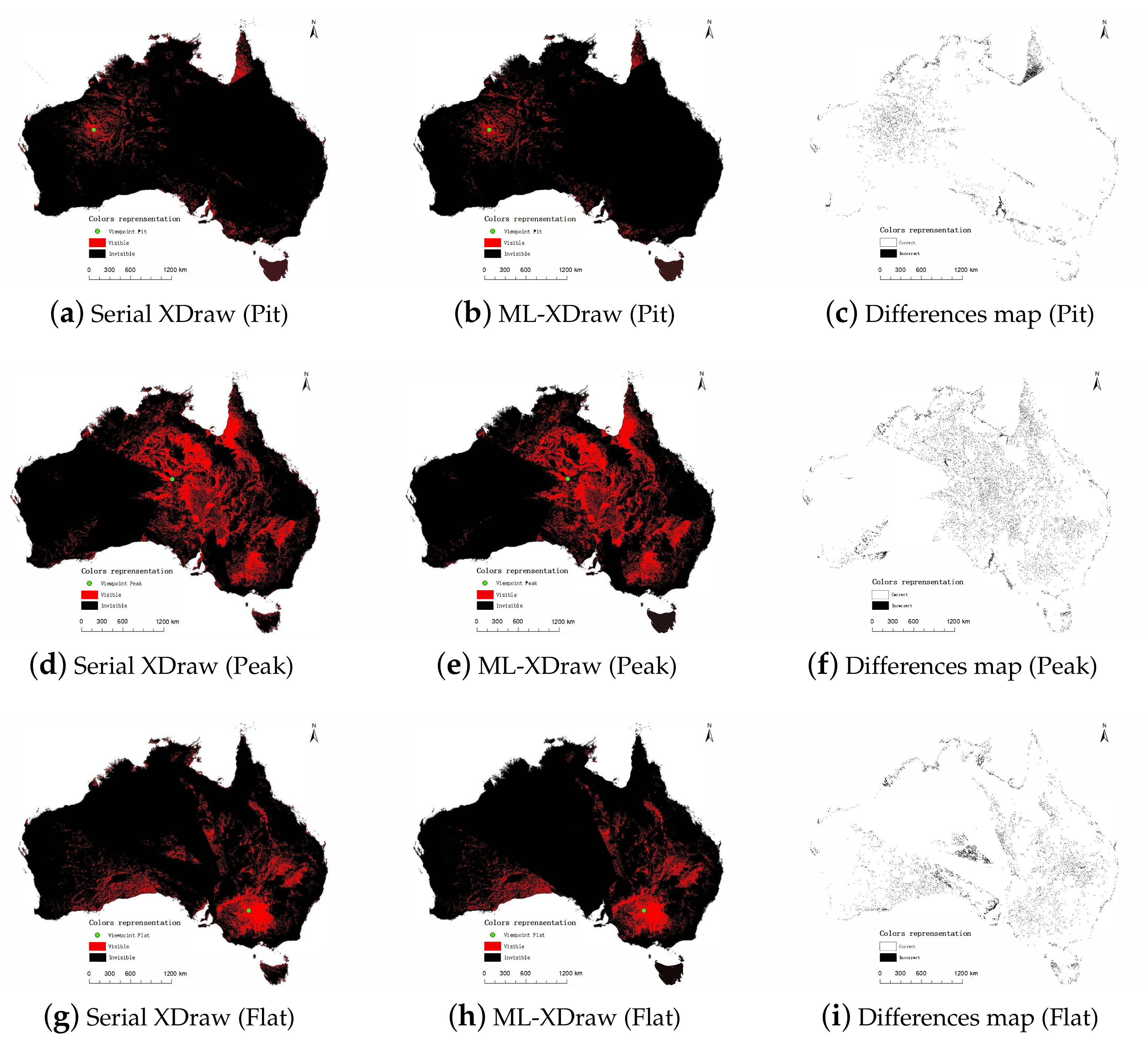
4.3. Accuracy Comparison of Algorithms
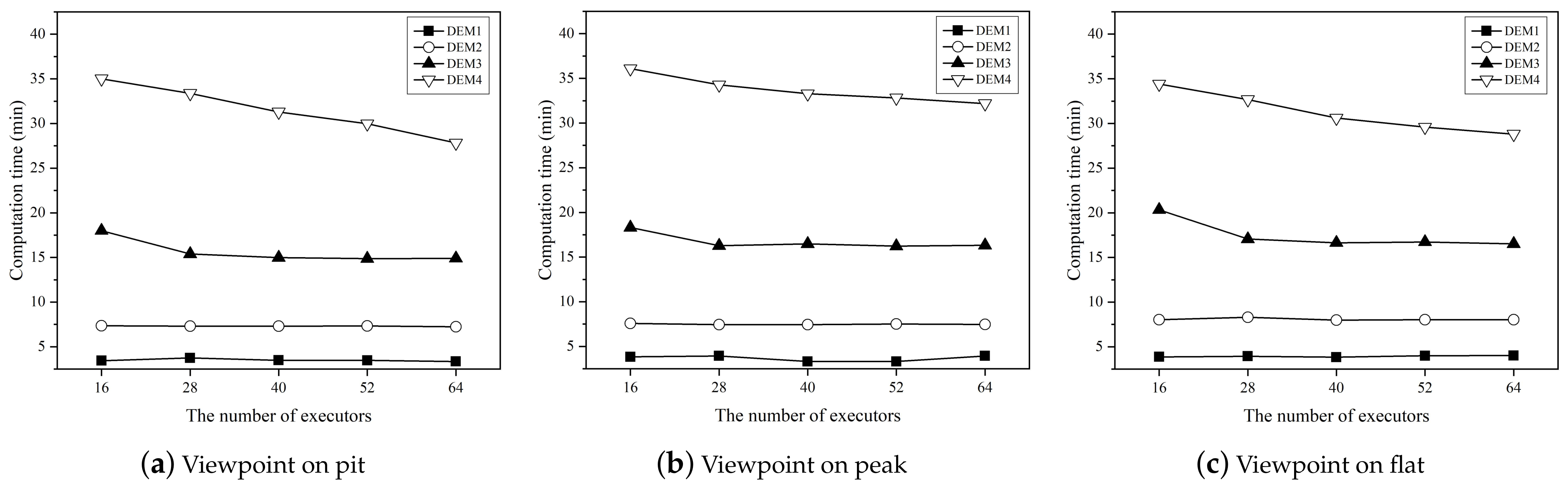
4.4. Scale-Out Performance of the Approach
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Larsen, M.V. Viewshed Algorithms for Strategic Positioning of Vehicles. Master’s Thesis, Faculty of Mathematics and Natural Sciences, University of Oslo, Oslo, Norway, May 2015. [Google Scholar]
- Łubczonek, J.; Kazimierski, W.; Pałczyński, M. Planning of combined system of radars and CCTV cameras for inland waterways surveillance by using various methods of visibility analyses. In Proceedings of the 2011 12th International Radar Symposium (IRS), Leipzig, Germany, 7–9 September 2011; pp. 731–736. [Google Scholar]
- Qiang, Y.; Shen, S.; Chen, Q. Visibility analysis of oceanic blue space using digital elevation models. Landsc. Urban Plan. 2019, 181, 92–102. [Google Scholar] [CrossRef]
- Tracy, D.M.; Franklin, W.R.; Cutler, B.; Luk, F.T.; Andrade, M. Path planning on a compressed terrain. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008; pp. 1–4. [Google Scholar]
- Yaagoubi, R.; El Yarmani, M.; Kamel, A.; Khemiri, W. HybVOR: A voronoi-based 3D GIS approach for camera surveillance network placement. ISPRS Int. J. Geo-Inf. 2015, 4, 754–782. [Google Scholar] [CrossRef]
- Bao, S.; Xiao, N.; Lai, Z.; Zhang, H.; Kim, C. Optimizing watchtower locations for forest fire monitoring using location models. Fire Saf. J. 2015, 71, 100–109. [Google Scholar] [CrossRef]
- Guo, H.; Nativi, S.; Liang, D.; Craglia, M.; Wang, L.; Schade, S.; Corban, C.; He, G.; Pesaresi, M.; Li, J.; et al. Big Earth Data science: An information framework for a sustainable planet. Int. J. Digit. Earth 2020, 13, 743–767. [Google Scholar] [CrossRef]
- Guo, H.; Liu, Z.; Jiang, H.; Wang, C.; Liu, J.; Liang, D. Big Earth Data: A new challenge and opportunity for Digital Earth’s development. Int. J. Digit. Earth 2017, 10, 1–12. [Google Scholar] [CrossRef]
- Mazumder, S.; Bhadoria, R.S.; Deka, G.C. Distributed computing in big data analytics. In InCon-Cepts, Technologies and Applications; Springer: New York, NY, USA, 2017. [Google Scholar]
- DAAC, L. The shuttle radar topography mission (SRTM) collection user guide. In NASA EOSDIS Land Processes DAAC; USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2015. [Google Scholar]
- Shook, E.; Hodgson, M.E.; Wang, S.; Behzad, B.; Soltani, K.; Hiscox, A.; Ajayakumar, J. Parallel cartographic modeling: A methodology for parallelizing spatial data processing. Int. J. Geogr. Inf. Sci. 2016, 30, 2355–2376. [Google Scholar] [CrossRef]
- Yang, C.; Raskin, R.; Goodchild, M.; Gahegan, M. Geospatial cyberinfrastructure: Past, present and future. Comput. Environ. Urban Syst. 2010, 34, 264–277. [Google Scholar] [CrossRef]
- Cheng, T.; Haworth, J.; Manley, E. Advances in geocomputation (1996–2011). Comput. Environ. Urban Syst. 2012, 36, 481–487. [Google Scholar] [CrossRef]
- De Floriani, L.; Marzano, P.; Puppo, E. Line-of-sight communication on terrain models. Int. J. Geogr. Inf. Syst. 1994, 8, 329–342. [Google Scholar] [CrossRef]
- Toma, L. Viewsheds on terrains in external memory. Sigspatial Spec. 2012, 4, 13–17. [Google Scholar] [CrossRef]
- Katz, M.J.; Overmars, M.H.; Sharir, M. Efficient hidden surface removal for objects with small union size. Comput. Geom. 1992, 2, 223–234. [Google Scholar] [CrossRef]
- Ozimek, A.; Ozimek, P. Viewshed analyses as support for objective landscape assessment. J. Digit. Landsc. Archit. JoDLA 2017, 2, 190–197. [Google Scholar]
- Franklin, W.R.; Ray, C.K.; Mehta, S. Geometric algorithms for siting of air defense missile batteries. Res. Proj. Battle 1994, 2756. [Google Scholar] [CrossRef]
- Franklin, W.R.; Ray, C. Higher isn’t necessarily better: Visibility algorithms and experiments. In Proceedings of the Advances in GIS Research: Sixth International Symposium on Spatial Data Handling; Taylor & Francis: Edinburgh, UK, 1994; Volume 2, pp. 751–770. [Google Scholar]
- Zhi, Y.; Wu, L.; Sui, Z.; Cai, H. An improved algorithm for computing viewshed based on reference planes. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–5. [Google Scholar]
- Xu, Z.Y.; Yao, Q. A novel algorithm for viewshed based on digital elevation model. In Proceedings of the 2009 Asia-Pacific Conference on Information Processing, Shenzhen, China, 18–19 July 2009; Volume 2, pp. 294–297. [Google Scholar]
- Yılmaz, G. Accelerating of Line of Sight Analysis Algorithms with Parallel Programming. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2017. [Google Scholar]
- Wu, H.; Pan, M.; Yao, L.; Luo, B. A partition-based serial algorithm for generating viewshed on massive DEMs. Int. J. Geogr. Inf. Sci. 2007, 21, 955–964. [Google Scholar] [CrossRef]
- Xia, Y.; Li, Y.; Shi, X. Parallel viewshed analysis on GPU using CUDA. In Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization, Huangshan, China, 28–31 May 2010; Volume 1, pp. 373–374. [Google Scholar]
- Zhao, Y.; Padmanabhan, A.; Wang, S. A parallel computing approach to viewshed analysis of large terrain data using graphics processing units. Int. J. Geogr. Inf. Sci. 2013, 27, 363–384. [Google Scholar] [CrossRef]
- Johansson, E.; Lundberg, J. Distributed Viewshed Analysis an Evaluation of Distribution Frameworks for Geospatial Information Systems. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2016. [Google Scholar]
- Gao, Y.; Yu, H.; Liu, Y.; Liu, Y.; Liu, M.; Zhao, Y. Optimization for viewshed analysis on GPU. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–5. [Google Scholar]
- Axell, T.; Fridén, M. Comparison between GPU and Parallel CPU Optimizations in Viewshed Analysis. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2015. [Google Scholar]
- Cauchi-Saunders, A.J.; Lewis, I.J. GPU enabled XDraw viewshed analysis. J. Parallel Distrib. Comput. 2015, 84, 87–93. [Google Scholar] [CrossRef]
- Carabaño, J.B.; Sarjakoski, T.; Westerholm, J. Efficient implementation of a fast viewshed algorithm on SIMD architectures. In Proceedings of the 2015 23rd Euromicro International Conference on Parallel, Distributed, and Network-Based Processing, Turku, Finland, 4–6 March 2015; pp. 199–202. [Google Scholar]
- Dou, W.; Li, Y.; Wang, Y. An equal-area triangulated partition method for parallel Xdraw viewshed analysis. Concurr. Comput. Pract. Exp. 2019, 31, e5216. [Google Scholar] [CrossRef]
- Li, Y.N.; Dou, W.F.; Wang, Y.L. Design and Implementation of parallel XDraw algorithm based on triangle region division. In Proceedings of the 2017 16th International Symposium on Distributed Computing and Applications to Business, Engineering and Science (DCABES), Anyang, China, 13–16 October 2017; pp. 41–44. [Google Scholar]
- Song, X.D.; Tang, G.A.; Liu, X.J.; Dou, W.F.; Li, F.Y. Parallel viewshed analysis on a PC cluster system using triple-based irregular partition scheme. Earth Sci. Inform. 2016, 9, 511–523. [Google Scholar] [CrossRef]
- Graham, R.L.; Shipman, G.M.; Barrett, B.W.; Castain, R.H.; Bosilca, G.; Lumsdaine, A. Open MPI: A high-performance, heterogeneous MPI. In Proceedings of the 2006 IEEE International Conference on Cluster Computing, Barcelona, Spain, 25–28 September 2006; pp. 1–9. [Google Scholar]
- Dou, W.; Li, Y.; Wang, Y. A fine-granularity scheduling algorithm for parallel XDraw viewshed analysis. Earth Sci. Inform. 2018, 11, 433–447. [Google Scholar] [CrossRef]
- Dou, W.; Li, Y. A fault-tolerant computing method for Xdraw parallel algorithm. J. Supercomput. 2018, 74, 2776–2800. [Google Scholar] [CrossRef]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, S.; Ye, Z. Spark-Enabled XDraw Viewshed Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2017–2029. [Google Scholar] [CrossRef]
- Jianbo, Z.; Caikun, C.; Tingnan, L.; Hao, X.; Simin, Z. A Parallel Implementation of an XDraw Viewshed Algorithm with Spark. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Zhangjiajie, China, 10–12 August 2019; pp. 19–28. [Google Scholar]
- Zhang, J.; Zhou, S.; Liang, T.; Li, Y.; Chen, C.; Xia, H. A two-level storage strategy for map-reduce enabled computation of local map algebra. Earth Sci. Inform. 2020, 13, 479–492. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, C.; Shi, L.; Du, Y. A tile-based scalable raster data management system based on HDFS. In Proceedings of the 2012 20th International Conference on Geoinformatics, Hong Kong, China, 15–17 June 2012; pp. 1–4. [Google Scholar]
- Liu, Z.; Hua, W.; Liu, X.; Liang, D.; Zhao, Y.; Shi, M. An Efficient Group-Based Replica Placement Policy for Large-Scale Geospatial 3D Raster Data on Hadoop. Sensors 2021, 21, 8132. [Google Scholar] [CrossRef] [PubMed]
- Shvachko, K.; Kuang, H.; Radia, S.; Chansler, R. The hadoop distributed file system. In Proceedings of the 2010 IEEE 26th Symposium on Mass Storage Systems and Technologies (MSST), Incline Village, NV, USA, 3–7 May 2010; pp. 1–10. [Google Scholar]

| Algorithm | Time Complexity | Space Complexity |
|---|---|---|
| R3 | ||
| R2 | ||
| XDraw |
| DataSet | Size (GB) | Grid-Cell Size | Columns | Rows | Total Grid Cells | Valid Grid Cells |
|---|---|---|---|---|---|---|
| DEM1 | 16.83 | 73,800 | 61,201 | 4,516,633,800 | 2,634,119,863 | |
| DEM2 | 29.91 | 98,399 | 81,602 | 8,029,555,198 | 4,682,469,269 | |
| DEM3 | 67.30 | 147,600 | 122,401 | 18,066,387,600 | 10,536,479,532 | |
| DEM4 | 105.16 | 184,500 | 153,001 | 28,228,684,500 | 16,462,348,871 |
| DataSet | Viewpoint | Serial XDraw (min) | ML-XDraw (min) | Speedup Ratio |
|---|---|---|---|---|
| DEM1 | Pit | 17.70 | 4.96 | 3.57 |
| Peak | 15.66 | 5.84 | 2.68 | |
| Flat | 12.44 | 5.44 | 2.29 | |
| DEM2 | Pit | 37.14 | 7.24 | 5.13 |
| Peak | 42.54 | 8.04 | 5.29 | |
| Flat | 30.64 | 7.46 | 4.11 | |
| DEM3 | Pit | 195.80 | 14.89 | 13.15 |
| Peak | 148.09 | 16.51 | 8.97 | |
| Flat | 137.81 | 16.31 | 8.45 | |
| DEM4 | Pit | - | 27.82 | - |
| Peak | - | 28.81 | - | |
| Flat | - | 32.18 | - |
| Dataset | Viewpoint | The Number of Correct Grid Cells with or without the Boundary Approximate Calculation Strategy | The Number of Total Valid Grid Cells | The Correctness Ratio (CR) with or without the Boundary Approximate Calculation Strategy | ||
|---|---|---|---|---|---|---|
| with | without | |||||
| DEM1 | Pit | 2,542,432,197 | 2,521,655,681 | 2,634,119,863 | 96.52% | 95.73% |
| Peak | 2,557,788,752 | 2,522,559,008 | 97.10% | 95.76% | ||
| Flat | 2,580,371,920 | 2,537,012,236 | 97.96% | 96.31% | ||
| DEM2 | Pit | 4,519,469,298 | 4,482,533,344 | 4,682,469,269 | 96.52% | 95.73% |
| Peak | 4,544,360,919 | 4,484,942,211 | 97.05% | 95.78% | ||
| Flat | 4,584,508,695 | 4,510,636,787 | 97.91% | 96.33% | ||
| DEM3 | Pit | 10,169,731,863 | 10,090,239,758 | 10,536,479,532 | 96.52% | 95.76% |
| Peak | 10,227,544,304 | 10,092,046,397 | 97.07% | 95.78% | ||
| Flat | 10,321,489,519 | 10,155,278,753 | 97.96% | 96.38% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Zhang, J. A Multi-Level Distributed Computing Approach to XDraw Viewshed Analysis Using Apache Spark. Remote Sens. 2023, 15, 761. https://doi.org/10.3390/rs15030761
Dong J, Zhang J. A Multi-Level Distributed Computing Approach to XDraw Viewshed Analysis Using Apache Spark. Remote Sensing. 2023; 15(3):761. https://doi.org/10.3390/rs15030761
Chicago/Turabian StyleDong, Junduo, and Jianbo Zhang. 2023. "A Multi-Level Distributed Computing Approach to XDraw Viewshed Analysis Using Apache Spark" Remote Sensing 15, no. 3: 761. https://doi.org/10.3390/rs15030761
APA StyleDong, J., & Zhang, J. (2023). A Multi-Level Distributed Computing Approach to XDraw Viewshed Analysis Using Apache Spark. Remote Sensing, 15(3), 761. https://doi.org/10.3390/rs15030761






