Spatial Prediction of Wildfire Susceptibility Using Hybrid Machine Learning Models Based on Support Vector Regression in Sydney, Australia
Abstract
1. Introduction
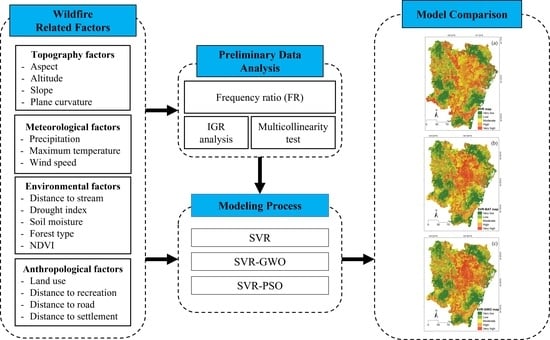
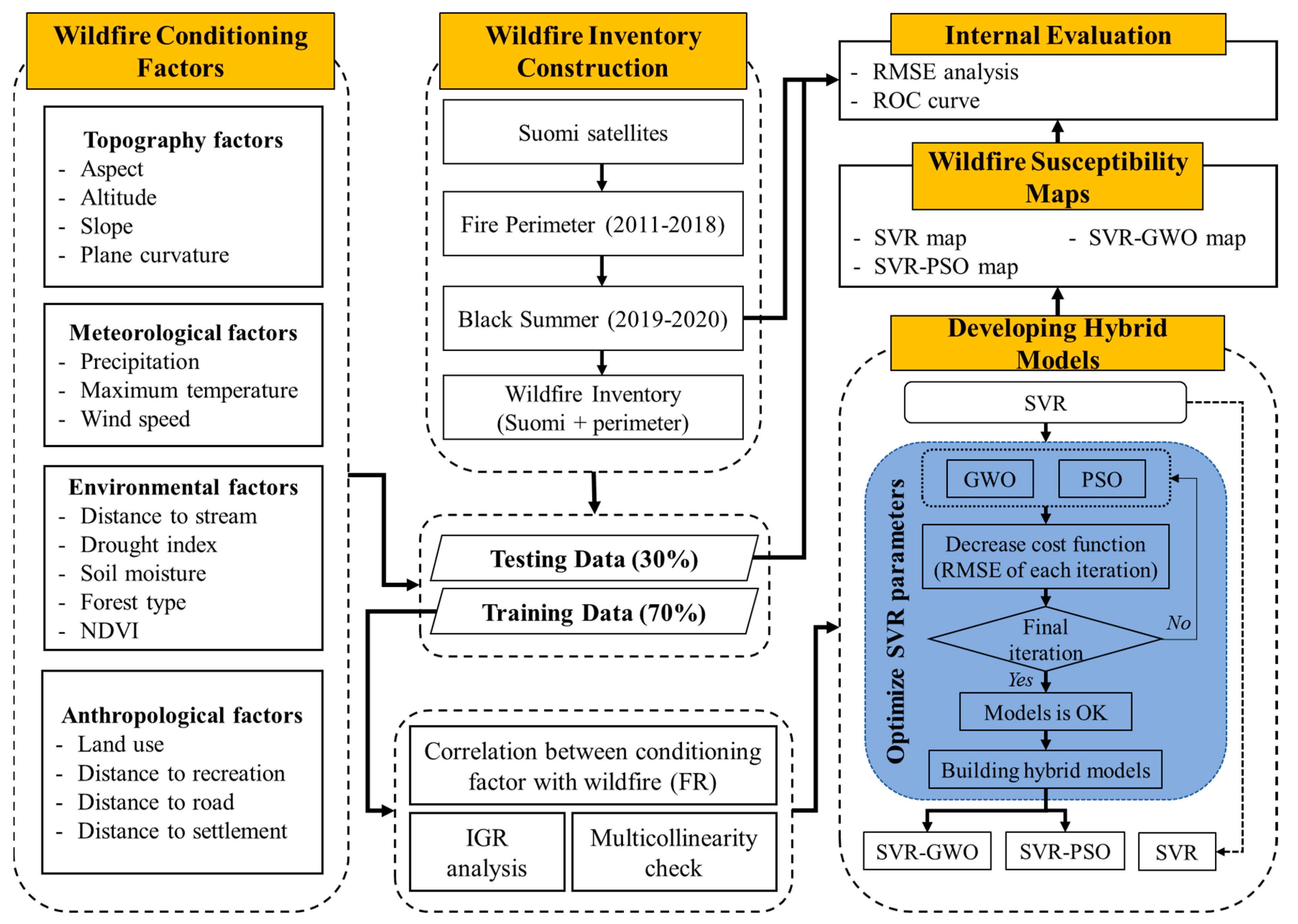
2. Materials and Methods
2.1. Study Area
2.2. Historical Fire Location
2.3. Additional Fire Data for Validation
2.4. Wildfire-Related Factors
2.4.1. Topographical
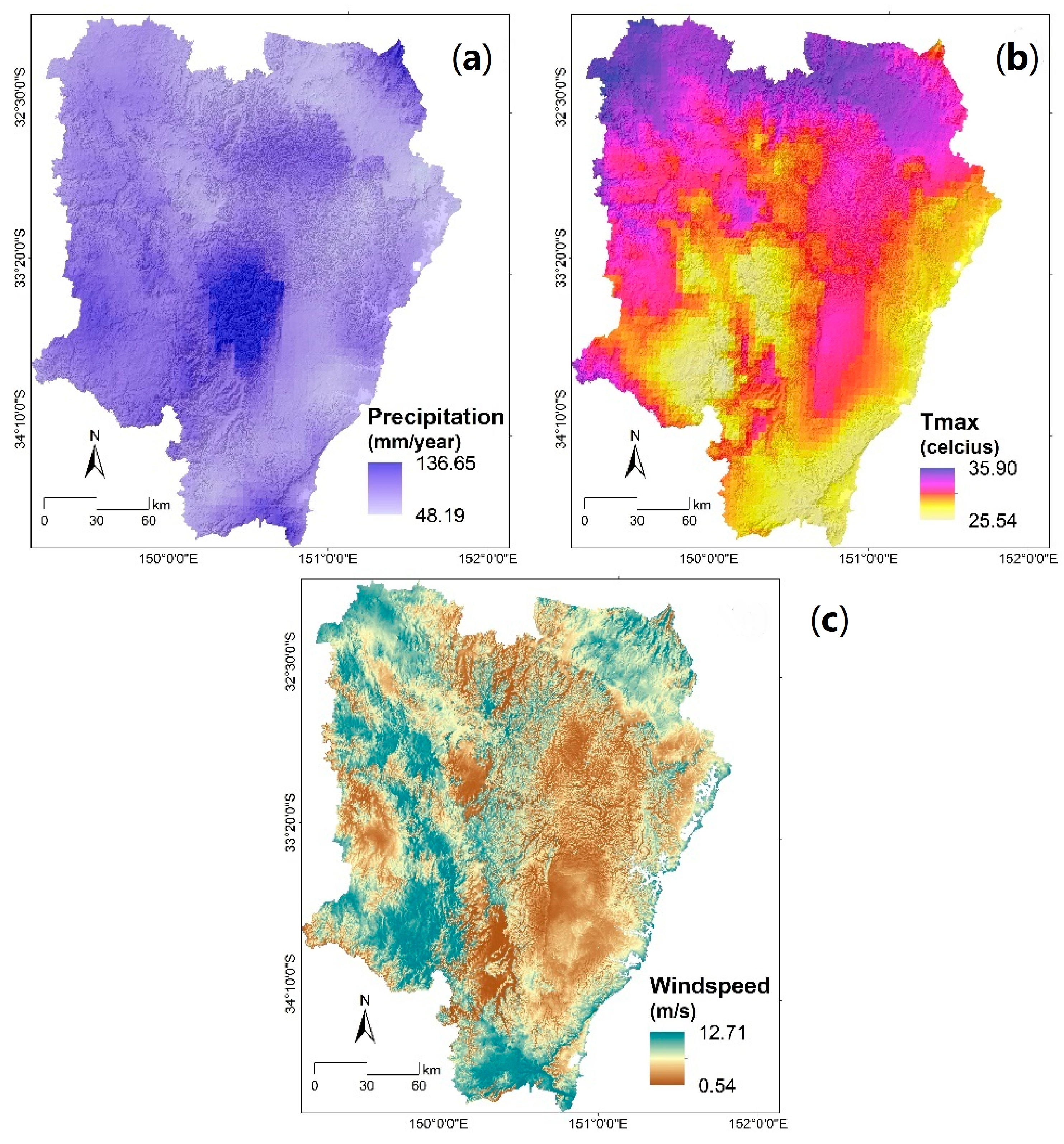
2.4.2. Meteorological
2.4.3. Environmental
2.4.4. Anthropological
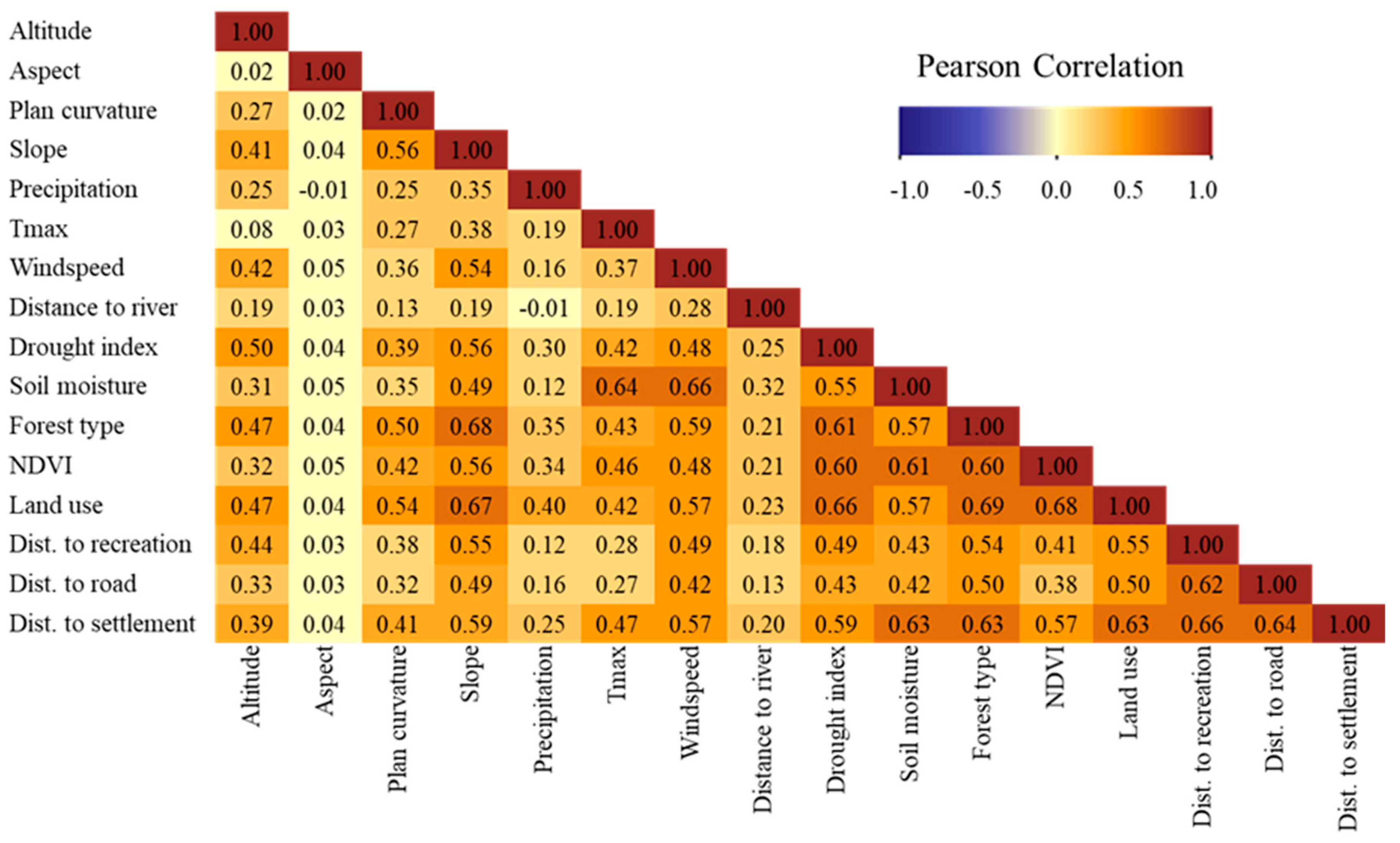
2.5. Spatial Correlation Analysis
2.6. Support Vector Regression (SVR)
2.7. Metaheuristic Optimization Approaches
2.7.1. Grey Wolf Optimization (GWO)
2.7.2. Particle Swarm Optimization (PSO)
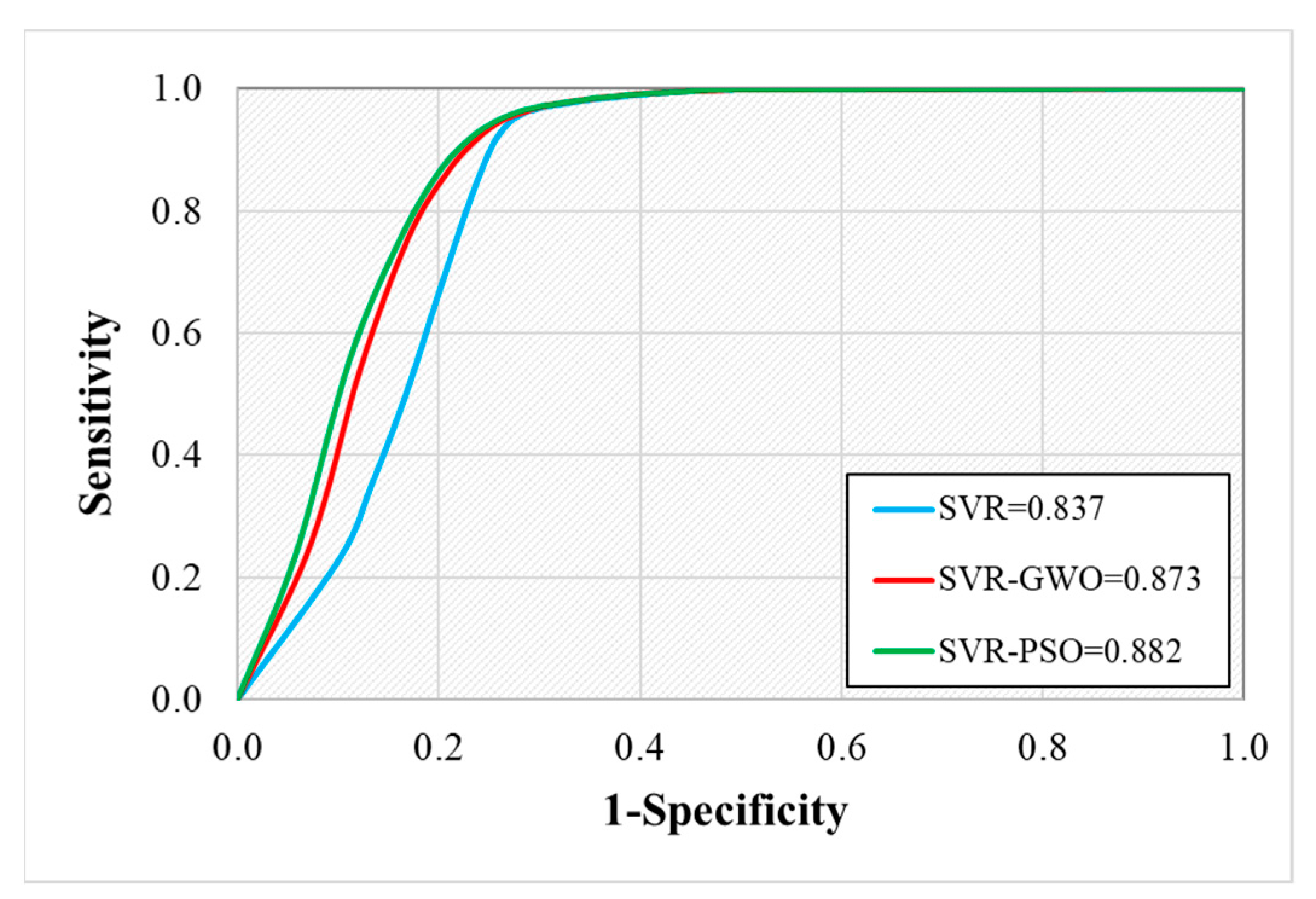
2.8. Performance Evaluation
3. Results
3.1. Correlation between Wildfire and Driving Factors
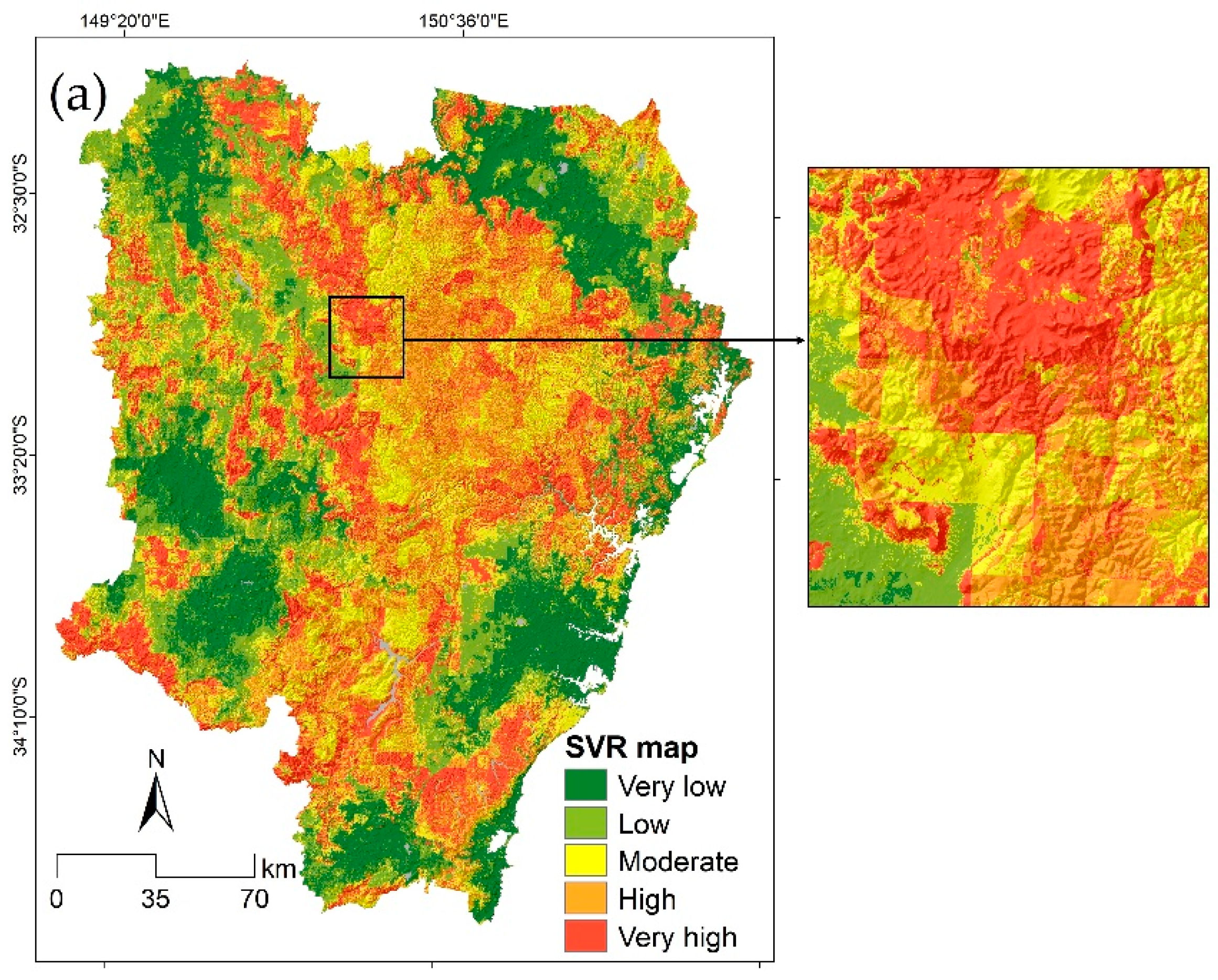
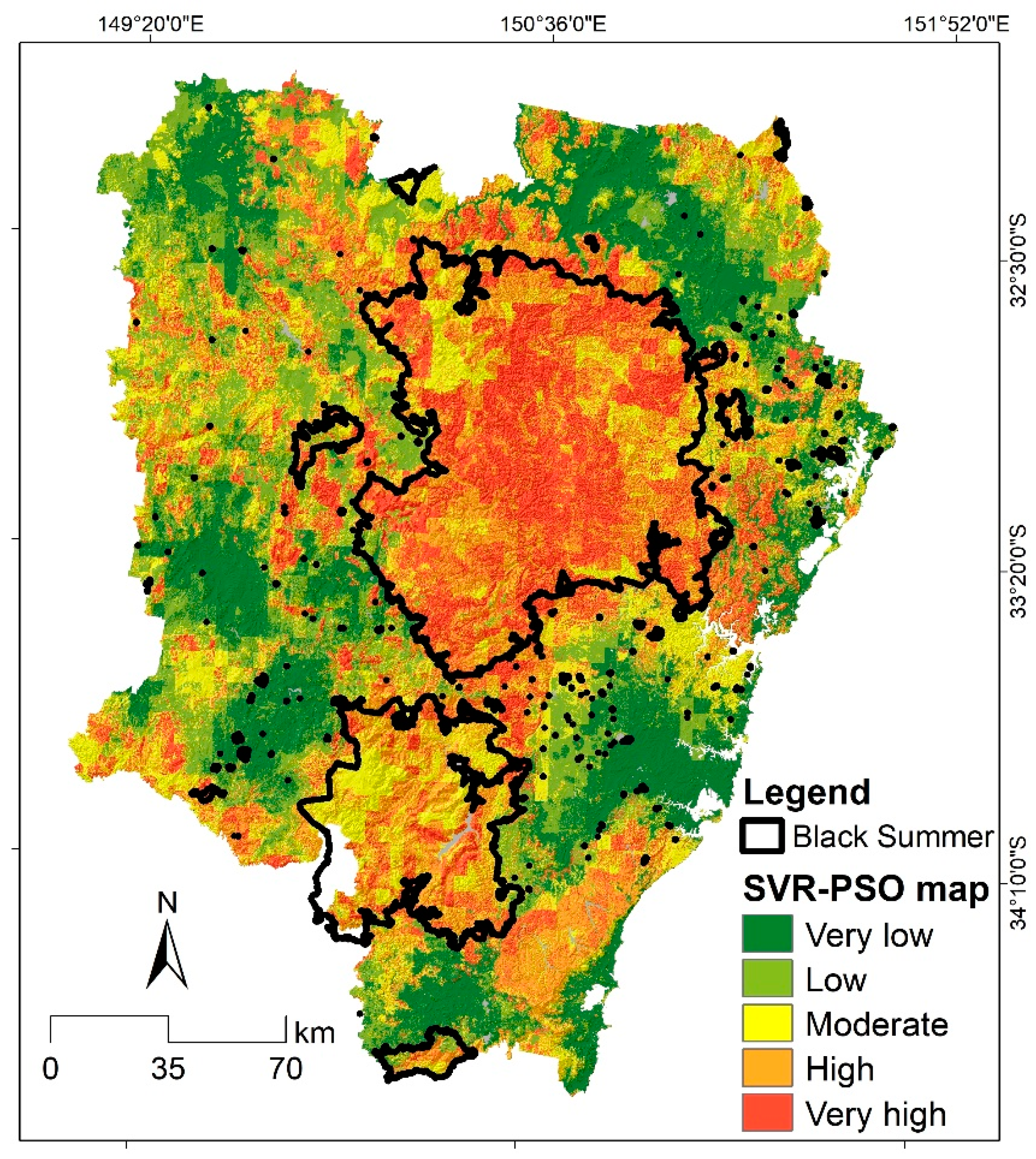
3.2. Susceptibility Map
3.3. Model Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bushfire|Understanding Hazards Collection. Available online: https://knowledge.aidr.org.au/resources/bushfire/ (accessed on 30 October 2022).
- Clarke, H.; Gibson, R.; Cirulis, B.; Bradstock, R.A.; Penman, T.D. Developing and Testing Models of the Drivers of Anthropogenic and Lightning-Caused Wildfire Ignitions in South-Eastern Australia. J. Environ. Manag. 2019, 235, 34–41. [Google Scholar] [CrossRef]
- Li, S.; Banerjee, T. Spatial and Temporal Pattern of Wildfires in California from 2000 to 2019. Sci. Rep. 2021, 11, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Bushfire Weather. Available online: http://www.bom.gov.au/weather-services/fire-weather-centre/bushfire-weather/index.shtml (accessed on 30 October 2022).
- Hosseini, M.; Lim, S. Gene Expression Programming and Data Mining Methods for Bushfire Susceptibility Mapping in New South Wales, Australia. Nat. Hazards 2022, 113, 1349–1365. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.P.; Jiang, F.; Gan, V.J.L.; Wang, M.; Zhai, C. Real-Time Detection of Wildfire Risk Caused by Powerline Vegetation Faults Using Advanced Machine Learning Techniques. Adv. Eng. Inform. 2020, 44, 101070. [Google Scholar] [CrossRef]
- Squire, D.T.; Richardson, D.; Risbey, J.S.; Black, A.S.; Kitsios, V.; Matear, R.J.; Monselesan, D.; Moore, T.S.; Tozer, C.R. Likelihood of Unprecedented Drought and Fire Weather during Australia’s 2019 Megafires. NPJ Clim. Atmos. Sci. 2021, 4, 1–12. [Google Scholar] [CrossRef]
- With Costs Approaching $100 Billion, the Fires Are Australia’s Costliest Natural Disaster. Available online: https://theconversation.com/with-costs-approaching-100-billion-the-fires-are-australias-costliest-natural-disaster-129433 (accessed on 30 October 2022).
- The Royal Commission into National Natural Disaster Arrangements. The Royal Commission into National Natural Disaster Arrangements Report. 2020. Available online: https://naturaldisaster.royalcommission.gov.au/publications/royal-commission-national-natural-disaster-arrangements-report (accessed on 30 October 2022).
- Zhang, Y.; Lim, S.; Sharples, J.J. Wildfire Occurrence Patterns in Ecoregions of New South Wales and Australian Capital Territory, Australia. Nat. Hazards 2017, 87, 415–435. [Google Scholar] [CrossRef]
- Cortes-Ramirez, J.; Michael, R.N.; Knibbs, L.D.; Bambrick, H.; Haswell, M.R.; Wraith, D. The Association of Wildfire Air Pollution with COVID-19 Incidence in New South Wales, Australia. Sci. Total Environ. 2022, 809, 151158. [Google Scholar] [CrossRef]
- Haque, M.K.; Azad, M.A.K.; Hossain, M.Y.; Ahmed, T.; Uddin, M.; Hossain, M.M.; Haque, M.K.; Azad, M.A.K.; Hossain, M.Y.; Ahmed, T.; et al. Wildfire in Australia during 2019-2020, Its Impact on Health, Biodiversity and Environment with Some Proposals for Risk Management: A Review. J. Environ. Prot. 2021, 12, 391–414. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Kamran, K.V.; Blaschke, T.; Aryal, J.; Naboureh, A.; Einali, J.; Bian, J. Spatial Prediction of Wildfire Susceptibility Using Field Survey Gps Data and Machine Learning Approaches. Fire 2019, 2, 43. [Google Scholar] [CrossRef]
- Sazib, N.; Bolten, J.D.; Mladenova, I.E. Leveraging NASA Soil Moisture Active Passive for Assessing Fire Susceptibility and Potential Impacts over Australia and California. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 779–787. [Google Scholar] [CrossRef]
- Buis, A. The Climate Connections of a Record Fire Year in the U.S. West. Available online: https://climate.nasa.gov/ask-nasa-climate/3066/the-climate-connections-of-a-record-fire-year-in-the-us-west/ (accessed on 4 April 2022).
- di Virgilio, G.; Evans, J.P.; Clarke, H.; Sharples, J.; Hirsch, A.L.; Hart, M.A. Climate Change Significantly Alters Future Wildfire Mitigation Opportunities in Southeastern Australia. Geophys. Res. Lett. 2020, 47, e2020GL088893. [Google Scholar] [CrossRef]
- Nur, A.S.; Kim, Y.J.; Lee, C.-W. Creation of Wildfire Susceptibility Maps in Plumas National Forest Using InSAR Coherence, Deep Learning, and Metaheuristic Optimization Approaches. Remote Sens. 2022, 14, 4416. [Google Scholar] [CrossRef]
- Zhang, Y.; Lim, S. Drivers of Wildfire Occurrence Patterns in the Inland Riverine Environment of New South Wales, Australia. Forests 2019, 10, 524. [Google Scholar] [CrossRef]
- Sulova, A.; Arsanjani, J.J. Exploratory Analysis of Driving Force of Wildfires in Australia: An Application of Machine Learning within Google Earth Engine. Remote Sens. 2020, 13, 10. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m Active Fire Detection Data Product: Algorithm Description and Initial Assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Nhongo, E.J.S.; Fontana, D.C.; Guasselli, L.A.; Bremm, C. Probabilistic Modelling of Wildfire Occurrence Based on Logistic Regression, Niassa Reserve, Mozambique. Geomat. Nat. Hazards Risk 2019, 10, 1772–1792. [Google Scholar] [CrossRef]
- Chicas, S.D.; Østergaard Nielsen, J.; Valdez, M.C.; Chen, C.F. Modelling Wildfire Susceptibility in Belize’s Ecosystems and Protected Areas Using Machine Learning and Knowledge-Based Methods. Geocarto Int. 2022, 1–23. [Google Scholar] [CrossRef]
- Al-Fugara, A.; Mabdeh, A.N.; Ahmadlou, M.; Pourghasemi, H.R.; Al-Adamat, R.; Pradhan, B.; Al-Shabeeb, A.R. Wildland Fire Susceptibility Mapping Using Support Vector Regression and Adaptive Neuro-Fuzzy Inference System-Based Whale Optimization Algorithm and Simulated Annealing. ISPRS Int. J. Geoinf. 2021, 10, 382. [Google Scholar] [CrossRef]
- Kaur, H.; Sood, S.K. Adaptive Neuro Fuzzy Inference System (ANFIS) Based Wildfire Risk Assessment. J. Exp. Theor. Artif. Intell. 2019, 31, 599–619. [Google Scholar] [CrossRef]
- Salavati, G.; Saniei, E.; Ghaderpour, E.; Hassan, Q.K. Wildfire Risk Forecasting Using Weights of Evidence and Statistical Index Models. Sustainability 2022, 14, 3881. [Google Scholar] [CrossRef]
- Nami, M.H.; Jaafari, A.; Fallah, M.; Nabiuni, S. Spatial Prediction of Wildfire Probability in the Hyrcanian Ecoregion Using Evidential Belief Function Model and GIS. Int. J. Environ. Sci. Technol. 2018, 15, 373–384. [Google Scholar] [CrossRef]
- Bayat, G.; Yildiz, K. Comparison of the Machine Learning Methods to Predict Wildfire Areas. Turk. J. Sci. Technol. 2022, 17, 241–250. [Google Scholar] [CrossRef]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial Prediction of Landslide Susceptibility Using Hybrid Support Vector Regression (SVR) and the Adaptive Neuro-Fuzzy Inference System (ANFIS) with Various Metaheuristic Algorithms. Sci. Total Environ. 2020, 741, 139937. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.; Er, M.J.; Wang, N. An Effective Semi-Cross-Validation Model Selection Method for Extreme Learning Machine with Ridge Regression. Neurocomputing 2015, 151, 933–942. [Google Scholar] [CrossRef]
- Wang, J.S.; Li, S.X. An Improved Grey Wolf Optimizer Based on Differential Evolution and Elimination Mechanism. Sci. Rep. 2019, 9, 1–21. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B. bin Applying Population-Based Evolutionary Algorithms and a Neuro-Fuzzy System for Modeling Landslide Susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Hakim, W.L.; Rezaie, F.; Nur, A.S.; Panahi, M.; Khosravi, K.; Lee, C.-W.; Lee, S. Convolutional Neural Network (CNN) with Metaheuristic Optimization Algorithms for Landslide Susceptibility Mapping in Icheon, South Korea. J. Environ. Manag. 2022, 305, 114367. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid Artificial Intelligence Models Based on a Neuro-Fuzzy System and Metaheuristic Optimization Algorithms for Spatial Prediction of Wildfire Probability. Agric. Meteorol. 2019, 266–267, 198–207. [Google Scholar] [CrossRef]
- Balogun, A.L.; Rezaie, F.; Pham, Q.B.; Gigović, L.; Drobnjak, S.; Aina, Y.A.; Panahi, M.; Yekeen, S.T.; Lee, S. Spatial Prediction of Landslide Susceptibility in Western Serbia Using Hybrid Support Vector Regression (SVR) with GWO, BAT and COA Algorithms. Geosci. Front. 2021, 12, 101104. [Google Scholar] [CrossRef]
- Fadhillah, M.F.; Lee, S.; Lee, C.W.; Park, Y.C. Application of Support Vector Regression and Metaheuristic Optimization Algorithms for Groundwater Potential Mapping in Gangneung-Si, South Korea. Remote Sens. 2021, 13, 1196. [Google Scholar] [CrossRef]
- Panahi, M.; Dodangeh, E.; Rezaie, F.; Khosravi, K.; van Le, H.; Lee, M.J.; Lee, S.; Thai Pham, B. Flood Spatial Prediction Modeling Using a Hybrid of Meta-Optimization and Support Vector Regression Modeling. Catena 2021, 199, 105114. [Google Scholar] [CrossRef]
- Australia Bureau of Statistics Regional Population. Available online: https://www.abs.gov.au/statistics/people/population/regional-population/2021 (accessed on 11 October 2022).
- NSW Map|NSW National Parks. Available online: https://www.nationalparks.nsw.gov.au/nsw-state-map (accessed on 17 October 2022).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Trucchia, A.; Meschi, G.; Fiorucci, P.; Gollini, A.; Negro, D. Defining Wildfire Susceptibility Maps in Italy for Understanding Seasonal Wildfire Regimes at the National Level. Fire 2022, 5, 30. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Pham, B.T. Wildfire Spatial Pattern Analysis in the Zagros Mountains, Iran: A Comparative Study of Decision Tree Based Classifiers. Ecol. Inf. 2018, 43, 200–211. [Google Scholar] [CrossRef]
- Hong, H.; Jaafari, A.; Zenner, E.K. Predicting Spatial Patterns of Wildfire Susceptibility in the Huichang County, China: An Integrated Model to Analysis of Landscape Indicators. Ecol. Indic. 2019, 101, 878–891. [Google Scholar] [CrossRef]
- Piralilou, S.T.; Einali, G.; Ghorbanzadeh, O.; Nachappa, T.G.; Gholamnia, K.; Blaschke, T.; Ghamisi, P. A Google Earth Engine Approach for Wildfire Susceptibility Prediction Fusion with Remote Sensing Data of Different Spatial Resolutions. Remote Sens. 2022, 14, 672. [Google Scholar] [CrossRef]
- Mabdeh, A.N.; Al-Fugara, A.; Khedher, K.M.; Mabdeh, M.; Al-Shabeeb, A.R.; Al-Adamat, R. Forest Fire Susceptibility Assessment and Mapping Using Support Vector Regression and Adaptive Neuro-Fuzzy Inference System-Based Evolutionary Algorithms. Sustainability 2022, 14, 9446. [Google Scholar] [CrossRef]
- Oliveira, S.; Gonçalves, A.; Zêzere, J.L. Reassessing Wildfire Susceptibility and Hazard for Mainland Portugal. Sci. Total Environ. 2021, 762, 143121. [Google Scholar] [CrossRef]
- de Santana, R.O.; Delgado, R.C.; Schiavetti, A. Modeling Susceptibility to Forest Fires in the Central Corridor of the Atlantic Forest Using the Frequency Ratio Method. J Environ. Manag. 2021, 296, 113343. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Idrees, M.O.; Janizadeh, S.; Ahmadi, K.; Shabani, F. Forest Fire Susceptibility Prediction Based on Machine Learning Models with Resampling Algorithms on Remote Sensing Data. Remote Sens. 2020, 12, 3682. [Google Scholar] [CrossRef]
- Sachdeva, S.; Bhatia, T.; Verma, A.K. GIS-Based Evolutionary Optimized Gradient Boosted Decision Trees for Forest Fire Susceptibility Mapping. Nat. Hazards 2018, 92, 1399–1418. [Google Scholar] [CrossRef]
- Bustillo Sánchez, M.; Tonini, M.; Mapelli, A.; Fiorucci, P. Spatial Assessment of Wildfires Susceptibility in Santa Cruz (Bolivia) Using Random Forest. Geosciences 2021, 11, 224. [Google Scholar] [CrossRef]
- Malik, A.; Rao, M.R.; Puppala, N.; Koouri, P.; Thota, V.A.K.; Liu, Q.; Chiao, S.; Gao, J. Data-Driven Wildfire Risk Prediction in Northern California. Atmosphere 2021, 12, 109. [Google Scholar] [CrossRef]
- Kant Sharma, L.A.; Gupta, R.A.; Fatima, N.A. Assessing the Predictive Efficacy of Six Machine Learning Algorithms for the Susceptibility of Indian Forests to Fire. Int. J. Wildland Fire 2022, 31, 735–758. [Google Scholar] [CrossRef]
- Gholamnia, K.; Nachappa, T.G.; Ghorbanzadeh, O.; Blaschke, T. Comparisons of Diverse Machine Learning Approaches for Wildfire Susceptibility Mapping. Symmetry 2020, 12, 604. [Google Scholar] [CrossRef]
- Tonini, M.; D’andrea, M.; Biondi, G.; Esposti, S.D.; Trucchia, A.; Fiorucci, P. A Machine Learning-Based Approach for Wildfire Susceptibility Mapping. The Case Study of the Liguria Region in Italy. Geosciences 2020, 10, 105. [Google Scholar] [CrossRef]
- Castro, R.; Chuvieco, E. Modeling Forest Fire Danger from Geographic Information Systems. Geocarto Int. 2008, 13, 15–23. [Google Scholar] [CrossRef]
- ABARES. Forests of Australia (2018). Canberra, Australia; 2019. Available online: https://www.agriculture.gov.au/abares/forestsaustralia/forest-data-maps-and-tools/spatial-data/forest-cover (accessed on 17 October 2022).
- Palmer, W.C. Meteorological Drought; Weather Bureau: Taiwan, China, 1965; Volume 30.
- Shang, C.; Wulder, M.A.; Coops, N.C.; White, J.C.; Hermosilla, T. Spatially-Explicit Prediction of Wildfire Burn Probability Using Remotely-Sensed and Ancillary Data. Can. J. Remote. Sens. 2020, 46, 313–329. [Google Scholar] [CrossRef]
- ABARES. Catchment Scale Land Use of Australia–Update December 2020. Canberra, Australia; 2021. Available online: https://www.agriculture.gov.au/abares/aclump/catchment-scale-land-use-of-australia-update-december-2020 (accessed on 17 October 2022).
- Tang, X.; Machimura, T.; Li, J.; Yu, H.; Liu, W. Evaluating Seasonal Wildfire Susceptibility and Wildfire Threats to Local Ecosystems in the Largest Forested Area of China. Earths Future 2022, 10, e2021EF002199. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Allocca, V.; di Napoli, M.; Coda, S.; Carotenuto, F.; Calcaterra, D.; di Martire, D.; de Vita, P. A Novel Methodology for Groundwater Flooding Susceptibility Assessment through Machine Learning Techniques in a Mixed-Land Use Aquifer. Sci. Total Environ. 2021, 790, 148067. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance Evaluation of the GIS-Based Data Mining Techniques of Best-First Decision Tree, Random Forest, and Naïve Bayes Tree for Landslide Susceptibility Modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Tanyu, B.F.; Abbaspour, A.; Alimohammadlou, Y.; Tecuci, G. Landslide Susceptibility Analyses Using Random Forest, C4.5, and C5.0 with Balanced and Unbalanced Datasets. Catena 2021, 203, 105355. [Google Scholar] [CrossRef]
- Hakim, W.L.; Nur, A.S.; Rezaie, F.; Panahi, M.; Lee, C.W.; Lee, S. Convolutional Neural Network and Long Short-Term Memory Algorithms for Groundwater Potential Mapping in Anseong, South Korea. J. Hydrol. Reg. Stud. 2022, 39, 100990. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Amedu, A.; Munda, J.L. Prediction of Global Solar Irradiation Using Hybridized K-Means and Support Vector Regression Algorithms. Renew. Energy Focus 2019, 29, 78–93. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary Bat Algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Mahapatra, S.; Daniel, R.; Dey, D.N.; Nayak, S.K. Induction Motor Control Using PSO-ANFIS. In Proceedings of the Procedia Computer Science; Elsevier: Amsterdam, The Netherlands, 2015; Volume 48, pp. 753–768. [Google Scholar]
- Liu, W.; Wang, Z.; Yuan, Y.; Zeng, N.; Hone, K.; Liu, X. A Novel Sigmoid-Function-Based Adaptive Weighted Particle Swarm Optimizer. IEEE Trans. Cybern. 2021, 51, 1085–1093. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial Prediction of Groundwater Potential Mapping Based on Convolutional Neural Network (CNN) and Support Vector Regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- He, Q.; Jiang, Z.; Wang, M.; Liu, K. Landslide and Wildfire Susceptibility Assessment in Southeast Asia Using Ensemble Machine Learning Methods. Remote Sens. 2021, 13, 1572. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, M.; Liu, K. Forest Fire Susceptibility Modeling Using a Convolutional Neural Network for Yunnan Province of China. Int. J. Disaster Risk Sci. 2019, 10, 386–403. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Özener, H.; Kalantar, B.; Ueda, N.; Habibi, M.R.; Shabani, F.; Saeidi, V.; Shabani, F. Application of an Ensemble Statistical Approach in Spatial Predictions of Bushfire Probability and Risk Mapping. J. Sens. 2021, 2021, 6638241. [Google Scholar] [CrossRef]
- Gigović, L.; Pourghasemi, H.R.; Drobnjak, S.; Bai, S. Testing a New Ensemble Model Based on SVM and Random Forest in Forest Fire Susceptibility Assessment and Its Mapping in Serbia’s Tara National Park. Forests 2019, 10, 408. [Google Scholar] [CrossRef]
- Kadavi, P.; Lee, C.-W.; Lee, S. Application of Ensemble-Based Machine Learning Models to Landslide Susceptibility Mapping. Remote Sens. 2018, 10, 1252. [Google Scholar] [CrossRef]
- Park, S.J.; Lee, C.W.; Lee, S.; Lee, M.J. Landslide Susceptibility Mapping and Comparison Using Decision Tree Models: A Case Study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.M. Potential of Hybrid Evolutionary Approaches for Assessment of Geo-Hazard Landslide Susceptibility Mapping. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Barker, J.W.; Price, O.F.; Jenkins, M.E.; Barker, C.; Price, O.F.; Jenkins, M.E. Patterns of Flammability after a Sequence of Mixed-Severity Wildfire in Dry Eucalypt Forests of Southern Australia. Ecosphere 2021, 12, e03715. [Google Scholar] [CrossRef]
- Band, S.S.; Janizadeh, S.; Pal, S.C.; Saha, A.; Chakrabortty, R.; Shokri, M.; Mosavi, A. Novel Ensemble Approach of Deep Learning Neural Network (DLNN) Model and Particle Swarm Optimization (PSO) Algorithm for Prediction of Gully Erosion Susceptibility. Sensors 2020, 20, 5609. [Google Scholar] [CrossRef]
- Nolan, R.H.; Bowman, D.M.J.S.; Clarke, H.; Haynes, K.; Ooi, M.K.J.; Price, O.F.; Williamson, G.J.; Whittaker, J.; Bedward, M.; Boer, M.M.; et al. What Do the Australian Black Summer Fires Signify for the Global Fire Crisis? Fire 2021, 4, 97. [Google Scholar] [CrossRef]



| Nomenclature | |||
|---|---|---|---|
| MODIS | moderate resolution imaging spectroradiometer | H | training dataset |
| VIIRS | visible infrared imaging radiometer suite | RF | related factors |
| GIS | geographic information system | FR | frequency ratio |
| RS | remote sensing | n | number of data points or samples |
| AHP | analytical hierarchy process | yi | output values |
| ANN | artificial neural network | xi | input data |
| WOE | weight of evidence | the transpose value of weight factor | |
| SVR | support vector regression | b | bias vectors |
| GWO | grey wolf optimization | φ(x) | nonlinear function |
| PSO | particle swarm optimization | C | penalty factor |
| FIRMS | fire information for resource management system | ξi | loose variables or distance between boundary |
| RMSE | root mean square error | ξi* | targets |
| ROC | the receiver operating characteristic | ε | insensitive loss function |
| AUC | area under ROC curve | αi | Lagrange multipliers |
| NSW | New South Wales | k(x,xi) | the kernel function |
| Cfa | humid subtropical climate | particle location | |
| S-NPP | Suomi-national polar-orbiting partnership | particle velocity | |
| GPS | global positioning system | t | iteration number |
| NDVI | normalized difference vegetation index | w | inertial weight |
| DEM | digital elevation model | Pi | the best position of particle i |
| ABARES | Australian bureau of agricultural and resource economics and sciences | G | the fittest position of the entire swarm |
| PDSI | Palmer drought severity index | c1 | cognitive acceleration constant |
| ACLUMP | Australian collaborative land use management program | c2 | social acceleration coefficient |
| IGR | information gain ratio | r | random coefficients range from 0 to 1 |
| TOL | tolerance | p | predicted value |
| VIF | variance inflation factor | o | actual value |
| Category | Variable Name | Resolution | Source of Data | Ref. |
|---|---|---|---|---|
| Topographical | Altitude | 30 m | Copernicus DEM | [43] |
| Aspect | [44] | |||
| Plan curvature | [13] | |||
| Slope | [45] | |||
| Meteorological | Precipitation | 4 km | Terra climate | [46] |
| Maximum temperature | [18] | |||
| Windspeed | 50 m | Global Wind Atlas | [42] | |
| Environmental | Dist. to rivers | 50 m | ABARES | [47] |
| Drought index | 4 km | Terra climate | [48] | |
| Soil moisture | [19] | |||
| Forest type | 100 m | ABARES | [49] | |
| NDVI | 375 m | MODIS | [50] | |
| Anthropological | Land use | 50 m | ABARES | [51] |
| Dist. to recreational areas | [52] | |||
| Dist. to roads | [53] | |||
| Dist. to human settlements | [21] |
| Factor | Multicollinearity Scores | IGR | |
|---|---|---|---|
| TOL | VIF | ||
| Altitude | 0.61 | 1.65 | 0.24 |
| Aspect | 0.99 | 1.00 | 0.01 |
| Plan curvature | 0.64 | 1.55 | 0.25 |
| Slope | 0.37 | 2.72 | 0.54 |
| Precipitation | 0.74 | 1.35 | 0.17 |
| Tmax | 0.53 | 1.90 | 0.19 |
| Windspeed | 0.45 | 2.21 | 0.32 |
| Dist. to rivers | 0.87 | 1.15 | 0.04 |
| Drought index | 0.44 | 2.27 | 0.40 |
| Soil moisture | 0.31 | 3.24 | 0.34 |
| Forest type | 0.31 | 3.22 | 0.85 |
| NDVI | 0.43 | 2.34 | 0.49 |
| Land use | 0.26 | 3.86 | 0.78 |
| Dist. to recreational | 0.40 | 2.53 | 0.35 |
| Dist. to roads | 0.52 | 1.92 | 0.27 |
| Dist. to human settlements | 0.30 | 3.28 | 0.52 |
| Variable Name | Class | Total % | Event % | FR Score |
|---|---|---|---|---|
| Altitude (m) | 0–154 | 19.83 | 6.02 | 0.30 |
| 154–367 | 20.42 | 31.38 | 1.54 | |
| 367–590 | 20.22 | 33.60 | 1.66 | |
| 590–792 | 20.12 | 16.98 | 0.84 | |
| 792–1356 | 19.41 | 12.02 | 0.62 | |
| Aspect | Flat | 0.35 | 0.02 | 0.07 |
| North | 12.51 | 13.73 | 1.10 | |
| Northeast | 12.78 | 13.34 | 1.04 | |
| East | 13.89 | 13.19 | 0.95 | |
| Southeast | 12.24 | 12.02 | 0.98 | |
| South | 10.69 | 11.39 | 1.07 | |
| Southwest | 11.24 | 11.36 | 1.01 | |
| West | 13.23 | 12.06 | 0.91 | |
| Northwest | 13.08 | 12.88 | 0.98 | |
| Plan curvature | Concave | 18.66 | 27.22 | 1.46 |
| Flat | 45.59 | 27.13 | 0.60 | |
| Convex | 35.75 | 45.65 | 1.28 | |
| Slope (degree) | 0–2.22 | 17.71 | 4.05 | 0.23 |
| 2.22–4.77 | 20.99 | 8.65 | 0.41 | |
| 4.77–9.54 | 20.87 | 16.91 | 0.81 | |
| 9.54–17.18 | 20.26 | 30.54 | 1.51 | |
| 17.18–81.15 | 19.96 | 39.85 | 2.00 | |
| Precipitation (mm) | 48.19–62.76 | 19.67 | 7.84 | 0.40 |
| 62.76–69.35 | 20.64 | 21.99 | 1.07 | |
| 69.35–75.94 | 19.82 | 20.13 | 1.02 | |
| 75.94–84.27 | 20.21 | 24.08 | 1.19 | |
| 84.27–136.64 | 19.67 | 26.00 | 1.32 | |
| Tmax (°C) | 25.54–28.63 | 19.09 | 16.66 | 0.87 |
| 28.63–30.09 | 21.06 | 17.50 | 0.83 | |
| 30.09–31.19 | 22.02 | 35.12 | 1.60 | |
| 31.19–32.77 | 19.45 | 23.70 | 1.22 | |
| 32.77–35.90 | 18.38 | 7.01 | 0.38 | |
| Windspeed (m/s) | 0.54–3.65 | 20.00 | 27.43 | 1.37 |
| 3.65–4.22 | 20.00 | 22.13 | 1.11 | |
| 4.22–4.78 | 20.00 | 20.90 | 1.05 | |
| 4.78–5.45 | 20.00 | 16.83 | 0.84 | |
| 5.45–12.71 | 20.00 | 12.70 | 0.64 | |
| Distance to rivers (m) | 30–180 | 22.80 | 21.77 | 0.95 |
| 180–421 | 21.99 | 19.15 | 0.87 | |
| 421–752 | 19.03 | 15.58 | 0.82 | |
| 752–1294 | 18.91 | 18.22 | 0.96 | |
| 1294–7708 | 17.27 | 25.28 | 1.46 | |
| Drought index | −6.75–−5.75 | 19.10 | 12.20 | 0.64 |
| −5.75–−5.50 | 20.57 | 29.59 | 1.44 | |
| −5.50–−5.29 | 28.36 | 47.30 | 1.67 | |
| −5.29–−5.09 | 20.78 | 8.62 | 0.41 | |
| −5.09–−4.30 | 11.19 | 2.31 | 0.21 | |
| Soil moisture (mm) | 1.85–4.20 | 20.21 | 7.41 | 0.37 |
| 4.20–7.10 | 20.36 | 25.67 | 1.26 | |
| 7.10–10.20 | 21.96 | 41.81 | 1.90 | |
| 10.20–15.70 | 19.49 | 13.49 | 0.69 | |
| 15.70–69.40 | 17.98 | 11.62 | 0.65 | |
| Forest type | Acacia | 0.04 | 0.01 | 0.32 |
| Callitris | 0.19 | 0.05 | 0.25 | |
| Casuarina | 1.91 | 2.25 | 1.18 | |
| Eucalypt | 52.29 | 93.08 | 1.78 | |
| Mangrove | 0.02 | 0.00 | 0.00 | |
| Melaleuca | 0.07 | 0.11 | 1.67 | |
| Mixed species | 0.00 | 0.00 | 0.00 | |
| Non-forest | 38.33 | 1.01 | 0.03 | |
| Unallocated type | 0.17 | 0.13 | 0.78 | |
| Other native forests | 4.42 | 2.28 | 0.52 | |
| Rainforest | 0.93 | 0.41 | 0.45 | |
| Softwood plantation | 1.59 | 0.66 | 0.41 | |
| Hardwood plantation | 0.03 | 0.00 | 0.00 | |
| NDVI | 0–0.55 | 20.01 | 0.27 | 0.01 |
| 0.55–0.62 | 20.00 | 5.42 | 0.27 | |
| 0.62–0.69 | 20.00 | 18.38 | 0.92 | |
| 0.69–0.76 | 20.00 | 45.95 | 2.30 | |
| 0.76–0.89 | 19.99 | 29.98 | 1.50 | |
| Land use | Nature conservation | 45.31 | 91.71 | 2.02 |
| Grazing native forest | 24.85 | 6.33 | 0.25 | |
| Dryland agriculture | 17.02 | 0.44 | 0.03 | |
| Irrigated agriculture | 0.64 | 0.00 | 0.00 | |
| Intensive uses | 10.37 | 1.24 | 0.12 | |
| Open water | 1.81 | 0.28 | 0.15 | |
| Dist. to recreational areas (m) | 30–2447 | 19.83 | 8.31 | 0.42 |
| 2447–6638 | 20.72 | 14.44 | 0.70 | |
| 6638–11,473 | 20.63 | 15.47 | 0.75 | |
| 11,473–17,920 | 19.78 | 24.67 | 1.25 | |
| 17,920–41,130 | 19.05 | 37.11 | 1.95 | |
| Dist. to roads (m) | 30–150 | 25.22 | 14.35 | 0.57 |
| 150–402 | 18.99 | 14.09 | 0.74 | |
| 402–823 | 18.57 | 14.92 | 0.80 | |
| 823–1663 | 18.55 | 16.72 | 0.90 | |
| 1663–12,385 | 18.67 | 39.91 | 2.14 | |
| Dist. to human settlements (m) | 30–456 | 18.92 | 4.49 | 0.24 |
| 456–1309 | 22.00 | 9.68 | 0.44 | |
| 1309–2589 | 20.15 | 13.36 | 0.66 | |
| 2589–5319 | 19.85 | 22.28 | 1.12 | |
| 5319–21,784 | 19.08 | 50.19 | 2.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nur, A.S.; Kim, Y.J.; Lee, J.H.; Lee, C.-W. Spatial Prediction of Wildfire Susceptibility Using Hybrid Machine Learning Models Based on Support Vector Regression in Sydney, Australia. Remote Sens. 2023, 15, 760. https://doi.org/10.3390/rs15030760
Nur AS, Kim YJ, Lee JH, Lee C-W. Spatial Prediction of Wildfire Susceptibility Using Hybrid Machine Learning Models Based on Support Vector Regression in Sydney, Australia. Remote Sensing. 2023; 15(3):760. https://doi.org/10.3390/rs15030760
Chicago/Turabian StyleNur, Arip Syaripudin, Yong Je Kim, Joon Ho Lee, and Chang-Wook Lee. 2023. "Spatial Prediction of Wildfire Susceptibility Using Hybrid Machine Learning Models Based on Support Vector Regression in Sydney, Australia" Remote Sensing 15, no. 3: 760. https://doi.org/10.3390/rs15030760
APA StyleNur, A. S., Kim, Y. J., Lee, J. H., & Lee, C.-W. (2023). Spatial Prediction of Wildfire Susceptibility Using Hybrid Machine Learning Models Based on Support Vector Regression in Sydney, Australia. Remote Sensing, 15(3), 760. https://doi.org/10.3390/rs15030760