An In-Flight Alignment Method for Global Positioning System-Assisted Low Cost Strapdown Inertial Navigation System in Flight Body with Short-Endurance and High-Speed Rotation

Abstract

Alignment technology plays an important role in navigation, and is used extensively throughout military and civilian applications. However, the existing in-flight alignment methods cannot be applied to the low-cost based strap-down inertial navigation system/global positioning system integrated navigation system, used in short-endurance and high-speed rotation flight bodies, since they cannot quickly obtain alignment results to meet the accuracy requirements of a flight body with special movement characteristics of short-endurance and high-speed rotation. In this paper, in order to solve this challenging problem of alignment for flight body with short-endurance and high-speed rotation, a fast in-flight alignment method based on the Lie group is proposed. First, an in-flight alignment model based on vector observations was established by using the Lie group. Second, addressing the problem that the alignment accuracy is greatly affected by the low-cost inertial sensor bias, an improved unscented Kalman filter was constructed in the Lie group on the basis of fully considering the characteristics of the system equations to estimate and feedback the correlated errors. Finally, a trajectory simulation of high-speed flight body and field semi-physical test was carried out to evaluate the proposed method. Evaluation of the system performance in comparison with existing state-of-the-art methods indicated that the proposed in-flight alignment method has better alignment accuracy and faster alignment velocity for a low-cost strap-down inertial navigation system/global positioning system integrated navigation system.

1. Introduction

Navigation technology is fundamental to many applications, such as unmanned systems and guided projectiles, and is widely applied in civil and military domains [1,2,3]. Developing a high-precision navigation method and technique is the key to realize miniaturized, autonomous and high-precision systems. Inertial sensors based on micro-electro-mechanical-system (MEMS) are more and more widely applied in the navigation. With the continuous and rapid development of MEMS sensing technology, strap-down inertial navigation systems (SINS) have become the first choice of navigation equipment due to advantages of good autonomous performance, small size and low cost [4]. At the present stage, the accuracy of existing MEMS-based low-cost SINS is comparatively low due to the accumulation of the accelerometer and gyroscope bias over time. SINS is often combined with other navigation systems to reduce the impact of this deficiency on navigation accuracy, and the global positioning system (GPS) is one of the most commonly used navigation systems to aid SINS. SINS/GPS integrated navigation system with GPS-assisted SINS is also one of the most widely used navigation systems. An integrated navigation system composed of SINS and GPS not only has great advantages, but also avoids disadvantages effectively. The initial alignment of SINS assisted by GPS is a key problem in navigation [5,6,7]. Determination of the initial state is the premise and foundation for the system to enter the navigation working state, and good initial alignment is key for the navigation system to achieve subsequent high-precision navigation parameter measurements [8,9,10,11]. In most practical applications, the alignment of the carrier often needs to be completed during movement, and the system model is often nonlinear. Therefore, it is of significance to study the initial alignment during movement.

The initial alignment of the air vehicle during flight is termed in-flight alignment (IFA). For the IFA problem of SINS assisted by GPS, the existing IFA methods can be divided into two categories: the deterministic method and the state estimation filter method. The deterministic method is mainly the optimization-based alignment (OBA) method [12]. According to the chain rule of attitude matrix decomposition, this method decomposes the real-time attitude matrix of the system into three sections, this decomposition being conducive to the solution. In the above three parts, one initial constant matrix estimated is the target attitude matrix for the alignment, as well as two time-varying matrices which are the easily solvable attitude change matrix of the body coordinate system and the navigation coordinate system, respectively [13,14]. Based on the principle of multi-vector attitude determination, the target matrix can be calculated by constructing the vector observations at different times from the latter two time-varying matrices [9,15,16,17]. The OBA method is a good alignment method for SINS with high precision inertial sensors, which can construct the attitude determination vectors to meet the accuracy requirement, and obtain a satisfactory alignment result. However, this kind of methods is not suitable for low-cost SINS consisting of moderate or low accuracy MEMS sensors because of the large device bias generated when constructing the observation vector, which seriously degrades the alignment accuracy. Another popular IFA method is the state estimation filtering method that directly estimates the objective attitude by establishing the state model of system and corresponding filter [9,18,19,20,21]. This type of method can obtain better alignment accuracy with an accurate system model and sufficient alignment time due to the consideration of sensor bias. Many alignment algorithms based on nonlinear filtering have been proposed for nonlinear error models, among which the extended Kalman filter (EKF) is the most commonly used [10,22,23,24]. However, in this kind of method, truncation errors of a high-order terms are caused by approximating nonlinearity through linear expansion, and a complicated Jacobian matrix needs to be calculated. This results in long alignment time and poor alignment accuracy, or even divergence for strongly nonlinear systems.

In addition, the traditional Euler angle or quaternion are generally adopted to describe rotation in the above methods. Unfortunately, there is a singular point problem in the Euler angle describing rotation. Using quaternion to describe rotation can avoid this singular problem but it also has a non-uniqueness problem; that is, the same rotation corresponds to two sets of quaternion, which will not only lead to longer computation time, but also may cause system divergence. It is widely known that alignment precision and alignment time are the important evaluation indexes of IFA. For some flight bodies with short flight time and rapid self-rotation, such as guided munitions, the requirements for alignment time are more stringent under the premise of ensuring alignment accuracy. Alignment methods with lengthy alignment process are obviously not suitable for such flying vehicles. Therefore, it is a challenging problem to achieve fast and accurate IFA in a special motion state of high spin and short flight time.

In recent years, rigid body rotation group theory has been successfully applied to the navigation field thanks to the gradual maturity of group theory [25,26,27,28]. The method based on the Lie group to describe the rotation of a space rigid body can avoid the singularity and ambiguity problems, and has the advantages of clear physical meaning, being complete and concise. This method has been applied in areas such as satellite and unmanned air vehicle navigation, and the feasibility and simplicity have been verified in navigation [29,30,31,32]. In this paper, an IFA method for low-cost SINS/GPS integrated navigation, which can be applied to short-endurance and high-speed rotation flight bodies, based on the Lie group is proposed. First, a multi-vector attitude determination alignment model was derived using the Li group description. Next, the errors of the OBA method based on multi-vector attitude determination were analyzed. Finally, on the basis of error analysis and according to the characteristics of the constructed system model, a simplified unscented Kalman filter (UKF) was designed on the Lie group to estimate and feedback the correlative errors and sensor bias to improve alignment accuracy. Compared with current research, the main contributions of our study can be summed up as: (1) a multi-vector alignment model was established for IFA problem based on Lie group, which can not only avoid the singularity and ambiguity, but also shorten the time of alignment and improve the alignment stability; (2) according to the constructed system model, a simplified UKF based on Lie group was designed to estimate and correct the correlative errors and the bias of low cost inertial sensors, thereby improving the alignment accuracy; (3) the proposed alignment method, for low-cost SINS, was demonstrated with good alignment performance through ground vehicle experiments.

The remaining part of this paper is arranged as follows. Section 2 describes the construction of the multi-vector alignment model based on the Lie group. Section 3 discusses the design of improved UKF based on the Lie group and shows a flow chart of the proposed IFA method. Section 4 presents simulation and experimental testing and the results of simulation and semi-physical experiment to show the validity, alignment accuracy and alignment time of the proposed IFA method. Finally, conclusions and future research focus are given in Section 5.

2. Construction of Multi-Vector Alignment Model on Lie Group

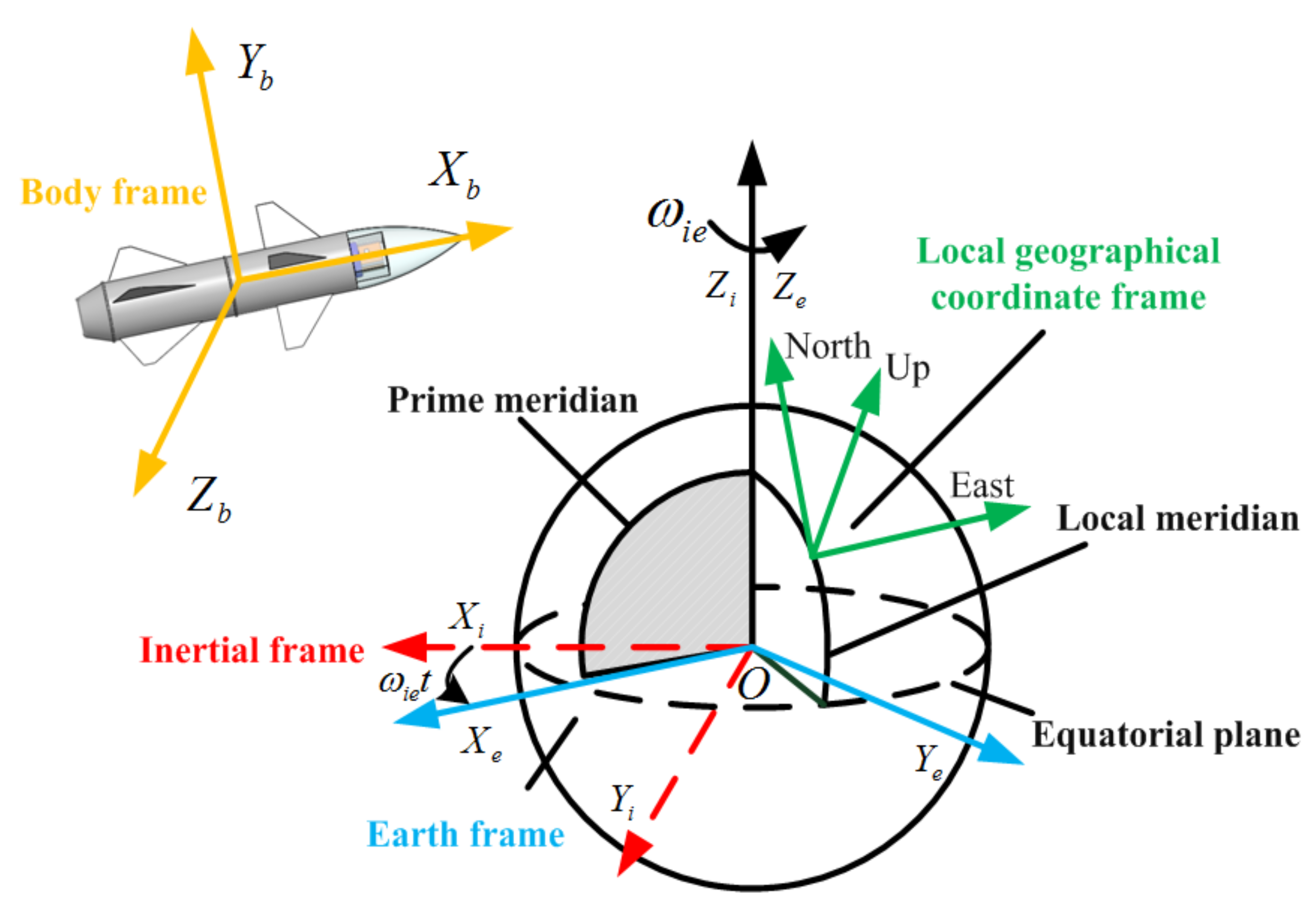
2.1. Mathematical Description of the Lie Group

A Lie group is a group with a continuous character, is a smooth differentiable manifold with a group structure, and the operation on the group is smooth. The Lie group satisfies the group operation and reversibility. The description of the Lie group and the orientation-space of the carrier correspond one by one, which avoids non uniqueness and singularity, and has explicit physical meaning and a concise expression [25,28].

The special orthogonal group $SO\left(3\right)$, an effective set of rotation matrices, is a special matrix Lie group. In essence, it is a group composed of a series of third-order square matrices in which the elements form a differentiable manifold. Therefore, the special orthogonal group $SO\left(3\right)$ can well describe the rotation of space and can be defined as follows:

$$SO\left(3\right)=\left\{\mathit{R}\in {ℝ}^{3\times 3}\left|\mathit{R}{\mathit{R}}^{\mathrm{T}}=\mathit{I},\det \left(\mathit{R}\right)=1\right.\right\},$$

(1)

where $ℝ$ represents the real number domain and $\det \left(\cdot \right)$ represents operation of matrix determinant. Orthogonality condition $\mathit{R}{\mathit{R}}^{\mathrm{T}}=\mathit{I}$ imposes six constraints on the matrix with nine components, making the degree of freedom of the matrix become three. For any attitude, it can correspond to a specific matrix $\mathit{R}\in SO\left(3\right)$. Therefore, in navigation and positioning, matrix Lie group $SO\left(3\right)$ can be introduced to denote the attitude information of carrier.

Each Lie group corresponds to a corresponding Lie algebra. The vector space of Lie algebra is a tangent space, which completely characterizes the local properties of the Lie group. The Lie algebra associated with $SO\left(3\right)$ is given by the following definition [30]:

$$so\left(3\right)=\left\{\mathit{\Phi }=({\mathit{\varphi }}^{\wedge })=(\mathit{\varphi }\times )\in {ℝ}^{3\times 3}\left|\mathit{\varphi }\in {ℝ}^3\right.\right\},$$

(2)

where $({\cdot }^{\wedge })$ represents a linear operation that maps that $\mathit{\varphi }\in {ℝ}^3$ to the $so\left(3\right)$; $(\cdot \times )$ denotes the skew-symmetric matrix operation and $(\mathit{\varphi }\times )=\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ {\varphi }_3& 0& -\varphi \\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]$ is the skew-symmetric matrix of the real matrix $\mathit{\varphi }=\left[\begin{array}{ccc}{\varphi }_1& {\varphi }_2& {\varphi }_3\end{array}\right]\in {ℝ}^3$. That is, the elements of the Lie algebra $so\left(3\right)$ corresponding to the rotation matrix special orthogonal group $SO\left(3\right)$ is a three-dimensional vector (three-dimensional antisymmetric matrix) of the real number field.

For the rotation, $SO\left(3\right)$ can be associated with $so\left(3\right)$ by matrix exponential map exp: $so\left(3\right)$ → $SO\left(3\right)$, as shown below:

$$\mathit{R}=\exp \left(\mathit{\varphi }\times \right)={\displaystyle \sum _{n=0}^{\infty }\frac{1}{n!}}{\left(\mathit{\varphi }\times \right)}^n,$$

(3)

where $\mathit{R}\in SO(3)$, $\mathit{\varphi }\in {ℝ}^3$, so $\left(\mathit{\varphi }\times \right)\in so(3)$.

Defining the module length and direction of three-dimensional vector $\mathit{\varphi }$ as $\varphi$ and $\mathit{p}$, respectively, $\mathit{\varphi }=\varphi \mathit{p}$. $\mathit{p}=\frac{\mathit{\varphi }}{\varphi }$ is the unit vector consistent with the direction of $\mathit{\varphi }$, and $‖\mathit{p}‖=1$. Furthermore, $\mathit{p}$ has the following characteristics:

$${\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }=\left[\begin{array}{ccc}-p_2^2-p_3^2& p_1{p}_2& p_1{p}_3\\ p_1{p}_2& -p_1^2-p_3^2& p_2{p}_3\\ p_1{p}_3& p_2{p}_3& -p_1^2-p_2^2\end{array}\right]=\mathit{p}{\mathit{p}}^{\mathrm{T}}-\mathit{I},$$

(4)

$${\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }={\mathit{p}}^{\wedge }(\mathit{p}{\mathit{p}}^{\mathrm{T}}-\mathit{I})=-{\mathit{p}}^{\wedge },$$

(5)

Combining (4) and (5), the exponential map (3) can be further deduced as:

$$\begin{array}{cc}\hfill & exp\left({\mathit{\varphi }}^{\wedge }\right)=exp\left(\varphi {\mathit{p}}^{\wedge }\right)={\displaystyle \sum _{n=0}^{\infty }}\frac{1}{n!}{\left(\varphi {\mathit{p}}^{\wedge }\right)}^n\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em} =\underset{p{p}^{\mathrm{T}}-p^{\wedge }{p}^{\wedge }}{\underbrace{\mathit{I}}}+\varphi {\mathit{p}}^{\wedge }+\frac{1}{2!}{\varphi }^2{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }+\frac{1}{3!}{\varphi }^3\underset{-p^{\wedge }}{\underbrace{{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }}}+\frac{1}{4!}{\varphi }^4\underset{-p^{\wedge }{p}^{\wedge }}{\underbrace{{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }}}+\cdots \hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em} =\mathit{p}{\mathit{p}}^{\mathrm{T}}-{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }+\varphi {\mathit{p}}^{\wedge }+\frac{1}{2!}{\varphi }^2{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }-\frac{1}{3!}{\varphi }^3{\mathit{p}}^{\wedge }-\frac{1}{4!}{\varphi }^4{\left({\mathit{p}}^{\wedge }\right)}^2+\cdots \hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em} =\mathit{p}{\mathit{p}}^{\mathrm{T}}+\underset{sin\varphi }{\underbrace{\left(\varphi -\frac{1}{3!}{\varphi }^3+\frac{1}{5!}{\varphi }^5-\cdots \right)}}{\mathit{p}}^{\wedge }-\underset{cos\varphi }{\underbrace{\left(1-\frac{1}{2!}{\varphi }^2+\frac{1}{4!}{\varphi }^4-\cdots \right)}}\underset{p{p}^{\mathrm{T}}-I}{\underbrace{{\mathit{p}}^{\wedge }{\mathit{p}}^{\wedge }}}\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em} =cos\varphi \mathit{I}+(1-cos\varphi )\mathit{p}{\mathit{p}}^{\mathrm{T}}+sin\varphi {\mathit{p}}^{\wedge }\hfill \end{array},$$

(6)

That is:

$$\mathit{R}=\cos \varphi \mathit{I}+(1-\cos \varphi )\mathit{p}{\mathit{p}}^{\mathrm{T}}+\sin \varphi {\mathit{p}}^{\wedge },$$

(7)

Correspondingly, the elements in $SO(3)$ can also be mapped to $so(3)$ through logarithmic mapping, namely:

$$\mathit{\varphi }=\log {(\mathit{R})}^{\vee }={\left({\displaystyle \sum _{n=0}^{\infty }\frac{{(-1)}^n}{n+1}}{(\mathit{R}-\mathit{I})}^{n+1}\right)}^{\vee },$$

(8)

Figure 1 visually describes the mathematical conversion relations among the vectors in Euclidean space, the Lie algebra $so(3)$ in tangent space, and the Lie group $SO(3)$ in manifold space.

The difference between the two rotations ${\mathit{R}}_1,{\mathit{R}}_2\in SO(3)$ can be defined by the following formula [26,27]:

$$d\left({\mathit{R}}_1,{\mathit{R}}_2\right)=‖\log \left({\mathit{R}}_1^{\mathrm{T}},{\mathit{R}}_2\right)‖,$$

(9)

where $‖\cdot ‖$ denotes the Frobenius matrix norm and $\log \left({\mathit{R}}_1^{\mathrm{T}},{\mathit{R}}_2\right)\in so(3)$. According to this definition, rotation $\mathit{R}\left(t\right)$ on $SO\left(3\right)$ at time t can be given by $\mathit{R}\left(t\right)=\exp \left[\left(\log \left({\mathit{R}}^{\mathrm{T}}(0)\mathit{R}(1)\right)\right)\cdot t\right]$.

2.2. Alignment Principle of Multi-Vector Attitude Determination on Lie Group

In the GPS-assisted SINS alignment method, exact initial values of velocity and position can be easily obtained, so obtaining accurate initial attitude values is the core problem in alignment, and it is also the pivot of our research in this paper. To describe the alignment model more clearly and concisely, defining relevant coordinates are shown in Figure 2, where b frame—body frame—selected as SINS coordinate frame fixed on the carrier; n frame—navigation frame—selected as local geographical coordinate frame with east-north-up axes, and e frame—earth frame- is fixed with the earth. The inertial body frame denoted by ib is in accordance with the b frame at the initial moment, and the inertial navigation frame represented by in coincides with the n frame at the initial time. In the inertial frame represented by i frame, the two coordinate systems ib frame and in frame are stationary.

The purpose of the alignment discussed is to obtain the attitude transfer matrix between the n frame and b frame at the initial time. The time-varying attitude matrix on $SO\left(3\right)$ based on matrix decomposition can be written as [30,32,33,34]:

$${\mathit{R}}_n^b\left(t\right)={\mathit{R}}_{n\left(t\right)}^{b\left(t\right)}={\mathit{R}}_{ib}^{b\left(t\right)}{\mathit{R}}_{in}^{ib}{\mathit{R}}_{n\left(t\right)}^{in},$$

(10)

where b(t) and n(t) respectively represent b frame and n frame at time t, ${\mathit{R}}_{in}^{ib}$ denotes the constant attitude matrix from in frame to ib frame, which is equal to the attitude transfer matrix between b frame and n frame at the beginning of alignment, ${\mathit{R}}_{in}^{n\left(t\right)}$ is the real-time attitude matrix from current n frame to in frame, and ${\mathit{R}}_{ib}^{b\left(t\right)}$ is the real-time attitude matrix from ib frame to current b frame, which describes the attitude change of the b frame during alignment. ${\mathit{R}}_{ib}^{b\left(t\right)}$ can be obtained by attitude tracking from gyroscope output because SINS is fixed to the carrier:

$${\dot{\mathit{R}}}_{ib}^{b\left(t\right)}=-\left({\mathit{\omega }}_{ib}^b\times \right){\mathit{R}}_{ib}^{b\left(t\right)},$$

(11)

where ${\mathit{\omega }}_{ib}^b$ is the angular rate measured by gyroscope, $\left({\mathit{\omega }}_{ib}^b\times \right)$ is the skew symmetric matrix of ${\mathit{\omega }}_{ib}^b$.

$R_{in}^{n\left(t\right)}$ describes the attitude change of the n frame in the alignment process, which can be calculated according to the real-time location of carrier and the alignment time [35,36]:

$${\mathit{R}}_{n\left(t\right)}^{in}=\left[\begin{array}{ccc}\cos \delta \lambda & -\sin L(t)\sin \delta \lambda & -\cos L(t)\sin \delta \lambda \\ \sin L_{in}\sin \delta \lambda & \cos L_{in}\cos L(t)+\sin L_{in}\sin L(t)\cos \delta \lambda & \cos L_{in}\sin L(t)-\sin L_{in}\cos L(t)\cos \delta \lambda \\ -\cos L_{in}\sin \delta \lambda & \sin L_{in}\cos L(t)-\cos L_{in}\sin L(t)\cos \delta \lambda & \sin L_{in}\sin L(t)+\cos L_{in}\cos L(t)\cos \delta \lambda \end{array}\right],$$

(12)

where $L_{in}$, ${\lambda }_{in}$, $L\left(t\right)$ and $\lambda \left(t\right)$ are the latitude and longitude of the carrier at the start time and t time, respectively, which can be directly provided by GPS; $\delta \lambda =\lambda (t)-{\lambda }_{in}+{\omega }_{ie}t$ is the longitude variation of the carrier during alignment, and the earth rotation rate ${\omega }_{ie}$ is constant.

From the above analysis, it can be seen that the constant matrix ${\mathit{R}}_{in}^{ib}$ is the only unknown term in the right of equal-sign crease of (10). Therefore, the alignment problem can be converted to the problem of solving $R_{in}^{ib}$. The existing alignment method for constant attitude matrix ${\mathit{R}}_{in}^{ib}$ is the optimization-based alignment method, which constructs multiple groups of non-coplanar vector pairs at different times in ib frame and in frame respectively, and the optimal solution is achieved by constructing the relevant cost function and adopting the optimal estimation method.

The specific force equation is the basis for constructing vector pair, the specific force equation of SINS in in frame can be written as [37,38]:

$${\dot{\mathit{v}}}^n={\mathit{R}}_{in}^{n\left(t\right)}{\mathit{R}}_{ib}^{in}{\mathit{R}}_{b\left(t\right)}^{ib}{\mathit{f}}^b-\left(2{\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n\right)\times {\mathit{v}}^n+{\mathit{g}}^n,$$

(13)

The above formula can be rewritten as:

$${\mathit{R}}_{ib}^{in}\left[{\mathit{R}}_{n\left(t\right)}^{in}\left({\dot{\mathit{v}}}^n+\left(2{\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n\right)\times {\mathit{v}}^n-{\mathit{g}}^n\right)\right]={\mathit{R}}_{b\left(t\right)}^{ib}{\mathit{f}}^b,$$

(14)

To avoid the effect of differential errors and improve anti-interference ability, the vector pair is constructed by integrating (9) twice [36,39]:

$${\mathit{R}}_{in}^{ib}{\mathit{V}}_k^{in}={\mathit{V}}_k^{ib},$$

(15)

where

$$\begin{array}{c}\left\{\begin{array}{c}{\mathit{V}}_k^{in}={\int }_0^t{\mathit{R}}_{n\left(t\right)}^{in}{\mathit{v}}^{n}dt-t{\mathit{v}}^n\left(0\right)+{\int }_0^t{\int }_0^{\tau }{\mathit{R}}_{n\left(t\right)}^{in}\left(2{\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n\right)\times {\mathit{v}}^{n}dtd\mathit{\tau }-{\int }_0^t{\int }_0^{\tau }{\mathit{R}}_{n\left(t\right)}^{in}{\mathit{g}}^{n}dtd\mathit{\tau }\\ {\mathit{V}}_k^{ib}={\int }_0^t{\int }_0^{\tau }{\mathit{R}}_{b\left(t\right)}^{ib}{\mathit{f}}^{b}dtd\mathit{\tau }\hfill \end{array}\right.,\hfill \end{array}$$

(16)

${\mathit{V}}_k^{in}$ and ${\mathit{V}}_k^{ib}$ denote the attitude determination vectors in ib frame and in frame respectively, which is called the vector pair. Multiple vector pairs can be obtained over time through (16). The objective matrix ${\mathit{R}}_{in}^{ib}$ satisfying the relationship as in (15) can be computed by the optimal estimating method. The optimal value of ${\mathit{R}}_{in}^{ib}$ is typically estimated by minimizing the following loss function (this can be considered as a classical Wahba’s Problem [40,41]):

$$\mathit{J}\left({\mathit{R}}_{in}^{ib}\right)=\frac{1}{2}{\displaystyle \sum _{k=1}^{\mathrm{K}}{w}_k{‖{\mathit{V}}_k^{ib}-{\mathit{R}}_{in}^{ib}{\mathit{V}}_k^{in}‖}^2},\begin{array}{c}\end{array}k=1,2,\cdots ,\mathrm{K},$$

(17)

where K is the number of vector pairs, $w_k$ denote positive weight and ${\displaystyle \sum _{k=1}^{\mathrm{K}}{w}_k}=1$.

Many mathematical methods based on quaternion or attitude matrix have been proposed to solve this optimal estimation problem. In this paper, the singular value decomposition optimization way is adopted, which is effective and intuitive and has excellent numerical stability.

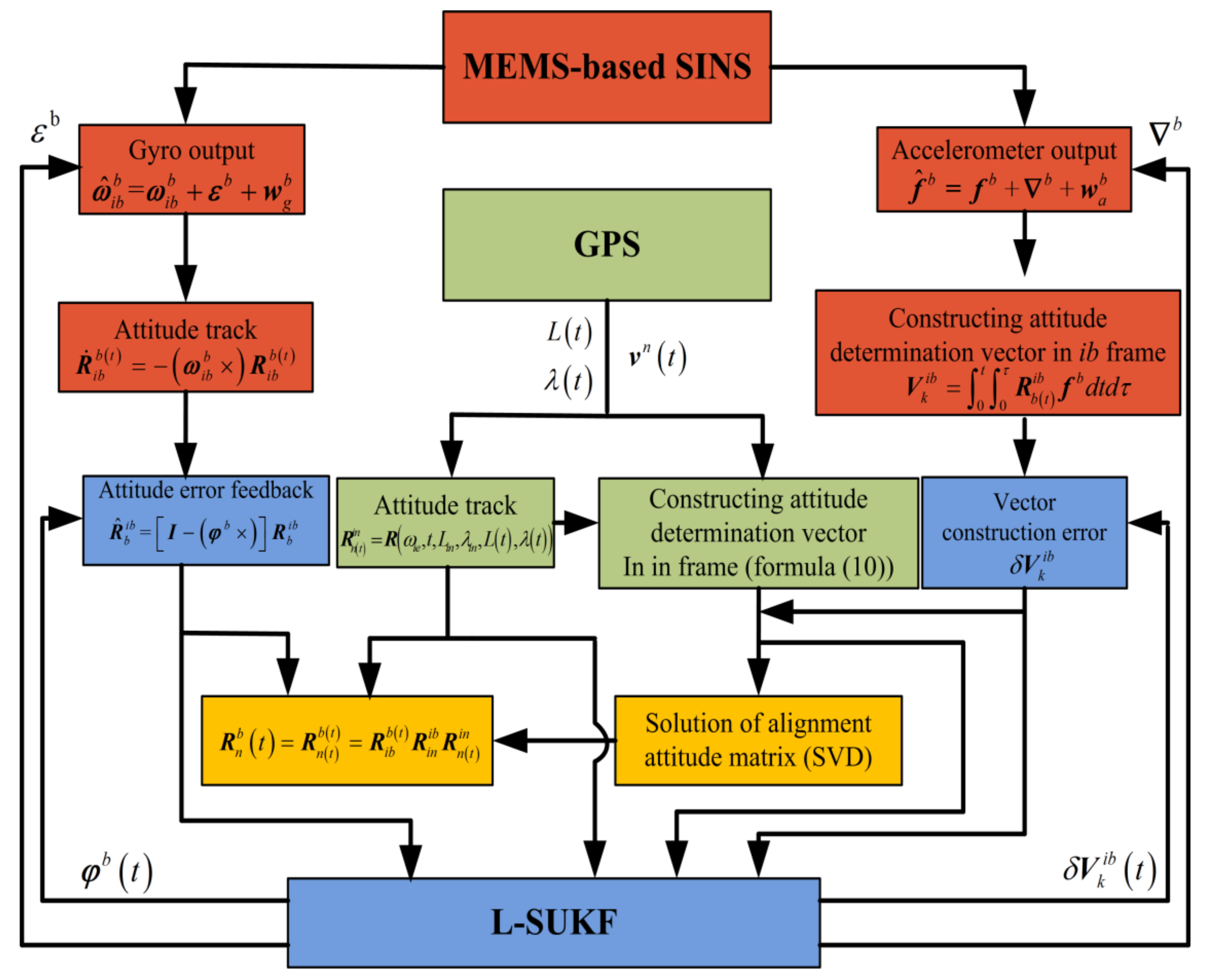
3. Improved UKF Based on Lie Group

The above method is perfect under ideal conditions. However, for inertial sensors, especially low-cost inertial devices, the device bias and measurement error cannot be ignored. Sensor error and integral error make the constructed attitude determination vector inaccurate, which causes great alignment error. In addition, the OBA method cannot estimate the real-time zero drift of the inertial sensors, and does not have the ability to estimate and correct the device bias.

In this section, aiming at dealing with the above-mentioned shortcoming, a simplified UKF based on the Lie group is described to estimate and correct the correlative error and sensor deviation during alignment in real time.

3.1. Error Analysis

For the ${\mathit{R}}_{ib}^{b\left(t\right)}$, it can be seen from (3) that the attitude matrix can be tracked by the gyroscope output. Considering the actual gyroscope bias and measurement error [42]:

$${\stackrel{\wedge }{\mathit{\omega }}}_{ib}^b={\mathit{\omega }}_{ib}^b+{\mathit{\epsilon }}^b+{\mathit{w}}_g^b,$$

(18)

Equation (6) can be rewritten as:

$$\left\{\begin{array}{c}{\stackrel{\wedge }{\mathit{R}}}_b^{ib}=\left[\mathit{I}-\left({\mathit{\phi }}^b\times \right)\right]{\mathit{R}}_b^{ib}\\ {\dot{\mathit{\phi }}}^b=-{\stackrel{\wedge }{\mathit{R}}}_b^{ib}\left({\mathit{\epsilon }}^b+{\mathit{w}}_g^b\right)\end{array}\right.,$$

(19)

For ${\mathit{\phi }}^b$, its equation in (19) is rewritten into discrete iterative form on $SO\left(3\right)$:

$${\mathit{\phi }}_k^b=-{\stackrel{\wedge }{\mathit{R}}}_{b,k-1}^{ib}\left({\mathit{\epsilon }}_{k-1}^b+{\mathit{w}}_{g,k-1}^b\right)\exp \left[\left({\mathit{\omega }}_{ib,k-1}^b-{\mathit{\epsilon }}_{k-1}^b-{\mathit{w}}_{g,k-1}^b\right)\mathrm{d}t\right],$$

(20)

where ${\stackrel{\wedge }{\mathit{\omega }}}_{ib}^b$ and ${\mathit{\omega }}_{ib}^b$ denote the theoretical and actual measurement values of the gyroscope respectively, ${\mathit{\phi }}^b$ is the tracking error of attitude matrix ${\mathit{R}}_{ib}^{b\left(t\right)}$, ${\mathit{\epsilon }}^b$ is the gyro constant bias, and ${\mathit{w}}_g^b$ denotes the gyro measurement noise, which can be assumed to be Gaussian white noise with zero mean. Therefore, it can be seen from the above analysis that the error of ${\mathit{R}}_{ib}^{b\left(t\right)}$ mainly comes from the gyro bias and measurement error.

For ${\mathit{R}}_{in}^{n\left(t\right)}$, the attitude matrix ${\mathit{R}}_{in}^{n\left(t\right)}$ can be directly calculated by (12), and it can be seen that the main error comes from the longitude and latitude error of GPS measurement. In fact, the error of ${\mathit{R}}_{in}^{n\left(t\right)}$ caused by this part of error is far less than the requirement of alignment accuracy. Therefore, the calculation error of ${\mathit{R}}_{in}^{n\left(t\right)}$ can be ignored.

For ${\mathit{V}}_k^{ib}$, taking into account the accelerometer bias and measurement error, the error $\delta {\mathit{V}}_k^{ib}$ between actual measurement ${\stackrel{\wedge }{\mathit{V}}}_k^{ib}$ and theoretical value ${\mathit{V}}_k^{ib}$ can be calculated by the following [14]:

$$\left\{\begin{array}{c}{\stackrel{\wedge }{\mathit{V}}}_k^{ib}={\mathit{V}}_k^{ib}+\delta {\mathit{V}}_k^{ib}\hfill \\ \delta {\dot{\mathit{V}}}_k^{ib}={\mathit{f}}^b\times {\mathit{\phi }}^b+{\stackrel{\wedge }{\mathit{R}}}_b^{ib}{\mathbf{\nabla }}^b+{\stackrel{\wedge }{\mathit{R}}}_b^{ib}{\mathit{w}}_a^b\end{array}\right.,$$

(21)

where ${\mathbf{\nabla }}^b$ denotes the bias of accelerometer, and ${\mathit{w}}_a^b$ is the measurement noise of accelerometer. It can be seen from (21) that the error of ${\mathit{V}}_k^{ib}$ mainly comes from the bias and measurement error of the accelerometer, and the calculation error of ${\stackrel{\wedge }{\mathit{R}}}_b^{ib}$.

For ${\mathit{V}}_k^{in}$, according to Equation (16), this can be directly computed by ${\mathit{R}}_{n\left(t\right)}^{in}$ and the position and velocity output of GPS. The error generated in this process is mainly caused by GPS measurement error, so the error of ${\mathit{V}}_k^{in}$ can be expressed directly as [36]:

$$\delta {\mathit{V}}_k^{in}=w_G^n,$$

(22)

where $w_G^n$ denotes the measurement noise of GPS.

3.2. Improved UKF Modeling on Lie Group

According to the above error analysis, the observation vector error $\delta {\mathit{V}}_k^{ib}$ in the b frame, the attitude tracking error ${\mathit{\phi }}^b$ of the b frame, the gyroscope bias ${\mathit{\epsilon }}^b$ and the accelerometer bias ${\mathbf{\nabla }}^b$ are selected as state variables:

$$\mathit{X}={\left[\begin{array}{cccc}\delta {\mathit{V}}_k^{ib}& {\phi }^b& {\mathit{\epsilon }}^b& {\mathit{\nabla }}^b\end{array}\right]}^{\mathrm{T}},$$

(23)

For the sake of convenience, the state variable at time k is set as ${\mathit{X}}_k:=\left[\begin{array}{c}{\mathit{\phi }}_k^b\end{array}\begin{array}{c},\end{array}\begin{array}{c}{\mathit{B}}_k\end{array}\right]$, where ${\mathit{B}}_k=\left[\begin{array}{c}\delta {\mathit{V}}_k^{ib}\end{array}\begin{array}{c},\end{array}\begin{array}{c}{\mathit{\epsilon }}_k^b\end{array}\begin{array}{c},\end{array}\begin{array}{c}{\mathit{\nabla }}_k^b\end{array}\right]$. In manifold space, the incremental description of the attitude tracking error matrix ${\mathit{\phi }}^b\in SO(3)$ needs to use exponential mapping because it is not closed for addition while the vector $\delta {\mathit{V}}_k^{ib}$, ${\mathit{\epsilon }}^b$ and ${\mathit{\nabla }}^b$ are closed for addition.

According to the differential Equations (11), (13), (19) and (21), the state equation of alignment filter model is:

$${\left[\begin{array}{cccc}\delta {\dot{\mathit{V}}}_k^{ib}& {\dot{\mathit{\phi }}}^b& {\dot{\mathit{\epsilon }}}^b& {\dot{\mathit{\nabla }}}^b\end{array}\right]}^{\mathrm{T}}=\left[\begin{array}{cccc}\mathbf{0}& {\stackrel{\wedge }{\mathit{f}}}^b\times & \mathbf{0}& {\stackrel{\wedge }{\mathbf{R}}}_b^{ib}\\ \mathbf{0}& \mathbf{0}& -{\stackrel{\wedge }{\mathbf{R}}}_b^{ib}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\delta {\mathit{V}}_k^{ib}\\ {\mathit{\phi }}^b\\ {\mathit{\epsilon }}^b\\ {\mathit{\nabla }}^b\end{array}\right]+\left[\begin{array}{cc}0& {\stackrel{\wedge }{\mathit{R}}}_b^{ib}\\ -{\stackrel{\wedge }{\mathit{R}}}_b^{ib}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}{\mathit{w}}_g^b\\ {\mathit{w}}_a^b\end{array}\right],$$

(24)

Considering the errors and rewriting (15) to:

$${\mathit{R}}_{in}^{ib}\left({\stackrel{\wedge }{\mathit{V}}}_k^{in}-\delta {\mathit{V}}_k^{in}\right)={\stackrel{\wedge }{\mathit{V}}}_k^{ib}-\delta {\mathit{V}}_k^{ib},$$

(25)

Therefore, the measured equation of the system can be obtained:

$${\stackrel{\wedge }{\mathit{V}}}_k^{ib}-{\mathit{R}}_{in}^{ib}{\stackrel{\wedge }{\mathit{V}}}_k^{in}=\delta {\mathit{V}}_k^{ib}-{\mathit{R}}_{in}^{ib}{w}_G^n,$$

(26)

The above system state equation and measurement equation can be discretized into the following form:

$$\left\{\begin{array}{c}{\mathit{X}}_k:=\left[{\mathit{\phi }}_k^b,{\mathit{B}}_k\right]=\mathit{f}\left({\mathit{X}}_{k-1}\right)+\mathit{j}\left({\mathit{X}}_{k-1}\right){\mathit{W}}_{k-1}=\mathit{f}\left({\mathit{\phi }}_{k-1}^b,\begin{array}{c}{\mathit{B}}_{k-1}\end{array}\right)+\mathit{j}\left({\mathit{\phi }}_{k-1}^b,{\mathit{B}}_{k-1}\right){\mathit{W}}_{k-1}\\ {\mathit{Z}}_k={\mathit{H}}_k{\mathit{X}}_k+{\mathit{M}}_k\end{array}\right.,$$

(27)

It can be seen that system model has the characteristic of nonlinear state equation and linear measurement equation. According to the characteristics of this system model, we designed a simplified UKF on the Lie group for correlative error estimation and correction.

1)

Initialization

Sigma sample points and their weights are calculated according to the sampling strategy. Set ${\stackrel{\wedge }{\mathit{X}}}_0=\left[\begin{array}{c}{\stackrel{\wedge }{\mathit{\phi }}}_0^b\end{array}\begin{array}{c},\end{array}\begin{array}{c}{\stackrel{\wedge }{\mathit{B}}}_0\end{array}\right]$ as the initial state and the initial value of the filter is defined:

$${\stackrel{\wedge }{\mathit{x}}}_0=E\left[{\mathit{x}}_0\right],{\mathit{P}}_0=E\left[({\mathit{x}}_0-{\stackrel{\wedge }{\mathit{x}}}_0)\cdot {({\mathit{x}}_0-{\stackrel{\wedge }{\mathit{x}}}_0)}^{\mathrm{T}}\right],$$

(28)

2)

Time Update

The sigma sampling points are used to calculate the one-step state model value of system through the state equation:

$${\mathit{\chi }}_{i,k|k-1}:=\left[{\mathit{\chi }}_{\phi ,k|k-1}^{\left(i\right)}\begin{array}{c},\begin{array}{c}{\mathit{\chi }}_{B,k|k-1}^{\left(i\right)}\end{array}\end{array}\right]=\mathit{f}\left({\mathit{\chi }}_{i,k-1}\right)=\mathit{f}\left({\mathit{\chi }}_{\phi ,k-1}^{\left(i\right)}\begin{array}{c},\begin{array}{c}{\mathit{\chi }}_{B,k-1}^{\left(i\right)}\end{array}\end{array}\right),$$

(29)

(a)

Predicting the model value at k + 1 time:

$${\stackrel{\wedge }{\mathit{x}}}_{k|k-1}:=\left[{\stackrel{\wedge }{\mathit{\phi }}}_{k|k-1}^b{\stackrel{\wedge }{\mathit{B}}}_{k|k-1}\right],$$

(30)

For ${\stackrel{\wedge }{\mathit{\phi }}}_{k|k-1}^b$, it can be calculated by Algorithm 1.

Algorithm 1: Calculation of ${\stackrel{\wedge }{\mathit{\phi }}}_{k|k-1}^b$ on $SO(3)$.

Input: Set of rotations $\left\{{\mathit{Z}}_0,\dots ,{\mathit{Z}}_{12}\right\}$ in $SO(3)$

1.$\mathit{H}\leftarrow {\mathit{Z}}_0$

2.$\mathit{\Omega }\leftarrow {\displaystyle {\sum }_{i=0}^{12}{W}_m^{(i)}\log \left({\mathit{Z}}_i{\mathit{H}}^{-1}\right)}$

3.$\mathit{H}\leftarrow \exp \left(\mathit{\Omega }\right)\mathit{H}$

4. return $\mathit{H}$

${\stackrel{\wedge }{\mathit{B}}}_{k|k-1}$ can be obtained by:

$${\stackrel{\wedge }{\mathit{B}}}_{k|k-1}={\displaystyle \sum _{i=0}^{L+1}{W}_m^{\left(i\right)}{\mathit{\chi }}_{B,k|k-1}^{\left(i\right)}},$$

(31)

(b)

Calculating the covariance matrix

Setting vector:

$$\left[{\mathit{\eta }}_i^{\left(a\right)}\right]:=\log \left({\mathit{\chi }}_{\phi ,k|k-1}^{\left(i\right)}\cdot \mathrm{inv}\left({\stackrel{\wedge }{\mathit{\phi }}}_{k|k-1}^b\right)\right),$$

(32)

$$\left[{\mathit{\eta }}_i^{\left(b\right)}\right]:={\mathit{\chi }}_{B,k|k-1}^{\left(i\right)}-{\stackrel{\wedge }{\mathit{B}}}_{k|k-1},$$

(33)

(c)

Combining vectors ${\mathit{\eta }}_i^{\left(a\right)}$ and ${\mathit{\eta }}_i^{\left(b\right)}$ into vector ${\mathit{\eta }}_i=({\mathit{\eta }}_i^{\left(a\right)},{\mathit{\eta }}_i^{\left(b\right)})\in {\mathbf{R}}^{12}$. The predicted covariance is then calculated as:

$${\mathit{P}}_{k|k-1}={\displaystyle \sum _{i=0}^{L+1}{W}_i^{(c)}{\mathit{\eta }}_i{\mathit{\eta }}_i^{\mathrm{T}}}+\mathit{j}({\mathit{x}}_{k-1}){\mathit{Q}}_{k-1}\mathit{j}{({\mathit{x}}_{k-1})}^{\mathrm{T}},$$

(34)

3)

Measurement Update

The UKF algorithm can be simplified, since the measure equation in the alignment filter (27) is linear. In (34), Sigma sampling points ${\mathit{\chi }}_{k|k-1}$ satisfy the following equation:

$$P_{k|k-1}={\displaystyle \sum _{i=0}^{L+1}{W}_c^{(i)}({\mathit{\chi }}_{i,k|k-1}-}{\stackrel{\wedge }{\mathit{x}}}_{k|k-1}){({\mathit{\chi }}_{i,k|k-1}-{\stackrel{\wedge }{\mathit{x}}}_{k|k-1})}^{{T}},$$

(35)

When the system measurement equation is a linear equation ${\mathit{Z}}_k={\mathit{H}}_k{\mathit{X}}_k+{\mathit{M}}_k$, ${\mathit{\chi }}_{i,k|k-1}$ can be propagated directly through the measurement equation:

$${\mathit{\gamma }}_{i,k|k-1}={\mathit{H}}_k{\mathit{\chi }}_{i,k|k-1},$$

(36)

Estimating the system measurement:

$${\stackrel{\wedge }{\mathit{z}}}_{k|k+1}={\mathit{H}}_k{\displaystyle \sum _{i=0}^{L+1}{W}_m^{(i)}{\mathit{\chi }}_{i,k|k-1}}={\mathit{H}}_k{\stackrel{\wedge }{\mathit{x}}}_{k|k+1},$$

(37)

4)

Calculation of Auto-Covariance Matrix and Cross-Covariance Matrix

The following relationship can be obtained from (35) and (37):

$${\displaystyle \sum _{i=0}^{L+1}{W}_c^{(i)}({\mathit{\gamma }}_{i,k|k-1}-}{\stackrel{\wedge }{\mathit{z}}}_{k|k-1}){({\mathit{\gamma }}_{i,k|k-1}-{\stackrel{\wedge }{\mathit{z}}}_{k|k-1})}^{\mathrm{T}}={\displaystyle \sum _{i=0}^{L+1}{W}_c^{(i)}\left({\mathit{H}}_k{\mathit{\eta }}_i\right){\left({\mathit{H}}_k{\mathit{\eta }}_i\right)}^{\mathrm{T}}}={\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}},$$

(38)

Since $\mathit{j}({\stackrel{\wedge }{\mathit{x}}}_{k|k-1})$ is an identity matrix, substituting (38) into (34), the auto-covariance matrix can be obtained as:

$${\mathit{P}}_{{\stackrel{\wedge }{z}}_k{\stackrel{\wedge }{z}}_k}={\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}+{\mathit{R}}_k,$$

(39)

Similarly, the cross-covariance is obtained:

$${\mathit{P}}_{{\stackrel{\wedge }{x}}_k{\stackrel{\wedge }{z}}_k}={\displaystyle \sum _{i=0}^{L+1}{W}_c^{(i)}{\mathit{\eta }}_i}{({\mathit{\gamma }}_{i,k|k-1}-{\stackrel{\wedge }{\mathit{z}}}_{k|k-1})}^{\mathrm{T}}={\displaystyle \sum _{i=0}^{L+1}{W}_c^{(i)}{\mathit{\eta }}_i}{({\mathit{H}}_k{\mathit{\eta }}_i)}^{\mathrm{T}}={\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}},$$

(40)

5)

Filtering Update

The filter measurement can be updated after the new measurement ${\mathit{z}}_k$ is obtained.

(a)

Calculating filter gain matrix:

$${\mathit{K}}_k={\mathit{P}}_{{\stackrel{\wedge }{x}}_k{\stackrel{\wedge }{z}}_k}{\mathit{P}}_{{\stackrel{\wedge }{z}}_k{\stackrel{\wedge }{z}}_k}^{-1},$$

(41)

(b)

Correcting the state prediction:

$${\stackrel{\wedge }{\mathit{x}}}_k={\stackrel{\wedge }{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k({\mathit{z}}_k-{\stackrel{\wedge }{\mathit{z}}}_{k|k-1}),$$

(42)

$$\delta {\stackrel{\wedge }{\mathit{x}}}_k=\left[\delta {\stackrel{\wedge }{\mathit{\phi }}}_k^b\begin{array}{c},\delta {\stackrel{\wedge }{\mathit{B}}}_k\end{array}\right]={\mathit{K}}_k({\mathit{z}}_k-{\stackrel{\wedge }{\mathit{z}}}_{k|k-1}),$$

(43)

$${\stackrel{\wedge }{\mathit{\phi }}}_k^b=\left[\exp (\delta {\stackrel{\wedge }{\mathit{\phi }}}_k^b)\right]{\stackrel{\wedge }{\mathit{\phi }}}_{k|k-1}^b,$$

(44)

$${\stackrel{\wedge }{\mathit{B}}}_k=\delta {\stackrel{\wedge }{\mathit{B}}}_k+{\stackrel{\wedge }{\mathit{B}}}_{k|k-1},$$

(45)

$${\stackrel{\wedge }{\mathit{x}}}_k=\left[{\stackrel{\wedge }{\mathit{\phi }}}_k^b,{\stackrel{\wedge }{\mathit{B}}}_k\right],$$

(46)

(c)

Updating the covariance of the system:

$${\mathit{P}}_k={\mathit{P}}_{k|k-1}-{\mathit{K}}_k{\mathit{P}}_{{\stackrel{\wedge }{z}}_k{\stackrel{\wedge }{z}}_k}{\mathit{K}}_k^{\mathrm{T}},$$

(47)

It can be seen that, except for using the method of unscented transformation (UT) to predict the state and its variance, the other operation steps are the same as for the normal Kalman filter. The proposed Lie group-based simplified UKF (termed as L-SUKF) avoids a series of complex operations such as re-sampling, solving prediction equation of measurement multiple times, and calculating predicted variance of measurement. In addition, different from the traditional UKF, the proposed L-SUKF samples the Sigma points on the Lie algebra space and projects them into the Lie group space. A Gaussian distribution is formed on the Lie algebra space based on the state model and the mapping between Lie group and Lie algebra to process the nonlinear transfer of covariance.

Noteworthy is that, for the Sigma sampling scheme, in order to reduce the number of sigma points and reduce the calculation cost with the premise of ensuring the accuracy, the simplex min skew sampling strategy is adopted in the process of UKF simplification. The specific process is as follows [10]:

Step 1: Selecting the initial state weight coefficient $0\le W_0<1$, and calculating the weight coefficient of Sigma sampling points:

$$W_i^{(m)}=\left\{\begin{array}{l}\frac{W_0}{{\alpha }^2}+(1-\frac{1}{{\alpha }^2}),i=0\\ \frac{1-W_0}{2^n\cdot {\alpha }^2},i=1,2\\ \frac{2^{i-2}\cdot W_1}{{\alpha }^2},i=3,4\cdots ,n+1\end{array}\right.,$$

(48)

$$W_i^{(c)}=\left\{\begin{array}{c}{W}_0^{(m)}+(W_0+1+\beta -{\alpha }^2),i=0\\ W_i^{(m)},i\ne 0\hfill \end{array}\right.,$$

(49)

Step 2: Iterating initial vector (when state dimension j = 1)

$${\mathit{\chi }}_0^1=\left[0\right],{\mathit{\chi }}_{1,2}^1=\left[\mp \frac{1}{\sqrt{2W_1^{(m)}}}\right],$$

(50)

For the input dimension j = 2, …, n, the recursive-iterative formula of this vector is:

$${\mathit{\chi }}_i^j=\left\{\begin{array}{c}\left[\begin{array}{c}{\mathit{\chi }}_0^{j-1}\\ 0\end{array}\right],i=0\hfill \\ \left[\begin{array}{c}{\mathit{\chi }}_i^{j-1}\\ -\frac{1}{\sqrt{2W_1^{(m)}}}\end{array}\right],i=1,2,\cdots ,j\hfill \\ \left[\begin{array}{c}0\\ \frac{1}{\sqrt{2W_1^{(m)}}}\end{array}\right],i=j+1\hfill \end{array}\right.,$$

(51)

Step 3: Adding the mean and covariance information of $\stackrel{\wedge }{x}$ to the generated Sigma points, the Sigma sampling point formula can be generated according to (51):

$${\mathit{\chi }}_i=\stackrel{\wedge }{\mathit{x}}+\alpha (\sqrt{\mathit{P}}){\mathit{\chi }}_i^j,i=0,1,\cdots ,j+1,$$

(52)

where $\alpha$ denotes a positive zooming factor, the value range is generally ${10}^{-4}\le \alpha \le 1$, which is used to determine the distribution of Sigma point near its mean value, and to reduce the influence of nonlocal effect of UT transformation by adjusting $\alpha$. $\sqrt{\mathit{P}}$ represents the square root matrix of matrix $\mathit{P}$ (such as the low triangle matrix $\mathit{C}$ that satisfies the matrix equation $\mathit{C}{\mathit{C}}^{\mathrm{T}}=\mathit{P}$ for Cholesky decomposition).

To summarize, the overall flowchart of the proposed in-flight alignment method is as shown in Figure 3.

4. Simulation and Experimental Results

In this section, simulation and ground experiments to verify and evaluate the performance of the proposed in-flight alignment method are described First, a numerical simulation was carried out for comparing the proposed in-flight alignment method with some existing traditional alignment methods. Later, a vehicle experiment was designed to further verify the effectiveness and superiority of the proposed in-flight alignment method in practical applications.

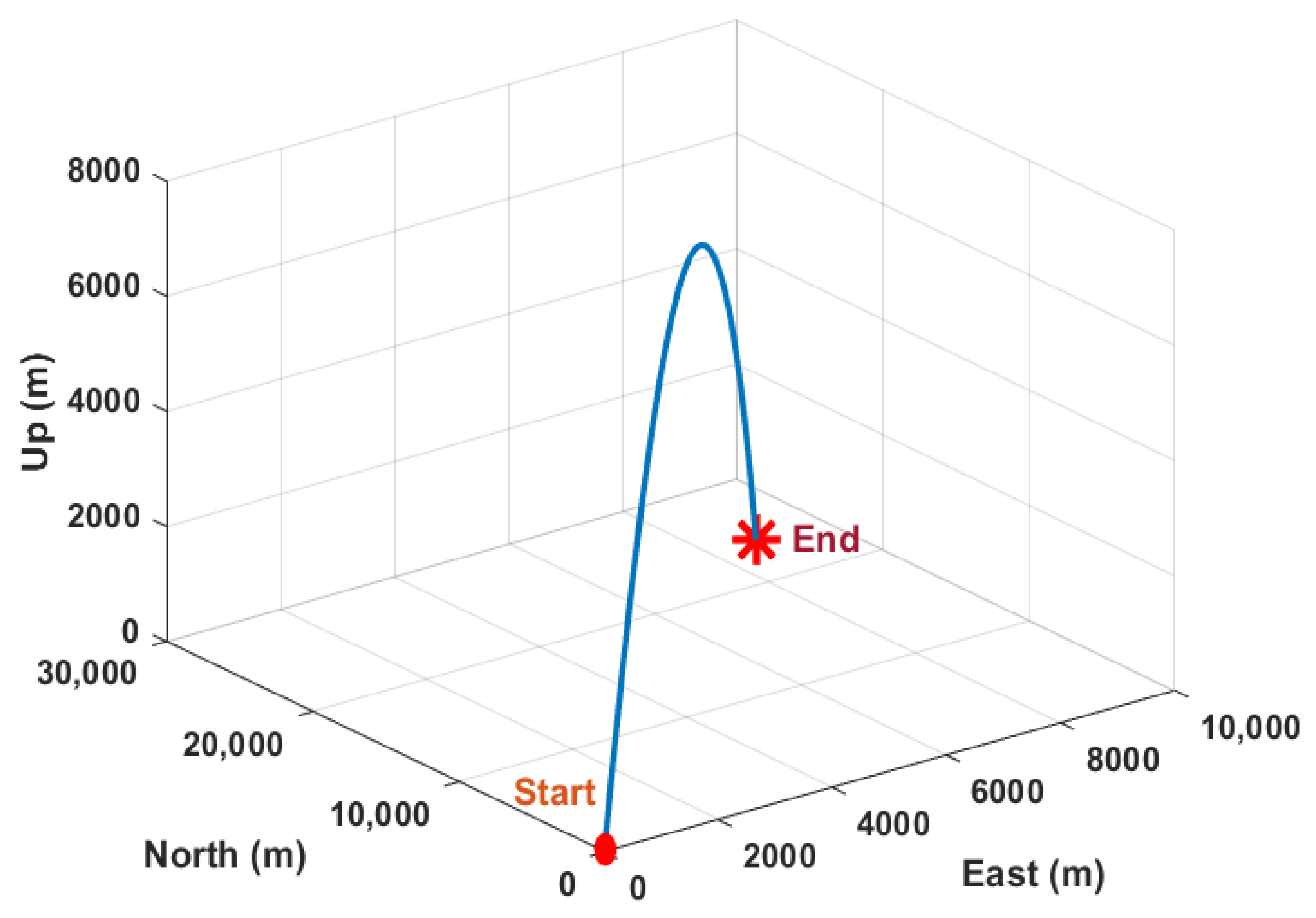
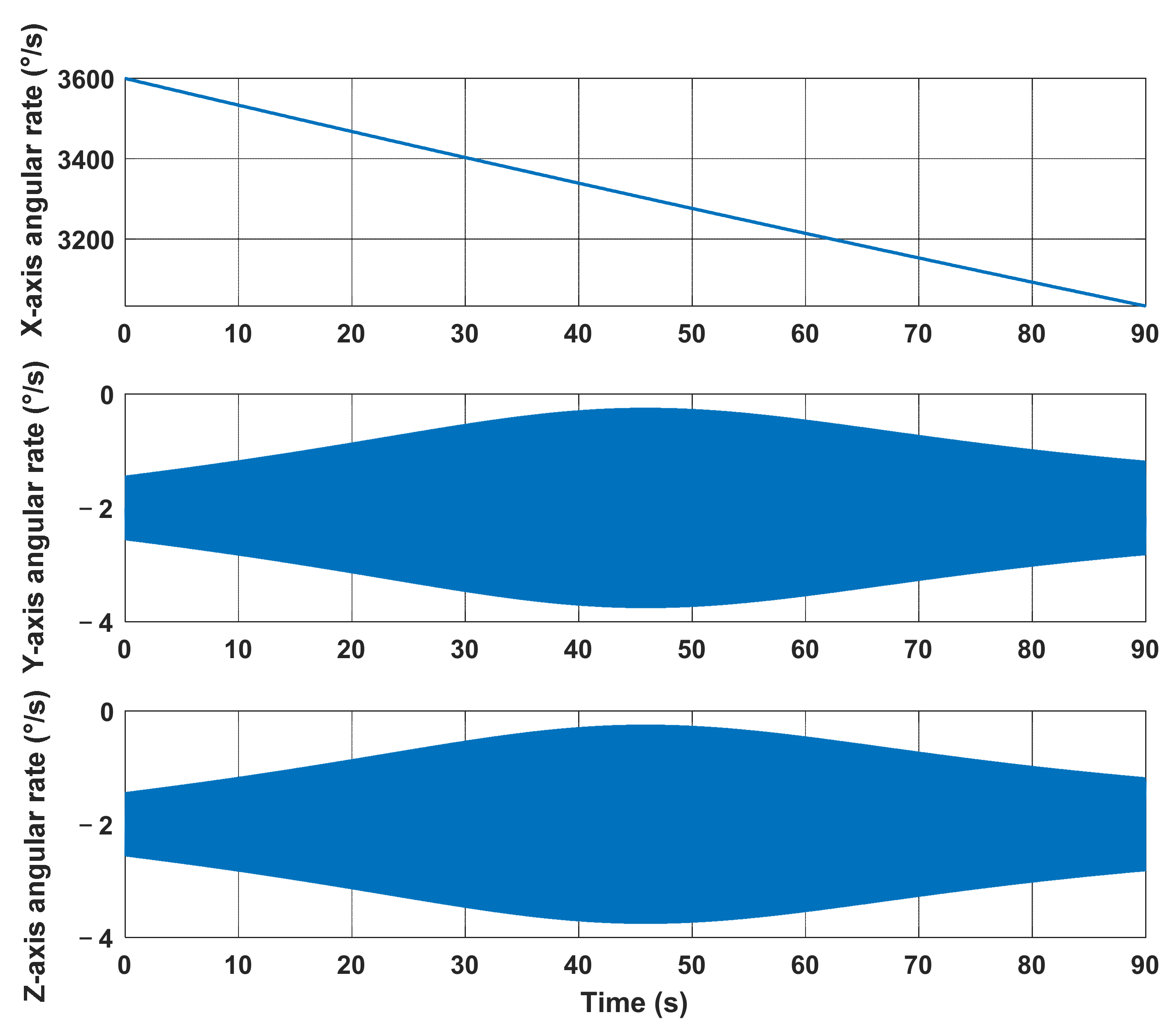
4.1. Simulation Results

In this section, a trajectory simulation of high-speed flight body is described to verify the effectiveness and superiority of the proposed in-flight alignment algorithm. The simulation trajectory of high-speed flight body is generated through the ballistic simulator. Accordingly, the specific parameters are set as follows: the projectile diameter is set to 125 mm, the projectile mass and length are, respectively, set as 40 kg and 130 mm, the aerodynamic coefficients of projectile shape is set to 1, the crosswind velocity and longitudinal wind speed are, respectively, set as 10 m/s and 5 m/s; the atmospheric pressure is set as $1\times {10}^5$ Pa; the launch point is set at 112°E and 30°N and the altitude is 800 m, the launch pitch angle and yaw angle are set to 30° and 35°, respectively, and the muzzle initial velocity and muzzle initial rotating speed of the projectile are set to 800 m/s and 10 r/s, respectively. The reference ballistic trajectory was generated as shown in Figure 4. The corresponding three-dimensional angular velocity, three-dimensional acceleration and three-dimensional velocity of the projectile are shown in Figure 5, Figure 6 and Figure 7, respectively.

In the simulation, the corresponding raw data of SINS and GPS are generated by the simulator. For the flying body with high-speed rotation characteristics, the inertial devices that can be used often have a large range, but the accuracy is low, and the measurement error is large. Therefore, according to the characteristics of inertial devices with low precision and large range, the constant bias of the three-axis gyroscopes and three-axis accelerometers in SINS are set to 60°/h and 5 mg, respectively, and the random noise intensity of gyroscopes and accelerometers are, respectively, set as 0.1°/$\sqrt{\mathrm{h}}$ and 100 ug/$\sqrt{\mathrm{Hz}}$. The constant error of GPS is set as zero, and its random velocity errors and position errors are set to 0.1 m/s and 1 m, respectively. The true pitch, roll and yaw angle at initial moment are 30°, 40° and 35°, respectively. The output frequency of SINS and GPS are respectively set as 100 Hz and 2 Hz, and the total simulation time for the ballistic trajectory is 90 s. Moreover, the existing classical OBA alignment method [34] and the EKF filter alignment method [23] widely applied in engineering are compared with the proposed alignment method, and the corresponding simulation comparison results as shown in Figure 8, Figure 9 and Figure 10.

From the above simulation comparison results, it can be seen that for SINS, where the device error cannot be ignored, the alignment attitude angle errors of both the classic OBA algorithm and the widely used EKF algorithm are relatively large when the inertial device errors and the related errors during alignment process are not effectively suppressed. For the traditional multi-vectors alignment method OBA, the effect of inertial device errors is not taken into account, and the bias of the gyroscopes and accelerometers accumulates over time. This leads to the optimal value of the objective function not being consistent with the true target attitude, resulting in poor multi-vectors construction accuracy. Thus, the classical conventional OBA method does not lead to the achievement of satisfactory alignment results when the bias of inertial devices cannot be ignored, or even diverge due to various errors. As for the filter alignment method EKF, this takes longer to reach convergence because it directly estimates the attitude angle by filtering. Moreover, the EKF method does not process well for a system with strong nonlinearity, which obviously fails to show good performance for high-speed flight body with short-endurance.

For the proposed alignment method, a simplified UKF was designed on the basis of OBA to identify the inertial bias and feedback to multi-vectors construction process, and the relevant errors were significantly suppressed, and the alignment velocity could be kept fast. This reduced the alignment time while ensuring alignment accuracy, and was more stable after convergence, with good robustness.

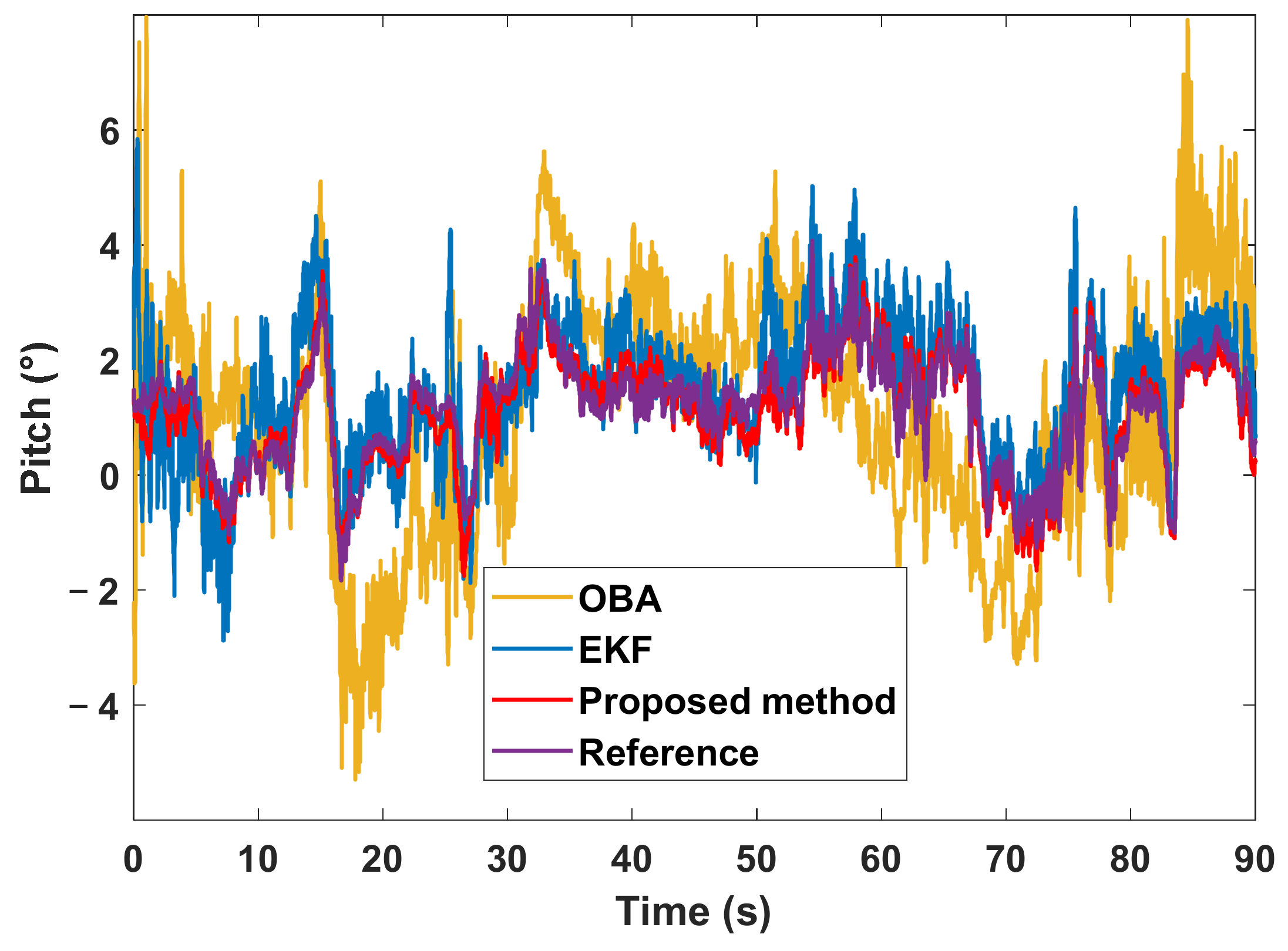
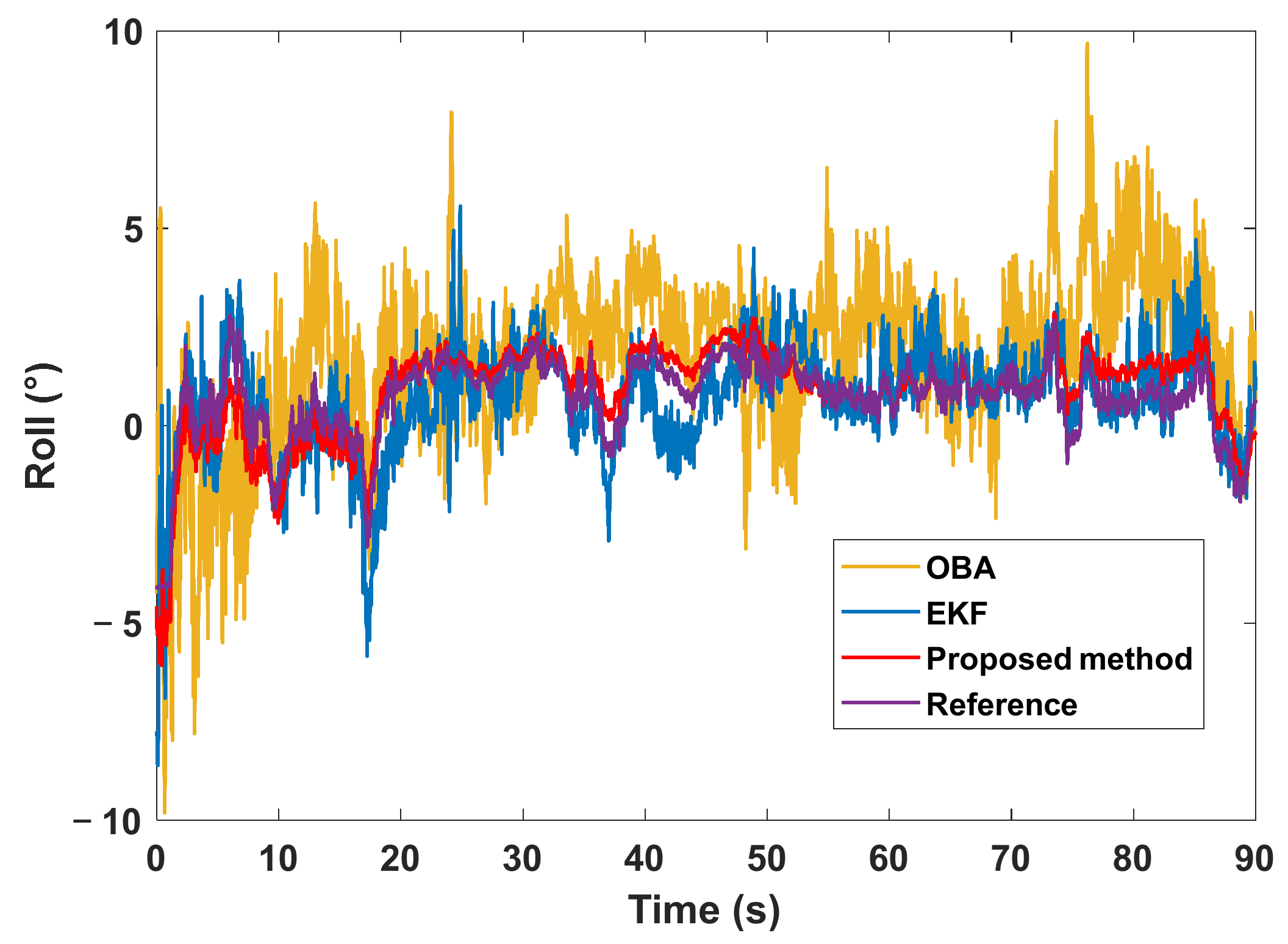
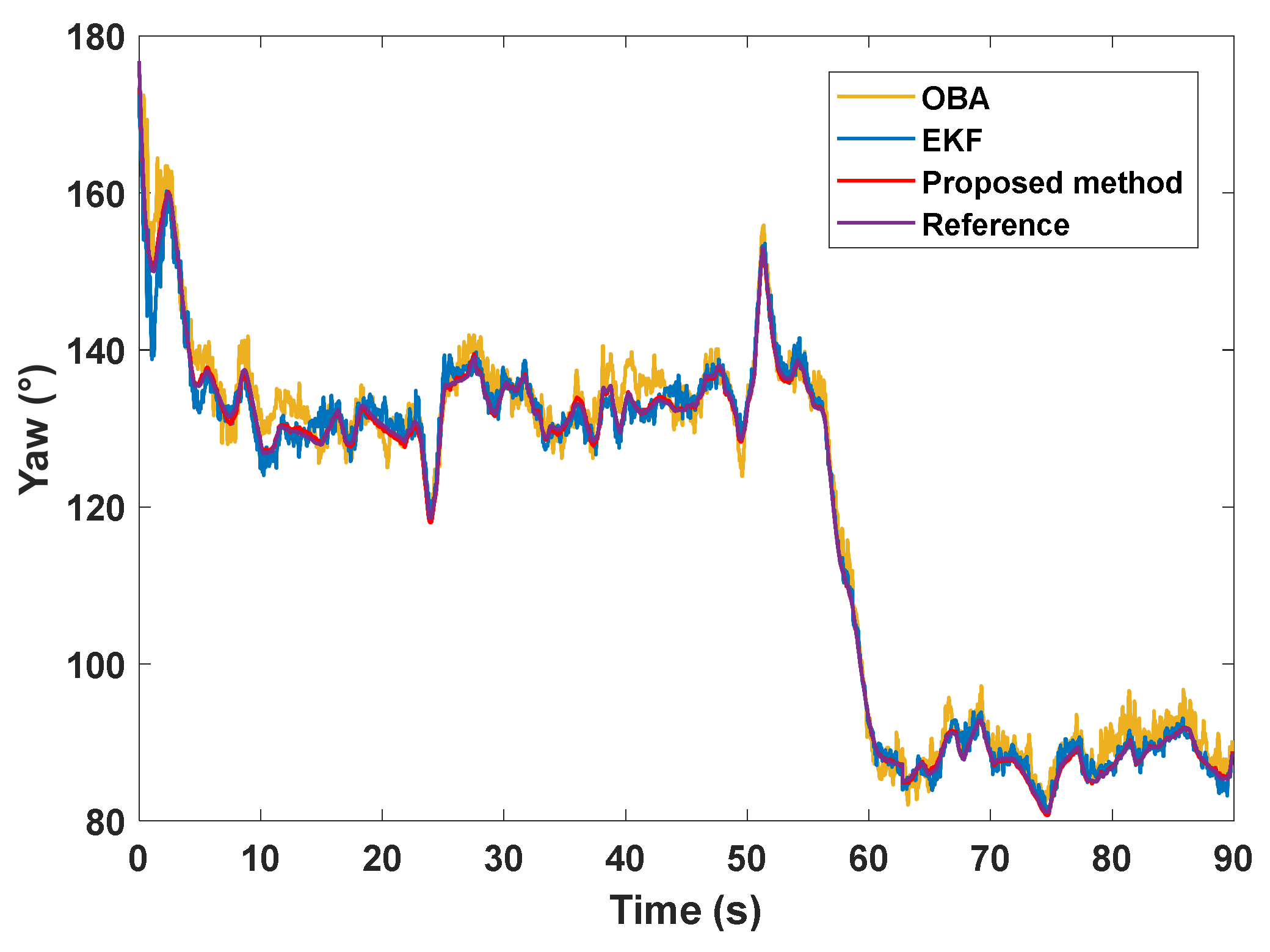
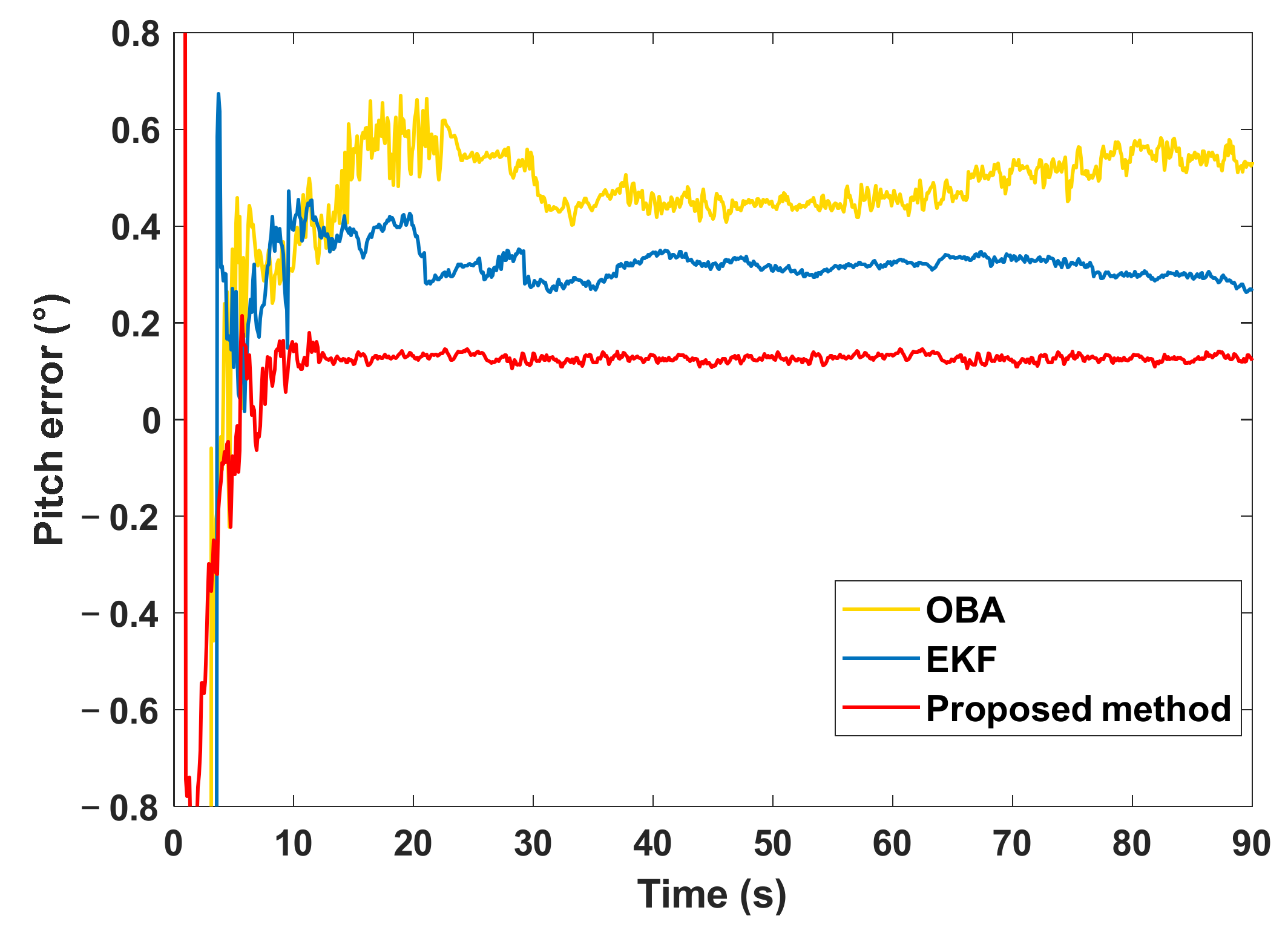
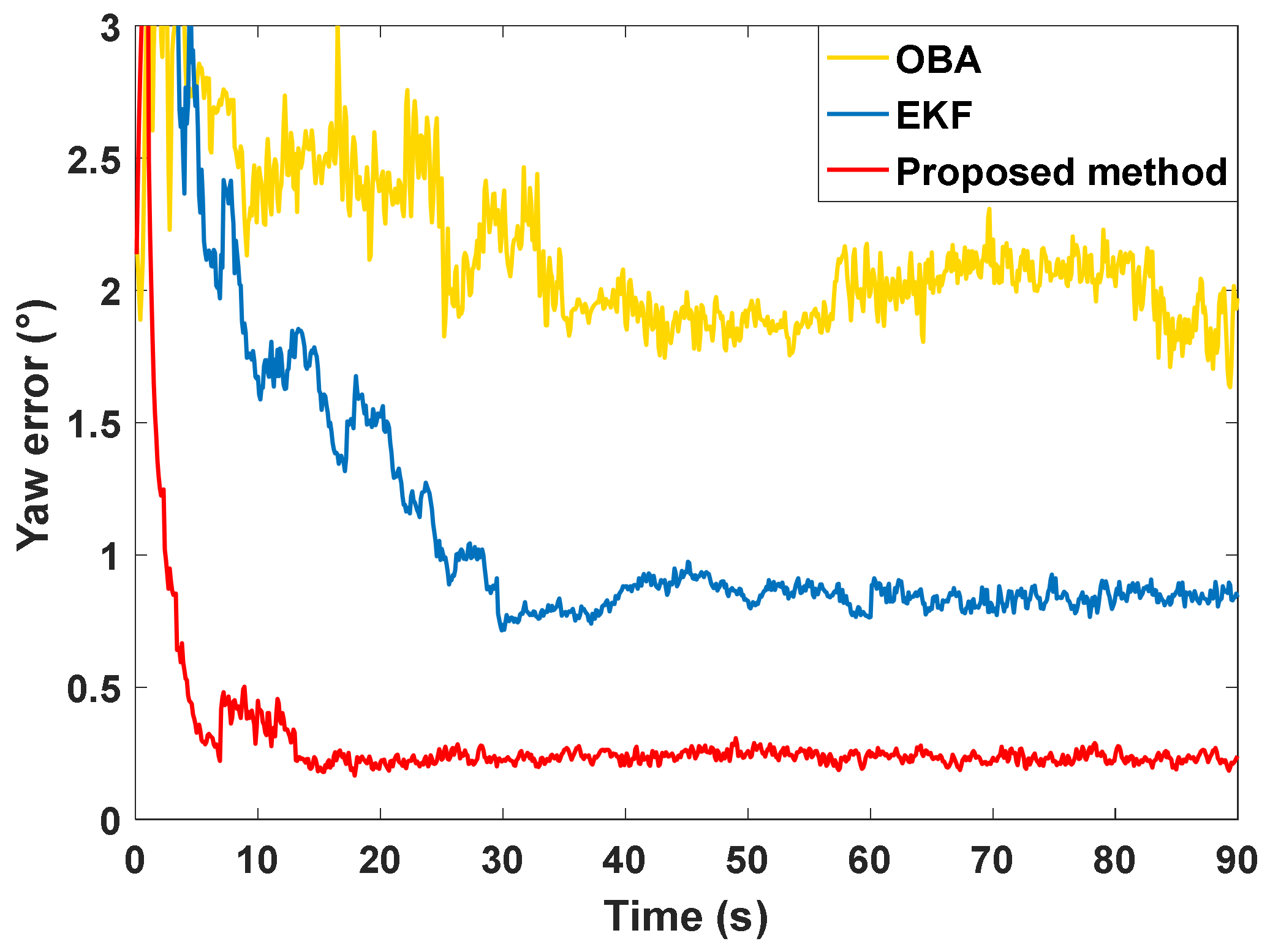
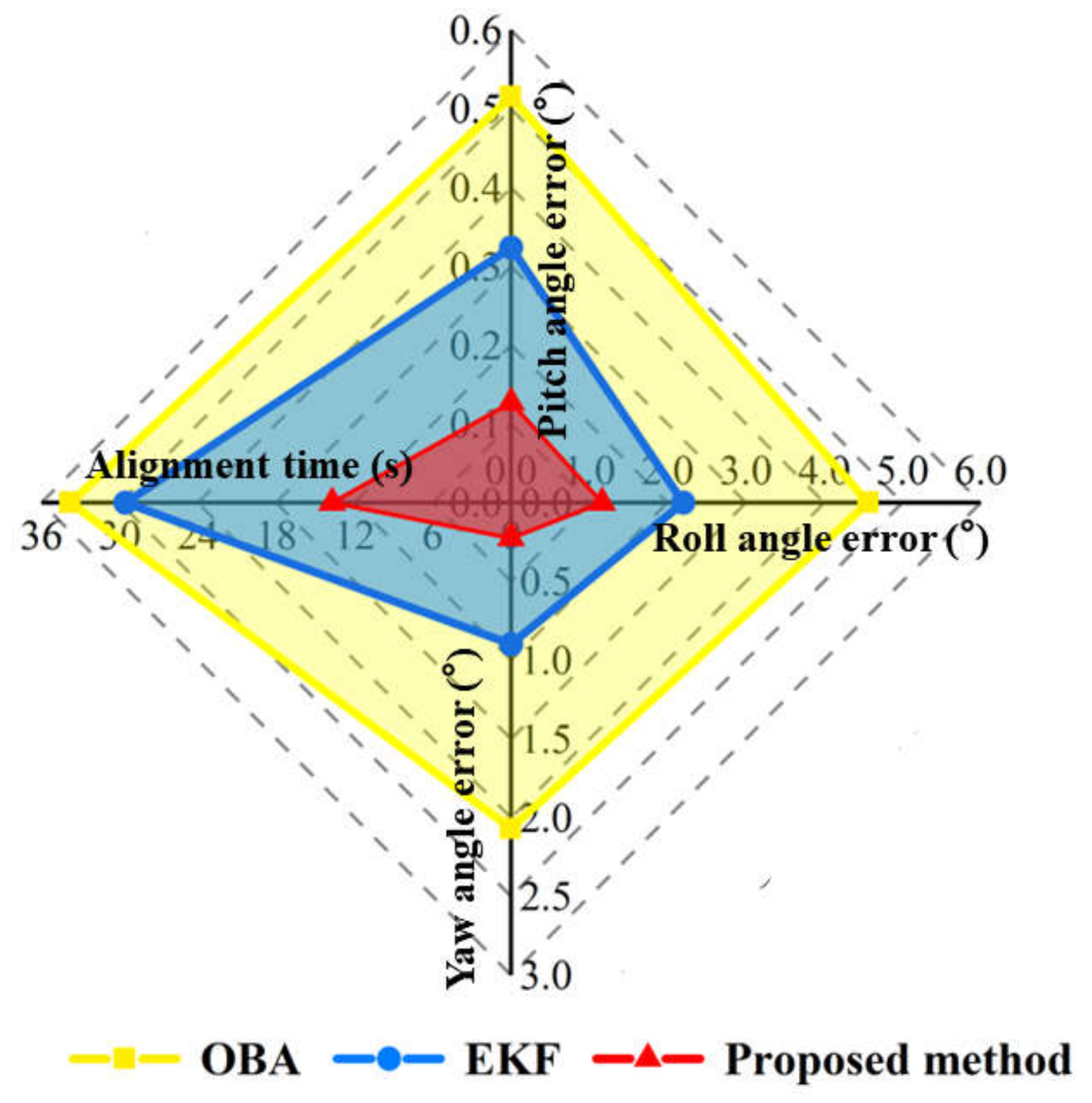
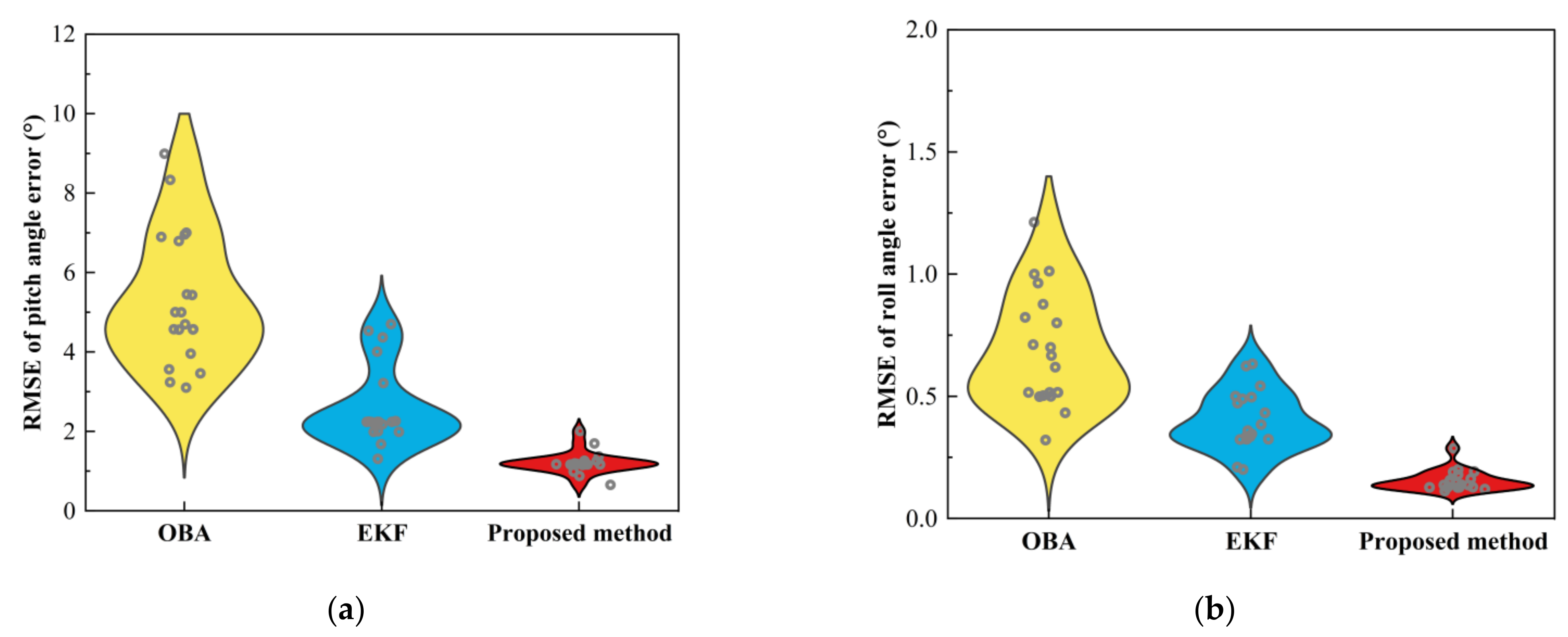
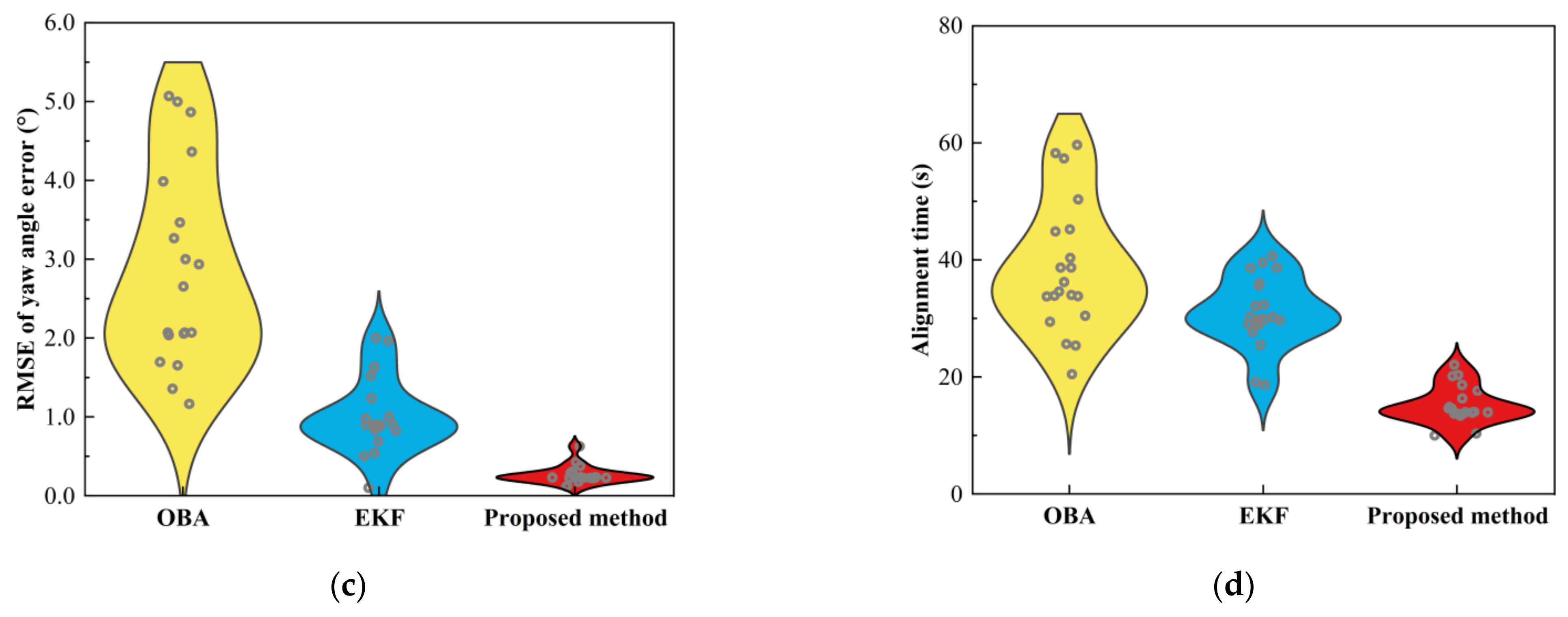
4.2. Experimental Results

In this section, a ground semi-physical experiment is described using the existing test platform to verify the validity and advantage of the proposed method. The experimental data were used to compare the performance of the proposed method with the existing advanced in-flight alignment algorithms. The experiment was carried out at 112°26′44″E, 38°0′39″N (North University of China, Taiyuan, China) and the experiment lasted 90 s. The vehicle experiment platform and vehicle experiment trajectory are as shown in Figure 11 and Figure 12.

In the SINS/GPS integrated navigation system as shown in Figure 11b, the SINS is composed of three MEMS accelerometers and three MEMS gyroscopes, and the experimental GPS receiver is CNS50. The vehicle platform is equipped with a high-precision vehicle turntable that can provide high-speed rotating state and high-precision roll attitude feedback information in real-time. The SINS/GPS integrated navigation system was installed on the on-board turntable, turntable configured for the vehicle and the high-speed rotation of the system can be realized by setting the turntable rolling speed. In fact, the rotating speed of the guided ammunition is generally 6~10 r/s, the rotating speed of vehicle turntable is set at 10 r/s during the experiment, so the turntable can meet the setting of such rotational motion state. In addition, a high-precision navigation system NovAtel SPAN-LCI shown in Figure 11b was used as a reference system for alignment. This system is a high-precision INS/GPS integrated navigation system with dual antennas as indicated in Figure 11a, which is installed on the vehicle experiment platform. The relevant system parameters are shown in

Table 1. Parameters of relevant devices.

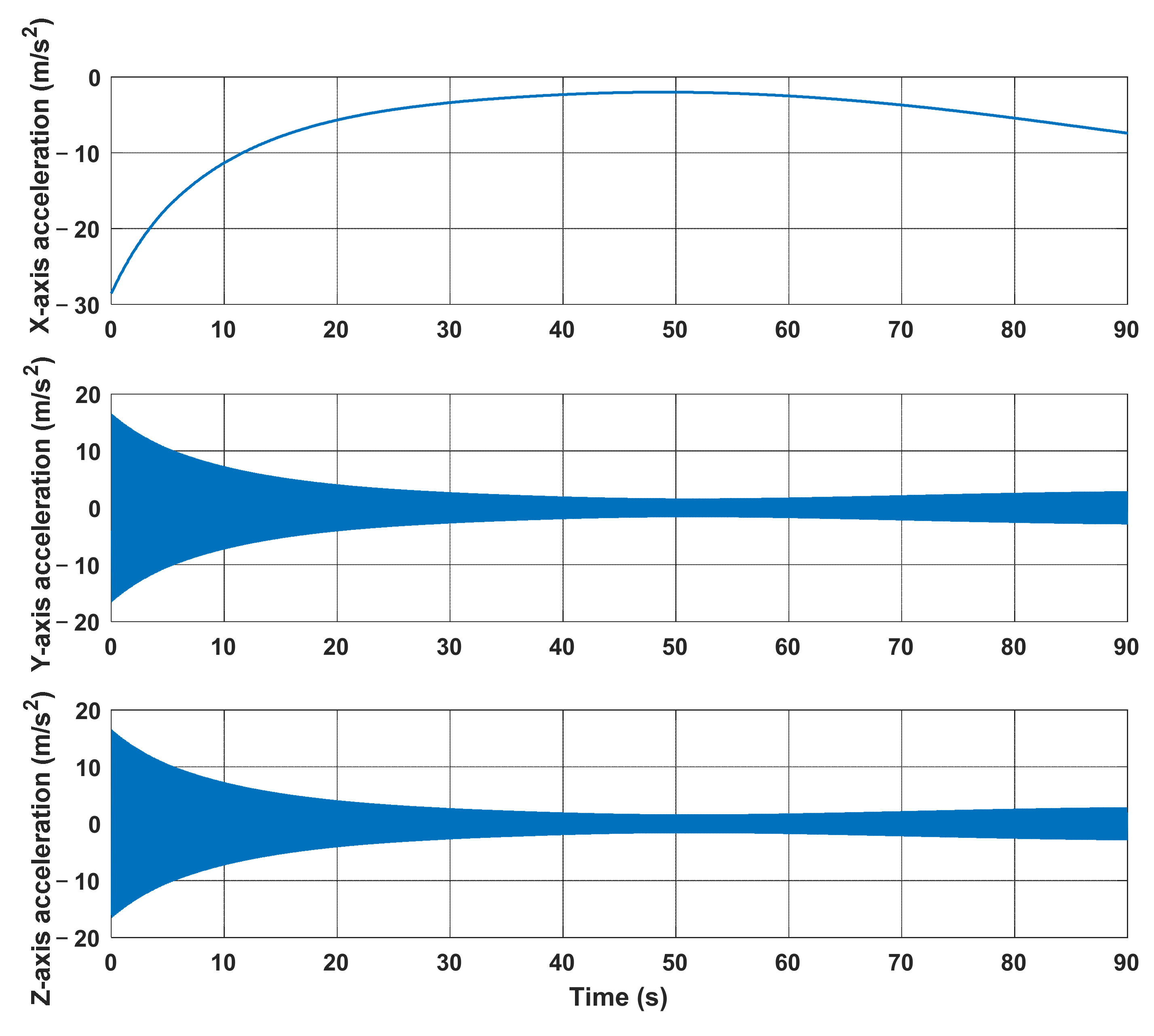
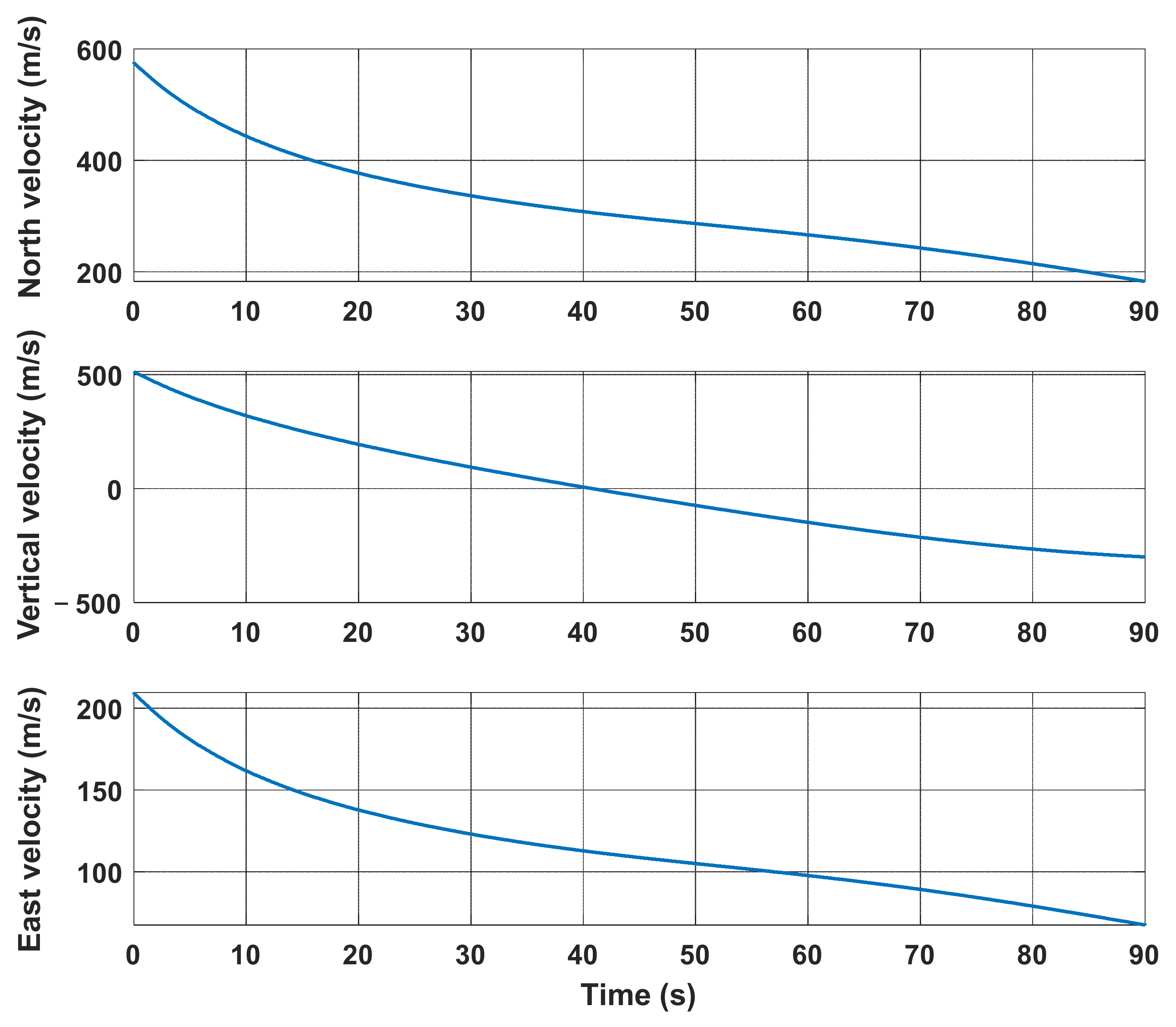
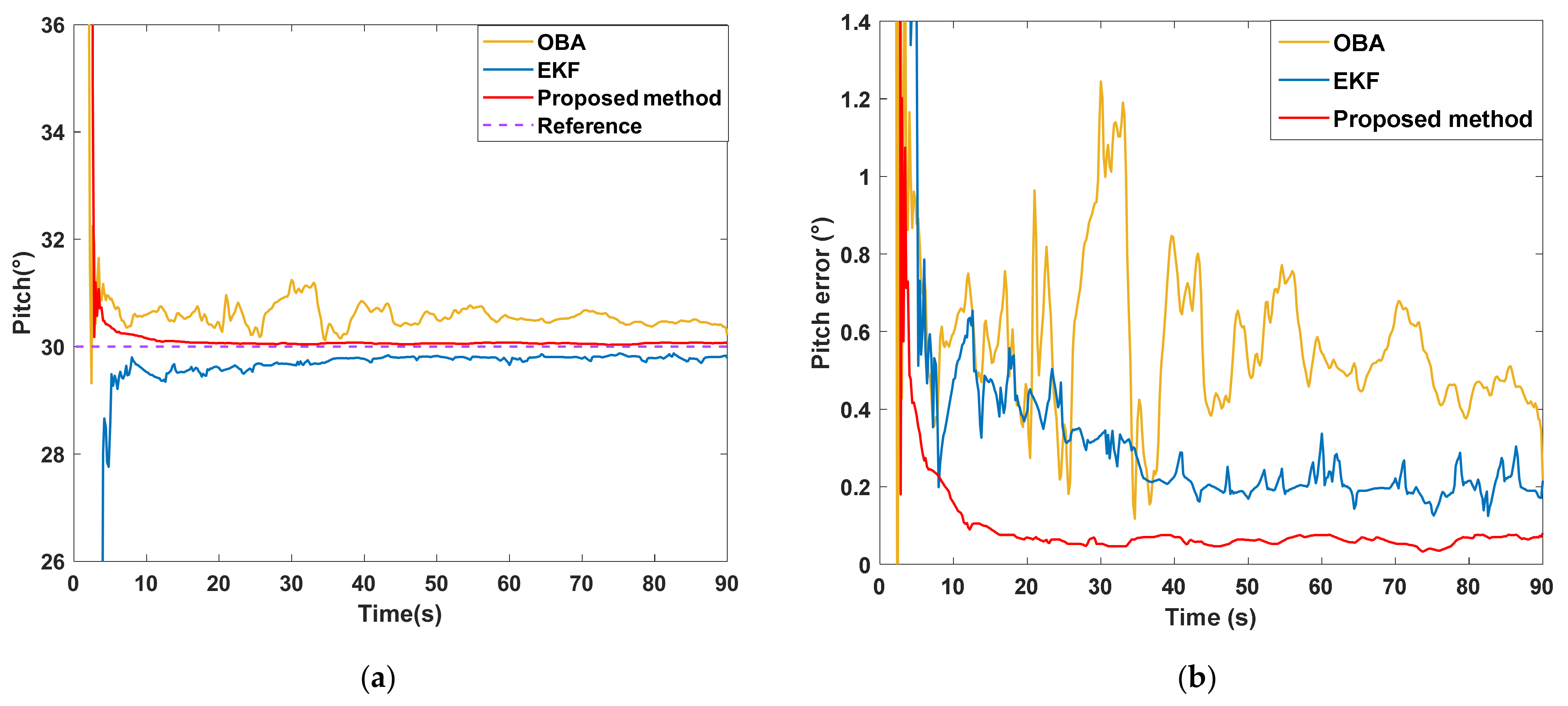
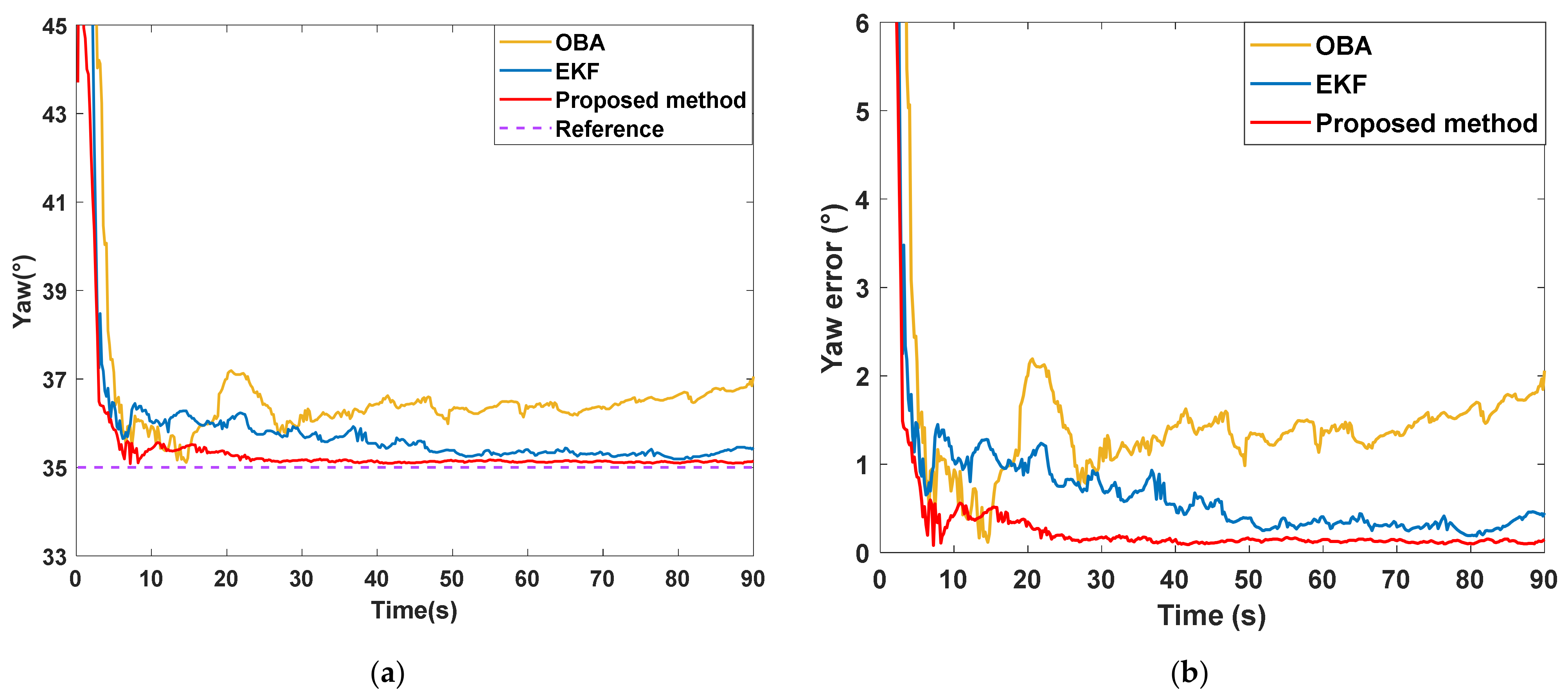
Device	Parameter	Value	Frequency
SINS	Gyro bias	50°/h	100 Hz
	Gyro random walk	$0.5°/\sqrt{\mathrm{h}}$
	Accelerometer bias	5 mg
GPS (CNS50)	Position accuracy	2 m	5 Hz
	Velocity accuracy	0.2 m/s
	Time accuracy	50 ns
Reference system (NovAtel SPAN-LCI)	Position accuracy	1 cm ± 1 ppm	100 Hz
	Velocity accuracy	0.03 m/s
	Time accuracy	20 ns
Vehicle turntable	Roll angle accuracy	0.05°	-

. The objective attitude, which is the attitude angle between the ib frame and in frame at the beginning of the alignment experiment, is respectively 1.47° (pitch), −4.09° (roll) and 176.85° (yaw) according to the reference system. All the algorithms run on the same Inter Core i5-6200U processor with 2.4 GHz and 8 GB RAM. For the lever arm effect between GPS and SINS, considering that the installation position between the GPS antenna and SINS is generally relatively fixed, the lever arm error was compensated by prior calibration before the ground experiment, so the lever arm effect was not considered in this experiment. The purpose of this was not only to reduce the amount of calculation in the alignment process, but also to prevent the inaccurate state estimation of the lever arm from affecting the estimation effect of other state parameters. [43,44].

Figure 13, Figure 14 and Figure 15 show the results of real-time attitude estimation using different alignment methods during real-time motion and alignment. For the roll angle, we subtracted the roll angle feedback of the vehicle high-precision turntable from the measured roll angle to make a clear comparison. Figure 16, Figure 17 and Figure 18 show the alignment error results of the proposed in-flight alignment method and two other existing and common in-flight alignment methods, which are OBA [34] and EKF [23]. The stated three IFA methods make use of the same set of experimental data to calculate the optimal value of attitude angle.

It can be seen from above comparison results that the alignment effect of the proposed in-flight alignment method is better than that of the other two methods. In terms of alignment accuracy, the alignment attitude error obtained by OBA method is obviously large, and the proposed alignment method can get a good and stable alignment results.

The root mean square error (RMSE) and standard deviation (Std) were adopted to compare the accuracy of the alignment after convergence.

Table 2. Std and RMSE of alignment attitude errors of different IFA methods after convergence in the experiment.

Alignment Error	Method	Std	RMSE
Pitch angle error (°)	OBA	0.04	0.52
	EKF	0.02	0.32
	Proposed method	0.01	0.13
Roll angle error (°)	OBA	1.02	4.56
	EKF	0.56	2.20
	Proposed method	0.08	1.16
Yaw angle error (°)	OBA	0.18	2.07
	EKF	0.09	0.90
	Proposed method	0.02	0.23

summarizes the RMSE and Std of alignment attitude errors of the three alignment methods and

Table 3. Alignment time of three different IFA methods in the experiment.

Method	OBA	EKF	Proposed Method
Alignment time (s)	33.79	29.56	13.71

compares the alignment time of the three alignment methods. For a more visual comparison of the alignment performance of different alignment methods, according to Table 2 and Table 3, the radar map for statistical data (RMSE) of alignment attitude errors and alignment time of different alignment methods is given in Figure 19.

From Table 2 and Table 3, and Figure 19, it can be seen that the proposed in-flight alignment method has higher alignment accuracy and shorter alignment time. The alignment error of the traditional OBA method based on multi-vector attitude determination is relatively large. The main reason is that the bias of gyroscopes and accelerometers accumulates with time, resulting in poor accuracy of the constructed multi vectors, which causes large or even divergent alignment error and the extension of alignment time. Therefore, when the bias of the inertial sensors cannot be ignored, it is necessary to estimate and correct the bias because of the poor accuracy of traditional vector construction method. For the in-flight alignment method based on EKF to directly estimate the attitude, the alignment accuracy is better than OBA method due to the estimation and correction of device bias, but not as good as the proposed method. The reason is that there is higher order truncation error when fitting nonlinear system, especially when the system is highly nonlinear, and the estimation accuracy of EKF is far lower than that of UKF.

In addition, the calculation process of EKF is complex and cumbersome, which requires more calculation cost, resulting in longer alignment time. For the proposed in-flight alignment method using UKF for error feedback based on the Lie group, the simplified UKF is used to estimate and feedback the device bias and the construction errors of attitude determination vectors, and the whole process is carried out on concise $SO\left(3\right)$, which greatly reduces the alignment time while improving the alignment accuracy. For the low cost SINS/GPS navigation system including accelerometers with bias 5 mg and gyroscopes with bias 50°/h, compared with the OBA and EKF alignment methods, the pitch angle error can be decreased from 0.52° and 0.32° to 0.13°, respectively, the roll angle error can be reduced from 4.56° and 2.20° to 1.16°, and the yaw angular error can be optimized from 2.07° and 0.90° to 0.23°, respectively. By adopting the proposed IFA method, the RMSE results of alignment accuracy is improved to more than 60% and 45%, respectively. Compared with the other two alignment methods, the proposed IFA method can reduce the alignment time from 33.79 s and 29.56 s to 12.71 s respectively, which means it can save on alignment time by over 62% and 57% respectively.

Moreover, when the estimated value of the proposed in-flight alignment method approaches the target attitude rapidly, the attitude alignment results tend to be stable and converge to the real attitude, maintaining relatively stable alignment accuracy. The proposed method still has good robustness even if the observation vector is noisy in practical applications.

In general, considering the true situation that single experimental results obtained may have uncertainty, field tests were repeated twenty times with the same SINS/GPS integrated navigation system and related experiment equipment under the same experimental environment, and the alignment performance of three alignment methods was evaluated in a statistical sense. The violin plot shown in Figure 20 illustrates the alignment time and RMSE of alignment attitude errors obtained from three alignment methods in the 20 field experiments.

It can be seen from Figure 20 that, compared with the other two alignment methods, the superior method has not only higher alignment accuracy and faster alignment speed, but also more stable alignment results. For the traditional OBA alignment approach, there is a large uncertainty during the construction of the observation vectors for alignment because of the failure to consider inertial sensor errors, which leads to the unstable alignment results. With the EKF-based filtering method for alignment, owing to the estimation and correction of the correlative alignment errors, this achieves better alignment results than the conventional OBA alignment method. However, since it does not handle nonlinear systems well, it makes the estimated alignment results unfocused and also affects the convergence speed and stability of the alignment.

The proposed alignment method has better alignment results relative to the above two alignment methods because the sensor errors and the correlation errors during the alignment process are fully considered and, in addition, the proposed UKF can effectively process nonlinear systems, which results in more centralized alignment results and more stable convergence. This further validates that the proposed in-flight alignment method can better achieve short-endurance alignment of low-cost SINS with the assistance of GPS.

5. Conclusions

This paper presented an in-flight alignment method with error feedback based on the Lie group for a special class of flight vehicles which has the characteristics of high-speed rotation and short flight time. First, taking advantage of the Lie group properties of the set of rotation matrices $SO\left(3\right)$, we redescribed the rigid body rotation to avoid the singularity and non-uniqueness of traditional methods, and the model of OBA method was derived on $SO\left(3\right)$ according to the principle of multi-vector attitude determination. Then, a simplified UKF algorithm on $SO\left(3\right)$ was proposed for estimating and correcting relevant error and sensor bias from low-cost SINS according to the characteristics of the system model. Simulation and ground semi-physical vehicle experiments demonstrated that the proposed method had better alignment accuracy and shorter alignment time in comparison with existing state-of-the-art in-flight alignment (IFA) methods. In addition, during the actual flight process of high-speed flight body, there were some random disturbing factors such as aerodynamics, attack angle, and sideslip angle. It was not possible to fully simulate the realistic flight environment of such high-speed flight body due to limited equipment. This will be the focus of our next work for fully considering other interference factors and evaluating the proposed IFA method in the actual flight environment.