Cooperated Moving Target Detection Approach for PA-FDA Dual-Mode Radar in Range-Ambiguous Clutter
Abstract
:1. Introduction
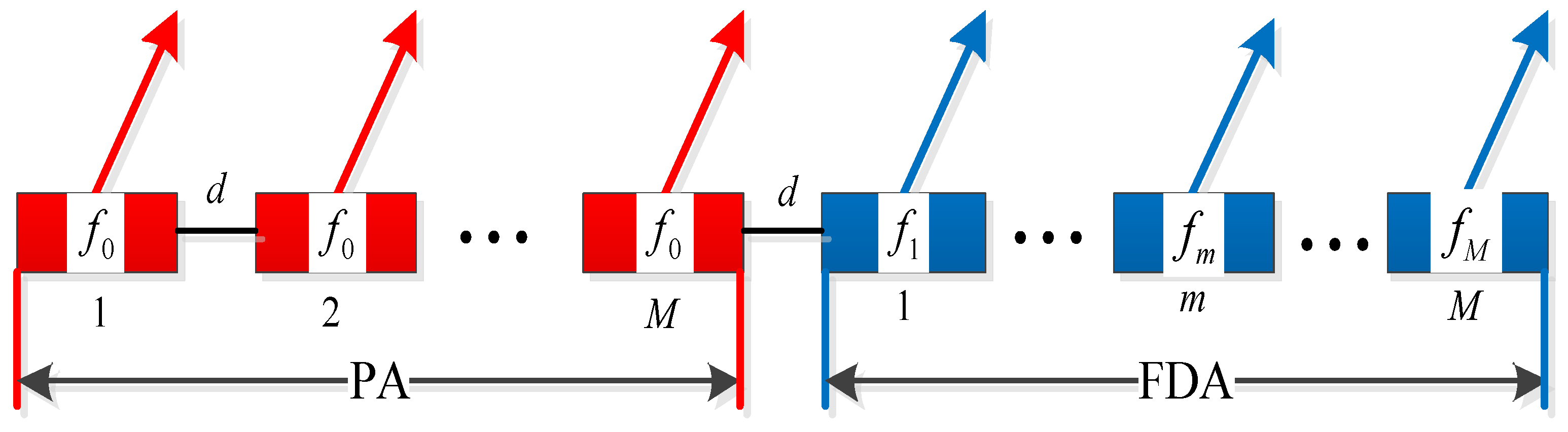
2. Signal Model of the PA-FDA Dual-Mode Radar
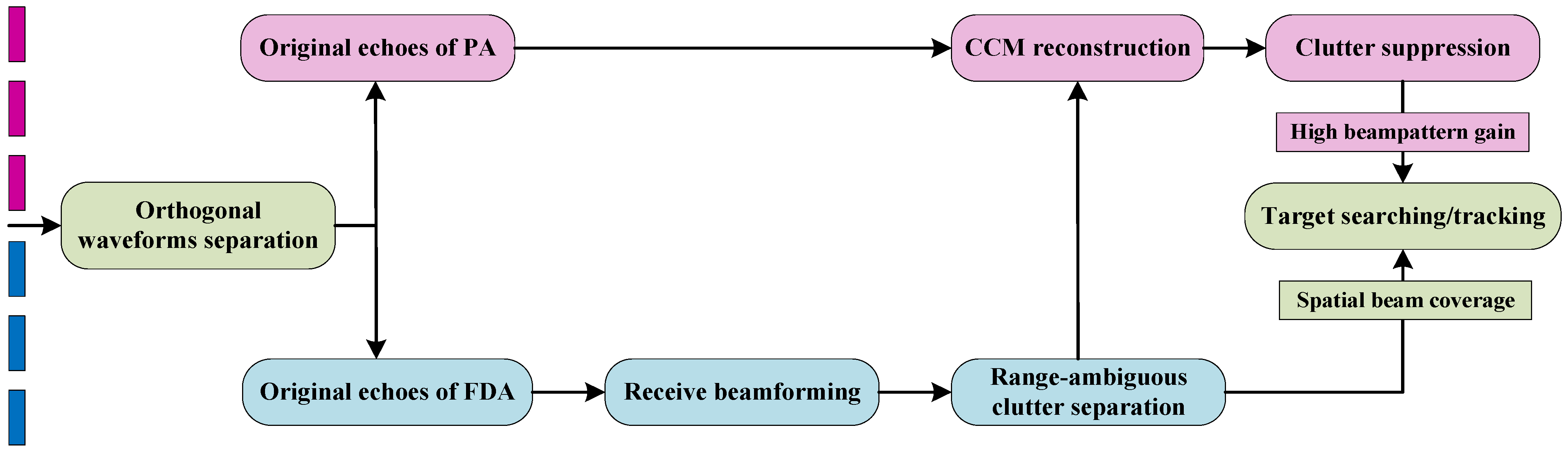
3. Cooperated Range Ambiguous Clutter Suppression with PA-FDA Dual-Mode Radar
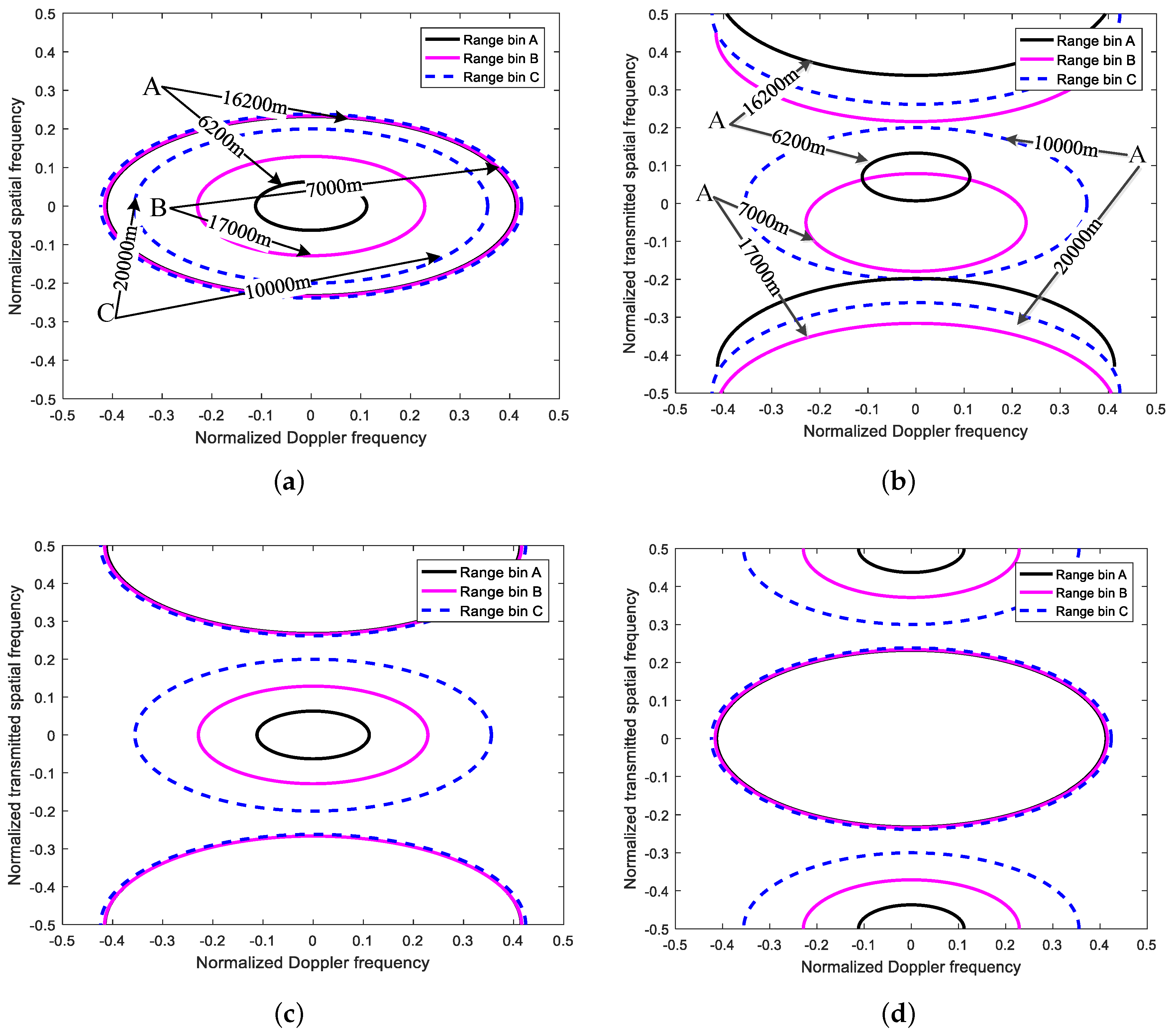
3.1. Range-Ambiguous Clutter Separation with FDA
3.2. Range-Ambiguous Clutter Suppression with PA
4. Simulation Result
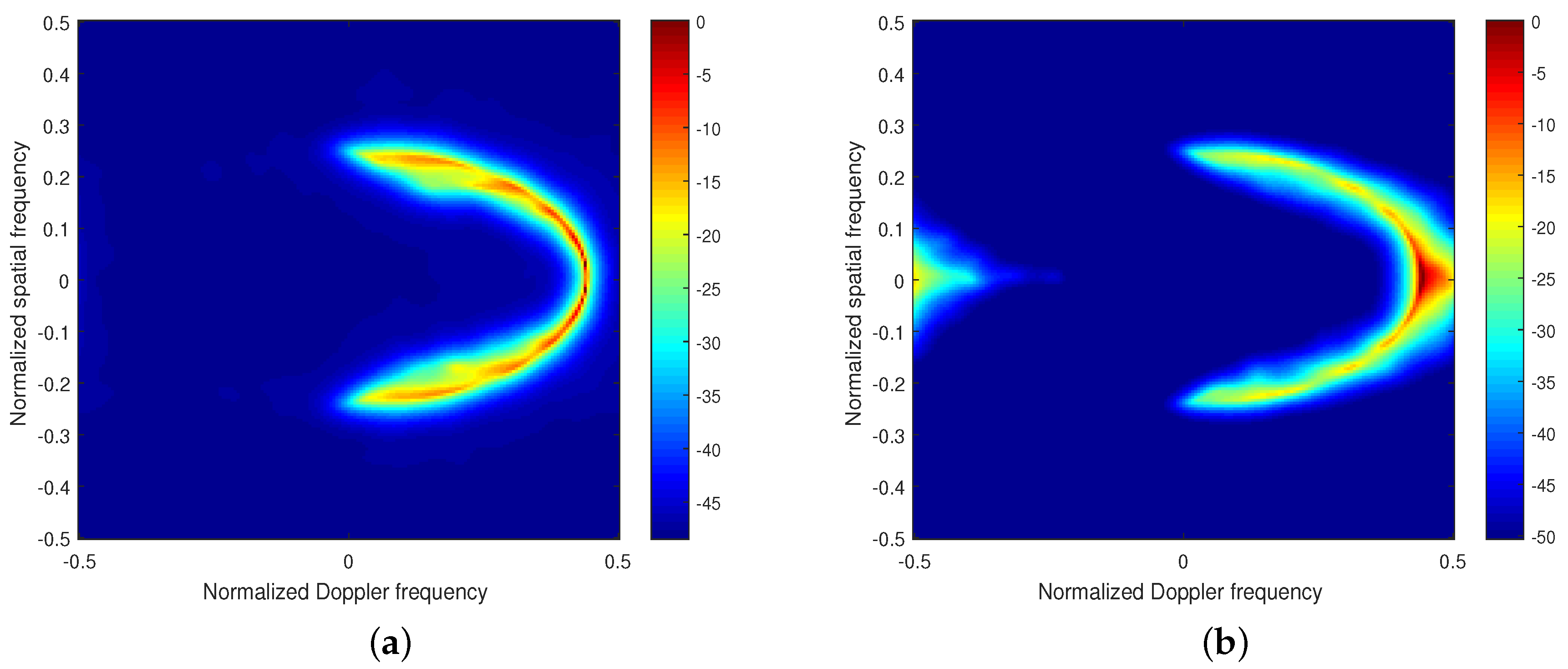
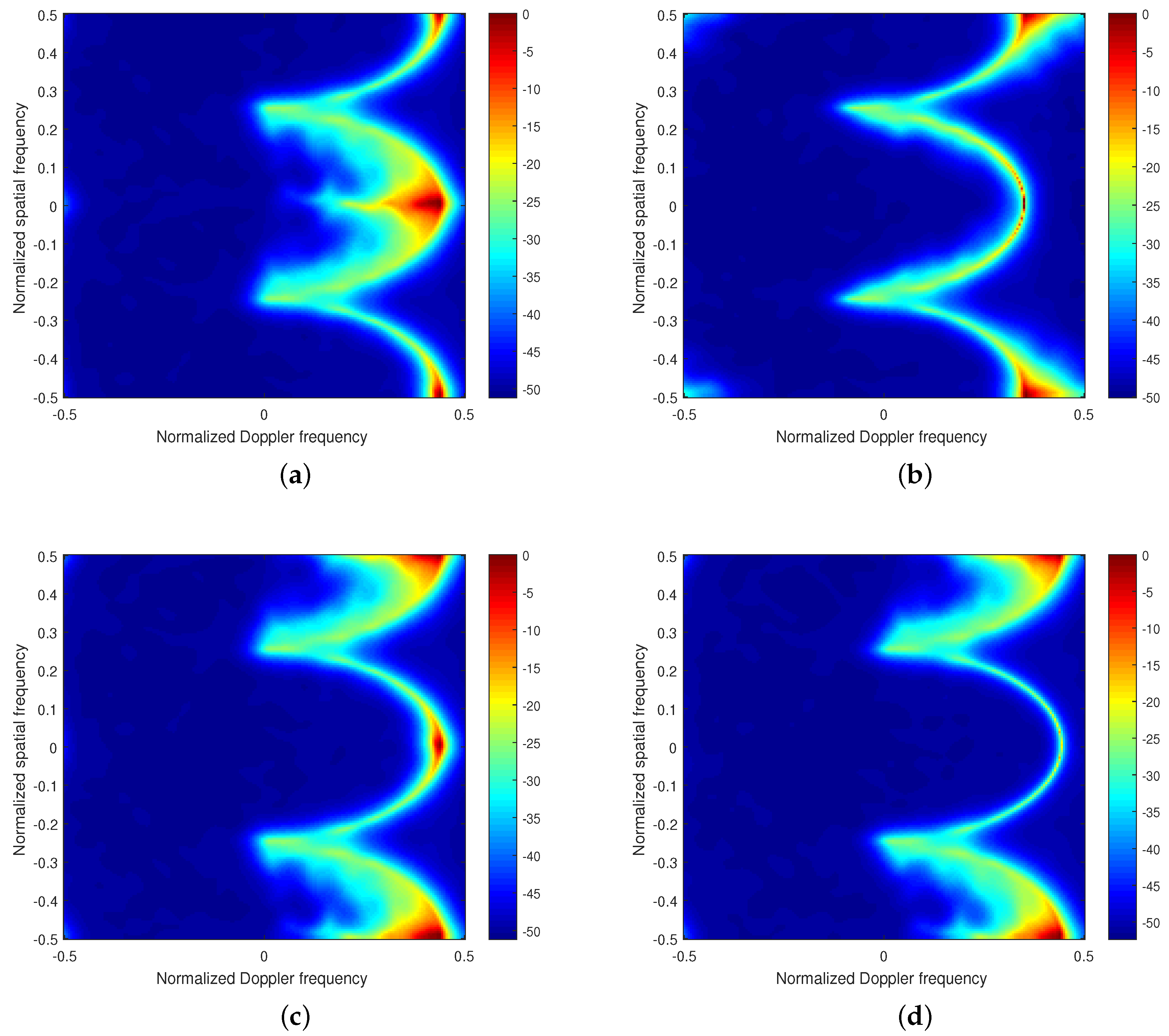
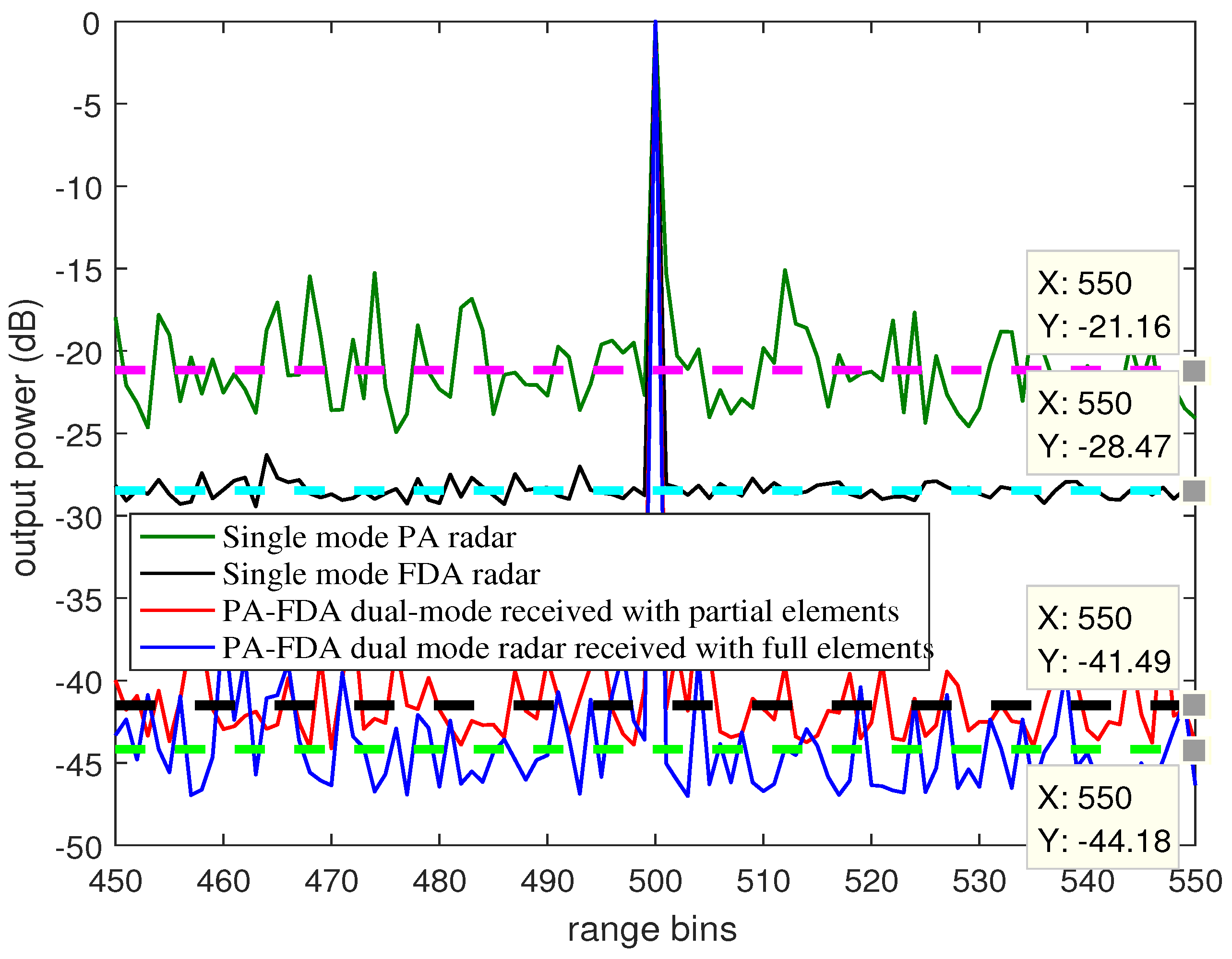
4.1. Comparison of Clutter Spectra
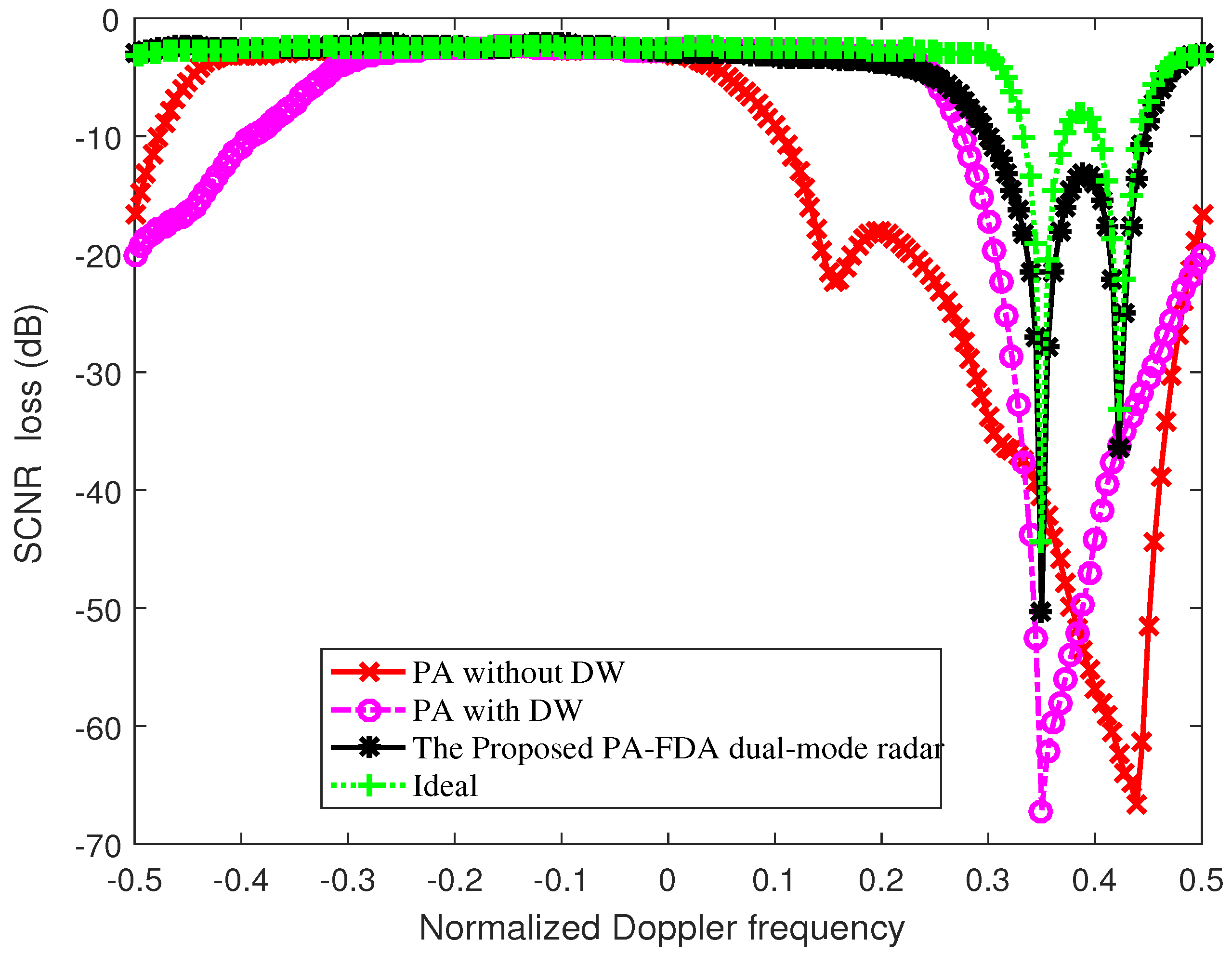
4.2. Comparison of SCNR Loss
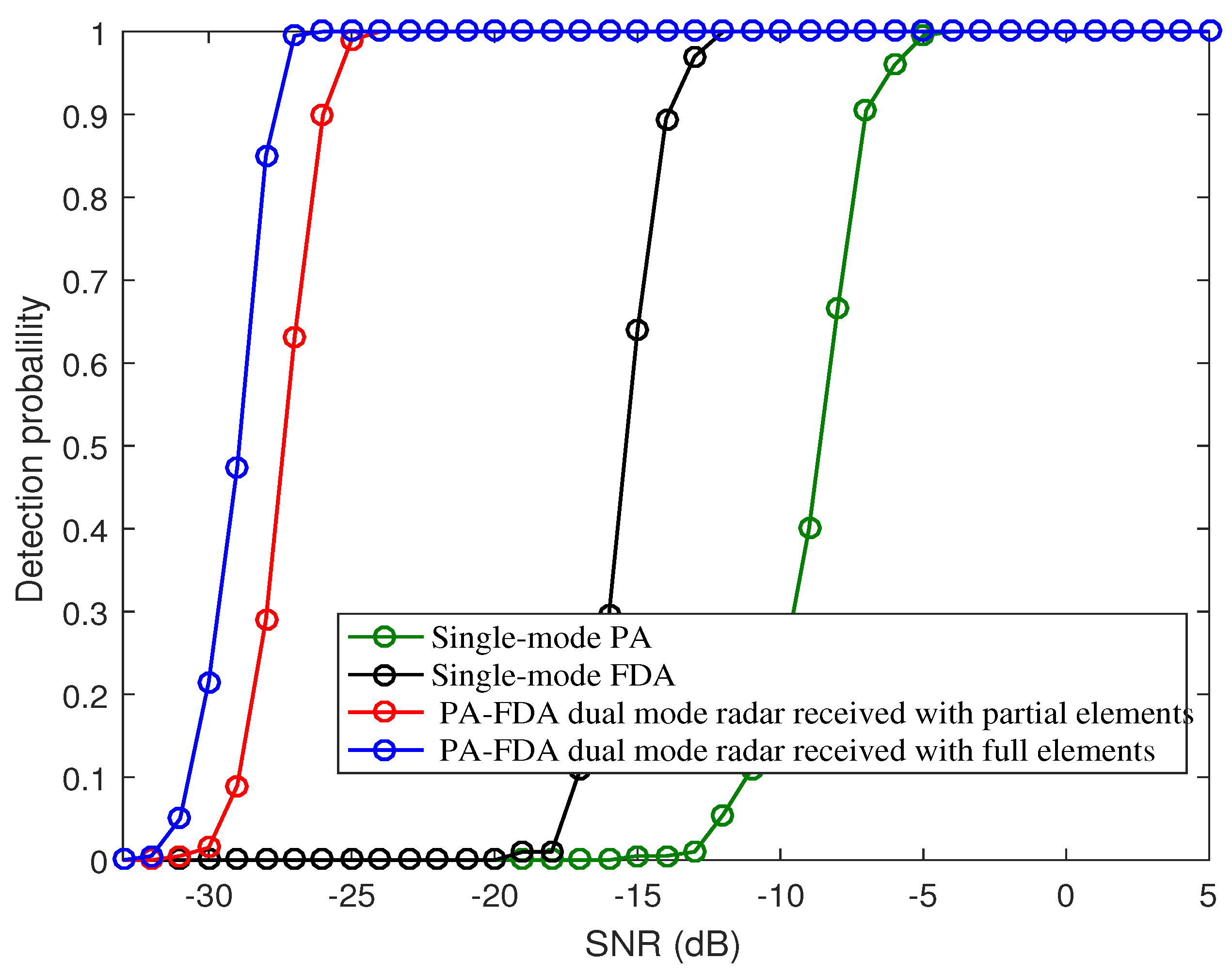
4.3. Analysis of Target Detection Probability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Melvin, W.L. A STAP overview. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 19–35. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.-G.; Liao, G.; Yang, Z.; Zhang, Y. Long-time coherent integration algorithm for radar maneuvering weak target with acceleration rate. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3528–3542. [Google Scholar] [CrossRef]
- Klemm, R. Adaptive airborne MTI: Comparison of sideways and forward looking radar. In Proceedings of the International Radar Conference, Alexandria, VA, USA, 8–11 May 1995; pp. 614–618. [Google Scholar]
- Kreyenkamp, O.; Klemm, R. Doppler compensation in forward-looking STAP radar. IEE Proc.—Radar Sonar Navig. 2001, 148, 253–258. [Google Scholar] [CrossRef]
- Jia, F.; He, Z.; Li, J.; Qian, J. Adaptive angle-Doppler compensation in airborne phased radar for planar array. In Proceedings of the IEEE 13th International Conference on Signal Processing, Chengdu, China, 6–10 November 2016; pp. 1585–1588. [Google Scholar]
- Varadarajan, V.; Krolik, J.L. Joint space-time interpolation for distorted linear and bistatic array geometries. IEEE Trans. Signal Process. 2006, 54, 848–860. [Google Scholar] [CrossRef]
- Cristallini, D.; Burger, W. A robust direct data domain approach for STAP. IEEE Trans. Signal Process. 2012, 60, 1283–1294. [Google Scholar] [CrossRef]
- Choi, W.; Sarkar, T.K. Minimum norm property for the sum of the adaptive weights for a direct data domain least squares algorithm. IEEE Trans. Antennas Propag. 2006, 54, 1045–1050. [Google Scholar] [CrossRef]
- Meng, X.; Wang, T.; Wu, J.; Bao, Z. Short-range clutter suppression for airborne radar by utilizing prefiltering in elevation. IEEE Geosci. Remote Sens. Lett. 2009, 6, 268–272. [Google Scholar] [CrossRef]
- Wu, J.; Wang, T.; Meng, X.; Bao, Z. Clutter suppression for airborne non sidelooking radar using ERCB-STAP algorithm. Radar Sonar Navig. IET 2010, 4, 497–506. [Google Scholar] [CrossRef]
- Chen, W.; Xie, W.; Wang, Y. Short-range clutter suppression for airborne radar using sparse recovery and orthogonal projection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Duan, K.; Xu, H.; Yuan, H.; Xie, H.; Wang, Y. Reduced-DOF three-dimensional STAP via subarray synthesis for nonsidelooking planar array airborne radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3311–3325. [Google Scholar] [CrossRef]
- Hale, T.B.; Temple, M.A.; Raquet, J.F.; Oxley, M.E.; Wicks, M.C. Localized three-dimensional adaptive spatial-temporal processing for airborne radar. IEE Proc.—Radar Sonar Navig. 2003, 150, 18–22. [Google Scholar] [CrossRef]
- Corbell, P.M.; Perez, J.J.; Rangaswamy, M. Enhancing GMTI performance in non-stationary clutter using 3D STAP. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 647–652. [Google Scholar]
- Cui, N.; Duan, K.; Xing, K.; Yu, Z. Beam-Space Reduced-Dimension 3D-STAP for Nonside-Looking Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Duan, K.; Xie, W. Subspace-augmented clutter suppression technique for STAP radar. IEEE Geosci. Remote Sens. Lett. 2016, 13, 462–466. [Google Scholar] [CrossRef]
- Huang, P.; Zou, Z.; Xia, X.-G.; Liu, X.; Liao, G. A Novel dimension-reduced space–time adaptive processing algorithm for spaceborne multichannel surveillance radar systems based on spatial–temporal 2-D sliding window. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S.; Huang, L.; So, H.C. Joint range and angle estimation using MIMO radar with frequency diverse array. IEEE Trans. Signal Process. 2015, 63, 3396–3410. [Google Scholar] [CrossRef]
- Lan, L.; Rosamilia, M.; Aubry, A.; Demaio, A.; Liao, G. Single-snapshot angle and incremental range estimation for FDA-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3705–3718. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.; Xu, J.; Zhang, Y.; Fioranelli, F. Suppression approach to main-beam deceptive jamming in FDA-MIMO radar using nonhomogeneous sample detection. IEEE Access 2018, 6, 34582–34597. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, S. Main-Beam Range deceptive jamming suppression with simulated annealing FDA-MIMO radar. IEEE Sens. J. 2020, 20, 9056–9070. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.; Liao, G.; Xu, X.; Zhang, Y. A range ambiguity resolution approach for high-resolution and wide-swath SAR imaging using frequency diverse array. IEEE J. Sel. Top. Signal Process. 2017, 11, 336–346. [Google Scholar] [CrossRef]
- Wang, W.-Q.; So, H.C.; Farina, A. An Overview on Time/Frequency Modulated Array Processing. IEEE J. Sel. Top. Signal Process. 2017, 11, 228–246. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhang, Y.; Ji, H.; Huang, L. An adaptive range-angle-doppler processing approach for FDA-MIMO radar using three-dimensional localization. IEEE J. Sel. Top. Signal Process. 2017, 11, 309–320. [Google Scholar] [CrossRef]
- Wen, C.; Ma, C.; Peng, J.; Wu, J. Bistatic FDA-MIMO radar space-time adaptive processing. Signal Process. 2019, 163, 201–212. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, S.; Liao, G. Range ambiguous clutter suppression for airborne FDA-STAP radar. IEEE J. Sel. Top. Signal Process. 2015, 9, 1620–1631. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; So, H.C. Space-time adaptive processing with vertical frequency diverse array for range-ambiguous clutter suppression. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5352–5364. [Google Scholar] [CrossRef]
- Wang, W.; Wan, P.; Zhang, J.; Liu, Z.; Xu, J. Enhanced Pre-STAP Beamforming for Range Ambiguous Clutter Separation with Vertical FDA Radar. Remote Sens. 2021, 13, 5145. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, S. Range ambiguous clutter suppression for FDA-MIMO forward looking airborne radar based on main lobe correction. IEEE Trans. Veh. Technol. 2021, 70, 2032–2046. [Google Scholar] [CrossRef]
- Wen, C.; Huang, Y.; Peng, J.; Wu, J.; Zheng, G.; Zhang, Y. Slow-Time FDA-MIMO Technique With Application to STAP Radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 74–95. [Google Scholar] [CrossRef]
- Wen, C.; Tao, M.; Peng, J.; Wu, J.; Wang, T. Clutter suppression for airborne FDA-MIMO radar using multi-waveform adaptive processing and auxiliary channel STAP. Signal Process. 2019, 154, 280–293. [Google Scholar] [CrossRef]
- Gao, C.; Teh, K.C.; Liu, A. Orthogonal frequency diversity waveform with range-Doppler optimization for MIMO Radar. IEEE Signal Process. Lett. 2014, 21, 1201–1205. [Google Scholar] [CrossRef]
- Hu, X.; Feng, C.; Wang, Y.; Guo, Y. Adaptive Waveform Optimization for MIMO Radar Imaging Based on Sparse Recovery. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2898–2914. [Google Scholar] [CrossRef]
- Chen, W.; Xie, W.; Wang, Y. Range-dependent ambiguous cutter Suppression for Airborne SSF-STAP Radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 855–867. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| CNR | 50 | PRF | 15 kHz |
| Platform height | 6000 m | Platform speed | 100 m/s |
| Element spacing | 0.0075 m | Frequency increment | 22.5 kHz |
| Carrier frequency | 10 GHz | Pulse number | 16 |
| Number of range bins | 800 | Rx element number | 34 |
| Tx element number of PA | 17 | Tx element number of FDA | 17 |
| Parameter | Value |
|---|---|
| Target speed | 10 m/s |
| Target azimuth | 0° |
| SNR | 0 dB |
| False probability |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhu, S.; Xu, J.; Lan, L.; He, X.; Li, X. Cooperated Moving Target Detection Approach for PA-FDA Dual-Mode Radar in Range-Ambiguous Clutter. Remote Sens. 2023, 15, 692. https://doi.org/10.3390/rs15030692
Liu Z, Zhu S, Xu J, Lan L, He X, Li X. Cooperated Moving Target Detection Approach for PA-FDA Dual-Mode Radar in Range-Ambiguous Clutter. Remote Sensing. 2023; 15(3):692. https://doi.org/10.3390/rs15030692
Chicago/Turabian StyleLiu, Zhixin, Shengqi Zhu, Jingwei Xu, Lan Lan, Xiongpeng He, and Ximin Li. 2023. "Cooperated Moving Target Detection Approach for PA-FDA Dual-Mode Radar in Range-Ambiguous Clutter" Remote Sensing 15, no. 3: 692. https://doi.org/10.3390/rs15030692
APA StyleLiu, Z., Zhu, S., Xu, J., Lan, L., He, X., & Li, X. (2023). Cooperated Moving Target Detection Approach for PA-FDA Dual-Mode Radar in Range-Ambiguous Clutter. Remote Sensing, 15(3), 692. https://doi.org/10.3390/rs15030692











