Passive Joint Emitter Localization with Sensor Self-Calibration

Abstract

This paper studies the problem surrounding distributed passive arrays (sensors) locating multiple emitters while performing self-calibration to correct possible errors in the assumed array directions. In our setting, only the angle-of-arrival (AoA) information is available for localization. However, such information may contain bias due to array directional errors. Hence, localization requires self-calibration. To achieve both, the key element behind our approach is that the received signals from the same emitter should be geometrically consistent if sensor arrays are successfully calibrated. This leads to our signal model, which is built on a mapping directly from emitter locations and array directional errors to received signals. Then we formulate an atomic norm minimization and use group sparsity to promote geometric consistency and align ‘ghost’ emitter locations from calibration errors. Simulations verify the effectiveness of the proposed scheme. We derive the Cramér Rao lower bound and numerically compare it to the simulations. Furthermore, we derive a necessary condition as a rule of thumb to decide the feasibility of joint localization and calibration.

1. Introduction

Localization is a fundamental issue for many applications, such as radar detection [1], acoustic sensing [2], and wireless communication [3]. This paper considers the problem of using spatially distributed passive antenna arrays to locate an unknown number of emitters in the presence of sensor errors. Passive joint emitter localization has received much attention, which is based on using parameters, including Angle of Arrival (AOA) [4], Time of Arrival (TOA) [5], Time Difference of Arrival (TDOA) [6], etc.

In practice, mobile and/or loosely synchronized systems are often used. We assume that emitters and sensors are non-collaborative and, hence, TOA information is absent. We also assume that sensor arrays are loosely synchronized in the sense that the synchronization error is much smaller than the time scale needed for relevant movements of emitters and sensors, i.e., the locations of emitters and sensors remain unchanged during the measuring process, but can be larger than that required for accurate TDOA measurements. Hence, we focus on using AOA information for localization.

It has been widely accepted that sensor errors can have large impacts on localization performance. There are many literature studies  [7,8,9,10,11,12,13,14,15,16,17] that have reviewed joint localization and calibration. The focus of calibration is on the non-ideal characteristics of a single antenna array, including mutual coupling, gain, and phase errors across antenna elements (antenna element placement errors can be modeled as element phase errors). It is noteworthy that the above errors are typically caused by hardware imperfections, remain constants for a long term, and typically do not require online calibration during operation.

In this work, we focused on possible errors in the array directions. We assumed that each sensor array in the system was well calibrated before operation so that mutual coupling, gain, and phase errors of antenna elements were negligible [18,19]. However, operation conditions can cause errors in the assumed array directions, for example, a sharp turn of autonomous vehicles [20], the unstable motion of aerial vehicles [21], the drifting of buoys [22], strong winds, and other unpredictable changes in the operating environment. Therefore, joint localization and calibration with array direction errors are significant in source localization using mobile platforms, such as the internet of vehicles, shipborne radars, and underwater sonars. To the best of our knowledge, this problem has not been formally studied in the literature despite its clear applicability.

In many early works, localization was achieved using a two-step procedure: first, some intermediate parameters were estimated, e.g., AoA, ToA, and/or TDoA, then emitters were located by fusing these parameters. Following this two-step procedure, self-calibration can be performed either in the first step [7,8,9] or in the second step [10,11,12]. There are two issues—data association and error propagation—that limit performance. For example, consider the case of localization using AoA information. Each sensor acquires multiple AoA parameters. These AoA parameters need to be associated with multiple emitters and then fused to calculate emitter locations. It is well known that data association is NP-hard in general [23], and that errors in parameter estimation and/or data association can deteriorate the localization performance severely.

To address the limitations of this two-step procedure, direct localization [24,25,26] has become the main approach in more recent works. The key idea is to build a mapping directly from locations to sensor measurements and then to search for locations that best match the measured data. In the context of joint localization and calibration, the mapping from locations to measurements is an operator specified by the parameters to be calibrated [13,14,15,16,17]. In [14,15,16], the authors studied the problem of positioning a single emitter with multiple snapshots. The authors of [17] studied the array calibration and direction estimation problems from a Bayesian perspective and provided a unified method to handle the single array errors of mutual coupling, gain, and phase errors. Recent work [13] extends the localization model to multiple emitters using a single moving array with gain and phase errors.

In this paper, we also followed the idea of direct localization. The main contributions are as follows:

• The signal model was built on a gridless mapping directly from emitter locations and array directional errors to received signals. Many localization [17] or imaging [27,28,29] methods discretize the parameter space into grids and assume that true parameters lie on the grids. However, in our setting, multiple arrays are involved, and there is nearly always a grid mismatch problem. For example, consider a system with three arrays positioned at different locations in different directions. The intersection of the discrete grids (in angle) of the arbitrary two arrays is a set of discrete irregular points. Most of these intersection points are off the grid of the discrete grid of the third array. This grid mismatch problem could result in severe degradation in performance [30]. To avoid this problem, both emitter locations and array directional errors are modeled as real numbers (hence, the parameter space is continuous) in our work. Similar modeling for joint localization and calibration also appeared in recent work [13].
• Atomic norm minimization (ANM) [31,32] is used to estimate the unknown number of emitters. The majority of the existing works assume prior knowledge of the number of emitters. In practice, such prior knowledge may not always be available. To handle this challenge, it is reasonable to assume that the number of emitters is relatively small, yielding a sparse model. Atomic norm can be viewed as a generalization of ${\ell }_1$-norm and promotes sparsity in the continuous parameter space.
• We apply group sparsity [33] to enforce geometric consistency. The feasibility of exploiting group sparsity lies in that we consider the multiple-measurement scenarios with a small number of emitters, where sparsity is generally exploited for performance improvement. Note that there are multiple sensor arrays for joint localization and the received signals from the same emitter should be geometrically consistent if these sensor arrays are perfectly calibrated. This means that source signals that originate from the same position but are received at different sensor arrays should be either all zero (no emitter at the location) or simultaneously nonzero (an emitter at the location). This consistency is naturally described by group sparsity.
  Group sparsity helps align ‘ghost’ emitter locations resulting from calibration errors. Due to calibration errors, source signals from the same location may be treated as from different locations from the view of different antenna arrays. Group sparsity promotes consensus locations where signal components originate, and eliminates possible ‘ghost’ locations caused by calibration errors.
  In this work, we apply the concept of group sparsity to source signal locations. This is similar to—but different from—its common usage for multiple measurement vector (MMV). In a typical MMV, multiple measurement vectors corresponding to directions share the same sparsity patterns, which are linear maps. Here, locations instead of directions (from views of different arrays) share the same sparsity patterns and there are nonlinear mappings from locations to measurement vectors. In fact, our model and simulations show that our scheme works for a single snapshot case where there is only a single measurement vector at each sensor array.
• A tailored optimization procedure has been developed for joint localization and calibration. There are several typical approaches used to solve an ANM problem in a continuous parameter space. When the atomic norm is defined on the set of steering vectors, it is possible to reformulate ANM to semi-definite programming (SDP) problem [32,34] and solve it efficiently using off-the-shelf convex toolboxes, such as CVX [35]. In the more general case, the alternating descent conditional gradient (ADCG) [36] can be adopted.
  The optimization problem for joint localization and calibration has a different nature. For a given calibration error, the optimization problem is a standard ANM problem and can be solved by ADCG. However, in the problem at hand, the optimization is with respect to calibration error as well. As a consequence, we designed our own optimization procedure that was inspired by the spirit of ADCG but significant modifications were made to simplify the process. Specifically, the optimization alternates between updating source signal locations and coefficients by fixing calibration errors and updating calibration errors by fixing locations. The objective function monotonically decreases during the optimization process and, hence, convergence is guaranteed.
• Other results presented in this paper include (1) simulations verifying the effectiveness of the proposed scheme; (2) the Cramér Rao lower bound; we numerically compare it to the simulations; and (3) a necessary condition as a rule of thumb to decide the feasibility of joint localization and calibration.

The rest of the paper is organized as follows. Section 2 describes the signal model. Section 3 derives a necessary condition for the feasibility of joint localization and calibration. Section 4 briefly reviews the basic concepts of group sparse recovery and ANM, followed by an optimization formulation of joint localization and calibration problems. Section 5 develops a tailored optimization method to solve the formulated optimization problem with a convergence guarantee. Numerical simulation results are shown in Section 6. We draw our conclusions in Section 7.

Notations used in this paper are depicted as follows. We use $\mathbb{R}$ and $\mathbb{C}$ to denote the sets of real and complex numbers, respectively. Notation $\mathrm{Re}(·)$ and $\mathrm{Im}(·)$ are used for the real and imaginary parts of a complex-valued argument. The amplitude of a scalar is represented by $|·|$. The largest integer less than the real number x is expressed as $\lfloor x\rfloor$. Uppercase boldface letters denote matrices(e.g., $\mathit{C}$) and lowercase boldface letters denote vectors (e.g., $\mathit{c}$). The element of matrix $\mathit{C}$ in the m-th row and the n-th column is written as ${\left[\mathit{C}\right]}_{m,n}$ and ${\left[\mathit{c}\right]}_n$ denotes the n-th entry of vector $\mathit{c}$. The complex conjugate operator, transpose operator, and the complex conjugate–transpose operator are denoted by ${}^{*}{,}^T{,}^H$, respectively. Denote the Hadamard product by ⊙ and matrix column vectorization by $\mathrm{vec}(·)$. We use ${\parallel ·\parallel }_p, p=1,2$ as the $l_p$ norm of an argument. We denote the imaginary unit for complex numbers by $j:=\sqrt{-1}$.

2. Signal Model

In this section, the signal model of the passive joint emitter localization with the array directional error is given.

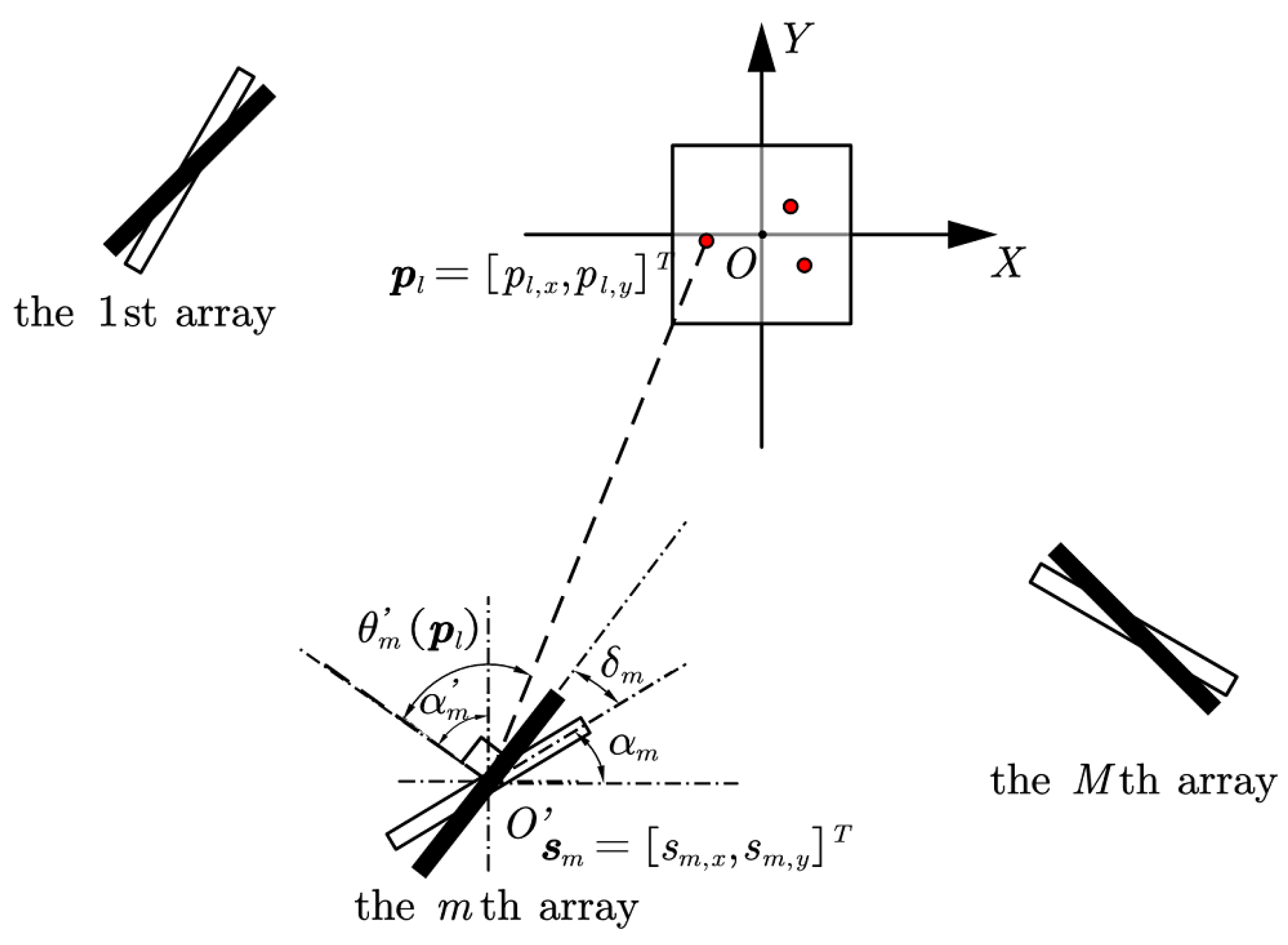
We consider a two-dimensional (2D) plane, denoted by $XOY$. Assume that there are L static emitters closely spaced near the origin point O, continuously transmitting signals at frequency $f_c=c/\lambda$, where c denotes the light speed and $\lambda$ denotes the wavelength. We denote the l-th emitter position by ${\mathit{p}}_l={[p_{l,x},p_{l,y}]}^T\in \mathcal{U}$, where $\mathcal{U}$ denotes the region of emitter positions. There are M sensors with passive uniform linear arrays (ULA) receiving the transmitted signals from the emitters. We assume that the manifold of each array is exactly known and there is no array element location perturbation. These errors are usually calibrated by offline or online [37] methods. Here we use ULAs for simplicity. Note that our optimization formulation and method (developed in Sections IV and V, respectively) do not rely on structured matrices tied to uniform arrays. They can be extended to other array geometries. Denote by $N_m$ the number of array elements and by $d_m$ the interval between adjacent elements in the m-th sensor. We use ${\mathbf{s}}_m={[s_{m,x},s_{m,y}]}^T$ and ${\alpha }_m$ to represent the position of the reference element in the m-th sensor and the angle of the m-th array surface versus the X axis, respectively, which determine the deployment of the array. The angle of the l-th emitter w.r.t. the normal direction of the m-th array, i.e., the AOA, is denoted by ${\theta }_m\left({\mathit{p}}_l\right)$, expressed as

$${\theta }_m\left({\mathit{p}}_l\right)=\arctan \frac{p_{l,x}-s_{m,x}}{p_{l,y}-s_{m,y}}+{\alpha }_m,$$

(1)

for $m=1,\dots ,M$ and $l=1,\dots ,L$.

In practice, the perturbations in the sensor deployment are inevitable, resulting in that the actual parameters ${\alpha }_m$ are different from their pre-assumed counterparts, denoted by ${\alpha }_m^{\prime }$. We denote array directional errors by ${\delta }_m={\alpha }_m^{\prime }-{\alpha }_m\in \Delta$, where $\Delta$ is a rough range of ${\delta }_m$. The AOA measurements, which are crucial in passive joint emitter localization, are affected by array directional errors. In particular, the AOA of the l-th emitter w.r.t. the pre-assumed m-th sensor, denoted by ${\theta }_m^{\prime }\left({\mathit{p}}_l\right)$, is expressed as

$${\theta }_m^{\prime }\left({\mathit{p}}_l\right)=arctan\frac{p_{l,x}-s_{m,x}}{p_{l,y}-s_{m,y}}+{\alpha }_m^{\prime }={\theta }_m\left({\mathit{p}}_l\right)+{\delta }_m,$$

(2)

for $m=1,\cdots ,M$ and $l=1,\cdots ,L$. Note that array directional error is highly structured, prevalent on mobile platforms, but not widely studied yet. What is the effect of the kind of error and how to achieve self-calibration well are still open problems, which are our focus in this paper. The geometry of the arrays and emitters is depicted in Figure 1.

Before introducing the signal model, there are some pre-conditions listed as follows: (1) The baseband signals of the transmitted signals from emitters are assumed to be narrow-band and wide-sense stationary. (2) The emitters are in the far field [38]. (3) In each array, one sample is expected to be taken at the same time as a single snapshot. Here, we do not assume that time synchronization is accurate for TDOA measurements. However, we assume a loosely synchronized system such that the locations of emitters and sensors remain unchanged during the measuring process. (We leave the multiple-snapshot case for future investigations.) Then, the received signal of the m-th array is given by

$${\mathit{r}}_m=\sum _{l=1}^L{\gamma }_{l,m}{\mathit{c}}_m\left(f_{l,m}\right)+{\mathit{w}}_m,$$

(3)

where ${\mathit{r}}_m\in {\mathbb{C}}^{N_m\times 1}$, ${\gamma }_{l,m}$ is a complex coefficient characterizing the unknown envelope of the transmitted signals from the l-th emitter to the m-th array, $f_{l,m}=\frac{d_m}{\lambda }sin{\theta }_m\left({\mathit{p}}_l\right)$ is often referred to the spatial frequency, ${\mathit{w}}_m\in {\mathbb{C}}^{N_m\times 1}$ denotes the additive noise, and the steering vector ${\mathit{c}}_m(·)$ is denoted by

$${\mathit{c}}_m\left(f_{l,m}\right)={\left[e^{j2\pi f_{l,m}·0},\cdots ,e^{j2\pi f_{l,m}·(N_m-1)}\right]}^T,$$

(4)

where $l=1,\dots ,L$ and $m=1,\dots ,M$.

By substituting (2) with (3), we recast the received signals as

$${\mathit{r}}_m=\sum _{l=1}^L{\gamma }_{l,m}{\mathit{c}}_m({\mathit{p}}_l,{\delta }_m)+{\mathit{w}}_m,$$

(5)

where the steering vector ${\mathit{c}}_m(·,·)$ is denoted by

$${\mathit{c}}_m(\mathit{p},{\delta }_m)={\left[e^{j2\pi \frac{d_m}{\lambda }\sin \left({\theta }_m^{\prime }\left(\mathit{p}\right)-{\delta }_m\right)·0},\cdots ,e^{j2\pi \frac{d_m}{\lambda }\sin \left({\theta }_m^{\prime }\left(\mathit{p}\right)-{\delta }_m\right)·(N_m-1)}\right]}^T.$$

(6)

For abbreviations, we use $\mathbf{\delta }={[{\delta }_1,\cdots ,{\delta }_M]}^T$, $\mathit{P}=[{\mathit{p}}_1,\cdots ,{\mathit{p}}_L]$, $\Gamma$ with ${[\Gamma ]}_{l,m}={\gamma }_{l,m}$ and $\mathcal{R}=\{{\mathit{r}}_1,\dots ,{\mathit{r}}_M\}$ to represent the directional errors vector, position matrix, complex coefficient matrix, and measurement set, respectively, $l=1,\cdots ,L,m=1,\cdots ,M$. In (5), we note that $\mathcal{R}$, M, $N_m$, and the function of ${\theta }_m^{\prime }(·)$ as (2) are known. Unknown parameters $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ and L are to be estimated.

Note that (5) is an incoherent model, which means that the intensity ${\gamma }_{l,m}$ of the l-th emitter varies in amplitude and phase w.r.t. different sensors and the relationship between them is unknown. Therefore, we do not require the time synchronization assumption that guarantees the specific relationship of ${\gamma }_{l,m}$ between all the sensor signals. Moreover, since only single-snapshot measurements are used, signal statistic assumptions for multiple-snapshot cases are also not required. The challenge of recovering emitter positions $\mathit{P}$ from (5) lies in the highly non-linear structure for frequencies $f_{l,m}$ w.r.t. ${\mathit{p}}_l$ and unknown array directional errors $\mathbf{\delta }$, $l=1,\dots ,L$ and $m=1,\dots ,M$.

3. Necessary Conditions

In this section, we explain the feasibility of self-calibrating array directional errors in passive joint emitter localization from the aspect of necessary conditions.

First, we give a necessary condition in our scenario by comparing the number of equations and unknowns. In particular, for the equations, we note that the principle of the passive joint emitter localization is to use distributed arrays to measure the emitters from different directions, and the intersections of the direction lines indicate the emitter positions. Each direction line corresponds to an equation as (2). Since there are L emitters and M arrays, i.e., $LM$ direction lines in total, the number of such equations is $LM$. For the unknowns, there are L emitter positions in the 2D plane, ${\mathit{p}}_l={[p_{l,x},p_{l,y}]}^T$, and M array directional errors to estimate, i.e., $2L+M$ real-valued unknown parameters in total. A necessary condition to achieve the joint estimation of $\{\mathit{P},\mathbf{\delta }\}$ is to guarantee that the number of equations is larger than the unknowns, i.e.,

$$LM⩾2L+M.$$

(7)

From (7), it is not hard to find that when $L⩾2$, many enough sensors M guarantee (7), yielding the potential of self-calibrating array directional errors. However, in practice, due to the impact of noises, sensor system settings, sensor and emitter spatial geometries, and so on, more sensors than the threshold in (7) are generally in demand.

When $L=1$, (7) does not always hold, no matter what M is, yielding the inevitable failure of the joint estimation of $\{\mathit{P},\mathbf{\delta }\}$. It implies that in the passive joint emitter localization, we are not able to calibrate all directional errors when $L=1$. Here, we further explain this phenomenon as follows: If $L=1$, for any true values $\{{\mathit{p}}_1,\mathbf{\delta }\}$ and a false emitter position ${\mathit{p}}_1^{\prime }$, it is always available to estimate the directional errors as ${\delta }_m^{\prime }={\theta }_m^{\prime }\left({\mathit{p}}_1^{\prime }\right)-{\theta }_m^{\prime }\left({\mathit{p}}_1\right)+{\delta }_m$, such that the following equation is satisfied:

$$\sin \left({\theta }_m^{\prime }\left({\mathit{p}}_1\right)-{\delta }_m\right)=\sin \left({\theta }_m^{\prime }\left({\mathit{p}}_1^{\prime }\right)-{\delta }_m^{\prime }\right),$$

(8)

where $m=1,\dots ,M$. Therefore, $\{{\mathit{p}}_1^{\prime },{\mathbf{\delta }}^{\prime }\}$ yields the same signals as $\{{\mathit{p}}_1,\mathbf{\delta }\}$ according to (5) when $\Gamma$ and noises are fixed. This indicates that $\{{\mathit{p}}_1^{\prime },{\mathbf{\delta }}^{\prime }\}$ and $\{{\mathit{p}}_1,\mathbf{\delta }\}$ cannot be distinguished only from the received signals $\mathcal{R}$. Correspondingly, the joint estimation of $\{\mathit{P},\mathbf{\delta }\}$ can be either one of them and will fail eventually.

To avoid the estimation failure when $L=1$, on the one hand, we assume that there are some precise arrays without errors. Denote the number of arrays with errors by $M_r$, $1<M_r<M$. A necessary condition in this case is $M⩾2+M_r$. On the other hand, we consider another scenario assuming that the directional errors in multiple sensors are the same. Similar assumptions on the errors can be seen in [13], where distributed sensor observations are obtained by sampling different moments of a single moving array with errors, and the position relationship of each array at different samplings is assumed to be exactly known. Under this $L=1$ condition, we have 3 unknowns (2 for emitter positions and 1 for the directional error) and M equations, yielding the necessary condition as $M⩾3$.

In summary, we explain the potential of self-calibrating the directional errors in terms of necessary conditions when $L⩾2$. For the $L=1$ case, where the necessary condition always does not hold, we also give the additional conditions for the self-calibration to be available. Note that in the sequel, our proposed method is suitable for both cases.

4. Optimization Formulation

In this section, a direct localization formulation is proposed, which encodes group sparsity and self-calibration together. In particular, we first explain the significance and the challenge of exploiting group sparsity in Section 4.1, and then review the typical gridless sparse recovery methods, ANM and group ANM, in Section 4.2. Finally, we extend group ANM for the passive joint emitter localization with sensor self-calibration in Section 4.3.

4.1. Group Sparsity Exploitation

In this subsection, we explain the significance and the challenge of exploiting group sparsity in passive joint emitter localization with sensor self-calibration.

The direct localization formulation incorporates multiple distributed sensors and realizes a direct mapping of their measurements to emitter positions, which avoids data association. Due to the sparsity of the emitters in the spatial distribution, it is a common belief of using sparse recovery methods to improve the localization performance. However, exploiting sparsity in the measurement of each sensor separately maps the same emitter to different positions, which results in many possible ‘ghost’ emitters.

To solve this problem, group sparsity, which aims to map the same emitter to the same position block, is generally used in the distributed sensor network and has proven to achieve better performance [39,40,41]. In particular, in our scenario, group sparsity promotes geometric consistency and has the potential to align ‘ghost’ emitter positions resulting from the errors. By exploiting group sparsity, the information of spatial geometry related to the array positions, emitter positions, and array directional errors is fully utilized, which yields a good localization performance.

The group sparse recovery methods are divided into two main categories, grid-based and gridless approaches. The grid-based approach assumes that the true parameter values exactly lie on some discrete grids of a known grid set and a sparse optimization problem is formulated to determine on which grids the true values are located. However, this assumption is usually impractical and the grid mismatch problem is inevitable, which results in significant performance degradation [30]. To this end, the gridless approach, such as ANM [31,32] uses more sophisticated mathematical tools to achieve sparse recovery on the continuum. There are some existing works [34,42] that extend the ANM approach to group sparse scenarios, named here as ’group ANM’. However, these methods are based on Fourier atoms and do not consider the model errors, yielding the challenge of applying them to our scenario directly.

A major difference between atomic norm minimization and typical low-rank norm minimization [43,44] lies in whether they have constraints on the basis. Atomic norm minimization assumes a specific basis/atoms and aims to recover the unknown frequencies of the atoms. Typical low-rank minimization mostly does not have constraints on the basis, i.e., the space of singular vectors, and solves a high-dimensional matrix completion problem. Since our scenario is a one-dimensional frequency estimation problem with a specific basis, it is more suitable to use atomic norm minimization to exploit more signal structure for better performance.

4.2. ANM and Group ANM

In this subsection, a brief review of ANM and group ANM is present in Section 4.2.1 and Section 4.2.2 as a preliminary, respectively.

4.2.1. ANM

Typical ANM stems from the frequency estimation from a superimposition of complex sinusoids, given by

$$\mathit{x}=\sum _{l=1}^L{s}_l\mathit{a}(f_l,{\varphi }_l)\in {\mathbb{C}}^{N\times 1},$$

(9)

where $f_l\in [0,1)$, $s_l>0$ and ${\varphi }_l\in [0,2\pi )$ are unknown parameters to estimate, denoting frequency, amplitude and phase of the l-th sinusoid, respectively, $\mathit{a}(f,\varphi )\in {\mathbb{C}}^{N\times 1}$ with entry ${\left[\mathit{a}(f,\varphi )\right]}_n=e^{j\left(2\pi f\right(n-1)+\varphi )}$ is defined as a linear spectral atom, $n=1,\dots ,N$, and L denotes the number of sinusoids. Denote by $\mathcal{A}=\left\{\mathit{a}\right(f,\varphi ):f\in [0,1),\varphi \in [0,2\pi \left)\right\}$ the set of atoms.

Then, atomic norm ${\parallel ·\parallel }_{\mathcal{A}}$ is defined by identifying its unit ball with the convex hull of $\mathcal{A}$, $\mathrm{conv}\left(\mathcal{A}\right)$, given by

$$\begin{array}{cc}\hfill {\parallel \mathit{x}\parallel }_{\mathcal{A}}& =inf\{t>0:\mathit{x}\in t\mathrm{conv}(\mathcal{A}\left)\right\}\hfill \\ \hfill & =\underset{\begin{array}{c}{s}_l>0,{\varphi }_l\in [0,2\pi ),\\ f_l\in [0,1)\end{array}}{inf}\left\{\sum _l{s}_l:\mathit{x}=\sum _l{s}_l\mathit{a}(f_l,{\varphi }_l)\right\}.\hfill \end{array}$$

(10)

The atomic norm in (10) is regarded as the continuous counterpart of the typical $l_1$ norm in grid-based sparse recovery methods. Moreover, ANM aims to solve a convex optimization problem minimizing (10). This ANM problem is proven to be equivalent to a semi-definite programming (SDP) problem and performs well when the frequencies $f_l$ in (10) are well separated [32].

4.2.2. Group ANM

Based on the ANM above, we consider that there are M measurement vectors of L complex sinusoids, with the m-th vector given by

$${\mathit{x}}_m=\sum _{l=1}^L{s}_{l,m}\mathit{a}(f_l,{\varphi }_{l,m})\in {\mathbb{C}}^{N_m\times 1},$$

(11)

where $f_l\in [0,1)$, $s_{l,m}>0$ and ${\varphi }_{l,m}\in [0,2\pi )$ denote the frequency, amplitude, and phase of m-th measurement w.r.t. the l-th sinusoid, respectively. These amplitudes and phases vary with m, indicating the incoherence of the signal models.

Compared with applying ANM separately to each measurement, group ANM utilizes an additional property where the positions of nonzero frequencies for different measurements are generally the same or close. Therefore, the group atomic norm, denoted by ${\parallel ·\parallel }_{\mathcal{G}}$, is defined as

$$\begin{array}{c}\hfill {\parallel \mathcal{X}\parallel }_{\mathcal{G}}=\underset{\begin{array}{c}{s}_{l,m}>0,\\ {\varphi }_{l,m}\in [0,2\pi ),\\ f_l\in [0,1)\end{array}}{\inf }\left\{\sum _l\sqrt{\sum _{m=1}^M{s}_{l,m}^2}:{\mathit{x}}_m=\sum _l{s}_{l,m}\mathit{a}\left(f_l,{\varphi }_{l,m}\right),m=1,\cdots ,M\right\},\end{array}$$

(12)

where $\mathcal{X}=\{{\mathit{x}}_1,\dots ,{\mathit{x}}_M\}$ denotes the set of multiple measurements. The group atomic norm in (12) is regarded as the continuous counterpart of the $l_{2,1}$ norm of grid-based group sparse recovery methods and group ANM is to solve a convex optimization problem minimizing (12) under certain constraints. Similar to ANM, group ANM has an equivalent SDP formulation [34], which is solved efficiently.

Here, we explain why the group ANM approach is not directly suitable for our scenario. In particular, we compare the multiple measurement vectors (MMV) model (11) with the received signals (5), and there are two main differences: (1) There exists the unknown directional error $\mathbf{\delta }$ in (5), which is not present in (11); (2) Atoms in (11) and (5) are different because $f_l$ in (11) are frequencies of the line spectrum, while ${\mathit{p}}_l$ in (5) is not, due to the non-linearity of the map ${\mathit{p}}_l\mapsto f_{l,m}$. Here, we exploit the geometrical consistency where the emitters share the same ${\mathit{p}}_l$, and note that the spatial frequencies of these emitters w.r.t. different sensor arrays are different. These differences hold back applying traditional group ANM directly in our scenario, which relies on consistency in the spatial frequency $f_l$.

4.3. Group ANM Incorporating Self-Calibration

In this subsection, to achieve passive joint emitter localization with sensor errors, we established a new sparse recovery model that encodes group ANM and self-calibration together.

In particular, we heuristically bring the array directional error $\mathbf{\delta }$ to the group atomic norm and then construct a new sparse representation operator, denoted by ${\parallel ·\parallel }_{\mathcal{S}}$,

$$\begin{array}{c}\hfill {\parallel \mathcal{X}\parallel }_{\mathcal{S}}=\underset{\mathit{P},\Gamma ,\mathbf{\delta }}{\inf }\left\{\sum _l\sqrt{\sum _{m=1}^M{\left|{\gamma }_{l,m}\right|}^2}:{\mathit{x}}_m=\sum _l{\gamma }_{l,m}{\mathit{c}}_m\left({\mathit{p}}_l,{\delta }_m\right),m=1,\dots ,M\right\},\end{array}$$

(13)

where $\mathcal{X}=\{{\mathit{x}}_1,\dots ,{\mathit{x}}_M\}$ denotes the set of noise-free measurements in passive joint emitter localization with sensor self-calibration and the new atoms ${\mathit{c}}_m$ are defined as (6). Imposing a new optimization problem based on this operator leads to a joint estimation of $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ and L. Therefore, we formulate a denoising lasso problem as

$$\underset{\mathit{P},\Gamma ,\mathbf{\delta }}{min}\frac{1}{2}\sum _{m=1}^M{∥{\mathit{r}}_m-{\mathit{x}}_m∥}_2^2+\mu {\parallel \mathcal{X}\parallel }_{\mathcal{S}},$$

(14)

where $\mu >0$ is the regularization parameter characterizing group sparsity and the bias between ${\mathit{r}}_m$ and ${\mathit{x}}_m$, different from group ANM in (12) and (14), which properly address the array directional error in the passive joint emitter localization and exploit group sparsity on the continuum. However, difficulty emerges since (14) is a non-convex optimization problem with multiple unknowns as $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$. This is a consequence of the fact that the proposed operator in (13) is not corresponding to convex hulls as atomic norms due to the existence of $\mathbf{\delta }$. To solve the above problem, we propose a tailored method, detailed in Section 5.

5. Solving Optimization Problems

In this section, we propose to solve (14), yielding the estimates of unknown parameters $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$. Overall, we implement rough position estimation emitter-by-emitter, while locally improving these estimates by a two-loop alternating gradient descent in both emitter positions and the sensor errors. The gradient descent procedure guarantees the decrease of the non-negative cost function at each step, and hence a convergence is achieved. To clearly introduce the proposed method called group sparsity exploitation for self-calibration (GSE−SC), the framework is shown in Section 5.1, and the local improvement is detailed in Section 5.2.

5.1. Framework

Our proposed method, GSE−SC, is based on such a scheme: the emitters are added to the support set one by one, then all the unknown variables are improved locally by alternating the gradient descent and support set prune. Before introducing this algorithm framework, we denote by t the counter of steps. Assume that after $t-1$ steps, we obtain the position matrix ${\widehat{\mathit{P}}}^{t-1}$ that contains $t-1$ emitter position estimates, i.e., ${\widehat{\mathit{P}}}^{t-1}=[{\widehat{\mathit{p}}}_1,\cdots ,{\widehat{\mathit{p}}}_{t-1}]$, the corresponding complex intensity matrix ${\widehat{\Gamma }}^{t-1}$ with the $(l,m)$-th entry ${\widehat{\gamma }}_{l,m}^{t-1}$, as well as the directional errors ${\widehat{\mathbf{\delta }}}^{t-1}={[{\widehat{\delta }}_1^{t-1},\cdots ,{\widehat{\delta }}_M^{t-1}]}^T$.

It is well-known that initialization plays an important role in iterative methods. In the GSE−SC, we initialize the emitter position in the t-th step by using grid-based group sparse recovery methods, particularly by solving the following $l_{2,1}$ norm minimization lasso problem as

$$\widehat{\mathit{S}}=\underset{\mathit{S}}{\mathrm{argmin}}\frac{1}{2}\sum _{m=1}^M{∥{\mathbf{e}}_m^{t-1}-{\mathit{A}}_m{\left[\mathit{S}\right]}_m∥}_2^2+{\mu }_s{\parallel \mathit{S}\parallel }_{2,1},$$

(15)

where ${\mu }_s>0$ is the regularization parameter, the $l_{2,1}$ norm is defined as

$$\begin{array}{c}\hfill {\parallel \mathit{S}\parallel }_{2,1}=\sum _{g=1}^G\sqrt{\sum _{m=1}^M{\left|{\left[\mathit{S}\right]}_{g,m}\right|}^2},\end{array}$$

(16)

and ${\mathit{A}}_m$ is the dictionary matrix constructed by uniformly dividing the range of emitter position $\mathcal{U}$ into $G=g_x\times g_y$ grids as ${\overline{\mathit{p}}}_g,g=1,\dots ,G$, and concatenating the corresponding atoms, i.e., ${\left[{\mathit{A}}_m\right]}_g={\mathit{c}}_m({\overline{\mathit{p}}}_g,0)$. Here, ${\mathbf{e}}_m^{t-1}$ is the residual signal of the m-th sensor in the $(t-1)$-th step, given by

$${\mathbf{e}}_m^{t-1}={\mathit{r}}_m-\sum _{l=1}^{t-1}{\widehat{\gamma }}_{l,m}^{t-1}{\mathit{c}}_m({\widehat{\mathit{p}}}_l,0).$$

(17)

The t-th initialization of the emitter position, ${\widehat{\mathit{p}}}_t$, is then derived from the optimal solution $\widehat{\mathit{S}}$ by selecting the grid with the largest intensity as

$${\widehat{\mathit{p}}}_t={\overline{\mathit{p}}}_{\widehat{g}},\widehat{g}=\underset{g}{argmax}{\parallel {\left[{\widehat{\mathit{S}}}^T\right]}_g\parallel }_2.$$

(18)

The t-th corresponding intensity matrix ${\Gamma }^t$ is then initialized by minimizing the temp residual as

$$\underset{{[\Gamma ]}_m}{\min }{∥{\mathit{r}}_m-\sum _{l=1}^t{\gamma }_{l,m}{\mathit{c}}_m({\widehat{\mathit{p}}}_l,0)∥}_2^2$$

(19)

for $m=1,\cdots ,M$, which is solved directly via the least square method, yielding the closed form solutions as

$${\left[{\widehat{\Gamma }}^t\right]}_m={\left({\mathit{B}}_m^H{\mathit{B}}_m\right)}^{-1}{\mathit{B}}_m{\mathit{r}}_m,$$

(20)

where ${\mathit{B}}_m=[{\mathit{c}}_m({\widehat{\mathit{p}}}_1,0),\dots ,{\mathit{c}}_m({\widehat{\mathit{p}}}_t,0)]$. Without prior knowledge, directional error ${\widehat{\mathbf{\delta }}}^t$ is, thus, initialized as $\mathbf{0}$.

The initialized $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ is then improved locally by an alternative gradient descent method to guarantee the decrease of the cost function in (14) and help self-calibrate errors, which is shown in the next subsection. Consequently, we will obtain $\{{\widehat{\mathit{P}}}^t,{\widehat{\Gamma }}^t,{\widehat{\mathbf{\delta }}}^t\}$, which implies the residuals ${\left\{{\mathbf{e}}_m^t\right\}}_{m=1}^M$. Then we repeat the procedures from (15) to (20) to continue the refinement of $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$, and this iteration terminates when t reaches the maximum number of steps, $t_{max}$. Empirically, $t_{max}$ is set to be larger than the emitter number L.

Lastly, for the identification of the emitter number L, we assume that the true L can be exactly estimated by our method, which is introduced in the next subsection. There are specific studies on this issue and some existing principles, such as AIC [45] and BIC [46], have been widely used. Our main contribution is not on this; previous related works are available for reference.

5.2. Joint Estimation of $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$

In this subsection, we detail the local improvement procedure, which aims to bring down the cost function in (14) by an alternating gradient descent method.

The difficulty of solving the optimization problem (14) reflects on two aspects: On the one hand, (14) is non-convex; therefore, a globally optimal solution is hardly guaranteed for most optimization methods. On the other hand, the array directional error $\mathbf{\delta }$ is key to the non-convexity and complexity of (14) and how to self-calibrate $\mathbf{\delta }$ is important for the precise emitter localization.

In response to the difficulties above, our strategy is based on an alternating gradient descent method with a two-loop structure containing an outer loop and an inner loop. In particular, we simultaneously improve the joint estimation of $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ and $\{\mathit{P},\Gamma \}$ by gradient descent in the outer and inner loop, respectively. In between, we prune the support set of $\mathit{P}$ by removing weak elements as $\mathrm{support}(·)$, a typical procedure commonly seen in ANM methods such as alternating descent conditional gradient (ADCG) [36] and greedy CoGEnT [47]. The proposed structure benefits from at least the following three points:

(A1)

The outer loop with gradient descent w.r.t. $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ guarantees bringing the cost function in (14) down.

(A2)

The inner loop inside an outer loop is used to refine $\{\mathit{P},\Gamma \}$ first. In this way, we reduce the probability of converging to local minimums in the outer loop iteration due to the imprecise initialization of $\{\mathit{P},\Gamma \}$.

(A3)

The two-loop structure is designed for self-calibrating $\mathbf{\delta }$ precisely. This is because after the inner loop, $\{\mathit{P},\Gamma \}$ reach their local minimums for a fixed $\mathbf{\delta }$. Then, the iteration direction and step size of gradient descent w.r.t. $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ in the outer loop mainly depends on $\mathbf{\delta }$, which forces $\mathbf{\delta }$ to move to a better estimate.

In particular, we introduce the details of the two-loop structure here. As a preliminary, we use k as the iteration counter of the outer loop, denote intermediate estimate by ${\widehat{·}}^{k-1}$ and initial ${\widehat{·}}^{k=0}$ by ${\widehat{·}}^{t-1}$, where · belongs to the set $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ or $\{{\mathit{p}}_l,{\gamma }_{l,m},{\delta }_m\}$. Moreover, denote by $C(\mathit{P},\Gamma ,\mathbf{\delta })$ the cost function in (14) and by ${\nabla }_{\circ }C({\widehat{\mathit{P}}}^{k-1},{\widehat{\Gamma }}^{k-1},{\widehat{\mathbf{\delta }}}^{k-1})$ the partial derivative of the cost function w.r.t. ∘ at $({\widehat{\mathit{P}}}^{k-1},{\widehat{\Gamma }}^{k-1},{\widehat{\mathbf{\delta }}}^{k-1})$, where ∘ belongs to the set $\{{\mathit{p}}_l,{\gamma }_{l,m},{\delta }_m\}$. For the convenience of the presentation, we remain the calculation of these derivatives in Appendix A.

In the k-th outer loop iteration, the inner loop is first carried out, i.e., $\{{\widehat{\mathit{p}}}_l^{k-1},{\widehat{\gamma }}_{l,m}^{k-1}\}$ are renewed by the gradient descent repeatedly until the maximum number of repetitions $i_{max}$, which is large enough to guarantee convergence. Note that we use this convergence criterion for a brief expression; other criteria (such as stopping the iteration when the gradients are small enough) are also available. Here, let i count the number of the inner loop repetitions, and initialize ${\widehat{·}}^{i=0}$ by ${\widehat{·}}^{k-1}$. Then, we perform

$$\left\{\begin{array}{cc}\hfill {\widehat{\mathit{p}}}_l^i& ={\widehat{\mathit{p}}}_l^{i-1}-{\kappa }^i{\nabla }_{{\mathit{p}}_l}C({\widehat{\mathit{P}}}^{i-1},{\widehat{\Gamma }}^{i-1},{\widehat{\mathbf{\delta }}}^{k-1}),\hfill \\ \hfill {\widehat{\gamma }}_{l,m}^i& ={\widehat{\gamma }}_{l,m}^{i-1}-{\kappa }^i{\nabla }_{{\gamma }_{l,m}}C({\widehat{\mathit{P}}}^{i-1},{\widehat{\Gamma }}^{i-1},{\widehat{\mathbf{\delta }}}^{k-1}),\hfill \end{array}\right.$$

(21)

where ${\kappa }^i$ denotes the step size in the i-th repetition and is determined via the Armijo line search [48]. When the inner loop ends, we achieve the updated parameters denoted by $\{{\tilde{\mathit{P}}}^k,{\tilde{\Gamma }}^k\}$. After the ‘prune support’ procedure, the array directional error ${\widehat{\mathbf{\delta }}}^k$ is then updated by gradient descent together with the immediate parameters $\{{\tilde{\mathit{P}}}^k,{\tilde{\Gamma }}^k\}$ as

$$\left\{\begin{array}{cc}\hfill {\widehat{\mathit{p}}}_l^k& ={\tilde{\mathit{p}}}_l^k-{\kappa }^k{\nabla }_{{\mathit{p}}_l}C({\tilde{\mathit{P}}}^k,{\tilde{\Gamma }}^k,{\widehat{\mathbf{\delta }}}^{k-1}),\hfill \\ \hfill {\widehat{\gamma }}_{l,m}^k& ={\tilde{\gamma }}_{l,m}^k-{\kappa }^k{\nabla }_{{\gamma }_{l,m}}C({\tilde{\mathit{P}}}^k,{\tilde{\Gamma }}^k,{\widehat{\mathbf{\delta }}}^{k-1}),\hfill \\ \hfill {\widehat{\delta }}_m^k& ={\widehat{\delta }}_m^{k-1}-{\kappa }^k{\nabla }_{{\delta }_m}C({\tilde{\mathit{P}}}^k,{\tilde{\Gamma }}^k,{\widehat{\mathbf{\delta }}}^{k-1}),\hfill \end{array}\right.$$

(22)

where the k-th step size ${\kappa }^k$ is also determined via the Armijo line search. The alternating iterations, (21) and (22), continue to be carried out until k reaches the maximum number of steps $k_{\max }$, yielding the end of the outer loop. The specific GSE−SC method is summarized in Algorithm 1.

Algorithm 1 GSE−SC

Input: Signal $\mathcal{R}$ and parameters $\mu$, ${\kappa }^0$, $t_{max}$, $k_{max}$, $i_{max}$. Initialization:${\widehat{\mathit{P}}}^0={\widehat{\Gamma }}^0=⌀$, ${\widehat{\mathbf{\delta }}}^0=\mathbf{0}$, ${\mathbf{e}}_m^0={\mathit{r}}_m$. Sett from 1 to $t_{max}$: (1) Localize the next emitter with (18), yielding ${\widehat{\mathit{p}}}_t$. (2) Update the supports as ${\widehat{\mathit{P}}}^t=[{\widehat{\mathit{P}}}^{t-1},{\widehat{\mathit{p}}}_t]$, the corresponding intensities $\Gamma$ as (20) and ${\widehat{\mathbf{\delta }}}^t=\mathbf{0}$. (3) Alternating gradient descent:   Setk from 1 to $k_{max}$ (outer loop): 1) Refine $\{\mathit{P},\Gamma \}$ using (21) while $i⩽i_{max}$ (inner loop). 2) Prune support as ${\widehat{\mathit{P}}}^t\leftarrow \mathrm{support}\left({\widehat{\Gamma }}^t\right)$. 3) Locally improve $\{\mathit{P},\Gamma ,\mathbf{\delta }\}$ together using (22). Output:${\widehat{\mathit{P}}}^{t_{max}}$, ${\widehat{\Gamma }}^{t_{max}}$ and ${\widehat{\mathbf{\delta }}}^{t_{max}}$.

Note that Algorithm 1 is proposed for the $L⩾2$ case, but is also available for the particular $L=1$ case mentioned in Section 3 by just viewing ${\delta }_m$ for $m=1,\cdots ,M$ as a single unknown parameter and iteratively update it, similarly to (22).

Here, we analyze the complexity of our proposed method. In particular, the complexity depends on the number of iterations. In each iteration, the calculation of the gradient contributes most to the computational burden. Therefore, we evaluate the complexity as follows:

• The number of complex-valued multiplications in each iteration: Executing Step 3.1 requires t times gradient calculation w.r.t. t emitters, respectively, and requires $O\left({\sum }_{m=1}^M{N}_m\right)$ complex-valued multiplications for each emitter. in Appendix A.
• The number of iterations: There are $i_{max}$ inner loops and $k_{max}$ outer loops.

In summary, the complexity of our proposed method is calculated as $O({\sum }_{t=1}^{t_{max}}t·i_{max}{k}_{max}·{\sum }_{m=1}^M{N}_m)$. Compared with grid-based methods, our proposed method has additional complexity in the refinement iterations, yielding more convergence time. This is a trade-off between performance improvement and complexity.

6. Numerical Simulation

In this section, we perform numerical simulations to compare our proposed method GSE−SC with some existing methods, including matched filtering (MF), grid-based group compressed sensing (GCS), ADCG [36], and Cramér-Rao Lower Bound (CRB). In particular, we examine the influence of noises, the array directional errors $\mathbf{\delta }$, the total number of sensors M and the number of biased sensors $M_r$ on the recovery of the emitter position $\mathit{P}$. Meanwhile, the estimation results of array directional error $\mathbf{\delta }$ are also presented. Finally, in the GSE−SC method, we consider the multipath effect on the performance, and the necessary conditions for a precise localization w.r.t. M and $M_r$ and.

6.1. Simulation Setting

We consider using M sensors to passively receive signals from $L=2$ emitters. Each sensor is equipped with a ULA array and the number of array elements is $N_m=12$, $m=1,2,\cdots ,M$. The intervals of the adjacent elements are set as half the wavelength, i.e., $d_m=\lambda /2$. The positions of these sensors are set randomly and uniformly in a circle with a center $(0,0)$ m and a radius of 120 m. The pre-assumed angles, ${\alpha }_m^{\prime }$, are set as 0. Among these M sensors, $M_r$ sensors have unknown array directional errors, denoted imprecise sensors, and the rest of the $M-M_r$ sensors are exactly located. It is assumed known that which sensor has errors and which is exactly located. In the simulations, each entry of $\mathbf{\delta }$ is a random variable, uniformly distributed in $(0,\pi /30]$. Emitter positions are set randomly and uniformly distributed in a circle with a center $(0,0)$ m and a radius of 40 m. The amplitude matrix $\Gamma$ is set as a standard complex Gaussian random matrix. We assume that the additive noise ${\mathit{w}}_m$ is i.i.d. white Gaussian with zero mean and variance ${\sigma }_w^2$, and the signal to noise ratio (SNR) is defined as $1/{\sigma }_w^2$.

We compare our proposed method GSE−SC with MF, GCS, ADCG methods and CRB. In particular, the MF method is used to solve the following optimization problem (23) w.r.t. $\mathit{p}\in \mathcal{U}$, given by

$$\widehat{\mathit{p}}=\underset{\mathit{p}\in \mathcal{U}}{argmax}\sum _{m=1}^M\frac{\parallel {\mathit{c}}_m^H(\mathit{p},0){\mathit{r}}_m{\parallel }_2^2}{N_m}.$$

(23)

Note that in this way, only one emitter is estimated. GCS method solves the lasso problem (15). The position estimates of the L emitters correspond to the L largest values in the set $\left\{\parallel {\left[{\widehat{\mathit{S}}}^T\right]}_i{\parallel }_2,i=1,2,\dots ,g_x\times g_y\right\}$. The ADCG method is detailed in [36]. The CRBs are calculated in Appendix B.

The parameter settings of these methods are shown as follows: The region of interest is set as $\mathcal{U}=[-50,50]\times [-50,50]$ m. The regularization parameter $\mu$ is set by borrowing the corresponding idea in [49]. In the GCS method, we set the grid number as $g_x=g_y=21$. In the GSE−SC method, we set the total iteration times $t_{max}=4$, the outer loop iteration times $k_{max}=200$, and the inner loop iteration times $i_{max}=50$.

We use the indicator root mean square error (RMSE) in the ${\log }_{10}$ scale to measure the recovery performance of $\{\mathit{P},\mathbf{\delta }\}$. In particular, we carry out $T_r$ Monte Carlo trials and denote the RMSE of $\{\mathit{P},\mathbf{\delta }\}$ by

$$\left\{\begin{array}{cc}\hfill & \mathrm{RMSE}\mathrm{of}\mathit{P}:\log \left(\sqrt{\frac{{\sum }_{t=1}^{T_r}{\sum }_{l=1}^L{\parallel {\widehat{\mathit{p}}}_l^t-{\tilde{\mathit{p}}}_l^t\parallel }_2^2}{L{T}_r}}\right),\hfill \\ \hfill & \mathrm{RMSE}\mathrm{of}\mathbf{\delta }:\log \left(\sqrt{\frac{{\sum }_{t=1}^{T_r}{\parallel {\widehat{\mathbf{\delta }}}^t-{\tilde{\mathbf{\delta }}}^t\parallel }_2^2}{M_r{T}_r}}\right),\hfill \end{array}\right.$$

(24)

where $\widetilde{·}$ and $\widehat{·}$ represent the true values and estimation of ·.

To further study the feasibility of the GSE−SC method in certain scenarios, such as $L=1$, we also use the hit rate as the evaluation index. In particular, it is recognized as a successful hit if the RMSE of emitter positions $\mathit{P}$ is less than a specific threshold, denoted by $T_p$. Then the hit rate is defined as the probability of a successful hit.

6.2. Convergence Behavior

Here, we use one numerical example to illustrate the convergence behavior of GSE−SC. We denote the iteration times by $(k-1)i_{\max }+i$. We set $M=8$, $M_r=4$, SNR=25 dB and ${\delta }_1=\frac{\pi }{40},{\delta }_2=\frac{\pi }{50},{\delta }_3=\frac{\pi }{60},{\delta }_4=\frac{\pi }{70},{\delta }_5=\cdots ={\delta }_8=0$. Denote the estimation error of $\mathit{P}$ and $\mathbf{\delta }$ by $\parallel {\mathit{P}}^{*}-\widehat{\mathit{P}}\parallel /\parallel {\mathit{P}}^{*}\parallel$ and $\parallel {\mathbf{\delta }}^{*}-\widehat{\mathbf{\delta }}\parallel /\parallel {\mathbf{\delta }}^{*}\parallel$, respectively, where ${(·)}^{*}$ is the true value and $\widehat{·}$ is the temp estimation in the iteration. The iteration convergence behavior of GSE−SC in a single trial is shown in Figure 2. From Figure 2a, we see that the cost function gradually approaches the true value in the iteration. From Figure 2b, we find that the estimation errors of $\mathit{P}$ and $\mathbf{\delta }$ are gradually close to 0 in the iteration. There is a zigzag in the curve of $\mathbf{\delta }$ because in the GSE−SC we only update $\mathbf{\delta }$ in the outer loop and keep $\mathbf{\delta }$ unchanged in the inner loop. Both simulation results show that GSE−SC converges in the iteration.

6.3. RMSE versus SNR

In this subsection, we compare the performances of MF, GCS, ADCG, and GSE−SC methods with CRB in terms of RMSE under different levels of noise.

In particular, we set the total sensor number $M=8$ and the imprecise sensor number $M_r=4$. We change SNR from 0 to 40 dB and perform $T_r=100$ Monte Carlo trials for each SNR and method. We plot the CRBs of $\mathit{P}$ and $\mathbf{\delta }$ when ${\delta }_m=\pi /30$ for $m=1,\cdots ,M$. Figure 3a,b show RMSEs of $\mathit{P}$ by the tested methods and RMSEs of $\mathbf{\delta }$ using the GSE−SC method, respectively.

From Figure 3a, we find that under the same SNR, the RMSE of $\mathit{P}$ using the GSE−SC method is significantly lower than the counterparts of MF, GCS, and ADCG methods, indicating that GSE−SC outperforms the other methods in the estimation accuracy of emitter positions. Moreover, the RMSE of $\mathit{P}$ by the GSE−SC method decreases much faster along with the increase of SNR compared to the MF, GCS, and ADCG methods. This is because array directional errors play more important roles than noise here, and GSE−SC efficiently alleviates the influence of the errors, while MF, GCS, and ADCG methods do not. Meanwhile, the RMSE of $\mathit{P}$ using the GSE−SC method is close to CRB when SNR is large enough. Figure 3b demonstrates that the RMSE of $\mathbf{\delta }$ using the GSE−SC method decreases along with the increase of SNR and is also close to CRB.

6.4. RMSE versus $\mathbf{\delta }$

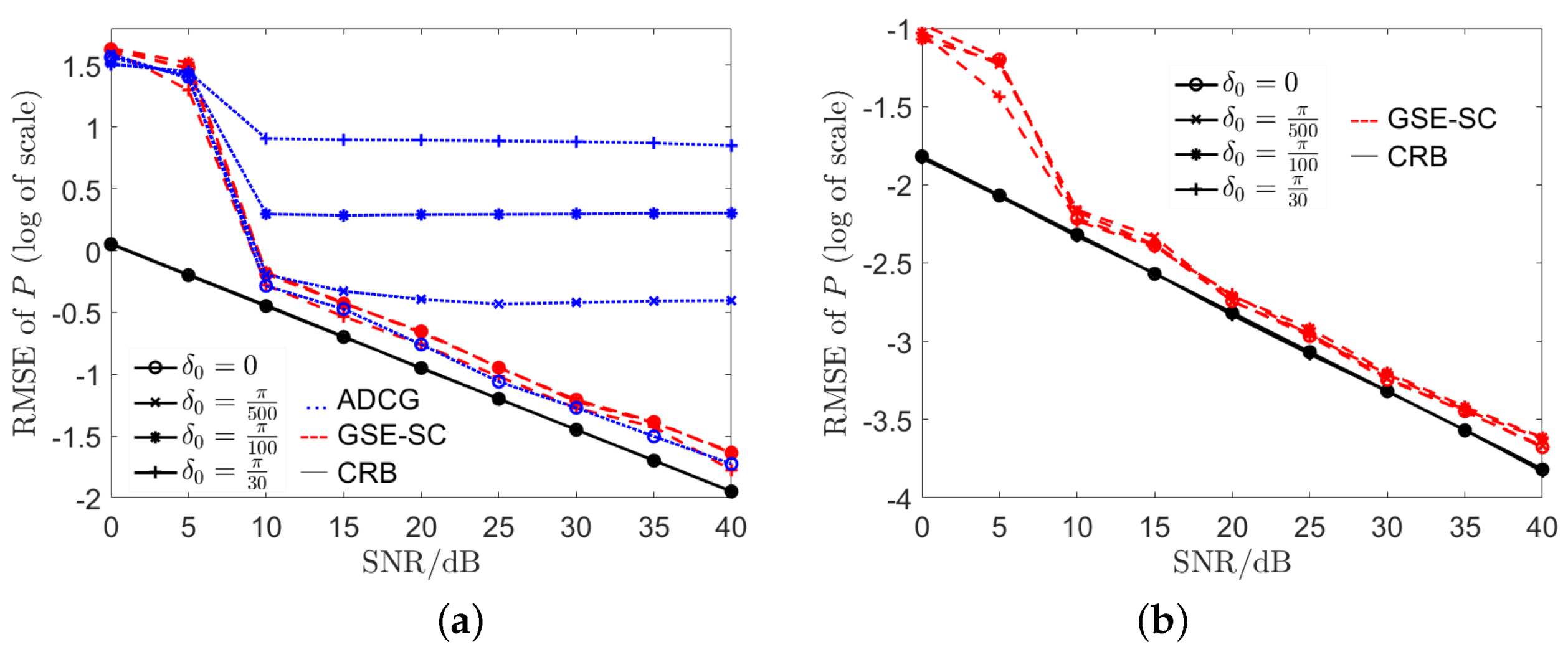
In this subsection, we quantify the effects of array directional errors $\mathbf{\delta }$ on the performance. In particular, we set ${\delta }_1=\cdots ={\delta }_{M_r}={\delta }_0$, and test ${\delta }_0$ with different levels, i.e., ${\delta }_0=0,\pi /500,\pi /100,\pi /30$. We also set $M=8$ and $M_r=4$. Then, we take the ADCG method [36] as a benchmark and compare its performance with GSE−SC for different ${\delta }_0$. The simulation results are shown in Figure 4.

There are 12 and 8 lines in Figure 4a,b, respectively. We find that the CRB lines w.r.t. different ${\delta }_0$ are very close.

From Figure 4a, we first find that GSE−SC is not sensitive to different ${\delta }_0$, and the RMSEs are all close to the CRB when SNR is reasonably large. Second, we find that when ${\delta }_0=0$, the performances of ADCG and GSE−SC are close. As ${\delta }_0$ increases, the performance of ADCG degrades gradually. These results demonstrate that array directional errors affect the localization performance significantly and our proposed method self-calibrates the errors well. From Figure 4b, we find that GSE−SC achieves a good estimation of $\mathbf{\delta }$ when SNR is reasonably large.

6.5. RMSE versus M

In this subsection, we investigate the impact of the number of sensors M on the estimation performance of $\{\mathit{P},\mathbf{\delta }\}$. Here, SNR is fixed as 25 dB, M varies from 2 to 10, and $M_r$ is set as $\lfloor M/2\rfloor$. We then carry out $T_r=100$ Monte Carlo trials in each case of M. The simulation results are given in Figure 5.

We observe from Figure 5 that the RMSEs of $\mathit{P}$ and $\mathbf{\delta }$ using the GSE−SC method first decrease along with the increase of M and then tend to level off. Remarkably, there is a sharp drop from $M=4$ to $M=5$, implying a necessary condition for the GSE−SC method, which in this case is $M⩾5$. In Figure 5a, we find that the RMSE of the GSE−SC method is much smaller than the other tested methods and close to CRB when M is large enough, $M⩾5$. However, as M increases, RMSE and CRB both decrease slowly. This phenomenon helps in the effective use of multiple arrays in practice. Figure 5b shows that the curve of the RMSE of $\mathbf{\delta }$ is similar to the RMSE of $\mathit{P}$. This is because more sensors are beneficial to the self-calibration of sensor errors, which further improves localization accuracy.

Note that in the setting, the number of unknown array directional errors, set as $M_r=\lfloor M/2\rfloor$, changes along with M. More biased sensors result in higher CRB. When $M=3,4$, we have $M_r=1,2$, respectively. Although $M=4$ is larger than 3, the former has more biased sensors to calibrate, $M_r=2>1$. This leads to a zigzag of the CRB curve at $M=3,4$.

6.6. RMSE versus $M_r$

In this subsection, when the total sensor number M and SNR are fixed, we analyze the effect of the number of sensors with errors $M_r$ on the localization performance. This indeed reflects the performance bound of the multiple-array system in self-calibrating directional errors. In particular, we set $M=8$, SNR = 25 dB, and then vary $M_r$ from 1 to 8. The simulation results are shown in Figure 6.

From Figure 6, we find that the RMSEs of $\mathit{P}$ and $\mathbf{\delta }$ using the GSE−SC method are close to CRB when $M_r⩽4$ and increase apparently when $M_r⩾5$. This reflects a performance bound of the GSE−SC method in self-calibrating array directional errors, and the limit is $M_r=4$ when $M=8$ in this scenario. However, in most cases, the GSE−SC method still performs better than other tested methods.

6.7. RMSE versus Multipath Effect

In this section, we consider the multipath effect on the performance of the GSE−SC method. We assume that the effects of the multipath results in spurious emitters, which are located in different positions from the true emitters, have the same/coherent emitted signals. The simulation setting is almost the same as in Figure 3. In particular, a true emitter and a spurious emitter resulted from the multipath (located in different positions), where we set the signals of the spurious emitter to be the same as the true emitter’s. In this way, the signals of the two emitters are coherent. We compare this multipath case with the results of Figure 3 in Figure 7.

From Figure 7, we find that the two results are close, yielding that the multipath scenarios have little effect on the estimation performance of the GSE−SC method. This shows the feasibility of our proposed method in the cases of coherent signals.

6.8. Hit Rate versus M

In this subsection, we look at how many sensors are required to achieve precise localization in the cases with $L=1,2$ when using the GSE−SC method. The corresponding results are compared with the necessary conditions.

Here, we fix the SNR as 25dB. Based on the simulation results in Figure 3 and Figure 5, the threshold of the hit rate is empirically set as $T_p=0.25$. In particular, we focus on the scenarios with $M_r=\lfloor M/2\rfloor$ or $M_r=M$ and $L=1,2$. We perform $T_r=100$ Monte Carlo trials in each case and the hit rate results, as well as the corresponding necessary conditions (distinguished by markers), as shown in Figure 8a. Then, assuming the same ${\delta }_m$ for $m=1,\cdots ,M$ for $L=1$ case in Section 3, we carry out $T_r=100$ trials and the hit rate results, as shown in Figure 8b.

From Figure 8a, we find that when $M_r=\lfloor M/2\rfloor$, the hit rates with $L=1,2$ tend to be 1 as M increases. Moreover, the least number of sensors for hit rates larger than 0.9 are 5 and 7 for $L=1,2$, respectively, which are larger than the necessary conditions. This indicates that the necessary conditions in our scenario are not very tight and more sensors are required in practice. When $M_r=M$ and $L=2$, the hit rates grow slowly as M increases, since more unknowns are to be estimated compared with the $M_r=\lfloor M/2\rfloor$ case. When $M_r=M$ and $L=1$, the failure of the joint estimation of $\{\mathit{P},\mathbf{\delta }\}$ is unavoidable as discussed in Section 3 and, hence, the hit rate is close to 0. Therefore, we do not mark its necessary condition. For the $L=1$ case, assuming the same ${\delta }_m$, Figure 8b indicates that a large enough M, such as $M=7$ in this scenario, guarantees a hit rate close to 1.

7. Conclusions

In this paper, we consider the passive joint emitter localization problem using multiple arrays with array directional errors. We first formulated a direct localization model with self-calibration on these errors; based on this model, group sparsity was exploited to improve the performance. We propose a novel method called GSE−SC to solve this non-convex optimization problem. In particular, a rough position estimation was implemented, emitter-by-emitter, while all unknowns were improved locally by a two-loop alternating gradient descent to bring the cost function down. Simulation results demonstrate that the GSE−SC method outperforms existing methods including MF, GCS, and ADCG methods.