Digital Mapping of Root-Zone Soil Moisture Using UAV-Based Multispectral Data in a Kiwifruit Orchard of Northwest China
Abstract
1. Introduction
2. Materials and Methods
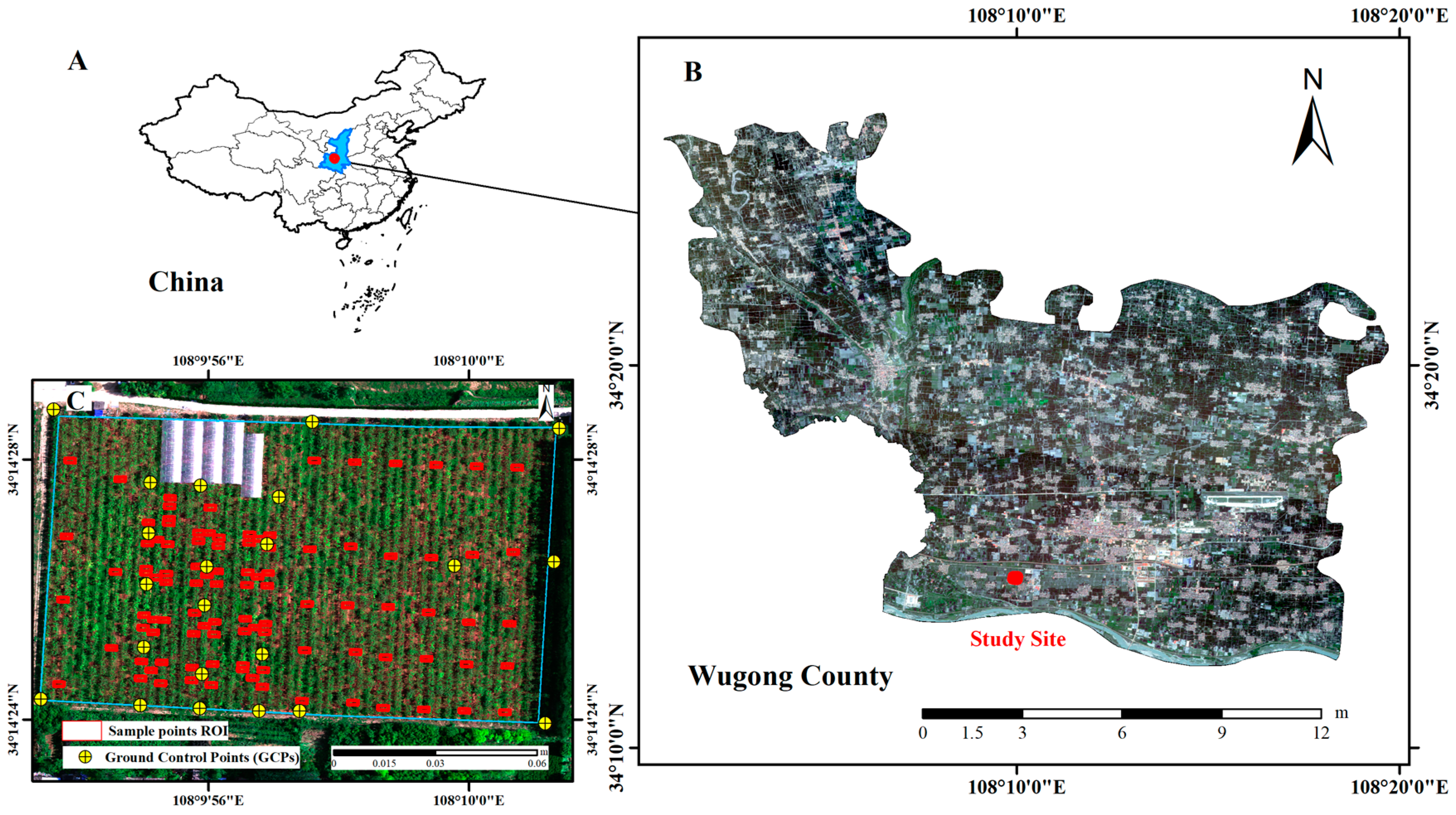
2.1. Test Site and Experimental Setup
2.2. Data Acquisition
2.2.1. SM Field Data Collection
2.2.2. UAV Multispectral Image Acquisition and Preprocessing
2.3. Canopy Spectral Information Extraction
2.4. The Calculation of Spectral Indices
2.5. The Feature Selection of Vegetation Indices
2.6. SM Prediction Model Calibration and Validation
2.6.1. RF Model
2.6.2. SVM Model
2.6.3. ELM Model
2.6.4. Model Calibration and Evaluation
3. Results
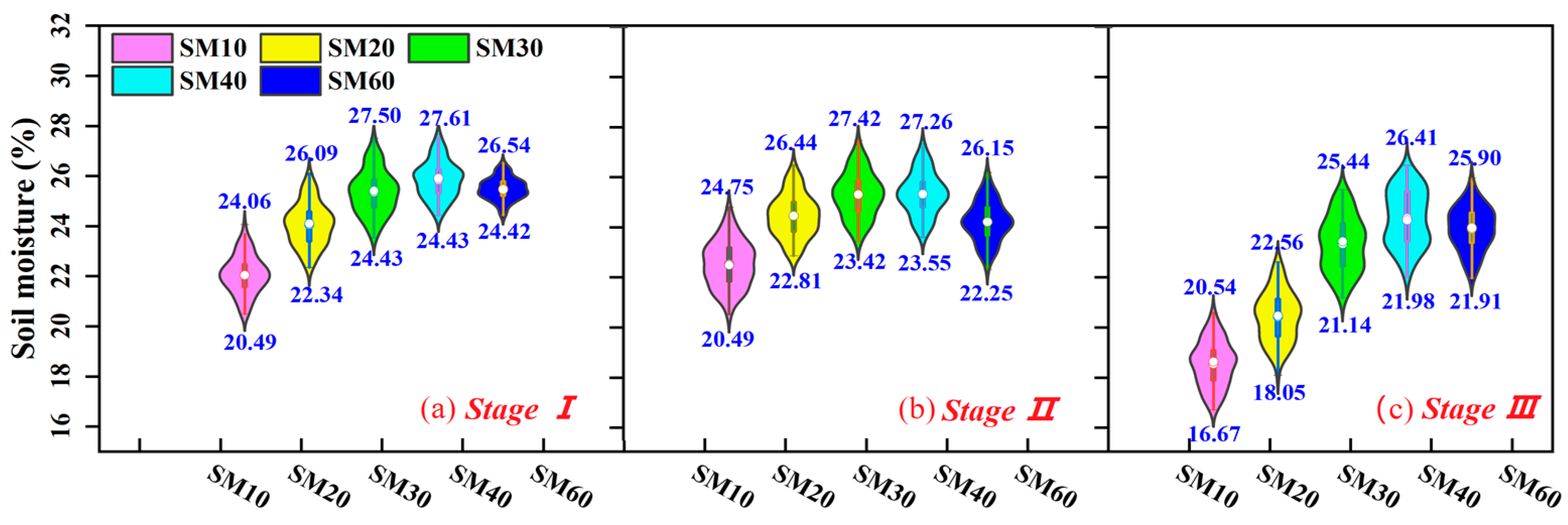
3.1. Changes of Root-Zone Soil Moisture in Fruit Growth Stages
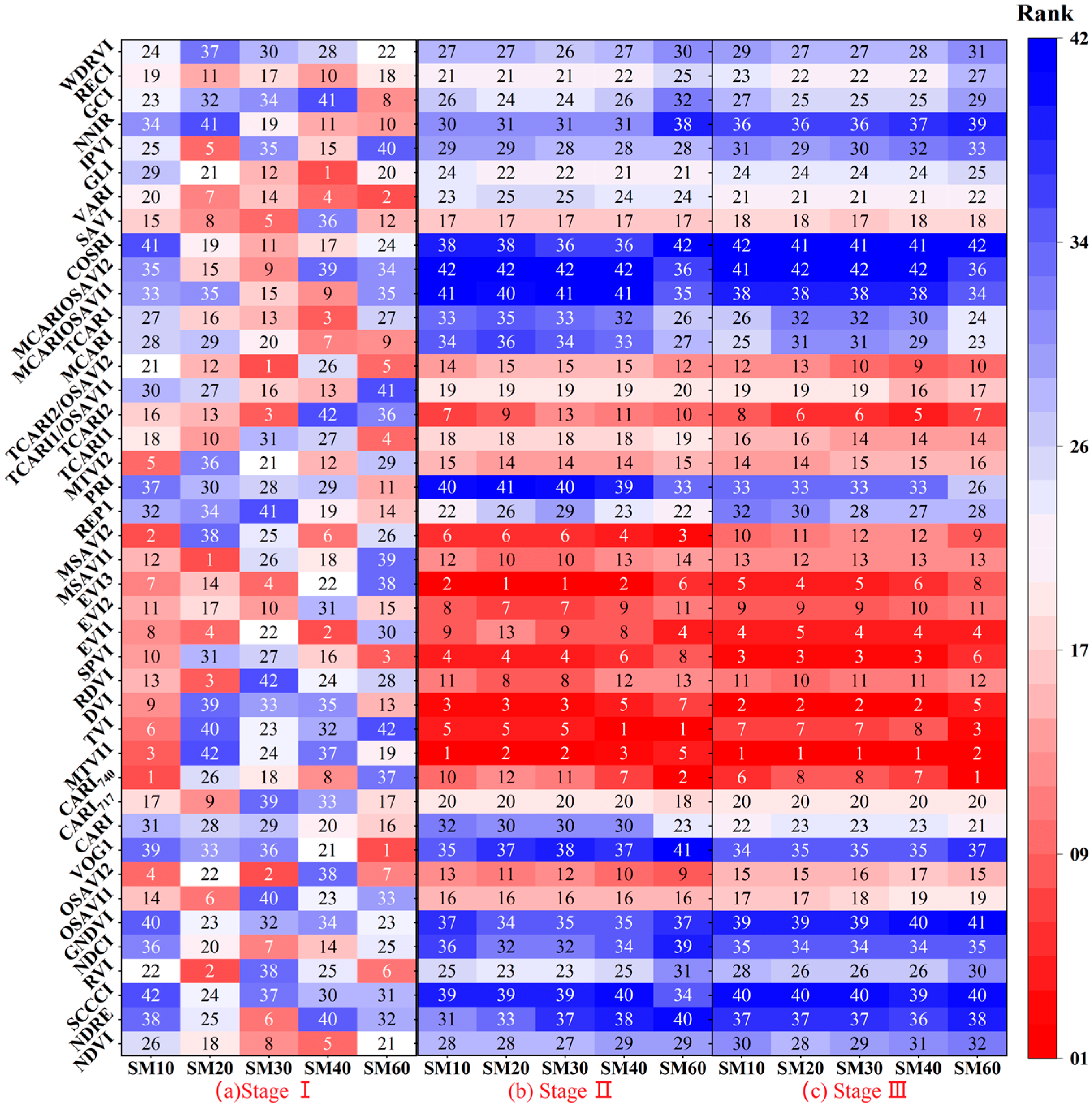
3.2. Appropriate Spectral Indices for Soil Moisture Estimation
3.3. Spatial Distribution of Root-Zone Soil Moisture in the Kiwi Field
4. Discussion
4.1. Comparison of Sensitive Spectral Variables with Soil Moisture
4.2. Performances of RF, SVM, and ELM Models
4.3. Research Limitations and Future Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guroo, I.; Sa, W.; Wani, S.M.; Ahmad, M.; Mir, S.A.; Masoodi, F.A. A Review of Production and Processing of Kiwifruit. J. Food Process. Technol. 2017, 8, 1–6. [Google Scholar]
- Wang, N.N.; Chen, Y.L.; Liu, B.; Yu, H.Y.; Hao, Y.; He, H.H.; Liu, Z.D.; Ma, F.W. Identification of the productivity-limiting nutrients of Xuxiang kiwifruit (Actiniadia chinensis) in China’s central Shaanxi province by analyzing soil fertility and leaf elements. Indian J. Agric. Sci. 2019, 89, 617–623. [Google Scholar] [CrossRef]
- Luo, W.; Xu, X.; Liu, W.Q.; Liu, M.; Li, Z.; Peng, T.; Xu, C.; Zhang, Y.; Zhang, R. UAV based soil moisture remote sensing in a karst mountainous catchment. Catena 2019, 174, 478–489. [Google Scholar] [CrossRef]
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.H.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, X.; Guo, W.; Wang, S.; Pan, Y.; Zhang, H.; Sang, H. Temporal and spatial distribution characteristics of irrigation water requirement for main crops in the plain area of Hebei Province. Irrig. Drain. 2020, 69, 1051–1062. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.W.; Ogden, F.L.; Selker, J.S.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Bai, X.; Chen, Y.; Chen, J.; Cui, W.; Tai, X.; Zhang, Z.; Cui, J.; Ning, J. Optimal window size selection for spectral information extraction of sampling points from UAV multispectral images for soil moisture content inversion. Comput. Electron. Agric. 2021, 190, 106456. [Google Scholar] [CrossRef]
- Khanna, A.; Kaur, S. Evolution of Internet of Things (IoT) and its significant impact in the field of Precision Agriculture. Comput. Electron. Agric. 2019, 157, 218–231. [Google Scholar] [CrossRef]
- Li, D.; Song, Z.; Quan, C.; Xu, X.; Liu, C. Recent advances in image fusion technology in agriculture. Comput. Electron. Agric. 2021, 191, 106491. [Google Scholar] [CrossRef]
- He, L.; Fang, W.; Zhao, G.; Wu, Z.; Fu, L.; Li, R.; Majeed, Y.; Dhupia, J.S. Fruit yield prediction and estimation in orchards: A state-of-the-art comprehensive review for both direct and indirect methods. Comput. Electron. Agric. 2022, 195, 106812. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Al-Asadi, R.A. Influence of soil moisture content on assessment of bulk density with combined frequency domain reflectometry and visible and near infrared spectroscopy under semi field conditions. Soil Tillage Res. 2018, 176, 95–103. [Google Scholar] [CrossRef]
- Aboutalebi, M.; Allen, L.N.; Torres-Rua, A.F.; McKee, M.; Coopmans, C. Estimation of soil moisture at different soil levels using machine learning techniques and unmanned aerial vehicle (UAV) multispectral imagery. In Proceedings of the Defense + Commercial Sensing Conference, Baltimore, MD, USA, 14–18 April 2019; p. 11008. [Google Scholar]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-based hyperspectral imagery and machine learning algorithms for soil moisture content monitoring. Peerj 2019, 7, e6926. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Jiao, X.; Liu, Y.; Shao, M.; Yu, X.; Bai, Y.; Wang, Z.; Wang, S.; Tuohuti, N.; Liu, S.; et al. Estimation of soil moisture content under high maize canopy coverage from UAV multimodal data and machine learning. Agric. Water Manag. 2022, 264, 107530. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Gobrecht, A.; Bendoula, R.; Roger, J.; Bellon-Maurel, V. A new optical method coupling light polarization and Vis-NIR spectroscopy to improve the measurement of soil carbon content. Soil Tillage Res. 2016, 155, 461–470. [Google Scholar] [CrossRef]
- Ding, J.; Yang, A.; Wang, J.; Sagan, V.; Yu, D. Machine-learning-based quantitative estimation of soil organic carbon content by VIS/NIR spectroscopy. Peerj 2018, 6, e5714. [Google Scholar] [CrossRef]
- Chen, H.; Liu, X.; Chen, A.; Cai, K.; Lin, B. Parametric-scaling optimization of pretreatment methods for the determination of trace/quasi-trace elements based on near infrared spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 229, 117959. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Xu, C.; Zeng, W.; Huang, J.; Wu, J.; Leeuwen, W.J. Prediction of Soil Moisture Content and Soil Salt Concentration from Hyperspectral Laboratory and Field Data. Remote Sens. 2016, 8, 42. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Q.; Wang, Y.; Liu, X.; Liu, X. Evaluation of MLSR and PLSR for estimating soil element contents using visible/near-infrared spectroscopy in apple orchards on the Jiaodong peninsula. Catena 2016, 137, 340–349. [Google Scholar] [CrossRef]
- Khosravi, V.; Ardejani, F.D.; Yousefi, S.; Aryafar, A. Monitoring soil lead and zinc contents via combination of spectroscopy with extreme learning machine and other data mining methods. Geoderma 2018, 318, 29–41. [Google Scholar] [CrossRef]
- Peng, X.; Chen, D.; Zhou, Z.; Zhang, Z.; Xu, C.; Zha, Q.; Wang, F.; Hu, X. Prediction of the Nitrogen, Phosphorus and Potassium Contents in Grape Leaves at Different Growth Stages Based on UAV Multispectral Remote Sensing. Remote Sens. 2022, 14, 2659. [Google Scholar] [CrossRef]
- Douglas, R.K.; Nawar, S.; Alamar, M.C.; Mouazen, A.M.; Coulon, F. Rapid prediction of total petroleum hydrocarbons concentration in contaminated soil using vis-NIR spectroscopy and regression techniques. Sci. Total Environ. 2018, 616, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, Y.; Chen, F.; Shi, T.; Wu, G. Wavelet-based coupling of leaf and canopy reflectance spectra to improve the estimation accuracy of foliar nitrogen concentration. Agric. For. Meteorol. 2018, 248, 306–315. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital mapping of soil properties using multiple machine learning in a semi-arid region, central Iran. Geoderma 2019, 338, 445–452. [Google Scholar]
- Liu, H.; Zhu, H.; Wang, P. Quantitative modelling for leaf nitrogen content of winter wheat using UAV-based hyperspectral data. Int. J. Remote Sens. 2017, 38, 2117–2134. [Google Scholar] [CrossRef]
- Li, W.; Zhu, X.; Yu, X.; Li, M.; Tang, X.; Zhang, J.; Xue, Y.; Zhang, C.; Jiang, Y.M. Inversion of Nitrogen Concentration in Apple Canopy Based on UAV Hyperspectral Images. Sensors 2022, 22, 3503. [Google Scholar] [CrossRef]
- Ndlovu, H.S.; Odindi, J.; Sibanda, M.; Mutanga, O.; Clulow, A.D.; Chimonyo, V.; Mabhaudhi, T. A Comparative Estimation of Maize Leaf Water Content Using Machine Learning Techniques and Unmanned Aerial Vehicle (UAV)-Based Proximal and Remotely Sensed Data. Remote Sens. 2021, 13, 4091. [Google Scholar] [CrossRef]
- Jin, J.; Huang, N.; Huang, Y.; Yan, Y.; Zhao, X.; Wu, M. Proximal Remote Sensing-Based Vegetation Indices for Monitoring Mango Tree Stem Sap Flux Density. Remote Sens. 2022, 14, 1483. [Google Scholar] [CrossRef]
- Wang, F.; Yang, M.; Ma, L.; Zhang, T.; Qin, W.; Li, W.; Zhang, Y.; Sun, Z.; Wang, Z.; Li, F.; et al. Estimation of Above-Ground Biomass of Winter Wheat Based on Consumer-Grade Multi-Spectral UAV. Remote Sens. 2022, 14, 1251. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Q.; Shang, J.; Liu, C.; Zhuang, T.; Ding, J.; Xian, Y.; Zhao, L.; Wang, W.; Zhou, G.; et al. UAV- and Machine Learning-Based Retrieval of Wheat SPAD Values at the Overwintering Stage for Variety Screening. Remote Sens. 2021, 13, 5166. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.; Shi, T.; Chen, Y.; Jiang, Q.; Linderman, M. Prediction of soil organic carbon stock by laboratory spectral data and airborne hyperspectral images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
- Savian, F.; Martini, M.; Ermacora, P.; Paulus, S.; Mahlein, A. Prediction of the Kiwifruit Decline Syndrome in Diseased Orchards by Remote Sensing. Remote Sens. 2020, 12, 2194. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; [Great Plains Corridor]; Remote Sensing Center; Texas A&M University: College Station, TX, USA, 1973. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; Leeuwen, W.J. A comparison of vegetation indices global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Raper, T.B.; Varco, J.J. Canopy-scale wavelength and vegetative index sensitivities to cotton growth parameters and nitrogen status. Precis. Agric. 2015, 16, 62–76. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red Edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Luo, W.; Xu, X.; Liu, W.Q.; Liu, M.; Li, Z.; Peng, T.; Xu, C.; Zhang, Y.; Zhang, R. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, X.; Yang, J.; Cao, W.; Zhu, Y. Extracting Red Edge Position Parameters from Ground- and Space-Based Hyperspectral Data for Estimation of Canopy Leaf Nitrogen Concentration in Rice. Plant Prod. Sci. 2011, 14, 270–281. [Google Scholar] [CrossRef]
- Yao, X.; Wang, N.; Liu, Y.; Cheng, T.; Tian, Y.; Chen, Q.; Zhu, Y. Estimation of Wheat LAI at Middle to High Levels Using Unmanned Aerial Vehicle Narrowband Multispectral Imagery. Remote Sens. 2017, 9, 1304. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.L.; Kim, M.S.; Colstoun, E.C.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Fernández-Buces, N.; Siebe, C.; Cram, S.; Palacio, J.L. Mapping soil salinity using a combined spectral response index for bare soil and vegetation: A case study in the former lake Texcoco, Mexico. J. Arid Environ. 2006, 65, 644–667. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atomspherically resistant vegetation resistant vegetation index (ARVI) for eos-modis. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J. Advanced vegetation indices optimized for up-coming sensors: Design, performance, and applications. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2489–2505. [Google Scholar]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Meijer, A.D. Aerial color infrared photography for determining late-season nitrogen requirements in corn. Agron. J. 2005, 97, 1443–1451. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.S.; Rundquist, D.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Peralta, N.R.; Assefa, Y.; Du, J.; Barden, C.J.; Ciampitti, I.A. Mid-Season High-Resolution Satellite Imagery for Forecasting Site-Specific Corn Yield. Remote Sens. 2016, 8, 848. [Google Scholar] [CrossRef]
- Huang, G.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Okin, G.S.; Roberts, D.A.; Murray, B.C.; Okin, W.J. Practical limits on hyperspectral vegetation discrimination in arid and semiarid environments. Remote Sens. Environ. 2001, 77, 212–225. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.L.; Gitelson, A.A.; Peng, Y.; Viña, A.; Arkebauer, T.J.; Rundquist, D. Green Leaf Area Index Estimation in Maize and Soybean: Combining Vegetation Indices to Achieve Maximal Sensitivity. Agron. J. 2012, 104, 1336–1347. [Google Scholar]
- Luo, S.; He, Y.; Li, Q.; Jiao, W.; Zhu, Y.; Zhao, X. Nondestructive estimation of potato yield using relative variables derived from multi-period LAI and hyperspectral data based on weighted growth stage. Plant Methods 2020, 16, 150. [Google Scholar]
- Lindner, C.; Bromiley, P.A.; Ionita, M.C.; Cootes, T.F. Robust and Accurate Shape Model Matching Using Random Forest Regression-Voting. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1862–1874. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, J.L.; Prueger, J.H. Value of Using Different Vegetative Indices to Quantify Agricultural Crop Characteristics at Different Growth Stages under Varying Management Practices. Remote Sens. 2010, 2, 562–578. [Google Scholar] [CrossRef]


| Band | Band Name | Spectral Wavelength (nm) | Bandwidth (nm) | Function |
|---|---|---|---|---|
| B1 | Blue444 | 444 | 28 | Strong absorption of chlorophyll a and carotenoids. |
| B2 | Blue | 475 | 32 | |
| B3 | Green531 | 531 | 14 | Strong absorption of chlorophyll and phycoerythrin absorption peak. |
| B4 | Green | 560 | 27 | Phycoerythrin absorption peak. |
| B5 | Red650 | 650 | 16 | Strong absorption of chlorophyll and phycoerythrin absorption peak. |
| B6 | Red | 668 | 14 | Strong absorption of chlorophyll, absorption trough of most vegetation. |
| B7 | Red-edge705 | 705 | 10 | Red edge region |
| B8 | Red-edge | 717 | 12 | |
| B9 | Red-edge740 | 740 | 18 | Strong absorption of chlorophyll |
| B10 | NIR | 842 | 57 | High reflection of vegetation and the top of red edge region |
| No. | Index | Formulation | Formula for on Red-Edge MX Dual Camera | Reference |
|---|---|---|---|---|
| 1 | NDVI | [36] | ||
| 2 | NDRE | [37] | ||
| 3 | SCCCI | / | [38] | |
| 4 | RVI | [39] | ||
| 5 | NDCI | [40] | ||
| 6 | GNDVI | [41] | ||
| 7 | OSAVI1 | [42] | ||
| 8 | OSAVI2 | (This study) | ||
| 9 | VOG1 | [43] | ||
| 10 | CARI | [44] | ||
| 11 | CARI717 | (This study) | ||
| 12 | CARI740 | (This study) | ||
| 13 | MTVI1 | [45] | ||
| 14 | TVI | [46] | ||
| 15 | DVI | [47] | ||
| 16 | RDVI | [48] | ||
| 17 | SPVI | [44] | ||
| 18 | EVI1 | [37] | ||
| 19 | EVI2 | [49] | ||
| 20 | EVI3 | [50] | ||
| 21 | MSAVI1 | [47] | ||
| 22 | MSAVI2 | (This study) | ||
| 23 | REP1 | (This study) | ||
| 24 | PRI | [51] | ||
| 25 | MTVI2 | [48] | ||
| 26 | TCARI1 | (This study) | ||
| 27 | TCARI2 | [52] | ||
| 28 | / | / | [52] | |
| 29 | / | / | (This study) | |
| 30 | MCARI | [53] | ||
| 31 | TCAR1 | [53] | ||
| 32 | / | / | [54] | |
| 33 | / | / | (This study) | |
| 34 | COSRI | [55] | ||
| 35 | SAVI | [37] | ||
| 36 | VARI | [56] | ||
| 37 | GLI | [57] | ||
| 38 | IPVI | [58] | ||
| 39 | NNIR | [59] | ||
| 40 | GCI | [60] | ||
| 41 | RECI | [60] | ||
| 42 | WDRVI | [61] |
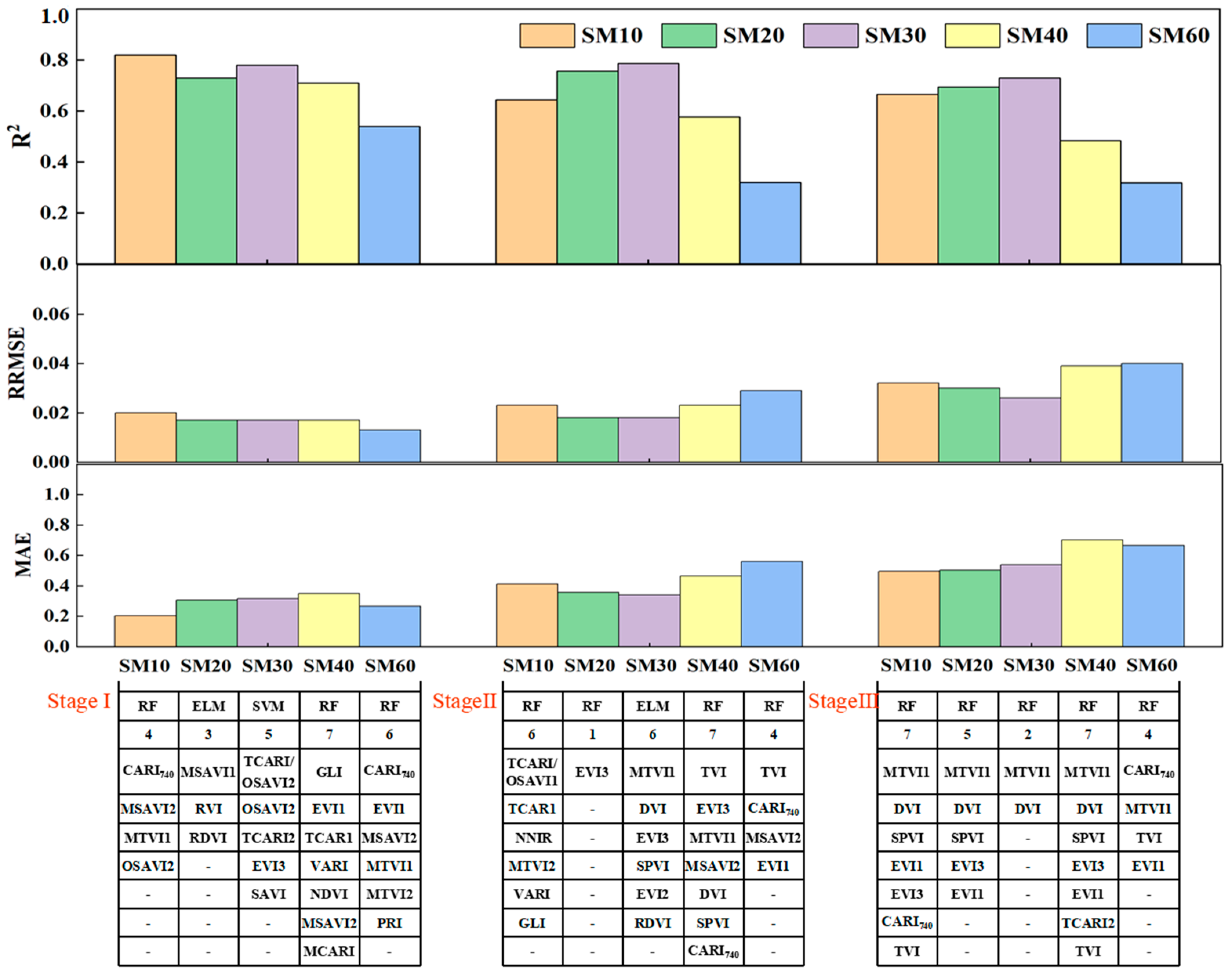
| Growth Stage | Response Variables | The Top 7 VIs | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Stage I | SM10 | CARI740 | MSAVI2 | MTVI1 | OSAVI2 | MTVI2 | TVI | EVI3 |
| SM20 | MSAVI1 | RVI | RDVI | EVI1 | IPVI | OSAVI1 | VARI | |
| SM30 | TCARI/OSAVI2 | OSAVI2 | TCARI2 | EVI3 | SAVI | NDRE | NDCI | |
| SM40 | GLI | EVI1 | TCAR1 | VARI | NDVI | MSAVI2 | MCARI | |
| SM60 | CARI740 | EVI1 | MSAVI2 | MTVI1 | MTVI2 | PRI | DVI | |
| Stage II | SM10 | TCARI/OSAVI1 | TCAR1 | NNIR | MTVI2 | VARI | GLI | RDVI |
| SM20 | EVI3 | SCCCI | NDRE | VOG1 | NDCI | EVI1 | OSAVI1 | |
| SM30 | EVI2 | RDVI | MTVI2 | MSAVI2 | SAVI | MSAVI1 | OSAVI1 | |
| SM40 | TVI | EVI3 | MTVI1 | MSAVI2 | DVI | SPVI | CARI740 | |
| SM60 | TVI | CARI740 | MSAVI2 | EVI1 | MTVI1 | EVI3 | DVI | |
| Stage III | SM10 | MTVI1 | DVI | SPVI | EVI1 | EVI3 | CARI740 | TVI |
| SM20 | MTVI1 | DVI | SPVI | EVI3 | EVI1 | TCARI2 | TVI | |
| SM30 | MTVI1 | DVI | SPVI | EVI1 | EVI3 | TCARI2 | TVI | |
| SM40 | MTVI1 | DVI | SPVI | EVI3 | EVI1 | TCARI2 | TVI | |
| SM60 | CARI740 | MTVI1 | TVI | EVI1 | DVI | SPVI | TCARI2 | |
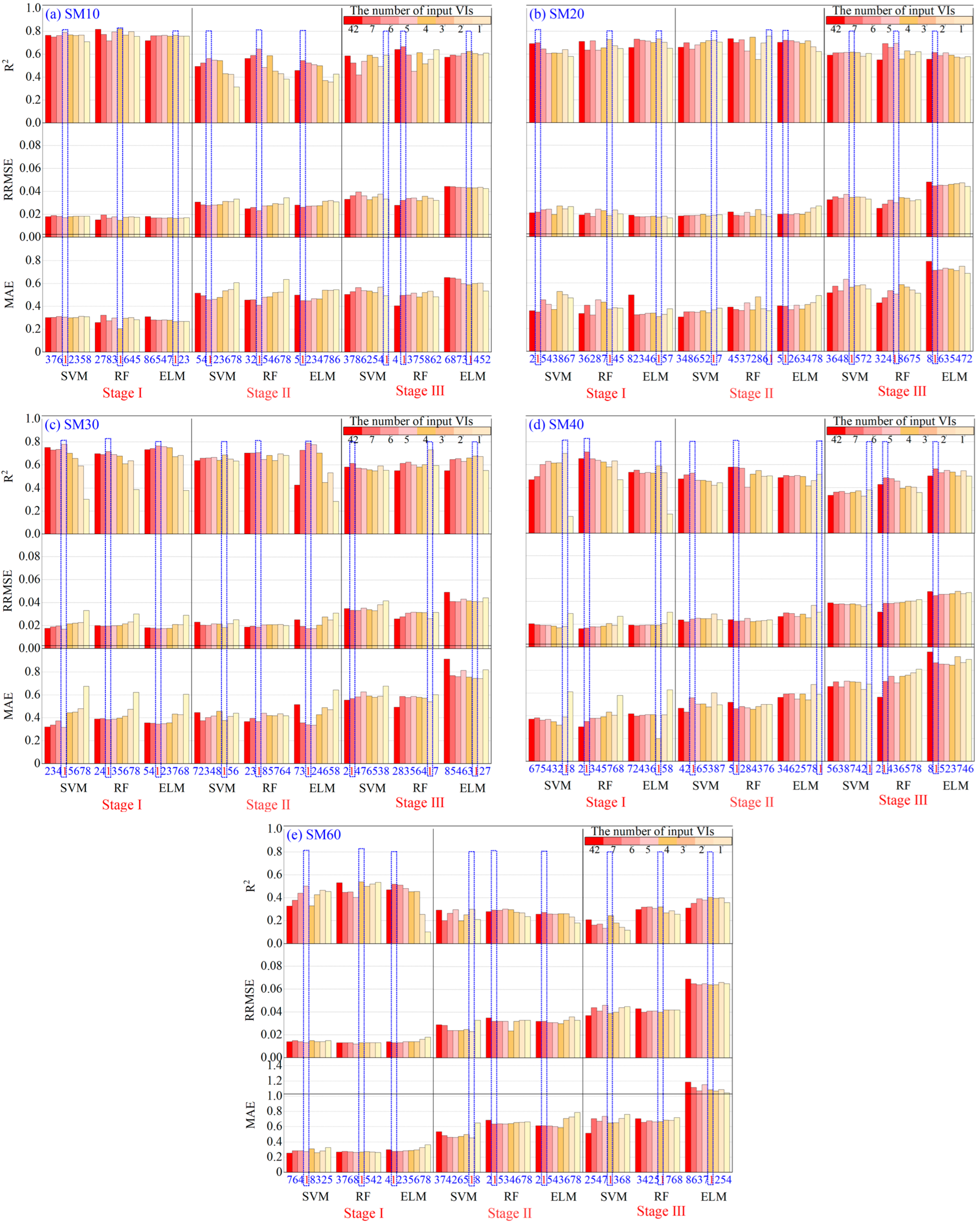
| Model | Response Variables | Number of VIs (No. of VIs) | Predictive Input VIs | R2 | RRMSE | MAE | GPI | Rank |
|---|---|---|---|---|---|---|---|---|
| SVM | SM10 | 5 (12, 22, 13, 8, 25) | CARI740, MSAVI2, MTVI1, OSAVI2, MTVI2 | 0.79 | 0.02 | 0.31 | 0.07 | 3 |
| SM20 | 7 (21, 4, 16, 18, 38, 7, 36) | MSAVI1, RVI, RDVI, EVI1, IPVI, OSAVI1, VARI | 0.70 | 0.02 | 0.35 | −0.06 | 10 | |
| SM30 | 5 (29, 8, 27. 20, 35) | TCARI/OSAVI2, OSAVI2, TCARI2, EVI3, SAVI | 0.78 | 0.02 | 0.32 | 0.06 | 4 | |
| SM40 | 2 (37, 18) | GLI, EVI1 | 0.70 | 0.02 | 0.39 | −0.10 | 12 | |
| SM60 | 5 (12, 18, 22, 13, 25) | CARI740, EVI1, MSAVI2, MTVI1, MTVI2 | 0.50 | 0.01 | 0.27 | −0.18 | 15 | |
| RF | SM10 | 4 (12, 22, 13, 8) | CARI740, MSAVI2, MTVI1, OSAVI2 | 0.82 | 0.02 | 0.20 | 0.21 | 1 |
| SM20 | 3 (21, 4, 16) | MSAVI1, RVI, RDVI | 0.73 | 0.02 | 0.31 | 0.01 | 7 | |
| SM30 | 6 (29, 8, 27. 20, 35, 2) | TCARI/OSAVI2, OSAVI2, TCARI2, EVI3, SAVI, NDRE | 0.72 | 0.02 | 0.38 | −0.08 | 11 | |
| SM40 | 7 (37, 18, 31, 36, 1, 22, 30) | GLI, EVI1, TCAR1, VARI, NDVI, MSAVI2, MCARI | 0.71 | 0.02 | 0.35 | −0.05 | 9 | |
| SM60 | 4(12, 18, 22, 13) | CARI740, EVI1, MSAVI2, MTVI1 | 0.54 | 0.01 | 0.27 | −0.13 | 13 | |
| ELM | SM10 | 3 (12, 22, 13) | CARI740, MSAVI2, MTVI1 | 0.77 | 0.02 | 0.27 | 0.09 | 2 |
| SM20 | 3 (21, 4, 16) | MSAVI1, RVI, RDVI | 0.73 | 0.02 | 0.31 | 0.02 | 5 | |
| SM30 | 6 (29, 8, 27. 20, 35, 2) | TCARI/OSAVI2, OSAVI2, TCARI2, EVI3, SAVI, NDRE | 0.77 | 0.02 | 0.34 | 0.01 | 6 | |
| SM40 | 3 (37, 18, 31) | GLI, EVI1, TCAR1 | 0.59 | 0.02 | 0.20 | −0.02 | 8 | |
| SM60 | 7 (12, 18, 22, 13, 25, 24,15) | CARI740, EVI1, MSAVI2, MTVI1, MTVI2, PRI, DVI | 0.52 | 0.01 | 0.28 | −0.16 | 14 |
| Model | Response Variables | Number of VIs (No. of VIs) | Predictive Input VIs | R2 | RRMSE | MAE | GPI | Rank |
|---|---|---|---|---|---|---|---|---|
| SVM | SM10 | 6 (28, 31, 39, 25, 36, 37) | TCARI/OSAVI1, TCAR1, NNIR, MTVI2, VARI, GLI | 0.56 | 0.03 | 0.46 | −0.03 | 9 |
| SM20 | 2 (20, 3) | EVI3, SCCCI | 0.72 | 0.02 | 0.34 | 0.25 | 3 | |
| SM30 | 3 (13,15. 20) | MTVI1, DVI, EVI3 | 0.69 | 0.02 | 0.38 | 0.19 | 6 | |
| SM40 | 6 (14. 20, 13, 22, 15, 17) | TVI, EVI3, MTVI1, MSAVI2, DVI, SPVI | 0.53 | 0.02 | 0.53 | −0.13 | 11 | |
| SM60 | 2 (14, 12) | TVI, CARI740 | 0.30 | 0.02 | 0.55 | −0.38 | 14 | |
| RF | SM10 | 6 (28, 31, 39, 25, 36, 37) | TCARI/OSAVI1, TCAR1, NNIR, MTVI2, VARI, GLI | 0.65 | 0.02 | 0.41 | 0.11 | 7 |
| SM20 | 1 (20) | EVI3 | 0.76 | 0.02 | 0.36 | 0.28 | 2 | |
| SM30 | 6 (13,15. 20, 17, 19, 16) | MTVI1, DVI, EVI3, SPVI, EVI2, RDVI | 0.71 | 0.02 | 0.37 | 0.22 | 5 | |
| SM40 | 7 (14. 20, 13, 22, 15, 17, 12) | TVI, EVI3, MTVI1, MSAVI2, DVI, SPVI, CARI740 | 0.58 | 0.02 | 0.46 | −0.01 | 8 | |
| SM60 | 7 (14, 12, 22, 18, 13. 20, 15) | TVI, CARI740, MSAVI2, EVI1, MTVI1, EVI3, DVI | 0.32 | 0.03 | 0.56 | −0.37 | 13 | |
| ELM | SM10 | 7 (28, 31, 39, 25, 36, 37, 16) | TCARI/OSAVI1, TCAR1, NNIR, MTVI2, VARI, GLI, RDVI | 0.54 | 0.03 | 0.45 | −0.04 | 10 |
| SM20 | 7 (20, 3, 2, 9, 5, 18, 7) | EVI3, SCCCI, NDRE, VOG1, NDCI, EVI1, OSAVI1 | 0.72 | 0.02 | 0.38 | 0.22 | 4 | |
| SM30 | 6 (13,15. 20, 17, 19, 16) | MTVI1, DVI, EVI3, SPVI, EVI2, RDVI | 0.79 | 0.02 | 0.34 | 0.33 | 1 | |
| SM40 | 1 (14) | TVI | 0.52 | 0.03 | 0.55 | −0.17 | 12 | |
| SM60 | 7 (14, 12, 22, 18, 13. 20, 15) | TVI, CARI740, MSAVI2, EVI1, MTVI1, EVI3, DVI | 0.27 | 0.03 | 0.53 | −0.40 | 15 |
| Model | Response Variables | Number of VIs (No. of VIs) | Predictive Input VIs | R2 | RRMSE | MAE | GPI | Rank |
|---|---|---|---|---|---|---|---|---|
| SVM | SM10 | 1 (13) | MTVI1 | 0.59 | 0.03 | 0.49 | 0.11 | 4 |
| SM20 | 4 (13, 15, 17. 20) | MTVI1, DVI, SPVI, EVI3 | 0.62 | 0.04 | 0.56 | 0.06 | 5 | |
| SM30 | 7 (13, 15, 17, 18. 20, 27, 14) | MTVI1, DVI, SPVI, EVI1, EVI3, TCARI2, TVI | 0.61 | 0.03 | 0.57 | 0.05 | 6 | |
| SM40 | 1 (13) | MTVI1 | 0.38 | 0.04 | 0.68 | −0.30 | 12 | |
| SM60 | 4(12,13,14,18) | CARI740, MTVI1, TVI, EVI1 | 0.25 | 0.04 | 0.62 | −0.37 | 14 | |
| RF | SM10 | 7 (13, 15, 17, 18. 20, 12, 14) | MTVI1, DVI, SPVI, EVI1, EVI3, CARI740, TVI | 0.67 | 0.03 | 0.50 | 0.18 | 3 |
| SM20 | 5 (13, 15, 17. 20, 18) | MTVI1, DVI, SPVI, EVI3, EVI1 | 0.69 | 0.03 | 0.50 | 0.20 | 2 | |
| SM30 | 2 (13, 15) | MTVI1, DVI | 0.73 | 0.03 | 0.54 | 0.21 | 1 | |
| SM40 | 7 (13, 15, 17. 20, 18, 27, 14) | MTVI1, DVI, SPVI, EVI3, EVI1, TCARI2, TVI | 0.49 | 0.04 | 0.70 | −0.22 | 10 | |
| SM60 | 4 (12, 13, 14, 18) | CARI740, MTVI1, TVI, EVI1 | 0.32 | 0.04 | 0.67 | −0.35 | 13 | |
| ELM | SM10 | 4 (13, 15, 17, 18) | MTVI1, DVI, SPVI, EVI1 | 0.63 | 0.04 | 0.59 | 0.03 | 7 |
| SM20 | 7 (13, 15, 17. 20, 18, 27,12) | MTVI1, DVI, SPVI, EVI3, EVI1, TCARI2, CARI740 | 0.62 | 0.05 | 0.71 | −0.10 | 9 | |
| SM30 | 3 (13, 15, 17) | MTVI1, DVI, SPVI | 0.68 | 0.04 | 0.74 | −0.07 | 8 | |
| SM40 | 7 (13, 15, 17. 20, 18, 27, 14) | MTVI1, DVI, SPVI, EVI3, EVI1, TCARI2, TVI | 0.56 | 0.05 | 0.85 | −0.29 | 11 | |
| SM60 | 4 (12, 13, 14, 18) | CARI740, MTVI1, TVI, EVI1 | 0.40 | 0.06 | 1.07 | −0.68 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Cui, N.; Zhou, J.; Xue, J.; Wang, Z.; Wu, Z.; Wang, M.; Deng, Q. Digital Mapping of Root-Zone Soil Moisture Using UAV-Based Multispectral Data in a Kiwifruit Orchard of Northwest China. Remote Sens. 2023, 15, 646. https://doi.org/10.3390/rs15030646
Zhu S, Cui N, Zhou J, Xue J, Wang Z, Wu Z, Wang M, Deng Q. Digital Mapping of Root-Zone Soil Moisture Using UAV-Based Multispectral Data in a Kiwifruit Orchard of Northwest China. Remote Sensing. 2023; 15(3):646. https://doi.org/10.3390/rs15030646
Chicago/Turabian StyleZhu, Shidan, Ningbo Cui, Ji Zhou, Jingyuan Xue, Zhihui Wang, Zongjun Wu, Mingjun Wang, and Qingling Deng. 2023. "Digital Mapping of Root-Zone Soil Moisture Using UAV-Based Multispectral Data in a Kiwifruit Orchard of Northwest China" Remote Sensing 15, no. 3: 646. https://doi.org/10.3390/rs15030646
APA StyleZhu, S., Cui, N., Zhou, J., Xue, J., Wang, Z., Wu, Z., Wang, M., & Deng, Q. (2023). Digital Mapping of Root-Zone Soil Moisture Using UAV-Based Multispectral Data in a Kiwifruit Orchard of Northwest China. Remote Sensing, 15(3), 646. https://doi.org/10.3390/rs15030646







