Abstract
Satellite image time series (SITS) classification is a challenging application concurrently driven by long-term, large-scale, and high spatial-resolution observations acquired by remote sensing satellites. The focus of current SITS classification research is to exploit the richness of temporal information in SITS data. In the literature, self-attention mechanism-based networks, which are capable of capturing global temporal attention, have achieved state-of-the-art results in SITS classification. However, these methods lack attention to local temporal information, which is also significant for SITS classification tasks. To explore the potential of different scales of temporal information in SITS data, a global–local temporal attention encoder (GL-TAE) is proposed in this paper. GL-TAE has two submodules set up in parallel, one of which is a lightweight temporal attention encoder (LTAE) for extracting global temporal attention and the other is lightweight convolution (LConv) for extracting local temporal attention. Compared with methods exploring global-only or local-only temporal features, the proposed GL-TAE can achieve better performance on two public SITS datasets, which proves the effectiveness of hybrid global–local temporal attention features. The experiments also demonstrate that GL-TAE is a lightweight model, which achieves the same performance as other models but with fewer parameters.
1. Introduction
With the availability of free remote sensing satellite images with regular temporal intervals, satellite image time series (SITS) data are becoming increasingly accessible. SITS plays an increasingly important role in land cover mapping due to the fact that single temporal data are unable to distinguish land cover types with similar structural and spectral characteristics and SITS has a wealth of temporal information that characterizes periodic changes in land cover to help us better classify different types of land cover. Many studies have shown that SITS outperforms single temporal data for land cover classification [1,2].
Various approaches have been developed to cope with the SITS classification, and some classical machine learning algorithms used for single temporal can be adapted to SITS classification, such as support vector machine (SVM) [3] and random forest (RF) [4]. References [5,6,7] adopted SVM for Sentinel or Landsat SITS-based cropland mapping. RF is widely used for land cover and crop type mapping in [8,9,10,11] due to its robustness and convenient operability. Although SVM and RF are theoretically interpretable and reliable, they have some limitations that are difficult to break through, the direct one of which is that they cannot handle input data with unequal dimensions. Due to the differences in the revisit periods of remote sensing satellites in different geographical areas, SITS with unequal temporal acquisitions is very common, especially for large area land cover-mapping tasks. One direct strategy is to flatten SITS into vectors with the same dimensions for SVM or RF, but it means that there have to be different degrees of information losses for different time series in SITS. Another drawback of SVM and RF is that they lack the mining of sequential information in SITS. Therefore, methods dedicated to various length time series analyses have received attention from researchers in the field of SITS classification.
One classical method compatible with input data with unequal lengths is dynamic time warp (DTW), which is originally used for time series similarity measures [12]. DTW is an elastic distance measure of time series with unequal lengths and it outperforms many classical distance measures, such as the Manhattan distance, Euclidean distance, and Pearson’s correlation [13]. Reference [14] first introduced DTW for SITS analysis and the results have proven that DTW is able to deal with irregularly sampled time series and allows the comparison of time series with different temporal lengths. DTW is capable of achieving good classification results when there are no sufficient training samples; thus, it is often used in clustering algorithms [15,16]. Reference [17] proposed a time-weighted dynamic time warping (TW-DTW), which has important improvements for the DTW-based method in SITS classification, which includes a temporal weight for characterizing the seasonality of land cover types. Many studies [18,19,20] have investigated the classification performance of TW-DTW compared with DTW, and the results show that the improvement in time weighting is significant. Although DTW-based methods have successfully been adopted in the SITS classification, the time-consuming computation of the DTW distance prevents its utility for big volumes of SITS datasets. Furthermore, this distance-based method performs poorly for SITS classification with many land cover types and unbalanced training samples.
The difficulty of SITS-based land cover classification lies in how to fully exploit the rich temporal information of SITS to generate discriminative features. The aforementioned traditional machine learning methods are insufficient to model temporal features from SITS. In the last decade, with the development of deep learning, many algorithms based on artificial neural networks have been proposed for SITS classification, and deep temporal features extracted from these deep neural networks have proven to be more effective. These deep learning methods are mainly categorized into three types according to which backbone neural network is employed to extract the temporal features: the recurrent neural network (RNN), convolutional neural network (CNN), and transformer with self-attention mechanisms.
RNN is the earliest DL method used for SITS classification [21,22]; it was initially designed to deal with sequence analysis [23] and is well-developed in NLP [24]. RNNs sequentially input each time step of a time series into recurrent cells and they are able to focus on information from a certain forward temporal range when extracting temporal features. Thus, RNNs can be viewed as local temporal attention-based methods. A recurrent cell is the basic unit of a RNN; long short-term memory (LSTM) and a gated recurrent unit (GRU) are the most widely used cells in RNN-based methods for SITS classifications [25,26,27,28]. A unidirectional recurrent cell pays attention to a unidirectional temporal range for each temporal acquisition in SITS when constructing new feature representations, while a bidirectional recurrent cell is capable of combining both forward and backward attention to encode the time series, which is more effective in some cases [29,30,31].
CNN-based methods—different from RNN-based methods—extract temporal features from SITS, focusing on local temporal information with a fixed symmetric range known as the perceptive field of convolution. Reference [32] proposed a temporal convolutional network (TempCNN), which applies multiple layers of 1D vanilla convolution for pixel-based SITS classification. Reference [33] combined 1D temporal convolutions via trainable attention to exploit information from object-based SITS for land cover classification. Reference [34] compared TempCNN and a generic temporal convolutional network (TCN) [35], which stacked causal convolutions with dilatation at powers of 2, and concluded that they could achieve comparable results. Reference [36] investigated more CNN-based methods, in addition to TempCNN, such as Time-CNN [37], multi-channel deep convolutional neural networks (MCDCNNs) [38,39], and InceptionTime [40], for SITS classification.
Local attention tends to capture information from temporal neighborhoods for each position of the time series, but global attention tends to capture information from all time steps for each position in the time series. Recently, with the remarkable achievements of transformer [41] in NLP [42,43,44,45] and CV [46,47,48], methods based on self-attention mechanisms, which extract global attention from sequence data have also been introduced into SITS classification and demonstrated to be superior to RNN/CNN-based methods. In [49], the authors explored the application of a pre-trained transformer in SITS classification. In [50], the authors adopted the encoder architecture of the transformer, in which the stage of the word-embedding was discarded because SITS is in a continuous space of spectral reflectance values, and global maximum pooling was applied to dimensionally reduce the representation of the last encoder layer. A temporal attention encoder (TAE) [51] simplified the architecture of [50] and defined a single master query to encode an entire time series into a single embedding and summarized the global temporal information. A lightweight temporal attention encoder (LTAE) [52] applied multi-head attention along the channel dimension and implemented the master query with query-as-a-parameter, which is more lightweight than TAE and better at understanding the global temporal information from the time series. LTAE was used in conjunction with U-Net [53] for semantic/panoptic segmentation of SITS [54]. All experiments from [50,51,52] demonstrated that such global attention is capable of focusing crucial positions by considering all temporal data within the input time series.
For DL-based SITS classification, attention is the most critical factor affecting the classification performance and existing methods are only capable of capturing single attention. Although global attention is able to automatically capture key phenological periods, it lacks sensitivity to changes in fixed periods, which is accurately captured by local attention. In theory, combining the attention of different sales is able to make classification features more discriminative. Reference [55] investigated a temporal encoder with two branches for SITS classification, in which one CNN branch has local attention and one RNN branch has forward local attention. The results of the experiments have shown that this two-branch architecture outperforms RNN-only and CNN-only architecture, which illustrates that hybrid attention is better than single attention. Thus, combining global attention with local attention has promising prospects from the perspective of improving the performance of SITS classification. For the design of a deep learning model, a straightforward idea is to make the model capable of obtaining both global and local features. LTAE is a state-of-the-art global attention-based and lightweight model. CNN-based methods are more focused on local temporal information than RNN-based methods [32,35] and are not bothered by the problems of vanishing and exploding gradients, where RNNs often occur. A lightweight convolution (LConv) is proposed in [56], which is capable of extracting local information with much fewer parameters. Thus, we propose a global–local temporal attention encoder (GL-TAE) to implement the idea. The key contributions of this paper are as follows.
- 1.
- The proposed GL-TAE is an early attempt to extract hybrid global–local temporal features for SITS classification, adopting self-attention mechanisms for global attention extraction and convolution for local attention extraction.
- 2.
- The proposed GL-TAE is a lightweight model. We selected and set two lightweight submodules (LTAE and LConv) in parallel and extracted global and local temporal features, respectively, in combination with dimensional split strategies, which further reduce the parameter numbers under the same hyperparameter settings.
2. Methodology
2.1. Overview
The overall architecture of our proposed GL-TAE is shown in Figure 1. Let us denote the input time series as x of size (T is the number of temporal acquisitions and is the number of channels of input data). x is firstly transformed into size by a channel feature enhancement layer composed of a 1D convolution with the LayerNorm that is also used in LTAE and TAE. Then it is processed by a positional encoding layer for catching sequential information of the time series according to the following equation:
where t refers to the time step in the time series, i refers to the i-th channel dimension, and is a constant set to 1000. The core module of our proposed encoder is the global–local attention-based temporal feature extractor, which combines LTAE (the latest self-attention mechanism variant for extracting global temporal features) with LConv for extracting local temporal features. In addition, there is a dimension split layer and a dimension concatenation layer before and after the module, respectively, both of which operate on the channel dimension. In this global–local attention extractor, the positional encoded time series is transformed into the size. The final multilayer perceptron (MLP) outputs the classification feature of size .
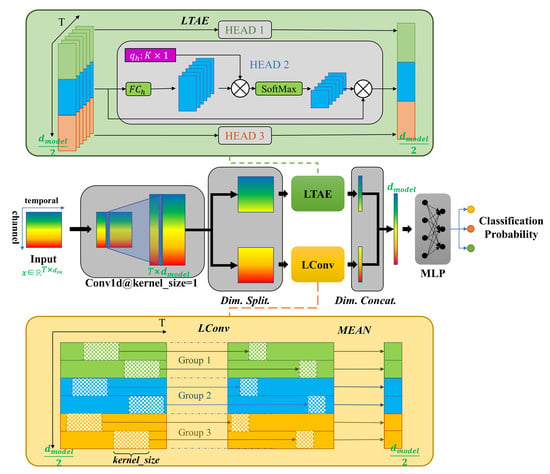
Figure 1.
Overall architecture of the proposed global–local temporal attention encoder (GL-TAE). The left part depicts the whole structure of GL-TAE and the right part portrays structures of LTAE and LConv with .
2.2. Self-Attention Mechanism
Reference [41] proposed the self-attention mechanism and applied it to the neural machine translation. The basic unit of the self-attention mechanism is the scaled dot-product attention (SDPA), which consists of the following steps:
- 1.
- Compute a triplet of the query–key–value for each time step t in the time series by three shared linear layers with transformation matrices to the input .
- 2.
- Compute the attention mask in which the weight assigned to each value is computed by a compatibility function of the query with the corresponding key. The compatibility function computes the dot products of the query with all keys, divides each by (dimension of keys), and applies a softmax function to obtain the weights on the values.
- 3.
- Compute the sum of the values weighted by the corresponding attention mask as the output for each time step.
In practice, we compute the output for each time step in the time series simultaneously and we compute Equation (2) as the matrix of the outputs, in which , , are projection transformation matrices, is the input time series, and softmax computes Equation (3) to normalize the attention mask (n is the number of weights and equals in Equation (2)).
Instead of performing a single SDPA to input the time series, multi-head attention (MHA) is proven to be beneficial with the diversity of feature representations, which compute H times SDPA simultaneously and then concatenates the outputs of H heads to yield the final output with projection matrix as the following equation:
In the processing of SDPA and MHA, all time steps are taken into account for each time step in the time series; with iterative training, the model will automatically assign different weights for time steps in the time series. Thus, the self-attention mechanism is capable of focusing on some crucial temporal positions through global temporal attention.
2.3. Lightweight Self-Attention for Global Attention Extraction
LTAE [52] is a lightweight self-attention mechanism variant in the classification of a remote sensing time series. Two crucial improvements allow LTAE to achieve strong feature extraction capabilities while reducing the number of trainable parameters:
- 1.
- Unlike the vanilla transformer [41], which computes multiple triplets for multi-head attention from the input sequence of size and produces an output size of ( is the number of heads), LTAE’s multi-head attention is applied along the channel dimensions, then the outputs of all heads are concatenated into a vector with the same channels as the input sequence, regardless of the number of heads. Such modified multi-head attention mechanism, while retaining the diversity of feature extraction, significantly reduces the number of trainable parameters.
- 2.
- Reference [52] defines a learnable query, named a master query, for each head in LTAE instead of computing from the input sequence by a linear layer, which further reduces the parameter numbers. The attention masks of each head are defined as the scaled softmax of the dot-product between the keys and the master query. The output of each head is defined as the sum of the corresponding inputs weighed by the attention mask in the temporal dimension.
LTAE’s attention mechanism can be summarized by the following equation for the h-th head, in which refers to the h-th channel group of x, refers to the h-th learnable master query, and refers to the h-th transformation matrix for keys.
2.4. Lightweight Convolution for Local Attention Extraction
LConv [56] has a fixed context window and it determines the importance of local neighborhood elements with a set of weights that are shared not only along the temporal dimension but also within certain output channels (channel group). Furthermore, weights are normalized across temporal dimensions using a softmax operation and then every entry of the normalized weights is dropped with probability p. A regular convolution requires trainable weights assuming that both input channels and output channels of convolution are . Nevertheless, LConv significantly reduces trainable parameters to ( is the number of channel groups in LConv) while maintaining the same local attention extraction capability. We set so LConv could have a diversity of feature extractions similar to multi-head attention in LTAE. LConv computes the following equation for the i-th time step in the time series and output channel c, in which W is the weight of LConv.
2.5. Channel Dimension Split and Concatenation
Instead of feeding the whole input time series into both two submodules, we used a Dim. Split layer to split the positional encoded time series into two parts of size . LTAE produces the global temporal feature of size and LConv produces the local temporal feature of size . The local temporal feature is then averaged along temporal dimensions into size and concatenated in a Dim. Concat. layer with the global temporal feature into the size.
3. Experiments and Results
In this section, we compare GL-TAE with other state-of-the-art competing methods in two publicly available datasets to evaluate the effectiveness of hybrid global–local attention.
3.1. Datasets
We selected two publicly available datasets for evaluating our proposed method in the experiments. Both datasets are pixel-based and imbalanced. Their data come from different sensors and geographic regions.
- (1)
- TiSeLaC: The study data come from the datasets provided by the 2017 Time Series Land Cover Classification Challenge (accessed on 20 December 2021) (https://sites.google.com/site/dinoienco/tiselac-time-series-land-cover-classification-challenge). The original data were generated from the level 2A Landsat, 8 images from 23 acquisition dates in 2014 above Reunion Island, shown in Figure 2. The spatial resolution was 30 m and 10 features were selected for each pixel, including the first 7 bands of Landsat-8 (Band1–Band7) and 3 complementary radiometric indices (normalized difference vegetation index, normalized difference water index, and brightness index) computed from original data. The original geographic coordinate information for each pixel was not considered in the experiments. The original dataset was officially divided into the train set and test set; we reintegrated the dataset to form a dataset consisting of 99,687 pixels distributed over 9 classes of land cover; the sample statistics are shown in Table 1. The ground truth label of each pixel is referenced from the 2012 Corine Land Cover map (https://www.eea.europa.eu/publications/COR0-landcover) and the 2014 local farmers’ graphical land parcel registration results.
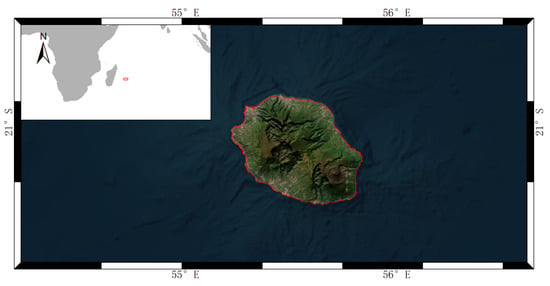 Figure 2. Study area of TiSeLaC: Reunion Island.
Figure 2. Study area of TiSeLaC: Reunion Island. Table 1. Sample Statistics of TiSeLaC.
Table 1. Sample Statistics of TiSeLaC.
- (2)
- TimeSen2Crop [57]: The data were collected from 15 Sentinel-2 tiles covering Austria, shown in Figure 3, between September 2017 and September 2018m with cloud coverage of less than 80% and atmospherically corrected using the radiative transfer model MODTRAN [58]. The number of acquisition dates of the time series varies for each tile, ranging from 23 to 38. The dataset has 16 crop types and 1.2 million pixels in total, and the sample statistics are shown in Table 2. For each pixel, there are 9 Sentinel-2 Bands (B2, B3, B4, B5, B6, B7, B8A, B11, B12) and 1 non-spectral band, indicating the condition of the pixel that was not considered in the experiments. The 20-m bands (B5, B6, B7, B8A, B11, B12) were resampled to 10 m and the final spatial resolution for each pixel is 10 m. The ground truth label of each pixel was extracted from the publicly available Austrian crop type map (https://www.data.gv.at/katalog/dataset/e21a731f).
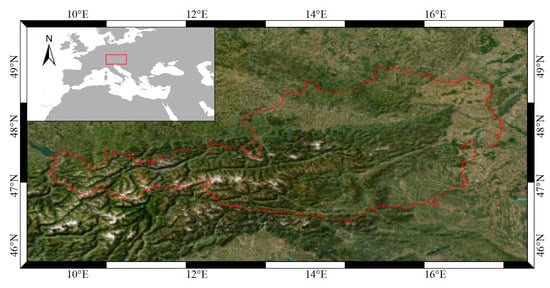 Figure 3. Study area of TimeSen2Crop: Austria.
Figure 3. Study area of TimeSen2Crop: Austria. Table 2. Sample Statistics of TimeSen2Crop.
Table 2. Sample Statistics of TimeSen2Crop.
3.2. Competing Methods and Classification Architecture
In order to verify the effectiveness of GL-TAE, the following temporal encoders were selected for comparison: TempCNN [32], TCN [35], LSTM [21], transformer [50], TAE [51], and LTAE [52].
- 1.
- TempCNN: TempCNN [32] has three vanilla convolutional layers that apply convolutions on the temporal dimensions with different kernels of kernel_size = 3. We added the same channel enhancement layer of GL-TAE before the convolutions. Then TempCNN flattens and dimensionally reduces the time series from to with a dense layer. However it is unable to handle the time series with variable temporal lengths; therefore, we replaced the flattened-dense layer with the global (temporal) average pooling layer for experiments on the TimeSen2Crop dataset.
- 2.
- TCN: TCN [35], which is different from TempCNN, has three causal convolutional layers with dilation and , which means TCN has a larger perceptive field than TempCNN along the temporal dimension.
- 3.
- LSTM: We adopted a one-layer LSTM with adjustable hyperparameters , and then used the last hidden state and transformed it into the size by a dense layer. A channel enhancement layer was also added before the LSTM layer.
- 4.
- Transformer: The architecture in [50] was adopted. In the original transformer, a query–key–value triplet was computed simultaneously for each time step in the time series and the attention mask was obtained by calculating the similarity of the queries and keys. The encoded result was defined as the sum of the values weighted by the attention mask. Reference [50] took the original transformer encoder with positional encoding, multi-head attention, and feedforward networks and used a global maximum average operation to achieve a dimensionality reduction from size to .
- 5.
- TAE: Reference [51] removed the feedforward networks and defined the master query as the mean of queries. The master query was then multiplied with the keys to determine a single attention mask for weighing the input time series.
- 6.
In the experiments, we followed the scheme in [51]: first, we extracted the temporal features and then used a multi-layer perceptron (MLP) as a common classifier. The purpose was to fairly compare the capabilities of different temporal encoders and exclude the influence of using different classifiers in practice.
3.3. Implementation Details
The five-fold cross-validation scheme was implemented to evaluate the performance of each method, and both datasets were divided into training, validation, and test sets at a 3:1:1 ratio. In the training stage, we trained models at a fixed batch size of 128, focal loss [59] as the objective function, and the Adam optimizer with the default setting (, ). Focal loss computes the following with being classification probability and y being the ground truth for binary classification.
The quantitative evaluation metrics used were overall accuracy (OA) and mean per-class intersect over union (mIoU). OA is the most commonly used metric for classification evaluation, but it is subject to the accuracy of classes, which take more proportions in the dataset. That is why mIoU was chosen as a classification metric that reflected the performance of a model on the imbalanced dataset. All networks were trained for 1000/100 epochs in each fold on the TiSeLaC/TimeSen2Crop dataset to ensure the convergence of the model; we selected the best mIoU epoch on the validation set and evaluated it on the test set. We adjusted the hyperparameters of each encoder to obtain models with parameters at different orders of magnitude due to the fact that the number of parameters of the model affected the classification performance [51,52]. The hyperparameters adjusted for each encoder and their candidates are listed in Table 3. The dropout probability p used for training all models was adjusted in the range of [0, 0.5].

Table 3.
Candidates of hyperparameters of different encoders.
3.4. Classification Results
In Table 4, we present the classification results of GL-TAE and competing methods under the condition of having approximately the same parameter numbers, all calculating the mean and standard deviations from a five-fold cross-validation scheme. Two convolutional networks (TempCNN, TCN) achieved comparable classification results compared with three self-attention mechanism-based models (LTAE, TAE, transformer) in two datasets, corroborating the importance of local temporal features. LTAE outperforms TAE and TAE outperforms the transformer, indicating that the setting of the master query and the modified mechanism of multi-head attention along the channel dimension have improvements in the self-attention mechanisms in extracting global temporal features. Our proposed GL-TAE outperformed all competing models in OA by 0.32–2.34% and 0.19–1.56% and mIoU by 1.70–5.41% and 0.39–4.1% on two datasets. Furthermore, GL-TAE achieved the best results in the per-class accuracy in most classes of two datasets. Specifically, GL-TAE yielded the best performances in the forest, sparse vegetation, grassland, and other crops of TiSeLaC, and yielded the best performances in legumes, soy, winter caraway, rye, rapeseed, beet, spring cereals, and winter wheat. For other classes where GL-TAE did not achieve the best results, the differences in the performance between GL-TAE and the best-performing model were negligible. For example, with TiSeLaC, TempCNN achieved the best results in urban areas and rocks and bare soil, which exceed GL-TAE by not more than 0.1%, and in TimeSen2Crop, GL-TAE achieved the best results in potato, winter barley, winter triticale, and permanent plantation, which exceed GL-TAE by 0.01–0.26%. It can be seen that our proposed GL-TAE, which is based on hybrid global–local temporal attention, is better than global-only or local-only attention-based methods for SITS classification under the same level of the model size.

Table 4.
Performance of GL-TAE and competing models all having approximate 160 K parameters on (a) TiSeLaC/140 K parameters and (b) TimeSen2Crop.
3.5. Comprehensive Comparison with Different Hyperparameter Settings
Figure 4 and Figure 5 show the performances in OA and mIoU of all models under different parameter numbers, ranging from 6 K to 4 M parameters. All models, except TAE, obtained better performances as the parameter numbers increased. Among the competing methods, TempCNN yielded the best results and LTAE yielded a slightly worse performance in TiSeLaC; however, LTAE yielded the best results in TimeSen2Crop—significantly better than TempCNN and TCN. Based on the above results, we argue that LTAE is more robust, and that with convolutional networks, it is hard to tackle larger datasets, even with larger perceptive fields. The vanilla self-attention mechanism method transformer and recurrent network LSTM yielded the worst results of the two datasets. GL-TAE yielded the best performance with parameters at different orders of magnitude on two datasets; this further demonstrates that our proposed hybrid global–local temporal attention-based approach is more robust and effective at extracting temporal features for classification compared to global-only and local-only attention-based methods.
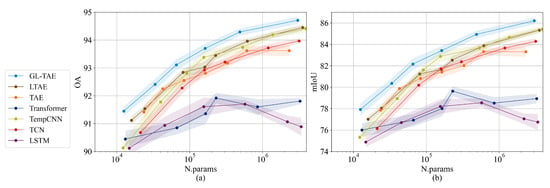
Figure 4.
Performance in (a) OA and (b) mIoU on TiSeLaC of different methods plotted with respect to the parameter numbers. The axis of parameters is given on a logarithmic scale and the light shaded areas represent the standard deviations of OA/mIoU across the five cross-validation folds.
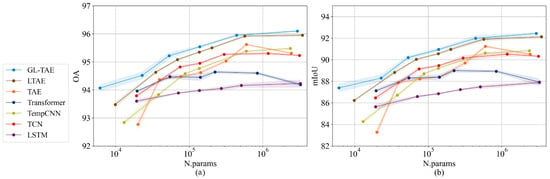
Figure 5.
Performances of (a) OA and (b) mIoU on TimeSen2Crop of the different methods plotted with respect to the parameter numbers.
Furthermore, we can conclude from Figure 4 and Figure 5 that smaller GL-TAE models can achieve comparable performances to other models. A GL-TAE with 163 K parameters achieves a similar performance to a TempCNN with 534 K parameters with mIoU, and OA on TiSeLaC. With TimeSen2Crop, a GL-TAE with 53 K parameters yields comparable results with most competing models with 300 K–3 M parameters and a GL-TAE with 440 K parameters yields mIoU and OA, which is slightly worse than a LTAE with 3.5 M parameters.
Overall, the hybrid global–local attention used in our proposed GL-TAE is better for SITS classification than global attention or local attention in terms of temporal feature extraction, and GL-TAE is a lightweight model, which is an advantage in practice for processing massive amounts of SITS data.
4. Discussion
We verified the effectiveness of GL-TAE and its hybrid global–local attention for SITS classification in two datasets in the last section. In this section, we further analyze which attention plays a more important role in the hybrid global–local attention of GL-TAE, whether the strategy is necessary, and what the impacts are of the different values of the hyperparameters in GL-TAE.
4.1. Importance Comparison of Global and Local Attention
Figure 6 and Figure 7 show the results of GL-TAE, LTAE, and LConv on two datasets under different parameter numbers. LTAE or LConv could outperform GL-TAE on the two datasets, which demonstrates the effectiveness of combining LTAE and LConv to extract global and local attention in GL-TAE. LConv outperforms LTAE with relatively fewer parameter numbers on TiSeLaC, but with the parameter numbers increasing, LTAE achieves a better performance than LConv. LTAE outperforms LConv on TimeSen2Crop with an obvious large margin, which is consistent with the conclusion in Section 3.5 that convolutional networks perform worse on large datasets. We can conclude that global attention extracted by LTAE plays a more important role in GL-TAE than local attention extracted by LConv. LTAE or LConv could outperform GL-TAE under any parameter numbers on the two datasets, which demonstrates the effectiveness and stability of hybrid global–local attention extracted by combining LTAE and LConv for SITS classification.
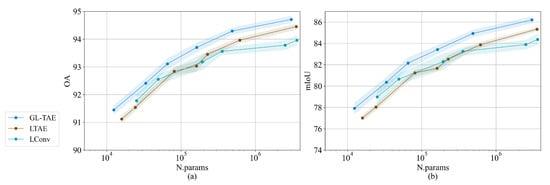
Figure 6.
Performance of (a) OA and (b) mIoU on the TiSeLaC of LTAE and LConv; plotted with respect to the parameter numbers.
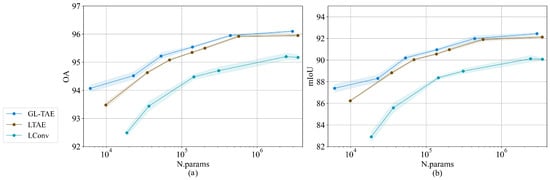
Figure 7.
Performance of (a) OA and (b) mIoU on the TimeSen2Crop of LTAE and LConv; plotted with respect to the parameter numbers.
4.2. Necessity of Channel Dimension Split
The original purpose of Dim. Split is to reduce the parameter numbers of GL-TAE under the same hyperparameter settings. If Dim. Split is discarded, we have to double to meet the consistency of the channel dimension; the channel numbers in each head of LTAE and each group in LConv will also be doubled. Consequently, the parameter numbers will be doubled under the same hyperparameter settings. Figure 8 and Figure 9 show the results of four hyperparameter settings of GL-TAE on the two datasets without Dim. Split, which corresponds to the second–fifth hyperparameter settings with Dim. Split. Obviously, GL-TAEs with Dim. Split exceed GL-TAEs without Dim. Split under the same order of magnitude of parameters. Furthermore, under the same hyperparameter settings, if we discard Dim. Split, the parameter numbers are almost doubled, but the performance is only slightly improved in some cases. For example, a GL-TAE with , , , and Dim. Split has 53 K parameters and yields mIoU, and OA on TimeSen2Crop. If we discard Dim. Split, a GL-TAE yields mIoU and OA with 103 K parameters. Therefore, Dim. Split is an effective and necessary strategy to feed input into two submodules in GL-TAE, which make the model lightweight, combined with two lightweight submodules, while maintaining comparable performances.
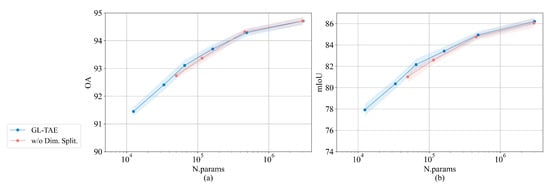
Figure 8.
Performance of (a) OA and (b) mIoU on the TiSeLaC of GL-TAE with/without Dim. Split; plotted with respect to the parameter numbers. GL-TAE without Dim. Split has four hyperparameter settings corresponding with the second to fifth hyperparameter settings of GL-TAE with Dim. Split.
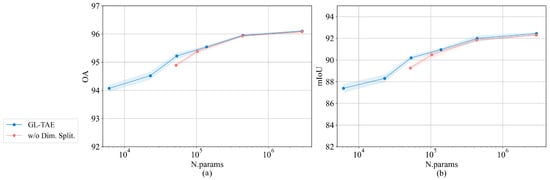
Figure 9.
Performance of (a) OA and (b) mIoU on the TimeSen2Crop of GL-TAE with/without Dim. Split; plotted with respect to the parameter numbers.
4.3. Impact of Different Values of Hyperparameters
In Table 5 and Table 6, we selected four crucial hyperparameters in GL-TAE and investigated the influences of different values for each hyperparameter on the performance of GL-TAE. The selected hyperparameters are the number of channels , the number of heads of LTAE and groups of LConv , and the dimension of keys in LTAE and of LConv. For each hyperparameter to be investigated, we only adjusted its value and kept the other hyperparameters as default settings.

Table 5.
The influence of four hyperparameters of GL-TAE on the performance of TiSeLaC. ’Underlines’ are default parameter values.

Table 6.
Influence of four hyperparameters of GL-TAE on the performance of TimeSen2Crop. Underlines are default parameter values.
The results of the two datasets show that the GL-TAE with a larger number of channels had a better performance, We argue that a larger has more parameter numbers and richer representation for the time series. We set in GL-TAE and it can be seen from the results that the performance first became better and then worse with increasing. We argue that there is a best for a fixed , smaller is insufficient to extract the diversity of global and local temporal information, and larger leads to each head of LTAE or each group of LConv lacking the representation of temporal information. Additionally, the dimension of keys in LTAE seems to have a limited effect on the performance and the difference caused by is negligible. We note that a larger leads (incrementally) to a slightly worse performance, which indicates is expected in practice.
5. Conclusions
In this paper, a novel temporal encoder named GL-TAE, which pays attention to both global and local temporal features, is proposed for remote sensing time series classifications. GL-TAE combines two lightweight submodules, LTAE and LConv, in parallel for extracting global–local attention features. We compared GL-TAE with other state-of-the-art models on two public datasets. GL-TAE has an average improvement of 1.18%/0.87% in OA and 2.77%/2.14% in mIoU on TiSeLaC/TimeSen2Crop with approximately 160 K/140 K parameters in comparison with existing models. We can conclude from the experiments that hybrid global–local temporal attention extraction is better than global-only or local-only attention feature extraction for SITS classification. Meanwhile, one thing noteworthy is that our proposed GL-TAE requires much fewer parameters when achieving the same performance as other models. A GL-TAE with 370 K fewer parameters is able to achieve similar performance to a TempCNN on TiSeLaC, and a GL-TAE with 53 K parameters is capable of achieving comparable results with most existing models with 300 K+ parameters. At this stage, we only focused on the extraction of temporal features from SITS data, but more applications are currently utilizing the spatial–temporal–spectral features for SITS classifications. Further modifications on the proposed GL-TAE to extract spatial–temporal–spectral features can be focused on in future work.
Author Contributions
Conceptualization, W.Z. and Z.Z. (Zheng Zhang); methodology, W.Z. and Z.Z. (Zhitao Zhao); software, W.Z. and H.Z.; validation, H.Z. and Z.Z. (Zhitao Zhao); writing—original draft preparation, W.Z.; writing—review and editing, P.T. and Z.Z. (Zheng Zhang); supervision, P.T. and Z.Z. (Zheng Zhang); project administration, P.T.; funding acquisition, Z.Z. (Zheng Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (grant no. 2021YFB3900503), the Self-Topic Fund of Aerospace Information Research Institute, CAS (grant no. E1Z211010F), and the Youth Innovation Promotion Association, CAS (no. 2022127).
Data Availability Statement
The data that support the findings of this study are openly available in (1) TiSeLaC (accessed on 20 December 2021) (https://sites.google.com/site/dinoienco/tiselac-time-series-land-cover-classification-challenge) and (2) TimeSen2Crop (accessed on 18 May 2022) (https://rslab.disi.unitn.it/timesen2crop/).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Langley, S.K.; Cheshire, H.M.; Humes, K.S. A comparison of single date and multitemporal satellite image classifications in a semi-arid grassland. J. Arid. Environ. 2001, 49, 401–411. [Google Scholar] [CrossRef]
- Franklin, S.E.; Ahmed, O.S.; Wulder, M.A.; White, J.C.; Hermosilla, T.; Coops, N.C. Large area mapping of annual land cover dynamics using multitemporal change detection and classification of Landsat time series data. Can. J. Remote Sens. 2015, 41, 293–314. [Google Scholar] [CrossRef]
- Zheng, B.; Myint, S.W.; Thenkabail, P.S.; Aggarwal, R.M. A support vector machine to identify irrigated crop types using time-series Landsat NDVI data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 103–112. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Dedieu, G. Assessing the robustness of Random Forests to map land cover with high resolution satellite image time series over large areas. Remote Sens. Environ. 2016, 187, 156–168. [Google Scholar] [CrossRef]
- Guo, Y.; Jia, X.; Paull, D. Effective sequential classifier training for SVM-based multitemporal remote sensing image classification. IEEE Trans. Image Process. 2018, 27, 3036–3048. [Google Scholar]
- Ouzemou, J.e.; El Harti, A.; Lhissou, R.; El Moujahid, A.; Bouch, N.; El Ouazzani, R.; Bachaoui, E.M.; El Ghmari, A. Crop type mapping from pansharpened Landsat 8 NDVI data: A case of a highly fragmented and intensive agricultural system. Remote Sens. Appl. Soc. Environ. 2018, 11, 94–103. [Google Scholar] [CrossRef]
- Kang, J.; Zhang, H.; Yang, H.; Zhang, L. Support vector machine classification of crop lands using Sentinel-2 imagery. In Proceedings of the 2018 7th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Hangzhou, China, 6–9 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Gbodjo, Y.J.E.; Ienco, D.; Leroux, L. Toward spatio–spectral analysis of sentinel-2 time series data for land cover mapping. IEEE Geosci. Remote Sens. Lett. 2019, 17, 307–311. [Google Scholar] [CrossRef]
- Zafari, A.; Zurita-Milla, R.; Izquierdo-Verdiguier, E. A multiscale random forest kernel for land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2842–2852. [Google Scholar] [CrossRef]
- Hao, P.; Zhan, Y.; Wang, L.; Niu, Z.; Shakir, M. Feature selection of time series MODIS data for early crop classification using random forest: A case study in Kansas, USA. Remote Sens. 2015, 7, 5347–5369. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, H.; Zhang, M. Mapping paddy rice by the object-based random forest method using time series Sentinel-1/Sentinel-2 data. Adv. Space Res. 2019, 64, 2233–2244. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series; KDD Workshop: Seattle, WA, USA, 1994; Volume 10, pp. 359–370. [Google Scholar]
- Jiang, W. Time series classification: Nearest neighbor versus deep learning models. SN Appl. Sci. 2020, 2, 1–17. [Google Scholar] [CrossRef]
- Petitjean, F.; Inglada, J.; Gançarski, P. Satellite image time series analysis under time warping. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3081–3095. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, P.; Huo, L.; Zhou, Z. MODIS NDVI time series clustering under dynamic time warping. Int. J. Wavelets Multiresolution Inf. Process. 2014, 12, 1461011. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, L.; Lu, W.; Meng, Y. Landsat time series clustering under modified Dynamic Time Warping. In Proceedings of the 2016 4th International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Guangzhou, China, 4–6 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 62–66. [Google Scholar]
- Maus, V.; Câmara, G.; Cartaxo, R.; Sanchez, A.; Ramos, F.M.; De Queiroz, G.R. A time-weighted dynamic time warping method for land-use and land-cover mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3729–3739. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Maus, V.; Câmara, G.; Appel, M.; Pebesma, E. dtwsat: Time-weighted dynamic time warping for satellite image time series analysis in r. J. Stat. Softw. 2019, 88, 1–31. [Google Scholar] [CrossRef]
- Belgiu, M.; Zhou, Y.; Marshall, M.; Stein, A. Dynamic time warping for crops mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 947–951. [Google Scholar] [CrossRef]
- Ienco, D.; Gaetano, R.; Dupaquier, C.; Maurel, P. Land cover classification via multitemporal spatial data by deep recurrent neural networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1685–1689. [Google Scholar] [CrossRef]
- Rußwurm, M.; Korner, M. Temporal vegetation modelling using long short-term memory networks for crop identification from medium-resolution multi-spectral satellite images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 June 2017; pp. 11–19. [Google Scholar]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Mikolov, T.; Karafiát, M.; Burget, L.; Cernockỳ, J.; Khudanpur, S. Recurrent neural network based language model. In Proceedings of the Interspeech, Makuhari, Japan, 26–30 September 2010; Volume 2, pp. 1045–1048. [Google Scholar]
- Sharma, A.; Liu, X.; Yang, X. Land cover classification from multi-temporal, multi-spectral remotely sensed imagery using patch-based recurrent neural networks. Neural Netw. 2018, 105, 346–355. [Google Scholar] [CrossRef]
- Minh, D.H.T.; Ienco, D.; Gaetano, R.; Lalande, N.; Ndikumana, E.; Osman, F.; Maurel, P. Deep recurrent neural networks for winter vegetation quality mapping via multitemporal SAR Sentinel-1. IEEE Geosci. Remote Sens. Lett. 2018, 15, 464–468. [Google Scholar] [CrossRef]
- Ienco, D.; Gaetano, R.; Interdonato, R.; Ose, K.; Minh, D.H.T. Combining sentinel-1 and sentinel-2 time series via rnn for object-based land cover classification. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4881–4884. [Google Scholar]
- Yin, R.; He, G.; Wang, G.; Long, T.; Li, H.; Zhou, D.; Gong, C. Automatic Framework of Mapping Impervious Surface Growth With Long-Term Landsat Imagery Based on Temporal Deep Learning Model. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Kwak, G.H.; Park, C.W.; Ahn, H.Y.; Na, S.I.; Lee, K.D.; Park, N.W. Potential of bidirectional long short-term memory networks for crop classification with multitemporal remote sensing images. Korean J. Remote. Sens. 2020, 36, 515–525. [Google Scholar]
- Crisóstomo de Castro Filho, H.; Abílio de Carvalho Júnior, O.; Ferreira de Carvalho, O.L.; Pozzobon de Bem, P.; dos Santos de Moura, R.; Olino de Albuquerque, A.; Rosa Silva, C.; Guimarães Ferreira, P.H.; Fontes Guimarães, R.; Trancoso Gomes, R.A. Rice crop detection using LSTM, Bi-LSTM, and machine learning models from sentinel-1 time series. Remote Sens. 2020, 12, 2655. [Google Scholar] [CrossRef]
- Bakhti, K.; Arabi, M.E.A.; Chaib, S.; Djerriri, K.; Karoui, M.S.; Boumaraf, S. Bi-Directional LSTM Model For Classification Of Vegetation From Satellite Time Series. In Proceedings of the 2020 Mediterranean and Middle-East Geoscience and Remote Sensing Symposium (M2GARSS), Tunis, Tunisia, 9–11 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 160–163. [Google Scholar]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef]
- Ienco, D.; Gbodjo, Y.J.E.; Gaetano, R.; Interdonato, R. Weakly supervised learning for land cover mapping of satellite image time series via attention-based CNN. IEEE Access 2020, 8, 179547–179560. [Google Scholar] [CrossRef]
- Račič, M.; Oštir, K.; Peressutti, D.; Zupanc, A.; Čehovin Zajc, L. Application of temporal convolutional neural network for the classification of crops on sentinel-2 time series. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 1337–1342. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Brock, J.; Abdallah, Z.S. Investigating Temporal Convolutional Neural Networks for Satellite Image Time Series Classification. arXiv 2022, arXiv:2204.08461. [Google Scholar]
- Zhao, B.; Lu, H.; Chen, S.; Liu, J.; Wu, D. Convolutional neural networks for time series classification. J. Syst. Eng. Electron. 2017, 28, 162–169. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time series classification using multi-channels deep convolutional neural networks. In Proceedings of the International Conference on Web-Age Information Management, Macau, China, 16–18 June 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 298–310. [Google Scholar]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Exploiting multi-channels deep convolutional neural networks for multivariate time series classification. Front. Comput. Sci. 2016, 10, 96–112. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. Inceptiontime: Finding alexnet for time series classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I.; Sutskever, I. Improving language understanding by generative pre-training. 2018. Available online: https://www.cs.ubc.ca/~amuham01/LING530/papers/radford2018improving.pdf (accessed on 15 March 2022).
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual Event, 18–24 July 2021; ACM: New York, NY, USA, 2021; pp. 10347–10357. [Google Scholar]
- Yuan, Y.; Lin, L. Self-supervised pretraining of transformers for satellite image time series classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 474–487. [Google Scholar] [CrossRef]
- Rußwurm, M.; Körner, M. Self-attention for raw optical satellite time series classification. ISPRS J. Photogramm. Remote. Sens. 2020, 169, 421–435. [Google Scholar] [CrossRef]
- Garnot, V.S.F.; Landrieu, L.; Giordano, S.; Chehata, N. Satellite image time series classification with pixel-set encoders and temporal self-attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12325–12334. [Google Scholar]
- Garnot, V.S.F.; Landrieu, L. Lightweight temporal self-attention for classifying satellite images time series. In Proceedings of the International Workshop on Advanced Analytics and Learning on Temporal Data, Ghent, Belgium, 18 September 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 171–181. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Garnot, V.S.F.; Landrieu, L. Panoptic segmentation of satellite image time series with convolutional temporal attention networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4872–4881. [Google Scholar]
- Interdonato, R.; Ienco, D.; Gaetano, R.; Ose, K. DuPLO: A DUal view Point deep Learning architecture for time series classificatiOn. ISPRS J. Photogramm. Remote Sens. 2019, 149, 91–104. [Google Scholar] [CrossRef]
- Wu, F.; Fan, A.; Baevski, A.; Dauphin, Y.N.; Auli, M. Pay less attention with lightweight and dynamic convolutions. arXiv 2019, arXiv:1901.10430. [Google Scholar]
- Weikmann, G.; Paris, C.; Bruzzone, L. Timesen2crop: A million labeled samples dataset of sentinel 2 image time series for crop-type classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4699–4708. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Richtsmeier, S.C.; Pukall, B.; et al. MODTRAN4 radiative transfer modeling for atmospheric correction. In Proceedings of the Optical spectroscopic techniques and instrumentation for atmospheric and space research III, Denver, CO, USA, 19–21 July 1999; SPIE: Bellingham, WA, USA, 1999; Volume 3756, pp. 348–353. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).