A New Method for Deformation Monitoring of Structures by Precise Point Positioning
Abstract
:1. Introduction
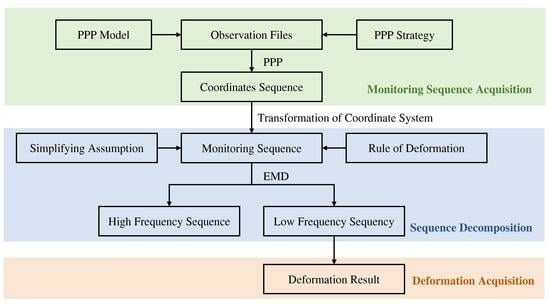
2. Materials and Methods
2.1. Original Monitoring Sequence of PPP
2.1.1. Precise Point Positioning
2.1.2. Acquiring Monitoring Sequence
2.1.3. Transformation of the Coordinate System
2.2. Analysis of the Monitoring Sequence
2.2.1. Simplifying Assumption
- The precision of the coordinates obtained under the same length of the monitoring arc segment was assumed to be the same and the errors were assumed to be independent and identically distributed among the monitoring coordinate sequence process.
- There are corresponding periods of fluctuation in the monitoring sequence. Random noise is related to the count of monitoring arc segments due to the unique data characteristics. Both parts can be seen as signals at a certain fixed frequency.
- Due to the structure of the project and the requirements of the engineering specifications, the deformation of the construction is inevitably slow. Compared to the periodic fluctuation signals and random errors, we can assume the period of static deformation information to be infinitely long, or a non-frequent signal.
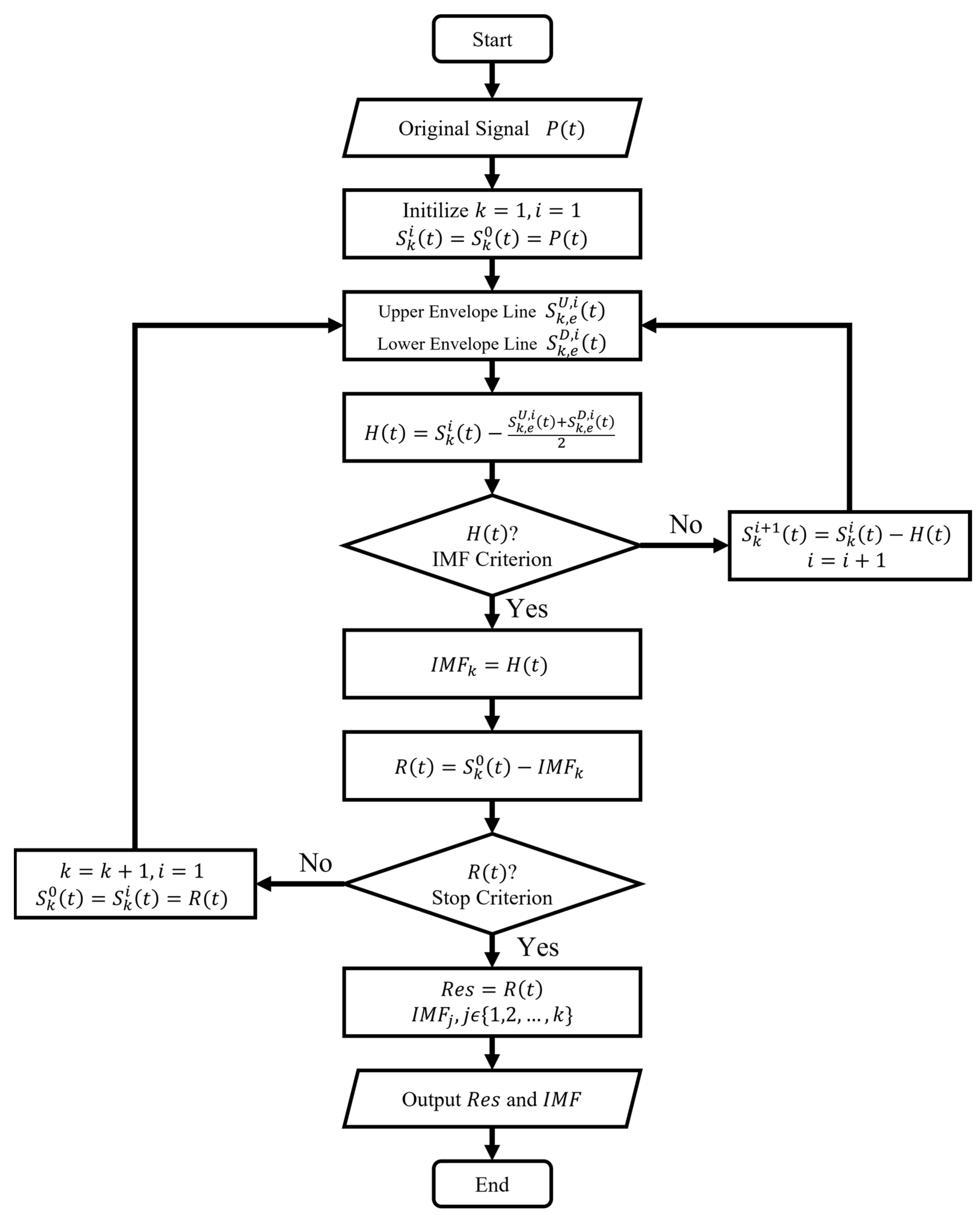
2.2.2. Empirical Mode Decomposition
- The numbers of extremum points and zero-crossing points in the entire signal sequence are the same or differ by one at most;
- The average of the upper and lower envelopes defined by the maximum and minimum values at any time is zero.
- Find all the maximum and minimum values in signal . Fit the maximum and minimum values, respectively, to obtain the upper and lower envelope lines in signal with the cubic spline curve.
- Calculate the average at each point of the upper and lower envelopes and obtain the average line, denoted as .
- Calculate and check whether conforms to the IMF component definition. If not, treat as the new , and redo Steps 1, 2 and 3 until meets the IMF component definition or the set screening threshold, denoted as .
- Recast as signal , and reiterate Steps 1, 2, 3, 4 until no new IMF component can be separated from signal . The remaining part is recorded as .
2.3. Experimentation
2.3.1. Data Resource
2.3.2. Configuration and Strategy
3. Results
4. Discussion
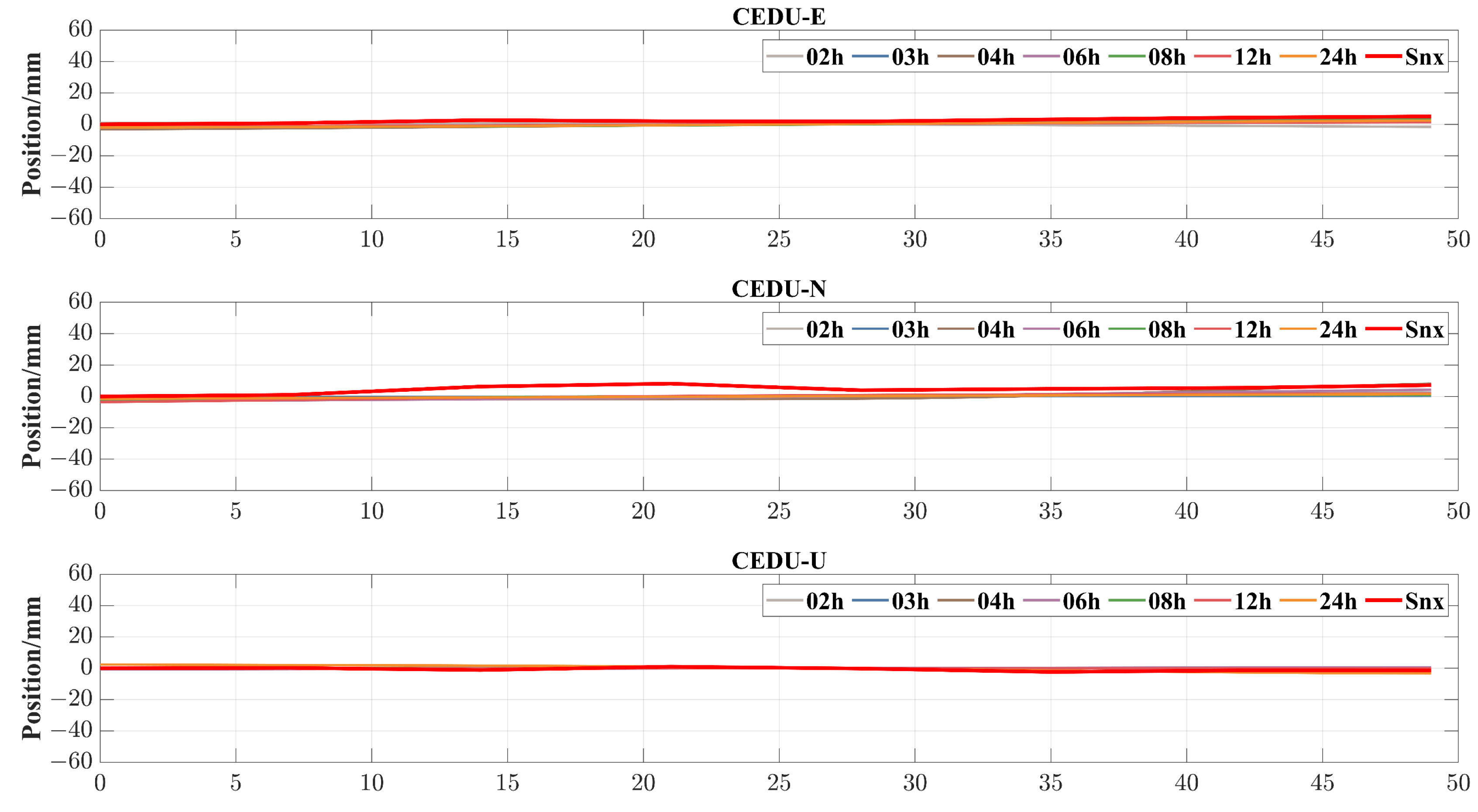
4.1. Monitoring Index Sd
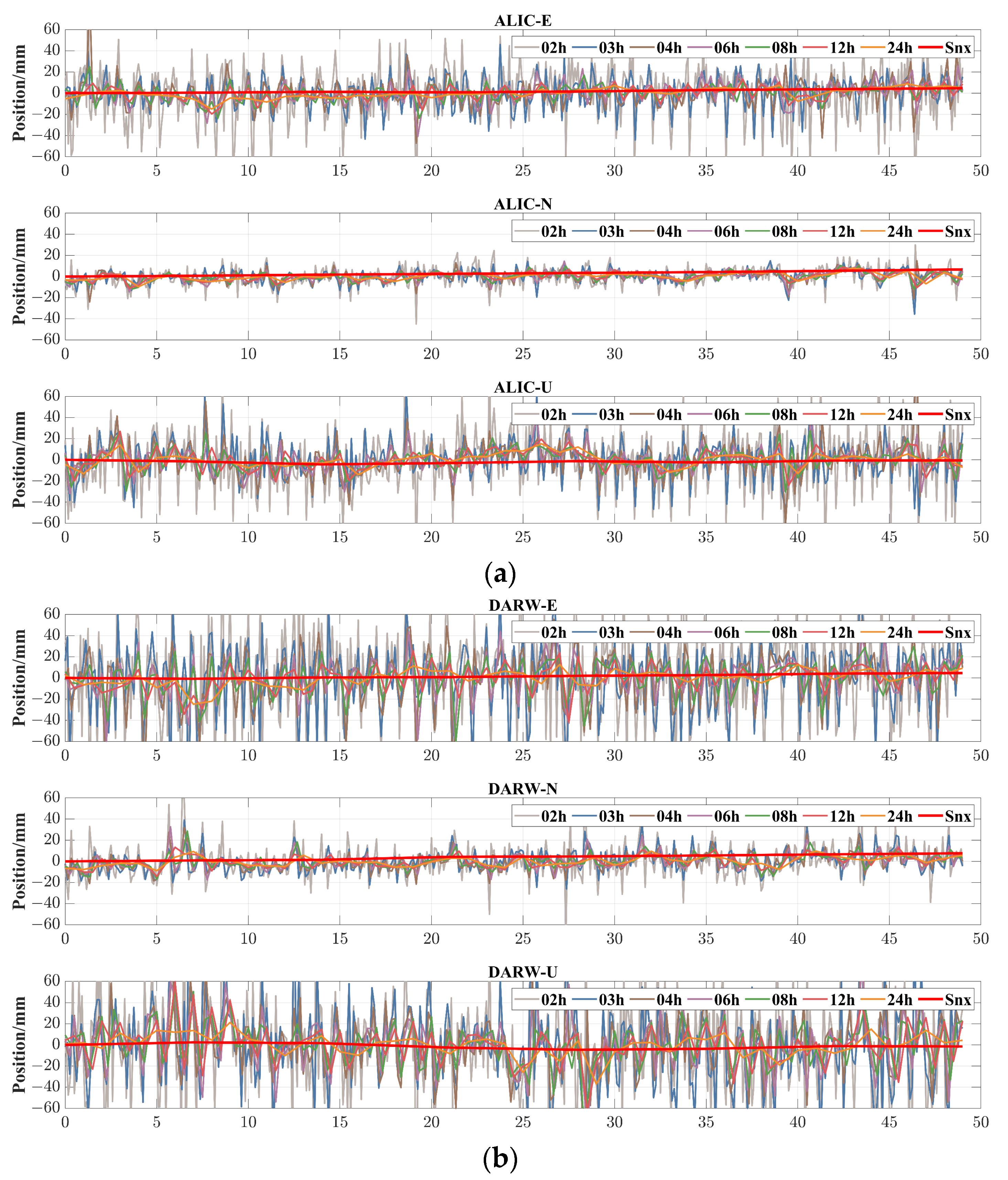
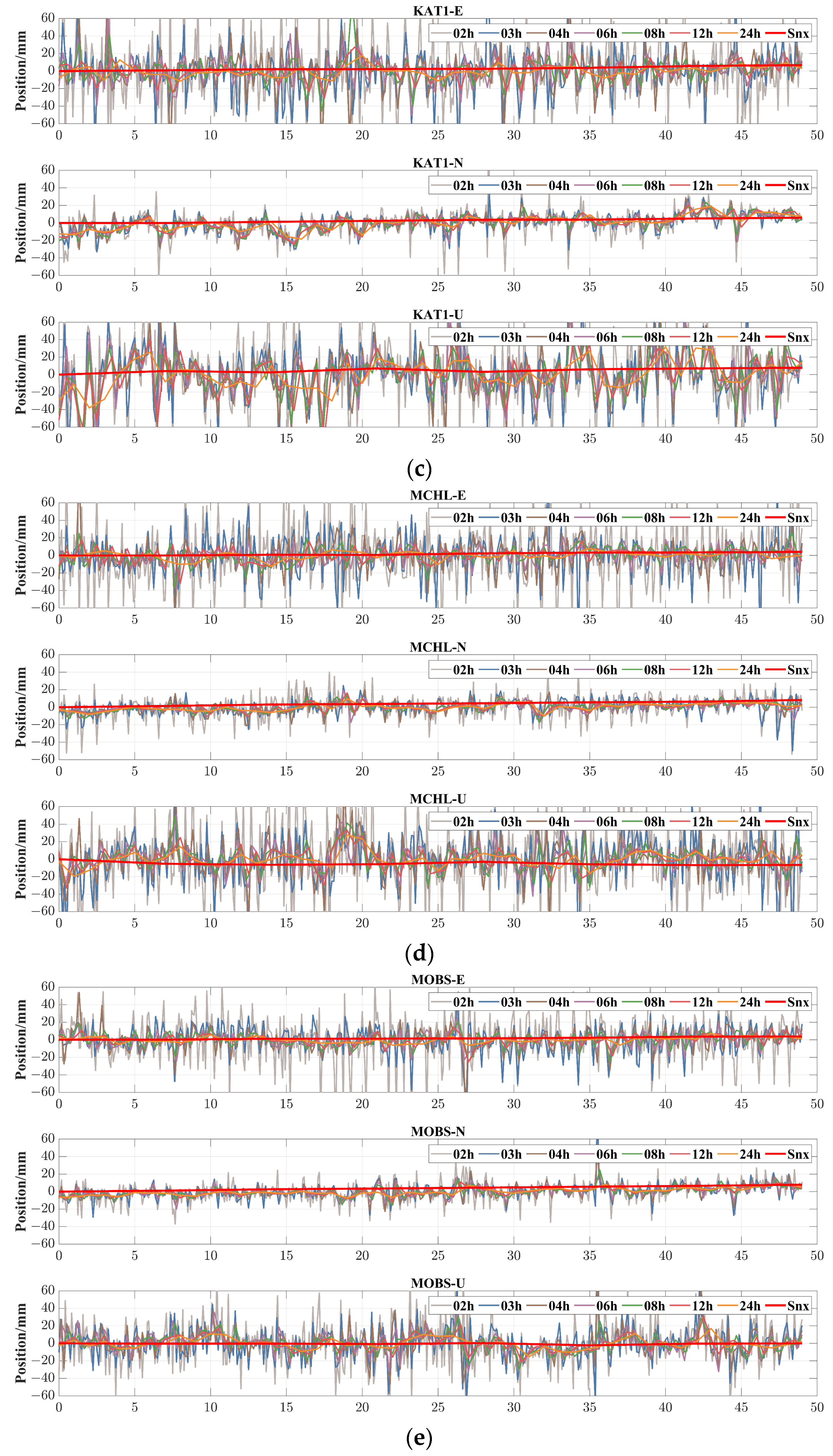
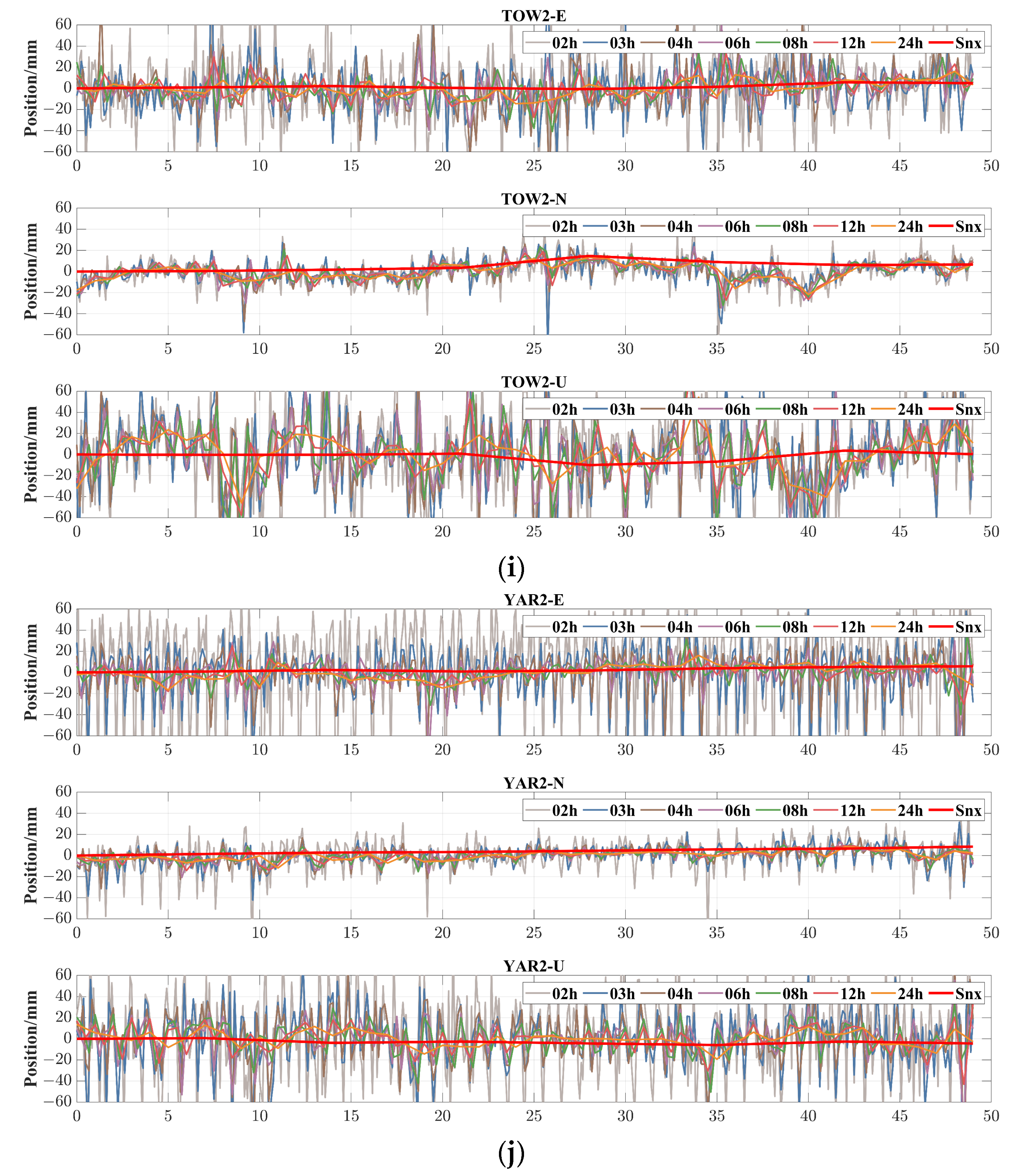
4.2. Analysis of the Monitoring Result
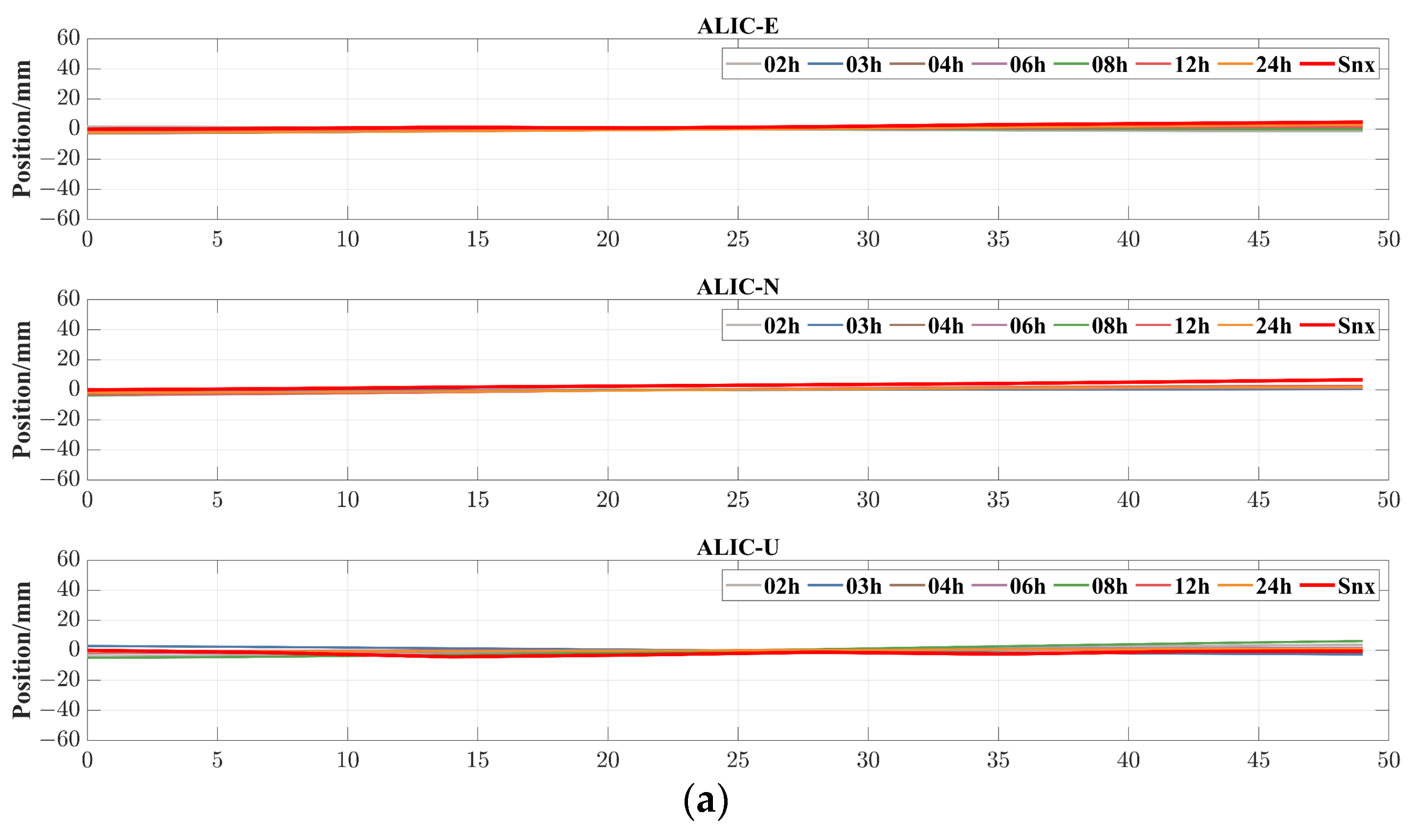
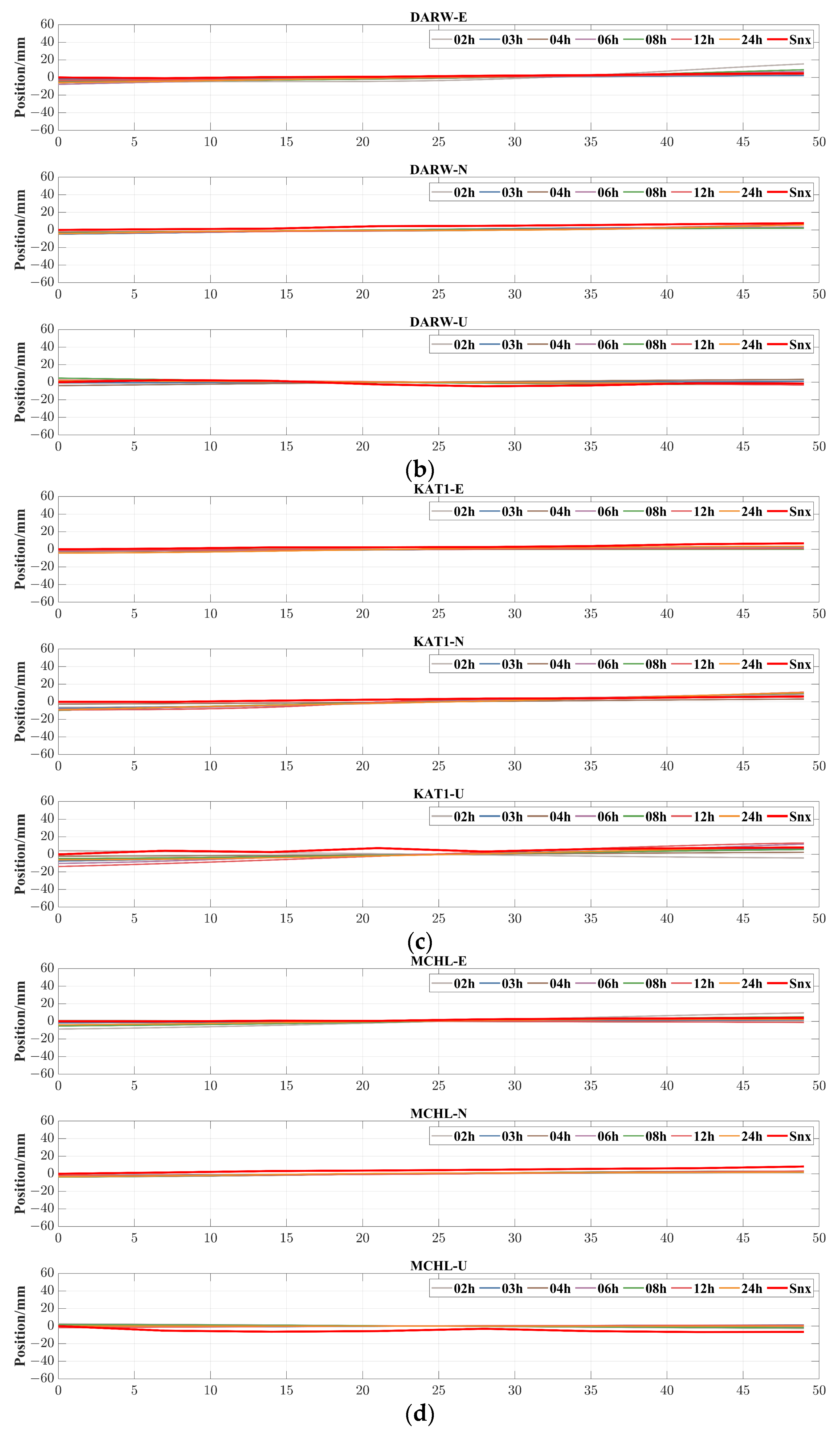
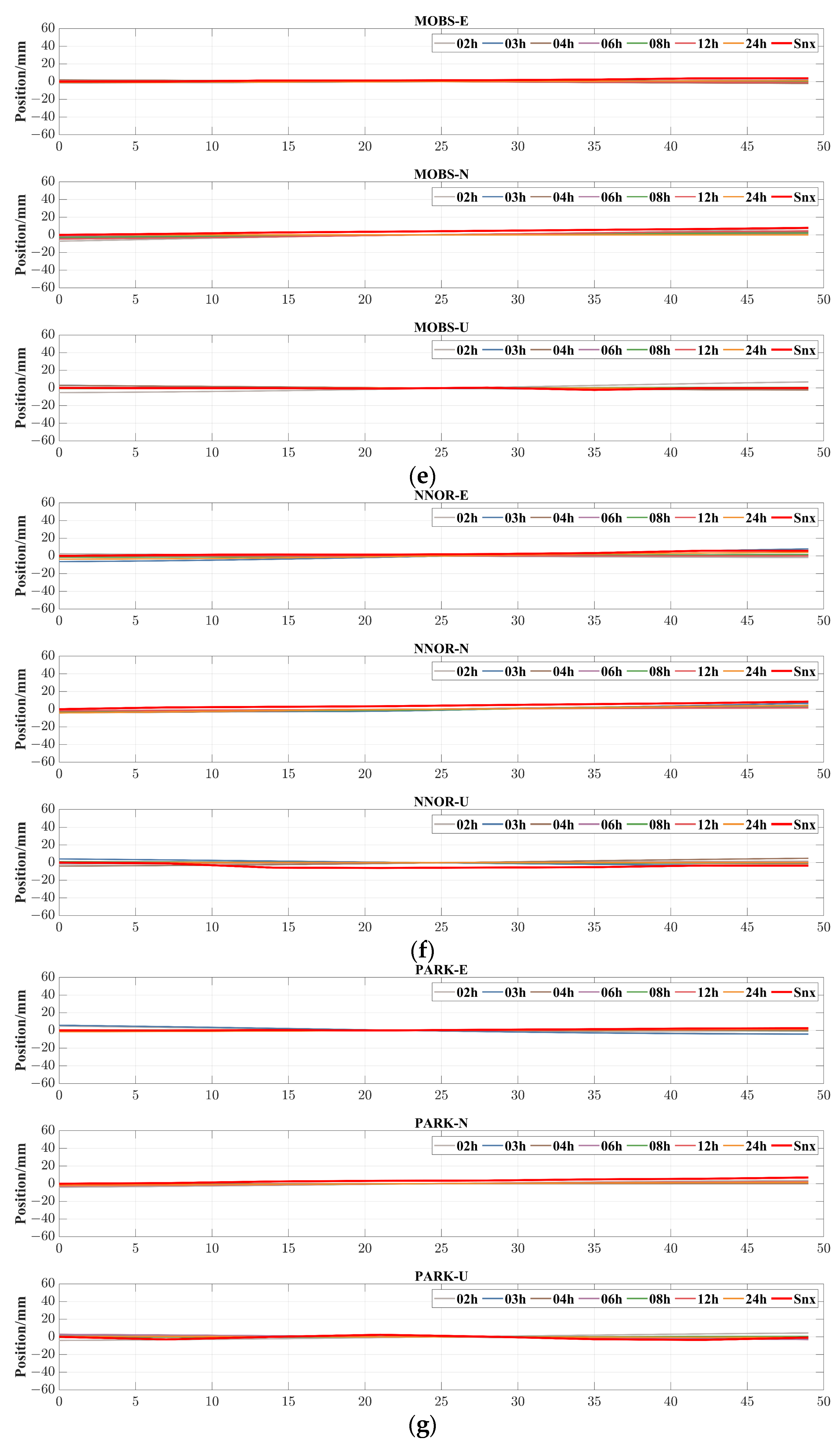
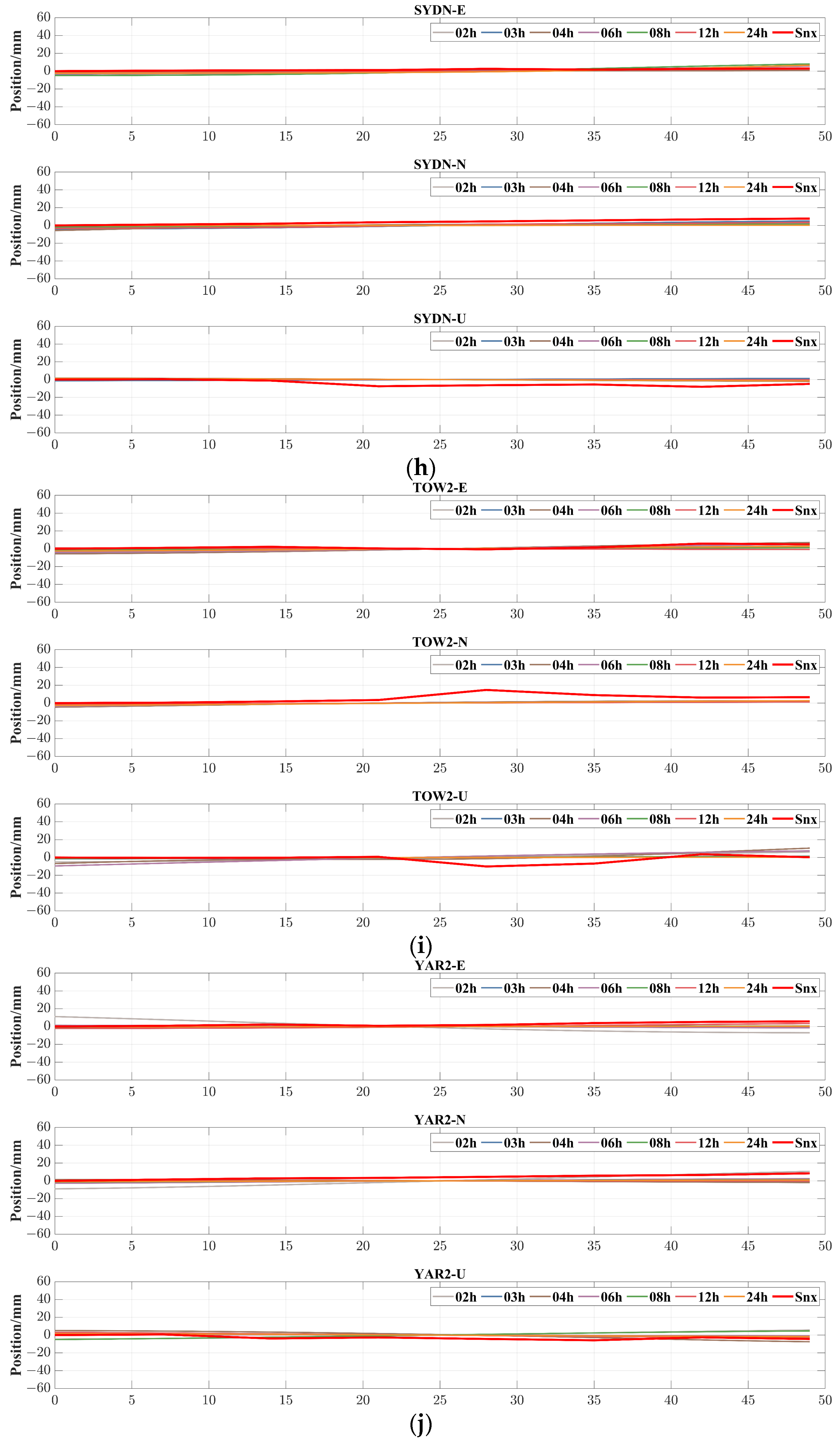
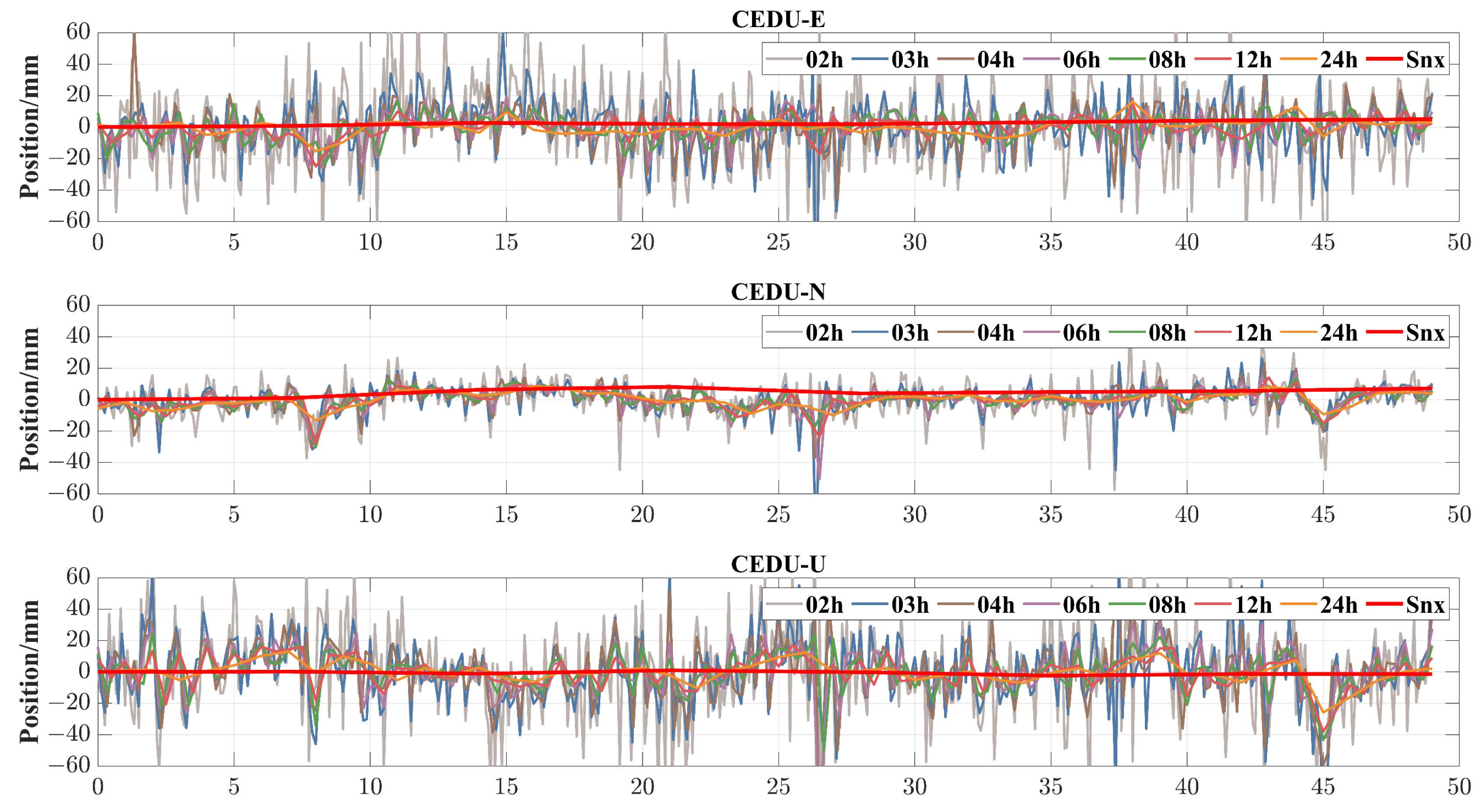
4.2.1. Original Monitoring Sequence of PPP
- Static deformation information is present in the original PPP deformation monitoring sequence.
- The static deformation information in the original PPP deformation monitoring sequence is drowned out by the fluctuations.
- As the monitoring arc shortens, the fluctuations in the original PPP deformation monitoring sequence become more pronounced, exacerbating the drowning out effect of static deformation information.
4.2.2. Extracting the Monitoring Sequence of PPP
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Du, Y.; Huang, G.; Zhang, Q.; Gao, Y.; Gao, Y. Asynchronous RTK Method for Detecting the Stability of the Reference Station in GNSS Deformation Monitoring. Sensors 2020, 20, 1320. [Google Scholar] [CrossRef] [PubMed]
- Nadarajah, N.; Khodabandeh, A.; Wang, K.; Choudhury, M.; Teunissen, P. Multi-GNSS PPP-RTK: From Large- to Small-Scale Networks. Sensors 2018, 18, 1078. [Google Scholar] [CrossRef]
- Gao, J.; Liu, C.; Wang, J.; Li, Z.; Meng, X. A New Method for Mining Deformation Monitoring with GPS-RTK. Trans. Nonferrous Met. Soc. China 2011, 21, S659–S664. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y.; Xiang, Z.; Zhang, S.; Li, X.; Wang, X.; Ma, X.; Hu, C.; Pan, J.; Zhou, Y.; et al. A Novel Low-Cost GNSS Solution for the Real-Time Deformation Monitoring of Cable Saddle Pushing: A Case Study of Guojiatuo Suspension Bridge. Remote Sens. 2022, 14, 5174. [Google Scholar] [CrossRef]
- Xi, R.; Jiang, W.; Meng, X.; Chen, H.; Chen, Q. Bridge Monitoring Using BDS-RTK and GPS-RTK Techniques. Measurement 2018, 120, 128–139. [Google Scholar] [CrossRef]
- Luo, L.; Ma, W.; Zhang, Z.; Zhuang, Y.; Zhang, Y.; Yang, J.; Cao, X.; Liang, S.; Mu, Y. Freeze/Thaw-Induced Deformation Monitoring and Assessment of the Slope in Permafrost Based on Terrestrial Laser Scanner and GNSS. Remote Sens. 2017, 9, 198. [Google Scholar] [CrossRef]
- Jing, C.; Huang, G.; Zhang, Q.; Li, X.; Bai, Z.; Du, Y. GNSS/Accelerometer Adaptive Coupled Landslide Deformation Monitoring Technology. Remote Sens. 2022, 14, 3537. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, W.; Meng, X.; Jiang, P.; Wang, K.; Xie, Y.; Ye, J. Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK. Remote Sens. 2018, 10, 364. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Xia, F.; Cheng, X.; Zhang, H.; Jiang, W. A Multipath Mitigation Method in Long-Range RTK for Deformation Monitoring. GPS Solut. 2022, 26, 1–12. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Feng, Y.; Gao, W.; Yang, L. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK. J. Geod. 2014, 88, 99–112. [Google Scholar] [CrossRef]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, R.; Gu, S. A New PPP Algorithm for Deformation Monitoring with Single-Frequency Receiver. J. Earth Syst. Sci. 2014, 123, 1919–1926. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Gao, Y.; Heck, B. A Unified Model for Multi-Frequency PPP Ambiguity Resolution and Test Results with Galileo and BeiDou Triple-Frequency Observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Ma, F.; Yuan, Y.; Zhang, K.; Zhou, F.; Zhang, X. Improved PPP Ambiguity Resolution with the Assistance of Multiple LEO Constellations and Signals. Remote Sens. 2019, 11, 408. [Google Scholar] [CrossRef]
- Katsigianni, G.; Loyer, S.; Perosanz, F. PPP and PPP-AR Kinematic Post-Processed Performance of GPS-Only, Galileo-Only and Multi-GNSS. Remote Sens. 2019, 11, 2477. [Google Scholar] [CrossRef]
- Bertiger, W.; Desai, S.; Haines, B.; Harvey, N.; Moore, A.; Owen, S.; Weiss, J. Single Receiver Phase Ambiguity Resolution with GPS Data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Yang, H.; Ji, S.; Weng, D.; Wang, Z.; He, K.; Chen, W. Assessment of the Feasibility of PPP-B2b Service for Real-Time Coseismic Displacement Retrieval. Remote Sens. 2021, 13, 5011. [Google Scholar] [CrossRef]
- Gao, R.; Liu, Z.; Odolinski, R.; Jing, Q.; Zhang, J.; Zhang, H.; Zhang, B. Hong Kong-Zhuhai-Macao Bridge Deformation Monitoring Using PPP-RTK with Multipath Correction Method. GPS Solut. 2023, 27, 195. [Google Scholar] [CrossRef]
- Araszkiewicz, A. Integration of Distributed Dense Polish GNSS Data for Monitoring the Low Deformation Rates of Earth’s Crust. Remote Sens. 2023, 15, 1504. [Google Scholar] [CrossRef]
- Zang, N.; Li, B.; Nie, L.; Shen, Y. Inter-System and Inter-Frequency Code Biases: Simultaneous Estimation, Daily Stability and Applications in Multi-GNSS Single-Frequency Precise Point Positioning. GPS Solut. 2019, 24, 18. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Li, X.; Li, P.; Chang, X.; Sang, J.; Ge, M.; Schuh, H. Mitigation of Unmodeled Error to Improve the Accuracy of Multi-GNSS PPP for Crustal Deformation Monitoring. Remote Sens. 2019, 11, 2232. [Google Scholar] [CrossRef]
- Wang, G.; Turco, M.; Soler, T.; Kearns, T.; Welch, J. Comparisons of OPUS and PPP Solutions for Subsidence Monitoring in the Greater Houston Area. J. Surv. Eng. 2017, 143, 05017005. [Google Scholar] [CrossRef]
- Alcay, S.; Ogutcu, S.; Kalayci, I.; Yigit, C. Displacement Monitoring Performance of Relative Positioning and Precise Point Positioning (PPP) Methods Using Simulation Apparatus. Adv. Space Res. 2019, 63, 1697–1707. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Huang, G.W.; Tu, R.; Zhang, S.C. Experiment Results and Analysis of Landslide Monitoring by Using GPS PPP Technology. Rock Soil Mech. 2014, 35, 2118–2124. [Google Scholar]
- Psimoulis, P.; Houlié, N.; Meindl, M.; Rothacher, M. Consistency of PPP GPS and Strong-Motion Records: Case Study of Mw9.0 Tohoku-Oki 2011 Earthquake. Smart Struct. Syst. 2015, 16, 347–366. [Google Scholar] [CrossRef]
- Song, W.; Zhang, R.; Yao, Y.; Liu, Y.; Hu, Y. PPP Sliding Window Algorithm and Its Application in Deformation Monitoring. Sci. Rep. 2016, 6, 26497. [Google Scholar] [CrossRef] [PubMed]
- Boudraa, A.; Cexus, J. EMD-Based Signal Filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Niu, Y.; Xiong, C. Analysis of the Dynamic Characteristics of a Suspension Bridge Based on RTK-GNSS Measurement Combining EEMD and a Wavelet Packet Technique. Meas. Sci. Technol. 2018, 29, 085103. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the Applications of EMD and EEMD on Time-Frequency Analysis of Seismic Signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Z.; Zang, N.; Wang, S. High-Precision GNSS Ocean Positioning with BeiDou Short-Message Communication. J. Geod. 2019, 93, 125–139. [Google Scholar] [CrossRef]


| Item | Strategy |
|---|---|
| Satellite orbit | IGS final precise orbit product-sp3 |
| Satellite clock | IGS final precise clock product-clk |
| Antenna bias | IGS18.atx |
| Ionospheric delay | Ionosphere-free combination |
| Ambiguity | Float resolution |
| Receiver coordinate | Parameter estimation |
| Receiver clock | Parameter estimation |
| Tropospheric delay | ZTD estimation |
| Solid tide correction | Spherical harmonic function correction |
| Item | Direction | East/mm | North/mm | Up/mm |
|---|---|---|---|---|
| Duration | 24 h | 4.82 | 3.86 | 9.87 |
| 12 h | 7.76 | 4.86 | 13.82 | |
| 08 h | 9.96 | 5.44 | 16.16 | |
| 06 h | 11.73 | 6.01 | 18.31 | |
| 04 h | 16.11 | 6.96 | 22.35 | |
| 03 h | 21.10 | 8.48 | 27.66 | |
| 02 h | 34.96 | 12.05 | 38.92 |
| Item | Direction | East/mm | North/mm | Up/mm |
|---|---|---|---|---|
| Duration | 24 h | 1.09 | 1.74 | 1.88 |
| 12 h | 1.18 | 1.55 | 2.25 | |
| 08 h | 1.63 | 1.42 | 2.20 | |
| 06 h | 1.41 | 1.40 | 2.35 | |
| 04 h | 1.52 | 1.40 | 2.49 | |
| 03 h | 1.47 | 1.46 | 2.47 | |
| 02 h | 2.81 | 1.71 | 3.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Zhang, Z.; Gao, Y.; Zhang, J.; Ge, H. A New Method for Deformation Monitoring of Structures by Precise Point Positioning. Remote Sens. 2023, 15, 5743. https://doi.org/10.3390/rs15245743
Li R, Zhang Z, Gao Y, Zhang J, Ge H. A New Method for Deformation Monitoring of Structures by Precise Point Positioning. Remote Sensing. 2023; 15(24):5743. https://doi.org/10.3390/rs15245743
Chicago/Turabian StyleLi, Ruihui, Zijian Zhang, Yu Gao, Junyi Zhang, and Haibo Ge. 2023. "A New Method for Deformation Monitoring of Structures by Precise Point Positioning" Remote Sensing 15, no. 24: 5743. https://doi.org/10.3390/rs15245743
APA StyleLi, R., Zhang, Z., Gao, Y., Zhang, J., & Ge, H. (2023). A New Method for Deformation Monitoring of Structures by Precise Point Positioning. Remote Sensing, 15(24), 5743. https://doi.org/10.3390/rs15245743