Abstract
The use of a transformer backbone in LiDAR point-cloud-based models for 3D object detection has recently gained significant interest. The larger receptive field of the transformer backbone improves its representation capability but also results in excessive attention being given to background regions. To solve this problem, we propose a novel approach called deformable voxel set attention, which we utilized to create a deformable voxel set transformer (DVST) backbone for 3D object detection from point clouds. The DVST aims to efficaciously integrate the flexible receptive field of the deformable mechanism and the powerful context modeling capability of the transformer. Specifically, we introduce the deformable mechanism into voxel-based set attention to selectively transfer candidate keys and values of foreground queries to important regions. An offset generation module was designed to learn the offsets of the foreground queries. Furthermore, a globally responsive convolutional feed-forward network with residual connection is presented to capture global feature interactions in hidden space. We verified the validity of the DVST on the KITTI and Waymo open datasets by constructing single-stage and two-stage models. The findings indicated that the DVST enhanced the average precision of the baseline model while preserving computational efficiency, achieving a performance comparable to state-of-the-art methods.
1. Introduction
Three-dimensional object detection based on LiDAR point clouds has attracted considerable attention, primarily for its applications in autonomous driving, virtual reality, and robotics [1,2]. There is immense potential in improving the performance of 3D object detection, both in industry and academia. Various methods for detecting 3D objects based on point clouds can be classified into point-based and voxel-based methods.
Point-based methods [3,4,5,6], such as PointNet and its variant models, take raw point clouds as inputs and extract key point feature representations by iterative sampling and group aggregation operations in point set abstraction modules, which are then used to predict object bounding boxes. Alternatively, voxel-based methods [7,8,9] divide the input raw point cloud into a regular grid to obtain a discrete voxel representation, which is processed using a deep convolutional neural network. Point-based methods can achieve precise spatial information from point clouds through larger receptive fields, enabling accurate positioning. However, these methods incur higher computational costs due to using point set abstraction [10]. Conversely, voxel-based methods prioritize computational efficiency but inevitably sacrifice information and reduce the precision of fine-grained localization [11]. This study focuses on voxel-based methods that aim to facilitate the development of 3D object detection from point clouds.
Voxel-based 3D object detection models frequently rely on 3D sparse convolutional networks [12] to extract voxel features. Although this method is computationally efficient, its limited receptive field prevents it from capturing rich contextual information, which can impede the detection of objects with only a small number of voxels. Additionally, efforts to mitigate this issue by increasing the maximum theoretical receptive field of each voxel, such as by modifying the voxel size, kernel size, downsampling stride, or number of layers, can result in numerous computational consumptions. To address these issues, Mao et al. proposed a voxel transformer (VoTr) [13], a voxel-based transformer backbone explicitly designed for 3D object detection. The VoTr utilized sparse voxel and submanifold voxel modules and employed self-attention mechanisms to model long-distance relationships between voxels. Moreover, it used local attention and dilated attention to expand the receptive field of attention without sacrificing computational efficiency. He et al. developed a voxel set transformer (VoxSeT) [14] to efficiently extract point cloud features for 3D object detection using set-to-set translation. The voxel-based set attention module, serving as the central component of VoxSeT, effectively overcomes the limitations of group-based and convolution-based attention modules and establishes long-distance dependencies more efficiently.
Despite their ability to utilize the transformer architecture for improved attention range, reduced information loss, and enriched contextual information, both the VoTr and VoxSeT models suffer from a limitation of not effectively focusing on foreground objects. As a result, the detection of naturally sparse and incomplete 3D objects is hindered. Given the potential increase in memory and computational costs associated with simply expanding the receptive field, as well as the possibility of feature interference from irrelevant parts beyond the region of interest, it is imperative to design a new architecture that can flexibly concentrate on foreground object areas and extract more informative features.
Recently, deformable mechanisms have been employed in 2D vision tasks due to their capability of selectively concentrating on areas with more information [15]. It has been demonstrated in references [16,17] that learning the deformable receptive field of a convolutional filter can efficiently selectively focus on more informative regions on a data-dependent basis. Xia et al. introduced a deformable attention transformer [18], which serves as a backbone model for tasks such as image classification and dense prediction. While the model chooses the positions of key-value pairs in self-attention based on data dependency to emphasize relevant regions, using a uniform reference point for all analyzed scenes hinders the detection of targets that may only have partial pixels or are positioned in the corners of the scene.
When applying the deformable mechanism to the detection of objects in 3D point clouds, previous studies have either built deformable self-attention modules for contextual feature extraction [19,20] or guided cross-domain feature aggregation [21]. However, it has not been recognized as a critical component in building a robust backbone, such as the deformable attention transformer. Two problems restrict the direct application of 2D deformable attention in detecting 3D point cloud objects. One problem arises from the sparsity of 3D point clouds, as the method used to determine reference points in the 2D deformable attention can lead to a substantial loss of information. Furthermore, numerous 3D point clouds in a scene exacerbate the quadratic computational complexity of self-attention, resulting in excessive memory usage and computational expenses.
To solve the problems above, we present a novel and efficient module called the deformable voxel set attention (DVSA) module for detecting objects in 3D point clouds. In general, the transformer-based 3D point cloud detection backbone has a larger receptive field, which enhances its representation capabilities. However, in object detection tasks, excessive attention to background areas is unnecessary and resource-consuming. Therefore, considering that the deformable mechanism can selectively focus on the target area, we tried to build a transformer backbone that selectively focuses on the foreground target area for 3D point cloud object detection. The target-region-sensitive deformable attention is constructed considering two factors when introducing the deformable mechanism. One factor is that performing operations involving the offset of all pixels in the deformable convolutional network feature map leads to a significant computational burden, and it also introduces confusion in the target area due to the offset of background points. Another factor is that, compared to only learning a few sets of query-independent offsets in 2D deformable attention, it is better to learn offsets for foreground queries to move the keys and values of the targets to important areas. Therefore, after the DVSA module divides the point clouds in the scene into foreground points and background points, it uses the newly constructed offset generation network to learn the offsets of the foreground queries. Then, the offset features carrying offset information are projected into keys and values, and the calculation of deformable attention is completed together with the input projected queries.
Specifically, after the DVSA divides all the points in the voxel grid into foreground and background points, the model learns the offsets of foreground points via an offset generation network. The offset features then serve as keys and values input to the multi-head attention, where the model derives the output features. Motivated by induced set attention [22], we reduce computational complexity by decomposing full self-attention into two consecutive cross-attention modules. This is based on the assumption that self-attention is low-rank [23] and can be approximated through low-rank projection [14]. The DVSA initially learns the offsets of foreground queries within the 3D voxel to acquire deformable features. Then, a set of inducing points is introduced to transform the features into hidden space by encoding cross-attention. Subsequently, a globally responsive convolutional feed-forward network (GRCFFN) enhances the hidden features. Lastly, output features are derived through decoding cross-attention.
With DVSA, we propose a novel approach called the deformable voxel set transformer (DVST) for 3D object detection from point clouds. The DVST employs deformable mechanisms to focus on and capture target-related features flexibly. It consists of multi-layer interconnected DVSA modules and a multi-layer perceptron (MLP). Through experiments conducted on the 3D detection benchmark KITTI and the Waymo open dataset, we demonstrate the effectiveness of the proposed model. The main contributions of our work are summarized as follows:
- (1)
- The DVST deformable backbone was developed to detect objects in 3D point clouds. It combines the flexibility of deformable mechanisms, the powerful long-range modeling capability of transformers, and the linear computational complexity of set attention in a cohesive manner. By solely focusing on learning the offsets of foreground queries, the target semantic information is strengthened, the background features are weakened, and the detection performance is improved.
- (2)
- DVSA, a deformable attention module for 3D point cloud learning, was designed for the first time. It utilizes deformable mechanisms to transfer the candidate keys and values of foreground queries to important regions. This enhancement provides the original self-attention with increased flexibility to capture target-related feature information.
- (3)
- A novel offset generation module (OGM) was constructed for learning the offsets of foreground queries in the DVSA module. This data-dependent method of generating offsets enhances the model’s robustness in detecting diverse scenarios. Moreover, a GRCFFN with a residual connection is proposed to facilitate global interaction and feature learning within the hidden space.
- (4)
- One-stage and two-stage detection models were developed based on the DVST, and experiments were performed on the KITTI and Waymo open datasets, widely used benchmarks for 3D object detection. The findings indicate that the proposed backbone enhances the performance of 3D detection while ensuring computational efficiency.
2. Related Work
2.1. Three-Dimensional Object Detection from Point Clouds
Point-Based methods. Point-based detectors typically abstract geometric information from unstructured point clouds using PointNet [3] and its variants [4,24], which process the point cloud directly to generate 3D boxes that preserve precise position information. Shi et al. introduced PointRCNN [25], a two-stage 3D object detection model that utilizes separate subnetworks for the first and second stages to generate and refine 3D proposals. To strike a balance between accuracy and efficiency, Yang et al. developed a point-based 3D single-stage object detector named 3DSSD [5]. This detector eliminates the feature propagation layer and refinement module and incorporates a novel fusion sampling strategy. Point-GNN [26] is a graph neural network comprising an auto-registration mechanism. Shi et al. constructed it for performing 3D point cloud object detection using graph representation. Given the significance of foreground points compared to background points in the detection of point clouds, two down-sampling strategies were proposed by Zhang et al. for the stratified selection of foreground points to the desired objects, resulting in the development of an efficient 3D detector named IA-SSD [6]. Ren et al. developed DGT-Det3D [10], a 3D object detection network that uses dynamic graph conversion to extract point-by-point semantic features that are beneficial in identifying distant and obstructed objects. Despite their ability to avoid the quantization errors caused by voxelization through direct feature learning, point-based methods have limited learning capabilities and efficiency.
Voxel-Based methods. Voxel-based detectors typically convert unordered point clouds into regular spatial units, usually of equal size. Yan et al. introduced sparse convolution into voxel-based 3D detectors and proposed a sparse embedded convolutional (SECOND) framework [14], improving detection accuracy and runtime speed. Lang et al. proposed PointPillars [7], which partitions point clouds into pillars, enabling faster encoding of point cloud features. To improve the detection accuracy with a coarse voxel granularity, Deng et al. developed the two-stage framework Voxel-RCNN [8], achieving comparable detection accuracy to point-based models with lower computational costs. Yin et al. presented an anchor-free detection framework called CenterPoint [27], which regresses other attributes based on detecting object centers. Yang et al. constructed an end-to-end multi-feature fusion network [28] composed of a voxel convolutional module, a local point feature module, and a detection head, obtaining a higher detection accuracy by extracting richer voxel features. Voxel-based methods can effectively balance accuracy and computational efficiency through the regular representation of point clouds. However, the introduction of inevitable quantization errors limits the learning ability of voxel-based methods on point cloud features, thereby restricting their detection performance.
Point–Voxel methods. Some approaches address the challenges posed by voxel-based and point-based methods by combining point and voxel representation. Shi et al. developed the PV-RCNN [11], which leverages 3D sparse convolution to extract voxel features and uses farthest-point sampling to sample key points. The voxel set abstraction module is then used to fuse point and voxel features, improving the detection accuracy. To fully utilize the structural information of point clouds, SA-SSD [29] incorporates an auxiliary network that transforms the convolutional features of the backbone into point-level representation. Noh et al. used hybrid voxel-point representation (HVPR) [30] for 3D object detection. Specifically, HVPR generates mixed 3D features by integrating point and voxel streams in the dual-stream encoder. Shuang et al. introduced AFE-RCNN [31], a point–voxel integrated network consisting of critical components such as the residual of dual attention proposal generation module, the multi-scale feature extraction module based on feature adaptive adjustment, and the refinement loss function module with vertex correlation. Nevertheless, achieving a balance between detection accuracy and efficiency poses a more significant challenge for these methods. Furthermore, the extensive reliance on handcrafted feature design in hybrid approaches hampers the potential for model improvement.
2.2. Transformers in 3D Object Detection
Transformer-based models are highly suitable for learning 3D point clouds with unordered and unstructured characteristics due to their capability of encoding positional information, long-range contextual information, and permutation invariance. Several 3D object detection models that incorporate transformers have recently been proposed. For instance, Mao et al. developed the VoTr model [13] to overcome the limitation of convolutional backbone networks in effectively capturing contextual information. Sheng et al. proposed CT3D [32], a two-stage 3D object detection framework that utilizes a channel-wise transformer to enhance the candidate boxes generated by the region proposal network. He et al. introduced the VoxSeT model [14], which leverages voxel-based set attention (VSA) for point cloud learning from sets. Guan et al. proposed M3DETR [33], a multi-representation and multi-scale integrated method that employs an M3 transformer to model point cloud features from multiple perspectives. Inspired by a window-based transformer, Sun et al. proposed a sparse window transformer [34] that fully exploits the sparsity of point clouds. In the weakly supervised point cloud transformer framework [35], Tang et al. adopted a self-attention mechanism to extract global features.
Moreover, Zhou et al. improved the performance of the anchor-free object detection network using the CenterFormer model [36], which utilizes the features of center candidates as query embeddings and incorporates cross-attention to fuse multi-frame features. Building upon the concept of anchor points, Liu et al. introduced the AnchorPoint model [37]. This detector encodes foreground points, which act as anchor points, as object queries. This encoding strategy allows each object query to possess a distinct and meaningful physical interpretation. Ning et al. proposed PV-SSD [38], a point–voxel and bird’s eye view (BEV) representation aggregation network for single-stage 3D detection, which adaptively integrates multi-level semantic features using a windows transformer spatial-semantic aggregation module. Ren et al. designed DGT-Det3D [10], a dynamic graph transformer 3D object detection network that captures long-range dependencies and refines candidate boxes through dynamic graph transformer and proposal-aware fusion modules.
Unlike the methods mentioned above, the proposed DVST combines the advantages of a deformable mechanism, voxel-based model, and set transformer, enabling a flexible focus on foreground target regions while efficiently modeling long-range contextual information and maintaining computational efficiency.
2.3. Deformable Mechanisms in 3D Object Detection
Deformable mechanisms are commonly incorporated into 3D object detection models using point clouds to enhance the extraction capability of salient and discriminative features. Bhattacharyya et al. introduced the Deformable PV-RCNN [19] model by integrating deformable mechanisms into the PV-RCNN. This model adaptively extracts informative and discriminative features through deformable convolution operations. Subsequently, Bhattacharyya et al. developed the deformable self-attention (DSA) module in SA-Det3D [20]. This module calculates offsets for sample points obtained through farthest-point sampling, extracting context information containing representative and informative feature subsets. Recognizing that relevant object information is mainly located in adjacent positions, Chen et al. proposed a deformable cross-attention feature alignment module [21]. This module guides the aggregation positions in the feature map using deformable convolutions. To learn more effective contextual features, Tang et al. designed a deformable offset self-attention (DOSA) structure [39]. This structure first samples a voxel subset using the farthest point sampling method and then learns offsets for this voxel subset. Offset self-attention is performed on the voxel subset, which is upsampled to cover each original voxel position.
It is evident that combining the deformable mechanism with the self-attention mechanism is a more appropriate approach for learning useful features of 3D point clouds, as opposed to solely utilizing deformable convolutions to process 2D feature maps. Nonetheless, it should be noted that the DSA and DOSA modules mentioned above do not effectively employ the deformable mechanism to modify the key-value pairs of each query during the computation of the attention mechanism. In other words, the adaptive capability of the deformable mechanism for extracting target-related features has not been fully utilized. Additionally, DSA and DOSA sample the same number of points or voxels using the farthest-point sampling method for all scenes, result in a somewhat diminished model performance. To fully integrate the ability of the deformable mechanism to attend to target regions and the power of the self-attention mechanism to extract contextual information, we propose the DVSA module for 3D point cloud object detection, taking inspiration from 2D deformable attention.
3. Deformable Voxel Set Transformer
3.1. Overall Architecture
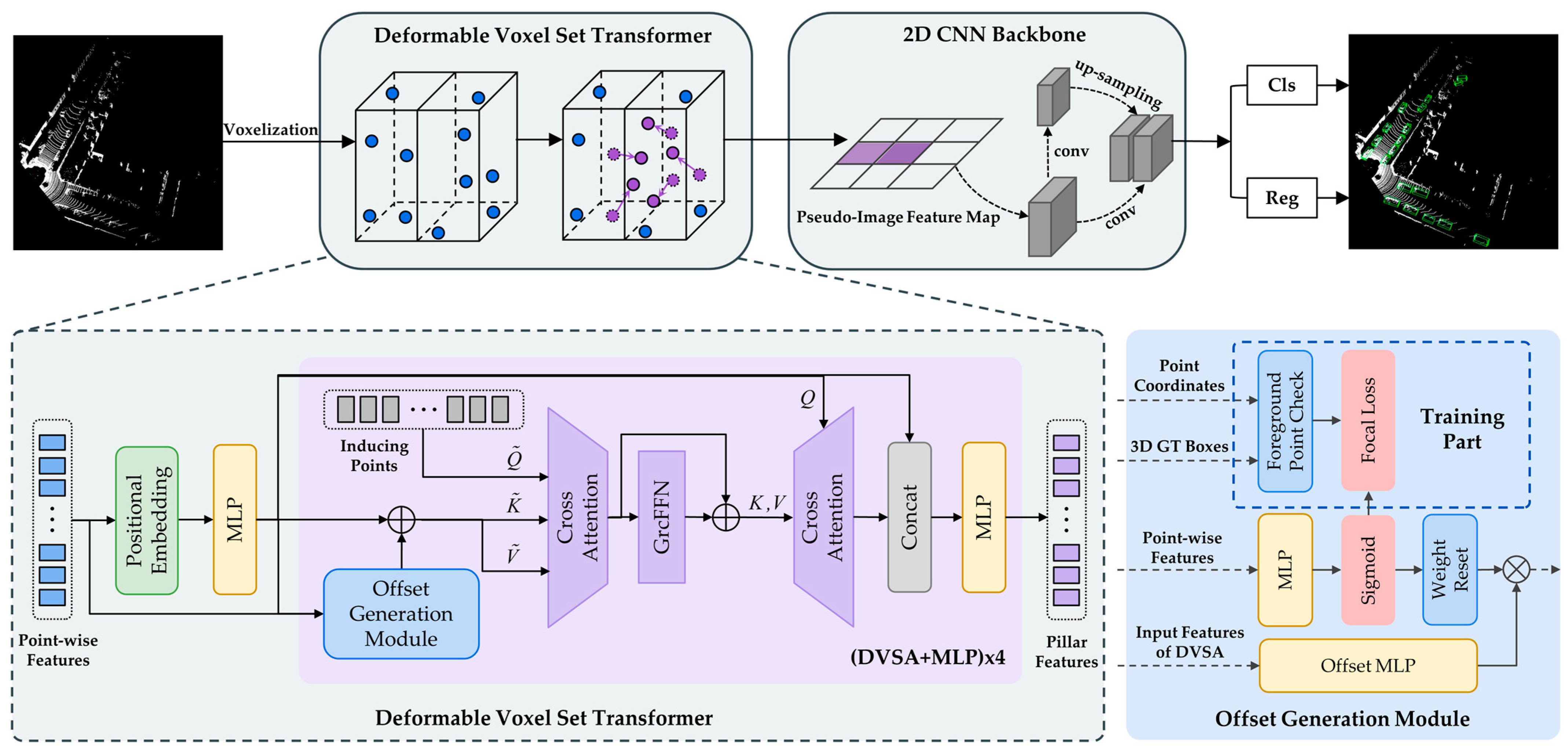
This paper presents a novel deformable voxel set transformer (DVST) for point-cloud-based 3D object detection. The DVST serves as a transformer-based 3D backbone, as depicted in Figure 1. By combining the deformable mechanism and transformer, the DVST can adaptively focus on the target region while possessing robust long-range modeling capabilities. We introduce induced set attention to reduce computational complexity, which breaks down full self-attention into two consecutive cross-attentions. Built upon the conventional voxel-based 3D detection pipeline [13], the DVST can seamlessly integrate into most voxel-based 3D detection frameworks. Specifically, the proposed 3D detector takes a voxelized point cloud as the input to extract features in the DVST backbone network, encodes them into BEV representation, applies a 2D convolutional neural network (CNN) to enhance the feature density further, and finally utilizes anchor-based detection heads to generate detection results. Following the traditional transformer paradigm, the DVST backbone consists of interconnected DVSA modules and MLPs. Moreover, we package the DVSA modules into residual blocks to ensure optimal gradient flow.
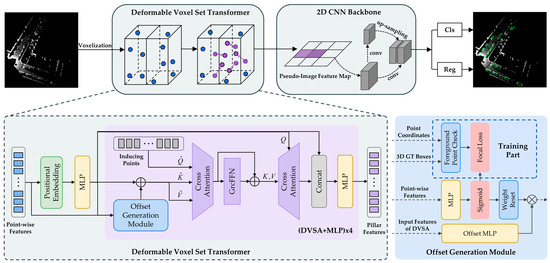
Figure 1.
The overall architecture of DVST. The DVST is a transformer-based 3D backbone that can be utilized in various voxel-based 3D detection frameworks. It comprises a sequence of DVSA modules and MLPs. The DVSA is a deformable attention module explicitly designed for learning from 3D point clouds. It consists of the OGM, encoding cross-attention, GRCFFN, and decoding cross-attention. The OGM is employed to generate deformable offsets.
The DVSA module is a vital component of the DVST and is purpose-built for processing 3D point cloud data. The query features are acquired by encoding the position of the voxelized point cloud and processing it using an MLP. Subsequently, these query features are utilized as inputs for the DVSA module. Inspired by the 2D deformable attention module [18], we propose a novel OGM to generate offsets for the queries. The OGM utilizes point-wise features to determine confidence scores for each query, indicating whether it is a foreground query. Using a threshold, we set the scores of non-foreground queries to zero. Meanwhile, the OGM employs an offset MLP to generate initial offsets for all queries multiplied by the confidence scores to obtain the final offset values. Through this approach, DVSA can adaptively learn the offsets of foreground queries for different scenes, overcoming the limitation of 2D deformable attention in learning the same position offsets for all scenes.
Motivated by induced set attention [22], which posits that a low-rank projection can approximate self-attention, we use two cross-attentions guided by a set of inducing points to approximate the complete self-attention within the set. The first cross-attention maps the inducing points to the hidden space by attending to the input set, while the second cross-attention directs its focus towards the hidden features and generates the output set. The output features are then encoded as BEV features and fed into a 2D backbone network. Finally, we employ a detection head for 3D object detection.
3.2. Deformable Voxel Set Attention
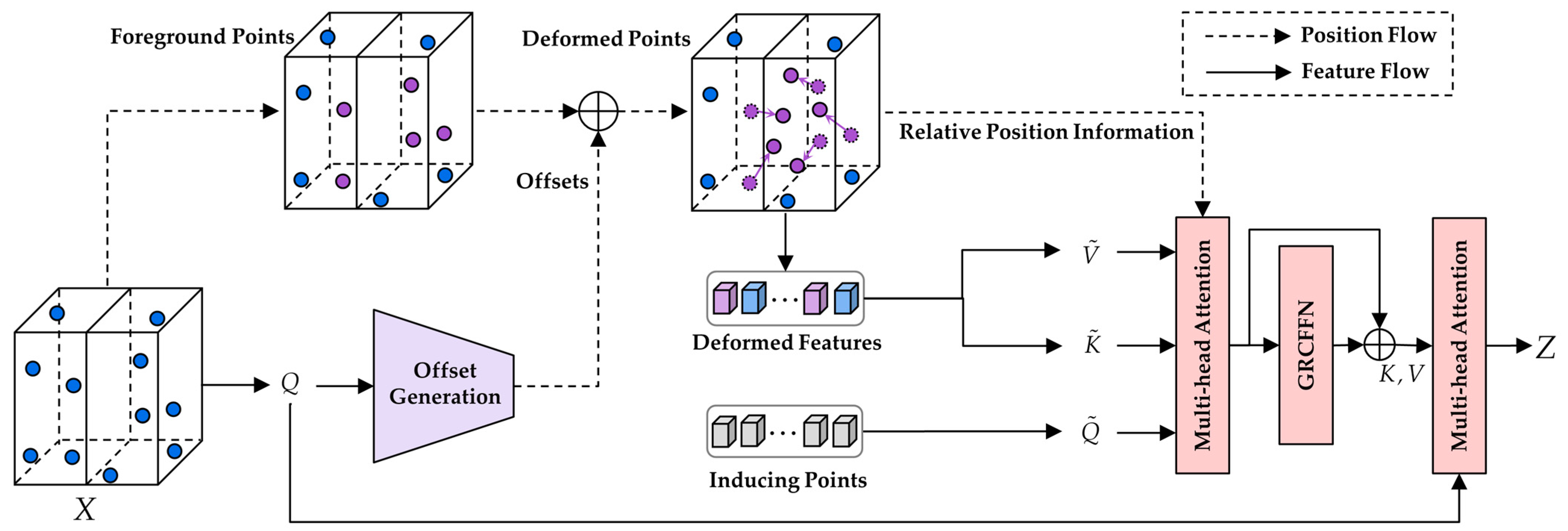
Unlike images, point clouds are extensively distributed and possess weak semantic correlations at the scene level, although they exhibit strong structural details in localized regions. Thus, we suggest using deformation attention to model the relationships between markers, guided by the significant regions in the voxel grid. These focused regions are determined by multiple sets of deformable foreground points, which are learned from queries using the OGM. Deformable features are extracted from these points and then projected to obtain deformed keys and values. Simultaneously, a set of inducing points is assigned for each voxel in the grid, and the deformable features are encoded into the hidden space using encoding cross-attention. Next, a GRCFFN with a residual connection enhances the global interaction of hidden space features. Finally, decoding cross-attention is applied to focus on the original queries and aggregate features from deformed values. This DVSA module specifically focuses on learning the point cloud features of important areas to detect 3D objects during the set-to-set transformation process. The overall architecture of the DVSA module can be observed in Figure 2, and the design of each module component will be elaborated below.
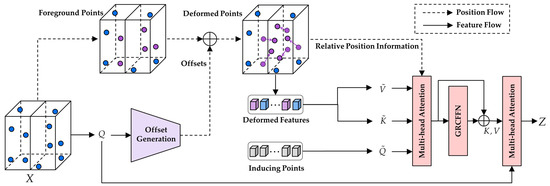
Figure 2.
An illustration of DVSA. The figure presents the information flow of the DVSA. A group of foreground points is identified, and their offsets are learned from the queries through the OGM. Then, the deformed keys and values are projected from the deformable features. Subsequently, the deformable features are compressed into a latent space using a set of inducing points, and the features are refined using the GRCFFN. Finally, the output features are obtained through multi-head attention. For clarity of presentation, only two voxel grids and five foreground points are shown, although there are more points in practical implementation.
3.2.1. Positional Embedding
Given the significance of preserving the local structure of point clouds to enhance detection performance [40], we introduce a positional embedding (PE) module. This module encodes the local coordinates of point clouds within voxels into high-dimensional features, which are subsequently fed into the DVSA. Specifically, the PE module applies Fourier parameterization to obtain values , where represents the normalized local coordinates and is the -th frequency with a bandwidth of . The resulting Fourier embedding has a dimension of , which is then mapped to the input dimension of the first MLP using a trainable linear layer. The positional encoding feature not only maintains the local structure of the point cloud but also aids in generating more precise deformable offsets.
3.2.2. Offset Generation Module
The 2D deformable attention [18] determines the focal area by deforming a fixed position reference point. However, this method is unsuitable for the deformable attention of three-dimensional point clouds, as they are sparse and unstructured. To resolve this problem, we introduce an intuitive and practical approach: dividing the point cloud into foreground and background points and determining the focal area by deforming the foreground points. We developed an OGM module, as illustrated in Figure 1.
The provided point cloud consists of points. It undergoes processing to extract -dimensional point-wise features , which are then encoded with the PE module to generate -dimensional DVSA input features . The OGM initially takes as the input to determine the confidence of the foreground as follows:
where represents a three-layer MLP with a sigmoid activation function designed for predicting the foreground confidence within the range of [0, 1]. Then, is obtained by resetting the confidence of non-foreground points to zero using a foreground confidence threshold , as shown in Equation (2):
The variable represents the foreground confidence of the -th point among points. The default threshold for the foreground confidence is set at 0.5. Afterward, the feature is fed into a shared subnetwork to generate the offset , as depicted in Equation (3):
where is a three-layer MLP network. The final offset value for each point in the foreground is determined by assigning the confidence of each point to the generated offset, referred to as in Equation (4):
After generating the offset of foreground points, it is added to the input vector to obtain the deformable feature , as described in Equation (5):
The OGM employs focal loss [41] with default hyperparameters in the training process. This technique addresses the imbalance between foreground and background points in the training set. By multiplying the confidence of foreground points with the corresponding offset, the module generates offset sizes that vary based on the confidence levels of the foreground points. This somewhat helps to mitigate the adverse effects caused by foreground threshold edge points. Moreover, the proposed OGM uses two learnable networks to identify foreground points and determine their offsets. This approach overcomes the drawbacks of manual offset generation design and enhances the DVST’s adaptive focusing capability on foreground regions.
3.2.3. Encoding Cross-Attention
As shown in Figure 2, the complete query of the deformable attention is acquired by projecting the input feature , while the keys and values are obtained by projecting the deformable feature . Following acquiring the deformable feature, we use an alternative approach to self-attention to model the global contextual relationship. To bypass the quadratic computational complexity of self-attention, we utilize VSA to learn the global features of the point clouds through set-to-set transformation. Given an input set with a size of and a dimension of , and by defining a -dimensional vector , known as inducing points, the output set from the VSA [14] can be represented as:
The inducing points are trainable parameters that are learned along with other parameters in the network. The first cross-attention transforms into hidden features by attending to the input set. The hidden features are then input to a convolutional feed-forward network (ConvFFN) for updating the information. The second cross-attention attends the input set to the resulting hidden features. For clarity, we refer to the first and second cross-attentions as encoding cross-attention and decoding cross-attention, respectively. Both cross-attentions utilize standard multi-head attention. Furthermore, we propose a novel GRCFFN with residual connection to enhance the comprehensiveness and flexibility of information updating.
In the encoding cross-attention, we begin by performing a linear projection to project the deformable features into the key and the value :
where and are projection matrices. Then, cross-attention is performed between the key and query to generate an attention matrix , as shown in Equation (10):
The query is the given induced vector. Next, the attention matrix is voxel-normalized using the scatter kernel function:
where denotes the voxel coordinates of points. Let represent the point cloud coordinates and be the size of the three-dimensional voxel. The voxel coordinates can be calculated using Equation (12):
where is the floor function. The CUDA kernel library scatter function allows for symmetric reductions on various matrix sections, including maximum, average, and sum. In DVSA, the input set is treated as a single matrix where each row represents a point-wise feature, and each voxel associated with a point-wise feature can be indexed by voxel coordinates. Given point-wise features, their reduced voxel form after the symmetric scatter function can be represented as:
where is the number of non-empty voxels. After obtaining the voxel-normalized attention matrix , it is multiplied by the values to produce the hidden feature :
After that, voxel reduction of the hidden features according to the voxel index is used for feature refinement in the hidden space, as shown in Equation (15):
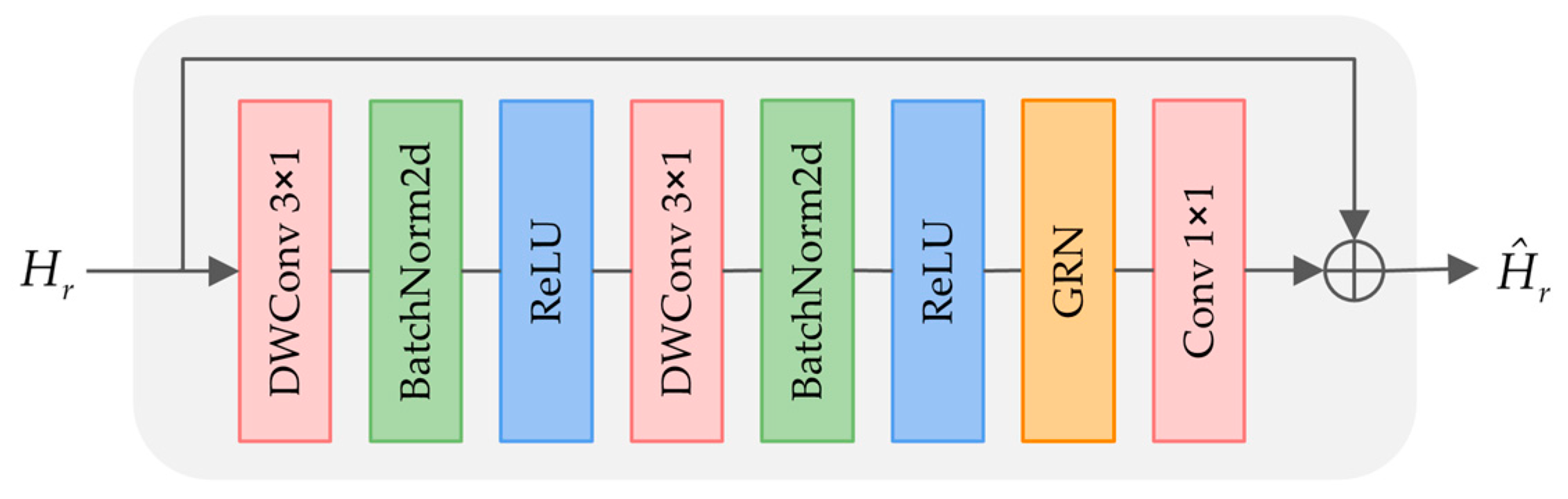
3.2.4. Globally Responsive Convolutional Feed-Forward Network
After encoding deformable features into the hidden space using inducing points, the hidden features are input into a feed-forward network to achieve more flexible and complex feature refinement. In a previous study [14], the hidden features were scattered into a 3D sparse tensor, and a ConvFFN was constructed to learn the information in the corresponding tensor. While this approach successfully captures inter-voxel information interaction, it may impede the model’s performance when dealing with deformable features due to limited feature diversity. To address this limitation, ConvNeXt V2 [42] proposed global response normalization (GRN), which normalizes the feature maps channel-wise, thereby enhancing feature competition and promoting feature diversity. Notably, GRN serves as a convolutional neural network layer that requires no additional parameters and has no learnable parameters. In light of this, we introduce the GRN into the ConvFFN to develop an improved version, GRCFFN, specifically designed to amplify feature diversity. The architecture of GRCFFN is illustrated in Figure 3.
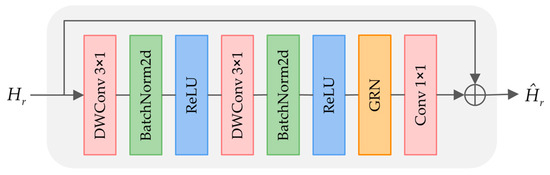
Figure 3.
The network structure of GRCFFN.
Specifically, we disperse the reduced hidden features into a 3D sparse tensor based on voxel coordinates to adaptively integrate voxel features and global dependencies. Subsequently, two depth-wise convolutions (DWConv) are applied to these 3D tensors to facilitate feature interactions in the spatial domain, and a GRN layer is used to enhance feature diversity. By incorporating a residual connection, we can retain the spatial information in the input hidden features and integrate this information after feature interaction. Given the reduced hidden features , the features obtained from performing two DWConvs can be written as:
where and are convolutional weights, and represent non-linear activation functions, denotes voxel coordinates, and refers to the formulation of sparse tensor.
When performing GRN, the first step is to use the global function to aggregate the feature into the vector :
Next, we apply the response normalization function to the aggregate value as follows:
where is the -th channel and is the L2-norm of the -th channel. The response normalization function computes the relative importance of each channel with the other channels. Finally, the normalized scores are used to correct the original input response:
After completing GRN, given the convolution weights , the rich hidden features from GRCFFN can be written as:
3.2.5. Decoding Cross-Attention
The output set is reconstructed by the decoding cross-attention, as demonstrated in Figure 2, using the rich hidden features . Initially, the hidden features are broadcasted to generate features with the same length as the input set. Then, the decoding cross-attention projects the input set onto the query and projects the rich hidden features containing offset information onto the key and the value :
where , , and are projection matrixes. Lastly, multi-head attention is performed on the query , key , and value . The output of the DVSA can be calculated as:
In summary, the DVSA module initially learns the offset of foreground queries through the proposed OGM module. Subsequently, it transforms the deformed features with offset information to the hidden space utilizing encoding cross-attention. The hidden features are then refined by the proposed GRCFFN. Finally, decoding cross-attention is employed to derive the output features. By dynamically prioritizing significant regions during the set-to-set transformation process, the DVSA can effectively detect 3D objects.
3.3. BEV Feature Encoding and Detection Head
As illustrated in Figure 1, the DVST backbone is employed to extract features from the input point cloud. Subsequently, these extracted features are encoded into BEV representation, and a shallow 2D CNN backbone is applied to enhance the feature density. The reason for performing BEV encoding is that, in the context of 3D point cloud detection, models utilizing dense BEV features [8,12] generally exhibit higher recall rates than models utilizing sparse point-wise features [25,43].
The 2D CNN network utilized in this study comprises two strides, with each stride encompassing three convolutions. The point-wise features generated by the DVST are aggregated into pillars measuring 0.36 m 0.36 m, which is followed by soft-pooling to generate BEV features. Given the point-wise output feature , the pooled pillar-wise feature can be represented as Equation (25):
The pillar features are then fed into a shallow 2D CNN. The convolution features of two strides are connected and passed into the detection head to predict bounding boxes. The detection head follows a traditional anchor-based design [7,12].
Our DVST can be extended to accommodate two-stage detectors. The CT3D [32] is a prime example of a two-stage detector that boasts exceptional performance and minimally relies on manual design. In the two-stage detector, we utilize the RoI head of CT3D as our second-stage module. This module performs proposal-aware embedding of point features and aggregates contextual information through a channel-wise transformer. We validate the DVST by constructing single-stage and two-stage detectors in the experimental section.
3.4. Training Losses
We employ an end-to-end strategy in training the DVST. The overall training loss is calculated by the OGM foreground segmentation loss , the bounding box classification loss , the bounding box regression loss , and the bounding box orientation loss :
where denotes the number of positive samples, both and adopt focal loss, adopts Smooth-L1 loss, and adopts binary entropy loss.
When the DVST is expanded to a two-stage model, in addition to the losses mentioned above, the loss from the second stage of the bounding box regression and confidence prediction must also be included.
4. Experiments and Results
In this section, we assess our proposed DVST using two publicly available 3D point cloud detection datasets, the KITTI and Waymo open datasets. We begin by presenting the implementation details and evaluation settings of DVST, followed by a comparison with state-of-the-art 3D point cloud detection models. Lastly, we perform a comprehensive analysis of the components of DVST through ablation experiments.
4.1. Dataset and Implementation Details
KITTI dataset. In 3D point cloud object detection, the KITTI dataset [44] is widely used for evaluating model performance. The dataset classifies the 3D detection task into three difficulty levels, i.e., easy, moderate, and hard, based on object size, occlusion status, and truncation level. It comprises a total of 7481 training samples and 7518 testing samples. According to the usual protocol, the training samples are subdivided into a training set containing 3712 annotated samples and a validation set containing 3769 annotated samples. To assess the effectiveness of the DVST, we conducted experiments on an online testing server. When evaluating the test set, the model was trained using 80% of the training set data, while the remaining 20% was employed for validation purposes.
According to the KITTI official evaluation criteria, the intersection over union (IoU) threshold for the car category was set to 0.7. For the pedestrian and cyclist categories, the IoU thresholds were set to 0.5. The mean average precision (mAP) and the average orientation similarity (AOS) results on the test set were computed using 40 recall positions on the online testing server. The mAP results on the validation set were computed using 11 recall positions to ensure a fair comparison with other methods. We present two DVST-based detection architectures, including a DVST single-stage detector (DVST-SSD) for single-stage detection and a DVST two-stage detector (DVST-TSD) for two-stage detection. The single-stage model adopts the anchor settings from SECOND [12], while the two-stage model utilizes the RoI head from CT3D [32].
Waymo open dataset. The Waymo open dataset [45], serving as a large-scale 3D detection dataset, comprises 1000 sequences, consisting of 798 training sequences and 202 validation sequences. The training set contains approximately 158 k point cloud samples, while the validation set contains around 40k samples. The validation process for the Waymo open dataset employs two main approaches. The first approach categorizes objects based on difficulty levels: LEVEL_1 pertains to objects with at least five lidar points, whereas LEVEL_2 encompasses objects directly labeled as second level or objects with at least one lidar point. The second approach organizes objects according to their distance from the sensor, with three distinct ranges: 0–30 m, 30–50 m, and >50 m.
The mAP and the mean average precision with heading accuracy weighting (mAPH) are official evaluation metrics. These metrics are calculated based on an IoU threshold of 0.7 for vehicles and 0.5 for other categories. The models were trained using 20% of the training data and validated using the complete validation data set. To evaluate the effectiveness of the DVST on the Waymo open dataset, we replaced the 3D backbone networks in the PointPillars [7] and CenterPoint [27] models with the DVST while keeping the other modules unchanged. Consequently, we used two detection architectures: DVST-SSD, an anchor-based single-stage detection architecture, and DVST-TSD, an anchor-free two-stage detection architecture.
Implementation details. On the KITTI dataset, the point cloud ranges for the X, Y, and Z axes were set to [0 m, 70.4 m], [−40 m, 40 m], and [−3 m, 1 m], respectively. The voxel size was set to [0.32 m, 0.32 m, 4 m]. The feature dimensions of the four DVSAs were 16, 32, 64, and 128. The number of inducing points for each DVSA was eight in the one-stage model and four in the two-stage model. The bandwidth of the PE module was set to 64. In the two-stage models, 512 RoIs were sampled during training, and 128 RoIs were sampled during inference. During the post-processing stage, both the one-stage and two-stage models utilized NMS with an IoU threshold of 0.01 to predict bounding boxes. For the final prediction, the one-stage and two-stage models selected bounding boxes with confidence scores surpassing 0.1 and 0.5, respectively. The models were trained end-to-end for 100 epochs using the Adam optimizer on four NVIDIA 3080Ti GPUs. The batch size and weight decay were set to 2 and 0.01, respectively. The one-stage model used a learning rate of 0.001, while the two-stage model utilized a learning rate 0.0005. Additionally, the learning rate decayed with the one-cycle strategy, where the momentum damping range was set to [85%, 95%]. For other default settings, please refer to the OpenPCDet [46] toolbox employed in this study.
On the Waymo open dataset, the point cloud ranges for the X, Y, and Z axes were set as [−75.2 m, 75.2 m], [−75.2 m, 75.2 m], and [−2 m, 4 m], respectively. The voxel size was set as [0.32 m, 0.32 m, 6 m]. The feature dimensions of the four DVSAs with four inducing points were 16, 32, 64, and 128. The bandwidth of the PE module was set to 64. During the post-processing stage, the DVST-SSD and DVST-TSD predicted the bounding boxes using an IoU threshold of 0.7. The final predictions were determined by selecting the bounding boxes with confidence scores above 0.1. The learning rates for the two models were set to 0.00075 and 0.001, respectively. Furthermore, both models were trained end-to-end using the Adam optimizer on four NVIDIA GeForce RTX 3080Ti GPUs. The training process involved 30 epochs with a batch size of 1 and a weight decay of 0.01.
4.2. Three-Dimensional Detection Results on KITTI Dataset
4.2.1. KITTI Test Set
The test set was evaluated by submitting the detection results of the DVST-TSD to the official KITTI test server, and the performance of the DVST was compared with state-of-the-art methods. The DVST-TSD adopted the anchor setting in SECOND and used the RoI head in CT3D. Table 1 and Table 2 present the results of the test set, including 3D detection mAP, BEV detection mAP, and 3D detection AOS metrics. Since some methods do not focus on the orientation evaluation of 3D objects, the results of the AOS metric are not listed in their respective literature. For these methods, the AOS metric was obtained either from the official KITTI leaderboard or was not compared in Table 2.

Table 1.
Performance evaluation of 3D object and BEV detection for the DVST on the KITTI test set. The results regarding mAP at an IoU threshold of 0.7, along with 40 recall positions, are reported. The results obtained using our DVST are in bold, while the top-three-ranked results are underlined.

Table 2.
Comparison of AOS performance of different methods on the KITTI test set. Our DVST results are shown in bold, and the top-three-ranking results are underlined.
A total of nine specific quantitative indicators are involved in Table 1 and Table 2. As shown in Table 1 and Table 2, our DVST had five top-three indicators. It can be seen that among the voxel-based detection methods, our DVST had apparent advantages in the number of the top-three indicators. In addition to the point–voxel combined PV-RCNN, which had the same number of top-three-ranked indicators, the DVST had more indicators ranked in the top three than the other methods in the table. Thus, the comprehensive performance of the DVST was validated. In other words, the DVST demonstrated exceptional overall performance in 3D car detection, BEV detection, and orientation estimations due to its incorporation of deformable mechanisms, which offer flexibility, and transformers, which facilitate powerful long-range modeling. Consequently, the DVST effectively concentrated on the target area and extracted rich intrinsic contextual features, enabling it to adapt better to various detection tasks and difficulty levels.
Specifically, for 3D car detection, the DVST outperformed most of the methods in Table 1 at the easy level with an mAP of 88.70%. Additionally, the DVST exhibited a higher mAP in 3D detection for the moderate and hard difficulty levels than all the point-based and point–voxel fusion methods in Table 1. Specifically, regarding the moderate-difficulty 3D detection, the DVST increased the mAP by at least 0.98% compared to the point-based methods and by at least 0.13% compared to the point–voxel fusion methods. For the hard-difficulty 3D detection, the proposed DVST showed mAP improvements of at least 1.16% and 0.15% compared to the point-based methods and point–voxel fusion methods, respectively. Similarly, when considering voxel-based methods, the DVST performed comparably to CT3D and VoxSeT for the medium- and hard-difficulty 3D detection mAP but outperformed them for the easy level.
Concerning car BEV detection, the point–voxel fusion method exhibited an advantage over the point-based and voxel-based methods. Notably, the DVST secured second place in the BEV detection mAP for the hard difficulty among the voxel-based methods, surpassing the third-ranked Part-A2 model by 1.36%. Regarding the car category orientation estimation, our DVST enhanced the AOS by at least 0.45% for the moderate difficulty compared to the point-based methods and by at least 0.04% compared to the point–voxel fusion methods. Among the voxel-based methods, our DVST achieved the highest AOS for the hard difficulty level, surpassing the second-ranked VoxSeT model by 1.65%. Based on the detailed analysis, it is evident that the DVST demonstrated a commendable overall performance on the KITTI test set.
4.2.2. KITTI Validation Set
We evaluated the performance of the DVST on the KITTI validation set, as presented in Table 3. For the VoxSeT, we reproduced the results based on the reference [14] utilizing the OpenPCDet toolbox [46]. Our findings are as follows: (1) For 3D car detection, the proposed DVST demonstrated competitive performance, achieving an mAP of 85.05% at moderate difficulty. The mAP was 0.23% higher than the point-based detector DGT-Det3D and at least 1.06% higher than the point–voxel detector. (2) Among the voxel-based detectors, the DVST-TSD outperformed VoTr-TSD and VoxSeT in the 3D detection of cars at the moderate difficulty level, surpassing them by 1.01% and 0.47% in terms of the mAP, respectively, despite all of them utilizing transformer-based backbone networks. (3) It is noteworthy that the DVST achieved the highest mAP of 78.99% among the voxel-based methods for the car type at the hard difficulty level.

Table 3.
Evaluation of the KITTI validation set. The results are reported using the mAP with a 0.7 IoU threshold and 11 recall positions. The results of our DVST are highlighted in bold, and the top-three-ranked results are underlined.
The mAP of the DVST for 3D car detection at moderate difficulty was lower than that of CT3D. After analysis, one primary reason for this discrepancy was the difference in the voxel size settings. In CT3D, the voxel size was set as [0.05 m, 0.05 m, 0.1 m], whereas in the DVST, it was set to [0.32 m, 0.32 m, 4 m]. Although a more minor voxel size resulted in higher precision in CT3D, it also led to increased computational complexity. We conducted experiments with a batch size of two on four NVIDIA RTX 3080Ti GPUs. The average floating-point operation of CT3D was 200.11 G with an inference time of 118.03 ms, while with the DVST, the values were only 89.61 G and 79.34 ms. Another relevant factor is the difference in the IoU threshold settings, with CT3D using 0.81 and the DVST using 0.7. Consequently, the following conclusions can be drawn: the DVST effectively utilized both deformable and attention mechanisms to extract rich object features from large voxels, and the DVST achieved a good balance between accuracy and speed in 3D object detection.
4.2.3. Performance on Pedestrian and Cyclist Classes
To assess the performance of the multi-class object detection model, we conducted experiments on the KITTI validation set using the single-stage DVST model. The DVST-SSD uses the proposed DVST as the backbone and adopts the same anchor settings as SECOND. The results of these experiments are presented in Table 4. We also compared the DVST-SSD with several baseline models, such as SECOND, PointPillars, and VoxSeT. The results in Table 4 illustrate the varying degrees of improvement in the mAP for the car, pedestrian, and cyclist categories across nine different situations of three difficulty levels. The corresponding improvements are shown in the last row of the table.

Table 4.
Performance of DVST-SSD on the KITTI validation set. All results are reported in terms of mAP with 40 recall positions, using an IoU threshold of 0.7 for the car category and 0.5 for the pedestrian and cyclist categories. Results from DVST-SSD are shown in bold, and the best result in each column is underscored. The improvements are displayed in italics.
The improvements demonstrate that the DVST exhibited strong detection capabilities for the car category and performed well in detecting pedestrians and cyclists, whose spatial sizes are smaller. The DVST-SSD achieved significant improvements of 2.60% and 2.05% in the mAP for the pedestrian category at the moderate and hard difficulty levels, respectively. Moreover, a substantial 2.54% increase in the mAP was observed for the cyclist category under moderate difficulty. These noteworthy enhancements suggest that the deformable attention utilized in the DVST-SSD effectively learned the target features under occlusion and truncation conditions. The overall improvement in the model performance further confirms the effectiveness of the DVST.
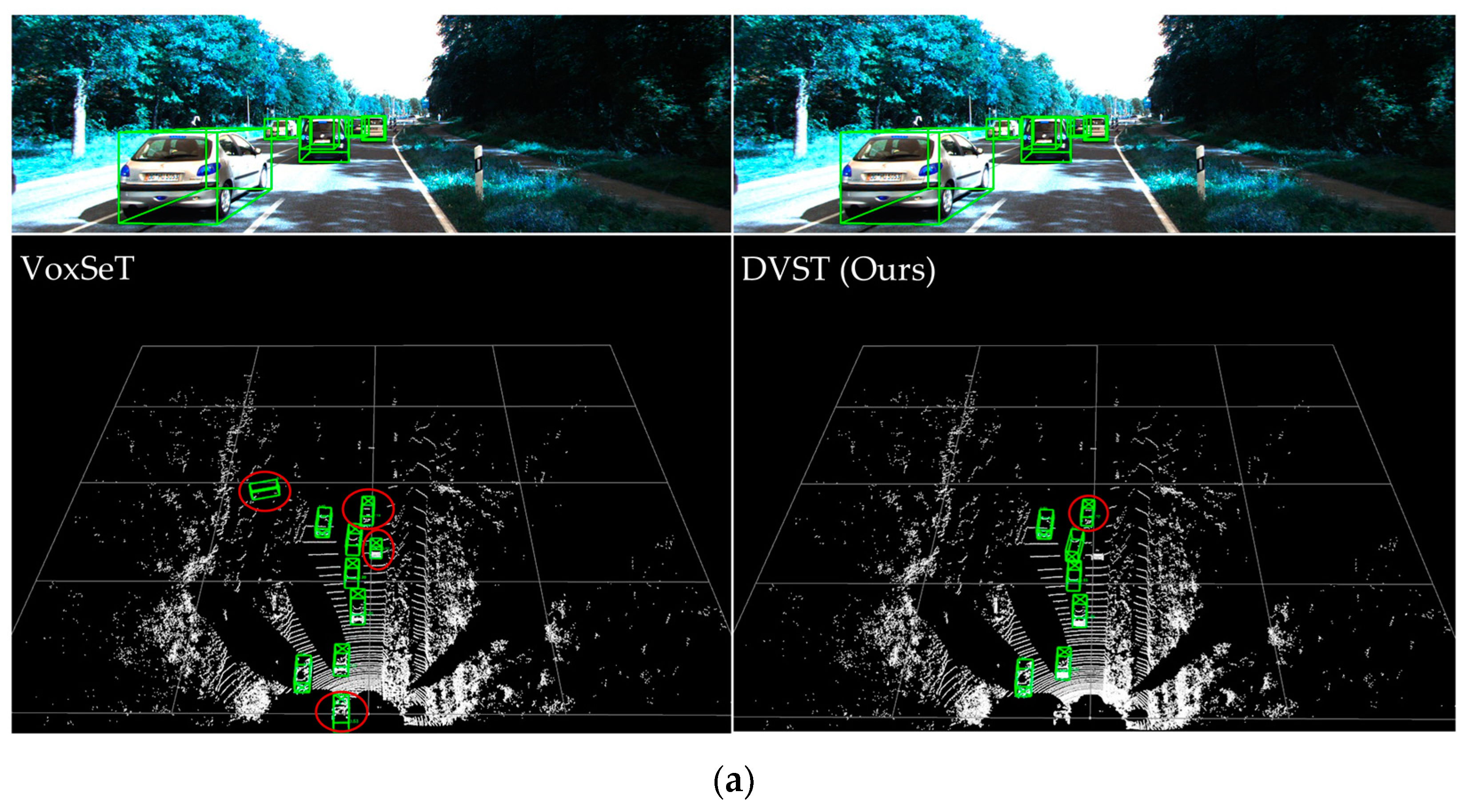
4.2.4. Qualitative Analysis
In this section, we present a comparison of the visualization results between VoxSeT and the DVST, as illustrated in Figure 4, where the circled parts are false-positive targets. Lidar-only detectors often suffer from a common failure mode: false-positive detections caused by more distant targets with similar shape characteristics. As shown in Figure 4a, VoxSeT and the DVST showed four and one false-positive detections, respectively. Figure 4b shows four false-positive detections for VoxSeT and two for the DVST. Figure 4c shows one false-positive detection for VoxSeT, while the DVST had none. From this comparison, we observed that the DVST used a deformable mechanism to transfer the candidate keys and values of the foreground query to essential areas to obtain more discriminative features, which can significantly reduce the number of false positives in the scene to be detected and improve the detection performance.
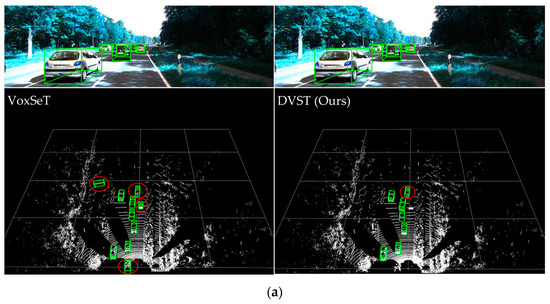

Figure 4.
Qualitative analysis results of 3D object detection on the KITTI dataset. Three scenes, denoted as (a–c), are showcased. Each scene includes the ground truth box. The detection results for each scene using VoxSeT and DVST models are depicted on the left and right sides, respectively. False detection targets are circled for clarity.
4.3. Three-Dimensional Detection Results on Waymo Open Dataset
We performed experiments on the large-scale Waymo open dataset to validate the effectiveness of the proposed DVST. The experimental results for the mAP and mAPH are presented in Table 5, encompassing the three categories of vehicles, pedestrians, and cyclists, evaluated at two difficulty levels: LEVEL_1 and LEVEL_2. We replaced the backbone networks of two 3D object detection models, PointPillars and VoxSeT, with the DVST to construct the DVST-SSD and DVST-TSD, respectively, for the experiments and comparisons.

Table 5.
Comparison of 3D detection results on 202 validation sequences from the Waymo open dataset. All models were trained using 20% of the training samples. ‘L1’ and ‘L2’ represent LEVEL_1 and LEVEL_2, respectively. The best results are underlined below. Results from DVST-SSD and DVST-TSD are shown in bold, and the improvements are displayed in italics.
From the results in Table 5, it can be observed that compared to PointPillars, the DVST-SSD achieved improvements in the mAP and mAPH across all twelve metrics for the vehicle, pedestrian, and cyclist classes at both the LEVEL_1 and LEVEL_2 difficulty levels. Mainly, the DVST-SSD showed significant improvements in the pedestrian and cyclist scores, increasing them by 5.44%, 11.44%, 5.37%, 10.42%, 6.52%, 7.85%, 6.28%, and 7.57% across the eight metrics. Similarly, the DVST-TSD exhibited improvements compared to VoxSeT, with increases of 1.20%, 1.20%, 1.16%, 1.16%, 1.39%, 1.48%, 1.55%, 1.59%, 1.93%, 1.92%, 1.85%, and 1.83% across the twelve metrics. These improvements across the metrics for the DVST-SSD and DVST-TSD provide strong evidence of the performance of the DVST in large-scale datasets. Compared to state-of-the-art models such as PV-RCNN, AFE-RCNN, IA-SSD, and AnchorPoint, although the DVST-TSD did not achieve the best performance in the vehicle class, it achieved the best accuracy in all eight metrics for the pedestrian and cyclist classes. The results were consistent with the results of the pedestrian and cyclist classes in the KITTI validation set, further validating the efficacy of the DVST for 3D object detection.
4.4. Ablation Studies
4.4.1. Effect of the DVST Components
We performed ablation experiments on the KITTI validation set to evaluate the various components of our method, and the results are presented in Table 6. As the DVST is built upon VoxSeT, we used VoxSeT as the baseline for comparison. The results in the first and second rows indicate that incorporating OGM improved the model’s mAP scores in the car category from 84.58% to 84.71%, which suggests that including the deformable mechanism enhances the model’s performance. Comparing the second and third rows, we observed a 0.09% increase in the moderate difficulty, demonstrating that our proposed GRCFFN can enrich global features in the hidden space. Furthermore, comparing the second and fourth rows reveals that adding residual connections played a critical role in boosting the model’s performance. Comparing the performance of the fourth and fifth rows indicates that GRCFFN outperformed the ConvFFN used in VoxSeT.

Table 6.
Ablation experiments on the KITTI validation set regarding the effects of the proposed OGM, GRCFFN, and residual connection (RC). The results are reported by the mAP with a 0.7 IoU threshold and 11 recall points. The best results are shown in bold.
4.4.2. Effect of the Number of Inducing Points
To analyze the impact of the number of inducing points used in the DVSA, we conducted experiments on the KITTI validation set using the DVST-SSD. As indicated in Table 7, we varied the number of inducing points between two, four, and eight, respectively, and evaluated the mAP across three difficulty levels within the car, pedestrian, and cyclist classes.

Table 7.
Ablation experiments on the KITTI validation set regarding the impact of the number of induction points. The results are reported with mAP at 0.7 IoU threshold and 11 recall positions. The best results for each column are shown in bold.
The results unveiled in the table show that an increase in the number of inducing points allowed for encoding more comprehensive contextual information, enhancing the DVST’s modeling capability and improving the detection. These findings are consistent with those observed in VoxSeT, which explored various latent codes. It is important to note that in the DVST-TSD, as indicated in the first and fifth rows of Table 6, the model achieved superior performance compared to VoxSeT when four inducing points were utilized, despite VoxSeT using eight inducing points. This phenomenon highlights that introducing deformable mechanisms strengthened the DVST’s ability to model context and global features, leading to more accurate detection outcomes using fewer inducing points.
4.5. Efficiency Analysis
Table 8 presents the mAP, the number of parameters, the number of floating-point operations (FLOPs), and the inference time of SECOND, PointPillars, VoxSeT, and the DVST-SSD on the KITTI validation set. All the models were executed using an NVIDIA 3080Ti GPU. Analyzing the results in Table 8 reveals that the DVST-SSD model outperformed the baseline models SECOND and PointPillars, exhibiting precision improvements of 0.33%, 4.36%, and 3.50% for cars, pedestrians, and cyclists under moderate difficulty, respectively, while having fewer parameters and FLOPs. Compared to VoxSeT, the DVST-SSD achieved a superior detection accuracy while only undergoing a slight increase in parameters, FLOPs, and inference time. This model offers a reliable solution for achieving a balance between efficiency and accuracy in 3D object detection tasks.

Table 8.
Performance comparison of DVST-SSD on the KITTI validation set. The best results in each column are shown in bold.
5. Discussion
In this paper, we used the proposed backbone network DVST to construct single-stage and two-stage models, respectively, conduct comprehensive experiments on the KITTI and Waymo datasets, and compare the proposed model with other methods on the corresponding benchmarks. In addition to the better results achieved by our approach, there are several points worthy of attention. As shown in Table 4 and Table 5, the improvements in the DVST were more prominent for the pedestrian and cyclist categories than for the vehicle categories. Combined with the overall performance of the DVST in the KITTI and Waymo datasets, we believe that there were two main reasons. One reason was that the proposed deformable voxel attention module could better learn the offsets of small-sized targets, thus significantly improving the detection accuracy of small-sized targets. For the larger vehicle categories, the original method achieved better detection results, so the DVST showed a relatively small improvement. Another reason was that the trained DVST could better adapt to the data distribution of the corresponding dataset than the other models. Another point worth noting is that the accuracy of the division of foreground and background points affected the performance of the DVST. The DVST uses a three-layer MLP and foreground threshold to divide foreground and background points. It is reasonable to suspect that DVST can achieve better results with the blessing of a deeper or more targeted network. Therefore, a more accurate division of foreground and background points is one of the focuses of our follow-up research. In addition, although the DVST provides a reliable solution to achieve a balance between efficiency and accuracy of 3D object detection from point clouds, in practical applications, higher accuracy and faster speed are still the goals we pursue.
6. Conclusions
In this work, we proposed a transformer-based method called the DVST for 3D object detection from point clouds. The DVST addresses the issue of excessive attention caused by the large receptive field of the transformer backbone network by employing deformable voxel set attention as its core. It also utilizes induced set attention to ensure computational efficiency. The DVST effectively learns target-related features and concentrates on significant foreground regions by selectively deforming only the foreground queries. The clever integration of a deformable mechanism, transformer, and induced set attention in the DVST strikes a favorable balance between average precision and computational efficiency. Moreover, as a voxel-based backbone network, the DVST can be applied to any voxel-based 3D detector. Extensive experiments on the KITTI and Waymo open datasets demonstrated that DVST performs similarly to state-of-the-art lidar-only detectors. However, to meet the higher accuracy and faster speed requirements of practical application scenarios, we will explore the integration of point cloud information with images and lightweight model optimization in future research.
Author Contributions
Conceptualization, Y.N., J.C. and C.B.; methodology, Y.N.; software, Y.N.; validation, Y.N.; formal analysis, Y.N. and J.C.; investigation, Y.N.; resources, J.C. and C.B.; data curation, Y.N.; writing—original draft preparation, Y.N.; writing—review and editing, Y.N., J.C. and C.B.; visualization, Y.N.; supervision, J.C. and Q.H.; project administration, Q.H.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets generated and analyzed during this study are available in the KITTI repository (https://www.cvlibs.net/datasets/kitti/eval_object.php?obj_benchmark=3d, accessed on 17 October 2023) and the Waymo open dataset (https://waymo.com/open/, accessed on 17 October 2023).
Acknowledgments
The authors thank Dexian Yin, Xue Huang, and Chang Zhou for their help in the paper and the anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, J.; Shi, S.; Wang, Z.; Li, H.; Qi, X. ST3D++: Denoised Self-Training for Unsupervised Domain Adaptation on 3D Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 6354–6371. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Chen, Q.; Fu, Z. LSNet: Learned Sampling Network for 3D Object Detection from Point Clouds. Remote Sens. 2022, 14, 1539. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 4 December 2017; pp. 5105–5114. [Google Scholar]
- Yang, Z.; Sun, Y.; Liu, S.; Jia, J. 3DSSD: Point-Based 3D Single Stage Object Detector. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11040–11048. [Google Scholar]
- Zhang, Y.; Hu, Q.; Xu, G.; Ma, Y.; Wan, J.; Guo, Y. Not All Points Are Equal: Learning Highly Efficient Point-Based Detectors for 3D LiDAR Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18931–18940. [Google Scholar]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. PointPillars: Fast Encoders for Object Detection from Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12689–12697. [Google Scholar]
- Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; Li, H. Voxel R-CNN: Towards High Performance Voxel-Based 3D Object Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; pp. 1201–1209. [Google Scholar]
- Wu, H.; Wen, C.; Li, W.; Li, X.; Yang, R.; Wang, C. Transformation-Equivariant 3D Object Detection for Autonomous Driving. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington DC, USA, 7–14 February 2023; pp. 2795–2802. [Google Scholar]
- Ren, S.; Pan, X.; Zhao, W.; Nie, B.; Han, B. Dynamic Graph Transformer for 3D Object Detection. Knowl.-Based Syst. 2023, 259, 110085. [Google Scholar] [CrossRef]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. PV-RCNN: Point-Voxel Feature Set Abstraction for 3D Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10529–10538. [Google Scholar]
- Yan, Y.; Mao, Y.; Li, B. SECOND: Sparsely Embedded Convolutional Detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Xue, Y.; Niu, M.; Bai, H.; Feng, J.; Liang, X.; Xu, H.; Xu, C. Voxel Transformer for 3D Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 3144–3153. [Google Scholar]
- He, C.; Li, R.; Li, S.; Zhang, L. Voxel Set Transformer: A Set-to-Set Approach to 3D Object Detection from Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8407–8417. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable DETR: Deformable Transformers for End-to-End Object Detection. In Proceedings of the International Conference on Learning Representations. arXiv 2020, arXiv:2010.04159. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Wang, W.; Dai, J.; Chen, Z.; Huang, Z.; Li, Z.; Zhu, X.; Hu, X.; Lu, T.; Lu, L.; Li, H.; et al. InternImage: Exploring Large-Scale Vision Foundation Models with Deformable Convolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 14408–14419. [Google Scholar]
- Xia, Z.; Pan, X.; Song, S.; Li, L.E.; Huang, G. Vision Transformer with Deformable Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4784–4793. [Google Scholar]
- Bhattacharyya, P.; Czarnecki, K. Deformable PV-RCNN: Improving 3D Object Detection with Learned Deformations. arXiv 2020, arXiv:2008.08766. [Google Scholar]
- Bhattacharyya, P.; Huang, C.; Czarnecki, K. SA-Det3D: Self-Attention Based Context-Aware 3D Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3022–3031. [Google Scholar]
- Chen, Z.; Li, Z.; Zhang, S.; Fang, L.; Jiang, Q.; Zhao, F. Deformable Feature Aggregation for Dynamic Multi-Modal 3D Object Detection. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 628–644. [Google Scholar]
- Lee, J.; Lee, Y.; Kim, J.; Kosiorek, A.R.; Choi, S.; Teh, Y.W. Set Transformer: A Framework for Attention-Based Permutation-Invariant Neural Networks. arXiv 2019, arXiv:1810.00825. [Google Scholar]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-Attention with Linear Complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Paigwar, A.; Erkent, O.; Wolf, C.; Laugier, C. Attentional PointNet for 3D-Object Detection in Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 1297–1306. [Google Scholar]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection from Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 770–779. [Google Scholar]
- Shi, W.; Rajkumar, R. Point-GNN: Graph Neural Network for 3D Object Detection in a Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1708–1716. [Google Scholar]
- Yin, T.; Zhou, X.; Krahenbuhl, P. Center-Based 3D Object Detection and Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11779–11788. [Google Scholar]
- Yang, S.; Lu, H.; Li, J. Multifeature Fusion-Based Object Detection for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1126–1133. [Google Scholar] [CrossRef]
- He, C.; Zeng, H.; Huang, J.; Hua, X.-S.; Zhang, L. Structure Aware Single-Stage 3D Object Detection from Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11870–11879. [Google Scholar]
- Noh, J.; Lee, S.; Ham, B. HVPR: Hybrid Voxel-Point Representation for Single-Stage 3D Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14600–14609. [Google Scholar]
- Shuang, F.; Huang, H.; Li, Y.; Qu, R.; Li, P. AFE-RCNN: Adaptive Feature Enhancement RCNN for 3D Object Detection. Remote Sens. 2022, 14, 1176. [Google Scholar] [CrossRef]
- Sheng, H.; Cai, S.; Liu, Y.; Deng, B.; Huang, J.; Hua, X.-S.; Zhao, M.-J. Improving 3D Object Detection with Channel-Wise Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 2723–2732. [Google Scholar]
- Guan, T.; Wang, J.; Lan, S.; Chandra, R.; Wu, Z.; Davis, L.; Manocha, D. M3DETR: Multi-Representation, Multi-Scale, Mutual-Relation 3D Object Detection with Transformers. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2293–2303. [Google Scholar]
- Sun, P.; Tan, M.; Wang, W.; Liu, C.; Xia, F.; Leng, Z.; Anguelov, D. SWFormer: Sparse Window Transformer for 3D Object Detection in Point Clouds. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 426–442. [Google Scholar]
- Tang, Z.; Sun, B.; Ma, T.; Li, D.; Xu, Z. Weakly Supervised Point Clouds Transformer for 3D Object Detection. In Proceedings of the IEEE 25th International Conference on Intelligent Transportation Systems, Macau, China, 8 October 2022; pp. 3948–3955. [Google Scholar]
- Zhou, Z.; Zhao, X.; Wang, Y.; Wang, P.; Foroosh, H. CenterFormer: Center-Based Transformer for 3D Object Detection. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 496–513. [Google Scholar]
- Liu, H.; Ma, Y.; Wang, H.; Zhang, C.; Guo, Y. AnchorPoint: Query Design for Transformer-Based 3D Object Detection and Tracking. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10988–11000. [Google Scholar] [CrossRef]
- Ning, K.; Liu, Y.; Su, Y.; Jiang, K. Point-Voxel and Bird-Eye-View Representation Aggregation Network for Single Stage 3D Object Detection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3223–3235. [Google Scholar] [CrossRef]
- Tang, Q.; Bai, X.; Guo, J.; Pan, B.; Jiang, W. DFAF3D: A Dual-Feature-Aware Anchor-Free Single-Stage 3D Detector for Point Clouds. Image Vis. Comput. 2023, 129, 104594. [Google Scholar] [CrossRef]
- Pan, X.; Xia, Z.; Song, S.; Li, L.E.; Huang, G. 3D Object Detection with Pointformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7459–7468. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Debnath, S.; Hu, R.; Chen, X.; Liu, Z.; Kweon, I.S.; Xie, S. ConvNeXt V2: Co-Designing and Scaling ConvNets with Masked Autoencoders. arXiv 2023, arXiv:2301.00808. [Google Scholar]
- Yang, Z.; Sun, Y.; Liu, S.; Shen, X.; Jia, J. STD: Sparse-to-Dense 3D Object Detector for Point Cloud. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019; pp. 1951–1960. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Sun, P.; Kretzschmar, H.; Dotiwalla, X.; Chouard, A.; Patnaik, V.; Tsui, P.; Guo, J.; Zhou, Y.; Chai, Y.; Caine, B.; et al. Scalability in Perception for Autonomous Driving: Waymo Open Dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2443–2451. [Google Scholar]
- OpenPCDet Development Team. OpenPCDet: An Open-Source Toolbox for 3D Object Detection from Point Clouds. 2020. Available online: https://github.com/open-mmlab/OpenPCDet (accessed on 17 October 2023).
- Huang, T.; Liu, Z.; Chen, X.; Bai, X. EPNet: Enhancing Point Features with Image Semantics for 3D Object Detection. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 35–52. [Google Scholar]
- He, Y.; Xia, G.; Luo, Y.; Su, L.; Zhang, Z.; Li, W.; Wang, P. DVFENet: Dual-Branch Voxel Feature Extraction Network for 3D Object Detection. Neurocomputing 2021, 459, 201–211. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, D.; Li, Y.; Zhao, L.; Su, R. FusionPillars: A 3D Object Detection Network with Cross-Fusion and Self-Fusion. Remote Sens. 2023, 15, 2692. [Google Scholar] [CrossRef]
- Shi, S.; Wang, Z.; Shi, J.; Wang, X.; Li, H. From Points to Parts: 3D Object Detection from Point Cloud with Part-Aware and Part-Aggregation Network. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 2647–2664. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhao, X.; Huang, T.; Hu, R.; Zhou, Y.; Bai, X. TANet: Robust 3D Object Detection from Point Clouds with Triple Attention. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 11677–11684. [Google Scholar]
- Zheng, W.; Tang, W.; Chen, S.; Jiang, L.; Fu, C.-W. CIA-SSD: Confident IoU-Aware Single-Stage Object Detector from Point Cloud. arXiv 2020, arXiv:2012.03015. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).